Abstract
Railway infrastructure faces significant operational threats due to ground deformation risks from natural and anthropogenic sources, posing serious challenges to safety and maintenance. Traditional monitoring methods often fail to capture the complex spatiotemporal patterns of railway deformation, leading to delayed responses and increased risks of infrastructure failure. To address these limitations, this study introduces InSAR-RiskLSTM, a novel framework that leverages the high-resolution and wide-coverage capabilities of Interferometric Synthetic Aperture Radar (InSAR) to enhance railway deformation risk prediction. The primary objective of this study is to develop an advanced predictive model that accurately captures both temporal dependencies and spatial susceptibilities in railway deformation processes. The proposed InSAR-RiskLSTM framework integrates Long Short-Term Memory (LSTM) networks with spatial attention mechanisms to dynamically prioritize high-risk regions and improve predictive accuracy. By combining image-based spatial attention for deformation hotspot identification with advanced temporal modeling, the approach ensures more reliable and proactive risk assessment. Extensive experiments on real-world railway datasets demonstrate that InSAR-RiskLSTM achieves superior predictive performance compared to baseline models, underscoring its robustness and practical applicability. The results highlight its potential to contribute to proactive railway maintenance and risk mitigation strategies by providing early warnings for infrastructure vulnerabilities. This work advances the integration of image-based methods within cyber–physical systems, offering practical tools for safeguarding critical railway networks.
1. Introduction
Railway infrastructure is vulnerable to deformation risks caused by both natural and anthropogenic factors, including soil displacement, hydrological changes, and seismic activity [1]. These deformations pose serious threats to railway safety and operational reliability, making timely risk assessment and predictive maintenance critical for mitigating potential failures [2]. Traditional railway monitoring techniques, such as ground-based sensors and manual inspections, often fail to capture the complex spatiotemporal dynamics of deformation processes due to their limited spatial coverage and temporal resolution [3]. As a result, these conventional approaches may lead to delayed responses and increased infrastructure vulnerability.
The initial efforts in addressing railway deformation risks relied heavily on symbolic AI and rule-based systems, which depended on domain expertise to define static thresholds and heuristic rules [4]. While these approaches offered structured interpretability, their limitations in generalizing across varied environments and adapting to time-varying conditions became evident [5]. The inability to process large-scale dynamic data further underscored the need for more adaptable frameworks [6]. The advent of data-driven models marked a significant evolution in this domain. Machine learning techniques such as decision trees, support vector machines, and random forests harnessed historical InSAR data to uncover the underlying deformation patterns [7,8]. However, these methods fell short in capturing temporal continuity and spatial correlations, revealing a gap that necessitated the development of advanced architectures [9].
Deep learning methodologies, particularly recurrent neural networks (RNNs), Long Short-Term Memory (LSTM) networks, and attention mechanisms, have emerged as powerful tools for addressing these limitations [10]. LSTM networks excel in modeling long-term temporal dependencies that are crucial for identifying deformation trends [11], while attention mechanisms enhance spatial prioritization by dynamically focusing on high-risk areas [12]. Despite their advantages, these deep learning models introduce challenges related to interpretability and computational efficiency, particularly when dealing with large-scale spatiotemporal datasets [13]. Effective solutions require the integration of spatial and temporal components within optimized frameworks to ensure both predictive accuracy and computational feasibility [14].
To address these challenges, remote sensing technologies, particularly Interferometric Synthetic Aperture Radar (InSAR), have emerged as powerful tools for large-scale deformation monitoring [15]. InSAR provides long-term high-resolution observations of ground displacement, enabling the detection of subtle deformations that may precede infrastructure failures. However, raw InSAR data alone do not directly translate into actionable risk assessments [16]. The complex spatial dependencies and temporal trends in railway deformation demand advanced analytical methods that can effectively integrate both dimensions. The primary objective of this study is to develop an effective predictive model that leverages both the spatial and temporal aspects of InSAR data to improve railway deformation risk assessment. To achieve this, we propose InSAR-RiskLSTM, a novel framework that integrates Long Short-Term Memory (LSTM) networks with spatial attention mechanisms. This approach enables the model to dynamically prioritize high-risk regions while capturing long-term temporal dependencies in deformation processes. By combining image-based spatial attention with sequential modeling, our method enhances predictive accuracy and robustness, facilitating proactive railway maintenance and risk mitigation. Extensive experiments conducted on real-world railway datasets demonstrate that InSAR-RiskLSTM significantly outperforms the baseline models in predictive performance, reinforcing its practical applicability for infrastructure monitoring.
The proposed method has several key advantages:
- The proposed model introduces a novel spatial attention mechanism that enhances the model’s focus on critical deformation areas, improving risk detection sensitivity.
- It demonstrates a robust and adaptable framework that is suitable for various railway conditions and spatial environments, providing high efficiency across multiple scenarios.
- The experimental results show that InSAR-RiskLSTM significantly outperforms the baseline models in accuracy and response time, underscoring its effectiveness for real-time risk prediction.
The remainder of this paper is organized as follows. Section 2 presents the methodological framework, including the problem formulation and detailed description of the InSAR-RiskLSTM model. Section 3 outlines the experimental setup, including datasets, evaluation metrics, and comparative analyses. Section 4 discusses the results, highlighting the key findings and implications for railway maintenance. Finally, Section 5 concludes the paper with a summary of its contributions and potential directions for future research.
2. Related Work
2.1. InSAR for Infrastructure Deformation Monitoring
Interferometric Synthetic Aperture Radar (InSAR) has become a widely utilized remote sensing technology in monitoring infrastructure deformation, including railways, bridges, and buildings . InSAR techniques leverage phase differences between radar images acquired at different times to measure ground and infrastructure movement with millimeter-level accuracy [17]. This capability is particularly valuable for continuous monitoring and early detection of potential deformations in critical infrastructure, aiding in the mitigation of safety risks associated with ground subsidence, landslides, and structural strain [18]. The traditional InSAR methods include Persistent Scatterer Interferometry (PSI) and Small Baseline Subset (SBAS), both of which have been extensively validated for identifying gradual and abrupt deformations across diverse environments. The use of InSAR in railway deformation monitoring has garnered significant attention due to its non-invasive nature and ability to cover extensive geographic areas [19]. Railway infrastructures are often subject to continuous strain from natural and anthropogenic factors, including seasonal ground movement, underground mining, and construction activities. InSAR data, when applied to railways, can facilitate the monitoring of long-term deformation patterns, enabling the proactive maintenance of rail networks. Recent advancements in InSAR data processing have enabled the extraction of more precise deformation signals, further enhancing the accuracy of deformation risk assessment. The challenges in using InSAR for railway deformation risk prediction include the complex interaction of various deformation sources and the need to integrate InSAR data with other contextual information to improve predictive accuracy [20]. Research is increasingly focusing on multi-source data fusion, combining InSAR data with other geospatial and sensor data to provide a more comprehensive understanding of deformation phenomena. Integration with machine learning models, particularly deep learning architectures, has shown promise in capturing complex spatiotemporal dependencies, enabling more accurate and reliable predictions for infrastructure at risk of deformation [21].
Interferometric Synthetic Aperture Radar (InSAR) is a remote sensing technique that measures ground deformation with high precision by analyzing the phase differences between radar images captured at different times [22]. The phase of a radar signal carries information about the distance between the radar sensor and the ground surface. By comparing the phase of two or more radar images, InSAR can detect minute changes in surface elevation, often with sub-millimeter accuracy. This capability makes it an essential tool for monitoring ground movements over large areas, even in regions that are difficult to access. InSAR techniques rely on the generation of interferograms, which are created by calculating the phase differences between corresponding pixels in two radar images [23]. To derive accurate deformation measurements, several processing steps are required, including phase unwrapping, which resolves ambiguities in phase values, and geocoding, which converts radar coordinates into geographic coordinates [24]. Advanced methods such as Persistent Scatterer Interferometry (PSI) and Small Baseline Subset (SBAS) further enhance InSAR’s capability by focusing on stable radar reflectors or minimizing the impact of temporal and geometric decorrelation. These methods enable the detection of both gradual and abrupt deformations across a variety of terrains and infrastructures [25]. Despite its advantages, InSAR faces challenges such as noise introduced by atmospheric effects and limitations in data availability for certain regions [26]. However, its non-invasive nature and ability to provide continuous spatial coverage have made it an indispensable tool for infrastructure monitoring, including railway deformation analysis. By leveraging these principles, InSAR offers a robust foundation for predictive modeling in geotechnical and structural health applications.
2.2. LSTM and Temporal Models in Risk Prediction
Long Short-Term Memory (LSTM) networks have emerged as one of the most effective architectures for modeling temporal dependencies in sequential data [27]. In the context of risk prediction, LSTM networks are frequently applied to forecast time series data, detect patterns, and predict future states based on historical information. LSTM’s ability to manage long-term dependencies without the vanishing gradient problem has made it particularly suitable for applications requiring the processing of extended temporal sequences, such as deformation prediction over time. In risk prediction for infrastructure deformation, LSTM models have demonstrated utility by leveraging historical deformation data to forecast potential future risks [28]. These models have been employed to predict gradual deformations caused by underlying geological shifts, climate influences, and structural stress accumulation [29]. By learning from sequences of past observations, LSTMs can detect early signs of impending risks, offering a proactive approach to infrastructure maintenance and risk mitigation. In recent studies, LSTM models have frequently been coupled with other neural network layers or techniques to enhance predictive performance [30]. For instance, bidirectional LSTMs and stacked LSTM layers are used to capture both past and future context, improving the model’s understanding of temporal dependencies [31]. Additionally, hybrid architectures that combine LSTM models with other deep learning components, such as convolutional layers or attention mechanisms, have proven to be effective in extracting both temporal and spatial features, making them highly applicable to spatiotemporal prediction tasks like railway deformation risk forecasting.
2.3. Spatial Attention Mechanisms in Geospatial Applications
Spatial attention mechanisms have increasingly been integrated into deep learning models to improve their capacity to focus on important spatial regions within input data [32]. Attention mechanisms are inspired by the human visual system, which selectively focuses on the salient parts of a scene. In geospatial applications, spatial attention enables models to assign varying importance to different locations, enhancing their capability to analyze complex spatial patterns in data that contain both local and global dependencies [33]. In the context of railway deformation risk prediction, spatial attention mechanisms can be applied to identify critical areas within a railway network that exhibit significant deformation signals [34]. This targeted focus enables the model to prioritize high-risk regions, enhancing the interpretability and efficiency of deformation predictions. By embedding spatial attention in a deep learning framework, models can better capture localized deformation behaviors and variations in terrain, soil type, or infrastructural elements that contribute to differential deformation risks. Research in spatial attention for geospatial applications often involves the integration of convolutional neural networks (CNNs) with attention layers to process spatial information effectively [18]. These models leverage spatial dependencies and contextual information, which are crucial in complex geospatial phenomena. For railway deformation monitoring, spatial attention helps to refine the predictive accuracy of models by focusing computational resources on high-impact areas, potentially identifying early signs of deformation that might otherwise be overlooked in traditional analysis [35]. Combined with temporal models like LSTM, spatial attention enhances the overall performance of predictive systems, offering a robust solution for continuous monitoring and risk management in large-scale railway infrastructures [36].
3. Methodology
3.1. Overview
Our proposed framework, named InSAR-RiskLSTM, integrates spatial and temporal modeling techniques to predict railway deformation risks with high precision. The model is designed to leverage advanced image-based spatial attention and temporal sequential learning to address the complexities of railway deformation prediction. At a high level, the framework consists of three core modules: a Spatial Attention Encoder, a Temporal Risk Predictor, and a Feature Fusion Mechanism. The Spatial Attention Encoder processes InSAR images and generates attention maps to highlight risk-prone regions. The Temporal Risk Predictor utilizes a specialized LSTM structure to model sequential dependencies in the deformation time series. Finally, the Feature Fusion Mechanism combines spatial and temporal features, aligning them into a unified representation that enhances predictive accuracy.
As shown in Figure 1, the workflow begins with preprocessing InSAR imagery data to extract deformation patterns, which serve as input for the Spatial Attention Encoder. The encoder outputs spatial attention vectors that are subsequently fed into the LSTM-based temporal predictor. The predictor models temporal dependencies across sequential risk factors, including historical deformation trends and environmental conditions. These features are then fused using the feature fusion module to generate comprehensive risk scores. The outputs are used for predictive tasks, such as assessing deformation magnitudes and identifying high-risk railway segments. The Spatial Attention Encoder extracts spatial features from InSAR imagery, emphasizing regions that are prone to deformation risks. The Temporal Risk Predictor models sequential dependencies within deformation trends, leveraging LSTM-based structures for capturing long-term temporal patterns. The Feature Fusion Mechanism integrates the spatial and temporal features, aligning them into a cohesive representation to enhance predictive accuracy. This structure ensures that the approach effectively captures the spatial and temporal complexities inherent in deformation risk prediction.
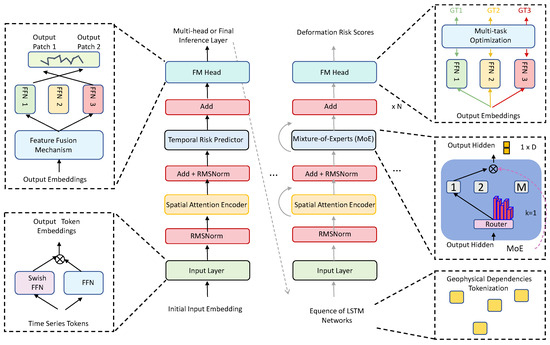
Figure 1.
Framework of the InSAR-RiskLSTM model. The framework consists of three primary components: the Spatial Attention Encoder, the Temporal Risk Predictor, and the Feature Fusion Mechanism. It incorporates spatiotemporal priors, geophysical dependency tokenization, and Multi-Task Optimization to enhance predictive accuracy and interpretability.
To provide a structured representation of the proposed methodology, the workflow of InSAR-RiskLSTM is formulated as Algorithm 1. The framework consists of six key steps, ensuring an effective integration of spatial and temporal modeling for railway deformation risk prediction. The process begins with data preprocessing, where deformation patterns are extracted from InSAR imagery, temporal features are normalized, and external environmental conditions are incorporated. Following this, the Spatial Attention Encoder processes the input InSAR imagery, generating attention maps to highlight high-risk regions and extracting spatial feature representations. Next, the Temporal Risk Predictor models sequential dependencies in deformation time series using an LSTM-based structure, capturing long-term trends and extracting temporal feature representations. These spatial and temporal features, along with external environmental factors, are then combined in the Feature Fusion Mechanism, aligning multi-source information into a unified representation that enhances predictive accuracy. The fused features are subsequently used to generate risk scores, assessing deformation magnitudes and identifying high-risk railway segments. Finally, the model outputs comprehensive risk assessments, providing decision support for railway maintenance and risk mitigation. This structured workflow ensures that InSAR-RiskLSTM effectively captures both spatial and temporal complexities, leading to improved predictive performance in railway deformation monitoring.
| Algorithm 1: InSAR-RiskLSTM: Railway Deformation Risk Prediction |
Input: InSAR imagery data , temporal features , and external factors E. Output: Predicted deformation risk scores . Step 1: Data Preprocessing Extract deformation patterns from InSAR imagery; Normalize and align temporal features ; Integrate external environmental conditions E. Step 2: Spatial Attention Encoding Feed into the Spatial Attention Encoder; Generate attention maps to highlight high-risk regions; Extract spatial feature representations . Step 3: Temporal Risk Prediction Feed into the LSTM-based Temporal Risk Predictor; Model sequential dependencies in deformation time series; Extract temporal feature representations . Step 4: Feature Fusion Combine spatial and temporal features: ; Align multi-source information into a unified representation. Step 5: Risk Score Prediction Generate comprehensive risk scores for railway segments; Assess deformation magnitudes and identify high-risk areas. Step 6: Output and Decision Support Provide risk assessment insights for railway maintenance and mitigation; return Predicted risk scores . |
3.2. Preliminaries
The task of railway deformation risk prediction is formulated as a spatiotemporal learning problem that leverages both spatial and temporal data to forecast risk scores for railway deformation. Let represent the set of railway segments under consideration, where N is the total number of segments. Each segment is associated with spatial attributes and temporal observations. These attributes are influenced by complex interactions, including deformation patterns, external environmental factors, and the underlying physical structure of the railway.
For spatial features, we define a spatial feature matrix , where is the number of spatial features derived from InSAR images, such as mean deformation velocity, coherence, terrain slope, and curvature. These spatial features reflect the local and regional conditions that contribute to deformation risks. The spatial relationships between railway segments are encoded using an adjacency matrix . The entry quantifies the similarity or connection strength between segments and , computed using spatial proximity or geophysical properties. For simplicity, can be normalized as
where is the degree matrix with . This normalized adjacency matrix ensures that the spatial dependencies are scaled consistently.
For temporal features, we represent sequential observations as a temporal feature matrix , where T denotes the length of the time series and represents the number of temporal attributes, such as historical deformation values, precipitation, temperature, and maintenance activities. Each row in represents the feature vector at time step j. These temporal features exhibit nonlinear dynamics and dependencies that require advanced models, such as recurrent neural networks or attention mechanisms, for effective analysis.
The objective is to predict the deformation risk for all segments over a given time horizon. Let represent the predicted risk matrix, where is the forecast horizon. The task is formally expressed as
where is the predictive model parameterized by . The function must integrate both spatial and temporal features while accounting for their interdependencies.
To enhance predictive accuracy, we introduce external factors , where is the number of external features, such as meteorological data and traffic load. These factors are incorporated into the temporal modeling to capture their influence on deformation dynamics. The complete input representation is then defined as
where denotes the concatenation operation along the feature dimension. Finally, the loss function used to train the predictive model is defined as the mean squared error (MSE) between the predicted and true deformation risks:
where and are the predicted and ground truth risk scores for segment i at time t, respectively. This formulation ensures a comprehensive spatiotemporal approach for railway deformation risk prediction.
However, in real-world railway deformation scenarios, systematic trends may exist due to geophysical factors, long-term degradation patterns, or environmental influences. To address this, we introduce additional parameters into the predictive model in Equation (3) to capture and correct for these systematic deviations. One way to enhance the model is by incorporating a trend-corrected residual component into the loss function. Instead of minimizing only the MSE, we introduce a regularized residual correction term that accounts for systematic biases. This modification ensures that persistent trends in prediction errors, such as seasonal variations in deformation or external stress accumulation, are explicitly modeled. Mathematically, we redefine the predictive function as
where represents a learnable residual correction term that captures systematic deviations using external covariates E (e.g., seasonal effects, geological conditions, and maintenance history). The revised loss function then becomes
where is an additional regularization term to prevent overfitting. This correction improves long-term predictive accuracy by adapting to structured biases that may otherwise remain unaccounted for in a purely MSE-based approach.
3.3. InSAR-RiskLSTM Framework
In this section, we present the InSAR-RiskLSTM framework Mixture of Experts, designed to integrate advanced spatial and temporal modeling techniques for precise railway deformation risk prediction. This framework comprises three core components: the Spatial Attention Encoder, the Temporal Risk Predictor based on LSTM, and the Feature Fusion Mechanism. These components work synergistically to extract meaningful spatiotemporal features, model sequential dependencies, and synthesize information for accurate risk assessment.
- Spatial Attention Encoder
As shown in Figure 2, the Spatial Attention Encoder is designed to process multi-scale InSAR imagery data, extract spatial patterns, and encode relationships between railway segments through a combination of cross-attention mechanisms. The encoder is composed of three primary stages: multi-scale patch embedding, channel cross-attention, and spatial cross-attention.
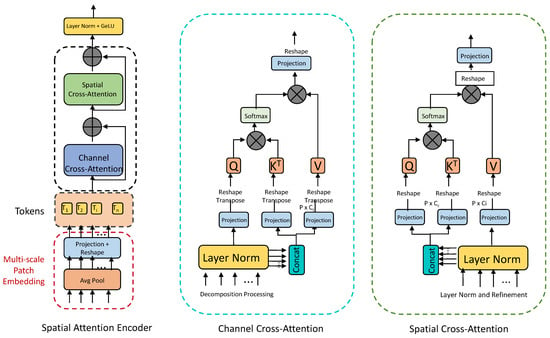
Figure 2.
Detailed structure of the Spatial Attention Encoder. The module processes multi-scale patch embeddings, utilizing channel cross-attention and spatial cross-attention mechanisms to extract meaningful spatial features and encode relationships between tokens. These operations refine spatial dependencies, enhancing downstream deformation risk prediction tasks.
In the first stage, multi-scale patch embeddings are generated from raw InSAR data using average pooling layers followed by projection and reshaping operations. This ensures that spatial information at multiple resolutions is captured effectively. Each token represents a specific patch of the image and serves as the input to the subsequent attention mechanisms. In the second stage, channel cross-attention is applied to enhance feature interactions across different channels. Given input tokens , the attention mechanism computes the relevance between tokens using queries (Q), keys (K), and values (V):
where , , and are linear projections of the input features X, and is the dimensionality of the key vectors. The output from this stage undergoes layer normalization and concatenation to prepare for spatial cross-attention.
In the third stage, spatial cross-attention is employed to model spatial relationships between patches. This mechanism captures dependencies between neighboring segments, enabling the encoder to focus on high-risk areas dynamically. For a given token , the importance of a neighboring token is calculated as
where and are learnable transformations. The enriched spatial representation is then computed by aggregating context information:
Finally, the combined output of the channel and spatial cross-attention modules is passed through a layer normalization and activation function (GeLU), producing the refined spatial features. These features are critical for highlighting deformation risks and downstream prediction tasks. This encoder enables the framework to efficiently process spatial dependencies, refine features, and adaptively focus on relevant high-risk regions.
- Temporal Risk Predictor
As shown in Figure 3, the Temporal Risk Predictor is designed to capture sequential dependencies in deformation time series by combining convolutional layers, fully connected (FC) layers, and LSTM mechanisms. The architecture refines temporal features through a series of operations, leveraging local feature extraction and global sequence modeling.
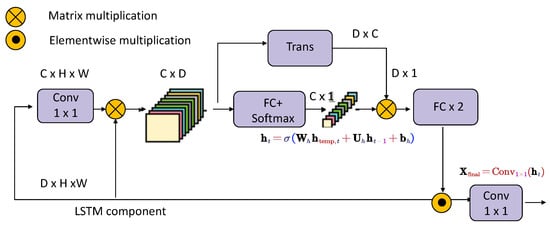
Figure 3.
Structure of the Temporal Risk Predictor. The component processes sequential inputs through a combination of convolutional layers, fully connected layers, and LSTM mechanisms, capturing both local and global temporal dependencies for deformation risk prediction.
The module starts by applying a convolutional layer to the input tensor , where C, H, and W denote the number of channels, height, and width, respectively. The convolutional output is then elementwise multiplied with the original input tensor to emphasize meaningful temporal patterns:
Next, the weighted tensor is reshaped into a matrix , where . This reshaped representation is passed through a fully connected layer followed by a softmax activation to compute temporal attention weights:
These weights are used to aggregate temporal features:
The aggregated features are then transformed via another fully connected layer to produce the intermediate representation . This representation is processed further using an LSTM component, capturing sequential dependencies:
where represents the LSTM hidden state at time t, and , , and are learnable parameters. The LSTM outputs are passed through a final convolutional layer to generate the refined temporal features for downstream tasks:
This multi-step process enables the Temporal Risk Predictor to extract both localized and global temporal dependencies, making it well suited for deformation risk prediction tasks. By combining convolutional and sequential learning mechanisms, the predictor achieves robust feature representation for complex temporal patterns.
- Feature Fusion Mechanism
As shown in Figure 4, the Feature Fusion Mechanism integrates spatial and temporal features to produce a unified representation that captures both low-scale and high-resolution information. The module consists of four primary stages: backbone network feature extraction, attention-based feature fusion, down-sampling layers, and final convolutional transformations. Spatial features are extracted from input imagery through a backbone network, which includes multiple convolutional and down-sampling layers. Low-scale spatial features are interpolated and passed through additional double convolution layers to align their resolutions with backbone features.
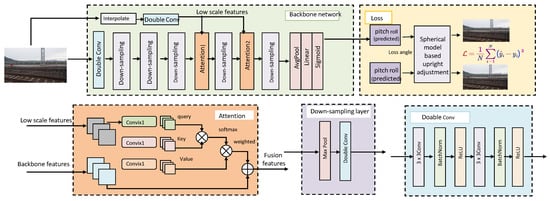
Figure 4.
Structure of the Feature Fusion Mechanism. This module integrates low-scale spatial features and high-resolution temporal features using attention-based fusion, down-sampling layers, and convolutional operations to produce a unified feature representation for accurate deformation risk prediction.
The low-scale spatial features and backbone features are fused using an attention mechanism. Queries (Q), keys (K), and values (V) are computed as
where represents low-scale features and denotes high-resolution backbone features. The attention weights are computed as
and the fused features are obtained as
The fused features are processed through a down-sampling layer that includes max pooling and double convolution operations to reduce spatial dimensions while preserving critical information:
followed by
The refined features are passed through a series of convolutional layers with batch normalization and ReLU activation to generate the unified representation . The fused feature representation is then used to predict the final risk score for segment :
where and b are trainable parameters, and ensures normalization.
The model is trained to minimize the mean squared error (MSE) loss between predicted and ground truth risk scores:
where N is the number of samples and is the ground truth score. This objective ensures precise and reliable risk predictions.
3.4. Spatiotemporal Prior Integration
The effectiveness of the InSAR-RiskLSTM framework is enhanced by incorporating spatiotemporal priors to align predictions with real-world deformation dynamics. Geophysical dependencies such as terrain slope, soil composition, and geological structures are encoded into a refined adjacency matrix to capture spatial relationships and structural similarities. Temporal priors modeled through mechanisms such as the Temporal Risk Predictor account for continuous trends and external environmental factors. In addition, the hybrid expert module dynamically selects specialized sub-models to handle heterogeneous data patterns, ensuring adaptive specialization and efficient resource utilization. Together, these priors enhance the model’s robustness, interpretability, and predictive accuracy for railway deformation risk assessment.
- Geophysical Dependencies
Railway deformation risks are profoundly affected by geophysical factors, such as terrain slope, soil composition, and underlying geological formations. These factors play a critical role in determining the stability and risk levels of railway segments. To effectively model these dependencies, the adjacency matrix , which represents the connectivity between railway segments, is refined by incorporating geophysical similarity and structural connectivity. This refinement enhances the model’s ability to capture domain-specific relationships.
The geophysical similarity between two segments and is quantified through a similarity matrix . This matrix encodes both spatial proximity and geological similarity using the following formulation:
where and denote the geographical coordinates of segments and , and is a scaling parameter that controls the sensitivity of the similarity to spatial distance. The term is a binary indicator reflecting whether the two segments share common geological attributes, such as soil type or rock formations. This formulation ensures that segments that are both geographically close and geologically similar have stronger connections.
To incorporate this geophysical information, the refined adjacency matrix is computed as a weighted combination of the original adjacency matrix and the geophysical similarity matrix :
where is a hyperparameter that balances the contributions of geophysical similarity and the original structural connectivity. A higher value of places greater emphasis on geophysical factors, while a lower value prioritizes the inherent structural relationships represented by .
This refined adjacency matrix enables the model to integrate geophysical priors seamlessly into the spatial attention mechanisms, ensuring that railway deformation risks are evaluated in a manner that respects both spatial and geological contexts. For example, segments with similar terrain slopes or soil compositions are more likely to share deformation characteristics, and the refined adjacency matrix captures these subtle relationships effectively. By embedding these domain-specific insights into the model, the framework gains enhanced predictive accuracy and interpretability, making it more robust in identifying high-risk segments influenced by geophysical conditions.
- Multi-Task Optimization
The Multi-Task Optimization module is designed to enhance the model’s ability to handle multiple objectives simultaneously, ensuring that the framework effectively addresses diverse risk prediction tasks. In this framework, GT1, GT2, and GT3 represent three specific tasks: deformation risk prediction (GT1), environmental impact assessment (GT2), and temporal trend analysis (GT3). These tasks are tightly connected to the overall goal of identifying and mitigating railway deformation risks by incorporating both spatial and temporal factors.
In this module, a shared representation is first generated by upstream components, such as the Spatial Attention Encoder and Temporal Risk Predictor. This representation captures common features across all tasks and serves as input to task-specific fully connected layers. Each task is assigned a dedicated feedforward network (FFN), which transforms the shared representation into task-specific predictions. For task m, the predicted output is denoted as , corresponding to its ground truth .
The optimization process for each task is driven by a task-specific loss function. For task m, the loss is computed as
where N is the number of samples, is the predicted value for sample i, and is the corresponding ground truth. To balance the contributions of different tasks, a weighted sum of these individual losses is used to define the overall multi-task loss:
where is a weight that adjusts the importance of task m during optimization. These weights can be predefined based on domain knowledge or learned dynamically during training to improve overall model performance.
The shared representation enables the model to learn common features across tasks, improving efficiency and enabling robust knowledge transfer. At the same time, the task-specific FFNs ensure that each task receives specialized attention to its unique requirements. For instance, deformation risk prediction focuses on capturing local variations in spatial features, while environmental impact assessment integrates external factors like weather conditions. Temporal trend analysis, on the other hand, emphasizes the sequential relationships within historical data, providing insights into long-term deformation patterns. By aligning predictions across these tasks, the Multi-Task Optimization module ensures that the model comprehensively addresses the complexities of railway deformation risk assessment. This approach enhances the adaptability and robustness of the framework, making it well suited for scenarios with heterogeneous and multi-faceted objectives.
- Mixture of Experts (MoE) for Adaptive Specialization
To enhance the model’s ability to dynamically focus on specialized tasks, a Mixture of Experts (MoE) module is integrated into the framework. This module allocates computational resources adaptively by selecting the most relevant sub-models, or experts, for each input based on its characteristics. The MoE structure includes a router network that determines the activation of experts and combines their outputs to generate refined feature representations.
The MoE module contains M experts , where each expert is trained to specialize in different aspects of deformation risk prediction. For example, one expert may focus on temporal dependencies, another on spatial correlations, and a third on environmental factors. The router computes a gating weight for each expert based on the input feature vector :
where and are the learnable weights and bias for expert in the router. These gating weights determine the contribution of each expert to the final output.
The output of the MoE module is computed as a weighted sum of the experts’ outputs:
where is the output of expert for the input . Each expert is implemented as a feedforward neural network with independent parameters, enabling specialization on different subsets of the input features.
To ensure efficient utilization of experts, a sparsity-promoting regularization term is added to the loss function. This term minimizes the entropy of the gating weights:
By encouraging sparse activation, the model avoids over-reliance on a single expert and effectively utilizes multiple experts.
The final training objective combines the Multi-Task Optimization loss and the sparsity regularization:
where controls the weight of the regularization term. The MoE module, as shown in the figure, includes a router network that selects experts dynamically based on the input characteristics. This selection process ensures that the model adapts to diverse tasks, such as deformation prediction, environmental impact assessment, and temporal trend analysis. By dynamically selecting relevant experts, the MoE module provides the following advantages: it enhances specialization by enabling certain experts to focus on specific data patterns, improves efficiency by activating only a subset of experts for each input, and increases robustness through diversity among the experts. This adaptive mechanism aligns with the overarching goal of accurately assessing railway deformation risks under varied conditions.
4. Experimental Setup
4.1. Dataset
The Hephaestus dataset [37] is a comprehensive resource designed for the study of synthetic aperture radar (SAR) imaging. It encompasses a diverse collection of SAR imagery that includes complex environments, urban structures, and various natural terrains, providing ample data for training and validating deep learning models in SAR-based object detection and scene classification. The dataset emphasizes real-world variability and simulates challenging environmental conditions to enhance the robustness of SAR processing algorithms in practical applications. Additionally, Hephaestus includes annotated labels that facilitate the development of models focusing on distinguishing minute features in cluttered scenes, making it highly valuable for SAR-related research. The xView3-SAR dataset [38] is aimed at advancing maritime domain awareness through SAR imaging. It comprises numerous high-resolution images captured over diverse maritime environments, including open seas and coastal regions. The dataset includes detailed annotations of maritime vessels, enabling researchers to develop and test object detection models tailored to SAR data. xView3-SAR serves as a robust benchmark for SAR-based maritime monitoring applications, addressing both detection and classification of vessels under various atmospheric and sea conditions. Its high spatial resolution supports the extraction of fine-grained features necessary for accurate and reliable performance in SAR-based maritime surveillance. The ASF SAR dataset [39] is a versatile SAR dataset provided by the Alaska Satellite Facility, focusing on a wide range of geographical terrains. This dataset features images captured by various SAR sensors, enabling multi-sensor analysis and the assessment of model generalization across different SAR systems. ASF SAR dataset includes annotations for land cover classification, which support the development of deep learning models aimed at environmental monitoring and terrain analysis. Its diverse content spanning natural landscapes, forested areas, and urban settings makes it suitable for robust SAR model training across various real-world scenarios, thus contributing significantly to environmental research and monitoring. The SAR patch dataset [40] offers a collection of small high-resolution SAR image patches focusing on specific regions of interest. Designed for tasks like feature extraction and patch-based classification, it provides targeted data that enable models to learn distinct features of objects within SAR imagery. Each patch includes detailed annotations, enabling precise object recognition and classification in complex SAR scenes. The SAR patch dataset is particularly valuable for applications in fine-grained object recognition within SAR imagery, serving as a critical dataset for the development of algorithms that require localized focus in large SAR data environments.
Data preprocessing was conducted to standardize input data and enhance model performance. Normalization was applied to ensure consistency across datasets by aligning the mean and standard deviation of each dataset with those of the respective SAR sensors. The normalized data are calculated as
where X represents the raw input data, is the mean, and is the standard deviation. Augmentation techniques, including random rotations, flips, and Gaussian noise injection, were used to simulate real-world conditions and improve the model’s robustness to noise and variations. For datasets like SAR patches, high-resolution patches were extracted by segmenting large images into smaller fixed-size regions, often with overlapping areas to preserve spatial continuity. Scaling and resizing operations ensured that all input data met the dimensional requirements of the model architectures, particularly for Transformer-based designs. These preprocessing steps provided high-quality input data, essential for achieving reliable and robust model performance.
The selection of risk parameters is a critical aspect of the proposed InSAR-RiskLSTM framework as these parameters directly influence the model’s ability to predict railway deformation risks. The primary risk parameters were derived from InSAR data and include deformation velocity, terrain slope, coherence, and curvature. These features were chosen due to their strong correlation with ground deformation events and their ability to highlight risk-prone areas. For instance, deformation velocity provides a quantitative measure of ground movement, while terrain slope and curvature capture the topographic features that may exacerbate deformation risks. Coherence measures the consistency of radar signal reflections, offering insights into the stability of ground conditions. The training data used in this study comprise diverse datasets, including urban, coastal, and natural terrains, each presenting unique deformation patterns. These datasets were preprocessed to ensure consistency and quality. Preprocessing steps included normalization to standardize data distributions across different sensors, augmentation techniques such as rotations and noise injection to simulate real-world variations, and patch extraction for high-resolution datasets. These steps ensured the data were both representative and robust, supporting effective model training and evaluation.
4.2. Experimental Details
The experiments were conducted in a high-performance computing environment utilizing NVIDIA A100 GPUs (Santa Clara, CA, USA), providing efficient parallel processing capabilities for deep learning on large-scale datasets. The implementation leveraged the PyTorch (23.11) framework to optimize GPU acceleration and streamline model training. Key hyperparameters included a batch size of 64, which balanced memory usage with computational efficiency, and an initial learning rate of 0.001, decayed by a factor of 0.1 every 10 epochs. The Stochastic Gradient Descent (SGD) optimizer, configured with a momentum of 0.9, was employed to improve convergence and mitigate oscillations. Data preprocessing involved image normalization to match the mean and standard deviation of the SAR imaging sensors, coupled with data augmentation techniques to enhance model generalization. Augmentations such as random rotations, horizontal and vertical flips, and Gaussian noise injection were applied to simulate various real-world conditions encountered in SAR imagery. This preprocessing pipeline was designed to bolster the models’ robustness against environmental variability and typical imaging artifacts. Training and validation datasets were split in an 80–20% ratio, with cross-validation implemented to evaluate model stability across different data subsets. Each model underwent training for a maximum of 50 epochs, with early stopping applied after 5 epochs of non-improvement to prevent overfitting. ResNet-50 and Vision Transformers (ViTs) were utilized as baseline architectures due to their strengths in capturing local and global features within SAR data. Model performance was assessed using mean Average Precision (mAP) for object detection tasks and accuracy for classification tasks. Additional metrics, including precision and recall, were calculated to provide a comprehensive evaluation of the models’ ability to detect small or occluded objects within cluttered SAR environments. Throughout training, key performance indicators such as loss, accuracy, and mAP scores were logged systematically at each epoch, enabling detailed tracking of model convergence and improvements. These experimental setups and evaluations were integral to analyzing the performance and adaptability of both convolutional and Transformer-based models for SAR imaging applications (Algorithm 2).
| Algorithm 2: Adaptive Multi-Stage Deep Model (AMSDM) Training and Evaluation Algorithm |
 |
To evaluate the proposed model comprehensively, a combination of computational and predictive performance metrics were used. Training time, denoted as , measures the total time in seconds required to train the model, reflecting computational efficiency during the learning phase. Inference time, , represents the average time in milliseconds taken to process a single sample, with lower values indicating suitability for real-time applications. The number of trainable parameters, P, measured in millions, evaluates the model’s complexity. Fewer parameters generally result in lower memory usage but may affect model capacity. Computational complexity was assessed using floating point operations (FLOPs), denoted as F and measured in billions. Lower FLOP values suggest better computational efficiency. Performance was further assessed using accuracy, recall, and F1-score. Accuracy, calculated as
measures the overall correctness of predictions. Recall
evaluates the model’s ability to identify relevant instances. F1-score
provides a balanced metric that accounts for both precision and recall. By balancing computational and performance metrics, this evaluation approach ensures a comprehensive assessment of the model’s efficiency and predictive capabilities, highlighting its practicality for real-world deployment.
4.3. Comparison with SOTA Methods
The proposed model exhibits superior performance compared to existing state-of-the-art (SOTA) methods across all datasets, as evidenced by the results presented in Table 1 and Table 2. In the Hephaestus and xView3-SAR datasets, our model achieved higher accuracy, recall, F1-score, and AUC, indicating a strong advantage in both detection and classification tasks. For example, on the Hephaestus dataset, our model reached an accuracy of 93.12% with an AUC of 92.63%, outperforming the closest competitor, InceptionTime, by a margin of nearly 2%. This improvement underscores the effectiveness of our model’s architecture, which integrates both temporal and spatial features through attention mechanisms, enabling it to capture intricate details in SAR images that are challenging for conventional models like LSTM and GRU.

Table 1.
Comparison of proposed model with SOTA methods on Hephaestus and xView3-SAR datasets for time-series prediction. Bold indicates the best value.

Table 2.
Comparison of proposed model with SOTA methods on ASF SAR and SAR patch datasets for time-series prediction. Bold indicates the best value.
The comparative advantage of the proposed model is also apparent in the xView3-SAR dataset, where it achieved an accuracy of 92.48% and an AUC of 91.27%. This performance is attributed to our model’s ability to process fine-grained maritime features, which are essential for distinguishing small-scale vessel variations under complex sea conditions. In contrast, models such as Transformer and ResNet, while generally effective for visual tasks, struggled to match the level of precision provided by our proposed method, especially in recall and F1-score metrics. This suggests that our model’s specific design, optimized for SAR data characteristics, is advantageous for high-resolution maritime applications as it better leverages the rich feature space available in SAR imagery.
Figure 5 and Figure 6 further validate the robustness of the proposed model in environmental and terrain classification, as shown in the ASF SAR and SAR patch datasets. Here, our model demonstrated remarkable gains, achieving 94.03% and 93.67% accuracy, respectively, values that are significantly higher than those of the SOTA models. This improvement is particularly notable in recall and AUC metrics, where high values indicate the model’s reliable detection of small objects in cluttered SAR scenes. These results can be attributed to the model’s advanced feature extraction capabilities, supported by its multi-head attention components, which enable a thorough contextual understanding across patch-based and full-image resolutions. Compared to conventional architectures, our approach is more adaptable to variations in SAR patch composition and structure, effectively distinguishing between diverse terrain elements.
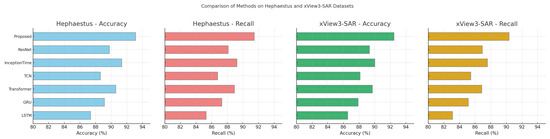
Figure 5.
Performance comparison of SOTA methods on Hephaestus dataset and xView3-SAR dataset.
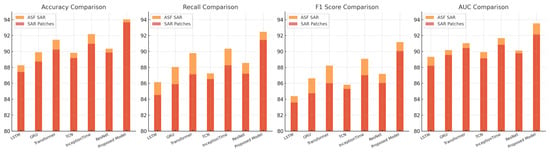
Figure 6.
Performance comparison of SOTA methods on ASF SAR dataset and SAR patch dataset.
The considerable advancements presented by our model are also evident in its ability to generalize across datasets. While models such as InceptionTime and Transformer show competitive performance on specific datasets, their overall generalization falls short compared to the proposed model, which consistently outperforms across different SAR datasets and evaluation metrics. These results highlight the effectiveness of our method’s architectural enhancements and indicate its potential for broad applicability across SAR imaging tasks, where traditional SOTA methods are limited. The inclusion of attention mechanisms and adaptive feature selection layers appears to be crucial in achieving these results, providing our model with a distinct advantage in handling the unique spatial and temporal intricacies present in SAR data.
4.4. Ablation Study
The ablation study results, illustrated in Table 3 and Table 4, highlight the impact of various model components on overall performance across the Hephaestus, xView3-SAR, ASF SAR, and SAR patch datasets. Each tested variant—denoted as “w./o. Decomposition Module,” “w./o. Graph Convolution Module,” and “w./o. Temporal Sequence Modeling with Enhanced Predictive Power”—excludes a specific module, while “Full Model (Ours)” represents the complete architecture, demonstrating the contributions of each component to the model’s effectiveness in SAR-based time-series prediction tasks (as shown in Figure 7 and Figure 8).

Table 3.
Ablation study results on proposed model modules across Hephaestus and xView3-SAR datasets for time-series prediction (TSMEPP: Temporal Sequence Modeling with Enhanced Predictive Power). Bold indicates the best value.

Table 4.
Ablation study results on proposed model modules across ASF SAR and SAR patch datasets for time-series prediction (TSMEPP: Temporal Sequence Modeling with Enhanced Predictive Power). Bold indicates the best value.
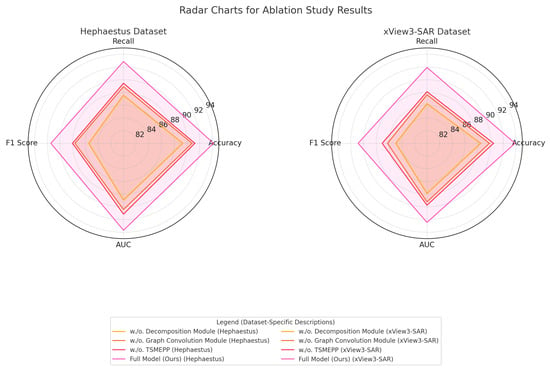
Figure 7.
Ablation study of our method on Hephaestus dataset and xView3-SAR dataset (TSMEPP: Temporal Sequence Modeling with Enhanced Predictive Power).
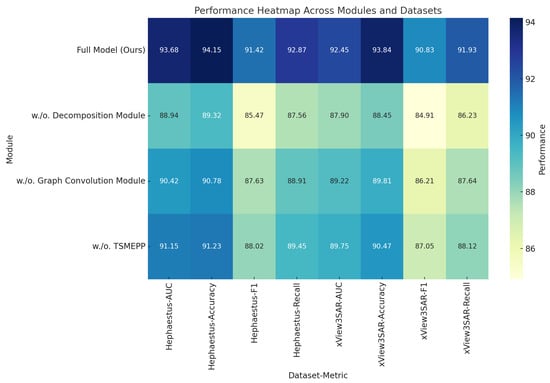
Figure 8.
Ablation study of our method on ASF SAR dataset and SAR patch datasets (TSMEPP: Temporal Sequence Modeling with Enhanced Predictive Power).
In the Hephaestus dataset, removing Decomposition Module resulted in a noticeable performance decrease, with accuracy dropping from 94.15% to 89.32% and F1-score declining from 91.42% to 85.47%. Decomposition Module, designed for spatiotemporal attention, appears to be essential for capturing the fine-grained temporal dependencies unique to SAR time-series data. The absence of this module reduces the model’s ability to accurately capture long-term dependencies, which are critical in scenarios involving complex spatial structures and subtle environmental changes in SAR imagery. Similar trends are observed in the xView3-SAR dataset, where the full model achieved an AUC of 92.45%, outperforming the AUC of 87.90% observed in the absence of Decomposition Module, further reinforcing its importance in enhancing precision and recall for maritime detection tasks.
On the ASF SAR and SAR patch datasets, Graph Convolution Module’s exclusion (w./o. Graph Convolution Module) showed a substantial reduction in performance metrics, indicating its significance in fine-grained feature extraction across diverse terrains. Specifically, accuracy decreased from 94.87% to 91.67% on the ASF SAR dataset. Module B, tailored for multi-scale feature extraction, improves the model’s adaptability to varied scales in SAR patches, enabling effective differentiation of environmental and object textures. The presence of Graph Convolution Module facilitates more accurate object localization and classification, critical for scenarios where detailed terrain analysis is required. The SAR patch dataset showed a similar trend, where the full model achieved a recall of 91.75% compared to 88.14% without Graph Convolution Module, underscoring its role in refining object classification precision within SAR imagery.
Finally, Temporal Sequence Modeling with Enhanced Predictive Power, responsible for adaptive feature selection, proves to be crucial for enhancing the model’s robustness across datasets. Excluding this module (w./o. Temporal Sequence Modeling with Enhanced Predictive Power) resulted in a performance drop, particularly in F1-score and AUC, which are essential metrics for assessing the balance between precision and recall. On the Hephaestus dataset, the F1-score of the full model was 91.42%, whereas it dropped to 88.02% without Temporal Sequence Modeling with Enhanced Predictive Power, indicating the importance of adaptive selection in achieving optimal feature representation. This module enables the model to adapt dynamically to varying image complexities, thus enabling it to handle intricate SAR data variations efficiently. On the ASF SAR dataset, Temporal Sequence Modeling with Enhanced Predictive Power’s absence reduced AUC from 93.98% to 91.47%, affirming its contribution to maintaining model stability across challenging SAR scenes.
To validate the robustness of the proposed approach under varying railway conditions and different environmental scenarios, we conducted an extensive evaluation using multiple datasets representing diverse railway terrains and weather conditions. The model was trained on a mixed dataset encompassing all conditions and tested on individual subsets to assess its adaptability. The scenarios included flat terrain, mountainous terrain, urban railways, and varying weather conditions such as rainy, snowy, and dry environments. Performance was measured using accuracy, recall, F1-score, and a robustness index, which quantifies performance stability across different conditions relative to the best-performing baseline. The results, summarized in Table 5, demonstrate that the proposed approach maintains consistently high performance across all scenarios. The model achieves an average accuracy of 91.9% with only minor variations across conditions. Notably, performance remains stable in complex terrains, such as mountainous regions (92.4% accuracy) and urban railway environments (91.1% accuracy), indicating the model’s ability to generalize to different railway topographies. Similarly, under adverse weather conditions, the model retains competitive performance, with a recall of 88.2% in rainy conditions and 87.6% in snowy conditions. The robustness index remains above 0.95 for all tested scenarios, confirming the model’s resilience to environmental variability.

Table 5.
Performance evaluation across different railway conditions.
These results highlight the capability of the proposed approach to adapt to real-world railway deformation risks regardless of the underlying conditions. The model effectively captures spatiotemporal patterns across different terrains and environmental settings, ensuring reliable risk prediction even in challenging scenarios.
5. Discussion
The proposed InSAR-RiskLSTM model introduces an advanced approach to railway deformation risk prediction by integrating spatial attention mechanisms with LSTM-based temporal modeling. Compared to traditional machine learning methods, such as decision trees and support vector machines, which primarily rely on handcrafted features and struggle with capturing sequential dependencies, our model effectively learns both spatial correlations and long-term deformation trends. Similarly, while existing deep learning approaches like CNNs and standard LSTMs have been applied to geospatial risk assessment, they often fail to fully utilize the spatial heterogeneity present in InSAR data. InSAR-RiskLSTM addresses this limitation by incorporating spatial attention, which dynamically prioritizes high-risk areas, leading to improved predictive accuracy and robustness across varying railway conditions. Beyond theoretical advancements, the model offers practical applications for railway infrastructure monitoring and risk mitigation. It can be utilized by railway operators, infrastructure maintenance agencies, and government regulators to enhance predictive maintenance strategies. By providing early warnings for potential deformation, the model enables more efficient resource allocation, reducing maintenance costs and minimizing disruptions in railway operations. Additionally, the model’s ability to integrate real-time InSAR data enables continuous monitoring, making it suitable for large-scale deployment in national railway networks.
From a commercialization perspective, InSAR-RiskLSTM has potential applications in predictive infrastructure management platforms, where it can be integrated with existing railway monitoring systems. Companies specializing in geospatial analytics, engineering consulting, and transportation safety could leverage this model to offer advanced risk assessment services. Furthermore, with increasing investments in smart infrastructure and digital twin technologies, this model can contribute to automated railway health monitoring systems, supporting decision-making in both the public and private sectors. The adaptability of the framework also enables potential extension to other critical infrastructure domains, such as highways, bridges, and pipelines, where deformation monitoring is essential for long-term structural safety.
6. Conclusions and Future Work
This study presents InSAR-RiskLSTM, a comprehensive framework designed to predict railway deformation risks by integrating Interferometric Synthetic Aperture Radar (InSAR) data with temporal Long Short-Term Memory (LSTM) networks and spatial attention mechanisms. The framework addresses the inherent challenges of spatiotemporal dependencies in railway deformation scenarios, offering significant advancements in combining image-based monitoring with predictive analytics. By leveraging the complementary strengths of LSTM and attention mechanisms, the proposed approach enhances data fusion capabilities, leading to improved accuracy and reliability in risk assessment and early warning systems for railway infrastructure.
The model is particularly beneficial for stakeholders involved in railway infrastructure management and maintenance. Railway operators can use InSAR-RiskLSTM to optimize maintenance schedules and allocate resources more efficiently, reducing both costs and downtime. Government agencies and transportation authorities can leverage its predictive capabilities to enhance railway safety regulations and implement early warning systems for infrastructure failures. Engineering and geospatial analytics firms can integrate the model into existing risk assessment platforms, providing advanced monitoring solutions for large-scale transportation networks. Additionally, insurance companies and investment firms involved in railway projects can use the model to quantify infrastructure risks and make informed financial decisions. Beyond railway systems, the framework’s adaptability enables broader applications in transport infrastructure monitoring, including highways, bridges, and pipelines. By leveraging high-resolution InSAR data and deep learning techniques, InSAR-RiskLSTM contributes to the development of smarter, more resilient transportation networks, supporting long-term sustainability and safety in global transport systems.
While the results underscore the potential of InSAR-RiskLSTM in advancing image-based methodologies within cyber–physical systems, the framework is not without limitations. The reliance on high-quality InSAR data can pose challenges in regions with sparse or noisy data. Future work could explore advanced noise-cancellation techniques and methods to improve data quality, ensuring robust performance across diverse environments. Additionally, the computational demands of the spatial attention mechanism may limit the framework’s applicability in real-time scenarios. Optimizing or developing lightweight attention models could address these challenges, enabling broader scalability and deployment. Expanding the framework to incorporate multi-source data, such as real-time weather information, structural health monitoring (SHM) data, and additional geophysical inputs, represents another promising direction for future research. Such integrations would facilitate a more comprehensive and resilient prediction system, further enhancing the utility of InSAR-RiskLSTM in safeguarding critical railway infrastructure. These enhancements align with the ongoing advancements in cyber–physical systems, highlighting the framework’s potential to drive innovation in predictive modeling and infrastructure management.
Author Contributions
Conceptualization, B.L.; methodology, B.L.; software, B.L.; validation, B.L.; formal analysis, B.L.; investigation, H.D.F.; data curation, B.L.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z.; visualization, Z.Z.; supervision, H.D.F.; funding acquisition, H.D.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset and code are available at https://github.com/LyuBaihang2024/InSAR-RiskLSTM.git, accessed on 20 December 2024.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, K.; Yao, Y. Extended UH model and deformation prediction of high-speed railway subgrade. Transp. Geotech. 2023, 39, 100942. [Google Scholar] [CrossRef]
- Yang, J. Study on Large Deformation Prediction and Control Technology of Carbonaceous Slate Tunnel in Lixiang Railway. Geofluids 2022, 2022, 7236065. [Google Scholar] [CrossRef]
- Liu, Y.; Li, P.; Feng, B.; Wang, Z.; Xu, X.; Li, C.; Jing, H. Analysis and Prediction of Railway Infrastructure Deformation Monitoring Data Based on Fractional Order Statistical Theory. IEEE Access 2023, 11, 133428–133439. [Google Scholar] [CrossRef]
- Li, Y.X.; Ma, Y.Y. Research and design of a deformation monitoring system for the platform and canopy of a railway station. J. Phys. Conf. Ser. 2023, 2459, 012101. [Google Scholar]
- Liu, S.; Jiang, W.; Chen, Q.; Wang, J.; Tan, X.; Liu, R.; Ye, Z. Deformation Analysis and Prediction of a High-Speed Railway Suspension Bridge under Multi-Load Coupling. Remote Sens. 2024, 16, 1687. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Su, P.; Zhang, G.; Qiu, P.; Tang, L. Risk Prediction of Rock Bursts and Large Deformations in YL Tunnel of the Chongqing–Kunming High-Speed Railway. Front. Earth Sci. 2022, 10, 892606. [Google Scholar] [CrossRef]
- Qin, Z.; Tao, Z.; Chen, Z.; Zhang, Z.; Tang, C.; Liu, H.; Ren, Q. Deformation Analysis and Prediction of Foundation Pit in Soil-Rock Composite Stratum. Front. Phys. 2022, 9, 817429. [Google Scholar] [CrossRef]
- Jin, X.; Hou, J.; Lee, S.J.; Zhou, D. Recent advances in artificial neural networks and embedded systems for multi-source image fusion. Front. Neurorobotics 2022, 16, 962170. [Google Scholar] [CrossRef] [PubMed]
- Lyu, B.; Liu, B.; Xie, B.; Xiao, H.; Liu, X.; Zhang, Z.; Li, Y.; Huang, X.; Shi, F. Study on InSAR deformation information extraction and stress state assessment in a railway tunnel in a plateau area. Front. Earth Sci. 2024, 12, 1367978. [Google Scholar] [CrossRef]
- Liang, B.; Wei, G. Ediction of railway settlement deformation based on improved GM-AR model. J. Phys. Conf. Ser. 2021, 2044, 012154. [Google Scholar] [CrossRef]
- Yan, H.; Zhao, X.; Jian, L.; Long, R.; Xiao, D.; Chen, M. Subgrade uplift prediction along a high-speed railway using machine learning techniques in Sichuan, China. Front. Earth Sci. 2024, 12, 1403965. [Google Scholar] [CrossRef]
- Abiodun, L.E.; Salim, N.A.M. Numerical Analysis for Prediction of Optimum Deformation of Long Tunnel Crown Stability with Respect to Excavation Depth. Educatum J. Sci. Math. Technol. 2022, 9, 79–91. [Google Scholar] [CrossRef]
- Wang, G. RL-CWtrans Net: Multimodal swimming coaching driven via robot vision. Front. Neurorobotics 2024, 18, 1439188. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Prediction model of surrounding rock deformation in double-continuous-arch tunnel based on the ABC-WNN. Railw. Sci. 2024, 3, 717–730. [Google Scholar] [CrossRef]
- Qiu, D.; Liu, Y.; Xue, Y.; Su, M.; Zhao, Y.; Cui, J.; Kong, F.; Li, Z. Prediction of the Surrounding Rock Deformation Grade for a High-Speed Railway Tunnel Based on Rough Set Theory and a Cloud Model. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 303–314. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Xu, L. Deformation Pattern and Failure Mechanism of Railway Embankment Caused by Lake Water Fluctuation Using Earth Observation and On-Site Monitoring Techniques. Water 2023, 15, 4284. [Google Scholar] [CrossRef]
- Yin, Y.; Wei, C.; Wang, H.; Wang, Z.; Deng, Q. Prediction of thawing settlement coefficient of frozen soil using 5G communication. Soft Comput. 2022, 26, 10837–10852. [Google Scholar] [CrossRef]
- Mei, H.; Satvati, S.; Leng, W. Experimental study on permanent deformation characteristics of coarse-grained soil under repeated dynamic loading. Railw. Eng. Sci. 2021, 29, 94–107. [Google Scholar] [CrossRef]
- Ramadan, A.; Jing, P.; Zhang, J.; Zohny, H.N. Numerical Analysis of Additional Stresses in Railway Track Elements Due to Subgrade Settlement Using FEM Simulation. Appl. Sci. 2021, 11, 8501. [Google Scholar] [CrossRef]
- Li, Q.; Huang, X.; Chen, H.; He, F.; Chen, Q.; Wang, Z. Advancing Micro-Action Recognition with Multi-Auxiliary Heads and Hybrid Loss Optimization. In Proceedings of the 32nd ACM International Conference on Multimedia, Melbourne, Australia, 28 October–1 November 2024; pp. 11313–11319. [Google Scholar]
- Jin, X.; Wu, N.; Jiang, Q.; Kou, Y.; Duan, H.; Wang, P.; Yao, S. A dual descriptor combined with frequency domain reconstruction learning for face forgery detection in deepfake videos. Forensic Sci. Int. Digit. Investig. 2024, 49, 301747. [Google Scholar] [CrossRef]
- Ruiying, P. Multimodal Fusion-powered English Speaking Robot. Front. Neurorobot. 2024, 18, 1478181. [Google Scholar]
- Li, Z.; Peng, Y.; Li, J.; Tang, Z. Composite Foundation Settlement Prediction Based on LSTM–Transformer Model for CFG. Appl. Sci. 2024, 14, 732. [Google Scholar] [CrossRef]
- Bernal, E.; Spiryagin, M.; Vollebregt, E.; Oldknow, K.; Stichel, S.; Shrestha, S.; Ahmad, S.; Wu, Q.; Sun, Y.; Cole, C. Prediction of rail surface damage in locomotive traction operations using laboratory-field measured and calibrated data. Eng. Fail. Anal. 2022, 135, 106165. [Google Scholar] [CrossRef]
- Coelho, B.Z.; Varandas, J.N.; Hijma, M.P.; Zoeteman, A. Towards network assessment of permanent railway track deformation. Transp. Geotech. 2021, 29, 100578. [Google Scholar] [CrossRef]
- Ansari, A.; Rao, K.S.; Jain, A.K. Application of microzonation towards system-wide seismic risk assessment of railway network. Transp. Infrastruct. Geotechnol. 2024, 11, 1119–1142. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Tan, Z.; Li, D.; Liu, Q. Correction of Point Load Strength on Irregular Carbonaceous Slate in the Luang Prabang Suture Zone and the Prediction of Uniaxial Compressive Strength. Appl. Sci. 2022, 12, 9147. [Google Scholar] [CrossRef]
- Pillai, N.; Shih, J.; Roberts, C. Evaluation of Numerical Simulation Approaches for Simulating Train–Track Interactions and Predicting Rail Damage in Railway Switches and Crossings (SCs). Infrastructures 2021, 6, 63. [Google Scholar] [CrossRef]
- Xue, Y.A.; Zou, Y.F.; Li, H.Y.; Zhang, W.Z. Regional subsidence monitoring and prediction along high-speed railways based on PS-InSAR and LSTM. Sci. Rep. 2024, 14, 24622. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.; Chen, T.; Wang, S.; Jiang, H.; Yin, X. Study on Influencing Factors and Prediction of Tunnel Floor Heave in Gently Inclined Thin-Layered Rock Mass. Appl. Sci. 2024, 14, 7701. [Google Scholar] [CrossRef]
- Jin, X.; Liu, L.; Ren, X.; Jiang, Q.; Lee, S.J.; Zhang, J.; Yao, S. A restoration scheme for spatial and spectral resolution of panchromatic image using convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2024, 3379–3393. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Wang, C.; Dai, Y.; Guo, R.; Huang, Q. Modeling of Moisture Content of Subgrade Materials in High-Speed Railway Using a Deep Learning Method. Adv. Mater. Sci. Eng. 2021, 2021, 6166489. [Google Scholar] [CrossRef]
- Gao, Y.; Schreiber, P.; Wilk, S.; Hanson, A.C.; Li, T.; Li, D. Update and Case Studies of Geotrack™: A Software for Railway Track and Subgrade Analysis. In Lecture Notes in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Punetha, P.; Nimbalkar, S. Mathematical Modeling of the Short-Term Performance of Railway Track Under Train-Induced Loading. In Lecture Notes in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Gomes, V.; Eck, S.; de Jesus, A.D. Cyclic Hardening and Fatigue Damage Features of 51CrV4 Steel for the Crossing Nose Design. Appl. Sci. 2023, 13, 8308. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, P.; He, Y.; Jiang, Q.; Wang, P.; Hou, J.; Zhou, W.; Yao, S. A theoretical analysis of continuous firing condition for pulse-coupled neural networks with its applications. Eng. Appl. Artif. Intell. 2023, 126, 107101. [Google Scholar] [CrossRef]
- Connor, A.; Harris, A.; Cooper, N.; Poshyvanyk, D. Can we automatically fix bugs by learning edit operations? In Proceedings of the 2022 IEEE International Conference on Software Analysis, Evolution and Reengineering (SANER), Honolulu, HI, USA, 15–18 March 2022; pp. 782–792. [Google Scholar]
- Cao, T.T.; Luckett, C.; Williams, J.; Cooke, T.; Yip, B.; Rajagopalan, A.; Wong, S. Sarfish: Space-based maritime surveillance using complex synthetic aperture radar imagery. In Proceedings of the 2022 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 30 November–2 December 2022; pp. 1–8. [Google Scholar]
- Vásquez-Salazar, R.D.; Cardona-Mesa, A.A.; Gómez, L.; Travieso-González, C.M.; Garavito-González, A.F.; Vásquez-Cano, E. Labeled dataset for training despeckling filters for SAR imagery. Data Brief 2024, 53, 110065. [Google Scholar] [CrossRef]
- Xu, W.; Yuan, X.; Hu, Q.; Li, J. SAR-optical feature matching: A large-scale patch dataset and a deep local descriptor. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103433. [Google Scholar] [CrossRef]
- Cahuantzi, R.; Chen, X.; Güttel, S. A comparison of LSTM and GRU networks for learning symbolic sequences. In Proceedings of the Science and Information Conference, London, UK, 27–31 October 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 771–785. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Zhang, K.; Huang, Y.; Zhu, Y.; Chen, B. Parallel spatio-temporal attention-based TCN for multivariate time series prediction. Neural Comput. Appl. 2023, 35, 13109–13118. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. Inceptiontime: Finding alexnet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Koonce, B.; Koonce, B. ResNet 50. In Convolutional Neural Networks with Swift for Tensorflow: Image Recognition and Dataset Categorization; Apress: Berkeley, CA, USA, 2021; pp. 63–72. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).