Qualitative Analysis of Sleeper Supporting Condition for Railway Ballasted Tracks Using Modal Test
Abstract
1. Introduction
2. Materials and Methods
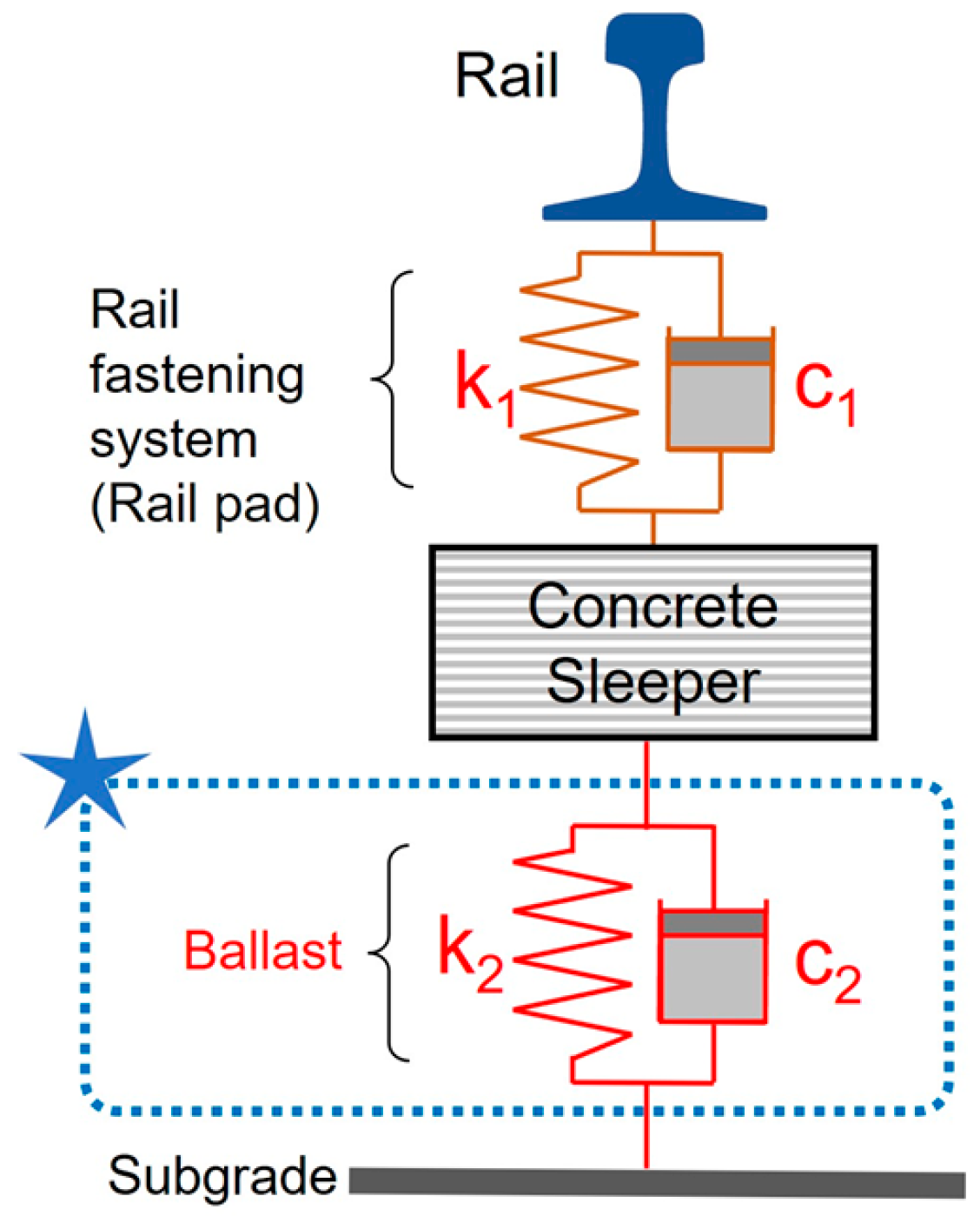
2.1. Materials
2.2. Dynamic Characteristic Analysis of Track Using Modal Testing
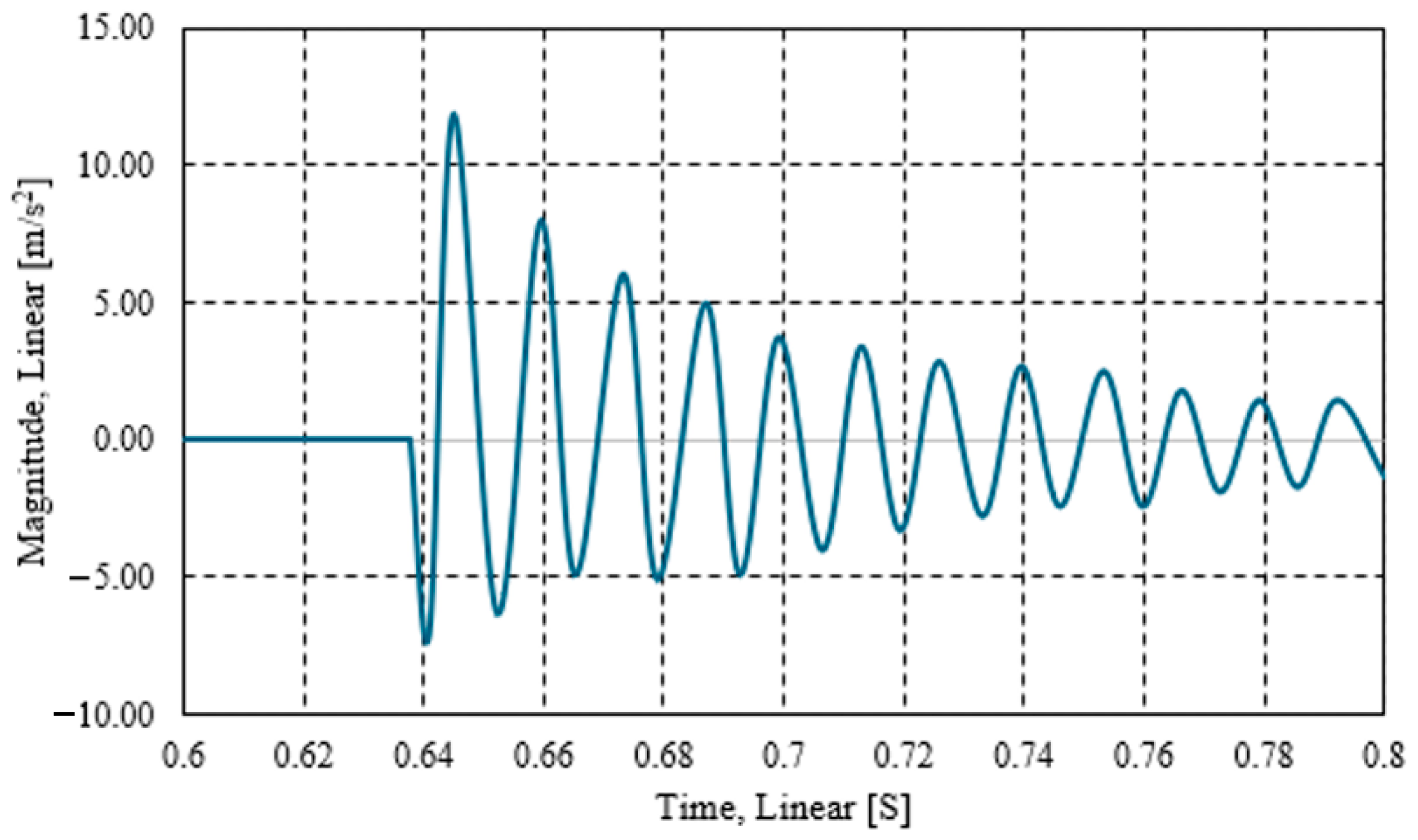
2.2.1. Testing Method
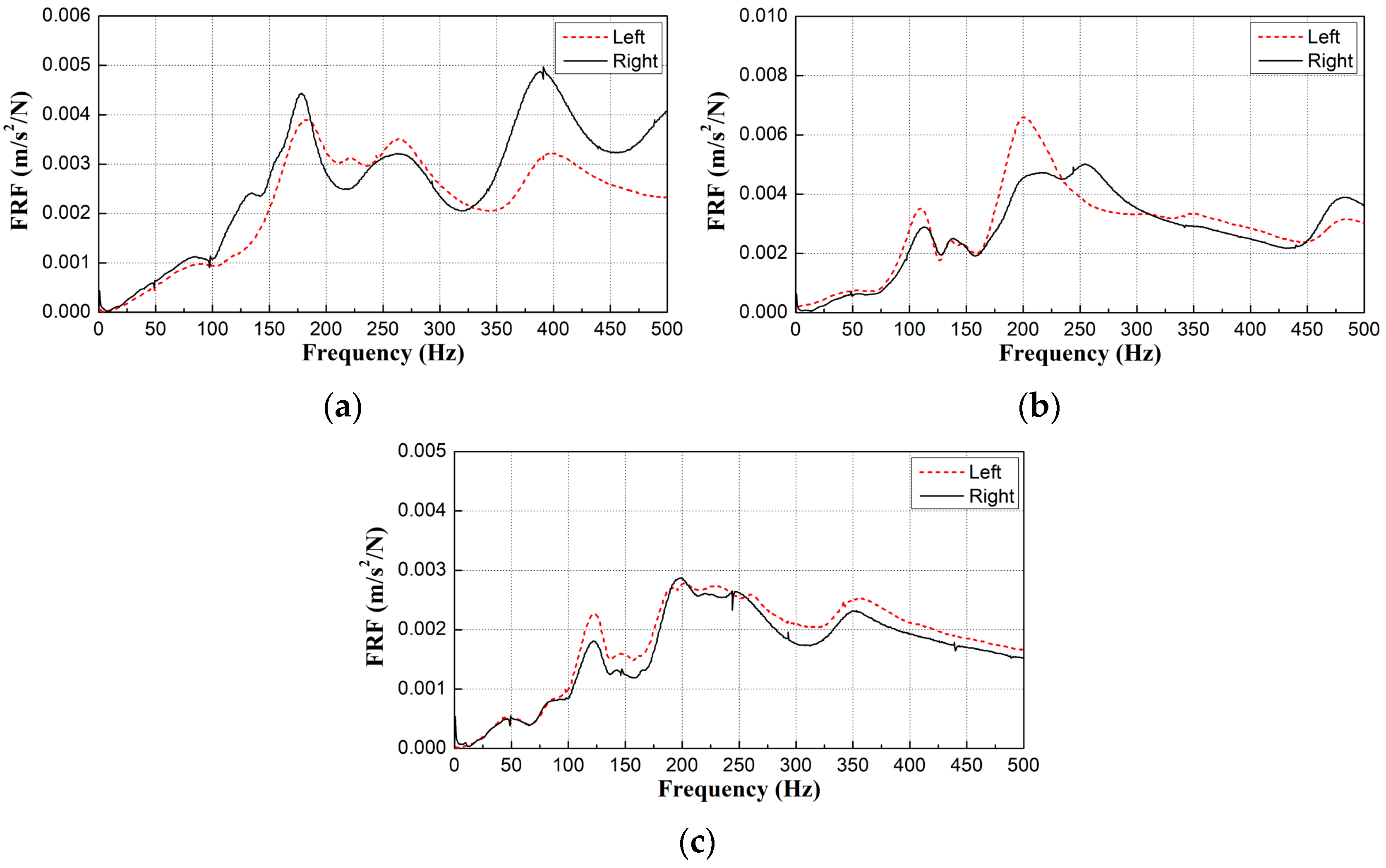
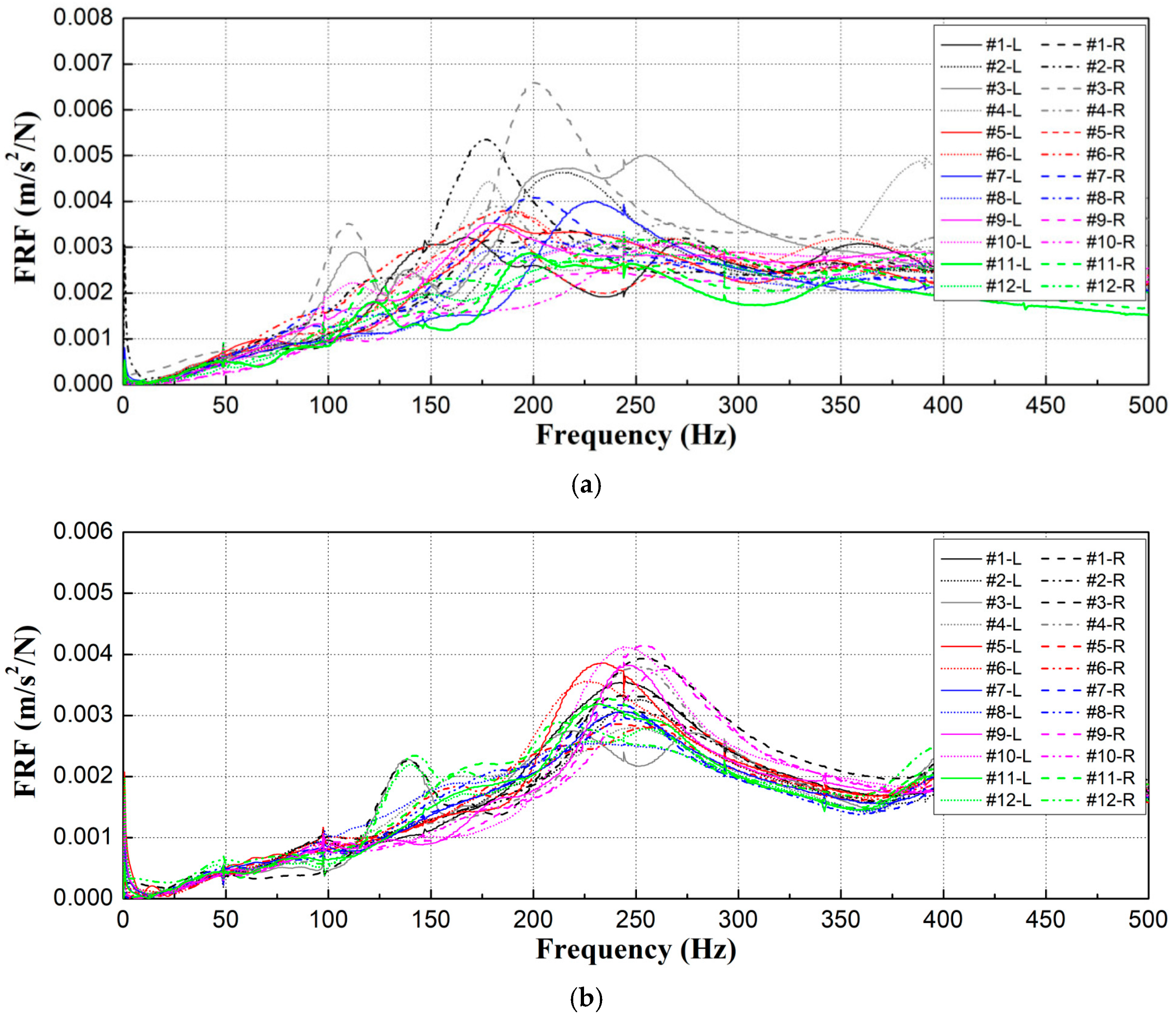
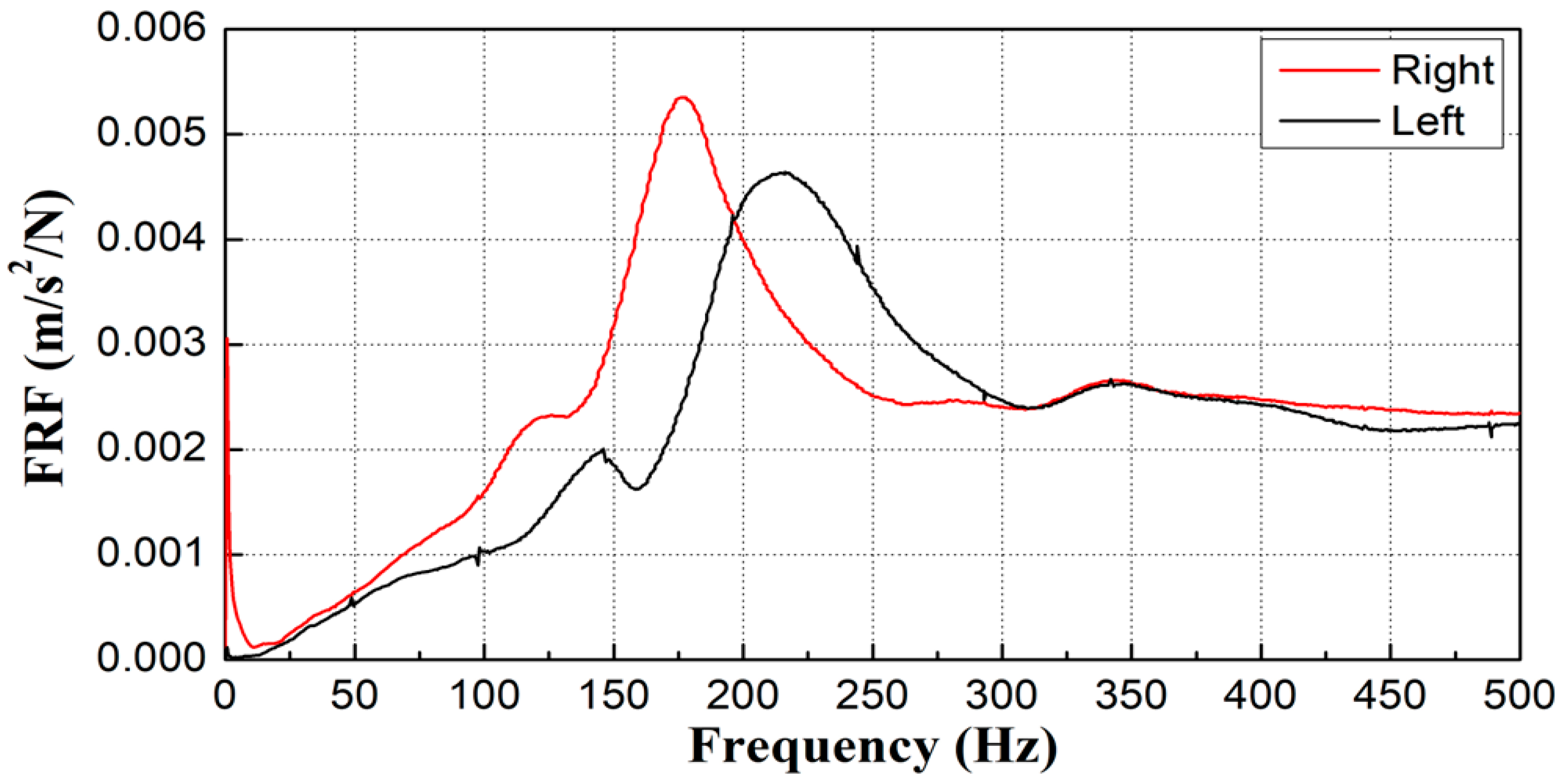
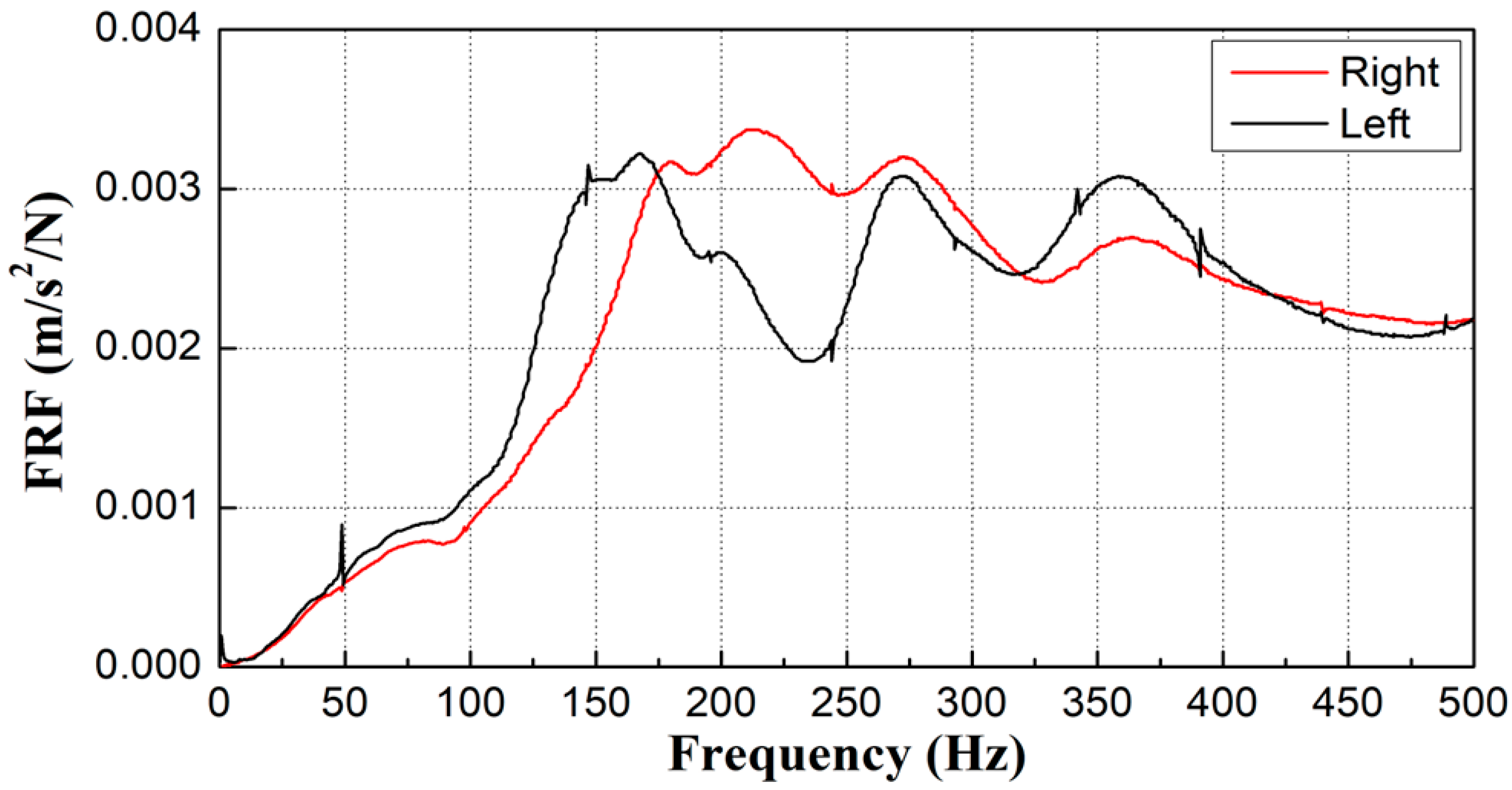
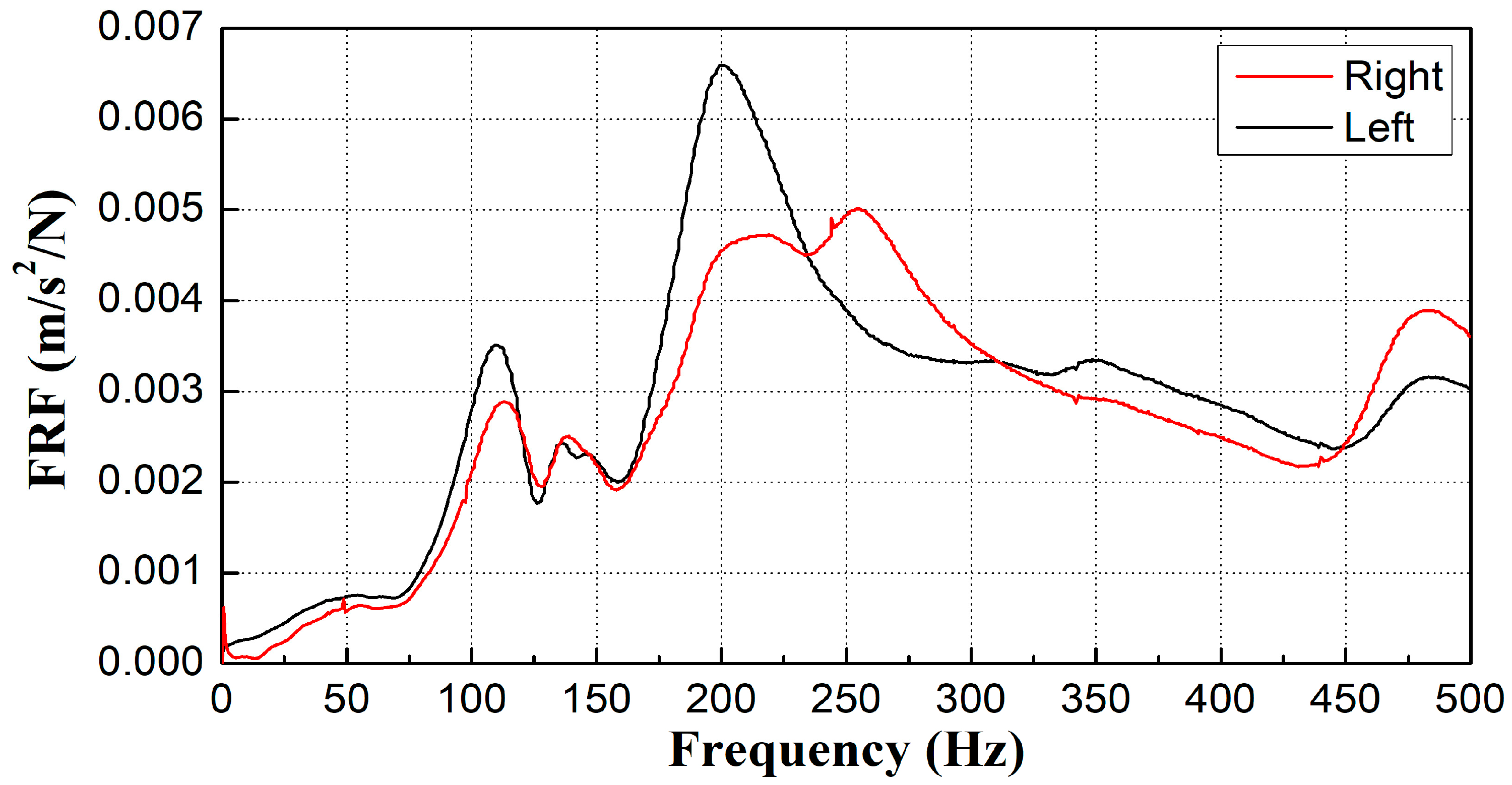
2.2.2. Test Results
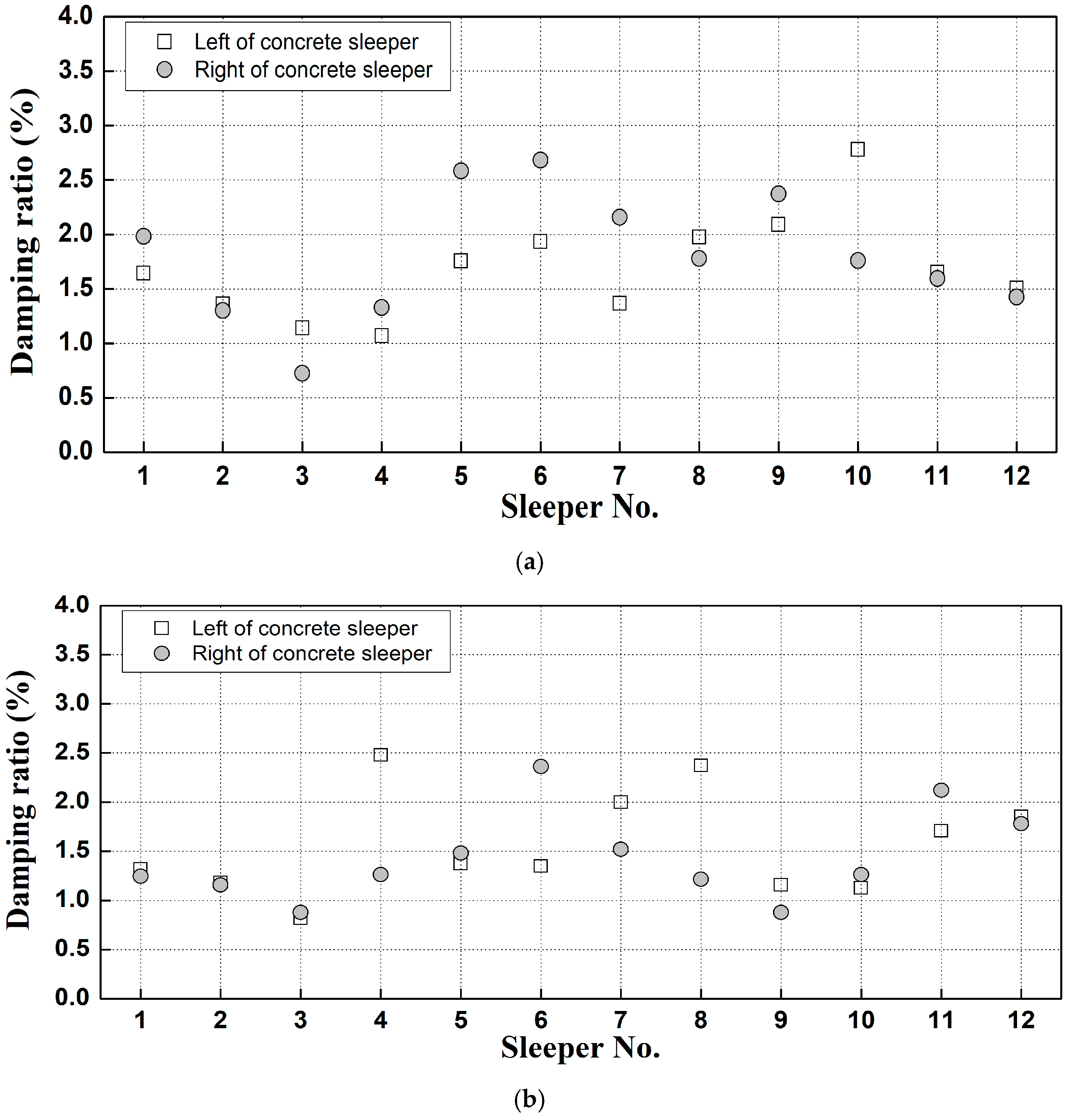
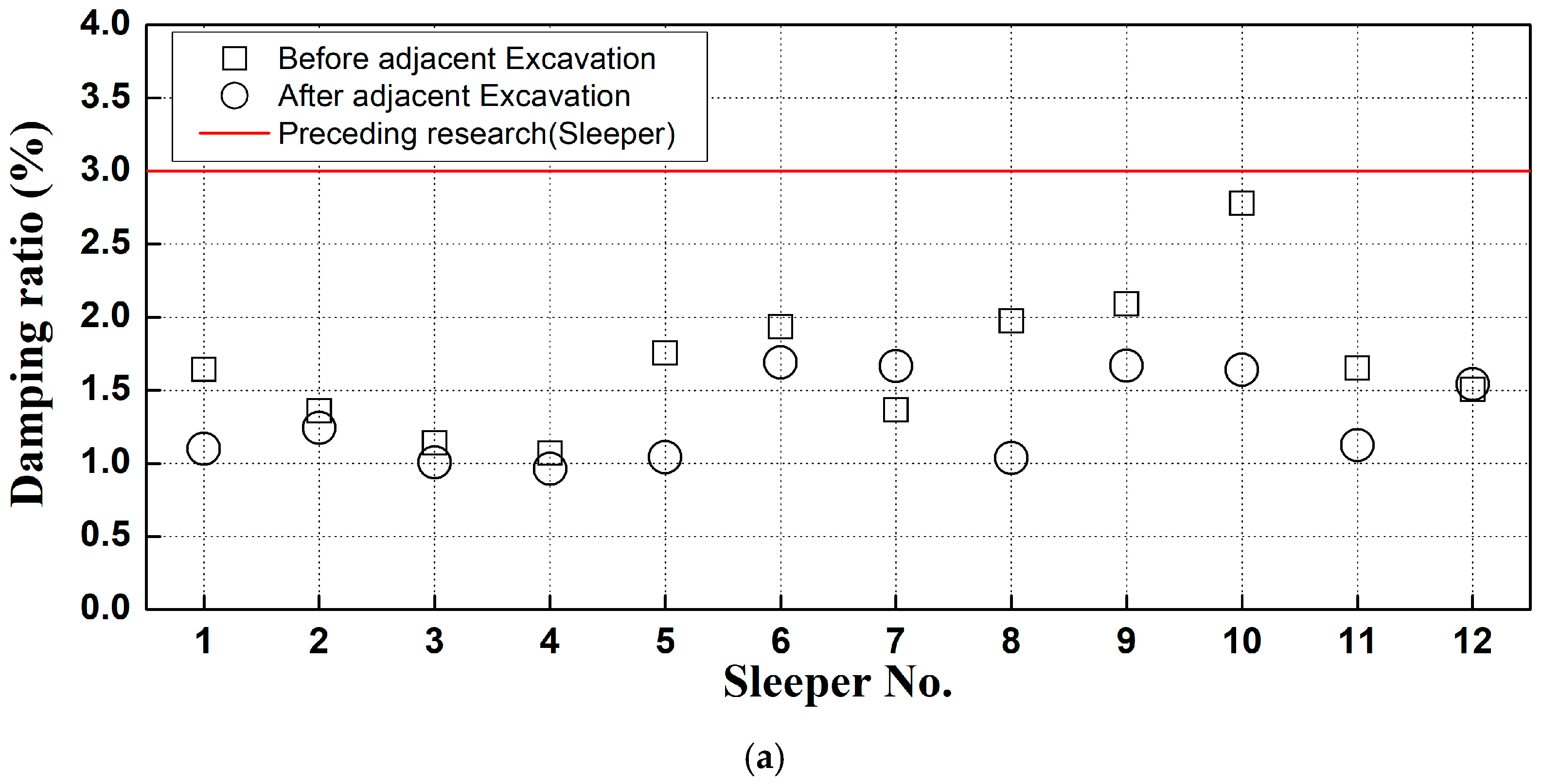
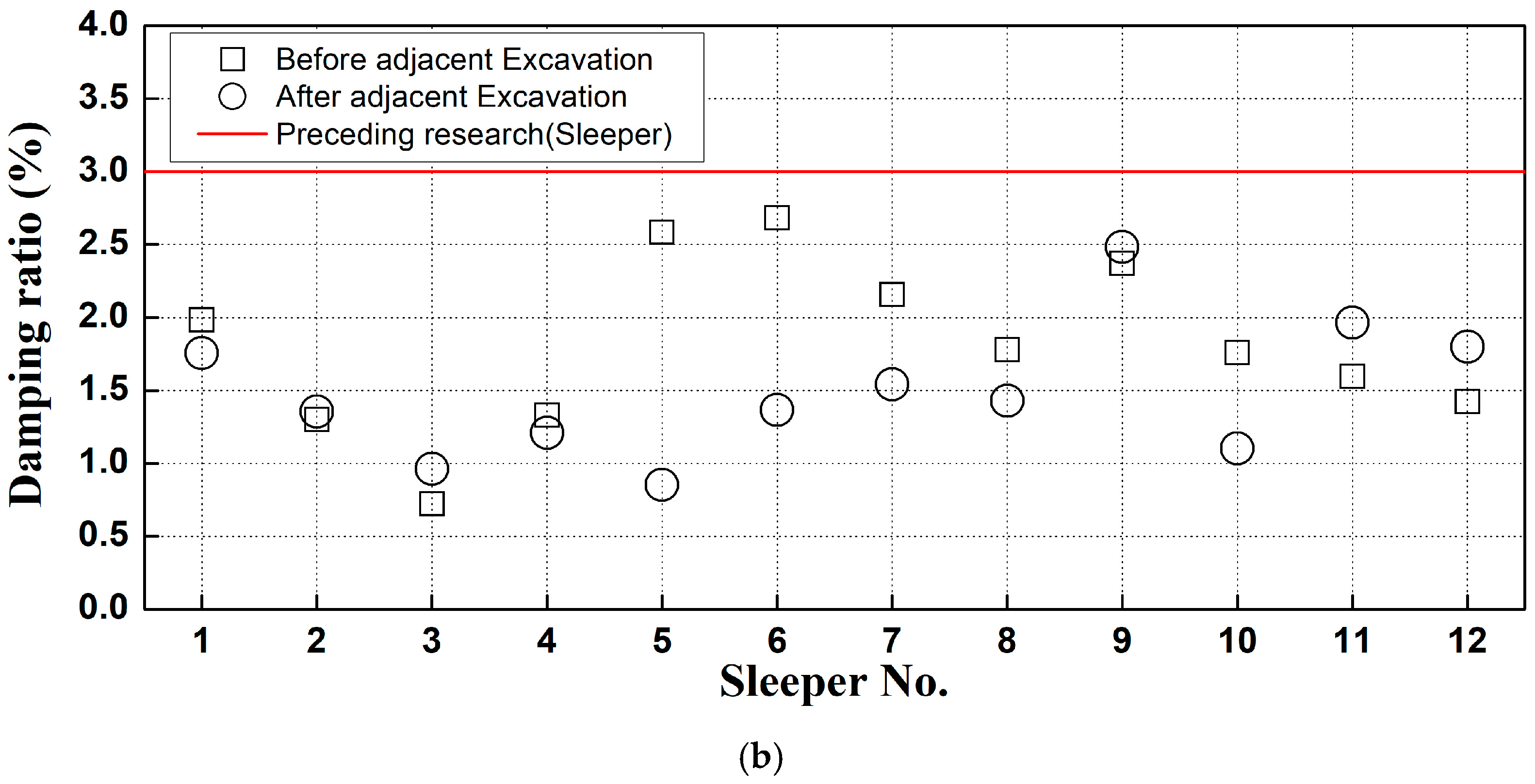
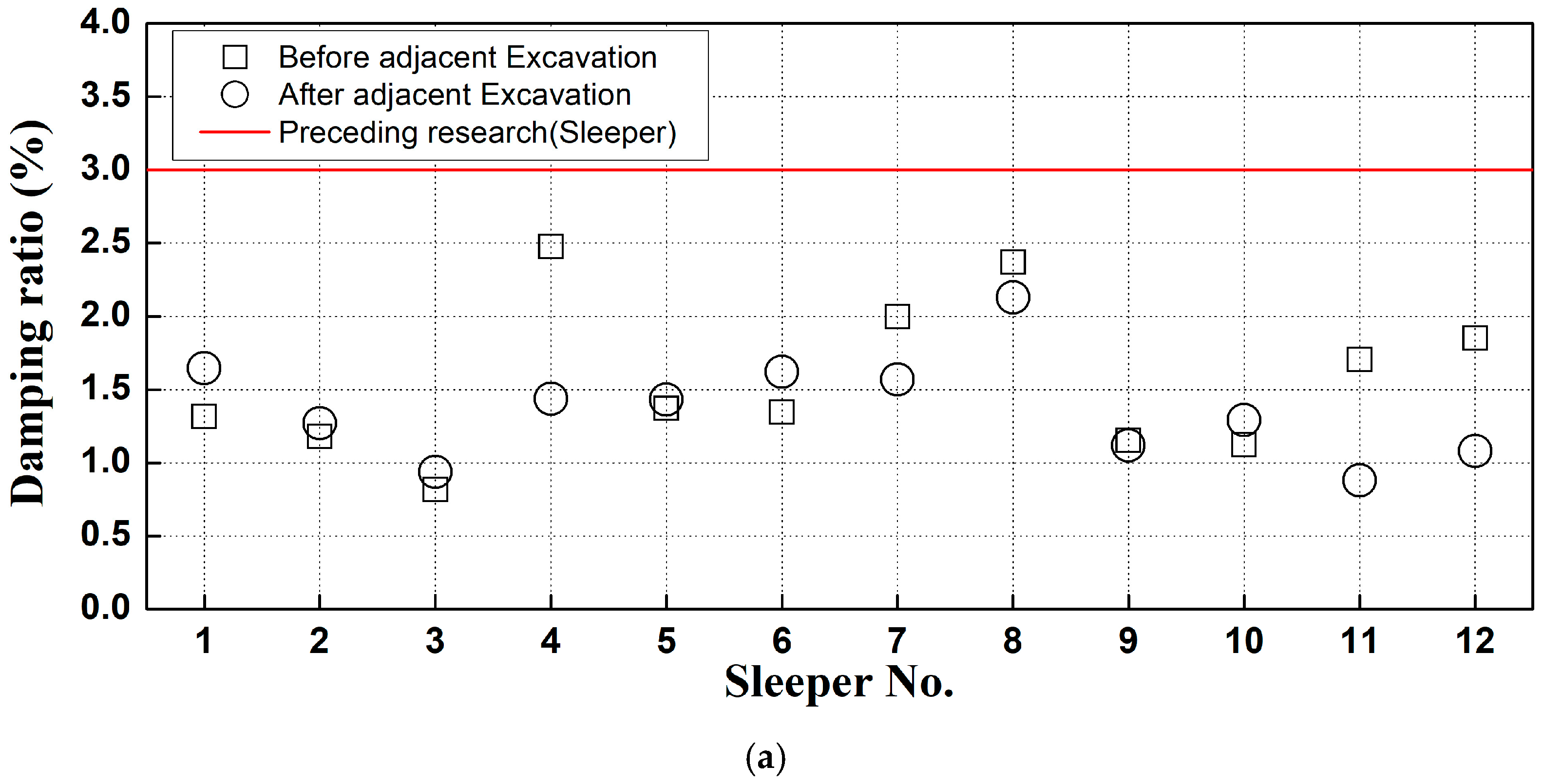
2.3. Damping Ratio Analysis
3. Natural Frequency Analysis of Ballasted Track Sleepers
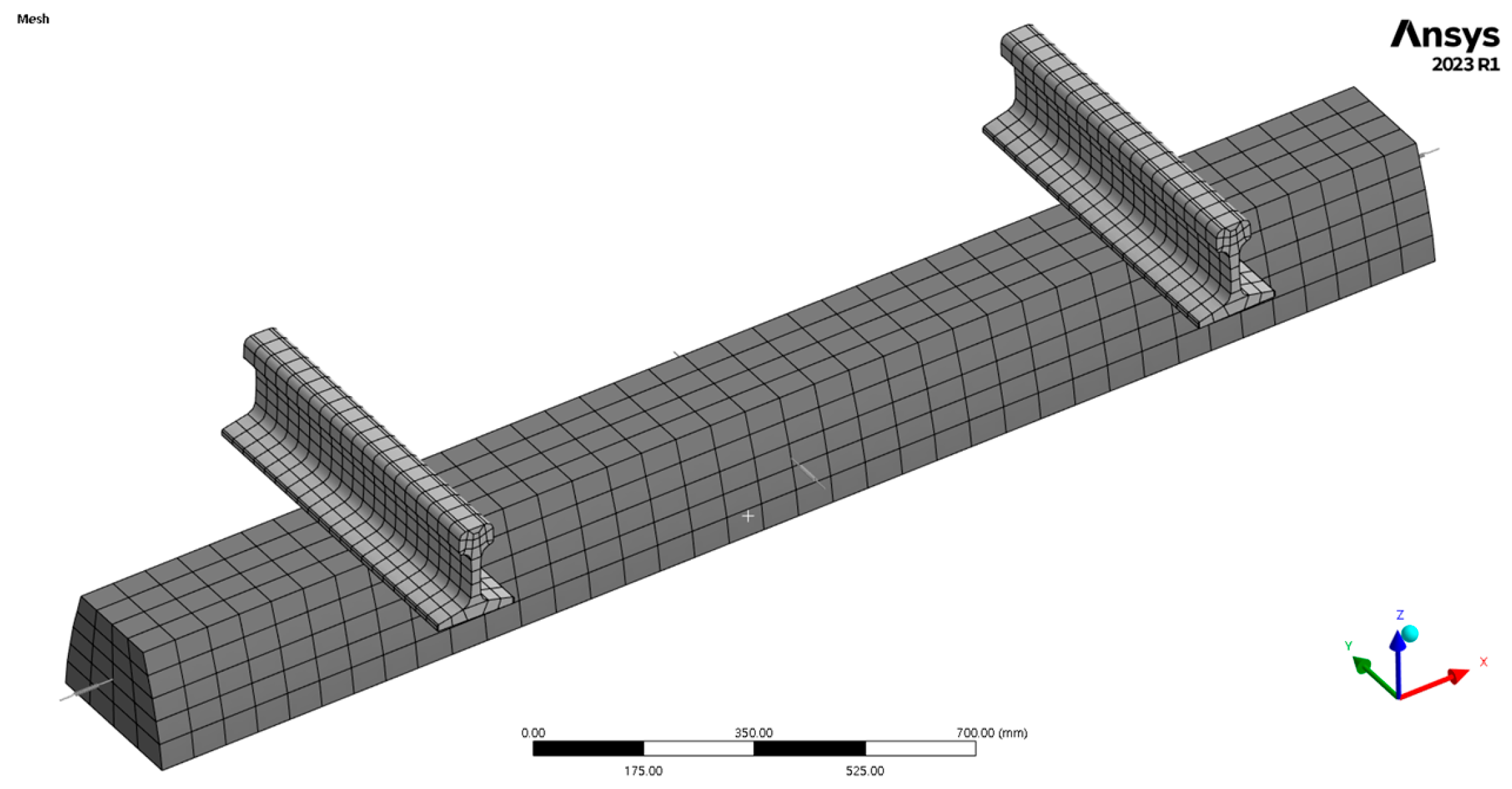
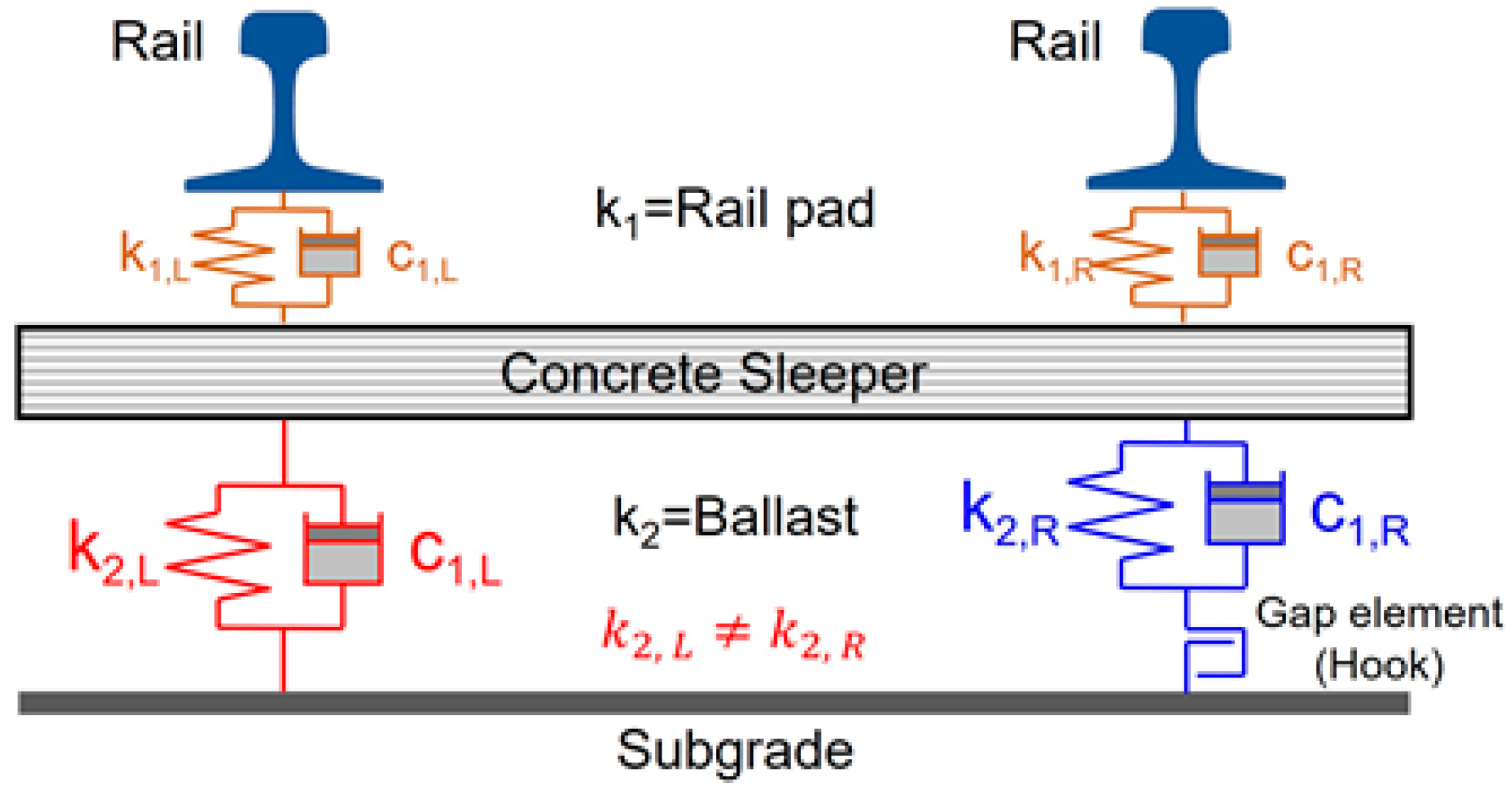
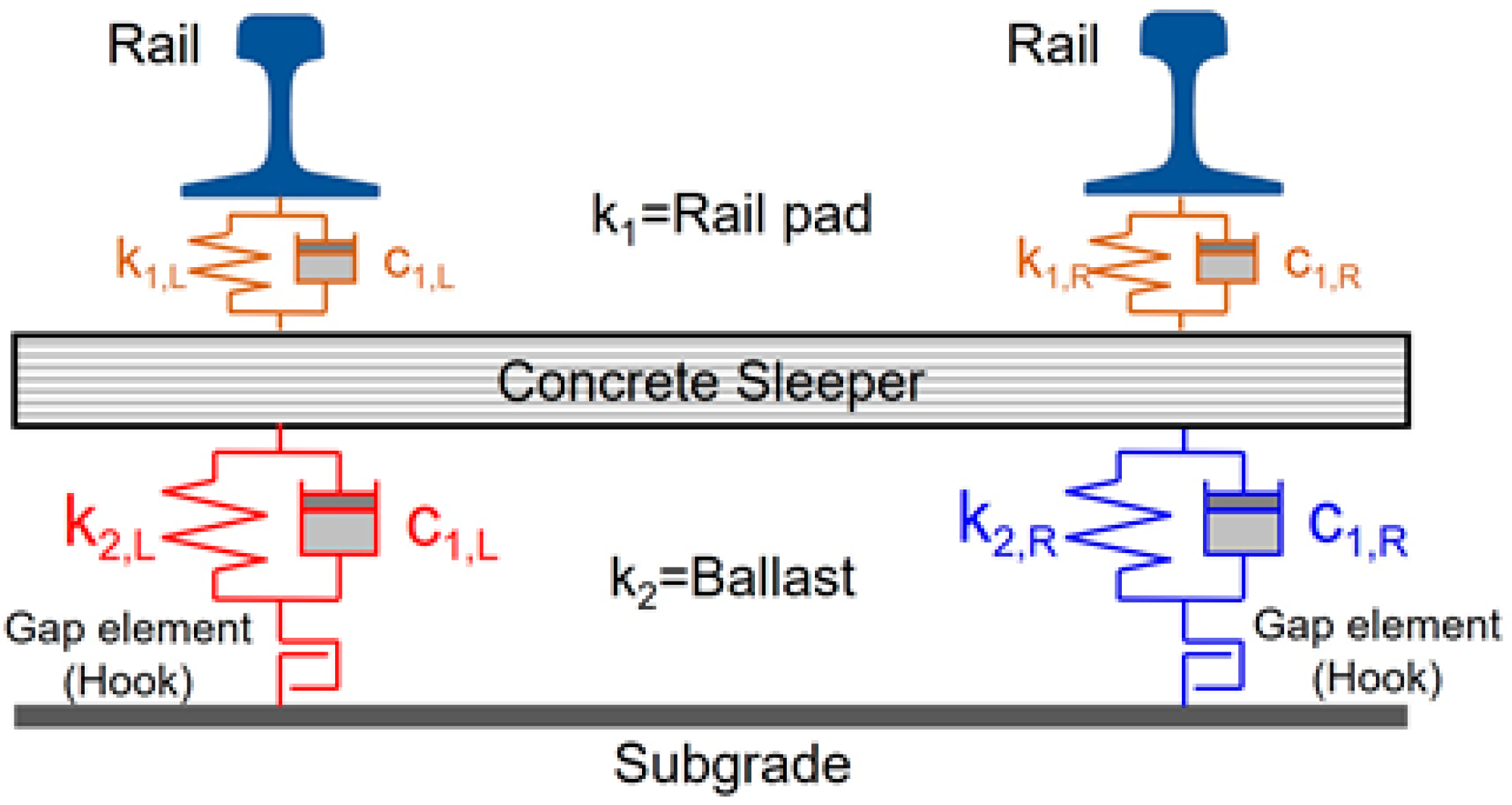
3.1. Modeling
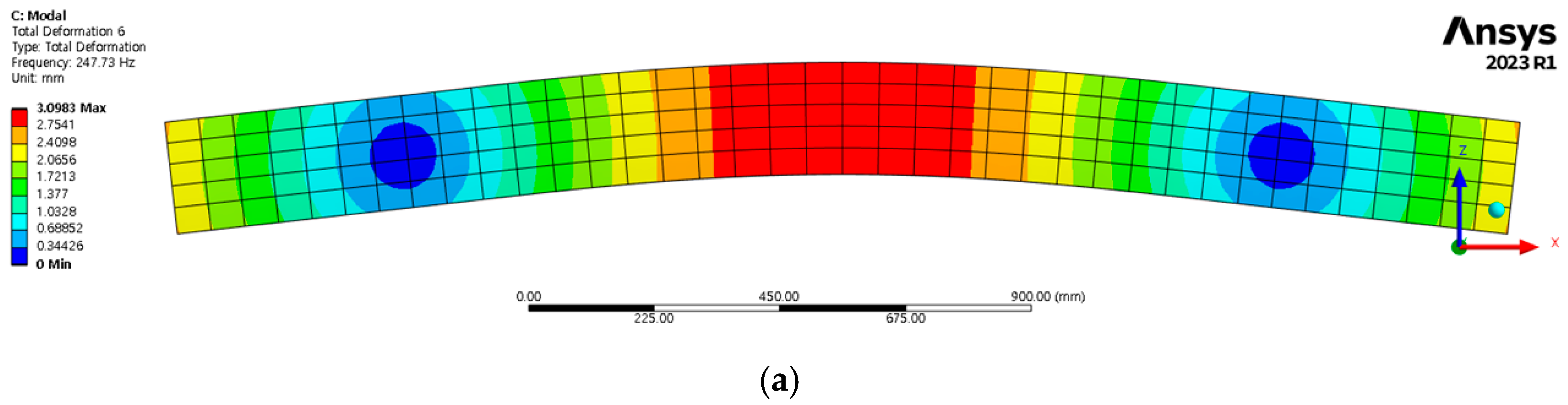
3.2. Numerical Analysis Results
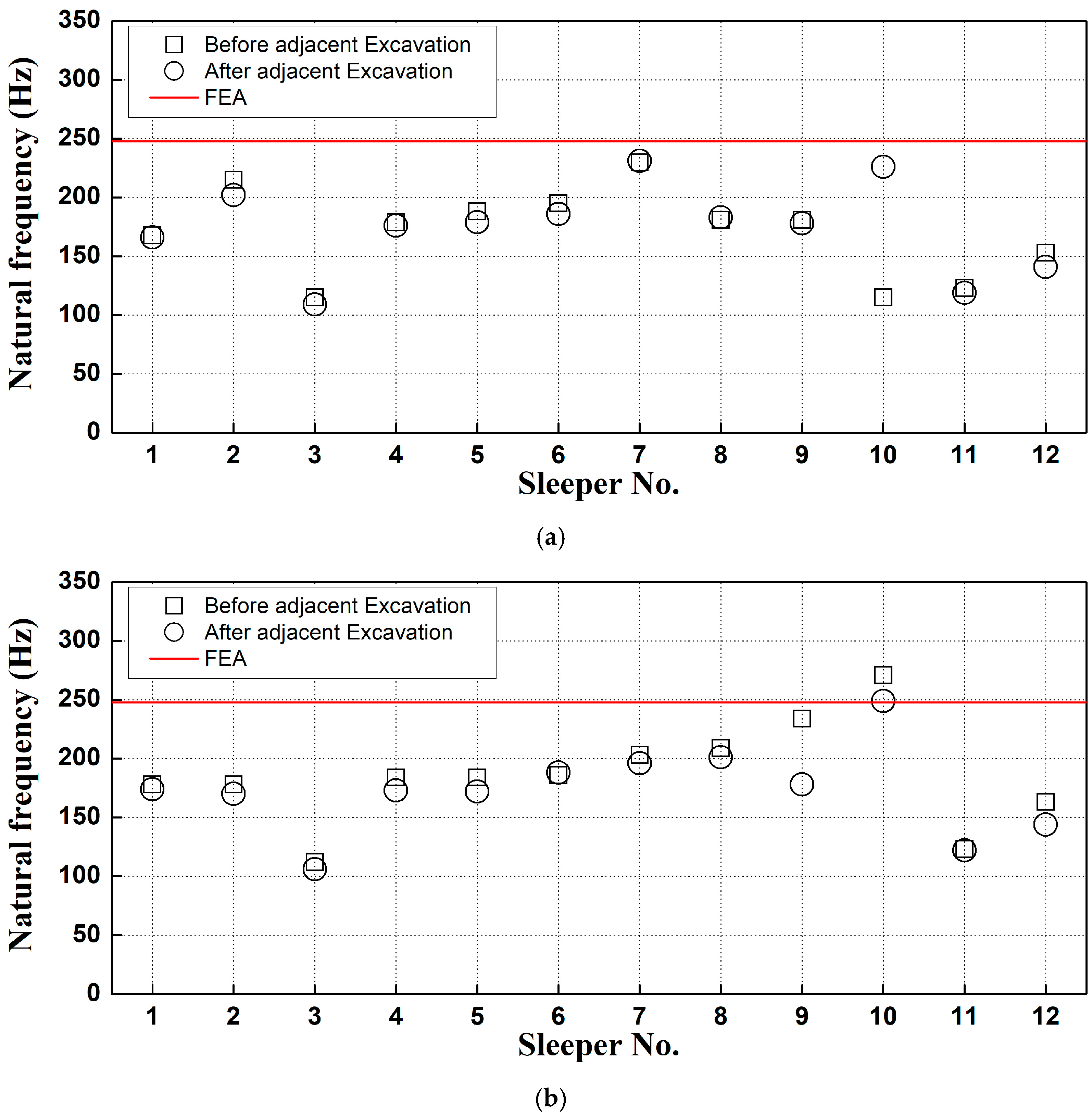
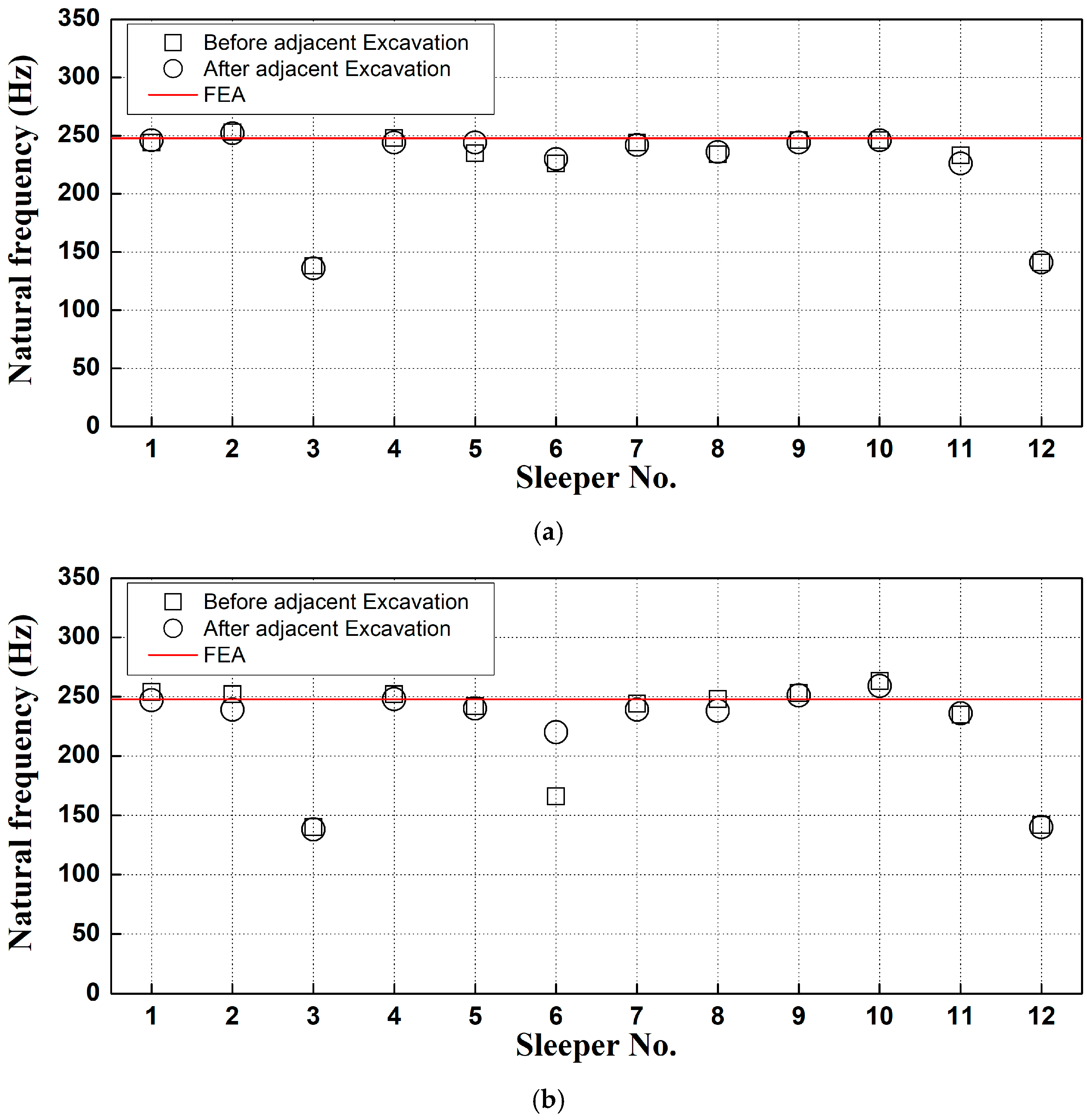
3.2.1. Natural Frequency of Sleepers in Normal Gravel Ballast Conditions
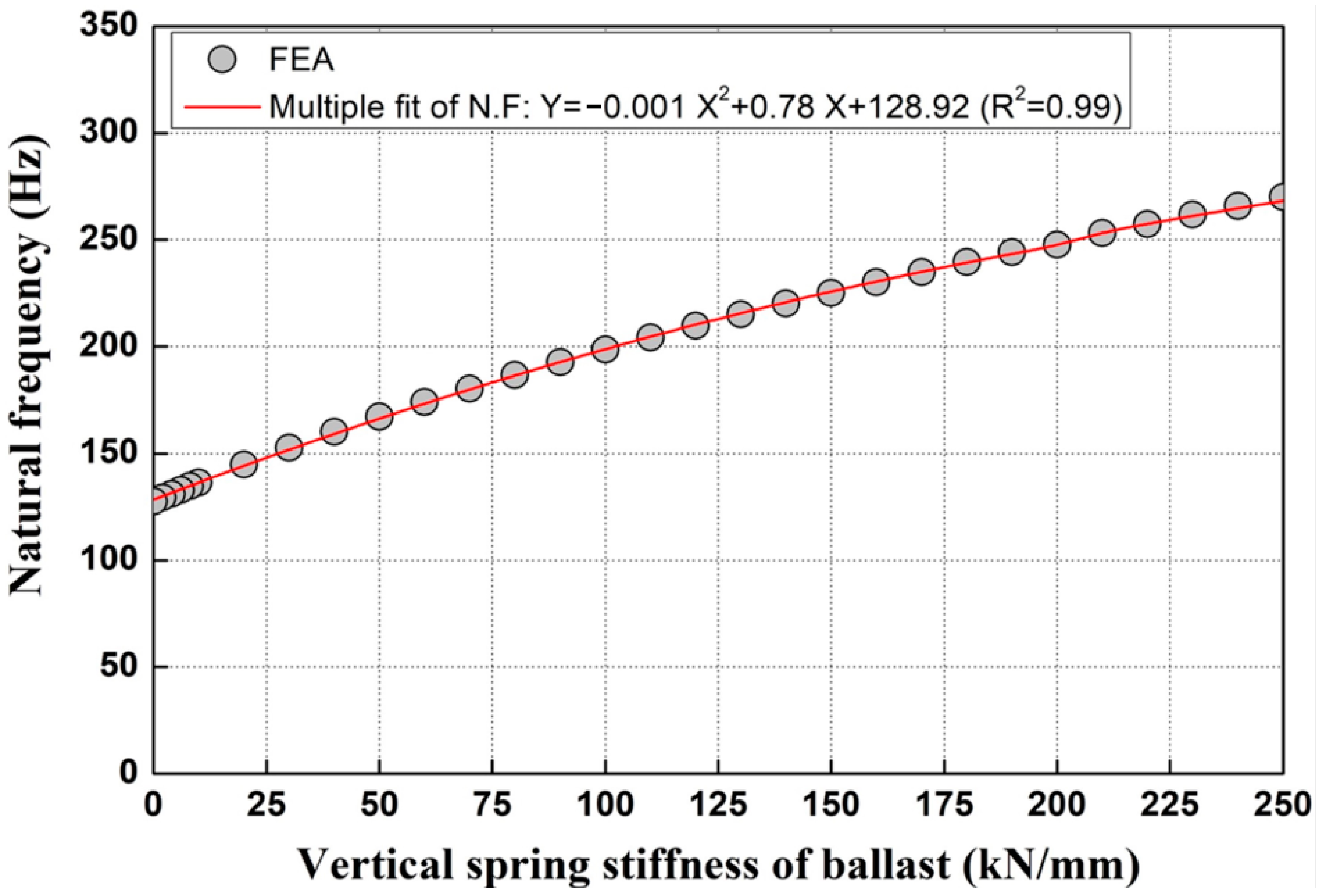
3.2.2. Natural Frequency Based on Changes in Spring Stiffness
4. Analysis and Discussion
4.1. Analysis of Natural Frequency Characteristics by Type of Sleeper Support Condition
4.2. Analysis of Changes in Natural Frequency and Damping Ratio of Graveled Track Sleepers
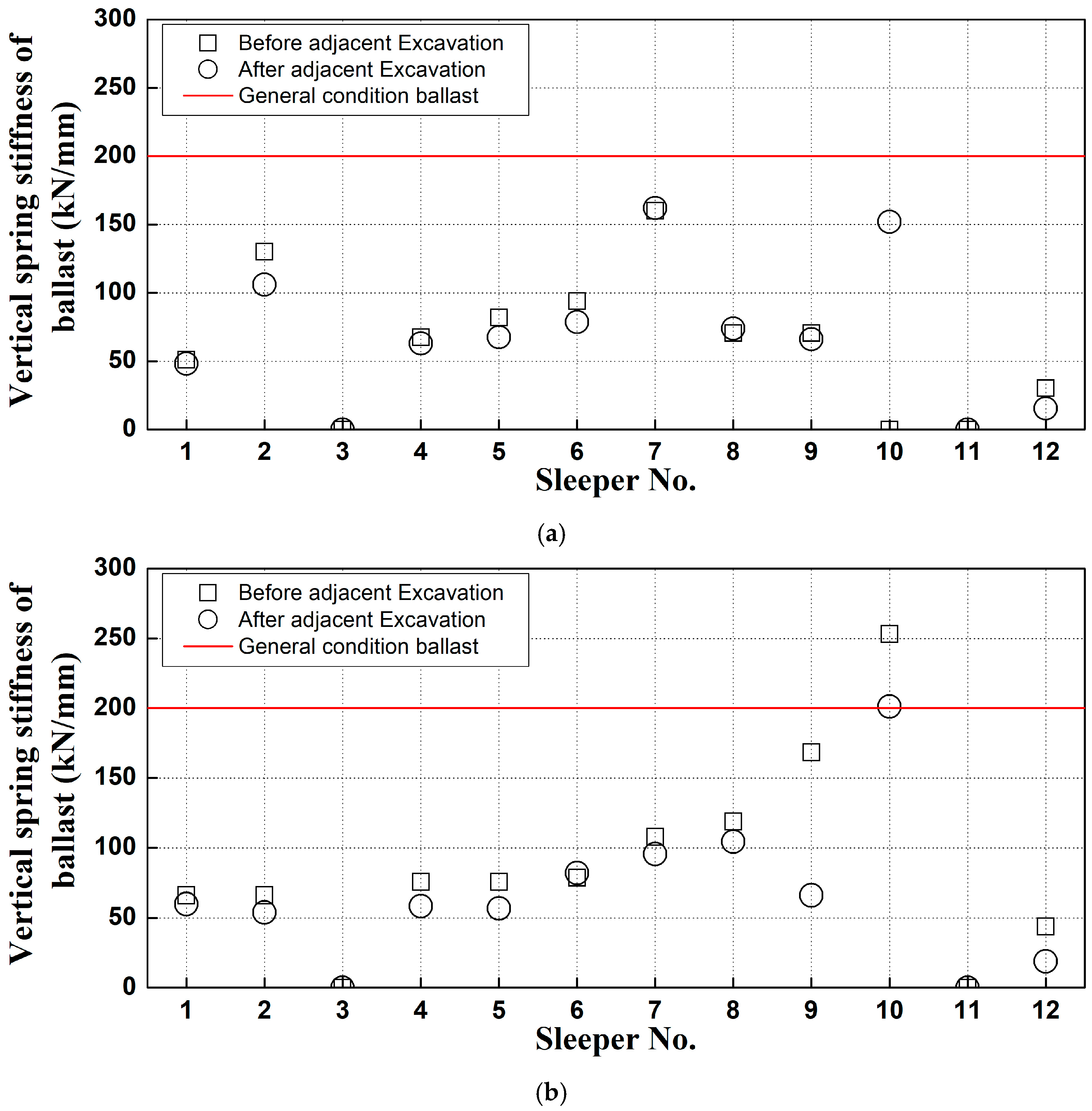
4.3. Analysis of Correlation Between Gravel Ballast Spring Stiffness and Natural Frequency
5. Conclusions
- (1)
- A field survey was conducted on gravel tracks adjacent to excavation sites, selecting sections with both good and poor conditions. Modal testing was employed to measure frequency response functions in areas where changes in sleeper support conditions were suspected within the ballast track. The first natural frequency at locations with floating sleepers was observed to be over 50 Hz lower than that of sleepers in good condition. Similarly, areas with insufficient ballast compaction also showed lower frequencies than those in normal conditions.
- (2)
- The study found that sleeper support conditions on both the left and right sides, previously assessed qualitatively through visual inspections, can be quantitatively evaluated using modal testing by analyzing frequency differences. Additionally, it experimentally confirmed that disparities in support conditions beneath the left and right sides of a sleeper—where two rails are affixed to a single sleeper, as typically seen with concrete sleepers on gravel tracks—can be effectively analyzed using this modal testing technique. Consequently, the frequency response function results from modal testing are instrumental in evaluating variations in sleeper support conditions and assessing differences in spring stiffness at rail support points.
- (3)
- This study treated the spring stiffness of the ballast as a variable and confirmed the natural frequency of the track through finite element analysis, corresponding to changes in this parameter. The finite element analysis results showed a maximum deviation of approximately 0.91% compared to the field measurement values. This close agreement validates the use of the finite element model for simulating the track behavior under varying ballast support conditions. Therefore, the spring stiffness of the ballast and finite element modeling can be used to predict damage to gravel-ballasted track sleepers.
- (4)
- A predictive formula was developed based on the correlation analysis between ballast spring stiffness and natural frequency, enabling the calculation of ballast spring stiffness at measurement sites based on observed natural frequencies. The analysis of the damping ratio shows that, in most cases, the damping ratio decreased during construction compared to before construction. Therefore, the modal testing technique developed in this study offers a robust quantitative method for assessing the condition of gravel ballast beneath the left and right sides of concrete sleepers in gravel tracks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oh, S.J.; Sung, D.Y.; Park, Y. The experimental study on the effect of loose sleeper on the integral behavior of ballasted track. J. Korean Soc. Hazard Mitig. 2017, 17, 209–216. [Google Scholar] [CrossRef]
- Choi, J.Y.; Shin, T.J.; Kim, S.H.; Chung, J.S. Experimental Study on Dynamic Characteristics of Damaged Post-Tensioning Concrete Sleepers Using Impact Hammer. Materials 2024, 17, 1581. [Google Scholar] [CrossRef] [PubMed]
- Remennikov, A.; Kaewunruen, S. Investigation of vibration characteristics of prestressed concrete sleepers in free-free and in-situ conditions. Fac. Eng. Inf. Sci. 2005, 1–11. [Google Scholar]
- Kaewunruen, S.; Remennikov, A.M. Sensitivity analysis of free vibration characteristics of an in situ railway concrete sleeper to variations of rail pad parameters. J. Sound Vib. 2006, 298, 453–461. [Google Scholar]
- Kim, J.W.; Jung, H.Y. Vibrational Characteristics of the Deteriorated Railway Plate Girder Bridge by Full-scale Experimental Modal Analysis. J. Korean Soc. Steel Constr. 2012, 24, 119–128. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A. Non-destructive evaluation for dynamic integrity of railway track structure. In Proceedings of the International Conference on Structural Integrity and Failure—SIF2006, Sydney, Australia, 27–29 September 2006; pp. 294–299. [Google Scholar]
- Ferdous, W.; Manalo, A.; Aravinthan, T.; Remennikov, A. Review of failures of railway sleepers and its consequences. In Proceedings of the 1st International Conference on Infrastructure Failures and Consequences (ICFC 2014), Melbourne, Australia, 16–20 July 2014. [Google Scholar]
- Kaewunruen, S.; Ishida, T.; Remennikov, A.M. Impact analyses for negative flexural responses (hogging) in railway prestressed concrete sleeper. J. Phys. Conf. Ser. 2016, 744, 012101. [Google Scholar] [CrossRef]
- Silva, R.; Silva, W.V.; Farias, J.Y.; Santos, M.A.A.; Neiva, L.O. Experimental and numerical analyses of the failure of prestressed concrete railway sleepers. Materials 2020, 13, 1704. [Google Scholar] [CrossRef] [PubMed]
- Tatarinov, A.; Rumjancevs, A.; Mironovs, V. Assessment of cracks in pre-stressed concrete railway sleepers by ultrasonic testing. Procedia Comput. Sci. 2019, 149, 324–330. [Google Scholar]
- Choi, J.Y.; Shin, T.H.; Chung, J.S. Damages cause analysis of concrete sleepers for sharp curved track on urban railway bridge. J. Converg. Cult. Technol. 2021, 7, 517–522. [Google Scholar]
- Shin, T.H. Integrity Assessment of Concrete Sleeper Using Modal Test Technique. Ph.D. Thesis, Dong Yang University, Yeongju-si, Republic of Korea, February 2023. [Google Scholar]
- Park, D.R. Evaluation for Ballasted Track on Serviced Railway Line. Ph.D. Thesis, Dong Yang University, Yeongju-si, Republic of Korea, August 2021. [Google Scholar]
- Chung, J.S.; Park, D.R.; Choi, J.Y. Evaluation of track irregularity effect due to adjacent excavation on serviced railway line. J. Converg. Cult. Technol. 2019, 5, 401–406. [Google Scholar]
- Sysyn, M.; Przybylowicz, M.; Nabochenko, O.; Kou, L. Identification of sleeper support conditions using mechanical model supported data-driven approach. Sensors 2021, 21, 3609. [Google Scholar] [CrossRef] [PubMed]
- Zakeri, J.A.; Esmaeili, M.; Mosayebi, S. Effect of sleeper support modulus on dynamic behaviour of railway tracks caused by moving wagon. Int. J. Heavy Veh. Syst. 2017, 24, 277–287. [Google Scholar]
- Esmaieili, M.; Zakeri, J.A.; Ebrahimi, H.; Sameni, M.K. Experimental study on dynamic properties of railway ballast mixed with tire derived aggregate by modal shaker test. Adv. Mech. Eng. 2016, 8, 5. [Google Scholar] [CrossRef]
- Liu, G.; Cong, J.; Wang, P.; Du, S.; Wang, L.; Chen, R. Study on vertical vibration and transmission characteristics of railway ballast using impact hammer test. Constr. Build. Mater. 2022, 316, 125898. [Google Scholar] [CrossRef]
- Feng, B.; Park, E.H.; Huang, H.; Li, W.; Tutumluer, E.; Hashash, Y.M.A.; Bian, X. Discrete element modeling of full-scale ballasted track dynamic responses from an innovative high-speed rail testing facility. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 107–116. [Google Scholar]
- Khan, M.R.; Dasaka, S.M. Quantification of ground-vibrations generated by high speed trains in ballasted railway tracks. Transp. Geotech. 2019, 20, 100245. [Google Scholar]
- Benedetto, A.; Tosti, F.; Ciampoli, L.B.; Calvi, A.; Brancadoro, M.G.; Alani, A.M. Railway ballast condition assessment using ground-penetrating radar-An experimental, numerical simulation and modelling development. Constr. Build. Mater. 2017, 140, 508–520. [Google Scholar] [CrossRef]
- Li, B.; Peng, Z.; Wang, S.; Guo, L. Identification of ballast fouling status and mechanized cleaning efficiency using FDTD method. Remote Sens. 2023, 15, 3437. [Google Scholar] [CrossRef]
- Wang, L.; Meguid, M.; Mitri, H.S. Impact of ballast fouling on the mechanical properties of railway ballast: Insights from discrete element analysis. Processes 2021, 9, 1331. [Google Scholar] [CrossRef]
- Lam, H.F.; Wong, M.T. A feasibility study on the use of simple vibration test in the detection of railway ballast damage. In Proceedings of the 1st International Workshop on High-Speed and Intercity Railways, Shenzhen and Hong Kong, China, 19–22 July 2011. [Google Scholar]
- Kim, S.I.; Yu, J.Y.; Mun, J.U.; Hong, S.M.; Kim, J.T. Modal tests of railway bridges considering the type of track structures. In Proceedings of the Korean Society for Railway, Daegu, Republic of Korea, 12–13 June 2008. [Google Scholar]
- Yoon, T.J. Assessment Method of Railway Ballasted Track Using Modal Test Technique. Ph.D. Thesis, Dong Yang University, Yeongju-si, Republic of Korea, February 2024. [Google Scholar]
- ANSYS. ANSYS®2007 ANSYS Workbench, version 2021 R2; ANSYS Inc.: Cannonsberg, PA, USA, 2021.
- KR C-14030; Ballasted Track Structures. Korea National Railway: Daejeon, Republic of Korea, 2021.
- KR C-14010; General Track Design. Korea National Railway: Daejeon, Republic of Korea, 2013.


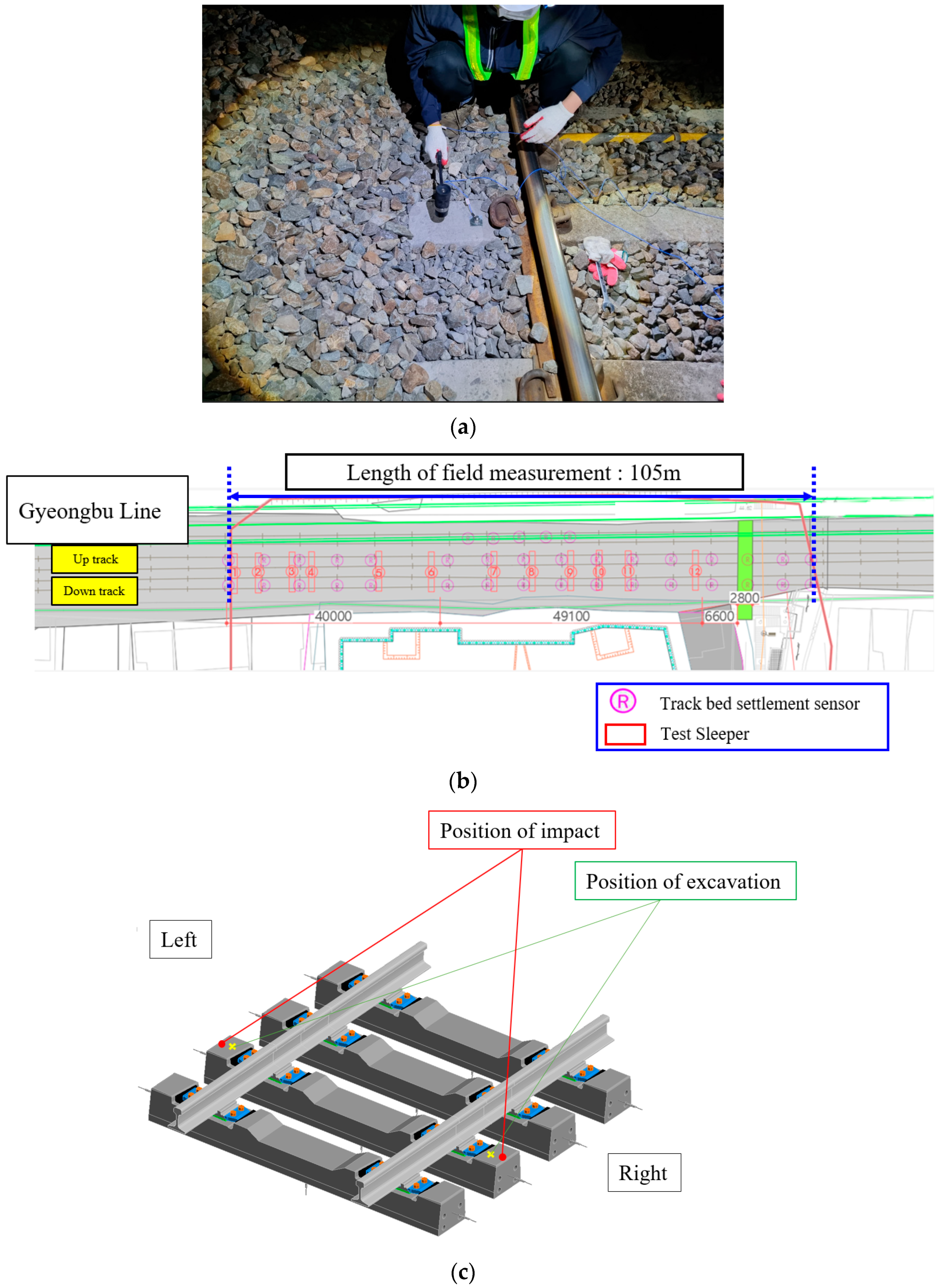


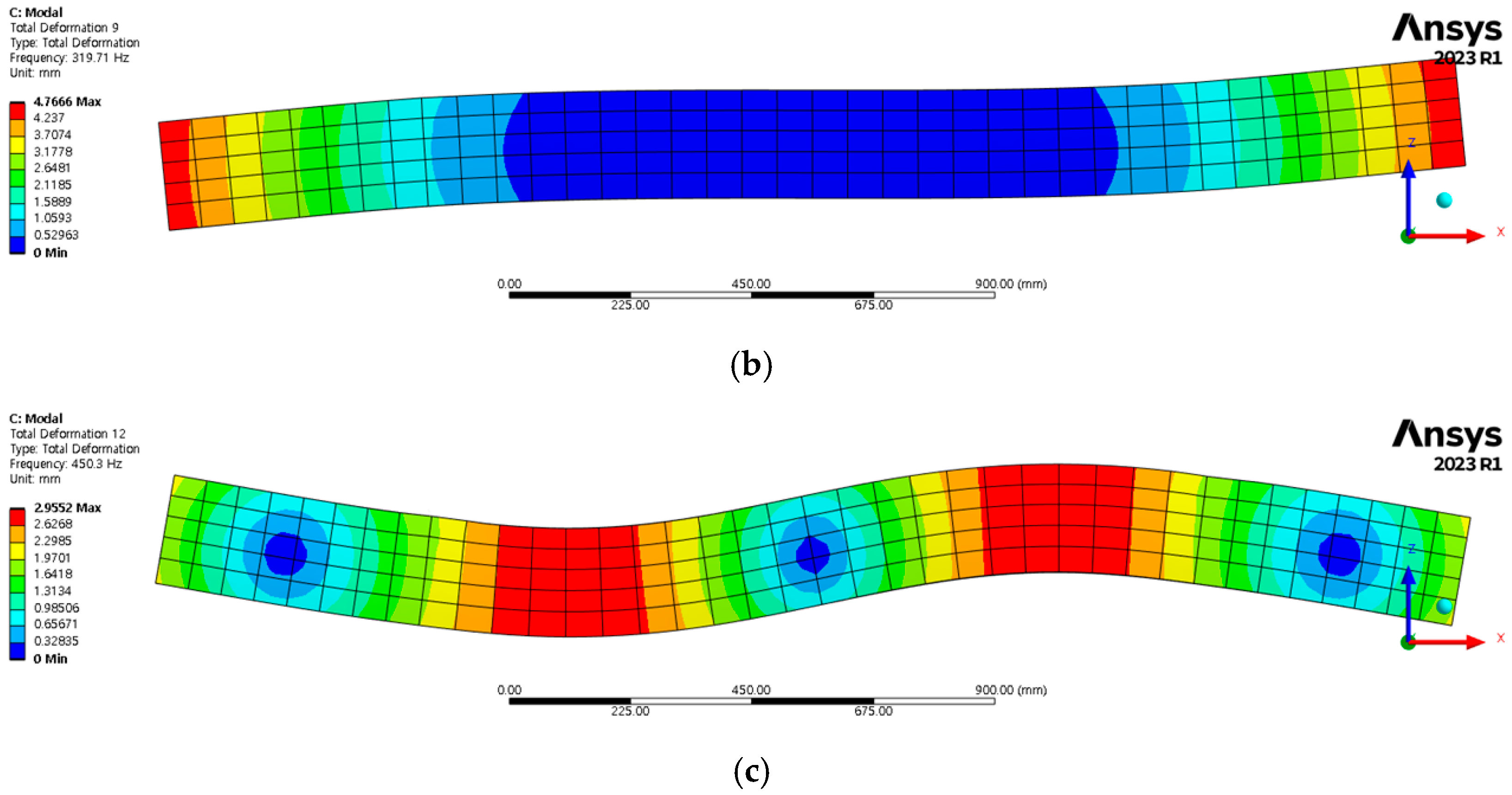
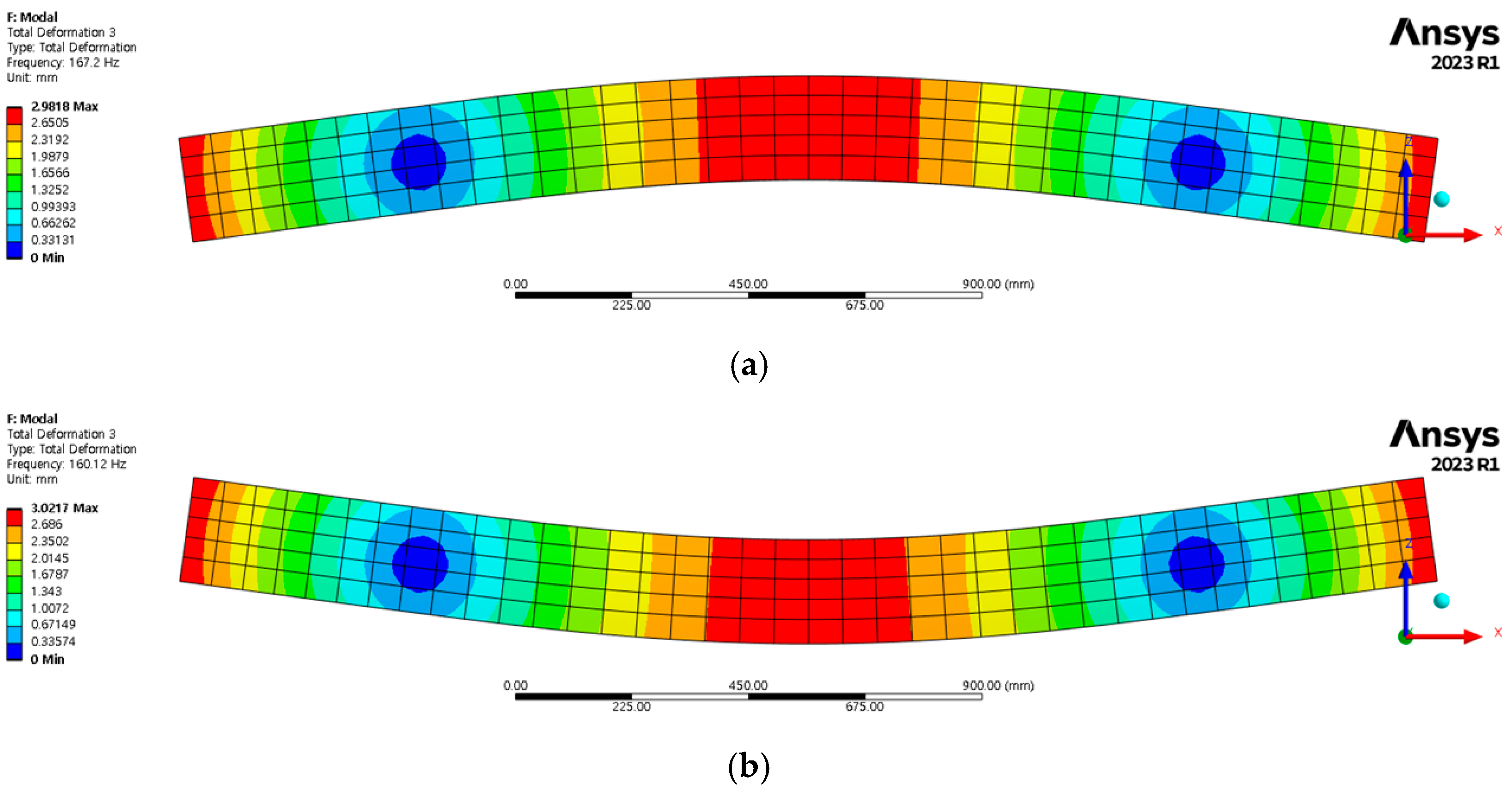
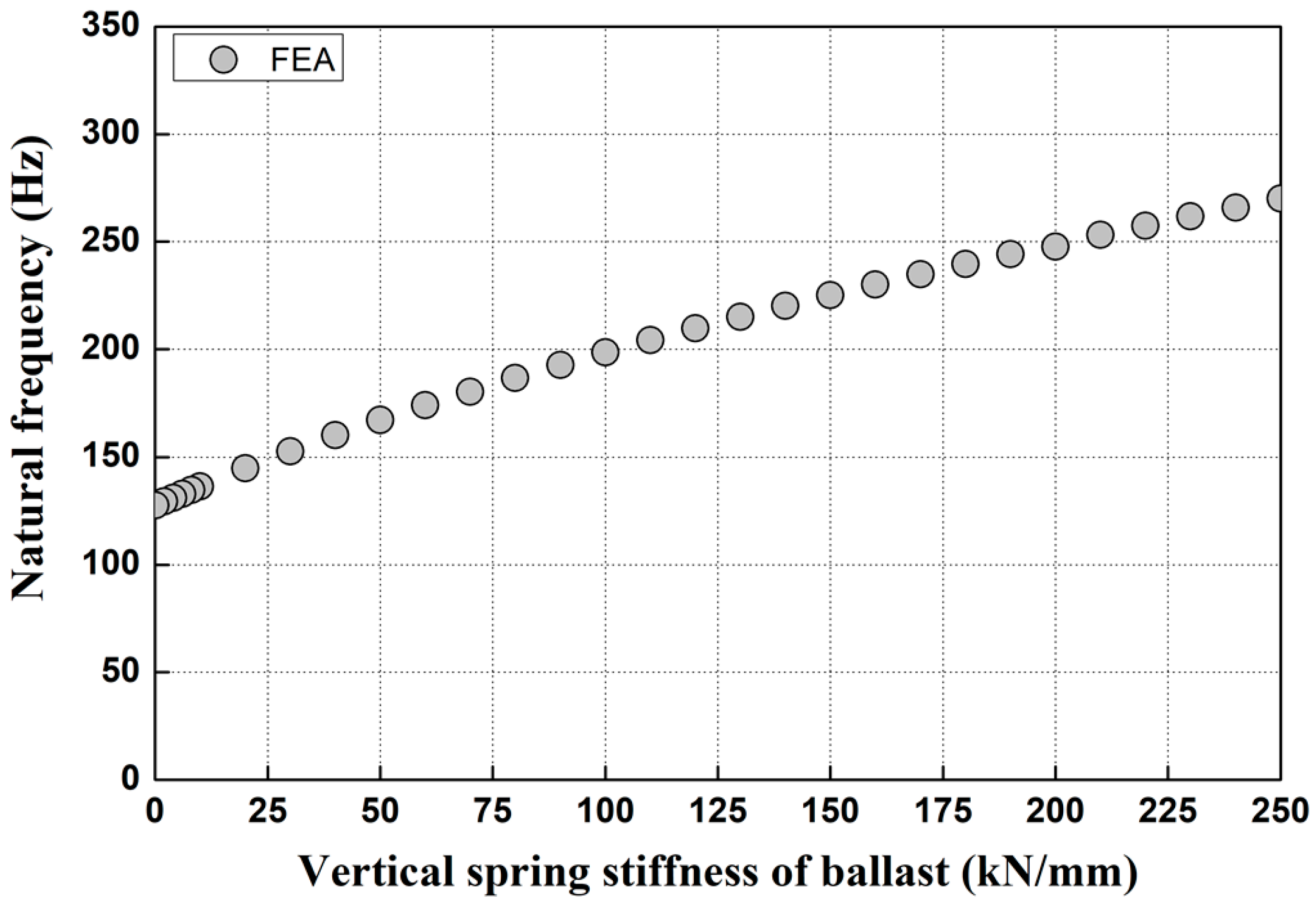

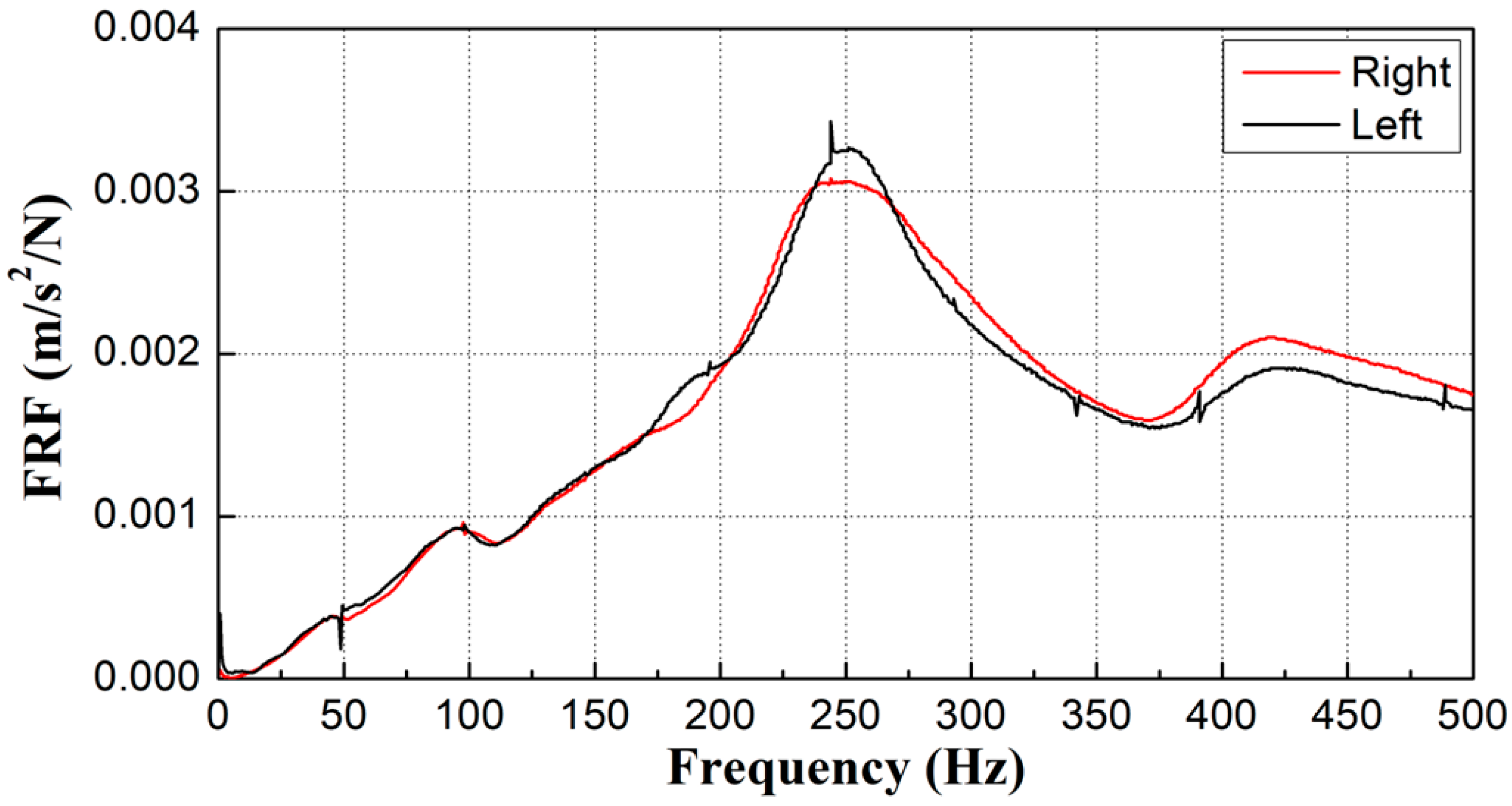


| Category | Impact Hammer (mV/N) | Accelerometer (mV/g) | |
|---|---|---|---|
| Left | Right | ||
| Sensitivity | 0.24 | 100 | 100 |
| Category | #4 | #3 | #11 | |||
|---|---|---|---|---|---|---|
| Left | Right | Left | Right | Left | Right | |
| First Natural Frequency | 183.8 | 178.8 | 111.9 | 115.0 | 123.1 | 122.5 |
| Components | Density (kg/m3) | Elastic Modulus (Mpa) | Poisson (ν) |
|---|---|---|---|
| Rail | 7850 | 200,000 | 0.3 |
| Sleeper | 2300 | 30,000 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.-Y.; Yoon, T.J.; Kim, S.-H. Qualitative Analysis of Sleeper Supporting Condition for Railway Ballasted Tracks Using Modal Test. Appl. Sci. 2025, 15, 3425. https://doi.org/10.3390/app15073425
Choi J-Y, Yoon TJ, Kim S-H. Qualitative Analysis of Sleeper Supporting Condition for Railway Ballasted Tracks Using Modal Test. Applied Sciences. 2025; 15(7):3425. https://doi.org/10.3390/app15073425
Chicago/Turabian StyleChoi, Jung-Youl, Tae Jung Yoon, and Sun-Hee Kim. 2025. "Qualitative Analysis of Sleeper Supporting Condition for Railway Ballasted Tracks Using Modal Test" Applied Sciences 15, no. 7: 3425. https://doi.org/10.3390/app15073425
APA StyleChoi, J.-Y., Yoon, T. J., & Kim, S.-H. (2025). Qualitative Analysis of Sleeper Supporting Condition for Railway Ballasted Tracks Using Modal Test. Applied Sciences, 15(7), 3425. https://doi.org/10.3390/app15073425






