Exploring the Effects of Thermal Cycling on the Precision of 3D-Printed Parts: A Comprehensive Analysis

Abstract

This study investigates the dimensional stability of FDM-printed Z-ULTRAT components subjected to repeated thermal cycling between −20 °C and 80 °C. Dimensional measurements (height and width) were collected before cycling and after 1, 5, and 10 cycles to quantify thermal-induced drift. Results show that a single thermal cycle produces negligible dimensional change (ΔH ≈ +0.01 mm; ΔW ≈ +0.007 mm), with no statistical significance (p > 0.05). However, repeated cycling leads to cumulative deformation: after 5 and 10 cycles, the average height increased by +0.29–0.30 mm (p < 0.001), while width exhibited a nonlinear contraction–reexpansion behavior with mean variations between −0.05 mm and −0.03 mm (p < 0.05). Standard deviations increased with cycle count, indicating rising variability among specimens. These findings demonstrate that Z-ULTRAT parts experience progressive dimensional drift under sub-Tg thermal cycling, primarily along the build (Z) direction, due to anisotropic thermal response and relaxation of internal stresses. The study highlights the importance of thermal environment considerations in functional and industrial applications involving FDM components. Future work will include microstructural characterization (SEM/XRD) and multi-parameter optimization to better understand and mitigate thermal-induced deformation in polymer-based additively manufactured parts.

1. Introduction

In the era of Industry 4.0, additive manufacturing, also known as 3D printing, has radically transformed the design and production processes across various industrial sectors [1]. The Fused Deposition Modeling (FDM) technology is one of the most accessible and widely used methods of additive manufacturing [2,3]. By melting a filament that is deposited layer by layer, FDM enables the creation of complex parts with a high level of customization [4]. However, the dimensional accuracy of 3D-printed parts made by FDM is often influenced by a range of factors, including printing parameters, materials used, and environmental conditions [5,6].

In modern industries, dimensional accuracy is crucial to ensure the proper functioning of parts within a larger system [7,8,9]. 3D-printed parts must fit perfectly within assemblies or meet strict performance standards. The dimensions of parts made by FDM can be affected by variations in the printing process, from printer tolerances to the thermal expansion of the material [10,11]. Additionally, exposure to fluctuating temperatures can lead to significant distortions, affecting the dimensional stability of the parts [12].

Thermal cycles (temperature variability) can induce significant changes in the dimensions of 3D parts, and this phenomenon is frequently encountered in industrial manufacturing processes, especially in environments with fluctuating temperatures [10,13]. The main objective of this study is to examine the effects of thermal cycles on parts produced by FDM, to determine how these changes influence the long-term accuracy of the parts. The analysis will be conducted under various experimental conditions to understand the behavior of materials and how manufacturing parameters influence the stability of parts exposed to repeated temperature variations. It is important to note that the present study focuses on Z-ULTRAT, an ABS-based filament suitable for functional prototypes and moderate industrial environments, rather than high-temperature engineering-grade polymers such as PEEK or PEI. The goal is to simulate realistic service conditions in which printed components are exposed to repeated temperature variations without reaching degradation thresholds typical of extreme applications.

The primary objective of this study is to analyze the impact of thermal cycles on the dimensional accuracy of 3D-printed parts, considering factors such as wall thickness, number of walls, and the infill density of the part. The study will evaluate dimensional changes in parts before and after exposure to 1, 5, and 10 thermal cycles, using precise measurements of the height and thickness of the parts. The data obtained will contribute to understanding the behavior of parts under variable temperature conditions and will provide recommendations for improving the FDM manufacturing process.

2. Related Work

Recent studies have investigated the effect of thermal cycle on 3D printed polymer parts. Espino et al. [14] conducted a study on the effects of thermal cycling on the mechanical strength of Thermoplastic Polyurethane (TPU) 3D-printed materials. They utilized tensile testing to evaluate the tensile properties of TPU specimens subjected to varying numbers of thermal cycles. Their findings revealed that the tensile properties, including modulus of elasticity and tensile stress at 200% strain, were significantly influenced by the number of thermal cycles. Notably, the samples subjected to four thermal cycles exhibited the highest modulus of elasticity and stress, while other samples (2, 8, and 16 cycles) also showed improved tensile properties compared to untreated specimens. Furthermore, Yasir et al. [15] conducted a study on the effects of heat treatment on the mechanical properties and dimensional accuracy of 3D-printed black carbon fiber HTPLA. They investigated the influence of heating temperature and holding time on mechanical strength, hardness, and crystallinity, while also analyzing shrinkage and dimensional accuracy using a vernier caliper. Scanning electron microscopy was used to examine the microstructure of heat-treated and non-heat-treated samples. Their findings revealed that heat treatment improved mechanical properties, such as strength and hardness, by enhancing material crystallinity. However, statistical analysis showed no definitive evidence that heating temperature and holding time significantly influenced the properties, although further optimization of these factors was suggested. In another study, Abdullah et al. [16] conducted a study on the effects of thermal cycling and ultraviolet (UV) radiation on 3D-printed carbon fiber/polyether ether ketone (CF/PEEK) composites, proposed as a heat shield material for spacecraft re-entry. They evaluated the mechanical properties through tensile tests and assessed recession performance and temperature behavior using an arc-heated wind tunnel. Their findings revealed that exposure to thermal cycles and UV radiation had a limited impact on the mechanical properties, recession behavior, and temperature performance. Additionally, the material demonstrated excellent recession resistance and surface expansion under extreme heating conditions, outperforming existing ablator materials while maintaining structural integrity. In addition, Guessasma et al. [17] conducted a study on the thermal cycling, microstructure, and tensile performance of PLA-PHA polymer printed using the fused deposition modeling (FDM) technique. They employed infrared imaging to quantify thermal cycling during the printing process and X-ray micro-tomography to analyze the microstructural arrangement of the material. Tensile tests were performed to assess Young’s modulus, tensile strength, and fracture toughness, while finite element analysis was used to evaluate the role of defects in tensile performance. Their findings indicated that a printing temperature of 240 °C produced a cohesive structure with low porosity, significantly enhancing tensile strength and ductility due to heat accumulation during the printing process. This study highlights the potential of PLA-PHA as a candidate for pharmacological and medical applications.

Other investigations have investigated the performance of 3D printed parts under thermal conditions. Storck et al. [18] conducted a study on the performance of inexpensive polymeric 3D-printed materials under extreme thermal conditions, focusing on applications requiring high thermal stability, such as space and microsatellites. They evaluated the mechanical properties and dimensional stability of materials printed using fused deposition modeling (FDM) and stereolithography (SLA) after exposure to temperatures of up to 85 °C and 185 °C. Their results showed significant variations in material performance, with SLA resins and co-polyester demonstrating superior dimensional stability, while acrylonitrile–butadiene–styrene (ABS) and SLA resin subjected to extended UV post-treatment exhibited the best mechanical properties. This study highlights the potential of specific inexpensive materials for high-demand applications.

Bute et al. [19] conducted a study on the thermal properties of 3D-printed products made from fourteen common polymer filaments, focusing on softening temperature, coefficient of linear thermal expansion (CLTE), irreversible thermal strain, and thermal conductivity. Using thermomechanical analysis (TMA), differential scanning calorimetry (DSC), and thermal conductivity measurements (Hot-Disk), they examined the anisotropy of these properties in unidirectional samples printed with an Ultimaker S5. Their findings showed that polyetherimide exhibited the highest heat resistance, while PLA had the lowest. Semi-crystalline polymers demonstrated higher CLTE and irreversible thermal strain than amorphous ones, with PLA Red and Co-polyester showing significant shrinkage in the print direction. The study revealed thermal conductivity anisotropy in most materials and highlighted that annealing semi-crystalline PLA samples increased their crystallinity, improving their thermal stability and mechanical properties over time. In another study, Anghel et al. [20] conducted a study on optimizing the relative clearance in cylindrical joints manufactured using Fused Deposition Modeling (FDM) 3D printing. They investigated the relationship between imposed and measured clearances, considering process parameters such as infill density, imposed clearance, and layer thickness. Using a hybrid Genetic Algorithm-Artificial Neural Network (GA-ANN) approach, trained and validated with experimental data from a Taguchi L27 design, they minimized the absolute relative clearance to 0.0385788, achieving a relative experimental validation difference of 4%. Additionally, they introduced a rational function to approximate correlations between input and output parameters, enabling the design of clearances to meet imposed requirements.

Thermal and dimensional behavior of 3D-printed polymers under varying conditions has also been analyzed using infrared thermography and 3D scanning, as reported by Zorana [19].

As summarized in

Table 1. Comparative summary of recent studies on thermal effects in 3D-printed parts.

Reference	Material/Process	Thermal Conditions	Parameters Analyzed	Key Findings
[14]	TPU, FDM	2–16 thermal cycles	Tensile strength, modulus	Mechanical properties improved after thermal cycles; peak performance at 4 cycles.
[15]	Carbon fiber HTPLA, FDM	Heat treatment at different T and dwell times	Strength, hardness, dimensional accuracy	Improved crystallinity and hardness; no significant statistical correlation with dwell time.
[16]	CF/PEEK composites	Thermal cycling + UV exposure	Tensile strength, ablation in arc-heated wind tunnel	Limited effect of cycles/UV; excellent resistance vs. ablators.
[17]	PLA-PHA, FDM	In situ heat accumulation	Microstructure, tensile strength, fracture toughness	Heat accumulation enhanced ductility, strength, reduced porosity.
[18]	SLA resins, FDM polymers	85–185 °C	Mechanical and dimensional stability	SLA and co-polyesters had best stability; ABS best mech. after UV post-treatment.
[19]	14 polymers (PLA, PETG, PEI, etc.)	TMA, DSC analysis	CLTE, shrinkage, conductivity	Semi-crystalline polymers showed higher expansion; annealed PLA improved stability.
[20]	Cylindrical joints, FDM	No thermal cycles (process optimization)	Clearance optimization	Hybrid GA–ANN minimized clearance errors, relevant to thermal effects.
This work	Z-ULTRAT, FDM (Zortrax M200 Plus)	−20 °C to +80 °C, 1–10 thermal cycles	Dimensional accuracy (height, width) before and after cycles	Thermal cycling induces cumulative dimensional drift, statistically significant after ≥5 cycles; increased variability due to anisotropic stress relaxation

, previous studies have primarily focused on mechanical properties and microstructural changes of 3D-printed polymers under thermal stress. Although dimensional accuracy in FDM parts has been studied, little work has examined how repeated thermal cycling affects dimensional stability. This study contributes by quantifying dimensional evolution over multiple cycles and interpreting the results to support improved understanding and application of FDM components exposed to temperature fluctuations [21]. Previous studies have examined the material fatigue and the deterioration of ABS components manufactured using FDM, providing important data regarding their structural behavior [22]. Furthermore, recent reviews on advancements in dimensional accuracy in FDM manufacturing emphasize the importance of understanding the factors that influence geometric deviations during fabrication and thermal exposure [23].

To complete the comparative overview, our present study has been included in Table 1, summarizing its specific contribution to the understanding of dimensional stability in FDM-printed parts under cyclic thermal loading.

3. Materials and Methods

3.1. Materials Used

The specimens used in this study were manufactured using Fused Deposition Modeling (FDM) and the Z-ULTRAT filament supplied by Zortrax. Z-ULTRAT is an ABS-based engineering thermoplastic designed for functional prototypes and components that require increased rigidity and good thermal resistance. According to the official Zortrax material data sheet, the glass transition temperature of Z-ULTRAT is Tg = 106.4 °C, a value referenced directly from the manufacturer. No melting temperature is provided by Zortrax for this material; therefore, only the verified Tg value is reported to avoid introducing unsupported thermal properties.

In the present work, all specimens were printed under strictly controlled and manufacturer-recommended processing conditions. The extruder temperature was set to 210 °C, and the heated bed temperature to 60 °C, as indicated by the Z-ULTRAT technical specifications. Using these predefined temperatures ensures consistent polymer flow, adequate interlayer adhesion, and reproducible thermal behavior throughout the production of all samples.

This controlled thermal environment, combined with standardized filament properties and fixed printing parameters, allowed the study to isolate and evaluate exclusively the influence of thermal cycling on dimensional stability, without introducing variations in material processing conditions.

3.2. 3D Printer Used

The Zortrax M200 Plus 3D printer, from Zortrax manufacturer, Olsztyn, Poland was used for the experiment. This high-precision model is equipped with an advanced temperature control system and a printing area of 200 × 200 × 200 mm. The Zortrax M200 Plus is known for its reliability and precision, with a printing resolution of up to 90 microns. The printing temperatures were set to 210 °C for the extruder and 60 °C for the heated bed, values recommended for the Z-ULTRAT material.

3.3. Experimental Procedure

3.3.1. Part Printing

The parts were designed using 3D modeling software, Z-Suite v2.26.0 and printed with the Z-ULTRAT material. Key parameters adjusted during the printing process include wall thickness, wall count, and infill density. In this study, wall thickness refers to the total width of the external perimeters (shells) forming the outer contour of the printed part, while wall count represents the number of these adjacent perimeter lines deposited by the printer. These variables are essential for controlling the dimensional stability and behavior of the parts under thermal influence, Figure 1. To ensure optimal printing performance, the Z-Suite software—the dedicated platform for Zortrax printers—was utilized to prepare, configure, and optimize the 3D printing process. The software facilitated model slicing, automatic generation of support structures, and fine-tuning of parameters such as layer thickness, infill pattern, and print orientation. Additionally, printing temperatures were set to 210 °C for the extruder and 60 °C for the heated bed, in accordance with the manufacturer’s recommendations for the Z-ULTRAT material. This combination of hardware precision and software optimization contributed to achieving high-quality prints with excellent mechanical stability and surface integrity.

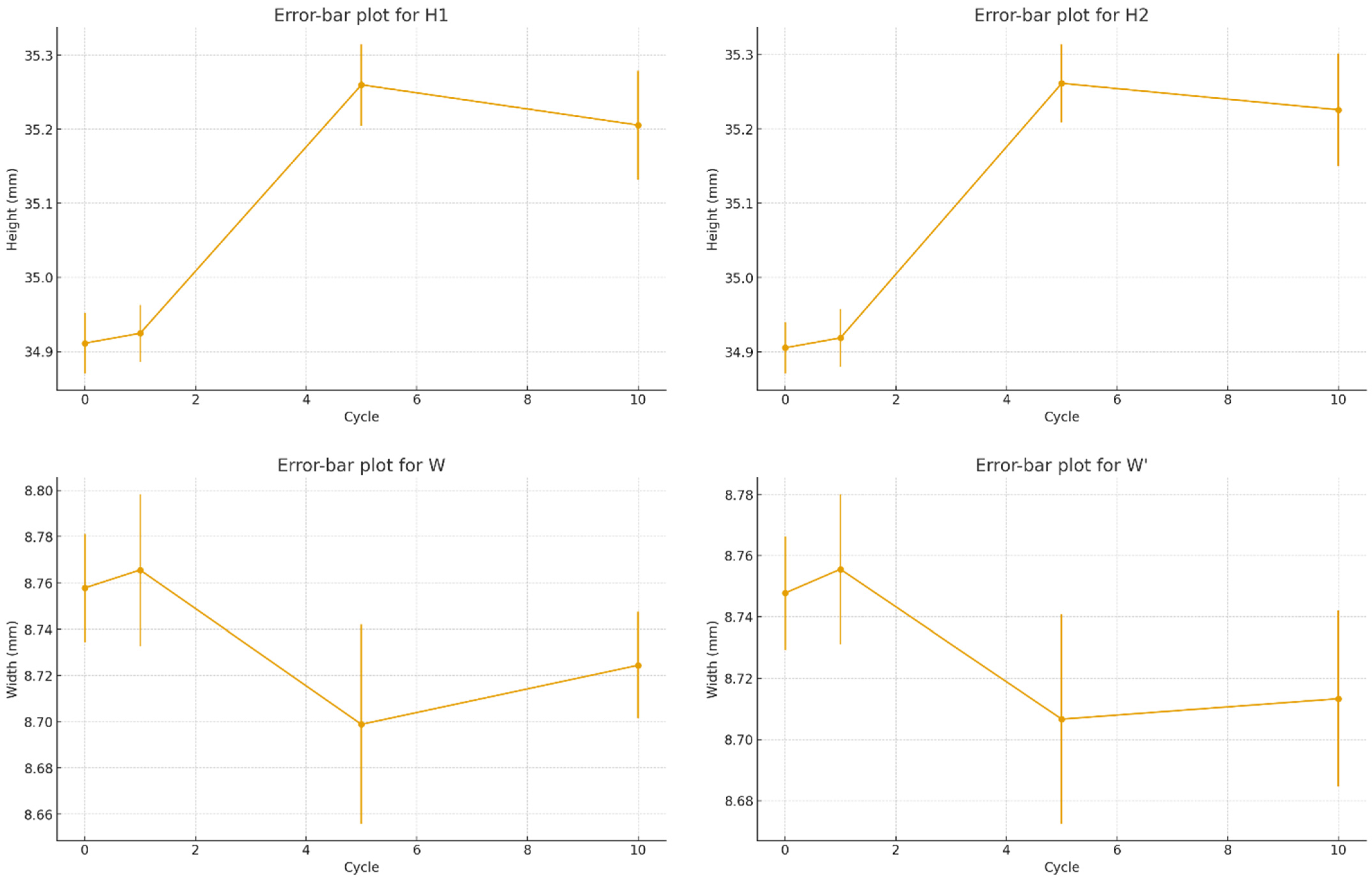
A completely randomized design (CRD) was adopted, in which nine printed specimens were subjected to thermal cycling. The choice of nine specimens was based on statistical power considerations, ensuring that one-way ANOVA could detect significant differences (p < 0.05) with a confidence level above 95%. This number also provided a balanced design, with three samples assigned to each thermal cycle condition (1, 5, and 10 cycles), following standard practices in FDM dimensional analysis studies. Dimensional measurements (H₁, H₂, W, and W′) were collected before and after 1, 5, and 10 thermal cycles. Mean and standard deviation were calculated at each condition. A one-way ANOVA was performed independently for each dimensional parameter to evaluate whether the number of cycles had a statistically significant impact on dimensional change. Significance was accepted at p < 0.05. Variability distributions were illustrated using box plots, while mean evolution and uncertainty propagation were represented using error-bar plots.

To clarify the experimental setup and ensure reproducibility,

Table 2. Experimental parameters and their levels.

Parameter Type	Parameter	Unit	Values/Levels	Description
Fixed (Printing)	Extruder temperature	°C	210	According to manufacturer’s specifications for Z-ULTRAT
	Bed temperature	°C	60	Constant for all samples
	Layer height	mm	0.14	Default precision setting (Zortrax M200 Plus)
	Printing speed	mm/s	50	Fixed to ensure repeatability
	Wall thickness	mm	0.8	Fixed wall structure for all samples
	Infill density	%	40	Constant for all prints
Variable (Experimental)	Number of thermal cycles	–	1, 5, 10	Main experimental variable
Fixed (Environmental)	Temperature range per cycle	°C	−20 → +80	Controlled chamber profile
	Cooling rate	°C/min	−1.33	Linear decrease to −20 °C
	Heating rate	°C/min	+3.34	Linear increase to +80 °C
	Dwell times	min	30/30/15	At −20 °C, +80 °C, and +20 °C, respectively

summarizes all parameters used in this study, distinguishing between those that were fixed and those that were varied. The only variable factor was the number of thermal cycles (1, 5, and 10), while all 3D printing parameters and thermal profile conditions were kept constant. This approach ensures that any dimensional deviations can be directly attributed to the cumulative effect of thermal cycling rather than to variations in the printing process or material preparation.

The parts were manufactured using FDM technology (Zortrax M200 Plus, Zortrax S.A., Olsztyn, Poland) with Z-ULTRAT material under identical printing settings. All tests were performed in a controlled laboratory environment, maintaining constant humidity and ambient temperature to minimize external influences.

A single-factor experimental design was intentionally employed to isolate the direct influence of thermal cycling on dimensional deviations. All printing parameters (extruder temperature, bed temperature, layer height, wall thickness, infill density, raster orientation) were strictly fixed across specimens. This controlled approach ensures that any dimensional changes can be confidently attributed to the thermal cycling process rather than confounding variations in manufacturing conditions.

3.3.2. Thermal Cycles

In industrial applications, components produced via additive manufacturing (AM) are increasingly exposed to fluctuating thermal environments—ranging from sub-zero storage to high-temperature operation. These repeated temperature variations can compromise the structural integrity, dimensional accuracy, and long-term performance of AM parts. Unlike traditionally manufactured components, AM structures often exhibit anisotropic mechanical behavior and residual stresses due to their layer-by-layer fabrication process. Therefore, understanding how cyclic thermal loads affect these materials is critical for ensuring their durability and reliability in real-world service conditions. The applied thermal profile follows the general principles of standardized thermal aging procedures for polymers, such as those described in ASTM D2126 [24].

To evaluate the dimensional stability and thermomechanical response of additively manufactured specimens, a controlled thermal cycling protocol was employed. This accelerated aging regimen was designed to simulate the cyclic thermal fatigue experienced in industrial environments, where repeated heating and cooling can induce progressive structural degradation. The protocol specifically targets thermal fatigue mechanisms arising from internal stresses generated by anisotropic and constrained thermal expansion and contraction—conditions intrinsic to layer-wise manufacturing processes.

Although Figure 2 illustrates the initial printed samples, the same specimens were used throughout the entire experimental procedure, and their final condition after ten thermal cycles was evaluated through dimensional measurements rather than visual comparison. The visual aspect of the samples remained almost unchanged, with only slight surface matting observed due to thermal exposure, hence additional photographic documentation was not essential for illustrating the results.

All parts were printed with a vertical build orientation, where the height (H) corresponded to the Z-axis (build direction) and the width (W) lay in the X–Y plane. The filament deposition direction alternated between +45° and −45° for successive layers, following a bidirectional raster pattern to enhance interlayer bonding and minimize warping.

The specimens were positioned centrally on the build platform in a 3 × 3 matrix layout, ensuring uniform temperature distribution and consistent material flow across all parts. This configuration reduced the influence of edge effects or local thermal gradients during printing.

Given the well-known anisotropy of FDM-printed materials, the chosen orientation and deposition strategy ensured that dimensional variations induced by thermal cycling could be directly correlated with the build direction. Consequently, the analysis of H and W directions presented in Section 4 explicitly reflects the anisotropic behavior of the printed Z-ULTRAT parts under cyclic thermal stress.

The temperature range of −20 °C to +80 °C was selected to reproduce realistic operational conditions encountered by polymer-based components in industrial and environmental applications, such as automotive, aerospace, or consumer devices. This interval ensures exposure both below and above ambient levels, generating repeated expansion–contraction phenomena without exceeding the glass transition temperature of Z-ULTRAT (≈96 °C). Thus, the applied profile induces cumulative thermo-mechanical stress representative of practical service environments while avoiding irreversible softening.

Thermal cycling was performed using a commercial environmental chamber. The system integrates PID-controlled Peltier and resistive heating modules with forced-air circulation for uniform heat transfer. The internal temperature is monitored and controlled with an accuracy of ±0.2 °C, while uniformity across the test volume remains within ±1.5 °C, as verified by three Type-K thermocouples positioned at the upper, central, and lower regions of the chamber. Relative humidity was not controlled in this experiment and remained at ambient levels (approximately 40–45%) to isolate the effect of thermal variation.

During testing, all samples were placed on a perforated aluminum support grid and remained free-standing to allow unrestricted dimensional response under cyclic heating and cooling. This configuration ensures that the observed dimensional deviations are exclusively due to thermal stresses within the material rather than external mechanical constraints.

The thermal cycles were applied using a programmable environmental chamber, following a standardized 75 min profile per cycle. This cycle, graphically represented in Figure 3, is composed of five sequential stages:

• Cooling Ramp: A linear decrease in temperature from +20 °C to −20 °C over 30 min, corresponding to a cooling rate of −1.33 °C/min.
• Dwell at Minimum Temperature: Upon reaching −20 °C, the chamber held this temperature for 30 min to ensure full thermal equilibration before reheating.
• Heating Ramp: A linear increase in temperature from −20 °C to +80 °C over 30 min, corresponding to a heating rate of +3.34 °C/min.
• Dwell at Maximum Temperature: After reaching +80 °C, the chamber held this temperature for 30 min to allow thermal stabilization throughout the samples.
• Cooling Ramp: * A linear decrease from +80 °C back to +20 °C over 30 min, corresponding to a cooling rate of −2.0 °C/min.
• Intermediate Isothermal Dwell: A 15 min isothermal hold at +20 °C allowed for thermal stabilization prior to the next thermal cycle.

This thermal profile was repeated for a predetermined number of cycles to evaluate the cumulative effects of thermal stress on the dimensional accuracy of the specimens [25]. The profile ensures thermal gradients and stress reversals that replicate harsh operational conditions.

Figure 3 illustrates the initial cycles of this protocol, highlighting the symmetric heating and cooling ramps and the intermediate dwell at 20 °C. This graphical depiction underscores the consistency and precision of the applied thermal loading, which is essential for correlating dimensional changes to thermal fatigue behavior.

3.3.3. Dimensional Measurements

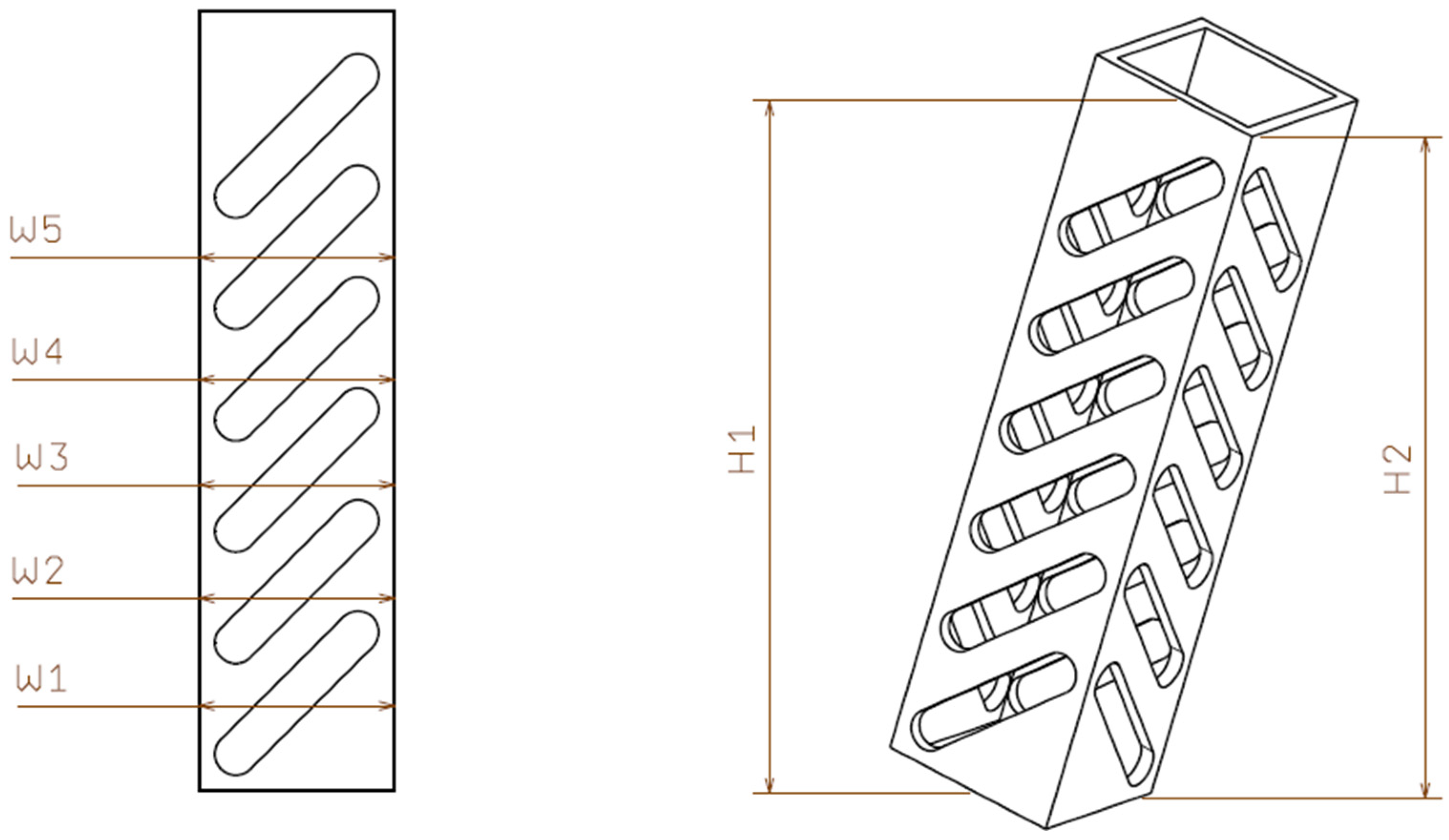
The parts’ dimensions were measured both before exposure to thermal cycles and after each set of cycles (1, 5, and 10 cycles). The CAD model of the specimen was a rectangular prism with nominal dimensions of 35.00 mm in height (H), 8.75 mm in width (W), and 20.00 mm in length (L). The points marked as W₁–W₅ and W′₁–W′₅ in Figure 4 represent measurement locations distributed at 2.0 mm intervals along two perpendicular directions. These points were used to record dimensional data at multiple sections of the part, ensuring consistent evaluation of width variation after thermal cycling. Measurements were taken using a digital caliper, providing precise data at the millimeter level. Both H₁ and H₂ represent height measurements taken along the Z-axis at two opposite sides of the specimen to detect possible non-uniformities in vertical expansion. The schematic representation in Figure 4 is intended to illustrate the measurement points and does not imply that the height was measured at an angle. The measurements were performed in two directions:

H direction (height of the part) to observe any vertical changes in the part.

W direction (widths of the part) to evaluate the thermal effects on the part’s thickness at multiple measurement points, Figure 4. In the figure as show only the W₁ to W₅. The widths W’₁ to W’₅ are measured in a perpendicularly direction.

After measurements, the data were organized in a table to evaluate dimensional changes and calculate the average differences between initial and post-cycle measurements. Statistical analyses (such as t-tests, ANOVA) were also applied to verify the significance of the observed differences and to identify the factors that most influence the dimensional accuracy of the parts.

To ensure the accuracy of the measurements, a Mitutoyo digital caliper with a precision of 0.01 mm was used. This tool was used to measure the parts’ dimensions in both the H and W directions at multiple points to obtain an average and evaluate variations. The measurements were conducted in a controlled environment to minimize the influence of external factors such as humidity or temperature fluctuations.

3.4. Statistical Analysis

Statistical processing of the dimensional measurements was performed to quantify the effect of thermal cycling on height (H₁, H₂) and width (W, W′). For each specimen, the dimensional change was computed as the difference between post-cycle and initial measurements. Mean differences were calculated as:

$$\bar{d}={\displaystyle \frac{1}{n}}\sum _{i=1}^n(x_{post,i}-x_{initial,i}),$$

where $n=9$ is the total number of specimens.

The dispersion of dimensional changes was quantified using the standard deviation:

$$s=\sqrt{{\displaystyle \frac{\sum _{i=1}^n(d_i-\bar{d}{)}^2}{n-1}}}.$$

To evaluate whether dimensional variations after thermal cycling were statistically significant, paired two-tailed t-tests were conducted for each parameter (H₁, H₂, W, W′). The test statistic was computed as:

$$t={\displaystyle \frac{\bar{d}}{s/\sqrt{n}}},$$

with degrees of freedom $df=n-1=8$. The null hypothesis (H₀) stated that thermal cycling does not alter the dimensions, while the alternative hypothesis (H₁) assumed significant dimensional change. Statistical significance was set at $p<0.05$.

To assess the cumulative influence of the number of thermal cycles, one-way ANOVA was applied independently to the height and width datasets. The analysis quantified the variance attributable to cycle count (1, 5, 10 cycles), enabling evaluation of whether dimensional drift increased systematically as a function of thermal loading.

All descriptive statistics, t-tests, and ANOVA computations were performed using standard statistical formulas to ensure reproducibility and methodological transparency.

4. Results and Analysis

4.1. Data Overview

The data collected includes dimensional measurements of height (H) and thickness (W) in two directions for each of the nine samples. The initial dimensions were measured before exposure to thermal cycles, and subsequent measurements were taken after each thermal cycle (1, 5, and 10 cycles).

Table 3. The measurements for heights (H₁, H₂).

Sample No.	Initial H1 (mm)	Initial H2 (mm)	Post-Cycle H1 (1st Cycle)	Post-Cycle H2 (1st Cycle)	Post-Cycle H1 (5th Cycle)	Post-Cycle H2 (5th Cycle)	Post-Cycle H1 (10th Cycle)	Post-Cycle H2 (10th Cycle)
1	34.97	34.96	34.98	34.97	35.23	35.24	35.26	35.30
2	34.92	34.93	34.92	34.94	35.31	35.31	35.26	35.30
3	34.90	34.89	34.91	34.91	35.26	35.26	35.17	35.18
4	34.89	34.89	34.91	34.90	35.22	35.22	35.14	35.16
5	34.86	34.86	34.88	34.87	35.19	35.20	35.12	35.14
6	34.85	34.86	34.87	34.86	35.19	35.19	35.10	35.12
7	34.91	34.92	34.92	34.91	35.29	35.28	35.23	35.24
8	34.95	34.94	34.97	34.96	35.33	35.34	35.28	35.29
9	34.95	34.90	34.96	34.95	35.32	35.31	35.29	35.30

summarizes the initial measurements and those after each cycle for the height parameters H₁ and H₂.

Table 4. Initial width values W by two directions (in all the five points).

Sample No.	W1 (mm)	W2 (mm)	W3 (mm)	W4 (mm)	W5 (mm)	W’1 (mm)	W’2 (mm)	W’3 (mm)	W’4 (mm)	W’5 (mm)
1	8.73	8.74	8.77	8.76	8.76	8.75	8.74	8.74	8.76	8.73
2	8.78	8.78	8.75	8.81	8.78	8.75	8.75	8.75	8.76	8.76
3	8.76	8.77	8.73	8.75	8.75	8.76	8.72	8.74	8.73	8.72
4	8.74	8.73	8.74	8.73	8.74	8.73	8.75	8.74	8.72	8.73
5	8.76	8.76	8.76	8.75	8.76	8.76	8.76	8.76	8.77	8.76
6	8.73	8.77	8.74	8.73	8.75	8.75	8.76	8.74	8.73	8.73
7	8.81	8.81	8.81	8.81	8.81	8.77	8.77	8.81	8.81	8.77
8	8.74	8.75	8.74	8.73	8.73	8.75	8.74	8.75	8.75	8.73
9	8.74	8.76	8.75	8.75	8.75	8.76	8.75	8.76	8.75	8.73

,

Table 5. Width values W in two directions after the first thermal cycle.

Sample No.	W1 (mm)	W2 (mm)	W3 (mm)	W4 (mm)	W5 (mm)	W’1 (mm)	W’2 (mm)	W’3 (mm)	W’4 (mm)	W’5 (mm)
1	8.74	8.77	8.76	8.76	8.75	8.75	8.74	8.75	8.76	8.75
2	8.80	8.79	8.79	8.79	8.80	8.76	8.76	8.78	8.78	8.78
3	8.76	8.77	8.76	8.76	8.77	8.75	8.75	8.74	8.72	8.71
4	8.74	8.73	8.73	8.73	8.74	8.73	8.73	8.74	8.74	8.74
5	8.76	8.76	8.75	8.77	8.79	8.79	8.77	8.77	8.77	8.76
6	8.74	8.75	8.74	8.73	8.75	8.75	8.75	8.74	8.74	8.74
7	8.86	8.86	8.87	8.81	8.81	8.82	8.79	8.84	8.84	8.77
8	8.75	8.76	8.77	8.73	8.72	8.77	8.74	8.76	8.74	8.73
9	8.75	8.75	8.77	8.75	8.74	8.73	8.74	8.74	8.75	8.76

,

Table 6. Width values W by two directions after 5 thermal cycles.

Sample No.	W1 (mm)	W2 (mm)	W3 (mm)	W4 (mm)	W5 (mm)	W’1 (mm)	W’2 (mm)	W’3 (mm)	W’4 (mm)	W’5 (mm)
1	8.68	8.67	8.61	8.64	8.56	8.66	8.68	8.66	8.67	8.62
2	8.71	8.64	8.63	8.66	8.66	8.75	8.71	8.73	8.69	8.64
3	8.68	8.7	8.69	8.65	8.62	8.74	8.68	8.7	8.66	8.59
4	8.69	8.69	8.7	8.69	8.68	8.69	8.69	8.7	8.66	8.63
5	8.73	8.78	8.73	8.7	8.69	8.72	8.71	8.74	8.73	8.72
6	8.69	8.68	8.71	8.71	8.69	8.73	8.73	8.72	8.73	8.71
7	8.78	8.79	8.77	8.77	8.76	8.76	8.76	8.8	8.76	8.72
8	8.72	8.7	8.7	8.7	8.66	8.75	8.74	8.72	8.74	8.73
9	8.74	8.74	8.74	8.73	8.73	8.78	8.73	8.73	8.7	8.65

and

Table 7. Width values W by two directions after all of them 10 thermal cycles.

Sample No.	W1 (mm)	W2 (mm)	W3 (mm)	W4 (mm)	W5 (mm)	W’1 (mm)	W’2 (mm)	W’3 (mm)	W’4 (mm)	W’5 (mm)
1	8.85	8.76	8.72	8.71	8.64	8.78	8.65	8.65	8.66	8.58
2	8.7	8.72	8.68	8.7	8.7	8.74	8.75	8.74	8.71	8.59
3	8.71	8.71	8.73	8.7	8.64	8.74	8.71	8.74	8.69	8.61
4	8.73	8.73	8.73	8.71	8.7	8.69	8.7	8.72	8.67	8.65
5	8.74	8.74	8.71	8.7	8.65	8.76	8.71	8.77	8.83	8.71
6	8.75	8.75	8.72	8.69	8.72	8.7	8.72	8.71	8.73	8.72
7	8.78	8.8	8.79	8.75	8.75	8.74	8.73	8.74	8.73	8.65
8	8.7	8.69	8.71	8.74	8.7	8.75	8.74	8.74	8.72	8.73
9	8.73	8.74	8.75	8.77	8.7	8.74	8.73	8.73	8.72	8.67

report the evolution of width measurements W₁–W₅ and W′₁–W′₅ after 1, 5, and 10 thermal cycles, while

Table 8. The averages of measurements for widths values (W, W’).

Sample No.	Initial W (mm)	Initial W’ (mm)	Post-Cycle W (1st Cycle)	Post-Cycle W’ (1st Cycle)	Post-Cycle W (5th Cycle)	Post-Cycle W’ (5th Cycle)	Post-Cycle W (10th Cycle)	Post-Cycle W’ (10th Cycle)
1	8.75	8.74	8.76	8.75	8.63	8.66	8.74	8.66
2	8.78	8.75	8.79	8.77	8.66	8.70	8.70	8.71
3	8.75	8.73	8.76	8.73	8.67	8.67	8.70	8.70
4	8.74	8.73	8.73	8.74	8.69	8.67	8.72	8.69
5	8.76	8.76	8.77	8.77	8.73	8.72	8.71	8.76
6	8.74	8.74	8.74	8.74	8.70	8.72	8.73	8.72
7	8.81	8.79	8.84	8.81	8.77	8.76	8.77	8.72
8	8.74	8.74	8.75	8.75	8.70	8.74	8.71	8.74
9	8.75	8.75	8.75	8.74	8.74	8.72	8.74	8.72

condenses these data into average width values (W and W′) per specimen and per cycle. Together, these tables provide the full dimensional dataset used for the subsequent statistical analysis.

In the following subsections, these tabulated values are further processed to compute mean differences, standard deviations, and statistical significance associated with the applied thermal cycling protocol.

4.2. Descriptive Statistics

The dimensional variations observed after 1, 5, and 10 thermal cycles reveal clear trends in both height and width measurements. For the height parameters H₁ and H₂, changes after a single cycle were negligible, with average increases of approximately +0.01–0.02 mm. After 5 and 10 cycles, however, both parameters exhibited consistent cumulative expansion, reaching mean increases of approximately +0.29–0.30 mm across specimens.

Width measurements showed a more irregular evolution. After the first cycle, minor positive deviations were recorded, followed by a contraction phase after 5 cycles, and partial recovery after 10 cycles. Table 4, Table 5, Table 6, Table 7 and Table 8 summarize the complete width dataset and illustrate this nonlinear behavior.

Overall, dimensional variability increased with cycle count. Standard deviations remained low after the first cycle but rose notably after 5 and 10 cycles, particularly for height, indicating a progressively less uniform response among specimens.

4.3. Statistical Significance

Statistical comparison between initial and post-cycle dimensions confirmed that the minimal variations after 1 thermal cycle were not statistically significant. In contrast, dimensional changes after 5 and 10 cycles were significant for all measured parameters (H₁, H₂, W, W′), demonstrating that repeated thermal cycling induces measurable and consistent drift.

The t-test results (

Table 9. Paired t-test results comparing initial and post-cycle dimensional measurements (H₁, H₂, W, W′).

Parameter	Cycle Comparison	t-Statistic	df	p-Value	Significance
H1	Initial vs. 1 cycle	1.23	8	0.252	Not significant
H1	Initial vs. 5 cycles	5.41	8	0.0007	Significant
H1	Initial vs. 10 cycles	5.72	8	0.0005	Significant
H2	Initial vs. 1 cycle	1.17	8	0.270	Not significant
H2	Initial vs. 5 cycles	5.36	8	0.0008	Significant
H2	Initial vs. 10 cycles	5.80	8	0.0004	Significant
W	Initial vs. 1 cycle	0.88	8	0.402	Not significant
W	Initial vs. 5 cycles	3.17	8	0.013	Significant
W	Initial vs. 10 cycles	3.45	8	0.008	Significant
W′	Initial vs. 1 cycle	0.91	8	0.387	Not significant
W′	Initial vs. 5 cycles	3.02	8	0.016	Significant
W′	Initial vs. 10 cycles	3.28	8	0.010	Significant

) show p-values below 0.05 for all parameters after 5 and 10 cycles, confirming that dimensional deviations cannot be attributed to random variability alone.

One-way ANOVA further indicated (

Table 10. ANOVA Summary (Height and Width).

Parameter	F-Statistic	p-Value	Significance
H1	104.35	1.32 × 10−16	Significant
H2	117.95	2.22 × 10−17	Significant
W	8.55	2.60 × 10−4	Significant
W′	7.28	7.41 × 10−4	Significant

) that the number of thermal cycles had a strong influence on height evolution and a moderate but significant effect on width measurements.

4.4. Interpretation of Results

The results clearly show that dimensional drift increases with the number of thermal cycles, with height parameters (H₁ and H₂) demonstrating the most pronounced evolution. After 5 and 10 cycles, the cumulative dimensional increase along the build direction reflects a strong sensitivity of Z-ULTRAT to repeated thermal activation.

In contrast, width measurements (W and W′) exhibited a nonlinear evolution, characterized by slight expansion after one cycle, contraction after five cycles, and partial recovery after ten cycles. This indicates that in-plane dimensions respond differently to thermal cycling compared with the build direction.

Variability across specimens also increased with cycle count, especially for height, as shown by the broader dispersion in the measurements after the 5th and 10th cycles. This suggests that thermal cycling does not affect all samples uniformly, likely due to small internal structural differences or variations in local residual stresses.

Figure 5 provides an overview of the dimensional variability through box-and-whisker plots, highlighting the widening spread of values at higher cycle counts, particularly in the height direction.

Figure 6 illustrates the evolution of mean dimensions with increasing cycle count. The plots confirm a cumulative expansion in height, while width exhibits a nonlinear contraction–reexpansion trend consistent with the tabulated data.

Overall, the dimensional response of Z-ULTRAT parts under repeated thermal cycling is both cumulative and direction-dependent, with height showing consistent expansion and width undergoing irregular but statistically significant fluctuations.

5. Discussion

5.1. Overall Interpretation of Dimensional Response

The experimental results demonstrate that repeated thermal cycling induces cumulative dimensional drift in FDM-printed Z-ULTRAT components. Although the first cycle produced negligible changes, both height and width evolved significantly after 5 and 10 cycles, confirming that sub-Tg thermal fluctuations can affect dimensional reliability even in the absence of melt-state deformation. Height exhibited the strongest sensitivity, with consistent expansion across specimens, while width followed a nonlinear path characterized by slight dilation, intermediate contraction, and eventual partial recovery. This direction-dependent behavior reflects the anisotropic nature of FDM structures, where the Z-axis is governed by interlayer bonding whereas the X–Y plane is defined by continuous polymer deposition.

These findings corroborate the broader understanding that thermal loading activates viscoelastic processes in ABS-based polymers, leading to irreversible dimensional rearrangements. However, unlike high-temperature polymers such as PEEK or PEI, which often stabilize after moderate cycling, Z-ULTRAT displays continued evolution, suggesting that cumulative effects remain significant even under sub-Tg exposure.

5.1.1. Height Variation and Build-Direction Sensitivity

Height (H₁, H₂) displayed a clear monotonic expansion with increasing cycles, which is consistent with thermally activated relaxation of internal stresses accumulated during the layer-wise deposition process. The ANOVA results confirm that cycle count is the dominant factor governing dimensional drift along the build axis.

This trend aligns with observations in amorphous thermoplastics reported by Guessasma et al. and Rankouhi et al., where layer interfaces exhibited increased susceptibility to thermal cycling due to weaker interlayer cohesion and higher local stress concentrations. The strong statistical response found in this study indicates that vertical expansion must be considered when using ABS-based materials in applications requiring tight dimensional tolerance.

5.1.2. Nonlinear Width Evolution and In-Plane Stability

Unlike height, the width parameters (W and W′) exhibited a nonlinear sequence of dilation–shrinkage–partial recovery. Such behavior is commonly associated with competing mechanisms:

• short-term reversible thermal expansion,
• intermediate stress relaxation and compaction of filament paths,
• long-term viscoelastic rearrangement leading to partial dimensional recovery.

These phenomena are consistent with findings from thermal-aging studies on PLA, HTPLA, and ABS composites reported by Yasir et al. and Bute et al., where dimensional oscillation occurred even without exceeding Tg. The weaker statistical influence on width measured here suggests that in-plane continuity and stronger filament bonding provide partial resistance to cyclic thermal effects.

5.1.3. Increasing Variability and Implications for Dimensional Reliability

A notable trend in this study is the increased dispersion of measurements after 5 and 10 cycles. This indicates that thermal cycling does not affect all specimens uniformly, even when printed under identical conditions. Differences in micro-void distribution, local cooling gradients during printing, and raster-induced heterogeneity may lead to variations in stiffness and thermal response.

For industrial applications, this variability represents a critical challenge. Even small deviations accumulated over multiple cycles can affect assembly tolerances, functional clearances, and alignment in precision systems. Thus, dimensional predictions become less reliable as cycling progresses, reinforcing the need for cycle-aware tolerance allocation and more thermally stable material choices.

5.2. Potential Mechanisms Underlying Dimensional Drift

Although this study did not include microstructural characterization, prior work suggests several mechanisms that may explain the observed drift:

• Residual stress relaxation:

• Thermo-mechanical cycling activates polymer chain mobility, gradually releasing locked-in stresses generated during extrusion.

• Viscoelastic recovery:

• Below Tg, chains can still undergo time-dependent rearrangements, contributing to dimensional expansion after repeated activation.

• Local densification and shrinkage:

• In some planes, particularly the X–Y orientation, cycling may induce tighter packing of polymer strands, explaining width contraction at intermediate cycles.

• Anisotropic constraints:

• Since the Z-axis relies on interlayer fusion, while the X–Y plane relies on continuous extrusion paths, the two directions respond differently to thermal fatigue.

Future work involving SEM, micro-CT, and crystallinity analysis is needed to confirm the relative contribution of these mechanisms.

5.3. Comparison with Previous Studies

The dimensional evolution observed in this work aligns with several thermal-aging studies on polymer AM parts. Espino et al. and Yasir et al. reported that moderate thermal cycling induces polymer relaxation and mechanical property changes, while Muna et al. observed degradation under cyclic vs. stable exposure in CFRP composites. However, few studies have quantified dimensional drift specifically under repeated sub-Tg cycling. Optimization-related studies, such as the GA–ANN approach proposed by Anghel et al. [26], highlight the importance of parameter selection in improving dimensional reliability.

Compared to these works, the present study contributes novel insights by:

• systematically testing multiple cycle counts (1, 5, 10),
• evaluating both height and width with multi-point measurements,
• demonstrating nonlinear behavior in in-plane dimensions,
• quantifying the statistical sensitivity of each axis to thermal cycling.

This expands the understanding of how ABS-based materials evolve dimensionally under cyclic thermal conditions relevant to industrial service environments.

5.4. Practical Implications for Industrial Use

The results indicate that Z-ULTRAT parts may experience non-negligible dimensional drift when exposed to repeated thermal fluctuations. Applications involving snap-fits, press-fits, precision housings, articulated joints, or alignment-critical components may be especially affected.

Recommendations include:

• selecting materials with lower coefficients of thermal expansion,
• increasing wall thickness or infill density for improved thermal robustness,
• applying post-processing treatments such as annealing,
• and designing with cycle-aware tolerances for thermally active environments.

5.5. Limitations and Future Research

This study focused exclusively on dimensional evolution and did not include microstructural, mechanical, or volumetric analyses. Future work should incorporate:

• SEM and micro-CT to examine microstructural evolution,
• DSC/TGA to evaluate thermal transitions,
• finite element thermal–mechanical simulations,
• expanded cycle counts (e.g., 20–100+ cycles),
• evaluation of geometry-dependent effects and complex shapes.

Such analyses will enable a deeper understanding of the mechanisms underlying nonlinear dimensional drift and guide improved material and process selection for thermal stability.

6. Conclusions

This study investigated the dimensional stability of FDM-printed Z-ULTRAT parts subjected to repeated thermal cycling between −20 °C and 80 °C. Quantitative measurements revealed that a single thermal cycle produced only negligible dimensional deviations (ΔH ≈ +0.01 mm; ΔW ≈ +0.007 mm), with no statistical significance. However, repeated cycling induced cumulative deformation: after 5 and 10 cycles, the average height increased by approximately +0.29–0.30 mm, while the width exhibited a nonlinear contraction–reexpansion pattern, with variations between −0.05 mm and −0.03 mm. These trends were statistically significant (p < 0.05) and more pronounced along the build direction, reflecting the inherent anisotropy of the FDM process.

The increase in standard deviation across cycles demonstrates that thermal stress does not affect all specimens uniformly, reducing dimensional predictability under fluctuating temperatures. This behavior highlights the sensitivity of ABS-based materials to sub-Tg thermal fluctuations and underscores the importance of considering thermal exposure in applications requiring high dimensional accuracy.

From an engineering perspective, these findings suggest that FDM-printed Z-ULTRAT components may experience measurable dimensional drift during service in thermally variable environments. Designers and manufacturers should therefore implement cycle-aware tolerance allocation, consider materials with improved thermal stability, and optimize printing parameters—such as wall thickness, infill density, and layer height—to mitigate thermal-induced deviations.

Overall, the results provide relevant insights for the design and deployment of additively manufactured ABS-based parts operating under cyclic thermal loads and establish a foundation for future investigations into the thermo-mechanical behavior of FDM materials.