Identifying and Predicting Changes in Behavioral Patterns for Temporal Data in Treatment of Neonatal Respiratory Failure

Abstract

In this paper, we present the findings of a study focused on discovering process models and tracking their evolution over time. The research specifically targets a distinct category of these models known as behavioral patterns. Consequently, the challenges and techniques addressed here involve temporal data. To demonstrate the issues and methodologies associated with identifying process patterns and their changes, we use illustrative data from the treatment of respiratory failure in premature infants. The main achievement of the paper is to successfully model behavioral patterns using machine learning models and predict changes in a neonate’s state. That was justified by comparing the classifier’s sensitivity for cases of deterioration, improvement, and stability. Classification quality is best when the pattern remains constant. However, in the proposed model, when the pattern deteriorates, the classification quality decreases only slightly.

1. Introduction

In this contribution, we describe the results of research aimed at developing a new data mining method for identifying process models and their changes. Specifically, a special type of such models, called behavioral patterns, is discussed. Therefore, the problems and methods considered here concern temporal data, i.e., data that takes into account the observation time of the represented objects. The presented results are based on exemplary data on the treatment of respiratory failure in premature infants, illustrating the problems and methods related to detecting process patterns and their changes.

Advances in medical science and technology over the past few decades have created new opportunities for intensive care. This makes it possible to keep premature neonates alive, including the smallest ones, those born at 20–24 weeks of gestation, and those weighing more than 500 g. Since premature infants experience several disorders in the first weeks of life, managing them is essential for avoiding severe multi-organ complications and ensuring survival. Prematurity is characterized by the incomplete maturity of various systems and organs, which contributes to the functional impairments observed after birth. Among them, breathing abnormalities occurring in the first hours of life are critical to the development of respiratory failure, the leading cause of death in those patients.

Efficient complex dynamical system monitoring very often requires the identification of so-called behavioral patterns or a specific type of such patterns called high-risk patterns or emergent patterns (see, e.g., [1] for more details). They are complex concepts concerning the dynamic properties of complex objects, which are dependent on time and space and expressed in natural language. Examples of behavioral patterns may include overtaking on a road, the behavior of a patient faced with a serious life-threatening situation, and ineffective behavior of a robot team. These types of concepts are much more difficult to approximate than complex concepts, for which approximation does not require following object changes over time. Identifying certain behavioral patterns can be crucial for recognizing or predicting the behavior of a complex dynamical system. Suppose specific risk patterns are identified in a certain situation; then the control object (a driver of a vehicle, a physician, a pilot of an aircraft, etc.) can use this information to adjust selected parameters and obtain the desirable behavior of the complex dynamical system. That can make it possible to overcome dangerous or uncomfortable situations (see, e.g., [1] for more details).

However, sometimes the identification of a behavioral pattern in relation to a monitored complex system may come too late to take action that could counteract the undesirable behavior. For example, if a patient undergoing treatment starts behaving according to a life-threatening pattern and we identify it at that point, it may already be too late to prevent the patient’s death. Therefore, it would be beneficial to predict in advance that the complex system is about to change its behavior and begin to match a different behavioral pattern. Therefore, recognizing changes in complex objects over time, also known as temporal change detection, has broad applications in many real-life areas. The goal of such a process is to detect, analyze, and sometimes predict how objects or systems evolve in time. This prediction is important, for example, in industrial systems (predictive maintenance—anticipating machine failure by analyzing sensor data; process optimization—predicting how production parameters will affect output over time), autonomous vehicles (trajectory prediction—forecasting the future positions of pedestrians, cars, or other agents), healthcare (disease progression modeling, patient monitoring—anticipating crises from continuous vital signs), climate and environmental systems (climate modeling, ecosystem change), and business and finance (customer behavior, market evolution). Diverse scientific tools were proposed in the literature to resolve these problems: time-series forecasting, Recurrent Neural Networks (RNNs), LSTMs, GRUs, transformers for time series, dynamical system modeling, and Graph Neural Networks (GNNs) (cf. [2,3]). In the case of healthcare and patient monitoring in the treatment of neonatal respiratory failure, machine learning methods have also previously been demonstrated (cf. [4,5,6,7]).

However, it is challenging to find methods in the literature for predicting changes in behavioral patterns that are manually defined by experts, possibly because this requires substantial support from domain experts. This study is dedicated to developing and exploring such methods.

The primary objective of this work is to identify and predict changes in the behavioral patterns of neonates in the treatment of respiratory failure. However, the proposed methodology may also be applied to other areas. The goal of this paper is to predict early (while the object matches the specific pattern) whether an object will later match another pattern. This method can be considered more advanced than the usually performed experiments, which are focused solely on identifying behavioral patterns. The results presented in this work are based on the concepts presented in [1]. The nodes in behavior graphs represent temporal concepts defined in time windows and requiring approximation. In this approach, the behavior graph of a complex object is interpreted as a complex classifier, enabling the identification of the behavior pattern described by this graph. That is achieved by observing the behavior of the complex object over time and verifying whether it aligns with a selected path of the behavior graph. If so, the behavior is determined to fit the behavior pattern represented by this graph, which enables the detection of specific behaviors of complex objects. It is worth adding that the structure of such a behavior graph (nodes and edges) is proposed by domain experts. In this paper, the proposed approach to defining and identifying behavior patterns differs slightly, although it also leverages the knowledge of domain experts. In particular, a behavior pattern is defined as a logical formula defined for a time window, describing the specific behavior of a complex object within that window. If the formula is true for the behavior of a given complex object, this means that the object behaves according to the pattern described by this formula.

The principal achievement of the paper is successfully modeling behavioral patterns and predicting changes in a neonate’s state. This was enabled by the use of machine learning methods, which utilized the classifier’s sensitivity for cases of deterioration, improvement, and stability. The analysis reveals that classification quality is best when the pattern remains constant. When the patient’s condition improves, the classification quality of such a change is also high. However, in the proposed model, when the pattern deteriorates, the classification quality decreases only slightly. Accurately predicting changes in these behaviors is complex due to noise, nonlinearity, and context dependency. The obtained results are excellent. They were obtained from a dataset collected at the Neonatal Pathology and Intensive Care Unit of the University Children’s Hospital in Krakow, Poland, from 2002 to 2004 using the Neonatal Information System (NIS).

However, the goal of this paper is not to build a computer-based system to support the treatment of infants. That would be practically impossible, as the data used is already quite old. Since their collection, these treatment methods have undergone significant evolution. Therefore, to develop a system supporting actual treatment, it would be necessary to collect current data. In this paper, we use the medical data solely to illustrate the method for predicting changes in behavior patterns.

The main results of this paper are as follows:

• Development of a method for defining behavior patterns and a method for identifying behavior patterns;
• Development of a method for perceiving changes in behavior patterns;
• Illustration of the proposed methods using medical data related to the treatment of respiratory failure in neonates;
• Verification of the quality of the proposed methods on medical data.

The structure of the paper is as follows: In Section 2, we provide the theoretical foundations of the work. In Section 3, we describe the methodology used in the experiments. In Section 4, we detail the characterization of the dataset, and in Section 5, we provided an overview of the proposed experimental approach. The classification procedure is described in Section 6. Finally, a discussion of the results is presented in Section 7.

2. Theoretical Foundations

An information system [8,9] is a pair of the form $\mathbf{IS}=(U,A)$, where

• U is a finite, non-empty set, called universum, and the elements of U are called objects: $U=\{u_1,u_2,\dots ,u_n\}$;
• A is a finite, non-empty set of attributes (properties, features): $A=\{a_1,a_2,\dots ,a_m\}$.

If in an information system one of the attributes indicates to which category each object belongs, then such a system is called a decision table.

A decision table is an information system of the form $\mathbf{DT}=(U,A\cup \{d\left\}\right)$, where

• $d\notin A$ is a decision attribute;
• Elements $a\in A$ are called conditional attributes, and A is called the set of conditional attributes.

If there is a need to represent the complex states of objects observed in complex dynamic systems, the standard concept of an information system needs to be extended. Therefore, a temporal information system is defined [1,10].

A temporal information system is a four-element tuple $\mathbf{TIS}=(U,A,a_{id},a_t)$, where

• $(U,A)$ is an information system;
• $a_{id}$ and $a_t$ are distinguished numerical attributes from set A.

We say that object $u\in U$ represents the current parameters of a complex object with identifier $a_{id}\left(u\right)$ at time point $a_t\left(u\right)$ in the temporal information system $\mathbf{TIS}$. It should be additionally noted that attribute $a_{id}$ is understood here as the identifier of a complex object that can be observed at multiple time points. Each such time point is represented in the system $\mathbf{TIS}$ by a single object (a row in the table). Then, for each object, the value of attribute $a_{id}$ is the same. For example, consider a complex object corresponding to a patient with a fixed identifier $p_{id}$. Information about this patient can be represented in $\mathbf{TIS}$ by a list of objects, where each object represents information about the patient at a single time point. In each of these objects, the value of attribute $a_{id}$ is the same and equal to $p_{id}$.

Moreover, we say that an object $u_1\in U$ precedes an object $u_2\in U$ in the temporal information system $\mathbf{TIS}$ if and only if

$$u_1\ne u_2\wedge a_{id}\left(u_1\right)=a_{id}\left(u_2\right)\wedge a_t\left(u_1\right)<a_t\left(u_2\right).$$

(1)

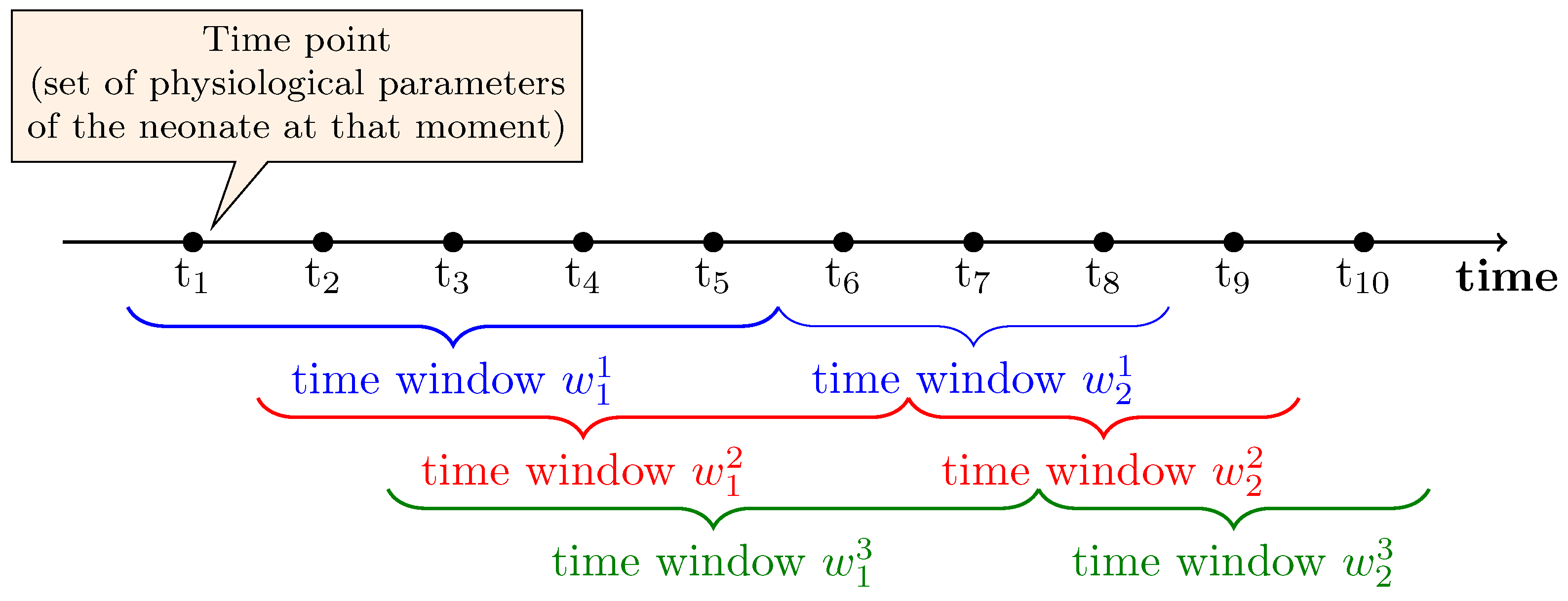
Objects from the temporal information system are grouped into time windows. For a time window w in a temporal information system $\mathbf{TIS}$ is any sequence $(u_1,\dots ,u_k)$ of objects from U, it follows that

• $k>1$;
• for any $i,j\in \{1,\dots ,k\}$, it holds that $a_{id}\left(u_i\right)=a_{id}\left(u_j\right)$;
• $a_t\left(u_i\right)<a_t\left(u_{i+1}\right)$, for $1\le i<k$.

The visualization of a time window is presented in Figure 1.

If w is a time window and u is one of the objects in that window, then we denote this fact as $u⊏w$. We denote the family of all time windows from the temporal information system $\mathbf{TIS}$ as $\mathbf{W}\left(\mathbf{TIS}\right)$.

For a given complex object (e.g., a patient undergoing treatment), a window of full size represents the entire history of changes in attribute values from the set $A\setminus \left\{a_{id}\right\}$ for that complex object (it is the entire history of a given complex object). The family of all such time windows from the temporal information system $\mathbf{TIS}$ is denoted as ${\mathbf{W}}_{tot}\left(\mathbf{TIS}\right)$ (where ${\mathbf{W}}_{tot}\left(\mathbf{TIS}\right)\subseteq \mathbf{W}\left(\mathbf{TIS}\right)$).

It is easy to see that for a given $u\in U$, there exists only one time window $w=(u_1,\dots ,u_k)\in {\mathbf{W}}_{tot}\left(\mathbf{TSI}\right)$ such that $u=u_i$ for exactly one $i\in 1,\dots ,k$. For a given $u\in U$, we denote such a time window by $w\left(u\right)$. In practice, there is a need to consider a number of decision problems that require the approximation of temporal concepts. In a temporal information system, these concepts are usually associated with time windows, and therefore the relationship of time windows with concepts must be represented in some way. As in the case of classical decision tables, we can use a special attribute here, called the decision attribute.

In principle, each time point within a given time window can have a distinct decision attribute value. However, in this paper, what is of particular interest to us is the situation in which each time point within the window has the same decision attribute value. In other words, a specific decision attribute value is associated with all time points representing information about a given time window. Therefore, the concept of a temporal information system requires yet another extension. Therefore, we define a temporal decision table.

A temporal decision table (TDT) is a seven-element tuple $\mathbf{TDT}=(U,A,a_{id},a_t,W,\tilde{A},\tilde{d})$, where

• $\mathbf{TIS}=(U,A,a_{id},a_t)$ is a temporal information system;
• $W\subseteq \mathbf{W}\left(\mathbf{TIS}\right)$ is a set of time windows selected by an expert;
• $\tilde{A}$ is a set of time window attributes (proposed by an expert or extracted using an automatic feature extraction method);
• $\tilde{d}\in \tilde{A}$ is a distinguished attribute of the time window, called the decision attribute of the time window.

The first four elements of the TDT tuple, i.e., U, A, $a_{id}$, and $a_t$, constitute the temporal information system and have been discussed earlier. The elements W, $\tilde{A}$, and $\tilde{d}$ require further explanation. W is the set of time windows prepared for the experiments. These windows were selected from the original dataset. In general, many different time windows of varying lengths and starting points can be selected from the original data. For this paper, a method for selecting time windows for experimental purposes had to be proposed. The proposed method generates time windows in such a way that, for a given patient, windows starting from any time point are created, but only windows of a fixed length are considered. Each window consists of eight time points, with the first five points forming the conditional part of the window (conditional subwindow) and the last three points forming the decision part of the window (decision subwindow). Thus, the length of each window in the set W is eight time points, with the lengths of the conditional and decision parts being five and three points, respectively. These lengths were chosen for practical reasons: with such lengths, the proposed method can be applied in a realistic manner. Extending the conditional part could reduce the classifier’s sensitivity to sudden changes at the end of the conditional part, while shortening it could reduce sensitivity due to insufficient context for the patient. Similarly, extending the decision part could lead to decision classes that are impossible to predict based on the conditional part (sudden changes at the end of the decision part could not be anticipated from the conditional observations). Shortening the decision part, on the other hand, would make pattern prediction less interesting, as it would concern only the very near future. These observations were confirmed by auxiliary experiments. $\tilde{A}$ is the set of temporal attributes calculated for the time windows in W. These attributes are necessary to approximate the decision attribute $\tilde{d}$. The values of the decision attribute $\tilde{d}$ are calculated based on the definition of behavior patterns (see the next subsection). By computing the decision attribute in this way, it is possible to construct a classifier that can predict the membership of a time window, represented by its conditional part, to the appropriate behavior pattern defined on the decision part of the window from the set W.

For a given temporal decision table $\mathbf{TDT}$, we also define an additional attribute d for objects from U (time points), called the decision attribute. It is computed for any $u\in U$ as follows: $d\left(u\right)=\tilde{d}\left(w\left(u\right)\right)$. It is easy to see that the value of the decision attribute d is always the same for all time points belonging to a given time window.

If $\mathbf{TDT}=(U,A,a_{id},a_t,W,\tilde{A},\tilde{d})$ is a temporal decision table (where $\mathbf{TIS}=(U,A,a_{id},a_t)$ is a temporal information system) and $W={\mathbf{W}}_{tot}\left(\mathbf{TIS}\right)$, then we call the temporal decision table $\mathbf{TDT}$ a temporal decision table with full time windows, and to simplify the description, we denote such a table as ${\mathbf{TDT}}_t$ instead of ${\mathbf{TDT}}_t=(U,A,a_{id},a_t,{\mathbf{W}}_{tot}\left(\mathbf{TIS}\right),\tilde{A},\tilde{d})$.

3. Methodology

3.1. Behavior Patterns Based on Domain Knowledge

In this paper, we concentrate on the problem of recognizing changes in a neonate’s behavioral patterns related to the treatment of respiratory failure. We will refer to it as the MED problem. In this paper, we understand a behavioral pattern as a description of the behavior of a complex object (e.g., a patient undergoing treatment) that characterizes a state of that object that cannot be immediately identified (i.e., at a single point in time) but requires observation of the object’s behavior over a period of time, i.e., observation of the object in a time window containing a sequence of time points. This refers to a situation where, in the available data, we have a recorded sequence of time points for each complex object, and at each time point, we have a description of the object represented by a fixed number of attributes, which we will call sensory attributes, as they are typically collected using specific sensors.

In the remainder of this paper, for the requirements of the experiments, we assume that there exists a complex object $id$ and a sequence of time points from the time window $w=(t_1,\dots ,t_n)$ describing the situation of an object $id$.

Furthermore, at each time point, we have available m sensory attributes $s_{a1},\dots ,s_{am}$ describing the state of object $id$ at individual time points. In addition to sensory attributes, additional attributes based on domain knowledge can be defined at time points to describe the behavior of the complex object at that time point. We will refer to these as expert attributes. In our case, let us say there are k attributes $e_{a1},\dots ,e_{ak}$. These additional attributes often require approximation based on sensory attributes, or their values are calculated using analytical formulas based on sensory attributes.

We often define a behavior pattern based on observing changes in expert attributes, but we must do this based on sequences of expert attribute values from individual time points. For example, suppose we are interested in an expert attribute $e\in \{e_{a1},\dots ,e_{ak}\}$, which we want to use to describe behavior patterns. In time window w, there is a sequence of attribute values e, which we denote by $v{e}_1,\dots ,v{e}_n$. Theoretically, we could label each such sequence as a behavior pattern characteristic of a specific complex object, but the data can contain many sequences that may correspond to different complex objects, or even different time windows for the same object. Therefore, to define temporal patterns that describe interesting behaviors of multiple objects (e.g., high-risk patterns, negative behavior patterns), we may consider grouping sequences of time points into clusters so that individual clusters have an interesting interpretation related to domain knowledge.

The problem of clustering sequences of time points has long been intensively studied in data mining. Existing methods often use sequence features computed as specific aggregations of sensory or expert characteristics from individual time points. For example, if time points have a numerical attribute a, then the aggregate features for this parameter could be, for example, the minimum value of a, the average value of a, the maximum value of a, etc. These aggregated features can then be used to cluster sequences of time points. Time points are typically clustered into fixed-length sequences, which are often called time windows. Therefore, clustering sequences is essentially clustering time windows. After clustering windows, each cluster can be labeled, associating with this cluster a specific behavior of the complex object.

In our example, if we have a time window with a sequence of values $e_1,\dots ,e_n$ of attribute e and we use the four aggregation functions $avg$ (average), $min$ (minimum), $max$ (maximum), and $stddev$ (standard deviation), then the attribute values of this window will be denoted as $avg(e1,\dots ,en)$, $min(e1,\dots ,en)$, $max(e1,\dots ,en)$, and $stddev(e1,\dots ,en)$, respectively. In this way, the calculated values of new attributes can be grouped, obtaining clusters of time windows.

Unfortunately, in practice, for specific datasets, fully automatic clustering of behavioral patterns encounters significant challenges. One such problem is that the data may not be sufficiently representative. As a result, automatically determined patterns may differ significantly from one data sample to another. This problem is particularly acute when discovering behavioral patterns related to phenomena that occur rarely (e.g., severe patient conditions). If the data contains few sequences describing such situations, it is difficult to predict the construction of clustering methods that would allow for the construction of classifiers that effectively classify test cases into such groups. Fortunately, domain experts (e.g., doctors) possess knowledge that can aid in the discovery of behavioral patterns. This means that instead of automatically clustering time windows, one can construct special formulas based on domain knowledge that allow for determining the behavioral pattern.

For example, in the MED problem, we have a sensory attribute $a_w$ that describes the patient’s current ventilation method, characterizing the patient’s current state during respiratory failure treatment. This attribute takes values in the range $[0,1]$, where 0 represents the most invasive form of mechanical ventilation used in the most severe cases of respiratory failure, and 1 represents the patient’s spontaneous breathing (without the need for respiratory support).

We therefore have values for this attribute for all time points in the window $a_{w1},\dots ,a_{wn}$. Let us also assume that we have calculated the values of the aggregated attributes: $avg(a_{w1},\dots ,a_{wn})$, $min(a_{w1},\dots ,a_{wn})$, and $max(a_{w1},\dots ,a_{wn})$.

As a result of an interview with an expert, it was determined that the following three patient behavior patterns should be monitored during respiratory failure treatment.

• Behavior pattern 0: This pattern is characterized by the formula

  $$avg(a_{w1},\dots ,a_{wn})<0.3\wedge max(a_{w1},\dots ,a_{wn})<0.4\wedge min(a_{w1},\dots ,a_{wn})\ge 0.0$$

  (2)
  —belonging to this pattern means that the patient’s condition is serious; their life may be in danger.
• Behavior pattern 2: This pattern is characterized by the formula

  $$avg(a_{w1},\dots ,a_{wn})>0.9\wedge max(a_{w1},\dots ,a_{wn})\le 1.0\wedge min(a_{w1},\dots ,a_{wn})>0.8$$

  (3)
  —belonging to this pattern means the patient is in a good condition, which promises successful completion of treatment for respiratory failure.
• Behavior pattern 1: This is an intermediate pattern between patterns 0 and 2, characterized by the formula

  $$avg(a_{w1},\dots ,a_{wn})\ge 0.3\wedge avg(a_{w1},\dots ,a_{wn})\le 0.9\wedge$$

  (4)

  $$max(a_{w1},\dots ,a_{wn})<1.0\wedge min(a_{w1},\dots ,a_{wn})\ge 0.0$$
  —belonging to this pattern indicates that the patient is in an average condition, requiring further treatment, especially in the event of complications, such as a bacterial, viral, or fungal infection.

The behavior patterns defined above were proposed based on domain knowledge. The physicians participating in the described studies indicated that, from a domain knowledge perspective, the most important parameter describing a patient’s condition in the context of respiratory failure is the parameter $a_w$ described earlier. Furthermore, the physicians proposed several thresholds for this parameter, which divide the patient’s states into better or worse conditions. These thresholds have the following values: 0.0, 0.3, 0.4, 0.8, 0.9, and 1.0. After defining the thresholds, the experts formulated three logical expressions describing three significantly different patient states. These formulas were then used to define three patient behavior patterns.

Once the above patterns are defined, it is easy to check whether a patient belongs to a particular pattern in a given time window. Certainly, in subsequent time windows, the patient may change their behavior pattern. For example, they may move from pattern 1 to pattern 0, indicating a significant deterioration in the patient’s condition.

Although this is not necessary, for practical applications related to this work, we define behavior patterns such that each time window matches exactly one behavior pattern (the sets of objects matching individual patterns are disjoint, non-empty, and together constitute the entire set).

3.2. Method for Predicting Changes in Behavior Patterns

In this paper, we present results related to the development of new methods for predicting the transition of a complex object from one behavioral pattern to another. This involves a situation where a complex object first matches one pattern and, after some time, another behavioral pattern. The goal is to predict early (while the object matches the first pattern) whether the object will later match the second pattern. This method can be considered more advanced than methods that are focused solely on identifying behavioral patterns [1]. For example, in the MED problem, a patient may transition from pattern 1 to pattern 0, indicating a significant deterioration in the patient’s condition. From a technical perspective, we consider a dataset consisting of a sequence of pairs of time windows $(w_1,w_2)$. Pairs of time windows may originate from different composite objects, but in a given pair $(w_1,w_2)$ both windows $(w_1$ and $w_2)$ originate from the same composite object, and window $w_1$ describes the situation of the object immediately before the situation in window $w_2$. Using the method described in detail in [1], we can determine for each pair of windows $(w_1,w_2)$ the behavior pattern to which window $w_2$ belongs, denoted by $W\left(w_2\right)$. This yields a dataset that is a sequence of pairs $(w_1,W\left(w_2\right))$. A visualization of a dataset created in the above described manner is given in Figure 2.

For this dataset, we construct classifiers that learn to make decisions for window $w_2$ regarding its behavior pattern membership based on the data in window $w_1$.

4. Dataset

Respiratory failure, which dominates the clinical picture of a premature infant, is not the only factor determining their recovery. Effective care for this type of patient requires consideration of all coexisting disorders, such as congenital and acquired infections, fluid and electrolyte imbalances, acid–base, circulatory, and renal disorders, etc. All of these factors are interconnected and interact with one another. Therefore, caring for premature infants in the first days of life requires continuous analysis of numerous vital signs and additional test results. These can be divided into stationary data (e.g., gestational age, birth weight, Apgar score) and continuous data (variables that change over time). Continuous variables can be examined ad hoc (e.g., arterial blood gas values) or monitored continuously, for example, using monitoring devices (hemoglobin oxygen saturation—SAT, heart rate, blood pressure, body temperature, and mechanical parameters of artificial ventilation). When caring for premature neonates, doctors also evaluate the results of imaging tests (e.g., brain ultrasound, echocardiography, chest X-ray). In addition to parameters that define the patient’s condition, comprehensive analysis also considers the treatment methods used. These can be qualitative (e.g., drug administration) or quantitative (e.g., ventilator settings). Daily analysis of parameters requires extensive theoretical knowledge and practical experience of physicians. Additionally, this analysis must be quick and precise. Assessments are often made in a rushed and stressful environment. A critical element of this analysis is the accurate assessment of the young patient’s risk of death due to respiratory failure in the coming hours and days. Therefore, the correct conclusions regarding life-threatening situations are based not only on current clinical condition, laboratory tests, and imaging studies of the neonate, but also on the recently observed dynamics and nature of changes in health status (e.g., deterioration in blood gas indicators of respiratory failure). Given the difficulties associated with analyzing all the necessary information at a given moment, IT methods can prove to be extremely helpful.

The analyzed dataset was collected at the Neonatal Pathology and Intensive Care Unit of the University Children’s Hospital in Krakow, Poland, from 2002 to 2004 using the Neonatal Information System (NIS) computer system. The dataset provides detailed information on the treatment of 340 neonates (row data). Detailed information was collected for each infant, including the mother’s pregnancy history, birth weight and age, laboratory and imaging test results, detailed diagnoses made during follow-up, medical procedures performed, and medications administered. The study group consisted of premature neonates with a birth weight of ≤1500 g, admitted to the hospital within 2 days of life. Additionally, for the purposes of the performed experiments, data from neonates were selected, removing those diagnosed with respiratory failure without a diagnosis of neonatal respiratory distress syndrome (RDS), patent ductus arteriosus (PDA), sepsis, or ureaplasma. In the original dataset obtained from NIS, complete information on cases of RDS, PDA, sepsis, and ureaplasma was represented. Therefore, it was possible to exclude patients who did not have these conditions. This approach was justified by the fact that the excluded cases were much less relevant to physicians from the perspective of developing computer-based methods to support treatment. The data of neonates who died in the hospital but did not have breathing problems (they died from another cause) were also removed.

A train and test split methodology was applied to perform the experiments. With a sufficiently large size, a dataset consisting of a sequence of pairs $(w_1,W\left(w_2\right))$ can be randomly divided into two parts to implement the train and test methods. However, when dividing the data into training and testing samples, it is necessary to ensure that the training part contains windows from different complex objects than the test sample. If this is not the case, the classifier may be trained and tested on data from the same complex object, which is inappropriate since it may lead to data leakage.

In the performed experiments, each patient’s data is used to generate pairs of windows: a conditional window $w_1$ (five time points were used) and a decision window $w_2$ (three time points were used). Visualization of the process of time window generation is presented in Figure 3.

As a result the data of neonates with less than eight observations (time points) were removed, which means that the neonate stayed in the hospital for too short a time to be examined using time-based methods (e.g., a neonate was transferred to another hospital or died almost immediately). Finally, for the purpose of the experiments performed in this paper, 173 neonates were chosen. The IDs were extracted (without repeats), and then the IDs were randomly divided in a 50% to 50% ratio. Therefore, there were 87 training patients and 86 test patients. These data served as the basis for determining window pairs for generating training and test data for the experiments.

The total number of pairs $(w_1,W\left(w_2\right))$ is 7186 (this refers to the total number of training and testing time windows). The decision window allowed for generating one of three decision values: 0 (bad state), 1 (medium state), or 2 (good state).

For the training portion, the class sizes were 0: 122 pairs $(w_1,W\left(w_2\right))$; 1: 1419 pairs $(w_1,W\left(w_2\right))$; 1: 2126 pairs $(w_1,W\left(w_2\right))$; and total: 3667 pairs $(w_1,W\left(w_2\right))$.

For the test portion, the class sizes were 0: 247 pairs $(w_1,W\left(w_2\right))$; 1: 1156 pairs $(w_1,W\left(w_2\right))$; 2: 2116 pairs $(w_1,W\left(w_2\right))$; and total: 3519 pairs $(w_1,W\left(w_2\right))$.

A short summary of the dataset details is provided as follows:

• Total data size: 7186 objects (this is the number of pairs $(w_1,W\left(w_2\right))$).
• Class 0: 360 objects (bad).
• Class 1: 2575 objects (medium).
• Class 2: 4242 objects (good).

This data is therefore unbalanced. This fact will influence the selection of the classification quality metric, which will be described in Section 6.

5. Proposed Approach Overview

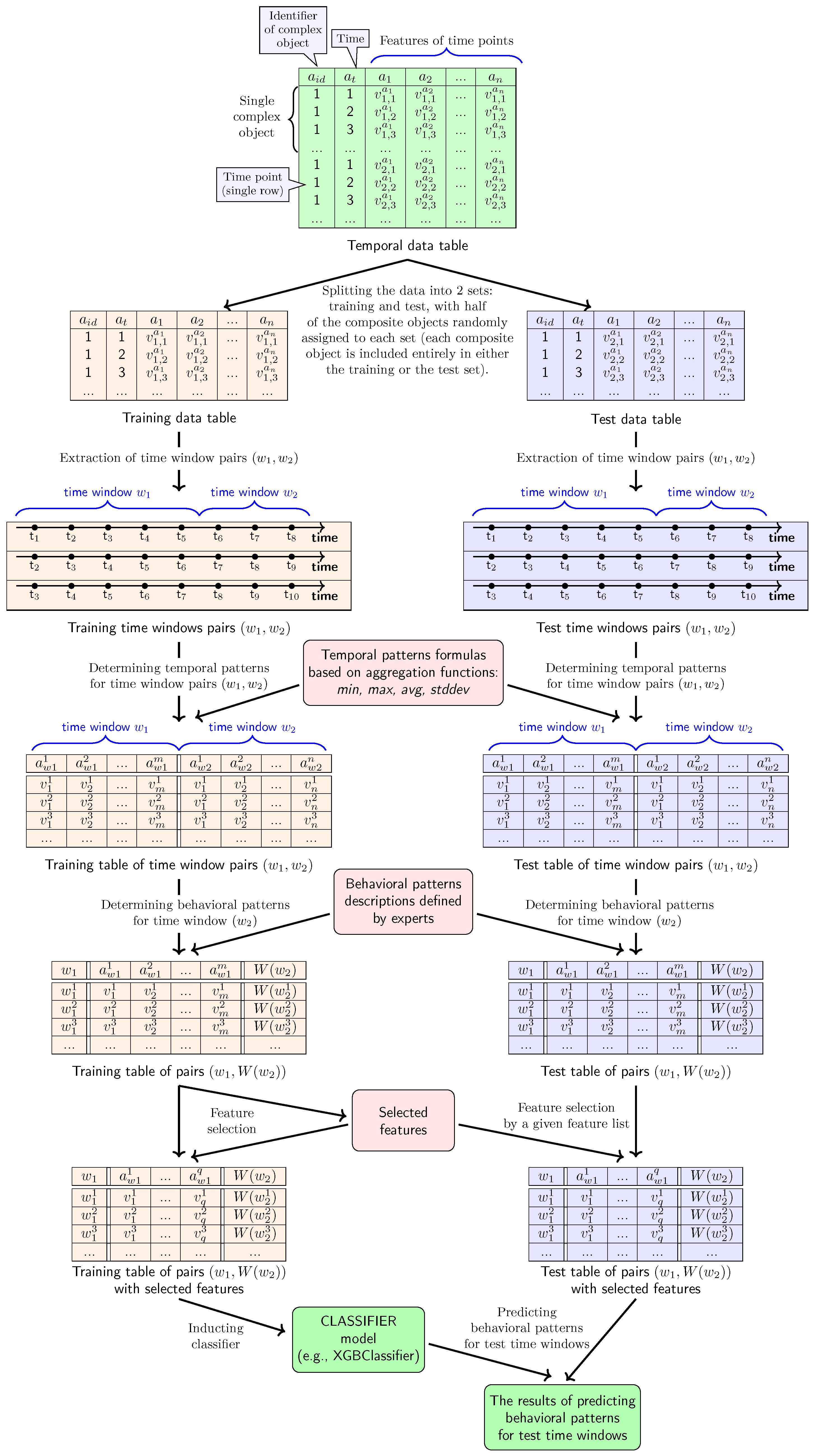
In this section, we present a comprehensive schematic of the proposed method. Figure 4 illustrates all stages of the proposed method for predicting changes in behavioral patterns, along with the relationships between them and the data flow. The individual objects in the diagram represent the main components of the method, while the arrows depict the flow of data and the corresponding actions.

The process begins with a temporal data table, where the rows correspond to time points of complex objects and the attributes describe the state of these objects at each time point. To enable model training and evaluation, the data are divided into two disjoint subsets: training and test sets, in a 50:50 ratio. The split is performed at the level of complex objects, ensuring that records belonging to the same object do not appear in both subsets simultaneously.

In the second step, pairs of time windows are generated separately for the training and test data using a sliding window mechanism, as illustrated in Figure 3. Each window covers a defined time interval, and sliding the window along the time axis enables capturing changes in behavior in a continuous and localized manner. For each complex object, successive pairs of windows $(w_1,w_2)$ are created, representing two adjacent segments of observations.

For each created pair of time windows $(w_1,w_2)$, temporal patterns are determined—a set of features describing the complex object within the given time interval. These patterns are computed using aggregation functions such as min, max, avg, and stddev, applied separately to windows $w_1$ and $w_2$. The result is a table of time window pairs $(w_1,w_2)$, where each pair is represented by a feature vector describing the properties of both windows.

Next, for each time window $w_2$ in the pair $(w_1,w_2)$, a corresponding behavioral pattern $W\left(w_2\right)$ is determined, using behavioral pattern descriptions defined by experts (see Section 3.1). This pattern reflects the characteristic behavior of the observed object within the given time window. The outcome of this process is a table of pairs $(w_1,W\left(w_2\right))$, containing a set of features for window $w_1$ along with the corresponding behavioral label for window $w_2$.

The next step involves feature selection from the set of attributes determined for each window $w_1$. The goal of this stage is to reduce data dimensionality and retain only those features that are most relevant for predicting behavioral patterns. Three alternative feature selection methods, described in Section 6.2, are employed, and separate experiments are conducted using each of these methods to evaluate their impact on classification performance.

Finally, for the training data, the table of pairs $(w_1,W\left(w_2\right))$ with the selected features serves as a decision table, where the pattern $W\left(w_2\right)$ is the decision attribute and the features of window $w_1$ are the conditional attributes. Based on this table, a classifier is induced (e.g., an XGBClassifier model). The trained classifier is then applied to the test data to predict behavioral patterns in time window $w_2$ for each test time window $w_1$. The outcome is a set of predicted patterns for each test window.

6. Classification Procedure

In this section, we describe the steps involved in selecting the optimal classifier model for data related to the MED problem. In the experiments, the PyCommoDM library, developed in Python (version 3.12.1) by researchers at the Institute of Computer Science, University of Rzeszów, was used. This library [11] was implemented using the Pandas [12] and Scikit-learn [13] packages in versions 2.2.3 and 1.5.2, respectively, as well as the Xgboost package in version 2.1.2. In cases where a pseudo random number generator was applied, no seed was set, relying instead on the generator’s default seeding. However, the experiments were repeated 10 times with the standard deviation calculated, which allows for an assessment of the reproducibility of the results. The classifiers used in the experiments were constructed based on the parameterless constructor of the class creating the given classifier.

6.1. Performance Metrics and Classifier Choice

We propose the F1-score as a measure of classifier quality. It combines precision and recall (sensitivity) into a single value and is especially useful when the data is unbalanced (it helps balance the impact of false positives and false negatives in classification). However, before we define the F1-score, we will define precision and sensitivity.

For the case of two decision classes (binary classification), precision tells us how many of the predicted positive cases were actually correct, namely

$$precision={\displaystyle \frac{Truepositives\left(TP\right)}{Truepositives\left(TP\right)+Falsepositives\left(FP\right)}}$$

(5)

where

• $Truepositives\left(TP\right)$—the number of cases that were classified as positive (so-called true positives),
• $Falsepositives\left(FP\right)$—the number of cases that were incorrectly classified as positive (so-called false positives).

Sensitivity, for the case of two decision classes, tells us how many of the actually positive cases the model detected. Namely,

$$sensitivity={\displaystyle \frac{Truepositives\left(TP\right)}{Truepositives\left(TP\right)+Falsenegatives\left(FN\right)}},$$

(6)

where

• $Falsenegatives\left(FN\right)$—the number of cases that were incorrectly classified as negative (omissions).

Precision and sensitivity are in conflict because increasing precision often reduces sensitivity. For example, we might have a model that detects cancer only in very obvious cases, resulting in high precision, but misses many less obvious cases (low sensitivity). On the other hand, increasing sensitivity often reduces precision, for example, a model detects cancer in almost all patients, but it leads to many false positives (low precision).

The F1-score for the case of two decision classes is defined as the harmonic mean of precision and sensitivity. Therefore, the F1-score combines both metrics into a single value that balances the trade-off between precision and sensitivity. Namely,

$$F1=2·{\displaystyle \frac{precision·sensitivity}{precision+sensitivity}}.$$

(7)

The harmonic mean is more stringent than the arithmetic mean because it penalizes a large difference between precision and sensitivity. If one of these values is very low, the $F1$ will also be low. This provides a good balance between precision and sensitivity, even for unbalanced data.

However, in this work, the classification problem is a multi-class one. Therefore, we need to generalize the precision, sensitivity, and F1-score defined above. Several methods for such generalization can be found in the literature. In this work, we use the approach that is probably most frequently used. When it comes to calculating precision and sensitivity, we calculate these measures separately for each class, treating each as “positive” and the others as “negative” (i.e., the so-called one-vs-rest strategy). Now we need to choose a method for aggregating the F1-score measures calculated for all decision classes. In the literature, three main aggregation approaches are typically distinguished:

• Micro F1—computes global TP, FP, and FN values for all classes and calculates a single F1-score (favors majority classes),
• Weighted F1—a weighted average of the F1-scores for each class, with weights based on class sizes (majority classes have a greater influence on the result),
• Macro F1—the arithmetic mean of the F1-scores for each class, where all classes are treated equally (majority classes do not have a greater impact on the result).

Since the data analyzed in this study are imbalanced, we use the macro F1 method, which handles the influence of dominant classes on the classification result best among the three approaches mentioned above.

The results of the experiment performed to select the best classifier model for the MED problem are based on the F1-score. In

Table 1. The results of the experiment performed to select the best classifier model for the MED problem.

Classifier	F1-Score	Standard Deviation
XGBClassifier	0.970	0.024
DecisionTree	0.964	0.021
GradientBoosting	0.954	0.022
RandomForest	0.909	0.047
AdaBoost	0.806	0.119
GaussianNB	0.745	0.105
MLPClassifier	0.714	0.054
LogisticRegression	0.666	0.064
k-NN (k = 3, Euclidean distance)	0.633	0.066

, the results of nine well-known classification methods are presented.

As we can see, XGBClassifier is the best, but it is not far ahead of several next-ranked classifiers.

6.2. Feature Selection Method

To justify the feature selection method used in this work, we compare the following three feature selection methods available in scikit-learn:

• f_classif—this is a function used in feature selection that uses one-way analysis of variance (ANOVA) to determine how strongly each feature is related to a decision variable (decision); it is a statistical method that examines whether the values of a feature differ significantly between different classes.
• mutual_info_classif—this is a function that calculates the mutual information between each conditional feature and the decision feature. It is a nonlinear measure of dependence and works well even when the dependencies between variables are more complex (it measures how much information about the decision variable a given feature provides).
• Feature selection using the RandomForestClassifier classifier—the features selected are those that have high importance from the point of view of the classifier structure.

In

Table 2. Results of the feature selection experiment using the selection method f_classif.

Number of Features	F1-Score	Standard Deviation
500	0.978	0.010
1500	0.975	0.019
1000	0.968	0.023
100	0.948	0.025
200	0.948	0.041
20	0.946	0.013
50	0.934	0.028
10	0.900	0.028
5	0.884	0.100

,

Table 3. Results of the feature selection experiment using the selection method mutual_info_classif.

Number of Features	F1-Score	Standard Deviation
1000	0.978	0.011
1500	0.972	0.021
500	0.960	0.026
200	0.957	0.023
100	0.934	0.023
50	0.922	0.045
20	0.910	0.025
10	0.855	0.061
5	0.810	0.041

and

Table 4. Results of the feature selection experiment using the selection method RandomForestClassifier.

Number of Features	F1-Score	Standard Deviation
1000	0.979	0.006
500	0.972	0.019
1500	0.971	0.022
100	0.971	0.012
200	0.970	0.014
50	0.956	0.018
20	0.937	0.025
10	0.935	0.019
5	0.870	0.059

, the experimental results of the above three feature selection methods are shown for different numbers of top features. In each experiment, we use XGBClassifier and perform 10 experiments, from which we calculate the mean and standard deviation values.

As can be seen, all three feature selection methods achieve very similar results. However, the random forest-based method achieved the best result for 1000 features. Therefore, for the purposes of this work, we use the random forest-based feature selection method.

The selected 1000 attributes describe all essential characteristics of the patient in the context of respiratory failure treatment. In particular, these include the following attributes or groups of attributes:

• information about the method of mechanical ventilation or spontaneous breathing,
• Information about the neonate’s birth weight.
• Attributes describing FiO2 values (FiO2—fraction of inspired oxygen; exactly the percentage of oxygen in the breathing mixture that the patient inhales), the PaO2/FiO2 ratio (assessment of the patient’s respiratory function, where PaO2 is the partial pressure of oxygen in arterial blood), and the results of other laboratory tests.
• Information about culture results for sepsis and ureaplasma.
• Information on the presence of PDA (patent ductus arteriosus) and whether it has been closed.
• Information about the administration of medications such as antibiotics, macrolides, steroids, surfactant, etc.
• Information about the presence of RDS (respiratory distress syndrome).

All these parameters are analyzed at each time point, and the conditional attributes in the decision table aggregate their values within a time window (e.g., the minimum, maximum, or average value of a numerical attribute within the window, the number of occurrences of a symbolic attribute value within the window, etc.).

6.3. Adjusting the Sensitivity Level to Decision Classes

Although the XGBClassifier achieves a very high $F1$-score, in practical applications it is often necessary to achieve high sensitivity (recall) for individual decision classes. For example, in the MED problem, doctors would prefer the highest-quality classifier for classes 0 and 1, because these are associated with a worse patient condition than class 2. Therefore, in this section, we describe an experiment related to adjusting the classifier’s sensitivity, performing experiments for different weight thresholds for classes 0 and 1. In these experiments, unlike the classical approach (where the class with the highest weight calculated for the test object is classified), we use a special approach based on the following Algorithm 1.

Algorithm 1: Classification rule for sensitivity adjustment

7. Results of the Experiments and Discussion

7.1. Results of Experiments with the Selection of Weight Thresholds

It is easy to see that the approach proposed in Section 6 allows the sensitivity to both classes (class 0 and class 1) to be adjusted. In

Table 5. Results of the experiments with the selection of weight thresholds for classes 0 and 1.

${\mathit{\theta }}_0$	${\mathit{\theta }}_1$	Recall0	StdDev	Recall1	StdDev	Recall2	StdDev
0.1	0.3	0.992	0.009	0.977	0.009	0.996	0.002
0.1	0.7	0.987	0.030	0.971	0.011	0.998	0.001
0.1	0.8	0.987	0.017	0.950	0.023	0.999	0.001
0.1	0.5	0.976	0.032	0.975	0.005	0.996	0.002
0.4	0.3	0.974	0.014	0.974	0.016	0.995	0.002
0.2	0.3	0.968	0.060	0.981	0.007	0.994	0.002
0.1	0.2	0.967	0.060	0.976	0.016	0.993	0.003
0.2	0.2	0.965	0.039	0.978	0.007	0.994	0.002
0.3	1.0	0.963	0.057	0.000	0.000	1.000	0.000
0.2	0.5	0.961	0.045	0.974	0.021	0.997	0.001
0.4	0.2	0.961	0.025	0.983	0.006	0.992	0.004
0.1	0.4	0.959	0.073	0.968	0.017	0.996	0.002
0.7	0.5	0.959	0.025	0.980	0.007	0.996	0.002
0.2	0.1	0.958	0.058	0.986	0.006	0.991	0.004
0.2	0.9	0.958	0.066	0.962	0.015	0.999	0.001
0.2	0.8	0.952	0.069	0.968	0.012	0.998	0.001
0.3	0.4	0.952	0.064	0.980	0.005	0.995	0.002

, we present the experimental results for different weight thresholds for class 0 and class 1. The method uses 1000 selected features.

Table 5 shows several interesting rows showing specific result configurations for both decision classes. It shows that by adjusting the weight threshold for classes 0 and 1, the sensitivity of the classifier can be fine-tuned. It is worth noting that in the table, columns Recall0, Recall1, and Recall2 correspond to sensitivities for classes 0, 1, and 2, respectively. For example, in order to achieve high sensitivity in detecting the improvement of a patient’s condition to class 2, the parameters should be set to ${\theta }_0=0.2$ and ${\theta }_1=0.9$. In this case, the sensitivity for class 2 recognition is 0.999, but the sensitivity for class 0 recognition is 0.958. On the other hand, to achieve high sensitivity in detecting the deterioration of a patient’s condition to class 0, the parameters should be set to ${\theta }_0=0.1$ and ${\theta }_1=0.3$. In this case, the sensitivity for class 0 recognition is 0.992, but the sensitivity for class 2 recognition is 0.996.

7.2. Summary of the Quality of Recognizing Deterioration, Improvement, and Permanent Transitions in Behavior Patterns

Although the classifier’s sensitivity results presented in Table 5 are very good and satisfactory from an application perspective, one might suspect that the classifier only performs well in cases where the patterns are stable, i.e., transitions from pattern 2 to 2, 1 to 1, or 0 to 0. If this is the case, the classifier’s quality would indeed be questionable. However, in medical practice, the most interesting transitions are those related to the deterioration of the patient’s condition, i.e., transitions from 2 to 1, 2 to 0, and 1 to 0. Therefore, we present the results of an experiment comparing the classifier’s sensitivity for cases of deterioration, improvement, and stability. In particular, four experiments were conducted with thresholds ${\theta }_0=0.2$ and ${\theta }_1=0.2$ on the test data used in the experiments from Table 5, where in each of these experiments the test objects were restricted to a specific subset:

• In the first experiment, the entire test set was evaluated (as in Table 5).
• In the second experiment, only those test cases representing a deterioration of the patient’s condition were evaluated.
• In the third experiment, only those test cases representing an improvement in the patient’s condition were evaluated.
• In the fourth experiment, only those test cases representing a stable patient condition were evaluated.

Table 6. Results of the experiment comparing the sensitivity of the classifier for the cases of deterioration, improvement, and stable level of the behavior pattern.

Direction	Recall0	STD	Recall1	STD	Recall2	STD
All	0.965	0.039	0.978	0.007	0.994	0.002
Worse	0.864	0.116	0.922	0.064	—	—
Better	—	—	0.921	0.062	0.947	0.018
Stable	0.998	0.004	0.982	0.006	1.000	0.001

shows that classification quality is indeed best when the pattern remains constant. When the pattern deteriorates, the classification quality decreases slightly, especially for class 0. However, the quality remains good, especially for class 1. Interestingly, when the patient’s condition improves, the classification quality of such a change is also high.

7.3. Discussion on Main Achievements

The goal of the study presented was to predict early on (while the object matches one behavioral pattern) whether the object will later match another behavioral pattern. This method can be considered more advanced than usually performed experiments, which are focused solely on identifying behavioral patterns. The overview of the literature on the treatment of neonate respiratory failure shows that many studies are retrospective. Open datasets specific to neonatal continuous monitoring for respiratory failure are less common, especially those including high-frequency signals (ventilator flow, oxygenation over time, etc.). Prediction horizons (i.e., how far ahead one can predict failure) are often not very short (minutes to an hour) in neonates and generally several days for more general outcomes (BPD, mortality).

There exist papers devoted to studying the treatment of neonatal respiratory failure and predicting neonatal health conditions. However, in these studies, the change in behavioral patterns is not predicted. In the paper [5], the authors demonstrated that machine learning models such as Random Forest and bagged CART can more accurately predict the mortality of critically ill neonates than conventional scoring systems such as the Neonatal Therapeutic Intervention Scoring System (NTISS) and Score for Neonatal Acute Physiology Perinatal Extension II (SNAPPE-II). The study in [6] identified the independent risk factors of respiratory failure in Neonatal Respiratory Distress Syndrome (NRDS) patients and used them to construct and evaluate a respiratory failure risk prediction model for NRDS, which may help clinicians to identify and intervene in the early stage. In [4], the authors used multiple ML methods (Random Forest, SVM, etc.) to predict respiratory distress syndrome (RDS) occurrence in premature infants. The best model, Random Forest, achieved an AUC of approx. 0.843 and an accuracy of approx. 0.815. In [7], the authors developed a decision-support tool for predicting extubation failure (EF) in neonates with bronchopulmonary dysplasia (BPD) using a set of machine learning algorithms. The study indicated that the XGBoost model was significant in predicting EF in BPD neonates with mechanical ventilation, which is helpful in determining the right extubation time among neonates with BPD to reduce the occurrence of complications.

The goal of this paper was achieved successfully (cf. Table 6). Comparing the classifier’s sensitivity for cases of deterioration, improvement, and stability shows that classification quality is the best when the pattern remains constant. When the patient’s condition improves, the classification quality of such a change is also high. Importantly, in the proposed model, when the pattern deteriorates, the classification quality decreases only slightly. Despite the good research results, it is worth noting that the presented method also has certain limitations. Firstly, as already mentioned, the data is outdated and therefore cannot be used to build a treatment-supporting system. Moreover, the number of time points where the patient’s condition is severe is small, which results in lower-quality prediction of the transition from a better pattern to a worse one. The number of behavioral patterns is small (only three), which certainly does not account for possible more detailed behavioral patterns that would be interesting from a practical perspective. Finally, the constructed classifier, which predicts changes in behavioral patterns, is of high quality, but no methods for explaining the decisions have been tested for them (e.g., methods known from XAI).

7.4. Linking Pattern Change Recognition with Concept Drift

The problem of predicting changes in process models can be treated as a special case considered in a subfield of machine learning called concept drift (cf. [14,15]). Generally speaking, it considers a situation where the properties of objects belonging to particular decision classes change over time. This makes it practically impossible to construct a classifier that operates effectively over time. Methods for fast and efficient adaptation of classifiers are needed. Therefore, if we treat a behavior pattern as the definition of a certain concept represented by a binary decision attribute (an object matches or does not match the pattern), then a change in the behavior pattern means a change in the concept, which in a sense “drifts” from one behavior pattern to another. Note that calculating the value of such an attribute requires knowledge of the behavioral pattern, which in the approach discussed here must be defined by domain experts. Incidentally, domain experts also define other patterns to which an object can fit. Following this line of thought, a more natural analogy is a decision table with a decision attribute with multiple values. Such a table would often be contradictory, because an object can fit multiple behavioral patterns simultaneously. Given this representation, the problem of predicting changes in the process may be treated as the problem of predicting changes in the decision class to which an object belongs. Nevertheless, the so-called active methods for dealing with concept drift discussed in the literature can be considered potential solutions to the problem in question. However, the proposed approach is not about recognizing that a behavioral pattern has changed (which requires adaptation, which is often the goal of methods developed in approaches related to concept drift), but about predicting that a behavioral pattern change will occur. This property significantly distinguishes the methods described in this paper from those typically used in concept drift. This is particularly evident in the case of predicting a potential change in a behavioral pattern caused by an important event that may trigger a change in the pattern.

8. Conclusions

The paper aimed to propose a model that can predict early on (while the object matches the first pattern) whether the object will match the second pattern in the near future. Our method can be considered more advanced than the experiments usually presented in the literature, which focus solely on identifying behavioral patterns. A crucial aspect of the study was domain knowledge, irreplaceable in defining patterns. In medical practice, the most interesting transitions are those related to the deterioration of the patient’s condition, i.e., transitions from 2 to 1, 2 to 0, and 1 to 0. Comparing the classifier’s sensitivity for cases of deterioration, improvement, and stability reveals that classification quality is best when the pattern remains constant. However, in the proposed model, when the pattern deteriorates, the classification quality decreases only slightly. When the patient’s condition improves, the classification quality of such a change is also high.

The approach to predicting changes in behavioral patterns can be applied in various domains. However, the prerequisite is that the behavioral patterns must be defined by experts based on selected parameters of complex objects. This relatively high level of involvement from domain experts may be regarded, on the one hand, as a drawback of the method. On the other hand, it enables the injection of domain knowledge into machine learning models, which can improve their quality, especially when the available datasets are relatively small. Moreover, such an approach may lead to the development of so-called AI agents, which have recently been gaining significant popularity. One can easily imagine an AI agent that interacts with a user (e.g., a physician) and answers questions regarding the possibility of a given patient transitioning to a different behavioral pattern. Furthermore, if, during such an interaction, the user wishes to change the definition of the behavioral patterns being used, the AI agent can recalculate all the models used in the AI framework in real time and then continue the dialogue with the user based on the new models. The authors of this study plan to develop an AI assistant to support the treatment of respiratory failure, including the prediction of patient transitions to different behavioral patterns.