Integration of Theoretical and Experimental Torsional Vibration Analysis in a Marine Propulsion System with Component Degradation

Abstract

This study investigates torsional vibration characteristics in an aged coastal car ferry propulsion system using theoretical calculations based on the Matrix method alongside experimental measurements. While the measured torsional vibration at the propeller shaft remained within the limits, it was significantly higher than the calculated values, particularly at the 5th harmonic order excited by engine combustion. Negative torque peaks observed during transient clutch engagement caused gear hammering. Structural vibration analysis identified potential gearbox defects, such as wear or misalignment. Multiple torsional vibration calculation models were developed considering various degrees of degradation of the aged rubber blocks and viscous torsional damper. A model assuming that the damping capacity of damper drops to about 1%, corresponding to the specified values at 125 °C, produced results that closely reproduced the measured vibration characteristics. The finding, confirmed by an actual inspection, identifies viscous oil leakage and deterioration of the damper as the primary cause of excessive vibration. Prompt replacement of the viscous oil is recommended to improve torsional vibration behavior.

1. Introduction

Propulsion systems are the most essential components in marine vessels, forming the mechanical backbone that transmits power from the main engine to the propeller. Ensuring the reliability of these systems is fundamental for the safe and efficient operation of ships [1]. Among the multiple dynamic factors affecting such systems, torsional vibration remains one of the most critical due to its ability to accelerate fatigue accumulation and reduce system reliability [2,3,4]. The primary excitation mechanisms arise from periodic torque fluctuations generated by the diesel engine combustion and from the propeller blade excitation during rotation in the surrounding water [5,6,7,8]. With modern engines producing higher power per cylinder for improved fuel efficiency, torsional oscillations have intensified [9,10,11]. An inappropriate consideration of torsional vibration can result in mechanical issues. At a certain engine speed, an excitation source may coincide with a natural frequency of the propulsion system, resulting in resonant vibration. Such conditions can produce excessive dynamic stress, endangering rotating components like shafts, couplings, and gearboxes, leading to accelerated fatigue or even cracking failures of shafting components [12,13]. Therefore, classification societies and international regulations specify the need for torsional vibration calculations (TVC) and measurements as a mandatory requirement for all newly constructed vessels [14,15,16,17]. For sister ships equipped with identical propulsion systems, verification is typically required only on a representative vessel, which helps reduce redundant testing while maintaining safety standards. These requirements are generally well observed in medium- and large-sized vessels, where shipbuilding budgets are comparatively higher and propulsion configurations relatively simple.

In contrast, small vessels face more challenges. Their propulsion systems often involve complex arrangements with multiple independent suppliers for the main engine, reduction gearbox, and propeller. Due to the lack of integrated design and review, torsional vibration analyses are frequently omitted or insufficiently performed. This has led to cases where excessive torsional vibration results in failures of engines or reduction gears, overheating, or even fire hazards, leading to serious marine accidents. The problem is further complicated by the fact that most small shipbuilders are small-scale enterprises that do not yet possess the technical capacity to carry out advanced vibration analyses at the system-integration level. Torsional vibration calculations are not thoroughly considered during the design stage. In such cases, propulsion system components may be selected hastily based on immediate stock availability.

From a safety engineering perspective, the importance of torsional vibration theory calculation cannot be overstated. Accurate calculation is essential for ensuring structural integrity, preventing fatigue damage, and prolonging service life. Early foundational work on torsional vibration in shafting was documented by Den Hartog [18] and later by Timoshenko et al. [19], who established the principles of mechanical vibration theory applied to rotating machinery. Simplified lumped-parameter models remain a mainstay in practical analysis, valued for their clarity and computational efficiency, and physical interpretability. Among these, the Matrix method is the most widely used analytical tool [20,21]. Accordingly, the method models a rotating shaft system as a sequence of discrete elements, each described by matrices that relate state variables (such as torque and angular displacement) across component interfaces. Major reviews by Pestel et al. [22] and Hatter [23] describe its advantages in forced vibration analysis, including its application to vibration isolation design and amplitude calculation under various loads. This method enables straightforward assembly of the overall system dynamic behavior and allows direct calculation of natural frequencies, mode shapes, and forced vibration response under periodic excitations common in marine environments. This also enables comprehensive analysis with practical constraints like multiple excitation sources, variable damping or variable coupling stiffness. Recent research has extended these classical methods further, accommodating nonlinearities and enabling advanced condition monitoring in marine shaft systems [24,25,26,27].

The foundation of a safe propulsion system lies in accurate TVCs performed during detailed design stages. This involves mathematically modeling the complete drivetrain, including mass inertias, stiffnesses, damping, gear ratios, and excitation sources, to calculate natural frequencies, forced vibration amplitudes, and resonance conditions [28]. The accuracy of a theoretical calculation can be accurate models validated through measurements under actual operating conditions. Direct measurement techniques, such as shaft-mounted strain gauges combined with a wireless telemetry system, provide actual torsional stress and torque data across the full operating speed range, enabling direct comparison with the theoretical calculation. Conversely, theoretical calculations are grateful in diagnosing anomalies observed in actual vibration measurements. When anomalies arise, effective troubleshooting requires an integrated approach. Engineers must combine empirical data analysis with recalculation based on plausible fault scenarios, which may include reduced damping at a critical component, gear mesh defects, flexible coupling deterioration, or incorrect assumptions regarding vibration mode shapes. By iteratively refining the model with measured data, root causes can be identified with greater confidence, enabling targeted interventions rather than costly trial-and-error repairs [29].

In the demanding operational environment of ferry propulsions, where high reliability must coexist with severe dynamic loads, torsional vibration theoretical calculation and measurement are inseparable. For new ships, theoretical calculations are essential during the design stage to ensure propulsion system performance and reliability, with subsequent measurements used to verify the calculations. In contrast, for aging ships, measurements are necessary for examining and evaluating the current condition, while theoretical calculations simulate potential scenarios to diagnose causes and mechanisms of observed abnormalities. Despite its widespread application, there is limited literature addressing the impact of component degradation, such as aged rubber couplings or torsional damper failures on torsional vibration behavior, despite their prevalence in service-related failures.

This paper studied the modeling method and conducted the vibration response characteristic analysis of a propulsion shaft system in a coastal car ferry with over 10 years of operation. The system was equipped with a high-speed diesel engine engaging a fixed pitched propeller through a reduction gear. The ship crew complained that there was abnormal noise from the gearbox at the maximum continuous rated (MCR) speed. To assess the condition of the propulsion system, a comprehensive series of vibration measurements were conducted. Multiple dynamic models were developed to identify the root causes of the observed anomalies, with particular focus on the degradation of rubber blocks and the torsional damper. Furthermore, the analysis explored how variations in torsional stiffness and damping capacity influence the torsional response, providing actionable insights for both design engineers and operators. Beyond conventional propulsions, the findings have direct relevance to the emerging field of autonomous ships, where human intervention is limited or absent. Understanding torsional vibration dynamics and the effects of component aging is crucial for predictive maintenance and ensuring uninterrupted operation under diverse and demanding conditions.

The remainder of this manuscript is organized as follows. Section 2 outlines the international standards relevant to torsional vibration of propeller shafts and gear transmissions. Section 3 describes the theoretical torsional vibration calculation developed using the specified design parameters. Section 4 presents the experimental measurement, including (a) normal firing steady-state tests and (b) transient tests during clutch engagements. Section 5 presents the root cause analysis through development of multiple TVC models that consider various degrees of degradation in the aged rubber blocks and viscous torsional damper. The finding has been confirmed by an actual component inspection. Finally, the main conclusions are summarized in Section 6.

2. International Standards for Torsional Vibration of Propeller Shafts and Gear Transmissions

The main international standards for torsional vibration of propeller shafts and gear transmissions are set by the International Organization for Standardization (ISO) and the International Association of Classification Societies (IACS), as well as by classification societies. These standards define design, calculation, measurement, and allowable limits to ensure safe operation under real-world conditions. IACS Unified Requirement M68 [30] specifies design formulas and permissible torsional vibration stress amplitudes for propeller and intermediate shafts. Accordingly, for continuous operation, the permissible torsional vibration stresses must not exceed the values determined by the following equations:

$$\pm {\tau }_c={\displaystyle \frac{{\sigma }_B+160}{18}}{·C}_K{·C}_D·(3-2·{\lambda }^2) \hspace{1em}\hspace{1em}\mathrm{for} \lambda <0.9$$

(1)

$$\pm {\tau }_c={\displaystyle \frac{{\sigma }_B+160}{18}}{·C}_K{·C}_D·1.38 \hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{for} 0.9\le \lambda <1.05$$

(2)

where

${\tau }_c$: permissible torsional stress amplitude for continuous operation [$\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$],

${\sigma }_B$: specified minimum ultimate tensile strength of the shaft material [$\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$],

$C_K$: factor for the particular shaft design features. For a propeller shaft, $C_K$ = 0.55.

$C_D=0.35+{0.93d_0}^{-0.2}$: size factor,

$d_0$: shaft outside diameter [$\mathrm{m}\mathrm{m}$],

$\lambda =n/n_0$: speed ratio,

$n$: speed under consideration [$\mathrm{r}\mathrm{p}\mathrm{m}$],

$n_0$: speed at rated power [$\mathrm{r}\mathrm{p}\mathrm{m}$].

If the stress amplitudes exceed the permissible limit for continuous operation, barred speed ranges must be imposed to be passed through rapidly. During quick pass through these barred speed ranges, the steady-state torsional vibration amplitudes must not exceed the value specified by the following formula:

$$\pm {\tau }_T=1.7·{\displaystyle \frac{{\tau }_c}{\sqrt{C_K}}}$$

(3)

In gear transmissions, the application factor, $K_A$, considers dynamic overloads from sources external to the gearing [31]. For gears designed for infinite lifespans, $K_A$ is defined as:

$$K_A={\displaystyle \frac{T_{max}}{T_0}}$$

(4)

where $T_{max}$ is the maximum repetitive cyclic torque applied to the gear set, and $T_0$ is the nominal rated torque determined by rated power and speed. Importantly, these rated values are determined by the gear manufacturer rather than by the main engine or propulsion system specifications. Gear manufacturers typically provide an application factor for their gear set, indicating the permissible cyclic torque that can be applied to the gears.

Lloyd’s Register (LR) requires that the sum of the mean and vibratory torques must not exceed four-thirds of the full transmission torque at MCR over the entire speed range [15]. In other words, the application factor is specified as $4/3$. In addition, Det Norske Veritas Germanischer Lloyd (DNV GL) [16] specifies that the permissible vibratory torque is limited to a value depending on the application factor provided by the gear manufacturer across the full speed and load range (above 90% of rated speed and load). DNV GL further limits the vibratory torque to 35% of $T_0$ throughout the entire operation range, effectively setting the application factor at 1.35, regardless of the value provided by the manufacturer. Gear hammering (negative torque) is generally not permitted except in unloaded power take-off branches, where up to 20% of $T_0$ (based on shaft speed). Transient vibrations shall not produce negative torques exceeding 25% of $T_0$, and transient peak torques shall not exceed the approved $\left(1.5T_0\right)$.

3. Theoretical Torsional Vibration Calculation

3.1. Methodology

In this study, the Matrix method was employed for torsional vibration calculations. In general, a propulsion system can be modeled as a series of discrete elements, with all major rotating components (such as the main engine, shafts, couplings, and propeller) represented by their equivalent mass moments of inertia interconnected by uniform shafts, idealized as springs. Each shaft segment is considered massless but assigned a defined torsional stiffness, determined by its geometry and material properties. Where applicable, relative damping is included to represent energy dissipation in flexible couplings or torsional dampers. Absolute damping is included for each engine cylinder and the propeller. The damped forced torsional vibration of the propulsion shafting system is governed by the following matrix equation of motion:

$$\left[\mathbf{J}\right]\left\{\ddot{\mathsf{\theta }}\left(t\right)\right\}+\left[\mathbf{C}\right]\left\{\dot{\mathsf{\theta }}\left(t\right)\right\}+\left[\mathbf{K}\right]\left\{\mathsf{\theta }\right(t\left)\right\}=\left\{\mathbf{Q}\right(t\left)\right\}$$

(5)

where [J] represents the mass moments of inertia matrix; [C] denotes the damping matrix; [K] is the stiffness matrix; $\left\{\ddot{\mathsf{\theta }}\left(t\right)\right\}$,$\left\{\dot{\mathsf{\theta }}\left(t\right)\right\},$ and $\left\{\mathsf{\theta }\right(t\left)\right\}$ are the angular acceleration, velocity and displacement vectors, respectively. The vector {Q(t)} corresponds to the excitation torque. When {Q(t)} is zero, the system undergoes free vibration. In the forced torsional vibration of a diesel engine propulsion system, the excitation vector is typically a periodic function representing both the combustion-induced torque fluctuations from the engine and the dynamic excitation caused by the rotating propeller. These excitation forces are decomposed into multiple harmonic components, each characterized by a specific excitation frequency and a corresponding phase angle. For every element in the system, the forced vibration response is computed for each harmonic order. The overall vibration response at each element is then obtained by synthesizing the individual responses from all harmonic components. Finally, the torsional vibration response must be evaluated in accordance with relevant international standards.

3.2. Specifications of Propulsion System

The propulsion system under this study is of a traditional design, with its key specifications summarized in

Table 1. Specifications of propulsion system.

Engine Model	DOOSAN V180TIH/M	Gearbox	HITACHI NICO MGN86EL-A
Engine type	4-stroke, V type	Gear ratio	3.93
Nominal output	441 kW at 1800 rpm	Application factor	1.5
Cylinder number	10	Coupling type	Rubber block
Vee angel	90°	Continuous Rating	617 kW at 1800 rpm
Bore	128 mm
Stroke	142 mm	Viscous damper	HASE & WREDE ASK 2060
Reciprocal mass	4.351 kg
Rotating mass	2.303 kg	Propeller type	Fixed pitch
Con–rod ratio	0.2773	Propeller shaft dia.	119 mm
Compression ratio	15:1	Propeller diameter	1450 mm
Tensile strength	≥850 N/mm2	Blade number	4
Firing order	1–6–5–10–2–7–3–8–4–9	M.O.I. in water	25.21 kg m2

. For analytical purposes, it was discretized into a lumped mass-spring model, as depicted in Figure 1. The main engine was a four-stroke, V-type configuration with ten cylinders. To attenuate the torsional vibration, a viscous torsional damper was installed at the free end of the crankshaft. The dynamic properties of the damper, including torsional stiffness and damping coefficient, vary with both vibration frequency and temperature; these dependencies follow log-log linear relationships, as illustrated in Figure 2. In this study, the damper parameters corresponding to 80 °C were utilized for the TVC.

In the gear transmission, the driving ring and spider gear were assembled through rubber blocks, which were designed not only to accommodate misalignment and absorb shock loads but also to provide additional torsional elasticity and damping. The reduction gear was configured with a ratio of 3.93, effectively matching the engine output to the operational envelope of a four-blade fixed pitch propeller. Detailed mass-elastic properties required for the TVC are described in

Table 2. Torsional system. (The data are not reduced to engine speed.)

No.	Mass Name	Inertia	Torsional Stiffness	Absolute Damping	Relative Damping	Speed Ratio
		${\mathbf{k}\mathbf{g}·\mathbf{m}}^2$	$\mathbf{M}\mathbf{N}\mathbf{m}/\mathbf{r}\mathbf{a}\mathbf{d}$		$\mathit{\eta } = \mathit{\psi }/2\mathit{\pi }$
1	Damper ring	0.3460				1
1–2			(*)		(*)	1
2	Pulley	0.2541				1
2–3			4.229			1
3	Throw No. 1	0.2546				1
3–4			2.714			1
4	Throw No. 2	0.2538				1
4–5			2.713			1
5	Throw No. 3	0.1592				1
5–6			2.721			1
6	Throw No. 4	0.2540				1
6–7			2.713			1
7	Throw No. 5	0.2569				1
7–8			4.521			1
8	Flywheel + disk	2.2375				1
8–9			rigid			1
9	Driving ring (I1)	1.774				1
9–10			6.368		0.00556	1
10	Spider gear (I2)	0.916				1
10–11			0.867			1
11	Reverse driving gear (I3)	0.160				1
11–12			rigid			1
12	Reverse driven gear (I4)	0.160				1
12–13			rigid			1
13	Steel plate (I8)	0.012				1
13–14			12.384			1
14	Pinion (I10)	0.034				1
14–15			rigid			1
15	Gear (I11)	5.435				1
15–18			4.9999			1
16	Steel plate (I7)	0.012				1
16–17			12.384			1
17	Pinion (I9)	0.034				1
17–15			rigid			1
18	Output flange (I12)	0.468				1:3.93
18–19			rigid			1:3.93
19	Companion flange (I13)	0.811				1:3.93
19–20			rigid			1:3.93
20	½ Propeller shaft	0.360				1:3.93
20–21			0.337			1:3.93
21	½ Tail shaft	0.360				1:3.93

(*) The torsional stiffness and damping of the torsional damper vary with vibration frequency.

, ensuring that all relevant inertia, stiffness, and damping values are systematically quantified. The TVC was conducted over the engine speed range of 500 to 1900 rpm, in normal firing conditions in all cylinders. This approach ensures precise characterization of the dynamic response across the full operational envelope of the propulsion system, capturing the variations in vibration amplitude and stress that may occur at different engine speeds.

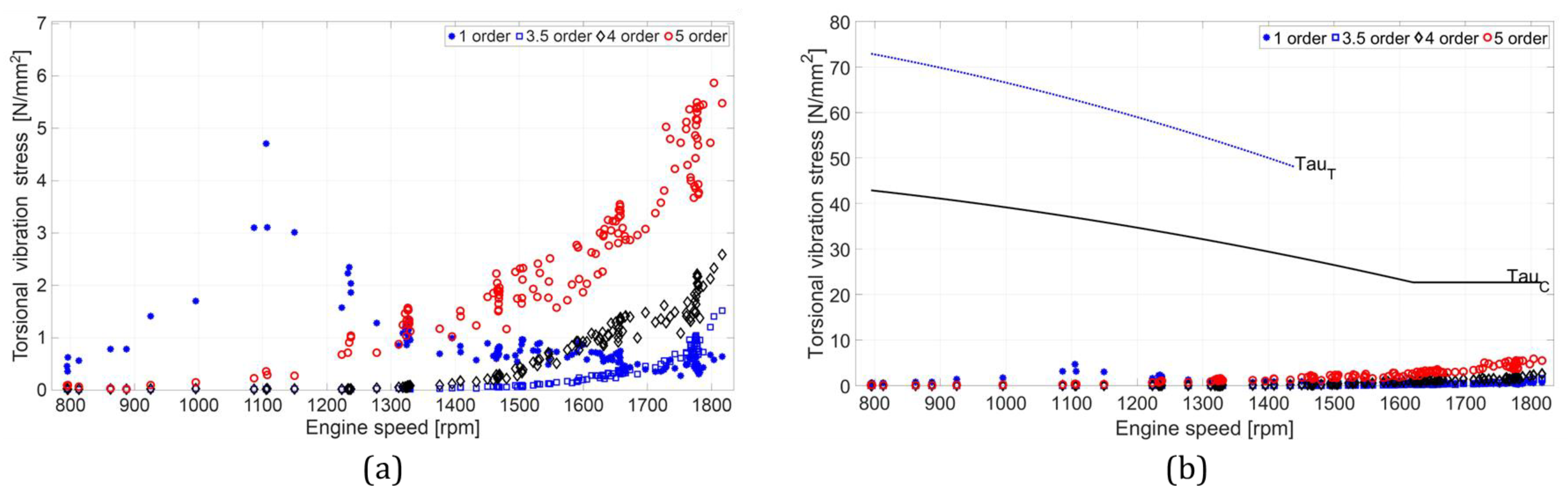
3.3. TVC Results

As shown in Table 1, the nominal output of the main engine was 441 kW at 1800 rpm, corresponding to a nominal transmitted torque of 2.34 kNm before speed reduction and 9.19 kNm after speed reduction. However, in marine applications, the manufacturer specifies the continuous duty rating for the gear as 617 kW at 1800 rpm. This corresponds to a rated transmitted torque of 3.27 kNm before speed reduction and 12.85 kNm after speed reduction.

Figure 3 presents the calculated vibratory torques for the driving ring, spider gear, output gear and propeller shaft. The 5th harmonic order represents vibration caused by the combustion processes in the ten cylinders of the main engine. The 1Z and 2Z harmonic orders correspond to vibrations at blade frequencies generated by the propeller rotating in water. Since the propeller has four blades and a speed reduction ratio of 1:3.93, the 1Z and 2Z orders closely match the frequencies of the 1st and 2nd harmonic orders of the propulsion system.

At MCR, the synthesized vibratory torque at the driving ring was 2.8 kNm, exceeding the permissible value of 1.15 kNm, which corresponds to 35% of the rated transmitted torque as specified by DNV GL. The vibratory torque also exceeded limit of 1.64 kNm, corresponding to the application factor, K_A = 1.5, provided by the gear manufacturer. Additionally, the sum of the mean and vibratory torques reached 5.14 kNm, surpassing the permissible limit of 4.36 kNm, equal to four-thirds of the rated transmitted torque, as specified by LR. The same issue was observed for the spider gear when the vibration was over the limits.

However, unlike conventional gear assemblies, as illustrated in Figure 4, the spider gear remained continuously engaged with the driving ring gear teeth, ensuring that the transmission torque was uniformly distributed across all teeth rather than concentrated on a single tooth pair. Consequently, the vibratory load per tooth was substantially reduced, maintaining safe operating conditions for the gear transmission system. It should be noted that the specified limits serve as reference values only and are not strictly applicable to this specific transmission configuration.

No issues were identified in the vibratory torques calculated for the output gear and propeller shaft, where the permissible limits were significantly higher after the speed reduction. Furthermore, the vibration behavior of the output gear closely mirrored that of the propeller shaft. Therefore, it is feasible to use the vibratory torque measurements of the propeller shaft to assess the condition of the output gear, where direct measurement of the vibratory torque is challenging.

Figure 5 shows the calculated torsional vibration stress of the propeller shaft. The results indicate no vibration issues, with all amplitude values remaining below the limits specified by the IACS rules. Similarly, no concerns were found for the calculated torsional vibration in other components of the system.

4. Torsional Vibration Measurement

4.1. Measurement Setup

Figure 6 illustrates the installation of vibration sensors. A laser tachometer (model A2103/LSR/001, Compact Instruments, Lancashire, UK) was employed to measure the shaft rotational speed. The torsional stress and transmitted torque at the propeller shaft were directly measured by a strain gauge (model CEA-06-250US-350, Micro-Measurements, Wendell, NC, USA) installed on the shaft surface. Signal transmission from the strain gauge was achieved via a telemetry system supplied by MANNER Sensortelemetrie (Spaichingen, Germany), which included a rotating sensor signal amplifier (model SV_8a) and a stationary receiver unit (model AW_22TE_Fu). The system exhibited an accuracy error below 0.02%/°C, with a sensitivity range of 0.05–20 mV/V and an operational bandwidth between 0 and 1000 Hz.

Structural vibrations of the gearbox casing were measured using industrial accelerometers (model 357A26) with a frequency range of 0.5 to 10,000 Hz. A signal conditioner (model 482C05) supplied current to the accelerometers and converted the signals to voltage. All accelerometers and the signal conditioner are manufactured by PCB Piezotronics (Depew, NY, USA). All measurement channels were synchronously acquired through a data acquisition system comprising an NI-9174 chassis and NI-9215 modules (National Instruments, Austin, TX, USA) operating at a sampling frequency of 8192 Hz, ensuring precise measurements.

4.2. Experiments and Results

The experiments were conducted according to ISO 20283-4:2012 [14], which covers the measurement and evaluation of vibrations in ship propulsion systems, under the following conditions:

• The ship loading condition was close to the designed nominal operating condition.
• Water depth was greater than five times the ship draught.
• Minimum turning, with the rudder angle not exceeding 2 degrees.
• Sea state 1.

a. 

Normal Firing Steady-State Measurement

In this experiment, the main engine was engaged with the propeller, maintaining an initial engine speed of 800 rpm. The engine speed was then gradually and steadily increased from 800 to 1800 rpm, with an acceleration rate of less than 270 rpm per minute, corresponding to 15% increments of the nominal speed, as specified by the ISO standard.

Figure 7 presents the measured torsional vibration of the propeller shaft. The vibration amplitudes were below the limits specified by the IACS rule. This indicated no safety concerns for the propeller shaft. However, the measured vibration amplitudes were significantly higher than the calculated results shown in Figure 5. Notably, the vibration at the 5th harmonic order, excited by the main engine combustion processes, intensified as the speed approached MCR. This phenomenon may be attributed to either a decline in the performance of the rubber blocks or torsional damper. Aged rubber blocks may inadequately isolate engine vibrations, transmitting them to the propeller shaft. Similarly, a damaged torsional damper may fail to effectively absorb vibrations originating from the main engine.

It is assumed that the vibration amplitudes of the output gear closely matched those of the propeller shaft, as shown in the TVC results. As illustrated in Figure 8, the vibratory torque on propeller shaft at MCR was 2.86 kNm. This value was below the permissible limit of 3.83 kNm, which corresponds to 35% of the rated transmitted torque as specified by DNV GL. The vibration amplitude also complied with the LR rule. No issues were identified in the vibratory torques for the output gear. However, the significantly higher measured vibration compared to the calculated values on propeller shaft indicated that torsional vibration in the other gears might be critical.

The gear mesh frequency (GMF) is a fundamental excitation related to gear tooth engagement. This is a defining characteristic of every gear assembly and is always present in the frequency spectrum at integer multiples of GMF, such as 1×, 2×, 3× … n × GMF. These harmonics appear due to repeated impacts between gear teeth regardless of gear condition [32]. Figure 9 illustrates the configuration of the gear transmission assembly. Gears (I3) and (I4) each have 42 teeth, corresponding to a gear mesh frequency of GMF_3–4 at the 42nd order. Gears (I9) and (I10) each have 28 teeth, and gear (I11) has 110 teeth, corresponding to the same gear mesh frequency of GMF_10–11 at the 28th order.

Figure 10 presents the results of the structural vibration analysis of the gearbox casing in longitudinal direction. The vibration at 42^nd, 84^th and 126^th orders was caused by the gear assembly I3–I4, corresponding to frequencies 1×, 2×, and 3× of GMF_3–4. However, the vibration observed at the 96th order does not correspond to an integer multiple of either 42 or 28. Instead, it falls between the second and third harmonics of GMF_3–4. This vibration order may indicate gearbox defects, such as wear or misalignment. Furthermore, this order matched a natural frequency of 2820 Hz near MCR, resulting in a structural resonance with an acceleration amplitude of 29 m/s², which caused the abnormal noise. However, this high-frequency vibration has no remarkable effect on the structure of reduction gear as its amplitude was much smaller than the limit specified in ISO 20816-9:2020 for gear units [33]. No remarkable issues were observed in the structural vibration measurements taken in the transversal and vertical directions.

b. 

Transient State Measurement

The torsional vibration behavior was examined during both clutch engagement and disengagement. The tests were conducted in both the ahead and astern rotational directions, following the same procedure as outlined below:

1.

Ensure the clutch is fully disengaged. Operate the main engine at approximately 800 rpm under no load condition.

2.

Engage the clutch while continuously measuring the torsional vibration and transmitted torque.

3.

Maintain engagement until stable torque transmission is achieved.

4.

Disengage the clutch and observe torsional vibration response during disengagement phase.

Figure 11 illustrates the transient torques measured at the propeller shaft during clutch engagements in both ahead and astern rotational directions. In the astern operation, the engine rotation direction remained the same as in the ahead operation; only the gear transmission mechanism was altered. For easier comparison, the measured torque recorded during the astern test was inverted in sign. In both directions, it was observed that the engine needed to produce a higher torque than during steady-state conditions to overcome the frictional and inertial forces of the shaft and propeller. Notably, the vibratory torque measured in the astern test was greater than that in the ahead test. The peak-to-peak torsional vibration stress amplitudes reached 17.9 kNm, which is 1.95 times the nominal transmitted torque at MCR. The negative torque peaks reached an absolute value of 4.1 kNm, close to the DNV GL limit of 4.5 kNm, corresponding to 35% of the rated transmitted torque. Although below the specified limit, these negative torque peaks still caused gear hammering, which increased noise, resulted in rougher engagement, and reduced the fatigue life of the gears. The maximum transient peak torque was 13.8 kNm, remaining below the approved limit of 19.3 kNm, equivalent to 1.5 times the rated transmitted torque. These evaluations assumed that the vibration amplitudes of the output gear closely corresponded to those of the propeller shaft, as indicated by the TVC results. It is also important to note that vibratory torque may increase when the ferry operates under harsh weather conditions. No significant vibration issues were observed during clutch disengagements.

5. Root Cause Analysis

The measured torsional vibrations at the propeller shaft were significantly higher than the calculated results. This propulsion system was over 10 years old and operates everyday under harsh conditions. The pronounced vibration occurred at the 5th harmonic order, corresponding to excitation generated by the main engine combustion process. Two primary groups of potential root causes were proposed. The first involves malfunctions of the main engine that could elevate excitation levels. The second concerns degradation of damping components, such as the torsional damper and flexible rubber blocks, which reduces the capacity to attenuate torsional vibration. Since the main engine, propeller, and shafting were reported to be well maintained, the abnormal vibration was therefore considered to be attributed to the second. In particular, degradation of the torsional viscous damper or rubber blocks may have reduced the damping and altered stiffness characteristics of the propulsion system, thereby increasing the vibration response. To verify these conjectures and clarify the mechanism of the excessive torsional vibration, several dynamic models of the propulsion system were developed and analyzed.

5.1. Degradation of Rubber Blocks

Over time, rubber blocks tend to harden due to environmental exposure, such as repeated impacts, heat and chemical attack. This results in a loss of elasticity and damping capacity, leading to less effective vibration mitigation and increased torsional vibrations [34,35]. In this study, the worst-case scenario was considered, assuming the rubber blocks lost all elasticity and damping capacity. The calculated torsional vibrations at propeller shaft are presented in Figure 12.

The TVC analysis shows that, even under the worst-case scenario of rubber block degradation, the torsional vibration behavior at the propeller shaft exhibits no significant changes compared to the original condition, as illustrated in Figure 4. This result indicates that while the rubber blocks may be degraded, they were not the main cause of the increased torsional vibration observed at the propeller shaft during measurements.

5.2. Degradation of Torsional Viscous Damper

The torsional stiffness and damping capacity of the viscous damper decrease as the operating temperature rises, especially under prolonged harsh conditions, as illustrated in Figure 2. This behavior aligns with the typical characteristics observed in aged viscous dampers. Additionally, after many years of service life, leakage of the viscous oil may occur, further accelerating the degradation of the damper [36]. A reduction in damping capacity leads to an increase in vibration amplitude, while a decrease in stiffness results in lower natural frequencies, causing resonances to occur at lower rotational speeds. To investigate the effects of such degradation, multiple TVC models were developed with varying levels of reduced stiffness and damping. Four representative cases were selected and are presented in Figure 13. The degradation parameters were simulated with reference to baseline values corresponding to the specified worst-case condition, represented by the highest temperature of 125 °C. The descriptions of 100%, 10%, and 1% indicate the relative amplitudes of the simulated stiffness or damping capacity compared to these baseline parameters.

In Case 1, where stiffness and damping are set to 100% as the baseline parameters, the calculated torsional stress at the propeller shaft is substantially higher than that calculated at 80 °C, as presented in Section 3.2. Nevertheless, the vibration amplitude at MCR remains comparatively small. In Case 2, maintaining 100% stiffness while reducing damping coefficients to 10% introduces a 5th order resonance at MCR. The vibration response shows a shift closer to the measured data, but the peak amplitude still remains below the experimental observation. Case 3, with both stiffness and damping reduced to 10%, shifts the 5th order resonance to a lower engine revolution, around 1700 rpm. This shift indicates that significantly decreased stiffness results in lower natural frequencies, causing the response to deviate substantially from the measurements. Case 4 yields result that closely reproduces the measured data. In this case, torsional stiffness is maintained at the baseline, whereas the damping capacity is almost completely lost (1% of the specified values). The corresponding properties are represented by the thick blue and red lines in Figure 2.

The findings demonstrate that the critical factor in reproducing the measured vibration characteristics is the loss of damping capacity. In practice, this means that long-term service, which accelerate damping degradation, directly compromise vibration suppression and can lead to resonance at critical operating speeds. Therefore, periodic inspection and maintenance of viscous dampers, with particular attention to damping capacity, are essential to ensure reliable torsional vibration control and the safe long-term operation of propulsion systems.

5.3. Discussion

The measurement and calculation results were reported to the ship owner. An inspection of the reduction gear and torsional viscous damper was performed by experts from the manufacturers. The inspection revealed degradation of the rubber blocks, resulting in reduced elasticity and damping capacity. However, this was not the primary cause of the excessive torsional vibration. Oil leakage was detected in the damper, and the quality of the viscous oil had deteriorated significantly. Consequently, the damper was unable to effectively attenuate the torsional vibrations generated by the main engine and propeller. A request was made to replace the viscous oil promptly to improve torsional vibration behavior.

This research identifies viscous oil leakage and damper degradation as the primary cause of excessive torsional vibration, whereas many other studies [37,38,39] emphasize rubber coupling degradation as dominant factors. This difference suggests that damper condition monitoring may be more critical than previously recognized and deserves further investigation.

6. Conclusions

This study examined torsional vibration in the propulsion system of a coastal car ferry with over 10 years of operation, using both theoretical calculations and experimental measurements. The key conclusions are as follows:

• The calculated torsional vibration of the output gear closely matched that of the propeller shaft. Therefore, measurements at the propeller shaft can be used to assess the condition of output gear, where a direct measurement is difficult. Vibration levels that satisfy propeller shaft criteria may still be critical for the gear system, highlighting the need to reference specific torsional vibration requirements for gears. This approach can be applied to propulsion systems that use gears to enhance condition monitoring and optimize maintenance strategies.
• Measured torsional vibration of the propeller shaft was below allowable limits but significantly higher than calculated values, particularly at the 5th harmonic order excited by the engine combustion process and increasing as the speed approached MCR. This suggested that torsional vibration in the gears may be critical.
• The transient torsional vibration during clutch engagements remained below, but close to, limits for gear transmissions. The vibration measured during the astern test was greater than that observed in the ahead test. The negative torque peaks, reaching an absolute value of 4.1 kNm, caused gear hammering, which increased noise, resulted in rougher gear engagement, and reduced the fatigue life of the gears. This is an important consideration, as ferries frequently alternate between ahead and astern operations, and harsh weather conditions can further amplify vibration amplitudes.
• Structural vibration at the 96th order observed in the gearbox casing did not correspond to an integer multiple of any gear mesh frequency. This indicates possible gearbox defects such as wear or misalignment. This resulted in a structural resonance of 29 m/s², which caused the abnormal noise at MCR. However, this vibration has no remarkable effect on the structure of reduction gear as its amplitude was much smaller than the limit.
• Multiple TVC models were analyzed to identify the root cause of excessive torsional vibration. The best match to the measured data was a damper degradation model where the torsional stiffness remains at 100%, but the damping capacity drops to about 1%, corresponding to the specified values at 125 °C. An inspection confirmed oil leakage and deteriorated viscous oil quality, necessitating prompt oil replacement to improve torsional vibration behavior. Furthermore, regular inspection and maintenance of viscous dampers, along with other related components, are essential to ensuring effective torsional vibration control and the safe long-term operation of propulsion systems.
• The limitation in this study is that the torsional vibration measurement was conducted only at the propeller shaft. Expanding measurements to multiple points, such as angular velocity fluctuations before and after the reduction gear, would enable a more detailed comparison between calculated and measured results, enhancing the accuracy of the analysis.