Damping Optimization Design of Plant Fiber-Reinforced Composites for Subway Interior Structures
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Numerical Analysis
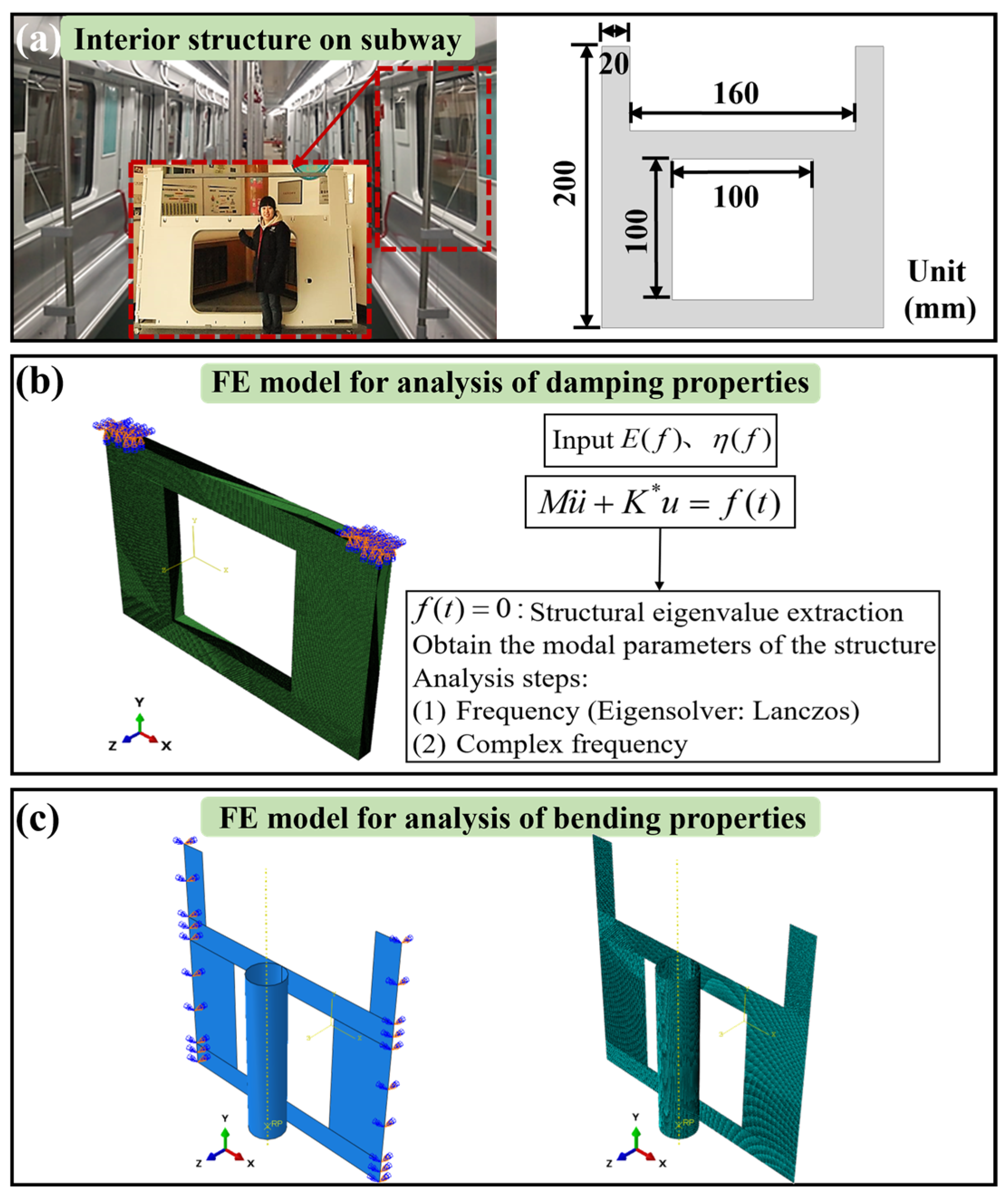
2.2.1. FE Model for Analysis of the Damping Properties
2.2.2. FE Model for Analysis of the Bending Properties
2.3. Experimental
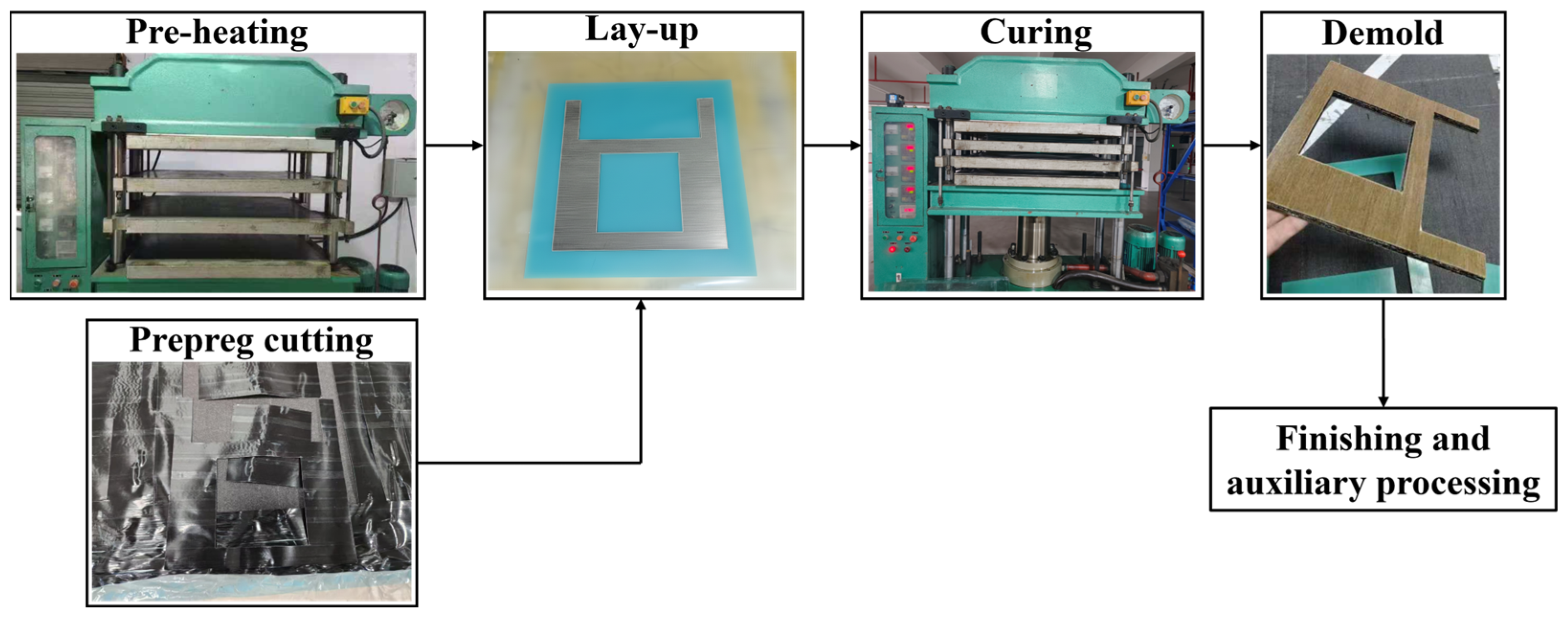
2.3.1. Preparation of the Composites
2.3.2. Vibration Tests
3. Results and Discussion
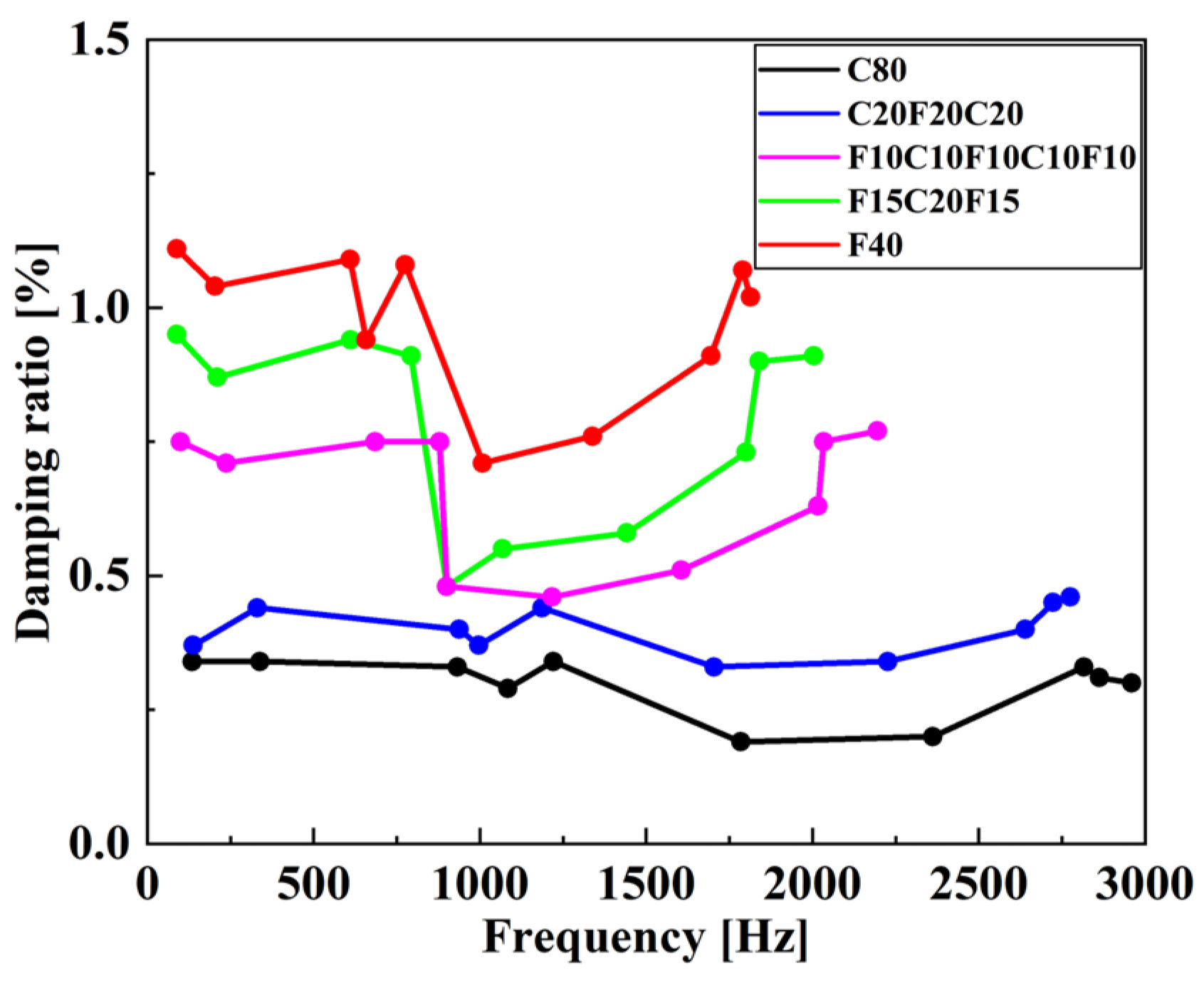
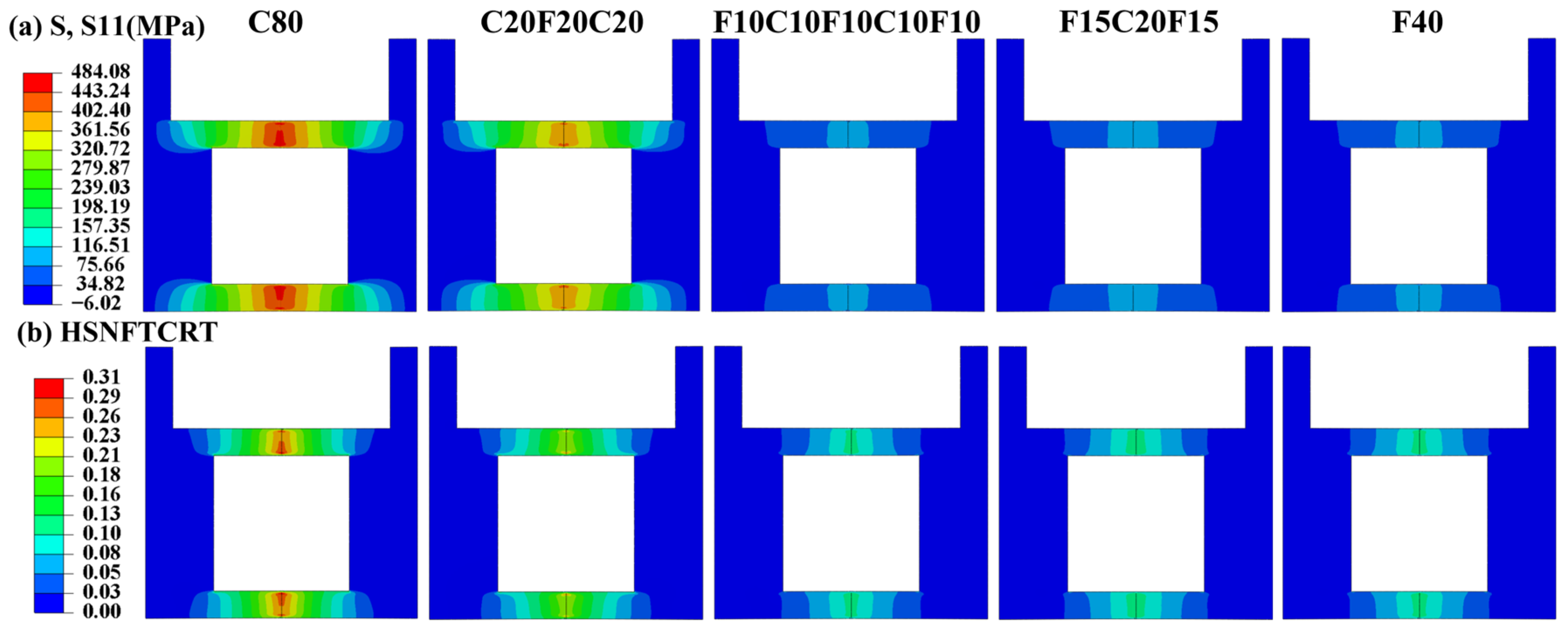
3.1. Effects of Stacking Sequences on the Damping Properties of CFFRC Structures
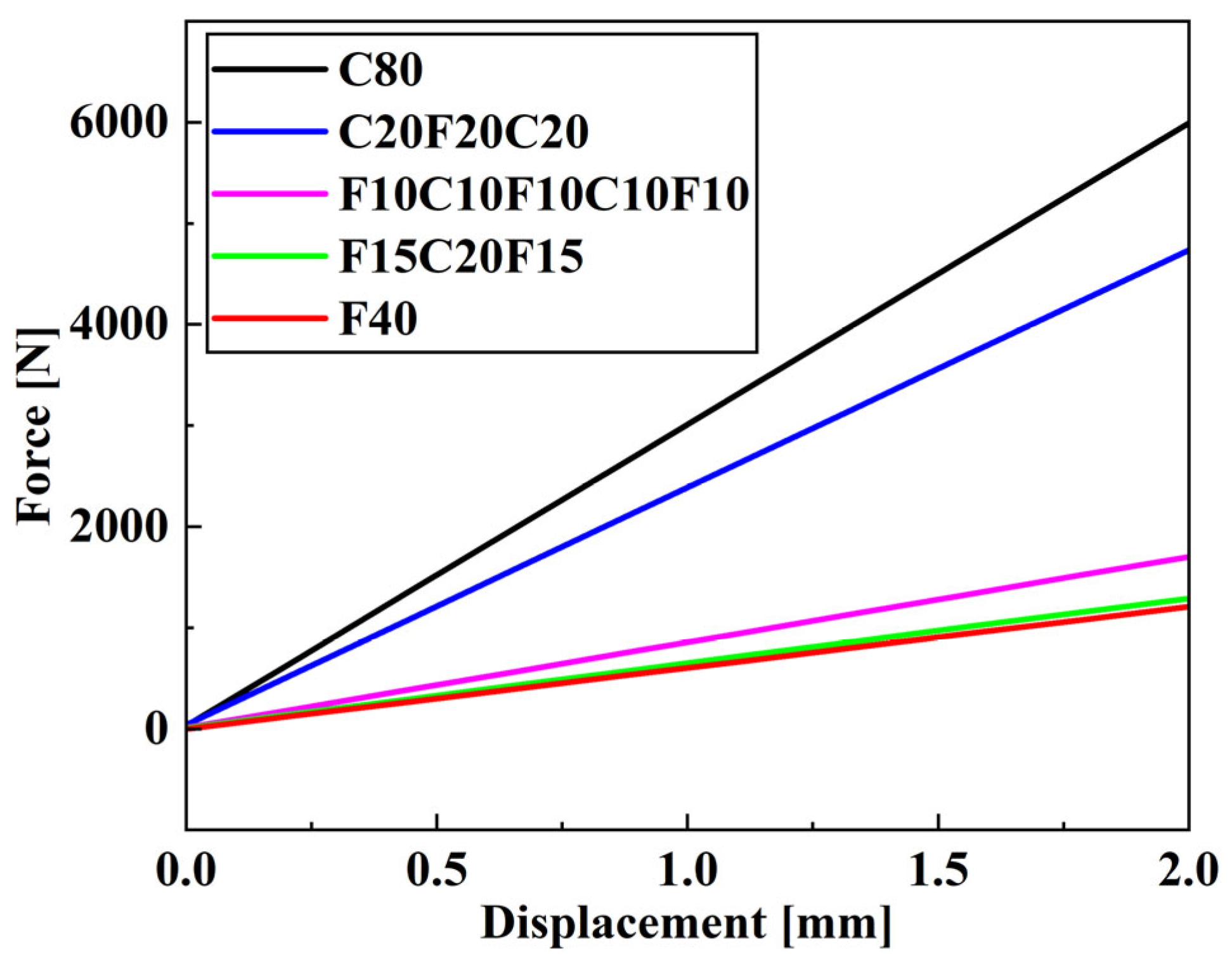
3.2. Effects of Stacking Sequences on the Bending Properties of CFFRC Structures
3.3. Mechanisms on Structural and Functional Integrated Optimization Design of CFFRC Structures
4. Conclusions
- (1)
- The effects of the stacking sequences on the bending and damping properties of CFFRC structures were evaluated by developing a finite element (FE) model integrating laminate theory, the Hashin failure criterion, and the complex eigenvalue method. The stacking sequence of carbon or flax fiber had a considerable impact on the damping ratio of the CFFRC structure, with the greatest improvement by placing the flax fibers in the outermost layer, whereas the bending strength decreased as the number of flax fiber layers positioned close to the outer layer. The balance between the damping and bending properties should be considered for structural design. The CFFRC structure with the stacking sequence of F10C10F10C10F10 exhibited balanced damping and bending properties.
- (2)
- Mechanisms of load-bearing and damping functional integrated optimization design of CFFRC structures were clarified. High damping capacity of the outer layers could absorb and dissipate effective vibrational energy before it propagates deep into the structure. The hierarchical structure and viscoelastic behaviors of flax fibers created additional pathways for energy dissipation at the interface between each cell wall layer and the micro-fibrillated sub-layers. The maximum compressive and tensile stresses were observed at the upper and lower layers of the CFFRC structures under bending load, with relatively low shear stress. When flax fiber as the outer layer was substituted with carbon fiber, the carbon fiber layer could sustain a high bending load.
- (3)
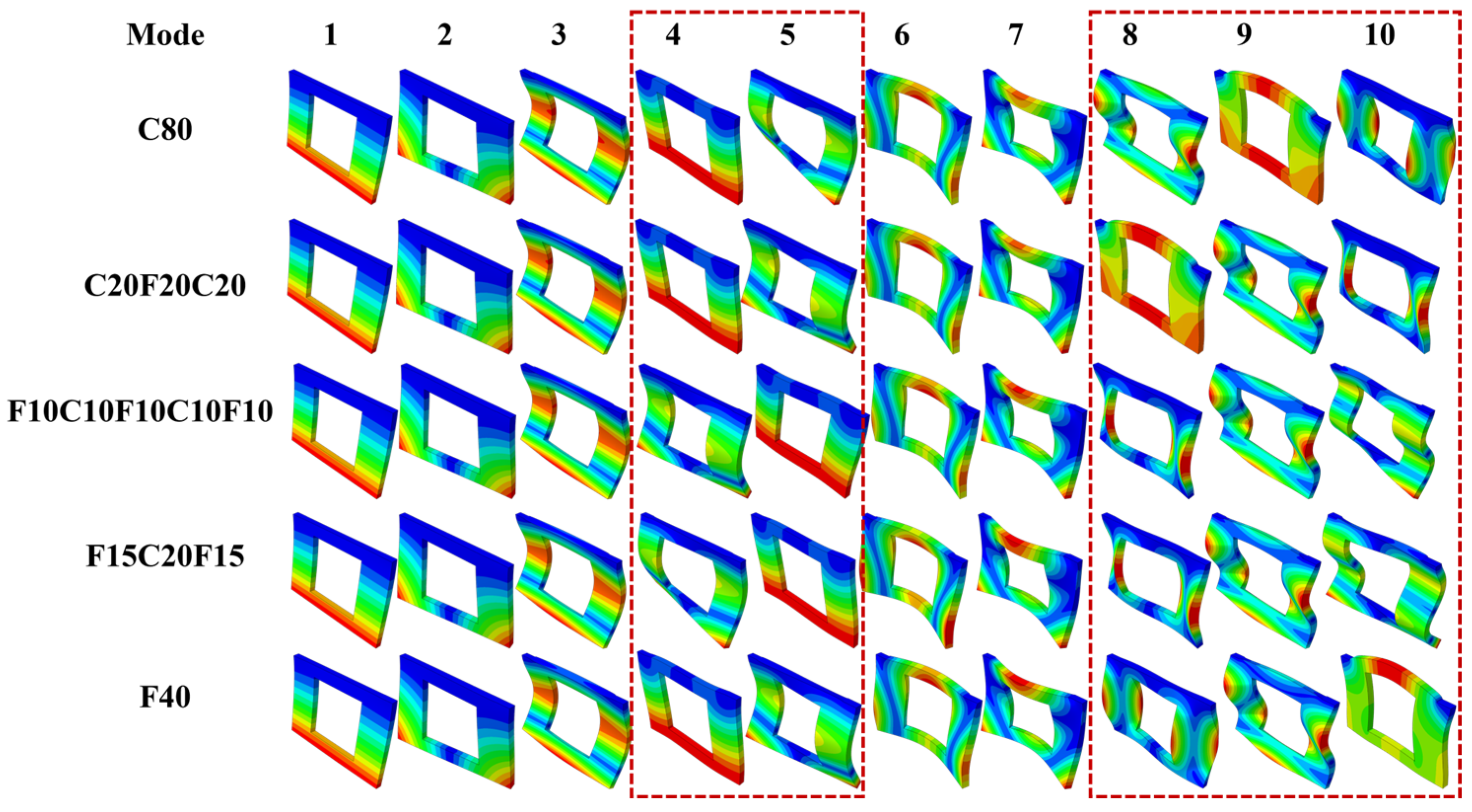
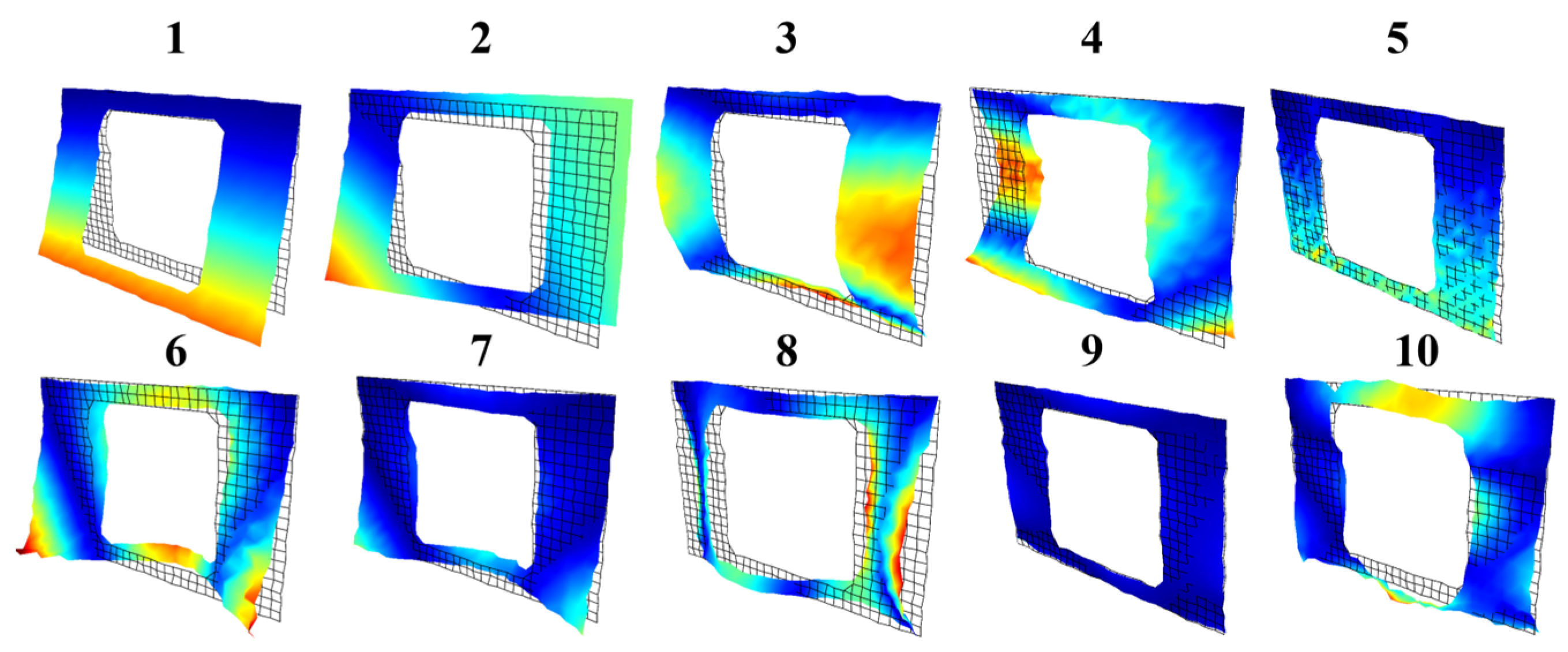
- The experimental modal behaviors (modal damping ratios, modal frequencies, and vibration mode shapes) of CFFRC structures with the optimal stacking sequence were identified by employing a non-contacting 3D Scanning Laser Doppler Vibrometer (SLDV) in vibration tests. The effects of the stacking sequences on the mode shapes tended to primarily occur in high-order modes. A significant agreement between the experimental first seven mode shapes and those derived from the established model was achieved. The findings provided essential parameters for designing subway interior structures that are both safe and reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PFRCs | Plant fiber-reinforced composites |
| CFFRCs | Carbon/flax fiber-reinforced epoxy composites |
| FRPs | Fiberglass-reinforced polymers |
| FE | Finite element |
| SLDV | Scanning Laser Doppler Vibrometer |
| CFRCs | Carbon fiber-reinforced composites |
| FFRCs | Flax fiber-reinforced composites |
| UMAT | User-defined material subroutine |
| ODS | Operational Deformation Shape |
References
- Saeedi, A.; Motavalli, M.; Shahverdi, M. Recent Advancements in the Applications of Fiber—Reinforced Polymer Structures in Railway Industry—A Review. Polym. Compos. 2024, 45, 77–97. [Google Scholar] [CrossRef]
- Chango, I.V.L.; Chen, J. Numerical and Statistical Evaluation of the Performance of Carbon Fiber-Reinforced Polymers as Tunnel Lining Reinforcement during Subway Operation. Buildings 2022, 12, 1913. [Google Scholar] [CrossRef]
- Navaratnam, S.; Selvaranjan, K.; Jayasooriya, D.; Rajeev, P.; Sanjayan, J. Applications of Natural and Synthetic Fiber Reinforced Polymer in Infrastructure: A Suitability Assessment. J. Build. Eng. 2023, 66, 105835. [Google Scholar] [CrossRef]
- Manso-Morato, J.; Hurtado-Alonso, N.; Revilla-Cuesta, V.; Skaf, M.; Ortega-López, V. Fiber-Reinforced Concrete and Its Life Cycle Assessment: A Systematic Review. J. Build. Eng. 2024, 94, 110062. [Google Scholar] [CrossRef]
- Zhang, Z.; Cai, S.; Li, Y.; Wang, Z.; Long, Y.; Yu, T.; Shen, Y. High Performances of Plant Fiber Reinforced Composites—A New Insight from Hierarchical Microstructures. Compos. Sci. Technol. 2020, 194, 108151. [Google Scholar] [CrossRef]
- Muneer Ahmed, M.; Dhakal, H.N.; Zhang, Z.Y.; Barouni, A.; Zahari, R. Enhancement of Impact Toughness and Damage Behaviour of Natural Fibre Reinforced Composites and Their Hybrids through Novel Improvement Techniques: A Critical Review. Compos. Struct. 2021, 259, 113496. [Google Scholar] [CrossRef]
- Li, M.; Pu, Y.; Thomas, V.M.; Yoo, C.G.; Ozcan, S.; Deng, Y.; Nelson, K.; Ragauskas, A.J. Recent Advancements of Plant-Based Natural Fiber–Reinforced Composites and Their Applications. Compos. Part B Eng. 2020, 200, 108254. [Google Scholar] [CrossRef]
- Pinto, F.; Boccarusso, L.; De Fazio, D.; Cuomo, S.; Durante, M.; Meo, M. Carbon/Hemp Bio-Hybrid Composites: Effects of the Stacking Sequence on Flexural, Damping and Impact Properties. Compos. Struct. 2020, 242, 112148. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Yang, L.; Du, J. Research on Mechanical Properties and Durability of Flax/Glass Fiber Bio-Hybrid FRP Composites Laminates. Compos. Struct. 2022, 290, 115566. [Google Scholar] [CrossRef]
- Tan, S.; Zhang, Z.; Li, Q.; Yang, W.; Yu, T.; Li, Y. Characterization and Prediction of Frequency- and Moisture-Dependent Damping Behaviors for Hierarchical Flax Fiber Reinforced Composite Laminates. Compos. Sci. Technol. 2024, 254, 110682. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Ma, H.; Cai, S.; Huang, X. Effect of Processing Temperature on the Static and Dynamic Mechanical Properties and Failure Mechanisms of Flax Fiber Reinforced Composites. Compos. Commun. 2020, 20, 100343. [Google Scholar] [CrossRef]
- Karthi, N.; Kumaresan, K.; Sathish, S.; Gokulkumar, S.; Prabhu, L.; Vigneshkumar, N. An Overview: Natural Fiber Reinforced Hybrid Composites, Chemical Treatments and Application Areas. Mater. Today Proc. 2020, 27, 2828–2834. [Google Scholar] [CrossRef]
- Mohammed, M.; Jawad, A.J.M.; Mohammed, A.M.; Oleiwi, J.K.; Adam, T.; Osman, A.F.; Dahham, O.S.; Betar, B.O.; Gopinath, S.C.B.; Jaafar, M. Challenges and Advancement in Water Absorption of Natural Fiber-Reinforced Polymer Composites. Polym. Test. 2023, 124, 108083. [Google Scholar] [CrossRef]
- Assarar, M.; Zouari, W.; Sabhi, H.; Ayad, R.; Berthelot, J.-M. Evaluation of the Damping of Hybrid Carbon–Flax Reinforced Composites. Compos. Struct. 2015, 132, 148–154. [Google Scholar] [CrossRef]
- Li, Y.; Cai, S.; Huang, X. Multi-Scaled Enhancement of Damping Property for Carbon Fiber Reinforced Composites. Compos. Sci. Technol. 2017, 143, 89–97. [Google Scholar] [CrossRef]
- Ben Ameur, M.; El Mahi, A.; Rebiere, J.-L.; Abdennadher, M.; Haddar, M. Damping Analysis of Unidirectional Carbon/Flax Fiber Hybrid Composites. Int. J. Appl. Mech. 2018, 10, 1850050. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q. Plant Fiber Reinforced Composites; Engineering Materials; Springer Nature: Singapore, 2022; pp. 220–221. [Google Scholar]
- He, Y.; Xiao, Y.; Liu, Y.; Zhang, Z. An Efficient Finite Element Method for Computing Modal Damping of Laminated Composites: Theory and Experiment. Compos. Struct. 2018, 184, 728–741. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Y.; Zhang, Z.; He, Y. Modal damping prediction of laminated composites using elastic-viscoelastic correspond-ence principle: Theory and finite element implementation. Acta Mater. Compos. Sin. 2017, 34, 1478–1488. [Google Scholar] [CrossRef]
- Hashin, Z. Complex Moduli of Viscoelastic Composites—II. Fiber Reinforced Materials. Int. J. Solids Struct. 1970, 6, 797–807. [Google Scholar] [CrossRef]
- Wan, Y.; Liu, Y.; Hu, C.; Yao, J.; Wang, F.; Yang, B. The Failure Mechanism of Curved Composite Laminates Subjected to Low-Velocity Impact. Acta Mech. Sin. 2023, 39, 423113. [Google Scholar] [CrossRef]
- Duc, F.; Bourban, P.E.; Månson, J.-A.E. The Role of Twist and Crimp on the Vibration Behaviour of Flax Fibre Composites. Compos. Sci. Technol. 2014, 102, 94–99. [Google Scholar] [CrossRef]
- Amenini, F.; Brocail, J.; Chauvin, M.; Thuillier, S. Dynamical Properties of Flax Fibre Reinforced PA11 over a Large Frequency Range. Compos. Sci. Technol. 2019, 171, 234–243. [Google Scholar] [CrossRef]
- Liu, T.; Butaud, P.; Placet, V.; Ouisse, M. Damping Behavior of Plant Fiber Composites: A Review. Compos. Struct. 2021, 275, 114392. [Google Scholar] [CrossRef]
- Wei, D.; Nurakhmetov, D.; Spitas, C.; Aniyarov, A.; Zhang, D. Nonlinear Dynamical Analysis of Some Microelectromechanical Resonators with Internal Damping. Acta Mech. Sin. 2021, 37, 1457–1466. [Google Scholar] [CrossRef]
- Li, Y.; Yi, X.; Yu, T.; Xian, G. An Overview of Structural-Functional-Integrated Composites Based on the Hierarchical Microstructures of Plant Fibers. Adv. Compos. Hybrid Mater. 2018, 1, 231–246. [Google Scholar] [CrossRef]

| E1 (GPa) | E2 (GPa) | E3 (GPa) | v12 | v13 | v23 | G12 (GPa) | G13 (GPa) | G23 (GPa) | Density | |
|---|---|---|---|---|---|---|---|---|---|---|
| CFRCs | 160 | 8.7 | 8.7 | 0.30 | 0.30 | 0.45 | 6.5 | 6.5 | 3.25 | 1690 (kg/m3) |
| FFRCs | 32 | 2.6 | 2.6 | 0.12 | 0.12 | 0.14 | 1.4 | 1.4 | 0.7 | 1120 (kg/m3) |
| Laminates | Ply Number Ratio (Flax/Carbon) | Stacking Sequence |
|---|---|---|
| C80 | 0/80 |  |
| C20F20C20 | 20/40 | 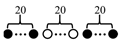 |
| F15C20F15 | 30/20 | 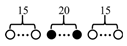 |
| F10C10F10C10F10 | 30/20 | 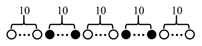 |
| F40 | 40 | 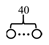 |
| Xt (MPa) | Xc (MPa) | Yt (MPa) | Yc (MPa) | S (MPa) | |
|---|---|---|---|---|---|
| CFRCs | 895 | 626 | 25 | 52 | 37 |
| FFRCs | 275 | 192 | 16 | 32 | 24 |
| Mode | Frequency (Hz) | Damping Ratio (%) | ||
|---|---|---|---|---|
| Num | Exp | Num | Exp | |
| 1 | 99.37 | 91.24 | 0.75 | 0.91 |
| 2 | 237.24 | 215.68 | 0.71 | 0.93 |
| 3 | 685.03 | 636.79 | 0.75 | 0.87 |
| 4 | 878.73 | 849.50 | 0.75 | 0.95 |
| 5 | 899.91 | 862.18 | 0.48 | 0.76 |
| 6 | 1216.6 | 1170.93 | 0.46 | 0.72 |
| 7 | 1605.3 | 1583.51 | 0.51 | 0.78 |
| 8 | 2016.1 | 1942.76 | 0.63 | 0.84 |
| 9 | 2033.8 | 1993.09 | 0.75 | 0.96 |
| 10 | 2195.5 | 2007.56 | 0.77 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, S.; Cao, A.; Zhang, Z.; Li, Q. Damping Optimization Design of Plant Fiber-Reinforced Composites for Subway Interior Structures. Appl. Sci. 2025, 15, 12281. https://doi.org/10.3390/app152212281
Tan S, Cao A, Zhang Z, Li Q. Damping Optimization Design of Plant Fiber-Reinforced Composites for Subway Interior Structures. Applied Sciences. 2025; 15(22):12281. https://doi.org/10.3390/app152212281
Chicago/Turabian StyleTan, Songli, Andong Cao, Zhen Zhang, and Qian Li. 2025. "Damping Optimization Design of Plant Fiber-Reinforced Composites for Subway Interior Structures" Applied Sciences 15, no. 22: 12281. https://doi.org/10.3390/app152212281
APA StyleTan, S., Cao, A., Zhang, Z., & Li, Q. (2025). Damping Optimization Design of Plant Fiber-Reinforced Composites for Subway Interior Structures. Applied Sciences, 15(22), 12281. https://doi.org/10.3390/app152212281





