Energy-Efficient Coaxial Electrocoagulation for Integrated Treatment of Urban Wastewater and Acid Mine Drainage: A Response-Surface Approach
Abstract
1. Introduction
2. Materials and Methods
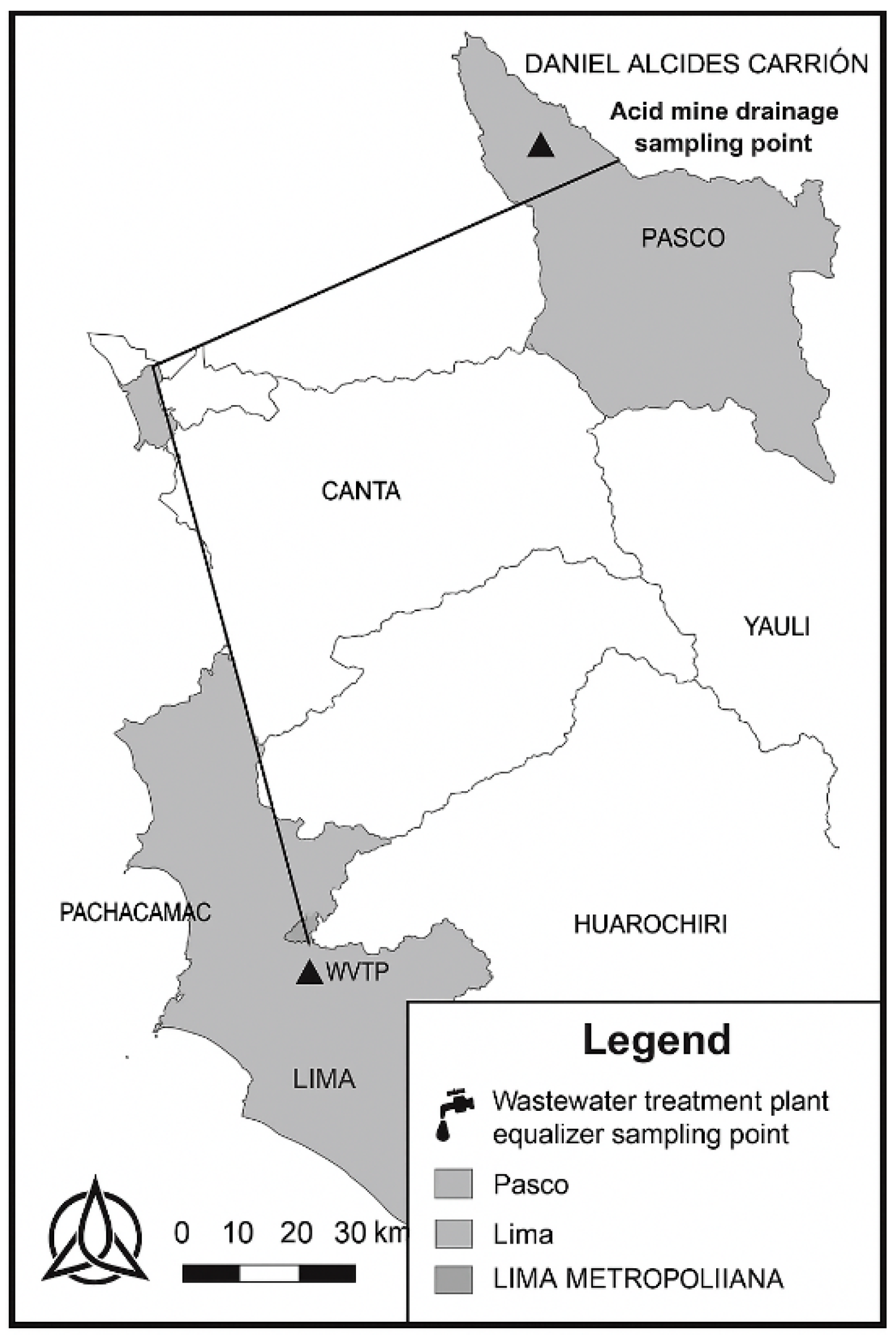
2.1. Sampling of MWW and AMD
2.2. Characterization of Municipal Wastewater and Acid Water
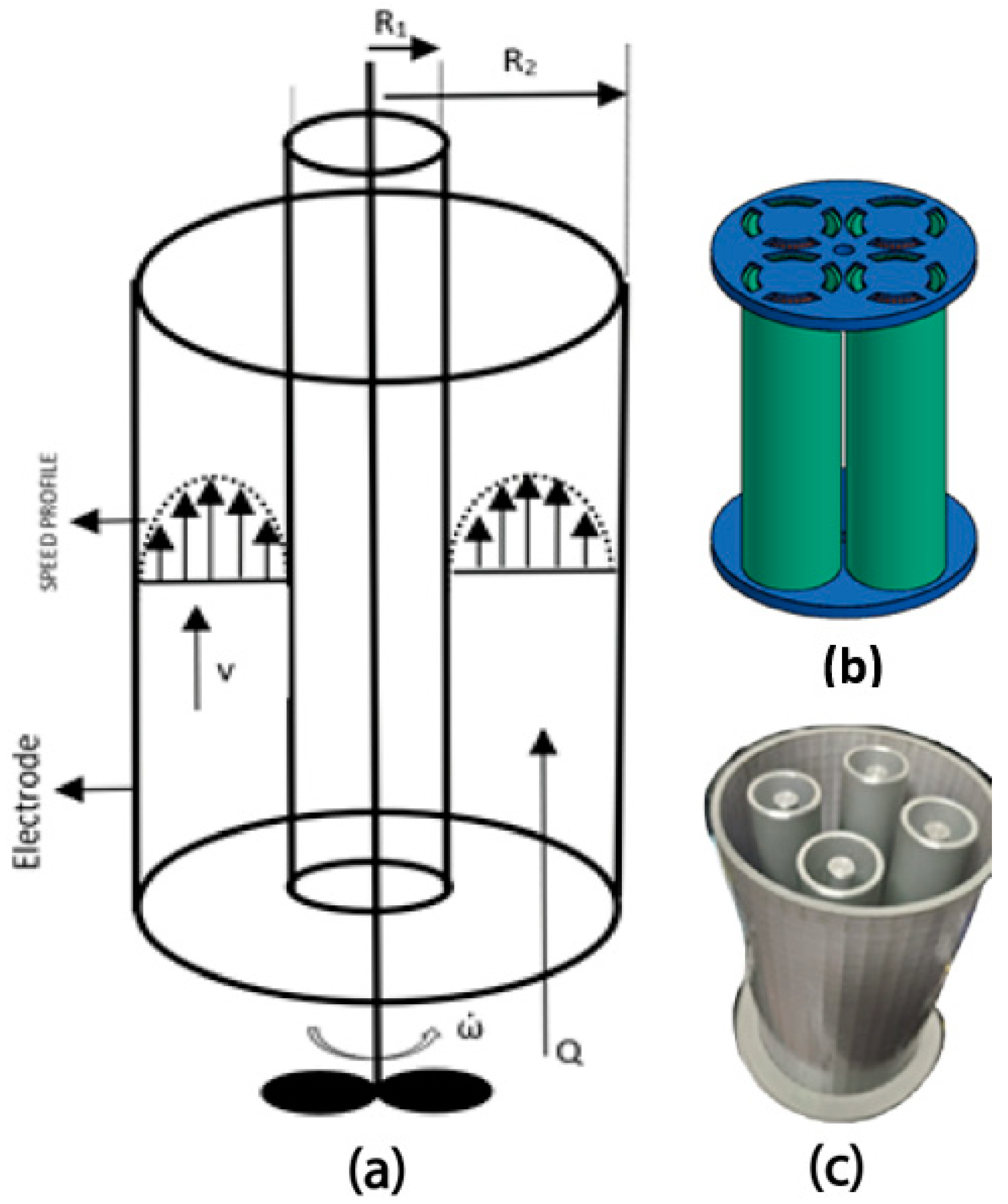
2.3. Design of Coaxial Electrode
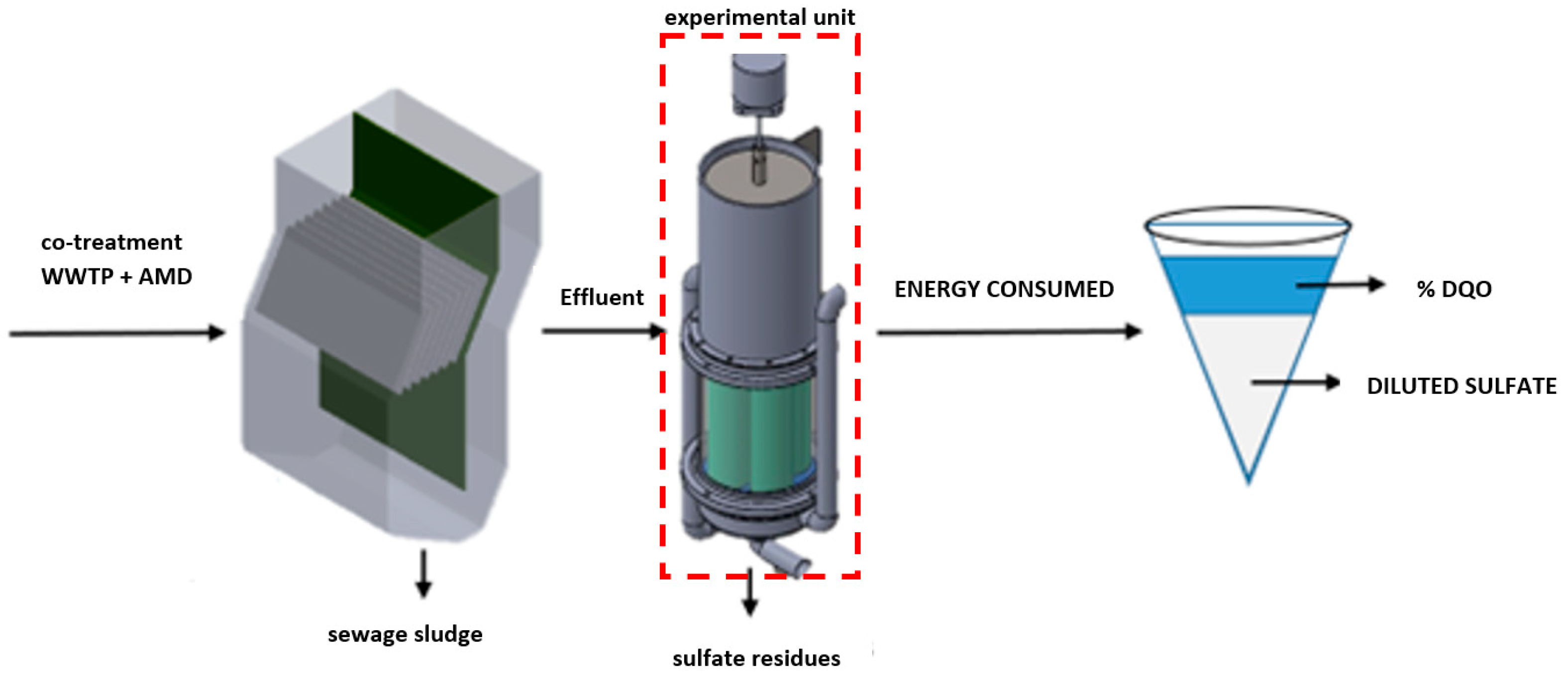
2.4. Coaxial Electrocoagulation Reactor
2.4.1. Electrode Maintenance and Cleaning
2.4.2. Pre-EC Clarification and Feed Quality
2.4.3. EC Operation

2.5. Experimental Procedure
2.5.1. Preliminary Experiments for the Volumetric Ratio of AMD and MWW
2.5.2. Operation of the Coaxial Electrocoagulation System
2.5.3. Experimental Design
2.5.4. Control Samples and Validation
2.6. COD Removal Efficiency
2.7. COD Determination
2.8. Energy Consumption
2.9. Statistical Analysis
2.9.1. Effects Analysis and Model Generation
2.9.2. Model Adjustment
2.9.3. Model Optimization
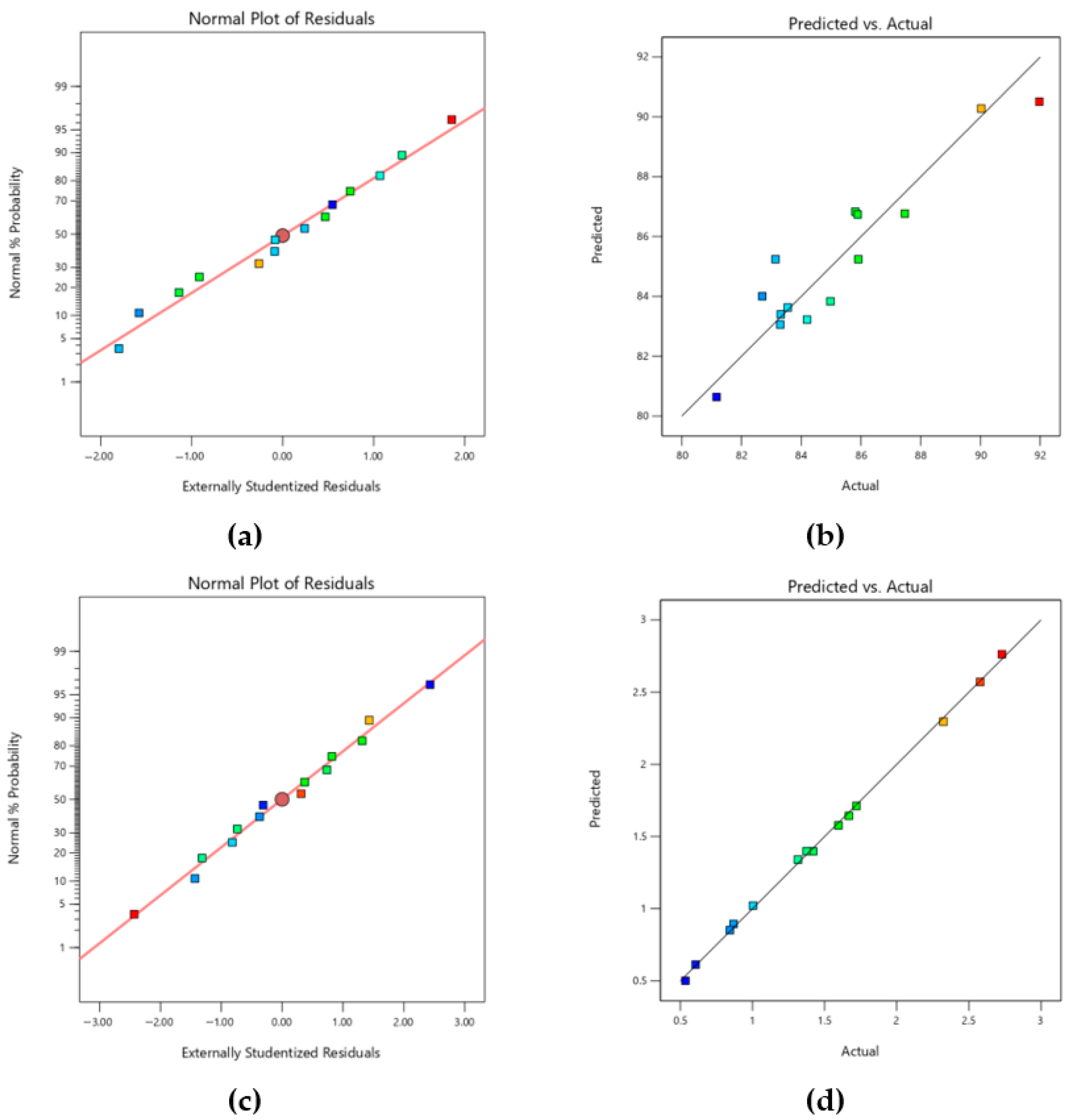
2.9.4. Cross-Validation and Influence Diagnostics
3. Results
3.1. Descriptive Results
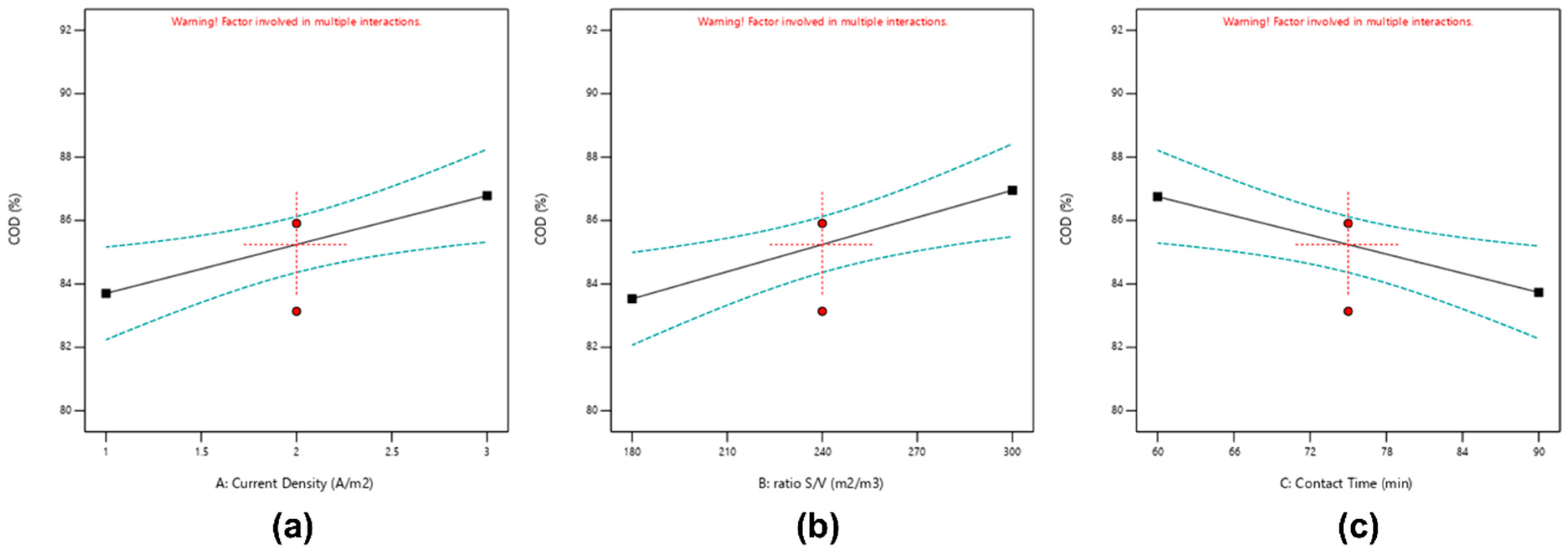
3.2. Effect of Experimental Factors
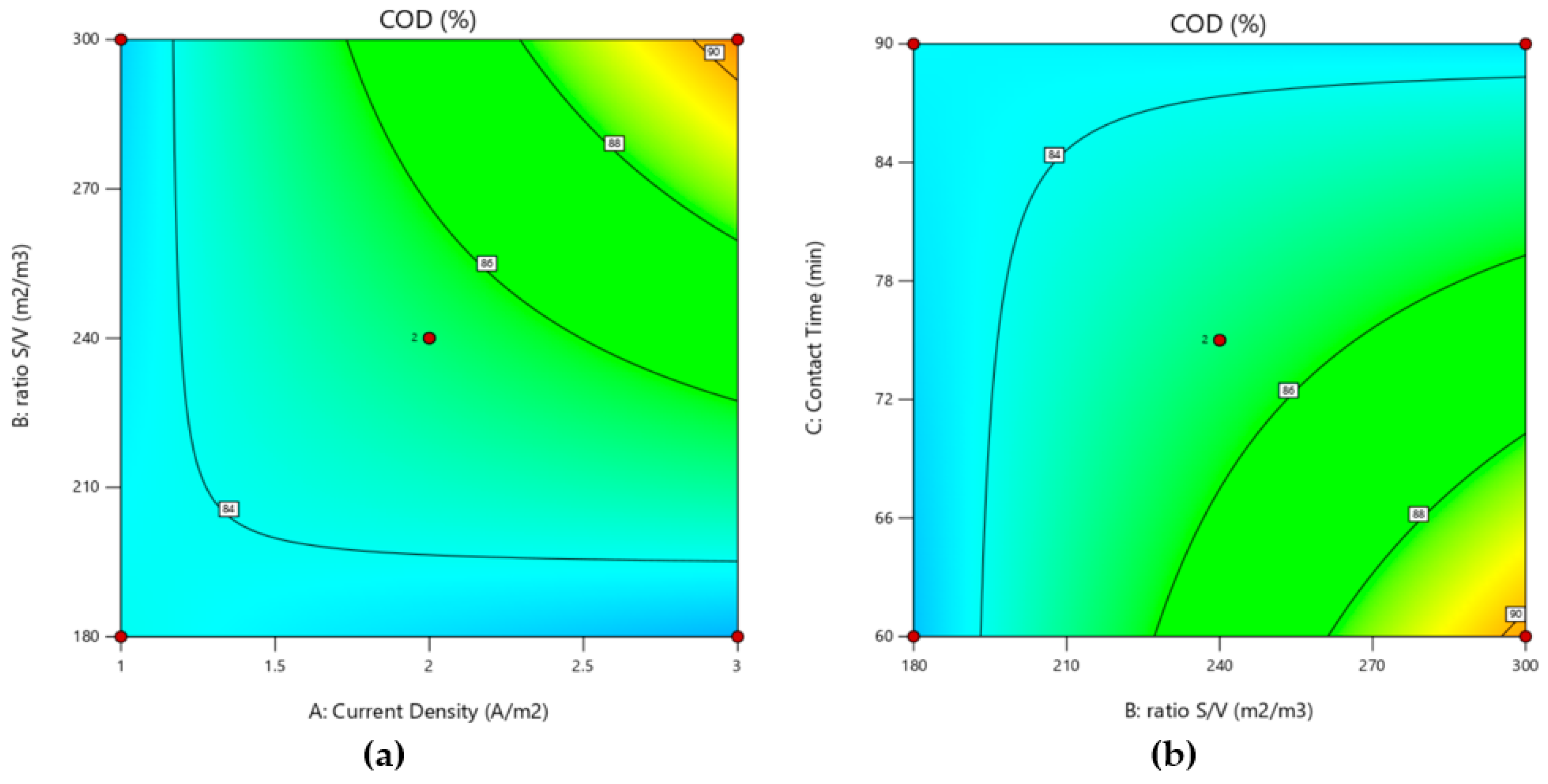
3.2.1. Effect of COD Removal
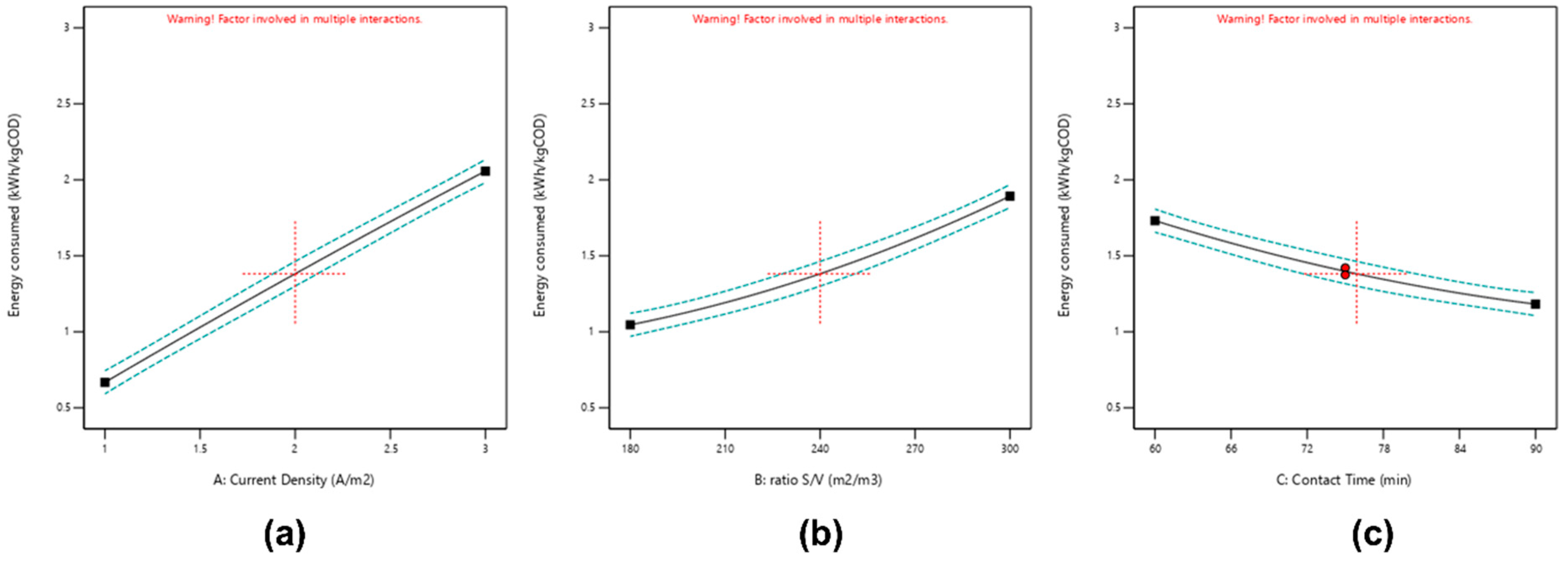
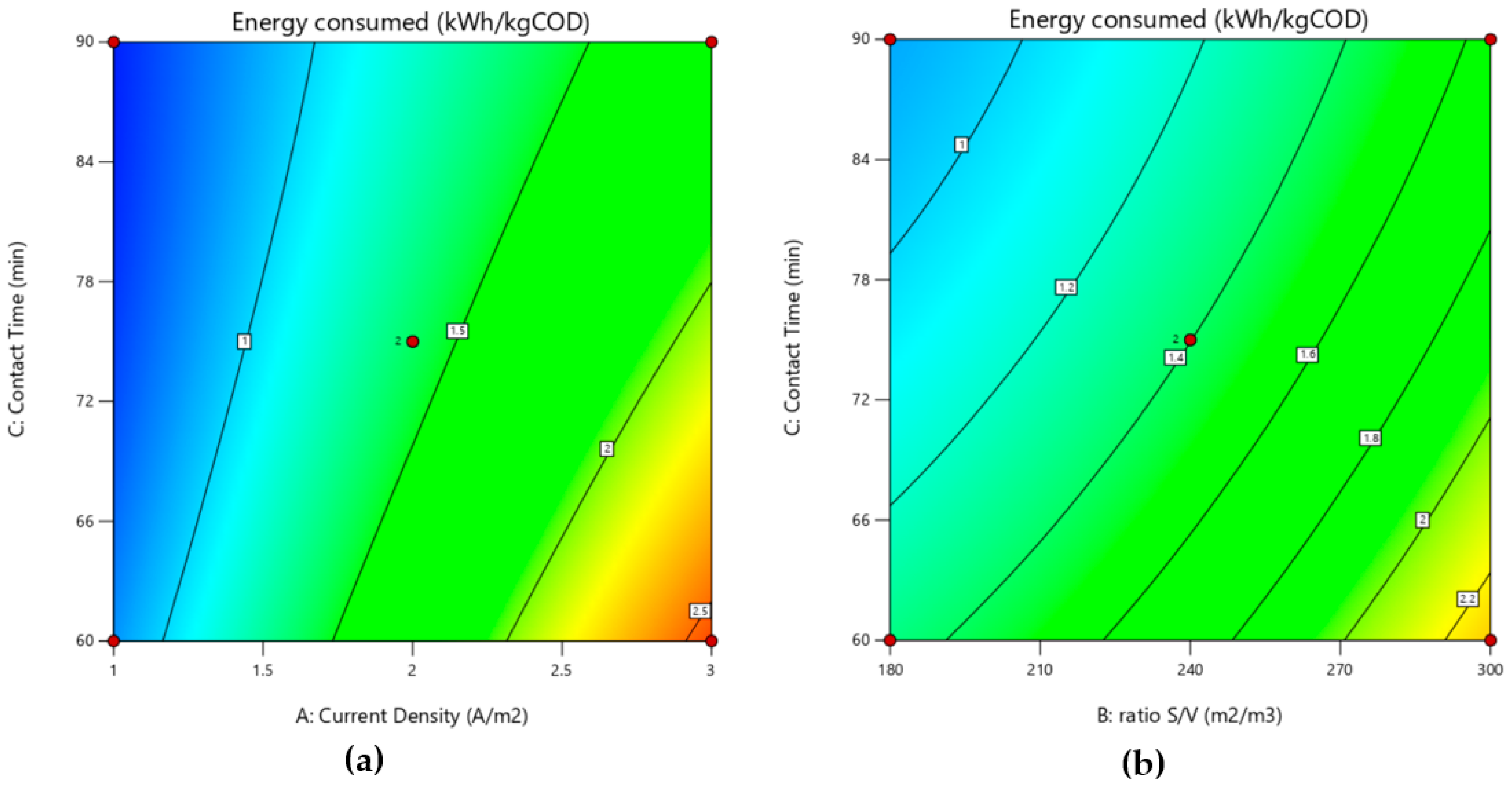
3.2.2. Effect of Energy Consumed
3.3. Analysis of Variance (ANOVA) and Fitting of the RSM-BBD Model
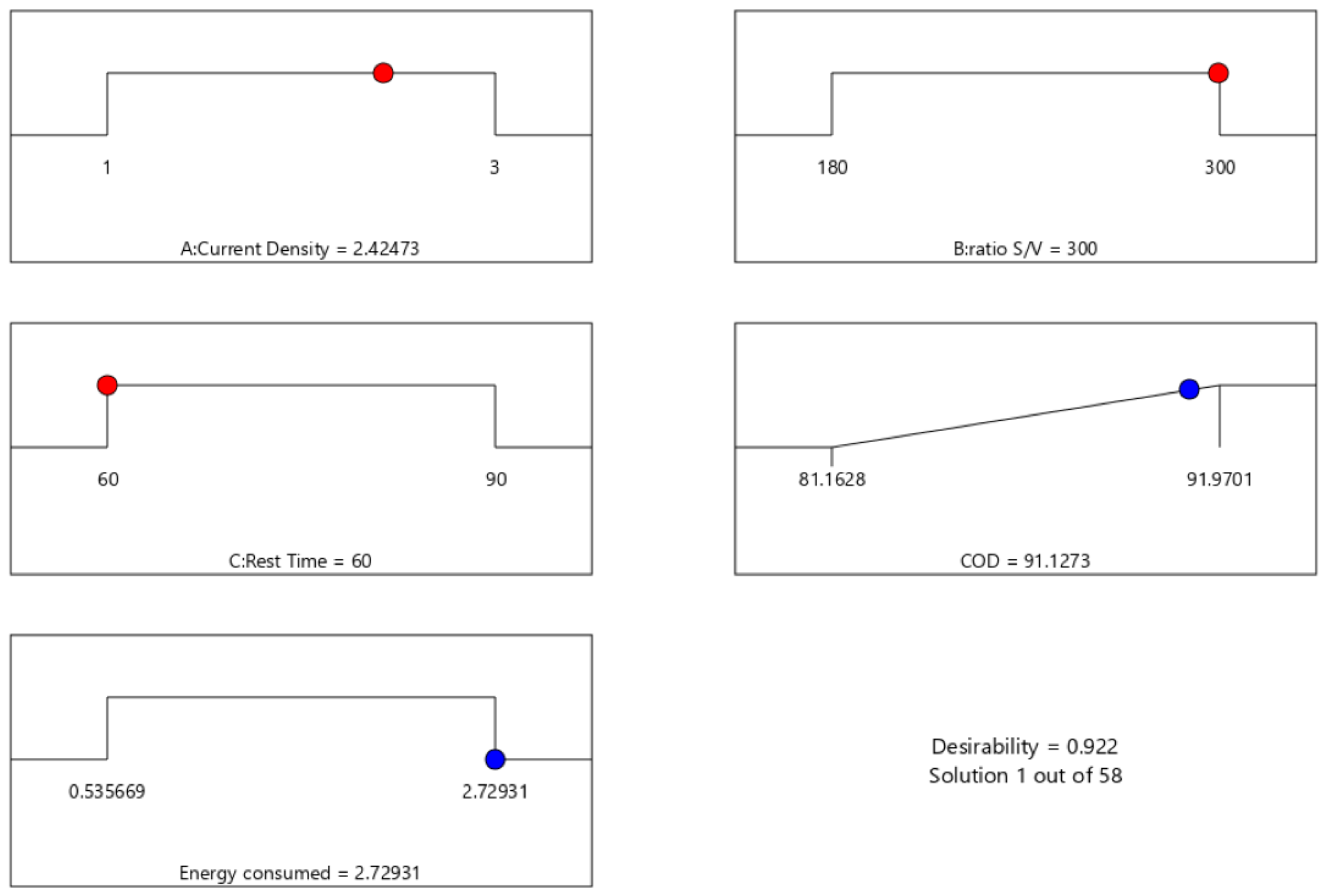
3.4. Optimization of Process Parameters
3.5. Sludge Generation and Post-EC Effluent Quality
3.6. Energy–Removal Trade-Off and Diminishing Returns
3.7. Reproducibility and Scope
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khosa, M.K.; Jamal, M.A.; Hussain, A.; Muneer, M.; Zia, K.M.; Hafeez, S. Efficiency of aluminum and iron electrodes for the removal of heavy metals [(Ni (II), Pb (II), Cd (II)] by electrocoagulation method. J. Korean Chem. Soc. 2013, 57, 316–321. [Google Scholar] [CrossRef]
- Stylianou, M.; Montel, E.; Zissimos, A.; Christoforou, I.; Dermentzis, K.; Agapiou, A. Removal of toxic metals and anions from acid mine drainage (AMD) by electrocoagulation: The case of North Mathiatis open cast mine. Sustain. Chem. Pharm. 2022, 29, 100737. [Google Scholar] [CrossRef]
- Mamelkina, M.A.; Cotillas, S.; Lacasa, E.; Sáez, C.; Tuunila, R.; Sillanpää, M.; Häkkinen, A.; Rodrigo, M.A. Removal of sulfate from mining waters by electrocoagulation. Sep. Purif. Technol. 2017, 182, 87–93. [Google Scholar] [CrossRef]
- Felipe, E.C.B.; Batista, K.A.; Ladeira, A.C.Q. Recovery of rare earth elements from acid mine drainage by ion exchange. Environ. Technol. 2021, 42, 2721–2732. [Google Scholar] [CrossRef] [PubMed]
- Nkuna, C.N.; Sadiku, E.R.; Perry, G.; Oboirien, B.; Dludlu, M.K.; Thompson, C. Treatment of acid mine drainage and chromium (VI) removal using synthesised chitosan composites blended with kenaf fibre and γ-Fe2O3 nanoparticles. Int. J. Environ. Sci. Technol. 2023, 20, 3599–3612. [Google Scholar] [CrossRef]
- Zendelska, A.; Golomeova, M.; Golomeov, B.; Krstev, B. Removal of zinc ions from acid aqueous solutions and acid mine drainage using zeolite-bearing tuff. Mine Water Environ. 2019, 38, 187–196. [Google Scholar] [CrossRef]
- Gugushe, A.S.; Nqombolo, A.; Nomngongo, P.N. Application of response surface methodology and desirability function in the optimization of adsorptive remediation of arsenic from acid mine drainage using magnetic nanocomposite: Equilibrium studies and application to real samples. Molecules 2019, 24, 1792. [Google Scholar] [CrossRef]
- Pino, L.; Vargas, C.; Schwarz, A.; Borquez, R. Influence of operating conditions on the removal of metals and sulfate from copper acid mine drainage by nanofiltration. Chem. Eng. J. 2018, 345, 114–125. [Google Scholar] [CrossRef]
- Ambiado, K.; Bustos, C.; Schwarz, A.; Bórquez, R. Membrane technology applied to acid mine drainage from copper mining. Water Sci. Technol. 2017, 75, 705–715. [Google Scholar] [CrossRef]
- Pramanik, B.K.; Shu, L.; Jegatheesan, J.; Shah, K.; Haque, N.; Bhuiyan, M.A. Rejection of rare earth elements from a simulated acid mine drainage using forward osmosis: The role of membrane orientation, solution pH, and temperature variation. Process Saf. Environ. Prot. 2019, 126, 53–59. [Google Scholar] [CrossRef]
- Buzzi, D.C.; Viegas, L.S.; Rodrigues, M.A.S.; Bernardes, A.M.; Tenório, J.A.S. Water recovery from acid mine drainage by electrodialysis. Miner. Eng. 2013, 40, 82–89. [Google Scholar] [CrossRef]
- Gao, H.; Wang, S.; Xu, D.; Wang, X.; Zhong, Q.; Zhong, Y.; Li, J.; Cao, W. Study of DC magnetron sputtered Nb films. Crystals 2021, 12, 31. [Google Scholar] [CrossRef]
- Bwapwa, J.K.; Jaiyeola, A.T.; Chetty, R. Bioremediation of acid mine drainage using algae strains: A review. S. Afr. J. Chem. Eng. 2017, 24, 62–70. [Google Scholar] [CrossRef]
- Oncel, M.S.; Muhcu, A.; Demirbas, E.; Kobya, M. A comparative study of chemical precipitation and electrocoagulation for treatment of coal acid drainage wastewater. J. Environ. Chem. Eng. 2013, 1, 989–995. [Google Scholar] [CrossRef]
- Roccaro, P. Treatment processes for municipal wastewater reclamation: The challenges of emerging contaminants and direct potable reuse. Curr. Opin. Environ. Sci. Health 2018, 2, 46–54. [Google Scholar] [CrossRef]
- Petrie, B.; Barden, R.; Kasprzyk-Hordern, B. A review on emerging contaminants in wastewaters and the environment: Current knowledge, understudied areas and recommendations for future monitoring. Water Res. 2015, 72, 3–27. [Google Scholar] [CrossRef] [PubMed]
- Vélez-Pérez, L.S.; Ramirez-Nava, J.; Hernández-Flores, G.; Talavera-Mendoza, O.; Escamilla-Alvarado, C.; Poggi-Varaldo, H.M.; Solorza-Feria, O.; López-Díaz, J.A. Industrial acid mine drainage and municipal wastewater co-treatment by dual-chamber microbial fuel cells. Int. J. Hydrogen Energy 2020, 45, 13757–13766. [Google Scholar] [CrossRef]
- Hughes, T.A.; Gray, N.F.; Sánchez Guillamón, O. Removal of Metals and Acidity from Acid Mine Drainage Using Liquid and Dried Digested Sewage Sludge and Cattle Slurry. Mine Water Environ. 2013, 32, 108–120. [Google Scholar] [CrossRef]
- Strosnider, W.H.; Nairn, R.W.; Peer, R.A.M.; Winfrey, B.K. Passive co-treatment of Zn-rich acid mine drainage and raw municipal wastewater. J. Geochem. Explor. 2013, 125, 110–116. [Google Scholar] [CrossRef]
- Smyntek, P.M.; Chastel, J.; Peer, R.A.M.; Anthony, E.; McCloskey, J.; Bach, E.; Wagner, R.C.; Bandstra, J.Z.; Strosnider, W.H.J. Assessment of sulphate and iron reduction rates during reactor start-up for passive anaerobic co-treatment of acid mine drainage and sewage. Geochem. Explor. Environ. Anal. 2018, 18, 76–84. [Google Scholar] [CrossRef]
- Masindi, V.; Foteinis, S.; Chatzisymeon, E. Co-treatment of acid mine drainage and municipal wastewater effluents: Emphasis on the fate and partitioning of chemical contaminants. J. Hazard. Mater. 2022, 421, 126677. [Google Scholar] [CrossRef]
- Johnson, K.L.; Younger, P.L. The co-treatment of sewage and mine waters in aerobic wetlands. Eng. Geol. 2006, 85, 53–61. [Google Scholar] [CrossRef]
- Deng, D.; Lin, L.S. Two-stage combined treatment of acid mine drainage and municipal wastewater. Water Sci. Technol. 2013, 67, 1000–1007. [Google Scholar] [CrossRef] [PubMed]
- Ruihua, L.; Lin, Z.; Tao, T.; Bo, L. Phosphorus removal performance of acid mine drainage from wastewater. J. Hazard. Mater. 2011, 190, 669–676. [Google Scholar] [CrossRef]
- Sánchez-Andrea, I.; Triana, D.; Sanz, J.L. Bioremediation of acid mine drainage coupled with domestic wastewater treatment. Water Sci. Technol. 2012, 66, 2425–2431. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Wang, X.; Luo, W.; Sun, J.; Xu, Q.; Chen, F.; Zhao, J.; Wang, S.; Yao, F.; Wang, D. Effectiveness and mechanisms of phosphate adsorption on iron-modified biochars derived from waste activated sludge. Bioresour. Technol. 2018, 247, 537–544. [Google Scholar] [CrossRef]
- Abdollahi, J.; Moghaddam, M.R.A.; Habibzadeh, S. The role of the current waveform in mitigating passivation and enhancing electrocoagulation performance: A critical review. Chemosphere 2023, 312, 137212. [Google Scholar] [CrossRef]
- Tegladza, I.D.; Xu, Q.; Xu, K.; Lv, G.; Lu, J. Electrocoagulation processes: A general review about role of electro-generated flocs in pollutant removal. Process Saf. Environ. Prot. 2021, 146, 169–189. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, P.; Li, J. Electrocoagulation technology for water purification: An update review on reactor design and some newly concerned pollutants removal. J. Environ. Manag. 2021, 296, 113259. [Google Scholar] [CrossRef]
- Ismail, M.M.; Erdemir, D.; Dincer, I. Hydrogen production with a novel coaxial cylindrical electrolyser: A CFD study. Int. J. Thermofluids 2024, 24, 100850. [Google Scholar] [CrossRef]
- Wang, J.-G.; Yang, Y.; Huang, Z.-H.; Kang, F. Coaxial carbon nanofibers/MnO2 nanocomposites as freestanding electrodes for high-performance electrochemical capacitors. Electrochim. Acta 2011, 56, 9240–9247. [Google Scholar] [CrossRef]
- Karajic, A.; Reculusa, S.; Heim, M.; Garrigue, P.; Ravaine, S.; Mano, N.; Kuhn, A. Bottom-up generation of miniaturized coaxial double electrodes with tunable porosity. Adv. Mater. Interfaces 2015, 2, 1–5. [Google Scholar] [CrossRef]
- Shemer, H.; Semiat, R. Comparing the effects of Cu-Ti/RuO2-IrO2 electrode configuration on the electro-reduction of nitrate. Water Sci. Technol. 2022, 86, 1642–1652. [Google Scholar] [CrossRef]
- Kupriashov, A.V.; Shestakov, I.Y. Influence of electrode arrangement method on specific energy consumption and productivity in electrosynthesis of fine graphite powder. Int. J. Adv. Manuf. Technol. 2022, 119, 7615–7628. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Dong, R.; Li, X. A large cathode surface area promotes electromethanogenesis at a proper external voltage in a single coaxial microbial electrolysis cell. Sci. Total Environ. 2023, 868, 161721. [Google Scholar] [CrossRef] [PubMed]
- Muddasar, M.; Liaquat, R.; Rahman, M.Z.U.; Khoja, A.H.; Aslam, A.; Basit, A. Coaxial microbial electrolysis cell for cost-effective bioenergy production and wastewater treatment of potato industry effluent. J. Chem. Technol. Biotechnol. 2023, 98, 2203–2213. [Google Scholar] [CrossRef]
- Wang, S.; Geng, Z.; Bi, S.; Wang, Y.; Gao, Z.; Jin, L.; Zhang, C. Recent advances and future prospects on Ni3S2-Based electrocatalysts for efficient alkaline water electrolysis. Green. Energy Environ. 2024, 9, 659–683. [Google Scholar] [CrossRef]
- Moussa, D.T.; El-Naas, M.H.; Nasser, M.; Al-Marri, M.J. A comprehensive review of electrocoagulation for water treatment: Potentials and challenges. J. Environ. Manag. 2017, 186, 24–41. [Google Scholar] [CrossRef]
- Hu, C.; Sun, J.; Wang, S.; Liu, R.; Liu, H.; Qu, J. Enhanced efficiency in HA removal by electrocoagulation through optimizing flocs properties: Role of current density and pH. Sep. Purif. Technol. 2017, 175, 248–254. [Google Scholar] [CrossRef]
- Deghles, A.; Kurt, U. Treatment of tannery wastewater by a hybrid electrocoagulation/electrodialysis process. Chem. Eng. Process Process Intensif. 2016, 104, 43–50. [Google Scholar] [CrossRef]
- Ji, M.; Jiang, X.; Wang, F. A mechanistic approach and response surface optimization of the removal of oil and grease from restaurant wastewater by electrocoagulation and electroflotation. Desalin Water Treat. 2015, 55, 2044–2052. [Google Scholar] [CrossRef]
- Holt, P.K.; Barton, G.W.; Mitchell, C.A. The future for electrocoagulation as a localised water treatment technology. Chemosphere 2005, 59, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Bravo-Toledo, L.; Virú-Vásquez, P.; Rodriguez-Flores, R.; Sierra-Flores, L.; Flores-Salinas, J.; Tineo-Cordova, F.; Palomino-Vildoso, R.; Madueño-Sulca, C.; Rios-Varillas de Oscanoa, C.; Pilco-Nuñez, A. Sustainability Prediction by Evaluating the Emergy of a Co-Treatment System for Municipal Wastewater and Acidic Water Using Intermittent Electrocoagulation. Water 2024, 16, 3081. [Google Scholar] [CrossRef]
- Coeuret, F. Introduccion a la Ingenieria Electroquimica; Editorial Reverte S.A: Ciudad de México, Mexico, 1992. [Google Scholar]
- Barreto-Pio, C.; Bravo-Toledo, L.; Virú-Vásquez, P.; Borda-Contreras, A.; Zarate-Sarapura, E.; Pilco, A. Optimization Applying Response Surface Methodology in the Co-treatment of Urban and Acid Wastewater from the Quiulacocha Lagoon, Pasco (Peru). Environ. Res. Eng. Manag. 2023, 79, 90–109. [Google Scholar] [CrossRef]
- Masindi, V.; Gitari, M.W.; Tutu, H.; De Beer, M.; Nekhwevha, N. Neutralization and attenuation of metal species in acid mine drainage and mine leachates using magnesite: A batch experimental approach. In Proceedings of the An Interdisciplinary Response to Mine Water Challenges—The Proceedings of the 12th IMWA Congress, Xuzhou, China, 18–22 August 2014; pp. 640–644. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Tir, M.; Moulai-Mostefa, N. Optimization of oil removal from oily wastewater by electrocoagulation using response surface method. J. Hazard. Mater. 2008, 158, 107–115. [Google Scholar] [CrossRef]
- Chen, X.; Chen, G.; Yue, P.L. Separation of pollutants from restaurant wastewater by electrocoagulation. Sep. Purif. Technol. 2000, 19, 65–76. [Google Scholar] [CrossRef]
- Ren, M.; Song, Y.; Xiao, S.; Zeng, P.; Peng, J. Treatment of berberine hydrochloride wastewater by using pulse electro-coagulation process with Fe electrode. Chem. Eng. J. 2011, 169, 84–90. [Google Scholar] [CrossRef]
- Dalvand, A.; Gholami, M.; Joneidi, A.; Mahmoodi, N.M. Dye removal, energy consumption and operating cost of electrocoagulation of textile wastewater as a clean process. Clean–Soil Air Water 2011, 39, 665–672. [Google Scholar] [CrossRef]
- Akkaya, G.K. Treatment of petroleum wastewater by electrocoagulation using scrap perforated (Fe-anode) and plate (Al and Fe-cathode) metals: Optimization of operating parameters by RSM. Chem. Eng. Res. Des. 2022, 187, 261–275. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, J.; Zhang, Y.; Lv, Y.; Dou, R.; Wen, S.; Li, L.; Chen, Y.; Hu, Y. Treatment of Ni-EDTA containing wastewater by electrocoagulation using iron scraps packed-bed anode. Chemosphere 2016, 164, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Un, U.T.; Aytac, E. Electrocoagulation in a packed bed reactor-complete treatment of color and cod from real textile wastewater. J. Environ. Manag. 2013, 123, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Hashim, K.S.; Shaw, A.; Al Khaddar, R.; Pedrola, M.O.; Phipps, D. Iron removal, energy consumption and operating cost of electrocoagulation of drinking water using a new flow column reactor. J. Environ. Manag. 2017, 189, 98–108. [Google Scholar] [CrossRef]
- Kambuyi, T.N.; Bejjany, B.; Lekhlif, B.; Mellouk, H.; Digua, K.; Dani, A. Design of a continuous-flow single-channel reactor using optimal experimental data from batch reactor for turbidity removal by electrocoagulation. J. Environ. Chem. Eng. 2021, 9, 104651. [Google Scholar] [CrossRef]
- Cheballah, K.; Sahmoune, A.; Messaoudi, K.; Drouiche, N.; Lounici, H. Simultaneous removal of hexavalent chromium and COD from industrial wastewater by bipolar electrocoagulation. Chem. Eng. Process Process Intensif. 2015, 96, 94–99. [Google Scholar] [CrossRef]
- Naje, A.S.; Chelliapan, S.; Zakaria, Z.; Abbas, S.A. Electrocoagulation using a rotated anode: A novel reactor design for textile wastewater treatment. J. Environ. Manag. 2016, 176, 34–44. [Google Scholar] [CrossRef]
- Naje, A.S.; Ajeel, M.A.; Alaba, P.A.; Chelliapan, S. Treatment of textile wastewater using a novel electrocoagulation reactor design. Wastewater Water Qual. 2018, 111–123. [Google Scholar]

| Parameter | Unit | Value |
|---|---|---|
| pH | pH unit | 5.70 |
| Turbidez | NTU | 3.60 |
| Conductivity | μS/cm | 2730.0 |
| BOD5 | mg/L | 151.20 |
| COD | mg/L | 255.50 |
| Sulfates | mg/L | 1542.8 |
| Total Phosphorus | mg/L | 8.50 |
| Parameter | Unit | Value |
|---|---|---|
| pH | pH unit | 1.74 |
| Turbidity | NTU | 23.07 |
| Conductivity | μS/cm | 1625.00 |
| Antimony | mg/L | 0.0050 |
| Arsenic | mg/L | 0.004 |
| Barium | mg/L | 0.0008 |
| Cadmium | mg/L | 0.28450 |
| Chromium | mg/L | 0.0040 |
| Total Iron | mg/L | 984.8 |
| Nickel | mg/L | 0.2075 |
| Lead | mg/L | 0.0010 |
| Selenium | mg/L | 0.004 |
| Thallium | mg/L | 0.0006 |
| Zinc | mg/L | 195.8 |
| Factors | Units | Minimum (−1) | Medium (0) | Maximum (+1) |
|---|---|---|---|---|
| Current density | A/m2 | 1 | 2 | 3 |
| Ratio S/V | m2/m3 | 180 | 240 | 300 |
| Contact time | min | 60 | 75 | 90 |
| Run | A: Current Density (A/m2) | B: Ratio S/V (m2/m3) | C: Electrolysis (Contact) Time (min) | COD Removal Efficiency % | Energy Consumption Efficiency (kWh/kg COD) |
|---|---|---|---|---|---|
| 1 | 2 | 180 | 60 | 84.19 | 1.32 |
| 2 | 2 | 240 | 75 | 85.91 | 1.37 |
| 3 | 1 | 180 | 75 | 82.69 | 0.54 |
| 4 | 2 | 300 | 60 | 90.02 | 2.32 |
| 5 | 3 | 240 | 90 | 85.81 | 1.72 |
| 6 | 3 | 240 | 60 | 85.89 | 2.58 |
| 7 | 2 | 300 | 90 | 83.55 | 1.67 |
| 8 | 2 | 240 | 75 | 83.14 | 1.42 |
| 9 | 3 | 300 | 75 | 91.97 | 2.73 |
| 10 | 1 | 240 | 60 | 87.47 | 0.84 |
| 11 | 2 | 180 | 90 | 84.98 | 0.87 |
| 12 | 1 | 240 | 90 | 81.16 | 0.61 |
| 13 | 1 | 300 | 75 | 83.31 | 1.00 |
| 14 | 3 | 180 | 75 | 83.30 | 1.60 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| %COD = 85.242 + 1.541 A + 1.712 B − 1.509 C + 2.01 AB + 1.556 AC − 1.815 BC | |||||
| Model | 99.76 | 6 | 16.63 | 8.54 | 0.0061 |
| A—current density | 19 | 1 | 19 | 9.76 | 0.0168 |
| B—ratio S/V | 23.44 | 1 | 23.44 | 12.04 | 0.0104 |
| C—electrolysis time | 18.23 | 1 | 18.23 | 9.36 | 0.0183 |
| AB | 16.23 | 1 | 16.23 | 8.33 | 0.0234 |
| AC | 9.69 | 1 | 9.69 | 4.98 | 0.0609 |
| BC | 13.17 | 1 | 13.17 | 6.77 | 0.0354 |
| Residual | 13.63 | 7 | 1.95 | ||
| Lack of fit | 9.78 | 6 | 1.63 | 0.4237 | 0.8246 |
| Pure error | 3.85 | 1 | 3.85 | ||
| Cor total | 113.39 | 13 | |||
| E (kWh/kg COD) = 1.39 + 0.70 A + 0.43 B − 0.275 C + 0.166 AB + 0.155 AC − 0.052 BC − 0.019 A2 + 0.088 B2 + 0.059 C2 | |||||
| Model | 6.28 | 9 | 0.6977 | 405.73 | <0.0001 |
| A—current density | 3.97 | 1 | 3.97 | 2307.09 | <0.0001 |
| B—ratio S/V | 1.45 | 1 | 1.45 | 845.83 | <0.0001 |
| C—electrolysis time | 0.6031 | 1 | 0.6031 | 350.74 | <0.0001 |
| AB | 0.1106 | 1 | 0.1106 | 64.34 | 0.0013 |
| AC | 0.0962 | 1 | 0.0962 | 55.94 | 0.0017 |
| BC | 0.0108 | 1 | 0.0108 | 6.29 | 0.0662 |
| A2 | 0.0012 | 1 | 0.0012 | 0.6895 | 0.453 |
| B2 | 0.0245 | 1 | 0.0245 | 14.25 | 0.0195 |
| C2 | 0.0111 | 1 | 0.0111 | 6.43 | 0.0642 |
| Residual | 0.0069 | 4 | 0.0017 | ||
| Lack of fit | 0.0058 | 3 | 0.0019 | 1.85 | 0.485 |
| Pure error | 0.0011 | 1 | 0.0011 | ||
| Cor total | 6.29 | 13 | |||
| Adjustment Statistics | %COD | E (kWh/kg COD) |
|---|---|---|
| R2 | 0.8798 | 0.9989 |
| Adjusted R2 | 0.7768 | 0.9964 |
| Predicted R2 | 0.5301 | 0.9845 |
| Adeq Precision | 10.01 | 64.52 |
| Std. Dev. | 1.4 | 0.0415 |
| Mean | 85.24 | 1.47 |
| C.V.% | 1.64 | 2.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quispe-Ramos, K.; Melgar-Izaguirre, E.; Rivera-Rodríguez, J.; Gutiérrez-Cuba, C.; Carrasco-Venegas, L.; Rodriguez-Aburto, C.; Ramos-Balcázar, Y.; Pilco-Nuñez, A. Energy-Efficient Coaxial Electrocoagulation for Integrated Treatment of Urban Wastewater and Acid Mine Drainage: A Response-Surface Approach. Appl. Sci. 2025, 15, 10452. https://doi.org/10.3390/app151910452
Quispe-Ramos K, Melgar-Izaguirre E, Rivera-Rodríguez J, Gutiérrez-Cuba C, Carrasco-Venegas L, Rodriguez-Aburto C, Ramos-Balcázar Y, Pilco-Nuñez A. Energy-Efficient Coaxial Electrocoagulation for Integrated Treatment of Urban Wastewater and Acid Mine Drainage: A Response-Surface Approach. Applied Sciences. 2025; 15(19):10452. https://doi.org/10.3390/app151910452
Chicago/Turabian StyleQuispe-Ramos, Katherin, Edilberto Melgar-Izaguirre, José Rivera-Rodríguez, César Gutiérrez-Cuba, Luis Carrasco-Venegas, Cesar Rodriguez-Aburto, Yone Ramos-Balcázar, and Alex Pilco-Nuñez. 2025. "Energy-Efficient Coaxial Electrocoagulation for Integrated Treatment of Urban Wastewater and Acid Mine Drainage: A Response-Surface Approach" Applied Sciences 15, no. 19: 10452. https://doi.org/10.3390/app151910452
APA StyleQuispe-Ramos, K., Melgar-Izaguirre, E., Rivera-Rodríguez, J., Gutiérrez-Cuba, C., Carrasco-Venegas, L., Rodriguez-Aburto, C., Ramos-Balcázar, Y., & Pilco-Nuñez, A. (2025). Energy-Efficient Coaxial Electrocoagulation for Integrated Treatment of Urban Wastewater and Acid Mine Drainage: A Response-Surface Approach. Applied Sciences, 15(19), 10452. https://doi.org/10.3390/app151910452






