Analysis of the Time Series of Compressed Air Flow and Pressure and Determining Criteria for Diagnosing Causes of Pressure Drop in Pneumatic Systems
Abstract
1. Introduction
- -
- -
- Reducing the speed and power of actuators;
- -
- Unpredictable production line shutdowns.
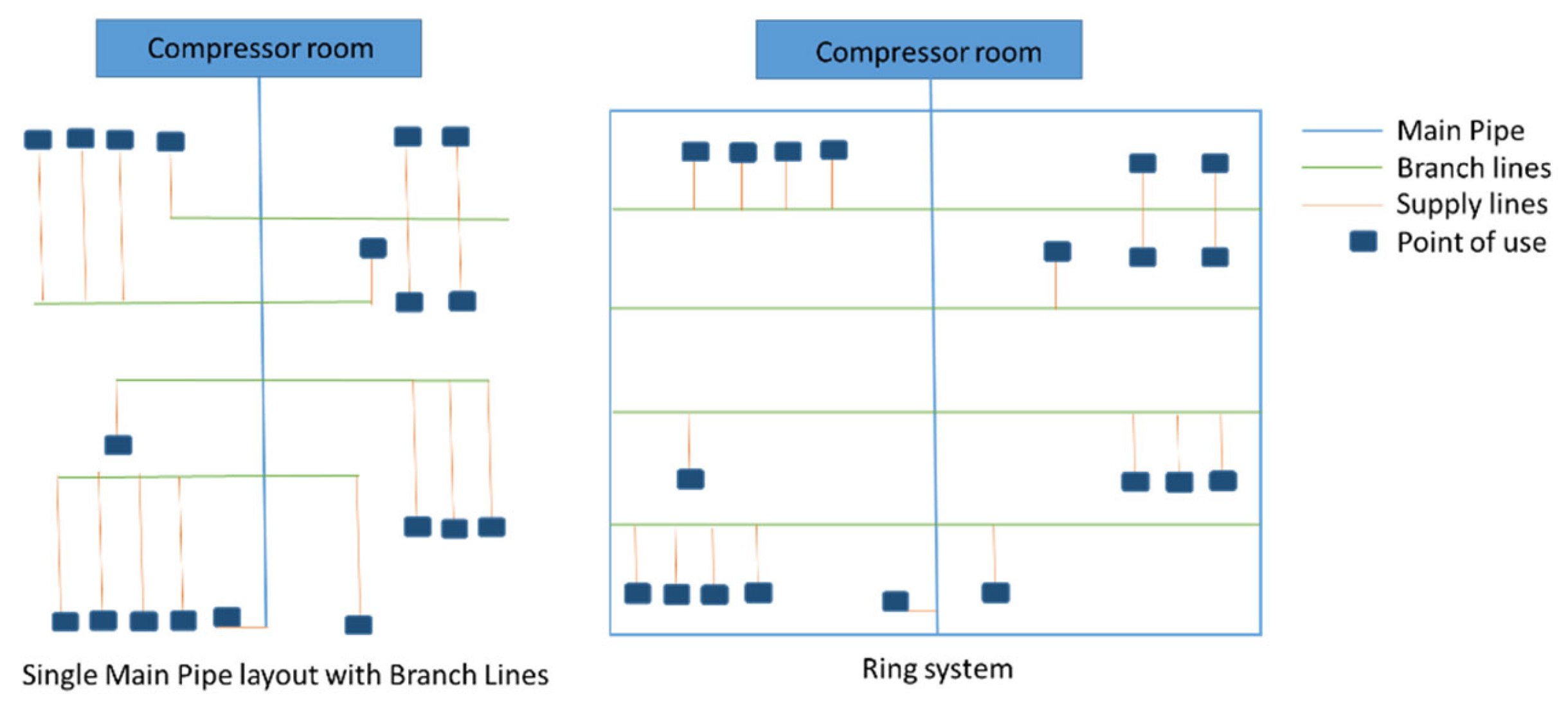
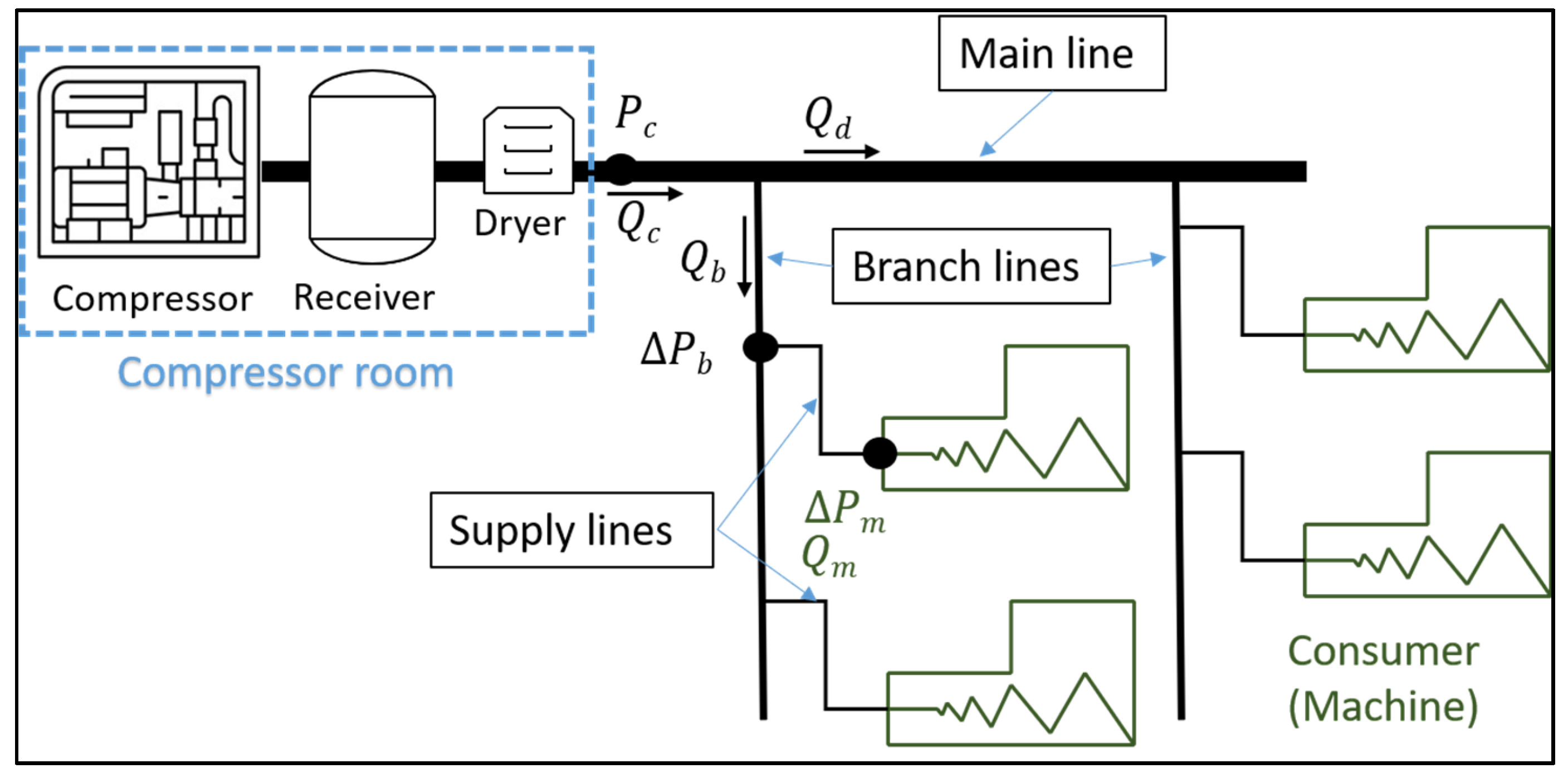
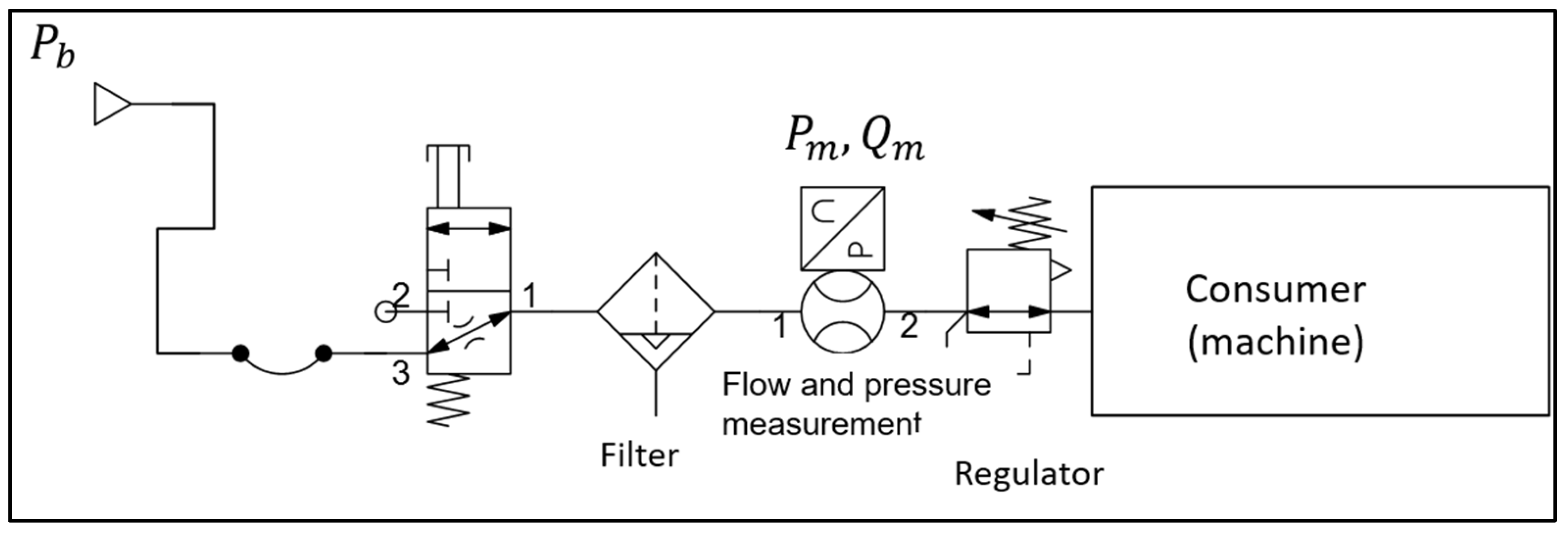
2. Materials and Methods
2.1. Correlation Analysis
- -
- Correlations between pairs of variables;
- -
- Correlations within and between sets of variables.
- -
- Whether there is a statistically significant relationship between two continuous variables;
- -
- The strength of the linear relationship (i.e., how close the relationship is to a perfectly straight line);
- -
- The direction of a linear relationship (increasing or decreasing).
- -
- Two or more continuous variables;
- -
- It is not permissible to have missing values for both variables;
- -
- Linear relationship between variables within the measurement range;
- -
- Independence of observations. The Pearson bivariate correlation coefficient and the corresponding significance test are not robust when independence is violated.
- -
- Bivariate normality:
- Each pair of variables is bivariately normally distributed;
- Each pair of variables is bivariately normally distributed at all levels of the other variable.
- -
- —the dependent variable Y is perfectly positively correlated with the independent variable X;
- -
- —this indicates a strong positive correlation of the dependent variable Y with the independent variable X;
- -
- —significant positive correlation of the dependent variable Y with the independent variable X;
- -
- —this indicates a moderate positive correlation of the dependent variable Y with the independent variable X;
- -
- —this indicates a weak positive correlation of the dependent variable Y with the independent variable X;
- -
- —what is considered the dependent variable Y does not have any kind of linear correlation with what is considered the independent variable X;
- -
- —this indicates a weak negative correlation of the dependent variable Y with the independent variable X;
- -
- —this indicates a moderate negative correlation of the dependent variable Y with the independent variable X;
- -
- —there is a significant negative correlation of the dependent variable Y with the independent variable X;
- -
- —this indicates a strong negative correlation of the dependent variable Y with the independent variable X;
- -
- —the dependent variable Y is perfectly negatively correlated with the independent variable X.
2.2. Diagnostic Criteria
- -
- A sign of a problem.
- -
- Indication of the problem being related to the supply line:
- -
- A sign of a structural or systemic problem in the design or implementation of the supply line—excessively large maximum theoretical pressure drop:
- 2.
- ;
- 3.
- ; ;.
- 4.
- ; ; .
3. Experimental Part
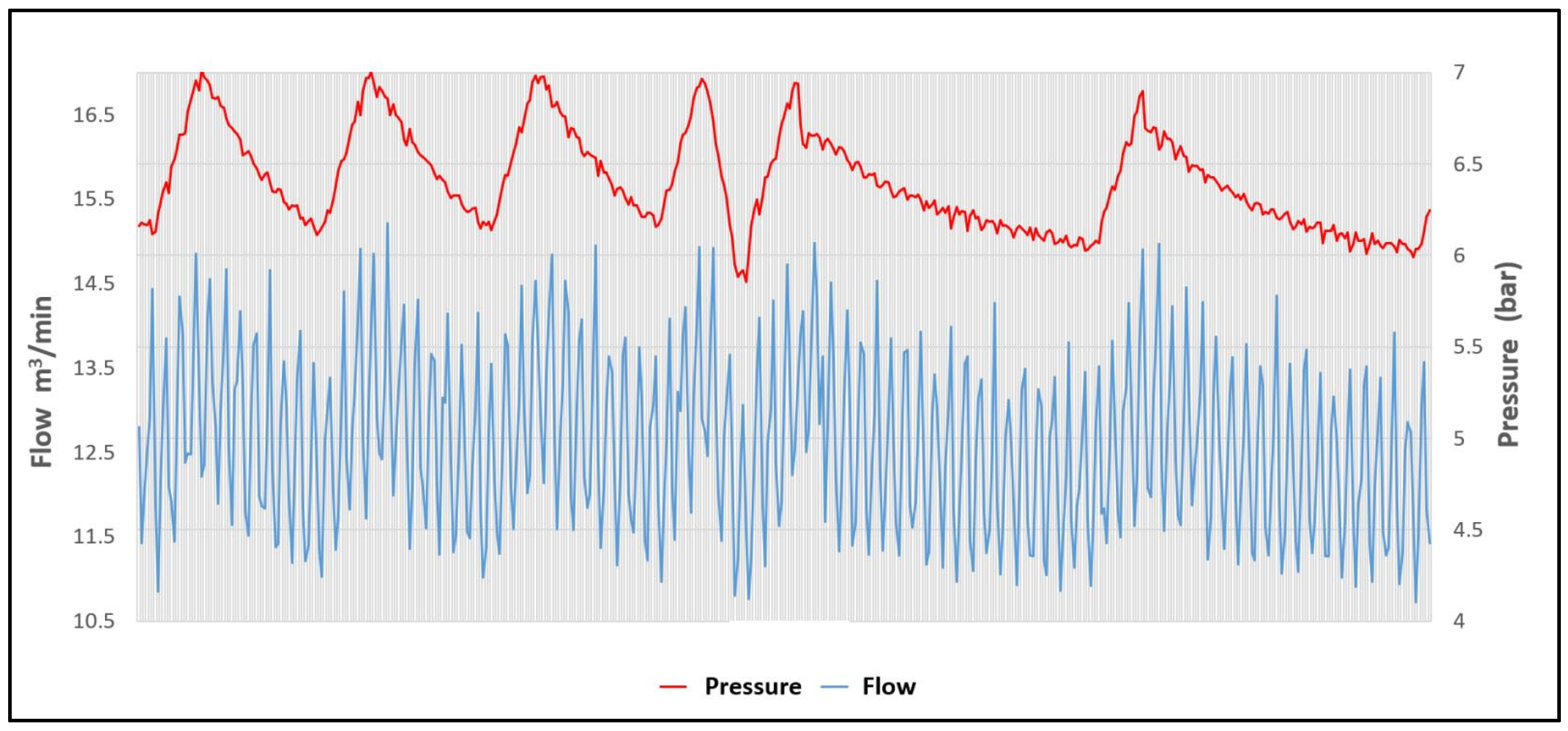
4. Results and Analyses
5. Discussion
- -
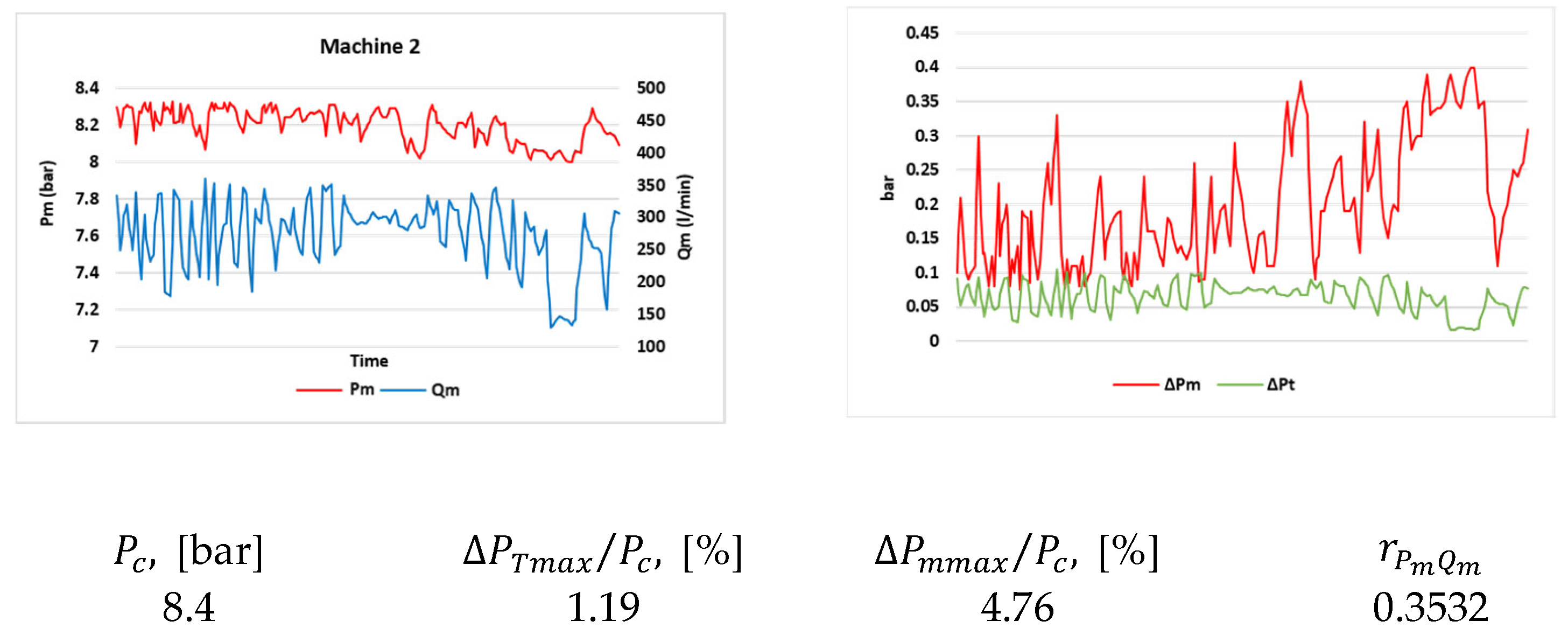
- The Pearson correlation coefficient between flow rate and end-user inlet pressure is a promising indicator for distinguishing whether pressure drop is due to supply line problems. This was confirmed both by actual troubleshooting of supply line problems on Machines 11 to 13 and by visual analysis of time diagrams on machines falling into Group 2. More real-world data are needed to empirically determine its threshold value more definitively;
- -
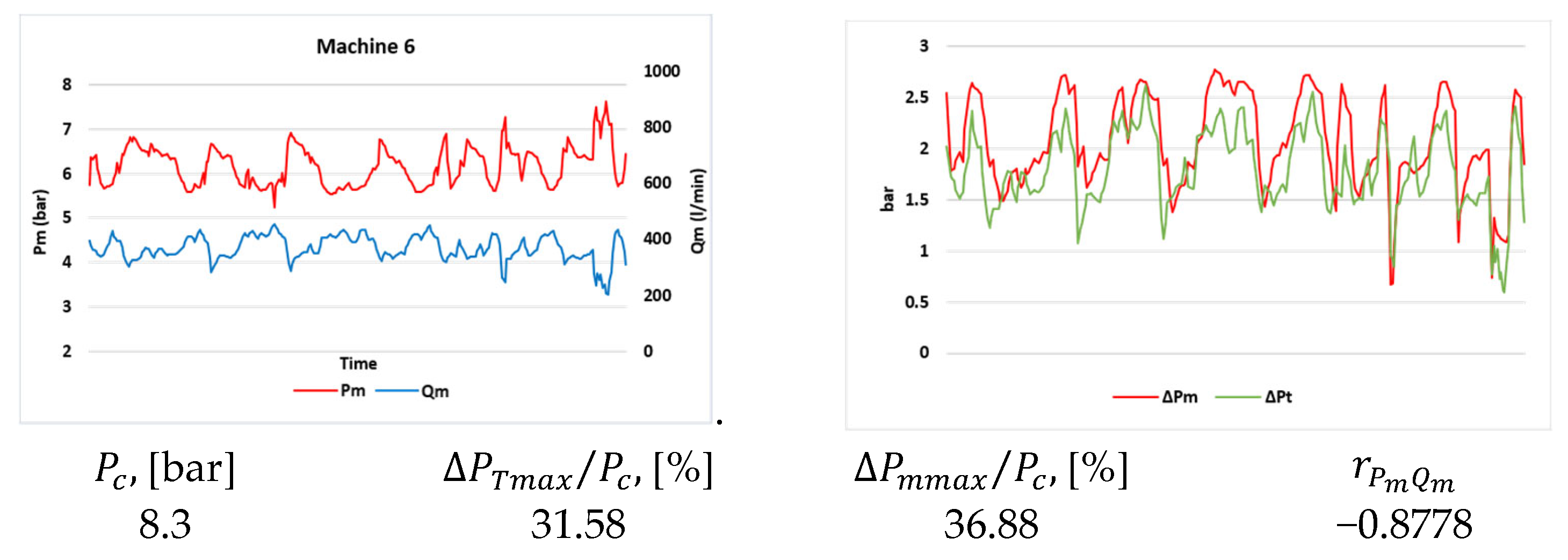
- Using the theoretical maximum pressure drop to separate the causes of problems in the supply line has practical application, but it requires additional knowledge of the supply line itself, and its parameters must be included in the calculations. From a practical point of view, it turns out that it is better for machines classified in Groups 3 and 4 to inspect the entire supply line and, if there are kinks, blockages, or leaks, to eliminate them. And, if after that, the pressure drop is still above the permissible level, optimize the internal diameter and length of the supply line;
- -
- The higher correlation coefficient above the specified threshold does not mean that the problem is only in the supply line. For example, in Machines 11 and 12, after eliminating the problems in the supply line, the pressure drop is still high, although within the specified permissible limits. However, searching for the causes of pressure drops in the main and branch lines is a significantly more complex task, often associated with stopping entire production sections. The proposed method can solve the problem to some extent without the need for unnecessary pressure increase in the compressor and the generation of artificial consumption.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaustein, E.; Radgen, P. Compressed Air Systems in the European Union; LOG_X Verlag GmbH: Stuttgart, Germany, 2001. [Google Scholar]
- Kosturkov, R.; Nachev, V.; Titova, T. System Analysis and Opportunities for Optimization of Pneumatic Systems in Manufacturing Plants. TEM J. 2019, 8, 749–763. [Google Scholar] [CrossRef]
- Werner, K.; Löbbe, S.; Büttner, S.; Schneider, C. Establishing Energy Efficiency—Drivers for Energy Efficiency in German Manufacturing Small- and Medium-Sized Enterprises. Energies 2020, 13, 5144. [Google Scholar] [CrossRef]
- Nehler, T.; Parra, R.; Thollander, P. Implementation of energy efficiency measures in compressed air systems: Barriers, drivers and non-energy benefits. Energy Effic. 2018, 11, 1281–1302. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, S.X.; Biao, H. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Cesarotti, V.; Orazi, S.D.; Introna, V. Improve Energy Efficiency in Manufacturing Plants through Consumption Forecasting and Real Time Control: Case Study from the Pharmaceutical Sector. In Proceedings of the International Conference on Advances in Production Management Systems (APMS 2010), Cernobbio, Italy, 11–13 October 2010. [Google Scholar]
- Qi, G.; Zhu, Z.; Erqinhu, K.; Chen, Y.; Chai, Y.; Sun, J. Fault-diagnosis for reciprocating compressors using big data and machine learning. Simul. Model. Pract. Theory 2018, 80, 104–127. [Google Scholar] [CrossRef]
- Magoulès, F.; Zhao, H.-X. Data Mining and Machine Learning in Building Energy Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Tran Yes, T.; Chen, Y.; Chau, M.Q.; Ning, B. A robust online fault detection and diagnosis strategy of centrifugal chiller systems for building energy efficiency. Energy Build. 2015, 108, 441–453. [Google Scholar] [CrossRef]
- Xiao, F.; Zheng, C.; Wang, S. A fault detection and diagnosis strategy with enhanced sensitivity for centrifugal chillers. Appl. Therm. Eng. 2011, 31, 3963–3970. [Google Scholar] [CrossRef]
- López, A.J.G.; Márquez, A.C.; Macchi, M.; Fernández, J.F.G. Prognostics and Health Management in Advanced Maintenance Systems. In Advanced Maintenance Modeling for Asset Management; Springer: Cham, Switzerland, 2018; pp. 79–106. [Google Scholar] [CrossRef]
- Xenos, D.P.; Cicciotti, M.; Kopanos, G.M.; Bouaswaig, A.E.; Kahrs, O.; Martinez-Botas, R.; Thornhill, N.F. Optimization of a network of compressors in parallel: Real Time Optimization (RTO) of compressors in chemical plants—An industrial case study. Appl. Energy 2015, 144, 51–63. [Google Scholar] [CrossRef]
- Lee, J.; Kao, H.-A.; Yang, S. Service Innovation and Smart Analytics for Industry 4.0 and Big Data Environment. Procedia CIRP 2014, 16, 3–8. [Google Scholar] [CrossRef]
- Benedetti, M.; Cesarotti, V.; Introna, V. From energy targets setting to energy-aware operations control and back: An advanced methodology for energy efficient manufacturing. J. Clean. Prod. 2017, 167, 1518–1533. [Google Scholar] [CrossRef]
- Zhang, K.; Peng, K.; Chu, R.; Dong, J. Implementing multivariate statistics-based process monitoring: A comparison of basic data modeling approaches. Neurocomputing 2018, 290, 172–184. [Google Scholar] [CrossRef]
- Xiao, W. A probabilistic machine learning approach to detect industrial plant faults. Int. J. Progn. Health Manag. 2016, 7. [Google Scholar] [CrossRef]
- Benedetti, M.; Bonfà, F.; Introna, V.; Santolamazza, A. Real Time Energy Performance Control for Industrial Compressed Air Systems: Methodology and Applications. Energies 2019, 12, 3935. [Google Scholar] [CrossRef]
- Semitela, Â.; Silva, J.; Girão, A.F.; Verdasca, S.; Futre, R.; Lau, N. Combining Infrared Thermography with Computer Vision Towards Automatic Detection and Localization of Air Leaks. Sensors 2025, 25, 3272. [Google Scholar] [CrossRef]
- Boyko, V.; Weber, J. Cycle Time-Based Fault Detection and Localization in Pneumatic Drive Systems. Actuators 2024, 13, 447. [Google Scholar] [CrossRef]
- Kosturkov, R.; Nachev, V.; Titova, T. Expert estimation of leakage in the pneumatic systems in the bottling industry. IOP Conf. Ser. Mater. Sci. Eng. 2020, 878, 012008. [Google Scholar] [CrossRef]
- Motazedi, N.; Beck, S. Leak detection using cepstrum of cross-correlation of transient pressure wave signals. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 2723–2735. [Google Scholar] [CrossRef]
- Kosturkov, R.; Titova, T.; Nachev, V. Diagnosis of Pneumatic Systems on the Basis of Time Series and Generalized Feature for Comparison with Standards for Normal Working Condition. TEM J. 2021, 10, 183–191. [Google Scholar] [CrossRef]
- Paramonov, A.; Starikov, A. Air Supply Systems for Enterprises; Lan: Moskow, Russia, 2011; Available online: https://elima.ru/books/?id=1752 (accessed on 12 January 2025). (In Russian)
- Silva, W.L.V.; Souza, L.C.O.; Bortolaia, L.A.; de Paula, M.R.; Leal, E.M. Study of the electricity consumption reduction of a compressed air system: The case of a steelmaking company. REM—Int. Eng. J. 2017, 70, 421–428. [Google Scholar] [CrossRef]
- Unger, M.; Radgen, P. Energy Efficiency in Compressed Air Systems: A review of energy efficiency potentials, technological development, energy policy actions and future importance. In Proceedings of the 10th International Conference on Energy Efficiency in Motor Driven Systems (EEMODS’2017), International Con-ference on Energy Efficiency in Motor Driven Systems EEMODS, Rome, Italy, 6–8 September 2017; Bertoldi, P., Ed.; Publications Office of the European Union: Luxembourg, 2018; pp. 207–233. [Google Scholar]
- Dindorf, R.; Wos, P. Automatic measurement system for determination of leakage flow rate in compressed air pipeline system. Metrol. Meas. Syst. 2018, 25, 59–70. [Google Scholar] [CrossRef]
- Eret, P.; Harris, C.; O’Donnell, G.; Meskell, C. A practical approach to investigating energy consumption of industrial compressed air systems. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 28–36. [Google Scholar] [CrossRef]
- Harman, A.; Baur, L.; Wolf, C.; Sauer, A. Detection of Anomalies in Compressed Air Systems using Time of Occurrence and KPI Analysis. In Proceedings of the 5th International Conference on Communications, Information, Electronic and Energy Systems (CIEES), Veliko Tarnovo, Bulgaria, 20–22 November 2024. [Google Scholar] [CrossRef]
- Thabet, M.; Sanders, D.A.; Bausch, N. Detection of Patterns in Pressure Signal of Compressed Air System Using Wavelet Transform. In Energy and Sustainable Futures, Proceedings of the 2nd ICESF 2020, Hatfield, UK, 10–11 September 2020; Springer: Cham, Switzerland, 2021; pp. 61–67. [Google Scholar] [CrossRef]
- Travaš, V.; Gal, E.; Lučin, I.; Žic, E. Digital twin for a real-time leakage detection and localization in pressurized piping systems. J. Hydroinformatics 2025, 27, 755–770. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C. Condition Monitoring of Pneumatic Drive Systems Based on the AI Method Feed-Forward Backpropagation Neural Network. Sensors 2024, 24, 1783. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.; Boyle, W.C.; Popel, I.H.J. Aeration: Principles and Practice, 1st ed.; CRC Press: Boca Raton, FL, USA, 2002; Volume 11. [Google Scholar] [CrossRef]
- Kissock, K.; Schmidt, C. Modeling and Simulation of Air Compressor Energy Use. ACEEE Summer Study Energy Effic. Ind. 2005, 1, 131–142. [Google Scholar]
- Perevoshchikov, S.I. Design and Operation of Compressor Stations; TyumGNTU: Tyumen, Russia, 1996; ISBN 5-88465-034-5. [Google Scholar]
- Popov, G.; Nikolov, G.; Boyadzhiev, M.; Klimentov, K. Investigation of errors in calculating friction coefficients in round pipes, Yearbook of the University of Mining and Geology “St. Ivan Rilski”, 2010, Volume 53, is. I. pp. 159–162. Available online: https://mgu.bg/wp-content/uploads/2025/05/Vol.-53-I-2010-159-162.pdf (accessed on 15 January 2025). (In Bulgarian).
- Barenblatt, G.I.; Chorin, A.; Prostokishin, V. Scaling Laws for Fully Developed Turbulent Flow in Pipes: Discussion of Experimental Data. Proc. Natl. Acad. Sci. USA 1997, 94, 773–776. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.D.; Leung, L.S.; Klinzing, G.E.; Rizk, F. Single Phase Flow in Pneumatic Conveying Systems of Solids; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- SMC Corporation. Energy Saving Manual. SMC Corporation: Tokyo, Japan, 2013. [Google Scholar]
- Engineering ToolBox, Compressed Air—Pressure Loss in Pipe Lines—Online Calculator with Metric and Imperial Units. Available online: https://www.engineeringtoolbox.com/pressure-drop-compressed-air-pipes-d_852.html (accessed on 1 November 2020).
- Atlas Copco. Atlas Copco Air Compendium; Atlas Sopco AB: Stockholm, Sweden, 1975. [Google Scholar]
- Rodgers, J.L.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. In The American Statistician; American Statistical Association: Alexandria, VA, USA, 1988; pp. 59–66. [Google Scholar]
- Hahs-Vaughn, D. Foundational methods: Descriptive statistics: Bivariate and multivariate data (correlations, associations). In International Encyclopedia of Education; Elsevier: Amsterdam, The Netherlands, 2023; pp. 734–750. [Google Scholar] [CrossRef]
- Rakova, E.; Weber, J. Process simulation of energy behaviour of pneumatic drives. Procedia Eng. 2015, 106, 149–157. [Google Scholar] [CrossRef]
- Taylor, B. What Is Compressed Air Pressure Drop and How Do You Minimize It. Fluid-Aire Dynamics Ltd. 21 September 2021. Available online: https://fluidairedynamics.com/blogs/articles/what-is-pressure-drop-and-how-its-costing-you-money#:~:text=An%20efficient%20compressed%20air%20system%20should%20lose,not%20receive%20enough%20pressure%20to%20operate%20correctly (accessed on 10 June 2025).
- Hernandez-Herrera, H.; Silva-Ortega, J.I.; Martínez Diaz, V.L.; Sanchez, Z.G.; García, G.G.; Escorcia, S.M.; Zarate, H.E. Energy Savings Measures in Compressed Air Systems. Int. J. Energy Econ. Policy 2020, 10, 414–422. [Google Scholar] [CrossRef]
- Oster, C. Detecting and Minimizing Air Pressure Drop in Compressed Air Systems. JHFOSTER Ltd. 2 April 2025. Available online: https://jhfoster.com/automation-blogs/what-is-a-pressure-drop-and-how-do-you-prevent-it/ (accessed on 10 June 2025).
- Taylor, B. Air Compressor Troubleshooting: Pressure Problems. Fluid-Aire Dynamics, 4 July 2023. Available online: https://fluidairedynamics.com/blogs/articles/air-compressor-troubleshooting-pressure-problems (accessed on 10 June 2025).






| Model | SMC ISE20A | |
|---|---|---|
| Fluid | Applicable fluid | Compressed air, non-flammable gases, non-corrosive gases |
| Temperature range | 0 to 50 °C | |
| Pressure | Measurement range | −0.100 to 1.000 MPa |
| Accuracy | Repeatability | ±0.2% FS |
| Analog output | ±2.5% FS (ambient temperature: 25 ± 3 °C) | |
| Analog output linearity | ±1% FS | |
| Analog Output | Type | Current output: 4 to 20 mA |
| Response time | 1.5 ms or less | |
| Model | CS VA 520 Standard | CS VA520 Max | |
|---|---|---|---|
| Fluid | Applicable fluid | Compressed air, N2; quality: ISO 8573-1 1.1.2 to 1.6.2. | |
| Temperature range | −30 to 80 °C | ||
| Measurement method | Thermal, in-line | ||
| Fluid velocity | 92.7 m/s | 185 m/s | |
| Pressure | Nominal working pressure | −0.1 to 1.6 MPa | |
| Accuracy | Repeatability | ±1.5% of the measured value ± 0.3% FS | |
| Analog output | Type | Current output: 4–20 mA | |
| Response time | Minimum: 0.05 s. | ||
| Digital output | RS 485 interface (Modbus-RTU), Ethernet, M-Bus | ||
| Model | CS Instruments DS 500 Mobile | ||
|---|---|---|---|
| Sensor inputs | Up to 12 sensor inputs—digital or analog. Programmable Digital CS sensors for dew-point measurement with SDI interface. Flow sensors on CS. Other sensors with RS 485/Modbus RTU. Analog CS sensors for pressure, flow, temperature, etc. Other analog sensors with outputs 0/4–20 mA, 0–1/10/30 V, pulse outputs Pt100/Pt1000, and KTY. | ||
| Input signals | Current signal (0–20 mA/4–20 mA) and internal or external power supply | Measurement range | 0–20 mA/4–20 mA |
| Resolution | 0.0001 mA | ||
| Accuracy | ±0.03 mA ±0.05% | ||
| Input resistance | 50 Ω | ||
| Sampling frequency | 10 ms, 100 Hz | ||
| Non-volatile memory | 4 GB | ||
| Machine | Pressure | Equivalent Length of the Supply Line | Inner Diameter of the Supply Line d | |
|---|---|---|---|---|
| [bar] | [m] | [mm] | ||
| Flexible water connection plant | Machine 1- Sealant application | 8.4 | 9 | 6 |
| Machine 2—Sealant application | 8.4 | 8 | 10 | |
| Machine 3—Automatic shear | 8.5 | 6 | 10 | |
| Machine 4—Pressing and molding | 8.4 | 7 | 16 | |
| Machine 5—Cutting and sorting | 8.5 | 2.5 | 8 | |
| Electronic components factory | Machine 6—Automatic soldering | 8.3 | 10 | 6 |
| Machine 7—Assembly unit | 8.4 | 12 | 10 | |
| Machine 8—Robotic assembly | 8.5 | 5 | 12 | |
| Machine 9—Robotic assembly | 8.4 | 5 | 12 | |
| Automobile hydraulic pump plant | Machine 10—Press | 6.7 | 3.5 | 8 |
| Machine 11—Press | 6.8 | 4.5 | 8 | |
| Machine 12—Automatic assembly | 6.8 | 10 | 10 | |
| Machine 13—Automatic assembly and test in clean room | 5.7 | 5 | 10 | |
| Household plastic products factory | Machine 14—Blast line | 7.3 | 5 | 50 |
| Machine 15—Sorting and arranging | 7.3 | 15 | 20 | |
| Machine 16—Packaging machine | 7.3 | 3 | 8 |
| Machine | [bar] | |||
|---|---|---|---|---|
| [%] | [%] | |||
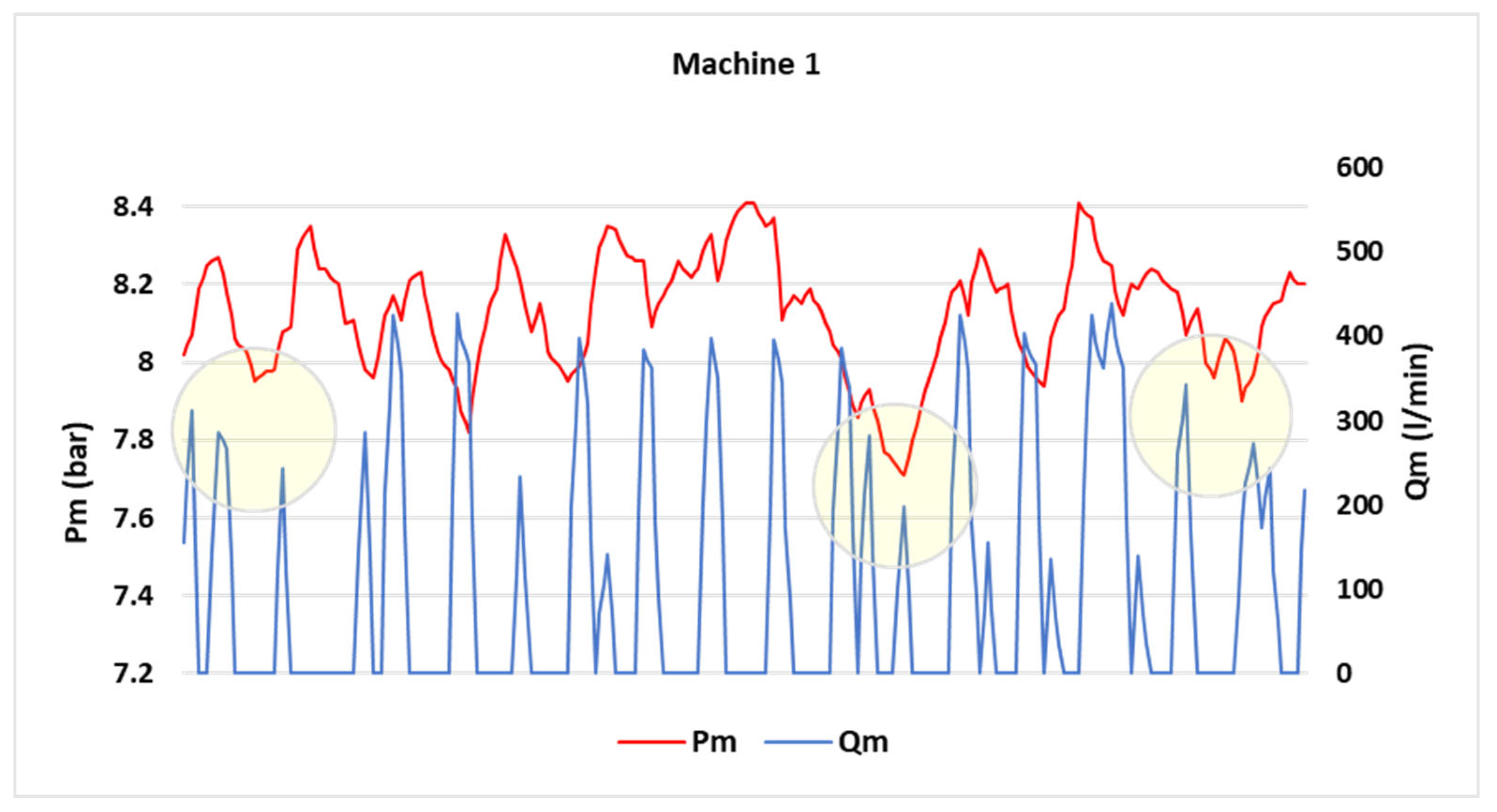
| Machine 1 | 8.4 | 2.02% | 8.33% | −0.0431 |
| Machine 2 | 8.4 | 1.19% | 4.76% | 0.3532 |
| Machine 3 | 8.5 | 2.12% | 16.00% | −0.3900 |
| Machine 4 | 8.4 | 1.43% | 4.76% | −0.2768 |
| Machine 5 | 8.5 | 3.60% | 16.59% | −0.9508 |
| Machine 6 | 8.3 | 31.58% | 36.88% | −0.8778 |
| Machine 7 | 8.4 | 3.38% | 9.40% | −0.7046 |
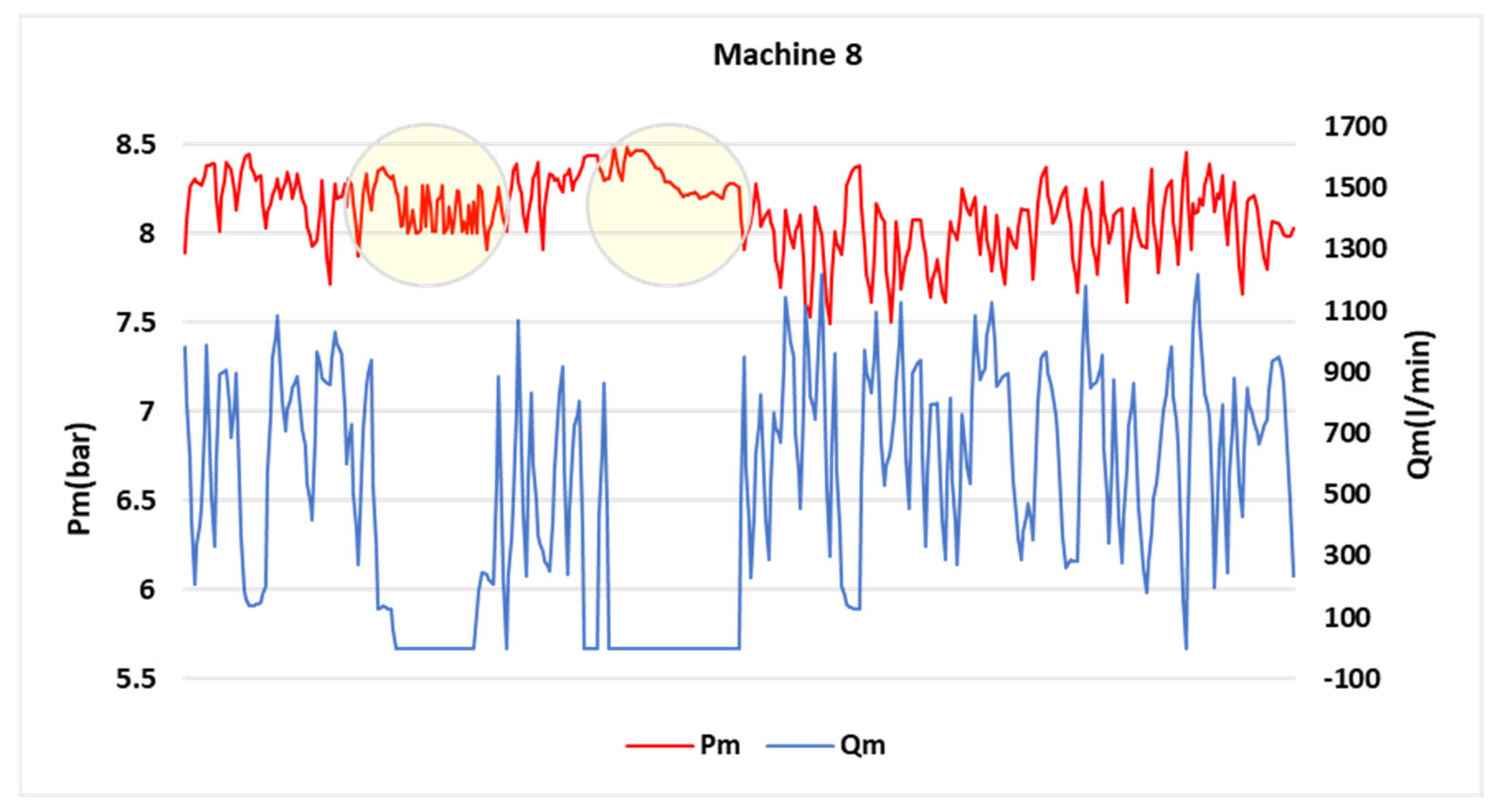
| Machine 8 | 8.5 | 2.92% | 11.41% | −0.4175 |
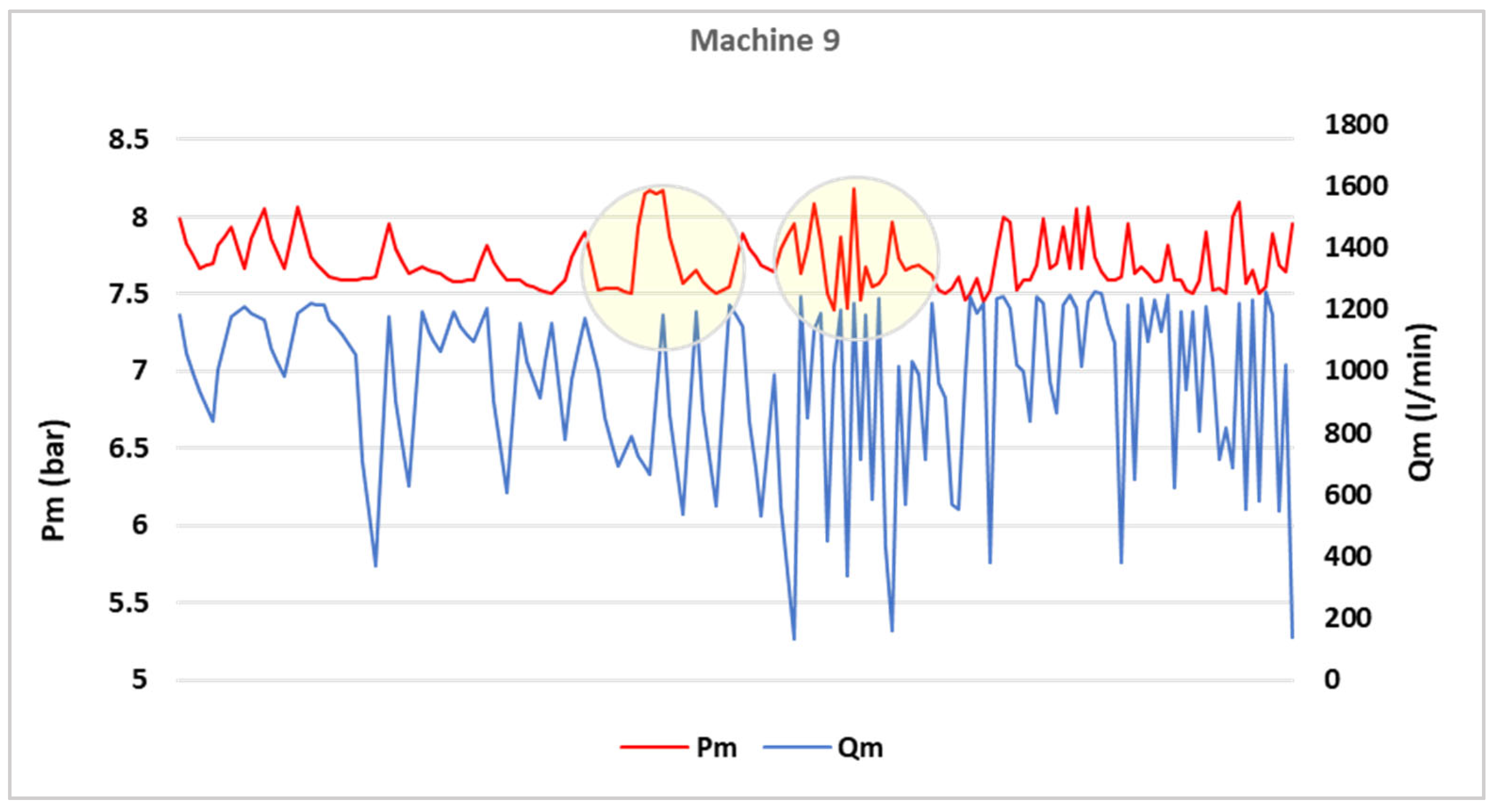
| Machine 9 | 8.4 | 2.98% | 11.90% | 0.1652 |
| Machine 10 | 6.7 | 16.17% | 17.91% | −0.9046 |
| Machine 11 | 6.8 | 14.19% | 23.09% | −0.8759 |
| Machine 12 | 6.8 | 4.42% | 21.76% | −0.7293 |
| Machine 13 | 5.7 | 5.11% | 5.79% | −0.9321 |
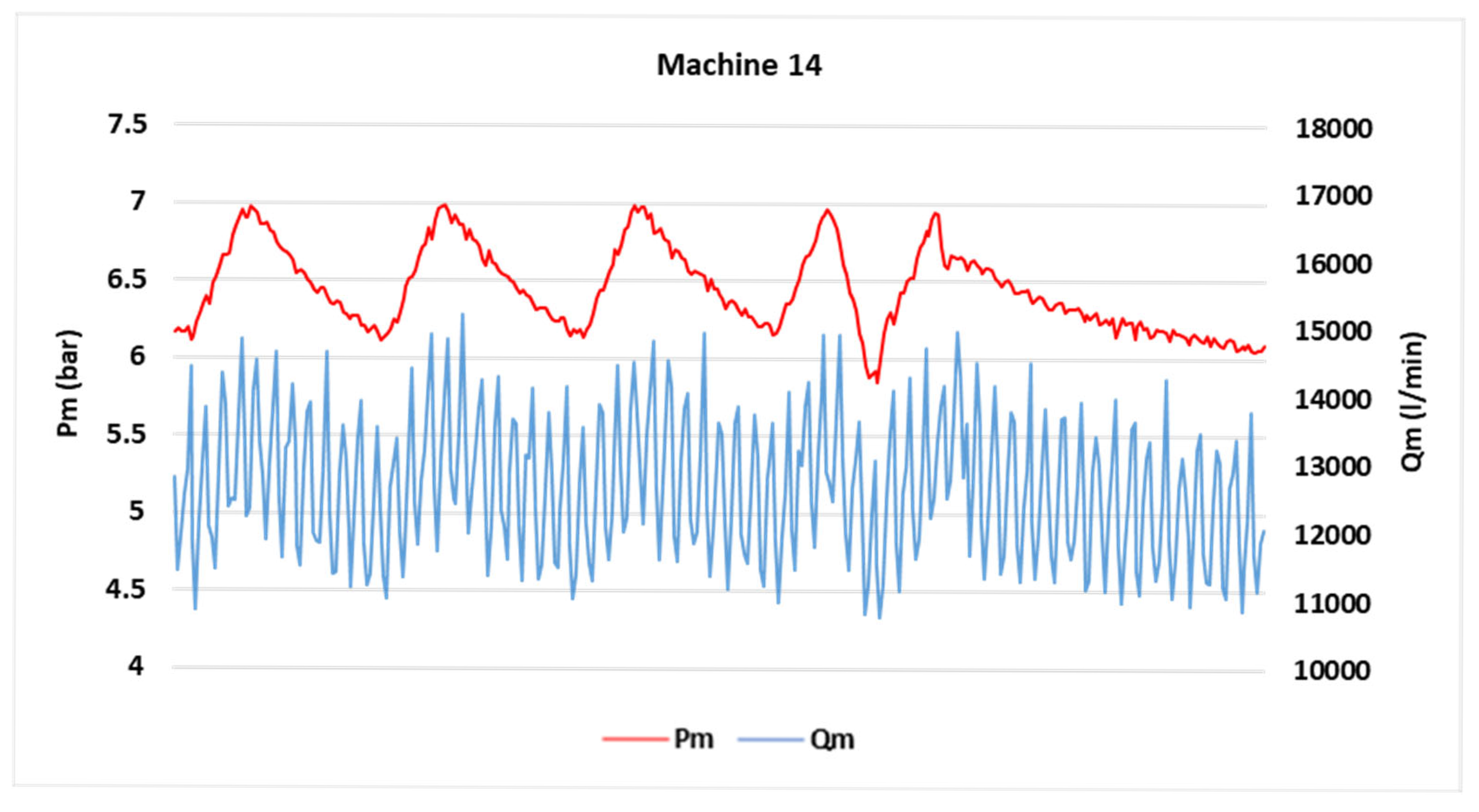
| Machine 14 | 7.3 | 0.34% | 19.81% | 0.3742 |
| Machine 15 | 7.3 | 2.35% | 23.56% | −0.3939 |
| Machine 16 | 7.3 | 4.18% | 29.59% | −0.8461 |
| Initial State | After Correction | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PC | Equivalent Length of the Supply Line L | Inner Diameter of the Supply Line d | ∆Pmmax | ∆Pmmax/Pc | Equivalent Length of the Supply Line L | Inner Diameter of the Supply Line d | ∆Pmmax | ∆Pmmax/Pc | |
| [bar] | [m] | [mm] | [bar] | [%] | [m] | [mm] | [bar] | [%] | |
| Machine 10 | 6.7 | 5 | 8 | 1.2 | 17.91% | 5 | 13 | 0.2 | 2.99% |
| Machine 11 | 6.8 | 4.5 | 8 | 1.57 | 23.09% | 5 | 13 | 0.3 | 4.41% |
| Machine 12 | 6.8 | 10 | 10 | 1.48 | 21.76% | 10 | 13 | 0.3 | 4.41% |
| Machine 13 | 5.7 | 5 | 10 | 0.33 | 5.79% | 5 | 13 | 0.1 | 1.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Titova, T.; Kosturkov, R. Analysis of the Time Series of Compressed Air Flow and Pressure and Determining Criteria for Diagnosing Causes of Pressure Drop in Pneumatic Systems. Appl. Sci. 2025, 15, 9536. https://doi.org/10.3390/app15179536
Titova T, Kosturkov R. Analysis of the Time Series of Compressed Air Flow and Pressure and Determining Criteria for Diagnosing Causes of Pressure Drop in Pneumatic Systems. Applied Sciences. 2025; 15(17):9536. https://doi.org/10.3390/app15179536
Chicago/Turabian StyleTitova, Tanya, and Rosen Kosturkov. 2025. "Analysis of the Time Series of Compressed Air Flow and Pressure and Determining Criteria for Diagnosing Causes of Pressure Drop in Pneumatic Systems" Applied Sciences 15, no. 17: 9536. https://doi.org/10.3390/app15179536
APA StyleTitova, T., & Kosturkov, R. (2025). Analysis of the Time Series of Compressed Air Flow and Pressure and Determining Criteria for Diagnosing Causes of Pressure Drop in Pneumatic Systems. Applied Sciences, 15(17), 9536. https://doi.org/10.3390/app15179536







