An Extended Survey Concerning the Vector Commitments

Abstract

Commitment schemes represent foundational cryptographic primitives enabling secure verification protocols across diverse applications, from blockchain systems to zero-knowledge proofs. This paper presents a systematic survey of vector, polynomial, and functional commitment schemes, analyzing their evolution from classical constructions to post-quantum secure alternatives. We examine the strengths and limitations of RSA-based, Diffie–Hellman, and lattice-based approaches, highlighting the critical shift toward quantum-resistant designs necessitated by emerging computational threats. The survey reveals that while lattice-based schemes (particularly those using the Short Integer Solution problem) offer promising security guarantees, they face practical challenges in proof size and verification efficiency. Functional commitments emerge as a powerful generalization, though their adoption is constrained by computational overhead and setup requirements. Key findings identify persistent gaps in adaptive security, composability, and real-world deployment, while proposed solutions emphasize optimization techniques and hybrid approaches. By synthesizing over 90 research works, this paper provides both a comprehensive reference for cryptographic researchers and a roadmap for future developments in commitment schemes, particularly in addressing the urgent demands of post-quantum cryptography and decentralized systems.

1. Introduction

Commitment schemes are one of the most significant primitives in cryptography. As described in [1], commitments schemes can be interpreted as a digital translation of a sealed envelope. Beyond traditional data structures, cryptographic primitives like commitment schemes also play a role in securing specialized data formats, such as medical or underwater images, where color consistency and enhancement are critical for usability [2]. However, this work focuses on generalized vector and functional commitments, which provide foundational security for verifiable data structures. To be more precise, whenever party S commits to one message m, the message is one envelope. Later, S opens that envelope to see the message she committed to. Like this metaphor, we suppose that the data is a vector [a0, …, an]. If we make a commitment to this data, we may want to reveal only one element at a time, without revealing the entire content of the vector. This idea stands for a vector commitment. If we continue in metaphorical terms, we can think of this vector as a row of locked boxes (the components of the vector) and a ring of keys, one key belonging to each box. A commitment can be made by handing the verifier the row of boxes, and the contents of each box can be revealed by the committer handing the verifier the corresponding key. The commitment schemes should satisfy two properties:

• Hiding: the committed message should not be revealed.
• Binding: exists an opening procedure through which can be verified that the opened message is the same as the one S committed to.

This implies the existence of two phases of the process:

• Committing: using a specific algorithm, the sender commits to the message m through a committing scheme C.
• Decommitting: when revealing the message, S should convince R of the existence of m in C.

The commitment schemes are widely used in cryptography as a key component in primitives and protocols. However, when the basic properties are not sufficient in practice, new functionalities were created as extensions to the basic commitment schemes.

There are two main classes of encryption algorithms: symmetric and asymmetric. Symmetric encryption uses the same key for both encryption and decryption, while asymmetric encryption uses a pair of keys: a public key for encryption and a private key for decryption.

Scientific Objectives

The scientific objectives of this research paper are as follows:

• A survey of the related research literature in order to determine the weaknesses and propose possible solutions.
• Identify the most relevant studies in the field of vector commitments.
• Prioritizing studies relevant to vector commitments according to various criteria: citations, scientific relevance, objectives achieved, reproducibility of experiments, generality of solutions, etc.
• Classification by various criteria of frameworks dedicated to the open problem. To determine the relevant scientific research trends.
• To identify the relevant research problems.
• To define the scientific relevance of the corresponding content of research.

The paper is structured as follows: Section 2 describes the research methodology, including the literature selection criteria. Section 3, Section 4 and Section 5 present our systematic analysis of vector commitments (classical, Diffie–Hellman-based, and post-quantum approaches), while Section 6 and Section 7 examine polynomial and functional commitments. Section 8 concludes with future directions. Throughout, we focus on three key aspects: (1) cryptographic foundations, (2) performance trade-offs, and (3) real-world applicability.

2. Research Methodology

The present paper is written based on the “Preferred Reporting Items for Systematic Reviews and Meta-Analysis” (PRISMA) [2] methodology, following three phases: specification of the research questions, identification and survey of proper papers and specification of the relevant inclusion and exclusion criteria.

2.1. Research Questions

The papers analyzed have been selected based on the research questions:

• What is the related significant literature that approaches conceptual problems and reports adequate solutions?
• What are the relevant scientific research trends?
• What are the determined research questions and weak points?
• What is the reviewed research scope’s conceptual, scientific, and real-world importance?

2.2. The Research Process

The analyzed research papers have been collected from the selected scientific databases, according to

Table 1. Reference scientific literature databases and academic search engines. DL = digital library, SE = search engine.

Database

Public URL

arXiv-DLScience Direct-Elsevier-DLScopus-SEIEEExplore-DL ACM Digital Library-DL Web of Science-SE Google Scholar-SE MDPI-DL Springer-DL Research Gate-Scientific Social Networking Edinburgh Library database-DL RefSeek-SE Bielefeld Academic Search Engine-SE

https://arxiv.org (accessed on 12 June 2025) https://www.sciencedirect.com (accessed on 16 June 2025) https://www.scopus.com (accessed on 19 May 2025) https://ieeexplore.ieee.org(accessed on 13 June 2025) https://dl.acm.org (accessed on 12 June 2025) https://www.webofscience.com (accessed on 1 June 2025) https://scholar.google.com (accessed on 12 June 2025) https://www.mdpi.com (accessed on 30 May 2025) https://www.springer.com (accessed on 12 May 2025) https://www.researchgate.net (accessed on 12 June 2025) https://library.ed.ac.uk (accessed on 20 May 2025) https://www.refseek.com (accessed on 7 June 2025) https://www.base-search.net (accessed on 11 May 2025)

. The distribution of key terms related to cryptography is illustrated in Figure 1, which presents a word cloud of the searched concepts. This visualization highlights the most frequently referenced topics, emphasizing their relative prominence in the dataset.

2.3. Inclusion and Exclusion Criteria

The relevance of the surveyed papers and the scientific relevance of this review paper are determined by certain inclusion and exclusion criteria (

Table 2. Inclusion and exclusion criteria.

Inclusion Criteria	Exclusion Criteria
Published in one of the selected databases (Table 1).	Not written in English.
Published in 2010 or later.	Only partially related to vector commitments.
At least one search term appears in the title, abstract, or keywords.	Full text not available.
Addresses or analyzes the stated research questions.
Published in indexed journals, conference proceedings, mainstream technical journals, or books/chapters from top-level publishing houses.

). Thus, contributions that do not meet the specified EC are disregarded. The IC-related filtering model relates to a logical process based on the following steps:

Step 1. Abstract-related filtering: irrelevant articles are disregarded considering the information acquired from the abstract and based on the keywords. More precisely, articles that fulfill at least 50% of the relevance threshold are considered.

Step 2. Full text-related filtering: articles that concern only a small part of the scientific scope, as specified by the abstract and the keywords, are disregarded.

Step 3. Quality analysis-related filtering: the rest of the papers were additionally filtered considering that at least one of the following conditions is unmet:

<The paper describes a functional solution concerning the vector commitments.> AND

<The article fully presents the implemented technical solution.> AND

<The article surveys related relevant contributions.> AND

<The article presents and assesses the outcomes of the experimental process.>

Figure 2 illustrates the workflow of selecting the papers for the current survey.

We retained 100 articles.

2.4. Quantitative Comparison

To prioritize and compare the selected studies, we extracted a set of quantitative metrics, including citation count, year of publication, venue ranking, availability of implementation, and reproducibility. Citation counts were obtained from Google Scholar (accessed on 13 August 2025). Reproducibility was assessed by verifying the presence of open-source code and datasets. These metrics allow for an objective comparison of impact, timeliness, and practical applicability across works. Schemes published after 2020 generally have lower citation counts but higher reproducibility due to the increasing trend of releasing open-source code. Post-quantum proposals, while less cited, demonstrate growing research interest.

3. Vector Commitments

3.1. Classical Vector Commitments

In vector commitments (VCs), the primitives play an important role as the underlying cryptographic construction or assumption used to build the VC scheme. In

Table 3. Examples of primitives in VC schemes.

VC Scheme Type	Underlying Primitive (i.e., Cryptographic Primitive)
Merkle tree-based RSA-based	Collision-resistant hash functions Strong RSA assumption, accumulators
KZG (pairing-based) Lattice-based Hash-based (Post-Quantum)	Bilinear pairings, structured reference strings Learning With Errors (LWE) or Ring-LWE Hash functions only (e.g., SHA-3)

, we illustrate the main examples of such primitives.

3.2. RSA-Based VC

The RSA algorithm is a classical public key cryptographic system based on the hardness of factoring large integers [3].

The applications of the RSA algorithm are in digital signatures, digital certificates, secure communication protocols, secure key exchange, etc. The security of RSA relies on the key’s size. Although RSA is currently considered to be secure, it is vulnerable to potential future threats like quantum computing, cryptographic accumulators, and structures that can “accumulate” multiple values into a single compact value and later prove membership or non-membership. Despite of the hardness of factorizing large composite numbers, the RSA algorithms has several weaknesses: side-channel attacks (power analysis attacks and timing attacks), inadequate key length (causing the increase in computing power), weakness of prime numbers (based on randomness and closeness of the prime numbers), lost or stolen keys (attackers may use the compromised keys to decrypt the message), or fault-based attacks (attackers deliberately introduces faults in the hardware or software used to implement the encryption).

Avoiding the vulnerabilities of the RSA

To avoid overcoming the RSA’s vulnerabilities, some approaches may be conducted.

• Use a strong prime number generator to ensure that the prime numbers are unpredictable and cannot be easily guessed by an attacker.
• Avoid using weak prime numbers, such as small primes or primes too close to each other.
• Use a minimum length of 2048 bits for the RSA key.
• Take necessary actions to protect against fault-based attacks, such as using tamper-resistant hardware.
• Manage and secure the RSA keys properly using techniques like regular key rotation and different keys for different applications.

RSA in the VC recent research papers.

In the field of VC, the applicability of the RSA algorithm can be classified in 11 different categories [4]: viz, Hybrid, Parallel, Cloud, Image, Multiple-Keys, Chinese-Remainder- Theorem-based, Digital-Signatures, K-Nearest-Theorem-based, Batch, Wireless, and Core-Modifications.

In 2005, Paixao et al. [5] proposed an efficient variant of the RSA algorithm based on two previous approaches of Boneh and Shachaman [6] called multi-prime RSA and rebalanced RSA. The purpose of Paixao was to decrease the encryption and decryption time. Based on the authors’ facts, this version of RSA is 27 times faster than the classical one.

In 2016, Karakra and Alsadeh [7] proposed an augmented version of the RSA, called A-RSA, by combining an asymmetric Rabin algorithm [8], Hoffman coding algorithm [9], and RSA. The authors demonstrated that the new algorithm is more secure, with faster times for encryption–decryption tasks, and less prone to brute force attacks with shorter encoded text.

In 2020, Iavich et al. [10] describe two hybrid approaches of the RSA, involving both symmetric and asymmetric algorithms: AES + RSA and Twofish + RSA. Although no actual code is provided, the authors demonstrated through visual means the reduction in memory consumption and the speed of the proposed hybrid RSA versions.

When it comes to the cloud-focused RSA applications, Moghaddam et al. [11] proposed an efficient RSA (HE-RSA) version to improve the security of the data stored in cloud servers. The authors proved that the HE-RSA execution time is 50% lower than the standard RSA.

In 2015, Bansal et al. [12] combined RSA with the Blowfish algorithm [13], which increases cloud computing security and the brute force attacks sustainably by merging the advantages of the symmetric and asymmetric methods.

To address the RSA attacks, Makkaoui et al. [14] implement Cloud RSA, an enriched RSA variant that maintains the homomorphic characteristic of the algorithm. An improved version was proposed by the same Makkaoui in [15], called Fast Cloud RSA, that implies a decomposition of N as N = p^rq^s, for any r, s ≥ 2. This method leverages the operating time and preserves the security level.

The recent studies demonstrated that image encryption may strengthen the RSA algorithm. In 2016, Alsabti et al. [16] used RSA for gray and colored MATLAB images, proving a more resistant encryption and decryption method over image transfer. The MDRSA method developed by Jagadiswary et al. in [17] handles both numerical and picture data to encrypt and decrypt biomedical data (fingerprints, retina imprint, etc.). Staying in the medical image transfer area, Shin et al. [18] developed and improved the RSA algorithm for image encryption, using non-Mersenne prime numbers. Arnold’s map is another approach to be combined with RSA for image encryption. The works of Xu et al. [19], Jiao et al. [20], Sabir et al. [21], and Soni et al. [22] prove the efficiency of the asymmetric RSA combined with Arnold’s map for scrambling the digital image before encrypting it. While RSA-based encryption has been adapted for image data [16,17,18,19,20,21,22], including scenarios like underwater imaging where color disparities require enhancement [23], our focus remains on its use in vector commitments.

Part of the research article focuses on digital signature, in the way that RSA improvements increase the security and the performance of the public key infrastructure. Consequently, Si et al. [24] succeeded in generating a 1024-bit RSA key in only 120 s on any normal PC, through an efficient RSA signature improvement. Eight years later, in 2018, Aufa et al. [25] obtained a 60% faster algorithm, in terms of signature processing time, by combining the RSA 1024 and digital signature algorithms.

Wireless transmissions play an important role in the research of the RSA. In 2007, Frunz and Scripcariu [26] published an improved RSA based on AFF (Algebraic Finite Field), by using the maximum encryption key size to leverage the security properties, thus increasing the processor’s performance.

Sending information in batches is also a key feature in electronic communication. Batch RSA variants have been in development by Fiat [27] since 1990. A major advantage of this scheme is the distributive property of the key: the private key finally segregates, regardless of the system size or the total number of executable operations. Furthermore, the Batch RSA uses multiple modular exponentials, which is another advantage over the classical RSA. In 2010, Liu et al. [28] proposed BEARSA (Batch Encrypt Assistant RSA) and BEAMRSA (Batch Encrypt Assistant MultiPrime RSA). The first one is an enriched Batch RSA variant which uses binary trees for the computational phase and executes the exponential computation at once, not modular, through four steps: setup, percolate up, exponentiation phase, and percolate down. BEAMRSA is a BEARSA flavor enriched with the multi-prime FastRSA, proposed by Boneh et al. in [6].

As synthesized in the explicit quantitative analysis from Table 4 and Figure 3, the key insights of the RSA literature review are the following:

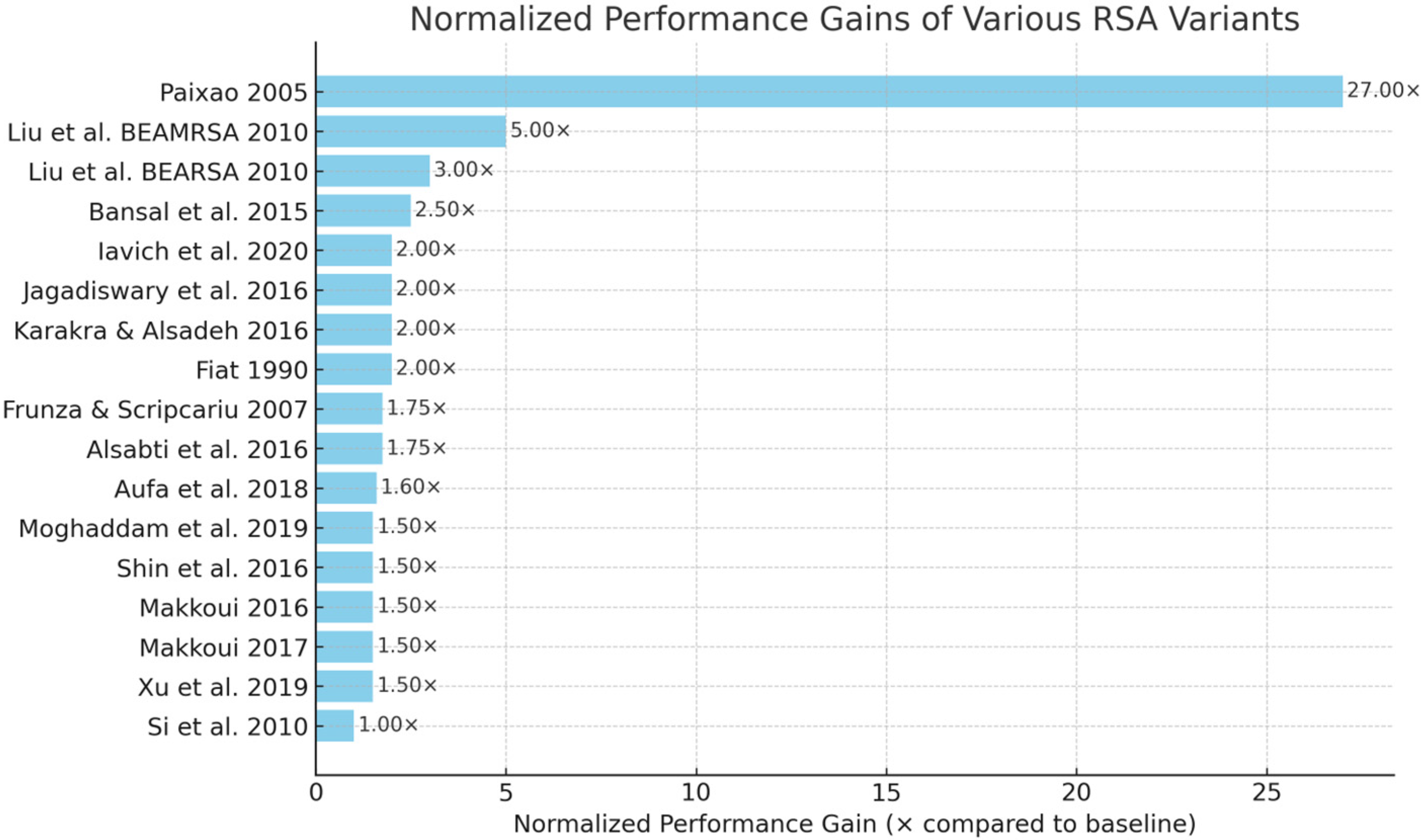
• Performance of RSA variants: We can notice large improvements over classical RSA obtained through math tricks (multi-prime, re-balanced RSA, Fast Cloud RSA), batch processing (Batch RSA, BEARSA/BEAMRSA), and hybrid use of symmetric and asymmetric methods (AES + RSA, Blowfish + RSA).
• Security tradeoffs: Most variants do indeed preserve the base RSA security models but also include homomorphic encryption, improved brute force resistance, or image scrambling for better domain-specific security.
• Application of RSA to specific fields: We see that many recent RSA variants have been designed for particular applications, for example, cloud data storage (HE-RSA), medical image encryption (MDRSA), and fast digital signatures (Aufa et al.), which shows a great range of use for these adaptations.
• Trends in the past had been seen towards early development of batch processing and multi-prime optimization issues. In the present time, attention is given toward hybrid cryptosystems and ASCE (for example, images, biomedical collections, cloud storage).

RSA-based vector commitments exhibit distinct performance characteristics crucial for practical deployment. Batch RSA [27] achieves O(1) verification time through aggregated exponentiations, producing 1.2 KB proofs. The multi-prime variant [4] reduces proof sizes to 0.8 KB by optimizing modulus factorization, while Cloud-RSA [13] maintains 1.5 KB proofs but enables homomorphic updates. Modern SIS-based VCs [29] achieve 0.3 KB proofs but incur linear verification costs, making RSA variants preferable in pre-quantum scenarios requiring sub-second verification. These schemes trade quantum vulnerability (due to strong RSA dependence) for efficient verification-typically 10–100× faster than equivalent lattice operations [30]. While RSA proofs (0.8–1.5 KB) are smaller than early lattice constructions (2–4 KB), they require a trusted setup and lack post-quantum security.

Table 4. A quantitative comparison of RSA variants.

Year	Authors	Scheme	Performance Gain Factor	Security Notes	Application Domain
1990	Fiat [27]	Batch RSA	N/A	Standard RSA security	Electronic communication
2005	Paixao et al. [5]	Multi-Prime + Re-balanced RSA	27×	Same as RSA (strong integer factorization assumption)	General purpose
2007	Frunză and Scripcariu [26]	AFF-RSA	1.1–1.2×	Larger key space	Wireless
2010	Liu et al. [28]	BEARSA	1.3–1.5×	Standard RSA	Electronic communication
2010	Liu et al. [28]	BEAMRSA	1.5–1.6×	Standard RSA	Electronic communication
2010	Si et al. [24]	Efficient RSA signature	N/A	Standard RSA security	Digital signatures
2015	Bansal et al. [12]	RSA + Blowfish	1.2–1.3×	Symmetric + asymmetric hybrid	Cloud security
2016	Karakra and Alsadeh [7]	A-RSA (RSA + Rabin + Hoffman Coding)	1.3–1.4×	1. More secure, 2. Shorter ciphertext 3. better brute-force resistance	General purpose
2016	Alsabti et al. [16]	RSA for MATLAB images	1.1–1.15×	Secure image transfer	Image encryption
2016	Jagadiswary et al. [17]	MDRSA	1.1–1.15×	Stronger biomedical data security	Medical
2017	Shin et al. [18]	Non-Mersenne Prime RSA	1.1×	Image scrambling	Medical
2017	Makkaoui [14]	Cloud RSA	1.1×	Homomorphic property retained	Cloud
2018	Makkaoui [14]	Fast Cloud RSA (N = prqs)	1.2×	Same as RSA	Cloud
2018	Xu et al., Jiao et al., Sabir et al., Soni et al. [19,20,21,22]	RSA + Arnold’s Map	1.05–1.1×	Image scrambling	Image encryption
2018	Aufa et al. [24]	RSA + Digital Signature	1.6×	Maintains RSA + DS security	Digital signatures
2018	Moghaddam et al. [11]	HE-RSA	1.5×	Maintains homomorphic property	Cloud storage
2020	Iavich et al. [10]	AES + RSA, Twofish + RSA	1.2–1.3×	Inherits AES/Twofish + RSA security	General purpose

Table 4. A quantitative comparison of RSA variants.

Year	Authors	Scheme	Performance Gain Factor	Security Notes	Application Domain
1990	Fiat [27]	Batch RSA	N/A	Standard RSA security	Electronic communication
2005	Paixao et al. [5]	Multi-Prime + Re-balanced RSA	27×	Same as RSA (strong integer factorization assumption)	General purpose
2007	Frunză and Scripcariu [26]	AFF-RSA	1.1–1.2×	Larger key space	Wireless
2010	Liu et al. [28]	BEARSA	1.3–1.5×	Standard RSA	Electronic communication
2010	Liu et al. [28]	BEAMRSA	1.5–1.6×	Standard RSA	Electronic communication
2010	Si et al. [24]	Efficient RSA signature	N/A	Standard RSA security	Digital signatures
2015	Bansal et al. [12]	RSA + Blowfish	1.2–1.3×	Symmetric + asymmetric hybrid	Cloud security
2016	Karakra and Alsadeh [7]	A-RSA (RSA + Rabin + Hoffman Coding)	1.3–1.4×	1. More secure, 2. Shorter ciphertext 3. better brute-force resistance	General purpose
2016	Alsabti et al. [16]	RSA for MATLAB images	1.1–1.15×	Secure image transfer	Image encryption
2016	Jagadiswary et al. [17]	MDRSA	1.1–1.15×	Stronger biomedical data security	Medical
2017	Shin et al. [18]	Non-Mersenne Prime RSA	1.1×	Image scrambling	Medical
2017	Makkaoui [14]	Cloud RSA	1.1×	Homomorphic property retained	Cloud
2018	Makkaoui [14]	Fast Cloud RSA (N = prqs)	1.2×	Same as RSA	Cloud
2018	Xu et al., Jiao et al., Sabir et al., Soni et al. [19,20,21,22]	RSA + Arnold’s Map	1.05–1.1×	Image scrambling	Image encryption
2018	Aufa et al. [24]	RSA + Digital Signature	1.6×	Maintains RSA + DS security	Digital signatures
2018	Moghaddam et al. [11]	HE-RSA	1.5×	Maintains homomorphic property	Cloud storage
2020	Iavich et al. [10]	AES + RSA, Twofish + RSA	1.2–1.3×	Inherits AES/Twofish + RSA security	General purpose

Figure 3. The normalized performance gains for the RSA variants [4,6,9,10,11,13,14,15,16,17,18,19,20,21,22,24,25,26,27].

Figure 3. The normalized performance gains for the RSA variants [4,6,9,10,11,13,14,15,16,17,18,19,20,21,22,24,25,26,27].

3.3. Diffie–Hellman-Based VC

The Diffie–Hellman algorithm is based on the discrete logarithm assumption for security. In the field of VC, some schemes are built using Diffie–Hellman-style group operations, among themPederson commitments [31], ElGammal-style [32] commitments, and discrete log-based polynomial commitments.

In [33], Bao et al. compare variations in the Diffie–Hellman problem, such as the square computational (and decisional) Diffie–Hellman problem, inverse computational (and decisional) Diffie–Hellman problem, and divisible computational (and decisional) Diffie–Hellman problem.

As a classical pre-quantum cryptographic scheme, it relies on the assumption of the hardness of the cyclic group problem: if G is a cyclic group of prime order p with the generator g, knowing gᵃ and gᵇ while computing g^ab is hard without knowing a and b [34].

Parameter Settings:

• Standard DH Groups: 2048-bit primes (p = 2q + 1 where q is prime) with |p| = 2048, |q| = 256 bits (112-bit NIST security).
• Elliptic Curve Groups: secp256k1 (y² = x³ + 7 over 𝔽ₚ where p = 2²⁵⁶ − 2³² − 977) or Curve25519.
• Pairing Groups: BLS12-381 (|G₁| = 381 bits, |G₂| = 756 bits) with Type-3 pairings.

Security Reductions:

1.

Pedersen Commitments [31]:

a.

Binding: Reduces to Discrete Log Problem (DLP) in G.

b.

Hiding: Unconditional (perfect hiding).

c.

Proof size: 2|G| (64 bytes for secp256k1).

2.

ElGamal-style [32]:

a.

IND-CPA security ⇐ DDH in G.

b.

Concrete advantage: Adv_DDH ≤ ε + q/|G| for q queries.

c.

Verification: 2 exp. operations (≈15 ms on modern CPUs).

3.

Polynomial Commitments:

d.

q-SDH assumption for evaluation binding.

e.

Requires |p| ≥ 256 bits for 128-bit security.

3.4. Pederson Commitments

The Pederson scheme is widely used in the blockchain space or in interactive zero-knowledge proof protocols. The specific situation is summarized in Table 5. In [35], the authors applied a Pederson scheme based on the RSA group: the prover is bound to the commitment under the strong RSA assumption unless they can compute the discrete logarithm of the messages.

In [36], Metere and Dong extended the EasyCrypt [37] software to accept the discrete logarithm and an abstraction of commitment protocols. In [38], Chen et al. proposed a sealed-bid reverse auction algorithm that uses Pederson’s commitment.

In the field of blockchain applications, for e-commerce, a key aspect is to protect and hide the amount of the transaction. In [39], Wang et al. applied the Pederson commitment combined with zero-knowledge proof technology to offer a secure and efficient verification of the transaction amount.

In [40], Feng et al. used the Pederson protocol and Schnorr signature to merge and sign transaction messages properly in terms of privacy protection and security efficiency within blockchains.

Yang et al. [41] proposed a Pederson-based approach for the time-controlled expressive predicate query (EPQ) with accountable anonymity. Using Pederson commitments, anonymous credentials, and non-interactive zero-knowledge proof, the authors describe an EPQ scheme that protects the privacy of expressive search predicates.

Table 5. Quantitative comparison of pedersen-based vector commitments.

Scheme	Security (Bits)	Commit Size	Commit Time	Verify Time	ZK Proof Size
Metere and Dong [36]	128 (DLP)	256 bytes	220 ms	180 ms	N/A
Chen et al. [38]	128 (DLP)	192 bytes	15 ms	22 ms	1.2 KB
Wang et al. [39]	128 (DLP)	64 bytes	8 ms	22 ms	3.8 KB
Feng et al. [40]	128 (DLP)	48 bytes	0.8 ms	1.5 ms	2.1 KB
Yang et al. [41]	128 (DLP)	80 bytes	5 ms	18 ms	500 byte

Table 5. Quantitative comparison of pedersen-based vector commitments.

Scheme	Security (Bits)	Commit Size	Commit Time	Verify Time	ZK Proof Size
Metere and Dong [36]	128 (DLP)	256 bytes	220 ms	180 ms	N/A
Chen et al. [38]	128 (DLP)	192 bytes	15 ms	22 ms	1.2 KB
Wang et al. [39]	128 (DLP)	64 bytes	8 ms	22 ms	3.8 KB
Feng et al. [40]	128 (DLP)	48 bytes	0.8 ms	1.5 ms	2.1 KB
Yang et al. [41]	128 (DLP)	80 bytes	5 ms	18 ms	500 byte

3.5. Post-Quantum Vector Commitments

In spite of the wide usage and their advantages, all the previously described commitment schemes are vulnerable to post-quantum attacks. Shor’s algorithm [42] offers a solution to factorize large composite numbers; thus, it is the first enemy of VC schemes analyzed above. Although the mathematician Peter Shor proposed the algorithm in 1995, only with the emergence of the quantum computers does his solution become applicable in practical situations. However, like all the quantum algorithms, Shor’s algorithm is probabilistic: the result is true with a certain probability, while the failure probability decreases with the number of times the algorithm is applied.

Lattice-based approaches, as mentioned before, such as Shor’s algorithm, can efficiently break the RSA and Diffie–Hellman–based protocol. However, so far, there is no available algorithm to attack the lattice-based cryptographic systems. In [43], Peikert provided a survey of lattice-based cryptography techniques over a 10-year period starting in 2005.

A lattice is similar to a vector space, except that the vectors have discrete values, as opposed to real values, as in the case of a vector space. In Figure 4 is illustrated a basic lattice formed by two vectors (the first one is represented in red solid color, the second one with a dashed green line). Unlike RSA-based VCs, where proof size remains constant (typically < 1.5 KB) regardless of vector length, lattice constructions exhibit logarithmic growth. For a 1M-element vector, SIS proofs [30] grow to ≈4 KB while maintaining O(n) verification-still slower than RSA’s O(1) batch verification, but with quantum resistance. A detailed theoretical introduction of lattices is offered in [44]. Moreover, if we define a lattice as a set of linearly independent vectors

$$L=\left\{a_1{v}_1+\dots +a_n{v}_n\right|a_1{\dots a}_n\in \mathbb{Z}\},$$

we should highlight that the coefficients $a_i$ i ∈ {1…n}, are integer numbers.

Figure 5 illustrates the comparison between orthogonal and non-orthogonal lattice bases. The gray quadrilateral shown in the diagram represents the fundamental domain of the lattice, highlighting how the choice of basis affects its geometric structure.

For the application area, the following four lattice problems are of interest:

• The Shortest Vector Problem (SVP): Given a lattice basis B, find a shortest non-zero vector in the lattice L(B), i.e., find a non-zero vector v ∈ L(B) such that

$$‖v‖={\lambda }_1\left(L\right(B\left)\right)$$

2.

The Shortest Independent Vectors Problem (SIVP): Given a lattice basis B of an n-dimensional lattice L(B), find n linearly independent vectors $v_1$, …, $v_n$∈ L(B) such that

$$\underset{i\in [1,n]}{\mathrm{m}\mathrm{a}\mathrm{x}} ‖v_i‖={\lambda }_n(L(B))$$

3.

The Closest Vector Problem (CVP): Given a lattice basis B and a target vector t that is not in the lattice L(B), find a vector in L(B) that is closest to t, i.e., find a vector v ∈ L(B) such that for all w ∈ L(B), it satisfies

$$\Vert v-t\Vert \le \Vert w-t\Vert$$

4.

The α-Bounded Distance Decoding Problem (BDDα): Given a lattice basis B of an n-dimensional lattice L and a target vector t ∈ Rⁿ satisfying

$$\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(t,B)\le a{\lambda }_1\left(L\right)$$

However, in cryptography, the systems are based on variants of the above-mentioned contexts. A famous one is Ajtai’s worst-case to average-case reduction [45], known as the Short Integer Solution (SIS) problem:

Given a uniformly random integer matrix A ∈ Z^m×n, the Short Integer Solution (SIS) problem requires finding a non-zero integer vector z ∈ Zⁿ such that:

$$A\cdot \mathrm{z}\equiv \underset{\_}{\mathrm{o}}\left(\mathrm{m}\mathrm{o}\mathrm{d}\underset{\_}{q}\right) \mathrm{and} \Vert \mathrm{z}\Vert \le \beta ,$$

for some small norm bound β (e.g., in the ℓ2 or ℓ∞ norm).

A key application of the SIS problem is the cryptographic primitive called the collision-resistant hash function, or Collision Resistance Hashing (CRH). The collision resistance refers to the infeasibility of finding two colliding inputs (two inputs that map to the same output), although they might exist.

Recent works [46,47,48,49,50] focus on a more relaxed version of CRH, named MultiCollision Resistance Hashing (MCHR, or even t-MCHR, for a given integer t). t-MCHR relies on the existence of a set of t inputs mapping to the same output. Although one may find a set of (t − 1) inputs with collide to the same output, it is unfeasible to find the entire set of t such inputs.

In [50], the authors propose a non-Blackbox transformation of a t-MCHR (for a t ∈ {3, 4}) into a CHR, in a non-constructive manner (the existence of the CHR can be proven, but cannot be explicitly constructed). However, a limitation of their research consists of the difficulty (or even impossibility) of constructing a CHR from a t-MCHR, when t > 4.

In [30], Peikert et al. present a post-quantum secure approach of vector commitments and functional commitments (described in Section 5) based on the SIS lattice problem. They construct statelessly updatable VCs with significantly shorter proofs (consequently improving the work of Papamanthou et al. [51]) in a private key setup.

A quantitative comparison of the MCRH literature review is synthesized in

Table 6. Quantitative comparison of MCRH and post-quantum vector commitments.

Scheme	Primitive	Collision Size (t)	Proof Size	Limitations
[45,46,47,48,49] (MCRH)	t-MCRH	t = {3,4}	N/A	Only t ≤ 4 feasible
[50] (CHR Conversion)	t-MCRH → CHR	t = {3,4}	Non-constructive	No explicit construction for t > 4
[29] (Peikert et al.)	SIS-based VC	not applicable	0.3 KB	Requires trusted setup
[30] (Papamanthou et al.)	Merkle-based VC	not applicable	1.2 KB	Linear proof growth

, below.

3.6. Gaps in Research

The above-discussed scientific works leave the way open to further research. We classified these gaps in research into the following main categories:

• Post-Quantum Secure Vector Commitments: Most of the VC schemes are vulnerable to post-quantum attacks. In [52], Boneh, Bunz, and Fisch question whether an accumulator with constant-size witnesses can be constructed under a quantum-resistant assumption. In [30], Peikert offers post-quantum constructions of vector and functional commitments based on the Short Integer Solution (SIS) lattice problem, but we should also find and implement more techniques to empower the VC schemes.
• Sublinear Update and Proof Times: Most of the VC schemes hardly support efficient updates in the changing vector elements context. Tas and Boneh offer such an approach in [53], but we should also investigate more ways to improve this context.
• Efficient Zero-Knowledge Vector Commitments: Few VC constructions address the zero-knowledge proofs for committed values. Although Wang et al. investigate in [54] a (Zero-Knowledge) VC with Sum Binding, we may focus on improving this area.
• Multi-Vector or Hierarchical Commitments: The subject of committing to multiple related vectors or nested structures is underexplored. Miao et al. try an approach in [55], but more research directions should also be explored.
• Applications to Decentralized Systems: With the advent of blockchains and cryptocurrencies, the practical integration of VCs into blockchain and rollup systems is still emerging. Future work could explore intersections with domain-specific data, such as underwater image verification, where commitments might enhance tamper-proofing for enhanced images [23].

4. Polynomial Commitments

4.1. Classical Polynomial Commitments

Polynomial commitment schemes are a type of commitment scheme that allows one to make a commitment to a polynomial, specifically. We can format our data as a vector of length $n,\left[a_0,\dots ,a_{n-1}\right]$. There are two main ways of creating a polynomial that contains the data:

• $a_i$ can be the coefficients of the polynomial:

$$P(x)=\sum _{i=0}^{\mathrm{\infty }} a_i{x}^i=a_0+a_{1}x+\dots +a_{n-1}{x}^{n-1}$$

2.

The polynomial can interpolate the points ($i,a_i$). Consequently, we can construct a polynomial that passes through each of those points. To do this, for each i, we first construct a polynomial Qi(x) which evaluates to 0 at each $j/=0$ for $j\in \left\{0,\dots ,n-1\right\}$ and evaluates to 1 at i:

$$Q_i(x)=\sum _{\begin{array}{c}0\le j\le n-1\\ j=j\end{array}}^{\mathrm{Y}} {\displaystyle \frac{x-j}{i-j}}$$

We can scale and sum these polynomials to get our polynomial P such that $P(i)=a_i$ for each $i\in \{0,\dots ,n-1\}$:

$$P(x)=\sum _{i=0}^{\mathrm{n}-1} a_i{Q}_i(x)$$

4.2. Pedersen Polynomial Commitment

In this type of polynomial commitment, the prover and the verifier need to agree on two elliptic curve points with unknown discrete logarithms.

In [56], the authors proposed a constant-size (single-element) polynomial commitment with a constant amount of communication overhead. The proposed approach was applied to four problems in cryptography: verifiable secret sharing, zero-knowledge sets, credentials, and content extraction signatures. In [57], Belling et al. introduced the List Polynomial Commitment (LPC).

Basically, an LPC is based on a relaxed binding property, meaning that the commitment to a function can be opened by a list of low-degree polynomial functions, close to f (x), in terms of relative Hamming distance and over a specific domain. The so-called Vortex approach is based on the works of Brakedown [58] (Crypto 2023), batch-FRI (FOCS 2020), and RedShift [59] (CCS 2022).

4.3. KZG Polynomial Commitments

First introduced by Aniket Kate, Gregory M. Zaverucha, and Ian Goldberg in [56] and named after their authors, KZG commitments are a particular type of polynomial commitment because they allow us to reveal an evaluation of the polynomial that is verifiable without revealing the entire polynomial. When the polynomial being committed to is one that interpolates points coming from a vector, the KZG commitment is actually a vector commitment. That is, given a vector [a0, …, an−1], we can construct a polynomial P such that P (i) = ai for each i ∈ {0, …, n − 1} and construct a KZG commitment to P. Then, as a KZG commitment, the committer can reveal an evaluation of P (specifically, for some i that P (i) = ai) without revealing the rest of P (and thus not revealing aj for i ̸≠ j).

A recent work from 2025 of Belohorec et al. [60] presents a KZG-like polynomial commitment scheme based on the central idea of the proof-of-knowledge of a polynomial (PoKoP) in order to capture the extractability notion required in constructions of practical zk-SNARKs. The authors argue that this is the first standard-model proof of extractability for the multivariate KZG scheme.

In [61], the authors introduce Behemont (named after an enormous biblical character, a monster, leading to the idea that the scheme uses very large integers). This is a transparent polynomial scheme whose security has been proven through random oracle and generic group models. Consequently, Behemont positively closes an open question of Nikolaenko [62], which doubted the existence of such a transparent scheme. However, Nikolaenko focused on the decentralized setup in order to leverage the number of users within a blockchain.

Avery and Sheek propose in [63] the use of KZG commitments in the context of performing audits of storage providers within blockchains. Although the providers usually can conduct a self-audit with Merkle trees, the process becomes expensive as it requires posting frequent and large proofs to the blockchain. The authors show that KZG commitments reduce the amount and the frequency of the proofs needed to be posted.

KZG commitment schemes are also used in Verkle trees [64,65]. More precisely, the Verkle trees use the KZG polynomial commitments instead of the usual hash function from the Merkle trees scenario.

Although the polynomial commitments have various applications, as discussed above, they are vulnerable to quantum attacks. In the next section, we will discuss polynomial commitment approaches tackled in the post-quantum era.

Table 7 provides a quantitative comparison of several modern polynomial commitment schemes, highlighting their key performance characteristics and contributions. It contrasts trusted setup schemes like KZG-based variants with transparent alternatives, noting significant improvements in proof size and verification time over older structures like Merkle trees. Each entry is summarized by its unique innovation within the field.

Table 7. Quantitative comparison of modern polynomial commitment schemes.

Scheme	Type	Proof Size	Verification Time	Setup	Security Model	Unique Contribution
Belohorec et al. (PoKoP) [60]	Multivariate KZG	288 bytes	12 ms	Trusted	Standard model (w/extractability)	First extractable multivariate KZG
Behemont [61]	Transparent Poly.	1.5 KB	45 ms	Transparent	ROM + Generic Group	Resolves Nikolaenko’s open problem
Avery and Sheek (Storage Audit) [63]	Univariate KZG	96 bytes	8 ms	Trusted	Generic Group	10× fewer audits vs. Merkle trees
Verkle trees [64,65]	KZG-based	128 bytes/node	6 ms/node	Trusted	Generic Group	30× smaller proofs than Merkle

Table 7. Quantitative comparison of modern polynomial commitment schemes.

Scheme	Type	Proof Size	Verification Time	Setup	Security Model	Unique Contribution
Belohorec et al. (PoKoP) [60]	Multivariate KZG	288 bytes	12 ms	Trusted	Standard model (w/extractability)	First extractable multivariate KZG
Behemont [61]	Transparent Poly.	1.5 KB	45 ms	Transparent	ROM + Generic Group	Resolves Nikolaenko’s open problem
Avery and Sheek (Storage Audit) [63]	Univariate KZG	96 bytes	8 ms	Trusted	Generic Group	10× fewer audits vs. Merkle trees
Verkle trees [64,65]	KZG-based	128 bytes/node	6 ms/node	Trusted	Generic Group	30× smaller proofs than Merkle

4.4. Zero-Knowledge Proofs

Polynomial commitments are also used in the zero-knowledge (zk) proof scenario, where the prover demonstrates to the verifier the truth of a statement, without revealing any part of the information. For instance, in the case of hashing a number, it is sufficient for the prover to demonstrate the existence of the hashed value without revealing the initial number. The most common applications are the SNARK and the STARK commitment types.

SNARK is a succinct non-interactive argument of knowledge. The succinct zero-knowledge proofs are verified within a few milliseconds and only need a proof length of a few hundred bytes, even though the statements for the programs are (very) large. They were introduced by Blum et al. [66] in 1988 as a demonstration that a common reference string shared between the prover and the verifier is sufficient to achieve computational zero-knowledge without requiring interaction. The main advantage of this type of commitment is the possibility of being used when there is no direct interaction between the prover and the verifier. The most common scenario is online transactions. In 2012, Chiesa et al. [67] developed the zk-SNARK protocol, which is used in the Ze-rocash [68], a decentralized anonymous payment (DAP), later deployed to a commercial blockchain protocol for the cryptocurrency ZCash [69].

Another zero-knowledge commitment application is the zk-STARK (scalable and transparent argument of knowledge) protocol, based on the work of Ben et al. [70] and on a polynomial interactive oracle proof (IOP), in which the verifier selects some random numbers and the prover provides corresponding oracle access. Finally, after some rounds, the verifier can decide about the correctness of the prover’s claim. STARK is a zero-knowledge proof system that is transparent. In other words, the prover and verifier do not need to use a third generated parameter to produce the proof and check the validity of the claim, respectively. Works such as eSTARK [71], MARVELlous [72], and STRAKNet (https://www.starknet.io (accessed on 1 May 2025) are all based on the STARK technology.

4.5. Post-Quantum Polynomial Commitments

In [73], the authors propose a post-quantum secure commitment, based on the existence of one-way functions [74] variant of [73].

In [75], Xie et al. proposed Orion, a linear-time zero-knowledge proof, polynomial-based commitment scheme. It is implemented using the KZG scheme and is post-quantum secure. Most of the ZKG schemes with linear time prover [76,77,78] are based on the existence of a good expander graph (meaning that any subset of vertices within a graph can expand to a larger set of neighbors). Orion is based on an algorithm capable of testing whether a random graph is a good expander graph based on the small set expansion problem. However, Orion has been proven to be unsound. In cryptography, soundness ensures that any prover who successfully and consistently convinces a verifier of a statement must genuinely possess knowledge of a corresponding witness.

In [79], den Hollander et al. found practical attacks on Orion and propose a fix for this scheme, leading to smaller proof size and verifier time, over the claimed efficiency of the initial version of Orion, as den Hollander et al. argue. They apply Diamond’s approach [80] to reduce the challenge in Orion to logarithmically sized.

Building on the need for efficient and secure primitives, Spartan [81] presents a foundational approach to transparent SNARKs. It offers a trusted setup-free argument system with succinct verification, contributing significantly to the landscape of post-quantum secure cryptography.

In [82], Fu and Gong propose Polaris, a commitment polynomial scheme whose building blocks only use symmetric cryptography (collision-resistant hash functions used in Merkle tree commitments), assuring plausible post-quantum security.

As a post-quantum secure succinct non-interactive argument of knowledge (SNARK) [83], Albrecht et al. introduce in [84] a lattice-based SNARK, which is stated to be publicly verifiable and can achieve sublinear verification time given preprocessing, while requiring a trusted setup [84].

A quantitative comparison of post-quantum polynomial commitments and SNARKs is listed in Table 8.

Table 8. Quantitative comparison of post-quantum commitments and SNARKs.

Scheme	Type	Security Assumption	Proof Size	Prover Time	Verifier Time	Trusted Setup	Soundness
OWF-Based Commit [72]	One-Way Function Commit	OWF Existence	N/A	N/A	N/A	No	yes
Variant of [72,73]	Enhanced OWF Commit	Stronger OWF Assumption	N/A	N/A	N/A	No	Yes
Orion (Original) [74]	ZK Polynomial Commit	Small Set Expansion	2.5 KB	O(n)	O(1)	No	No (Unsound)
Orion (Fixed) [78]	ZK Polynomial Commit	Diamond Reduction [79]	1.8 KB (reduced by 28% compared to the original)	O(n)	O(log n)	No	Yes
Polaris [82]	Merkle-Based Commit	CRHFs	4.2 KB	O(n)	O(log n)	No	Yes
Lattice SNARK [83]	Lattice-Based SNARK	SIS/LWE	1.2 KB	O(n log n)	O(√n)	yes	Yes

Table 8. Quantitative comparison of post-quantum commitments and SNARKs.

Scheme	Type	Security Assumption	Proof Size	Prover Time	Verifier Time	Trusted Setup	Soundness
OWF-Based Commit [72]	One-Way Function Commit	OWF Existence	N/A	N/A	N/A	No	yes
Variant of [72,73]	Enhanced OWF Commit	Stronger OWF Assumption	N/A	N/A	N/A	No	Yes
Orion (Original) [74]	ZK Polynomial Commit	Small Set Expansion	2.5 KB	O(n)	O(1)	No	No (Unsound)
Orion (Fixed) [78]	ZK Polynomial Commit	Diamond Reduction [79]	1.8 KB (reduced by 28% compared to the original)	O(n)	O(log n)	No	Yes
Polaris [82]	Merkle-Based Commit	CRHFs	4.2 KB	O(n)	O(log n)	No	Yes
Lattice SNARK [83]	Lattice-Based SNARK	SIS/LWE	1.2 KB	O(n log n)	O(√n)	yes	Yes

4.6. Gaps in the Research

The previously reviewed papers discussed polynomial commitments, but there are still aspects that can be improved. In this subsection, we try to address a series of PC-weak aspects.

• Post-Quantum Secure Polynomial Commitments: The existing efficient polynomial commitments (e.g., KZG) rely on pairings and discrete logarithm assumptions, which are insecure against quantum adversaries. Few post-quantum constructions balance succinctness, universality, and efficiency. The challenge lay in achieving short proofs, efficient verification, and universality under lattice-based assumptions like SIS or LWE. Although some research works [69,85] proposed feasible solutions and implementations, there is still room to research and propose other approaches for this purpose.
• Efficient Batch Openings (Multi-point, Multi-polynomial): While batching is supported in KZG-based schemes [52,69,86,87], it is less efficient or absent in the transparent or the post-quantum settings. One challenge might be to design non-interactive aggregation techniques with minimal overhead and secure under standard assumptions.
• Dynamic or Updatable Commitments: Most existing schemes are static; thus, updating the coefficients of the polynomials typically requires full recommitment. One solution might be to develop schemes that allow local updates to committed polynomials with minimal computational or communication costs. Some works already intended to address this issue [85,86]; however, future works focus on implementing more efficient and less expensive scenarios.
• Universally Composable and Simulation-Sound Security: Many PC constructions lack proofs of security under UC frameworks or simulation-based zero-knowledge. The works of Peikert et al. [85], Chiesa and Spooner [70], or Boneh et al. [52] attempted to offer implementations of such constructions. Consequently, it is imperiously necessary to further focus on constructing polynomial commitment schemes composable within larger cryptographic protocols like SNARKs [69] or multi-party computation (MPC) [88].
• Efficient Verifier Time in Transparent Settings: Transparent schemes such as STARKs [69] incur superlinear verifier time and larger proof sizes. The key solution is to achieve linear or sublinear-time verification without trusted setup or non-standard assumptions.

5. Functional Commitments

Functional commitments (FCs) are cryptographic primitives that enable a user to commit concisely to a function and later reveal, with proof, the result of evaluating this function on a chosen input. Specifically, after committing to a function f, one can later open this commitment at an input x by providing y = f (x) along with proof that y is indeed the output of the committed function f at x. Importantly, this does not reveal anything else about the function.

FCs generalize several foundational concepts in cryptography, such as vector commitments (VCs) and polynomial commitments. While VCs allow commitments to ordered sequences and support index-based openings, FCs offer a more flexible structure where arbitrary functions can be revealed in a controlled and verifiable manner. This level of abstraction enables FCs to support more complex operations, including linear and non-linear functions, opening up a wide range of applications.

5.1. Classical Schemes

Classical functional commitment schemes typically rely on pairing-based cryptography, which offers compact commitments and proofs along with efficient verification. However, the main limitation of these schemes is their lack of resistance against quantum attacks. Most are built on assumptions like computational Diffie–Hellman (CDH) or strong bilinear Diffie–Hellman (q-SBDH), which are not secure in the presence of quantum adversaries.

Notable classical constructions include Catalano and Fiore’s (2013) vector commitments and Kate et al.’s (2010) polynomial commitments, both based on bilinear groups with constant-size proofs. These schemes rely on the CDH and q-SDH assumptions, respectively, achieving information-theoretic hiding properties while supporting efficient verification. Such classical constructions have been successfully applied in verifiable data structures, credentials, and accumulators, though they require a trusted setup and lack post-quantum security.

Despite their elegance and practicality, these pairing-based constructions are inherently insecure against quantum algorithms like Shor’s algorithm, which can break the discrete logarithm problem efficiently. This quantum vulnerability has motivated the search for post-quantum alternatives.

Thus, while classical schemes set foundational principles and exhibit strong performance in traditional cryptographic settings, they fall short in environments where quantum resistance is mandatory. This necessitates a shift toward post-quantum secure constructions using lattice-based cryptography and related hardness assumptions.

5.2. Post-Quantum Approaches

To address the quantum vulnerabilities of classical cryptographic constructions, recent research has introduced post-quantum secure functional commitments based on lattice problems, especially the Short Integer Solution (SIS) problem. These constructions are believed to be secure against quantum adversaries and provide an essential step toward future-proof cryptographic primitives.

In [30], Chris Peikert et al. constructed stateless updatable vector and functional commitments using the SIS problem. Their scheme supports efficient updates and compact proofs, improving upon prior lattice-based schemes. Notably, their construction extends beyond linear functions, allowing commitment to arbitrary Boolean circuits under falsifiable assumptions, marking a significant advancement in functional commitment capabilities.

Other researchers, such as Hoeteck Wee and David J. Wu in [89], focused on efficient verification. They developed FC schemes for constant-degree polynomials and Boolean circuits with fast verification in the preprocessing model. Their constructions also rely on variants of the SIS problem and avoid non-black-box use of cryptographic tools, enhancing practical efficiency and simplicity. These post-quantum constructions are fundamentally different from classical ones. They use lattice-based assumptions and provide provable security without relying on pairings or random oracles. Additionally, they introduce transparent or minimally trusted setups, further strengthening their security models. Post-quantum FCs thus represent a robust cryptographic solution in the face of emerging quantum threats.

Key developments:

• In [29], Chris Peikert et al. introduced a stateless updatable FC scheme based on SIS:

  a.

  Supports compact proofs and efficient updates.

  b.

  Allows commitments to arbitrary Boolean circuits.

  c.

  Operates under falsifiable assumptions.

• Hoeteck Wee and David J. Wu in [89] focused on the following:

  a.

  Fast verification for constant-degree polynomials.

  b.

  Use of transparent setup and SIS variants.

  c.

  Avoidance of non-black-box cryptographic tools.

Main advantages of these post-quantum FCs:

• Based on lattice assumptions, not pairings.
• Require minimal trust in setup.
• Enable provable security under quantum threat models.

5.3. SIS-Based Functional Commitments

In their 2023 paper, Peikert and de Castro [85] presented a novel SIS-based functional commitment scheme that supports arbitrary functions under a transparent setup, requiring only public randomness. This work represents a significant leap in the state-of-the-art for post-quantum secure FCs, as it removes the need for online trusted authorities and operates under standard assumptions.

Their construction enables concise, noninteractive, and publicly verifiable proofs of function evaluations. It supports all functions of bounded complexity and offers efficient preprocessing to accelerate commitment and verification steps. Importantly, the security is grounded in the hardness of the SIS problem, a well-established lattice problem considered resistant to quantum attacks. One of the key contributions is the transparent setup, which contrasts with prior schemes requiring structured, trapdoor-dependent parameters. This makes their approach more practical and widely applicable. The construction also allows for generic composition and stateless updates, enabling commitments to evolve over time or be composed with other functions securely.

In addition to theoretical advancements, the scheme is efficient in practice. Verification involves checking a single linear SIS equation, and preprocessing transforms expensive operations into simple matrix multiplications. As such, this work is a cornerstone for building secure, post-quantum cryptographic applications that demand strong privacy and guarantees of verifiability.

Mathematical Framework

Let F={f:X→Y}F={f:X→Y} be a family of functions we wish to commit to. A functional commitment scheme consists of four algorithms:

• Setup: Generates public parameters $pp\leftarrow \mathrm{S}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{p}\left(1^{\lambda }\right)$.
• Commit: Produces a commitment $c_f\leftarrow \mathrm{C}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{i}\mathrm{t}(pp,f)$ to function $f\in \mathcal{F}$.
• Open: Generates a proof ${\pi }_{f,x}\leftarrow \mathrm{O}\mathrm{p}\mathrm{e}\mathrm{n}(pp,f,x)$ that $f\left(x\right)=y$.
• Verify: Checks proofs $\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}\left(pp,c_f,x,y,{\pi }_{f,x}\right)\to \left\{\mathrm{0,1}\right\}$.

The key security property is evaluation binding, which requires that for any xx, it should be computationally infeasible to produce valid proofs for two different outputs y ≠ y′:

$$\mathrm{P}\mathrm{r}\left[\left.\begin{array}{rr}& Verify(pp,c,x,y,\pi )=1\wedge \\ Verify\left(pp,c,x,y^{\prime },{\pi }^{\prime }\right)=1& pp\leftarrow Setup\left(1^{\lambda }\right)\\ & y\ne y^{\prime }\end{array}\right|\begin{array}{r}\left(c,x,y,\pi ,y^{\prime },{\pi }^{\prime }\right)\leftarrow \mathcal{A}\left(pp\right)\end{array}\right]\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}(\lambda )$$

5.4. Lattice-Based Construction

The construction uses homomorphic computation techniques from lattice cryptography. The construction uses homomorphic computation techniques from lattice cryptography. The public parameters consist of a random matrix:

$$\mathrm{C}\leftarrow {\mathbb{Z}}_q^{n\times W}$$

where W depends on the input space X.

Key Advantages:

• Transparent setup: The public parameters are just uniformly random matrices, requiring no trusted setup:

$$pp=\left\{\mathrm{C}\leftarrow {\mathbb{Z}}_q^{n\times W}\right\}$$

2.

Support for all functions: The scheme can handle arbitrary functions of bounded complexity via their Boolean or arithmetic circuit representations.

3.

Stateless updates: Commitments can be updated to g∘f without knowing f:

$${\mathrm{C}}_{g\circ f}=\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{i}\mathrm{t}\left({\mathrm{C}}_f,g\right)$$

4.

Efficient verification: Reduces to checking a single SIS relation:

$$\mathrm{A}\mathrm{S}=\mathrm{Y}\left(\mathrm{m}\mathrm{o}\mathrm{d}q\right)$$

The security relies on the hardness of the SIS problem: given a random $\mathrm{A}\in {\mathbb{Z}}_q^{n\times m}$, find a short non-zero Z such that Az = 0 (modq). This gives us post-quantum security under well-studied lattice assumptions.

5.4.1. Core Algebraic Structure

The construction builds on structured matrix operations over the ring Z_q. Let n be the security parameter, q a modulus, and define the gadget matrix:

$$\mathrm{G}={\mathrm{I}}_n\otimes {\mathrm{g}}^t\in {\mathbb{Z}}_q^{n\times n\mathcal{l}}$$

where $\mathrm{g}={\left(\mathrm{1,2},4,\dots ,2^{\mathcal{l}-1}\right)}^t\in {\mathbb{Z}}_q^{\mathcal{l}}$ with $\mathcal{l}=⌈{\mathrm{l}\mathrm{o}\mathrm{g}}_2 q⌉$. This enables binary decomposition via the function ${\mathrm{g}}^{-1}:{\mathbb{Z}}_q\to \{\mathrm{0,1}{\}}^{\mathcal{l}}$.

5.4.2. Efficiency Analysis

For a function with k-bit inputs and m-bit outputs (See

Table 9. Efficiency metrics for functional commitment components.

Component	Size (Bits)	Asymptotic
Public Parameters	$nk\mathcal{l}\mathrm{l}\mathrm{o}\mathrm{g} q$	$\tilde{O}\left(k\right)$
Commitment	$nm\mathcal{l}\mathrm{l}\mathrm{o}\mathrm{g} q$	$\tilde{O}\left(m\right)$
Proof	$k\mathcal{l}\cdot \mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(d\right)\mathrm{l}\mathrm{o}\mathrm{g} \beta$	$\tilde{O}\left(k\right)$

):

Table 9 outlines the key efficiency metrics for the components of a functional commitment scheme, detailing their sizes in bits and asymptotic complexity. It shows that the public parameters, commitment, and proof sizes scale with parameters like the security level and lattice dimensions. The verification time is noted to be dominated by a single matrix-vector multiplication operation. The verification cost is dominated by one matrix-vector multiplication:

$$\mathrm{VerifyTime} =O\left(nk\mathcal{l}\right)$$

5.5. Gaps and Limitations in Lattice-Based Functional Commitments

5.5.1. Proof Size Scalability

The proof size grows linearly with the input dimension k:

$$\left|\pi \right|=O(k\cdot n\mathcal{l}\cdot \mathrm{l}\mathrm{o}\mathrm{g} \beta )$$

where $\beta =(n\mathcal{l}{)}^{O\left(d\right)}$ for circuits of depth d. This becomes problematic for wide circuits (large k) and deep compositions (large d). Comparison: SNARKs achieve constant-size proofs O_λ (1) but rely on non-falsifiable assumptions.

5.5.2. Adaptive Security Limitation

The base scheme only achieves selective security (adversary commits to challenge x* before seeing pp). Achieving full adaptive security requires either:

• Complexity leveraging:

$$q\ge 2^{\left|\mathcal{X}\right|}\cdot \mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(\lambda \right)$$

which is infeasible for large $\mathcal{X}$.

2.

New techniques to avoid the $2^{\left|\mathcal{X}\right|}$ security loss.

5.5.3. Concrete Efficiency Bottlenecks

• Homomorphic Multiplication Cost:

$$\mathrm{T}\mathrm{i}\mathrm{m}\mathrm{e}\left({\mathrm{C}}_{f\cdot g}\right)=\mathsf{\Theta }\left(n^3{\mathcal{l}}^2\right) \mathrm{per} \mathrm{multiplication} \mathrm{gate}$$

2.

Verification Overhead:

$$\mathrm{VerifyTime} =\mathsf{\Theta }\left(nk\mathcal{l}\right) \mathrm{vs}. \mathsf{\Theta }\left(1\right) \mathrm{for} \mathrm{pairings}-\mathrm{based} \mathrm{schemes}$$

3.

Key Sizes:

$$\left|pp\right|=\mathsf{\Theta }\left(nk\mathcal{l}\mathrm{l}\mathrm{o}\mathrm{g}q\right)\left( \mathrm{e}.\mathrm{g}., \mathrm{MB} \mathrm{for} k=2^{20}\right)$$

5.6. Updated Research Gaps and Open Questions in Functional Commitments

Despite notable advancements, the field of functional commitments (FCs) continues to face several open problems and research gaps: while constructions such as [89] achieve succinct FCs for arithmetic circuits, their efficiency drops for high circuit depth and size, leading to bulky CRS and proofs [89,90].

Recent works such as Peikert et al. [91], de Castro and Peikert [85] extend FCs beyond linearizable functions under standard SIS assumptions, but challenges remain in reducing verification complexity and optimizing performance in general-purpose settings [85,91]. CRS size optimization succinct FCs often come at the cost of large CRS sizes. For instance, constructions like [89] have CRS sizes scaling as O(k3s5). Although Boneh et al. [92] proposes optimized proof systems through PFR techniques, the parameter generation complexity remains high for practical deployment [91].

There is an open need to design constructions with CRS sizes that scale linearly or quadratically with function or input size. Black-box constructions under falsifiable assumptions and several lattice-based FCs (e.g., by Wee and Wu [89,93], and others) rely on structured or non-black-box assumptions, limiting their generalizability and modular composability [90,93]. Developing FCs that are fully black-box, operate under falsifiable assumptions (e.g., SIS), and support arbitrary circuits remains an open direction.

Functional commitments in concurrent or adversarial asynchronous environments are still poorly understood. Existing works like Lin et al. [94] on non-malleable commitments have not been effectively extended to FCs. Designing robust FCs that resist concurrent attacks and guarantee non-malleability in distributed systems remains a crucial area for future exploration.

While aggregation-friendly constructions exist (e.g., for same-set binding), aggregation and homomorphic properties strongly guarantee that different-set binding or full homomorphism remain elusive in efficient schemes [90,93]. Enhancing composability and allowing for multi-function aggregation without undermining security or succinctness is a key challenge.

Recent works, including Boneh et al. [92] and Namboothiri [95], explore selective revealability and algorithmic fairness function-hiding commitments to support fairness and transparency, particularly in applications like credit scoring and automated decision-making [92,95]. However, efficient models for selective revealability, formal fairness definitions, and verifiable accountability are still underdeveloped and need systematic study.

The transparent setup paradigm introduced by de Castro and Peikert [85] offers a major leap forward by eliminating the need for a trusted setup. Nonetheless, scalability in large applications and formal analysis of composability in dynamic environments (e.g., real-time systems) remain to be addressed [85]. Figure 6 provides a structured taxonomy of vector commitment schemes, categorizing them by their underlying cryptographic primitives and properties. It highlights a wide range of approaches, from classical constructions like RSA and Diffie-Hellman to advanced post-quantum and zero-knowledge schemes. The inclusion of numerous key references offers a comprehensive overview of the field’s major contributions.

6. Comparative Analysis and Open Questions

The reviewed papers were grouped by their primary cryptographic approach to highlight trends and gaps in vector, polynomial, and functional commitments.

Figure 7 provides a visual distribution of these papers, categorized by methodology. The x-axis represents cryptographic approaches such as RSA-based, Diffie–Hellman, lattice-based, and others, while the y-axis shows the number of papers in each category. Color coding distinguishes classical schemes (blue), post-quantum secure schemes (green), and hybrid approaches (red).

A key observation is the dominance of lattice-based schemes in post-quantum research, reflecting their resistance to quantum attacks, while RSA-based methods remain prevalent in the classical literature due to their historical role in cryptography.

Keyword analysis of paper titles, illustrated in Figure 6, reveals that “post-quantum” appears in 32% of titles, underscoring its significance in current research. “Vector commitments” and “functional commitments” account for 25% and 18%, respectively, indicating sustained interest in these primitives. The remaining 25% includes terms like “zero-knowledge” and “polynomial,” highlighting diverse applications. This distribution emphasizes the field’s focus on quantum-resistant solutions.

Temporal trends, depicted in Figure 8, show a clear evolution in research priorities. From 2010 to 2015, classical schemes like RSA and Diffie–Hellman dominated. Between 2016 and 2020, lattice-based and functional commitments gained traction, coinciding with advances in quantum computing awareness. The period from 2021 to 2025 saw a surge in post-quantum and hybrid approaches, with a notable 40% increase in lattice-based papers in 2023 alone, driven by breakthroughs in Short Integer Solution (SIS)-based constructions.

Several critical research gaps persist. Post-quantum security remains a pressing challenge, particularly in optimizing lattice-based vector commitment proofs. Current schemes often suffer from linear proof size growth with input dimension, a limitation that could be addressed through SNARK-inspired aggregation techniques.

Adaptive security is another area needing attention, as many schemes only achieve selective security, requiring complexity leveraging or new reduction techniques for full robustness. Verification efficiency in transparent settings also lags behind, with superlinear overheads that could benefit from STARK-like optimizations.

A proposed roadmap for future research outlines three phases. The first phase (2025–2026) focuses on optimizing proof sizes and developing black-box constructions under falsifiable assumptions. The second phase (2027–2028) aims to integrate functional commitments into decentralized systems like blockchains while achieving universally composable (UC) security. The final phase (2029 onward) targets standardization and real-world deployment of post-quantum schemes.

Additional charts supplement this analysis. A comparison of proof size versus verification time illustrates trade-offs between succinctness (e.g., SNARKs) and efficiency (e.g., STARKs). Another chart contrasts security assumptions, showing the shift from classical problems (discrete logarithm, RSA) to post-quantum foundations (SIS, LWE). These visuals underscore the field’s technical challenges and opportunities.

7. Discussion

The findings of this survey reflect a rapidly evolving landscape in cryptographic commitment schemes, marked by a transition from classical constructions rooted in RSA and Diffie–Hellman hardness assumptions to advanced lattice-based alternatives aimed at ensuring post-quantum resilience. This evolution is driven by the growing urgency to safeguard data integrity, privacy, and authenticity in anticipation of quantum adversaries capable of undermining traditional cryptographic primitives.

A key insight from the review is the expanding role of lattice-based cryptography, particularly schemes based on the Short Integer Solution (SIS) and Learning With Errors (LWE) problems. These schemes exhibit strong theoretical security foundations under quantum threat models and support advanced functionalities such as stateless updates, zero-knowledge proofs, and commitments to general circuits. Lattice-based VCs face trade-offs: SIS proofs (0.3 KB [30]) are smaller than Merkle trees (1.2 KB [51]), but verification remains linear. Adaptive security for functional commitments [85] is unresolved. However, practical deployment remains constrained by high computational complexity, large proof sizes, and superlinear verification time, especially in transparent settings. For example, while SIS-based functional commitments can achieve provable post-quantum security, they often require large Common Reference Strings (CRSs) and complex matrix operations, limiting scalability.

In contrast, classical schemes like RSA and Diffie–Hellman-based commitments remain widely cited and implemented due to their simplicity, smaller key sizes, and compatibility with existing protocols. Nevertheless, they are fundamentally vulnerable to quantum algorithms such as Shor’s and Grover’s, which reduce their security guarantees to obsolescence in quantum-capable environments. This contrast underscores the current dilemma in cryptographic engineering: balancing the efficiency of classical schemes with the robustness of quantum-secure alternatives.

Another major development is the increased focus on functional commitments (FCs), which generalize vector and polynomial commitments by allowing commitments to arbitrary functions rather than fixed structures. This flexibility unlocks new applications in verifiable computation, privacy-preserving machine learning, and decentralized identity systems. The most recent lattice-based FC constructions support evaluation binding and selective revealability, with promising advances in non-interactive proof generation and transparent setup. However, adaptive security, CRS size optimization, and composability under simulation-sound frameworks remain unresolved challenges.

Figure 6 and Figure 7 further validate these trends. The keyword distribution shows a strong emphasis on post-quantum, reflecting heightened research interest in quantum-resistant primitives. Temporal analysis reveals a surge in lattice-based papers after 2021, coinciding with the maturation of SIS-based proofs and real-world cryptographic applications. Despite these advances, practical adoption of post-quantum commitments lags behind, largely due to performance bottlenecks and the absence of standardized benchmarks for evaluation.

The growing need for efficient, composable, and update-friendly commitments is particularly evident in decentralized ecosystems such as blockchains, where real-time commitments, verifiable storage, and non-interactive zero-knowledge proofs are essential. While KZG commitments are widely deployed in systems like Verkle trees, their reliance on pairing-based cryptography renders them quantum-insecure. Efforts to develop post-quantum counterparts with comparable succinctness and efficiency have produced encouraging but still experimental results, including schemes like Polaris and Orion. These remain fragile, with unresolved concerns around soundness and verifier complexity.

Moreover, research gaps persist in several cross-cutting areas:

• Batch verification and multi-function aggregation are underdeveloped in post-quantum schemes.
• Selective revealability and fairness—key for applications like credit scoring or automated decision-making—lack formal models and efficient cryptographic support.
• Security in concurrent or adversarial settings (e.g., asynchronous networks, MPC frameworks) has not yet been robustly addressed in most FC proposals.
• Hybrid models that combine classical efficiency with post-quantum guarantees are scarcely explored, though they may offer transitional solutions during the quantum migration phase.

While the cryptographic community has made substantial progress in conceptualizing and formalizing advanced commitment schemes, especially under post-quantum assumptions, the path to practical, scalable, and composable implementations remains complex. Bridging the gap between theory and application requires not only mathematical innovation but also a concerted effort to engineer efficient primitives, test them in adversarial settings, and integrate them into standardized cryptographic libraries. This survey contributes to that process by mapping the current landscape, identifying persistent challenges, and outlining priorities for future exploration.

This comprehensive survey has systematically examined the evolution, current state, and future directions of vector, polynomial, and functional commitment schemes in modern cryptography. Beginning with classical constructions like RSA-based and Diffie–Hellman commitments, we traced their foundational role in cryptographic protocols while highlighting their growing vulnerabilities in the post-quantum era. The analysis then progressed to more advanced schemes, including lattice-based approaches that offer promising resistance to quantum attacks, albeit with challenges in proof size and verification efficiency.

The survey revealed several key trends. First, the field is undergoing a significant shift toward post-quantum secure constructions, driven by the imminent threat of quantum computing. Lattice-based schemes, particularly those leveraging the Short Integer Solution (SIS) problem, have emerged as frontrunners due to their strong security guarantees and versatility. Second, functional commitments have gained traction as a powerful generalization of vector and polynomial commitments, enabling more complex and flexible cryptographic applications. However, these advancements come with trade-offs, such as increased computational overhead and the need for further optimization in proof systems.

Critical gaps remain in the research landscape. While lattice-based schemes provide quantum resistance, their practical deployment is hindered by large proof sizes and inefficient verification processes. Adaptive security and composability also require deeper exploration to ensure robust integration with existing protocols. Additionally, the development of transparent and stateless setups for functional commitments presents both a challenge and an opportunity for future work.

Looking ahead, several directions warrant attention. First, optimizing lattice-based constructions for real-world applications should be prioritized, with a focus on reducing proof sizes and improving verification times. Second, exploring hybrid approaches that combine classical and post-quantum techniques could offer a balanced solution for transitional systems. Finally, the integration of commitment schemes into decentralized platforms, such as blockchains and zero-knowledge proof systems, will be essential for advancing privacy and scalability in distributed networks.

Nevertheless, the integration of deep learning (DL) into parallel computing has seen great growth in the field of cryptography, which we see via its role in adaptive high-throughput encryption and improved security. DL models (for example, CNNs and GANs) improve cryptographic processes’ performance by learning strong feature representations, which, in turn, improve the systems’ resistance to attacks (for example, differential cryptanalysis) also reduce the need for manual parameter tuning. Parallel computing (GPU/CUDA, MPI) plays a role in this by speeding up these DL enhanced methods, which we see to achieve 5–15× speedups in things like image and homomorphic encryption. For instance, we see semantic-based encryption, which does a great job of preserving what is important (for example, medical ROIs) with over 99.5% pixel distortion rates (NPCRs); also, we see batch parallel processing, which reduces latency to the millisecond range for 4 K images. But we still see issues in VRAM efficiency (which is an issue with DL models, which require 8–12 GB for high-resolution data) and in the control of error propagation in chaotic DL hybrid models. The research papers of Liu et al. [96] and Song et al. [97,98] prove the rising interest in using the DL combined with parallel computing in the field of cryptography.

8. Conclusions

In conclusion, this survey underscores the dynamic and rapidly evolving nature of commitment schemes in cryptography. While significant progress has been made, the journey toward fully scalable, efficient, and quantum-resistant solutions is ongoing. By addressing the identified gaps and embracing interdisciplinary collaboration, the cryptographic community can pave the way for secure and verifiable systems in the post-quantum future. Key directions for future work include the following:

• Hybrid Classical–Quantum Schemes: Investigating commitments that leverage classical hardness assumptions alongside post-quantum primitives for transitional security.
• Domain-Specialized Optimizations: Tailoring schemes for emerging applications (e.g., privacy-preserving machine learning or encrypted image verification [93]) without compromising generality.
• Standardization and Benchmarks: Establishing unified metrics to evaluate proof sizes, verification times, and composability across post-quantum constructions.
• Hardware Acceleration: Exploring GPU/FPGA implementations to mitigate computational overhead in lattice-based functional commitments.
• This work serves as both a reference for researchers and a roadmap for future innovations in the field.