Upper Bound Solution for Stability Analysis of Deep Underground Cavities Under the Influence of Varying Saturation
Abstract
Featured Application
Abstract
1. Introduction
2. Basic Theory
2.1. Upper Limit Theorem Under High-Geostress Action
2.2. Hoek–Brown Destruction Criteria
2.3. Rock Strength and Saturation Relationships
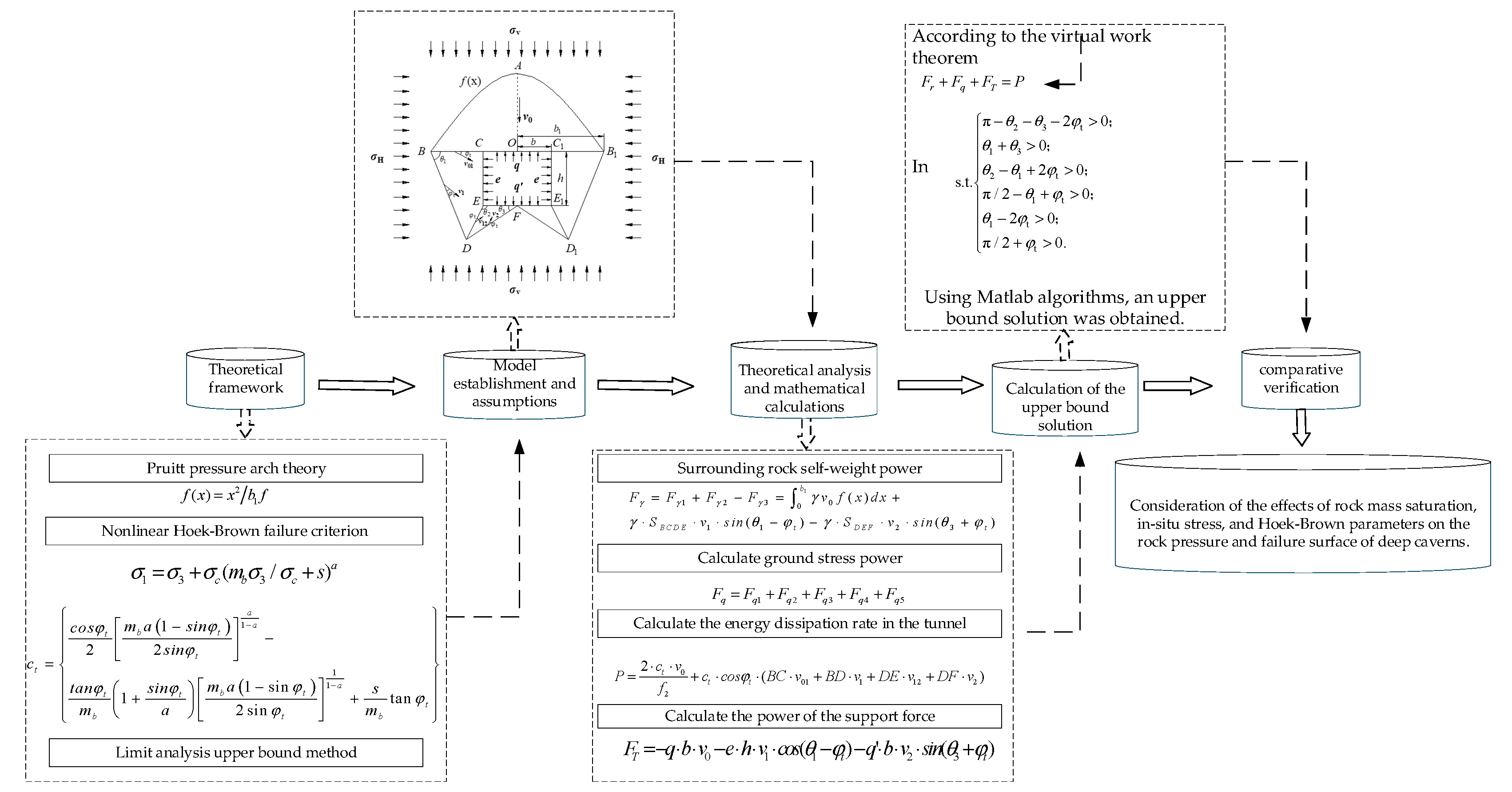
3. Destruction Model
4. Upper Bound Solution
4.1. Geometric Relationships
4.2. Internal Energy Dissipation Power
4.3. Self-Weight Power of the Surrounding Rock
4.4. Geostress Power
4.5. Support Force Power
4.6. Upper Limit Solution for Perimeter Rock Pressure
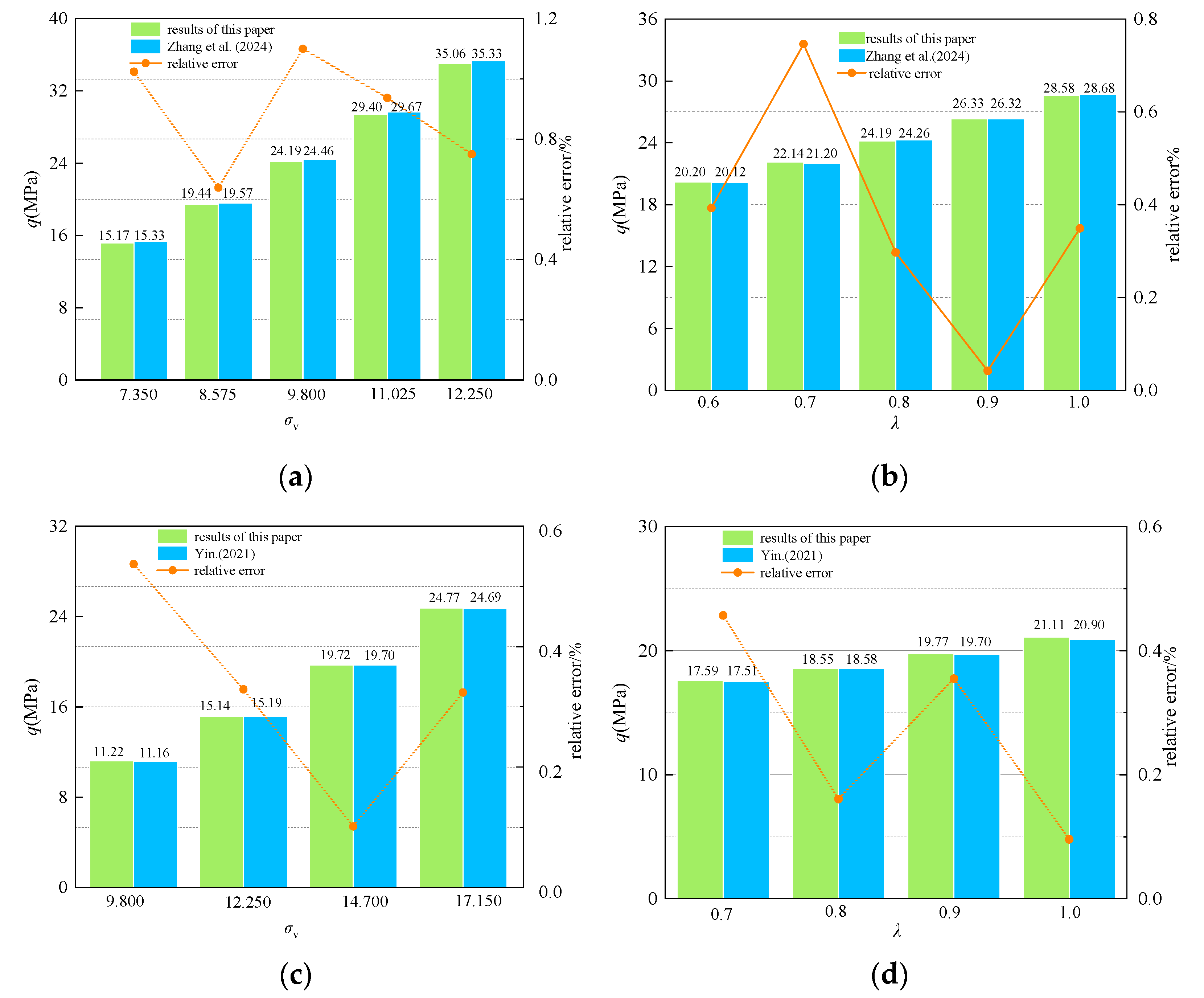
5. Comparative Verification
6. Analysis of Results
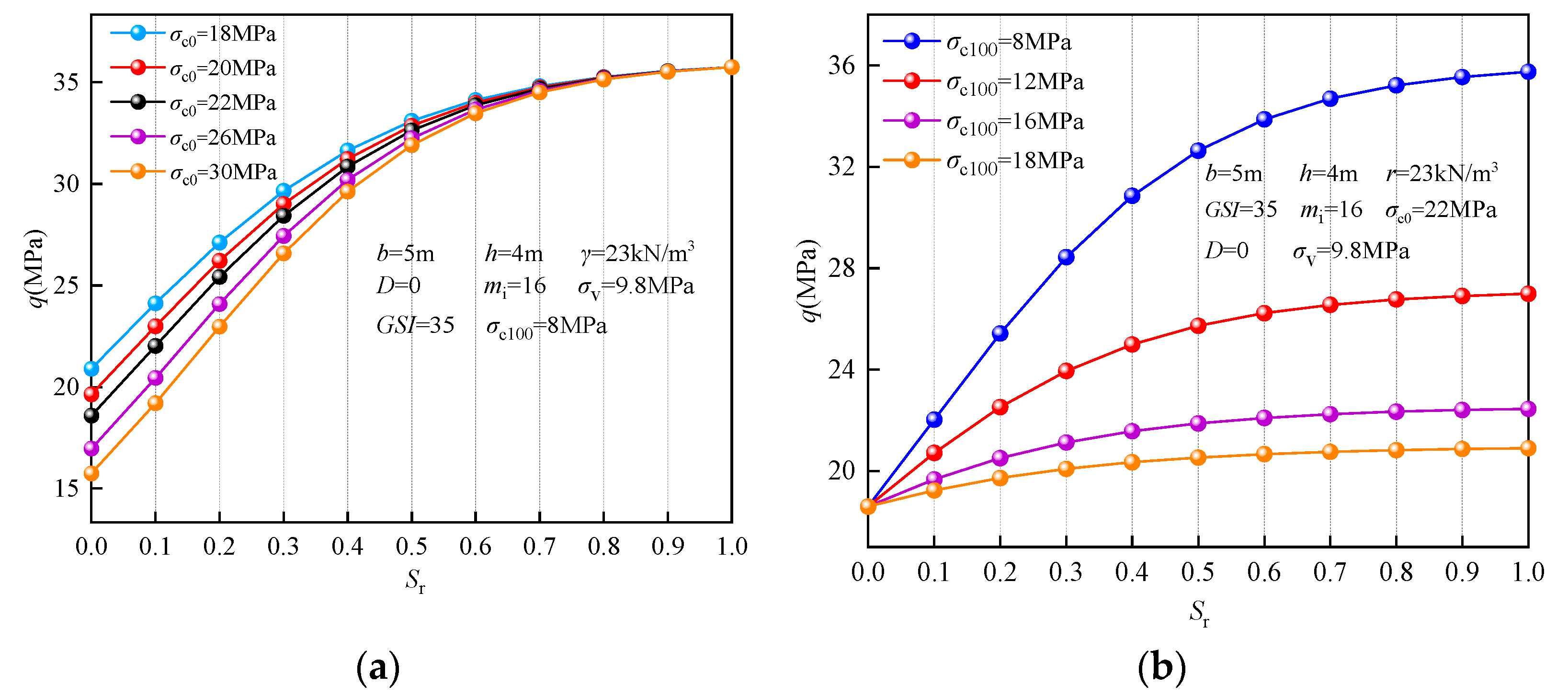
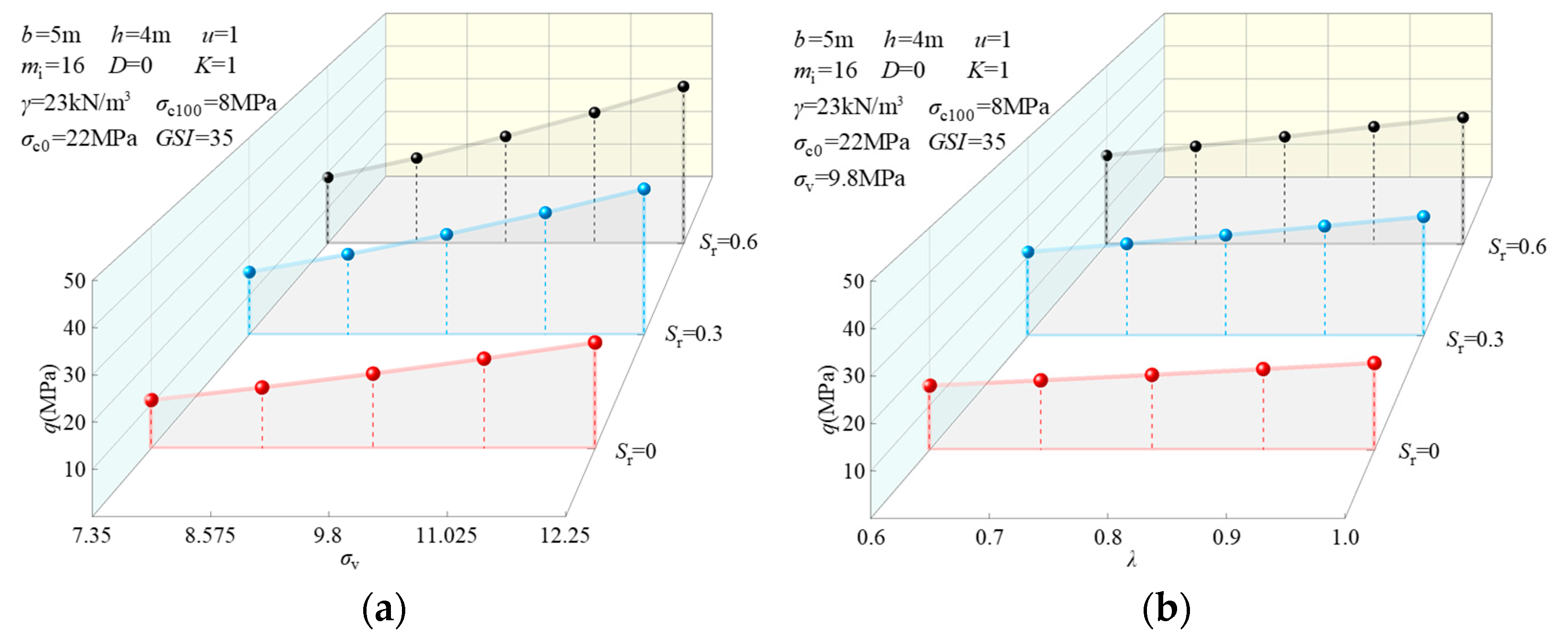
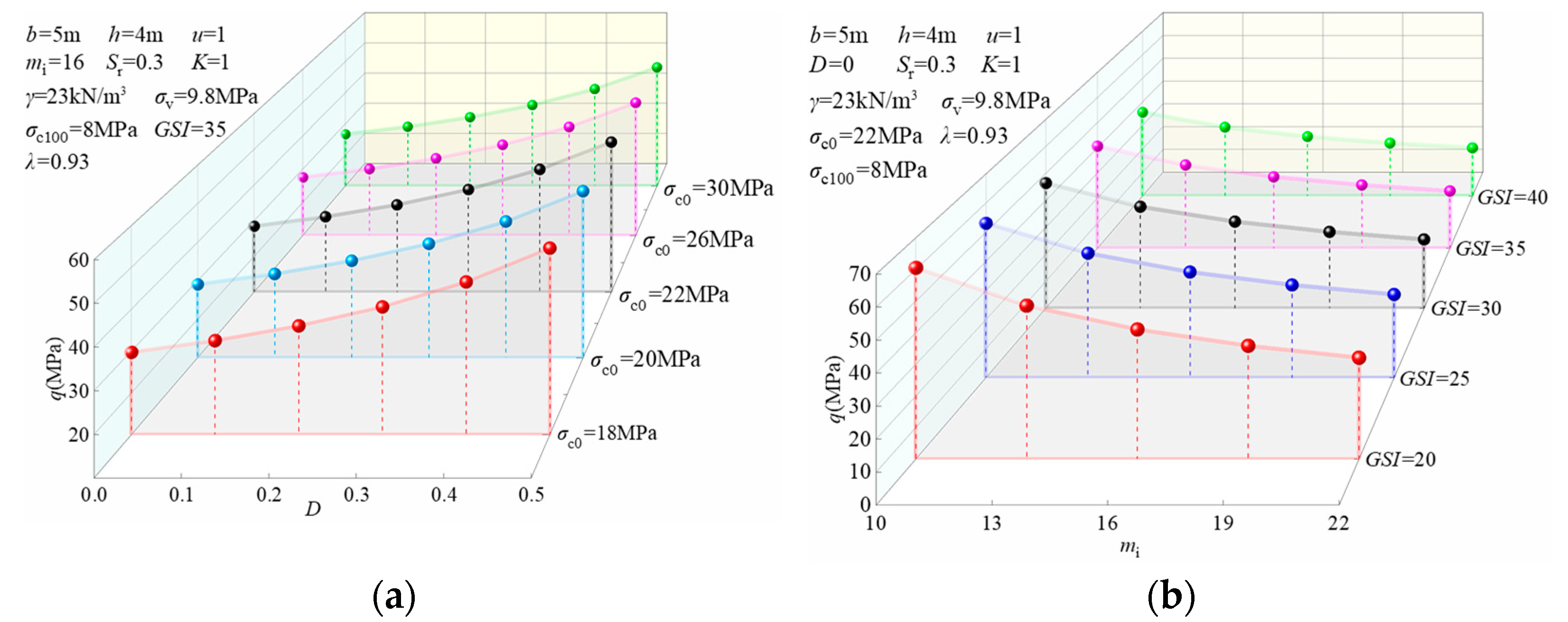
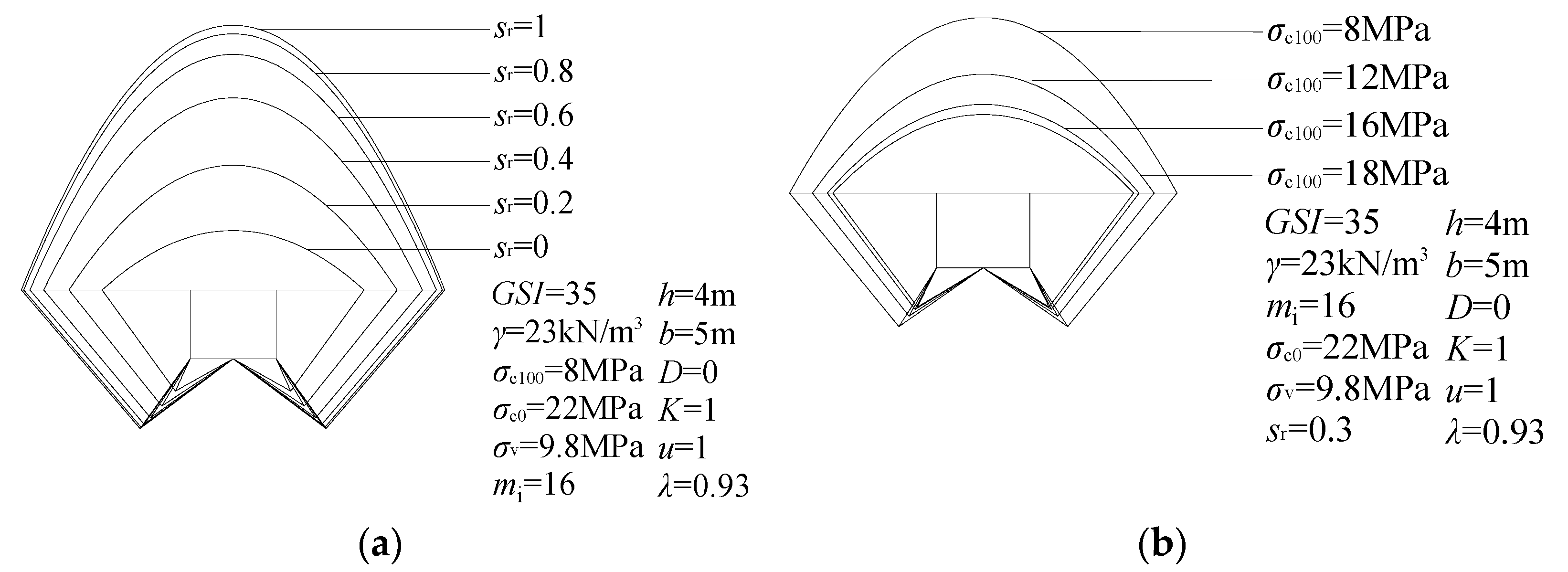
6.1. Effect of Saturation
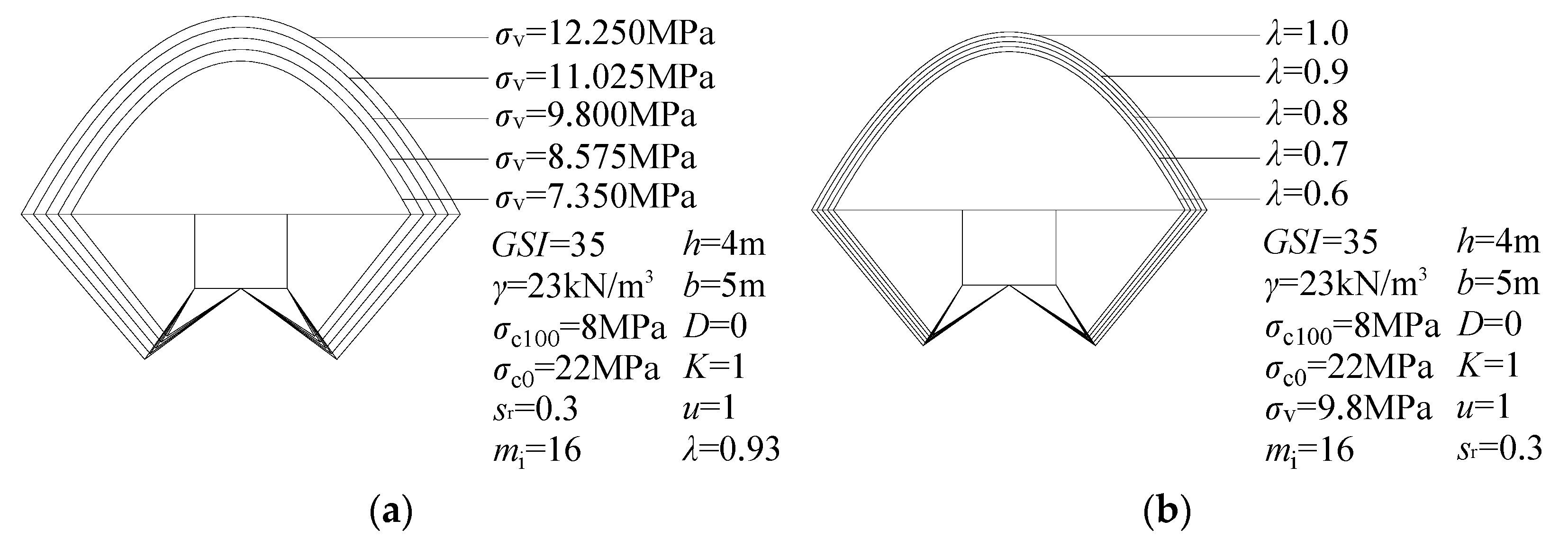
6.2. The Influence of Ground Stress
6.3. The Influence of Hoek–Brown Parameters
6.4. Damage Surfaces
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin, C.D.; Kaiser, P.K.; Christiansson, R. Stress, instability and design of underground excavations. Int. J. Rock Mech. Min. Sci. 2003, 40, 1027–1047. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W. Reliability assessment of stability of underground rock caverns. Int. J. Rock Mech. Min. Sci. 2012, 55, 157–163. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Q.; Jia, H.L.; Shen, Y.J.; Li, G.Y. Fracture mechanical properties of frozen sandstone at different initial saturation degrees. Rock Mech. Rock Eng. 2022, 55, 3235–3252. [Google Scholar] [CrossRef]
- Yin, T.B.; Yin, J.W.; Wu, Y.; Yang, Z.; Liu, X.L.; Zhuang, D.D. Water saturation effects on the mechanical characteristics and fracture evolution of sandstone containing pre-existing flaws. Theor. Appl. Fract. Mech. 2022, 122, 103605. [Google Scholar] [CrossRef]
- Ou, X.; Ouyang, L.; Xu, X.; Wang, L. Case study on floor heave failure of highway tunnels in gently inclined coal seam. Eng. Fail. Anal. 2022, 136, 106224. [Google Scholar] [CrossRef]
- Feng, J.Q.; Gong, L.; Wang, L.H.; Zhou, P.; Zhang, P.; Li, Y.; Liu, Z.Q. Study on failure mechanism and treatment measures of floor heave of high-speed railway tunnel in the interbedded surrounding rock with high geostress. Eng. Fail. Anal. 2023, 150, 107365. [Google Scholar] [CrossRef]
- Wang, M.; Guo, G.L.; Wang, X.Y.; Guo, Y.; Dao, V. Floor heave characteristics and control technology of the roadway driven in deep inclined-strata. Int. J. Min. Sci. Technol. 2015, 25, 267–273. [Google Scholar] [CrossRef]
- Wagner, H. Deep mining: A rock engineering challenge. Rock Mech. Rock Eng. 2019, 52, 1417–1446. [Google Scholar] [CrossRef]
- An, H.; Mu, X. Contributions to Rock Fracture Induced by High Ground Stress in Deep Mining: A Review. Rock Mech. Rock Eng. 2025, 58, 463–511. [Google Scholar] [CrossRef]
- Abdellah, W.R.; Ali, M.A.; Yang, H.S. Studying the effect of some parameters on the stability of shallow tunnels. J. Sustain. Min. 2018, 17, 20–33. [Google Scholar] [CrossRef]
- Hernández, Y.Z.; Farfán, A.D.; de Assis, A.P. Three-dimensional analysis of excavation face stability of shallow tunnels. Tunn. Undergr. Space Technol. 2019, 92, 103062. [Google Scholar] [CrossRef]
- Liang, J.Y.; Cui, J.; Lu, Y.D.; Shan, Y. Limit Analysis of Shallow Tunnels Collapse Problem with Optimized Solution. Appl. Math. Model. 2022, 109, 98–116. [Google Scholar] [CrossRef]
- Yang, Z.W.; Chen, F.Q.; Fang, S.Q. Slip-Line Analysis of Passive Limit Support Pressure for Shallow-Buried Shield Tunnel Face. Int. J. Geomech. 2024, 24, 04024295. [Google Scholar] [CrossRef]
- Lei, M.; Peng, L.; Shi, C. Calculation of the surrounding rock pressure on a shallow buried tunnel using linear and nonlinear failure criteria. Autom. Constr. 2014, 37, 191–195. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, X.; Zhang, J.S.; Zhang, J.H.; Cheng, H. Safe range analysis of clear distance of twin shallow tunnels based on limit analysis and reliability theory. J. Cent. South Univ. 2018, 25, 196–207. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Two-dimensional face stability analysis in rock masses governed by the Hoek-Brown strength criterion with a new multi-horn mechanism. Int. J. Min. Sci. Technol. 2023, 33, 963–976. [Google Scholar] [CrossRef]
- Luo, W.; Xiao, G.Q.; Tao, Z.; Chen, J.Y.; Lu, X.; Wang, H.F. Nonlinear Stability Analysis of Shallow-Buried Bias Tunnel Based on Failure Mode Improvement. Appl. Sci. 2025, 15, 3153. [Google Scholar] [CrossRef]
- Zhan, S.Q.; Liu, Y.H.; Xiao, M.; Du, X.W.; Chen, Y.C.; Xing, T.; Kong, C. Numerical Simulation Analysis Method for Rockburst Control in Deeply Buried Caverns. Appl. Sci. 2023, 13, 11197. [Google Scholar] [CrossRef]
- Zuo, J.; Wang, J.; Jiang, Y. Macro/meso failure behavior of surrounding rock in deep roadway and its control technology. Int. J. Coal Sci. Technol. 2019, 6, 301–319. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, Z.W.; Liu, Z.A.; Xiao, H.B. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media. J. Cent. South Univ. 2017, 24, 957–966. [Google Scholar] [CrossRef]
- Zhang, D.B.; Zeng, L.H.; Lv, Z.L.; Yu, X.C.; Liu, C.; Jiang, A.M.; Jiang, X.Y.; Li, Q.; Yang, Y.X. Failure Mode of Deep-Buried Rectangular Chamber and Upper Bound Solution of Surrounding Rock Pressure. Mathematics 2024, 13, 69. [Google Scholar] [CrossRef]
- Huang, F.; Zhao, L.H.; Ling, T.H.; Yang, X.L. Rock mass collapse mechanism of concealed karst cave beneath deep tunnel. Int. J. Rock Mech. Min. Sci. 2017, 91, 133–138. [Google Scholar] [CrossRef]
- Liu, Y.R.; Zhang, R.J.; Hou, S.K.; Zhu, L.; Pang, Z.Y.; Zhuang, W.Y. Investigation of energy evolution process of rock mass during deep tunnel excavation based on elasto-visco plastic damage model and time-dependent energy indices. Acta Geotech. 2025, 20, 1549–1570. [Google Scholar] [CrossRef]
- Xu, J.C.; Wen, H.Y.; Sun, C.; Yang, C.B.; Rui, G.R. Numerical simulation of non-stationary parameter creep large deformation mechanism of deep soft rock tunnel. Appl. Sci. 2022, 12, 5311. [Google Scholar] [CrossRef]
- Kang, H.P.; Yi, B.D.; Gao, F.Q.; Lu, H.W. Database and characteristics of underground in-situ stress distribution in Chinese coal mines. J. Chin. Coal. Soc. 2019, 44, 23–33. (In Chinese) [Google Scholar]
- Yi, B.D. Development and research of in-situ stress parameters database for underground coal mines of China. Saf. Coal Mines 2021, 52, 134–138. (In Chinese) [Google Scholar]
- Chen, W.F. Limit Analysis and Soil Plasticity; J Ross Publishing, Inc: Plantation, FL, USA, 2007. [Google Scholar]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2018, 11, 445–463. [Google Scholar] [CrossRef]
- Xu, Y.; Li, L.; Zou, J.F. Generalized Hoek-Brown solution of circular tunnel considering effects of axial stress and seepage force. Rock Soil Mech. 2015, 36, 2837–2846+2854. (In Chinese) [Google Scholar]
- Gao, Y.F.; Ye, M.; Zhang, F. Three-dimensional analysis of slopes reinforced with piles. J. Cent. South Univ. 2015, 22, 2322–2327. [Google Scholar] [CrossRef]
- Vásárhelyi, B.; Ván, P. Influence of water content on the strength of rock. Eng. Geol. 2005, 84, 70–74. [Google Scholar] [CrossRef]
- Jiang, B.; Li, S.C.; Wang, Q.; Wang, F.Q.; Zhang, J. Design method of roof anchor cable for deep large section mining roadways based on the upper bound method. Rock Soil Mech. 2017, 38, 2351–2357+2367. (In Chinese) [Google Scholar]
- Wang, W.J.; Hou, C.J. Study on mechanical principle and control technique of floor heave in roadway driven along next goaf. Chin. J. Rock Mech. Eng. 2004, 23, 69–74. (In Chinese) [Google Scholar]
- Zhang, D.B.; Yin, H.D.; Hu, A.P.; Zhu, Y.N.; Peng, X.J.; Zhang, S.; An, F.X. Analysis on the Stability of Surrounding Rock Damaged by the Floor Drum of Deep Underground Chamber under High In-Situ Stress. J. Disaster Prev. Mitig. Eng. 2024, 44, 660–669. (In Chinese) [Google Scholar]
- Yin, H.D. Upper Bound Analysis of Surrounding Rock Pressure and Reliability Study for Roadway Considering Floor Heave Failure. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, 2021. (In Chinese). [Google Scholar]
- Yang, Z.H.; Yang, X.L.; Zhang, J.H.; Li, Y.X. Upper bound analysis of collapsing area of tunnel face in broken soft rocks under different saturations. J. Cent. South Univ. Sci. Technol. 2015, 46, 2267–2273. (In Chinese) [Google Scholar]



| Serial Number | Sr | q (MPa) | Δ1 | Δ2 |
|---|---|---|---|---|
| 1 | 0 | 15.747 | ||
| 2 | 0.1 | 19.208 | 21.98% | 21.98% |
| 3 | 0.2 | 22.977 | 45.91% | 19.62% |
| 4 | 0.3 | 26.585 | 68.83% | 15.7% |
| 5 | 0.4 | 29.623 | 88.12% | 11.43% |
| 6 | 0.5 | 31.908 | 102.63% | 7.71% |
| 7 | 0.6 | 33.484 | 112.64% | 4.94% |
| 8 | 0.7 | 34.505 | 119.12% | 3.05% |
| 9 | 0.8 | 35.14 | 123.15% | 1.84% |
| 10 | 0.9 | 35.325 | 124.33% | 0.53% |
| 11 | 1.0 | 35.754 | 127.05% | 1.21% |
| Sr | Scope of Damage | ||
|---|---|---|---|
| Depth of Vault (m) | Width of Sheet Gang (m) | Length of Base Drum (m) | |
| 1.0 | 15.47 | 9.83 | 4.06 |
| 0.8 | 14.91 | 9.68 | 3.99 |
| 0.6 | 13.71 | 9.33 | 3.82 |
| 0.4 | 11.19 | 8.52 | 3.44 |
| 0.2 | 7.26 | 7.05 | 2.75 |
| 0 | 3.46 | 5.12 | 1.88 |
| Parameters | Retrieve a Value | Scope of Damage | ||
|---|---|---|---|---|
| Depth of Vault (m) | Width of Sheet Gang (m) | Length of Base Drum (m) | ||
| σv (MPa) | 12.250 | 17.87 | 11.62 | 4.92 |
| 11.025 | 16.80 | 10.77 | 4.51 | |
| 9.800 | 15.71 | 9.91 | 4.10 | |
| 8.575 | 14.61 | 9.04 | 3.68 | |
| 7.350 | 13.48 | 8.15 | 3.26 | |
| λ | 1.0 | 16.04 | 10.17 | 4.23 |
| 0.9 | 15.57 | 9.80 | 4.05 | |
| 0.8 | 15.10 | 9.43 | 3.86 | |
| 0.7 | 14.62 | 9.05 | 3.68 | |
| 0.6 | 14.13 | 8.66 | 3.49 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Zhang, D.; Zhang, J.; Zhang, B.; Yin, H.; Jiang, A.; Li, Q. Upper Bound Solution for Stability Analysis of Deep Underground Cavities Under the Influence of Varying Saturation. Appl. Sci. 2025, 15, 9295. https://doi.org/10.3390/app15179295
Xie S, Zhang D, Zhang J, Zhang B, Yin H, Jiang A, Li Q. Upper Bound Solution for Stability Analysis of Deep Underground Cavities Under the Influence of Varying Saturation. Applied Sciences. 2025; 15(17):9295. https://doi.org/10.3390/app15179295
Chicago/Turabian StyleXie, Shaoxiang, Daobing Zhang, Jiahua Zhang, Biao Zhang, Huadong Yin, Anmin Jiang, and Qi Li. 2025. "Upper Bound Solution for Stability Analysis of Deep Underground Cavities Under the Influence of Varying Saturation" Applied Sciences 15, no. 17: 9295. https://doi.org/10.3390/app15179295
APA StyleXie, S., Zhang, D., Zhang, J., Zhang, B., Yin, H., Jiang, A., & Li, Q. (2025). Upper Bound Solution for Stability Analysis of Deep Underground Cavities Under the Influence of Varying Saturation. Applied Sciences, 15(17), 9295. https://doi.org/10.3390/app15179295






