Stability Analysis of Shield Tunnels Considering Spatial Nonhomogeneity and Anisotropy of Soils with Tensile Strength Cut-Off
Abstract
1. Introduction
2. Theoretical Basis
2.1. Tensile Strength Cut-Off
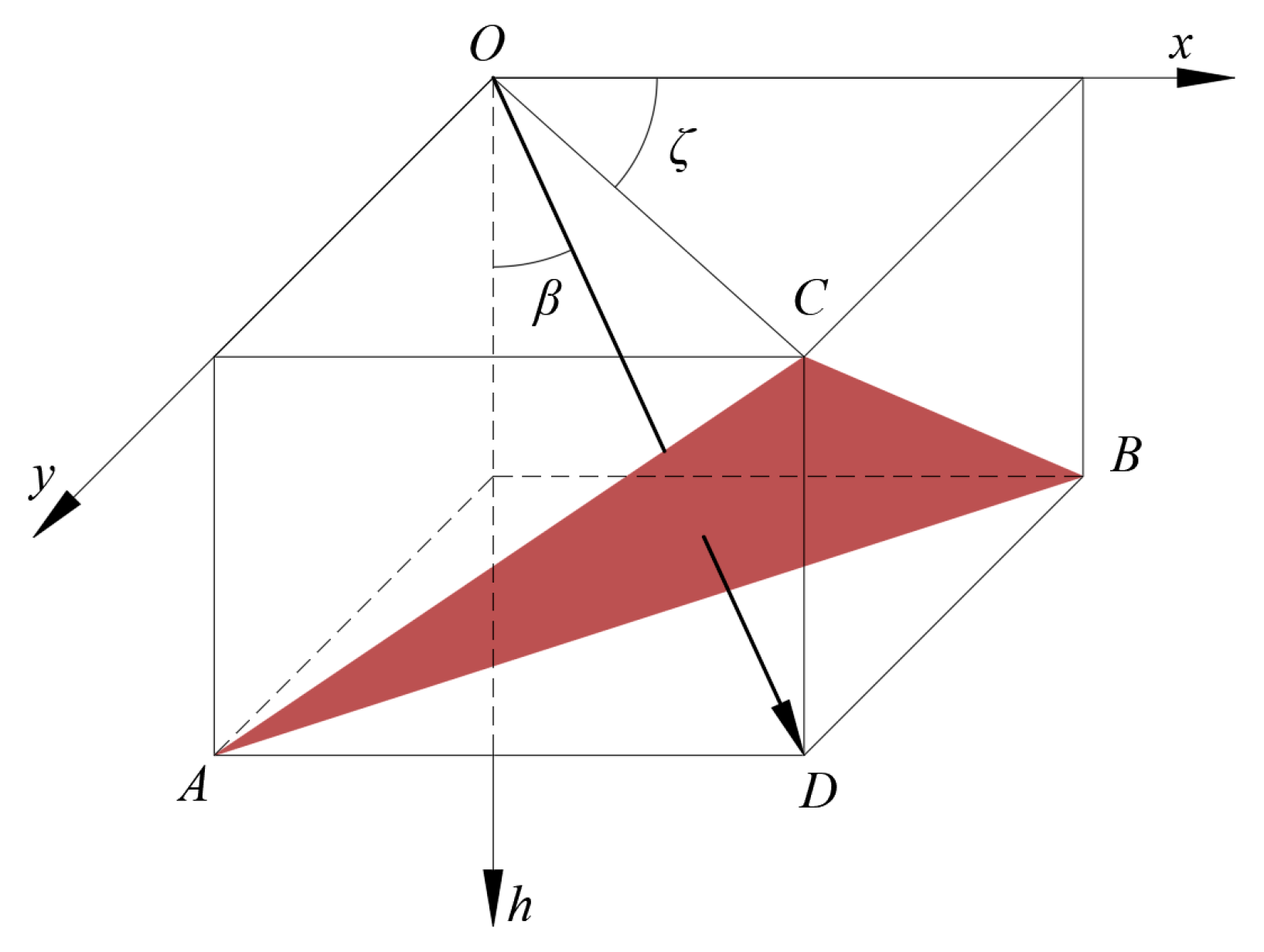
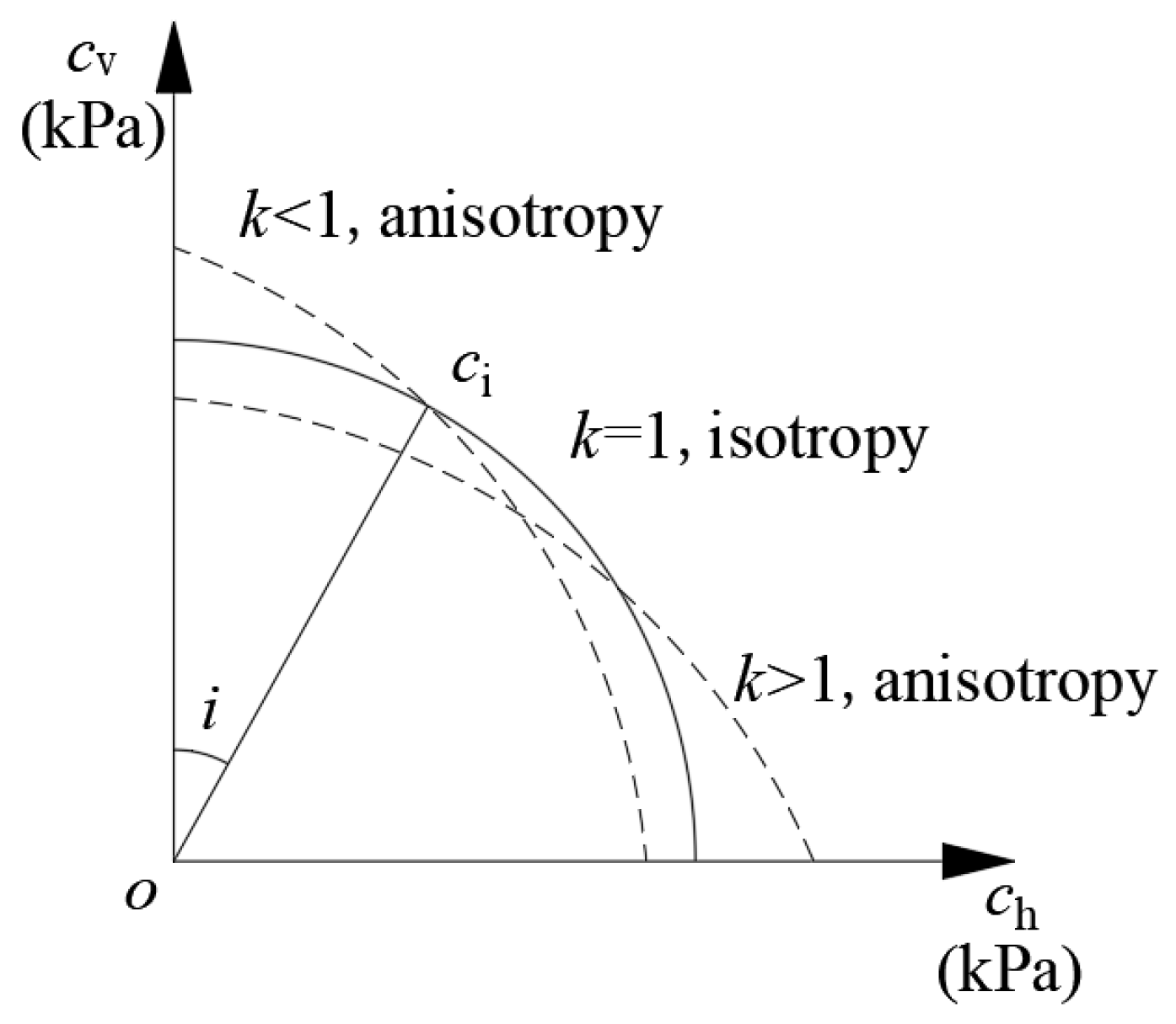
2.2. Spatial Inhomogeneity and Anisotropy Soil Cohesion
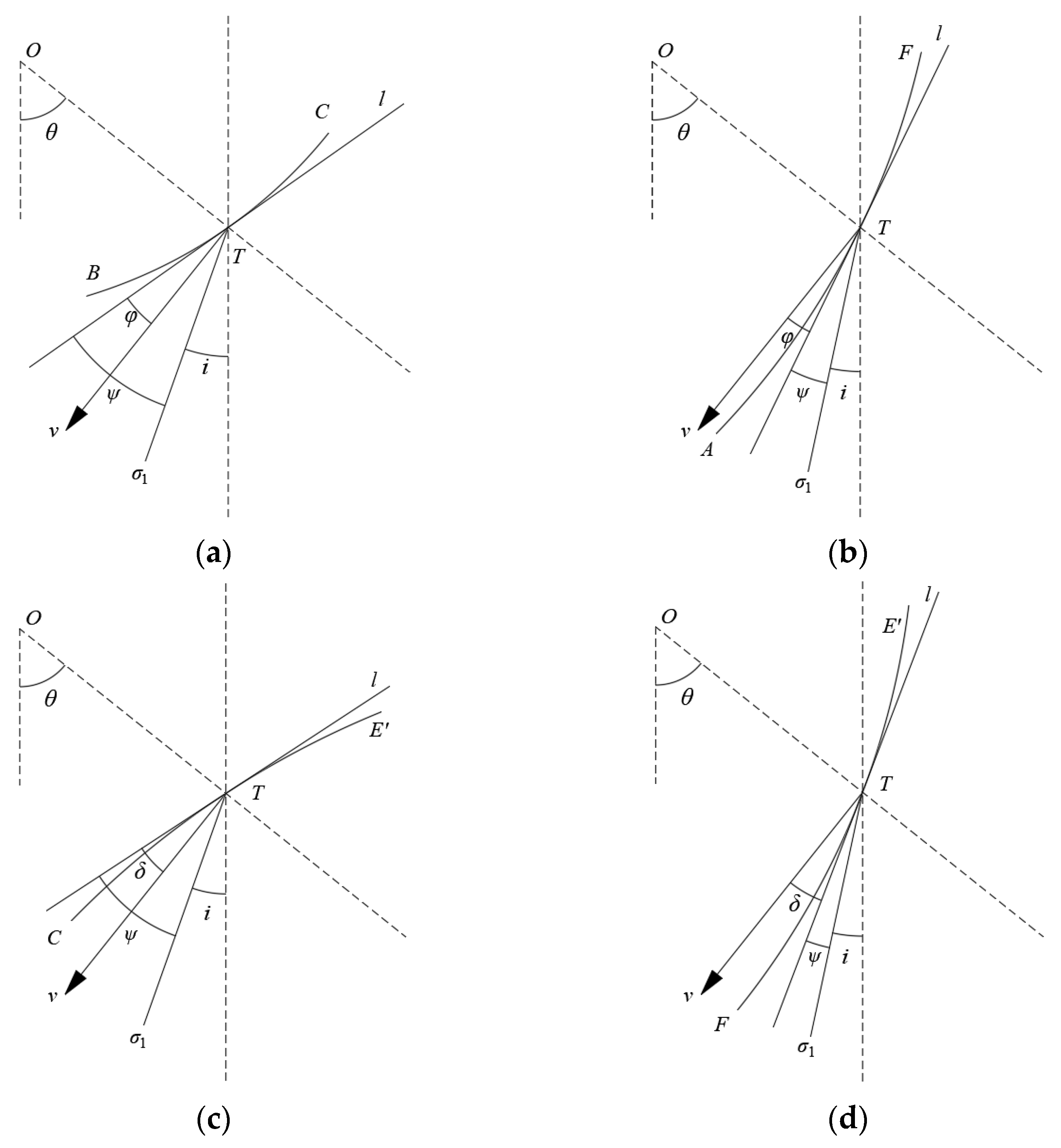
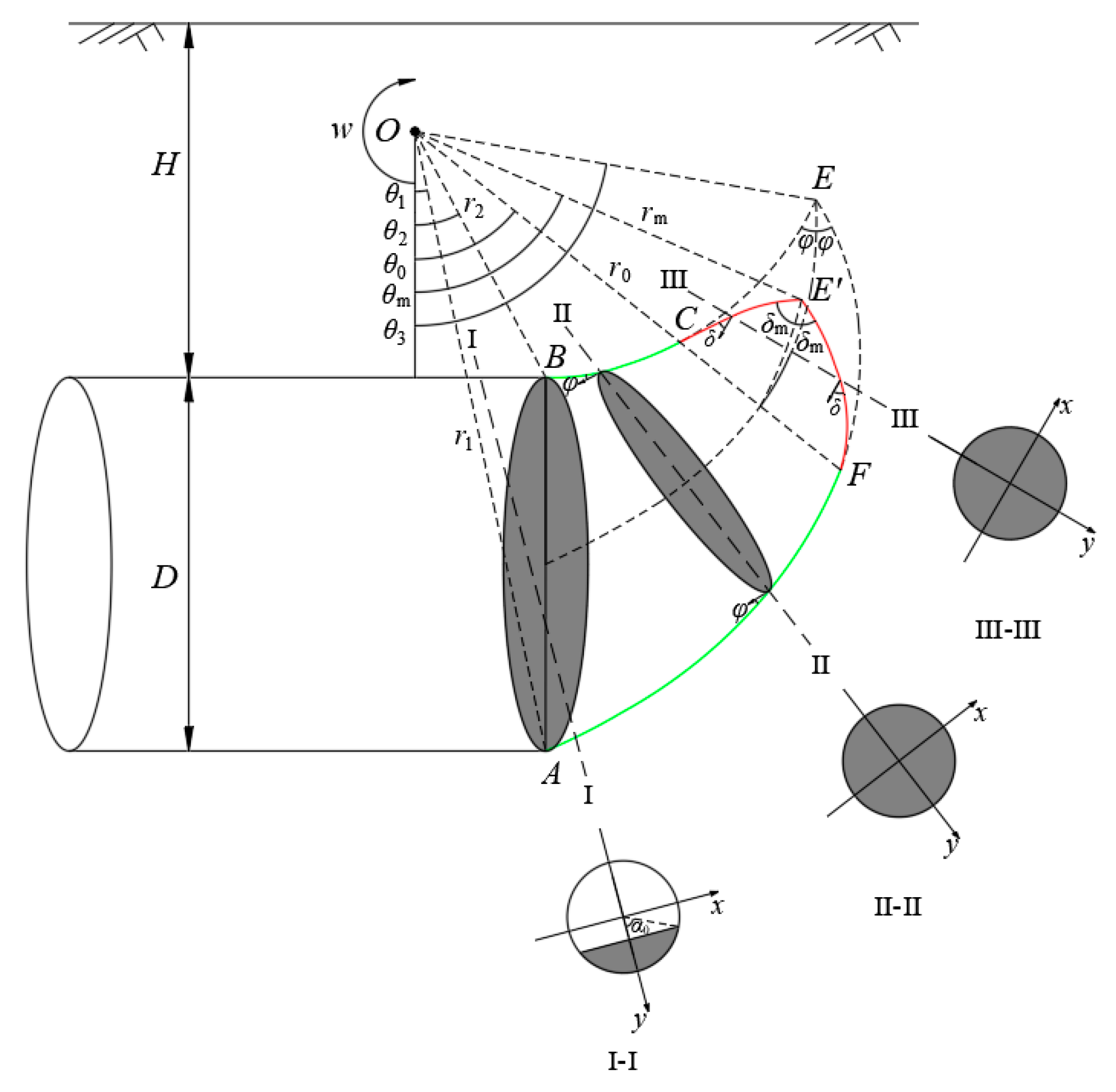
3. Destruction Mode
4. Upper Bound Solution
- (1)
- Assume that the rock mass is an ideal elastic–plastic material and obeys the associated flow law.
- (2)
- Assume that the failure body is a rigid body, and its volume does not change during the failure process, with energy dissipated only along the velocity discontinuity line.
- (3)
- Assume that, after applying a uniformly distributed minimum support force to the working face in the horizontal direction to the right, the failure body is in a limit state.
4.1. Gravitational Work Power
4.2. Internal Energy Dissipation
4.3. Power Generated by Support Force
4.4. Ultimate Support Force
5. Comparative Verification
6. Results Analysis
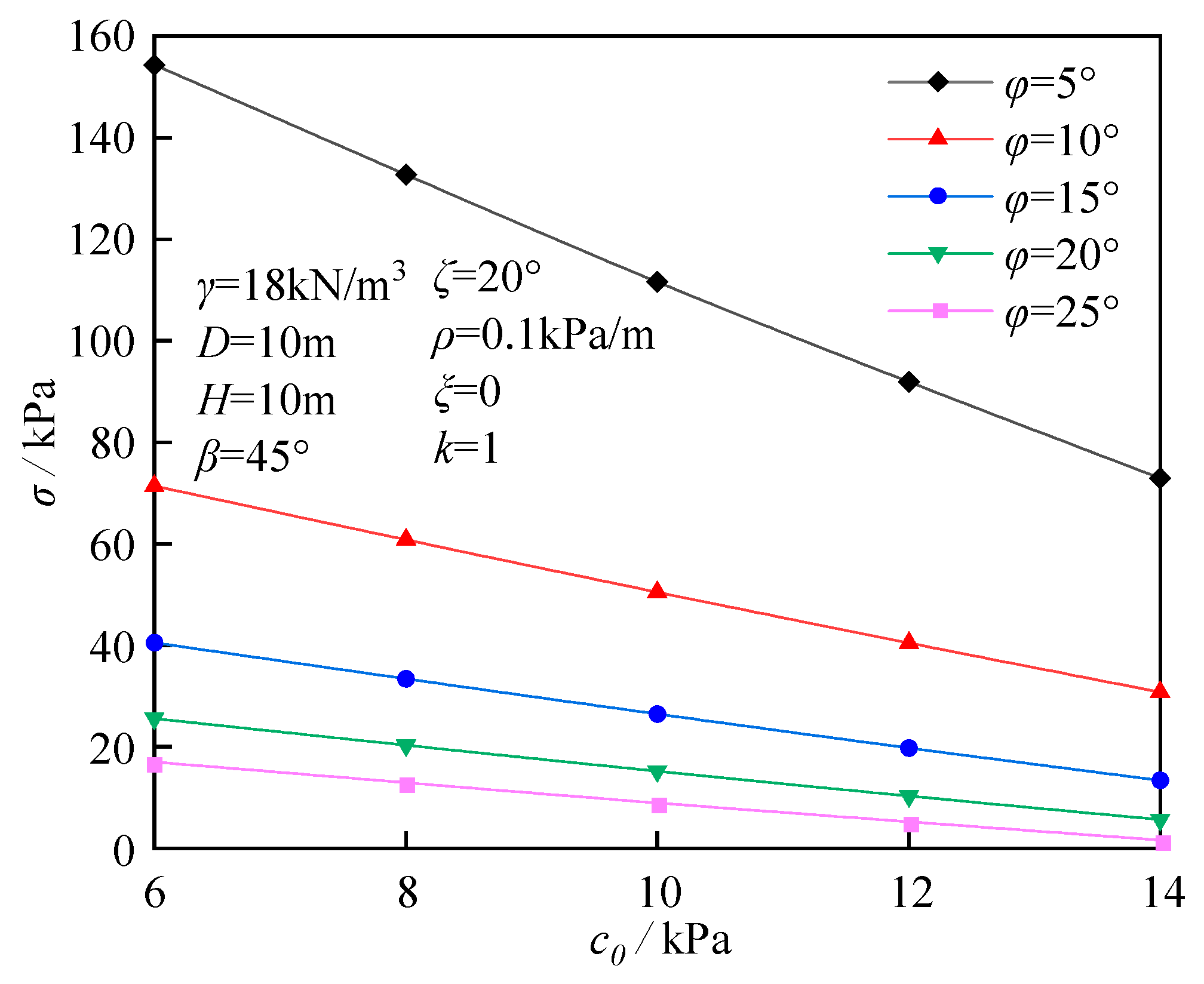
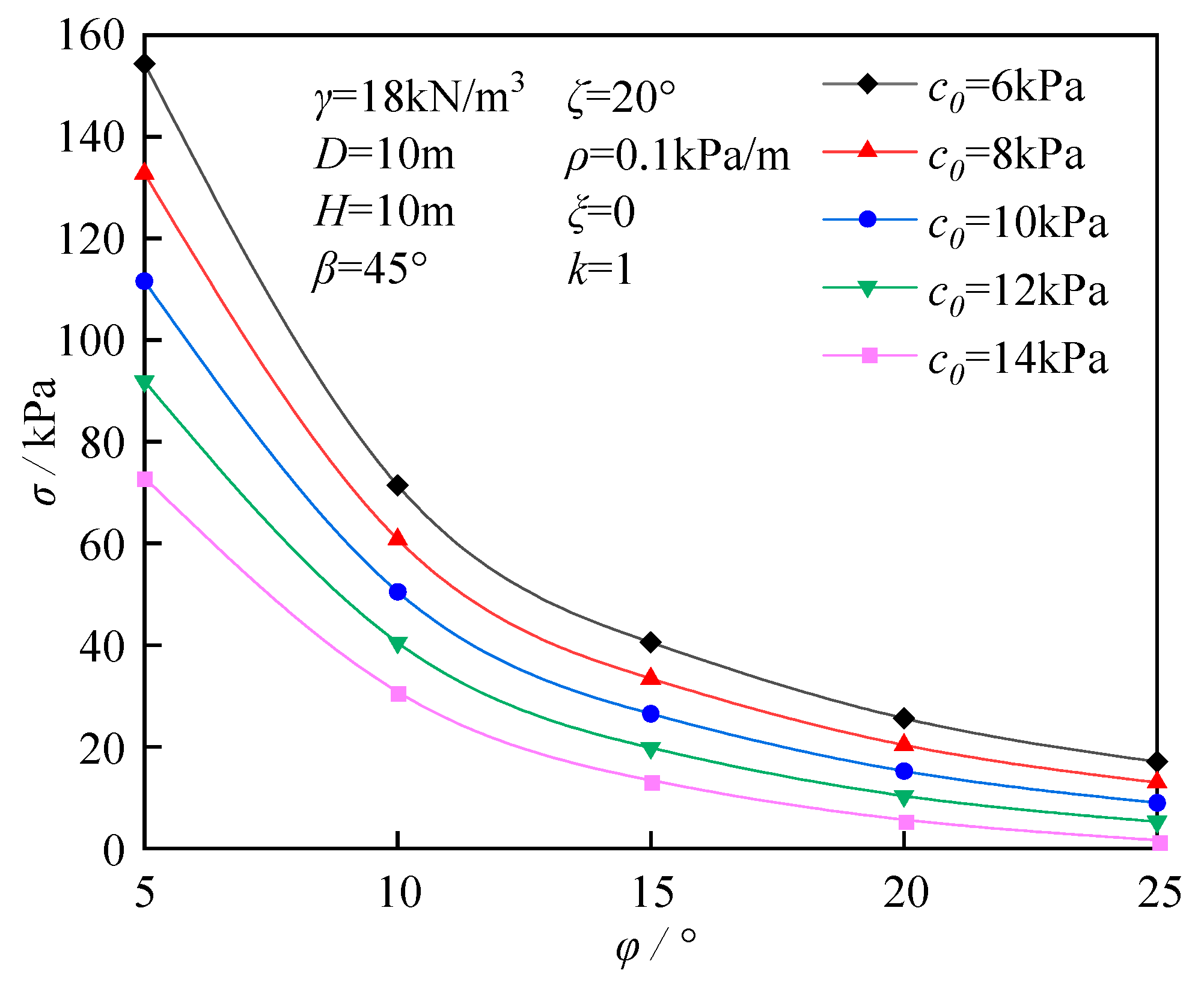
6.1. The Influence of Soil Strength Indicators
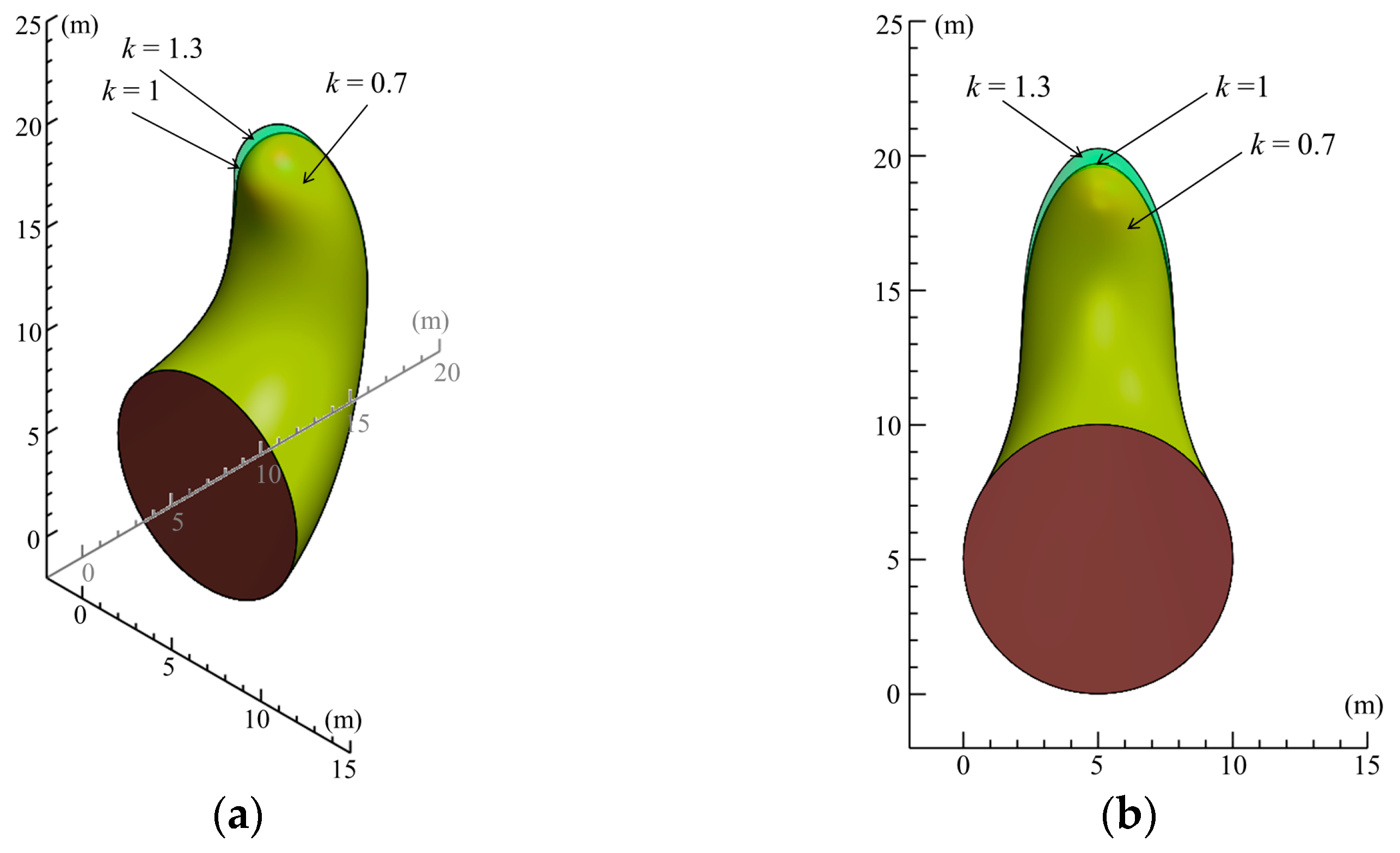
6.2. The Influence of Tensile Strength Reduction Parameter
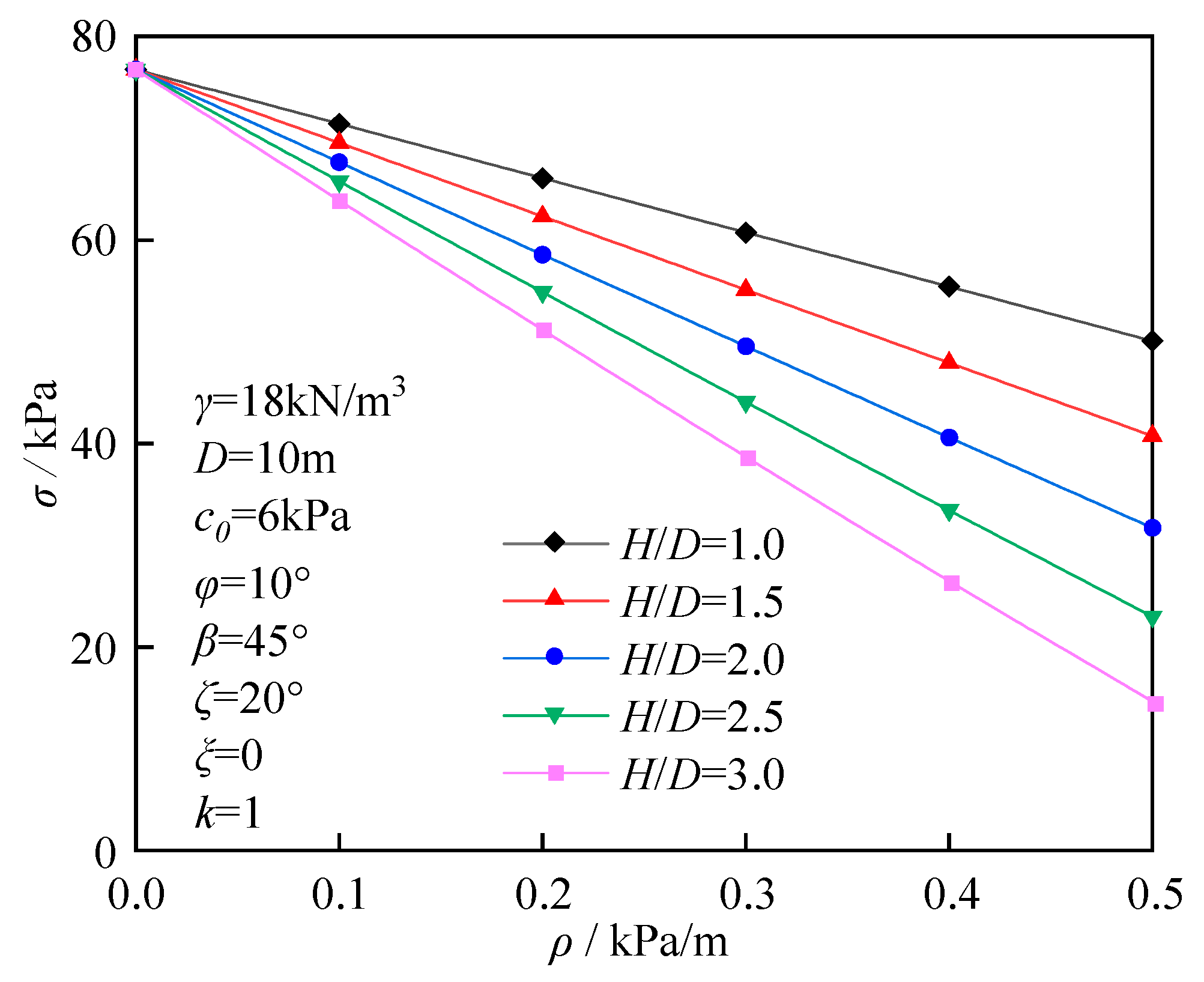
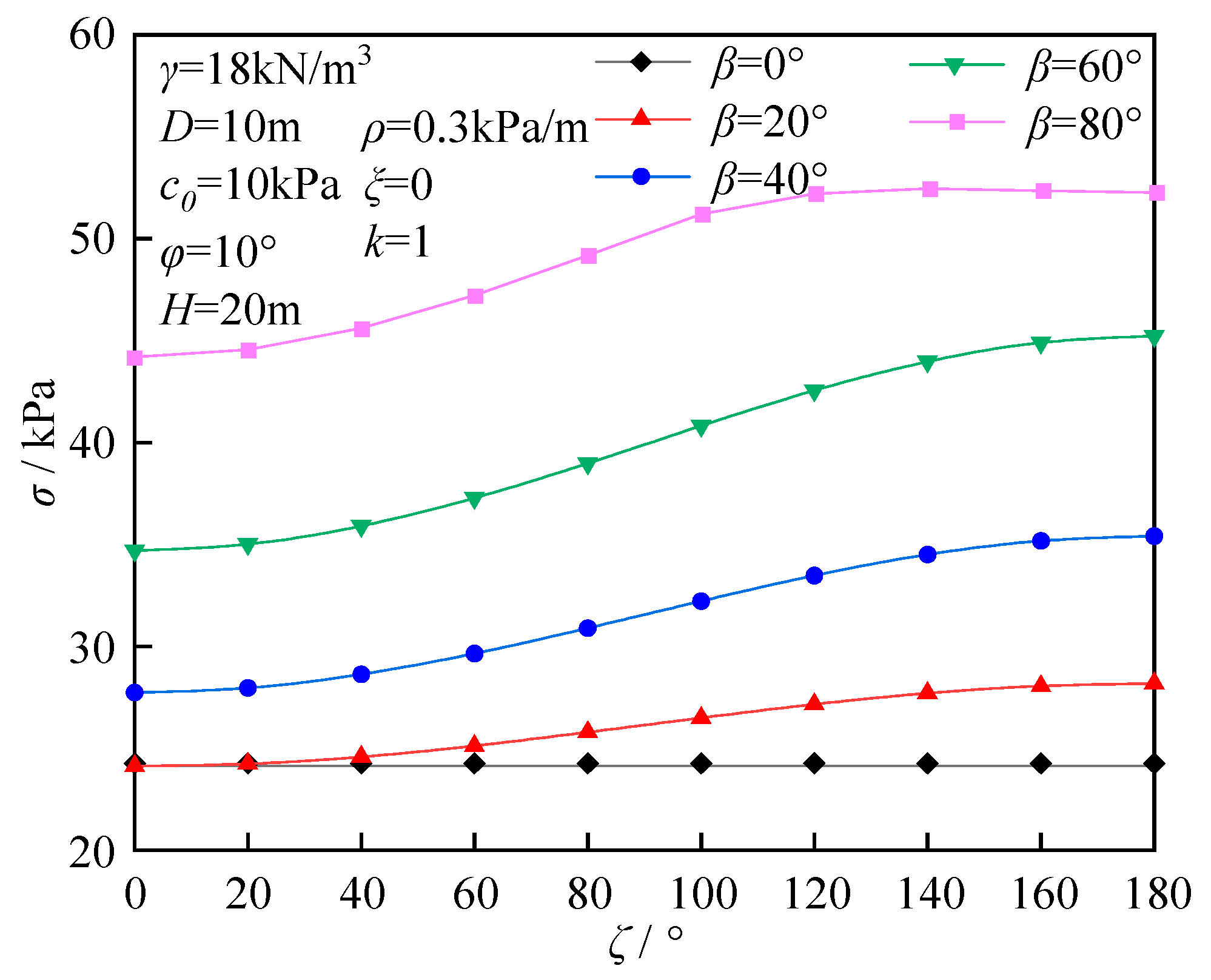
6.3. The Effect of Nonhomogeneity of Soil
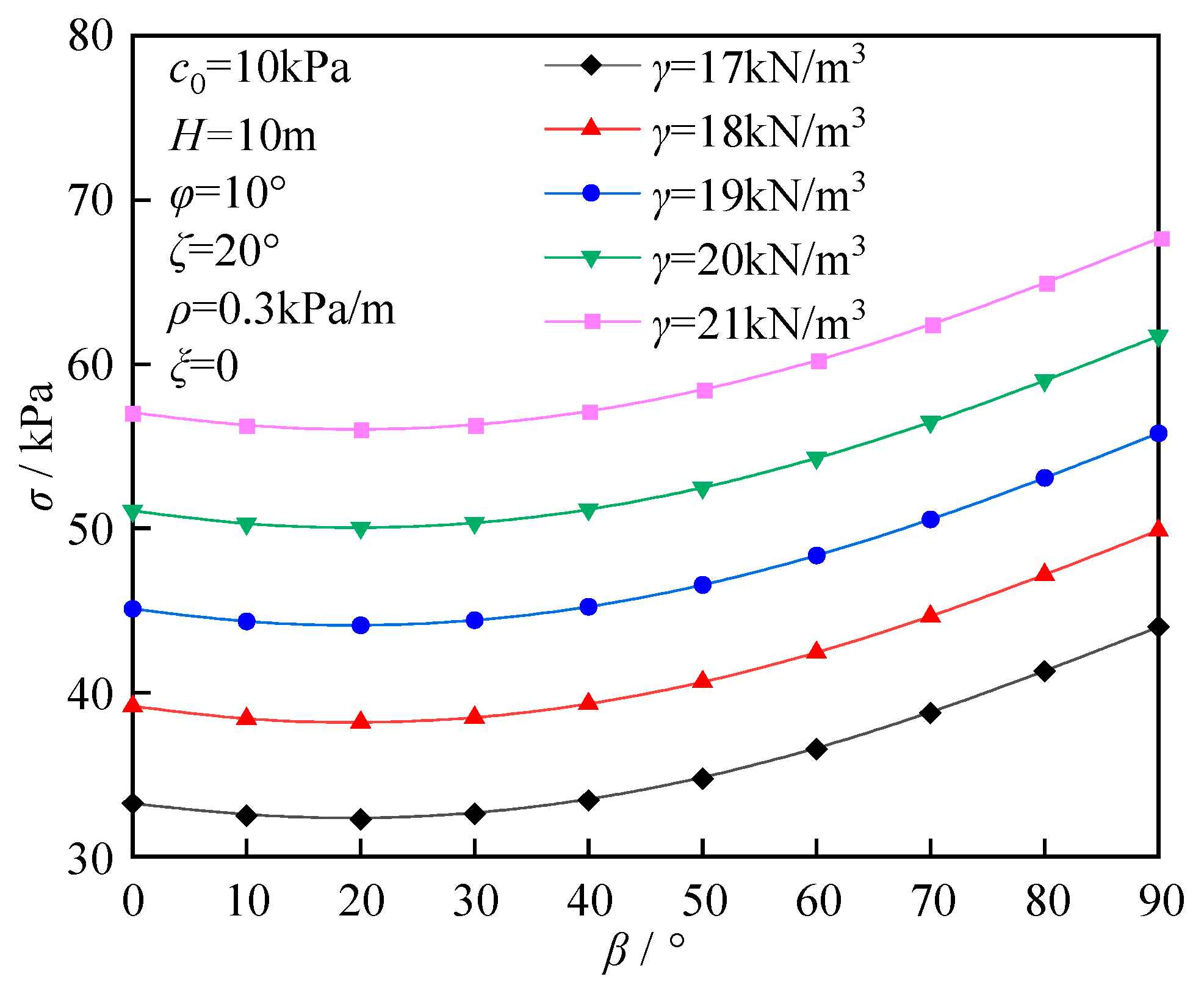
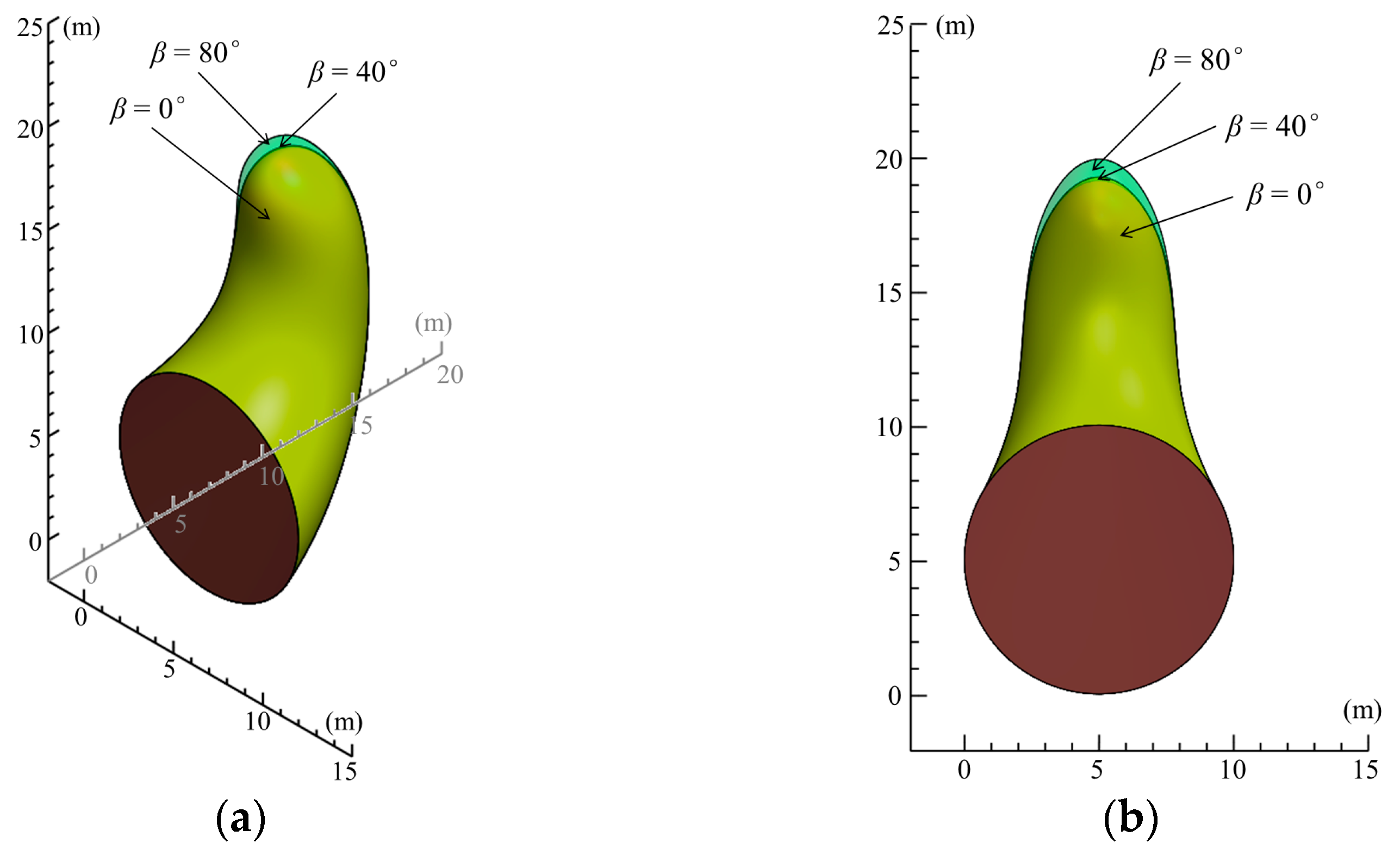
6.4. The Effect of Soil Anisotropy
7. Engineering Case Comparison
8. Conclusions
- (1)
- The ultimate support force decreases linearly with an increasing initial cohesion, decreases nonlinearly with an increasing internal friction angle, and decreases gradually with an increasing tensile strength reduction parameter. Among these, when the initial cohesion is relatively high, changes in the tensile strength reduction factor exert a more pronounced influence on the support force. For example, under the conditions of initial cohesion being 16 kPa and internal friction angle being 20°, increasing its tensile strength reduction parameter from 0 to 1 causes the ultimate support force to decline by approximately 58.3%.
- (2)
- When the nonhomogeneous directional angle increases, the ultimate support force demonstrates a progressive growth pattern. When ζ is 90°, the rate of increase reaches its maximum value. As the inclined angle of soil layer increases, the ultimate support force exhibits a nonlinear change, first decreasing and then increasing. The ultimate support force reaches its minimum value within the inclined angle of soil layer range of 10° to 30°. Additionally, under conditions of low internal friction angle, the effect exerted by the anisotropic coefficient on the ultimate support force diminishes.
- (3)
- Changes in the nonhomogeneous coefficient have a significant impact on the failure plane position, while the nonhomogeneously directional angle has a relatively minor influence on the location of the failure plane. The inclined angle of soil layer and anisotropy have a negligible impact on the failure plane position. As demonstrated by engineering examples, the application of the tensile strength cut-off to the computation of tunnel face support force results in an error margin of approximately 1.92% relative to field measurements. This enhancement in the precision of tunnel face stability evaluation is a key finding of this study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Cui, H.; Tao, R.; Bao, X.; Wu, X.; Qiu, T.; Shen, J.; Han, Z.; Chen, X. Seismic Resilience Evolution of Shield Tunnel with Structure Degradation. Appl. Sci. 2023, 14, 72. [Google Scholar] [CrossRef]
- Yang, X.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Tu, S.; Chen, W.; Ma, M. Face stability analysis of a shield tunnel excavated along inclined strata. Undergr. Space 2023, 13, 183–204. [Google Scholar] [CrossRef]
- Shi, X.; Liu, B.; Tannant, D.; Qi, Y. Influence of consolidation settlement on the stability of inclined TBM tunnels in a coal mine. Tunn. Undergr. Space Technol. 2017, 69, 64–71. [Google Scholar] [CrossRef]
- Li, L.; Shang, C.; Chu, K.; Zhou, Z.; Song, S.; Liu, Z.; Chen, Y. Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel. Tunn. Undergr. Space Technol. 2021, 109, 103756. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, Y.; Shi, P.; Li, J.; Gan, P. Face stability analysis of shield-driven tunnels shallowly buried in dry sand using 1-g large-scale model tests. Acta Geotech. 2018, 13, 693–705. [Google Scholar] [CrossRef]
- Wu, W.; Liu, X.; Guo, J.; Sun, F.; Huang, X.; Zhu, Z. Upper limit analysis of stability of the water-resistant rock mass of a Karst tunnel face considering the seepage force. Bull. Eng. Geol. Environ. 2021, 80, 5813–5830. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Cao, M.; Wang, Z. Study on excavation sequence of pilot tunnels for a rectangular tunnel using numerical simulation and field monitoring method. Rock Mech. Rock Eng. 2022, 55, 3507–3523. [Google Scholar] [CrossRef]
- Zhang, B.; Jiang, J.; Zhang, D.; Liu, Z. Upper bound solution of collapse pressure and permanent displacement of 3D tunnel faces using the pseudo-dynamic method and the kinematic approach. Geomech. Eng. 2021, 25, 521–533. [Google Scholar]
- Zhong, J.; Yang, X. Two-dimensional face stability analysis in rock masses governed by the Hoek-Brown strength criterion with a new multi-horn mechanism. Int. J. Min. Sci. Technol. 2023, 33, 963–976. [Google Scholar] [CrossRef]
- Song, Q.; Su, D.; Pan, Q.; Han, W.; Chen, X. Limit equilibrium models for passive failure of a large-diameter shield tunnel face in reinforced soft clay. Acta Geotech. 2024, 19, 5231–5247. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Face stability analysis of circular tunnels driven by a pressurized shield. J. Geotech. Geoenviron. Eng. 2010, 136, 215–229. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, F. Stability analysis of unsaturated soils at the end of starting point of shield tunnels after well dewatering. KSCE J. Civ. Eng. 2025, 29, 100030. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, W.; Wang, C.; Yu, B. Reliability Analysis of Seismic Stability of Shield Tunnel Face under Multiple Correlated Failure Modes. KSCE J. Civ. Eng. 2021, 25, 3172–3185. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B. Reliability analysis for seismic stability of tunnel faces in soft rock masses based on a 3D stochastic collapse model. J. Cent. South Univ. 2019, 26, 1706–1718. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Three-dimensional stability analysis of slopes in hard soil/soft rock with tensile strength cut-off. Eng. Geol. 2017, 229, 73–84. [Google Scholar] [CrossRef]
- Liu, J.; Luo, W.; Liu, L. Seismic Stability of 3D Tunnel Face considering Tensile Strength Cut-Off. KSCE J. Civ. Eng. 2022, 26, 3620–3632. [Google Scholar] [CrossRef]
- Park, D. Influence of the Hoek–Brown failure criterion with tensile strength cut-off on the roof stability in deep rock tunnels. Tunn. Undergr. Space Technol. 2023, 136, 105016. [Google Scholar] [CrossRef]
- Huang, F.; Wang, Y.; Zhang, M.; Yang, Z. Face stability analysis of longitudinally inclined shield tunnel considering the effect of tensile strength cut-off and pore water pressure. J. Cent. South Univ. 2025, 32, 1080–1098. [Google Scholar] [CrossRef]
- Hou, C.; Yang, X. Seismic stability of 3D tunnel face considering tensile strength cut-off. KSCE J. Civ. Eng. 2020, 24, 2232–2243. [Google Scholar] [CrossRef]
- Zou, J.; Qian, Z.; Xiang, X.; Chen, G. Face stability of a tunnel excavated in saturated nonhomogeneous soils. Tunn. Undergr. Space Technol. 2019, 83, 1–17. [Google Scholar] [CrossRef]
- Du, D.; Dias, D.; Yang, X. Analysis of earth pressure for shallow square tunnels in anisotropic and non-homogeneous soils. Comput. Geotech. 2018, 104, 226–236. [Google Scholar] [CrossRef]
- Meng, Q.; Qu, X.; Wang, X.; Yuanita, V.; Wong, S. Quantitative risk assessment modeling for nonhomogeneous urban road tunnels. Risk Anal. 2011, 31, 382–403. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H.; Deng, R.; Wang, Y. Active stability analysis of 3D tunnel face in nonhomogeneous and anisotropic soils. Geotech. Geol. Eng. 2023, 41, 3013–3033. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, K.; Wang, W. Seismic stability analysis of tunnel faces in heterogeneous and anisotropic soils using modified pseudodynamic method. Sustainability 2023, 15, 11083. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Design equation for stability of a circular tunnel in anisotropic and heterogeneous clay. Undergr. Space 2022, 7, 76–93. [Google Scholar] [CrossRef]
- Zhang, T.; Baroth, J.; Dias, D. Probabilistic basal heave stability analyses of supported circular shafts in non-homogeneous clayey soils. Comput. Geotech. 2021, 140, 104457. [Google Scholar] [CrossRef]
- Zou, J.; Peng, Z. Stability analyses of shallow rectangular tunnels in anisotropic and nonhomogeneous soils using a kinematic approach. Int. J. Geomech. 2024, 24, 04024127. [Google Scholar] [CrossRef]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Application of the soil parameter random field in the 3D random finite element analysis of Guanyinyan composite dam. Case Stud. Constr. Mater. 2022, 17, e01329. [Google Scholar] [CrossRef]
- Jamhiri, B.; Xu, Y.; Shadabfar, M.; Jalal, F.E. Probabilistic estimation of thermal crack propagation in clays with Gaussian processes and random fields. Geomech. Energy Environ. 2023, 34, 100454. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Zhang, L.; Tian, Y.; Cassidy, M.J.; Zhang, L. Random finite element method for spudcan foundations in spatially variable soils. Eng. Geol. 2016, 205, 146–155. [Google Scholar] [CrossRef]
- Li, M.; Cai, G.; LI, H.; Yang, B.; Zhao, C. Infinite unsaturated soil slopes stability with tensile strength cut-off. Chin. J. Geotech. Eng. 2020, 42, 705–713. [Google Scholar]
- Michalowski, R.L. Stability of intact slopes with tensile strength cut-off. Géotechnique 2017, 67, 720–727. [Google Scholar] [CrossRef]
- Luan, M.T.; Nian, T.K.; Yang, Q. Stability analysis of pile-stabilized slopes considering both nonhomogeneity and anisotropy of soil strength using upper bound method of limit analysis. Rock Soil Mech. 2006, 27, 530–536. [Google Scholar]
- Liao, B.; Huang, M.; Lu, Y.; Huang, Y.; Xu, J. Upper bound solution of shield tunnel face supporting pressure in non-homogeneous fault fracture zone. J. Eng. Geol. 2023, 31, 2008–2019. [Google Scholar]
- Zhang, D.; Zhang, B. Stability analysis of the pressurized 3D tunnel face in anisotropic and nonhomogeneous soils. Int. J. Geomech. 2020, 20, 04020018. [Google Scholar] [CrossRef]
- Li, T.; Yang, X. Three-dimensional face stability of shallow-buried tunnels with tensile strength cut-off. Comput. Geotech. 2019, 110, 82–93. [Google Scholar] [CrossRef]

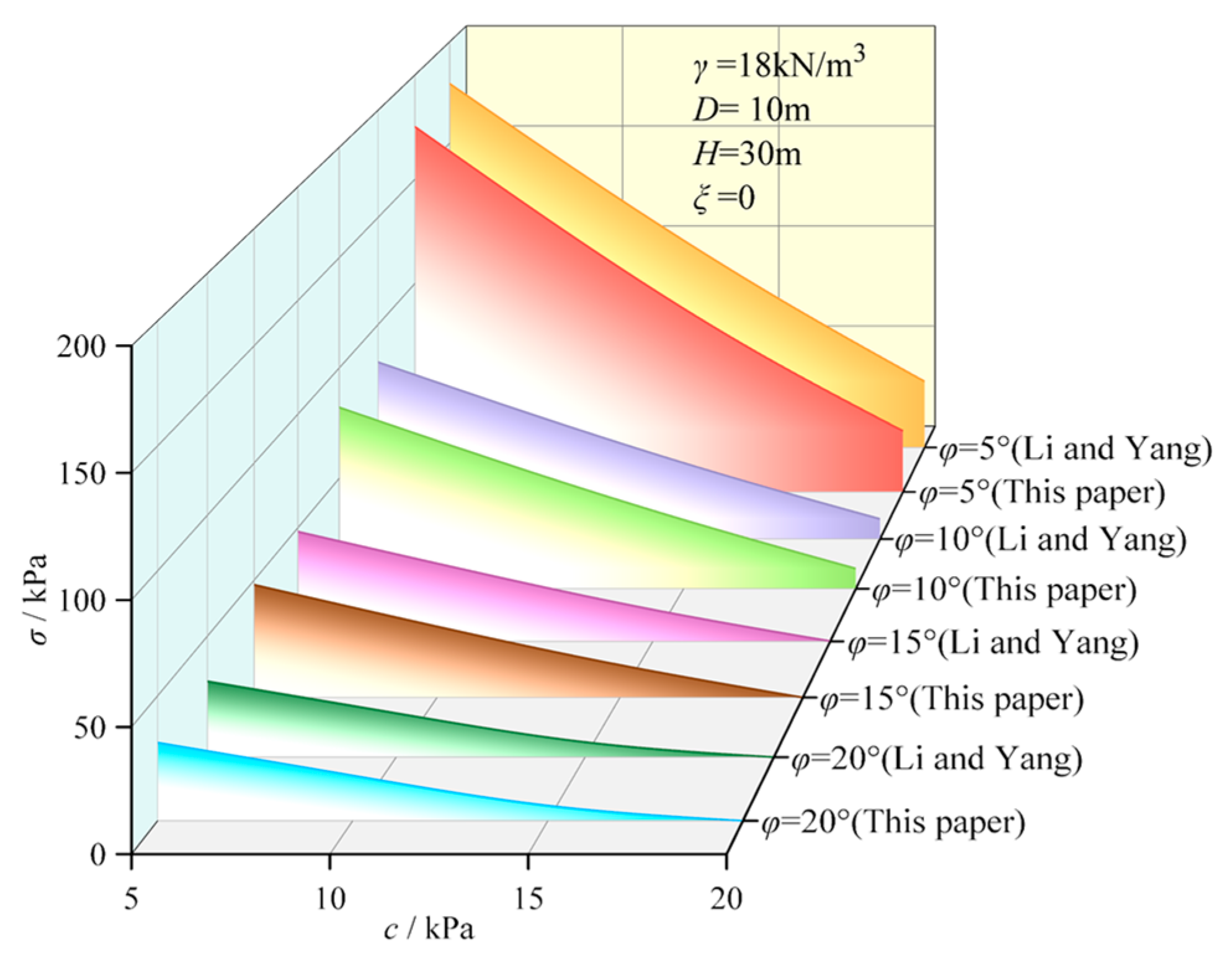



| n | γ (kN/m3) | c0 (kPa) | φ (°) | σ (kPa) | Relative Error | |
|---|---|---|---|---|---|---|
| Li and Yang [39] | This Paper (ξ = 0) | |||||
| 1 | 18 | 5 | 5 | 179.360 | 175.226 | 2.31% |
| 2 | 18 | 5 | 10 | 82.450 | 82.161 | 0.35% |
| 3 | 18 | 5 | 15 | 48.310 | 48.115 | 0.40% |
| 4 | 18 | 5 | 20 | 31.370 | 31.272 | 0.31% |
| 5 | 18 | 10 | 5 | 126.290 | 121.042 | 4.16% |
| 6 | 18 | 10 | 10 | 56.030 | 55.783 | 0.44% |
| 7 | 18 | 10 | 15 | 30.550 | 30.319 | 0.76% |
| 8 | 18 | 10 | 20 | 18.200 | 18.122 | 0.43% |
| 9 | 18 | 15 | 5 | 76.980 | 71.603 | 6.98% |
| 10 | 18 | 15 | 10 | 31.380 | 31.229 | 0.48% |
| 11 | 18 | 15 | 15 | 14.010 | 13.884 | 0.90% |
| 12 | 18 | 15 | 20 | 6.250 | 6.101 | 2.38% |
| n | ρ (kPa/m) | σ | Relative Error | |
|---|---|---|---|---|
| Zhang and Zhang [38] | This Paper (ξ = 0) | |||
| 1 | 0 | 75.9224 | 76.7554 | 1.10% |
| 2 | 0.1 | 70.4588 | 71.2001 | 1.05% |
| 3 | 0.2 | 64.9952 | 65.6448 | 1.00% |
| 4 | 0.3 | 59.5315 | 60.0899 | 0.94% |
| 5 | 0.4 | 54.0679 | 54.5352 | 0.86% |
| 6 | 0.5 | 48.6043 | 48.981 | 0.78% |
| 7 | 0.6 | 43.1827 | 43.4263 | 0.56% |
| 8 | 0.7 | 37.7728 | 37.8722 | 0.26% |
| 9 | 0.8 | 32.3629 | 32.3181 | 0.14% |
| 10 | 0.9 | 26.953 | 26.7642 | 0.70% |
| 11 | 1 | 21.543 | 21.2106 | 1.54% |
| n | k | σ | Relative Error | |
|---|---|---|---|---|
| Zhang and Zhang [38] | This Paper (ξ = 0) | |||
| 1 | 0.6 | 63.5904 | 60.4151 | 4.99% |
| 2 | 0.7 | 67.9947 | 66.2505 | 2.57% |
| 3 | 0.8 | 71.2979 | 70.6275 | 0.94% |
| 4 | 0.9 | 73.8671 | 74.0319 | 0.22% |
| 5 | 1 | 75.9224 | 76.7554 | 1.10% |
| 6 | 1.1 | 77.6041 | 78.9839 | 1.78% |
| 7 | 1.2 | 79.0054 | 80.841 | 2.32% |
| 8 | 1.3 | 80.1912 | 82.4124 | 2.77% |
| n | c0 (kPa) | φ (°) | Mohr–Coulomb | Cut-Off | ||
|---|---|---|---|---|---|---|
| ξ = 0 | ξ = 0.5 | ξ = 1 | ||||
| 1 | 6 | 5 | 166.011 | 164.114 | 163.963 | 163.812 |
| 2 | 6 | 10 | 75.930 | 76.749 | 76.586 | 76.576 |
| 3 | 6 | 15 | 44.236 | 44.484 | 44.379 | 44.371 |
| 4 | 6 | 20 | 28.443 | 28.594 | 28.524 | 28.520 |
| 5 | 8 | 5 | 143.153 | 142.324 | 141.971 | 141.637 |
| 6 | 8 | 10 | 64.590 | 66.142 | 65.821 | 65.802 |
| 7 | 8 | 15 | 36.774 | 37.323 | 37.181 | 37.170 |
| 8 | 8 | 20 | 22.950 | 23.299 | 23.145 | 23.122 |
| 9 | 10 | 5 | 120.296 | 121.042 | 120.405 | 119.782 |
| 10 | 10 | 10 | 53.250 | 55.783 | 55.091 | 55.067 |
| 11 | 10 | 15 | 29.312 | 30.319 | 29.983 | 29.969 |
| 12 | 10 | 20 | 17.457 | 18.122 | 17.781 | 17.752 |
| 13 | 12 | 5 | 97.438 | 100.359 | 99.316 | 98.273 |
| 14 | 12 | 10 | 41.910 | 45.696 | 44.575 | 44.332 |
| 15 | 12 | 15 | 21.850 | 23.539 | 22.785 | 22.768 |
| 16 | 12 | 20 | 11.964 | 13.128 | 12.455 | 12.382 |
| 17 | 14 | 5 | 74.581 | 80.873 | 78.756 | 77.243 |
| 18 | 14 | 10 | 30.570 | 35.948 | 34.307 | 33.597 |
| 19 | 14 | 15 | 14.388 | 17.028 | 15.745 | 15.568 |
| 20 | 14 | 20 | 6.471 | 8.355 | 7.246 | 7.012 |
| 21 | 16 | 5 | 51.723 | 62.646 | 59.481 | 56.868 |
| 22 | 16 | 10 | 19.230 | 26.574 | 24.297 | 22.862 |
| 23 | 16 | 15 | 6.926 | 10.799 | 8.919 | 8.367 |
| 24 | 16 | 20 | 0.977 | 3.942 | 2.143 | 1.643 |
| Soil Layer | γ (kN/m3) | c0 (kPa) | φ (°) | Thickness (m) |
|---|---|---|---|---|
| artificial fill | 17.3 | 12.0 | 28.0 | 1.4 |
| silty soil | 18.5 | 6.0 | 18.0 | 7.6 |
| alluvial deposits | 19.5 | 0.8 | 18.0 | 6.0 |
| Strongly weathered mudstone | 21.6 | 200.0 | 24.0 | 23.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Zhao, Y.; Zhang, D.; Zhang, S. Stability Analysis of Shield Tunnels Considering Spatial Nonhomogeneity and Anisotropy of Soils with Tensile Strength Cut-Off. Appl. Sci. 2025, 15, 9507. https://doi.org/10.3390/app15179507
Zhang B, Zhao Y, Zhang D, Zhang S. Stability Analysis of Shield Tunnels Considering Spatial Nonhomogeneity and Anisotropy of Soils with Tensile Strength Cut-Off. Applied Sciences. 2025; 15(17):9507. https://doi.org/10.3390/app15179507
Chicago/Turabian StyleZhang, Biao, Yanbin Zhao, Daobing Zhang, and Shunshun Zhang. 2025. "Stability Analysis of Shield Tunnels Considering Spatial Nonhomogeneity and Anisotropy of Soils with Tensile Strength Cut-Off" Applied Sciences 15, no. 17: 9507. https://doi.org/10.3390/app15179507
APA StyleZhang, B., Zhao, Y., Zhang, D., & Zhang, S. (2025). Stability Analysis of Shield Tunnels Considering Spatial Nonhomogeneity and Anisotropy of Soils with Tensile Strength Cut-Off. Applied Sciences, 15(17), 9507. https://doi.org/10.3390/app15179507





