Determining Factors Influencing Operating Speeds on Road Tangents
Abstract
1. Introduction
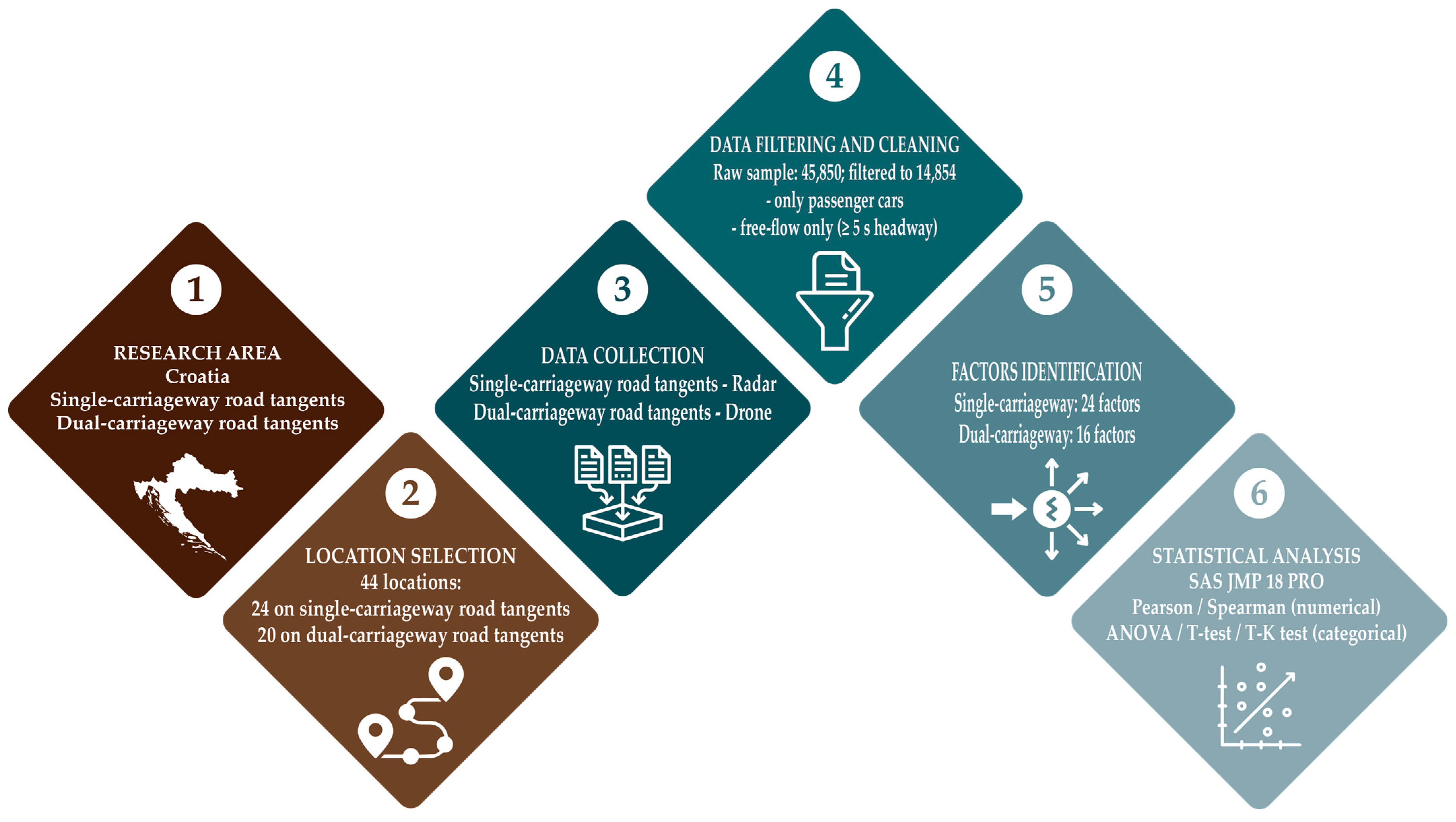
2. Methodology
2.1. Research Context
2.2. Data Collection
- Dual-carriageway roads—motorways;
- Single carriageway roads:
- ⚬
- State roads,
- ⚬
- County roads.
2.2.1. Locations Selection
- Efforts were made to select locations as randomly as possible within the constraints of the road network, ensuring national representativeness and covering all major geographic regions (Central Croatia, Slavonia and Baranja, Lika, Istria, Dalmatia);
- Existing speed limit (70, 80, 90 km/h for single-carriageway roads; 100, 110, 120, 130 km/h for dual-carriageway roads). It should be noted that, in Croatia, the default speed limit outside of urban areas is 90 km/h, unless otherwise indicated by a posted speed limit sign;
- Other relevant road design, vehicle structure, road capacity, and other contributing elements;
- Speeds were measured during the week (from Monday to Friday) at off-peak hours so that the established patterns of driver behavior could be disregarded or excluded from consideration;
- To maintain data integrity and to avoid behavioral bias, all selected locations were situated away from fixed or mobile speed enforcement zones;
- Only extra-urban areas were considered to eliminate the influence of urban traffic patterns and to minimize the impact of pedestrian activity;
- Measurements were conducted exclusively on tangent segments, with a minimum tangent length of 100 m;
- Within each tangent, measurements were performed at various positions (beginning, middle, and end) to account for potential intra-segment speed variations;
- Each location also met the following geometric and environmental criteria:
- ⚬
- A straight and uniform road section, free from nearby horizontal curves that could affect vehicle speed;
- ⚬
- This study did not consider the horizontal tangents in vertical curves;
- ⚬
- A section where it is technically possible to exceed the posted speed limit;
- ⚬
- Sections exhibiting a range of longitudinal slopes (from −5.20% to +5.20% (single-carriageway roads); from −4.00% to 4.00% (dual-carriageway roads));
- ⚬
- Locations chosen across different terrain types (flat, hilly, mountainous);
- ⚬
- Locations exhibiting a variety of AADT and ASDT values.
2.2.2. Speed Measurement
- Speed Measurement—Single-carriageway Road tangents
- Speed Measurement—Dual-carriageway Road Tangents
2.2.3. Data Cleaning and Finalizing
2.2.4. Factors Identification
- Factors Identified—Single-carriageway Road Tangents
- Factors Identified—Dual-carriageway Road Tangents
2.3. Data Analysis
3. Results
3.1. Single-Carriageway Road Tangents
3.2. Dual-Carriageway Road Tangents
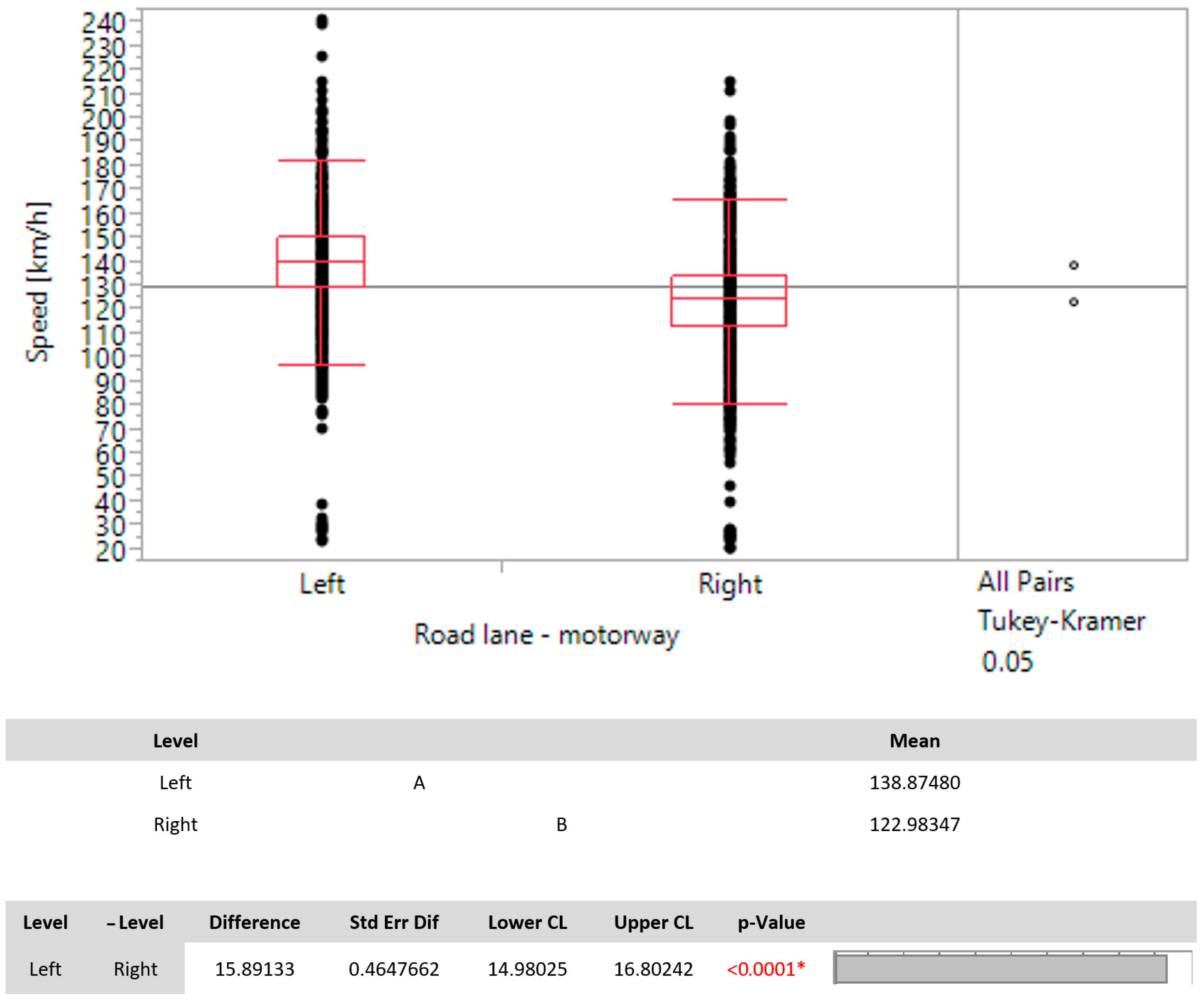
3.2.1. Left (Overtaking) Lane
3.2.2. Right (Driving) Lane
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Road Type | Road Category | Road Name | Direction | Speed Limit [km/h] | AADT | ASDT | Total Sample Size (All Vehicle Categories) [veh] | Filtered Sample Size (Passenger Cars) [veh] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| [veh/day] | [veh/day] | |||||||||
| Single-carriageway road | State road | Dubrovnik | towards Dubrovnik | 90 | 18,292 | 25,757 | 8222 | 1024 | ||
| towards Čilipi | 90 | 18,292 | 25,757 | 6802 | 1287 | |||||
| Single-carriageway road | County road | Gospić | from toll | 90 | 878 | 1118 | 242 | 161 | ||
| towards toll | 90 | 878 | 1118 | 176 | 119 | |||||
| Single-carriageway road | County road | Knin | from Knin | 90 | 1216 | 1450 | 88 | 70 | ||
| towards Knin | 90 | 1216 | 1450 | 76 | 56 | |||||
| Single-carriageway road | County road | Osijek | from Osijek | 70 | 8717 | 8438 | 2433 | 933 | ||
| towards Osijek | 70 | 8717 | 8438 | 3526 | 1147 | |||||
| Single-carriageway road | State road | Pazin | from Pazin | 90 | 3391 | 3847 | 492 | 335 | ||
| towards Pazin | 90 | 3391 | 3847 | 488 | 338 | |||||
| Single-carriageway road | County road | Požega | from Požega | 90 | 1656 | 1655 | 836 | 323 | ||
| towards Požega | 90 | 1656 | 1655 | 928 | 429 | |||||
| Single-carriageway road | State road | Pula | from Pula | 90 | 2873 | 4375 | 1602 | 771 | ||
| towards Pula | 90 | 2873 | 4375 | 1557 | 762 | |||||
| Single-carriageway road | State road | Sisak | towards Sisak | 90 | 3953 | 4550 | 479 | 248 | ||
| towards Stružec | 90 | 3953 | 4550 | 516 | 234 | |||||
| Single-carriageway road | State road | Split | from Klis | 80 | 2404 | 3522 | 823 | 299 | ||
| towards Klis | 80 | 2404 | 3522 | 1234 | 359 | |||||
| Single-carriageway road | State road | Varaždin | from Varaždin | 90 | 8947 | 8773 | 1603 | 564 | ||
| towards Varaždin | 90 | 8947 | 8773 | 1696 | 661 | |||||
| Single-carriageway road | County road | Virovitica | from Novaki | 90 | 380 | 410 | 74 | 62 | ||
| towards Novaki | 90 | 380 | 410 | 75 | 63 | |||||
| Single-carriageway road | State road | Zadar | towards Zadar | 90 | 13,022 | 22,904 | 1914 | 906 | ||
| towards Nin | 90 | 13,022 | 22,904 | 1211 | 502 | |||||
| Total: | 37,093 | 11,653 | ||||||||
| Road type | Road Category | Road name | Carriageway/Direction | Speed limit [km/h] | AADT | ASDT | Total sample size (all vehicle categories) | Filtered sample size (passenger cars) | ||
| [veh/day] | [veh/day] | Left lane [veh] | Right lane [veh] | Left lane [veh] | Right lane [veh] | |||||
| Dual-carriageway road | Motorway | Motorway A1 | Bisko—Blato na Cetini | 130 | 5253 | 11,059 | 391 | 739 | 86 | 113 |
| Blato na Cetini—Bisko | 130 | 5253 | 11,059 | 340 | 614 | 86 | 113 | |||
| Dual-carriageway road | Motorway | Motorway A1 | Bosiljevo 2—Ogulin | 100 | 10,511 | 24,747 | 414 | 600 | 94 | 106 |
| Ogulin—Bosiljevo 2 | 100 | 10,511 | 24,747 | 506 | 703 | 102 | 105 | |||
| Dual-carriageway road | Motorway | Motorway A1 | Donja Zdenčina—Jastrebarsko | 130 | 20,603 | 34,474 | 773 | 550 | 99 | 79 |
| Jastrebarsko—Donja Zdenčina | 130 | 20,603 | 34,474 | 863 | 585 | 86 | 79 | |||
| Dual-carriageway road | Motorway | Motorway A1 | Gornja Ploča—Gospić | 100 | 9255 | 22,581 | 243 | 468 | 25 | 73 |
| Gospić—Gornja Ploča | 120 | 9255 | 22,581 | 443 | 688 | 82 | 114 | |||
| Dual-carriageway road | Motorway | Motorway A1 | Zadar Center—Zadar East | 130 | 7857 | 19,279 | 574 | 753 | 94 | 110 |
| Zadar East—Zadar Center | 130 | 7857 | 19,279 | 611 | 770 | 85 | 106 | |||
| Dual-carriageway road | Motorway | Motorway A2 | Zabok—Zaprešić | 130 | 9999 | 15,473 | 137 | 355 | 29 | 86 |
| Zaprešić—Zabok | 130 | 9999 | 15,473 | 232 | 502 | 43 | 108 | |||
| Dual-carriageway road | Motorway | Motorway A3 | Babina Greda—Županja | 100 | 5988 | 9184 | 167 | 261 | 60 | 81 |
| Županja—Babina Greda | 100 | 5988 | 9184 | 87 | 211 | 32 | 62 | |||
| Dual-carriageway road | Motorway | Motorway A3 | Križ—Popovača | 130 | 13,425 | 18,067 | 242 | 443 | 52 | 72 |
| Popovača—Križ | 130 | 13,425 | 18,067 | 273 | 420 | 73 | 81 | |||
| Dual-carriageway road | Motorway | Motorway A3 | Lužani—Nova Gradiška | 130 | 9007 | 12,947 | 265 | 362 | 65 | 70 |
| Nova Gradiška—Lužani | 130 | 9007 | 12,947 | 350 | 383 | 78 | 74 | |||
| Dual-carriageway road | Motorway | Motorway A6 | Delnice—Ravna Gora | 110 | 7981 | 13,233 | 158 | 438 | 54 | 99 |
| Ravna Gora—Delnice | 110 | 7981 | 13,233 | 380 | 463 | 63 | 82 | |||
| Total: | 7449 | 10,308 | 1388 | 1813 | ||||||
| 17,757 | 3201 | |||||||||
Appendix B
| Operating Speed Values | Symbol | Unit of Measure | Type | Mean | StDev | Min | Max | Median |
|---|---|---|---|---|---|---|---|---|
| Operating speed (V85) for single-carriageway road tangents | V85 | [km/h] | Continuous | 93.18 | 14.37 | 74.00 | 128.00 | 91.50 |
| Operating speed (V85) for dual-carriageway road tangents (left lane) | V85L | [km/h] | Continuous | 159.20 | 7.19 | 148.00 | 173.00 | 157.00 |
| Operating speed (V85) for dual-carriageway road tangents (right lane) | V85R | [km/h] | Continuous | 142.70 | 8.22 | 131.00 | 157.00 | 141.50 |
| Factors—Single-carriageway roads | Symbol | Unit of measure | Type | Mean | StDev | Min | Max | Median |
| Passenger side | PS | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Shoulder type | ST | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Edge line quality | ELQ | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Visibility | Vsb | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Pavement quality | PQ | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Lateral access density | LAD | [-] | Continuous | 1.63 | 1.55 | 0 | 6 | 1 |
| Tangent length (up to measurement point) | TL1 | [m] | Continuous | 848.75 | 619.25 | 110.00 | 2500.00 | 715.00 |
| Tangent length (from measurement point) | TL2 | [m] | Continuous | 848.75 | 619.25 | 110.00 | 2500.00 | 715.00 |
| Speed limit | SL | [km/h] | Categorical—Multi-level; | 87.50 | 6.08 | 70.00 | 90.00 | 90.00 |
| AADT | AADT | [veh/day] | Continuous | 5477.42 | 5488.92 | 380.00 | 18,292.00 | 3132.00 |
| ASDT | ASDT | [veh/day] | Continuous | 7233.25 | 8244.36 | 410.00 | 25,757.00 | 4111.00 |
| Lane width | LW | [m] | Categorical—Multi-level; | 3.02 | 0.30 | 2.50 | 3.50 | 3.00 |
| Longitudinal slope | LS | [%] | Continuous | 0.00 | 3.364 | -5.20 | 5.20 | 0.00 |
| Crash ratio | CR | [-] | Continuous | 0.003785 | 0.002544 | 0.002108 | 0.011545 | 0.003098 |
| Design speed | Vp | [km/h] | Categorical—Multi-level; | 69.167 | 18.86 | 40.00 | 100.00 | 70.00 |
| Terrain type | TT | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Guardrail presence | GP | [-] | Binary | 0.17 | 0.38 | 0 | 1 | 0 |
| Shoulder lane presence | ELP | [-] | Binary | 0.63 | 0.49 | 0 | 1 | 1 |
| Radius of previous curve | RpC | [m] | Continuous | 418.75 | 372.51 | 25.00 | 1500.00 | 315.00 |
| Radius of following curve | RfC | [m] | Continuous | 418.75 | 372.51 | 25.00 | 1500.00 | 315.00 |
| Road category | RC | [-] | Binary | 0.58 | 0.50 | 0 | 1 | 1 |
| Overtaking allowed | OA | [-] | Binary | 0.88 | 0.34 | 0 | 1 | 1 |
| Heavy goods vehicles share | HVS | [%] | Continuous | 3.60 | 1.90 | 1.20 | 8.40 | 3.20 |
| Disruptive factor presence | DFP | [-] | Binary | 0.13 | 0.34 | 0 | 1 | 0 |
| Factors—Dual-carriageway roads | Symbol | Unit of measure | Type | Mean | StDev | Min | Max | Median |
| Total tunnel length in last 20 km | TTL | [m] | Continuous | 274.50 | 662.05 | 0 | 2640.00 | 0 |
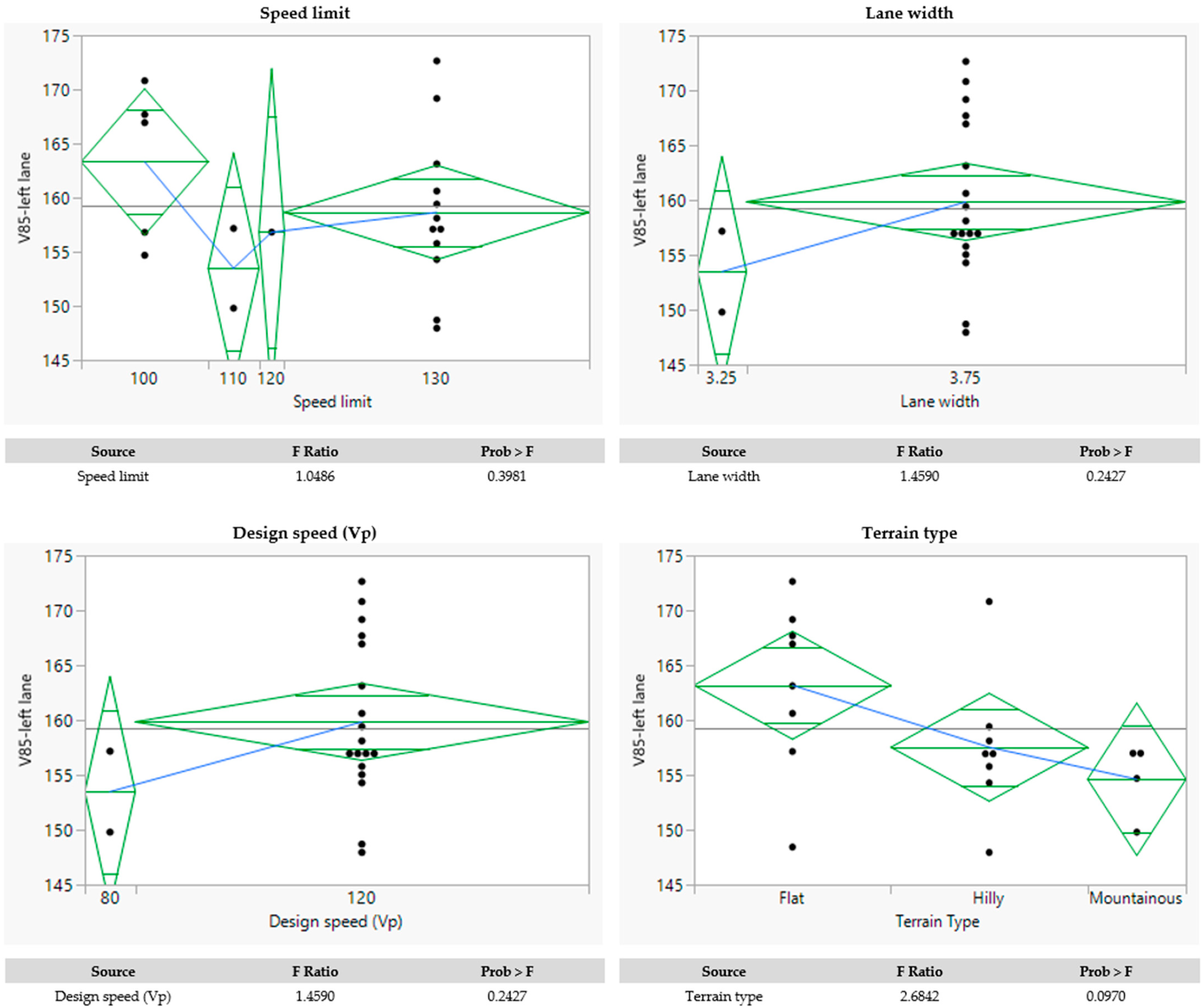
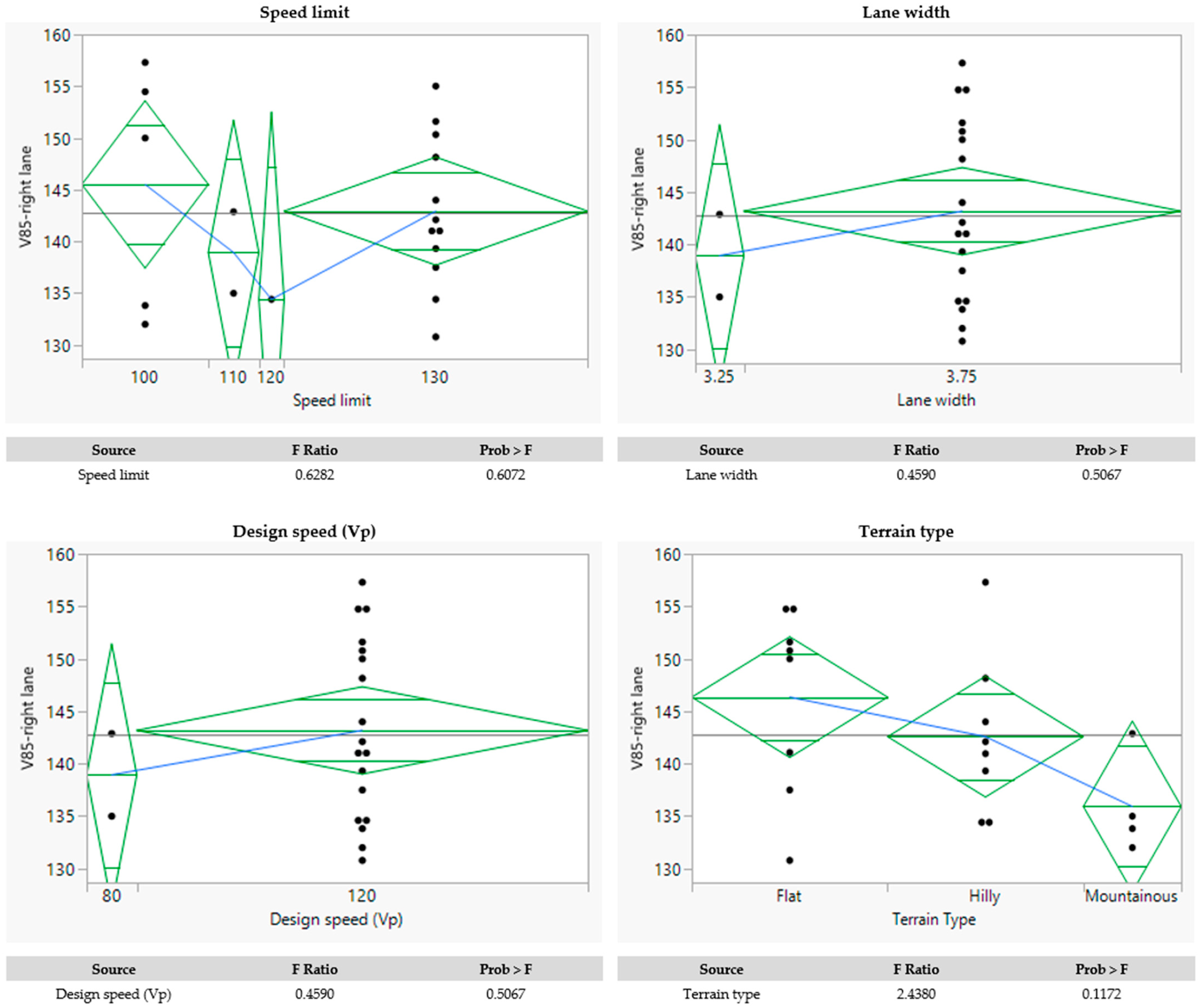
| Speed limit | SL | [km/h] | Categorical—Multi-level; | 120.00 | 13.38 | 100.00 | 130.00 | 130.00 |
| Lane width | LW | [m] | Categorical—Multi-level; | 3.70 | 0.15 | 3.25 | 3.75 | 3.75 |
| Design speed | Vp | [km/h] | Categorical—Multi-level; | 116.00 | 12.31 | 80.00 | 120.00 | 120.00 |
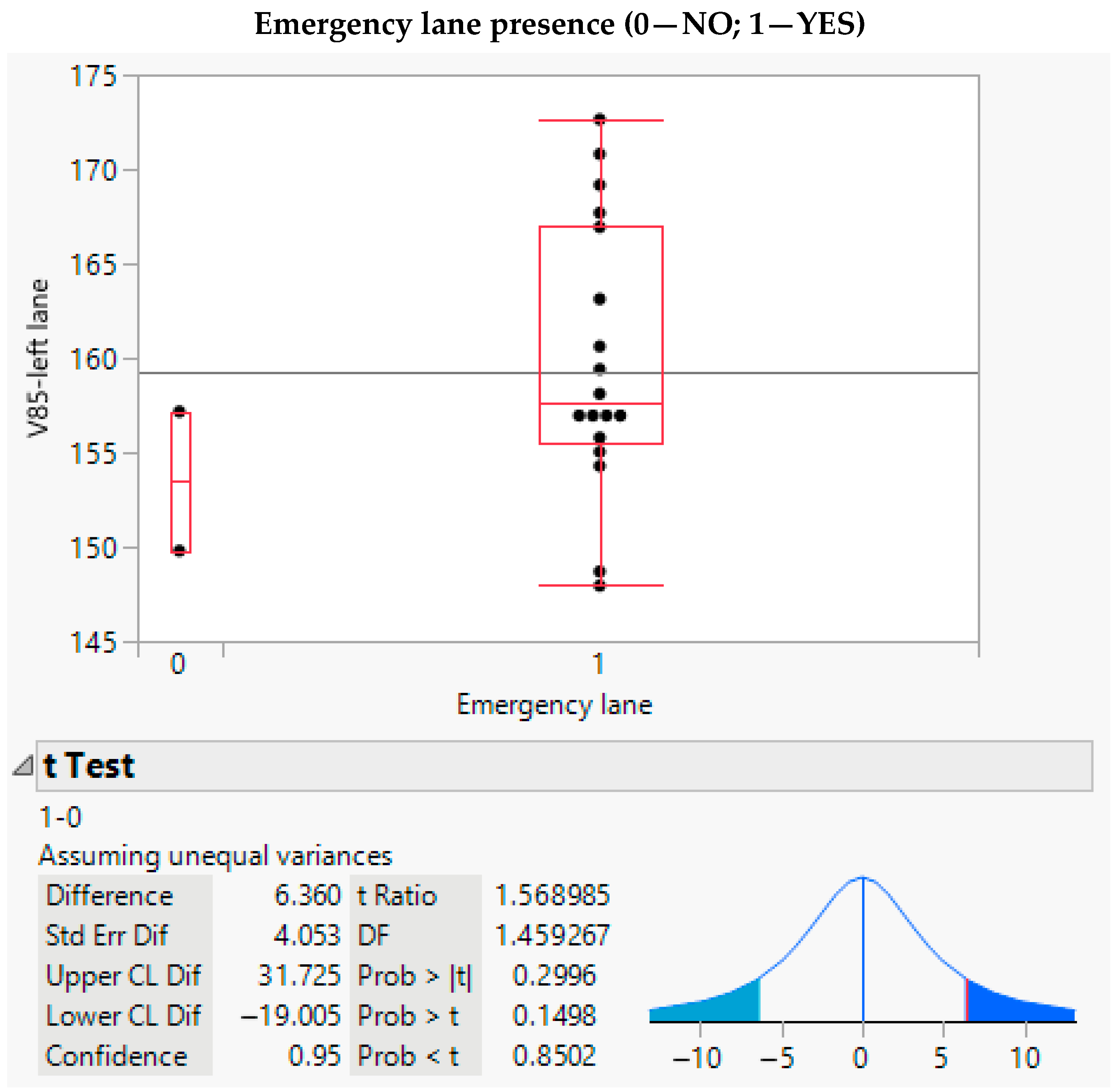
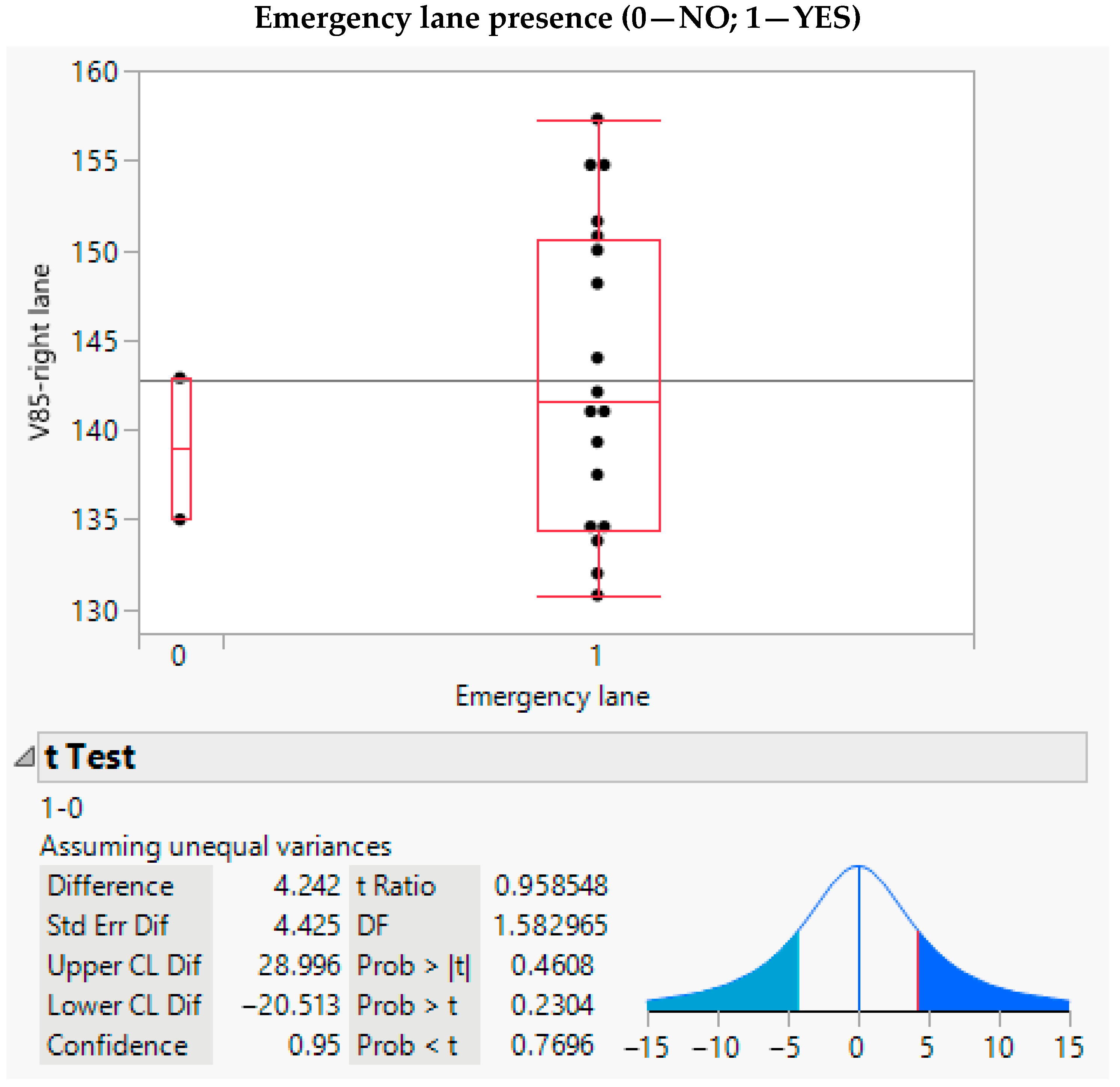
| Emergency lane presence | SLP | [-] | Binary | 0.90 | 0.31 | 0 | 1 | 1 |
| Previous object distance | POD | [m] | Continuous | 4810.00 | 3066.96 | 0 | 13,400.00 | 4400.00 |
| Following object distance | FOD | [m] | Continuous | 4400.00 | 3067.66 | 0 | 13,400.00 | 3650.00 |
| Longitudinal slope | LS | [%] | Continuous | 0.43 | 1.81 | -4.00 | 4.00 | 0.00 |
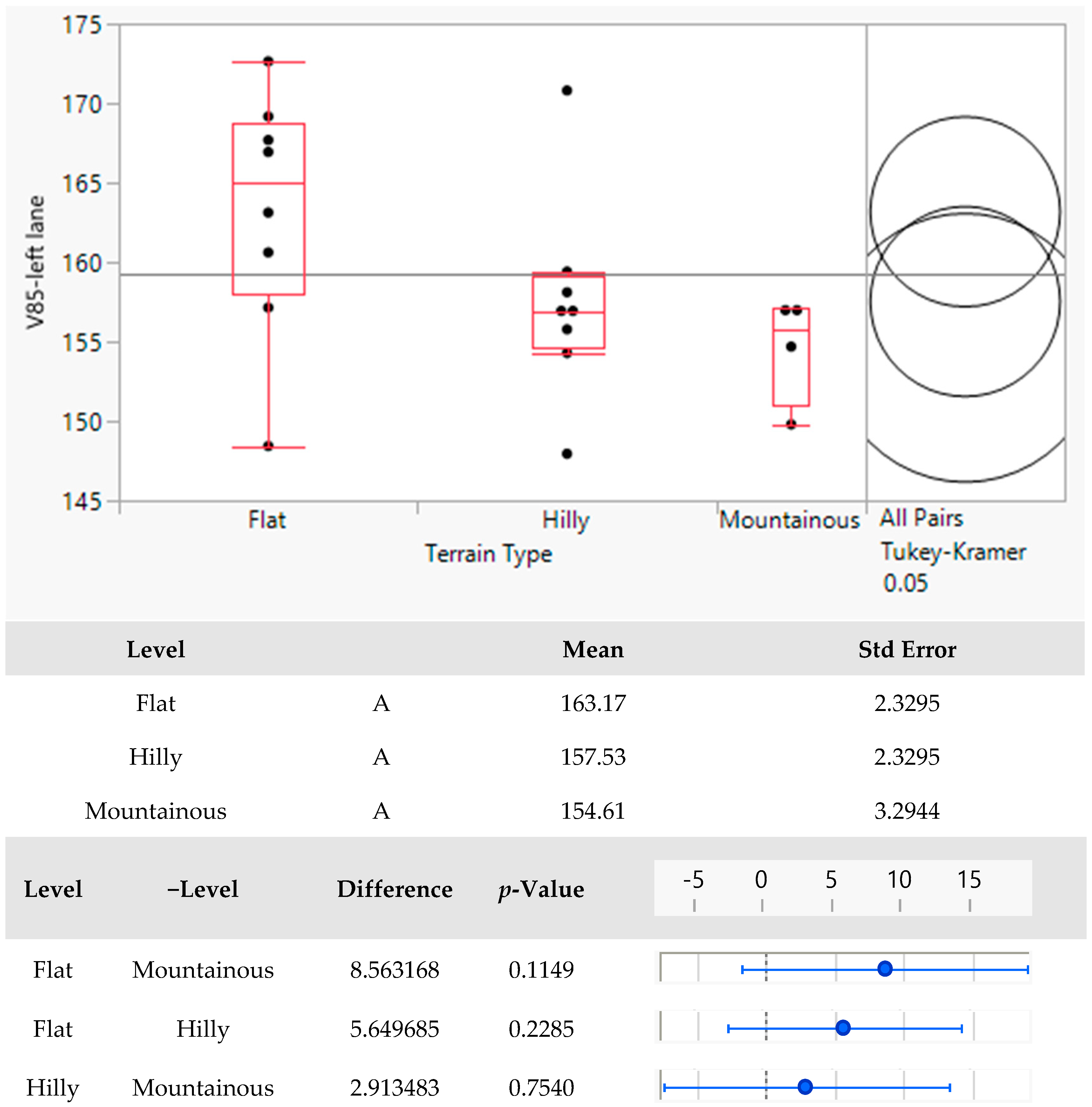
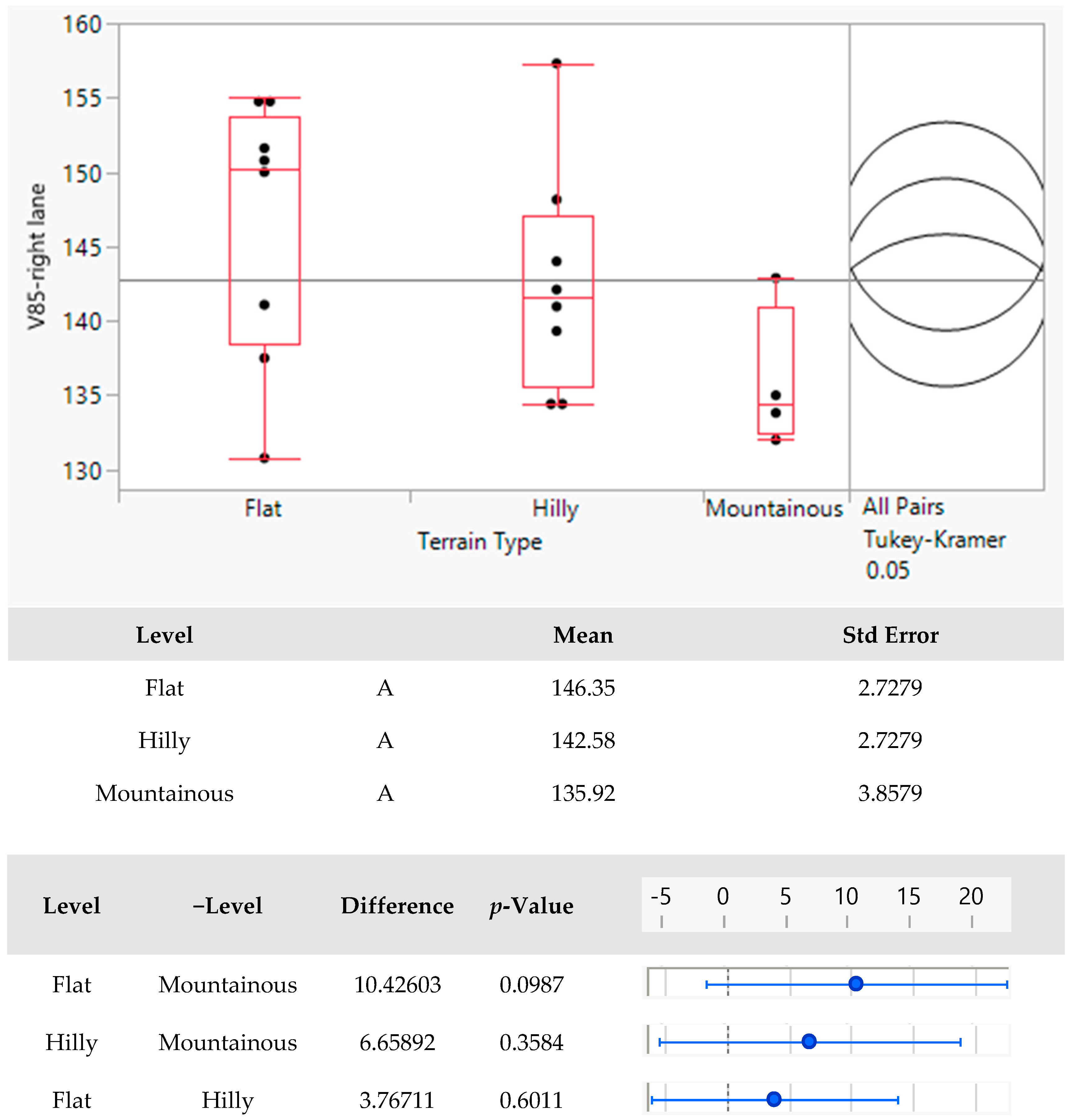
| Terrain type | TT | [-] | Categorical—Multi-level; | --- | --- | --- | --- | --- |
| Heavy goods vehicles share (left lane) | HVS_LL | [%] | Continuous | 0.87 | 0.93 | 0.00 | 2.92 | 0.54 |
| Heavy goods vehicles share (left lane) | HVS_RL | [%] | Continuous | 17.12 | 9.38 | 4.52 | 35.08 | 14.83 |
| Heavy goods vehicles share (both lanes) | HVS_2L | [%] | Continuous | 10.53 | 5.81 | 2.56 | 22.82 | 10.09 |
| AADT | AADT | [veh/day] | Continuous | 9.99 | 4.27 | 5.25 | 20.60 | 9.13 |
| ASDT | ASDT | [veh/day] | Continuous | 18.10 | 7.39 | 9.18 | 34.47 | 16.77 |
| Traffic flow density (left lane) | TFD_LL | [veh/km/lane] | Continuous | 2.49 | 1.42 | 0.70 | 4.80 | 2.15 |
| Traffic flow density (right lane) | TFD_RL | [veh/km/lane] | Continuous | 4.33 | 1.63 | 1.80 | 7.00 | 3.80 |
References
- World Health Organization. Global Status Report on Road Safety 2023; WHO: Geneva, Switzerland, 2023. [Google Scholar]
- Ministry of the Interior, Republic of Croatia. National Road Safety Plan of the Republic of Croatia for the Period 2021–2030; Ministry of the Interior: Zagreb, Croatia, 2021.
- International Transport Forum (ITF). Road Safety Annual Report 2018; OECD Publishing: Paris, France, 2018. [Google Scholar] [CrossRef]
- SWOV Institute for Road Safety Research. Speed and Speed Management; SWOV: The Hague, The Netherlands, 2021. [Google Scholar]
- National Highway Traffic Safety Administration (NHTSA). Traffic Safety Facts: Speeding; NHTSA: Washington, DC, USA, 2022. [Google Scholar]
- Insurance Institute for Highway Safety (IIHS). Speed and Fatality Statistics; IIHS: Arlington, VA, USA, 2022. [Google Scholar]
- National Highway Traffic Safety Administration (NHTSA). Crash Data Analysis; NHTSA: Washington, DC, USA, 2022. [Google Scholar]
- World Health Organization (WHO). Speed and Road Safety; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- Fitzpatrick, K.; Carlson, P.; Brewer, M.; Wooldridge, M. Design Speed, Operating Speed, and Posted Speed Practices; Transportation Research Board: Washington, DC, USA, 2003. [Google Scholar]
- Transport for New South Wales (Transport NSW). Annual Report 2010; Transport NSW: Sydney, Australia, 2010. Available online: https://www.transport.nsw.gov.au/system/files/media/documents/2023/2010-annual-report-overview.pdf (accessed on 10 March 2025).
- European Automobile Manufacturers Association. Road Safety: Safe Vehicles, Safe Drivers, Safe Roads; European Automobile Manufacturers Association: Brussels, Belgium, 2019; Available online: https://www.roadsafetyfacts.eu/themes/ACEA-Road-Safety-Facts/img/ACEA_Road_Safety.pdf (accessed on 10 March 2025).
- Tabish, S.A. Road Traffic & Safety: Risk Factors & Recommendations; Nova Science Publishers Inc: Hauppauge, NY, USA, 2017. [Google Scholar]
- European Transport Safety Council. Reducing Speeding in Europe. PIN Flash Report 36; European Transport Safety Council: Brussels, Belgium, 2019; Available online: https://etsc.eu/wp-content/uploads/PIN-flash-report-36-Final.pdf (accessed on 10 March 2025).
- Eluru, N.; Bhat, C.R. A Joint Econometric Analysis of Seat Belt Use and Crash-Related Injury Severity. Accid. Anal. Prev. 2007, 39, 1037–1049. [Google Scholar] [CrossRef]
- Maji, A.; Singh, D.; Agrawal, N.; Zaman, M. Operating Speed Prediction Models for Tangent Sections of Two-Lane Rural Highways in Oklahoma State. Transp. Lett. 2020, 12, 130–137. [Google Scholar] [CrossRef]
- Wang, B.; Hallmark, S.; Savolainen, P.; Dong, J. Examining Vehicle Operating Speeds on Rural Two-Lane Curves Using Naturalistic Driving Data. Accid. Anal. Prev. 2018, 118, 236–243. [Google Scholar] [CrossRef]
- Abdul-Mawjoud, A.A.; Sofia, G.G. Development of Models for Predicting Speed on Horizontal Curves for Two-Lane Rural Highways. Arab. J. Sci. Eng. 2008, 33, 365–377. [Google Scholar]
- Echaveguren, T.; Díaz, Á.; Vargas-Tejeda, S. Operating Speed Models for Horizontal Reverse Curves. Proc. Inst. Civ. Eng. Transp. 2015, 168, 510–522. [Google Scholar] [CrossRef]
- Shallam, R.D.K.; Ahmed, M.A. Operating Speed Models on Horizontal Curves for Two-Lane Highways. Transp. Res. Procedia 2016, 17, 445–451. [Google Scholar] [CrossRef]
- Malaghan, V.; Pawar, D.S.; Dia, H. Modeling Operating Speed Using Continuous Speed Profiles on Two-Lane Rural Highways in India. J. Transp. Eng. Part A Syst. 2020, 146, 04020124. [Google Scholar] [CrossRef]
- Russo, F.; Biancardo, S.A.; Busiello, M. Operating Speed as a Key Factor in Studying Driver Behaviour in a Rural Context. Transport 2016, 31, 260–270. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Miaou, S.P.; Brewer, M.; Carlson, P.; Wooldridge, M.D. Exploration of the Relationship between Operating Speed and Roadway Features on Tangent Sections. J. Transp. Eng. 2005, 131, 261–269. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Safety Performance Functions: Development and Application; U.S. Department of Transportation: Washington, DC, USA, 2015. Available online: https://www.fhwa.dot.gov/publications/research/safety/15030/006.cfm#073 (accessed on 10 March 2025).
- Özkan, T.; Lajunen, T.; El Chliaoutakis, J.; Parker, D.; Summala, H. Cross-Cultural Differences in Driving Behaviours: A Comparison of Six Countries. Transp. Res. Part F Traffic Psychol. Behav. 2006, 9, 227–242. [Google Scholar] [CrossRef]
- Jiang, Z.; Jadaan, K.; Ouyang, Y.; University of Illinois; Illinois Department of Transportation; Federal Highway Administration. Speed Harmonization—Design Speed vs. Operating Speed; Civil Engineering Studies, Illinois Center for Transportation Series No. 16-021; Illinois Center for Transportation: Rantoul, IL, USA, 2016; Available online: https://apps.ict.illinois.edu/projects/getfile.asp?id=5056 (accessed on 10 March 2025).
- Zuriaga, A.M.P.; García, A.G.; Torregrosa, F.J.C.; D’Attoma, P. Modeling Operating Speed and Deceleration on Two-Lane Rural Roads with Global Positioning System Data. Transp. Res. Rec. 2010, 2171, 11–20. [Google Scholar] [CrossRef]
- Dell’Acqua, G.; Russo, F. Speed Factors on Low-Volume Roads for Horizontal Curves and Tangents. Balt. J. Road Bridge Eng. 2010, 5, 89–97. [Google Scholar] [CrossRef]
- Abbondati, F.; Capaldo, F.S.; Lamberti, R. Predicting Driver Speed Behavior on Tangent Sections of Low-Volume Roads. Int. J. Civ. Eng. Technol. 2017, 8, 1047–1060. [Google Scholar]
- Eboli, L.; Guido, G.; Mazzulla, G.; Pungillo, G. Experimental Relationships between Operating Speeds of Successive Road Design Elements in Two-Lane Rural Highways. Transport 2015, 32, 138–145. [Google Scholar] [CrossRef]
- Montella, A.; Galante, F.; Mauriello, F.; Aria, M. Continuous Speed Profiles to Investigate Drivers’ Behavior on Two-Lane Rural Highways. Transp. Res. Rec. 2015, 2521, 3–11. [Google Scholar] [CrossRef]
- Dell’Acqua, G.; Esposito, T.; Lamberti, R.; Abate, D. Operating Speed Model on Tangents of Two-Lane Rural Highways. In Proceedings of the 4th International SIIV Congress, Palermo, Italy, 12–14 September 2007; p. 2848. Available online: https://www.siiv.net/site/sites/default/files/Documenti/palermo/63_2848_20080110105803.pdf (accessed on 10 March 2025).
- Crisman, B.; Marchionna, A.; Perco, P.; Robba, A.; Roberti, R. Operating Speed Prediction Model for Two-Lane Rural Roads. In Proceedings of the 3rd International Symposium on Highway Geometric Design, Chicago, IL, USA, 29 June–l July 2005; Available online: https://www.siiv.net/site/sites/default/files/Documenti/firenze/firenze05.pdf (accessed on 10 March 2025).
- Lobo, A.; Amorim, M.; Rodrigues, C.; Couto, A. Modelling the Operating Speed in Segments of Two-Lane Highways from Probe Vehicle Data: A Stochastic Frontier Approach. J. Adv. Transp. 2018, 2018, 3540785. [Google Scholar] [CrossRef]
- Stamatiadis, N.; Gong, H. Analysis of Inconsistency Related to Design Speed, Operating Speed, and Speed Limit; Kentucky Transportation Center Report KTC-06-12/SPR286-05-1F; University of Kentucky: Lexington, KY, USA, 2006. [Google Scholar]
- Abbas, S.K.S.; Adnan, M.A.; Endut, I.R. Exploration of 85th Percentile Operating Speed Model on Horizontal Curve: A Case Study for Two-Lane Rural Highways. Procedia-Soc. Behav. Sci. 2011, 16, 352–363. [Google Scholar] [CrossRef]
- Medina, A.M.F.; Tarko, A.P. Speed Changes in the Vicinity of Horizontal Curves on Two-Lane Rural Roads. J. Transp. Eng. 2007, 133, 215–222. [Google Scholar] [CrossRef]
- Gong, H.; Stamatiadis, N. Operating Speed Prediction Models for Horizontal Curves on Rural Four-Lane Highways. Transp. Res. Rec. 2008, 2075, 1–7. [Google Scholar] [CrossRef]
- Croatian Bureau of Statistics. Estimation of the Population of the Republic of Croatia in 2023; Croatian Bureau of Statistics: Zagreb, Croatia, 2024. Available online: https://podaci.dzs.hr/2024/hr/76804 (accessed on 10 March 2025).
- Croatian Bureau of Statistics. 1731 Tourism, 2023, Statistical Reports; Croatian Bureau of Statistics: Zagreb, Croatia, 2024; ISSN 1331-341X. Available online: https://podaci.dzs.hr/2024/hr/79000 (accessed on 10 March 2025).
- Republic of Croatia. Road Traffic Safety Act (Zakon o sigurnosti prometa na cestama). Narodne Novine 2020, 60, 1225. [Google Scholar]
- Ministry of the Sea, Transport and Infrastructure of the Republic of Croatia. Highways. Available online: https://mmpi.gov.hr/infrastruktura/prometna-infrastruktura-137/autoceste/8272 (accessed on 10 March 2025).
- Ministry of the Sea, Transport and Infrastructure of the Republic of Croatia. The Republic of Croatia Manages the Following Basic Traffic Infrastructure Network. Available online: https://mmpi.gov.hr/infrastruktura/prometna-infrastruktura-137/republika-hrvatska-raspolaze-sa-sljedecom-osnovnom-mrezom-prometne-infrastrukture/10402 (accessed on 10 March 2025).
- Croatian Roads Ltd. In Traffic Counting on the Roads of the Republic of Croatia, 2023; Croatian Roads Ltd.: Zagreb, Croatia, 2023; Available online: https://hrvatske-ceste.hr/uploads/documents/attachment_file/file/1804/Brojenje_prometa_na_cestama_Republike_Hrvatske_godine_2023.pdf (accessed on 10 March 2025).
- Kiss, B.; Ballagi, Á.; Kuczmann, M. An Efficiency Examination of the DJI Mavic 2 Pro’s Precision Landings. Preprints 2024. [Google Scholar] [CrossRef]
- Jovanović, B. Fundamental Probabilistic Traffic Flow Model for High-Performance Roads in the Republic of Croatia. Ph.D Thesis, University of Zagreb, Zagreb, Croatia, 2024. [Google Scholar]
- Van Driel, C.J.G.; Davidse, R.J.; Van Maarseveen, M.F.A.M. The Effects of an Edgeline on Speed and Lateral Position: A Meta-Analysis. Accid. Anal. Prev. 2004, 36, 671–682. [Google Scholar] [CrossRef]
- Boroujerdian, A.M.; Seyedabrishami, E.; Akbarpour, H. Analysis of Geometric Design Impacts on Vehicle Operating Speed on Two-Lane Rural Roads. Procedia Eng. 2016, 161, 1144–1151. [Google Scholar] [CrossRef]
- Yan, Y.; Li, G.; Tang, J.; Guo, Z. A Novel Approach for Operating Speed Continuous Prediction Based on Alignment Space Comprehensive Index. J. Adv. Transp. 2017, 2017, 9862949. [Google Scholar] [CrossRef]
- Li, Y.F.; Chen, M.N.; Lu, X.D.; Zhao, W.Z. Research on Optimized GA-SVM Vehicle Speed Prediction Model Based on Driver-Vehicle-Road-Traffic System. Sci. China Technol. Sci. 2018, 61, 782–790. [Google Scholar] [CrossRef]
- Croatia. Ordinance on Basic Conditions That Public Roads Outside Settlements and Their Elements Must Meet from the Point of View of Traffic Safety (OG 110/2001 and 90/2022); Ministry of the Sea, Transport and Infrastructure: Zagreb, Croatia, 2022.
- Martinelli, V.; Ventura, R.; Bonera, M.; Barabino, B.; Maternini, G. Estimating Operating Speed for County Road Segments—Evidence from Italy. Int. J. Transp. Sci. Technol. 2022, 12, 560–577. [Google Scholar] [CrossRef]
- Charef, A.; Jarir, Z.; Quafafou, M. The Impact of Pedestrian Crossings on Speed Patterns and Roundabout Capacity. Int. J. Sci. Res. Innov. Stud. 2024, 3, 13–20. [Google Scholar]
- Prakash, C.M.; Navandar, Y.V.; Golakiya, H.D.; Dhamaniya, A. Analysis of the Impact of Pedestrian Crossing Activity on Traffic Characteristics at Urban Midblock Sections Using a Simulation Technique. In Recent Advances in Transportation Systems Engineering and Management; Anjaneyulu, M.V.L.R., Harikrishna, M., Arkatkar, S.S., Veeraragavan, A., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2023; Volume 261. [Google Scholar] [CrossRef]
- Aram, A. Effective Safety Factors on Horizontal Curves of Two-Lane Highways. J. Appl. Sci. 2010, 10, 2814–2822. [Google Scholar] [CrossRef][Green Version]
- Liu, S.; Wang, J.; Fu, T. Effects of Lane Width, Lane Position, and Edge Shoulder Width on Driving Behavior in Underground Urban Expressways: A Driving Simulator Study. Int. J. Environ. Res. Public Health 2016, 13, 1010. [Google Scholar] [CrossRef]
- Gaddam, H.K.; Rao, K.R. Speed–Density Functional Relationship for Heterogeneous Traffic Data: A Statistical and Theoretical Investigation. J. Mod. Transp. 2019, 27, 61–74. [Google Scholar] [CrossRef]
- Croatian Bureau of Metrology. Ordinance on Metrological and Technical Requirements for Speedometers in Road Traffic; Official Gazette 60/2020; Croatian Bureau of Metrology: Zagreb, Croatia, 2020.




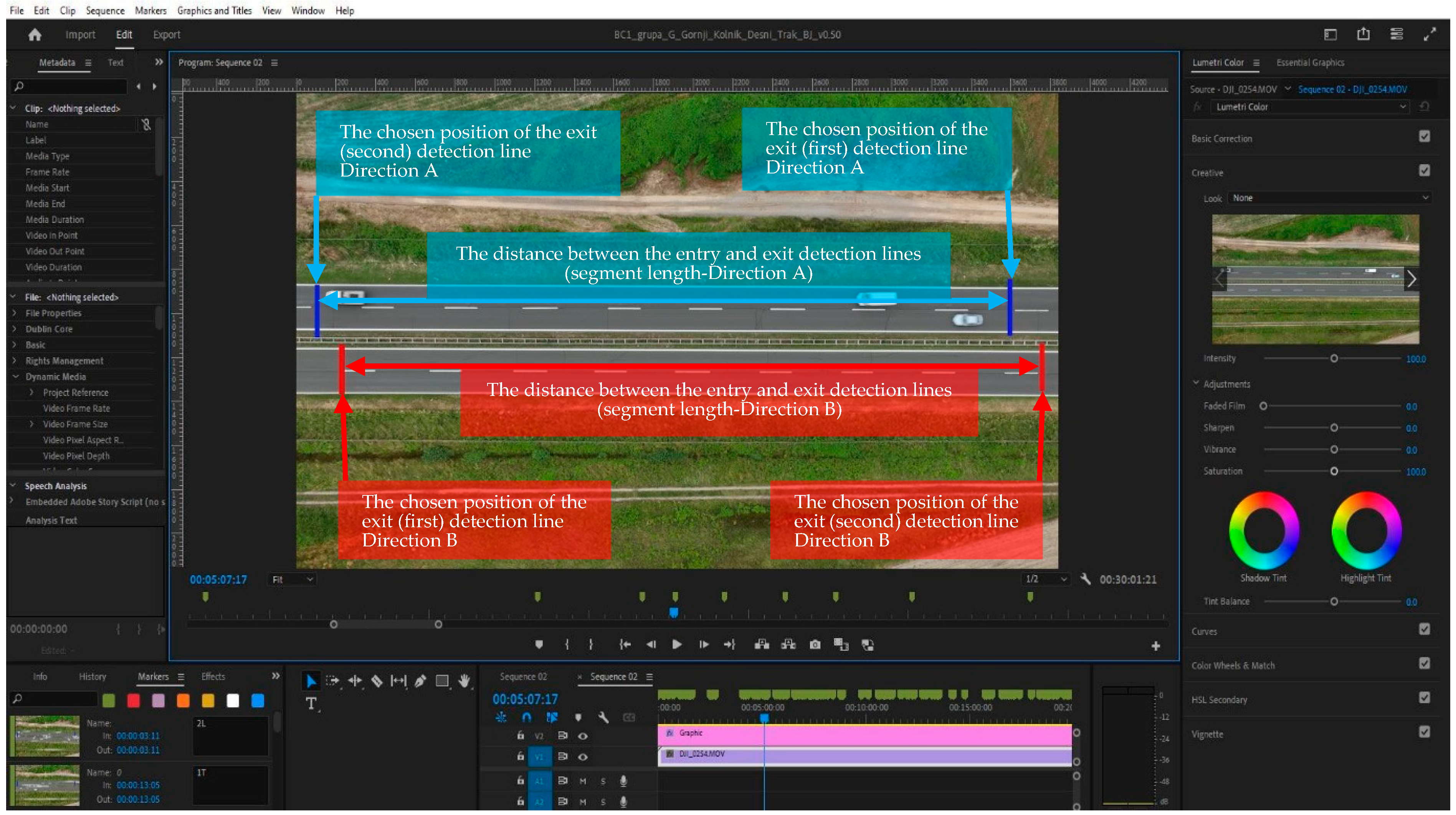
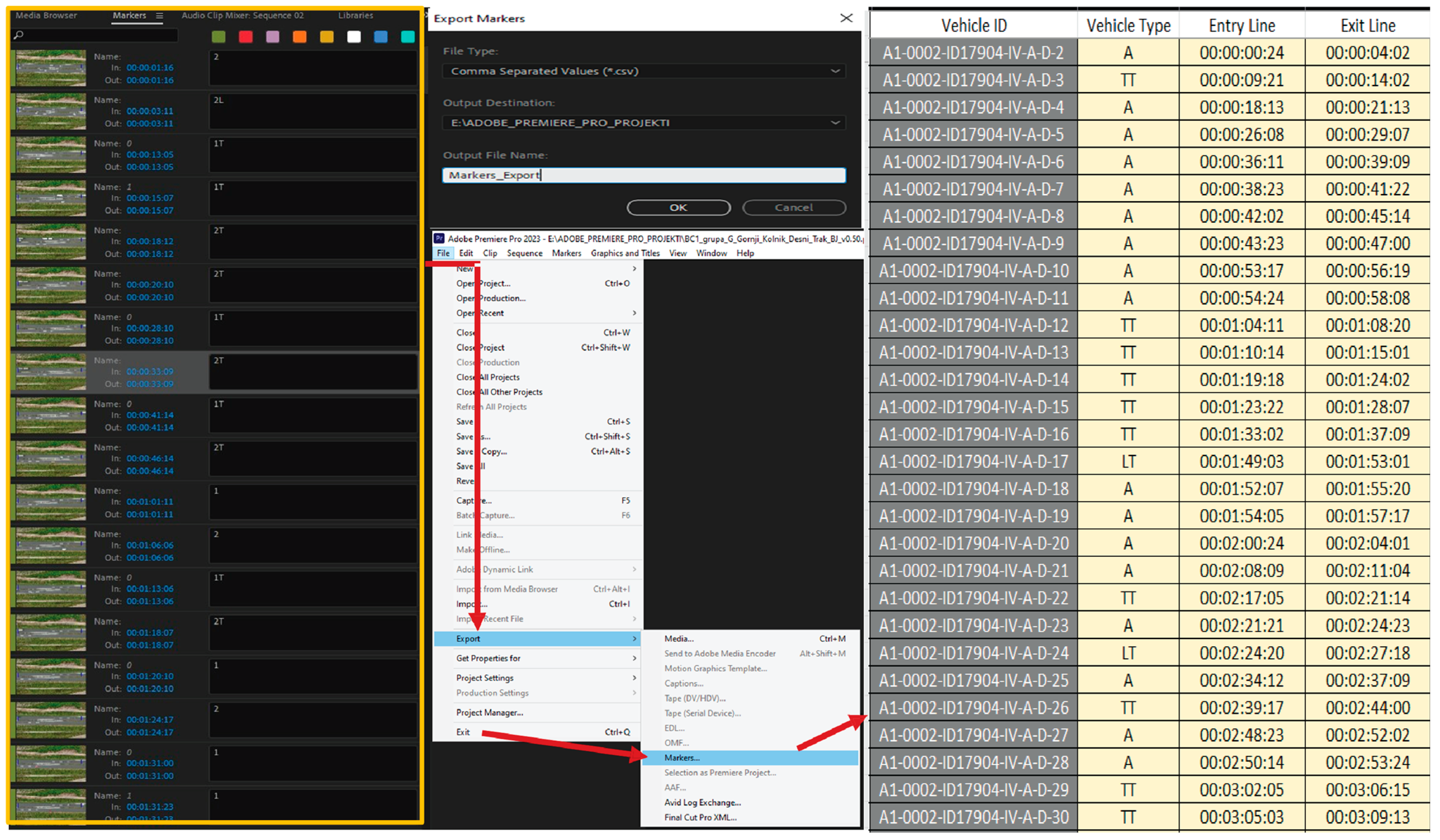


| Road Name | Carriageway/Direction | Aerial Video Recording Date | Off-Peak Hour Selected for Recording |
|---|---|---|---|
| Motorway A1 | Bisko–Blato na Cetini | Monday, 31 July 2023 | 12:00–13:00 |
| Blato na Cetini–Bisko | |||
| Motorway A1 | Bosiljevo 2–Ogulin | Tuesday, 18 July 2023 | 13:00–14:00 |
| Ogulin–Bosiljevo 2 | |||
| Motorway A1 | Donja Zdenčina–Jastrebarsko | Tuesday, 11 July 2023 | 18:45–19:45 |
| Jastrebarsko–Donja Zdenčina | |||
| Motorway A1 | Gornja Ploča–Gospić | Tuesday, 18 July 2023 | 07:00–08:00 |
| Gospić–Gornja Ploča | |||
| Motorway A1 | Zadar Center–Zadar East | Tuesday, 8 August 2023 | 12:00–13:00 |
| Zadar East–Zadar Center | |||
| Motorway A2 | Zabok–Zaprešić | Tuesday, 11 July 2023 | 18:45–19:45 |
| Zaprešić–Zabok | |||
| Motorway A3 | Babina Greda–Županja | Monday, 24 July 2023 | 18:30–19:30 |
| Županja–Babina Greda | |||
| Motorway A3 | Križ–Popovača | Wednesday, 12 July 2023 | 06:00–07:00 |
| Popovača–Križ | |||
| Motorway A3 | Lužani–Nova Gradiška | Monday, 24 July 2023 | 13:00–14:00 |
| Nova Gradiška–Lužani | |||
| Motorway A6 | Delnice–Ravna Gora | Monday, 7 July 2023 | 18:30–19:30 |
| Ravna Gora–Delnice |
| Factors—Single-Carriageway Roads | Type | Normal Distribution | Test Used |
|---|---|---|---|
| Passenger side | Categorical—Multi-level | --- | ANOVA |
| Shoulder type | Categorical—Multi-level | --- | ANOVA |
| Edge line quality | Categorical—Multi-level | --- | ANOVA |
| Visibility | Categorical—Multi-level | --- | ANOVA |
| Pavement quality | Categorical—Multi-level | --- | ANOVA |
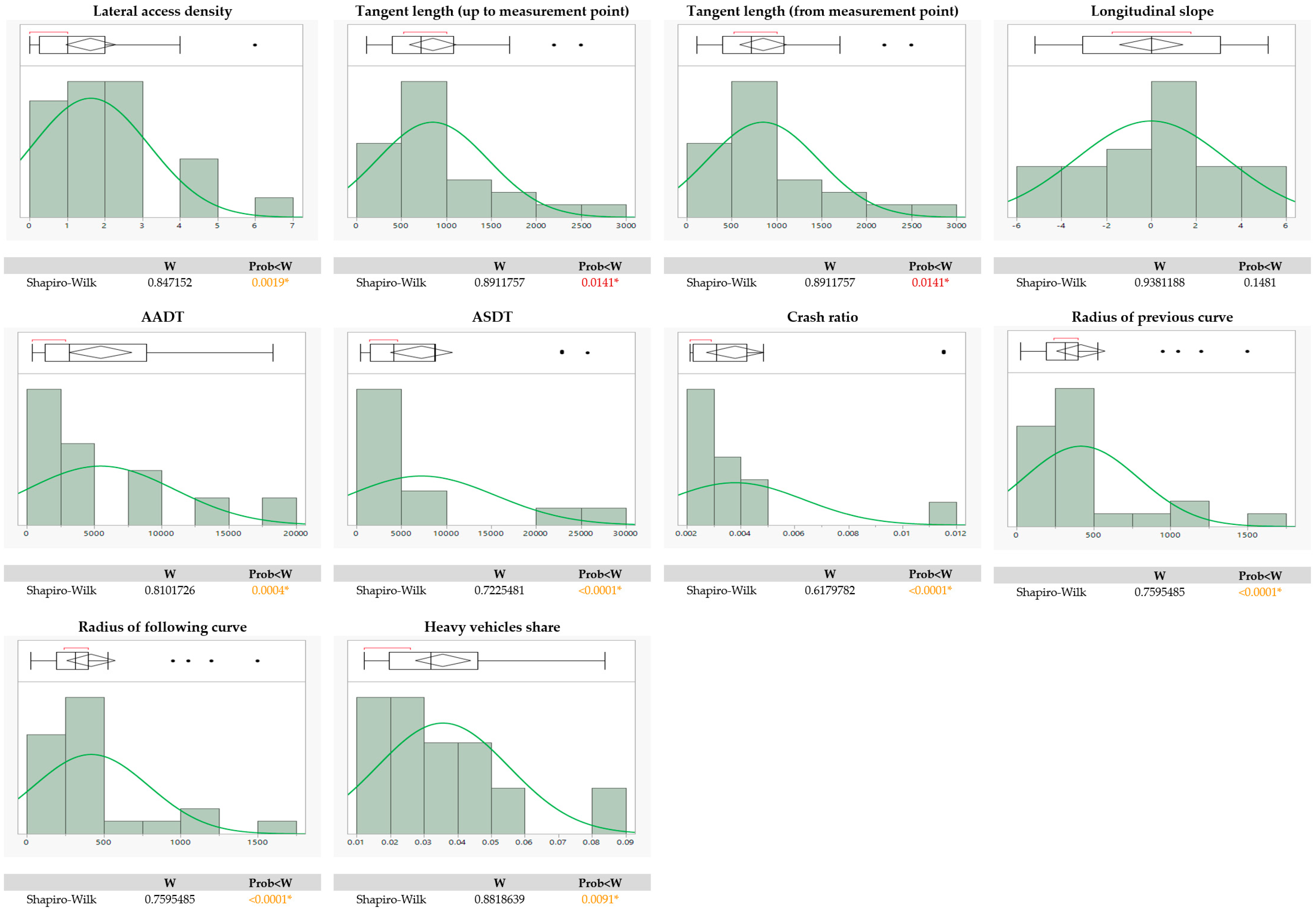
| Lateral access density | Continuous | NO | Spearman |
| Tangent length (up to measurement point) | Continuous | NO | Spearman |
| Tangent length (from measurement point) | Continuous | NO | Spearman |
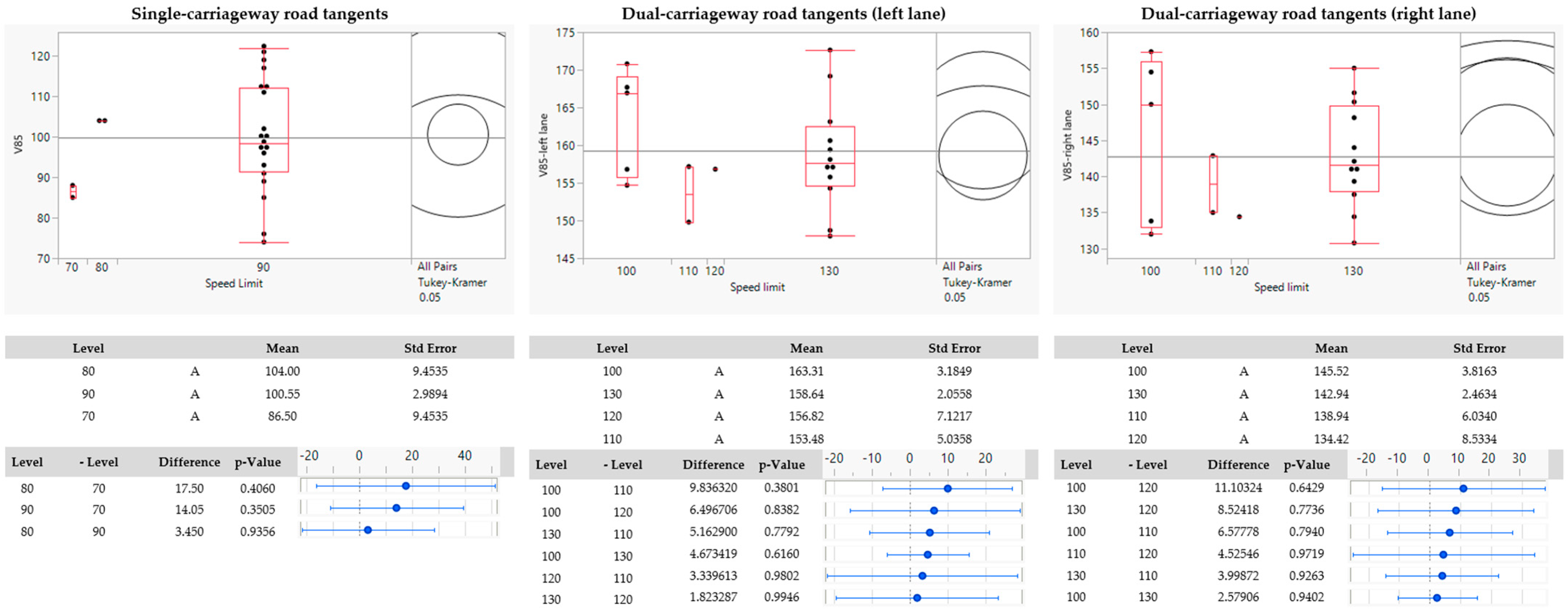
| Speed limit | Categorical—Multi-level | --- | ANOVA |
| AADT | Continuous | NO | Spearman |
| ASDT | Continuous | NO | Spearman |
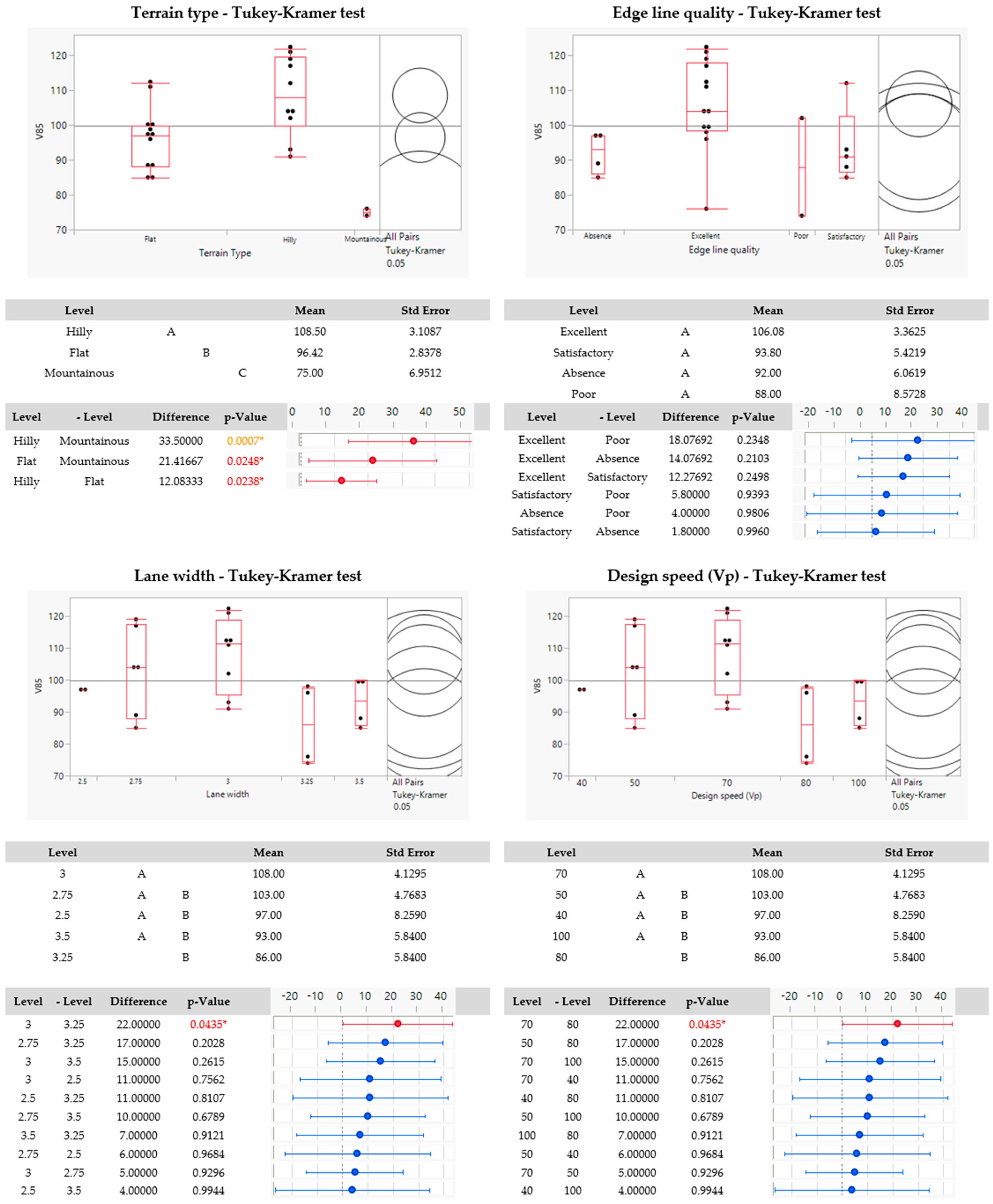
| Lane width | Categorical—Multi-level | --- | ANOVA |
| Longitudinal slope | Continuous | YES | Pearson |
| Crash ratio | Continuous | NO | Spearman |
| Design speed | Categorical—Multi-level | --- | ANOVA |
| Terrain type | Categorical—Multi-level | --- | ANOVA |
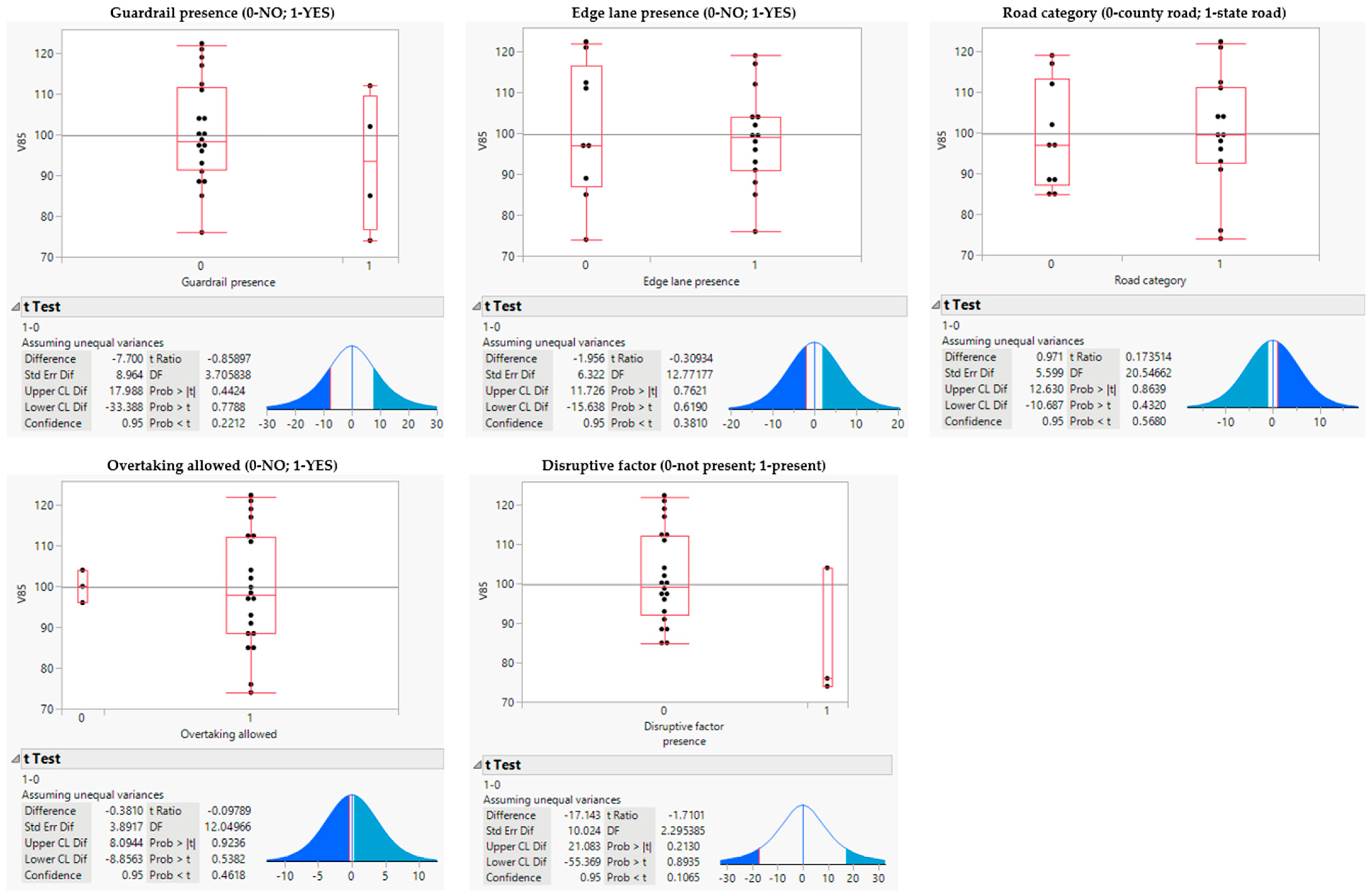
| Guardrail presence | Binary | --- | t-test |
| Shoulder lane presence | Binary | --- | t-test |
| Radius of previous curve | Continuous | NO | Spearman |
| Radius of following curve | Continuous | NO | Spearman |
| Road category | Binary | --- | t-test |
| Overtaking allowed | Binary | --- | t-test |
| Heavy goods vehicles share | Continuous | NO | Spearman |
| Disruptive factor presence | Binary | --- | t-test |
| Continuous Factors Single-Carriageway Roads | Test Used | Pearson Coefficient/Spearman’s ρ | Significance Level (p-Value) |
|---|---|---|---|
| Lateral access density | Spearman | −0.0540 | 0.8020 |
| Tangent length (up to measurement point) | Spearman | 0.1076 | 0.6168 |
| Tangent length (from measurement point) | Spearman | 0.1568 | 0.4643 |
| AADT | Spearman | −0.3970 | 0.0547 |
| ASDT | Spearman | −0.3412 | 0.1028 |
| Longitudinal slope | Pearson | −0.03352 | 0.8764 |
| Crash ratio | Spearman | 0.3628 | 0.0815 |
| Radius of previous curve | Spearman | 0.3242 | 0.1222 |
| Radius of following curve | Spearman | 0.3349 | 0.1097 |
| Heavy goods vehicles share | Spearman | 0.0829 | 0.7002 |
| Factors—Dual-Carriageway Roads | Type | Normal Distribution | Test Used |
|---|---|---|---|
| Total tunnel length in last 20 km | Continuous | NO | Spearman |
| Speed limit | Categorical—Multi-level | --- | ANOVA |
| Lane width | Categorical—Multi-level | --- | ANOVA |
| Design speed | Categorical—Multi-level | --- | ANOVA |
| Emergency lane presence | Binary | --- | t-test |
| Previous object distance | Continuous | YES | Pearson |
| Following object distance | Continuous | YES | Pearson |
| Longitudinal slope | Continuous | YES | Pearson |
| Terrain type | Categorical—Multi-level | --- | ANOVA |
| Heavy goods vehicles share (left lane) | Continuous | NO | Spearman |
| Heavy goods vehicles share (right lane) | Continuous | YES | Pearson |
| Heavy goods vehicles share (both lanes) | Continuous | YES | Pearson |
| AADT | Continuous | NO | Spearman |
| ASDT | Continuous | NO | Spearman |
| Traffic flow density (left lane) | Continuous | NO | Spearman |
| Traffic flow density (right lane) | Continuous | YES | Pearson |
| Continuous Factors Dual-Carriageway Roads—Left (Overtaking) Lane | Test Used | Pearson Coefficient/Spearman’s ρ | Significance Level (p-Value) |
|---|---|---|---|
| Total tunnel length in last 20 km | Spearman | −0.2194 | 0.3527 |
| Previous object distance | Pearson | 0.170952 | 0.4711 |
| Following object distance | Pearson | 0.188981 | 0.4249 |
| Longitudinal slope | Pearson | −0.1876 | 0.4283 |
| Heavy goods vehicles share (left lane) | Spearman | 0.6152 | 0.0039 * |
| Heavy goods vehicles share (right lane) | Pearson | 0.115168 | 0.6287 |
| Heavy goods vehicles share (both lanes) | Pearson | 0.284816 | 0.2236 |
| AADT | Spearman | −0.1117 | 0.6392 |
| ASDT | Spearman | −0.4649 | 0.0389 * |
| Traffic flow density (left lane) | Spearman | −0.7434 | 0.0002 * |
| Traffic flow density (right lane) | Pearson | −0.66612 | 0.0013 * |
| Continuous Factors Dual-Carriageway Roads—Right (Driving) Lane | Test Used | Pearson Coefficient/Spearman’s ρ | Significance Level (p-Value) |
|---|---|---|---|
| Total tunnel length in last 20 km | Spearman | −0.2095 | 0.3754 |
| Previous object distance | Pearson | 0.25115 | 0.2855 |
| Following object distance | Pearson | 0.083631 | 0.7259 |
| Longitudinal slope | Pearson | −0.10003 | 0.6748 |
| Heavy goods vehicles share (left lane) | Spearman | 0.2591 | 0.2700 |
| Heavy goods vehicles share (right lane) | Pearson | 0.25593 | 0.2761 |
| Heavy goods vehicles share (both lanes) | Pearson | 0.430092 | 0.0584 |
| AADT | Spearman | −0.3170 | 0.1733 |
| ASDT | Spearman | −0.5525 | 0.0115 * |
| Traffic flow density (left lane) | Spearman | −0.7901 | <0.0001 * |
| Traffic flow density (right lane) | Pearson | −0.70432 | 0.0005 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vertlberg, J.L.; Jakovljević, M.; Abramović, B.; Ševrović, M. Determining Factors Influencing Operating Speeds on Road Tangents. Appl. Sci. 2025, 15, 7549. https://doi.org/10.3390/app15137549
Vertlberg JL, Jakovljević M, Abramović B, Ševrović M. Determining Factors Influencing Operating Speeds on Road Tangents. Applied Sciences. 2025; 15(13):7549. https://doi.org/10.3390/app15137549
Chicago/Turabian StyleVertlberg, Juraj Leonard, Marijan Jakovljević, Borna Abramović, and Marko Ševrović. 2025. "Determining Factors Influencing Operating Speeds on Road Tangents" Applied Sciences 15, no. 13: 7549. https://doi.org/10.3390/app15137549
APA StyleVertlberg, J. L., Jakovljević, M., Abramović, B., & Ševrović, M. (2025). Determining Factors Influencing Operating Speeds on Road Tangents. Applied Sciences, 15(13), 7549. https://doi.org/10.3390/app15137549









