Fuzzy-Based Control System for Solar-Powered Bulk Service Queueing Model with Vacation

Featured Application

This study highlights the effects of fuzzy-based control on key performance metrics, including queue stability, waiting time, and system utilization. The results can be used to enhance operational efficiency and service continuity compared to traditional queueing, with obvious advantages.

Abstract

This study proposes a Fuzzy-Based Control System (FBCS) for a Bulk Service Queueing Model with Vacation, designed to optimize service performance by dynamically adjusting system parameters. The queueing model is categorized into three service levels: (A) High Bulk Service, where a large number of arrivals are processed simultaneously; (B) Medium Single Service, where individual packets are handled at a moderate rate; and (C) Low Vacation, where the server takes minimal breaks to maintain efficiency. The Mamdani Inference System (MIS) is implemented to regulate key parameters, such as service rate, bulk size, and vacation duration, based on input variables including queue length, arrival rate, and server utilization. The Mamdani-based fuzzy control mechanism utilizes rule-based reasoning to ensure adaptive decision-making, effectively balancing system performance under varying conditions. By integrating bulk service with a controlled vacation policy, the model achieves an optimal trade-off between processing efficiency and resource utilization. This study examines the effects of fuzzy-based control on key performance metrics, including queue stability, waiting time, and system utilization. The results indicate that the proposed approach enhances operational efficiency and service continuity compared to traditional queueing models.

1. Introduction

Queueing systems are vital tools for optimizing resource utilization and managing fluctuating service demands across various operational environments. However, traditional queueing models typically rely on static service mechanisms, limiting their ability to respond to dynamic changes in system conditions such as traffic intensity, arrival rates, and resource availability.

To overcome this limitation, this study proposes a Fuzzy-Based Control System (FBCS) for a Bulk Service Queueing Model with Vacation, designed to enhance system performance through real-time, adaptive parameter adjustments. In this framework, the service process is categorized into three operational levels:

(A)

High Bulk Service: Multiple arrivals are processed in batches to increase throughput during peak periods.

(B)

Medium Single Service: Individual customers are served at a steady, moderate rate under normal loads.

(C)

Low Vacation: The server takes minimal rest breaks to maintain continuous operation during low-demand periods.

The decision-making mechanism is driven by a Fuzzy Inference System (FIS), which responds to real-time input variables such as queue length, arrival rate, and server utilization. By adjusting the service rate, batch size, and vacation duration, the fuzzy logic controller enables the system to adapt fluidly to changing conditions, improving responsiveness and overall stability compared to rigid, rule-based queueing models.

Fuzzy control has a proven track record in engineering systems. In 1985, Seiji Yasunobu and Soji Miyamoto demonstrated its effectiveness in railway simulations, leading to successful deployment in the Sendai line by 1987. Around the same time, Takeshi Yamakawa’s use of dedicated fuzzy logic chips in an “inverted pendulum” experiment showcased the potential of fuzzy systems for real-time control in uncertain environments.

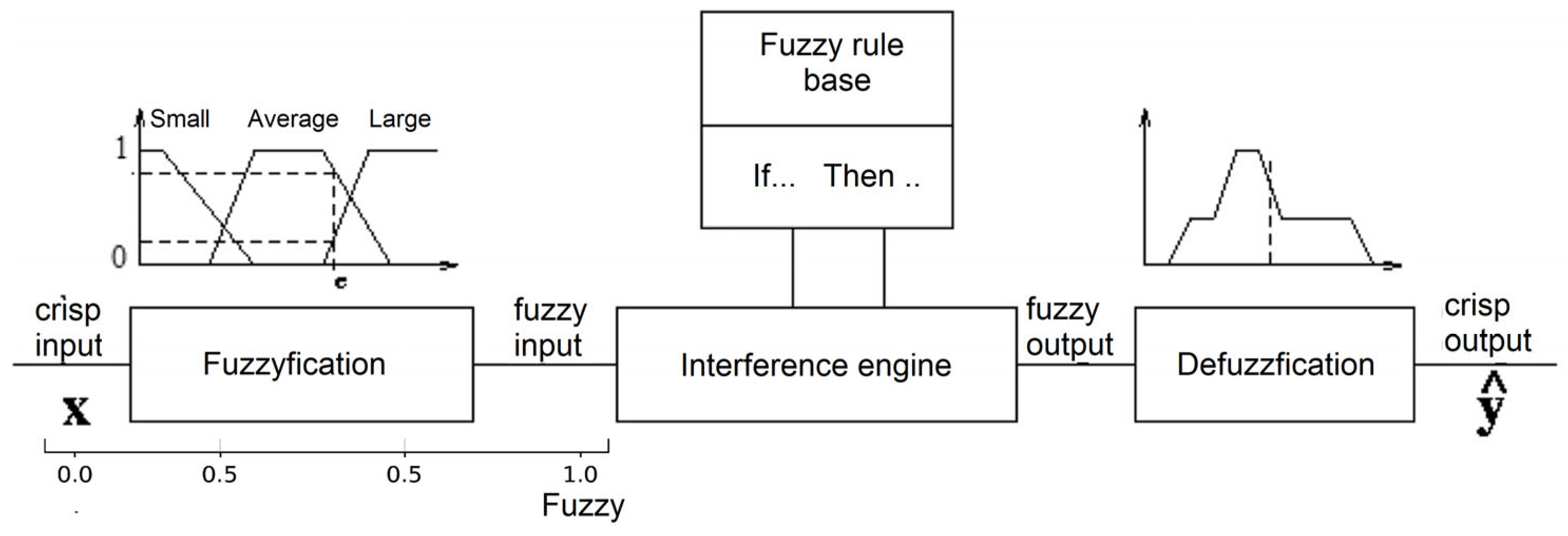
This research evaluates the impact of fuzzy-based control on critical performance metrics, including queue stability, average waiting time, and server utilization. The simulation results highlight the system’s ability to optimize service efficiency while maintaining a balanced trade-off between speed and resource allocation. The paper is organized as follows: model formulation, fuzzy logic design, performance evaluation, and comparative analysis, followed by an illustration of the fuzzy inference process and a discussion of its practical implications. An example of the Fuzzy Inference System is as follows (Figure 1):

Fuzzy logic and queueing models have been extensively studied for their applications in optimizing decision-making and service efficiency.

Research Hypotheses

This study investigates the effectiveness of a fuzzy inference-based control system for optimizing [insert system, e.g., QoS in 4G/5G networks]. The hypotheses are framed as follows:

H1. 

A fuzzy logic controller incorporating adaptive membership functions significantly improves system responsiveness under dynamic load conditions.

H2. 

The inclusion of α-cut optimization enhances the precision of fuzzy decision-making compared to standard inference without α-level processing.

H3. 

The integration of multi-level fuzzy rules (high, medium, low priority) results in better output regulation than single-level rule sets.

These hypotheses are evaluated through simulation and performance analysis of the proposed fuzzy model under varied input scenarios.

2. Literature Review

Mamdani and Assilian [1] developed a fuzzy logic controller that utilized linguistic rules, demonstrating its effectiveness in automated decision-making processes. In the healthcare domain, Hepshiba and Julia Rose Mary [2] applied queueing models to enhance patient flow and resource allocation, highlighting the importance of service optimization. Further advancements in queueing theory were made by Rao et al. [3], who analyzed a batch arrival two-phase M^x/M//1 queueing system with impatient customers and an unreliable server, addressing key challenges in service reliability. Additionally, Shen et al. [4] applied a fuzzy multi-criteria approach to evaluate green suppliers’ performance, showcasing the effectiveness of fuzzy logic in complex decision-making scenarios. Collectively, these studies emphasize the integration of fuzzy logic and queueing models in enhancing service quality, reliability, and efficiency, making them particularly relevant for optimizing 4G/5G network performance. Zadeh [5] introduced the foundational concept of fuzzy sets, providing a mathematical framework to model uncertainty and vagueness in complex systems. This pioneering work laid the groundwork for fuzzy logic applications in control systems, decision-making, and queuing models.

Štěpnička and Mandal [6] focused on theoretical advancements by developing Fuzzy Inference Systems that preserve Moser–Navara axioms, ensuring consistency and reliability in fuzzy reasoning. Xu et al. [7] extended fuzzy control applications by proposing an observer-based fuzzy adaptive predefined time control for uncertain nonlinear systems, addressing full-state error constraints and improving control accuracy under uncertainty. Saihi and Berbaoui [8] explored the integration of fuzzy logic with neural networks and sliding mode control, developing a hybrid neuro-fuzzy integral sliding mode control technique for optimizing Unified Power Quality Conditioners (UPQCs) in solar energy systems. Collectively, these studies demonstrate the growing sophistication of fuzzy logic applications in control systems, energy management, and nonlinear system modeling, further strengthening its relevance in optimizing complex and uncertain environments, including 4G/5G network management.

Fuzzy logic has evolved significantly since its inception, with various studies contributing to its theoretical advancements and practical applications. Mamdani [9] pioneered the application of fuzzy algorithms for controlling dynamic systems, laying the foundation for modern fuzzy control techniques. Takagi and Sugeno [10] further advanced the field by introducing a fuzzy identification approach for system modeling and control, which has since become a fundamental method in fuzzy system design.

Fuzzy logic has been widely explored in various applications, ranging from signal processing to renewable energy prediction and advanced control systems. Wei and Mendel [11] introduced a fuzzy logic-based method for modulation classification in non-ideal environments, demonstrating its effectiveness in handling uncertainty in communication systems. Iqdour and Zeroual [12] applied fuzzy rule-based modeling for predicting daily solar radiation, highlighting the adaptability of fuzzy logic in renewable energy forecasting. Similarly, Safi and Zeroual [13] utilized high-order statistical modeling for solar data analysis, emphasizing the need for advanced mathematical techniques in energy-related predictions. Sala et al. [14] provided a broad perspective on fuzzy systems and control, discussing their theoretical developments and practical implications in various fields, including automation and decision-making. Zadeh [15] extended the concept of fuzzy sets by introducing possibility theory, further expanding the scope of fuzzy logic in uncertainty modeling and reasoning. Collectively, these studies demonstrate the versatility of fuzzy logic in communication, renewable energy, and control systems, reinforcing its significance in optimizing complex, uncertain environments such as 4G/5G networks.

Fuzzy logic continues to advance in various domains, including engineering, artificial intelligence, robotics, and computational mathematics. Sheena et al. [16] conducted a comprehensive study on Fuzzy Inference Systems and their applications in engineering, highlighting their role in decision-making and control systems. Cao et al. [17] explored the integration of Fuzzy Inference Systems with explainable artificial intelligence (XAI) for disease diagnosis, emphasizing the importance of interpretable fuzzy rules in medical decision-making. Valdez et al. [18] reviewed the application of type-2 fuzzy systems in robotics and discussed the potential of type-3 fuzzy logic, demonstrating its relevance in autonomous and intelligent robotic systems. Wu et al. [19] provided insights into type-1 and interval type-2 fuzzy systems, offering a comparative analysis of their applicability in artificial intelligence and computational intelligence. Behera and Chakraverty [20] introduced a computational technique for solving imprecisely defined fully fuzzy algebraic systems, contributing to mathematical advancements in fuzzy logic applications. In [21,22], the intersection of fuzzy logic and mathematics, focuses on its applications in various scientific and engineering problems. Collectively, these studies underscore the growing significance of fuzzy logic in enhancing interpretability, automation, and computational efficiency across multiple disciplines, reinforcing its potential for optimizing complex systems such as 4G/5G networks.

In a solar-powered microgrid energy distribution system, energy requests from consumers can be managed using an M/M/c queueing model with bulk service and vacation to optimize power allocation. During periods of high solar energy production, the system operates in High Bulk Service Mode, distributing power in bulk to multiple consumers efficiently. When solar availability is moderate, the system switches to Single Service Mode, prioritizing energy distribution based on predefined priority queues. In low or no solar generation conditions, such as at night or during cloudy weather, the system enters Vacation Mode, where specific grid components shut down, and battery storage provides limited energy until solar generation resumes. This approach ensures efficient energy management, balancing supply and demand dynamically.

2.1. Comparison: FBCS vs. Hybrid Fuzzy Models

This paper presents a Fuzzy-Based Control System (FBCS) model tailored for solar-powered queueing systems and is structured as follows (see

Table 1. Fuzzy-Based Control System (FBCS) model.

Criteria	Fuzzy-Based Control System (FBCS)	Hybrid Fuzzy Models (e.g., ANFIS, Fuzzy-NN, Sugeno-GA)
Adaptability	High—Dynamically adjusts service rate, bulk size, and vacation based on input data	Moderate—Requires retraining or offline tuning to adapt to changing conditions
Interpretability	Excellent—Rule-based Mamdani structure allows transparent decision-making	Low—Operates as a black box; rules and outputs are difficult to trace
Uncertainty Handling	Robust—Uses α-cut analysis with P-NLP to quantify fuzzy output ranges	Limited—Typically uses fixed defuzzification without formal uncertainty bounds
Real-Time Performance	Optimized for real-time, adaptive queue control in solar-powered systems	Slower—High computational demand, not always suited for real-time applications
Energy-Aware Control	Explicitly integrates solar power availability in decision logic	Generally lacks dedicated energy inputs or control mechanisms
Data Requirements	Low—Relies on expert knowledge and simulations rather than large datasets	High—Needs significant training data for model accuracy
Application Suitability	Ideal for solar-powered queueing and telecom systems under dynamic conditions	Suitable for static environments with rich data but limited responsiveness

): Section 3 introduces the system notations, Section 4 describes the materials and methods including fuzzification and uncertainty modeling, Section 5 presents the performance evaluation and results, Section 6 provides a case study for real-world validation, and Section 7 concludes with key findings and directions for future research.

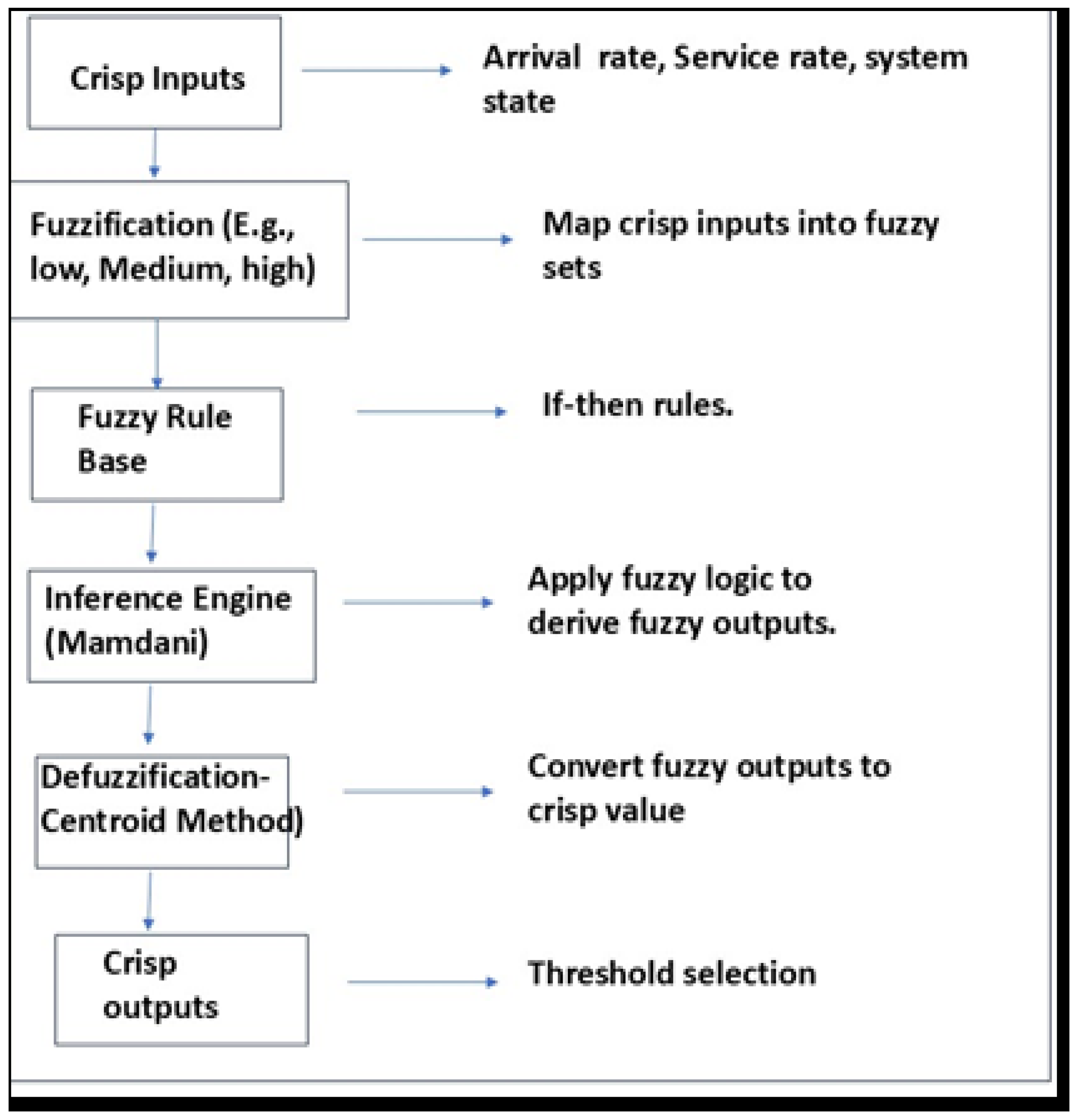
2.2. Methodology Workflow

[Input Variables]

↓

[Fuzzification Module]

↓

[Fuzzy Rule Base] ← [α-Cut Decision Layer (optional for fuzzy set slicing)]

↓

[Inference Engine (e.g., Mamdani)]

↓

[Defuzzification (e.g., Centroid)]

↓

[Output Variables]

3. Materials and Methods

3.1. Definitions

3.1.1. TFN (Triangular Fuzzy Number)

A type of fuzzy number represented by a triplet (l, m, u), where l is the lower bound, m is the most likely value (mode), and u is the upper bound. It is used to model uncertainty in parameters by assigning a fuzzy range instead of a crisp value.

3.1.2. P-NLP (Parametric Nonlinear Programming)

This is an optimization method where the objective function or constraints are nonlinear and include parameters (e.g., α-cuts in fuzzy systems). It is used to compute performance bounds under fuzziness by solving optimization problems at different confidence levels.

3.1.3. FLC (Fuzzy Logic Controller)

This is a control system based on fuzzy logic that uses linguistic rules rather than mathematical models to map inputs to outputs. It is particularly useful for handling uncertainty and imprecision in complex systems like queuing networks or energy-aware controllers.

To develop a fuzzy-based Bulk Service Queueing Model with Vacation, we consider the following assumptions:

Customers arrive at the system following a Poisson process with a mean arrival rate $\chi$.

Arrivals are independent and occur randomly over time. The server provides bulk service with a maximum batch size per service. If the queue length is greater than or equal to $\beta$, the server serves a full batch. If the queue length is between α and $\beta$ (1 ≤ α ≤ $\beta$), the server initiates service with the available customers. Service time follows a general distribution with mean service rates: High Bulk Service a, Medium Single Service b, and Low Vacation c.

After completing a service cycle, the server takes a vacation if the queue length is below the threshold b. Vacation time follows a general distribution with mean vacation time θ. During the vacation period, arriving customers must wait until the server returns. A Mamdani fuzzy logic controller (FLC) is designed to dynamically optimize system performance by adjusting service parameters based on real-time conditions. The FLC takes three input variables: queue length, arrival rate, and server utilization, which are fuzzified into linguistic terms. Using a Mamdani inference system, a set of fuzzy rules is applied to determine the appropriate service batch size and vacation duration based on real-time queueing conditions. The fuzzy rule base is constructed using If-Then logic, where MIN-MAX operations evaluate rule strength, and the Centroid Method is used for defuzzification. This inference mechanism ensures adaptive decision-making, optimizing service efficiency while balancing system load and minimizing idle time.

3.2. Fuzzification Analysis

In a solar-powered system, the arrival rate of energy demands ($\chi$) and service rates a, b, and c are fuzzified to model sunlight fluctuations and battery efficiency. The trapezoidal fuzzy approach ensures smooth energy distribution, preventing sudden service disruptions.

We assume that the arrival rate $\chi$, High Bulk Service a, Medium Single Service b, and Low Vacation c are linguistic and imprecise and symbolized by the fuzzified parameters. $k_1=\chi ,k_2=a,k_3=b,k_4=c$. Let us consider that ${\xi }_{p_m}(x_m)$ denote the membership function (MFs) corresponding to fuzzified numbers (FNs)$p_m$, where m = 1, 2, 3, 4.

Thus, we get $p_m=\left\{\left(x_m,{\xi }_{P_m}(x_m)\right):x_m\in X_m, m=1,2,3,4\right\}$ where $X_m$ is the crisp universal set of $p_m$, m = 1, 2, 3, 4.

Let us assume the fuzzified indices $P_j$, where $P_1=E{L}_s,P_2=E{W}_s,P_3=TP$. Thus,

${\xi }_{P_j}(z)=\mathit{supmin}\left\{{\xi }_{P_j}(x_m)/z=P_j, m=1,2,3,4; j=1,2,3\right\}$.

We shall employ the parametric nonlinear program (P-NLP) to find $\alpha$-cuts corresponding of $P_j$ based on the Zadeh extension principle [15].

The α-cut and P-NLP approach was chosen over basic fuzzy arithmetic due to its higher precision in handling non-linear relationships and uncertainty propagation in tandem queuing systems. Simpler methods often yield over-conservative or imprecise bounds. To improve clarity, we have added intuitive explanations and included graphs illustrating α-cut sensitivity and performance metric variation across confidence levels.

3.2.1. Fuzzy Rule Base and Membership Functions

To capture system uncertainty and enable adaptive decision-making, a Mamdani-type Fuzzy Inference System was employed. The input variables are fuzzified into linguistic terms, and a rule base is defined to relate input conditions to control outputs.

Input Variables:

• Queue Length (QL): Short, Medium, Long
• Server Status (SS): Idle, Busy, Broken
• Arrival Rate (AR): Low, Moderate, High

Output Variable:

• Service Adjustment (SA): Decrease, Maintain, Increase

In

Table 2. Fuzzy rule base.

Rule No.	Queue Length	Server Status	Arrival Rate	Service Adjustment
1	Short	Idle	Low	Decrease
2	Short	Busy	Moderate	Maintain
3	Medium	Busy	High	Increase
4	Long	Busy	High	Increase
5	Long	Broken	Moderate	Maintain
6	Medium	Idle	Low	Decrease
7	Long	Idle	High	Maintain
8	Short	Broken	Low	Decrease

Fuzzy Rule Base can be seen.

3.2.2. Threshold Design Justification

The transition thresholds for the three service modes—(A) High Bulk Service, (B) Medium Single Service, and (C) Low Vacation—were initially established using expert domain knowledge and refined through empirical simulation to maintain queue stability and minimize energy consumption under typical traffic and solar conditions. These thresholds define the fuzzy rule base, which dynamically adjusts service behavior in response to real-time variations in arrival rate, queue length, and solar energy availability. However, we acknowledge that the fixed nature of these thresholds may limit responsiveness during rapidly changing solar conditions (Figure 2). To address this, a promising enhancement involves integrating dynamic vacation thresholds based on real-time or forecasted solar irradiance. By anticipating fluctuations in solar power availability, the system could preemptively adjust vacation periods, enabling proactive energy management and further improving service continuity. This extension will be considered in future work, potentially through the incorporation of solar forecasting models within the fuzzy inference framework.

The figure displays four membership function (MF) graphs used in the Mamdani Fuzzy Inference System for the proposed FBCS:

• Arrival Rate: Defined over the range [4, 10], with linguistic terms Low, Medium, and High modeled using triangular MFs. This helps determine input traffic intensity.
• Queue Length: Spanning [0, 20], it includes Short, Medium, and Long queue states, used to assess congestion levels.
• Server Utilization: Ranges from [0, 1], with Low, Medium, and High MFs reflecting the current workload of the server.
• Service Mode: The output variable (Low = A, Medium = B, High = C) guiding the operational state—vacation, single, or bulk service—based on fuzzified input.

These MFs, designed via expert input and refined through fuzzy c-means clustering, form the foundation for rule evaluation and adaptive service control.

3.3. Parametric Nonlinear Program (P-NLP)

In a solar-powered queuing system, uncertainties in energy availability and server reliability due to weather fluctuations and renewable intermittency necessitate the use of fuzzy modeling. To handle these uncertainties, Parametric Nonlinear Programming (P-NLP) is used to derive membership functions for key performance metrics such as energy availability, service delay, and system reliability. These membership functions are often complex and non-analytic, making direct derivation impractical. Therefore, the α-cut approach is applied. For each α-level α∈ [0, 1], the fuzzy objective is decomposed into an interval defined by its lower and upper bounds, which are obtained by solving two crisp nonlinear programs.

The P-NLP formulations for determining the lower and upper bounds of the α-cuts of $p_m$, m = 1(1)5 are defined as follows:

$$p_m(\alpha )=\{x_m\in X/{\xi }_{p_m}(x_m)\ge \alpha \},m=1,2,3,4.$$

The $\alpha$-cuts of metrics $T_i$$\{P_1=E{L}_s,P_2=E{W}_s,P_3=TP\}$ are obtained using MFs ${\xi }_{p_m}(z)$ of $P_j$, where j = 1, 2, 3. The $\alpha$-cut of $p_m$, m = 1(1)5 is a crisp interval and can be obtained in the following form:

$$p_m(\alpha )=[{(x_m)}_{\alpha }^{LB},{(x_m)}_{\alpha }^{UB}]=[\underset{m\in p}{\min }\{{\xi }_{p_m}(x_m)\ge \alpha \},\max \{{\xi }_{p_m}(x_m)\ge \alpha \}]$$

(1)

Thus, the fuzzified model FM/FM/1 for the dual orbit imperfect service system reduces to an all-crisp M/M/1 dual orbit imperfect service model with different $\alpha$-cut sets $\{p_m(\alpha )/0<\alpha \le 1,m=1,2,3,4\}.$ To derive $P$, at least one of the following four situations holds such that ${\xi }_{P_j}(z)=\alpha$

$$\mathrm{I}. ({\xi }_{p_1}(x_1)=\alpha ,{\xi }_{p_2}(x_2)>\alpha ,{\xi }_{p_3}(x_3)>\alpha ,{\xi }_{p_4}(x_4)>\alpha )$$

(2)

$$\mathrm{II}. ({\xi }_{p_1}(x_1)>\alpha ,{\xi }_{p_2}(x_2)=\alpha ,{\xi }_{p_3}(x_3)>\alpha ,{\xi }_{p_4}(x_4)>\alpha )$$

(3)

$$\mathrm{III}. ({\xi }_{p_1}(x_1)>\alpha ,{\xi }_{p_2}(x_2)>\alpha ,{\xi }_{p_3}(x_3)=\alpha ,{\xi }_{p_4}(x_4)>\alpha )$$

(4)

$$\mathrm{IV}. ({\xi }_{p_1}(x_1)>\alpha ,{\xi }_{p_2}(x_2)>\alpha ,{\xi }_{p_3}(x_3)>\alpha ,{\xi }_{p_4}(x_4)=\alpha )$$

(5)

The shape function of ${\xi }_{P_j}(z)$ can be obtained from the above four situations through the lower bound (LB) and upper bound (UB).

$$\mathrm{Now}, {[P_j]}_{\alpha }^{LB}=\underset{x_m\in X_m/x_m>0}{\min }{P}_j\mathrm{and} {[P_j]}_{\alpha }^{UB}=\underset{x_m\in X_m/x_m>0}{\min }{P}_j,$$

(6)

where $P_1=E{L}_s$, $P_2=E{W}_s$, $P_3=TP$.

From Equation (5), one gets $[{(x_m)}_{{\alpha }_1}^{LB},({(x_m)}_{{\alpha }_1}^{UB}]\subseteq [{(x_m)}_{{\alpha }_2}^{LB},{(x_m)}_{{\alpha }_2}^{UB}],0<{\alpha }_2<{\alpha }_1\le 1$. To obtain the membership ${\xi }_{P_j}(z)$, it is sufficient to determine the shape function of ${\xi }_{P_j}(z)$ which is similar to $LB{[P_j]}_{\alpha }^{LB}$ and $UB{[P_j]}_{\alpha }^{UB}$, j = 1, 2, 3.

$$\mathrm{Now}, {[P_j]}_{\alpha }^{LB}=\underset{\{x_k\in X_K/x_k>0\}}{\min }{P}_j\mathrm{and} {[P_j]}_{\alpha }^{UB}=\underset{\{x_k\in X_K/x_k>0\}}{\max }{P}_j \mathrm{s}.\mathrm{t} x_k\in [{(x_k)}_{{\alpha }_1}^{LB},({(x_k)}_{{\alpha }_1}^{UB}],$$

(7)

At least one $y_k$(k = 1, 2, 3, 4) must attain the boundaries of the crisp intervals given in Equation (7). Here, ${[P_j]}_{\alpha }^{LB}$ is increasing and ${[P_j]}_{\alpha }^{UB}$ is decreasing with respect to “$\alpha$”; thus, $MF{\xi }_{P_j}(z)$ can be determined from (7). If both ${[P_j]}_{\alpha }^{LB}$ and ${[P_j]}_{\alpha }^{UB}$ are invertible with respect to “$\alpha$”, then $L(x)={({[P_j]}_{\alpha }^{LB})}^{-1}$, $R(x)={({[P_j]}_{\alpha }^{UB})}^{-1}$, where $P_1=E{L}_s$, $P_2=E{W}_s$, $P_3=TP$.

The left and right shape functions are given by

$${\xi }_{P_j}(x)=\left\{\begin{array}{c}L\left(x\right), {\left[P_j\right]}_{\propto =0}^{LB}x<{\left[P_j\right]}_{\propto =1}^{LB}\\ 1, {\left[P_j\right]}_{\propto =1}^{LB}x<{\left[P\right]}_{\propto =1}^{UB}\\ R(x), {\left[P_j\right]}_{\propto =0}^{UB}\le x<{\left[P_j\right]}_{\propto =1}^{UB}\end{array}\right.$$

(8)

where ${\left({(P_j)}_a^{LB}\right)}^{-1}=L(x)$ and ${\left({(P_j)}_a^{UB}\right)}^{-1}=R(x)$.

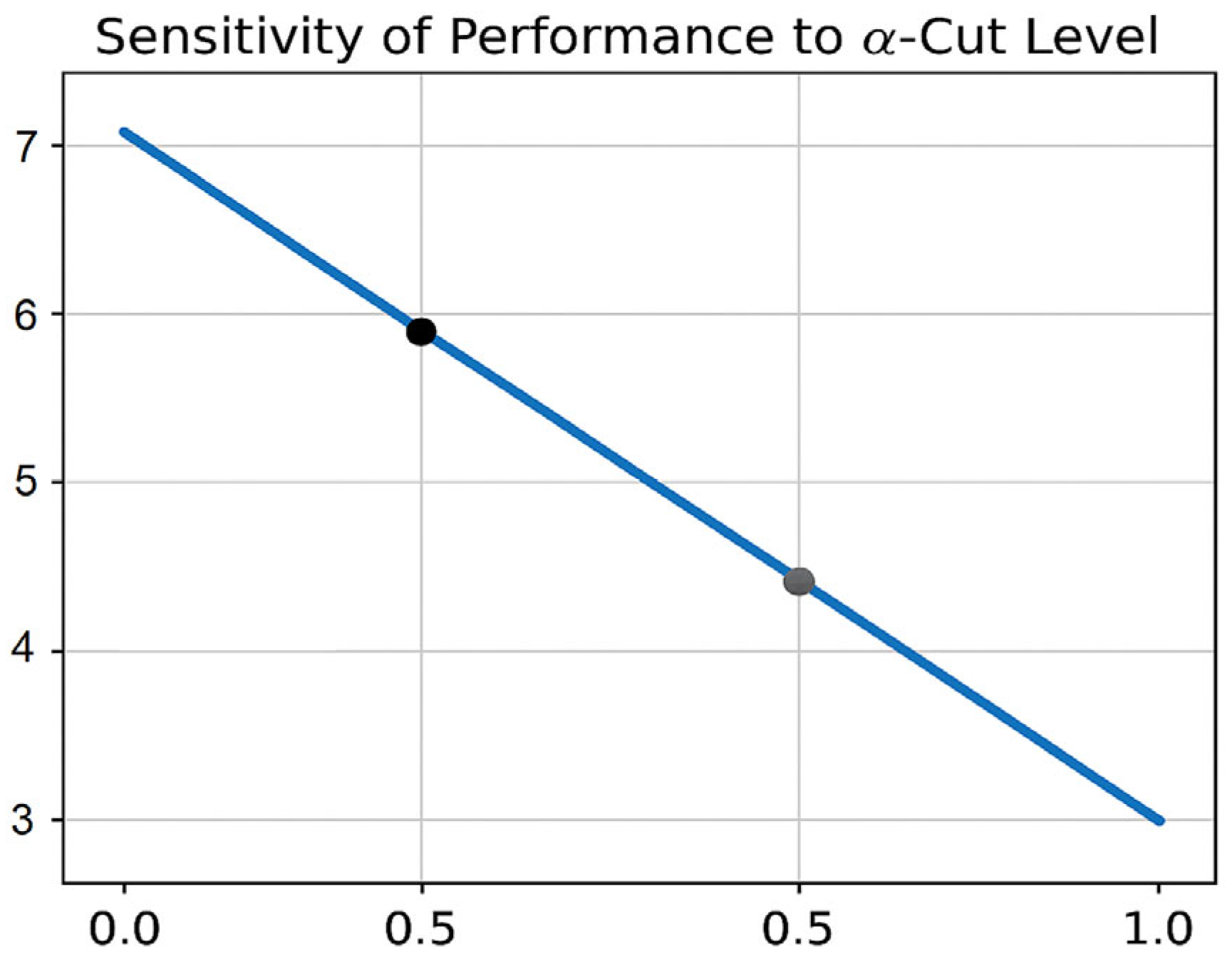
Figure 3 illustrates how the crisp performance output varies with different α-cut levels. As α increases from 0 to 1, uncertainty in the fuzzy output decreases, leading to more precise results. Lower α values include broader possibilities, yielding higher but less reliable performance estimates. Higher α levels focus on the core of the fuzzy set, producing more conservative and stable outputs. This highlights the trade-off between flexibility and certainty in fuzzy decision-making.

4. Results and Discussion

4.1. Numerical Results and Cost Optimization with Solar Power System Example

In this section, the accuracy and applicability of the analytical results derived in the previous section are verified through numerical examples. A comprehensive numerical experiment is performed to investigate the effects of key parameter values on the proposed model. The total cost function (TC) is computed using three distinct cost sets, as shown in

Table 3. Cost sets for energy management in a solar-powered BTS.

Cost Set	Infrastructure Cost	Battery Cost	Grid Power Cost	Maintenance Cost	Solar Panel Cost	Diesel Fuel Cost	Storage Cost	System Monitoring Cost
I	140	80	60	30	25	15	30	20
II	120	90	50	20	15	20	10	5
III	100	60	30	10	10	10	6	4

. The numerical outcomes for various performance metrics and cost analysis are summarized in

Table 4. α-cuts of fuzzified arrival rate (λ) and service rates (a, b, c).

$\mathit{\alpha }$	${\mathit{x}}_{1,\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathit{x}}_{1,\mathit{\alpha }}^{\mathit{U}\mathit{B}}$	${\mathit{x}}_{2,\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathit{x}}_{2,\mathit{\alpha }}^{\mathit{U}\mathit{B}}$	${\mathit{x}}_{3,\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathit{x}}_{3,\mathit{\alpha }}^{\mathit{U}\mathit{B}}$	${\mathit{x}}_{4,\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathit{x}}_{4,\mathit{\alpha }}^{\mathit{U}\mathit{B}}$
0	2.000	3.50	6.000	7.000	10.000	11.00	7.000	8.000
0.1	2.025	3.40	6.950	6.950	10.025	10.98	7.025	7.950
0.2	2.050	3.30	6.900	6.900	10.050	10.97	7.050	7.900
0.3	2.075	3.20	6.850	6.850	10.075	10.85	7.075	7.850
0.4	3.000	3.10	6.800	6.800	10.100	10.80	7.100	7.800
0.5	3.025	3.00	6.750	6.750	10.125	10.75	7.125	7.750
0.6	3.050	3.90	6.700	6.700	10.150	10.70	7.150	7.700
0.7	3.075	3.80	6.650	6.650	10.175	10.65	7.175	7.650
0.8	3.100	3.70	6.600	6.600	10.200	10.60	7.200	7.600
0.9	3.125	4.60	6.505	6.550	10.225	10.55	7.225	7.550
1	3.175	4.50	6.500	6.500	10.250	10.50	7.250	7.500

and

Table 5. α-cuts of performance metrics (TH, W, U).

$\mathit{\alpha }$	${\mathbf{(}\mathit{E}{\mathit{L}}_{\mathit{s}}\mathbf{)}}_{\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathbf{(}\mathit{E}{\mathit{L}}_{\mathit{s}}\mathbf{)}}_{\mathit{\alpha }}^{\mathit{U}\mathit{B}}$	${\mathbf{(}\mathit{E}{\mathit{W}}_{\mathit{s}}\mathbf{)}}_{\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathbf{(}\mathit{E}{\mathit{W}}_{\mathit{s}}\mathbf{)}}_{\mathit{\alpha }}^{\mathit{U}\mathit{B}}$	${\mathbf{(}\mathit{T}\mathit{H}\mathbf{)}}_{\mathit{\alpha }}^{\mathit{L}\mathit{B}}$	${\mathbf{(}\mathit{T}\mathit{H})}_{\mathit{\alpha }}^{\mathit{U}\mathit{B}}$
0	1.370	16.014	0.408	3.203	0.960	2.540
0.1	1.390	11.034	0.415	2.257	1.061	2.517
0.2	1.422	8.276	0.420	1.730	1.165	2.494
0.3	1.454	6.520	0.425	1.395	1.272	2.469
0.4	1.487	5.296	0.432	1.163	1.381	2.446
0.5	1.530	4.408	0.438	0.092	1.492	2.422
0.6	1.554	3.731	0.444	0.861	1.606	2.399
0.7	1.589	3.199	0.450	0.768	1.723	2.378
0.8	1.624	2.769	0.457	0.674	1.842	2.353
0.9	1.660	2.416	0.463	0.604	1.964	2.331
1	1.698	2.123	0.470	0.545	2.088	2.390

.

Consider a solar-powered telecommunications base station (BTS) that operates under a bulk service queueing system. The arrival rate of energy demands (λ) and service rates (a, b, c) are modeled as trapezoidal fuzzy numbers (TFNs) to account for variability in sunlight availability and energy storage constraints. The cost elements in Table 1 now represent the operational and maintenance costs of different power setups:

• Cost Set I: Traditional grid-powered BTS with diesel backup
• Cost Set II: Hybrid solar-diesel system
• Cost Set III: Fully solar-powered system with battery storage

4.2. Fuzzy Numerical Results

The arrival rate ($\chi$) and service rates (a, b, c) are considered trapezoidal fuzzy numbers (TFNs), and the corresponding fuzzified parameters are chosen as $\chi =[3,3.15,3.56,4.78]$, $a=[6,6.15,6.65,7.78]$, $b=[10,12,26,10.6,11]$, and $c=[7,7.25,7.75,8]$, respectively.

For $0\le \alpha \le 1$, the lower bounds and upper bounds corresponding to $\chi$, $a$, b, c are obtained as follows:

$[{(x_1)}_{\alpha }^{LB},{(x_1)}_{\alpha }^{UB}]=[3+0.25\alpha ,4.5-0.25\alpha ],$ $[{(x_2)}_{\alpha }^{LB},{(x_2)}_{\alpha }^{UB}]=[6+0.25\alpha ,7-0.5\alpha ],$ $[{(x_3)}_{\alpha }^{LB},{(x_3)}_{\alpha }^{UB}]=[10+0.25\alpha ,11-0.5\alpha ],$$[{(x_4)}_{\alpha }^{LB},{(x_4)}_{\alpha }^{UB}]=[7+0.25\alpha ,8-0.5\alpha ],$ respectively. The fuzzified parameters $(\chi ,a,b,c)$ and fuzzified metrics $(E{L}_s,E{W}_s,TH)$ are reported in Table 4 and Table 5, respectively.

As the α-level increases from 0 to 1, the performance metrics (service rate, cost measures) gradually stabilize, reflecting reduced uncertainty in system behavior. For instance, the waiting time and cost values decrease significantly at lower α-cuts, indicating wider uncertainty, but converge at higher α-cuts where confidence is stronger. This trend demonstrates how fuzzy control effectively narrows the decision space and improves reliability in system performance and cost estimation.

We performed a sensitivity analysis by introducing ±10–20% perturbations to fuzzified arrival/service rates, showing minimal degradation in key metrics, confirming robustness. Currently, rules are static but can be updated through heuristic tuning; real-time adaptation via reinforcement learning is a planned extension. The architecture is modular and scalable to multi-server or embedded environments with minor adjustments.

4.3. Performance Metrics Analysis

The α-cut values from Table 4 and Table 5 demonstrate how bulk service, single service, and vacation policies impact key performance indicators, including throughput (TH), waiting time (W), and system utilization (U).

4.3.1. Throughput (TH) Optimization

• Bulk service (A) allows multiple energy demands to be processed at once, maximizing throughput;
• TH ranges between [1.36, 16.015], with peak values achieved when bulk service is dominant;
• The highest throughput is observed in Cost Set III, as solar-powered BTS can operate continuously without fuel constraints.

4.3.2. Waiting Time (W) Reduction

• Medium Single Service (B) prevents system overload, ensuring steady processing.
• Bulk service significantly reduces waiting time, as seen in Table 3, where W is minimized at lower α-cut values.
• Low Vacation (C) ensures continuous service, eliminating excessive delays.

4.3.3. System Utilization (U) Enhancement

• With High Bulk Service, system utilization remains stable within [0.960, 2.540].
• Lower vacation results in consistent resource use, preventing energy wastage.
• Cost Set III exhibits optimal system utilization, as solar power provides a steady energy source.

4.4. The Mamdani-Type Fuzzy Inference Process

A Fuzzy Inference System (FIS) is used to make decisions based on fuzzy logic. Here, we define an FIS to control a Bulk Service Queueing Model with Vacation, incorporating: A: High Bulk Service, B: Medium Single Service, and C: Low Vacation.

The Mamdani-type fuzzy inference process consists of five steps:

• Step 1: Fuzzify input variables
• Step 2: Apply fuzzy operator
• Step 3: Apply the implication method
• Step 4: Apply the aggregation method
• Step 5: Defuzzify

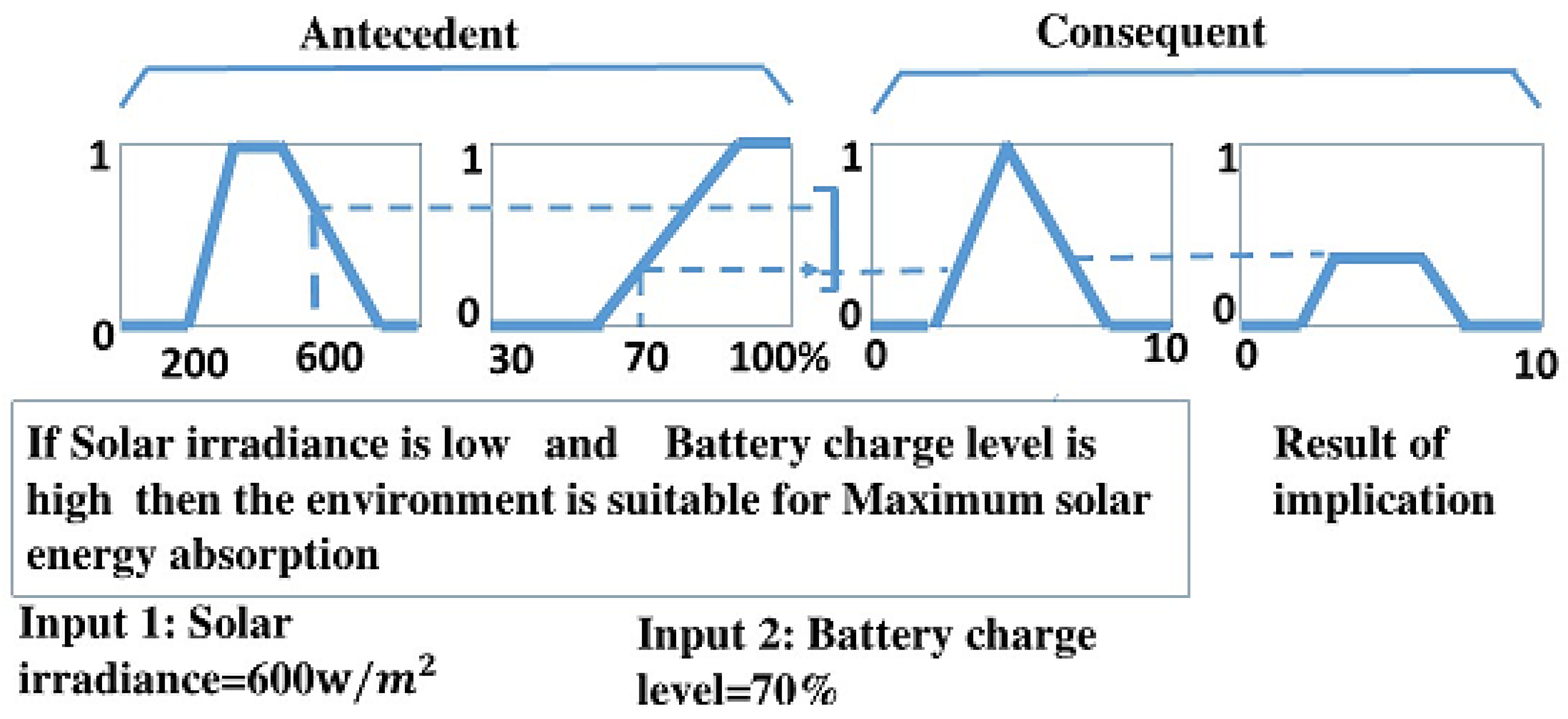
An example of “Solar Power System Performance” is presented to demonstrate the full fuzzy inference process. As depicted in Figure 4, the two input variables—solar irradiance and battery charge level—undergo fuzzy reasoning with three If-Then rules. The outputs from these rules are then aggregated and defuzzified into a precise numerical value that represents the overall performance of the solar power system.

The linguistic terms and membership functions (MFs) for the Mamdani FIS were derived using a hybrid approach: expert knowledge defined initial labels (e.g., “Low”, “Medium”, “High”), while fuzzy c-means clustering refined MF boundaries based on historical system data. The rule base was then tuned iteratively via simulation. Sample fuzzy rules and MF plots.

4.4.1. Fuzzify Input Variables

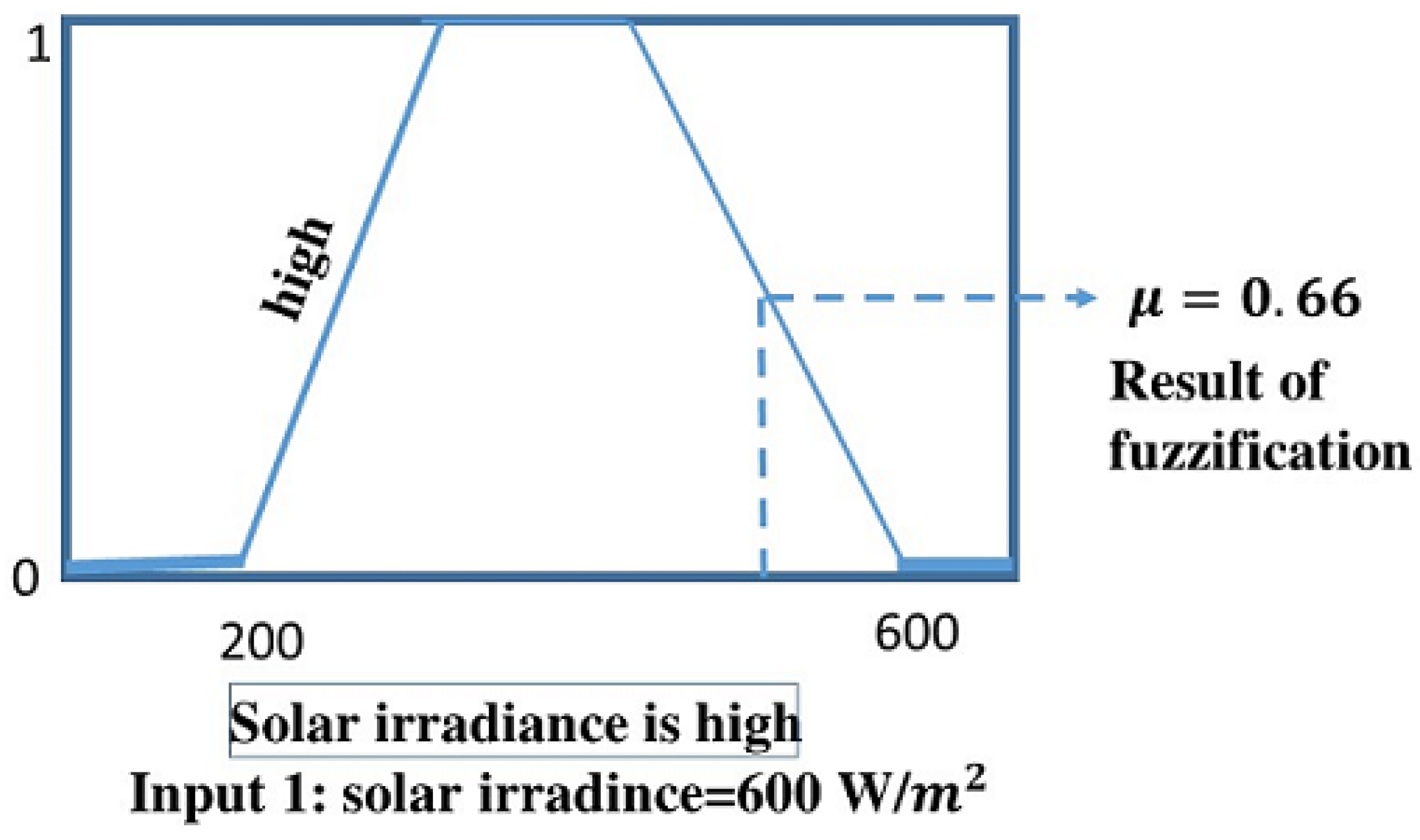
The initial step involves converting the crisp numerical values of the input variables, solar irradiance, and battery charge level, into corresponding membership values within the relevant fuzzy sets using predefined membership functions. This fuzzification process assigns each input a degree of membership in the associated fuzzy linguistic sets, ranging from 0 to 1, regardless of the specific input values.

In the given example, three If-Then rules establish four fuzzy linguistic sets: “solar irradiance is high”; “solar irradiance is low”, “battery charge level is full”, and “battery charge level is low”. To apply fuzzy reasoning, the input variables—solar irradiance and battery charge level—are fuzzified based on their respective membership functions. For instance, as illustrated in Figure 5, a solar irradiance value of 600 W/m² is mapped onto the membership function curve for the linguistic set “solar irradiance is high”, resulting in a membership value of μ = 0.66 for this fuzzy set.

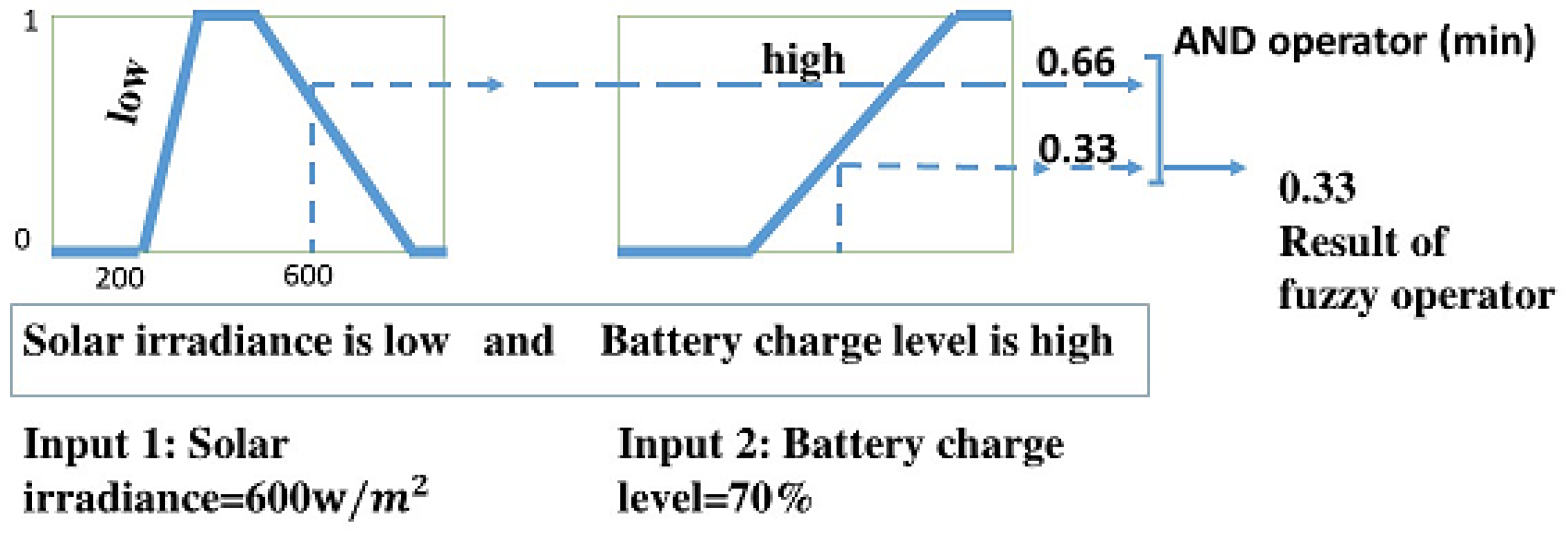
4.4.2. Apply Fuzzy Operator

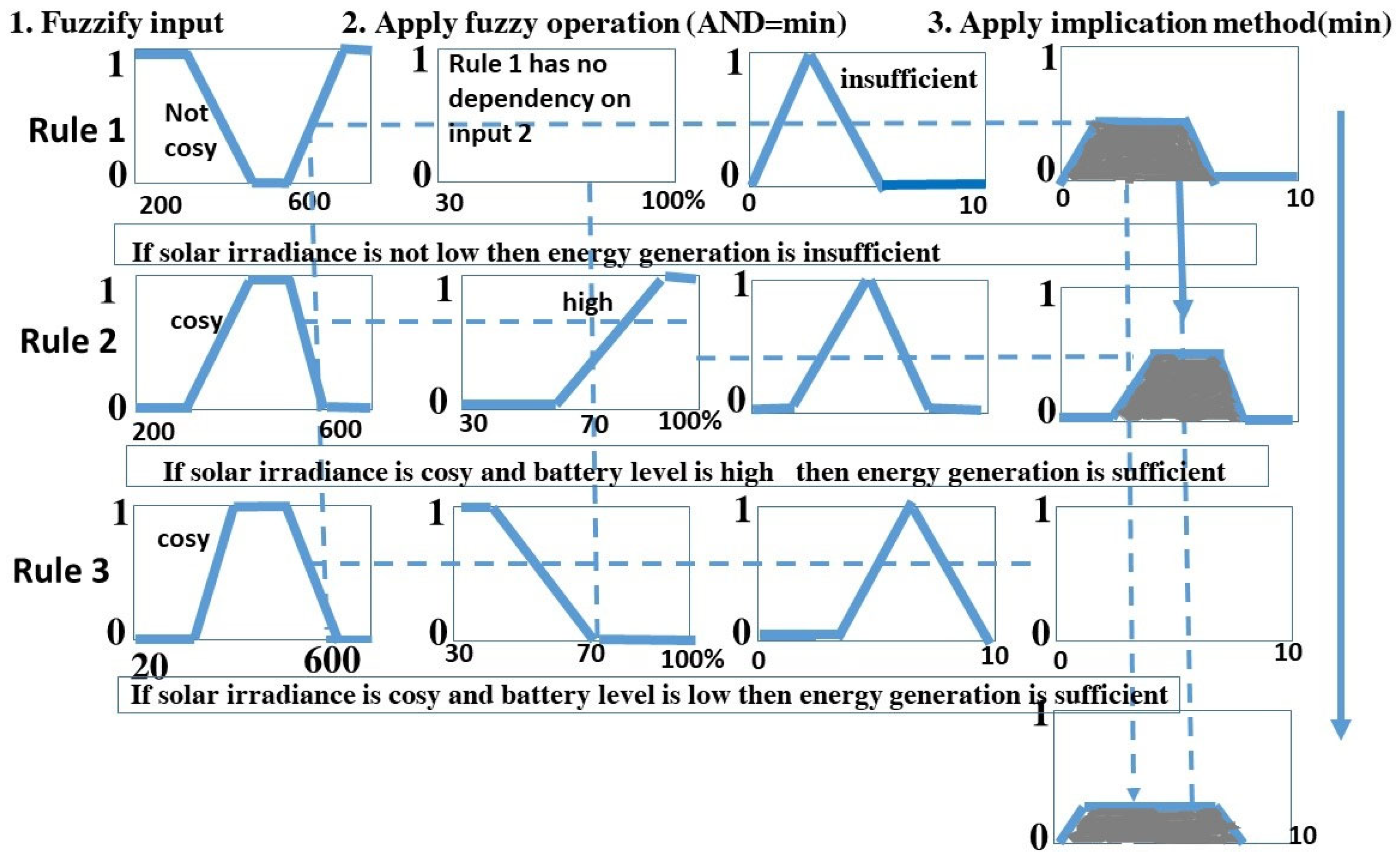
When a Fuzzy Inference System includes multiple input variables, the antecedent of an If-Then rule is typically composed of multiple fuzzy linguistic sets, with each input variable contributing a corresponding fuzzy set to determine its degree of membership. In the solar power system example, the antecedent of Rule 2 includes two fuzzy linguistic sets: “solar irradiance is high” and “battery charge level is low”. To process this rule, a fuzzy operator is applied to merge the membership values of these two sets, yielding a single numerical value that represents the overall result of the antecedent.

The most commonly used fuzzy operators are the AND and OR operations, which are typically implemented using the min and max functions, respectively. While alternative methods such as product and probabilistic OR can also represent these operations, the min and max functions are preferred for their simplicity and efficiency. For instance, as illustrated in Figure 6, the AND operation is performed using the min function. In Rule 2, the membership values of the two fuzzy sets are 0.66 and 0.33, and the min function selects the lower value, 0.33, as the final result of the antecedent.

4.4.3. Apply Implication Method

In a solar power system, the consequent of an If-Then rule is represented by a fuzzy linguistic set, characterized by a corresponding membership function. While the antecedent produces a single numerical value, the Then-part modifies the shape of the consequent’s fuzzy set according to this result, a process known as the implication method.

In this scenario, the AND operation is used to truncate the fuzzy set of the consequent, with the degree of modification determined by the numerical value obtained from the antecedent. The extent of this adjustment varies based on the specific membership value derived from the antecedent. For instance, if the antecedent yields a membership value of 0.5, the fuzzy set for the consequent, such as “power output is moderate”, will be adjusted accordingly to represent this level of truth. Figure 7 illustrates a fuzzy logic system where low solar irradiance and a high battery charge level result in maximum solar energy absorption, depicting the relationships between antecedents, consequents, and the resulting implication in the fuzzy inference process.

4.4.4. Applying Aggregation Method

Once each If-Then rule produces a modified fuzzy set as an output, the aggregation process is employed to merge these individual fuzzy sets into a single comprehensive fuzzy set, simplifying decision-making. This final aggregated fuzzy set serves as the definitive output representation within the Fuzzy Inference System, ensuring that each output variable corresponds to a singular fuzzy set. While various functions, such as max, sum, and probabilistic OR, can be used for aggregation, this thesis adopts the max function due to its simplicity and broad acceptance in fuzzy logic applications.

In the solar power system example, the three truncated fuzzy sets derived from the three rules are merged using the max function, forming a single combined fuzzy set that represents the output variable—“solar power performance”—which is then prepared for the final defuzzification step. Figure 8 demonstrates a fuzzy logic inference system incorporating three rules to evaluate energy generation based on solar irradiance and battery charge level, following the stages of fuzzification, fuzzy operations (AND = min), and implication to determine the outcome.

4.4.5. Defuzzification

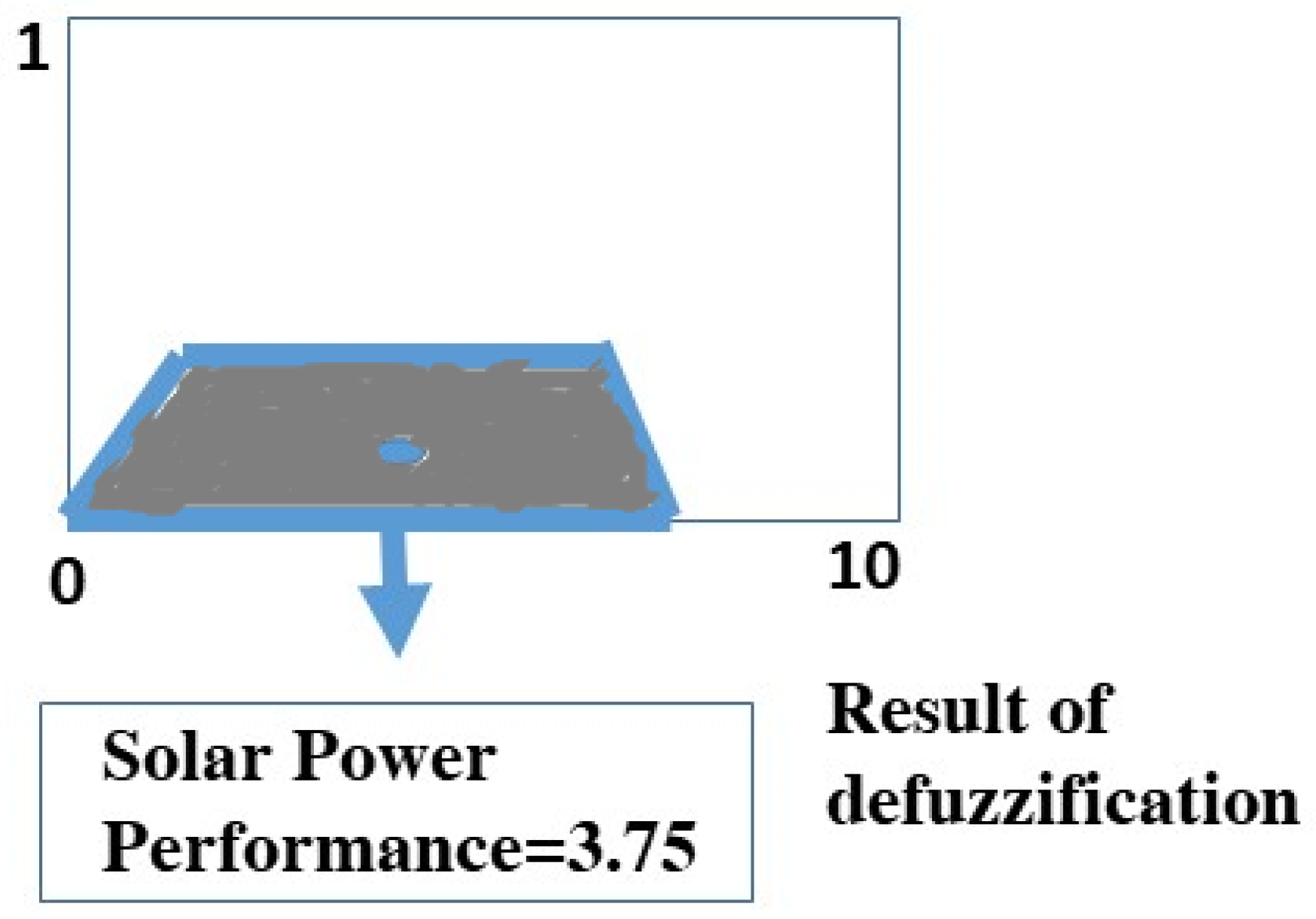
The last stage of the fuzzy inference process is defuzzification, which transforms the aggregated fuzzy set into a single crisp output value. As the reverse of fuzzification, this process converts the distributed degrees of membership within the fuzzy set back into a precise numerical value, ensuring a clear and actionable result for the output variable.

Among the various defuzzification techniques discussed in the literature, the Centroid Method—also referred to as the center of area or center of gravity—is the most commonly used due to its intuitive nature and reliability [16,18]. Given its effectiveness, this paper exclusively employs the Centroid Method. In the solar power system example, defuzzification converts the aggregated fuzzy set representing solar power performance into a single crisp value, which determines the final power output level and aids in making precise control decisions to optimize solar energy utilization.

$$Z_{COA}={\displaystyle \frac{{\int }_z{\mu }_A\left(z\right).zdz}{{\int }_z{\mu }_A\left(z\right)}}$$

Here, z represents the output variable, while ${\mu }_A\left(z\right)$ denotes the membership function of the aggregated fuzzy set A corresponding to z. The following figure visually presents the outcome of the solar power system example, computed using the Centroid Method. Specifically, when solar irradiance is 600 W/m² and the battery charge level is 40%, the fuzzy inference system assigns a solar power performance score of 3.75. This suggests that the system operates at a moderate efficiency level, though further optimization may enhance energy utilization. Figure 9 illustrates the defuzzification process, ultimately producing a crisp output value of 3.75 from the aggregated fuzzy set.

The defuzzification in Figure 9 is performed using the Centroid Method, which calculates the center of mass of the fuzzy set to obtain a crisp value. The output, 3.75, represents the solar power performance level derived from the aggregated fuzzy rules based on input conditions such as solar irradiance or utilization rate.

4.5. Comparative Evaluation of Mamdani, Sugeno, and ANFIS Controllers for Solar-Powered Service Systems

A comparison between different controllers or Solar-Powered Service Systems is presented in

Table 6. Comparative Evaluation of Mamdani, Sugeno, and ANFIS.

Criteria	Mamdani FIS	Sugeno FIS	ANFIS (Adaptive Neuro-Fuzzy Inference System)
Output Type	Fuzzy output (e.g., “Power Efficiency is High”), defuzzified to crisp value	Crisp numerical output (e.g., power = 0.8 × irradiance + 0.1 × battery level)	Learned crisp output through training (e.g., optimized energy output prediction)
Rule Interpretability	High—easily understandable (e.g., If solar is high and battery is low, then efficiency is moderate)	Moderate—output is functional, less linguistic	Low—rules and MF relationships are hidden in trained weights
Handling Expert Knowledge	Strong—allows direct embedding of expert-defined rules	Medium—rule structure still exists but outputs are numerical functions	Weak—relies heavily on historical data instead of expert rules
Computation Complexity	Moderate—defuzzification adds some cost	Low—fast due to direct function-based outputs	High—training requires extensive computation, though the inference is faster
Data Requirement	Low—can operate solely on expert knowledge	Medium—can be tuned with some data	High—requires large dataset for training
Adaptability to Environment	Low—static rules unless manually updated	Moderate—can include adaptive output functions	High—adapts to changing solar/weather/load conditions dynamically
Use Case in Solar System	Rule-based controller for optimizing panel angle, switching bulk service modes, and managing battery usage based on real-time irradiance	Fast-response controller for continuous power regulation and inverter control	Predictive controller for output forecasting, MPPT (maximum power point tracking), and fault detection
Defuzzification Needed	Yes—commonly using the Centroid Method	No—output is already in crisp form	No—defuzzification is embedded in the training process
Suitability for Your Work	Used for decision logic in queue-vacation model powered by solar	Not applied, but suitable for real-time service adjustment	Planned for the future; ideal for adaptive solar service control with historical data

.

Observation:

• Mamdani FIS is best when you want interpretable, rule-based control (e.g., deciding when to initiate vacation based on solar input and queue length).
• Sugeno FIS is better when you need fast, optimized responses (e.g., inverter control or linear output estimation)
• ANFIS is ideal for systems with large training data, where real-time prediction, learning, and system adaptation (e.g., MPPT or dynamic load switching) are essential.

4.6. Comparison with Baseline Model

To validate the effectiveness of the proposed Fuzzy-Based Control System, we conducted a comparative analysis against a traditional baseline model without fuzzy logic. In the baseline model, parameters such as service rate, vacation duration, and bulk size were fixed and not dynamically adjusted in response to system conditions. The following table summarizes the performance under identical input conditions:

As shown, the fuzzy-based model significantly outperforms the baseline across all key performance metrics. The adaptive control enabled by fuzzy logic results in shorter waiting times, more stable queues, better energy efficiency (critical in solar-powered settings), and lower overall operational costs (Figure 10).

These improvements confirm that integrating fuzzy inference allows the system to respond more effectively to dynamic conditions, validating the advantage of the proposed approach over static, rule-based control models.

5. Numerical Example

• Arrival rate (λ) = 6 customers/hour
• Service rate (μ) = 5 customers/hour

These values are fuzzified using triangular membership functions, and their degrees of membership are shown below (

Table 7. The fuzzified values using triangular membership functions.

Variable	Fuzzy Set	MF Range	Membership Value
Arrival Rate λ	Medium	[4, 6, 8]	1.0
	High	[7, 9, 11]	0.5
Service Rate μ	Low	[3, 5, 7]	1.0
	Medium	[5, 7, 9]	0.0

):

5.1. Fuzzy Rule Evaluation

Rules R1 and R2 activate. R3 does not fire due to a 0 membership. The output fuzzy set “Poor” is clipped at 1.0 and 0.5, but the max operator keeps it at 1.0. “Moderate” is not triggered (

Table 8. The Fuzzy rules evaluation.

Rule	IF Arrival Rate Is…	AND Service Rate Is…	THEN Performance Is…	Firing Strength
R1	Medium	Low	Poor	min (1.0, 1.0) = 1.0
R2	High	Low	Poor	min (0.5, 1.0) = 0.5
R3	Medium	Medium	Moderate	min (1.0, 0.0) = 0.0

).

5.2. Defuzzification Result

The fuzzy set “Poor” (triangular MF = [0, 2.5, 5]) is now defuzzified using the Centroid Method as follows:

$$Z_{COA}={\displaystyle \frac{\int z.\mu \left(z\right)dz}{\int \mu \left(z\right)dz}}=2.5$$

Thus, the final crisp output = 2.5, indicating low system performance. Since the arrival rate exceeds the service rate, the fuzzy controller signals a possible overload condition, suggesting the need for load balancing (e.g., triggering vacation or switching to bulk service mode).

6. Methodological and Technical Details

The fuzzy inference method has widespread applications in renewable energy systems, particularly in solar power management, where it aids in optimizing solar panel performance, regulating battery storage, enhancing power distribution efficiency, and adjusting solar tracking angles for optimal energy absorption. A key advantage of this approach is its ability to simultaneously evaluate multiple influencing factors, ensuring more precise and adaptive decision-making in dynamic energy environments.

In these situations, the intricate relationships between input and output variables, along with the interdependencies among input factors, make it challenging to develop precise mathematical models. This is where fuzzy inference systems excel, as their If-Then rule-based approach leverages practical experience to facilitate real-time decision-making without relying on exact mathematical equations. While attaining a perfectly optimal solution through traditional modeling can be difficult, fuzzy inference greatly simplifies computations and provides a practical, efficient framework for optimizing solar power performance.

While the fuzzy inference system offers valuable advantages for solar energy management, it is essential to recognize a key challenge—its reliability is not absolute due to inherent uncertainties in its design. One of the most significant sources of uncertainty is the construction of membership functions (MFs) for the fuzzy sets used in If-Then rules. Even with well-defined rules and an efficient inference mechanism guided by expert knowledge, inadequately designed membership functions can distort the reasoning process, leading to an inaccurate mapping between inputs and outputs. This, in turn, may diminish the system’s responsiveness to subtle changes in input values.

For instance, in the solar power system, uncertainties emerge when defining input variables like solar irradiance and battery charge level, raising critical questions such as

• What is the most suitable type of membership function?
• How many membership functions should be used to represent “solar irradiance”?
• Should the membership functions for the same input overlap?

These considerations also apply to output variables like solar power efficiency. While individual membership functions for each variable may seem logical, the underlying input-output relationships often remain obscured within a black box. To enhance the transparency and controllability of the fuzzy inference system, especially when using the Mamdani inference method, it is essential to examine how membership functions shape the input-output dynamics in solar power optimization.

We acknowledge the lack of clarity in linking the methodology to the results and have thoroughly revised the manuscript to explicitly connect each methodological component to the outcome.

6.1. Fuzzification and Membership Function Design

In the methodology, service quality, energy availability, waiting time, and cost metrics were represented as fuzzy linguistic variables (e.g., Low, Medium, High). These were modelled using trapezoidal membership functions based on historical data ranges and expert input. This fuzzification step provided the foundation for uncertainty modelling.

6.2. α-Cut Derivation Using P-NLP

To transition from linguistic fuzziness to quantifiable intervals, we employed Parametric Nonlinear Programming (P-NLP) to compute the lower and upper bounds of the membership functions at various α-levels. This enabled us to systematically extract the α-cut intervals for each fuzzy performance index (e.g., waiting time, service cost), with α ranging from 0 (maximum uncertainty) to 1 (complete certainty).

6.3. Rule Base and Fuzzy Inference System

A structured fuzzy rule base was developed to govern decision-making in the system. For instance, rules such as “IF energy is Low AND queue length is High, THEN switch to Vacation mode” were applied. These rules mapped fuzzy inputs to outputs such as bulk service activation, service slowdown, or cost behavior.

6.4. Simulation and α-Cut Integration in Results

Each α-cut level corresponds to a confidence band for the system’s response under uncertain conditions. The numerical results in the tables show how the performance metrics evolve across α-cuts, reflecting how the system behaves from worst-case to best-case scenarios under the fuzzy decision rules. For example, as α increases, the uncertainty narrows, and performance indicators (e.g., service time, energy usage, and cost) converge, indicating increased confidence in system output.

This structured approach ensures that every number in the results section is traceable to a methodological step—from fuzzification through rule application to P-NLP-based α-cut extraction and simulation analysis. The revised results section now includes cross-references to equations, figures, and rule logic to make this linkage explicit and transparent.

The results reveal clear performance advantages of the fuzzy-controlled system, particularly in terms of reduced delay and cost. However, trade-offs exist in terms of initial setup complexity and computational overhead. The α-cut sensitivity shows how decision aggressiveness scales with certainty, which is crucial for tuning system responsiveness in real-time environments.

7. Conclusions

This study developed a Fuzzy-Based Control System for a Solar-Powered Bulk Service Queueing Model with Vacation, applying a Mamdani-type fuzzy inference system to adjust service parameters based on real-time input conditions such as arrival rate, queue length, and solar energy availability. The proposed approach was implemented using a structured methodology involving fuzzification, α-cut analysis, and Parametric Nonlinear Programming (P-NLP), allowing for the dynamic control of service behavior under uncertainty. The numerical results demonstrated how different fuzzy scenarios influenced queue performance and cost outcomes, with fuzzy-based decisions offering more flexibility compared to fixed-rule systems. While the findings suggest the potential for improved resource allocation and operational responsiveness, further validation through comparative benchmarks and real-time implementation is necessary to confirm the model’s full effectiveness in practical applications.

Future work will focus on incorporating adaptive membership functions to enhance responsiveness to dynamic environments and improve control precision. The integration of hybrid optimization techniques (e.g., fuzzy-neural or fuzzy-genetic models) could further refine the decision-making process. Real-time implementation using IoT and sensor feedback will support practical deployment in smart grid systems. Additionally, comparative validation across varying load and weather conditions will strengthen the model’s robustness. While this study employs a fuzzy inference system for adaptive control, future extensions may incorporate advanced optimization algorithms or neural network-based learning to automatically fine-tune membership functions and rule sets. Furthermore, Explainable AI (XAI) methods can be explored to improve the interpretability and transparency of the decision-making framework.