Freezing Behavior of Clayey Sand and Spatiotemporal Evolution of Seasonally Frozen Soil Distribution in the Qinghai–Tibet Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area Overview
2.2. Preparation of Clayey Sand Samples
2.3. Test Equipment and Methods
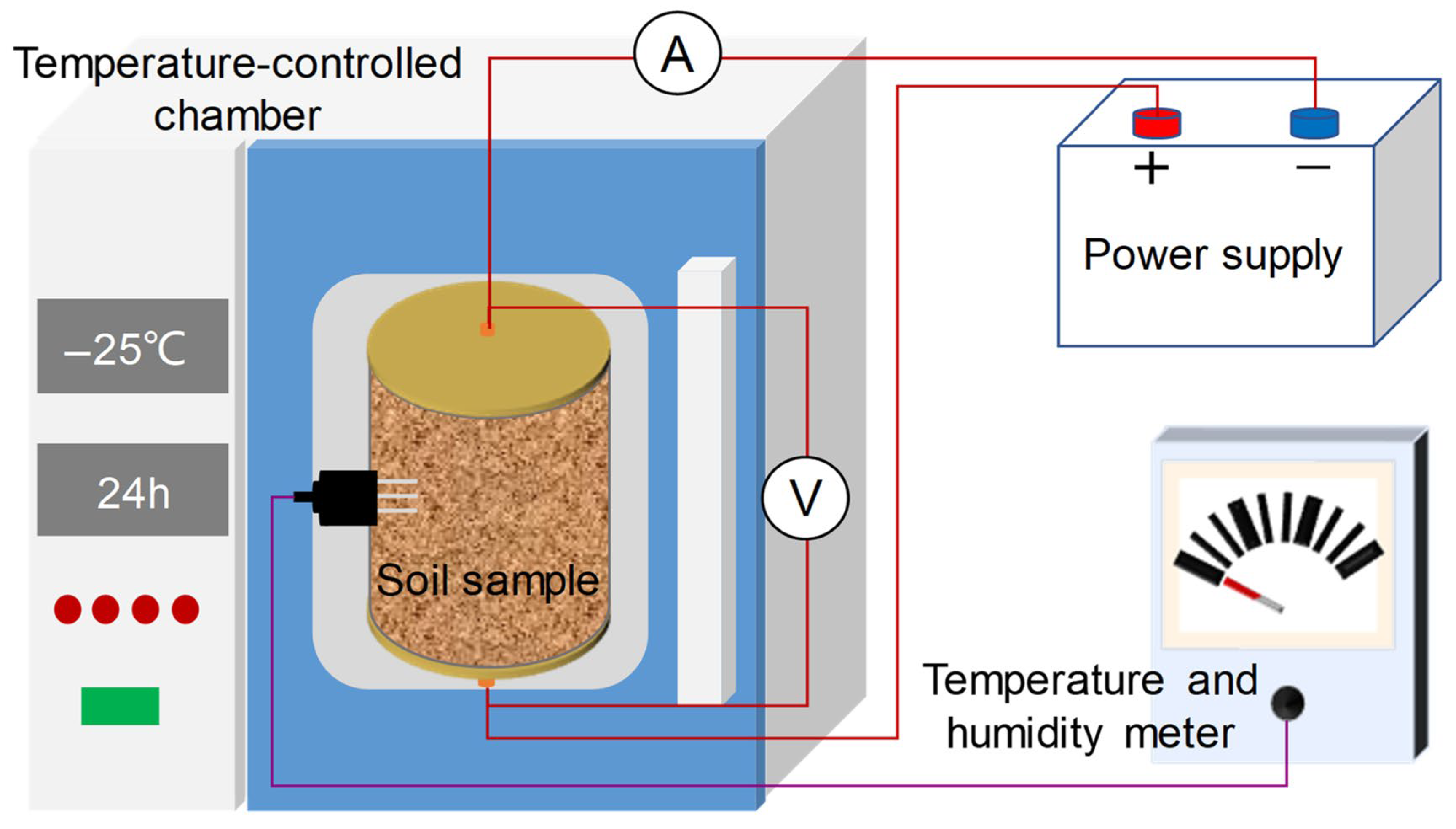
2.3.1. Freezing–Thawing Test Apparatus and Procedure
2.3.2. ERT Tests Apparatus and Procedure
3. Results and Discussion
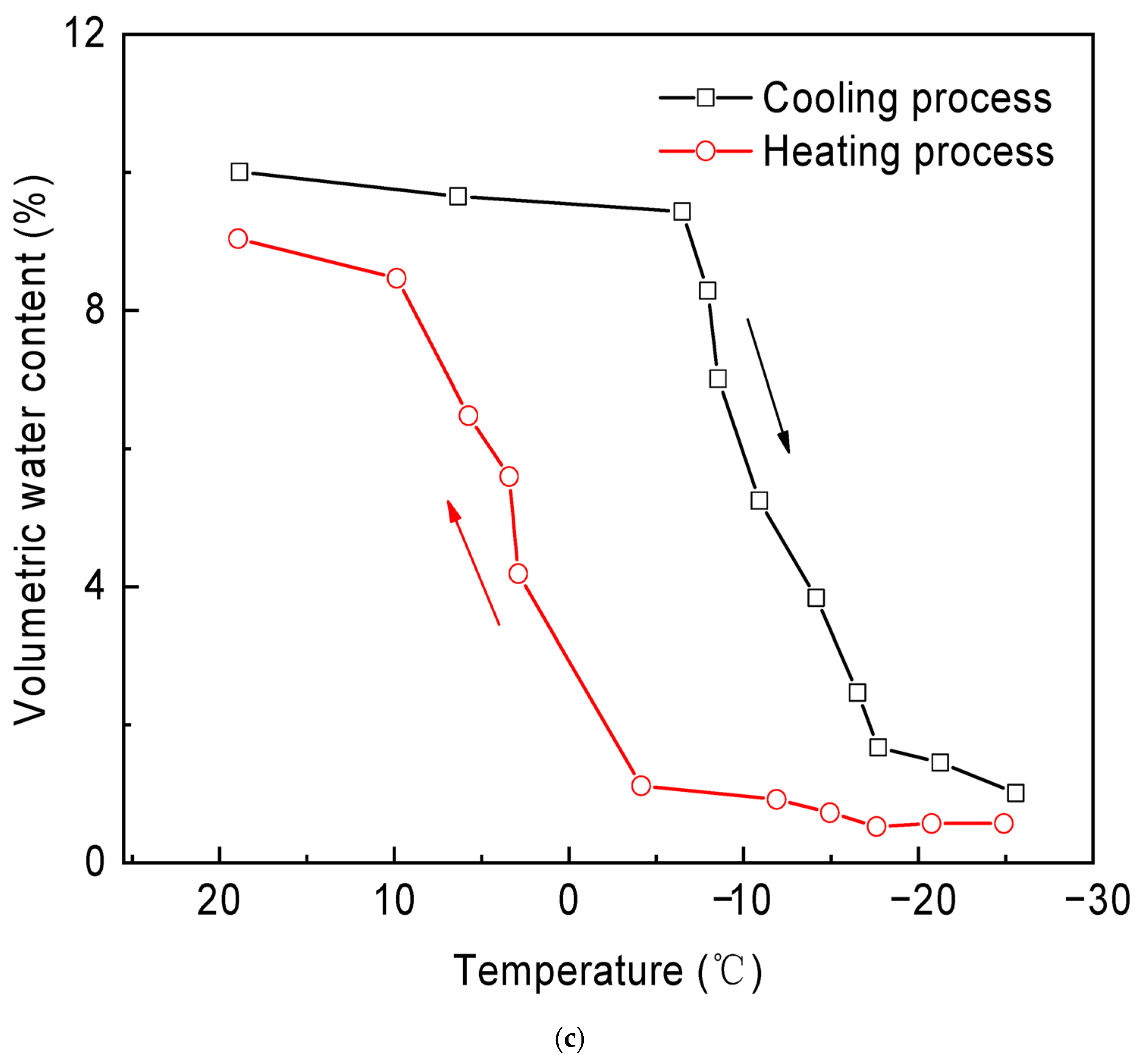
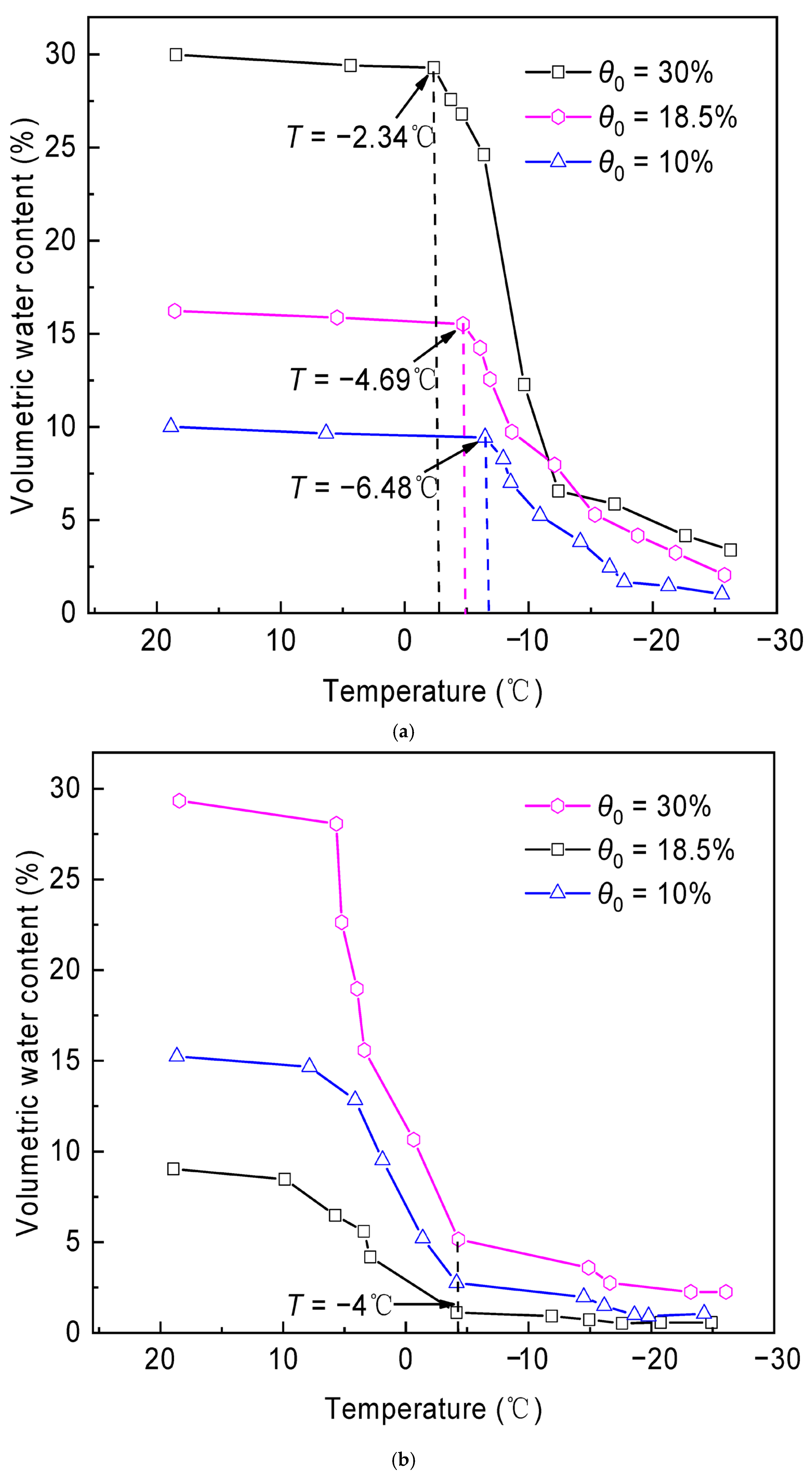
3.1. Freezing Characteristics of Clayey Sand
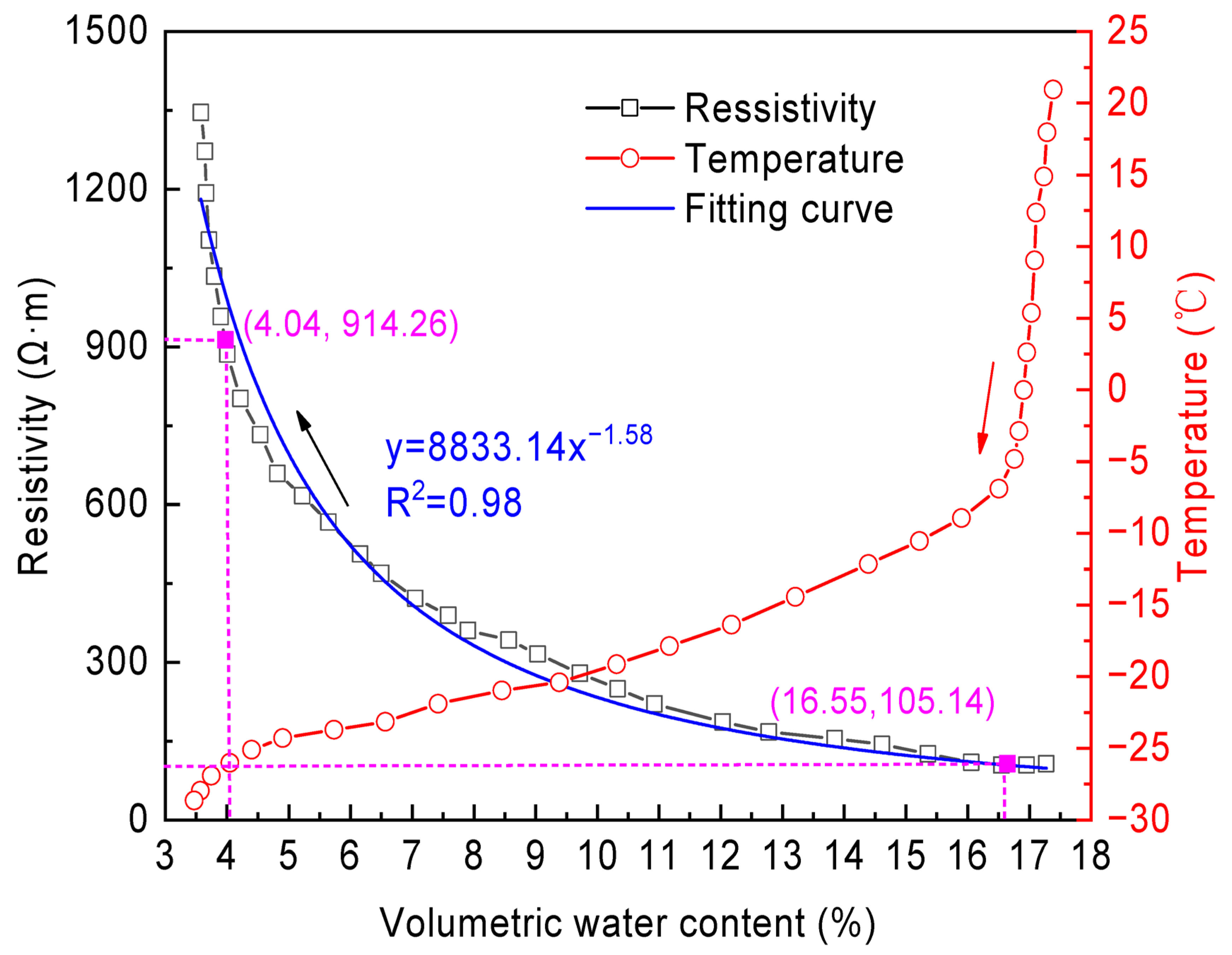
3.2. Resistivity Variation Characteristics of Frozen Clayey Sand
3.2.1. Influence of Unfrozen Water Content on the Resistivity of Clayey Sand
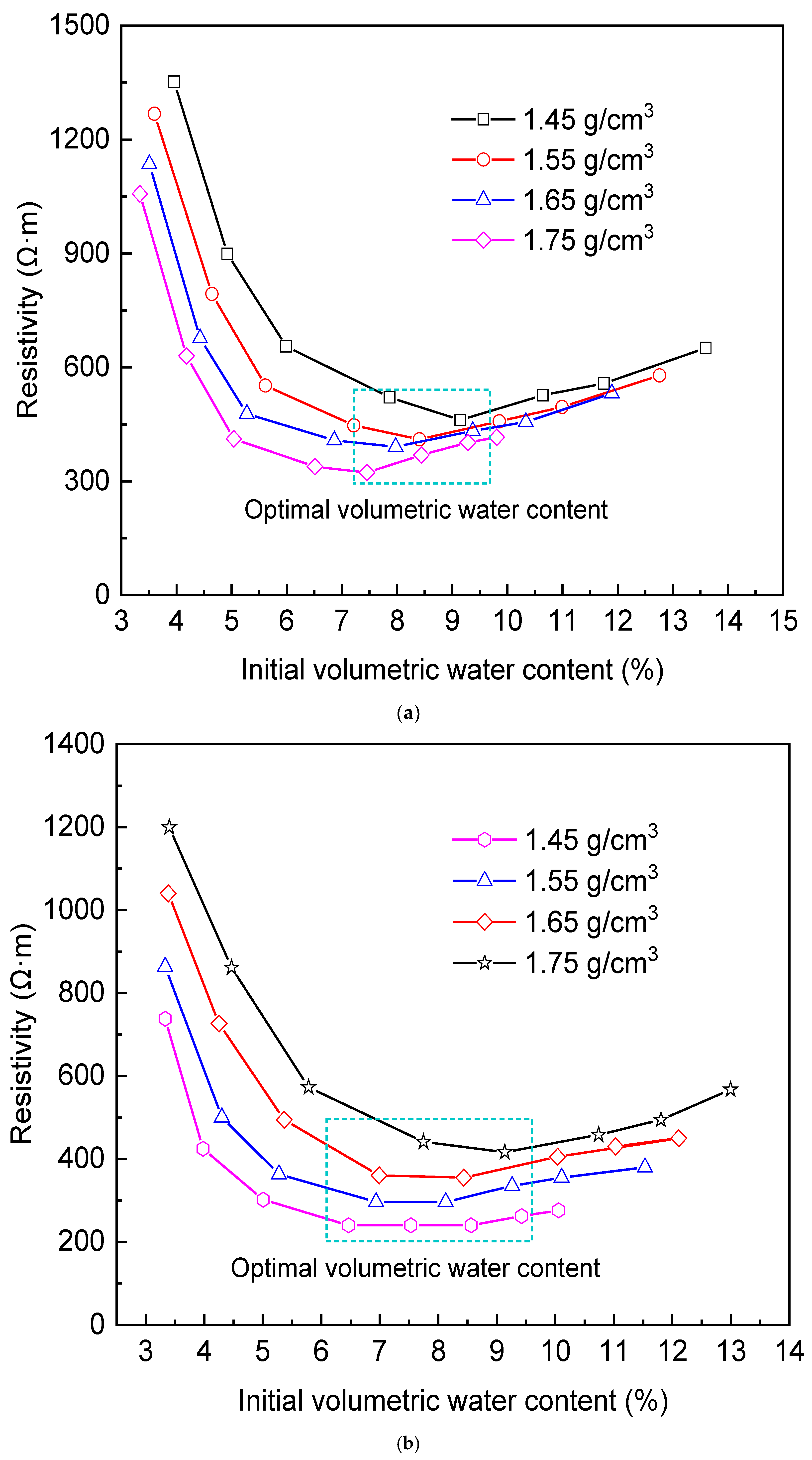
3.2.2. Influence of Initial Volumetric Water Content on the Resistivity of Frozen Clayey Sand
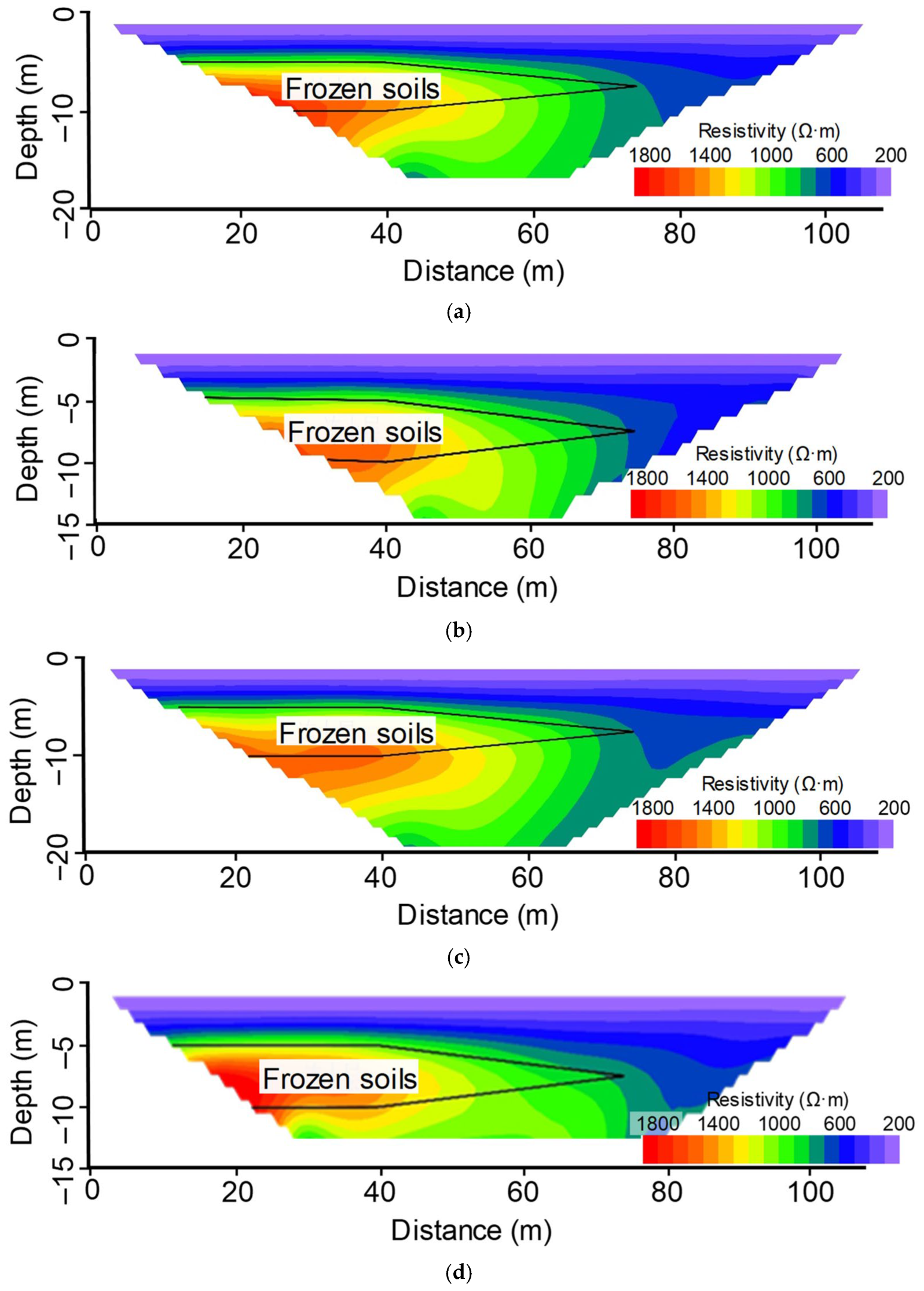
3.3. Evolution of Frozen Soil Distribution in the Study Area
3.3.1. Forward Modeling
3.3.2. Field ERT Test Inversion
4. Conclusions
- (1)
- During the freezing process, clayey sand samples with different initial volumetric water contents exhibited S-shaped curves characterized by gentle slopes at both ends and a steep transition in the middle. This process can be divided into three stages: rapid heat release, rapid freezing, and stable freezing. A higher initial volumetric water content led to a higher freezing temperature and faster freezing rate, whereas the melting temperature remained consistent at approximately −4 °C.
- (2)
- As soil temperature decreased, the unfrozen water content gradually declined, accompanied by a significant increase in resistivity. An inverse relationship between these two parameters was observed within the test range, confirming the dominant influence of unfrozen water content on the resistivity of frozen soil. This finding provides a basis for distinguishing seasonal and perennial frozen soils in the Qinghai–Tibet Plateau. For fully frozen soils, resistivity exhibited a U-shaped variation with respect to initial volumetric water content, reaching a minimum at an optimal initial volumetric water content. Additionally, the resistivity decreased with increasing dry density.
- (3)
- Forward modeling demonstrated that both Wenner-α and Schlumberger arrays exhibited good resolution for the upper and lower boundaries of frozen soil layers. However, the Wenner-α configuration showed stronger resistance to interference. Considering the harsh geological conditions in the study area, Wenner-α was selected as the primary electrode arrangement for field electrical surveys of frozen soils.
- (4)
- Field high-density resistivity profiles revealed minimal differences between summer (July) and early autumn (September). In contrast, by winter (December), the intermediate transition layer exhibited a pronounced increase in vertical thickness and horizontal extent, indicating the seasonal evolution of frozen soil. Once frozen, this transition layer acts as a “hydraulic barrier”, effectively reducing the downward infiltration of surface and shallow water, thereby supporting surface vegetation survival.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, M.; Wang, X.; Pang, G.; Wang, G.; Liu, Z. The Tibetan Plateau Cryosphere: Observations and Model Simulations for Current Status and Recent Changes. Earth-Sci. Rev. 2019, 190, 353–369. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, F.; Li, H.; Cheng, D.; Sun, B. The Influence Mechanism of Freeze-Thaw on Soil Erosion: A Review. Water 2021, 13, 1010. [Google Scholar] [CrossRef]
- Pan, Y.; Sun, Z.; Pan, Z.; Zhang, S.; Li, X.; Ma, R. Influence of Permafrost and Hydrogeology on Seasonal and Spatial Variations in Water Chemistry of An Alpine River in the Northeastern Qinghai-Tibet Plateau, China. Sci. Total Environ. 2022, 834, 155227. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, T.; Chen, J.; Wu, X.; Wang, P.; Zou, D.; Yue, G.; Yan, X.; Ma, X.; Wang, D.; et al. Summer Heat Wave in 2022 Led to Rapid Warming of Permafrost in the Central Qinghai-Tibet Plateau. NPJ Clim. Atmos. Sci. 2024, 7, 216. [Google Scholar] [CrossRef]
- Xu, Z.; Jiang, L.; Guo, R.; Huang, R.; Zhou, Z.; Niu, F.; Jiao, Z. Interaction of Permafrost Degradation and Thermokarst Lakes in the Qinghai-Tibet Plateau. Geomorphology 2023, 425, 108582. [Google Scholar] [CrossRef]
- Xie, S.; Qu, J.; Zu, R.; Zhang, K.; Han, Q.; Niu, Q. Effect of Sandy Sediments Produced by the Mechanical Control of Sand Deposition on the Thermal Regime of Underlying Permafrost Along the Qinghai-Tibet Railway. Land Degrad. Dev. 2013, 24, 453–462. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, W.; Zhang, Z. Scientific Concept and Application of Frozen Soil Engineering System. Cold Reg. Sci. Technol. 2018, 146, 127–132. [Google Scholar] [CrossRef]
- Kong, B.; Yan, Y.; He, H.; Yu, J.; Zou, B.; Chen, Q. Strength and Fractal Characteristics of Artificial Frozen-Thawed Sandy Soft Soil. Fractal Fract. 2024, 8, 393. [Google Scholar] [CrossRef]
- Shan, W.; Liu, Y.; Hu, Z.; Xiao, J. A Model for the Electrical Resistivity of Frozen Soils and an Experimental Verification of the Model. Cold Reg. Sci. Technol. 2015, 119, 75–83. [Google Scholar] [CrossRef]
- Pan, Y.; Zhou, S.; Li, Z.; Zhang, M.; Zhang, Z. Hydrothermal Changes and Physicochemical Characteristics of Subtropical Subalpine Soils Under Freezing and Thawing. Sustainability 2022, 14, 13115. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, M.; Gao, J. Research Progress of Constitutive Models of Frozen Soils: A Review. Cold Reg. Sci. Technol. 2023, 206, 103720. [Google Scholar] [CrossRef]
- Peng, S.; Xiong, F.; Yang, F.; Hu, L.; Wang, X. Study on the Effects of Artificial Trapezoidal Freezing Soil Mass on the Stability of Large-diameter Shield Tunnel Portal. Appl. Sci. 2022, 12, 12250. [Google Scholar] [CrossRef]
- Dong, C.; Chen, X.; Mu, Y.; Duan, Z.; Xue, Q.; Sun, C.; Li, J. Microscopic Analysis of Deformation and Water-Salt Transport in Chlorine Saline Soils Under Unidirectional Freezing in Cold and Arid Zones. J. Rock Mech. Geotech. Eng. 2024, 17, 2445–2460. [Google Scholar] [CrossRef]
- Tang, L.; Wang, K.; Jin, L.; Yang, G.; Jia, H.; Taoum, A. A Resistivity Model for Testing Unfrozen Water Content of Frozen Soil. Cold Reg. Sci. Technol. 2018, 153, 55–63. [Google Scholar] [CrossRef]
- Keating, K.; Binley, A.; Bense, V.; Van Dam, R.L.; Christiansen, H.H. Combined Geophysical Measurements Provide Evidence for Unfrozen Water in Permafrost in the Adventdalen Valley in Svalbard. Geophys. Res. Lett. 2018, 45, 7606–7614. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Y.; Ma, W.; Lei, L.; Wen, Z. Study on the Freezing-Induced Soil Moisture Redistribution Under the Applied High Pressure. Cold Reg. Sci. Technol. 2018, 145, 135–141. [Google Scholar] [CrossRef]
- Kim, J.; Lee, A.H.; Chang, W. Manipulation of Unfrozen Water Retention for Enhancing Petroleum Hydrocarbon Biodegradation in Seasonally Freezing and Frozen Soil. Environ. Sci. Technol. 2021, 55, 9172–9180. [Google Scholar] [CrossRef]
- Meisner, A.; Snoek, B.L.; Nesme, J.; Dent, E.; Jacquiod, S.; Classen, A.T.; Prieme, A. Soil Microbial Legacies Differ Following Drying-Rewetting and Freezing-Thawing Cycles. ISME J. 2021, 15, 1207–1221. [Google Scholar] [CrossRef]
- Chen, M.; Mei, J.; Shen, K.; Gao, Y. Response of Sandy Soil-Water Migration to Different Conditions Under Unidirectional Freezing. Sustainability 2024, 16, 3597. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, H.; Li, J.; Li, H.; Ma, W. Study on the Changing Rules of Silty Clay’s Pore Structure Under Freeze-Thaw Cycles. Adv. Civ. Eng. 2019, 2019, 7493872. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Hu, C.; Zhen, X.; Xu, Z.; Xue, Y. Review and Prospect of the Effects of Freeze-Thaw on Soil Geotechnical Properties. Sci. Cold Arid Reg. 2021, 13, 349–356. [Google Scholar]
- Léger, E.; Dafflon, B.; Soom, F.; Peterson, J.; Ulrich, C.; Hubbard, S. Quantification of Arctic Soil and Permafrost Properties Using Ground-Penetrating Radar and Electrical Resistivity Tomography Datasets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4348–4359. [Google Scholar] [CrossRef]
- Krzeminska, D.; Bloem, E.; Starkloff, T.; Stolte, J. Combining FDR and ERT for Monitoring Soil Moisture and Temperature Patterns in Undulating Terrain in South-Eastern Norway. Catena 2022, 212, 106100. [Google Scholar] [CrossRef]
- Tomaškovičová, S.; Ingeman-Nielsen, T. Quantification of Freeze-thaw Hysteresis of Unfrozen Water Content and Electrical Resistivity from time Lapse Measurements in the Active Layer and Permafrost. Permafr. Periglac. Process. 2024, 35, 79–97. [Google Scholar] [CrossRef]
- Gu, Z.; Yoo, C.; Chen, J. Behavior of Geosynthetic-Encased Stone Column Reinforced Foundation Under Freeze-Thaw Cycles. Geotext. Geomembr. 2024, 52, 479–493. [Google Scholar] [CrossRef]
- Teng, F.; Sie, Y.; Kuo, C. Field Experimental and Numerical Study on the Formation and Frost Heave Development of Frozen Soil Under Rapid Freezing. Case Stud. Constr. Mater. 2025, 22, e04239. [Google Scholar] [CrossRef]
- Ge, J.; Sun, H.; Liu, R.; Huang, Z.; Tian, B.; Liu, L.; Zheng, Z. Permafrost Thawing Characterization in Engineering Scale by Multi-Geophysical Methods: A Case Study from the Tibet Plateau. Eng. Geol. 2025, 350, 108012. [Google Scholar] [CrossRef]
- Zhang, T.; Armstrong, R.L. Soil Freeze/Thaw Cycles Over Snow-Free Land Detected by Passive Microwave Remote Sensing. Geophys. Res. Lett. 2001, 28, 763–766. [Google Scholar] [CrossRef]
- Geng, L.; Cong, S.; Luo, J.; Ling, X.; Du, X.; Yu, Y. Stress-Strain Model for Freezing Silty Clay Under Frost Heave Based on Modified Takashi’s Equation. Appl. Sci. 2020, 10, 7753. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y. Influence of Soil Heterogeneity on the Behavior of Frozen Soil Slope Under Freeze-Thaw Cycles. CMES-Comput. Model. Eng. Sci. 2022, 131, 119–135. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban Rural Development of the People’s Republic of China. GB/T 50123-2019; Standard for Geotechnical Testing Method. China Planning Press: Beijing, China, 2019.
- Watanabe, K.; Kito, T.; Wake, T.; Sakai, M. Freezing Experiments on Unsaturated Sand, Loam and Silt Loam. Ann. Glaciol. 2011, 52, 37–43. [Google Scholar] [CrossRef]
- Lei, H.; Wang, L.; Feng, S.; Zhang, W.; Bo, Y.; Tu, C. Laboratory Studies on the Influence of Freezing Methodology on the Shear Strength Behavior of Artificially Frozen Clays. Int. J. Geomech. 2023, 23, 04023122. [Google Scholar] [CrossRef]
- Qu, Y.; Ni, W.; Niu, F.; Mu, Y.; Chen, G.; Luo, J. Mechanical and Electrical Properties of Coarse-Grained Soil Affected by Cyclic Freeze-thaw in High Cold Regions. J. Cent. South Univ. 2020, 27, 853–866. [Google Scholar] [CrossRef]
- Tang, L.; Chen, W.; Luo, X.; Zhang, G.; Feng, X.; Guo, L.; Gao, W.; He, J.; Zhao, G.; Jiang, J.; et al. Multi-Technological Integration in a Smelting Site: Visualizing Pollution Characteristics and Migration Pattern. J. Hazard. Mater. 2023, 459, 132135. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, M.; Cai, H.; Chen, P. Numerical Simulation of the Temperature Fields in the Shielding Walls of Frozen Soil with Multi-Circle-Pipe Freezing in Shaft Sinking. Therm. Sci. 2019, 23, 647–652. [Google Scholar] [CrossRef]
- Shi, Y.; Ma, W.; Zhang, L.; Yang, C.; Shang, F.; Chen, C. Change of Pore Water Near the Freezing Front During Soil Freezing: Migration and Mechanisms. Pedosphere 2024, 34, 770–782. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, L. A Theoretical Model of Soil Freezing Characteristic Curve Considering the Freezing of Adsorbed Water and Capillary Water. Water Resour. Res. 2023, 59, e2023WR034662. [Google Scholar] [CrossRef]
- Teng, J.; Dong, A.; Zhang, S.; Zhang, X.; Sheng, D. Freezing-Thawing Hysteretic Behavior of Soils. Water Resour. Res. 2024, 60, e2024WR037280. [Google Scholar] [CrossRef]
- Zhao, Y.; Si, B.; He, H.; Xu, J.; Peth, S.; Horn, R. Modeling of Coupled Water and Heat Transfer in Freezing and Thawing Soils, Inner Mongolia. Water 2016, 8, 424. [Google Scholar] [CrossRef]
- Bai, R.; Lai, Y.; Zhang, M.; Yu, F. Theory and Application of a Novel Soil Freezing Characteristic Curve. Appl. Therm. Eng. 2018, 129, 1106–1114. [Google Scholar] [CrossRef]
- Nagare, R.M.; Schincariol, R.A.; Quinton, W.L.; Hayashi, M. Effects of Freezing On Soil Temperature, Freezing Front Propagation and Moisture Redistribution In Peat, Laboratory Investigations. Hydrol. Earth Syst. Sci. 2012, 16, 501–515. [Google Scholar] [CrossRef]
- Sun, K.; Tao, X.; Zhou, A. Phase Field Modeling of Freezing Characteristics of Saturated Soil with Different Particle Sizes. Comput. Geotech. 2023, 164, 105794. [Google Scholar] [CrossRef]
- Yang, H.; Lei, B.; Xie, L.; Hu, C.; Liu, J. Experimental Study on Water and Salt Migration and the Aggregate Insulating Effect in Coarse-grained Saline Soil Subgrade Under Freeze-thaw Cycles. Appl. Sci. 2024, 14, 8970. [Google Scholar] [CrossRef]
- Yu, Z.; Fang, J.; Xu, A.; Zhou, W. The Study of Influence of Freeze-Thaw Cycles on Silty Sand in Seasonally Frozen Soil Regions. Geofluids 2022, 2022, 6886108. [Google Scholar] [CrossRef]
- Han, S.; Cao, W.; Chou, Y.; Peng, E. Experimental Study on the Change in Freezing Temperature During the Remediation of Pb-Contaminated Soils with Biochar. Atmosphere 2024, 15, 1483. [Google Scholar] [CrossRef]
- Teng, J.; Kou, J.; Yan, X.; Zhang, S.; Sheng, D. Parameterization of Soil Freezing Characteristic Curve for Unsaturated Soils. Cold Reg. Sci. Technol. 2020, 170, 102928. [Google Scholar] [CrossRef]
- Miao, Y.; Cao, W.; Zhang, L.; Zhao, Q.; Ding, R.; Wang, S. Distribution of BTEX in Freeze-Thaw Soil System and Its Relationship with Soil Physical and Chemical Properties. Fresenius Environ. Bull. 2022, 31, 3483–3491. [Google Scholar]
- Wang, C.; Li, K.; Tian, J.; Meng, F.; Yang, H.; Ren, J.; Li, S. Quantification of Chloride Saline Soil Freezing-Thawing Temperature Threshold Based on Thermodynamic Theory. Acta Geotech. 2025, 20, 1049–1068. [Google Scholar] [CrossRef]
- Wan, X.; Lai, Y.; Wang, C. Experimental Study on the Freezing Temperatures of Saline Silty Soils. Permafr. Periglac. Process. 2015, 26, 175–187. [Google Scholar] [CrossRef]
- Xu, J.; Li, F.; Gao, W.; Ding, H.; Zhang, J.; Wen, H.; Yu, X. Study on the Evolution of the Dielectric Properties of Artificially Frozen Sand Under Temperature Variation. Environ. Earth Sci. 2024, 83, 355. [Google Scholar] [CrossRef]
- Ding, B.; Zhang, Y.; Yu, X.; Jia, G.; Wang, Y.; Zheng, P.; Li, Z. Comparative Study of Seasonal Freeze-thaw on Soil Water Transport in Farmland and Its Shelterbelt. Catena 2023, 225, 106982. [Google Scholar] [CrossRef]
- Henry, H.A.L. Soil Freeze-Thaw Cycle Experiments: Trends, Methodological Weaknesses and Suggested Improvements. Soil Biol. Biochem. 2007, 39, 977–986. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, B.; Jiang, H.; Li, T.; Zhang, B.; Wu, W. Initial Soil Moisture Prewinter Affects the Freeze-Thaw Profile Dynamics of a Mollisol in Northeast China. Catena 2024, 234, 107648. [Google Scholar] [CrossRef]
- Yuan, G.; Che, A.; Tang, H. Evaluation of Soil Damage Degree Under Freeze-Thaw Cycles Through Electrical Measurements. Eng. Geol. 2021, 293, 106297. [Google Scholar] [CrossRef]
- Li, G.; Zhang, J.; Zhou, Z.; Wang, F.; Chen, D.; Cao, Y.; Wu, G. A Novel Freezing Point Determination Method for Oil-Contaminated Soils Based on Electrical Resistance Measurement and Its Influencing Factors. Sci. Total Environ. 2020, 721, 137821. [Google Scholar] [CrossRef]
- Yuan, G.; Che, A.; Feng, S. Evaluation Method for the Physical Parameter Evolutions of Highway Subgrade Soil Using Electrical Measurements. Constr. Build. Mater. 2020, 231, 117162. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Sun, J.; Ding, L.; Wang, Y.; Wang, H. Effect of Seasonal Freeze-Thaw Process on Spatial and Temporal Distribution of Soil Water and Its Infiltration to Recharge Groundwater. Hydrol. Process. 2024, 38, e15110. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, L.; Mu, Y.; Ma, W.; Kong, X.; Yang, C. Dynamic Characteristics of Soil Pore Structure and Water-heat Variations During Freeze-thaw Process. Eng. Geol. 2024, 343, 107785. [Google Scholar] [CrossRef]
- Kalyuzhnyi, I.L.; Lavrov, S.A. Mechanism of the Influence of Soil Freezing Depth on Winter Runoff. Water Resour. 2017, 44, 604–613. [Google Scholar] [CrossRef]
- Stuurop, J.C.; van der Zee, S.E.A.T.M.; French, H.K. The Influence of Soil Texture and Environmental Conditions on Frozen Soil Infiltration: A Numerical Investigation. Cold Reg. Sci. Technol. 2022, 194, 103456. [Google Scholar] [CrossRef]
- Li, N.; Cuo, L.; Zhang, Y. On the Freeze-Thaw Cycles of Shallow Soil and Connections with Environmental Factors Over the Tibetan Plateau. Clim. Dyn. 2021, 57, 3183–3206. [Google Scholar] [CrossRef]
- Huang, M.; Jia, J.; Liu, K. Probabilistic Analysis of the Frozen Depth of Soil Foundations Considering Thermal and Hydraulic Coupling by COMSOL. KSCE J. Civ. Eng. 2024, 28, 3671–3680. [Google Scholar] [CrossRef]

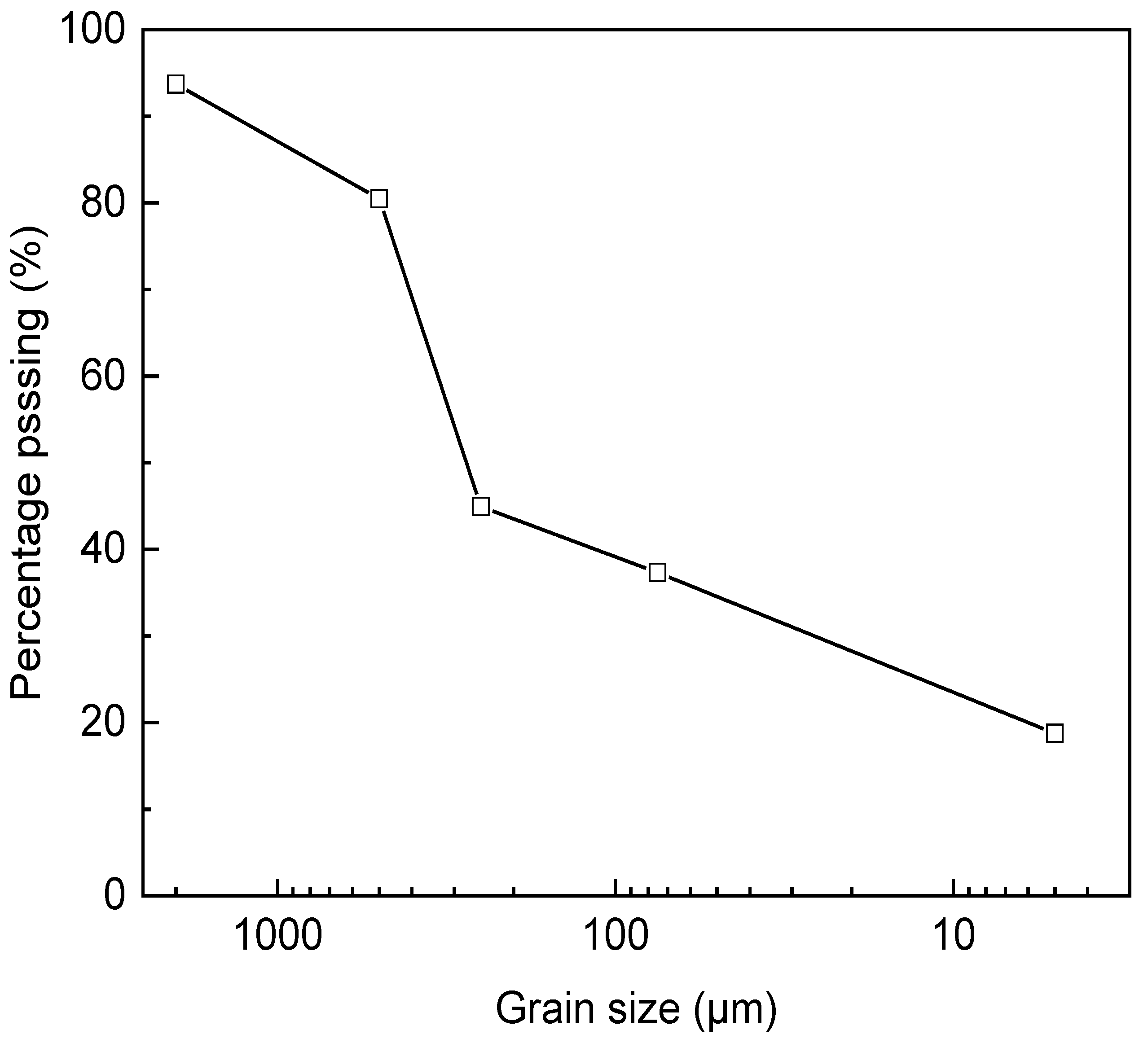



| Natural Volumetric Water Content (%) | Natural Dry Density (g·cm−3) | Specific Gravity | Plastic Limit (%) | Liquid Limit (%) | Plasticity Index | pH |
|---|---|---|---|---|---|---|
| 18.5% | 1.55 | 2.65 | 23.7 | 34.1 | 10.4 | 6.78 |
| No. | Parameter | Description | Resistivity (Ω·m) |
|---|---|---|---|
| I | ρ1 | First layer medium, thawed layer, 2 m parallel strata. | 200 |
| II | ρ2 | Second layer medium, freezing transition zone, 3~8 m inclined strata. | 500 |
| III | ρ3 | Third layer medium, seasonally frozen soil layer, 4~6 m inclined strata. | 2000 |
| IV | ρ4 | Fourth layer medium, bedrock layer, 20 m depth. | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Yang, H.; Yue, J.; Wei, H.; Che, R.; Duan, Q.; Zhou, S.; Sun, M. Freezing Behavior of Clayey Sand and Spatiotemporal Evolution of Seasonally Frozen Soil Distribution in the Qinghai–Tibet Plateau. Appl. Sci. 2025, 15, 7498. https://doi.org/10.3390/app15137498
Xu Y, Yang H, Yue J, Wei H, Che R, Duan Q, Zhou S, Sun M. Freezing Behavior of Clayey Sand and Spatiotemporal Evolution of Seasonally Frozen Soil Distribution in the Qinghai–Tibet Plateau. Applied Sciences. 2025; 15(13):7498. https://doi.org/10.3390/app15137498
Chicago/Turabian StyleXu, Yunlei, Haiyan Yang, Jianhua Yue, He Wei, Rongqi Che, Qibao Duan, Shulong Zhou, and Meng Sun. 2025. "Freezing Behavior of Clayey Sand and Spatiotemporal Evolution of Seasonally Frozen Soil Distribution in the Qinghai–Tibet Plateau" Applied Sciences 15, no. 13: 7498. https://doi.org/10.3390/app15137498
APA StyleXu, Y., Yang, H., Yue, J., Wei, H., Che, R., Duan, Q., Zhou, S., & Sun, M. (2025). Freezing Behavior of Clayey Sand and Spatiotemporal Evolution of Seasonally Frozen Soil Distribution in the Qinghai–Tibet Plateau. Applied Sciences, 15(13), 7498. https://doi.org/10.3390/app15137498







