Distributed Prediction-Enhanced Beamforming Using LR/SVR Fusion and MUSIC Refinement in 5G O-RAN Systems

Abstract

Low-latency and robust beamforming are vital for sustaining signal quality and spectral efficiency in emerging high-mobility 5G and future 6G wireless networks. Conventional beam management approaches, which rely on periodic Channel State Information feedback and static codebooks, as outlined in 3GPP standards, are insufficient in rapidly varying propagation environments. In this work, we propose a Dominance-Enforced Adaptive Clustered Sliding Window Regression (DE-ACSW-R) framework for predictive beamforming in O-RAN Split 7-2x architectures. DE-ACSW-R leverages a sliding window of recent angle of arrival (AoA) estimates, applying in-window change-point detection to segment user trajectories and performing both Linear Regression (LR) and curvature-adaptive Support Vector Regression (SVR) for short-term and non-linear prediction. A confidence-weighted fusion mechanism adaptively blends LR and SVR outputs, incorporating robust outlier detection and a dominance-enforced selection regime to address strong disagreements. The Open Radio Unit (O-RU) autonomously triggers localised MUSIC scans when prediction confidence degrades, minimising unnecessary full-spectrum searches and saving delay. Simulation results demonstrate that the proposed DE-ACSW-R approach significantly enhances AoA tracking accuracy, beamforming gain, and adaptability under realistic high-mobility conditions, surpassing conventional LR/SVR baselines. This AI-native modular pipeline aligns with O-RAN architectural principles, enabling scalable and real-time beam management for next-generation wireless deployments.

1. Introduction

Precise and timely beamforming has emerged as a cornerstone of network performance in recent wireless communication systems, particularly in the context of 5G and the upcoming 6G technology. Conventional beamforming in 3GPP New Radio (NR) hinges on the systematic acquisition of Channel State Information (CSI) via CSI reference signal (CSI-RS) transmissions and their associated feedback mechanisms [1]. In high-mobility scenarios, the time lag between measurement, feedback, and beam adaptations can cause beam misalignment and a decreased signal-to-noise ratio (SNR), resulting in system throughput degradation [2]. Additionally, the complexities of real-world deployment are exacerbated in high-density urban areas, where user equipment (UE) mobility is rapid and channel conditions are highly variable. Moreover, conventional static-beam management approaches lack sufficient adaptability to mitigate rapidly varying propagation conditions, multipaths, and non-linear user mobility patterns [3,4,5]. Angle of arrival (AoA) estimation in these conditions is inherently difficult, especially if the system assumes constant velocity or flat user trajectories. These issues are exacerbated by periodic signal oscillation, interference, and the limitations of traditional codebook-based beamforming systems [6,7,8].

Within this context, we propose a novel predictive beamforming framework, termed Dominance-Enforced Adaptive Clustered Sliding Window Regression (DE-ACSW-R). In this framework, the Radio Unit performs immediate low-latency AoA prediction using weighted Linear Regression (LR), while the Distributed Unit concurrently applies a curvature-adaptive Support Vector Regression (SVR) and executes the dynamic fusion and dominance logic. This approach ensures both fast slot-level responsiveness and robust, Mean Squared Error (MSE)-optimised prediction blending, enhancing overall performance in rapidly varying environments.

The DE-ACSW-R system also incorporates an intelligent fallback mechanism to further enhance beam alignment precision and reliability under highly dynamic or unpredictable channel conditions. Specifically, when sudden AoA deviations or drops in prediction confidence are detected, the Radio Unit autonomously triggers a localised Multiple Signal Classification (MUSIC) scan, thereby promptly refining AoA estimation without incurring significant computational overhead or latency.

Our solution is well embedded in the Open Radio Access Network (O-RAN) framework introduced by the O-RAN Alliance. O-RAN offers a virtualised and disaggregated architecture that incorporates flexibility, openness, and intelligence into the Radio Access Network (RAN). In particular, the O-RAN Category B functional split (Split 7-2x) enables the centralisation of beamforming decisions at the Open Distributed Unit (O-DU) while allowing for real-time signal processing in the Open Radio Unit (O-RU). This architecture facilitates improved flexibility in beam control by leveraging AI-based models, low-latency interfaces, and predictive algorithms running in near-real-time Radio Intelligent Controller (RIC) platforms [9,10,11,12].

Despite O-RAN’s architectural flexibility, predictive AoA modelling still presents several practical challenges:

The first challenge arises from the assumptions inherent in the traditional Linear Regression assumptions, which assumes a constant-speed trajectory, treating all historical AoA samples equally. In reality, user motion is subject to dynamic behaviour acceleration, deceleration, and non-linear changes in direction. This leads to prediction errors, particularly during transitions and curved motion [13,14,15]. To address this, we implement a Weighted Linear Regression (WLR) model, assigning greater importance to more recent AoA samples, thus better capturing recent non-linear or abrupt mobility patterns.

A second critical challenge is the sensitivity of Support Vector Regression (SVR) parameters to varying mobility dynamics. While SVR provides powerful modelling capabilities, its performance heavily depends on kernel hyperparameters like Gaussian width (σ) and regularisation strength (λ). Static settings of these parameters can lead to underfitting in environments with minimal mobility or overfitting in scenarios involving high speeds or multipath-rich conditions [16,17]. To mitigate this, we introduce a Curvature-Adaptive SVR kernel, dynamically adjusting the Gaussian width (σ) based on real-time estimated AoA trajectory curvature. This adaptation allows for the SVR model to respond to rapid and non-linear changes in user motion more effectively.

A third challenge involves the overreliance on confidence without the sufficient consideration of physical insights. Current switching mechanisms between LR and SVR often rely solely on statistical metrics, such as the confidence derived from AoA spread. However, this alone may misrepresent actual reliability, particularly in cases of high SNRs with erratic movement or low SNRs with steady motion [18,19].

Our system employs a Dominance-Enforced Adaptive Fusion approach. This method first uses a clustered sliding window: when a sharp AoA jump is detected, only the most recent post-jump samples are used for both LR and SVR. Then, both predictions are blended using a dynamic fusion rule that assigns a higher weight to the method with a lower instantaneous Mean Squared Error (MSE) over the window. If one predictor is clearly more accurate, a “dominance-enforced override” forces the fused prediction to select that value, ensuring optimal reliability under both linear and non-linear mobility. This system leverages adaptive predictions combined with the real-time signal processing capabilities that are uniquely enabled by O-RAN’s Split 7-2x architecture.

The key novel contributions of this work are as follows:

• Parallel distributed prediction architecture: We uniquely leverage the O-RAN Split 7-2x architecture to distribute prediction tasks. Lightweight LR inference is executed at the O-RU for immediate slot-level responsiveness, while adaptive, curvature-aware SVR is performed at the O-DU. This parallel dual-pipeline eliminates the latency overhead and instability associated with switching between reactive or sequential models.
• Dominance-Enforced Adaptive Clustered Sliding Window Fusion (DE-ACSW-R): Our core innovation is a mathematically novel fusion framework that (1) detects sharp AoA jumps within the sliding prediction window and clusters (selects) only post-jump samples for subsequent regression and SVR inference, maximising reliability after rapid trajectory changes, and also (2) applies a dynamic, dominance-enforced fusion rule: the fused AoA prediction is weighted toward the model (LR or SVR) that exhibits the lowest MSE against the most recent ground truth, with a “dominance-enforced” override when there is a clear performance gap.
• Curvature-adaptive SVR kernel: We introduce a dynamic SVR kernel-width adaptation strategy, where the Gaussian width (σ) is modulated by real-time AoA trajectory curvature. This enables highly responsive and robust prediction under non-linear or unpredictable mobility.
• Autonomous MUSIC-based fallback: When a jump is detected or when the confidence in prediction drops, the O-RU autonomously triggers a localised high-speed MUSIC scan, refining AoA estimation within a reduced angular search space. This approach enables a rapid and robust recovery without the cost of a full-spectrum search.

Simulation results show that our DE-ACSW-R approach consistently achieves lower AoA-predicted Root Mean Squared Error (RMSE) than classical LR/SVR switching or static-fusion approaches and significantly sharpens MUSIC spectrum peak localisation. These improvements result in more accurate beam selection, a higher average signal-to-noise ratio (SNR), and faster, more robust beam alignment in O-RAN-based 5G and 6G systems.

2. Related Work

The increasing complexity of wireless communication environments in 5G and emerging 6G networks has accelerated the development of intelligent beamforming and AoA estimation techniques. These efforts aim to address core challenges, including user mobility, multipath propagation, and latency-sensitive processing. Traditional subspace methods like MUSIC offer high resolution in AoA estimation, but suffer from computational limitations under dynamic conditions. Meanwhile, machine learning (ML)-based approaches have shown promise in enhancing prediction accuracy and adapting to fast-changing propagation characteristics. In parallel, the O-RAN architecture has emerged as a modular and flexible framework for enabling AI-driven signal processing, distributed inference, and real-time beam management.

In this context, a range of research works have explored techniques spanning from classical signal estimation to predictive modelling and AI-native RAN architectures. The following studies provide a representative overview of prior work and serve as a basis for comparison with our DE-ACSW-R framework.

Spanos et al. present an enhanced MUSIC-based AoA estimation approach for 5G NR uplink by leveraging Sounding Reference Signals (SRS) [20]. Their method improves resolution under mobility using a full subspace decomposition, but does not address the latency and does not consider the predictive mechanisms for proactive real-time beam steering. In contrast, our work introduces lightweight prediction pipelines to proactively steer beams, thereby reducing reliance on full-spectrum scanning in real-time.

Elsisi et al. propose a computationally efficient 2D-MUSIC method tailored for joint range and angle estimation in 5G and 6G sensing applications [21]. While their focus is on reducing complexity for static and linear tracking, their solution lacks a predictive mechanism for AoA evolution. Their approach is limited to static scenarios, making it less suitable for high-mobility or non-linear environments. Our approach extends these by introducing (1) clustered sliding window regression to adaptively re-centre the prediction window after AoA jumps, (2) dominance-enforced fusion to privilege the most accurate predictor (LR or SVR) per window based on instantaneous error, and (3) a dominance-enforced override for sharply non-stationary scenarios.

Shan et al. explore the use of SVR combined with AoA and chaos mapping to forecast tunnel crown displacement under dynamic excavation [22]. Although not wireless-focused, the paper demonstrates how SVR performance improves when paired with dynamic trajectory modelling, supporting our adoption of curvature-adaptive SVR for non-linear AoA prediction in mobile environments. We selected this study as it illustrates the effectiveness of SVR in capturing non-linear dynamics, reinforcing our approach’s validity in complex AoA trajectory prediction.

Mohamed et al. introduce a machine learning-aided approach to optimise beam selection and update timing in mmWave 5G systems [23]. Their solution uses historical measurements to reduce handover delays, but does not explicitly model AoA prediction or support distributed O-RAN integration. Their lack of direct AoA predictive modelling highlights a key gap addressed by our method, which integrates predictive AoA modelling within distributed O-RAN architectures.

Al-Shehri et al. propose a low-complexity machine-learning design for mmWave beam prediction using time-series inputs [24]. While effective for low-latency inference, the method lacks a fallback mechanism or kernel adaptation for trajectory curvature. Their static kernel limits adaptability in dynamic scenarios. Our framework addresses both issues by combining clustered LR and curvature-sensitive SVR with a dominance-enforced and error-weighted fusion, along with an autonomous, localised MUSIC fallback, which uniquely enables both rapid adaptation and robust recovery without relying solely on confidence metrics or static thresholds.

Jin et al. present a model-driven neural network to enhance AoA estimation accuracy in non-line-of-sight and multipath-rich conditions [25]. While powerful, their approach relies on deep learning and retraining for environment changes, which may not suit low-latency O-RAN deployment. Compared to our approach, their approach involves significant overhead due to retraining requirements. We have avoided this overhead by employing interpretable, dynamically clustered regression, error-driven fusion, and real-time decentralised prediction, delivering both high accuracy and practical O-RAN deployability.

These studies were selected based on their significant contributions to AoA estimation, predictive beamforming, and the integration of machine learning techniques in wireless systems. Each chosen work represents significant advancements and provides critical benchmarks against which the unique contributions of our DE-ACSW-R framework can be effectively demonstrated and contrasted.

Table 1. Summary of related works and key advancements in DE-ACSW-R.

Reference	Methodology	Key Contributions	Limitations	Comparison with DE-ACSW-R
[20] Spanos et al.	MUSIC (SRS-based)	High-resolution AoA estimation	Lacks predictive and latency-sensitive real-time beam steering	DE-ACSW-R incorporates predictive modelling for proactive beamforming
[21] Elsisi et al.	Computationally Efficient 2D MUSIC	Reduced complexity for static scenarios	No predictive mechanism, limited mobility handling	DE-ACSW-R provides dynamic clustering and adaptive prediction, suitable for non-linear mobility
[22] Shan et al.	SVR with Chaos Mapping	Improved SVR predictive capability	Lacks AoA predictive modelling in mobile scenarios	DE-ACSW-R leverages SVR with curvature-adaptive kernels for wireless AoA
[23] Mohamed et al.	ML-based beam selection	Optimises beam selection and timing	Lacks distributed integration, no direct AoA modelling	DE-ACSW-R integrates directly into O-RAN with distributed inference
[24] Al-Shehri et al.	Low-complexity ML beam prediction	Effective low-latency prediction	No fallback mechanism, static kernel	DE-ACSW-R provides dynamic adaptation and MUSIC-based fallback mechanisms
[25] Jin et al.	Neural network-driven AoA estimation	Enhances accuracy under multipath	Deep learning overhead, lacks low-latency deployment	DE-ACSW-R avoids overhead through adaptive regression and real-time prediction

highlights both the strengths of prior approaches and how our method addresses their limitations.

3. Proposed Solution to Predict the AoA

In the following sub-sections, we present the solution proposed to predict the movement of the user in advance. Concretely, Section 3.1 presents the system and the assumptions that we consider, whereas Section 3.2 shows the predictive AoA framework and the decision logic for determining the position of the user. Section 3.3 mathematically analyses the predictive framework, and, lastly, Section 3.4 explains how this framework should be used for improving beamforming operations.

3.1. System Overview and Assumptions

The Open Radio Access Network (O-RAN) Alliance promotes openness, intelligence, and interoperability in next-generation RAN deployments [26]. Among its key architectural innovations is the functional split framework, particularly Split 7-2x, which is associated with Category B O-RAN deployments. This split delineates the distribution of physical (PHY) layer processing between the O-RU (Radio Unit) and the O-DU (Distributed Unit), enabling flexible deployment and more efficient beamforming control [27].

In Split 7-2x, the lower PHY functions (such as cyclic prefix insertion/removal and digital front-end operations) are handled by the O-RU. In contrast, the upper PHY functions (e.g., modulation/demodulation, coding, scrambling, and precoding) are centralised at the O-DU. This allows for the O-DU to manage beamforming and precoding operations across multiple RUs in a coordinated fashion, leveraging centralised CSI feedback and scheduling decisions [28,29].

The advantage of Split 7-2x lies in its ability to support high-bandwidth low-latency fronthaul (e.g., eCPRI) while enabling real-time signal processing closer to the antenna. This is particularly beneficial for beamforming in high-mobility environments, where quick adaptation to AoA variations is required.

O-RAN Category B, designed for massive MIMO and intelligent beam management, aligns closely with our research goal: to realise a parallel, distributed prediction and fusion architecture leveraging DE-ACSW-R. In this system, the O-RU performs clustered jump-aware Weighted Linear Regression (WLR) for fast, local AoA prediction, while the O-DU concurrently executes curvature-adaptive SVR and applies dynamic dominance-based error fusion (dominance-enforced override). This dual-pipeline approach ensures that the most reliable predictor (LR or SVR) is adaptively privileged based on instantaneous window performance, while also supporting rapid window clustering in the presence of sudden AoA shifts. The result is robust low-latency beamforming, fully exploiting the flexibility and modularity of Split 7-2x O-RAN.

While the distributed processing model of Split 7-2x enables centralised beamforming, it also introduces the following challenges:

• The O-DU lacks an immediate physical-layer awareness of rapid changes at the O-RU.
• CSI-RS-based feedback loops incur latency and cannot adapt quickly in high-mobility scenarios [30,31].
• Codebook-based beam selection often underperforms in multipath and NLoS (non-line-of-sight) conditions.

Nevertheless, to fully appreciate the motivation behind predictive AoA estimation within the O-RAN architecture, it is essential to contrast it with conventional beamforming techniques defined by 3GPP standards [32,33]. While Split 7-2x enables a more responsive and modular beamforming pipeline, legacy NR systems continue to rely heavily on feedback-driven mechanisms, which are susceptible to significant latency and cannot react promptly to abrupt changes in user direction or channel conditions. Our results and analysis demonstrate that, in high-mobility and densely urban scenarios, the time lag and granularity of CSI-RS-based feedback are insufficient to maintain beam alignment, resulting in increased prediction error and degraded SNR. This contrast underscores the need for real-time prediction-enhanced frameworks such as our proposed DE-ACSW-R dual-pipeline architecture, which proactively adapts to user mobility by (1) dynamically clustering prediction windows after AoA jumps, (2) enforcing dominance-based fusion according to error metrics, and (3) fusing physical-layer trends with adaptive learning models for robust, anticipatory beam management.

3.1.1. 3GPP Beamforming Limitations

In traditional 3GPP-compliant radio access networks (e.g., LTE and 5G NR), beamforming is typically executed through periodic channel measurements and feedback cycles. User Equipment (UE) receives reference signals, such as CSI-RS (Channel State Information Reference Signals), from the gNB, which then relies on feedback from the UE to estimate the preferred beam indices or channel quality indicators (CQI). The gNB uses this information to perform beam selection, adaptation, and scheduling. However, the latency between reference signal transmission, feedback reporting, and actual beam update creates a bottleneck, especially in high-speed or dense urban environments where the AoA may change faster than the feedback loop can track.

Moreover, the 3GPP beam management procedures, which include beam sweeping, measurement, reporting, and refinement, are optimised for semi-static or low-mobility scenarios. In high-mobility use cases, such as vehicular or UAV applications, these procedures may fail to respond quickly enough, resulting in outdated beam decisions and degraded link quality. Another limitation lies in the discrete nature of codebook-based beamforming: UE can only choose from a predefined set of beams, which may not align well with the instantaneous channel geometry, especially under multipath fading or non-line-of-sight (NLoS) conditions [34,35].

Consequently, while the 3GPP standard supports beamforming through explicit feedback mechanisms, its performance heavily depends on the feedback rate, channel coherence time, and codebook granularity. These limitations underscore the need for predictive and intelligent beamforming strategies. Our proposed DE-ACSW-R framework directly addresses these gaps by adaptively clustering prediction windows after AoA jumps, enforcing dominance-based fusion (dominance-enforced override) when one predictor outperforms the other, and continuously learning from mobility and AoA trajectory patterns. This results in adaptive, low-latency predictions that fully exploit the architectural flexibility of O-RAN Split 7-2x. Our solution enables proactive beam steering even in the presence of abrupt motion changes or non-linear trajectories, as confirmed by our simulation results and empirical model validation.

In contrast to these 3GPP-defined mechanisms, the architectural openness and functional disaggregation of O-RAN, particularly under the Split 7-2x configuration, provide a fundamentally more flexible and intelligent platform for predictive beamforming. Unlike legacy systems that rely on reactive feedback loops, the O-RAN architecture enables proactive and adaptive beam steering by separating real-time lower-layer signal processing (at the O-RU) from higher-level computation-intensive prediction and decision-making (at the O-DU) [36,37,38,39].

In our model, the O-RU executes low-latency jump-aware clustered Weighted Linear Regression (WLR) predictions in real-time, dynamically splitting the prediction window when abrupt AoA changes are detected. Simultaneously, the O-DU leverages a broader history and additional context, including curvature-adaptive SVR, real-time confidence, and recent error metrics to refine, override, or fuse O-RU predictions using dynamic dominance-enforced error fusion logic.

This dual-pipeline prediction architecture achieves two goals:

• Immediate low-latency AoA adjustment at the RU for fast mobility or sudden AoA jumps;
• Continuous validation, correction, or fusion of predictions at the DU for robustness and overall performance.

The O-RU can also autonomously trigger localised MUSIC scans based on detected AoA jumps or drops in prediction confidence, further refining AoA estimates in near-real-time without requiring DU intervention.

By explicitly distributing, clustering, and fusing predictive intelligence across both layers while enforcing dynamic dominance (dominance-enforced override) when one model substantially outperforms the other, our architecture enhances AoA estimation accuracy, robustness, and beamforming adaptability. This approach is fully aligned with O-RAN’s modular design principles and the high-performance low-latency demands of next-generation networks.

To overcome these limitations and fully exploit the architectural flexibility of Split 7-2x, we propose a distributed DE-ACSW-R beamforming strategy. In our framework, the following factors are observed:

• The O-RU performs real-time AoA tracking using a jump-aware, clustered, WLR model. Upon detecting an abrupt AoA jump within the window, the O-RU recentres its prediction on the most recent (post-jump) samples to maximise its responsiveness to non-linear user mobility.
• The O-RU maintains per-user AoA history buffers and precomputes beamforming weights for the predicted angles, ensuring slot-level adaptation and low-latency response.
• Concurrently, the O-DU executes a curvature-adaptive SVR prediction process using a broader AoA history, real-time SNR, and physical and statistical confidence metrics. The O-DU can override, validate, or dynamically fuse O-RU predictions using a dominance-enforced logic that always selects the most reliable predictor based on windowed mean squared error (MSE).
• At every slot boundary, the O-RU transmits updated AoA histories to the O-DU. The O-DU replies with either a dynamically fused AoA prediction (a dominance-enforced confidence-curvature-weighted combination of LR and SVR, or an explicit override/fallback command if low confidence or outlier behaviour is detected).

Whenever a sudden AoA jump or confidence drop is observed, the O-RU autonomously triggers a localised MUSIC scan, refining the AoA estimate with minimal latency and computational overhead. This dual-path approach ensures both ultra-fast adaptation to real-time conditions and robust, centrally validated prediction, delivering reliable beamforming under fast mobility and multipath environments.

This layered prediction and control design guarantees that latency-critical low-complexity decisions are made directly at the O-RU, close to the antenna, while more advanced and computationally intensive predictions are performed centrally at the O-DU.

When uncertainty or abrupt changes are detected, such as non-linear AoA shifts, mobility-induced Doppler jumps, or sudden SNR drops, the O-RU autonomously triggers a localised enhanced MUSIC scan. This scan operates over a narrowed angular window, dramatically reducing computational cost and delay compared to full-spectrum searches, and thus maintains real-time responsiveness without waiting for O-DU coordination.

3.1.2. Key Technical Contributions

Key technical contributions and enablers within O-RAN Split 7-2x include the following:

• Parallel distributed inference: The system executes lightweight Weighted LR prediction at the O-RU (for immediate reaction) and advanced curvature-adaptive SVR at the O-DU (for robust, longer-term modelling), running in true parallel to eliminate the inherent latency of reactive model switching.
• Dominance-enforced confidence–curvature weighted fusion: LR and SVR predictions are fused in real-time via a dynamic weighting algorithm that incorporates statistical spread (confidence), trajectory curvature, and instantaneous windowed prediction error. Whenever a clear winner is present (as determined by MSE), the fusion “dominance-enforced” overrides the privileges of that predictor, ensuring that the most reliable result drives beam updates at each slot.
• Autonomous MUSIC-based fallback: Upon detection of a sharp AoA jump or drop in prediction confidence, the O-RU immediately triggers a localised MUSIC estimation within a reduced angular sector, providing rapid and robust AoA refinement and protecting against outlier or adversarial conditions.
• Jump-aware window clustering: When sudden AoA jumps are detected within the sliding window, the regression window is split, and predictions are recalculated only on the most recent post-jump segment, reducing prediction error during abrupt trajectory changes.
• Modular and practical integration: The prediction architecture is fully modular and designed for seamless integration with standard O-DU scheduling and control logic. No changes are required at the O-RU’s hardware level, facilitating practical adoption and interoperability within existing O-RAN deployments.

Overall, this architecture leverages the flexibility of O-RAN Split 7-2x to optimise both responsiveness and accuracy, enabling predictive AI-driven beam management that is well-suited for 5G and future 6G RANs.

3.2. Predictive AoA Framework and Decision Logic

In high-mobility environments, conventional AoA estimation approaches that rely solely on real-time MUSIC scanning are often limited by computational overhead and scanning latency. To address these challenges, our proposed DE-ACSW-R framework integrates a jump-aware predictive pipeline that exploits the clustered structure of recent AoA history to improve prediction robustness and adaptivity. The predicted AoA is used proactively to update beamforming weights, allowing for beams to be dynamically steered for the next transmission interval with minimal latency and improved resilience to abrupt mobility changes.

As depicted in Figure 1, DE-ACSW-R operates in a dual-layer distributed architecture conforming to O-RAN Split 7-2x: the O-RU runs a lightweight, clustered, WLR predictor using a sliding window of recent AoA estimates, dynamically detecting and isolating abrupt trajectory jumps. This ensures that sudden mobility events are rapidly captured and that predictions are focused on the most relevant, recent samples. In parallel, the O-DU receives updated AoA histories and performs curvature-adaptive SVR with windowed error and curvature-based kernel adaptation. A dominance-enforced logic fuses the LR and SVR predictions, always selecting or favouring the predictor with the lower observed windowed MSE for each prediction step [40].

Additionally, an enhanced fallback mechanism is triggered at the O-RU whenever the prediction confidence drops or a jump is detected. In such cases, the O-RU autonomously initiates a localised MUSIC scan over a reduced angular sector, refining the AoA estimate without the computational penalty of a full-spectrum search.

The choice of LR and SVR is motivated by their complementary strengths: LR provides fast, interpretable, and low-complexity predictions, ideal for real-time execution at the RU, while SVR, enhanced by curvature adaptation, runs at the DU and provides robustness in the presence of non-linear mobility and multipath effects. The clustering and weighting in the sliding window ensure its responsiveness to dynamic scenarios, while the dominance-enforced fusion strategy guarantees that only the most reliable prediction influences the final beam update at each time slot.

In contrast, SVR provides enhanced flexibility for modelling non-linear AoA paths, especially under NLoS and dynamic mobility conditions. Its accuracy, however, depends critically on the selection of kernel parameters. To address this, our O-DU implementation utilises a curvature-adaptive SVR, dynamically adjusting the Gaussian kernel width based on the estimated AoA curvature using second-order differences within the sliding window. This adaptation ensures stable operation and steady-state mobility while allowing for SVR to respond rapidly to sharp non-linear trajectory changes. Given the higher computational requirements, SVR is executed at the O-DU, where an extended AoA history and additional physical layer information, such as SNR and ToA, are available.

Unlike conventional approaches that switch between LR and SVR based on confidence or error metrics, our framework applies a dominance-enforced fusion logic at the O-DU. The fusion process first checks for in-window jumps and then enforces a clustered window for regression when a jump is detected. LR and SVR predictions are both computed over the current (or clustered) window, and their mean squared errors (MSE) against recent AoA ground truth are compared. The predictor with the lower MSE is assigned a dominant weight in the final fused output. Only if the two predictors are within a small error margin is a weighted average used; otherwise, the more accurate model is selected for that time slot. This approach robustly mitigates the impact of outlier predictions and ensures optimal tracking across varying mobility patterns.

In parallel, the O-RU continuously uses its LR (or clustered LR) prediction to precompute and update beamforming weights for immediate and near-future slots. These predictions are stored and indexed by user ID (UEID) to support rapid beam scheduling and handover decisions. The O-DU, using the fused or dominant AoA predictions, may override or refine these weights as needed based on a broader temporal and physical context, further increasing system adaptability.

By explicitly combining the low-latency responsiveness of LR (including clustered and jump-aware variants) with the non-linear modelling capacity of curvature-adaptive SVR, the proposed framework achieves a substantial improvement in AoA prediction accuracy. The dominance-enforced fusion approach guarantees that, at every time step, the most statistically reliable predictor controls the beam update, providing both robustness to outliers and fast adaptation to sudden trajectory shifts. This aligns precisely with O-RAN’s principles of modular and distributed intelligence, with the O-RU handling latency-critical decisions and the O-DU ensuring global accuracy and consistency through advanced predictive analytics and CSI-based validation.

The resulting prediction pipeline is scalable, latency-aware, and robust for high-mobility multipath-rich urban environments. The proposed dual-layered jump-aware regression and dominance-enforced fusion not only support real-time prediction and fallback, but also maintain full compatibility with standard O-RAN Split 7-2x deployments, offering a practical path toward AI-native self-optimising beamforming in future RANs.

3.3. System Model and Mathematical Formulation

3.3.1. System Geometry and Architecture

The proposed beamforming framework is implemented within an O-RAN Category B deployment, adhering to the Split 7-2x functional disaggregation model defined by the O-RAN Alliance. In this architecture, the O-RU) is physically co-located with the antenna array and is responsible for performing real-time lower PHY processing, including localised beamforming operations. Specifically, the O-RU is equipped with a uniform linear array (ULA) consisting of N antenna elements spaced at half the carrier wavelength, which provides high angular resolution for effective AoA discrimination, even under dense multipath conditions.

In contrast to conventional centralised RAN systems that rely on periodic CSI feedback and gNB-side beam index selection, our design follows a decentralised philosophy. Each O-RU maintains a local per-user angle history buffer and signal observation statistics indexed by unique User Equipment Identifiers (UEIDs). This memory enables the O-RU to track the AoA trajectory of each user u ∈ {1, 2, …, U} using a clustered, weighted sliding window approach. The O-RU employs jump detection logic within this history, segmenting the window and applying adaptive Linear Regression only to the most relevant post-jump segment for each user. This advanced buffer logic allows for the O-RU to perform slot-level, cluster-based AoA prediction, enabling highly responsive and robust beamforming, even during rapid mobility events or abrupt trajectory changes, without waiting for explicit feedback or full CSI reports.

Meanwhile, the O-DU acts as a higher-layer coordination node, executing curvature-adaptive SVR on a broader AoA history for each user and dynamically fusing these predictions with O-RU results. It manages the confidence metrics, orchestrates fallback logic (including MUSIC re-scans), and ensures overall system robustness via long-term trajectory tracking and model calibration. This decoupled design minimises latency, improves responsiveness, and aligns with the distributed processing goals of the Split 7-2x model, where near-field prediction and beam alignment decisions are made autonomously at the edge (O-RU). At the same time, centralised learning and validation occur asynchronously at the O-DU.

3.3.2. Predictive Signal Model Under User Mobility

To realistically capture the dynamic propagation environment in high-mobility O-RAN scenarios, we adopt a predictive baseband signal model that incorporates both deterministic and stochastic signal components. This model is designed to reflect the composite nature of the received signal under time-varying user movement, multipath reflections, fading, and background noise. It serves as the basis for slot-level AoA tracking and prediction using a clustered, adaptive sliding window pipeline, which includes in-window jump detection and cluster-specific regression modelling.

The user signal received at the ith antenna element from user u at time t is modelled as follows:

$$\begin{gathered} r_{i,u}\left(t\right)=G_{\mathrm{u}}{e}^{j\left({\omega }_{\mathrm{c}}t-{\displaystyle \frac{{\omega }_{\mathrm{c}}}{c}}\left(i-1\right)d\sin \left({\theta }_u\left(t\right)\right)\right)}+s_{\mathrm{m}\mathrm{p},\mathrm{u}}\left(t\right)+f_{\mathrm{N}\mathrm{L}\mathrm{O}\mathrm{S},\mathrm{u}}\left(t\right)+n_{i,u}(\mathrm{t}) \\ Fori=\mathrm{1,2},\dots ,N\left(i-thantennaelement\right)andu=\mathrm{1,2},\dots ,U\left(Userindex\right) \end{gathered}$$

(1)

where $G_{\mathrm{u}}$ denotes the amplitude gain of the line-of-sight (LOS) signal component for the user $u$, and ${\omega }_{\mathrm{c}}=2\pi f_c$ is the angular frequency corresponding to the carrier frequency $f_c$. The term ${\displaystyle \frac{{\omega }_{\mathrm{c}}}{c}}\left(i-1\right)d\sin \left({\theta }_u\left(t\right)\right)$ accounts for the phase difference introduced by spatial delays between antenna elements, where ccc is the speed of light, $d=\lambda /2$ is the inter-antenna spacing, and ${\theta }_u\left(t\right)$ represents the instantaneous AoA of the dominant signal path at time $t$.

$M_{\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}}\left(t\right)$ present the multiple paths due to reflections, diffractions, and scattering.

The total received signal includes contributions from $M$ number of multipath components ($s_{\mathrm{m}\mathrm{p},\mathrm{u}}\left(t\right)$). The $f_{\mathrm{N}\mathrm{L}\mathrm{O}\mathrm{S},\mathrm{u}}\left(t\right)$ represents the effect of scattered signals in non-line-of-sight (NLOS) environments, it is generally modelled as a complex Gaussian random variable. The $n_{i,u}$ additive Gaussian noise at the ith antenna. These components cause phase and amplitude distortions, increasing the complexity of AoA estimation.

The model accounts for both spatial diversity across the antenna array and temporal variation induced by user mobility, forming a foundation for evaluating AoA tracking and prediction algorithms in realistic O-RAN deployments.

The choice of this hybrid deterministic–stochastic signal model is guided by its close approximation to real-world wireless propagation, particularly under the constraints and capabilities of O-RAN Category B deployments. In practice, the signal received at each antenna results from a superposition of direct LOS components, scattered multipath replicas, fast-fading variations, and thermal noise. Our model integrates all of these aspects and introduces time dependency through ${\mathsf{\theta }}_{\mathrm{u}}\left(t\right)$, which evolves non-linearly over time.

This non-linear AoA trajectory is especially relevant for high-mobility users (e.g., vehicular or pedestrian motion through cluttered environments), where abrupt changes in direction or velocity can drastically alter the spatial signature of the received signal. Such behaviour challenges static beamforming systems and motivates the need for predictive models capable of forecasting AoA with low latency. Our framework explicitly detects such abrupt changes within the AoA window and adaptively selects clusters of recent samples for linear or SVR-based regression, ensuring robust prediction even during non-linear user trajectories.

By incorporating multipath $s_{\mathrm{m}\mathrm{p},\mathrm{u}}\left(t\right)$ and fading $f_{\mathrm{N}\mathrm{L}\mathrm{O}\mathrm{S},\mathrm{u}}\left(t\right)$ components, the simulation environment also allows us to evaluate the robustness of prediction-enhanced beamforming under challenging channel conditions, such as inter-cell interference, non-line-of-sight (NLoS) dominance, and fading-induced signal dropout.

Furthermore, the statistical properties of each term in Equation (1) allow for controlled experimentation. For example, the number of multipath components and their angular spread can be adjusted to simulate rich-scattering or corridor-type environments.

In the broader beamforming context, Equation (1) serves as the foundation for constructing the received snapshot matrix $X\left(t\right)\in {\mathbb{C}}^{NxT}$ which aggregates signals across antennas and time. This matrix is used to compute the spatial covariance matrix $R_x={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}X\left(t\right)X^H\left(t\right)$, which feeds into subspace-based AoA estimation algorithms such as MUSIC, enhanced MUSIC, or CW-P-MUSIC. The accuracy of these estimators and the efficacy of the beamforming weights derived from them depend critically on how well the signal model reflects true propagation characteristics.

By simulating ${\mathsf{\theta }}_{\mathrm{u}}\left(t\right)$ as a time-varying signal and augmenting it with multipath and fading effects, we create a rigorous testbed for predictive AoA estimation. The AoA traces produced by this model directly feed into our clustered sliding window regression pipeline, where adaptive LR and curvature-adaptive SVR are executed on the most relevant segment of each AoA history. This enables us to quantify improvements in estimation accuracy, spectrum sharpness, and beamforming gain when using models like LR, SVR, or the proposed DE-ACSW-R.

3.3.3. Snapshot Matrix and Predictive Normalisation

In a multi-antenna system with time-varying user mobility, the signal received at the antenna array must be aggregated over both space (antenna elements) and time (snapshots) to form the observation basis for AoA estimation and subsequent prediction. To this end, we construct a snapshot matrix. $X_u\in {\mathbb{C}}^{NxT}$ for each user, u, capturing the spatio-temporal characteristics of their received signal. The matrix is defined as follows:

$$R_u=\left[\begin{array}{cccc}{r}_{1,u}\left(t_1\right)& r_{1,u}\left(t_2\right)& \dots & r_{1,u}\left(t_T\right)\\ r_{2,u}\left(t_1\right)& r_{2,u}\left(t_2\right)& \dots & r_{2,u}\left(t_T\right)\\ ⋮& ⋮& \ddots & ⋮\\ r_{N,u}\left(t_1\right)& r_{N,u}\left(t_1\right)& \dots & r_{N,u}\left(t_T\right)\end{array}\right]$$

(2)

where N is the number of antenna elements and T is the number of time-domain snapshots considered per estimation window. This matrix formulation serves as the input for spatial covariance analysis, subspace decomposition (e.g., via MUSIC), and predictive learning (e.g., LR, SVR). Each column in $X_u$ corresponds to a spatial sample of the received waveform at a particular time instant, t, and the rows span the antenna array dimension.

The average signal and noise power for the ith antenna element over the observation window is computed as follows:

$$P_{r,i}={\displaystyle \frac{1}{T}}{\sum }_t{\left|r_{i,u}\left(t\right)\right|}^2$$

(3)

$$P_{r,i}={\displaystyle \frac{1}{T}}{\sum }_t{\left|n_{i,u}\left(t\right)\right|}^2$$

(4)

Here, $r_i\left(t\right)$ and $n_i\left(t\right)$ represent the instantaneous signal and additive noise at the $i^{\mathrm{t}\mathrm{h}}$ element, respectively. These quantities may be computed individually for each user or globally across all users and antennas, depending on the normalisation strategy.

Once the power levels are estimated, the received signal is scaled to produce a normalised signal $P_r\left(t\right)$ as follows:

$$z_{i,u}(t)={\displaystyle \frac{r_{i,u}\left(t\right)}{\sqrt{P_{r,u}}}}+{\displaystyle \frac{n_{i,u}\left(t\right)}{\sqrt{P_{n,i}}}}\times {10}^{-{\displaystyle \frac{SNR}{20}}}$$

(5)

This equation ensures that the signal component is unity-normalised, while the noise component is scaled according to the target SNR, expressed in decibels. The term ${10}^{-{\displaystyle \frac{SNR}{20}}}$ translates SNR from dB to a linear scale, applying an attenuation factor to the noise to reflect realistic receiver conditions.

This modelling rigour makes the simulation environment highly suitable for evaluating the effectiveness of hybrid MUSIC–prediction techniques, adaptive regression models, and fallback mechanisms, like enhanced MUSIC scanning, under practical urban mobility patterns.

3.3.4. Predictive AoA Models (DE-ACSW-R)

• Weighted and Clustered Linear Regression for Predictive AoA Estimation

Linear Regression (LR) is a fundamental technique for forecasting a signal’s future AoA. In the proposed DE-ACSW-R framework, LR is employed at the O-RU level due to its computational efficiency and suitability for real-time low-latency prediction in O-RAN Split 7-2x architecture. To improve performance in realistic high-mobility scenarios, our model extends classical LR with both temporal weighting and clustered sliding window logic, referred to as Adaptive DE-ACSW-R.

Let $\theta \left(t\right)$ denote the estimated AoA at a discrete time index, $t$, and let the O-RU maintain a sliding window, $D_t$, of the $W$ most recent AoA samples:

$$D_t={\{{(t}_i,{\theta }_i)\}}_{i=t-W+1}^t$$

(6)

where $t_i$ is the discrete time index (e.g., snapshot or frame number), ${\theta }_i={(t}_i)$ is the estimated AoA at the time, and $t_i$ W is the prediction window size. We fit a simple linear model of the following form:

$$\widehat{\theta }(t+∆)=at+b$$

(7)

where a is the slope representing an angular rate of change (AoA velocity), b is the intercept, and $∆$ is the forward prediction step (typically Δ = 1 for next-slot prediction).

The parameters a and b are computed via ordinary least squares (OLS) minimization:

$$\left(a,b\right)=arg\underset{a,b}{\min }{\sum }_{i=t-W+1}^t{\left({\theta }_i-(a{t}_i+b)\right)}^2$$

(8)

This minimisation yields closed-form solutions:

$$a={\displaystyle \frac{W\sum {t_i\theta }_i-\sum t_i\sum {\theta }_i}{W\sum t_i^2-{(\sum t_i)}^2}},a={\displaystyle \frac{\sum {\theta }_i-a\sum t_i}{W}}$$

(9)

Once the model is trained, the predicted AoA for future time $t+∆$ is given by the following:

$${\widehat{\theta }}_{LR}(t+∆)=a(t+∆)+b$$

(10)

Depending on the system confidence level, this prediction is then passed to the enhanced MUSIC estimator or is directly used for precoding.

• Weighted Linear Regression (WLR) Extension

To improve robustness in rapidly changing mobility scenarios, we implement a WLR variant. This model gives more importance to recent AoA values by assigning temporal weights.

$$\left(a,b\right)=arg\underset{a,b}{\min }{\sum }_{i=t-W+1}^t{w}_i\left({\theta }_i-(a{t}_i+b)\right)$$

(11)

where $w_i$ is a monotonically increasing function over time (e.g., exponential weights):

$$w_i=\mathrm{e}\mathrm{x}\mathrm{p}(\mathsf{\gamma }\left(t_i-t_W)\right),\mathsf{\gamma }>0$$

(12)

This ensures that recent AoAs are prioritised, allowing for faster adaptation to mobility-induced angular shifts while maintaining mathematical tractability.

• Adaptive Clustered Sliding Window Regression (Jump Detection)

To further improve prediction under abrupt mobility changes, we introduce a jump-detection and clustering logic:

• If $|{\theta }_{\mathrm{k}+1}-{\theta }_{\mathrm{k}}|>jumpthreshold$ for some k in the window, then only the samples after the last jump (i.e., from $t_{\mathrm{k}+1}tot$) are used in the weighted regression.
• If no jump is detected, the entire window is used.

The prediction is then as follows:

$${\theta }_{ACSW-R}\left(t+\Delta \right)=a^{*}\left(t+\mathit{\Delta }\right)+b^{*}$$

(13)

where $a,b$ are obtained by weighted regression on the “clustered” (post-jump) segment.

• Linear Regression-based AoA prediction relies on the following assumptions:
  • Short-term linear trend: The AoA trajectory over the prediction window is approximately linear, valid for low-speed UEs or over short time scales.
  • Stationarity within window: The angular velocity ${\displaystyle \frac{\mathrm{d}\mathsf{\theta }}{\mathrm{d}\mathrm{t}}}$ remains roughly constant within the window, W.
  • High-quality historical AoAs: The recent AoA estimates ${\theta }_i$ are accurate and not corrupted by multipath-induced ambiguity or outliers.

Given its simplicity and efficiency, LR is ideally suited for execution at the O-RU layer, where real-time responsiveness and minimal computational overhead are critical. When the Mean Squared Error (MSE) of the LR model falls below a predefined threshold (e.g., ${MSE}_{LR}$ < 1), the prediction is accepted. Otherwise, the system waits for the O-DU’s SVR output or triggers fallback to MUSIC, as described in the section Support Vector Regression (SVR) for Non-Linear AoA Prediction and Section 3.3.6.

LR predictions serve as the first-pass estimation mechanism in the dual-layered prediction structure of DE-ACSW-R. At each time step, the O-RU locally computes ${\widehat{\theta }}_{LR}(t+∆).$ Furthermore, forward it to the following:

• The enhanced MUSIC module, which constrains its angular search window using ${\widehat{\theta }}_{LR}$.
• The confidence-weighted fusion logic blends it with SVR-based predictions for robust output.

In high-confidence regimes, LR alone suffices for both prediction and beam steering. In lower-confidence regimes, the LR prediction still provides directional prior knowledge to constrain subsequent spectrum computation, forming the backbone of latency-aware adaptive beamforming in Split 7-2x O-RAN systems.

• Support Vector Regression (SVR) for Non-Linear AoA Prediction

While LR provides a computationally efficient solution for short-term AoA forecasting, it is inherently limited to linear angular trajectories. In dynamic or non-linear user mobility scenarios, such as abrupt direction changes, curved pedestrian movement, or multipath-induced angular deviation, the linearity assumption breaks down. To address this, we extend the DE-ACSW-R framework with SVR, a kernel-based non-linear model capable of learning complex AoA evolution patterns from historical data.

SVR operates at the O-DU layer, where more computational resources and a broader temporal context are available. SVR predictions complement those of LR and are dynamically fused via a confidence and error-weighted scheme, as detailed in our adaptive fusion logic.

Given a window of AoA observations $D_t={\{{(t}_i,{\theta }_i)\}}_{i=t-W+1}^t$, the SVR aims to find a non-linear $f\left(t\right)$ that approximates the underlying AoA trajectory:

$${\widehat{\theta }}_{SVR}\left(t+∆\right)=f\left(t+∆\right)=〈W,\mathsf{\varphi }(t+∆)〉+b_{SVR}$$

(14)

where $\mathsf{\varphi }\left(t\right)$ is a non-linear mapping to a high-dimensional feature space, W is the weight vector in the transformed space, $b_{SVR}$ is the SVR bias term, and 〈⋅,⋅〉 denotes the inner product.

The SVR learning problem minimises a regularised hinge-loss objective

$$\underset{{w,b,\mathit{\xi }}_t,{\xi }_t^{*}}{\mathit{min}}{\displaystyle \frac{1}{2}}{‖w‖}^2+C{\sum }_{i=1}^w({\xi }_t+{\xi }_t^{*})$$

(15)

subject to the following constraints:

$$\left\{\begin{array}{c}{\theta }_i-〈2,\varphi \left(t_i\right)〉-b_{SVR}\le ϵ+{\xi }_t\\ ⟨w,\varphi \left(t_i\right)⟩+b_{SVR}-{\theta }_i\le ϵ+{\xi }_t^{*}\\ {\xi }_t,{\xi }_t^{*}\ge 0\end{array}\right.\mathrm{for}i-1,\dots ,W$$

(16)

where $ϵ$ is the maximum allowable prediction error (insensitive margin), ${\xi }_i,{\xi }_i^{*}$ are slack variables penalising violations beyond $ϵ$, and C > 0 is the regularisation parameter controlling the trade-off between margin width and tolerance to error.

In practice, the SVR is implemented using a Gaussian (RBF) kernel whose width is dynamically adapted according to the estimated curvature of the AoA trajectory within the window. This curvature-adaptive kernel allows for the SVR model to respond to both slow and sharp changes in user motion. The SVR prediction for time $t+\Delta$ is computed as a weighted sum over support vectors, utilising the curvature-adapted kernel:

$${\widehat{\theta }}_{SVR}\left(t+∆\right)={\sum }_{i=1}^w({\mathsf{\alpha }}_i-{\mathsf{\alpha }}_i^{\mathrm{*}})K\left({\mathrm{t}}_i,t+∆\right)+b_{SVR}$$

(17)

where ${\mathsf{\alpha }}_i-{\mathsf{\alpha }}_i^{\mathrm{*}}$ are dual coefficients learned from training and $K({\mathrm{t}}_i,t)=\langle \varphi \left({\mathrm{t}}_i\right),\varphi \left({\mathrm{t}}_j\right)\rangle$ is a kernel function (Radial Basis Function kernel) defining the similarity between inputs.

SVR-based AoA prediction is particularly beneficial in the following scenarios:

• Non-linear or curved mobility patterns, such as turns, roundabouts, or urban obstacles.
• Multipath-dominated environments, where reflection-induced AoA shifts create non-monotonic signal behaviour.
• Longer-term history exploitation, where patterns are not well approximated by short-window linear trends.

Compared to LR, SVR can exploit a more extended history and capture non-linear AoA evolution, providing improved generalisation for irregular mobility or channel conditions. However, SVR’s computational cost and the need for additional parameters make it better suited for O-DU or near-real-time RIC layers rather than for immediate O-RU prediction.

At each slot, the O-DU runs the SVR model based on the recent AoA history (provided by the O-RU). The predicted value ${\widehat{\theta }}_{SVR}\left(t+∆\right)$ is combined with the LR prediction through a confidence- and error-weighted fusion logic (see Section 3.3.5). This fused prediction constrains the search region for enhanced MUSIC estimation or, if confidence falls below a threshold, can trigger full-range MUSIC fallback at the O-RU. The SVR’s prediction error and window curvature are also continuously monitored to dynamically adapt kernel width and fusion weights (see the section Curvature-Adaptive Kernel for Non-Linear Mobility).

• Curvature-Adaptive Kernel for Non-Linear Mobility

The performance of SVR in dynamic AoA prediction is susceptible to kernel choice, especially the Gaussian (RBF) kernel width σ. Using a fixed σ may be adequate in stable linear-mobility cases, but cannot adapt to the fast non-linear AoA shifts commonly seen in urban or vehicular scenarios. To address this, our model employs a Curvature-Adaptive Kernel, in which the kernel width is updated in real-time according to the local curvature of the AoA trajectory. This approach enables the SVR to adjust its locality and smooth it flexibly, tracking both gradual and abrupt AoA changes without the need for retraining or system reconfiguration.

This method allows for the SVR model to respond to trajectory nonlinearities in real-time, enhancing its prediction accuracy under variable mobility without requiring architectural or training changes.

In a trajectory defined by discrete AoA observations $\theta$($t_i$), the curvature reflects how sharply the AoA changes with respect to time. A nearly linear AoA change indicates low curvature, where wide kernels (i.e., large σ) are beneficial due to smooth variations. In contrast, rapid AoA transitions (e.g., due to turns or multipath transitions) induce high curvature and require narrower kernels to maintain local sensitivity.

Thus, we define a time-dependent kernel width σ(t) based on the instantaneous angular curvature κ(t), which is calculated from the recent AoA window using finite differences:

$$\kappa \left(t\right)=\theta (t+1)-2\theta \left(t\right)+\theta (t-1)$$

(18)

This expression resembles the second derivative of θ(t) and quantifies angular acceleration. A significant value of ∣κ(t)∣ implies a sharp AoA transition.

We define the kernel width σ(t) for the RBF kernel as a function of AoA curvature:

$$\sigma \left(t\right)=\alpha +\beta \cdot \mid \kappa \left(t\right)\mid$$

(19)

where α > 0 is a baseline kernel width (ensures non-zero minimum smoothing), β > 0 scales the influence of curvature on kernel size, and $\mid \kappa \left(t\right)\mid$ is the absolute curvature, ensuring positive σ(t).

Substituting this into the standard RBF kernel, we obtain the curvature-adaptive kernel:

$$K(t_i,t_j)=exp\left(-{\displaystyle \frac{{(t_i-t_j)}^2}{{2\sigma \left(t\right)}^2}}\right)$$

(20)

Note that σ(t) is recomputed at every prediction step using the most recent AoA window, making the SVR kernel adaptive and responsive to current trajectory dynamics.

This is a practical implementation strategy starting from compute $\kappa \left(t\right)$ from the most recent AoA window $\left\{\theta \left(t-1\right),\theta \left(t\right),\theta \left(t+1\right)\right\}.$ Set σ(t) using Equation (18), with the parameters $\alpha$ and $\beta$ chosen based on empirical observations and systematic cross-validation using representative training data, reflecting various mobility scenarios and propagation conditions. To further enhance performance robustness and generalisation, future implementations may incorporate online parameter optimisation methods to dynamically tune α and β according to observed real-time trajectory curvature and mobility characteristics, with empirically chosen or cross-validated parameters α and β. Pass σ(t) to the SVR model kernel function for the next prediction. Repeat the adaptation at every new slot, ensuring real-time kernel adjustment for each user’s mobility pattern.

This method’s benefits include responsiveness, stability, and continuity. When users undergo rapid directional changes, the model adaptively narrows the kernel width to preserve local learning accuracy. During linear or slow movement, a wider kernel suppresses overfitting and promotes smoother predictions. This dynamic adjustment eliminates the need for explicit switching logic or model replacement, relying solely on real-time kernel recalibration.

This approach enables the SVR model to generalise across a wide range of mobility profiles within a unified modelling framework, reducing the reliance on handcrafted heuristics or scenario-specific tuning. By continuously adapting to curvature dynamics, the model maintains robust prediction quality across diverse and time-varying propagation conditions.

The Clustered and Curvature-Adaptive kernel is fully integrated into the SVR layer of the system, operating transparently to the O-RU. It enables the O-DU to perform the following:

• Maintain prediction robustness across time-varying dynamics;
• Inform the confidence-weighted fusion module of trajectory nonlinearity, enhancing global prediction quality;
• Reduce fallback events by improving prediction precision in conditions where LR fails due to curvature;
• Operate asynchronously while allowing for the RU to continue local operations.

• Adaptive Dynamic Fusion of LR and SVR Predictions (DE-ACSW-R Fusion)

In mobility-aware beamforming, no single model, whether linear or non-linear, consistently outperforms in all scenarios. While Weighted Linear Regression (WLR) enables low-latency real-time tracking on near-linear AoA segments, it can underperform in the presence of non-linear mobility or sudden trajectory jumps. Conversely, curvature-adaptive SVR (CA-SVR) is more robust to non-linearities and trajectory curvature, but relies on longer context and increased computation.

To optimally leverage the strengths of both predictors, our system applies a DE-ACSW-R Fusion scheme. Here, both LR and SVR are computed on the current (possibly clustered) AoA window, and their outputs are dynamically fused. The fusion weights are not fixed. Instead, they are assigned to ensure that the predictor with the lower mean squared error (MSE) receives at least 65% of the total weight while the other predictor receives the remainder. If MSEs are similar, the weights default to a confidence-weighted scheme that accounts for prediction spread, residuals, and real-time SNR trends. Dominance-enforced weighting means that whenever one predictor outperforms the other, it is guaranteed to have the majority influence on the fused result while still allowing, the secondary predictor to contribute in ambiguous or transition cases. This dynamically rebalanced fusion approach provides the following:

• Smooth, adaptive transitions between LR and SVR predictions without abrupt switching.
• Robustness to abrupt mobility changes as the fusion rapidly increases the influence of the more reliable predictor.
• Physical-layer awareness is achieved by optionally incorporating SNR or error statistics in the weighting logic.

Outlier detection is incorporated; if the difference between LR and SVR predictions exceeds a threshold (e.g., 10°), the fusion automatically selects the prediction closer to the recent history as the final output.

The resulting fused prediction ${\widehat{\theta }}_{fused}\left(t+∆\right)$ is then used both for beamforming weight calculation and to restrict the angular search space in MUSIC-based fallback procedures. This hybrid fusion guarantees robust and low-latency AoA prediction under a wide range of user mobility and channel conditions.

Let ${\widehat{\theta }}_{LR}\left(t+∆\right)$ and ${\widehat{\theta }}_{SVR}\left(t+∆\right)$ denote the predicted AoA from the Linear Regression (LR) and Support Vector Regression (SVR) models, respectively, at time t + Δ. Let ${MSE}_{LR}\mathrm{a}\mathrm{n}\mathrm{d}{MSE}_{SVR}$ denote their respective mean squared prediction errors computed on the current window. Let $ϵ>0$ be a small regularisation constant to avoid division by zero.

We define the confidence of each model $c_i$ as the inverse of its prediction error:

$$c_i={\displaystyle \frac{1}{{MSE}_i+ϵ}},iϵ\{LR,SVR\}$$

(21)

A weighted average gives the fused AoA prediction:

$${\widehat{\theta }}_{fused}\left(t+∆\right)={\displaystyle \frac{w_{LR}\cdot c_{LR}\cdot {\widehat{\theta }}_{LR}\left(t+∆\right)+w_{SVR}\cdot c_{SVR}\cdot {\widehat{\theta }}_{SVR}\left(t+∆\right)}{w_{LR}\cdot c_{LR}+w_{SVR}\cdot c_{SVR}}}$$

(22)

where $w_{LR}$ and $w_{SVR}$ implement minimum dominance logic:

• If LR is more accurate (${MSE}_{LR}<{MSE}_{SVR}$):

  ○

  $w_{LR}=\max \left(\mathrm{0.65,1}-w_{SVR}\right)$

  ○

  $w_{SVR}=1-w_{LR}$

• If LR is more accurate (${MSE}_{SVR}<{MSE}_{LR}$):

  ○

  $w_{SVR}=\max \left(\mathrm{0.65,1}-w_{LR}\right)$

  ○

  $w_{LR}=1-w_{SVR}$

The main features of the models are as follows: (1) the better model receives ≥ 65% weight, (2) both models contribute in a similar way when their performance is comparable, and (3) smooth transitions between dominance regimes are guaranteed.

To further refine confidence scoring, we extend the confidence metric to include SNR:

$$c_i^{\prime }={\displaystyle \frac{\gamma .SNR+\left(1-\gamma \right).\frac{1}{{MSE}_i+ϵ}}{max\left(confidence\right)}}$$

(23)

The parameter γ balances statistical and physical-layer confidence, with the result normalised to maintain scale consistency, a critical consideration in real-world O-RAN settings, where high SNR may coexist with unstable trajectories (risking false confidence) or noisy AoA histories, despite steady user movement.

At each time step, the framework computes both the LR prediction ${\widehat{\theta }}_{LR}$ and the SVR prediction ${\widehat{\theta }}_{SVR}$, evaluates their recent prediction mean squared error (MSE) over a sliding validation window, and retrieves local SNRs from PHY measurements or RU power levels if available. The fused estimate ${\widehat{\theta }}_{fused}$, generated from the dynamically adapted weights ($c_{LR}$, $c_{SVR}$ $w_{LR}$, $w_{SVR}$) is then used for steering vector computation, beamforming weight calculation, and constraining the MUSIC angular search region if fallback is needed.

This adaptive fusion approach ensures stable and high-quality AoA prediction across all mobility regimes. It avoids abrupt switching between models, provides smooth transitions near decision boundaries, and is fully compatible with the distributed O-RAN architecture: LR and clustering at the O-RU for immediate local prediction and SVR plus fusion at the O-DU or near-real-time RIC. As a result, the DE-ACSW-R system delivers robust, low-latency, and data-driven beamforming even under fast mobility and dense multipath conditions, meeting the requirements for 5G and 6G RAN.

3.3.5. Enhanced MUSIC AoA Estimation with Predictive Window Constraints

In standard implementations, MUSIC-based AoA estimation requires scanning the entire angular domain, which introduces high computational latency, particularly in distributed O-RAN systems. To overcome this challenge, our framework uses the fused AoA prediction ${\widehat{\theta }}_{pred}$ from the DE-ACSW-R pipeline to dynamically restrict the angular search region for MUSIC.

Specifically, the enhanced MUSIC algorithm scans only a localised angular window, defined as follows:

$${\Theta }_{local}=\left\{\mathsf{\theta }|\mathsf{\theta }\in [{\widehat{\theta }}_{pred}-w,{\widehat{\theta }}_{pred}+w]\right\}$$

(24)

where ${\widehat{\theta }}_{pred}$ is the current fused prediction (from LR and SVR fusion) and $w$ is a tunable half-width (e.g., 10°).

Within this window, the MUSIC pseudo-spectrum is computed as follows:

$$P_{music}(\theta )={\displaystyle \frac{1}{a^H\left(\theta \right)E_n{E}_n^{H}a\left(\theta \right)}}$$

(25)

where $a\left(\theta \right)$ is the array steering vector at an angle theta and $E_n$ is the noise eigenvector matrix.

By limiting the search to ${\Theta }_{local}$, rather than the entire angular range, the proposed method significantly reduces computation time while retaining the high-resolution characteristics of MUSIC, especially when the user’s mobility is smooth or predictable. If the system detects high uncertainty or abrupt mobility, it can revert to a broader or full-range search as needed.

3.3.6. Confidence-Driven MUSIC Fallback Mechanism

While predictive AoA estimation using weighted LR, curvature-adaptive SVR, and enhanced MUSIC windowing significantly reduce latency and computational overhead, these methods may still degrade in performance under rapid user trajectory changes, multipath anomalies, or temporary signal loss. In such cases, relying solely on predicted AoAs risks beam misalignment and reduced signal quality. To address this, we integrate a confidence-driven fallback mechanism that autonomously reverts to classical full-spectrum MUSIC scanning whenever predictive estimates become unreliable.

This mechanism acts as a fail-safe within the DE-ACSW-R framework, ensuring estimation accuracy and robust beamforming, even when the prediction models (LR, SVR, and fusion) encounter outliers, trajectory discontinuities, or low-SNR conditions.

• Fallback Triggering Conditions

The fallback logic is minimally invasive, activating only when prediction reliability is clearly compromised. The switch to full MUSIC is triggered under the following conditions:

• Low Prediction Confidence

If the confidence score $\gamma \left(t\right)\in \left[\mathrm{0,1}\right]$, derived from recent AoA history (such as standard deviation and model residuals), falls below a system-defined threshold, ${\tau }_{conf},$

$$\gamma \left(t\right)<{\tau }_{conf}$$

This threshold is typically chosen based on the system tuning and environmental noise characteristics.

• Abrupt AoA Discontinuity (Jump Detection)

If the difference between consecutive AoA estimates exceeds a preset jump threshold ${\delta }_{jump}$,

$$\mid \theta \left(t\right)-\theta \left(t-1\right)\mid >{\delta }_{jump}$$

(26)

The jump detection threshold, ${\delta }_{jump}$, used in this system was determined using simulation experiments covering a wide range of user mobility scenarios, including linear, non-linear, and abrupt directional changes under varying speeds and multipath intensities. The threshold was evaluated by comparing the current AoA with the previous AoA in each time slot, with candidate thresholds ranging from 5° to 25°. For each case, user speed was derived from AoA evolution over time and distance, allowing us to correlate angular variation with mobility dynamics. This approach enabled us to select an optimal threshold that consistently balanced between the target AoA and false AoA caused by noise or minor fluctuations.

• Prediction Residual Thresholding

If the absolute difference between the predicted AoA and the current observed AoA exceeds a residual tolerance, ${ϵ}_r$,

$$\mid {\widehat{\theta }}_{est}\left(t\right)-{\theta }_{est}\left(t\right)\mid >{ϵ}_r$$

(27)

Any of these conditions, low confidence, an AoA jump, or a significant prediction residual will bypass the enhanced (windowed) MUSIC scan in favour of a full-spectrum search.

When fallback is triggered, the system performs a comprehensive MUSIC scan over the entire angular domain. This resets and resynchronizes the AoA estimation logic with the real channel environment, discarding potentially outdated predictions. The new AoA estimate is then added back to the O-RU’s local AoA buffer, enabling the DE-ACSW-R models to resume predictions for subsequent slots unless fallback is invoked again.

Some important implementation details are as follows:

• All fallback logic, confidence calculations, and jump detections operate at the O-RU level, and no O-DU or RIC interventions are required.
• Fallback decisions are updated slot-by-slot, ensuring rapid adaptation to dynamic propagation conditions.
• When the fallback AoA ${\theta }_{MUSIC-full}$ is obtained, it is immediately used to update steering vectors and realign the beam.
• The updated AoA is reinserted into the O-RU’s history window, enabling the seamless recovery and transition back to predictive operation.

This confidence-driven fallback strategy enhances the DE-ACSW-R system’s overall robustness, ensuring reliable operation in stable and volatile scenarios and supporting the fully autonomous real-time correction of trajectory estimation errors in practical O-RAN deployments.

3.4. Beamforming and Precoding Strategy

Accurate beamforming and precoding are essential to fully exploit spatial degrees of freedom in multi-antenna systems, especially under high-user-mobility and urban multipath conditions. In the proposed system, the integration of real-time AoA prediction (via LR), SVR-based refinement at the DU, and localised MUSIC estimation enables a dynamic and adaptive beamforming strategy that is tightly coupled with the O-RAN Split 7-2x architecture.

This section outlines the beamforming and precoding methodology employed, the mathematical formulation of weight generation using predicted AoAs, and the considerations for interference mitigation in multi-user scenarios.

3.4.1. Beamforming Weight Computation Using Predicted AoA

Let ${\widehat{\theta }}_u(t)$ denote the predicted or estimated AoA of user, u, at time, t, as provided by the DE-ACSW-R prediction pipeline (i.e., fused LR/SVR with clustering and jump detection). For a uniform linear array (ULA) of N antennas with inter-element spacing, the corresponding steering vector is as follows:

$$a({\widehat{\theta }}_u)={\left[{1,e}^{-j{\displaystyle \frac{2\pi }{\lambda }}dsin({\widehat{\theta }}_u)},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}\left(N-1\right)dsin({\widehat{\theta }}_u)}\right]}^T$$

(28)

This steering vector is normalised and used to compute the beamforming weights for user, u. In a matched filter formulation (i.e., maximum ratio transmission), the beamforming vector is as follows:

$$w_u={\displaystyle \frac{a\left({\widehat{\theta }}_u\right)}{‖a\left({\widehat{\theta }}_u\right)‖}}$$

(29)

These weights are applied to the transmit signals to spatially focus the beam in the direction of the predicted AoA.

3.4.2. Multi-User Beamforming and Interference Management

In our DE-ACSW-R-based framework, multi-user MIMO beamforming is achieved by generating orthogonal (or near-orthogonal) beams using the predicted AoAs for each active user, as determined by the latest slot-level fusion result. When the AoAs are sufficiently separated, direct steering suffices. For closer or overlapping users, Zero-Forcing (ZF) precoding is applied to mitigate inter-user interference by ensuring the following:

$$w_i^H{w}_j\approx 0\mathrm{for}i\ne j$$

(30)

In practice, this is achieved by applying a Zero-Forcing precoding process on the set $\left\{a\right({\widehat{\theta }}_1),\dots ,a({\widehat{\theta }}_k\left)\right\}$ to generate beamforming weights that maximise the desired signal power while suppressing interference [41,42].

This precoding process ensures that each user’s beam remains spatially isolated, thereby suppressing cross-user interference at the transmitter. Because the AoAs are predicted one or more slots ahead, the O-RU can proactively update and apply the ZF weights without waiting for real-time CSI feedback, improving responsiveness in highly mobile environments. This lightweight ZF strategy aligns with Split 7-2x constraints, where the O-RU executes latency-sensitive beam updates based on local prediction, while broader coordination and UEID validation are handled at the O-DU.

3.4.3. Predictive Precoding with Slot-Level Responsiveness

The use of DE-ACSW-R predictive AoA models allows for the beamforming vectors to be computed one or more time slots in advance, enabling proactive beam steering. Let ${\widehat{\theta }}_u(t+\Delta )$ be the predicted AoA at a future time, $t+\Delta$. The precoder $w_u(t+\Delta )$ is constructed from ${\widehat{\theta }}_u\left(t+\Delta \right).$ Moreover, it is applied at the scheduled transmission time without waiting for CSI feedback or explicit uplink measurements.

This proactive approach addresses the latency and coherence time challenges in high-mobility scenarios and is particularly beneficial when fronthaul delays exist between the O-DU and O-RU.

3.4.4. Practical Considerations for O-RAN Integration

The beamforming logic in the proposed framework is architecturally decoupled and mapped onto the O-RAN functional split as follows:

• At the O-RU, a rapid generation of beamforming weights using LR-based AoA predictions, jump-detection clustering, and enhanced MUSIC (with window constraints) allows for near-instantaneous adaptation at the network edge.
• At the O-DU, longer-term refinement based on curvature-adaptive SVR, confidence-weighted fusion, and user classification can be sent to the O-RU for synchronised future-slot updates over eCPRI.
• Slot-to-Slot Update Capability offers beam weight updates at each TTI based on the most recent DE-ACSW-R prediction or MUSIC result, maintaining a rapid response in mobile scenarios.

3.4.5. Robustness to Prediction Error

Given the presence of prediction uncertainty, robustness is ensured through the following:

• Fallback AoA estimation: When prediction confidence falls below the threshold, or an AoA jump is detected (as per DE-ACSW-R logic), the O-RU triggers a localised or full MUSIC scan, restoring alignment using direct subspace estimation.
• Beam width adjustment: Upon low confidence, the beam pattern is widened via tapering (e.g., Taylor window), sacrificing some gain to improve coverage and avoid mis-steering.
• SNR and SINR monitoring: Continuous monitoring of received SNR/SINR informs both prediction window size and beam pattern adaptation, increasing system resilience in rapidly changing conditions.

By integrating predictive modelling (LR, SVR with clustering, adaptive fusion) with subspace estimation, the DE-ACSW-R-enabled beamforming and precoding framework delivers low-latency accurate directional transmission that is adaptable to O-RAN Split 7-2x deployments and robust in dense high-mobility scenarios, without relying on continuous CSI feedback or centralised optimisation.

4. Simulation Setup and Parameters

4.1. Channel and Interference Modelling

The simulation environment replicates a dense urban environment, where the radio channel is characterised by both line-of-sight (LoS) and non-line-of-sight (NLoS) propagation. Each user’s received signal is modelled as a combination of a dominant LoS path, multiple reflected multipath components, and Rayleigh fading to capture small-scale variations. Multipath arrivals are simulated with random angular spreads and delays, emulating reflections from buildings and obstacles typical of city environments. Additive white Gaussian noise (AWGN) is present at each antenna element, and a configurable signal-to-noise ratio (SNR) range between 0 and 30 dB allows for stress-testing under both favourable and adverse channel conditions. Interference is explicitly modelled by injecting additional signal sources at fixed or time-varying angles, permitting the evaluation of spatial suppression and inter-user isolation by the beamforming subsystem. Doppler effects, dynamically calculated according to user velocity and trajectory, further enhance realism by introducing frequency shifts and rapid channel variation.

4.2. Mobility and User Behaviour Models

User trajectories in the simulation environment are designed to capture both linear and non-linear mobility patterns that are representative of realistic urban communication scenarios. Linear mobility models simulate vehicular movement with constant velocity and direction, while non-linear models emulate pedestrian or urban motion, including curves, zigzag patterns, and city-block-style routes, as shown in Figure 2. Each user begins at a defined offset from the base station and follows an independent, randomly assigned path with updates processed at every simulation step. The user positions are refreshed every 1 ms to align with standard CSI reporting intervals, which may range from 1 ms to 160 ms based on user mobility and network configuration (as specified in 3GPP TS 38.214, Clause 5.2.1.4.1, and in TS 38.331).

For clarity, and to focus on the core predictive beamforming mechanisms, the simulation results presented in this paper primarily consider a single-user scenario. This controlled setup allows us to isolate and demonstrate the core innovations, such as adaptive AoA prediction, clustered regression, SVR fusion, and fallback refinement, without introducing the added complexity of inter-user interference. However, the underlying architecture is explicitly designed for multi-user support, as detailed in Section 3.4.2. The same predictive and precoding mechanisms, including UEID-indexed steering and Zero-Forcing beamforming, are readily applicable in multi-user deployments. Future extensions will focus on validating these principles under dense interference-rich scenarios.

4.3. Antenna Array and System Parameters

The base station is configured with a uniform linear antenna array (ULA) comprising 8, 16, and 32 elements, each spaced at half the carrier wavelength. The array is mounted at a height of 20 m, reflecting typical urban deployments, while user equipment is modelled at a height of 1.5 m. The system operates at a carrier frequency of 5.9 GHz with a bandwidth of 20 MHz—parameters aligned with contemporary 5G NR standards. The AoA prediction algorithm uses a sliding window of five recent measurements to predict user direction. Fronthaul latency between the O-RU and O-DU is modelled within the range of 100–200 microseconds, reflecting O-RAN Split 7-2x deployments using eCPRI transport. All parameters are summarised in

Table 2. Simulation parameters.

Parameter	Value/Range
Carrier Frequency (fc)	5.9 GHz
Number of Antenna Elements (N)	8, 16, 32
Antenna Height	20 m
Number of Users (U)	1–8
User Height (fixed)	1.5 m
Antenna Spacing (d)	λ/2
Snapshots (T)	20, 100, 1000 (per scenario)
Time Interval (t)	1 ms–160 ms
User Initial Distance	10 m
User Distance	150–200 m
User Speed	30 km/h and 50 km/h
SNR Levels	0–30 dB
Number of Multipath (M)	3 per user
Window Size	5 (with tests at 10 and 20)
AWGN Power	8.004 × 10−13 W (calculated for TH_noise = 290 K, B = 20 MHz)
Rayleigh Fading	Variance = 0.8, Mean = 0

.

4.4. Predictive Beamforming, DE-ACSW-R, and System Integration

At every slot, the system generates the full signal environment using MATLAB 9.13, where all model equations have been developed for simulation, producing realistic baseband data for all users, including interference and channel impairments. The O-RU performs MUSIC-based AoA estimation and stores per-user AoA histories. DE-ACSW-R is applied to these histories, detecting in-window angular jumps and segmenting stable clusters for improved prediction. Real-Time Weighted Linear Regression is run at the O-RU for fast slot-level AoA prediction. At the same time, curvature-adaptive SVR is executed at the O-DU to model non-linear trajectories. Fused predictions are computed using confidence- and error-weighted logic, and a fallback to full MUSIC is triggered whenever model residuals, abrupt jumps, or low-confidence scores are detected. Beamforming weights for each user are generated based on the most recent fused AoA estimate, and multi-user spatial orthogonality is enforced through orthogonal or MMSE precoding. All key signals, predictions, and performance data are logged for post-processing and visualisation.

4.5. Performance Metrics

System performance is assessed using several key metrics: Root Mean Squared Error (RMSE) between predicted and true AoAs, average SNR improvement compared to non-predictive beamforming, and the percentage of slots where beam selection aligns with the optimal direction. The system also tracks throughput per user, calculates it using the Shannon capacity formula, and analyses latency at each layer (O-RU, O-DU, and fallback MUSIC). The robustness of prediction and fallback is stress-tested by introducing trajectory curvature, Doppler, and substantial interference, as well as by monitoring the frequency of fallback events. Results are visualised using plots of AoA error, SNR over time, and spatial heatmaps, providing a comprehensive assessment of system adaptability, responsiveness, and practical O-RAN integration.

5. Simulation Results and Discussion

In this section, we evaluate the performance of the proposed DE-ACSW-R framework for predictive AoA estimation and robust beamforming under dynamic mobility scenarios. The simulation emulates challenging high-mobility conditions in O-RAN deployments, where users may exhibit both smooth trajectories and abrupt direction changes, resulting in non-linear non-stationary AoA evolution.

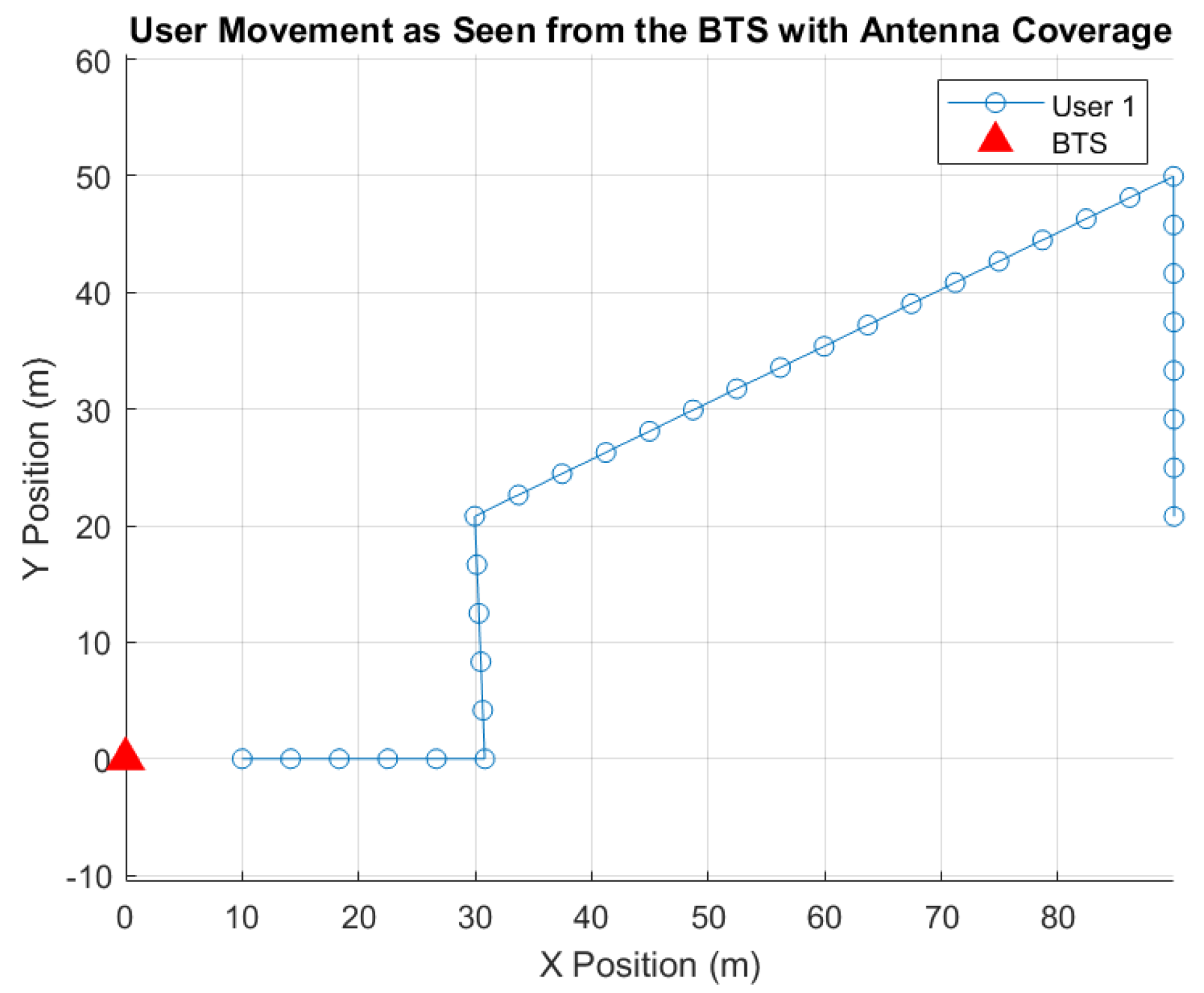
5.1. Model Adaptation Logic and Window Clustering Behaviour

Figure 3 illustrates the decision step in the DE-ACSW-R model when an abrupt AoA trajectory jump is detected within the sliding prediction window. The plot shows the AoA values inside the prediction window at time t = 5, along with LR fits for the entire window and the dynamically clustered window after a trajectory jump is detected.

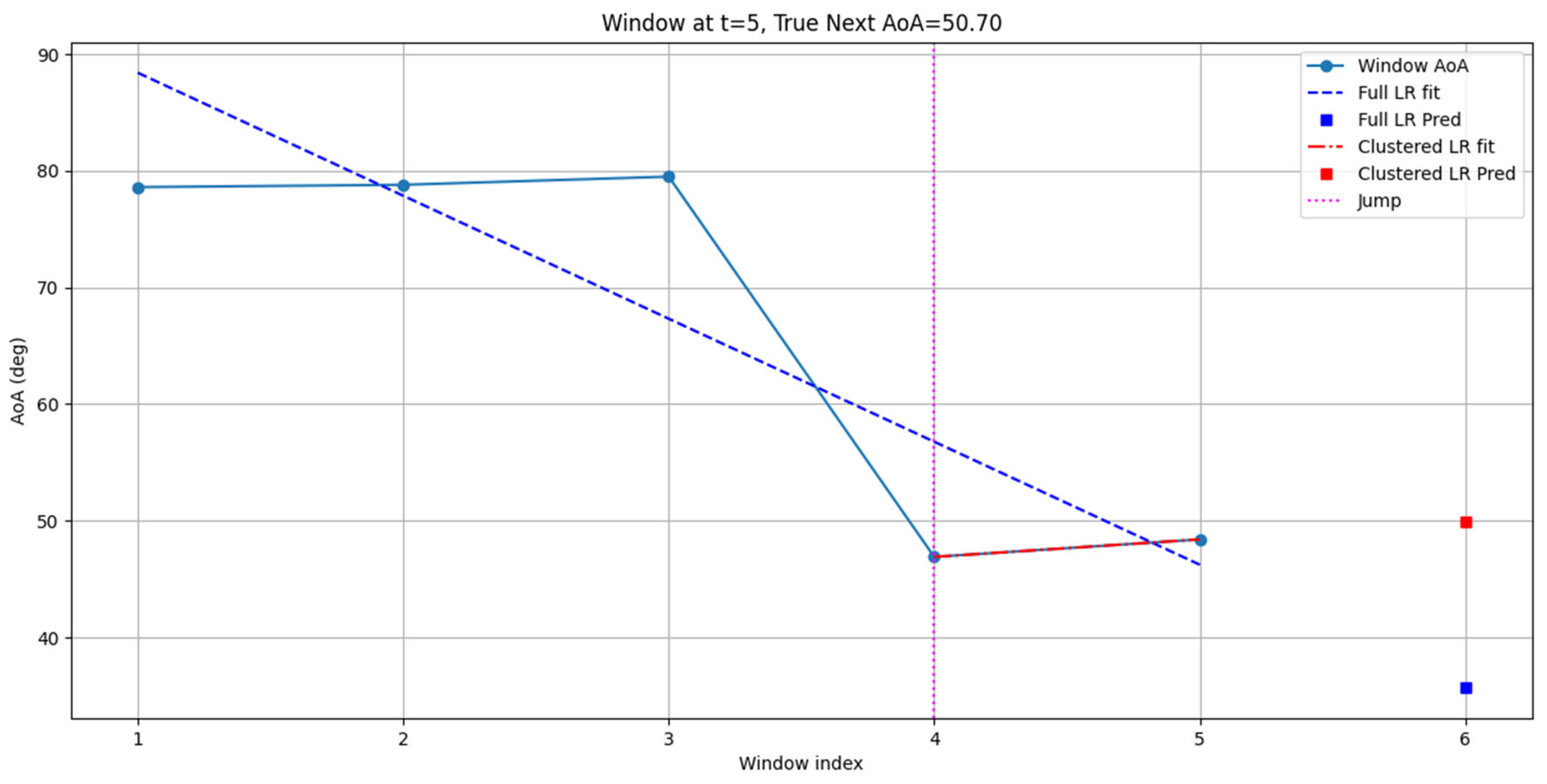
• Window AoA: The blue points and line indicate the sequence of recent AoA measurements (window history), which the model uses for prediction.
• Full LR fit and prediction: The blue dashed line is the Linear Regression fit across the full window. The corresponding blue dot at index 6 is the predicted AoA for the next time slot, assuming no change in trajectory.
• Jump detection and clustering: At window index 4, the model detects a sudden, significant change in AoA identified as a trajectory jump. The DE-ACSW-R logic immediately re-clusters the window, discarding older points that do not reflect the new direction.
• Clustered LR fit and prediction: The red dashed-dotted line represents the LR fit applied only to the most recent cluster of AoA points after the jump. The red square at index 6 is the resulting predicted AoA for the next slot, based solely on the recent post-jump samples.

The key model behaviour may be described as follows:

• When the trajectory is smooth, the model uses the full window to fit and predict the next AoA, leveraging maximum history for noise averaging.
• Upon detecting a jump, the window is clustered so that only the recent (relevant) points influence the LR fit and prediction. This avoids “lag” and prevents stale trajectory data from biassing the result.
• The clustered LR fit and its prediction are visibly better aligned with the new AoA trend than the full-window fit, demonstrating the model’s ability to adapt in real-time.

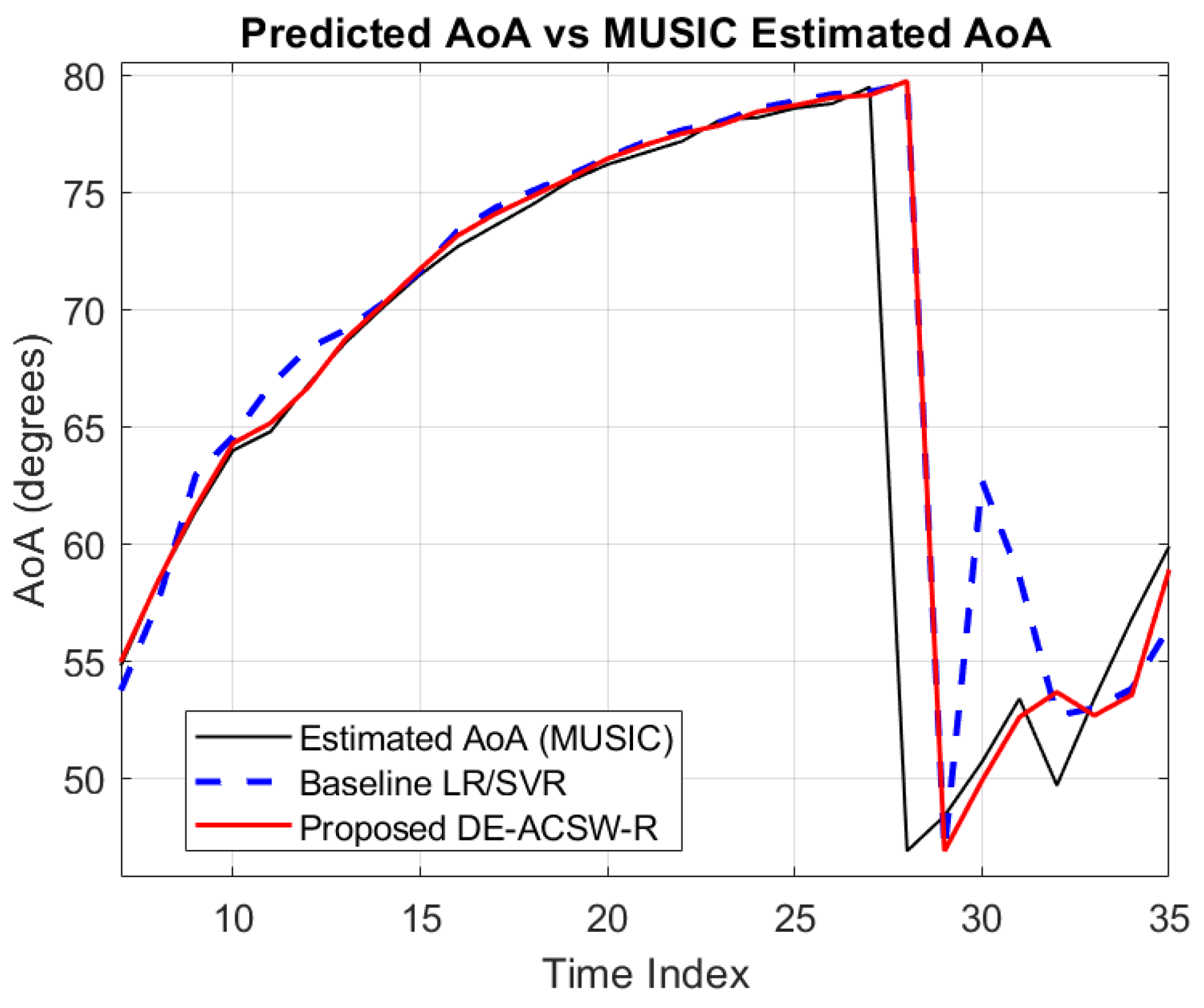
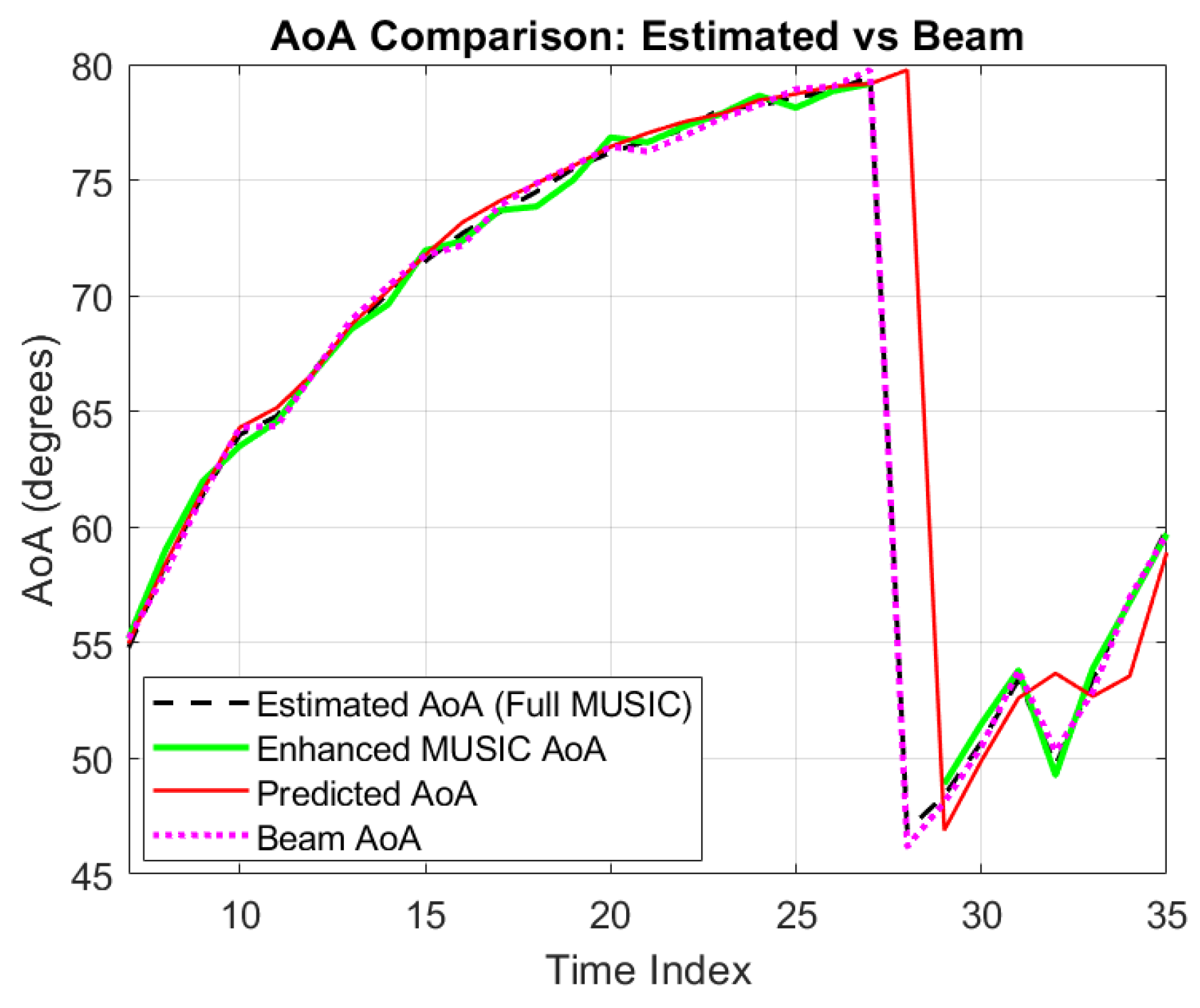
5.2. Baseline Model Performance and Comparative Analysis with the DE-ACSW-R Model

The DE-ACSW-R model fuses two predictive engines: LR for low-latency near-linear mobility, and curvature-adaptive SVR for handling non-linear trajectories and abrupt jumps. Unlike traditional single-model or reactive switching schemes, DE-ACSW-R dynamically balances the influence of LR and SVR based on real-time prediction error and model confidence. When an abrupt change (“jump”) is detected within the sliding AoA history window, the framework automatically clusters the window to focus on the most recent relevant samples, resets outliers, and re-weights model contributions. This enables the system to rapidly “forget” outdated trajectory data, avoid model lag, and achieve fast realignment with the user’s actual movement.

Figure 4 illustrates this process using a representative segment of AoA evolution with both smooth movement and sudden jumps.

As shown in the figure, both predictors closely follow the Estimated AoA during steady movement (indices 6–26), but their differences become pronounced around abrupt mobility changes. At index 28, the user’s AoA drops sharply from 79.5° to 46.9°. The baseline predictor, which lacks jump detection and adaptive fusion, produces a value of 62.7°, demonstrating significant lag and prediction error. In contrast, the DE-ACSW-R model immediately detects the jump, clusters the history, and produces a much more accurate estimate of 49.9°. This advantage persists in subsequent indices (29–30), where the new model’s outlier logic and window clustering rapidly stabilise its predictions near the ground truth, whereas the baseline remains slow to recover and displays greater oscillation.

Across the full trajectory, DE-ACSW-R consistently demonstrates the following:

• Faster adaptation after abrupt mobility changes due to window clustering and dominance-enforced fusion.
• Reduced prediction error and variance during both linear and non-linear segments, owing to smooth confidence-weighted transitions between models.
• Increased robustness to outliers and history contamination by actively re-centring on relevant trajectory clusters after a jump.

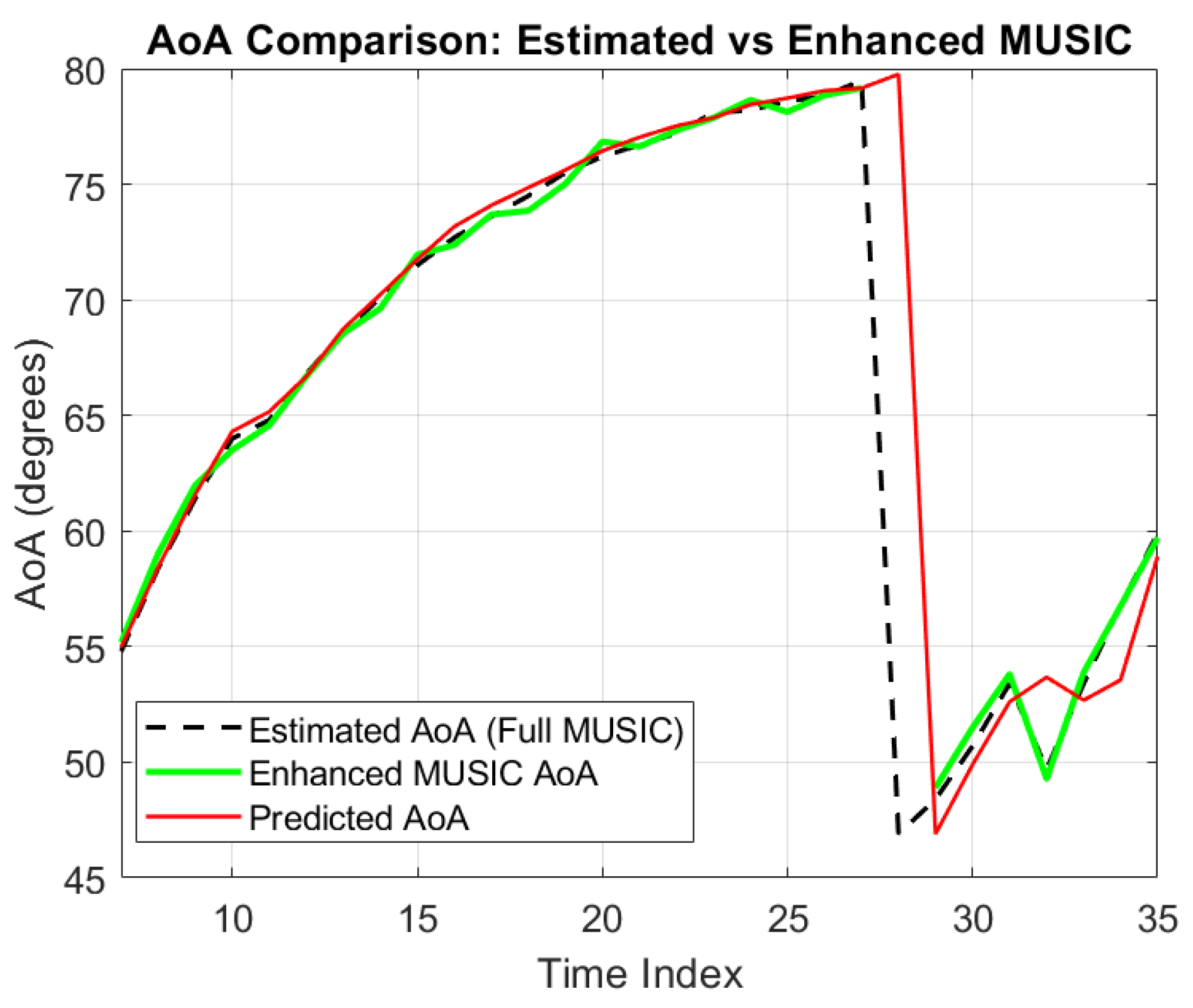
5.3. Prediction-Aided Fallback and Beam Alignment Behaviour

To further illustrate the interplay between prediction, fallback logic, and beamforming, Figure 5 depicts the system’s operation during an abrupt AoA change, highlighting the sequence of events as the system switches from enhanced MUSIC to a full MUSIC search. Here, the predicted AoA anticipates the sudden trajectory change, and the enhanced MUSIC estimator steps out of the tracking loop, as indicated by the activation of the fallback mode.

At index 27, the system detects a significant discrepancy between the ongoing prediction and the estimated AoA. The enhanced MUSIC estimator, which typically tracks the predicted AoA with a narrow high-gain beam, is automatically disabled to prevent incorrect beam steering. The fallback control is triggered, causing the system to suspend enhanced MUSIC and revert to full MUSIC for direct angle estimation. During this phase, the predicted AoA and the full MUSIC AoA remain closely aligned with the estimated trajectory, while enhanced MUSIC is temporarily disabled to avoid misaligned beamforming.

Supporting data shows that, at index 27, the AoA prediction abruptly drops from 79.16° to 46.9°, corresponding to a jump in the estimated AoA. The system, recognising this jump, triggers a model re-clustering and disables enhanced MUSIC, switching to full MUSIC at index 28. This fallback mechanism prevents the narrow enhanced beam from steering toward an incorrect angle, thereby avoiding significant SNR loss and potential coverage gaps.

Figure 6 further demonstrates the beam alignment behaviour in this regime. The “Beam Angle” closely follows the full MUSIC estimation during fallback and only resumes tracking the enhanced MUSIC output when confidence is restored. This mechanism prevents the risk of steering beams in the wrong direction during periods of high trajectory uncertainty or model disagreement.

Subsequent indices show that, as the prediction stabilises and the clustered history realigns with the new trajectory, the system resumes enhanced MUSIC beamforming. This adaptive switching ensures that beam alignment, as shown in Figure 5, remains closely coupled to the ground-truth AoA, even in the presence of abrupt user movement or prediction failure. The beam angle output and source selection trace the full MUSIC estimator during periods of uncertainty (indices 28–30) and seamlessly return to enhanced MUSIC as prediction confidence is restored.

This dynamic prediction-aided fallback process provides several key advantages for next-generation RAN systems. First, it ensures fault tolerance by immediately disabling the enhanced beam during prediction failures, thereby preventing the system from steering beams in incorrect directions, which minimises packet loss and maximises the received SNR. Second, the framework offers self-healing alignment capabilities by enabling rapid recovery: it leverages the full MUSIC estimator to quickly reacquire the proper user direction before re-enabling high-gain beams once model confidence is restored. Finally, this adaptive control logic is particularly valuable for O-RAN Category B deployments, where the ability to select beams and realign with low latency autonomously is crucial for supporting high-mobility users without centralised intervention.

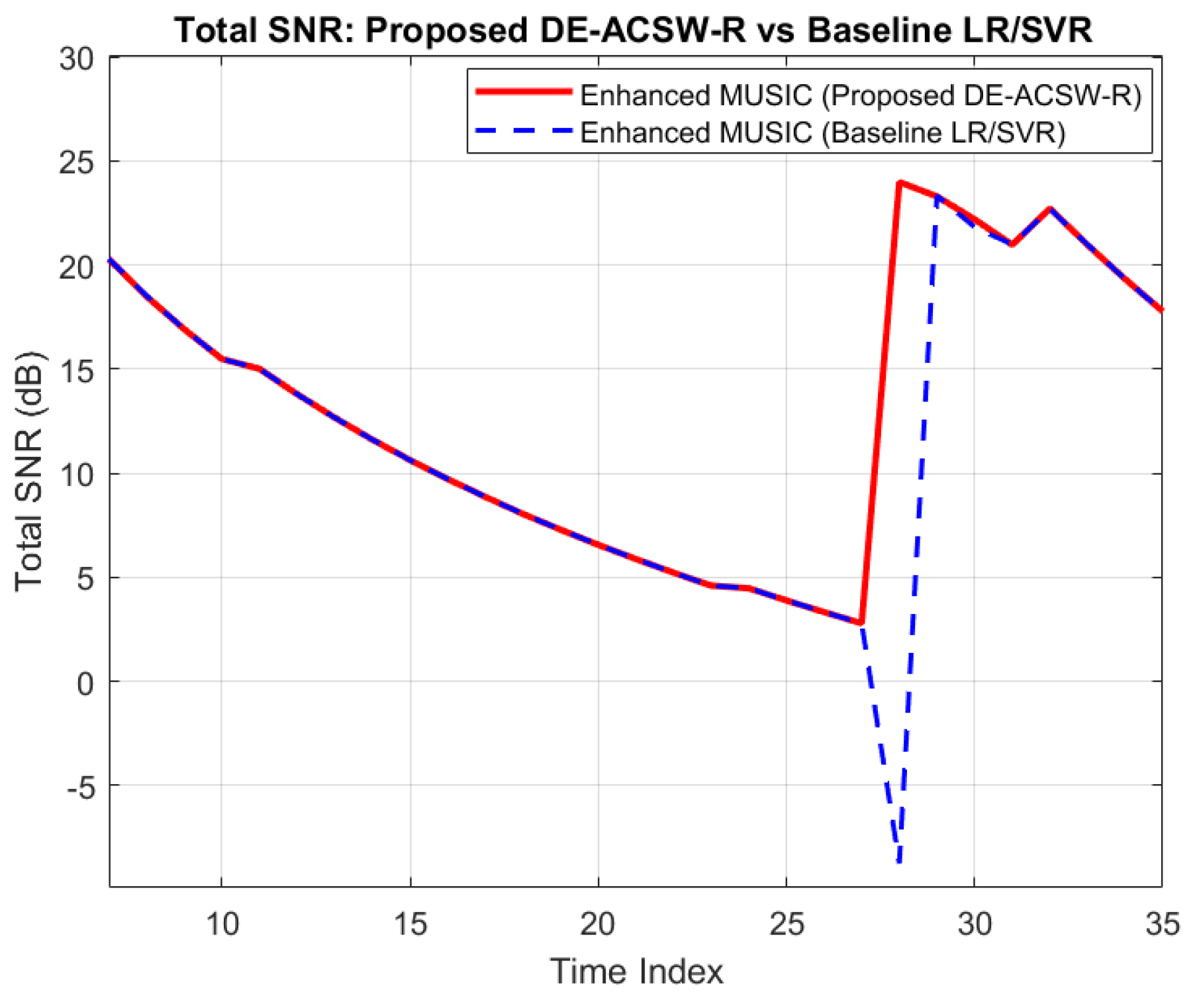
5.4. SNR Performance: Robustness Under Mobility and Prediction Failures

Figure 7 presents the time evolution of the total SNR (dB) achieved by the DE-ACSW-R system compared to the baseline LR/SVR-enhanced MUSIC approach. Both systems exhibit similar SNR trends during steady near-linear user movement (indices 6–26), where predictive and beamforming models track the trajectory without interruption. However, the distinction between the two approaches becomes pronounced during abrupt mobility changes.

A key difference is observed following the sharp AoA jump at index 27. The baseline system, lacking robust jump detection and fallback logic, continues to track with the outdated prediction, causing the enhanced MUSIC estimator to steer the beam incorrectly and resulting in a severe SNR collapse (dropping below −8.75 dB at indices 28–29). In contrast, the DE-ACSW-R model detects the anomaly and immediately disables enhanced MUSIC, switching to full MUSIC-based estimation. For index 28, the baseline system reports a total SNR of −8.75 dB, whereas the DE-ACSW-R approach maintains the SNR at 23.98 dB by leveraging prediction-aided fallback. This proactive fallback prevents SNR degradation, with the system rapidly restoring link quality to above 20 dB within just two time slots after the jump.

The key advantages demonstrated by the DE-ACSW-R framework are substantial. Most notably, the prediction-aware fallback logic effectively eliminates the risk of severe outages by preventing catastrophic SNR drops that would otherwise result from abrupt user movement or prediction errors. Furthermore, the system exhibits rapid SNR recovery, as its ability to quickly re-centre on the correct angle of arrival (AoA) using full MUSIC ensures that optimal beamforming performance is restored with minimal latency, even following extreme mobility events. Over the entire user trajectory, the DE-ACSW-R framework consistently maintains high SNR, substantially outperforming the baseline model, particularly during periods of trajectory instability. These results underscore the critical importance of adaptive prediction-aided fallback mechanisms for O-RAN deployments, where unpredictable user mobility and the need for robust link maintenance are essential for achieving system reliability and a high-quality user experience.

6. Conclusions

This work presents a novel, distributed prediction-enhanced beamforming framework called Dominance-Enforced Adaptive Clustered Sliding Window Regression (DE-ACSW-R), designed explicitly for O-RAN Split 7-2x architectures in high-mobility 5G environments. By combining clustered, jump-aware Weighted Linear Regression (WLR) at the O-RU with curvature-adaptive SVR and dynamic dominance-based fusion at the O-DU, the proposed framework overcomes the core limitations of conventional LR/SVR switching and static fusion approaches.

Simulation results demonstrate that DE-ACSW-R provides a decisive improvement in AoA prediction accuracy and beamforming robustness under challenging user mobility scenarios. The introduction of a window clustering mechanism allows for the system to adapt immediately to abrupt trajectory changes, avoiding lag and minimising prediction errors that would otherwise degrade beam alignment. The dynamic fusion logic ensures that the most statistically reliable predictor, whether linear or non-linear, always guides the system. At the same time, the autonomous fallback to full MUSIC estimation enables rapid self-recovery in the presence of prediction outliers or confidence drops.

Crucially, these innovations translate into a significant reduction in SNR collapse events, the rapid restoration of link quality after mobility-induced anomalies, and sustained high SNR across the entire user trajectory. The DE-ACSW-R framework consistently maintains optimal beam alignment, minimises the risk of misdirected beams, and adapts beam width and selection in real-time without the need for centralised intervention or excessive computational overhead.

These advances are fully aligned with the architectural principles of O-RAN Category B and are compatible with 3GPP New Radio requirements for ultra-reliable low-latency communication (URLLC). The proposed approach offers a practical, AI-native solution for future O-RAN deployments, supporting scalable, modular, and resilient beamforming in dense urban and high-mobility environments. By integrating predictive intelligence at both the edge (O-RU) and higher layers (O-DU), DE-ACSW-R paves the way for robust self-optimising RANs, meeting the evolving demands of 5G and emerging 6G networks.

Future work will extend the model to multi-user coordination, further optimise computational resource allocation between the O-RU and O-DU, and explore its integration with real-time AI/ML pipelines, as defined by the latest O-RAN specifications.