Abstract
Timely status updates are essential for Internet of Things (IoT) services. The freshness of these updates can be quantified using Age of Information (AoI). The worst-case behavior of AoI is evaluated by peak AoI (PAoI), denoting the maximum AoI just before each successful update. To characterize the time-averaged evolution of the PAoI over a long time horizon, we adopt the average PAoI as a performance metric. In this paper, we consider a two-hop status update system in IoT monitoring networks, where sensors periodically transmit short status packets to a remote edge server via a sink node. The sink node encodes status packets received from multiple sensors into a single longer packet to enhance the transmission reliability of short-packet communications. Here, we analyze the average PAoI in this setup as a function of system parameters and minimize this function by jointly optimizing three key parameters: (i) the number of status packets for joint coding at the sink node, (ii) the blocklength of a status packet in the first hop, and (iii) the blocklength of a coded packet in the second hop. Through numerical studies, we demonstrate the effectiveness of the proposed optimization in reducing the average PAoI.
1. Introduction
The freshness of status updates has emerged as a key performance indicator in Internet of Things (IoT) monitoring networks, where sensors periodically transmit packets to a remote destination to update real-time status information (e.g., temperature, humidity, wind speed) [1]. To quantify the freshness of status updates, Age of Information (AoI) was introduced as a performance metric in the seminal works [2,3]. This metric represents the time elapsed since the generation of the latest successfully decoded status packet at the destination. Peak AoI (PAoI) was introduced to evaluate the worst-case AoI, denoting the maximum AoI just before a status packet is successfully decoded at the destination [4]. This metric is particularly useful for supporting IoT services that require an upper bound on AoI. To characterize the time-averaged evolution of the PAoI over a long time horizon, we focus on the average PAoI as a performance metric.
In this paper, we investigate a status update system for IoT monitoring networks, where sensors periodically transmit status packets to a remote edge server via a sink node, as illustrated in Figure 1. Similar two-hop status update systems have been studied in prior works [5,6,7,8], and Section 2 provides a detailed comparison with these studies, highlighting the unique aspects of our work. Practical use cases of such systems include factory automation and smart environmental monitoring in IoT networks.
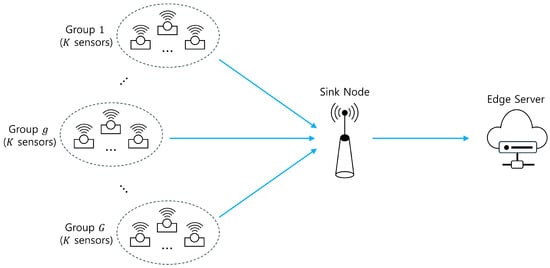
Figure 1.
A two-hop status update system consisting of G groups of K sensors, a sink node, and an edge server.
In IoT monitoring networks, status packets are typically short (e.g., tens of bytes) to meet stringent low-latency requirements [9]. However, short-packet communications are prone to decoding errors due to operation in the finite blocklength regime. This contrasts with the infinite blocklength regime, where error-free channel capacity can be achieved based on Shannon’s formula, but at the cost of large transmission delays. In [10], Polyanskiy et al. established a theoretical framework for error probability in the finite blocklength regime, providing a tight approximation formula for the PER as a function of blocklength. In this paper, we use this approximation formula to capture the PERs in two-hop transmissions, i.e., from a sensor to the sink node (first hop) and from the sink node to the edge server (second hop).
To enhance the reliability of short-packet communications, multiple short packets can be concatenated into a longer packet [11,12]. In this paper, we adopt joint packet coding at the sink node to concatenate status packets, following the approach in [5]. This approach involves dividing the sensors into groups. The sink node then collects status packets from each group, jointly encodes them into a longer packet, and transmits the coded packet to the edge server.
For this system, we first note that the number of sensors per group significantly affects the AoI performance. We refer to this number as the group size throughout the paper. In addition to group size, blocklength is a key parameter that determines AoI performance in short-packet communications. In recent years, there have been growing efforts to analyze and minimize AoI in the finite blocklength regime through blocklength optimization for various systems, e.g., [13,14,15,16,17,18]. These studies derive optimal (or suboptimal) blocklengths to minimize the average AoI and, in some cases, the average PAoI. A detailed discussion and comparison with our work are provided in Section 2.
Motivated by these observations and prior studies, we optimize the following three key parameters to minimize the average PAoI in a two-hop status update system with joint packet coding:
- (1)
- The group size for joint packet coding;
- (2)
- The blocklength of a status packet in the first hop;
- (3)
- The blocklength of a coded packet in the second hop.
This paper is inspired by [5], where the status update system shown in Figure 1 was studied under short-packet communication conditions. The key differences between our work and [5] are summarized as follows. In [5], the impact of group size was analyzed from various perspectives, and the optimal group size was derived to minimize average AoI and bounded AoI. However, the optimization was performed under a fixed PER constraint, implying that the blocklengths of the status packet and the coded packet are determined by their respective PERs. Departing from [5], we treat blocklengths and group size as control variables to be optimized, thereby further exploiting the potential for AoI reduction. Since blocklengths and group size are coupled, we jointly optimize them to minimize the average PAoI and propose joint blocklength and group size (JBG) optimization. Furthermore, we adopt the average PAoI as a performance metric to evaluate the freshness of status updates from the worst-case perspective.
The contributions of this paper are summarized as follows.
- We present a closed-form formula for the average PAoI in a two-hop status update system with joint packet coding in the finite blocklength regime.
- Based on this formula, we jointly optimize the first-hop blocklength, second-hop blocklength, and group size to minimize the average PAoI.
- Through numerical studies, we validate the effectiveness of our analysis and optimization. In particular, the results show that the proposed scheme reduces the average PAoI by around 8% compared to the existing approach, with more significant gains observed under poor wireless channel conditions.
The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 describes the system model. In Section 4, we analyze the average PAoI. Based on this analysis, Section 5 details the procedure for minimizing the average PAoI. Numerical results are provided in Section 6. Section 7 discusses the applicability of our framework to fading channels and other key AoI metrics, such as the average and variance of AoI. Finally, Section 8 concludes the paper.
2. Related Work
Since the seminal works [2,3], extensive research has analyzed AoI through queueing models under various service disciplines, such as first-come-first-served (FCFS) and last-come-first-served (LCFS), with or without preemption [19,20]. Building on these foundational studies, AoI has attracted significant attention for enabling timely status updates in IoT networks. Comprehensive surveys on recent advances in AoI for IoT networks are available in [21,22]. In this section, we discuss prior studies relevant to our work, with a focus on three key aspects of AoI reduction in short-packet communications: (i) blocklength optimization, (ii) packet concatenation, and (iii) error control techniques.
2.1. Blocklength Optimization for AoI Reduction
Among various considerations, short-packet communications are particularly important in IoT networks, as they inevitably lead to decoding errors due to operation in the finite blocklength regime [9]. The seminal work by Polyanskiy et al. [10] established a theoretical framework for characterizing the PER as a function of blocklength. A longer blocklength can reduce AoI as it improves the PER, but it can also increase AoI due to a longer transmission time. Accordingly, finding an optimal blocklength that balances this tradeoff has been considered an important problem, and many studies (e.g., [13,14,15,16,17,18]) have investigated it in the context of AoI minimization.
Specifically, the study in [13] analyzes the average AoI under various packet management schemes, namely non-preemption, preemption, and retransmission, and optimizes the blocklength to minimize the average AoI under an AWGN channel. The work in [14] further examines the correlation and tradeoff among the average AoI, PAoI, and delay in an LCFS system with retransmission and non-preemption, and it proposes a joint optimization of blocklength and update rate to minimize the weighted sum of delay and the average PAoI under an AWGN channel. More recently, the study in [15] considers a slotted ALOHA network in which multiple devices transmit short status packets to a common access point, and it derives the optimal blocklengths that minimize the average AoI and PAoI, respectively, under AWGN channels.
Blocklength optimization for AoI reduction has also been studied in fading environments. The study in [16] evaluates two classic transmission protocols for machine-type communications under Rayleigh fading and derives suboptimal blocklengths to minimize the average AoI for each protocol. The work in [17] analyzes decode-and-forward relaying in both half-duplex and full-duplex modes, and it jointly optimizes the transmit power and blocklength to minimize the average AoI under Rayleigh fading. The study in [18] focuses on a two-hop status update system with energy harvesting (EH) and optimizes the blocklengths for both hops to minimize the average AoI under Rayleigh fading.
2.2. Packet Concatenation for AoI Reduction
Concatenating multiple short packets into a longer packet can enhance the reliability of short-packet communications [11,12]. Unlike the aforementioned studies [13,14,15,16,17,18], this paper focuses on leveraging such concatenation, along with blocklength optimization, to support timely status updates in IoT networks under short-packet communication conditions.
The most relevant work in this context is [5], which considers a two-hop status update system, as illustrated in Figure 1, and proposes joint packet coding at the sink node. The study analyzes information freshness and reliability in terms of AoI and PER, respectively, and derives the optimal group size under fixed PER constraints. Other relevant works include [6,7,8], which consider two-hop status update systems similar to the one in Figure 1, specifically focusing on uplink scenarios in [6,7] and a downlink scenario in [8]. The work in [6] applies a product code (i.e., a type of parallel concatenated code) to implement joint packet coding at the sink node. It demonstrates that product coding reduces the average AoI compared to conventional block-coded schemes and also investigates the optimal group size under fixed PER constraints, as in [5]. The study [7] compares the performance of two encoding schemes in terms of the average AoI: a joint encoding scheme and a distributed encoding scheme. These schemes correspond to the system in Figure 1 with group sizes fixed at N and 1, respectively. It derives the optimal blocklength for each scheme under a fixed group size constraint (i.e., N or 1). Furthermore, the work in [8] investigates the tradeoff between average AoI and EH in a downlink scenario and demonstrates that an optimal group size exists that simultaneously achieves high EH and low average AoI under a fixed PER constraint.
While these works [5,6,7,8] provide valuable insights into the effectiveness of concatenation for AoI reduction in short-packet communications, they either fix the blocklength (i.e., impose a fixed PER constraint) or treat the group size independently. Consequently, the joint optimization of blocklengths and group size for AoI reduction in two-hop status update systems remains only partially explored.
2.3. Error Control Techniques for AoI Reduction
Besides packet concatenation, several reliability-enhancing mechanisms can also be used to improve the reliability of short-packet communications, including forward error correction (FEC); automatic repeat request (ARQ); a combination of FEC and ARQ, namely hybrid ARQ (HARQ); and network coding. Recent studies have explored combining HARQ mechanisms with two-hop links to optimize AoI [23,24]. Nonetheless, these methods still depend on explicit feedback and iterative decoding, which increase the real-time computational load with every retransmission and require relay nodes to maintain multi-packet buffers. Network-coding-based schemes improve performance by replacing retransmissions with algebraic mixing of packets [25,26]; however, they also demand finite-field matrix operations and additional memory to store coding coefficients and partially decoded blocks. In contrast, the scheme proposed in this paper preserves the packet-level real-time processing path and confines added computations to a one-time offline optimization step. Consequently, it retains nearly the same runtime complexity and buffer requirements as the approach in [5], while delivering substantial AoI gains under finite blocklength constraints.
3. System Model
In this section, we provide a detailed description of the system model depicted in Figure 1. We consider a status update system comprising N homogeneous sensors, a sink node, and an edge server. The sensors are divided into groups, where K represents the group size, i.e., the number of sensors per group. The k-th sensor in group g is indexed as , where .
We consider an uplink scenario in which status packets are transmitted from each sensor to the edge server via the sink node in two hops. We assume that the sink node operates in half-duplex mode; thus, no first-hop transmissions occur during the second-hop transmission, and vice versa. The uplink transmissions follow a round-robin schedule on a group-by-group basis, as described below.
Suppose that group g is scheduled for the first-hop transmissions. Then, each sensor in group g, from sensor to sensor , transmits its status packet to the sink node in order. Specifically, once sensor completes its transmission to the sink node, the next sensor immediately begins transmitting its status packet. (The analysis in this paper remains applicable to other TDMA-based policies for scheduling sensors in a group, provided that sensor is defined as the k-th scheduled sensor in group g.) At the same time, the sink node continuously collects status packets from all sensors in group g. The transmission time of each status packet to the sink node is given by , where denotes the blocklength of each status packet and B represents the system bandwidth. Hence, the total duration of the first-hop transmissions in group g is given by .
Once the first-hop transmissions for group g are completed, i.e., the sink node has collected K status packets from all sensors in group g, it jointly encodes these K status packets into a single coded packet and transmits it to the edge server in the second-hop transmission. The transmission time in the second hop is given by , where denotes the blocklength of the coded packet.
Once the second-hop transmission for group g is completed, i.e., the edge server has received the coded packet of group g from the sink node, the next group (or group 1 if ) is scheduled for the first-hop transmissions to the sink node. These first-hop transmissions are followed by the second-hop transmission of the corresponding coded packet from the sink node to the edge server, and this process repeats for all groups.
We now analyze the PER in short-packet communications based on the results of [10]. We assume that packets are transmitted over additive white Gaussian noise (AWGN) channels. Then, the PER in the i-th hop for can be tightly approximated as follows:
Here, is the Q-function, is the received signal-to-noise ratio (SNR) at the sink node () or the edge server (), and is the number of information bits per status packet () or coded packet (). A status packet sent by a sensor is successfully received and decoded at the edge server if and only if no packet error occurs in either the first-hop or second-hop transmission. Hence, the probability of successful decoding at the edge server is given by
Next, we describe the status update procedure at the edge server. Upon receiving a coded packet of a group (e.g., group g), the edge server decodes it to recover the status information of all sensors in group g. If the k-th status packet in group g is successfully decoded (with probability ), the edge server updates the status of sensor using the information contained in the packet. On the other hand, if the k-th status packet in group g fails to decode (with probability ), the edge server cannot update the status of sensor . In the latter case, the failed packet is not retransmitted and is considered lost.
Last, we describe the packet arrival model. We assume a generate-at-will model, as adopted in e.g., [5], where each sensor generates a status packet whenever needed. Accordingly, when a sensor is scheduled for transmission, it generates a packet just before transmission. As a result, each sensor always transmits a new status packet, regardless of whether the previous one was successfully decoded at the edge server. Furthermore, under this generate-at-will model, status packets from each sensor are generated periodically, with a period of
It is worth noting that this packet arrival model effectively captures IoT networks with periodic and synchronous updates, such as those in periodic wireless sensor networks [27,28]. In contrast, for event-driven or asynchronous systems where status packets are generated randomly, a more general arrival model would be required. The AoI performance under such models remains an active research topic; see, e.g., [21,22,29] and references therein.
4. Average PAoI Analysis
In this section, we derive a closed-form formula for the average PAoI. For the analysis, we consider sensor as a tagged sensor and track its behavior. For any given time instant , let denote the generation time of the most recently successfully decoded status packet of sensor at the edge server. Then,
represents the instantaneous AoI of sensor at time t [3].
Whenever the status packet of sensor is successfully decoded at the edge server, the AoI is reset to the sojourn time of this packet, given by
Here, the first term represents the time required for the sink node to collect all status packets from the k-th to the K-th sensors in group g during the first-hop transmissions; the second term represents the time needed for the sink node to transmit the jointly coded packet of group g to the edge server during the second-hop transmission.
Once the AoI is reset to , it increases linearly with a slope of 1 until the next successful decoding of a status packet from sensor at the edge server. As a result, the AoI reaches its local peak just before every successful decoding of a status packet from sensor at the edge server. This local peak is referred to as the PAoI, representing the worst-case AoI performance. Let denote the i-th PAoI of sensor . Then, we have
where and denote the generation times of the i-th and -th successfully decoded status packets, respectively, of sensor at the edge server, and is given in (4). Figure 2 shows a sample path of .
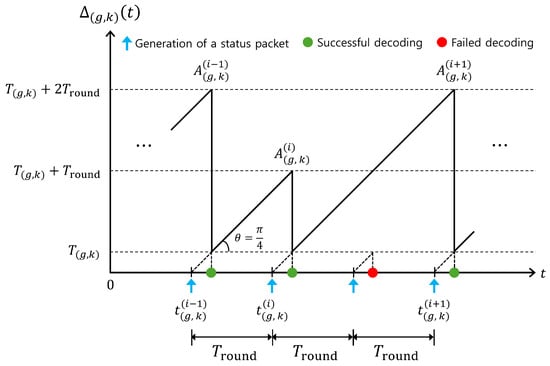
Figure 2.
A sample path of the instantaneous AoI over time t.
The term in (5) is probabilistically determined as follows: (i) Sensor generates its status packets periodically with a period of , as given in (3). (ii) The decoding of each status packet at the edge server is successful with probability or fails with probability , where is given in (2). (iii) These decoding outcomes are independent across the status packets of sensor . From (i) and (ii), it follows that
where is a random variable representing the total number of status packets generated by sensor between and that fail to decode at the edge server. Furthermore, from (ii) and (iii), this random variable follows a geometric distribution with parameter and support . Specifically,
Substituting (6) into (5), we obtain
The average PAoI of sensor , denoted by , is expressed as ([30], Equation (5))
Using the expression for in (8), we obtain
Here, holds because and are independent of i, and follows from the law of large numbers, as for are independent and identically distributed random variables. From (7), the expected value of is obtained as . Hence, the average PAoI of sensor is given by
5. Average PAoI Minimization
Based on the analysis in Section 4, we minimize the average PAoI through the JBG optimization, treating the blocklengths and the group size K as control variables. We begin by formulating the average PAoI as a function defined on the domain , where denotes the set of all divisors of N. Based on the relation
the average PAoI minimization is performed in two sequential steps. In the first step, we fix and solve
Then, the minimum average PAoI for a given group size K is obtained as
In the second step, we determine the optimal group size by minimizing over all :
Then, the optimal blocklengths for transmissions in the first and second hops are given by
Finally, the minimum average PAoI is obtained as
In the above procedure, solving (11) is crucial to arrive at (13)–(15). To this end, we relax the constraint to and solve the system of equations and . Note that such relaxation has been used in the recent literature to optimize blocklength, e.g., [15,16,17,18]. Differentiating in (10) with respect to for , we obtain
where for is derived as
with
We note that the partial derivatives in (16) and (17) represent the rate of change of the average PAoI with respect to the blocklengths and , with and held fixed, respectively. In other words, they quantify the sensitivity of the average PAoI to variations in blocklength. The right-hand sides of (16) and (17) explicitly capture the effects of the control variables K, , and . In particular, the term corresponds to the average number of failed transmissions between two consecutive successful decodings at the edge server. Consequently, the partial derivative in (18) characterizes how this average changes with the blocklength , highlighting the tradeoff between reliability and transmission delay.
By setting and , we obtain the following fixed-point problem for the two variables and :
For a given set of system parameters , we can numerically solve for and by applying a fixed-point iteration method [31] to Equations (19) and (20). The blocklengths in (11) are then calculated as and , where denotes rounding to the nearest integer.
We note that even for large-scale systems (i.e., systems with a large number of sensors N), the fixed-point problem remains scalable, as N is treated as a constant in Equations (19) and (20), and a conventional fixed-point algorithm can be applied. However, the subsequent step in the optimization procedure, formulated in (13), involves comparisons over all , resulting in a computational complexity of with respect to the system size N. Since the fixed-point iteration can be executed offline using standard numerical methods, the proposed scheme is considered computationally feasible for real-time or resource-constrained systems.
6. Numerical Studies
6.1. Parameter Setting
In this section, we present numerical studies to evaluate the performance of the proposed JBG optimization. For this study, we use the parameters from ([5], Section V) unless stated otherwise. Specifically, the system consists of sensors, and, thus, the group size K is chosen from the set . The system bandwidth is normalized to . Each status packet sent by a sensor contains information bits. The average SNR at the sink node and the edge server is set to , where dB. Table 1 summarizes the parameter settings used in the numerical studies.

Table 1.
Parameter settings.
6.2. Validation via Monte Carlo Simulations
The average PAoI expression in (10) forms the basis for the JBG optimization. Accordingly, we first validated this expression prior to performing the optimization. To this end, we developed a MATLAB-based simulator that emulates the two-hop status update system illustrated in Figure 1 under AWGN channels. Using this simulator, we conducted Monte Carlo simulations with different random seeds for each run. To validate our analysis under various channel conditions, we considered different SNR settings, specifically dB. Furthermore, we performed simulations over two different time scales—long-term and short-term. For the long-term case, we performed 100,000 runs and computed the empirical mean. For the short-term case, we performed 30 runs and computed the 95% confidence interval. We then compared the simulation results with the analytical values obtained from (10). Figure 3 presents this comparison. As shown in the figure, the analytical results closely match the simulation results at both long-term and short-term time scales across different SNR settings, thereby confirming the correctness of the derived expression.
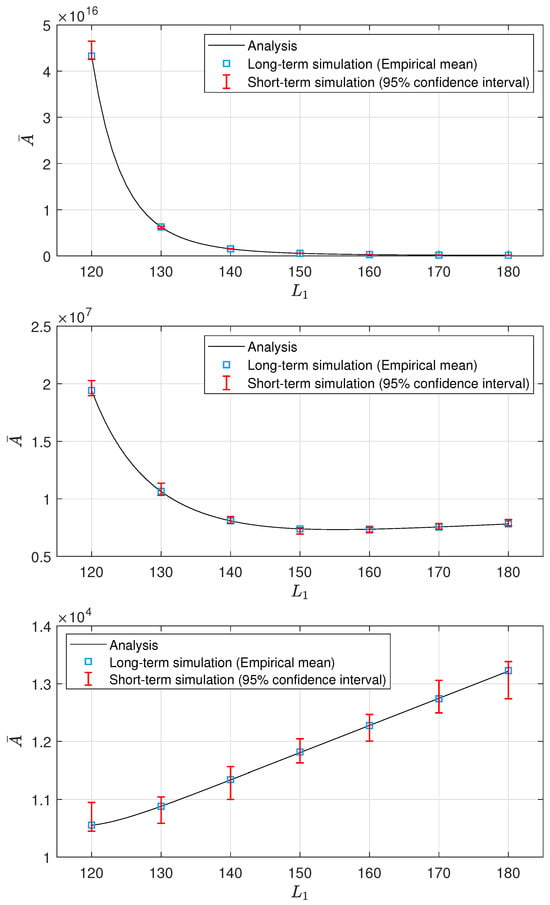
Figure 3.
Comparison between analytical and simulation results when and . Results are presented for different SNR settings: dB (top), dB (middle), and dB (bottom).
6.3. JBG Optimization
Based on the formula (10), we proceed with the JBG optimization. We begin by investigating the impact of the blocklengths on the average PAoI, assuming a fixed group size. Figure 4 shows the average PAoI obtained from (10) for varying blocklengths and , with the group size fixed at and the average SNR set to dB. The figure shows that the average PAoI initially decreases and then increases as the blocklengths increase, attaining a minimum at an intermediate point. The circular marker on the surface in Figure 4 indicates the minimum point found through an exhaustive search, where reaches its minimum value of at . The star-shaped markers on the x- and y-axes denote the solutions to (19) and (20), showing that and , which match the exhaustive search results.
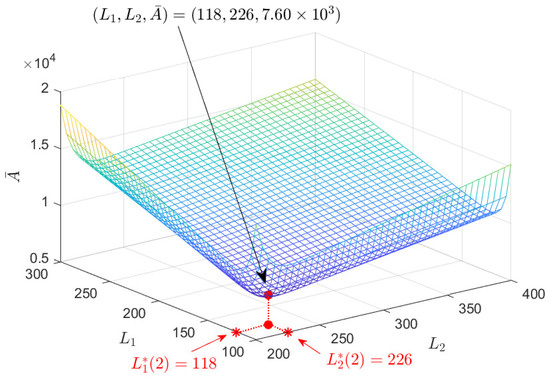
Figure 4.
Average PAoI in (10) for varying blocklengths and , with the group size fixed at and dB.
Now, we vary the group size K within the set and compute the optimal blocklengths and in (11) for each K by solving (19) and (20). Figure 5 presents the results, where increases with K, whereas remains nearly constant with a slight decrease as K increases. This behavior arises because joint packet coding is performed at the sink node for second-hop transmission, making the blocklength strongly dependent on the group size.
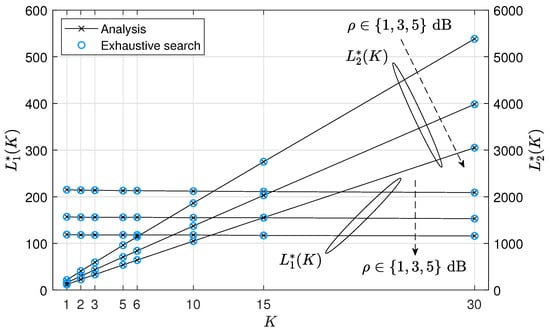
Figure 5.
Optimal blocklengths and in (11) for each group size .
The use of and minimizes the average PAoI when the group size is fixed at K. The resulting average PAoI is obtained from (12) and shown in Figure 6 for . The average PAoI is minimized at for each SNR dB, meaning the optimal group size is for these values of .
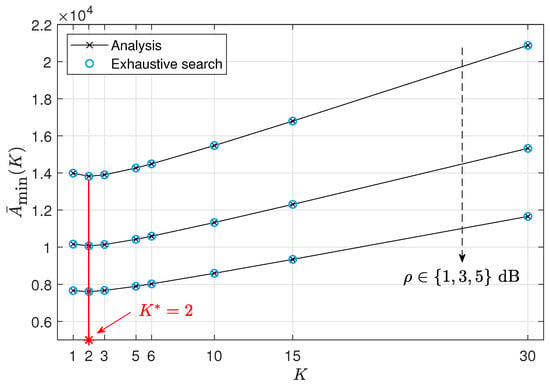
Figure 6.
Minimum average PAoI in (12) for each group size .
This result in Figure 6, combined with that in Figure 5, determines the optimal solutions for the control variables , as presented in Table 2. The minimum average PAoI achieved with is calculated using (15) and given by for dB. Here, decreases with because a higher SNR improves the PER, allowing for a shorter blocklength.
6.4. Impact of the Number of Sensors
So far, we have fixed the number of sensors at . In this subsection, we vary N from 10 to 200 and investigate its impact on the optimal group size and the optimal blocklengths for different average SNRs dB. To this end, we repeated the JBG optimization presented in Section 6.3 for each and summarize the results in Table 3.

From the table, we observe that a larger N generally leads to a larger . Conversely, when N is small (e.g., ), the optimal group size becomes , indicating that joint packet coding is no longer beneficial. In such cases, optimizing blocklengths alone can be a more effective approach to minimizing the average PAoI. Furthermore, the results in Table 3 show that under low-SNR conditions, a larger group size or longer blocklengths can help reduce the average PAoI, as they enhance the reliability of short-packet communications.
6.5. Comparison
Last, we evaluate the effectiveness of the proposed JBG optimization in minimizing the average PAoI. To this end, we adopt the method in [5] as a reference benchmark and compare its performance with that of our proposed scheme. In [5], the group size K is optimized to minimize the average AoI and the bounded AoI, while the blocklengths and are determined from (1), under the constraint that the PERs and are fixed (e.g., ). We apply the approach from [5] to minimize the average PAoI and present the results in Figure 7 for . Our proposed scheme outperforms the benchmark in [5] in terms of average PAoI, achieving reduction rates of % on average for dB. This demonstrates that optimizing the blocklengths in addition to the group size further reduces the average PAoI, with the effect being more pronounced in lower SNR environments, though at the cost of additional computation required to solve (19) and (20).
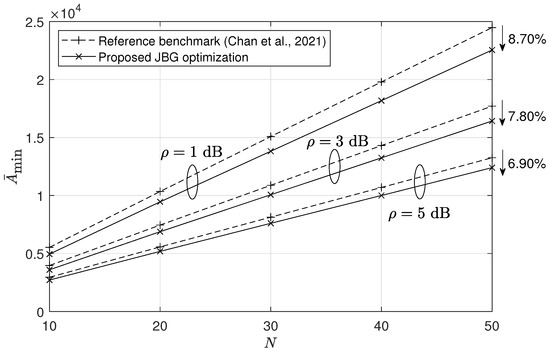
Figure 7.
Comparison of the minimum average PAoI between group size optimization in [5] and JBG optimization for varying numbers of sensors N.
We note that PAoI is closely related to packet delay, which is also a critical performance metric in IoT networks. Under the generate-at-will model, the sojourn time of a packet corresponds to its delay, as there is no queueing delay. Consequently, the packet delay of sensor is given , as specified in (4). It follows from (9) that this delay is bounded above by the average PAoI of sensor , implying that a lower average PAoI generally leads to reduced packet delays. Hence, in industrial-IoT monitoring scenarios—where an end-to-end latency budget on the order of 100 ms is common—even a modest decrease in the average PAoI can help reduce the share of packets that miss the latency deadline, delivering a tangible benefit. Importantly, the only additional cost introduced by the proposed JBG optimization is a single offline fixed-point computation; at run time, the decoder still performs one FEC pass, and the sink node maintains the same single-packet buffer as in [5]. Therefore, the proposed scheme increases the latency margin without changing the control cycle or protocol, and the performance gain remains evident while imposing virtually no extra memory overhead.
7. Discussion
7.1. Applicability to Fading Channels
In this paper, we have assumed AWGN channels with a constant SNR in the i-th hop for . However, in real-world scenarios, wireless channels often experience random fluctuations due to fading and path loss [32,33]. In this subsection, we discuss the applicability of our analysis and optimization framework under such conditions.
First, in the average PAoI analysis, the PER expression in (1) can be replaced with its expected value , which accounts for random fluctuations in the SNR . Suppose that the instantaneous SNR is modeled as a random variable with probability density function . Then, the average PER can be computed as
Details can be found in ([14], Footnote 2), ([16], Equation (20)), ([17], Equation (3)), ([34], Section V.A), ([35], Equation (11)), and ([36], Equation (8)). This approach is well suited to block-fading channels, where the channel coefficient remains constant during each packet transmission and varies independently between transmissions. Among various models, the Rayleigh block-fading channel has been widely adopted in prior studies on AoI analysis in the context of short-packet communications [16,17,35,36]. It is also worth noting that the Q-function in (21) can be tightly approximated by a segmented linear function [37], which has been employed in recent studies to simplify the evaluation of (e.g., [16,17,35,36,38,39]).
Given the average PERs and , the term in (2) can be replaced with , resulting in an average PAoI expression of the same form as in (10). Consequently, the optimization procedure described in Section 5 remains applicable, provided that the partial derivative in (18) is reformulated to account for the dependence on for .
7.2. Applicability to Average and Variance of AoI
This work is also readily extensible to other key AoI metrics, such as the average and variance of AoI. Specifically, the optimal group size and blocklengths that minimize either the average AoI or its variance can be obtained by applying the analysis and optimization framework presented in this work. For the analysis, the average AoI of sensor , denoted by , and its second moment, denoted by , are expressed as follows:
These expressions are derived in ([5], Equations (7) and (9)) for a two-hop status update system with joint packet coding, as illustrated in Figure 1. The system-wide average AoI and variance are given by
The optimization procedure described in Section 5 can then be applied to the functions and . Since the variance is associated with a second-order moment, its minimization can involve additional technical challenges.
8. Conclusions
In this paper, we addressed the minimization of the average PAoI in a two-hop IoT network employing joint packet coding, with the aim of achieving timely status updates. To this end, we derived a closed-form expression for the average PAoI and jointly optimized the blocklengths and the group size. Numerical results demonstrate that the proposed optimization reduces the average PAoI compared to the existing approach, with more substantial reductions observed under lower SNR conditions.
We validated our analysis using Monte Carlo simulations in MATLAB 2024. While this confirms the accuracy of our analytical results, it serves as an initial step and requires a further extension to adequately capture real-world system behaviors. As a next step, we plan to evaluate the proposed scheme using dedicated network simulators (e.g., ns-3) that account for factors such as protocol stack operations, traffic patterns, and channel fading.
For future work, we also plan to extend the system model to more practical scenarios, including heterogeneous sensors located at varying distances from the sink node and full-duplex operation at the sink node. In addition, we aim to extend the model to allow a different number of sensors per group, which, in turn, raises fairness considerations. We expect the analysis in this paper to provide a foundation for these extensions.
Author Contributions
Conceptualization, Y.K.; methodology, J.-H.C. and Y.K.; software, Y.K.; validation, J.-H.C.; formal analysis, Y.K.; investigation, J.-H.C. and Y.K.; writing—original draft preparation, Y.K.; writing—review and editing, J.-H.C.; visualization, J.-H.C.; funding acquisition, J.-H.C. and Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2019R1F1A1060743 and No. RS-2023-00279714).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in this study are openly available in FigShare at https://doi.org/10.6084/m9.figshare.29322113.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gu, Y.; Chen, H.; Zhou, Y.; Li, Y.; Vucetic, B. Timely status update in Internet of Things monitoring systems: An age–energy tradeoff. IEEE Internet Things J. 2019, 6, 5324–5335. [Google Scholar] [CrossRef]
- Kaul, S.; Gruteser, M.; Rai, V.; Kenney, J. Minimizing age of information in vehicular networks. In Proceedings of the IEEE SECON 2011, Salt Lake City, UT, USA, 27–30 June 2011; pp. 350–358. [Google Scholar] [CrossRef]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? In Proceedings of the IEEE INFOCOM 2012, Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar] [CrossRef]
- Costa, M.; Codreanu, M.; Ephremides, A. On the age of information in status update systems with packet management. IEEE Trans. Inf. Theory 2016, 62, 1897–1910. [Google Scholar] [CrossRef]
- Chan, T.-T.; Pan, H.; Liang, J. Age of information with joint packet coding in industrial IoT. IEEE Wirel. Commun. Lett. 2021, 10, 2499–2503. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, M.; Zhao, C. Age of information with product coded IoT systems. In Proceedings of the 2022 International Symposium on Wireless Communication Systems (ISWCS), Hangzhou, China, 19–22 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, N.; Sadeghi, P.; Zhou, X. The age of information of short-packet communications: Joint or distributed encoding? In Proceedings of the IEEE ICC, Seoul, Republic of Korea, 16–20 May 2022; pp. 2175–2180. [Google Scholar] [CrossRef]
- Zou, Z.; Chan, T.-T.; Pan, H.; Lok, T.-M. Age of information and energy harvesting tradeoff for joint packet coding in downlink IoT networks. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, M.; Mohammadi, M.S.; Abbas, R.; Minja, A.; Yue, C.; Matuz, B.; Han, G.; Lin, Z.; Liu, W.; Li, Y.; et al. Short block-length codes for ultra-reliable low latency communications. IEEE Commun. Mag. 2019, 57, 130–137. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdú, S. Channel coding rate in the finite blocklength regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Durisi, G.; Koch, T.; Popovski, P. Toward massive, ultrareliable, and low-latency wireless communication with short packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef]
- Trillingsgaard, K.F.; Popovski, P. Downlink transmission of short packets: Framing and control information revisited. IEEE Trans. Commun. 2017, 65, 2048–2061. [Google Scholar] [CrossRef]
- Wang, R.; Gu, Y.; Chen, H.; Li, Y.; Vucetic, B. On the age of information of short-packet communications with packet management. In Proceedings of the IEEE GLOBECOM, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, J.; Zhu, X.; Jiang, Y.; Wei, Z.; Sun, S. Information age-delay correlation and optimization with finite block length. IEEE Trans. Commun. 2021, 69, 7236–7250. [Google Scholar] [CrossRef]
- Kim, Y. Minimizing age of information in slotted ALOHA with short-packet communications. IEEE Access 2024, 12, 186779–186793. [Google Scholar] [CrossRef]
- Yu, B.; Cai, Y.; Wu, D.; Xiang, Z. Average age of information in short packet based machine type communication. IEEE Trans. Veh. Technol. 2020, 69, 10306–10319. [Google Scholar] [CrossRef]
- Zheng, D.; Yang, Y.; Wei, L.; Jiao, B. Decode-and-forward short-packet relaying in the Internet of Things: Timely status updates. IEEE Trans. Wirel. Commun. 2021, 20, 8423–8437. [Google Scholar] [CrossRef]
- Xie, M.; Jia, X.; Yin, J.; Wang, Q.; Zhou, M. Age of information for partial earliest relay aided short packet status update with energy harvesting. IEEE Trans. Wirel. Commun. 2024, 23, 699–719. [Google Scholar] [CrossRef]
- Bedewy, A.M.; Sun, Y.; Shroff, N.B. Minimizing the age of information through queues. IEEE Trans. Inf. Theory 2019, 65, 5215–5232. [Google Scholar] [CrossRef]
- Moltafet, M.; Leinonen, M.; Codreanu, M. On the age of information in multi-source queueing models. IEEE Trans. Commun. 2020, 68, 5003–5017. [Google Scholar] [CrossRef]
- Kahraman, İ.; Köse, A.; Koca, M.; Anarım, E. Age of information in Internet of Things: A survey. IEEE Internet Things J. 2023, 11, 9896–9914. [Google Scholar] [CrossRef]
- Abbas, Q.; Hassan, S.A.; Qureshi, H.K.; Dev, K.; Jung, H. A comprehensive survey on age of information in massive IoT networks. Comput. Commun. 2023, 197, 199–213. [Google Scholar] [CrossRef]
- Li, A.; Wu, S.; Jiao, J.; Zhang, N.; Zhang, Q. Age of information with Hybrid-ARQ: A unified explicit result. IEEE Trans. Commun. 2022, 70, 7899–7914. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Ren, J.; Wang, F.; Wang, S.; Yu, J. On AoI of grant-free access with HARQ. IEEE Trans. Commun. 2024, 72, 924–937. [Google Scholar] [CrossRef]
- Pan, H.; Chan, T.-T.; Leung, V.C.M.; Li, J. Age of information in physical-layer network coding enabled two-way relay networks. IEEE Trans. Mob. Comput. 2023, 22, 4485–4499. [Google Scholar] [CrossRef]
- Kahraman, İ.; Köse, A.; Koca, M.; Anarim, E. Impact of network coding on age of information in multi-source multi-hop IoT networks. IEEE Internet Things J. 2024, 11, 33053–33063. [Google Scholar] [CrossRef]
- Bae, Y.H.; Baek, J.W. Age of information and throughput in random access-based IoT systems with periodic updating. IEEE Wirel. Commun. Lett. 2022, 11, 821–825. [Google Scholar] [CrossRef]
- Al-Qurabat, A.K.M.; Abdulzahra, S.A. An overview of periodic wireless sensor networks to the Internet of Things. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 032055. [Google Scholar] [CrossRef]
- Chen, L.; Dong, Y. Estimating age of information in wireless systems with unknown distributions of inter-arrival/service time. IEEE Trans. Netw. Sci. Eng. 2024, 11, 6090–6104. [Google Scholar] [CrossRef]
- Yates, R.D.; Sun, Y.; Brown, D.R.; Kaul, S.K.; Modiano, E.; Ulukus, S. Age of information: An introduction and survey. IEEE J. Sel. Areas Commun. 2021, 39, 1183–1210. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Singh, A.; Danish, S.M.; Prasad, G.; Kumar, S. A unified α–η–κ–μ fading model based real-time localization on IoT edge devices. IEEE Trans. Netw. Sci. Eng. 2024, 11, 6207–6218. [Google Scholar] [CrossRef]
- Blagojević, V.; Kozić, N.; Cvetković, A.; Ivaniš, P. Secrecy outage performance analysis of wirelessly powered IoT system with randomly moving receiving nodes. Sensors 2025, 25, 1386. [Google Scholar] [CrossRef]
- Han, C.; Gu, Y.; Li, Y.; Vucetic, B. Optimal blocklength allocation towards reduced age of information in wireless sensor networks. In Proceedings of the IEEE GLOBECOM Workshops, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Li, J.; Tang, J.; Liu, Z. On the data freshness for industrial Internet of Things with mobile-edge computing. IEEE Internet Things J. 2022, 9, 13542–13554. [Google Scholar] [CrossRef]
- Sung, H.; Kim, M.; Lee, S.; Lee, J. Age of information analysis for finite blocklength regime in downlink cellular networks. IEEE Wirel. Commun. Lett. 2022, 11, 683–687. [Google Scholar] [CrossRef]
- Makki, B.; Svensson, T.; Zorzi, M. Finite block-length analysis of spectrum sharing networks using rate adaptation. IEEE Trans. Commun. 2015, 63, 2823–2835. [Google Scholar] [CrossRef]
- Cao, J.; Zhu, X.; Jiang, Y.; Wei, Z. Can AoI and delay be minimized simultaneously with short-packet transmission? In Proceedings of the IEEE INFOCOM Workshops, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, W.; Lu, X.; Yan, S.; Shu, F.; Li, Z. Age of information for short-packet covert communication. IEEE Wirel. Commun. Lett. 2021, 10, 1890–1894. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).