Analysis of Strength Effects on the Dynamic Response of a Shaped-Charge Under Lateral Disturbances
Abstract
1. Introduction
2. Finite Element Model and Research Scheme
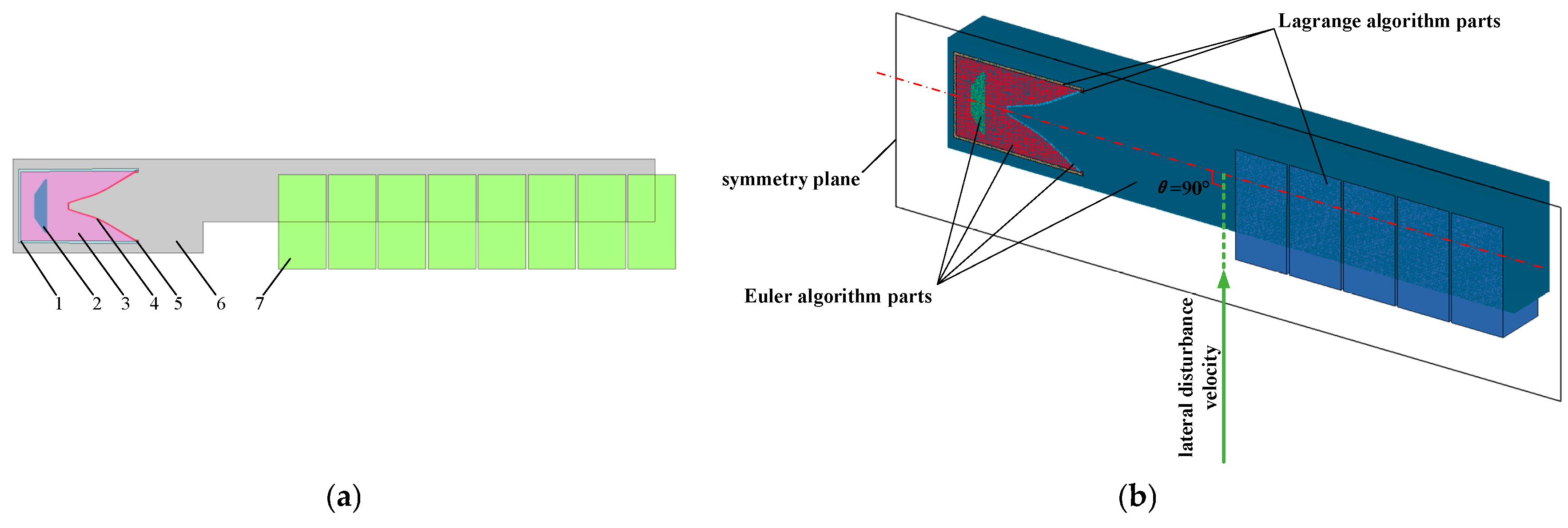
2.1. Simplified and Numerical Simulation Models
2.2. Material Model and Parameters
3. Dynamic Impact Process of the Jet Under the Influence of Target Strength
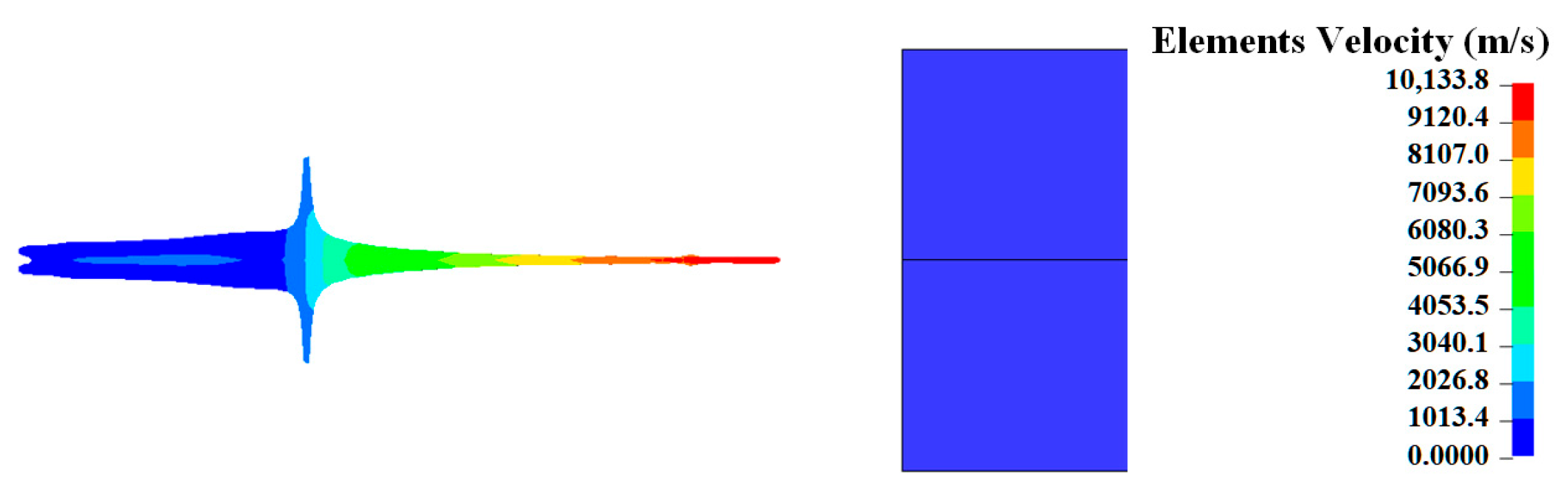
3.1. Typical Jet Dynamic Impact Process
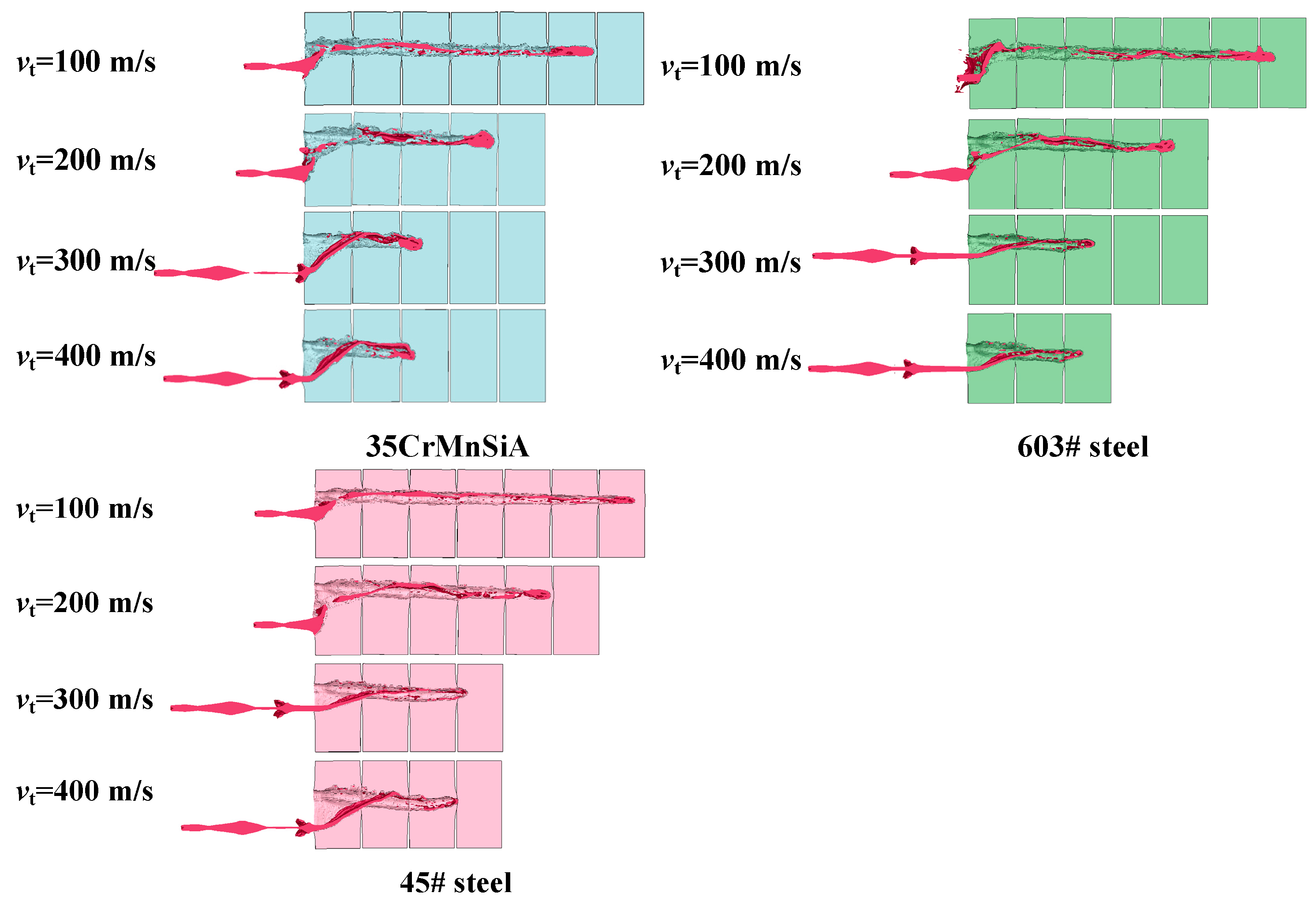
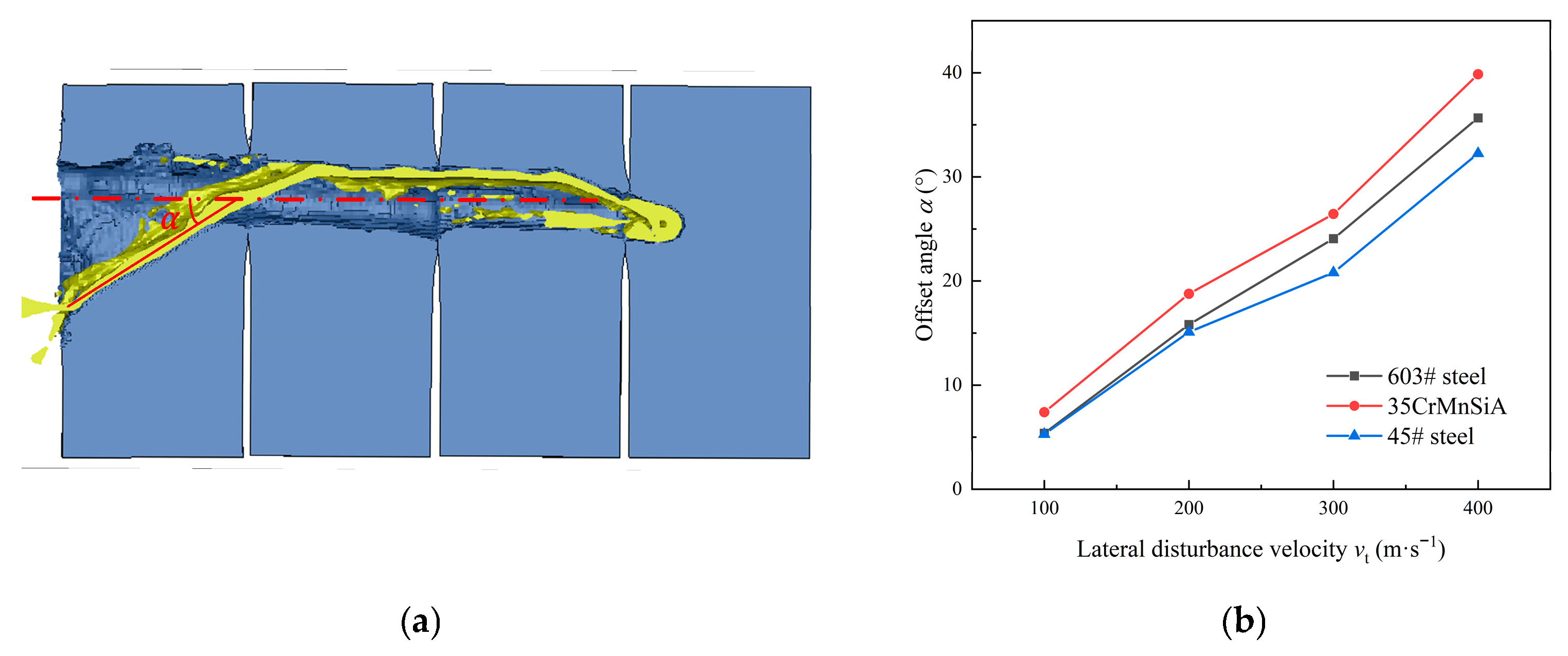
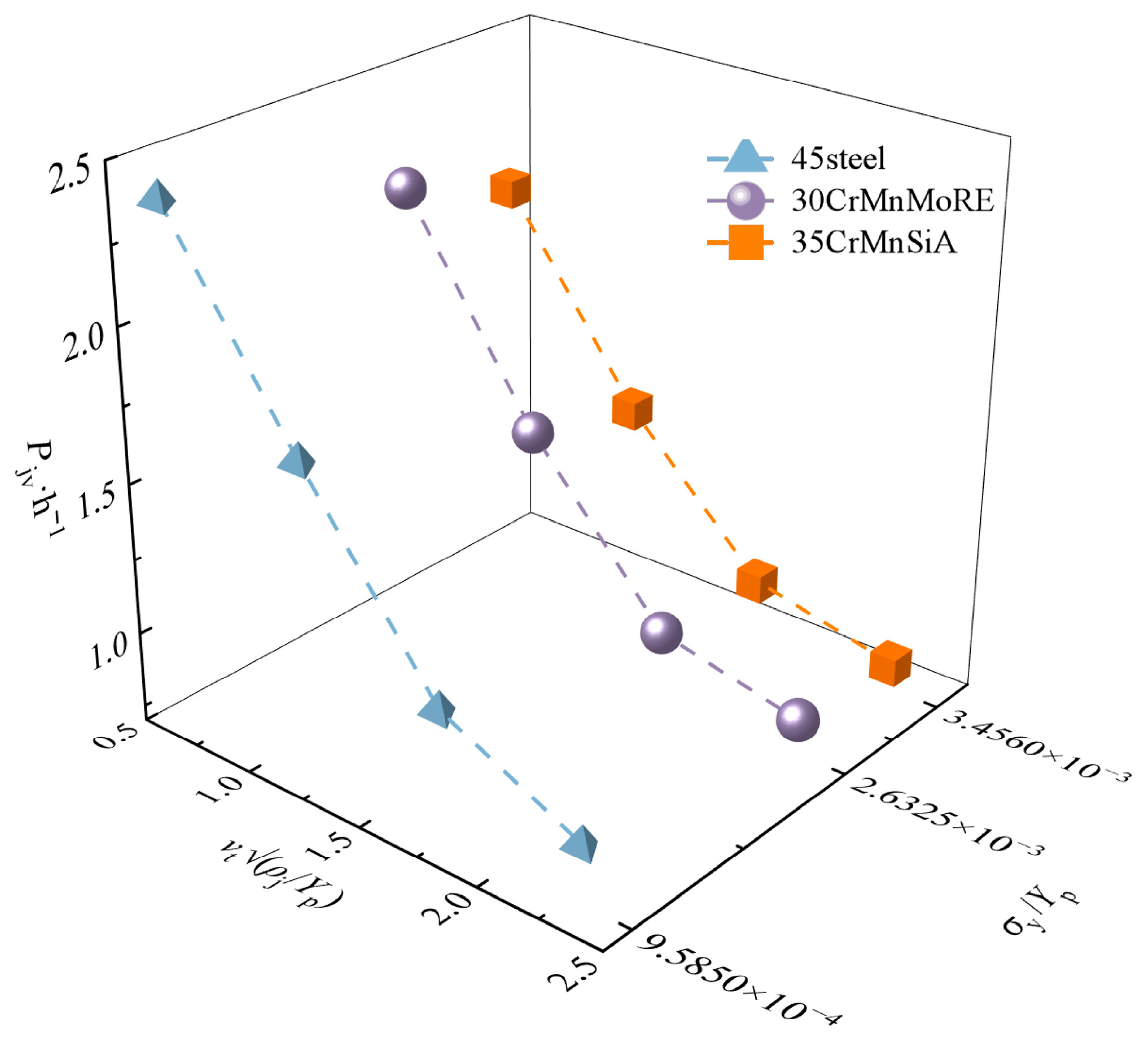
3.2. Analysis of Disturbed Impact Process
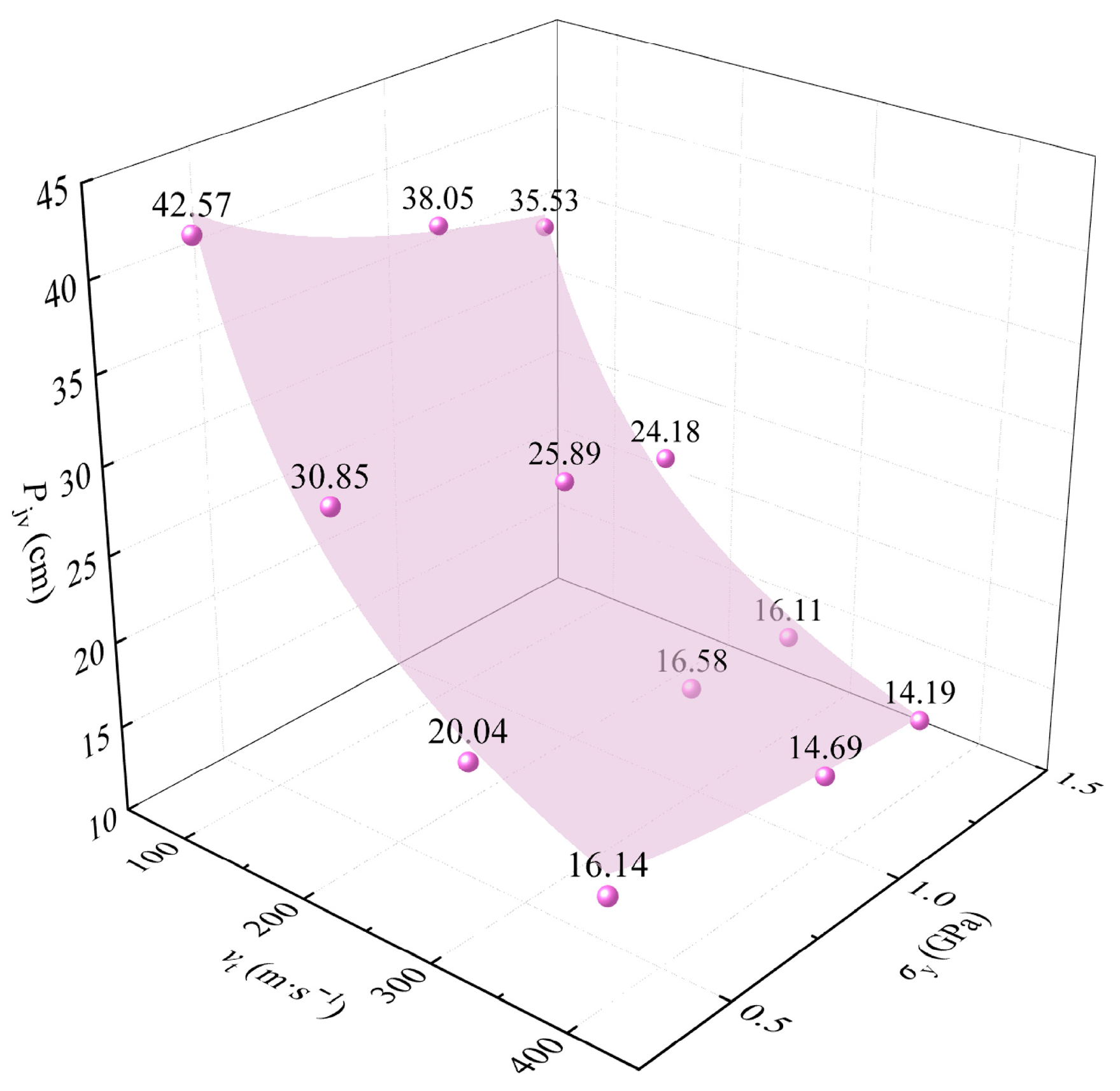
3.3. Establishment of Prediction Model
4. Dynamic Impact Test of Shaped-Charge Jet
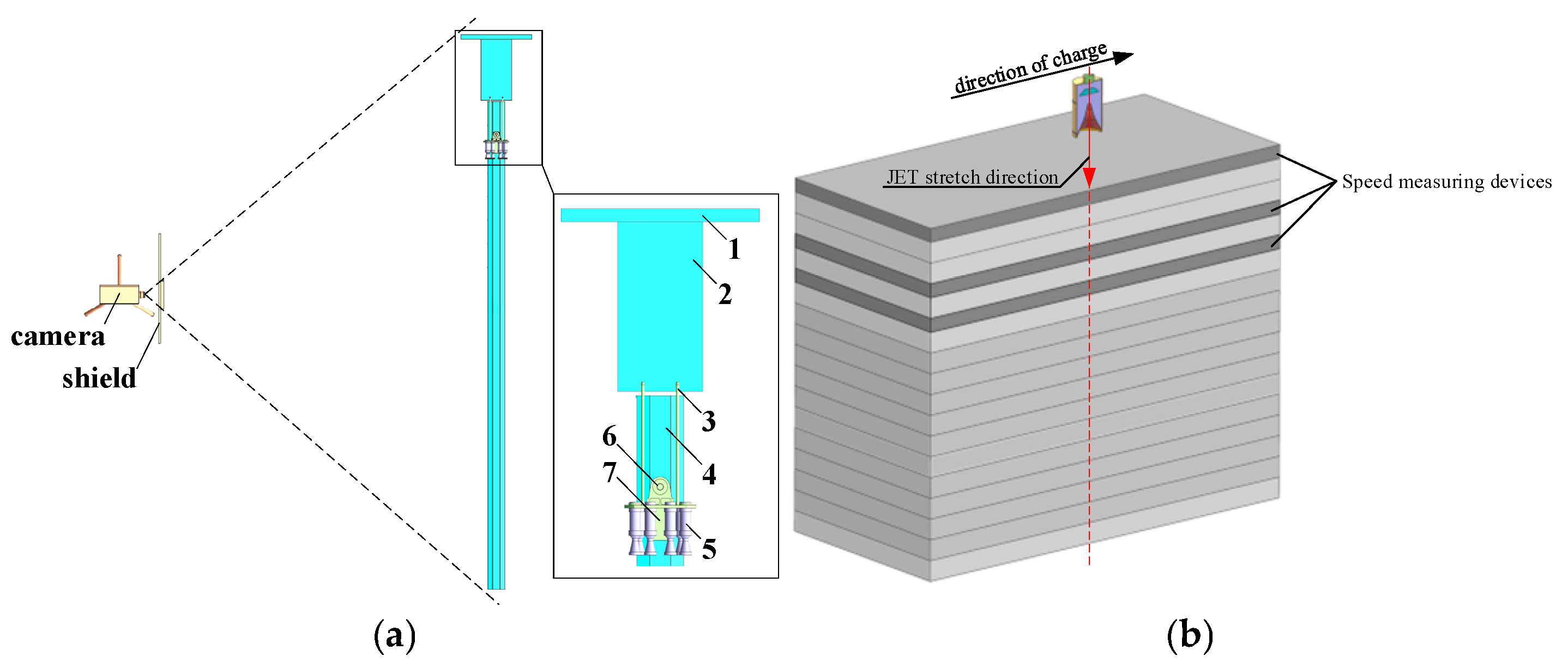
4.1. Dynamic Impact Test Principle
4.2. Numerical Simulation and Validity Verification of Prediction Model
5. Conclusions
- When the lateral disturbance velocity increases within the range of 100–400 m/s, the jet offset angle increases with the increase of the lateral disturbance velocity across all target yield strengths. At a fixed lateral disturbance velocity, the offset angle is negatively correlated with the yield strength of the target plate;
- Based on dimensional analysis, considering the influence of lateral disturbance velocity, jet strength and target strength, it is found that there is a strong exponential relationship between the dimensionless variable Pj,dyn/l and the respective influencing variables;
- A comparison of the numerical simulation, the prediction model and the experimental data under different target velocities, reveals that the relative errors between the established prediction model, numerical simulation and experimental data are all below 15%, showing good consistency. The established engineering model can characterize the influence of target strength.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hao, Z.; Wang, Z.J.; Xu, Y.J.; Duan, C.; Wang, Y. Study on the detonation wave propagation of shaped charge with three-layer liner and its driving characteristics to liner. Sci. Rep. 2024, 14, 8778. [Google Scholar] [CrossRef]
- Fang, Y.Z.; Zhang, X.F.; Xiong, W.; Liu, C.; Tan, M.T. Characteristics of After-effect Parameters of Shaped Charge Jet Penetrating Finite Thickness Steel Target. Chin. J. Energetic Mater. 2024, 32, 899–910. [Google Scholar]
- Guo, Y.; Peng, S.; Yang, R. Experimental and numerical simulation study on penetration damage effect of parabolic-shaped charge. Braz. Soc. Mech. Sci. Eng. 2025, 47, 91. [Google Scholar] [CrossRef]
- Park, J.; Kwon, S. Study on the penetration performance of a double-angle linear shaped charge: Performance improvement and miniaturization. Aerospace. 2024, 11, 310. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Z. Ammunition; Beijing Institute of Technology Press: Beijing, China, 2015; pp. 134–135. [Google Scholar]
- Liu, Z.; Yang, R.; Zuo, J.; Xu, P.; Zhao, Y.; Yang, Z. Research on the crack formation mechanism of shaped charge blasting and the new dual-shaped charge blasting technology. Mech. Adv. Mater. Struct. 2024, 32, 374–390. [Google Scholar] [CrossRef]
- Jia, X.; Huang, Z.; Xu, M.; Xiao, Q. Theoretical model and numerical study of shaped charge jet penetrating into thick moving target. Acta Armamentarii 2019, 40, 1553–1561. [Google Scholar]
- Li, J.; Lu, Y.; Liang, B.; Xu, H.; Chen, X.; Zhang, J. Numerical Study and Theoretical Model of Shaped Charge Jet Penetrating into Thick-Walled Target with Following Velocity. Int. J. Aerosp. Eng. 2024, 2024, 7646255. [Google Scholar] [CrossRef]
- Held, M. Shaped Charge Jet Against a Transverse Moving Target. Propellants Explos. Pyrotech. 1999, 24, 325–327. [Google Scholar] [CrossRef]
- Frankel, I.; Weihs, D. Hydrodynamic theory of glancing impact. J. Fluid Mech. 1990, 216, 213–229. [Google Scholar] [CrossRef]
- Walters, W.P.; Zukas, J.A. Fundamentals of Shaped Charges; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Golesworthy, R.C. The effect of transverse velocity on shaped charge performance. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 1–15. [Google Scholar]
- Jia, X.; Huang, Z.; Xu, M.; Xiao, Q.; Liu, X.; Zhang, X.; Yin, D. Study on Interaction Mechanism between the Shaped Charge Jet and Thick Moving Target. Prop. Explos. Pyrotech. 2019, 44, 1033. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D.; Weihs, D. Effect of target velocity on damage patterns in hypervelocity glancing collisions. Int. J. Impact Eng. 2020, 144, 103664. [Google Scholar] [CrossRef]
- Kobylkin, I.F.; Dorokhov, N.S. Interaction of a shaped-charge jet with moving reactive armor plates. Combust. Explos. Shock Waves 2013, 49, 495–500. [Google Scholar] [CrossRef]
- Li, G.; Chen, X. A compressible model of radial crater growth by shaped-charge jet impact. Explos. Shock Waves 2022, 42, 97–105. [Google Scholar]
- Held, M.; Fischer, R. Penetration theory for inclined and moving shaped charges. Propellants Explos. Pyrotech. 1986, 11, 115–122. [Google Scholar] [CrossRef]
- Han, S. Simulation Research on Sunder Armor Oblique Penetrate High Speed Movement; North University of China: Taiyuan, China, 2015. [Google Scholar]
- Tan, L.; Zhang, T.; Qiao, L.; Ma, C. Numerical Simulation of Shaped Jet Penetrating Moving Steel Target. Ordnance Ind. Autom. 2021, 40, 6–9. [Google Scholar]
- Rassokha, S.S. Numerical Simulation of Jet Formation from a Rotating Shaped Charge. Combust Explos Shock Waves 2024, 60, 811–818. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, H.; Zhao, P.; Shao, X.; Zhang, X. Study on Damage Effectiveness of Shaped Warhead in Air Defense and Anti-missile. Ordnance Ind. Autom. 2018, 37, 60–63, 72. [Google Scholar]
- Chen, Z. Analysis of the Characteristics of the Jet from HEAT Projectile with the Error and Simulation Research on Impact into the High-Speed Target in an Angle; North University of China: Taiyuan, China, 2015. [Google Scholar]
- Li, R.; Han, H.; Sun, S.; Liu, T. Ballistic resistance capabilities of explosive reactive armors encapsulated by ceramic layers. Explos. Shock. Waves 2014, 34, 47–51. [Google Scholar]
- Liang, Y. Study on the Factors Affecting Shaped Energy Jet Oblique Impact into Thin Layer Charge Reactive Armor; North University of China: Taiyuan, China, 2023. [Google Scholar]
- Nan, Y.; Jiang, J.; Wang, S.; Fang, Y. Numerical simulation and test for impact response of submunitions drop. J. Vib. Shock. 2013, 32, 182–187. [Google Scholar]
- Zuo, H.; Guo, W.; Xu, F.; Zou, J.; Kang, X. Laboratory simulation of deceleration and acceleration process. In Proceedings of the 10th National Conference on Shock Dynamics College of Aeronautics, Taiyuan, China, 1 July 2011; pp. 162–170. Available online: https://d.wanfangdata.com.cn/conference/7559575 (accessed on 1 July 2011).
- Zaouk, A.K. Development and Validation of a US Side Impact Moveable Deformable Barrier Fe Model. In Proceedings of the 3rd European LS-DYNA Conference, Paris, France, 18–19 June 2001. [Google Scholar]
- Wang, Y.; Yin, J.; Zhang, X.; Yi, J.; Li, X. Study on jet dynamic impact performance under the influence of standoff. Sci. Rep. 2024, 14, 31462. [Google Scholar] [CrossRef]
- Feng, K.; Yang, Y.; Chen, Y. Study on Penetrating Stability of Shaped Charge Jet. Ordnance Ind. Autom. 2022, 41, 87–92. [Google Scholar]
- Jia, X.; Xu, M.; Huang, Z.; Xiao, Q.; Chen, S.; Ma, B. Theoretical analysis and experimental study of the performance of shaped charge jet penetration into thick-walled moving target by rocket sled testing method. Int. J. Impact Eng. 2021, 155, 103894. [Google Scholar] [CrossRef]



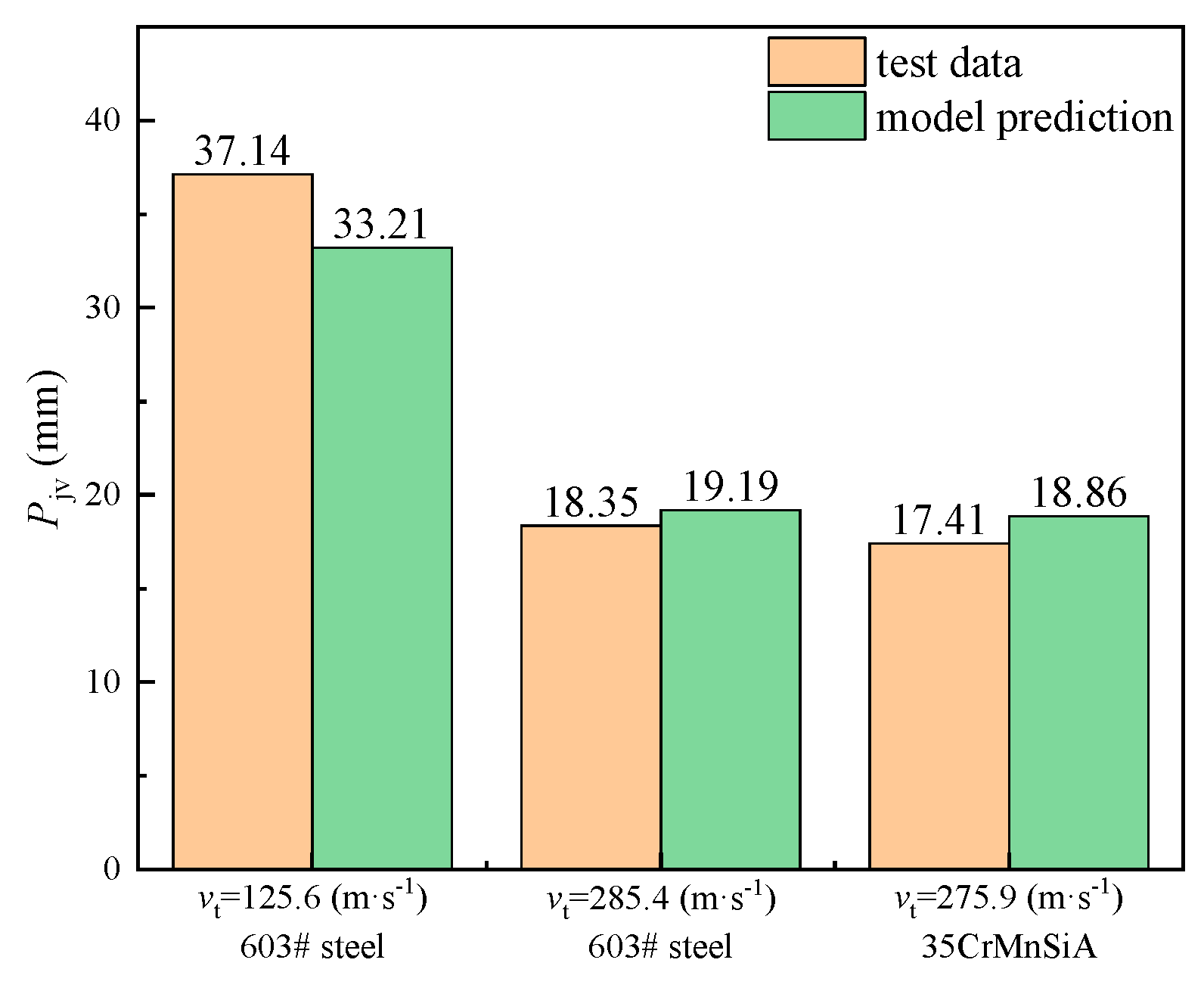
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ρ/(kg·m−3) | 8960 | Tm/°C | 1356 |
| A/GPa | 0.09 | Cp/J·kg−1·K−1 | 383 |
| B/GPa | 0.292 | /s−1 | 1 |
| C | 0.025 | C/(m·s−1) | 3940 |
| N | 0.31 | s | 1.489 |
| M | 1.09 | γ | 2.02 |
| Tr/°C | 293 | A | 0.47 |
| ρ/(kg·m−3) | D/(m·s−1) | PCJ | A/GPa | B/GPa | R1 | R2 | ω |
|---|---|---|---|---|---|---|---|
| 1717 | 8320 | 0.37 | 524.23 | 7.68 | 4.2 | 1.1 | 0.34 |
| Material | ρ/(kg·m−3) | E/GPa | σY/GPa | β |
|---|---|---|---|---|
| aluminum alloy | 2780 | 72.4 | 0.345 | 0.5 |
| phenolic resin | 1130 | 0.35 | 0.12 | 1 |
| 603# steel | 7830 | 202.8 | 0.975 | 1 |
| 35CrMnSiA | 8000 | 210 | 1.275 | 1 |
| 45# steel | 7830 | 210 | 0.355 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xu, C.; Yi, J.; Li, X.; Yin, J. Analysis of Strength Effects on the Dynamic Response of a Shaped-Charge Under Lateral Disturbances. Appl. Sci. 2025, 15, 6313. https://doi.org/10.3390/app15116313
Zhang X, Xu C, Yi J, Li X, Yin J. Analysis of Strength Effects on the Dynamic Response of a Shaped-Charge Under Lateral Disturbances. Applied Sciences. 2025; 15(11):6313. https://doi.org/10.3390/app15116313
Chicago/Turabian StyleZhang, Xuepeng, Can Xu, Jianya Yi, Xudong Li, and Jianping Yin. 2025. "Analysis of Strength Effects on the Dynamic Response of a Shaped-Charge Under Lateral Disturbances" Applied Sciences 15, no. 11: 6313. https://doi.org/10.3390/app15116313
APA StyleZhang, X., Xu, C., Yi, J., Li, X., & Yin, J. (2025). Analysis of Strength Effects on the Dynamic Response of a Shaped-Charge Under Lateral Disturbances. Applied Sciences, 15(11), 6313. https://doi.org/10.3390/app15116313






