Prediction of Blast Crushing Lumpiness Based on CPO-BP Modeling
Abstract
1. Introduction
- (1)
- A novel hybrid model CPO-BP is developed that significantly improves the stability and prediction accuracy of BP networks under complex geological conditions;
- (2)
- A real engineering database is constructed, and key variables are selected using the MIV method to optimize the model’s input structure;
- (3)
- The proposed CPO-BP model outperforms the standard BP model in terms of RMSE, MAE, and MAPE, and demonstrates strong potential for practical application in engineering blasting design.
2. Research Methods
2.1. BP Algorithm
2.2. CPO Algorithm
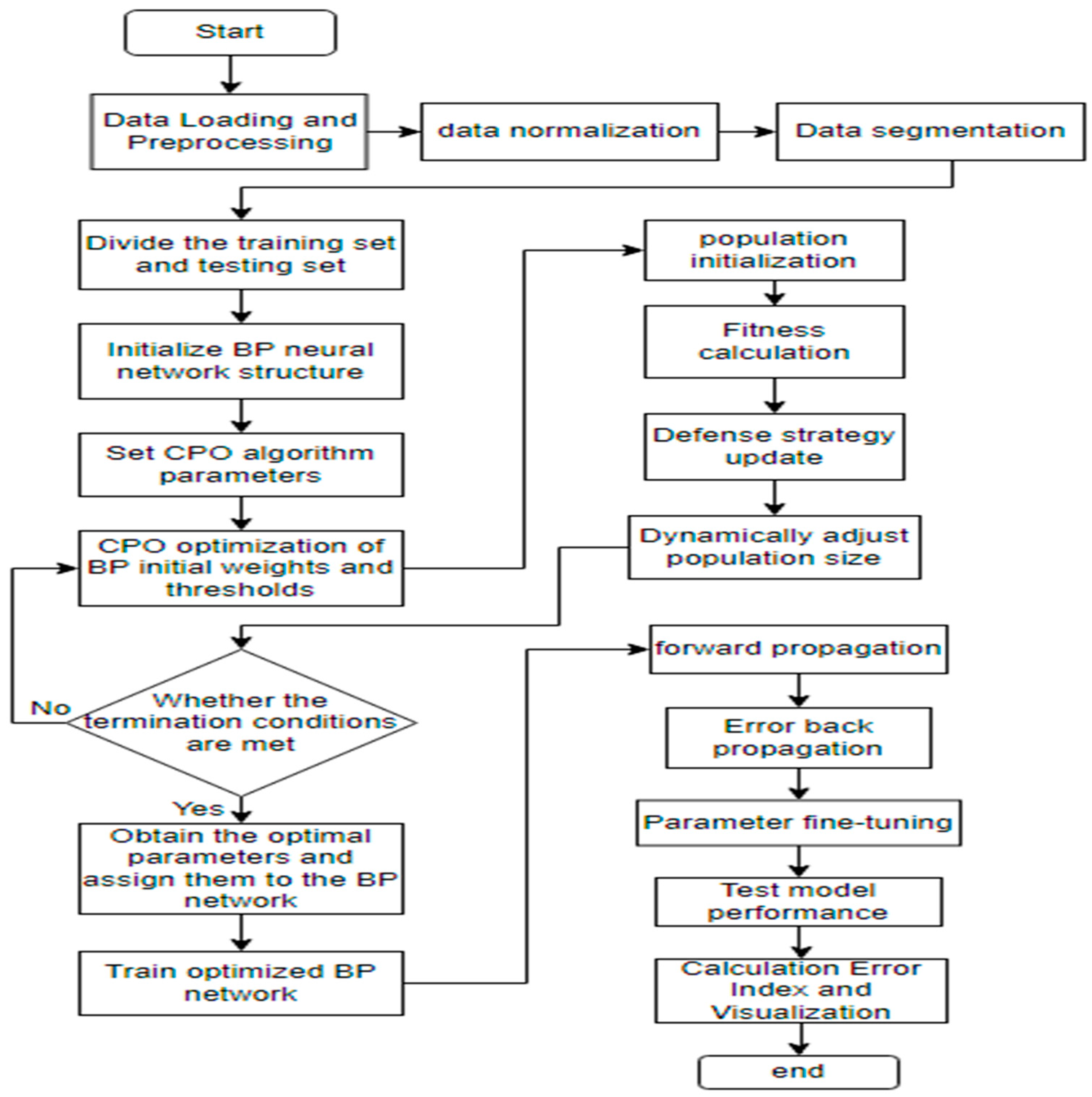
2.3. CPO-BP Algorithm
3. Construction and Validation of CPO-BP Prediction Models
3.1. CPO-BP Model Parameterization
3.2. CPO-BP Model Evaluation Indicators
3.3. CPO-BP Model Validation
4. Engineering Applications
4.1. Project
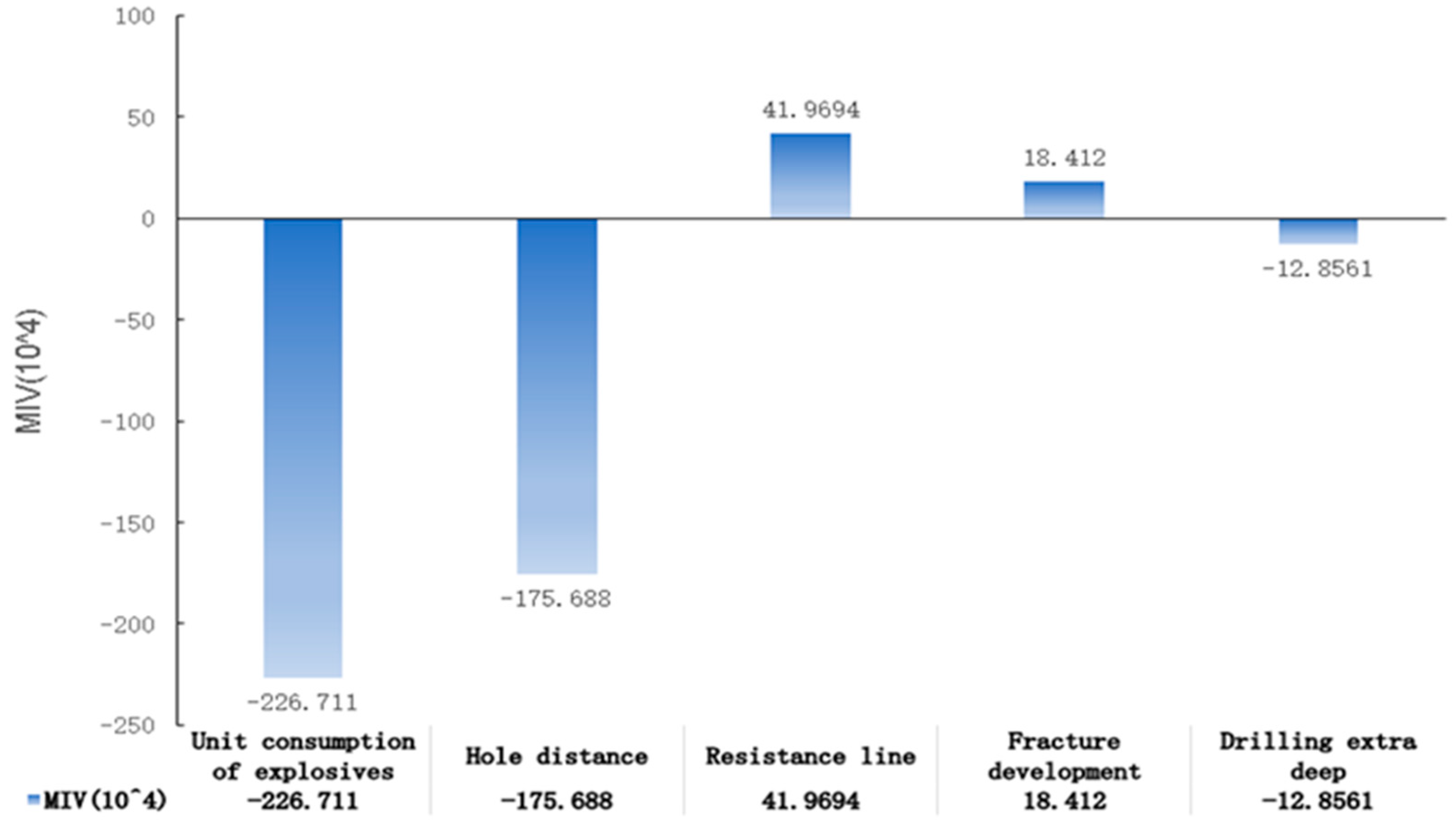
4.2. Parameter Selection
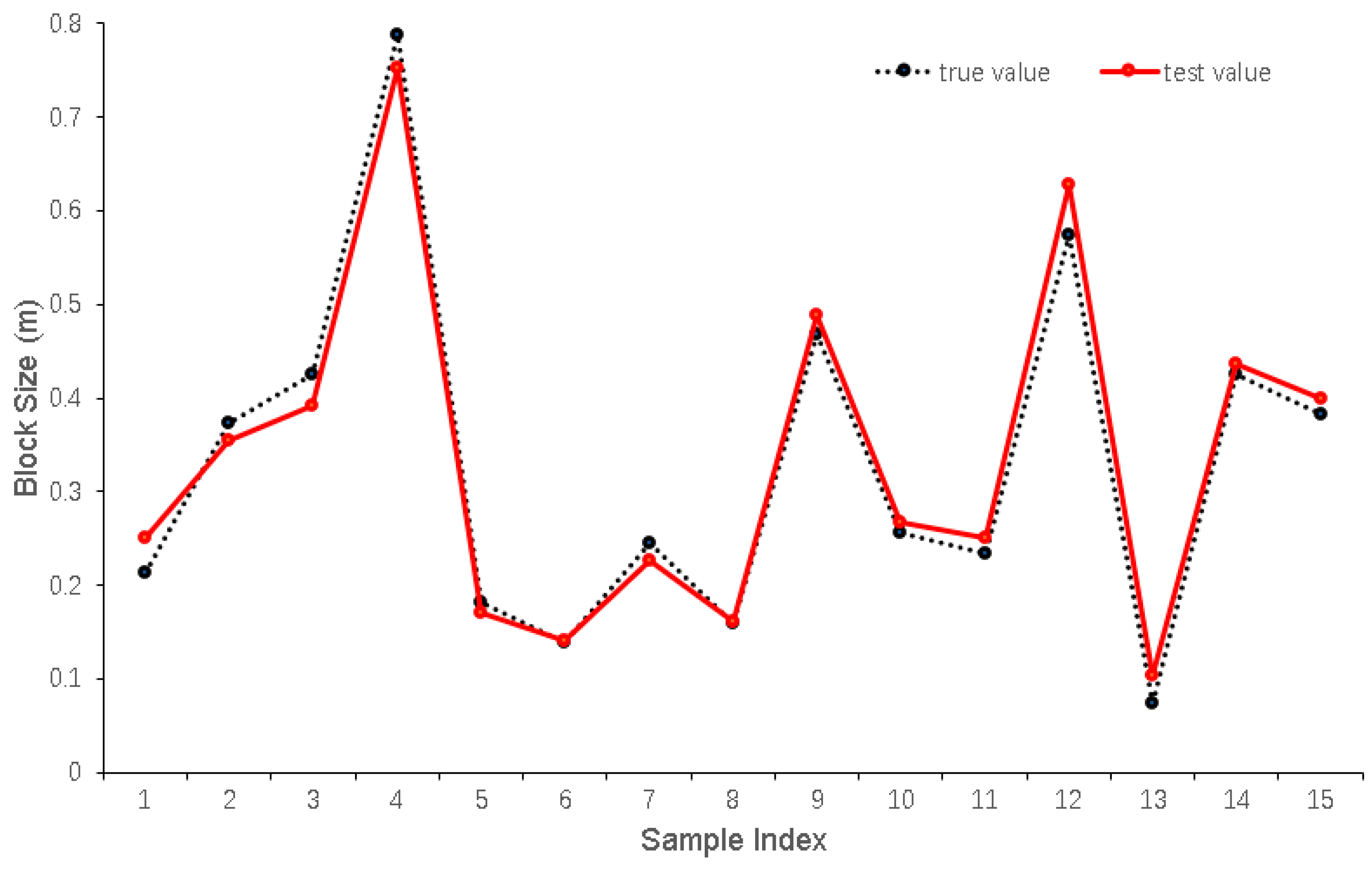
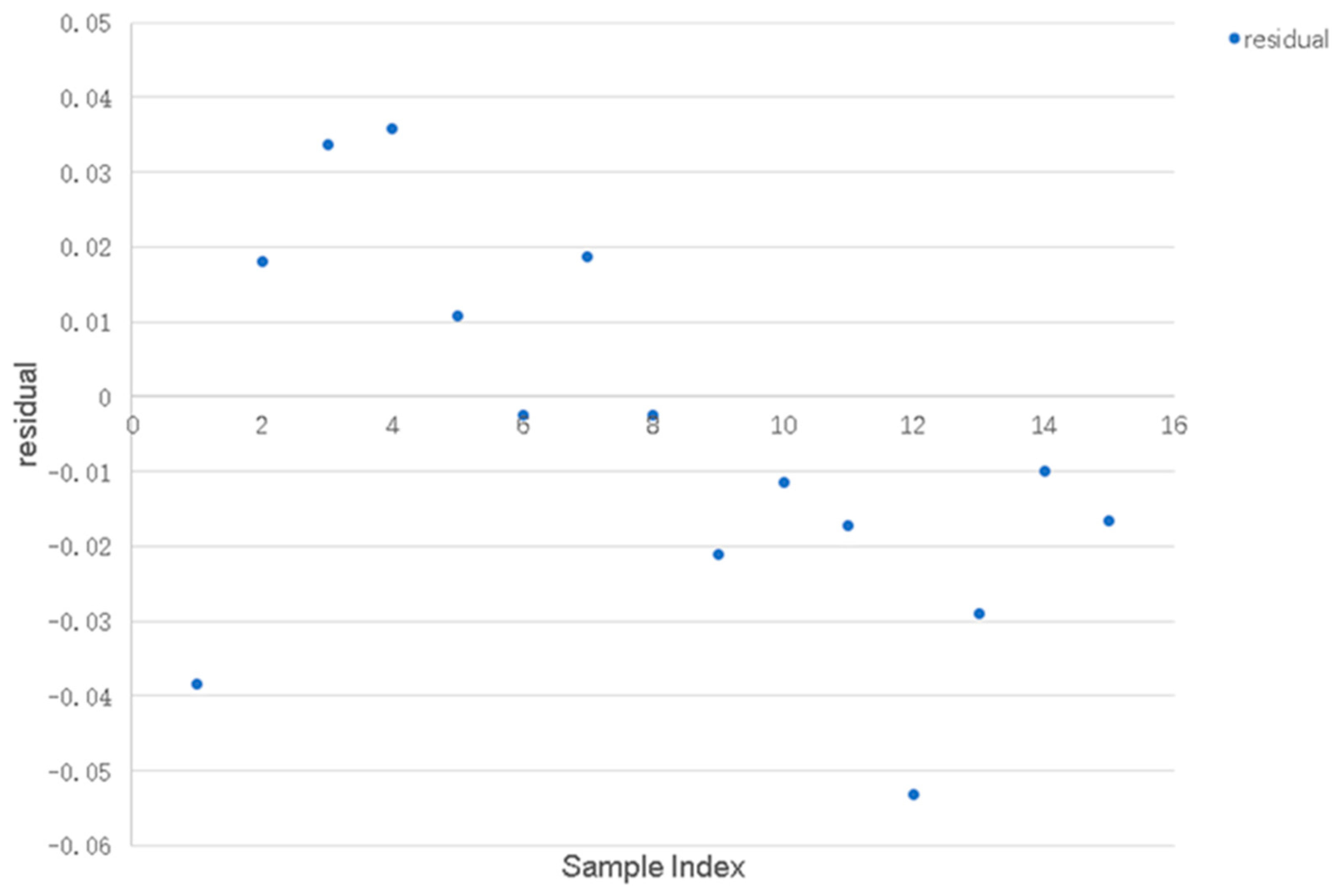
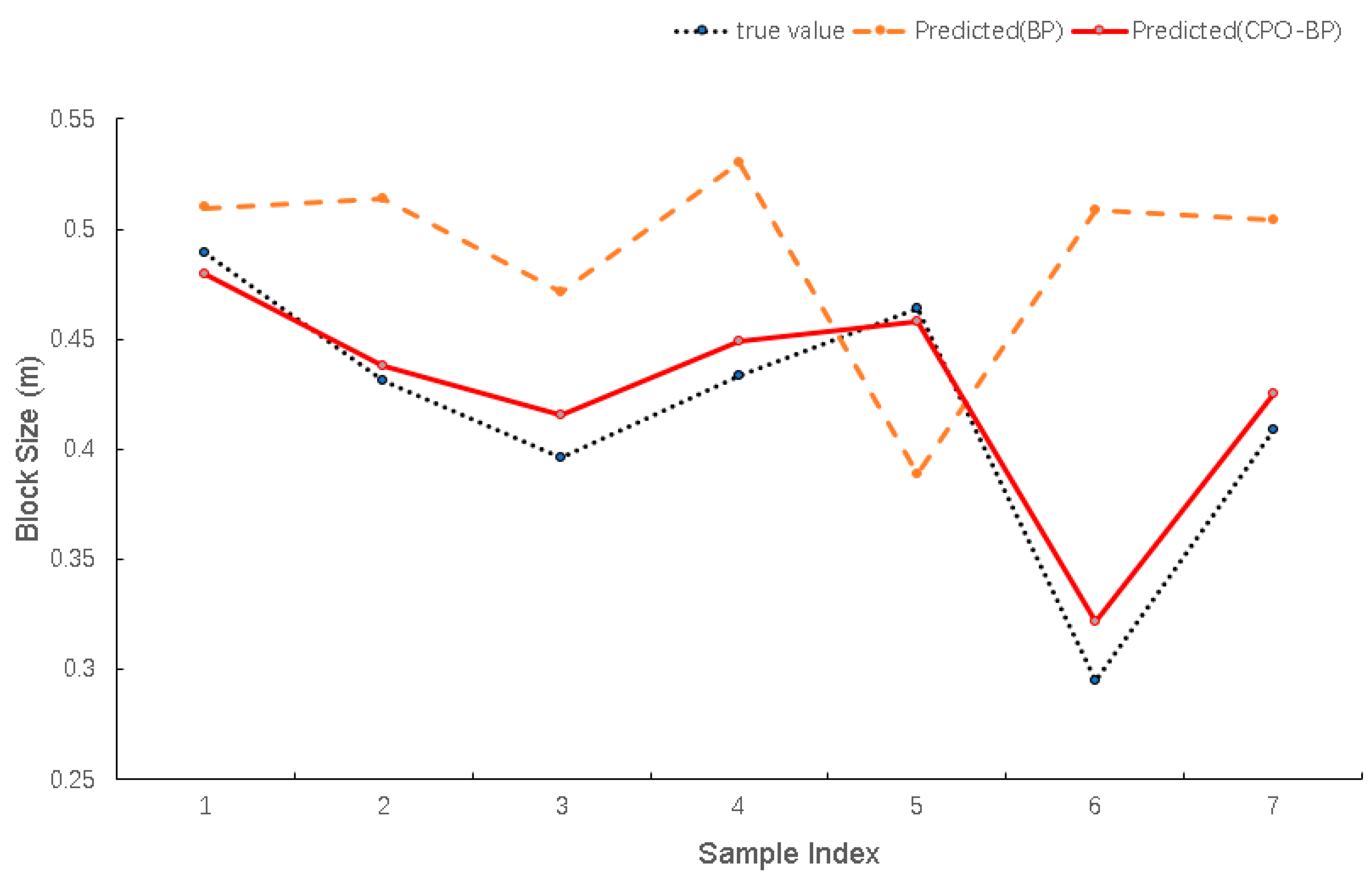
4.3. Blast Block Size Prediction and Validation Based on CPO-BP Modeling
5. Limitations and Future Work
6. Conclusions
- (1)
- The CPO-BP model was trained and tested using the Hudaverdi blasting dataset, a representative and widely used database in blasting research. To verify its practical utility, the model was also applied to a real-world iron ore mine in Hunan Province, China. Results from both the benchmark dataset and the field validation confirm that the model can generalize well across different blasting conditions and deliver high prediction accuracy, indicating its potential for broad engineering application.
- (2)
- Although the model demonstrated high accuracy on the current dataset, its generalization ability across different geological conditions and blasting environments remains to be verified. Future research will explore applying the CPO-BP model to other datasets to further evaluate its robustness and practical transferability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peleg, M. Determination of the parameters of the Rosin-Rammler and beta distributions from their mode and variance using equation-solving software. Powder Technol. 1996, 87, 181–184. [Google Scholar] [CrossRef]
- Kuznetsov, V.M. The mean diameter of the fragments formed by blasting rock. Sov. Min. Sci. 1973, 9, 144–148. [Google Scholar] [CrossRef]
- Cunningham, C. The Kuz-Ram model for prediction of fragmentation from blasting. First Int. Symp. Rock Fragm. Blasting 1983, 2, 439–453. [Google Scholar]
- Zheng, R.C. Bond-Ram model for rockburst lumpiness distribution prediction. Met. Mine 1988, 23, 11–15+29. [Google Scholar]
- Zhou, D.X. A three-dimensional mathematical model for calculating the blasting blockiness distribution of an open-pit mine step. Explos. Shock. Waves 1984, 4, 48–59. [Google Scholar]
- Liu, W.Z. Three-dimensional mathematical model of energy flux distribution and fragmentation composition in step blasting. Met. Mine 1987, 22, 25–28. [Google Scholar]
- Kanchibotla, S.S.; Valery, W.; Morrell, S. Modelling fines in blast fragmentation and its impact on crushing and grinding. Proc. Explo 1999, 99, 137–144. [Google Scholar]
- Ouchterlony, F. The Swebrec© function: Linking fragmentation by blasting and crushing. Min. Technol. 2005, 114, 29–44. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.H.; Li, L.N.; Chen, J.W.; Yao, Y.K.; Liu, C.B. Prediction of blast vibration velocity in mines based on particle swarm—Least squares support vector machine model. Met. Mine 2022, 57, 145–150. [Google Scholar] [CrossRef]
- Kulatilake, P.; Qiong, W.; Hudaverdi, T.; Kuzu, C. Mean particle size prediction in rock blast fragmentation using neural networks. Eng. Geol. 2010, 114, 298–311. [Google Scholar] [CrossRef]
- Asl, P.F.; Monjezi, M.; Hamidi, J.K.; Armaghani, D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm. Eng. Comput. 2018, 34, 241–251. [Google Scholar] [CrossRef]
- Hudaverdi, T.; Kulatilake, P.; Kuzu, C. Prediction of blast fragmentation using multivariate analysis procedures. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1318–1333. [Google Scholar] [CrossRef]
- Shi, X.; Jian, Z.; Wu, B.; Huang, D. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction. Trans. Nonferrous Met. Soc. China 2012, 22, 432–441. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Z.Q.; Gao, Q.; Xue, G. Prediction of rock mass fragmentation based on joint network simulation and fractal theory. J. Taiyuan Univ. Technol. 2015, 46, 318–322. [Google Scholar]
- Duan, B.F.; Fe, H.L. Application of neural network model in step blasting blockiness prediction. Eng. Blasting 1999, 5, 25–29. [Google Scholar]
- Liu, Y.; Tan, K.X.; Guo, Q.P. Prediction of rock blasting fragmentation using random forest and GA. BP Neural Netw. Ming Res. Dev. 2021, 41, 135–140. [Google Scholar]
- Liu, X.B.; Yuan, P.Z.; Zhang, X.F. Research on prediction of blasting effect in open pit mines based on RBF neural network. China Min. Mag. 2020, 19, 81–84. [Google Scholar]
- Ye, H.W.; Hu, J.J.; Lei, T.; Li, N.; Wang, Q.Z. LOO-XGBoost model prediction of rock blasting fragmentation. Blasting 2022, 39, 16–21. [Google Scholar]
- Guan, F.S.; Wu, M.F.; Luo, Z.; Yao, Q.; Liao, Y.B.; Li, H.T. Prediction of rock mass blasting blockage based on grey correlation analysis and GA-BP model. Explos. Mater. 2021, 50, 40–47+53. [Google Scholar]
- Liu, X.; Xie, T.; Wang, X.H.; Yi, Z.B.; He, Q.Z. Rock blasting fragmentation prediction based on improved random forest algorithm. Ming Res. Dev. 2022, 42, 25–29. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, Y.; Xu, S.C.; Li, B.; Gu, Y.; Zhang, J.K.; Jiang, N. Prediction of blast blockiness based on PSO-BPNN model. Blasting 2024, 41, 136–142. [Google Scholar]
- Hu, X.B.; Chen, Z.Y.; Wei, G.P.; Wei, Z.; Wang, G.; Song, J.W. Blasting vibration prediction system based on BP neural network. Min. Res. Dev. 2020, 40, 154–158. [Google Scholar] [CrossRef]
- Dai, S.; Su, H.Z.; Gu, Y. Dam deformation monitoring model based on HO-BP-AdaBoost. Water Resour. Power 2025, 43, 153–156+108. [Google Scholar]
- Wang, X.M.; Zhao, B.; Wang, X.L. Optimization of rock drilling and blasting parameters based on BP neural network. J. Cent. South Univ. (Sci. Technol.) 2009, 40, 1411–1416. [Google Scholar]
- Bo, Z. Prediction of NEP of Rotor Spinning Yarn by Means of Intelligent Theory. In Information Engineering Research Institute, USA, Proceedings of the 2012 2nd International Conference on Mechanical, Industrial, and Manufacturing Engineering (Volume 1 · 2012), Singapore, 27–28 June 2012; College of Textiles, Zhongyuan University of Technology: Zhengzhou, China, 2012; Volume 6. [Google Scholar]
- Zhou, Y. Research on Rolling Bearing Fault Diagnosis Technology Based on MIV Feature Screening and BP Neural Network. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2011. [Google Scholar]
- Zhang, Z.Y.; Jin, J.X. Prediction of Peak Velocity of Blasting Vibration Based on Artificial Neural Network Optimized by Dimensionality Reduction of FA-MIV. Math. Probl. Eng. 2018, 2018, 8473547. [Google Scholar] [CrossRef]
- Hu, Y.H.; He, M.; Zhou, C.J.; Ding, Z.H.; Cai, C.G.; Ma, X.Y.; Zhang, J.J. Research on prediction of vibration velocity of millisecond delay blasting based on GA-BP neural network. China Min. Mag. 2022, 31, 72–77. [Google Scholar]
- Zhao, G.Y.; Sun, G.D.; Dai, B.; Chen, Y. Application of BP network improved by PSO in optimization of blasting rate. Blasting 2017, 34, 15–19. [Google Scholar]
- Wong, T.T.; Yeh, P.Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]

| Hole Distance (m) | Resistance Line (m) | Unit Consumption of Explosives (kg-m−3) | Drilling Extra Deep (m) | Fracture Development (T) | p50 (m) |
|---|---|---|---|---|---|
| 5.80 | 4.30 | 0.45 | 0.80 | 1 | 0.357 |
| 5.80 | 4.30 | 0.49 | 1.20 | 1 | 0.314 |
| 5.80 | 4.30 | 0.49 | 2.20 | 1 | 0.318 |
| 5.80 | 4.30 | 0.47 | 2.00 | 1 | 0.324 |
| 5.80 | 4.80 | 0.41 | 1.50 | 1 | 0.397 |
| 5.80 | 4.80 | 0.38 | 2.00 | 2 | 0.450 |
| 5.80 | 4.30 | 0.46 | 0.50 | 1 | 0.349 |
| 5.80 | 4.30 | 0.48 | 2.50 | 1 | 0.317 |
| 5.80 | 4.30 | 0.36 | 1.50 | 2 | 0.480 |
| 5.80 | 4.80 | 0.33 | 1.50 | 1 | 0.530 |
| 5.50 | 4.30 | 0.48 | 1.50 | 1 | 0.321 |
| 5.80 | 4.30 | 0.51 | 1.50 | 1 | 0.298 |
| 4.30 | 5.50 | 0.36 | 1.50 | 2 | 0.443 |
| 5.50 | 4.50 | 0.35 | 0.50 | 1 | 0.458 |
| 5.80 | 4.30 | 0.40 | 2.50 | 1 | 0.406 |
| 5.80 | 4.80 | 0.32 | 0.50 | 1 | 0.557 |
| 5.50 | 4.30 | 0.40 | 2.50 | 1 | 0.398 |
| 5.80 | 4.30 | 0.42 | 1.00 | 1 | 0.391 |
| 5.50 | 4.30 | 0.40 | 1.00 | 2 | 0.401 |
| 5.80 | 4.50 | 0.39 | 1.50 | 2 | 0.447 |
| 5.80 | 4.50 | 0.37 | 1.50 | 1 | 0.505 |
| 5.50 | 4.30 | 0.42 | 20.00 | 2 | 0.388 |
| 5.50 | 4.50 | 0.39 | 2.00 | 1 | 0.441 |
| 5.50 | 4.30 | 0.45 | 2.00 | 1 | 0.350 |
| 5.80 | 4.30 | 0.42 | 1.50 | 1 | 0.395 |
| 5.80 | 4.30 | 0.37 | 1.50 | 1 | 0.486 |
| 5.80 | 4.30 | 0.41 | 1.50 | 1 | 0.402 |
| 5.50 | 4.30 | 0.49 | 2.00 | 2 | 0.308 |
| 5.50 | 4.30 | 0.47 | 1.50 | 1 | 0.495 |
| 5.80 | 4.50 | 0.37 | 2.00 | 1 | 0.516 |
| 5.50 | 4.50 | 0.36 | 1.50 | 1 | 0.489 |
| 5.50 | 4.30 | 0.39 | 1.50 | 1 | 0.431 |
| 5.50 | 4.50 | 0.40 | 1.50 | 1 | 0.396 |
| 5.50 | 4.30 | 0.39 | 1.50 | 2 | 0.433 |
| 5.80 | 4.80 | 0.39 | 1.50 | 1 | 0.464 |
| 5.00 | 4.00 | 0.54 | 2.00 | 1 | 0.295 |
| 5.50 | 4.30 | 0.40 | 2.00 | 1 | 0.409 |
| Mould | CPO-BP | BP |
|---|---|---|
| Mean Absolute Error MAE | 0.014341 | 0.094344 |
| Mean Square Error MSE | 0.00025004 | 0.011837 |
| Root Mean Square Error RMSE | 0.015813 | 0.1088 |
| Mean Absolute Percentage Error MAPE | 0.037595% | 0.25274% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Huang, C. Prediction of Blast Crushing Lumpiness Based on CPO-BP Modeling. Appl. Sci. 2025, 15, 6312. https://doi.org/10.3390/app15116312
Xie X, Huang C. Prediction of Blast Crushing Lumpiness Based on CPO-BP Modeling. Applied Sciences. 2025; 15(11):6312. https://doi.org/10.3390/app15116312
Chicago/Turabian StyleXie, Xuebin, and Chuanqi Huang. 2025. "Prediction of Blast Crushing Lumpiness Based on CPO-BP Modeling" Applied Sciences 15, no. 11: 6312. https://doi.org/10.3390/app15116312
APA StyleXie, X., & Huang, C. (2025). Prediction of Blast Crushing Lumpiness Based on CPO-BP Modeling. Applied Sciences, 15(11), 6312. https://doi.org/10.3390/app15116312






