Research on Data-Driven Performance Assessment and Fault Early Warning of Marine Diesel Engine

Abstract

To enable proactive prediction of marine diesel engine failure time and root causes, thereby reserving sufficient time for maintenance, this study proposes a data-driven multi-algorithm integration framework for performance assessment and fault early warning in marine diesel engines. By integrating the SSD (steady-state detection) algorithm, a data-driven CLIQUE clustering algorithm was chosen for automatic multi-parameter high-dimensional running condition partitioning. This innovative approach overcomes the limitations of traditional single-parameter approaches or dimensionality reduction techniques, significantly enhancing state classification accuracy. The improved classification results subsequently increase the reliability of Mahalanobis distance as a performance indicator for marine diesel engine condition assessment. Finally, the cumulative anomaly method combined with the Yamamoto test was employed for anomaly detection analysis, enabling precise identification of fault occurrence time and establishing an effective early-warning mechanism. The study demonstrates that this technique effectively characterizes the overall performance of marine diesel engines and captures their performance degradation features. Implemented on a 6RT-flex82T marine diesel engine dataset, the method achieved precise prediction of fault occurrence time with early warnings, providing approximately 20 days advance notice for maintenance planning. Furthermore, comparative analyses with existing studies revealed its superior capability in pinpointing the anomaly to the jacket cooling water outlet temperature of cylinder #2. These results confirm the method’s effectiveness in both performance assessment and fault early warning for marine diesel engines, offering a novel approach for intelligent maintenance of shipboard equipment.

1. Introduction

As the core power generation unit of marine vessels, marine main diesel engines are prone to frequent failures due to prolonged high-load operations under harsh marine conditions. Performance evaluation of these engines enables early prediction of impending failures and proactive warnings, thereby allocating sufficient time for corrective maintenance or preventive interventions. However, the structural complexity and variable operational conditions of marine diesel main engines present significant challenges in achieving reliable performance assessments. Conventional onboard data acquisition systems typically record limited operational parameters that insufficiently reflect the engine’s actual performance state, while critical deep-seated condition parameters remain unmonitored. All measurable parameters exhibit operational condition dependency, with early-stage performance degradation often manifesting as subtle fluctuations in these parameters. Such incipient anomalies are frequently obscured by strong background noise interference, rendering traditional threshold-based warning methods inadequate due to insufficient sensitivity and high false-alarm rates.

With the advancement of big data and communication network technologies, new requirements have been proposed for the intelligent operation and maintenance of marine diesel engines. The concept of the “smart ship” was first introduced by Det Norske Veritas (DNV) in its Future Shipping Industry report in 2014, which significantly promoted global research in this field [1]. In 2015, the China Classification Society (CCS) released the world’s first smart ship code, marking a major step forward for China in the development of smart ship technologies [2]. Subsequently, in 2017, Lloyd’s Register published the Design Rules for Intelligent Ship Systems, further providing technical guidance for this domain [3]. To accelerate the development of intelligent ships, Prognostics and Health Management (PHM) technologies have been gradually introduced into the maritime industry [4]. Data-driven PHM techniques establish fault prediction models by analyzing large volumes of historical data and use real-time equipment data for health management. From early sensor and data logging systems to today’s cloud computing and artificial intelligence technologies, PHM has continuously improved the reliability and availability of equipment [5] while becoming increasingly intelligent and autonomous. Li et al. investigated the application of PHM in marine diesel engines, described the characteristics of traditional fault diagnosis methods, proposed a system architecture for diesel engine PHM, summarized the key enabling technologies, and provided insights into data analysis, fault diagnosis, early warning, and health management [6]. It is evident that health assessment and fault diagnosis of marine diesel engines based on monitoring data, intelligent algorithms, and condition monitoring have become an inevitable trend in the intelligent operation and maintenance of ship propulsion systems. The core objective of intelligent marine diesel engine management lies in the real-time monitoring, evaluation, and analysis of engine health and operational performance to enable timely fault prediction. This technological pathway primarily relies on big data and information technologies to uncover latent correlations among performance parameters through data mining, allowing for accurate identification of both visible and latent fault features. Such approaches significantly enhance the level of intelligent decision making for marine diesel engines [7]. Based on this objective, this study conducts research utilizing monitoring data to analyze and assess the health condition of marine main diesel engines. It quantifies the overall engine performance to visually observe operational trend variations and proposes a fault early-warning technique according to the degradation trend of holistic engine performance. This technique can issue pre-failure alerts before abnormal performance parameters emerge, thereby preventing potential malfunctions. The implementation of this technology enhances navigation safety and reliability while providing theoretical foundations and technical tools for intelligent ship maintenance systems.

During ship navigation, the vessel is not always in a steady state. Monitored data from navigation states such as acceleration, deceleration, and shutdown cannot characterize the overall performance of marine diesel main engines but rather reduce the accuracy of performance evaluation. Therefore, stable running intervals must be identified prior to analysis, with only steady-state navigation data used for performance assessment. Current mainstream steady-state detection algorithms fall into quantitative and qualitative categories. Qualitative methods include the confidence interval method, R-test, combined statistical testing, and SSD algorithm, while quantitative approaches encompass physics-informed neural networks (PINN) and modified adaptive polynomial filtering algorithms. The combined statistical test and confidence interval method proposed by Narasimhan [8] in the 1980s detects steady states by comparing dual means and variances. However, its assumption of zero-mean normal distribution makes it vulnerable to interference in practical applications with insufficient robustness. The R-test improves F-test through variance ratio analysis, yet its threshold is significantly affected by filtering parameters and shows sensitivity to random noise with poor stability. Physics-informed neural networks integrate physical equations (e.g., partial differential equations, conservation laws, etc.) into loss functions to jointly optimize data fitting and physical constraints but exhibit convergence instability for high-dimensional nonlinear problems [9]. The robust adaptive polynomial filtering algorithm (ASF) based on M-estimation detects states through threshold parameter comparison, offering advantages of fewer parameters and strong noise resistance, yet requires manual parameter setting and shows poor adaptability to steady-state fluctuations [10]. In contrast, Kelly et al. used the SSD algorithm, hich constructs threshold criteria using Student’s t-test within window widths and requires only two parameters (window width and significance level), while demonstrating superior performance in multivariate collaborative detection [11]. Given that marine diesel main engine stability identification involves coupled analysis of multiple thermodynamic parameters, this study adopted the SSD algorithm to identify stable operating intervals. Its concise parameter system and multivariate compatibility effectively support steady-state discrimination requirements under complex operating conditions.

Current research on fault prediction can generally be categorized into two approaches: state prediction and state classification. State prediction, constrained by human factors and data quality, suffers from insufficient model accuracy due to challenges in realistically simulating diesel engine operating conditions and quantitative/qualitative modeling with scarce samples. For instance, Liu et al. developed a CNN-BiGRU-based exhaust temperature prediction model for marine diesel engines in which only exhaust temperature data were utilized for prediction. By artificially linearly adjusting the dataset to simulate abnormal exhaust temperature changes when potential faults occur in diesel engines, the model revealed prediction errors [12]. Su et al. innovatively proposed a PCA-CNN-BiLSTM hybrid model, which employs only two parameters (after PCA dimensionality reduction) to represent overall engine performance and considers solely stable operating conditions of a specific diesel engine model with minimal load variations [13]. Consequently, such prediction models struggle to establish corresponding fault prediction frameworks for complex, multivariate, and correlated fault systems [14]. This study addresses this issue by adopting state classification with statistical data analysis methods to process multi-dimensional real-ship monitoring data, capturing temporal variations in statistical features while eliminating subjective influences, followed by autonomous operating condition partitioning. Current mainstream data analysis methods include principal component analysis (PCA), data mining clustering algorithms, and time series analysis. For example, Su et al. used PCA to extract two feature parameters that explained more than half of the characteristics in the sample data [13], while Liu et al. derived performance parameters through coefficient and correlation efficiency definitions, established initial diesel engine performance maps via surface fitting, and tracked performance degradation trends by comparing real-time and initial performance maps [15]. Fault warning methodologies are divided into physics-based models and data-driven approaches. Physics-based methods require precise mathematical or physical models to describe equipment operation [14]. However, under dynamic load conditions, these models often produce larger errors, resulting in systemic biases in the data. In contrast, data-driven approaches construct analytical models based on historical operational data and utilize algorithms to mine potential fault features, effectively circumventing the complexities of physical modeling. With the advancement of intelligent algorithms, data-driven methods have become the dominant research direction in fault prediction for marine diesel engines.

The technical methods employed in this study include data mining clustering algorithms and time series analysis. Clustering algorithms are particularly suitable for solving complex operating condition partitioning in marine main diesel engines. For instance, Zheng et al. utilized the K-means clustering algorithm to partition engine operating intervals, followed by quadratic polynomial fitting to derive relationships between engine load and fuel consumption rates [16]. Perera et al. applied the EM algorithm to identify the frequent operating ranges of marine diesel engines and analyzed engine performance using PCA [17,18]. Erik Vanem et al. explored methods including K-means clustering, Gaussian mixture models, density-based clustering, self-organizing maps, and support vector machines after data dimensionality reduction, concluding that dimensionality reduction may cause information loss. Although these methods are straightforward to implement, they require parameter tuning and validation prior to practical application [19]. Time series analysis investigates statistical regularities in the temporal evolution of sequential data, enabling prediction and control of future events, such as preventing fault occurrences. Zhang et al. integrated time–domain analysis with deep learning algorithms, focusing on temporal characteristics of faults and resulting in higher diagnostic accuracy compared to traditional methods [20]. Je-Gal H et al. proposed combining time–domain and frequency–domain analyses, achieving superior accuracy over frequency–domain methods alone [21].

In current research on marine diesel engine fault prediction, the use of single or limited data sources to evaluate overall engine performance often results in incomplete assessments and introduces systematic bias into model predictions. Moreover, existing studies that focus solely on predicting stable operating conditions for a specific diesel engine model fail to adequately support the evolving dynamic requirements of intelligent ship engine operation and maintenance. To address these limitations, this study selected 22 performance parameters of a marine diesel engine over an extended time span. By incorporating the SSD steady-state detection algorithm, a data-driven approach using the CLIQUE clustering algorithm is herein proposed for autonomous classification of multi-parameter operating conditions. This approach overcomes the constraints of traditional single-variable or dimensionality-reduced methods, enabling objective and precise condition partitioning. The Mahalanobis distance was computed across different time points to construct a time series that provides a more comprehensive and accurate foundation for evaluating engine performance. Finally, a time–domain analysis method was employed for mutation detection in the performance degradation curve, thereby improving the accuracy of fault warning timing. The effectiveness of the proposed methodology was validated through experimental data.

2. Introduction to Performance Assessment and Fault Warning Methods

2.1. Steady-State Interval Identification Algorithm

Ships operate under various navigation states, such as acceleration, deceleration, and stoppage, resulting in the collection of substantial non-steady-state data by sensors. These transient datasets introduce significant interference in the performance evaluation of marine diesel main engines. The SSD (slope sign detection) steady-state detection algorithm, which requires minimal manual parameter configuration and demonstrates strong capability in multi-variable steady-state detection, is particularly suitable for identifying the stable operating ranges of marine diesel main engines [11]. The fundamental principle of the SSD algorithm is as follows:

The SSD algorithm is based on the assumption that the system exhibits dynamic drift. The univariate process signal y(t) of the system is constructed by multiplying the relative time by a non-zero slope, with the mathematical expression formulated as follows:

$$y_t=mt+\mu +a_t$$

(1)

In the equation, $mt$ represents the dynamic drift component; $t$ denotes the cycle index; $\mu$ is the mean under the assumed steady-state condition, whose value equals the arithmetic mean or sample mean of the window when the slope is zero; $a_t$ corresponds to a white noise or random error sequence following a normal distribution (0,${\sigma }_a$).

The difference between the signal $y_{t-1}$ at the previous time step and the signal $y_t$ at the current time step is

$$m={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n(y_t-y_{t-1})}$$

(2)

The steady-state judgment criterion is constructed using Student’s t-test, with the mathematical expression formulated as follows:

$$\left|y_t-\mu \right|\le t_{crit}{\sigma }_a$$

(3)

In the equation, $t_{crit}$ is the critical value of Student’s t-test, determined from statistical tables based on the significance level $a$ and degrees of freedom v; when the significance level is set to 0.05, it implies a 5% Type I error rate (i.e., 5 non-steady-state data points out of 100 tested); ${\sigma }_a$ represents the standard deviation of the window sample, calculated as follows:

$${\sigma }_a=\sqrt{{\displaystyle \frac{1}{n-2}}{\displaystyle \sum _{t=1}^n{(x_t-mt-\mu )}^2}}$$

(4)

2.2. Operational Condition Classification Algorithm

Clustering algorithms demonstrate advantages in analyzing unlabeled marine diesel engine monitoring data through their capacity to automatically determine optimal cluster numbers via performance metrics, eliminating the need for manual intervention. The grid-based CLIQUE (Clustering In QUEst) algorithm, also recognized as a high-dimensional clustering approach, exhibits particular suitability for this study due to its inherent strengths in autonomous processing of high-dimensional datasets and independence from operator-specific domain expertise.

The fundamental principle of CLIQUE involves partitioning the multidimensional data space into non-overlapping rectangular cells of equal size. Cluster formation operates through density-based evaluation, where a cell exceeding a predefined density threshold qualifies as a dense unit. Cell density is defined by the number of data points contained within it. The final clusters emerge as maximally connected regions composed of adjacent dense cells [22,23].

A Priori Properties of the CLIQUE Clustering Algorithm:

Theorem 1.

Anti-Monotonicity: If a k-dimensional spatial unit is dense, its projection onto any (k − 1)-dimensional subspace is also dense.

Theorem 2.

If any projection of a k-dimensional spatial unit onto a (k − 1)-dimensional subspace contains one or more sparse units, the k-dimensional unit is necessarily non-dense.

Three-Step Procedure for CLIQUE Clustering in Multidimensional Space:

Step 1: Identification of All Dense Subspaces Containing Clusters

The multidimensional space is partitioned into disjoint rectangular units. Dense units are identified using the a priori properties via a bottom-up approach:

The multidimensional space is first partitioned into disjoint rectangular units, and the a priori properties are then utilized to determine whether these units are dense. The identification of dense units employs a “bottom-up” approach, which incrementally processes data from lower to higher dimensions. For instance, once the set of dense units Dk − 1 in the (k − 1)-dimensional space is identified, the candidate dense unit set $D_k\prime$ for the k-dimensional space can be derived using the a priori properties. If $D_k\prime$ is empty, the highest-dimensional subspace $S_{k-1}=D_1\times D_2\times \dots \times D_{k-1}$ containing clusters is obtained. If $D_k\prime$ is non-empty, the k-dimensional data are traversed again to eliminate non-dense units in $D_k\prime$ using the a priori properties, yielding the dense unit set $D_k$ for the k-dimensional space. Subsequently, the candidate dense unit set $D_{k+1}\prime$ for the (k + 1)-dimensional space is generated. This process iterates until the candidate dense unit set for a certain dimension becomes empty.

Step 2: Cluster Identification

Input: A set D of dense units in a k-dimensional subspace.

Output: A partition $\left\{D_1,D_2,\dots D_q\right\}$ of D into connected components, where no two distinct components $u_i\in D_i,u_j\in D_j(i\ne j)$ are interconnected.

This step is analogous to searching for connected components in a graph, where the units in the multidimensional space are treated as vertices, and an edge exists between two units if they are connected.

Step 3: Cluster Description Generation

Input: A dense unit set in a k-dimensional subspace, forming a cluster C.

Output: A collection R within the same subspace, where R ∈ C, and every unit in C belongs to at least one member of R. For each cluster, generate concise descriptions using the minimal covering hyper-rectangles of R.

From the analysis of the above clustering process, the CLIQUE algorithm implementation for marine diesel engine operational mode classification proceeds through the following systematized workflow:

(1)

Dimensionality Specification: Determine the dimensionality of the multidimensional space according to the number of performance parameters required for operational mode differentiation;

(2)

Grid Partitioning: Define parameter λ to partition each dimension into λ equal-length intervals, establishing the fundamental grid structure;

(3)

Initial Candidate Generation: At k = 1 (where k denotes subspace dimensionality), designate all rectangular units as candidate dense units;

(4)

Density Computation: Systematically examine each k-dimensional subspace to calculate unit densities, quantified as the number of data points contained within individual units;

(5)

Dense Unit Identification: Apply density threshold τ to classify units exceeding this value as k-dimensional dense units;

(6)

Subspace Pruning: Eliminate subspaces failing to meet minimum density criteria through iterative validation;

(7)

Dimensionality Expansion: Generate (k + 1)-dimensional candidate dense units from the intersection of k-dimensional dense unit sets;

(8)

Cluster Extraction: Identify final clusters as maximally connected regions within k-dimensional dense unit assemblies;

(9)

Data Archiving: Store derived cluster characteristics and metadata in designated databases for subsequent operational mode analysis.

2.3. Performance Evaluation Metrics—Mahalanobis Distance

Marine diesel main engine performance parameters exhibit strong interdependencies with heterogeneous dimensionality and variation ranges. To address this multivariate challenge, the Mahalanobis distance (MD)—a covariance-based metric proposed by P.C. Mahalanobis—was adopted for its efficacy in quantifying similarity between multidimensional datasets. Consider a sample_x. The Mahalanobis distance from X to another sample set can be mathematically expressed as

$${\rho }_{Mah}(x)=\sqrt{{\left(x-\mu \right)}^T{S}^{-1}\left(x-\mu \right)}$$

(5)

In the equation, $\mu$ denotes the sample mean of the dataset, and $S$ represents the covariance matrix. When $S$ reduces to an identity matrix, the Mahalanobis distance becomes equivalent to the Euclidean distance. Two critical properties emerge from this formulation: First, the Mahalanobis distance calculation is scale-invariant [24], meaning it remains unaffected by measurement unit variations across parameters in different datasets. Second, through explicit incorporation of the covariance matrix, this metric inherently eliminates parameter correlations and incorporates the overall distribution characteristics of the dataset.

2.4. Fault Early Warning Method

The cumulative anomaly curve method and Yamamoto detection method were employed for abrupt change identification in the Mahalanobis distance time series.

2.4.1. Cumulative Anomaly Curve Method

The cumulative anomaly method calculates cumulative anomaly values for each temporal node, generating a time-indexed curve that visually represents trend variations. The curve’s inflection points, determined by slope direction reversals (ascending-to-descending or vice versa), approximate the timing of abrupt changes in the target time series [25]. For a given time series X, the cumulative anomaly at time t is defined as

$$x_t={\displaystyle \sum _{i=1}^t(x_i-\overline{x})}$$

(6)

In the equation, $\overline{x}$ denotes the mean value of series _x.

2.4.2. Yamamoto Detection Method

The Yamamoto detection method identifies abrupt changes by assessing the statistical significance of mean differences between pre- and post-test point subsequences [26]. This methodology conceptualizes abrupt change detection as a hypothesis-testing problem concerning population mean equivalence. For a given series _x, let $n_1$ and $n_2$ represent the sample sizes of the pre- and post-test subsequences, respectively. The signal-to-noise ratio (SNR) is defined as

$$SNR={\displaystyle \frac{\left|\overline{x_1}-\overline{x_2}\right|}{s_1+s_2}}$$

(7)

In the equation, $\overline{x_1}$ and $\overline{x_2}$ represent the mean values of the pre- and post subsequences, respectively, with s₁ and s₂ denoting their standard deviations.

If the signal-to-noise ratio (SNR) is greater than 1.0, it is considered that an abrupt change occurs at that moment. If the SNR exceeds 2.0, the abrupt change is classified as a strong mutation. If the value of the SNR is set to 10, it corresponds to a confidence level of 95%, while a value of 14 corresponds to a confidence level of over 99.5%.

3. Performance Degradation Trend Analysis and Fault Early Warning of Marine Diesel Main Engines

3.1. Data Processing

3.1.1. Data Sources

The monitoring data were collected from a 6RT-flex82T marine diesel main engine (Wärtsilä, Helsinki, Finland) installed on a commercial vessel, comprising 43,186 performance samples spanning 9 June 2020 06:20 to 14 May 2021 08:10. Key technical specifications of the engine are detailed in

Table 1. Technical parameters of the 6RT-flex82T host.

Technical Parameter	Parameter Value
Number of Cylinders	6
Bore Diameter/mm	820
Stroke/mm	3375
Firing Order	1-5-3-4-2-6
Rated Power/kW	25,200
Rated Speed/(r/min)	76
Rated Specific Fuel Consumption (g/kW·h)	176.7
Control Modes	Bridge Control-ECR Control-Local Control
Service Power	22,680
Service Speed (r/min)	72
Service Fuel Consumption (g/kW·h)	200.02
Critical Speed Range (r/min)	34–45
Number of Turbochargers	2
Engine Type	Vertical Two-Stroke

.

The monitoring parameters were collected and stored using a dedicated data acquisition system with sampling intervals of 1 s, 1 min, 10 min, and 1 h. Each recorded sample includes timestamps, data types, parameter values, and parameter classifications. As shown in Figure 1, the 10 min interval dataset spanning 16 June 2020 05:30 to 23 June 2020 04:00 exhibited significant anomalies, necessitating preprocessing prior to analysis.

3.1.2. Performance Parameter Selection

Standard thermodynamic parameters of marine diesel main engines effectively reflect operational health and performance, with most parameters now being automatically monitored, collected, and stored in real-time [27]. Performance degradation manifests as deviations of these parameters from factory-set baselines, where the magnitude of deviation serves as the primary evaluation metric.

Rational parameter selection forms the foundation of engine performance assessment. This study selected 22 parameters encompassing power output, fuel type, rotational speed, scavenge air temperature, fuel flow rate, specific fuel oil consumption (SFOC), exhaust temperatures of cylinders #1–6, jacket cooling water outlet temperatures of cylinders #1–6, lubricating oil inlet temperature, jacket cooling water inlet temperature, scavenge air pressure, and jacket cooling water inlet pressure. Due to sensor limitations, engine room ambient temperature was approximated using scavenge air temperature, while sea condition influences were excluded through operational condition partitioning. As a critical indicator of fuel efficiency, SFOC was calculated using

$$SFOC={\displaystyle \frac{Q}{P}}$$

(8)

In the equation, $Q$ denotes fuel flow rate (kg/h), and P represents engine power (kW). The selected parameters comprehensively cover major engine subsystems, ensuring holistic performance characterization. The performance parameter table is as shown in

Table 2. Performance parameters information.

Performance Parameter	The Performance of a Marine Diesel Main Engine Reflects
Speed, Power	The power performance of the marine diesel main engine
Fuel Type, Fuel Flow Rate, SFOC	The performance of the fuel system
Cylinder Exhaust Temperature (Six-cylinder)	The performance of the combustion system
Lubricating Oil Inlet Temperature	The performance of the lubrication system
Scavenge Air Temperature, Scavenge Air Pressure	The performance of the turbocharging system
Jacket Cooling Water Inlet Temperature, Jacket Cooling Water Inlet Pressure Jacket Cooling Water Outlet Temperature (Six-cylinder)	The performance of the cooling system

. Storage specifications for all parameters except SFOC are detailed in

Table 3. Performance parameters store information.

Performance Parameter	Data Type	Unit	Nullable	Lower Limit	Upper Limit
Speed	float (8, 3)	RPM	Yes	−200	200
Power	float (8, 1)	kW	Yes	−20,000	20,000
Fuel Tcype	int (11)	1: HFO, 2: MGO, 3: LSHFO, 4: MDO	Yes	\	\
Fuel Flow Rate	float (12, 2)	kg/h	Yes	\	\
Cylinder Exhaust Temperature (Six-cylinder)	float (8, 3)	°C	Yes	0	600
Lubricating Oil Inlet Temperature	float (8, 3)	°C	Yes	0	200
Jacket Cooling Water Inlet Temperature	float (8, 3)	°C	Yes	0	200
Jacket Cooling Water Inlet Pressure	float (8, 3)	Mpa	Yes	−0.1	0.6
Jacket Cooling Water Outlet Temperature (Six-cylinder)	float (8, 3)	°C	Yes	0	200
Scavenge Air Temperature	float (8, 3)	°C	Yes	0	200
Scavenge Air Pressure	float (8, 3)	Mpa	Yes	0	0.6

.

3.1.3. Data Preprocessing

Data preprocessing is one of the critical steps to ensure the accuracy of marine diesel main engine performance evaluation, aiming to eliminate abnormal performance samples. The primary causes of abnormal data include the following: First, sensor malfunctions during data acquisition lead to invalid values such as negative numbers, constant values, or abrupt fluctuations. Second, data packet loss occurs due to communication issues, resulting in parsing errors during data reception. Third, inconsistent sampling frequencies among sensors, causing missing parameters in monitoring data. The main categories of abnormal data are as follows:

(1) Missing parameters: One or more performance parameters are absent in a sample, preventing the calculation of performance evaluation metrics;

(2) Parameter anomalies: One or more parameters exhibit abrupt deviations or values far from the mean under current operating conditions (e.g., rotational speed below the minimum stable threshold, abnormally low shaft power, or fuel flow rate below operational limits). These anomalies are caused by sensor failures or data parsing errors and do not reflect the actual performance of the marine diesel main engine.

Criteria for abnormal performance samples are as follows:

Any performance parameter in the sample is null.

Rotational speed falls below the minimum stable threshold (20 RPM).

Power output is lower than 10 kW.

Fuel flow rate is less than 0.0001 kg/h.

Table 4. Sample basic information.

Feature	Basic Information
Data Acquisition Period	9 June 2020 06:20–14 May 2021 08:10
Sample Size	43,186
Sampling Interval	10 min

summarizes the statistical characteristics of the preprocessed dataset. As visualized in Figure 2, the postprocessed data (red curve) effectively eliminates subthreshold rotational speed anomalies (black raw data segments) through this protocol.

3.2. Steady-State Interval Identification

This paper employs the SSD steady-state detection algorithm with the first parameter (window width) set to 12,the window size is selected based on practical scenarios and; determined through multiple experiments. The second parameter is the critical value of Student’s t-test. The critical value is derived from statistical tables based on degrees of freedom ν and significance level α. Configured with α = 0.025, the degrees of freedom are calculated as

$$\nu =n-2$$

(9)

In the equation, ν represents the number of independent parameters in statistical estimation, and n denotes the window width.

Steady-state operation is confirmed when thermodynamic parameters satisfy the stability criterion, thereby indicating nominal engine operation. The identified stable intervals are statistically summarized in

Table 5. Basic information of samples after steady-state identification.

Feature	Basic Information
Data Acquisition Period	14 June 2020 3:00–14 May 2021 7:40
Sample Size	37,026
Sampling Interval	10 min

.

Figure 3 illustrates the rotational speed trend before and after steady-state detection. The black curve represents the preprocessed rotational speed profile, while the red curve denotes the post-detection steady-state sequence. As evident from the raw data (black curve), two pronounced fluctuations occur, likely corresponding to acceleration/deceleration maneuvers or shutdown events. The steady-state detection protocol successfully eliminates these transient disturbances (red curve), yielding a stabilized operational profile that better reflects nominal engine behavior.

3.3. Operational Condition Classification

The 37,026 steady-state processed sample data were used as the data source. Performance parameters such as fuel type, power, speed, scavenge air temperature, and scavenge air pressure were selected as the grid dimensions (i.e., input dimensions) to establish a five-dimensional sample space. The remaining performance parameters were used as output samples, with the output sample dimensions being 17. The dimensional information of the sample space is shown in

Table 6. Information of each dimension of sample space.

Grid Dimension	Minimum	Maximum	Segments
Fuel Type	0	4	8
Speed/RPM	0	20,000	500
Power/kW	20	80	240
Scavenge Air Temperature/°C	20	80	240
Scavenge Air Pressure/MPa	0	0.6	60

. The density threshold is used to determine whether a cell is a dense unit. In this study, the density threshold was set to 0.002. If the number of samples within a cell exceeds the product of the total number of samples and the density threshold, the cell is considered a dense unit; otherwise, it is classified as a non-dense unit. The maximum connected region of adjacent dense units is defined as a cluster. The clustering results are shown in Figure 4, which generated 33 operating conditions (clusters), with condition 1 containing 23,720 performance samples, the largest cluster, and condition 33 containing only 8 performance samples. When a ship is sailing at sea, the engine speed is usually set according to the shipowner’s requirements, ensuring that the main engine’s operating condition remains stable for a certain period of time or a single voyage. The operating condition that the ship’s main engine frequently operates under is called the common operating range, and the cluster with the largest number of samples represents the common operating range condition, which is condition 1 in Figure 4. The basic information of the common operating range condition is shown in

Table 7. Basic information about common working conditions.

Parameter		Range
Input Dimension Parameters	Fuel Type	Low-Sulfur Heavy Fuel Oil (LSHFO)
	Power (kW)	10,520–12,240
	Rotational Speed (RPM)	57.5–58.75
	Scavenge Air Temperature (°C)	46.75–52
	Scavenge Air Pressure (MPa)	0.07–0.1
Output Dimension Parameters	Cylinder 1 Exhaust Temperature (°C)	352.71–361.28
	Cylinder 2 Exhaust Temperature (°C)	350.05–360.57
	Cylinder 3 Exhaust Temperature (°C)	351.51–361.32
	Cylinder 4 Exhaust Temperature (°C)	346.1–356.28
	Cylinder 5 Exhaust Temperature (°C)	355.71–363.86
	Cylinder 6 Exhaust Temperature (°C)	353.67–361.62
	Lubricating Oil Inlet Temperature (°C)	45.19–46.34
	Cylinder 1 Jacket Cooling Water Outlet Temperature (°C)	88.29–89.69
	Cylinder 2 Jacket Cooling Water Outlet Temperature (°C)	88.21–89.87
	Cylinder 3 Jacket Cooling Water Outlet Temperature (°C)	87.86–89.31
	Cylinder 4 Jacket Cooling Water Outlet Temperature (°C)	88.02–89.37
	Cylinder 5 Jacket Cooling Water Outlet Temperature (°C)	88.6–90.01
	Cylinder 6 Jacket Cooling Water Outlet Temperature (°C)	88.32–89.74
	Jacket Cooling Water Inlet Pressure (MPa)	0.4685–0.4791
	Fuel Flow Rate (kg/h)	1935.52–2022.81
	Specific Fuel Consumption (g/kWh)	172.42–182.04
	Jacket Cooling Water Inlet Temperature (°C)	84.05 (Fixed)

, with 23,720 performance samples under the common operating range condition, spanning from 19:00 on 7 July 2020 to 07:40 on 14 May 2021.

3.4. Performance Degradation Analysis and Fault Early Warning

3.4.1. Performance Evaluation Metrics—Calculation of Mahalanobis Distance

Following operational condition partitioning of marine diesel main engines using the CLIQUE clustering algorithm, a time series of Mahalanobis distances was established by calculating the distances between performance samples at different time points under identical operational conditions. This study established an initial performance dataset $Y={\left[Y_1,Y_2,T_3,\dots ,Y_{100}\right]}^T$ comprising the first 1000 sets of performance samples, where each synchronized parameter configuration constitutes a performance sample. We subsequently calculated the Mahalanobis distance between temporal performance samples and this reference dataset. For a given performance sample X at time t, its Mahalanobis distance to dataset Y is formulated as

$$MD=\sqrt{\left(x-\mu \right)S^{-1}{\left(x-\mu \right)}^T}$$

(10)

In the equation, µ denotes the mean vector of the initial performance dataset Y, and S represents its covariance matrix. These statistical descriptors are formally defined as

$$\mu ={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{Y}_i}$$

(11)

$$S={\displaystyle \frac{1}{n-1}}{\displaystyle \sum _{i=1}^n\left(Y_i-\mu \right)}{\left(Y_i-\mu \right)}^T$$

(12)

In the equation, n = 1000, denoting the sample size of the reference dataset. The Mahalanobis distance serves as a robust metric for marine diesel engine performance assessment, quantitatively characterizing the engine’s degradation trajectory. A monotonic relationship exists between the distance magnitude and degradation severity: larger Mahalanobis distances indicate more pronounced performance deterioration, while smaller values correspond to preserved operational integrity.

3.4.2. Performance Evaluation and Degradation Trend Analysis

Using the frequently encountered operational condition range as a case study, comprehensive performance evaluation and degradation analysis were conducted for marine diesel main engines. The first 1000 performance samples (collected from 19:00 on 7 July 2020 to 07:20 on 6 September 2020) were selected as the baseline performance sample space, with their statistical means summarized in

Table 8. Mean Values of Performance Parameters in the Initial Performance Sample Space for the Common Operating Range Condition.

Performance Parameter	Mean Value
Cylinder Jacket Cooling Water Inlet Temperature (°C)	83.773101089477535
Cylinder 1 Jacket Cooling Water Outlet Temperature (°C)	89.696554016113282
Cylinder 2 Jacket Cooling Water Outlet Temperature (°C)	89.845977897644048
Cylinder 3 Jacket Cooling Water Outlet Temperature (°C)	89.163089996337888
Cylinder 4 Jacket Cooling Water Outlet Temperature (°C)	89.092101951599119
Cylinder 5 Jacket Cooling Water Outlet Temperature (°C)	89.833513893127446
Cylinder 6 Jacket Cooling Water Outlet Temperature (°C)	89.516971015930181
Cylinder Jacket Cooling Water Inlet Pressure (MPa)	0.47260199856758117
Cylinder 1 Exhaust Temperature (°C)	358.57207760620116
Cylinder 2 Exhaust Temperature (°C)	352.28291729736327
Cylinder 3 Exhaust Temperature (°C)	351.78961108398437
Cylinder 4 Exhaust Temperature (°C)	343.9371090698242
Cylinder 5 Exhaust Temperature (°C)	356.3969108276367
Cylinder 6 Exhaust Temperature (°C)	352.38188513183593
Lubricating Oil Inlet Temperature (°C)	45.5445690536499
Scavenge Air Temperature (°C)	51.23264501571655
Scavenge Air Pressure (MPa)	0.084497000284492974
Speed (RPM)	58.234216999053956
Power (kW)	11,815.623912109375
Fuel Flow Rate (kg/h)	2035.4115
Specific Fuel Consumption (g/kW·h)	172.31603485696255
Fuel Type	3

. Subsequent calculation of Mahalanobis distances between performance samples from different time intervals and this baseline space yielded a time series comprising 22,720 data points. The resultant performance degradation trend curve is presented in Figure 5.

Figure 5 demonstrates that the Mahalanobis distance exhibited a gradual increase from September 2020 to late January 2021, aligning with empirical patterns of marine diesel main engine performance degradation. However, a sharp surge and pronounced fluctuations in Mahalanobis distances were observed between mid-January and March 2021, indicative of acute systemic performance deterioration. After March 2021, the growth rate of Mahalanobis distances stabilized, demonstrating restoration of normative degradation patterns. This temporal pattern suggests anomalous parameter deviations during the mid-January–March 2021 period, potentially attributable to transient mechanical faults. The subsequent normalization of degradation trends implies successful fault mitigation through operational interventions.

To validate this hypothesis, sequential elimination of individual performance parameters was conducted with subsequent Mahalanobis distance recalculations to reconstruct degradation trend curves. The results demonstrate that removal of the “No. 2 cylinder jacket cooling water outlet temperature” parameter yielded a gradual degradation profile devoid of abrupt surges or significant fluctuations (Figure 6). In contrast, elimination of other parameters maintained degradation trends consistent with Figure 5 (Figure 7 and Figure 8). Subsequent analysis revealed substantial amplitude variations in the No. 2 cylinder jacket cooling water temperature profile between late February and March 2021 (Figure 9), suggesting probable mechanical fault occurrence within this period. The localized temperature anomalies indicate fault origination proximate to the No. 2 cylinder jacket cooling water outlet, consistent with the observed performance deviations.

3.4.3. Fault Early Warning

Fault early warning aims to provide alerts before a failure occurs. In practical navigation, if a warning is only issued after a significant change in the performance degradation trend, it may be too late. This paper proposes a fault early warning technique based on time–domain analysis. The core idea is to analyze the performance degradation curve of the ship’s main engine, identify the time of the first abrupt change in the curve as the fault warning time, and analyze the cause of the anomaly to prevent potential failures.

The cumulative anomaly curve method and Yamamoto detection method were employed for abrupt change identification in the Mahalanobis distance time series. The effectiveness of this technique was validated through experimental verification. As shown in Figure 10, between late February and March 2021, the outlet temperature of the jacket cooling water for cylinder #2 exhibited abnormal fluctuations, accompanied by a significant increase in performance variation. However, from late January to early February 2021, the performance degradation curve of the marine diesel engine already showed the first abrupt change, while the “outlet temperature of the cylinder jacket cooling water for cylinder #2” only slightly deviated from the normal mean without showing any significant anomaly. Therefore, by identifying the first abrupt change in the performance degradation curve during this period, fault warning can be effectively triggered.

Implementing time–domain analysis for precise abrupt change identification involves a two-stage methodology: preliminary temporal range estimation via the cumulative anomaly method, followed by Yamamoto-based exact localization. The cumulative anomaly curve provides visual detection of degradation trend transitions. As shown in Figure 11, the Mahalanobis distances exhibit progressive growth over time, accompanied by decreasing cumulative anomaly values—a pattern consistent with typical marine diesel main engine degradation. However, a marked inflection in the cumulative anomaly curve occurred in late January 2021, indicating an abrupt change in the degradation trajectory. This initial inflection phase was temporally bounded between January 23 and 26 February 2021.

Subsequent refinement using the Yamamoto method entailed SNR calculations for performance sequences within this critical window, with results fitted to a validation curve (Figure 12 and Figure 13). The detection threshold (SNR > 1.0) was first breached at 18:10 on 25 January 2021, establishing this timestamp as “The definitive onset of degradation curve destabilization; The optimal fault early-warning trigger point”.

Figure 14, Figure 15 and Figure 16 further demonstrate a significant temporal separation between the initial inflection of the engine’s overall performance degradation curve and subsequent parametric anomalies, providing additional validation of the effectiveness and timeliness of the degradation-based fault early-warning technology.

4. Conclusions

This study proposes a data-driven methodology for marine diesel engine performance assessment, effectively revealing performance degradation trends and enabling proactive fault warning through degradation pattern analysis. The results demonstrate the capability to detect and issue warnings for impending faults 20–30 days prior to measurable parameter anomalies. Key findings are summarized as follows:

(1) Utilizing 43,186 operational data points collected over one year, 37,026 stable samples were obtained through preprocessing and steady-state detection. The CLIQUE clustering algorithm automatically partitioned these samples into 33 operational conditions, with Condition 1 (containing 23,720 samples) identified as the dominant operational range. These results quantitatively validate the algorithm’s efficacy in automatic operational condition classification;

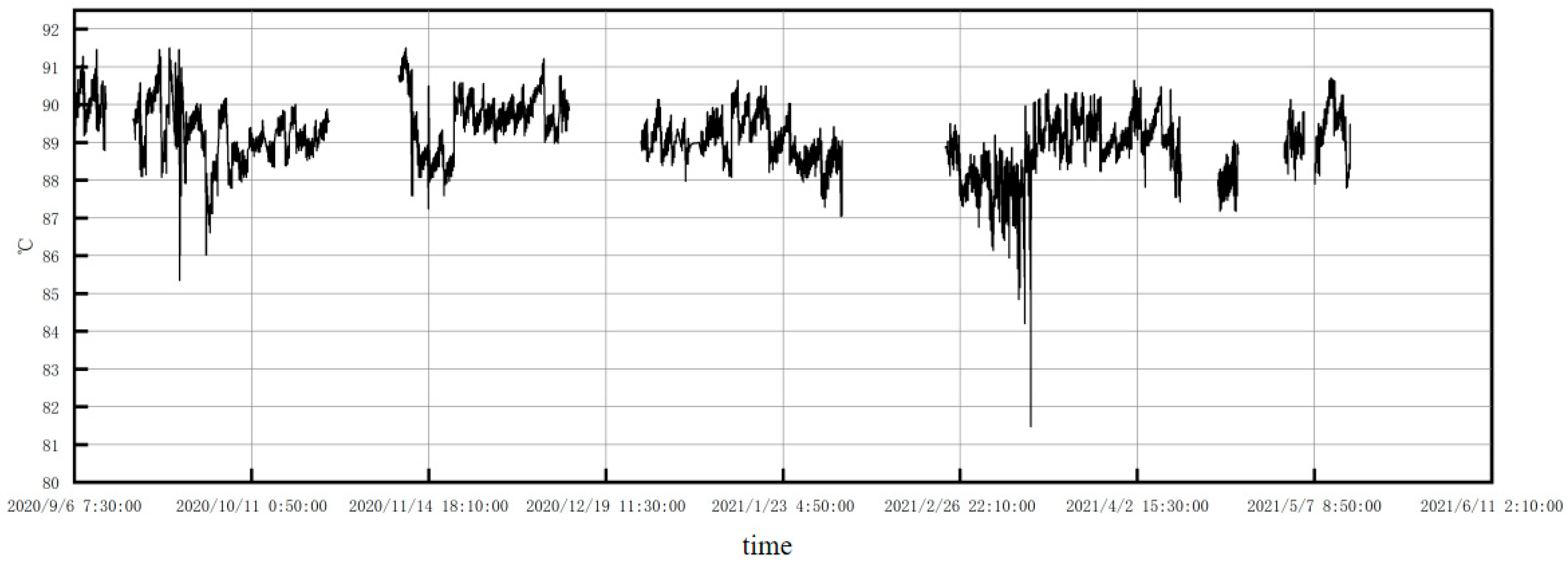
(2) Analysis of the Mahalanobis distances within the dominant operational range yielded a fitted performance degradation curve. While the initial phase followed empirical degradation patterns, subsequent abrupt changes and fluctuations indicated systemic anomalies. Sequential parameter elimination localized the anomaly near the No. 2 cylinder jacket cooling water outlet, with temporal analysis confirming abnormal parameter deviations.

(3) Comparative analysis revealed that degradation curve destabilization preceded measurable temperature fluctuations at the No. 2 cylinder outlet by approximately 20 days, establishing a critical early-warning window. The time–domain analysis-based warning system demonstrated operational validity, with precise warning triggering at 18:10 on 25 January 2021.

The proposed methodology provides novel insights for marine diesel engine health management while offering methodological references for intelligent marine equipment condition classification and abrupt change detection. Future research will incorporate additional conventional thermodynamic parameters to enhance holistic engine performance characterization. Concurrently, algorithmic refinements to the SSD framework will implement adaptive window width configuration, establishing a data-driven foundation for integrated ship–shore performance diagnostics.