ML-Empowered Microservice Workload Prediction by Dual-Regularized Matrix Factorization

Abstract

A technical challenge for workload prediction in microservice systems is how to capture both the dynamic features of workload and evolving dependencies among microservices. The existing work focused mainly on modeling dynamic features without taking adequate account of evolving dependencies due to their unpredictable temporal dynamics. To fill this gap, as an illustration of bridging theory and real-work solutions by integrating machine learning with data analysis, we propose a novel framework of Temporality-Dependence Dual-Regularized Matrix Factorization (TDDRMF) by combining matrix factorization with regularization on both workload temporality and microservice dependencies. It models the workload matrix as the product of a microservice dependency matrix W and workload feature matrix X applying matrix factorization, and computes X by temporal regularization and W by low-rank norm regularization as a convex relaxation of rank minimization. To further enhance its adaptability to workload variations in real-time environments, we deploy a dynamic error detection and update mechanism. Experiments on the Alibaba dataset show that TDDRMF achieves 18.5% lower RMSE than TAMF in 10-step prediction, improving the existing matrix factorization methods in accuracy. In comparison with ML-based methods, as TDDRMF uses only 5% of their training data, it requires only a small fraction of their training time.

1. Introduction

In the era of cloud computing, microservice architectures [1] have become the cornerstone of modern distributed systems such as the booming data center networks, supported by their scalability, flexibility, and rapid deployability. However, this paradigm introduces significant complexities in resource management [2], particularly under dynamic workload conditions of real-world applications such as advanced manufacturing and smart agriculture, where achieving a balance among performance, cost, and energy efficiency is critical [3]. As a core component of resource management, workload prediction [4] plays a pivotal role by enabling real-time responses to sudden workload surges and identifying long-term trends to optimize resource allocation. Yet, the intricate characteristics of microservice workloads pose substantial challenges to achieving accurate predictions.

Microservice workload prediction is not only affected by the dynamics of workload evolution over time but also driven by the complex synergistic relationships among microservices. Most of the existing research draws on the framework of time series prediction to capture the temporal dynamics of the workload [5,6] through statistical methods [7,8,9,10], machine learning models [11,12,13,14] and ensemble learning methods [15,16,17]. These methods show a strong ability to model time dynamics but give less consideration to the complex synergistic relationship between microservices. The inter-dependency and interaction characteristics of microservices often directly affect the propagation pattern and change rule of the load, which may lead to biased prediction results. Some studies address modeling the synergistic relationship between microservices [18,19,20]. However, they mainly focus on microservice dependency modeling and pay insufficient attention to the temporal dynamic characteristics of workload, making it difficult to fully reflect the multi-scale characteristics of workload changes. In addition, traditional microservice workload prediction methods have high requirements on data volume and data integrity. Machine learning-based methods suffer from long training time, high computing and latency costs, making their applicability limited in cold start and resource-constrained microservice environments.

In contrast, matrix factorization [21], originally deployed to impute missing entries in high-dimensional data by performing dimensionality reduction and denoising after augmentation with temporal regularization, enables the direct modeling of short-term fluctuations, long-term trends, and periodic behaviors to capture the essential modes of workload evolution without a prohibitive compute overhead. However, existing matrix-factorization approaches typically ignore the rich dependency structure among microservices.

To address the knowledge gap, existing works studied workload prediction and microservice dependency separately due to the lack of a joint portrayal of modeling time dynamics and microservice dependencies, making them unable to achieve a satisfactory performance. We will study how to construct a unified prediction framework of jointly modeling the temporal features of workloads and microservice dependencies so as to capture the multidimensional dynamic characteristics of workloads more accurately.

Our prediction framework, namely Temporality-Dependency Dual-Regularized Matrix Factorization (TDDRMF), effectively integrates relevant techniques of machine learning with data analysis by combining matrix factorization with temporal regularization and low-rank dependency modeling: matrix factorization decomposes high-dimensional workload data into low-dimensional latent feature matrices capturing short-term fluctuations, long-term trends, and periodic patterns; temporal regularization integrates autoregressive and periodic constraints [22,23] to enhance multi-scale temporal dynamics modeling; low-rank nuclear norm regularization [24] models key inter-service dependencies by imposing structured constraints on the microservice relationship matrix. To adapt to workload variations in real-time environments, the framework incorporates a dynamic error detection and parameter update mechanism, providing a balanced trade-off between prediction accuracy and computational efficiency.

The contributions of this paper are summarized as follows:

• Workload dynamics modeling: We apply matrix factorization with temporal regularization to model the dynamics of microservice workloads for more accurately capturing the principal patterns of workloads.
• Microservice dependency capturing: We apply nuclear norm regularization to capture the primary dependencies between microservices by constraining the low-rank structure of the microservice feature matrix.
• Workload variation capturing: We introduce a dynamic error detection and update mechanism that leverages localized window data to capture workload variations in real-time environments and enable the framework adaptive to dynamic and evolving environments.

The rest of this paper is organized as follows. Section 2 presents an overview of related work, Section 3 presents the proposed methodology, Section 4 shows the empirical results, and Section 5 concludes the paper and evaluates paths for future work.

2. Related Work

In this section, we review and summarize relevant research in the field of workload forecasting, especially the application of statistical methods, machine learning and deep learning techniques, ensemble learning methods, and time-dynamic modeling techniques based on matrix factorization. These methods provide solution ideas for workload forecasting from different perspectives and also have certain limitations.

Statistical methods are used as an early research focus for workload forecasting, capturing short-term trends in workload data through time series analysis. For example, Ref. [9] predicts future performance trends based on statistical models and triggers system expansion using response time as an indicator; Ref. [25] applies an ARIMA model to enable medium-term workload forecasting for power systems; Ref. [10] uses an ARIMA model to optimize CPU utilization prediction and resource allocation to reduce energy consumption. These methods utilize time series autocorrelation and perform well in scenarios where the workload data are stable and linear in nature. However, they typically assume data linearity and hence are unable to handle nonlinear data arising in diverse scenarios.

Machine learning (ML) methods are capable of modeling complex temporal dynamics and nonlinear relationships and are important tools for workload forecasting. For example, Ref. [12] uses decision tree regression to dynamically adapt a resource forecasting model for short-term workload measurements, and Ref. [13] transforms workload request forecasts into resource utilization forecasts to optimize system stability. These methods enhance the ability to adapt to nonlinear variations by learning complex patterns in historical data. These models focus only on the temporal dynamic properties of a single microservice and fail to capture the inter-service dependencies that are critical in workload propagation. Further research attempts to combine temporal dynamics with dependency modeling. For example, Ref. [20] improves the prediction ability of the microservice workflow by integrating the dependency structure into deep learning models through the directed acyclic graph (DAG). Ref. [26] proposes a workload prediction method based on spatio-temporal graph neural networks, which combines temporal dynamics with inter-microservice dependencies to significantly improve prediction performance.

However, these methods rely on complex graph neural network architectures and capture only static dependencies. ASTMGCNet [27] is designed to improve prediction accuracy in dynamic urban traffic systems by effectively capturing complex spatio-temporal correlations through multi-scale feature extraction and dual attention mechanisms to effectively capture complex spatio-temporal correlations within traffic sequences, enhancing prediction accuracy. Based on it, Ref. [28] employs a resource allocation strategy within edge computing to reduce energy usage during prediction, where the attention mechanism helps quickly decide which services are most important. Using this information, smart cities can assign tasks and allocate resources based on priority to ensure high-quality service. The work [29] discusses the limitations of current deep-learning architectures in using publicly available spatial data to capture crop-yield complexity, and integrates process-based methods to enhance the reliability and interpretability of data-driven forecasting models. Overall, ML methods, especially deep learning methods, are highly dependent on the quality of data. They have limited generalization ability in diverse scenarios using a single model since it would require frequent adjustments and retraining, making the maintenance cost excessively high.

To cope with the limitations of a single model, ensemble learning has gradually become a hot research direction in the field of workload prediction. Ensemble learning techniques improve the accuracy and robustness of prediction by combining the advantages of multiple models. For example, Ref. [16] compares the prediction effects of LSTM, AR, and HTM and dynamically selects the best performing model; Ref. [15] proposes an ensemble approach based on metaheuristics combined with an Extreme Learning Machine (ELM) in order to reduce the training time and improve the prediction performance. Ref. [17] further integrates multiple models (e.g., ARIMA, multilayer perceptron, support vector regression, Random Forest, and LSTM) and dynamically adjusts the model configurations to adapt to changes in the workload environment. These methods solve the problem of unstable performance of a single model to a certain extent, while improving the adaptability in complex workload scenarios. However, they inherit the disadvantage of single-model ML and are unable to fully capture the underlying structure of the workload data and the dynamic and collaborative relationships between microservices.

Matrix factorization has been widely applied in time series forecasting due to its advantages in capturing latent features and temporal dynamics. For example, Ref. [30] proposes a spatio-temporal modeling framework (MF-STN) that combines matrix factorization with neural networks to capture regional characteristics and correlations through latent embeddings, thereby improving the accuracy of urban flow prediction. Similarly, Ref. [31] develops a non-stationary time matrix factorization model (NoTMF), which integrates matrix factorization with vector autoregression (VAR) to address high-dimensional time series forecasting problems. Furthermore, Ref. [22] introduces a matrix factorization method incorporating temporal regularization and autoregressive processes to model nonlinear dynamics and detailed properties in time series. Ref. [23] designs the Temporal Autoregressive Matrix Factorization (TAMF) framework, which uses trend and periodic regularization to uncover latent characteristics of time series while handling data sparsity issues. Then, BTAMF [32] splits the direct variables in the traditional decomposition into two parts—a trend component and a periodic component—and then uses an autoregressive model over the target series’ preceding time steps to capture trend fluctuations, alongside a second autoregressive model built on strongly correlated historical segments to characterize periodic patterns. This design enables both the accurate imputation of missing values and effective forecasting of future observations without sacrificing the original time series characteristics.

These studies demonstrate the potential of matrix factorization in capturing complex data change trends and handling sparse data. However, most of the current matrix factorization approaches focus mainly on modeling temporal dynamics of datasets and ignore their dynamic relationships existing in many applications such as microservice workload scheduling.

In summary, existing approaches to microservice workload prediction have their strengths and limitations: statistical methods are efficient in linear, stable scenarios but struggle with nonlinearity and sparse data; machine learning and deep learning models with the attention mechanism can capture complex temporal dynamics and dependencies but rely on large, complete datasets and incur heavy training and computing overheads; ensemble learning improves robustness by combining multiple models but inherits the high costs and structural blind spots of its base learners; and traditional matrix factorization excels at imputing missing values and denoising but typically focuses only on temporal patterns and overlooks the critical collaborative dependencies that drive load propagation among microservices.

In contrast to existing methods, our TDDRMF employs matrix factorization with temporal and nuclear-norm regularization to jointly model multi-scale workload dynamics and low-rank service dependencies. Its convex optimization backbone ensures fast convergence, and its low-rank design naturally denoises and handles missing data. However, TDDRMF has a lower capability of capturing highly nonlinear interactions than deep-learning models, and requires to tune the rank parameter to accommodate evolving dependency complexity. To address these issues, we integrate an error-detection trigger that selectively retrains on local data only when the error exceeds a predefined threshold, thereby preserving model agility at minimal overhead.

3. Methodology

This section provides the problem definition, conceptual design and key technical details of our framework.

3.1. Problem Definition

In modern microservice architectures, workload prediction is a critical task aimed at optimizing resource allocation and system performance. The primary goal is to accurately forecast future workload fluctuations based on historical data so as to enable efficient resource scheduling and system maximize system performance.

Let the workload data be represented as a matrix $Y\in {\mathbb{R}}^{n\times T}$, where n denotes the number of microservices, T represents the historical time steps, and $Y_{i,t}$ indicates the workload of the i-th microservice at time t. The prediction task can be formulated as learning a mapping function $f(·)$, which maps historical workloads $Y_{1:T}$ to future workloads $Y_{T+1:T+h}$:

$$f:Y_{1:T}\to Y_{T+1:T+h},$$

where $f(·)$ represents the learned prediction model.

To facilitate workload prediction, we make the following assumptions:

• The workload matrix Y can be approximated in a low-dimensional latent space, i.e., $\mathrm{rank}\left(Y\right)\ll min(n,T)$, based on the inherent correlations of microservice interactions and workload patterns (low-rank assumption).
• Workload changes exhibit temporal continuity, where adjacent time steps have strong dependencies.

Workload prediction in microservice systems faces multiple challenges. On one hand, workload data exhibit multi-scale temporal dynamics, encompassing short-term fluctuations, long-term trends, and periodic patterns, which require accurate modeling without overfitting. On the other hand, the complex and dynamic interdependencies among microservices introduce significant modeling challenges, necessitating the extraction of key interactions to enhance efficiency and interpretability. Furthermore, in cold-start or data-scarce scenarios, models must demonstrate robustness to handle uncertainty caused by limited historical data.

3.2. Framework Overview

We propose the framework of Temporality-Dependency Dual-Regularized Matrix Factorization (TDDRMF) to address the challenges of workload prediction in dynamic microservice environments. TDDRMF leverages matrix factorization to jointly model temporal workload dynamics and inter-microservice dependencies. It employs temporal regularization to capture multi-scale temporal patterns and nuclear norm constraints to enforce the low-rank structure of microservice dependencies. Furthermore, a dynamic detection and update mechanism is introduced to adapt to environmental changes effectively.

(a) Matrix Factorization Modeling: The workload matrix Y is factorized into the product of a microservice matrix W and a temporal feature matrix X [21]:

$$Y\approx WX,$$

(1)

where we have the following:

• $W\in {\mathbb{R}}^{n\times r}$: Represents the dependency relationships among n microservices, where the rows are n microservices and the columns are r latent patterns. W encodes each service’s weights across those patterns, capturing both inter-service dependencies and their collaborative workload.
• $X\in {\mathbb{R}}^{r\times T}$: Represents the temporal dynamics of r latent features over T time steps, where the rows are r latent patterns and the columns are T time steps. X records how each pattern varies over time.

(b) Temporal Dynamics Capturing: The temporal feature matrix X is further decomposed into a trend component and a periodic component [23]:

$$X_T\approx X_T^{\mathrm{trend}}+X_T^{\mathrm{period}},$$

(2)

where we have the following:

• $X_T^{\mathrm{trend}}$: Captures short-term fluctuations using autoregressive modeling;
• $X_T^{\mathrm{period}}$: Extracts periodic patterns, representing recurring behaviors over time.

The temporal regularization term is defined as

$$R_{\mathrm{AR}}\left(X\right)={\displaystyle \frac{1}{2}}\sum _{t=d+1}^T\parallel X_t-X_t^{\mathrm{trend}}-X_t^{\mathrm{period}}{\parallel }_F^2+{\displaystyle \frac{\eta }{2}}{\parallel X\parallel }_F^2$$

(3)

ensuring accurate temporal representation and low complexity.

(c) Low-Rank Dependency Capturing: The microservice matrix W is regularized using the nuclear norm [33] to enforce its low-rank structure:

$$N\left(W\right)={\parallel W\parallel }_{*},$$

(4)

where ${\parallel \parallel }_{*}$ is the nuclear norm, i.e., the sum of matrix singular values. Nuclear norm regularization can capture tightly knit inter-service dependencies and enhancing model generalization.

(d) Dynamic Detection and Update Mechanism: To adapt to changing environments, TDDRMF introduces a dynamic detection mechanism that monitors prediction errors:

$$E_t={\parallel Y_t-W{X}_t\parallel }_F^2.$$

(5)

When $E_t$ exceeds a predefined threshold, the microservice matrix W and temporal feature matrix X are incrementally updated to maintain prediction accuracy and robustness.

(e) Objective Function: The overall optimization objective of TDDRMF is defined as

$$\mathcal{L}={\displaystyle \frac{1}{2}}min{\parallel Y-WX\parallel }_F^2+{\lambda }_1{R}_{\mathrm{AR}}\left(X\right)+{\lambda }_{2}N\left(W\right),$$

(6)

where we have the following:

• ${\parallel Y-WX\parallel }_F^2$: Measures the prediction error;
• $R_{\mathrm{AR}}\left(X\right)$: Temporal regularization term to capture multi-scale temporal dynamics;
• $N\left(W\right)$: Nuclear norm regularization to enforce low-rank dependencies;
• ${\lambda }_1,{\lambda }_2$: Hyperparameters balancing the contributions of regularization terms.

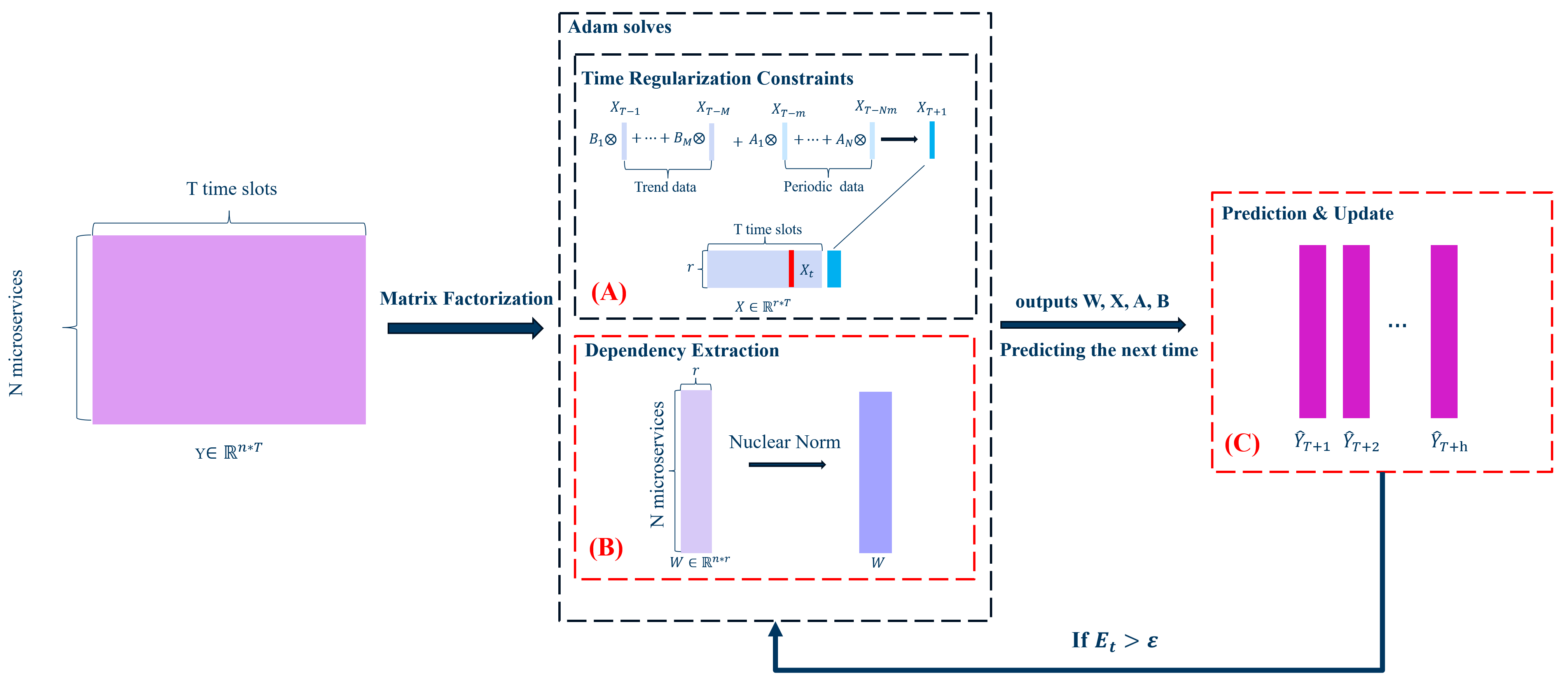
The TDDRMF framework combines temporal dynamics modeling and low-rank dependency capturing, offering accurate workload predictions and robust handling of evolving microservice environments. Figure 1 presents a block diagram of the TDDRMF architecture, depicting the core modules and their interactions from workload decomposition to the prediction of future workloads whose functions are outlined as follows:

• (A) Feature Matrix Computation: Compute temporal feature matrix X from workload matrix Y that satisfies the periodic and tendency constraints A and B obtained by autoregression to fit r latent workload patterns over time, applying the Adam optimizer.
• (B) Dependency Extraction: Compute microservice matrix W from workload matrix Y under the nuclear-norm low-rank constraint to uncover strong inter-service dependencies and their weights on the r patterns applying the Adam optimizer.
• (C) Prediction and Update: Predict ${\widehat{Y}}_{T+1}$ based on $W,X,A,B$; if $\parallel Y_{T+1}-{\widehat{Y}}_{T+1}\parallel >ϵ$, trigger the localized retraining of $W,X,A,B$.

Building on this foundation, the subsequent sections explore the technical implementation of the framework, including the optimization of temporal regularization, the integration of low-rank constraints, and the dynamic update mechanism.

3.3. Temporal Dynamics Modeling

To capture the multi-scale temporal characteristics of the workload data, the temporal dynamics modeling module decomposes the temporal feature matrix X into short-term trends $X_T^{\mathrm{trend}}$ and periodic patterns $X_T^{\mathrm{period}}$. This decomposition provides precise temporal representations for the framework. The implementation details of these modules are given in [23] as follows:

(a) Short-Term Trend Modeling: The short-term dynamics are modeled using an autoregressive approach:

$$X_T^{\mathrm{trend}}\approx \sum _{h=1}^M{B}_h·X_{T-h},$$

(7)

where we have the following:

• M: Number of past time steps considered for short-term dynamics.
• $B_h$: Autoregressive coefficients that capture the influence of previous time steps.

This formulation leverages neighboring historical data to model transient workload fluctuations.

(b) Periodic Pattern Modeling: The periodic characteristics are modeled as

$$X_T^{\mathrm{period}}\approx \sum _{l=1}^N{A}_l·X_{T-lm},$$

(8)

where we have the following:

• N: Number of past periodic patterns considered.
• m: Length of the periodic cycle.
• $A_l$: Regression coefficients for periodic dependencies.

This model captures recurring workload patterns over longer-term periodic cycles, such as daily or weekly trends.

(c) Temporal Regularization: Obviously, the associated parameters A and B play a key role in modeling the dynamic behaviors, so Equation (3) is re-expressed as

$$R_{\mathrm{AR}}\left(X\right|A,B)={\displaystyle \frac{1}{2}}\sum _{t=d+1}^T\parallel X_t-X_t^{\mathrm{trend}}-X_t^{\mathrm{period}}{\parallel }_F^2+{\displaystyle \frac{\eta }{2}}{\parallel X\parallel }_F^2,$$

(9)

where $d=max\{M,N\ast m\}$, and we have the following:

• The first term minimizes the reconstruction error of $X_t$ using its trend and periodic components.
• The second term applies Frobenius norm regularization to X, constraining its complexity and improving generalization.

While temporal dynamics modeling focuses on capturing multi-scale workload patterns over time, it is equally critical to represent the intrinsic relationships among microservices. To this end, we introduce a nuclear norm regularization on the microservice matrix W, which ensures a compact and interpretable representation of microservice dependencies.

3.4. Microservice Dependency Capturing

Modeling dependencies among microservices presents a significant challenge due to their high-dimensional complexity and dynamic evolution. Capturing critical interactions while avoiding redundant dependencies is crucial for solving workload prediction problems. To address this, we initially aimed to impose a rank minimization constraint on the microservice matrix W, enabling the model to preserve the key dependencies between microservices by leveraging the low-rank structure inherent in the microservice feature matrix. The rank minimization problem [24] can be formalized as

$$\underset{W}{min}\mathrm{rank}\left(W\right),\mathrm{s}.\mathrm{t}.Y\approx WX,$$

(10)

However, rank minimization is a non-convex problem [34], making its computational complexity prohibitively high for large-scale systems.

To overcome this limitation, TDDRMF employs nuclear norm minimization [33] as a convex relaxation of rank minimization to achieve efficient optimization. The nuclear norm of W is defined as

$${\parallel W\parallel }_{*}=\sum _{i=1}^{min(n,r)}{\sigma }_i,$$

(11)

where ${\sigma }_i$ are the singular values of W. By minimizing the sum of singular values, the nuclear norm enforces low-rank constraints while simultaneously driving the model to capture the similarity structure within the microservice feature matrix, thereby enabling more accurate capturing of the primary dependencies between microservices.

Nuclear norm regularization is seamlessly integrated into the overall optimization objective of TDDRMF and co-optimized with temporal dynamics modeling. Therefore, based on the objective function from [23], we redefine the meaning of the microservice matrix W and replace the original Frobenius norm with nuclear norm regularization. The complete objective function is expressed as

$$\mathcal{L}={\displaystyle \frac{1}{2}}\underset{W,X,A,B}{min}{\parallel Y-WX\parallel }_F^2+{\lambda }_1{R}_{\mathrm{AR}}\left(X\right|A,B)+{\lambda }_2{\parallel W\parallel }_{*},$$

(12)

The integration of temporal regularization and nuclear norm regularization in TDDRMF demonstrates significant synergy in modeling the temporal dynamics of workloads and modeling microservice dependencies. Temporal regularization effectively extracts short-term trends and periodic patterns, while nuclear norm regularization enforces low-rank constraints on the microservice matrix W, enabling the compact and efficient representation of microservice interactions. This joint optimization not only enhances the model’s generalization ability by reducing the impact of noise and redundant dependencies but also improves computational efficiency, making the framework well suited for large-scale microservice systems.

However, in long-term prediction tasks, the dynamic nature of workloads and the evolving interdependencies among microservices can pose additional challenges. If the parameters remain fixed, the model may struggle to adapt to significant changes over time. To address this, TDDRMF incorporates an error detection mechanism that dynamically triggers parameter updates. The following section elaborates on the design and implementation of this mechanism.

3.5. Dynamic Detection and Updating

The dynamic detection and update mechanism ensures the TDDRMF adapts to evolving workload patterns by monitoring prediction accuracy in real time. When the prediction error at a specific time step exceeds a predefined threshold, the mechanism triggers a parameter update, avoiding frequent retraining while maintaining efficiency and robustness.

At each prediction step t, the prediction error is computed as

$$E_t={\parallel Y-{\widehat{Y}}_t\parallel }_F^2,$$

(13)

where $Y_t$ represents the observed workload at time t, and ${\widehat{Y}}_t$ is the predicted workload. If $E_t>ϵ$, where $ϵ$ is a predefined error threshold, the mechanism identifies a significant drift in workload patterns and triggers an update of the model parameters.

After triggering the update, TDDRMF first extracts only the most recent d observation lengths and performs retraining on this local window rather than the entire history to obtain the optimized microservice matrix W, temporal feature matrix X, and error detection parameters A and B to minimize the objective function, thereby accelerating convergence and ensuring smooth parameter transition, significantly reducing the computational overhead.

The dynamic detection and update mechanism ensures the real-time adaptation to workload changes by focusing updates on significant prediction deviations, thereby maintaining high prediction accuracy without unnecessary computational overhead. Using the low-rank structure of W, it achieves scalability and robustness, even in large-scale microservice systems. This mechanism seamlessly integrates with temporal dynamics modeling and low-rank dependency capturing, providing a cohesive foundation for the framework’s overall optimization process.

To provide a clear overview of the TDDRMF framework’s optimization process, Algorithm 1 summarizes the core steps for parameter optimization and multi-step prediction.

Algorithm 1 TDDRMF framework prediction and dynamic update process.

Require: Historical workload matrix Y, initial parameters $W_0,X_0,A_0,B_0$; Regularization coefficients ${\lambda }_1,{\lambda }_2$, error threshold $ϵ$, prediction horizon h, initial error$e_t$, trend and period parameters $M,N,m$ and maximum iterations MaxIter. Ensure: Optimized parameters $W,X,A,B$; predictions ${\widehat{Y}}_{T+1:T+h}$.  Initialize $W\leftarrow W_0,X\leftarrow X_0,A\leftarrow A_0,B\leftarrow B_0$;  Initialize ${\widehat{Y}}_{T+1:T+h}$ as an empty matrix.  for $t=T+1$ to $T+h$ do        if $e_t>ϵ$ then    Step 1: Trigger parameter optimization:           for $i=1$ to MaxIter do               Define the optimization objective: $$\mathcal{L}={\displaystyle \frac{1}{2}}\underset{W,X,A,B}{min}{\parallel Y-WX\parallel }_F^2+{\lambda }_1{R}_{\mathrm{AR}}\left(X\right|A,B)+{\lambda }_2{\parallel W\parallel }_{*}.$$               Compute gradients: $${\nabla }_W,{\nabla }_X,{\nabla }_A,{\nabla }_B\leftarrow {\displaystyle \frac{\partial \mathcal{L}}{\partial W}},{\displaystyle \frac{\partial \mathcal{L}}{\partial X}},{\displaystyle \frac{\partial \mathcal{L}}{\partial A}},{\displaystyle \frac{\partial \mathcal{L}}{\partial B}}.$$               Update parameters using Adam optimizer: $$W,X,A,B\leftarrow \mathrm{Adam}\mathrm{updates}.$$           end for       end if       Step 2: Update temporal feature vector $X_t$: $$X_T=\sum _{h=1}^M{B}_h\otimes X_{T-h}+\sum _{l=1}^N{A}_l\otimes X_{T-lm}.$$       Step 3: Predict workload for the current time step: $${\widehat{Y}}_t=W{X}_T.$$       Store the predicted value ${\widehat{Y}}_t$ in ${\widehat{Y}}_{T+1:T+h}$.       Step 4: Compute prediction error: $$E_t={\parallel Y-{\widehat{Y}}_t\parallel }_F^2.$$ end for return Optimized parameters $W,X,A,B$ and predictions ${\widehat{Y}}_{T+1:T+h}$.

The TDDRMF framework effectively addresses key challenges in dynamic microservice workload prediction through collaborative modular design. To tackle the complexity of temporal dynamics, the framework employs matrix factorization combined with temporal regularization, enabling more accurate modeling across multiple time scales by disentangling short-term trends and periodic patterns. For the dynamic evolution of microservice dependencies, the framework leverages low-rank constraints to capture critical interactions while integrating a dynamic detection mechanism to adapt parameters in real time, ensuring rapid responsiveness to environmental changes. Lastly, the low-rank property of matrix factorization allows TDDRMF to perform efficiently even in data-scarce scenarios, while the dynamic detection mechanism further enhances the framework’s robustness and practicality during cold-start phases. These features enable TDDRMF to maintain efficiency, adaptability, and stability in complex and dynamic microservice environments.

3.6. Complexity Analysis

The proposed TDDRMF framework achieves workload prediction by combining matrix factorization, temporal regularization, and nuclear norm regularization. Below, we analyze the computational complexity of each component and compare TDDRMF with related baseline models.

Matrix factorization updates the microservice matrix W and temporal feature matrix X iteratively, with a per-iteration complexity of $O(n·T·r)$. Temporal regularization incorporates autoregressive and periodic constraints to enhance temporal dynamics modeling, with a complexity of $O((M+N)(T-d)·r^2·T)$. Additionally, nuclear norm regularization involves the computation of the singular value decomposition (SVD) of W, which has a complexity of $O(n·r^2)$. Combining these components, the overall complexity of TDDRMF per iteration is

$$O\left(k(n·T·r+(M+N)(T-d)·r^2·T+n·r^2)\right).$$

Under the assumptions $r\ll n,T$ and $M,N,d$ are constants, the complexity simplifies to

$$O\left(k((T-d)·r^2·T)\right).$$

To evaluate TDDRMF’s computational efficiency, we compare its complexity with statistical models (e.g., ARIMA), ensemble models (e.g., Random Forest), neural network models (e.g., LSTM), and matrix factorization models (e.g., TAMF). The updated complexity comparison is shown in

Table 1. Training complexity comparison.

Model	Training Complexity
TDDRMF	$O\left(k((T-d)·r^2·T)\right)$
TAMF	$O\left(k((T-d)·r^2·T)\right)$
ARIMA	$O(n·p^2·T)$
Random Forest	$O(L·n·(T-p)·p·log(n·(T-p)\left)\right)$
LSTM	$O(k·n·(T-p)·(p·r_h+r_h^2))$

.

The computational complexity of TDDRMF and TAMF mainly arises from the low-rank constraints in matrix factorization and temporal regularization. Its global optimization approach eliminates redundant calculations caused by sliding windows, achieving lower computational costs and higher efficiency for multi-sequence modeling. In contrast, ARIMA’s complexity is determined by the independent fitting of each sequence and the lag order p, with recursive predictions significantly increasing the training time. However, ARIMA performs well for single-sequence modeling. The complexity of Random Forest is influenced by the sliding window size p, the number of windows $T-p$, and the number of trees L, making it suitable for short-term pattern extraction but computationally expensive for long sequences. The complexity of LSTM is dominated by the hidden state dimension $r_h$ and the number of training iterations k, which allows it to capture long-term dependencies effectively, but its high computational cost limits its application in large-scale data scenarios. Overall, TDDRMF demonstrates the best efficiency and complexity control for multi-sequence modeling, while LSTM excels in capturing nonlinear dynamics, and Random Forest and ARIMA are more suitable for short sequences or low-dimensional tasks.

4. Performance Evaluation

This section evaluates the TDDRMF model in microservice workload prediction tasks. The experiments aim to answer the following research questions:

RQ1: How does TDDRMF compare to state-of-the-art methods in terms of prediction accuracy?

RQ2: How effective are the temporal and nuclear norm regularization components in improving model performance?

RQ3: Can TDDRMF achieve efficient and robust predictions in challenging scenarios, such as cold-start or dynamic dependency environments?

4.1. Experiment Setup

To validate the performance of the proposed TDDRMF framework in workload prediction tasks, we conduct experiments on a dataset tracked by the Alibaba cluster. Load data from some consecutive time periods are extracted for collation and preprocessing to ensure consistency and reliability. In the first two experiments, the dataset is divided into 80% for training and the rest for testing. Subsequent experiments are conducted in a special way to simulate a cold start environment.

We compare TDDRMF with a variety of methods, including ARIMA [10], RF [35], LSTM [36], TRMF [37], and TAMF [23]. The evaluation focuses on three aspects: prediction accuracy, training efficiency, and robustness. Prediction accuracy is measured using Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and the Coefficient of Determination ($R^2$). Training efficiency is evaluated based on training time, while robustness is assessed under cold-start scenarios.

The specific computer configuration is as follows: processor Intel(R) Core(TM) i7-10510U CPU at 1.80 GHz (2.30 GHz Turbo); RAM 16.0 GB; storage 512 GB SSD; Windows 10 64-bit operating system. All models are implemented using the PyTorch framework. To ensure reliability, each experiment is repeated five times, and the average results are reported to minimize the impact of random variations. The experiments in this article are conducted on a locally available computer.

Since we use RMSE as our primary prediction-error metric in all experiments, the dynamic update mechanism directly compares the per-timestep RMSE against the threshold $ϵ$ to decide whether to trigger local retraining. This maintains consistency with our evaluation and reduces hyperparameter complexity. All key parameters (regularization coefficients ${\lambda }_1,{\lambda }_2$ and error-detection threshold $ϵ$) are selected via a two-stage grid search on a 5% validation subset as follows. Initially, we search over broad ranges (${\lambda }_1,{\lambda }_2\in [{10}^{-4},{10}^2],ϵ\in [0.01,10]$) with coarse intervals to identify promising regions. Then, we perform fine-grained tuning within narrowed ranges around the best-performing values to select the parameters that minimize RMSE. Final values are as follows: ${\lambda }_1=3\ast {10}^{-1}$, ${\lambda }_2=1\ast {10}^{-1}$, and $ϵ=0.3$. All reported results use these settings, except RQ2 which uses $ϵ=0.5$.

4.2. Prediction Accuracy Comparison (RQ1)

To evaluate the effectiveness of the proposed TDDRMF framework, we conduct multi-step prediction experiments for both $T+1$ (1-step prediction) and $T+10$ (10-step prediction) scenarios. The performance of TDDRMF is compared against several baseline models to assess prediction accuracy and computational efficiency.

The experimental results for 1-step and 10-step predictions are summarized in

Table 2. Performance comparison across models (1-step).

Metric	TDDRMF	TAMF	TRMF	ARIMA	RF	LSTM
RMSE	0.3353	0.3368	0.4391	0.4101	0.2773	0.2319
$R^2$	0.9808	0.9808	0.9730	−6.3680	0.9989	0.9992
Train Time (s)	2.33	1.12	1.11	580.96	9890.77	44,451.21
Pred Time (s)	0.001	0.002	0.001	3.14	5.07	0.29

and

Table 3. Performance comparison across models (10-step).

Metric	TDDRMF	TAMF	TRMF	ARIMA	RF	LSTM
RMSE	0.3784	0.4645	0.5782	0.4311	0.3548	0.3192
$R^2$	0.9771	0.9715	0.9612	−3.2 × 1034	0.9983	0.9986
Train Time (s)	2.24	12.95	12.31	675.29	9890.77	44,451.21
Pred Time (s)	0.009	0.011	0.011	3.90	14.62	1.61

, respectively.

The Q1 experiment evaluates various models in both single-step and multi-step prediction tasks, demonstrating that matrix factorization-based methods strike a good balance between computational efficiency and prediction accuracy.

In single-step prediction tasks, although LSTM achieves the best precision with the lowest RMSE and highest $R^2$, its training and prediction times are significantly higher than those of other models, highlighting its high computational cost. In contrast, TDDRMF maintains a lower computational time while achieving superior prediction accuracy compared to other matrix factorization methods, such as TAMF and TRMF. This can be attributed to the synergistic optimization of temporal regularization and nuclear norm constraints.

In multi-step prediction tasks, the advantages of TDDRMF become even more apparent. It achieves the lowest training and prediction times among all models while delivering accuracy second only to LSTM, and it significantly outperforms traditional statistical models such as ARIMA and other matrix factorization methods. Notably, ARIMA exhibits anomalies in $R^2$ values during multi-step prediction, indicating its limited applicability in dynamic workload scenarios.

Overall, TDDRMF effectively balances computational efficiency and prediction accuracy through the joint optimization of temporal regularization and nuclear norm regularization. It demonstrates robust performance in both single-step and multi-step prediction tasks, providing an efficient and reliable solution for dynamic workload prediction.

4.3. Ablation Study (RQ2)

This experiment aims to validate the independent contributions of the core components in the proposed TDDRMF framework, including trend regularization, periodic regularization, nuclear norm constraints, and the dynamic error detection mechanism. An incremental modeling approach is adopted, where components are progressively added to analyze their impact on multi-step prediction performance. The experiment includes the following four model configurations (with abbreviations):

1. Matrix Factorization + Trend Regularization (MF + T): Captures short-term changes and long-term trends.

2. Matrix Factorization + Trend Regularization + Periodic Regularization (MF + T + P): Adds periodic modeling on top of trend modeling.

3. Matrix Factorization + Trend Regularization + Periodic Regularization + Nuclear Norm Constraints (MF + T + P + N): Introduces low-rank constraints to model inter-service dependencies.

4. Full model (TDDRMF): Incorporates all components to evaluate the combined effect of dynamic updates and regularizations.

The results are summarized in

Table 4. Ablation study results (500-step).

Metric	MF + T	MF + T + P	MF + T + P + N	TDDRMF
RMSE	0.9312	0.7137	0.7115	0.6870
MAE	0.8237	0.5524	0.5532	0.5282
$R^2$	0.9529	0.9672	0.9670	0.9703
Train Time (s)	8030.86	6267.20	6587.21	831.46
Pred Time (s)	0.91	0.70	0.59	0.42

, demonstrating that prediction accuracy improves significantly with the gradual integration of these components, while computational efficiency is also enhanced. The baseline matrix factorization model captures only the low-dimensional structure of workloads, resulting in lower accuracy and longer training time. By incorporating temporal regularization (MF + T + P), the model significantly improves its ability to capture short-term trends and periodic patterns, reducing prediction error. The nuclear norm constraints (MF + T + P + N) optimize the low-rank representation of microservice dependencies, enhancing the accuracy of multi-step prediction tasks. However, due to the necessity of retraining the model for each prediction and the inability to fully leverage historical errors for timely adjustments, its performance does not reach the optimal level. In contrast, the complete model incorporating the dynamic error detection and update mechanism (TDDRMF) achieves real-time error correction, maintaining the continuity and stability of predictions, significantly reducing both training and prediction times, while simultaneously improving accuracy.

In summary, the Q2 experimental results validate the rational design of the TDDRMF framework. The integration of temporal regularization, nuclear norm constraints, and the dynamic error detection mechanism significantly enhances prediction accuracy and computational efficiency. The synergistic effect of these components enables TDDRMF to excel in dynamic and complex environments, offering an efficient and accurate solution for workload prediction tasks.

4.4. Cold-Start Performance Comparison (RQ3)

To evaluate the performance of the proposed TDDRMF framework in cold-start environments, this experiment focuses on single-step prediction under a limited training data scenario. The proportion of training data is set to 5%, simulating a cold start condition. The results are summarized in

Table 5. Cold-start performance at 5% training data (10-step).

Metric	TDDRMF	TAMF	TRMF	ARIMA	RF	LSTM
RMSE	0.3042	0.4379	0.3343	0.2016	0.3106	0.4908
$R^2$	0.9740	0.9711	0.9733	−4.5 × 1020	0.9987	0.9767
Train Time (s)	2.13	19.39	18.98	251.36	121.61	2268.53
Pred Time (s)	0.008	0.009	0.009	3.59	0.682	1.952

.

In the cold-start scenario for multi-step prediction, ARIMA achieves the best RMSE performance; however, its results exhibit significant instability. In particular, the model struggles to adapt to sparse data or evolving trends in certain scenarios, resulting in unreliable $R^2$ values. This highlights that while ARIMA excels in short-term time series modeling, its robustness and applicability are limited in dynamic or complex environments.

TDDRMF achieves the second-best prediction accuracy and demonstrates superior stability and adaptability compared to other matrix factorization-based methods. This performance can be attributed to the synergistic effects of nuclear norm regularization and temporal regularization, which effectively capture key microservice dependencies and multi-step temporal dynamics. Additionally, TDDRMF exhibits the highest computational efficiency, with both the shortest training and shortest prediction times among all models, making it highly suitable for resource-constrained or real-time scenarios.

4.5. Discussion

The exceptional performance of TDDRMF, achieved with only 5% training data, highlights its suitability for dynamic microservice environments. Our experiments demonstrate that TDDRMF effectively captures both short-term and long-horizon dynamics while maintaining low computational overhead. In single-step forecasting, the incorporation of temporal regularization enables the model to learn multi-scale patterns—short-run trends and periodic behaviors—resulting in an RMSE of 0.3353, moderately higher than LSTM, yet with training and inference times reduced by orders of magnitude. For 10-step horizons, the nuclear-norm constraint further refines the representation of microservice dependencies, driving an 18.5% RMSE improvement over TAMF while reducing the training time from 12.95 s to 2.24 s. These results highlight how the synergy of low-rank approximation and global convex optimization can rival deep architectures in accuracy while vastly improving efficiency.

Under cold-start conditions, TDDRMF maintains robust performance, remarkably outperforming ARIMA and TAMF in stability and precision. The ability of low-rank regularization to suppress noise in sparse samples, coupled with the dynamic error-detection mechanism that selectively triggers updates, enables dependancy predictions even when historical data are scarce.

Finally, the error threshold $ϵ$ in our dynamic update scheme governs a critical trade-off between accuracy and efficiency. A larger $ϵ$ reduces update frequency—thereby lowering overall training cost—but risks missing gradual workload shifts and elevating RMSE, whereas a smaller $ϵ$ offers marginal RMSE gains at the expense of frequent retraining and high computational burden. We thus tune $ϵ$ via grid search for the value at which RMSE improvements plateau while the update overhead remains moderate. This sensitivity analysis confirms that $ϵ$ is a key lever for practitioners to balance real-time responsiveness against resource constraints. However, increasing the data volume may decrease the model’s prediction accuracy and stability. To address this challenge, our model can be enhanced by incremental learning, dynamic data adjustment, and the integration with sliding window methods, for better handling long-term prediction tasks.

5. Conclusions

Accurate workload prediction is essential for optimizing resource allocation and ensuring system stability in dynamic microservice environments. However, existing methods face significant challenges in capturing both multi-scale temporal dynamics of workloads and complex dependencies among microservices. In particular, they typically rely on static assumptions for microservice dependency, which limits their ability to comprehensively represent the dynamic collaborative patterns among microservices. To address this challenge, we propose a novel framework Temporality-Dependency Dual-Regularized Matrix Factorization (TDDRMF) which combines matrix factorization with regularization on both workload temporality and microservice dependencies as an illustration of effective integration of machine learning and data analysis. It employs temporal regularization to effectively capture short-term fluctuations, long-term trends, and periodic patterns in workload data, and nuclear norm regularization to extract critical microservice dependencies by enforcing low-rank constraints on the microservice relationship matrix. TDDRMF also incorporates a dynamic error detection and update mechanism to reflect workload variation in dynamic environments, enabling rapid model adaptation when performance degradation occurs, thereby improving its robustness and efficiency.

Experimental results demonstrate that TDDRMF outperforms traditional matrix factorization methods in both single-step and multi-step prediction tasks, achieving a superior balance between prediction accuracy and computational efficiency. Furthermore, TDDRMF exhibits exceptional adaptability in cold-start and highly dynamic scenarios. To enhance its practical impact, future work will deploy TDDRMF in production environments, integrating it with orchestration platforms such as Kubernetes and Prometheus with optimal resource allocation at reduced costs and resource consumption.

However, the framework primarily relies on low-rank constraints for the implicit modeling of microservice relationships, which may limit its effectiveness in handling more complex dynamic dependency scenarios. Future research will explore graph-based explicit modeling methods to more accurately capture direct collaboration patterns among microservices, and validate robustness by simulating service failures and drastic workload changes in real-world microservice cluster systems. This direction has the potential to address the limitations of current methods and provide a more comprehensive theoretical foundation and practical support for performing complex workload prediction tasks.