Abstract
Computed tomography scans are among the most used medical imaging modalities. With increased popularity and usage, the need for maintenance also increases. In this work, the problem is tackled using machine learning methods to create a predictive maintenance system for the classification of faulty X-ray tubes. Data for 137 different CT machines were collected, with 128 deemed to fulfil the quality criteria of the study. Of these, 66 have had X-ray tubes subsequently replaced. Afterwards, auto-regressive model coefficients and wavelet coefficients, as standard features in the area, are extracted. For classification, a set of different classical machine learning approaches is used alongside two different architectures of neural networks—1D VGG-style CNN and LSTM RNN. In total, seven different machine learning models are investigated. The best-performing model proved to be an LSTM trained on trimmed and normalised input data, with an accuracy of 87% and a recall of 100% for the faulty class. The developed model has the potential to maximise the uptime of CT machines and help mitigate the adverse effects of machine breakdowns.
1. Introduction
Medical CT devices play a crucial role in modern healthcare by providing accurate and detailed images for diagnostic purposes. According to the UNSCEAR report [1], an estimated 403 million CT exams/procedures are performed in the world annually. However, like all medical diagnostic machines, they can suffer from failures affecting their performance and reliability. These failures cause numerous problems for both medical providers and patients. For patients, they usually increase the time to diagnose and cause inconvenience related to longer waiting times or rescheduling. For medical providers, they mostly cause financial losses. In some cases, the malfunctions can lead to decreased diagnostic accuracy, and in the most extreme and rare cases, even to injuries or deaths. Traditional approaches to diagnosing and predicting failures in CT devices often rely on manual inspection combined with expert knowledge.
Maintenance can be generally grouped into three groups [2,3]:
- Corrective maintenance—Existing errors are corrected when they occur;
- Preventive maintenance—Maintenance is performed periodically, on predetermined intervals;
- Predictive maintenance (PdM)—Predicting a malfunction before it happens.
PdM is the newest of the approaches, and it is deeply tied to data [4]. Compared to preventive maintenance, it does not rely on predetermined service intervals but tries to intelligently determine when the maintenance is needed/will be needed. This is possible thanks to the ever-increasing utilisation of sensors and the increasing amount of big data. There are two essential parts of PdM [4]—anomaly detection and remaining useful life (RUL) prediction. In this work, we will focus on the former, which is concerned with detecting undesired behaviour in the machines. As it utilises detection and prediction and is tied to data, PdM is strongly tied to machine learning. In the last several years, machine learning has become an increasingly effective way to automate the fault detection process in different domains [5,6], including healthcare [3], as it can uncover hidden patterns and relationships in complex data. From the perspective of the review [4], our work would fall under the umbrella of “behavioural/collective anomalies”. In these anomalies, a data point and a data pattern can differ from the normal/expected state. In our case, this would be a behaviour and data pattern of the sensors of a CT machine.
This work investigates the application of ML algorithms in a practical problem—PdM of medical CT devices. Our PdM system is based on the classification of the current state of the X-ray tube, which is based on the sensor data from sensors present in a CT machine. The problem is rather specific and under-investigated; our review identified only one directly related work within a still rather sparse field—PdM in healthcare devices, where we identified 10 works. We leverage historical data to learn patterns and relationships that can help identify potential failures and provide early warnings, enabling proactive maintenance and minimising equipment downtime. To do so, we utilise both hand-crafted and learned/extracted features in combination with several machine learning models.
2. Related Work
The utilisation of the PM in the medical equipment has been considerably slower than in other areas. A review by Manchadi, Ben-Bouazza and Jioudi [3] from 2023 was only able to identify nine different “PdM applications on ME (medical equipment)”. Of those, only two were related to the same class of devices—an Infant incubator and seven others used different classes of medical equipment. The authors also try to explore and name possible reasons, such as regulatory (missing guidelines), complexity and fragmentation of devices, variety of device manufacturers, data privacy/security, and costs. They also try to propose possible solutions to overcome these challenges. Another reason for such a small number of studies could be that, to the best of our knowledge, no medical equipment-related PM dataset is currently released under a permissive licence. This fact leads to a situation where studies in this area are trying to create a PdM system for different machine types, with different input data and labelling, and through different means/with different models being utilised.
When selecting the studies from the review by the type of used medical equipment, the most relevant study mentioned in the review would be that of Wahed, Sharawi, and Badawi [7]. They analysed past failures in MRI (six years) and CT (3 years) and utilised ARMA and LPC methods to model availability, reliability, and performance efficiency. From the perspective of the used data, we identified three works in which a higher number of machine-generated features related to different aspects of the devices were considered.
Packianather et al. [8] employed the k-NN algorithm to predict the failures of clinical chemistry analysers. Starting from 27 analyser-generated features, they cleaned the data and applied PCA to obtain 9 features. Their best-performing model was a 10-NN model, which was able to obtain an accuracy of 94.98%.
Two other works related to classifying devices as fit or unfit for duty after the yearly “safety and performance inspection”. The work of Kovacevic et al. [9] classified infant incubators into two classes—requiring maintenance and safe for usage. They gathered 140 samples with 30 features and applied 5 different classifiers—NB, DT, RF, k-NN, and SVM. The best-performing algorithm was DT, with an accuracy of 98.5%.
The work of Badnjevic et al. [10] concerned classifying defibrillators as fit to be used or faulty. They utilised a dataset of 1221 samples with 38 samples each. Firstly, they tried to utilise four different feature selection techniques by using all features and extraction via the InfoGain algorithm, extraction via the genetic algorithm, and extraction via the wrapper algorithm. Second, they combined these feature selection approaches with DT, RF, k-NN, SVM, and NB algorithms. Their best performance was achieved by genetic algorithm feature selection combined with an RF classifier (100%). When RF was combined with other feature extraction algorithms, it was able to achieve an accuracy of 99.6%.
As the proposed system should be used for the PdM of an X-ray tube, we have tried to find and analyse further works that concern CT/X-ray machines or the X-ray tube itself.
González-Domínguez et al. [11] used Markov chains to model one of the five health states of the CT machine—ranging from very good to unacceptable, to estimate the need for maintenance. They used the failure history of 8 CTs from different Spanish hospitals over 4 years to extract states for different machines. In the end, they proved that Markov chains could model the CT machine’s lifetime accurately.
Ortegón and Guerrero [12] applied a continuous-time Markov chain to model 3 different states of the CT—“perfect”, “deteriorated”, and “damaged” and optimise maintenance policies to maximise the profit/maintenance ratio. This work was more about when and how to assign technicians/repair machines and optimise the repair cycle than how to detect when to repair.
Shazril et al. used external sensors installed on a CT to detect abnormalities in sensory data that could signal malfunction in two studies [13,14]. Both studies used five external sensors measuring current, radiation, humidity, temperature, and vibration (acceleration in the x and y axes) to predict the chance of a CT breakdown as “low” or “high”. Both studies used synthetically generated data because of the lack of abnormal readings, where they expanded the data distribution. Both studies used an ANN with an input layer of 6 neurons (mentioned values, as single points) and two hidden layers of 6 neurons, each with RELU activations. The output layer had a single neuron with a sigmoid activation function. They achieved an average accuracy of 95.91 % and 97.58 %, respectively.
Zhou et al. [15] used their custom SAX-HCBOP feature representation, which merges the Histogram-based Information Gain Binning (HIGB) and Coefficient improved Bag of Pattern (CoBOP) alongside the LightGBDT model to predict the X-ray tube arcing. After an analysis, the authors asserted that X-ray tube arcing might be a good indicator of CT malfunction, as it may lead to damage of some of the components or deterioration of CT image quality. They used a private dataset provided by Sichuan University that contains a time series with five features (including arcing used as a label). They were able to achieve an accuracy of 90.4% and a recall of 74.7%.
Zhong et al. [16] created a system to predict both future cathode filament currents of an X-ray tube, based on the historical values, and filament failure. In order to be able to demask this degradation, they needed to maintain consistent settings of the CT. Afterwards, they extracted historical data about filament current and used three modules with different sizes of 1D convolutions (1, 3, 5) followed by a scale attention module and MLP to produce their proposed MSAP model (“multiscale attention prediction model”). Afterwards, on the basis of the measured currents and their changes, they were also able to formulate a framework for the prediction of filament failure.
To sum up the state of the art, not much work has been conducted in the area of PdM of medical devices. Even then, most of the works, pretty much all outside of [15,16], either work with singular data points (such as [9,10,13,14]) or are concerned more with probabilities of transitioning to states based on the past observed behaviour than based on current data itself [11,12]. Both [15,16] try to detect a partial problem that is a possible sign of X-ray tube failure. Our work concerns itself with detection of any failure from historical data monitoring most of the available CT variables. To the best of our knowledge, this is one of the first works to address the problem of PdM, based on the long-term data, in the medical equipment field.
3. Diagnosing Failures in Medical Equipment
Failures in medical devices [17,18] can arise from various factors such as defects, manufacturing issues, improper design, wear, misuse, or environmental effects [19]. Recognising these causes is critical for developing effective failure-prevention strategies. In this section, we introduce the structure of the CT device, with a focus on the X-ray tube, alongside its risk factors.
3.1. Structure of the CT Device
CT scanners consist of three main components: the gantry, X-ray tube, and detector arrays. The gantry, a large rotating ring, houses the X-ray tube and detectors, rotating around the patient to capture multiple images. The X-ray tube emits X-rays that pass through the patient’s body. The detector array on the opposite side of the gantry captures these X-rays, which are converted into electrical signals that the system processes to reconstruct 3D images of the body’s internal structures. The operator controls key operational parameters of the CT, such as tube voltage, current, and rotation speed, by selecting specific scan protocols, ensuring detailed images suited to diagnostic needs. Continuous monitoring of critical performance metrics is essential to ensure CT systems operate efficiently and safely. These include the following:
- Image Quality Parameters: Resolution and noise levels must be consistently monitored to ensure diagnostic accuracy.
- Dose Parameters: Monitoring radiation exposure to patients is crucial for safety.
- Operational Parameters: Metrics like X-ray tube voltage and current, gantry rotation time, and table movement are critical for system longevity and performance.
Sensors embedded within the CT system monitor these parameters in real time. For example, voltage and current sensors in the high-voltage generator track the X-ray tube’s input, preventing image quality issues and reducing wear on the equipment. Temperature sensors monitor both the cooling system and the X-ray tube to avoid overheating, which can cause irreversible damage.
Real-time monitoring [16] can prevent failures, reduce downtime, and ensure accurate diagnostics by continuously tracking these factors.
3.2. X-Ray Tube Failures
X-ray tubes have always been somewhat problematic parts [20] of the medical products for X-ray-based imaging techniques. In over 130 years of their continual evolution, there have been many milestones improving their performance, reliability or both. For a more detailed breakdown of the history and development of X-ray tubes, see [21].
Ref. [21] lists possible failures of the X-ray tube as related to either ageing or manufacturing defects. For ageing, they list eight different reasons, “cathode filament burnout”, “target micro-cracking”, or “X-ray tube arcing”, among others. Some of them are related to tungsten evaporation caused by different effects (listed as “cathode filament burnout”, “target micro-cracking”, “glass crazing or etching”), others to reduction of vacuum levels (listed as “X-ray tube arcing”, “slow leaks in X-ray tube”, “inactivity”), failure of ball bearings (listed as “ball bearings of rotating anode”) and others fall within the category of “accidental damage”. The work showcases that there are diverse reasons for X-ray tube failure or degradation that need to be taken into consideration when creating a PdM system for the X-ray tube.
There are two possible ways to address the creation of the X-ray tube PdM system.
The first approach consists of creating a classification system for classifying possible X-ray tube failures into several classes. The approach would require pinpointing and monitoring variables related to those specific failures. Causes of both “cathode filament burnout” and “target micro-cracking” are visible only on a microscopic level; “slow leaks in X-ray tube” would, on the other hand, require non-stop granular monitoring of the gas environment within the X-ray tube. While the continuous adoption of the IoT in the MedTech industry could lead to the development of required monitoring systems, current X-ray tubes may lack such sensors with granular data. On the other hand, some metrics would already be available, for example, the “X-ray tube arcing”, as it is part of our dataset. However, this approach has another major obstacle. To create such a specific system, one would need to ask the X-ray tube manufacturers to conduct a post-failure inspection and examination of every X-ray tube to pinpoint the specific failure category and obtain the necessary labels for AI systems. The primary benefit of such a system is that such an approach could allow for easy refurbishing of some of the X-ray tubes, as only specific problematic parts could be repaired.
The second approach is based on a binary classification of the current X-ray tube state into a working state and a faulty state. We will not further investigate specific reasons for this failure, as, anyway, once deemed faulty, the X-ray tube is replaced with a new one. This approach could lead to some minor label noise, for example, when the X-ray tube is replaced due to external mechanical damage. In such a case, the parameters of the X-ray tube could correspond to the working class while still being replaced. Another possible case could be if maintenance were performed preemptively. Such a case would be when a technician was already present for other reasons, but an X-ray tube was also close to the end of its useful life. We do not expect such occurrences to be frequent. Also, these preemptive changes should not create a significant noise as the lifespan of X-ray tubes is usually in years, while such preemptive changes would be in days or a few weeks early. In such a time, X-ray tubes should be classified as faulty anyway. This approach was selected based on the available data explained below.
4. Data
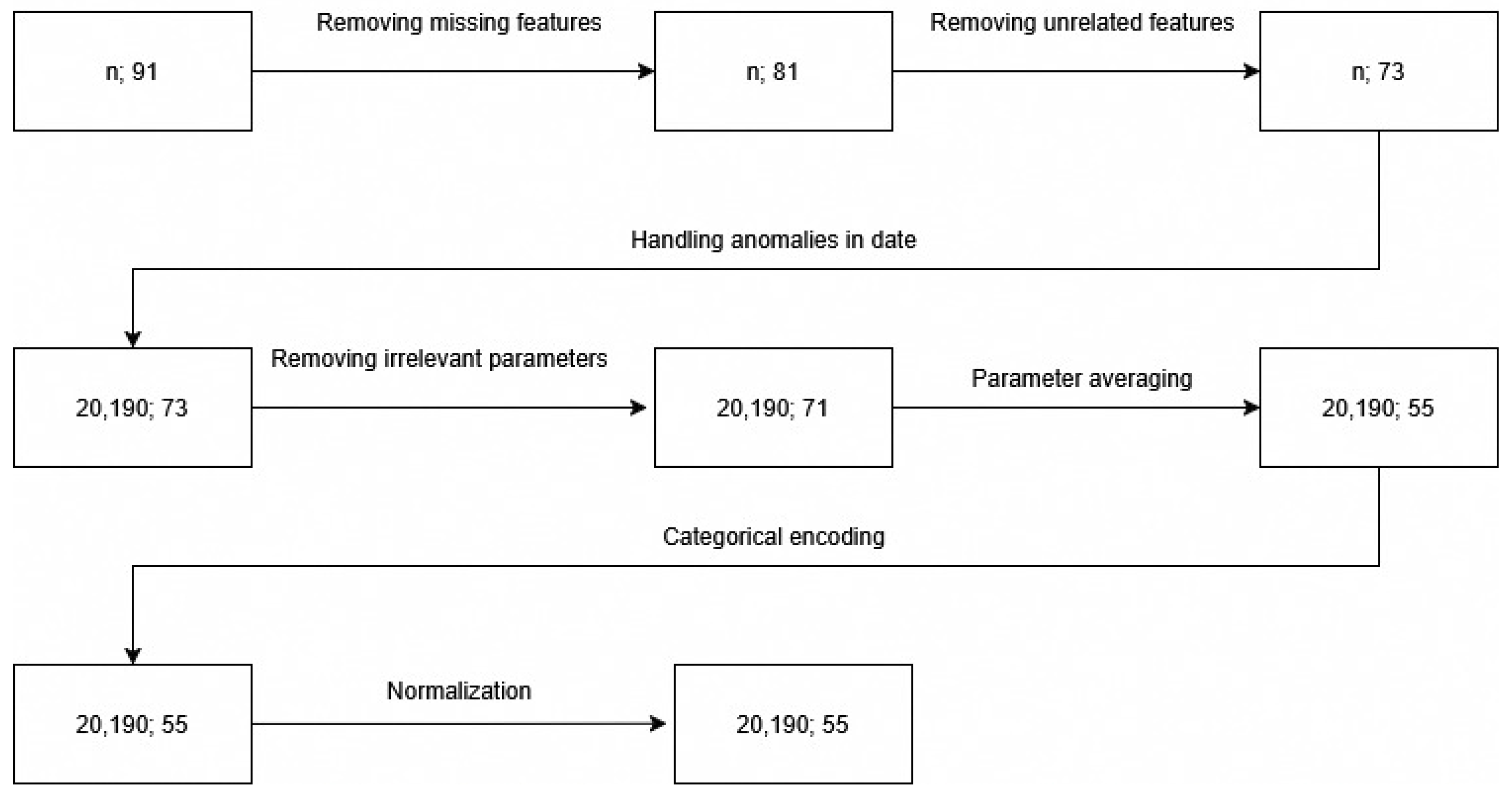
This section explains the obtained dataset with 137 CT time series. Later on, we explain how noise and inconsistencies in the data were addressed, how data were normalised and what kind of features are extracted before the data are passed to the classifier. This process, up to but not including feature extraction, is visible in Figure 1.
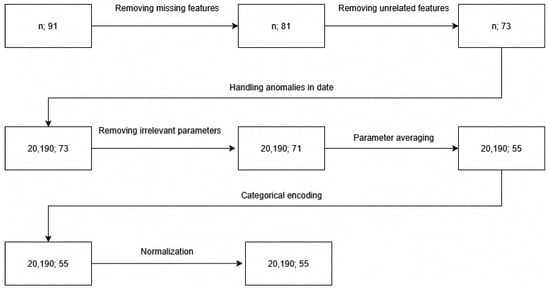
Figure 1.
Data processing steps and shape of the CT data point.
4.1. Data Description
The obtained dataset featured 137 tables, each representing one CT device, with an average length of 320,000 rows. Of these, 66 corresponded to CTs, where X-ray tubes were subsequently replaced (the logs ended with the date of replacement), and 71 of those were still functional at the time of the data collection. However, the data do not present the precise reason or moment of the breakdown. Hence, it is only possible to say whether such behaviour led to the breakdown. Metrics were collected during each scan performed (intervals of a few seconds), giving an extensive overview of the machine’s behaviour during scanning. The measurements are not isochronous but rather depend on the scanning type, length, etc.
The original collected dataset contained 91 features. Ten parameters with only NULL values, such as “tank expansion” and “arcs:”, were removed from the dataset due to the lack of available measurements for interpolation. Parameters without NULL values were retained without further interpolation.
After removing features deemed useless (such as the machine’s serial number, the tube’s serial number, scan ID, region, etc.), we have tables that include 73 features. Most of the retained features are related to the X-ray tube. Some of them are only indirectly related to the X-ray tube:
- Rotation time—Deviations in the rotation time could indicate a mechanical problem in the gantry rotation system, such as worn bearings or motor malfunction. Such problems might result in excessive vibrations during scanning, which could lead to lower quality of the images or even damage to the X-ray tube and other components.
- Scan duration—Deviation from the expected scanning time may indicate a problem with the patient table or a mechanical issue with the gantry, which can cause reduced image quality and may increase radiation dose. Prolonged scanning times may lead to overheating of components, mechanical wear, and increased radiation exposure, potentially resulting in decreased performance and shorter device lifespan.
- Frequency and current of the cooling pump—could signalise problems with the cooling system in general.
4.2. Data Cleaning
4.2.1. Identifying Anomalies and Handling Them
It is important to assess the regularity of the data-gathering process to guarantee the correctness and dependability of the CT scanner data. Graphs plotting scan counts over time reveal two significant anomalies within our data.
Firstly, while every single scan is labelled with both id and date, sometimes, these do not quite fit into the big picture with other data points. Usually, this means that while id is somehow continuous, the date would be shifted by several days compared to neighbouring data points if sorted by id. Anomalies found suggest that specific measurements were recorded at the wrong time, possibly due to incorrect computer date and time settings. These data were excluded, as it is impossible to accurately determine the corresponding number of scans and the time when the data were recorded.
Additionally, there are observable gaps in the data, which point to times when the CT machine was not in use or when data collection failed. Most of the time, it would be the latter, as in the case of a CT scanner being used, it is being used daily, at worst, with a 2-day pause during the weekend. Hence, to mitigate this problem, it is important to select an interval where the data were routinely gathered in order to achieve relevant results. Our usage observations are also supported by the existing literature. For example, the 2015 report about CT equipment in NHS [22] states that the average CT scanned 32 patients daily and was in normal (not emergency on-call) operation for 48.8 h per week. Another NHS report from 2019 [23] also notes increasing 7-day usage of CTs. In Canada, as reported by CMII 2022–2023 survey [24], daily usage of an average CT was reported as 14.2 h, with 91.1 h being the weekly average, and 75.7% of surveyed sites reported 7 days/week operation.
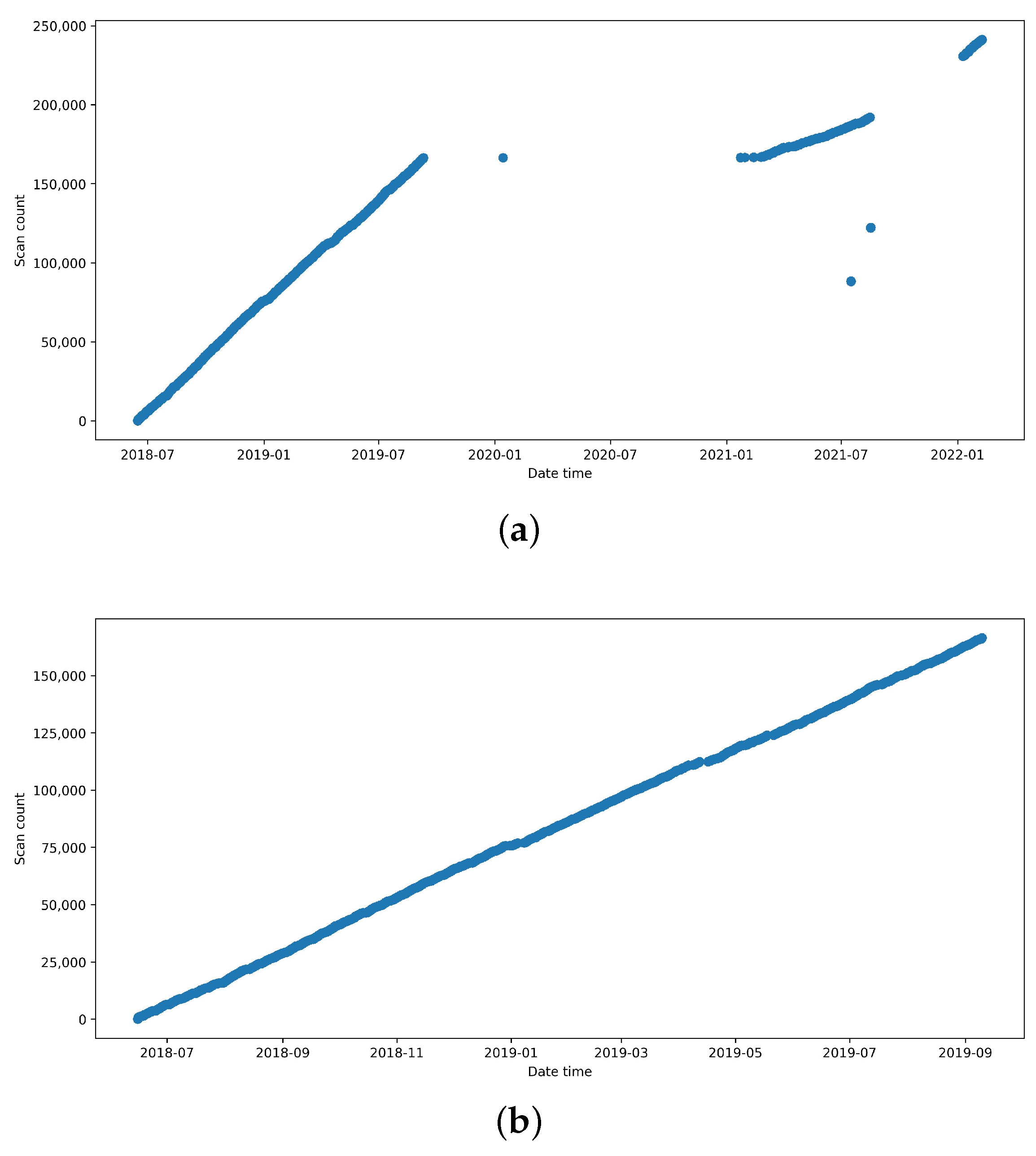
For working CT devices, data from the beginning of the graph were chosen. The selection was made this way as it is hard to estimate the reason for the gap, and a consistent interval ensures there was no hidden malfunction. This phenomenon can be seen in Figure 2. The initial long interval spanning from the start of the measuring until September 2019 is extracted and used as data for working CT.
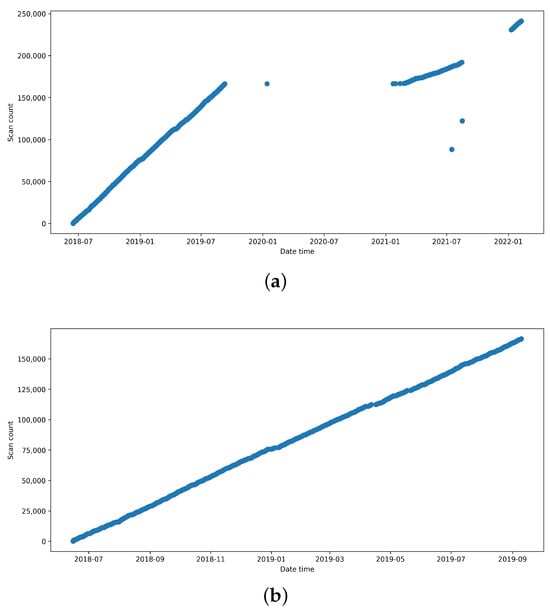
Figure 2.
Number of scans over time for the working tube. (a) Before handling anomalies. (b) After handling anomalies.
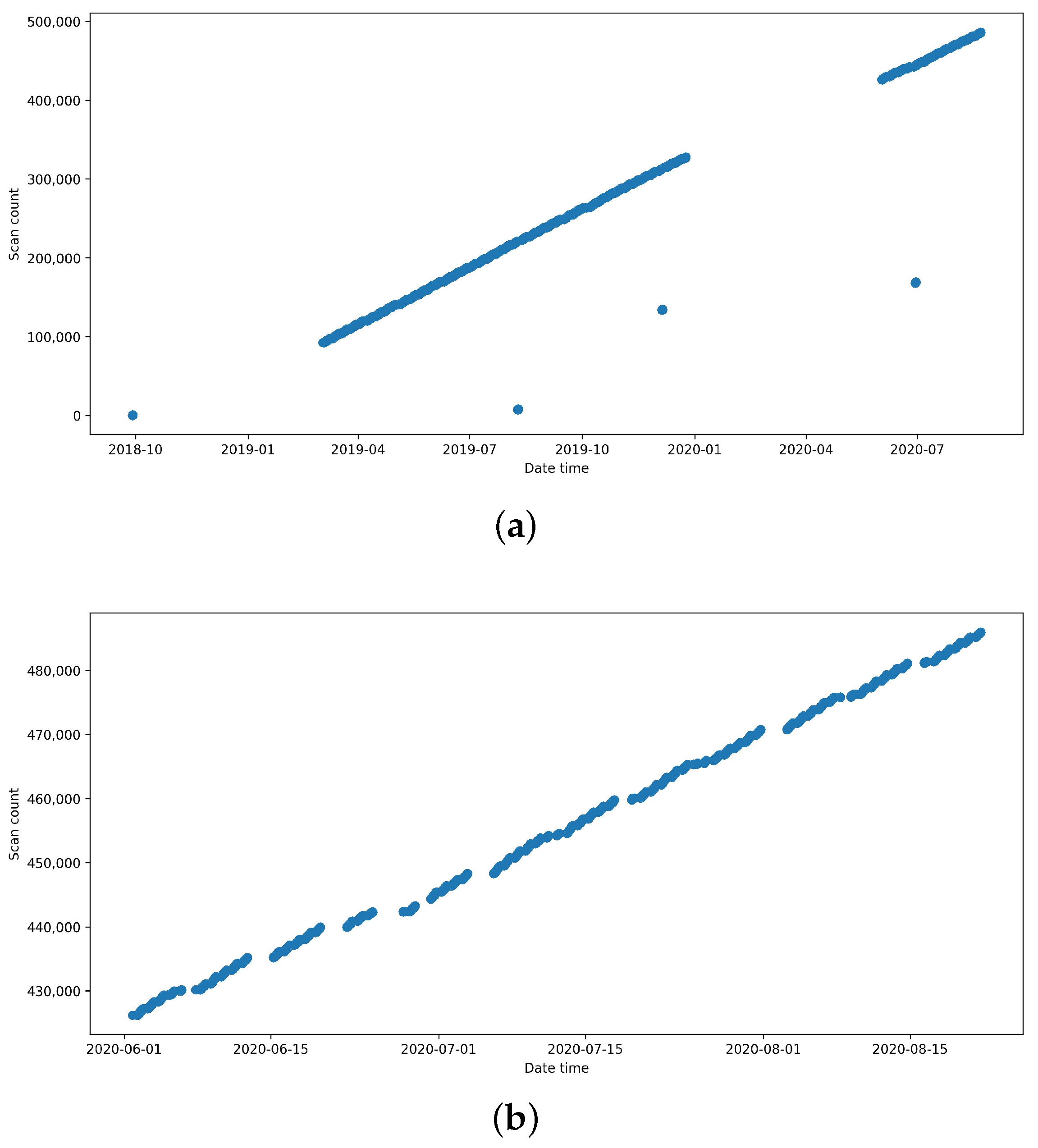
For malfunctioning devices, data closer to the failure point was used. It is logical that the transition from functional to slowly malfunctioning devices, or a device already malfunctioning and failing slowly, should happen in this window; hence, it is important to capture this moment. This approach’s application is visible in Figure 3, where the top right interval is selected.
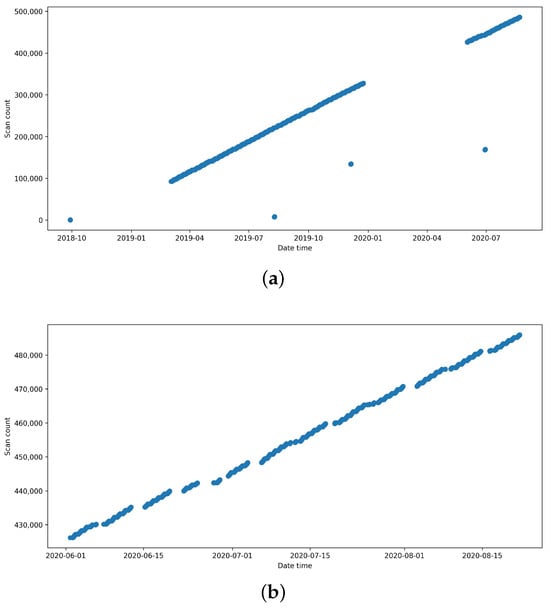
Figure 3.
Number of scans over for malfunctioning tube. (a) Before handling anomalies. (b) After handling anomalies.
As we opted to use classifiers, where consistent input dimensions are usually required, it was also necessary to agree on the input vector size. After some consideration, it was agreed to keep all the vectors bigger than 20,000 samples and truncate them to fit the smallest vector bigger than 20,000—20,190 data points. On average, this vector represents data from 69 days. We have selected this number of samples because we were able to retain most of the original dataset, given that we have already been operating with a low number of data samples, and excluding more could compromise the model’s sensitivity. Additionally, 69 days should provide sufficient data to smooth out any noise that may occur due to variations in scanning procedures and protocols. We do not have any information about the day of the first reported malfunction or when the staff perceived the CT to degrade. We do not have information on when the X-ray tube perceived as functional has been replaced. Therefore, we cannot comment on the inflection point, where the functional X-ray tube starts to degrade towards the faulty one. Making this vector long could cause label noise, as it could include these transitional states. While they are important for long-term forecasts, the provided dataset is likely not big enough to deal with this noise. Resorting to shorter time reduces the chance of such label noise and possibly makes our model more accurate on the short-term data. On the other hand, this choice may remove some important insights from the data. This way, the number of samples dropped from the original 137 to 128: 66 of those are still working, and 62 are malfunctioning.
4.2.2. Excluding Irrelevant Parameters
After this detailed analysis, another two parameters were removed from the dataset, as while helpful for data analysis and exploration, they do not have a value for classifiers:
- Scan Count: Not indicative of the CT device’s condition.
- Date-Time: Assumed constant environmental conditions.
4.3. Data Preparation
4.3.1. Parameter Averaging
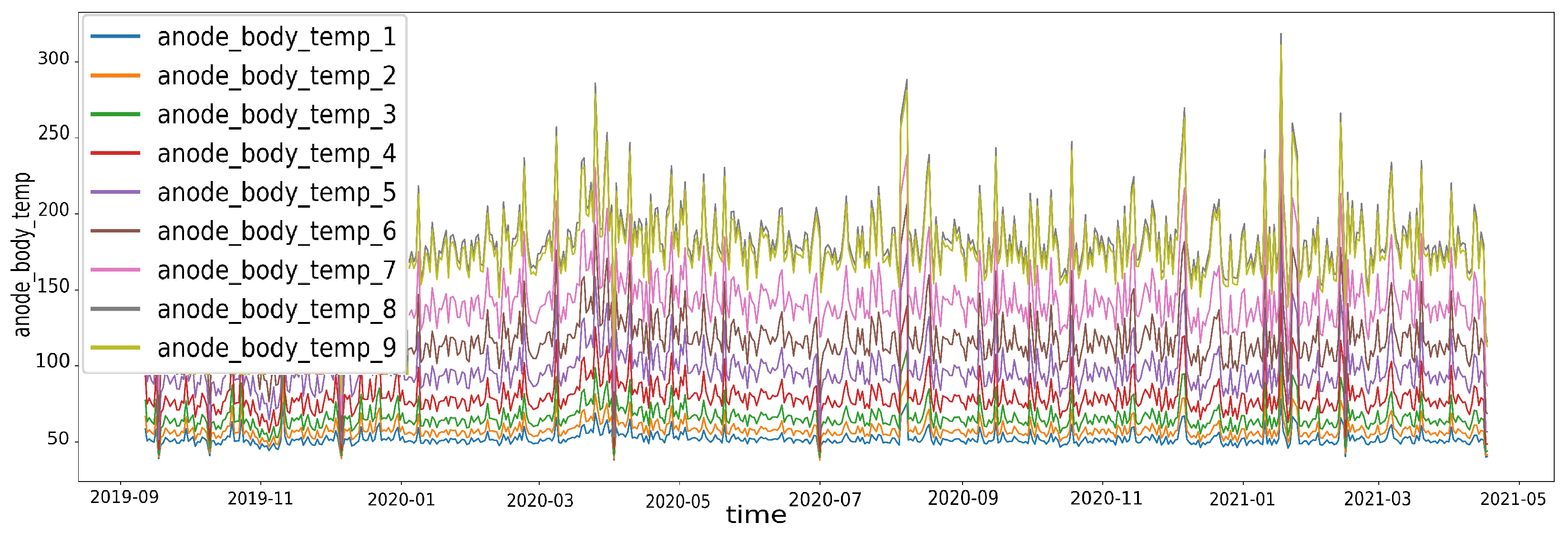
To simplify the data and reduce redundancy, two features, possibly represented multiple times in the dataset, were identified—anode body temperature and focal track temperature. Firstly, they were analysed visually. Figure 4 shows anode temperatures for one of the samples. It was apparent that these values are highly correlated. To make sure, we also plotted a correlation matrix, where the weakest correlation between two features of anode body temperature was 0.96. Afterwards, we calculated the average of these and created two new features—average anode temperature and average focal track temperature. This approach reduced the 18 original temperature parameters (9 for each) to a more concise set, capturing essential temperature characteristics.
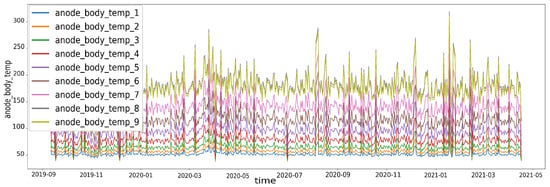
Figure 4.
Anode temperatures.
From a dimensionality standpoint, this step has achieved a final dimensionality of our input data—20,190 data points, each representing a single measurement. Every measurement has 55 different values—features. The distance between measurements depends on several aspects, but the input matrix represents, on average, 69 days of data from CT devices. This matrix, representing a single CT, is then input to a feature extraction process/classifier. For a more detailed breakdown of 55 parameters remaining for each data point after this averaging process, please see Appendix A Table A1. For a sample value just after this step, please see Appendix B Table A2.
4.3.2. Categorical Encoding
Non-numerical parameters, like “kind” and “focus”, were converted into numerical values using categorical encoding. This process involved assigning unique numerical codes to each verbal value, allowing the machine learning models to process the data effectively.
4.3.3. Normalisation
Normalisation is crucial to ensure that all features contribute equally to the machine learning model, preventing features with larger scales from dominating. The Min–Max normalisation was used to normalise data, scaling all features to a range between 0 and 1.
4.4. Feature Extraction
As we are dealing with time series, we will be applying two particularly popular methods in time series/signal processing: autoregressive models and Discrete Wavelet Transformation.
4.4.1. Autoregressive Models
Autoregressive models have been used to model time series data since at least the 1970s [25]. In the autoregressive model, the next value of a regressed variable depends on the linear combination of its past values. In general, in autoregressive model [26], the current value y in time t can be written as follows:
where p is so-called lag, or, to put it simply, how many past values of y are taken into account, and represents white noise. denotes the parameters of the model that will be learned. In this case, the input to the ML models is these parameters. Their quantity depends on a lag p, which is treated as a hyperparameter.
In our case, we are not using autoregressive models as regressors. We are instead trying to use the autoregressive coefficients as features for other classifiers. This method is used to process time series, for example, in the domain of EEG classification [27]. This approach is based on the fact that a properly selected autoregressive model fits and describes the time series; hence, its parameters should be descriptive enough for the classifier as well. Also, the auto-regression patterns for faulty parts close to the end of life should be different from normal progression, as, for example, filament enters the stage of “rapid degradation” [16].
4.4.2. Discrete Wavelet Transformation
Discrete Wavelet Transformation (DWT) is a linear transformation that breaks down the original signal into smaller parts called wavelets. There is an infinite number of possible wavelets, but they need to fulfil admissibility and should fulfil regularity conditions [28]. Hence, over time, several waves fulfilling these criteria were created, called mother waves, that are typically used to generate the wavelets. Child wavelets are generated from these mother wavelets via translation (k) and scaling (j) as shown in Equation (3).
Following the notation by Burrus, Gopinath, and Guo [29], any square-integrable signal/function can be described as follows:
where the mother wavelet, can be described as follows:
and the are the DWT coefficients.
Compared to Fourier transformation (FT), which breaks down the signal into a list of sine and cosine waves lasting the whole sample, DWT considers not only frequency information but also where this frequency occurs (temporal information) in the signal. We try to exploit this property, as the indications of faults can be very localised events or cause sudden changes to the time series.
As our samples are considerable in length, we have opted for a discrete, not continuous, version that is more computationally expensive while providing better feature extraction.
DWT has been used in the domain of PdM in the past; see, for example, [30,31].
5. Classifiers
5.1. Classifier Selection
As we are dealing with a rather small dataset, we opted for both models that need hand-crafted features as inputs and models that can extract features from the data themselves. Depending on the complexity of the data and the fact that we do not utilise transfer learning, the latter models’ performance could be problematic, as they usually require more data to learn the underlying patterns. As we are dealing with time series data, many different classifiers can be used.
For the classification of hand-crafted features, we have selected the following classifiers:
- Logistic Regression (LR);
- Decision Trees (DT);
- Random Forest (RF);
- Gradient Boosting decision trees (GBDT);
- Support Vector Machines (SVM).
When selecting the classifiers, we went for both performance and diversity. GBDT, RF, SVM, and DT all rank among the top-5 classification algorithms [32]. Together with LR, they also create a diverse group with different principles being applied.
For the models that can learn underlying patterns themselves, we have selected the following:
- Long short-term memory (LSTM);
- Convolutional Neural Networks (CNN).
5.1.1. Decision Trees, Logistic Regression and SVM
DTs are among the oldest models used for classification and prediction [33]. It is characterised by recursively splitting the dataset based on the values of the selected features, creating decision rules. This way, it splits the datasets into smaller, more homogeneous datasets until only examples of one class remain in the dataset. This type of node is called a leaf node. How the tree is built and how to define homogeneity depends on the algorithm used.
Logistic regression [34] is a probabilistic model using the logistic (sigmoid) function to model probability. It models the relationship between n independent variables and produces a binary output for a dependent variable. While logistic regression is a linear model in the log-odds space, the relationship between independent variables and probability is nonlinear due to the logistic function.
With the modern form introduced in 1992 [35], SVM is also used for classification and regression. The simplest version tries to create a linear separation hyperplane between classes that is maximally and equally distanced from the nearest samples (support vectors) of both classes (maximum-margin hyperplane). Not all classes are separable by a linear hyperplane, so it uses a kernel trick to separate them in a higher-dimensional feature space.
5.1.2. Gradient Boosting Machines and Random Forest
Both GBDT [36] and RF [37] are based on an ensemble of decision trees. They take different approaches to how the trees are created, as GBDT belong to a family of algorithms called boosting, while RF belongs to a family called bagging [38]. There are two primary sources of error in ML: bias and variance. In order to mitigate the error, boosting and bagging attempt to balance them in different ways. For bagging methods, an ensemble of models that are as strong (accurate) as possible is created, resulting in low bias but high variance. Bagging tries to reduce the variance while keeping the bias low. It is the other way for a boosting approach—weaker models with less bias but more variance.
In this case, boosting with decision trees as a base classifier is used. These trees are a group of weak classifiers that together act on the outside as a strong classifier. This is possible under the assumption that the voting of weak classifiers can provide an opinion of a strong classifier or even out-compete it.
For Random forests, the trees are always trained only on a subset of the samples and features. This approach is taken to create as strong a classifier as possible, as the generalisation error is constrained by the ratio between the correlation and the strength of the classifiers. To minimise this ratio, it is necessary to maximise the strength of the classifier while maintaining low correlation.
5.1.3. Convolutional Neural Networks
Convolutional neural networks have had much success over the years in different domains, including signal processing [39,40], image processing [41,42], or video processing [43]. Since the breakthrough of AlexNet in 2011, many different architectures have emerged.
CNNs are good at processing grid-shaped data of different dimensionality. Different sequential data of one order can be formulated as a grid structure of higher order—for example, 2D + time data such as video can be processed through 3D convolution. As our data can be formulated as a rectangle [samples, features], we will utilise it. However, there might be a caveat in the fact that CNNs struggle with modelling long-term dependencies, as convolution and pooling are relatively local operations. If our data have long-term dependencies, CNNs may not perform as well as architectures created for sequential modelling.
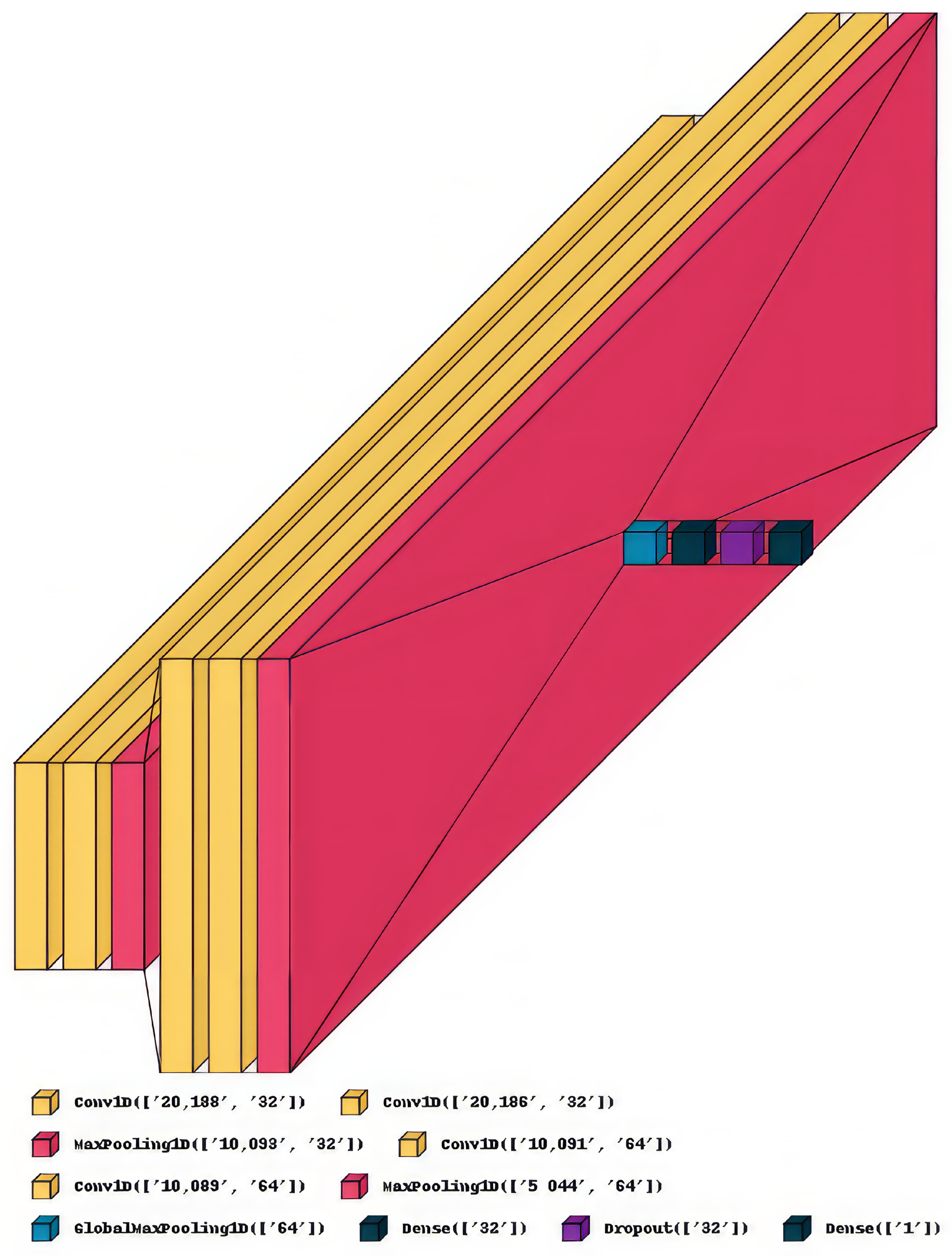
Our architecture is inspired by the VGG family [44]. These networks comprise blocks consisting of 2 or 3 convolutional layers followed by max pooling. Both convolutional layers have the same number of channels, and every consecutive block has twice the number of channels of the former block. Theoretically, every block should allow the model to extract relevant features for that semantic level, subsequently “zoom out”, and focus on a higher semantic level in consecutive blocks. As our network will work with time series data, which has the shape of [data points, features], we will apply 1D Convolutions instead of 2D, as seen in the image classification problems.
We will need to train from scratch because there are very few 1D CNNs to conduct transfer learning from. With our limited dataset, we will not be able to train the whole model of VGG16 or VGG19 as proposed in the original article. Hence, we will treat both the number of VGG blocks and the number of filters in convolutions of these blocks as hyperparameters, which we will try to optimise. An example of this CNN is visible in Figure 5.
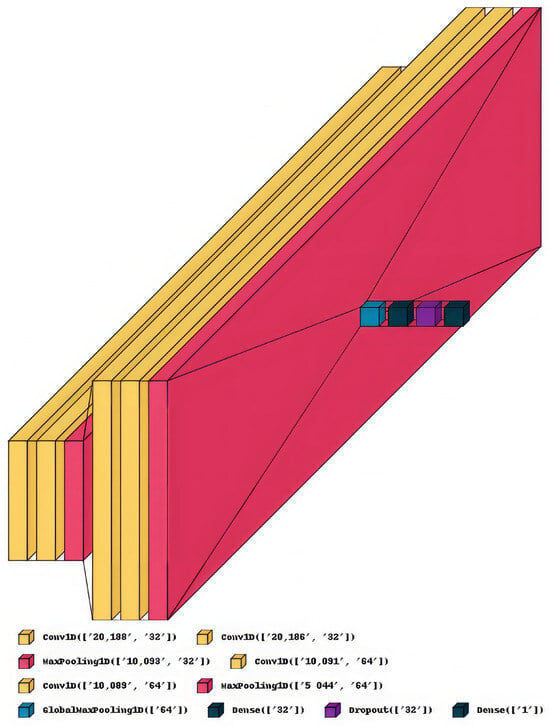
Figure 5.
Schema of a CNN with 32 and 64 filters.
5.1.4. LSTM
Compared to CNNs, which can work on any grid-structured data, recurrent neural networks (RNNs) specialise in processing sequential data. This specialisation is possible due to their specialised structure. While classical feed-forward networks only feed information in one direction (forward), the RNNs can also pass the information back. As such, they have found their applications [45] in different areas with inherently sequential data, such as natural language processing, sentiment analysis, machine translation, or time series analysis. As such, RNNs are a natural fit for our use case.
There are different architectures of RNNs, such as Long short-term memory (LSTM), Gated recurrent unit (GRU), or Bidirectional RNN. For a more detailed breakdown of RNN architectures, please see [46].
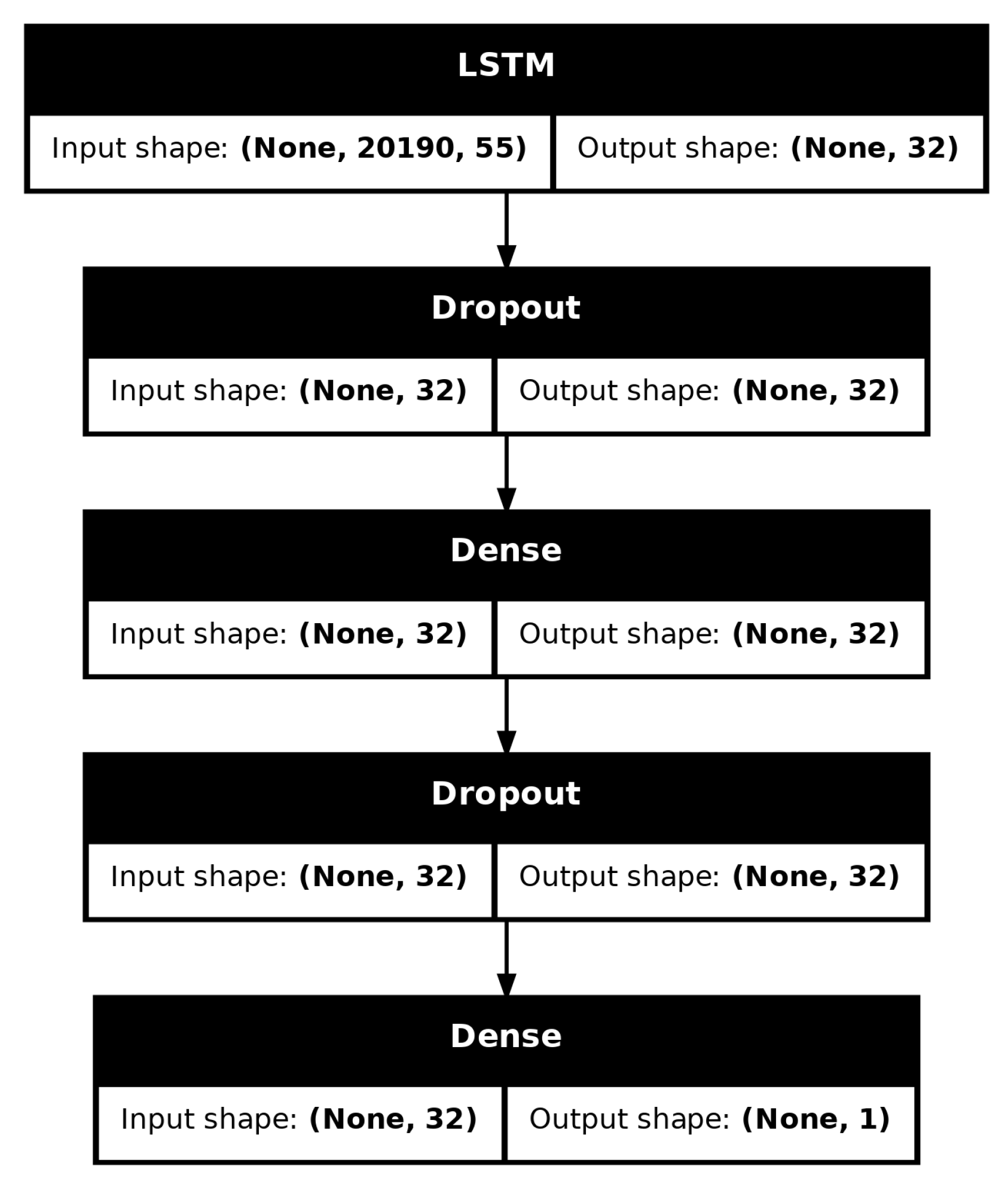
For our work, we selected an LSTM. Proposed first time by Hochreiter in 1991 [47] is one of the most popular RNN architectures. It utilises the gating mechanism with three different types of gates:
- Input gate
- Forget gate
- Output gate
that are responsible for managing and optimising the cell state/memory and hidden state . These states are computed from the current input , last cell state , and last cell state , passing through the mentioned gates. Utilising these gates, when appropriately trained, an LSTM can remember relevant (and forget irrelevant) information.
The number of cells of our LSTM is being treated as a hyperparameter. To allow for a classification of the sequence, the LSTM is connected to a layer of 32 neurons (with “relu” activation), which is consequently connected to an output neuron with sigmoid activation. In between both these connections, there are also dropout layers, with 20% of inputs being set to zero. The inclusion of dropout layers is performed to improve the network’s generalisation. The diagram of this LSTM is visible in Figure 6.
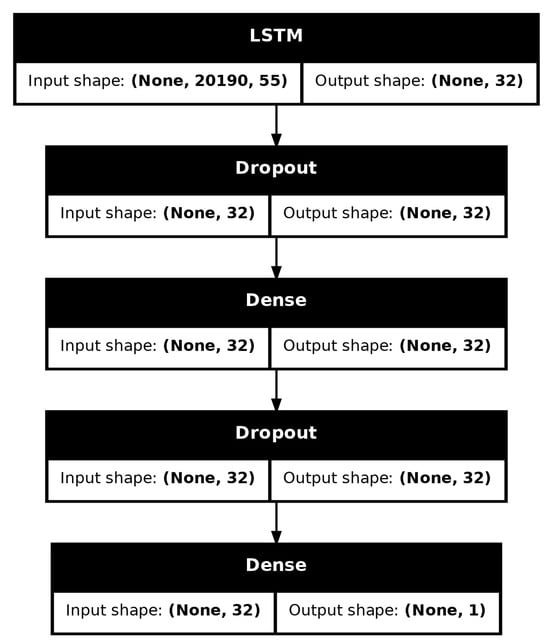
Figure 6.
Diagram of used LSTM.
6. Experiments
6.1. Methodology
First, the data were split into 2, in the 80:20 ratio. Afterwards, 5-fold cross-validation was performed on the 80% percent of the data, always training on 4 folds and validating on the 5th one. This was performed to tune the hyper-parameters and select the best candidate models. Afterwards, these were tested on the 20% per cent test set that was split out initially. All the splits were stratified to account for the class distribution in the dataset despite the rather small imbalance (66:62). The seed was held constant across experiments to make the experiments reproducible.
As an evaluation metric, accuracy was selected. Before calculating accuracy, every sample was rounded—samples with output of 0.5 and lower were classified as 0 (working), others as 1 (not working). In the case of a binary problem, the micro-f1 score corresponds to the accuracy (as also noted by scikit-learn’s documentation). Hence, we write accuracy/micro F1-score in the tables below, as they are equal. As the dataset is approximately balanced, the calculated macro F1-score would also be very close to this number. As models were evaluated through cross-validation, the reported values are averages through the 5-folds.
For hyperparameter selection, the optimised parameters were as follows:
- LR
- –
- penalty—In the range of [l1, l2 and None]
- –
- c—Parameter related to regularisation strength (inverse), in the range of [0.1, 1, 10, 100]
- SVC
- –
- kernels—Selected kernel function, in the range of [“rbf”, “linear”, “poly”]
- –
- c—Same as for LR (1)
- –
- gamma—kernel coefficient, in the range of [0.01, 0.1, 1, 10], base was ’scale’
- RF
- –
- Number of estimators—number of constructed trees, values in [10, 100, 1000, 10,000]
- –
- Distance criterion—possible values were [gini, entropy, log_loss]
- –
- Minimal number of samples in leaf nodes—values were in the range of 1–9 with step 2, base was 1
- DT
- –
- Distance criterion—same as RF
- –
- Minimal number of samples in leaf nodes—same as RF
- GBDT
- –
- Number of estimators—[100, 1000, 10,000]
- –
- Subsamples—Ratio of samples used for training base of learners—[0.75, 1], base 1
- –
- Maximum depth for base learners—[5, 7, 9], base 6
- –
- Learning rate—[0.1, 0.2], base 0.3
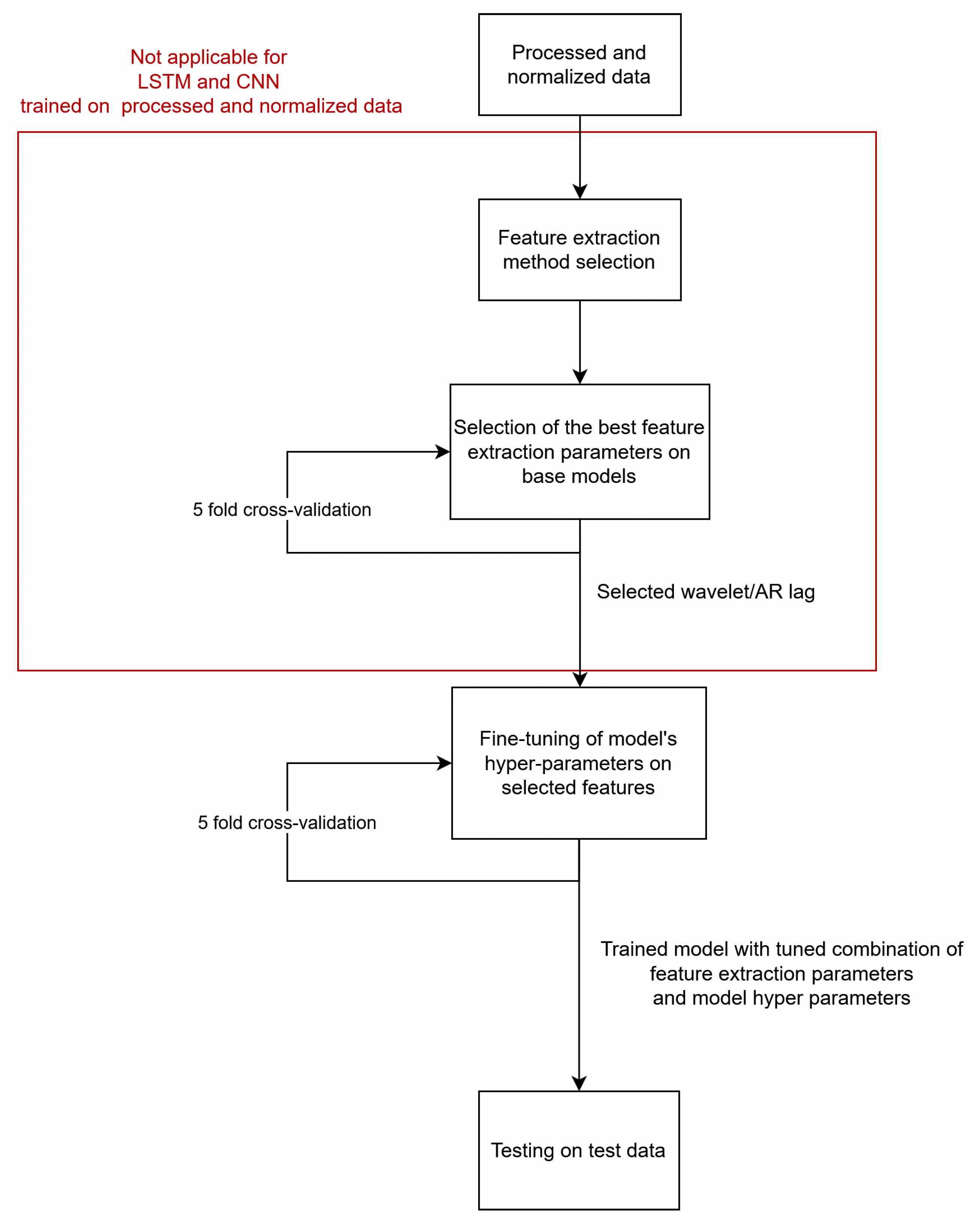
Hyperparameters were selected in an exhaustive grid search. GBDT in combination with 10,000 estimators was dropped for the wavelet experiment, as cross-validation took days. The base settings, used for the initial search for AR lag/wavelet shape below, are indicated in bold. The general schema is shown in Figure 7.
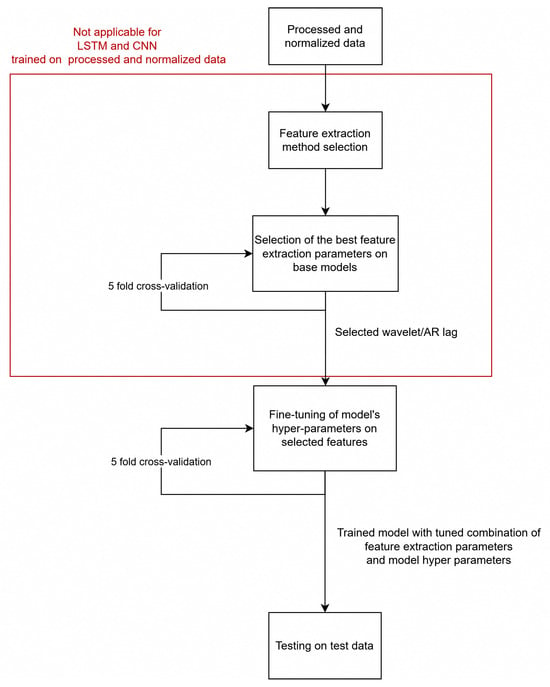
Figure 7.
Diagram of the model selection scheme.
All of our experiments were performed in the Python 3.11 programming language. We utilised Keras 3.9.1 [48] with TensorFlow 2.19.0 [49] backend for neural networks. The scikit-learn [50] library in version 1.6.1 was utilised for classical ML algorithms. For GBDT, we utilised XGBoost 3.0.0 [51] library in order to leverage the parallel implementations. For autoregressive models, we utilised statsmodel [52] library 0.14.4 version and for wavelets, we utilised PyWavelets [53] library in version 1.8.0. Figure 5 was visualised through Visualkeras 0.1.4 [54].
6.2. Autoregressive Model Coefficients as Features
In order to even use autoregressive models, we needed to check whether the features of processed samples were stationary time series. In order to evaluate this, we employed an augmented Dickey–Fuller test [55]. As the results were usually in the realm of −20 and smaller, we could reject the null hypothesis and proclaim the time series stationary.
In this experiment, every feature of every sample was modelled as an autoregressive model. Afterwards, the array was flattened and fed into classifiers. As the search space was rather large, we decided to proceed as follows:
- As mentioned in Section 4.4.1, we treated lag as an hyperparameter. We selected lags spanning from 0 to 10 for testing
- For every lag, every classifier with default parameters was trained
- Afterwards, we selected the best lag for every model based on the accuracy score on the validation set
- We tried to optimise the classifier-specific hyperparameters (listed in Section 6.1) to maximise the validation accuracy
- Finally, we tested the best candidate for every classifier
For LR, there was a phenomenon when lags 5–7 performed the same during the initial model fitting. Afterwards, the hyperparameters for lags 5, 6, and 7 were explored, and finally, the best model was selected from all of the possible models. The results are visible in Table 1.

Table 1.
Performance of classifiers when AR coefficients were used as features.
6.3. DWT Coefficients as Features
We empirically tested different mother wavelets—Haar, Daubechies, Symlets, and Coiflets. In pywt, they are referred to as “haar”, “dbx”, “symx”, and “coifx”, where x is a parameter representing a number of vanishing moments of the wavelet. Haar wavelet does not feature a configurable vanishing moment and hence was only used once. Testing was performed in a similar way as we did with AR model coefficients:
- We treated the wavelet shape as a hyperparameter. We selected and tried haar, db1-db10, sym2-sym10, coif1-10
- For every wavelet, every classifier with default parameters was trained
- Afterwards, we selected the best wavelet for every model based on the accuracy score on the validation set
- We tried to optimise the classifier-specific hyperparameters (listed in Section 6.1) to maximise the validation accuracy
- Finally, we tested the best candidate for every classifier
Results are visible in Table 2. The performance of LR and SVC was relatively stable. Sixteen different configurations achieved the same performance—all of the combinations of c and gamma for the linear kernel. While the LR had a clear winner, 10 of 12 possible setups achieved the same accuracy.

Table 2.
Performance of classifiers when DWT coefficients were used as features.
The downfall of tree-based methods is rather interesting. We hypothesise that this can be attributed to the feature selection process. It likely means that DWT coefficients alone are not as distinctive as needed for these methods. Even more so, during the initial wavelet selection, rather simple wavelets performed the best.
To sum up these experiments, DWT coefficients seem more suitable for SVC and LR classifiers, while AR coefficients seem more suitable for tree-based methods. The difference between the best method utilising DWT coefficients and AR coefficients is negligible (0.6%).
6.4. Experiments with CNN
For CNNs, we decided to try two different approaches:
The first approach consists of giving a CNN trimmed and normalised data. Here, the goal is for CNNs to learn how to extract features themselves and find the hidden patterns in the data.
The second approach is based on the assumption that DWT coefficients might not be representative enough of the features or may contain unnecessary features. In many works, DWT coefficients are only used as an intermediate step and more features are extracted over time. In this case, the goal is for a CNN to learn additional needed processing on top of the DWT. Another possible upside is that data processed with DWT could be easier to learn for CNNs and allow for easier/faster convergence.
During the experiments, we constantly monitored the validation accuracy, and the best model of every epoch was always saved after the epoch and loaded during the final evaluation. Together with limiting the number of epochs, it has the approximate effects of the early stopping mechanism. As a loss function, binary cross-entropy was utilised with the Adam optimiser.
For a VGG-type CNN, we utilise 5-fold cross-validation with possible duos/triplets of filters in consecutive blocks:
- 8, 16
- 16, 32
- 32, 64
- 64, 128
- 8, 16, 32
- 16, 32, 64
- 32, 64, 128
- 64, 128, 256
This choice was made for several reasons. Firstly, we did not have enough data to train a 1D CNN as massive as VGG16 or 19 from scratch, so we proceeded with continuous slashing of VGG blocks. This approach brought us to a setup with three blocks—64, 128, and 256. This was the largest network that did not either diverge or heavily oscillate on our data. Compared to the original VGG architecture, the 256 filter block did not have 3 but only 2 convolutional layers. We also tweaked the architecture with a global average pooling layer, followed by a 32-neuron dense layer, a dropout layer with a 20% chance, and finally, an activated dense layer with one neuron. From here, we decided to experiment with the number of filters and modules.
For the normalised and trimmed data, with no prior feature extraction, the VGG-like network setup with 32 and 64 filters performed the best, achieving an accuracy of 75.4%.
For the combination with DWT, we first needed to select candidate wavelets for different sizes of filters. We have experimented with (16, 32), (32, 64), and (64, 128) filter combinations. We noticed that VGG-style architecture was a fast learner on our data and rarely ever improved over epoch 50. Hence, we first tried to train the 3 selected VGG-style architectures on all selected wavelets (same as in Section 6.3). Afterwards, based on the validation accuracy, we picked the best-performing wavelet for every of the 3 filters. During this experiment, the best-performing coefficients of wavelets for the filters were “sym2”, “haar”, and “coif7”, respectively.
Afterwards, we cross-validated all filter combinations mentioned above on the 3 selected wavelets. As we have been training different filter sizes and numbers of blocks, we trained for 100 epochs. The best performance with this approach was achieved by combining a 32 and 64-filter (two-module) network and the “coif7” wavelet, with an accuracy of 78.6%.
While it seems that further processing helped the VGG-style network achieve approximately 3% better accuracy, it still could not beat the best-performing LR and SVC models. The result is likely due to the size and complexity of the dataset. It has already been proven in different studies [56] that hand-crafted features combined with a classifier usually beat the CNN on a smaller dataset.
6.5. RNN-Based Processing
For RNN-based processing, we treated the number of LSTM units as a hyperparameter. We first cross-validated the setups with 16, 32, and 64 units on the trimmed and normalised features for 75 epochs. Empirically, we have not seen an LSTM learn anything beyond 75 epochs.
The best-performing LSTM was 32 units, which achieved an accuracy of 87%. This was also our best-performing model overall. Confusion matrices for this model on all 5-folds are visible in Appendix C. We see that the model achieves a 100% recall for the faulty class—it never classifies an X-ray tube as working if it is soon to be replaced.
An LSTM model with 32 units was also cross-validated across different wavelets to decrease the search space. The best-performing coefficients were for the Haar wavelet with 61.8%. This result is a significant regression compared to training an LSTM on trimmed and normalised data. The regression is likely related to the fact that DWT coefficients cannot model complex long-term dependencies in our data properly. Hence, LSTM performance actually degrades with such feature extraction.
The results of all the NN-based methods are visible in Table 3.

Table 3.
Performance of NN-based methods.
7. Summary
As mentioned before, this was our first study on these data. In this study, the obtained CT data were described, cleaned, and prepared, and every step was documented. Afterwards, AR model coefficients and DWT coefficients were used as features for different classical machine learning models. Later, two different NN families were applied to DWT coefficients and also applied to trimmed and preprocessed data without a feature extraction step. The best-performing architecture proved to be an LSTM with 64 units, with 87% accuracy on trimmed and preprocessed data. The second place was jointly shared by LR and SVC trained with DWT coefficients, and the fourth place was held by RF trained on AR coefficients.
We view 87% accuracy as a success, given the possible data quantity. However, it is necessary to put the performance of the LSTM model into a real-world context. Confusion matrices for this model on all 5-folds are visible in Appendix C. On these folds, the model has never classified a faulty X-ray tube as a working one. This way, we can conclude two qualities of the LSTM model:
- The model likely can spot all the malfunctioning X-ray tubes.
- If the model classifies an X-ray tube as working, it has only a small chance (never before seen malfunctions) of the tube being replaced too soon.
The obvious downside is that, sometimes, a working machine is classified as soon-to-fail. Depending on the priorities of the companies/clinics, this could be a costly problem. However, it would help maximise the machines’ uptime.
As of execution time, once the data are trimmed and normalised, the LSTM model takes approximately 540 ms to execute on an older workstation-grade CPU (AMD Ryzen™ Threadripper™ 2920X 12-Core Processor). As the classified data represents, on average, 69 days, running such a model daily should not cause any computational problems for CT machines.
As for the related work, there are several possible extensions. One of the biggest challenges was to trim and preprocess the data. When trimming, we selected a relatively safe approach—selecting only intervals where we were sure either there was no malfunction occurring for the functioning class or the malfunction was relatively imminent for the malfunction class. While this approach may help diagnose the malfunction a few days before the failure, it does not help quantify the device’s health somewhere in the middle of the life cycle nor does it quantify the possibility of the failure or the mean time to failure. We view this as the biggest limitation of this work and a significant area for improvement in future work.
To do so, it would be necessary to perform the following:
- Gather more data—Data quantity is essential for good performance and generalisation, which is even more so for deep learning-based models.
- Create a fully retrospective study—All the X-ray tubes classified as working during the study were still working by the time of log gathering. That means there was no way to obtain more information about their expected life cycle. While, for the purpose of classification as being malfunctioning or still working, this was not a problem, it became a problem when intervals from the start of the life cycle were selected. For future work, this would allow us to obtain more information on the life cycle.
- Inspect failed X-ray tubes—In order to allow for more granular classification, a detailed understanding of the cause of failure would be needed.
- Conduct a deeper analysis of the features and their impact on the model—as different features can contribute to various types of faults at different stages of the life cycle. There is room for further experimentation with different features. Afterwards, explainable AI methods such as SHAP [57], or its extension to recurrent models—TimeSHAP [58], could be utilised.
Another possible future work could include trying to experiment with the size of the vector, as we suspect that the malfunction can become fully apparent later than we expect it to be with the current vector size.
We also tried to train a ResNet-style network [59], but we could not obtain this family of networks to train correctly and converge, despite trying to downsize the network all the way to only using 1 ResNet block. The size and the ambiguity in our dataset likely explain this. Possible future work here also includes the possibility of finding a similar but much bigger dataset and trying to learn the more powerful CNN architectures via transfer learning.
Another possible improvement is trying new models based on transformers. According to some of the literature [60], they are an efficient and accurate alternative to traditional RNN-based methods, while other parts of the literature are sceptical [61].
Author Contributions
Conceptualisation, M.K. and I.Z.; methodology, L.P. and M.T.; software, M.T., L.P. and M.K.; validation, L.P., M.K. and I.Z.; formal analysis, M.T. and L.P.; investigation, M.T., L.P. and M.K.; resources, I.Z. and L.P.; data curation, M.T., M.K. and L.P.; writing—original draft preparation, M.T., L.P. and I.Z.; writing—review and editing, M.T., L.P. and I.Z.; visualisation, M.T.; supervision, I.Z.; project administration, I.Z.; funding acquisition, I.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by VEGA (Vedecká grantová agentúra)—Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic, under the grant named EDEN: EDge-Enabled intelligeNt systems, grant number VEGA 1/0480/22.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
Description of the provided parameters.
Table A1.
Description of the provided parameters.
| Parameter Name | Description |
|---|---|
| scan_count | Number of scans since installation of tube. |
| date_time | Scan date and time (up to seconds). |
| rot_time | 10 ms Time of rotation for this scan. |
| voltage | 1/100 V Tube voltage during scan, represented by two parameters: nominal and actual voltage. |
| scan_time | 1/10 ms Scan duration (with X-ray), represent by two parameters: nominal and actual scan time. |
| stator_frequency | Hz Stator magnetic field rotation speed. |
| anode_frequency | Hz Anode rotation speed. |
| kind | Type of scanning: STA—the table does not move, SPI—the X-ray tube rotates while the table with the patient moves, a spiral is created, SEQ—sequence of scans, ROT—the X-ray tube rotates while the table does not move, it moves only after completing the rotation, ZIG—the table moves back and forth during the entire scan for a specific purpose, TOP—an image is created from one angle, the table moves, like a regular X-ray image. |
| flying_focal_spot | Position of the focal spot (the area of the anode surface which receives the beam of electrons from the cathode) of the X-ray tube: DIAG—flying focal spot is positioned diagonally relative to the gantry, PHI—flying focal spot is positioned along a fixed angle relative to the gantry, PHIs—is similar to the Phi mode, but the angle of the flying focal spot can be adjusted, NONE—fixed focal spot is used. |
| current | mA Current supplied to the tube, represented by seven parameters: current that is displayed to the user on the interface (ui), nominal, minimum, maximum, mean during scan, at scan begin, at scan end. |
| focus | The size of the X-ray beam at the point where it is emitted from the X-ray tube: SHR—super high resolution, SUHR—super ultra-high resolution, FHR—fine high resolution, UHR—ultra-high resolution, GET—geometry enhanced tool, LO—low output, SP—super position. |
| filament_current | mA Current supplied to the filament, represent by three parameters: filament current nominal, at scan begin, at scan end. |
| dose | mV Amount of radiation released, represent by four parameters: dose nominal, minimum, maximum, at scan end. |
| water_inlet_temp | 1 °C water temperature at tube inlet, represent by two parameters: temperature for scan begin and after scan end. |
| water_outlet_temp | 1 °C water temperature at tube outlet, represent by two parameters: temperature for scan begin and after scan end. |
| oil_temp | 1 °C Temperature of the tube system, represent by two parameters: temperature for scan begin and after scan end. |
| cooling_liquid_temp | 1 °C The calculated anode temperature at the scan end. |
| anode_body_temp | 1 °C Calculated anode surface temperature at scan end, represent by nine parameters, where each parameter is a point on the anode. |
| focal_track_temp | 1 °C Calculated focal track temperature at scan end, represent by nine parameters, where each parameter is a point on focal track. |
| temp_focal_spot | 1 °C Temperature of focal spot of the X-ray tube. |
| e_catcher_temp | 1 °C Calculated E-catcher temperature at scan end. |
| tank_expansion | mm Indicates the status of the expansion cooling tank with an distance sensor. |
| gantry_temp | 1 °C Gantry temperature at scan end. |
| cooling_pump_frequency | Hz Cooling pump rotation speed. |
| cooling_pump_current | mA Cooling pump current. |
| hv_block_temp | 1 °C High Voltage block temperature. |
| stator_current | mA Current of the stator. |
| arcs | Number of tube arcings during scan. |
| arcs_half_ut | Number of tube half arcings during scan. |
| xc_drops | Sum over the whole scan of signal stop inverter. |
| hv_drops | Sum of High Voltage drops over the whole scan. |
| start_angle | Angle for first valid reading. |
| readings | Total sum of all readings over the scan. |
| defective_readings | Total sum of all defect readings over the scan. |
| last_defective_reading | Last defect reading. |
| mode | Scan Mode (A,B)—using of 1 or 2 X-rays. |
| abort_reason | Reason why a CT scan was aborted: SuspendedByUser—scan was intentionally paused or suspended by the user, StoppedByUser—the scan was stopped by the user before completion, Comp—scan was interrupted due to a problem with the CT system’s computer, Abort— interruption of the scan for some reason other than the above. |
| abort_controller | Specific type of abort controller that stops the scan. |
| DOM_type | Type of digital output module used in the control system. |
| eco | State refers to the eco mode setting of the machine (off, on). |
Appendix B

Table A2.
Parameters before normalisation and conversion.
Table A2.
Parameters before normalisation and conversion.
| Parameter Name | Value |
|---|---|
| scan_count | 301,196 |
| kind | SEQ |
| date_time | 8 January 2023 18:56:36 |
| rot_time | 1.0 |
| scan_time_nom | 2.0 |
| scan_time_act | 2.0 |
| voltage_nom | 120 |
| voltage_act | 119.9 |
| current_ui | 165 |
| current_nom | 156 |
| current_min | 130 |
| current_max | 133 |
| current_control | 133 |
| current_mean | 133 |
| current_begin | 147 |
| current_end | 133 |
| focus | LO |
| stator_frequency | 220 |
| anode_frequency | 199 |
| filament_current_nom | 1621 |
| filament_current_begin | 1604 |
| filament_current_control | 1605 |
| filament_current_end | 1605 |
| filament_push_current | 1627 |
| dose_nom | 4131 |
| dose_min | 2576 |
| dose_max | 3874 |
| dose_end | 3476 |
| flying_focal_spot | Phi |
| water_inlet_temp_begin | 41 |
| water_inlet_temp_end | 41 |
| water_outlet_temp_begin | 41 |
| water_outlet_temp_end | 41 |
| oil_temp_1_begin | 42 |
| oil_temp_1_end | 42 |
| oil_temp_2_begin | 43 |
| oil_temp_2_end | 44 |
| e_catcher_temp | 43 |
| cooling_liquid_temp | 32 |
| temp_focal_spot | 214 |
| gantry_temp | 28 |
| cooling_pump_frequency | 83 |
| cooling_pump_current | 6277 |
| hv_block_temp | 40 |
| stator_current | 12,891 |
| xc_drops | 1 |
| hv_drops | 0 |
| start_angle | 48,928 |
| readings | 5600 |
| defective_readings | 0 |
| last_defective_reading | 0 |
| DOM_type | ZEC |
| mode | A |
| abort_reason | Comp |
| abort_controller | NaN |
| focal_track_temp | 193.0 |
| anode_body_temp | 71.666667 |
Appendix C
Confusion matrices for all 5 folds of the best, LSTM-based model.

Table A3.
Confusion matrix for fold 1.
Table A3.
Confusion matrix for fold 1.
| Predicted Working | Predicted Replaced | |
|---|---|---|
| Actual working | 10 | 4 |
| Actual replaced | 0 | 12 |

Table A4.
Confusion matrix for fold 2.
Table A4.
Confusion matrix for fold 2.
| Predicted Working | Predicted Replaced | |
|---|---|---|
| Actual working | 12 | 2 |
| Actual replaced | 0 | 12 |

Table A5.
Confusion matrix for fold 3.
Table A5.
Confusion matrix for fold 3.
| Predicted Working | Predicted Replaced | |
|---|---|---|
| Actual working | 9 | 5 |
| Actual replaced | 0 | 12 |

Table A6.
Confusion matrix for fold 4.
Table A6.
Confusion matrix for fold 4.
| Predicted Working | Predicted Replaced | |
|---|---|---|
| Actual working | 10 | 4 |
| Actual replaced | 0 | 12 |

Table A7.
Confusion matrix for fold 5.
Table A7.
Confusion matrix for fold 5.
| Predicted Working | Predicted Replaced | |
|---|---|---|
| Actual working | 12 | 2 |
| Actual replaced | 0 | 12 |
References
- UNSCEAR. Sources, Effects and Risks of Ionizing Radiation, United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) 2020/2021 Report, Volume IV: Scientific Annex D-Evaluation of Occupational Exposure to Ionizing Radiation; United Nations: New York, NY, USA, 2022. [Google Scholar]
- Achouch, M.; Dimitrova, M.; Ziane, K.; Sattarpanah Karganroudi, S.; Dhouib, R.; Ibrahim, H.; Adda, M. On predictive maintenance in industry 4.0: Overview, models, and challenges. Appl. Sci. 2022, 12, 8081. [Google Scholar] [CrossRef]
- Manchadi, O.; Ben-Bouazza, F.E.; Jioudi, B. Predictive maintenance in healthcare system: A survey. IEEE Access 2023, 11, 61313–61330. [Google Scholar] [CrossRef]
- Nunes, P.; Santos, J.; Rocha, E. Challenges in predictive maintenance–A review. CIRP J. Manuf. Sci. Technol. 2023, 40, 53–67. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Challenges and opportunities of deep learning models for machinery fault detection and diagnosis: A review. IEEE Access 2019, 7, 122644–122662. [Google Scholar] [CrossRef]
- Cen, J.; Yang, Z.; Liu, X.; Xiong, J.; Chen, H. A review of data-driven machinery fault diagnosis using machine learning algorithms. J. Vib. Eng. Technol. 2022, 10, 2481–2507. [Google Scholar] [CrossRef]
- Wahed, M.A.; Sharawi, A.A.; Badawi, H.A. Modeling of medical equipment maintenance in health care facilities to support decision making. In Proceedings of the 2010 5th Cairo International Biomedical Engineering Conference, Cairo, Egypt, 16–18 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 202–205. [Google Scholar]
- Packianather, M.S.; Munizaga, N.L.; Zouwail, S.; Saunders, M. Development of soft computing tools and IoT for improving the performance assessment of analysers in a clinical laboratory. In Proceedings of the 2019 14th Annual Conference System of Systems Engineering (SoSE), Cairo, Egypt, 16–18 December 2010; IEEE: Piscataway, NJ, USA, 2019; pp. 158–163. [Google Scholar]
- Kovačević, Ž.; Gurbeta Pokvić, L.; Spahić, L.; Badnjević, A. Prediction of medical device performance using machine learning techniques: Infant incubator case study. Health Technol. 2020, 10, 151–155. [Google Scholar] [CrossRef]
- Badnjević, A.; Pokvić, L.G.; Hasičić, M.; Bandić, L.; Mašetić, Z.; Kovačević, Ž.; Kevrić, J.; Pecchia, L. Evidence-based clinical engineering: Machine learning algorithms for prediction of defibrillator performance. Biomed. Signal Process. Control 2019, 54, 101629. [Google Scholar] [CrossRef]
- Gonzalez-Dominguez, J.; Sánchez-Barroso, G.; Aunion-Villa, J.; Garcia-Sanz-Calcedo, J. Markov model of computed tomography equipment. Eng. Fail. Anal. 2021, 127, 105506. [Google Scholar] [CrossRef]
- Cardona Ortegón, A.F.; Guerrero, W.J. Optimizing maintenance policies of computed tomography scanners with stochastic failures. In Service Oriented, Holonic and Multi-Agent Manufacturing Systems for Industry of the Future: Proceedings of SOHOMA LATIN AMERICA 2021, Bogota, Colombia, 27–28 January 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 331–342. [Google Scholar]
- Mohd, M.H.S.E.B.; Shazril, A.; Mashohor, S.; Amran, M.E.; Hafiz, N.F.; Rahman, A.A.; Ali, A.; Rasid, M.F.A.; Kamil, A.S.A.; Azilah, N.F. Predictive Maintenance Method using Machine Learning for IoT Connected Computed Tomography Scan Machine. In Proceedings of the 2023 IEEE 2nd National Biomedical Engineering Conference (NBEC), Melaka, Malaysia, 5–7 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 42–47. [Google Scholar]
- Azrul, M.H.S.E.M.; Mashohor, S.; Amran, M.E.; Hafiz, N.F.; Ali, A.M.; Naseri, M.S.; Rasid, M.F.A. Assessment of IoT-Driven Predictive Maintenance Strategies for Computed Tomography Equipment: A Machine Learning Approach. IEEE Access 2024. [Google Scholar]
- Zhou, H.; Liu, Q.; Liu, H.; Chen, Z.; Li, Z.; Zhuo, Y.; Li, K.; Wang, C.; Huang, J. Healthcare facilities management: A novel data-driven model for predictive maintenance of computed tomography equipment. Artif. Intell. Med. 2024, 149, 102807. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Liu, Q.; Miao, Q.; Huang, J. Prognosis for Filament Degradation of X-Ray Tubes Based on IoMT Time Series Data. IEEE Internet Things J. 2024, 12, 8084–8094. [Google Scholar] [CrossRef]
- Amoore, J.N. A structured approach for investigating the causes of medical device adverse events. J. Med Eng. 2014, 2014, 314138. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.R.; Clarkson, P.J. An analysis of medical device-related errors: Prevalence and possible solutions. J. Med Eng. Technol. 2004, 28, 2–21. [Google Scholar] [CrossRef] [PubMed]
- Laganà, F.; Bibbɂ, L.; Calcagno, S.; De Carlo, D.; Pullano, S.A.; Pratticɂ, D.; Angiulli, G. Smart Electronic Device-Based Monitoring of SAR and Temperature Variations in Indoor Human Tissue Interaction. Appl. Sci. 2025, 15, 2439. [Google Scholar] [CrossRef]
- Kemerink, M.; Dierichs, T.J.; Dierichs, J.; Huynen, H.; Wildberger, J.E.; van Engelshoven, J.M.; Kemerink, G.J. The application of X-rays in radiology: From difficult and dangerous to simple and safe. Am. J. Roentgenol. 2012, 198, 754–759. [Google Scholar] [CrossRef]
- Anburajan, M.; Sharma, J.K. Overview of X-Ray Tube Technology. Biomedical Engineering and its Applications in Healthcare; Springer: Singapore, 2019; pp. 519–547. [Google Scholar]
- The Royal College of Radiologists; Society and College of Radiographers; Institute of Physics and Engineering in Medicine. CT Equipment, Operations, Capacity and Planning in the NHS; Technical report; Institute of Physics and Engineering in Medicine: London, UK, 2015. [Google Scholar]
- England, N.; Improvement, N. Transforming imaging services in England: A national strategy for imaging networks. NHS Improv. Publ. Code CG 2019, 51, 19. [Google Scholar]
- Canadian Agency for Drugs and Technologies in Health. Canadian Medical Imaging Inventory 2022–2023: CT: CMII Report; Canadian Agency for Drugs and Technologies in Health: Ottawa, ON, USA, 2024.
- Parzen, E. Some recent advances in time series modeling. IEEE Trans. Autom. Control 1974, 19, 723–730. [Google Scholar] [CrossRef]
- Kotu, V.; Deshpande, B. Data Science: Concepts and Practice; Morgan Kaufmann: Cambridge, MA, USA, 2018. [Google Scholar]
- Kurzynski, M.; Krysmann, M.; Trajdos, P.; Wolczowski, A. Multiclassifier system with hybrid learning applied to the control of bioprosthetic hand. Comput. Biol. Med. 2016, 69, 286–297. [Google Scholar] [CrossRef]
- Poularikas, A.D. The Transforms and Applications Handbook; Technical report; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Burrus, C.S.; Gopinath, R.A.; Guo, H. Wavelets and wavelet transforms. Rice Univ. Houst. Ed. 1998, 98, 7–8. [Google Scholar]
- Bonnevay, S.; Cugliari, J.; Granger, V. Predictive maintenance from event logs using wavelet-based features: An industrial application. In Proceedings of the 14th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2019), Seville, Spain, 13–15 May 2019; Proceedings 14. Springer: Cham, Switzerland, 2020; pp. 132–141. [Google Scholar]
- Bhavsar, K.; Vakharia, V.; Chaudhari, R.; Vora, J.; Pimenov, D.Y.; Giasin, K. A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models. Machines 2022, 10, 176. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Zhang, X.; Almpanidis, G. An up-to-date comparison of state-of-the-art classification algorithms. Expert Syst. Appl. 2017, 82, 128–150. [Google Scholar] [CrossRef]
- De Ville, B. Decision trees. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 448–455. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Dietz, K.; Gail, M.; Klein, M.; Klein, M. Logistic Regression; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, New York, NY, USA, 27–29 July 1992; COLT ’92. pp. 144–152. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Shang, L.; Zhang, Z.; Tang, F.; Cao, Q.; Pan, H.; Lin, Z. CNN-LSTM hybrid model to promote signal processing of ultrasonic guided lamb waves for damage detection in metallic pipelines. Sensors 2023, 23, 7059. [Google Scholar] [CrossRef] [PubMed]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D convolutional neural networks for signal processing applications. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 8360–8364. [Google Scholar]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of image classification algorithms based on convolutional neural networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Sharma, V.; Gupta, M.; Kumar, A.; Mishra, D. Video processing using deep learning techniques: A systematic literature review. IEEE Access 2021, 9, 139489–139507. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Schmidt, R.M. Recurrent neural networks (rnns): A gentle introduction and overview. arXiv 2019, arXiv:1912.05911. [Google Scholar]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent neural networks: A comprehensive review of architectures, variants, and applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Hochreiter, S. Untersuchungen zu dynamischen neuronalen Netzen. Diploma, Tech. Univ. München 1991, 91, 31. [Google Scholar]
- Keras. 2015. Available online: https://keras.io (accessed on 10 April 2025).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 10 April 2025).
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; KDD ’16. pp. 785–794. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28–30 June 2010. [Google Scholar]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Gavrikov, P. Visualkeras. 2020. Available online: https://github.com/paulgavrikov/visualkeras (accessed on 10 April 2025).
- Dickey, D.; Fuller, W. Distribution of the Estimators for Autoregressive Time Series With a Unit Root. JASA J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Lin, W.; Hasenstab, K.; Moura Cunha, G.; Schwartzman, A. Comparison of handcrafted features and convolutional neural networks for liver MR image adequacy assessment. Sci. Rep. 2020, 10, 20336. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Bento, J.; Saleiro, P.; Cruz, A.F.; Figueiredo, M.A.; Bizarro, P. Timeshap: Explaining recurrent models through sequence perturbations. In Proceedings of the 27th ACM SIGKDD conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 2565–2573. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Ahmed, S.; Nielsen, I.E.; Tripathi, A.; Siddiqui, S.; Ramachandran, R.P.; Rasool, G. Transformers in time-series analysis: A tutorial. Circuits Syst. Signal Process. 2023, 42, 7433–7466. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).