IW-NeRF: Using Implicit Watermarks to Protect the Copyright of Neural Radiation Fields
Abstract
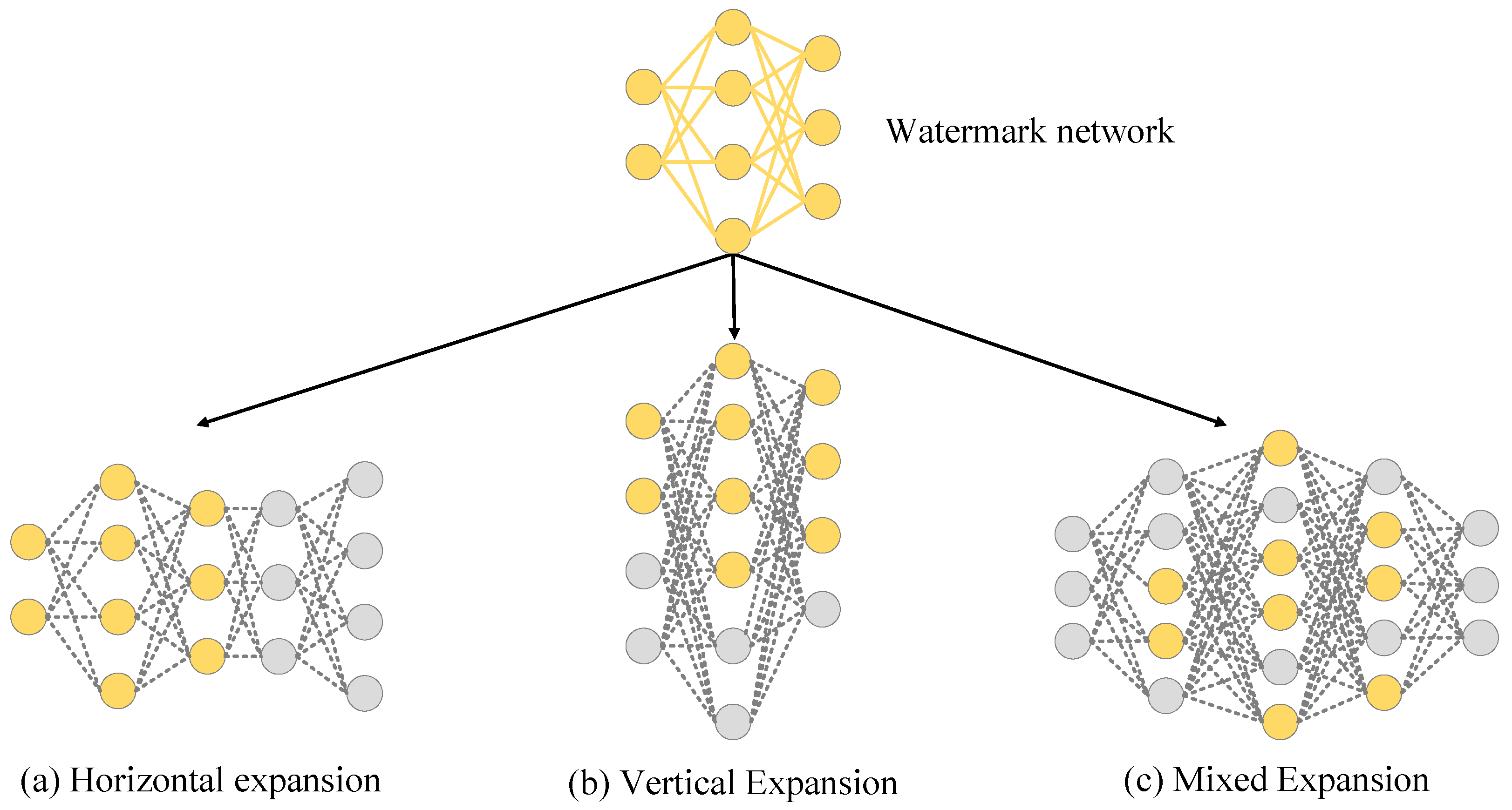
1. Introduction
- The first application of implicit representations in NeRF copyright protection to address existing NeRF watermarking challenges.
- A key-based carrier network construction method for lossless watermark information extraction.
- Validation of our method across various datasets, ensuring model quality and successful watermark extraction.
- Testing the robustness of our model to demonstrate that any attempts to remove the watermark would render the NeRF model unusable.
2. Related Work
2.1. Digital Watermarking for 2D Data
2.2. Digital Watermarking for 3D Data
2.3. Model Watermarking Algorithm
2.4. Watermark Algorithm for Neural Radiation Field
3. Preliminaries
4. Proposed Method
4.1. Framework
4.2. Data Representation and Transformation
4.3. Watermark Information Embedding Stage
4.4. Training of Carrier Networks
4.5. Watermark Information Extraction
| Algorithm 1 Training process of IW-NeRF. |
|
5. Experiments
5.1. Experimental Settings
- (1)
- PSNR (peak signal-to-noise ratio).
- (2)
- SSIM (structural similarity).
- (3)
- LPIPS (learned perceptual image patch similarity).
5.2. Reconstruction and Watermark Extraction Quality
5.3. Algorithm Capacity
5.4. The Robustness of the Model
5.5. Security Assessment
6. Limitations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Yang, Z.; Jin, X. Zero watermarking scheme for 3D triangle mesh model based on global and local geometric features. Multimed. Tools Appl. 2023, 82, 43635–43648. [Google Scholar] [CrossRef]
- Wu, H.; Liu, G.; Yao, Y.; Zhang, X. Watermarking Neural Networks with Watermarked Images. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 2591–2601. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, X. Watermarking Neural Network with Compensation Mechanism. In Knowledge Science, Engineering and Management; Lecture Notes in Computer Science; Li, G., Shen, H.T., Yuan, Y., Wang, X., Liu, H., Zhao, X., Eds.; Springer: Cham, Swtzerland, 2020; pp. 363–375. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2022, 65, 99–106. [Google Scholar] [CrossRef]
- Kuang, X.; Ling, W.A.; Ke, L.S.; Lei, G.; Ping, P.J.; Yue, L.Z.; Ping, L.F. Watermark embedding and extraction based on LSB and four-step phase shift method. In Proceedings of the 2019 7th International Conference on Information Technology: IoT and Smart City, Shanghai, China, 20–23 December 2019; pp. 243–247. [Google Scholar]
- Muyco, S.D.; Hernandez, A.A. Least significant bit hash algorithm for digital image watermarking authentication. In Proceedings of the 2019 5th International Conference on Computing and Artificial Intelligence, Bali, Indonesia, 17–20 April 2019; pp. 150–154. [Google Scholar]
- Van Schyndel, R.G.; Tirkel, A.Z.; Osborne, C.F. A digital watermark. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; Volume 2, pp. 86–90. [Google Scholar]
- Chen, L.; Liu, J.; Dong, W.; Sun, W. Image Hiding Scheme Based on Dense Residual Networks. Sci. Technol. Eng. 2024, 24, 03719-08. [Google Scholar]
- Singh, H.K.; Singh, A.K. Digital image watermarking using deep learning. Multimed. Tools Appl. 2024, 83, 2979–2994. [Google Scholar] [CrossRef]
- Charfeddine, M.; Mezghani, E.; Masmoudi, S.; Amar, C.B.; Alhumyani, H. Audio watermarking for security and non-security applications. IEEE Access 2022, 10, 12654–12677. [Google Scholar] [CrossRef]
- Luo, X.; Li, Y.; Chang, H.; Liu, C.; Milanfar, P.; Yang, F. DVMark: A deep multiscale framework for video watermarking. arXiv 2023, arXiv:2104.12734. [Google Scholar] [CrossRef] [PubMed]
- Uchida, Y.; Nagai, Y.; Sakazawa, S.; Satoh, S. Embedding Watermarks into Deep Neural Networks. In Proceedings of the 2017 ACM on International Conference on Multimedia Retrieval, Bucharest, Romania, 6–9 June 2017; pp. 269–277. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.Y.; Fan, Z.; Pan, P.; Wang, Z. StegaNeRF: Embedding Invisible Information within Neural Radiance Fields. arXiv 2022, arXiv:2212.01602. [Google Scholar]
- Luo, Z.; Guo, Q.; Cheung, K.C.; See, S.; Wan, R. CopyRNeRF: Protecting the CopyRight of Neural Radiance Fields. arXiv 2023, arXiv:2307.11526. [Google Scholar]
- Chen, W.; Zhu, C.; Ren, N.; Seppänen, T.; Keskinarkaus, A. Screen-cam robust and blind watermarking for tile satellite images. IEEE Access 2020, 8, 125274–125294. [Google Scholar] [CrossRef]
- Singh, O.P.; Singh, A.K. Image fusion-based watermarking in IWT-SVD domain. In Advanced Machine Intelligence and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2022; pp. 163–175. [Google Scholar]
- Thomas, R.; Sucharitha, M. Contourlet and Gould transforms for hybrid image watermarking in RGB color images. Intell. Autom. Soft Comput. 2022, 33, 879–889. [Google Scholar] [CrossRef]
- Kandi, H.; Mishra, D.; Gorthi, S.R.S. Exploring the learning capabilities of convolutional neural networks for robust image watermarking. Comput. Secur. 2017, 65, 247–268. [Google Scholar] [CrossRef]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. Hidden: Hiding data with deep networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 657–672. [Google Scholar]
- Zhang, C.; Karjauv, A.; Benz, P.; Kweon, I.S. Towards robust deep hiding under non-differentiable distortions for practical blind watermarking. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, 20–24 October 2021; pp. 5158–5166. [Google Scholar]
- Zhang, G.; Liu, J. Research on Watermark Algorithm for 3D Color Point Cloud Models. Comput. Technol. Dev. 2023, 33, 62–68. [Google Scholar]
- Li, B.; Wu, J.; Zhang, B. Improved Image Digital Watermark Algorithm for Zero Parallax Pixel Reorganization. Comput. Simul. 2023, 40, 244–248. [Google Scholar]
- Cui, J.; Zhang, G. Anti simplification blind watermarking algorithm based on vertex norm 3D mesh model. Comput. Eng. Des. 2023, 44, 692–698. [Google Scholar] [CrossRef]
- Xiong, X.; Wei, L.; Xie, G. A robust color image watermarking algorithm based on 3D-DCT and SVD. Comput. Eng. Sci. Gongcheng Kexue 2015, 37, 8. [Google Scholar]
- Pham, G.N.; Lee, S.H.; Kwon, O.H.; Kwon, K.R. A 3D Printing Model Watermarking Algorithm Based on 3D Slicing and Feature Points. Electronics 2018, 7, 23. [Google Scholar] [CrossRef]
- Hou, J.U.; Kim, D.G.; Lee, H.K. Blind 3D mesh watermarking for 3D printed model by analyzing layering artifact. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2712–2725. [Google Scholar] [CrossRef]
- Hamidi, M.; Chetouani, A.; El Haziti, M.; El Hassouni, M.; Cherifi, H. Blind robust 3D mesh watermarking based on mesh saliency and wavelet transform for copyright protection. Information 2019, 10, 67. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, H.; Fang, H.; Zhang, W.; Yu, N. Deep 3D mesh watermarking with self-adaptive robustness. Cybersecurity 2022, 5, 24. [Google Scholar] [CrossRef]
- Yoo, I.; Chang, H.; Luo, X.; Stava, O.; Liu, C.; Milanfar, P.; Yang, F. Deep 3D-to-2D Watermarking: Embedding Messages in 3D Meshes and Extracting Them from 2D Renderings. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10021–10030. [Google Scholar] [CrossRef]
- Wang, J.; Wu, H.; Zhang, X.; Yao, Y. Watermarking in Deep Neural Networks via Error Back-propagation. Electron. Imaging 2020, 32, 22-1–22-9. [Google Scholar] [CrossRef]
- Fan, L.; Ng, K.W.; Chan, C.S. Rethinking Deep Neural Network Ownership Verification: Embedding Passports to Defeat Ambiguity Attacks. 2019. Available online: https://proceedings.neurips.cc/paper_files/paper/2019/file/75455e062929d32a333868084286bb68-Paper.pdf (accessed on 16 September 2019).
- Rouhani, B.D.; Chen, H.; Koushanfar, F. DeepSigns: A Generic Watermarking Framework for IP Protection of Deep Learning Models. arXiv 2018, arXiv:1804.00750. [Google Scholar]
- Adi, Y.; Baum, C.; Cisse, M.; Keshet, J.; Pinkas, B. Turning Your Weakness Into a Strength: Watermarking Deep Neural Networks by Backdooring. 2018. Available online: https://www.usenix.org/system/files/conference/usenixsecurity18/sec18-adi.pdf (accessed on 13 February 2018).
- Shafieinejad, M.; Wang, J.; Lukas, N.; Li, X.; Kerschbaum, F. On the Robustness of the Backdoor-based Watermarking in Deep Neural Networks. arXiv 2019, arXiv:1906.07745. [Google Scholar]
- Liu, J.; Luo, P.; Ke, Y. Hiding Functions within Functions: Steganography by Implicit Neural Representations. arXiv 2023, arXiv:2312.04743. [Google Scholar]
- Chen, L.; Liu, J.; Ke, Y.; Sun, W.; Dong, W.; Pan, X. MarkNerf: Watermarking for Neural Radiance Field. arXiv 2023, arXiv:2309.11747. [Google Scholar] [CrossRef]
- Baluja, S. Hiding Images in Plain Sight: Deep Steganography. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]















| Method | NeRF Rendering | Watermark Extraction | |||
|---|---|---|---|---|---|
| PSNR ↑ | SSIM ↑ | LPIPS ↓ | Acc (%) ↑ | SSIM ↑ | |
| Standard NeRF | 33.23 | 0.9143 | 0.1113 | N/A | N/A |
| LSB + NeRF | 27.45 | 0.8446 | 0.1410 | N/A | N/A |
| DeepStega + NeRF | 26.41 | 0.8457 | 0.1429 | N/A | N/A |
| HiDDeN + NeRF | 27.88 | 0.8964 | 0.1418 | N/A | N/A |
| StegaNeRF | 30.31 | 0.9847 | 0.0276 | 100 | 0.9643 |
| CopyRNeRF | 30.54 | 0.9689 | 0.0327 | 100 | N/A |
| IW-NeRF (ours) | 21.32 | 0.6364 | 0.2852 | 100 | 1 |
| Method | NeRF Rendering | Watermark Extraction | |||
|---|---|---|---|---|---|
| PSNR ↑ | SSIM ↑ | LPIPS ↓ | Acc (%) ↑ | SSIM ↑ | |
| Standard NeRF | 27.76 | 0.8546 | 0.1453 | N/A | N/A |
| LSB + NeRF | 27.59 | 0.8435 | 0.1399 | N/A | N/A |
| DeepStega + NeRF | 26.98 | 0.8356 | 0.1269 | N/A | N/A |
| HiDDeN + NeRF | 27.64 | 0.8865 | 0.1512 | N/A | N/A |
| StegaNeRF | 28.21 | 0.8453 | 0.1423 | 100 | 0.9698 |
| CopyRNeRF | 30.67 | 0.9683 | 0.0457 | 100 | N/A |
| IW-NeRF (ours) | 22.54 | 0.6539 | 0.2798 | 100 | 1 |
| Expansion Rate | 1.75 | 2.14 | 2.66 | 3.40 | 4.50 |
| PSNR | 19.88 | 21.67 | 22.99 | 23.41 | 25.86 |
| Expansion Rate | 2.60 | 3.00 | 3.40 | 3.80 | 4.20 |
| PSNR | 20.94 | 21.58 | 23.21 | 24.34 | 25.66 |
| Dataset | Hot Dog | Lego | Fern | Flower |
|---|---|---|---|---|
| PSNR (dB) | 46.34 | 45.28 | 44.57 | 46.13 |
| SSIM | 0.9843 | 0.9789 | 0.9648 | 0.9881 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Song, C.; Liu, J.; Sun, W.; Dong, W.; Di, F. IW-NeRF: Using Implicit Watermarks to Protect the Copyright of Neural Radiation Fields. Appl. Sci. 2024, 14, 6184. https://doi.org/10.3390/app14146184
Chen L, Song C, Liu J, Sun W, Dong W, Di F. IW-NeRF: Using Implicit Watermarks to Protect the Copyright of Neural Radiation Fields. Applied Sciences. 2024; 14(14):6184. https://doi.org/10.3390/app14146184
Chicago/Turabian StyleChen, Lifeng, Chaoyue Song, Jia Liu, Wenquan Sun, Weina Dong, and Fuqiang Di. 2024. "IW-NeRF: Using Implicit Watermarks to Protect the Copyright of Neural Radiation Fields" Applied Sciences 14, no. 14: 6184. https://doi.org/10.3390/app14146184
APA StyleChen, L., Song, C., Liu, J., Sun, W., Dong, W., & Di, F. (2024). IW-NeRF: Using Implicit Watermarks to Protect the Copyright of Neural Radiation Fields. Applied Sciences, 14(14), 6184. https://doi.org/10.3390/app14146184






