A Novel Computational Paradigm for Reconstructing Solid CAD Features from a Segmented Manifold Triangular Mesh

Abstract

We introduce a novel computational paradigm for reconstructing solid computer-aided design (CAD) features from the surface of a segmented manifold triangular mesh. This paradigm addresses the challenge of capturing high-level design semantics for manifold triangular meshes and facilitates parametric and variational design capabilities. We categorize four prevalent features, namely extrusion, rotation, sweep, and loft, as generalized swept bodies driven by cross-sectional sketches and feature paths, providing a unified mathematical representation for various feature types. The numerical optimization-based approach conducts geometric processing on the segmented manifold triangular mesh patch, extracting cross-sectional sketch curves and feature paths from its surface, and then reconstructing appropriate features using the Open CASCADE kernel. We employ the personalized three-dimensional (3D) printed model as a case study. Parametric and variant designs of the 3D-printed models are achieved through feature reconstruction of the manifold triangular mesh obtained via 3D scanning.

1. Introduction

In the comprehensive industry chain of engineering software, reverse engineering computer-aided design (CAD) software plays a pivotal role [1]. Through the utilization of computers and three-dimensional (3D) scanning devices, this software assists engineers in swiftly realizing 3D reconstructions of physical objects in reverse and facilitates variant design [2]. It significantly improves the efficiency of product design in enterprises, shortens the research and development cycle, and is increasingly acknowledged as a crucial design tool for industrial enterprises.

Currently, digital 3D models in reverse engineering CAD software are commonly represented as manifold meshes [3] derived from scanned 3D point clouds. A manifold triangular mesh is a surface model that discretizes the surface of a CAD model and produces triangular facets to approximate the surface [4]. Manifold triangular mesh data can express only the geometric and topological relationships among the vertices and edges of triangular facets, and they lack the ability to represent the high-level semantic and design aspects of CAD models. Furthermore, CAD model surfaces often include planar and quadratic surfaces, resulting in sparse and sharp-edged manifold meshes [5]. Reconstructing manifold meshes into continuous geometric objects such as B-splines or NURBS and applying them to CAD software can lead to shape distortion and the loss of semantic features.

The development of geometric modeling technology has advanced through four distinct stages: wireframe modeling, surface modeling, solid modeling, and feature modeling [6]. Feature modeling acts as a direct representation of the design intentions within solid CAD models, enabling the expression of elevated semantics and design details [7]. This function significantly aids in the seamless integration of CAD/CAM and propels progress towards higher-dimensional digital twin modeling [8]. Hence, the reconstruction of solid CAD features from manifold triangular meshes acquired through reverse engineering CAD software is crucial.

In this paper, we present a novel computational paradigm for reconstructing solid CAD features from the surface of a segmented manifold triangular mesh. We make the following contributions in this paper.

• We present a unified mathematical representation for categorizing four common solid CAD features as generalized swept bodies driven by cross-sectional sketches and feature paths. It facilitates the efficient realization of feature reconstruction through the CAD kernel.
• Utilizing a numerical optimization-based approach, we perform geometric processing on the segmented manifold triangular mesh patch, leading to the extraction of cross-sectional sketch curves and feature paths from its surface.
• We demonstrate how this computational paradigm enables parametric and variant designs of the manifold triangular meshes acquired from 3D scanning, enhancing their compatibility with personalized 3D-printed models.

The remaining sections of the paper are structured as follows: Section 2 presents a review of prior efforts in recovering or extracting solid CAD features from unstructured data like 3D point clouds or polygon meshes. Section 3 outlines our computational paradigm. In Section 4, we detail our method for extracting cross-sectional sketch curves and feature paths of four types of solid CAD features from segmented manifold triangular mesh patches. Section 5 presents the experimental results of our approach for reconstructing four types of solid CAD features. Concluding remarks end the paper.

2. Related Work

The technologies most relevant to this article are primitive fitting from unconstructed data and solid feature reconstruction, which we briefly describe in this section.

2.1. Primitive Fitting

Fitting primitives from unstructured 3D data holds significant industrial applications [9] and has garnered considerable attention in computer-aided design research, especially within the realm of reverse engineering [10]. Previous studies have concentrated on segmenting input data—such as point clouds or triangular meshes—into regions and subsequently matching them with geometric primitives characterized by diverse types and parameters, with a focus on numerical optimization.

Early methodologies incorporated probabilistic search techniques such as RANSAC [11] or variational optimization methods [12,13] that iterated between primitive fitting and segmentation to accurately match primitive surface patches to input shapes represented as point clouds or triangular meshes. Subsequently, global optimization with structural constraints was applied to enhance local primitive fitting and ensure overall consistency [14,15,16]. Benkő et al. [17] introduced a methodology for fitting primitives from multi-view 3D point clouds. Rather than determining the geometric primitive type in each segmented patch, the authors employed various approximation tests to fit a parameterized geometric primitive. The accuracy of edges plays a pivotal role in the efficacy of this method, which produces intriguing outcomes when applied to dense 3D meshes with edges aligned well with the continuous boundaries of the actual object. Romanengo et al. [18] introduced a robust method utilizing the Hough transform to recognize geometric primitives within 3D point clouds of mechanical CAD objects. The proposed approach effectively handles noise and outliers by detecting the primitives present in the point cloud and determining the optimal geometric parameters associated with them.

In recent years, the emergence of machine learning has led to the adoption of more advanced techniques utilizing neural networks for learning data-driven priors. Convolutional neural networks (CNNs) have become common machine learning models in computer graphics, applied for identifying primitives and parameters from discrete datasets like point clouds and triangular meshes. CNN-based methods typically begin by classifying input points as potential segment anchors and then consolidating these classified points into groups through clustering and searching procedures. Li et al. [19], Sharma et al. [20], Yan et al. [21], and Huang et al. [22] trained point-based CNNs to allocate patch primitive types and parameters to each input point, effectively addressing segmentation and fitting challenges. This was accomplished by training on extensively annotated CAD datasets.

The existing literature on primitive fitting primarily focuses on fitting basic geometric shapes, such as planes, cylinders, spheres, and cones, to point cloud data or mesh surfaces. Common techniques include least squares fitting, RANSAC algorithms, and hybrid approaches. Despite their widespread use, these methods frequently encounter several issues: high sensitivity to noise and outliers, difficulties handling complex geometries with intersecting primitives and intricate surface details, inefficiencies in processing large datasets, and the necessity for significant user intervention to guide the fitting process.

Our proposed computational paradigm addresses these issues by employing a robust numerical optimization approach that minimizes sensitivity to noise and outliers, ensuring more accurate fitting of primitives. The unified mathematical framework we introduce can handle various primitive types, simplifying the process for complex geometries. Additionally, our method is designed to efficiently process large datasets with minimal computational overhead and reduces the need for user intervention by automating the extraction of cross-sectional sketches and feature paths from segmented mesh surfaces.

2.2. Solid Feature Reconstruction

In the field of reverse engineering, triangular mesh models reconstructed from unstructured data are no longer adequate for the requirements of product parametric design and variant design. It is essential that a reconstructed 3D model includes solid CAD features that precisely convey forward design information through a process referred to as solid feature reconstruction.

In recent years, Huang and Menq [23] proposed a methodology for reconstructing a solid model from a 3D point cloud. Initially, the target object’s shape is reconstructed by iteratively merging multiple input point clouds into a watertight triangular mesh. Subsequent to this, mesh segmentation is employed to isolate individual geometric feature surfaces from the triangular mesh. Eventually, the manifold topology, which delineates the connectivity between different geometric surfaces, is automatically derived, and a mathematical representation of each geometric feature is generated. The accuracy of the 3D mesh edges significantly impacts the efficacy of this method, consequently constraining the complexity of the reconstructed CAD model. Bénière et al. [24] introduced a comprehensive approach for reconstructing a solid model from a 3D mesh, comprising three sequential steps: primitive extraction, wire construction, and solid creation. Initially, the matching geometric primitive (such as a plane, sphere, cylinder, or cone) corresponding locally to the 3D mesh of interest is determined by analyzing differential geometry operators. Subsequently, the relationships among all the extracted geometric primitives are established to calculate the intersection curves between pairs of these primitives. These curves are then amalgamated to construct a continuous wire. Subsequently, a consistent solid CAD model is composed by amalgamating the information extracted or reconstructed throughout the prior two steps. Goyal et al. [25] focused on the comprehensive and detailed shape analysis of a triangular mesh. They explored the utilization of protruding section sets (PCSs) to highlight model features. Additionally, they introduced a linear embedded algorithm (LLE) for examining these protruding sections based on cross-sectional geometric properties. Subsequently, they developed a solid model and introduced an affinity propagation algorithm (AP) to cluster these protruding sections, forming distinct scanning parts by propagating constraint relationships among them. Wang et al. [26] presented a method for transforming a triangular mesh model into a solid model. Initially, preprocessing is utilized to eliminate noise from the input mesh, followed by mesh segmentation to extract distinct geometric feature blocks. Through tailored approaches for entity and surface features, the original characteristics are reconstructed from the segmented feature blocks. Subsequently, Boolean or trimming operations are employed on both the entity and surface features to shape the final solid model. Subsequently, Wang et al. [27] focused on the triangular mesh as their research subject. They delved into techniques for extracting characteristic parameters related to four types of features, namely extrusion, rotation, sweep, and loft, and analyzed the two-dimensional cross-sectional profiles of these features using piecewise fitting and global optimization methods. Marinov et al. [28,29] presented an innovative technique for converting an open triangular mesh, with its perimeter bounded by a set of smooth curves, into a T-NURCC surface that smoothly approximates both the mesh and curve geometry. Initially, a transfinite interpolation construction process is utilized to define a $C^0$ patch network that interpolates the curves at the boundaries and coincides with the mesh internally. Following that, an approximation algorithm is implemented to transform the network into a T-NURCC surface. Finally, the resulting T-NURCCs with adjacent faces are integrated to form a watertight, low-tolerance solid CAD model.

Existing methods aim to convert point cloud data or mesh surfaces into solid CAD models with high-level design semantics. Traditional approaches often include direct conversion techniques, feature recognition, and model fitting. However, these methods face several challenges: they frequently fail to capture and preserve the original design intent and high-level semantics, struggle with accurate recognition of complex features such as sweeps and lofts, are computationally intensive, and have difficulties ensuring seamless integration with existing CAD software for parametric and variational design capabilities.

Our novel computational paradigm significantly improves upon traditional methods by capturing high-level design semantics through the use of cross-sectional sketches and feature paths, thereby preserving the original design intent in the reconstructed model. The robust numerical optimization approach ensures the accurate extraction and reconstruction of complex features. Our method also enhances computational efficiency by optimizing the geometric processing of segmented manifold triangular mesh patches. Furthermore, leveraging the Open CASCADE kernel ensures seamless integration with existing CAD systems, enabling parametric and variational design capabilities for the reconstructed models.

3. Overview

Our proposed computational paradigm unfolds in two primary phases, as illustrated in Figure 1.

Extracting feature paths. The principal curvatures of each vertex in the triangular meshes are calculated, and every segmented patch is considered a distinct solid feature for reconstruction. To acquire feature sections, initial sampling points are determined based on the vertex principal curvature values, and the initial feature section ($S^{\prime }$) is defined by the vertex principal directions. Utilizing Gaussian mapping of ($S^{\prime }$) and iterative optimization of its direction, the feature section ($S$) is obtained. The acquisition of feature paths involves obtaining all vertices of the triangular mesh model intersected by each feature section, calculating the centroids of these vertices, sequentially connecting the centroids to form a polyline $\mathsf{\Lambda }$, identifying various line patterns (line, arc, B-spline) within the polyline ($\mathsf{\Lambda }$), and ultimately deriving the characteristic path Γ.

Extracting cross-sectional sketches. Based on the intersection points of the characteristic section and the triangular surface fragment, the initial section sketch is generated. The types of lines (line, arc, B-spline) are selected based on the curvatures and normal vectors of the individual points within the sketch. Segment fitting and application of geometric constraints are then carried out for each line type. Furthermore, global geometric constraint optimization equations are developed and resolved to obtain the optimal cross-sectional sketch ($C$) globally, thus avoiding concerns arising from excessive constraint definition. Ultimately, guided by the feature path $\Gamma$ and the set of cross-sectional sketch curves $C\left(t\right)$, the segmented feature patch is reconstructed to incorporate the designated basic features, such as stretching, rotating, sweeping, and releasing, utilizing the feature modeling capabilities of Open CASCADE [30].

In the CAD software for solid modeling, solid features are defined as a geometric entity that embodies the design intent, influenced by cross-sectional sketch curves and feature paths, while also facilitating parametric editing [31]. Hence, to reconstruct solid features from manifold meshes, it is essential to extract two fundamental components from the segmented triangular mesh patches: the cross-section sketch curves and the feature paths. Four typical entity features—extrusion, rotation, sweep, and loft—are classified into a generalized sweep volume (GSV), thereby establishing a unified mathematical representation for various basic features. GSV is formulated as

$$\mathrm{G}\mathrm{S}\mathrm{V}={\int }_{\Gamma }C\left(t\right)ds={\int }_0^{L}C\left(t\right)ds$$

(1)

where $C\left(t\right)$ represents the cross-sectional sketch curves that evolve over the parameter t, where t ranges from 0 to 1. $\Gamma$ denotes the feature path, and $ds$ represents the differential of the arc length along the feature path $\Gamma$, where s ranges from 0 to the full length of the arc L. Essentially, GSV involves the spatial curve integral of the cross-sectional sketch curve along the feature path. Figure 2 illustrates the GSV representations of the four typical solid features.

4. Methodology

This chapter deals with the methodology for reconstructing solid CAD features from segmented manifold triangular mesh patches.

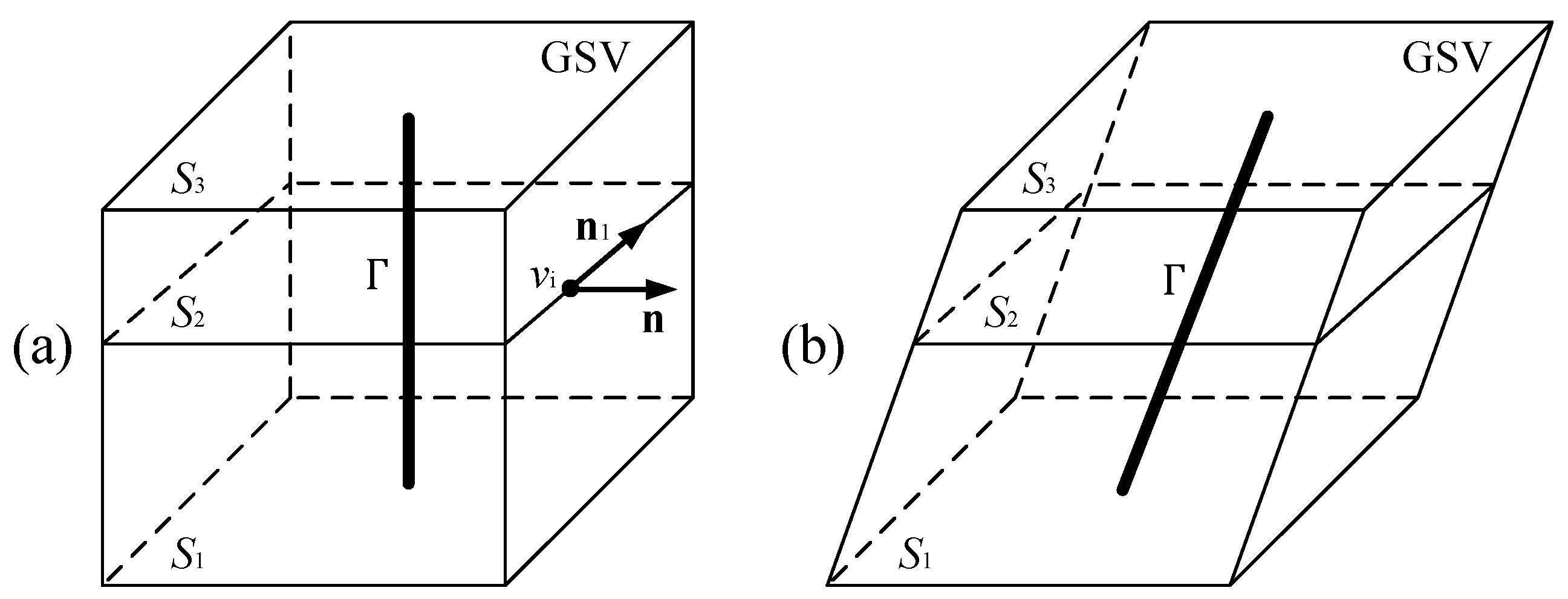
4.1. Extract Feature Paths

This section outlines the process of extracting feature paths from the segmented mesh.

4.1.1. Estimate Principal Curvatures of Each Vertex

At a point $v$ on a surface $\mathsf{\Pi }$, the principal curvatures, denoted as $K_1$ and $K_2$, represent the maximum and minimum normal curvatures, occurring in orthogonal directions known as principal directions, denoted as $T_1$ and $T_2$ [32]. $R_1$ and $R_2$ represent the curvature radii associated with $K_1$ and $K_2$, respectively, as depicted in Figure 3. Each point on a smooth surface possesses a unique tangent plane that offers a linear approximation of the surface at that location. By examining the normal curvature in various directions within this tangent plane, one can determine the principal directions, which correspond to the eigenvectors of the shape operator. These principal directions are orthogonal to each other. Understanding the principal curvatures and principal directions is essential for defining feature paths and cross-sectional sketches in our CAD reconstruction methodology, as they provide detailed insights into the local geometric properties of the surface.

This study employs the curvature estimation method introduced by Mao et al. [34], which involves interpolating three endpoints and their respective normal vectors of each triangle to form a curved patch. Subsequently, the curvature per triangle is computed for the neighboring triangles surrounding a specific mesh point of interest. Similar to deriving per-vertex normal vectors from adjacent per-triangle normals, the per-vertex curvature is calculated by determining a weighted average of the per-triangle curvatures.

Upon determining the principal curvatures $K_1$ and $K_2$ of the vertices, the computational approach presented by Taubin [35] is employed to derive the principal directions $T_1$ and $T_2$. This method involves constructing symmetric matrices to identify the two eigenvectors that correspond to the principal directions $T_1$ and $T_2$. Following this, the directions of the feature sections are determined utilizing the previously obtained principal directions.

4.1.2. Generate Feature Sections via Gaussian Mapping

According to the geometric relationship between the feature section $S$ and the feature path $\Gamma$, solid features can be classified into two groups, as shown in Figure 4.

Given the widespread application of solid features in CAD software, our study exclusively addresses the reconstruction of the first type of solid features. As is shown in Figure 4a, feature section $S$ is consistently perpendicular to the tangent direction of the Frenet–Serret frame along the path $\Gamma$. Moreover, at any intersection point $v_i$ of the feature section $S$ with the manifold mesh surface, it aligns orthogonally with the tangent direction of the Darboux frame at that specific location. Consequently, the parametric expression for the initial feature section $S^{\prime }$ can be established using the principal direction vector ${\mathbf{n}}_1$, correlated with the maximum curvature $K_1$ of the primary curvature at $v_i$, the normal vector $\mathbf{n}$ at $v_i$, and $v_i$: $S^{\prime }=v_i+\lambda {\mathbf{n}}_1+\mu \mathbf{n}$, where $\lambda$ and $\mu$ range from 0 to 1.

According to Sellamani et al. [36], cross-section Gaussian mapping is characterized by utilizing the cross-section normal vector at a specific point on the manifold grid surface as the normal vector of the Gaussian sphere’s great circle (Gaussian sphere polar axis). Gaussian mapping has been introduced that effectively generates significant cross-sections at any point on the manifold mesh, approximating the local sweep. This novel concept offers an innovative idea for us to create the initial feature section $S^{\prime }$.

It is imperative to carefully select the initial sampling points on the manifold mesh surface. The curvature radius vector $\mathbf{e}$ at vertex $v_i$ is classified as concave (−) if it is oriented opposite to the normal vector, and as convex (+) if it aligns with the normal vector. Given that a vertex possesses two principal curvatures, the concave–convex characteristics of vertex $v_i$ on the mesh are determined as follows: (−,−) convex feature; (+,−) or (−,+) saddle feature; (+,+) concave feature; (0,0) flat. Inaccurate selection of initial sampling points can result in a reduction in the precision of the Gaussian mapping. Hence, the following selection principles are defined:

• Sampling at points where the concave and convex features are (0,0) is prohibited, meaning sampling the cross-section of the segmented area to be reconstructed is not allowed;
• Aim to sample at concave features (+,+) or convex features (−,−), ensuring that the discrepancy between the two principal curvature values meets the requirement: $\left|K_1-K_2\right|\ge \left[K\right]$. Here, $\left[K\right]$ represents the main curvature difference threshold set at 0.005 [36].

Under the condition that the aforementioned principles are met, RANSAC [11] can be employed to determine the initial sampling point. Subsequently, the initial characteristic section $S^{\prime }$ is defined based on the primary curvature and primary direction of the sampling point. The direction of $S^{\prime }$ undergoes continuous iterative optimization through Gaussian mapping. To execute Gaussian mapping effectively, it is crucial to identify the intersection of $S^{\prime }$ with the triangles and locate all intersections between $S^{\prime }$ and the mesh. When a plane intersects with a triangle, it can occur at only two instances: intersecting with a vertex or an edge of the triangle. This process initiates from the initial sampling point vi on the initial characteristic section $S^{\prime }$ and traverses the neighboring points in the primary direction until returning to point $v_i$. The discussion will explore two scenarios.

If a point $v_j$ is present on $S^{\prime }$ among the first-order neighborhood points of $v_i$, then the new point $v_j$ should be adopted as the starting point for further exploration of its neighbors. It is crucial to avoid returning to $v_i$ to prevent the algorithm from getting stuck in an infinite loop. On the other hand, if there are no points on $S^{\prime }$ within the first-order neighborhood of $v_i$, each of $v_i$’s first-order neighbors should be successively substituted into the parametric equation of $S^{\prime }$. When two adjacent first-order neighbors $v_m$ and $v_n$ result in a negative product upon substitution into the equation, it indicates that the edge $\overline{v_m{v}_n}$ intersects with $S^{\prime }$. The point of intersection $v_l$ is determined, and its normal vector ${\mathbf{n}}_l$ is calculated using linear interpolation between the normal vectors of $v_m$ and $v_n$ for Gaussian mapping:

$${\mathbf{n}}_l={\displaystyle \frac{a{\mathbf{n}}_m+b{\mathbf{n}}_n}{‖a{\mathbf{n}}_m+b{\mathbf{n}}_n‖}}$$

(2)

where ${\mathit{n}}_m$ and ${\mathbf{n}}_n$ represent the normal vectors of points $v_m$ and $v_n$, while $a$ and $b$ denote the distances from $v_l$ to $v_m$ and $v_n$, respectively.

To create cross-sectional Gaussian mapping, the initial points of the normal vectors of intersections between $S^{\prime }$ and the manifold mesh are translated to the center of the Gaussian sphere. Given the discrete distribution characteristics of the endpoints of all normal vectors, it becomes imperative to conduct plane fitting based on the least squares method. Subsequently, the angle between the normal vector ${\mathbf{n}}_f$ of the fitting plane $S_f$ and the normal vector ${\mathbf{n}}_s$ of the original section $S^{\prime }$ is examined for iterative corrections. Compute the cosine of the angle between ${\mathbf{n}}_f$ and ${\mathbf{n}}_s$ represented as $\mathrm{c}\mathrm{o}\mathrm{s}〈{\mathbf{n}}_f,{\mathbf{n}}_s〉$, and proceed with the following discussion:

(1) If $\left(1-\mathrm{c}\mathrm{o}\mathrm{s}〈{\mathbf{n}}_f,{\mathbf{n}}_s〉\right)\ge 0.0001$, adjustments to the orientation of the fitting plane are necessary. This involves translating the initial section normal vector ${\mathbf{n}}_s$ to the center of the Gaussian sphere, utilizing it as the polar axis of the sphere to compute the normal vector and angle at each intersection point. The included angle ${\theta }_i$ of the axis is then determined, followed by calculating the mean $E$ and standard deviation $\sigma$ of all included angles. Subsequently, a Gaussian probability distribution function is established, and normal vectors beyond $\pm 3\sigma$ are eliminated. The process continues by refitting the remaining normal vectors until the specified criteria are satisfied.

(2) If $\left(1-\mathrm{c}\mathrm{o}\mathrm{s}〈{\mathbf{n}}_f,{\mathbf{n}}_s〉\right)<0.0001$, the current fitting plane is accepted as the definitive feature section.

4.1.3. Generate Feature Paths from Centroids

A set of feature sections, denoted as $\left\{S_i\right\}$, is positioned to encompass the segmented manifold mesh patch of the solid feature being reconstructed. This is achieved by connecting the center of mass of the vertices intercepted by each section sequentially, resulting in the formation of a polyline. The detailed steps involved in this process are outlined below:

Step 1: From feature section $S_1$, the algorithm iterates through all the first-order neighboring points of the initial sampling point $v_i$ to identify the point $v_j$ that has the smallest angle with respect to the vector connecting it to $v_i$ and the normal vector of $S_1$.

Step 2: Continue traversing all first-order neighborhood points, starting from $v_j$, and repeat Step 1 until the algorithm returns to $v_i$.

Step 3: Calculate the centroid for all the vertices extracted in Step 2 using the Formula (3), where $x_c$, $y_c$, $z_c$ represent the X, Y, and Z coordinates of the centroid, respectively. $N$ represents the total number of sampling points in the current feature section. Repeat Step 1 and Step 2 until the centroids of all the feature sections have been calculated, then connect the centroids that have already been calculated sequentially to form polyline $\mathsf{\Lambda }$.

$$\left\{\begin{array}{c}{x}_c={\sum }_{k=1}^N{x}_k/N\\ y_c={\sum }_{k=1}^N{y}_k/N\\ z_c={\sum }_{k=1}^N{z}_k/N\end{array}\right.$$

(3)

The subsequent procedure involves classifying the line type of polyline $\mathsf{\Lambda }$ using the curvature and normal vector of the centroids, as illustrated in Figure 5.

For the discrete centroid point sequence $\left\{v_1^c,v_2^c,\cdots ,v_n^c\right\}$, the curvature $K_i$ of centroid $v_i^c$ is determined based on itself, as well as its preceding and succeeding neighbor points $v_{i-1}^c$ and $v_{i+1}^c$, calculated using the following formula [27]:

$$K_i={\displaystyle \frac{4S_{△}{v}_{i-1}^c{v}_i^c{v}_{i+1}^c}{\overline{v_i^c{v}_{i-1}^c}\cdot \overline{v_{i+1}^c{v}_i^c}\cdot \overline{v_{i+1}^c{v}_{i-1}^c}}}$$

(4)

where $S_{△}{v}_{i-1}^c{v}_i^c{v}_{i+1}^c$ represents the area of the triangle formed by vertices $v_{i-1}^c$, $v_i^c$, and $v_{i+1}^c$, calculated using Heron’s formula based on the triangle’s side lengths. In addressing the curvature calculation for the polyline $\mathsf{\Lambda }$’s endpoints $v_1^c$ and $v_n^c$, the edges $\overline{v_1^c{v}_2^c}$ and $\overline{v_{n-1}^c{v}_n^c}$ are extended equidistantly in opposite directions to points $v_0^c$ and $v_{n+1}^c$, ensuring $K_0=K_{n+1}=0$. Additionally, the normal vector of the centroid $v_i^c$ is formulated as:

$${\mathbf{n}}_i={\displaystyle \frac{{\mathbf{n}}_{i-1,i}\times {\mathbf{n}}_{i,i+1}}{‖{\mathbf{n}}_{i-1,i}\times {\mathbf{n}}_{i,i+1}‖}}$$

(5)

where ${\mathbf{n}}_{i-1,i}$ and ${\mathbf{n}}_{i,i+1}$ represent the normal vectors of edges $\overline{v_{i-1}^c{v}_i^c}$ and $\overline{v_i^c{v}_{i+1}^c}$, which are formulated as:

$$\left\{\begin{array}{c}{\mathbf{n}}_{i-1,i}={\displaystyle \frac{{\mathbf{s}}_{i-1,i}\times \left({\mathbf{s}}_{i-1,i}\times {\mathbf{s}}_{i,i+1}\right)}{‖{\mathbf{s}}_{i-1,i}\times \left({\mathbf{s}}_{i-1,i}\times {\mathbf{s}}_{i,i+1}\right)‖}}\\ {\mathbf{n}}_{i,i+1}={\displaystyle \frac{{\mathbf{s}}_{i,i+1}\times \left({\mathbf{s}}_{i-1,i}\times {\mathbf{s}}_{i,i+1}\right)}{‖{\mathbf{s}}_{i,i+1}\times \left({\mathbf{s}}_{i-1,i}\times {\mathbf{s}}_{i,i+1}\right)‖}}\end{array}\right.$$

(6)

where ${\mathbf{s}}_{i-1,i}$ and ${\mathbf{s}}_{i,i+1}$ represent the direction vectors of edges $\overline{v_{i-1}^c{v}_i^c}$ and $\overline{v_i^c{v}_{i+1}^c}$, respectively.

Commencing from the initial point $v_1^c$ of polyline $\mathsf{\Lambda }$, tolerance processing is conducted on the centroid curvature $K_i$ and the angle between the normal vector ${\phi }_{i-1,i}$. The defined tolerance conditions are as follows:

$$\left\{\begin{array}{c}0\le K_i\le 0.1\\ 0\le {\phi }_{i-1,i}\le 2°\end{array}\right.$$

(7)

Line type judgment rules dictate that if, in the path from the initial point $v_1^c$ to a certain point $v_i^c$, either the curvature tolerance condition or the normal vector angle tolerance condition is not met, the segment between $v_1^c$ and $v_{i-1}^c$ is considered a straight line. This section is removed, and a straight-line segment is created connecting $v_1^c$ and $v_{i-1}^c$. Similarly, if from point $v_i^c$ to point $v_j^c$ the curvature tolerance condition is met but the normal vector angle tolerance condition is not, the segment from $v_i^c$ to $v_j^c$ is recognized as an arc. The arc is then fitted utilizing the RANSAC [11], ensuring that $v_i^c$ and $v_j^c$ are positioned at the arc’s start and end points. For points in polyline $\mathsf{\Lambda }$ that cannot be classified as either straight lines or arcs, a B-spline curve fitting process [37] is employed.

4.2. Extract Cross-Sectional Sketches and Reconstruct Features

This section describes the extraction of cross-sectional sketches necessary for feature reconstruction.

4.2.1. Segmental Fitting of Curves on Sketch

Intersecting a feature section $S$ in the basic feature with an edge or vertex of the triangular mesh feature area forms a continuous ordered set of ring data points $\left\{p_1,p_2,\cdots ,p_N\right\}$, which are sequentially connected to create a polyline $\sum$. The analysis of various basic line shapes within the polyline $\sum$ follows the method outlined in Section 4.1.3. This method categorizes the basic line shapes into three types: straight lines, arcs, and B-splines. The judgment considers both the curvature of the data points and the normal vectors. As the curvature value of the set of ring data points intercepted by the feature section is notably higher than that of the center of mass points of the feature path $\Gamma$ presented in Section 4.1, with a potential abrupt change in curvature, a modification to the tolerance condition is necessary:

$$\left\{\begin{array}{c}0\le K_i\le 0.5\\ 0\le {\phi }_{i-1,i}\le 5°\end{array}\right.$$

(8)

As the line pattern judgment method was outlined in Section 4.1.3, this section will not reiterate the precise procedure. Each categorized line pattern requires a sequential fitting operation to fully convert it into the respective line pattern type.

Spatial straight lines are fitted using the least squares method [38]. Consider the set of points to be fitted as $\sum \left(x_i,y_i,z_i\right)$, the parametric equation for a spatial straight line is presented as follows:

$${\displaystyle \frac{\left(x-m\right)}{p}}={\displaystyle \frac{\left(y-n\right)}{q}}={\displaystyle \frac{z}{1}}$$

(9)

where parameters to be determined are $m$, $n$, $p$, and $q$.

To fit spatial circular arcs, the Lagrange multiplier method [39] is employed. Consider the set of points to be fitted as $\sum \left(x_i,y_i,z_i\right)$ and designate the coordinates of the center of the circular arc as $C_O\left(x_O,y_O,z_O\right)$. The spatial circular parametric equation is then constructed as follows:

$$\left\{\begin{array}{c}Ax+By+Cz+D=0\\ {\left(x-x_o\right)}^2+{\left(y-y_o\right)}^2+{\left(z-z_o\right)}^2=r^2\end{array}\right.$$

(10)

where parameters to be determined are $A$, $B$, $C$, $D$, $x_o$, $y_o$, $z_o$, and $r$.

Similarly, for points in polyline $\sum$ that cannot be classified as either straight lines or arcs, a B-spline curve fitting process [37] is employed. The points to be fit as B-spline curves are located on the flow mesh surface, reflecting the contour characteristics of the model. To optimize the alignment between the fitted B-spline curve and the original mesh surface contour, these points should be used as the data points for the reverse calculation of the B-spline curve’s control points [40].

4.2.2. Solving Geometry Constraints and Optimization

When intersecting the line segments, arcs, and B-spline curves resulting from fitting multiple segments of polyline $\sum$ at their endpoints, one must take into account the potential geometric constraints among the fitted curves of each segment. Additionally, to prevent the issue of over-constraining that could arise from sequentially adding geometric constraints, constraint solving is essential to achieve the globally optimal cross-sectional sketch.

Graphic elements are classified into three types: straight lines, arcs, and B-splines. The types of geometric constraints are categorized as coincident, parallel, angular, perpendicular, tangent, concentric, internally tangent, externally tangent, and concentric constraints. We employ the Python package from GeoSolver [41,42] for constraint resolution to achieve a globally optimal cross-sectional sketch.

4.2.3. Reconstructing Features Based on Open CASCADE

Utilizing the application programming interface (API) functions of Open CASCADE, guided by the cross-sectional sketch curve $C\left(t\right)$ and the feature path $\Gamma$, the reconstruction of four distinct features (extrusion, rotation, sweep, lofting) is conducted. The subsequent section elaborates on the specific methodologies for reconstructing these four features.

(a)

Extrusion feature

For extrusion features, the pseudocode snippet for this process is provided as Algorithm 1:

Algorithm 1. Procedure of reconstructing extrusion feature

(b)

Sweep feature

For sweep features, the pseudocode snippet for this process is provided as Algorithm 2:

Algorithm 2. Procedure of reconstructing sweep feature

(c)

Rotation feature

For rotation features, the pseudocode snippet for this process is provided as Algorithm 3:

Algorithm 3. Procedure of reconstructing rotation feature

(d)

Lofting feature

For lofting features, the pseudocode snippet for this process is provided as Algorithm 4:

Algorithm 4. Procedure of reconstructing lofting feature

5. Experimental Results

5.1. Implementation for Extracting Feature Paths and Cross-Sectional Sketches

In order to evaluate the feasibility of the feature path acquisition method detailed in Section 4.1, a case study was conducted to optimize the orientation of feature cross-sections and extract feature paths. The results of the implementation are presented as follows.

Figure 6 demonstrates the comparative effects before and after the optimization of the feature cross-sectional orientation across six types of triangular mesh models. For the initial four CAD models with clearly defined sharp features, the test findings indicate that the number of iterations required is consistently below five cycles. In contrast, for the fifth and sixth models characterized by noise and intricate surfaces common in cultural and creative designs, the iteration times can be controlled within 10 cycles. The results validate the capability of our approach to reduce the duration of this process while ensuring the accurate extraction of feature cross-sections.

Figure 7 depicts the extraction of four typical feature sections and paths to assess their significance. Feature sections are obtained from the CAD meshes, showcasing distinctive boundary features in Figure 7a–c, as well as the intricate surface in Figure 7b. These sections are aimed at accurately reconstructing the original triangular mesh without any visible intersections or repetitions. Likewise, feature paths, exemplified in Figure 7a,c for arc-type paths, Figure 7b for straight-line paths, and Figure 7d for B-spline paths, are also acquired. The validation results validate that the discussed feature extraction method effectively captures these attributes for reconstruction within the triangular mesh region. Specifically tailored for CAD triangular mesh models, this approach minimizes the number of sections utilized to streamline subsequent feature reconstruction, thereby reducing computational complexity.

To evaluate the feasibility of the cross-sectional sketch extraction approach outlined in Section 4.2, four types of features (extrusion, rotation, sweep, and lofting) were selected for verification analysis. The triangular mesh region designated for transforming into the mentioned features was conceptualized as a generalized sweep volume (GSV) defined by the cross-sectional sketch and feature path. The reconstruction procedure was divided into four phases: point sampling, piecewise fitting of curves, applying geometric constraints, and feature reconstruction. The results of the implementation are elaborated upon below:

(a)

Point sampling

Figure 8 presents the segmented mesh area designated for reconstructing the four types of features, depicting the extracted results of the cross-sectional sampling points. The results highlight the efficacy of our method in precisely capturing the sampling points from the triangular mesh contour intercepted by the feature section. Notably, areas with pronounced curvature, such as fillets and chamfers, exhibit a significantly higher density of sampling points compared to regions with lower curvature, such as straight lines. This varying distribution guarantees that the sampling point contour successfully replicates the true cross-sectional shape to a substantial extent.

(b)

Piecewise fitting of curves

The sampling point contour undergoes piecewise fitting, incorporating straight line segments (L), arcs (C), and B-spline curves (B) as illustrated in Figure 9. For the extrusion feature, 10 straight lines and two arc segments are utilized. In the rotation feature, two complete arc segments are employed. The sweep feature involves two arc segments and two B-spline curve segments. The lofting feature transforms the sampling point contour into a closed B-spline curve. It is important to note that while the segmented fitting results in a closed and well-reconstructed sketch, the absence of geometric constraints and dimensions results in irregular shaping that inadequately represents the original design intent.

(c)

Applying geometric constraints

Geometric constraints are applied to each segmented curve upon fitting, dimensions are labeled accordingly, and the over-defined constraint issue is optimized. This effect is demonstrated in Figure 10, where the curve highlighted in red represents an over-defined curve, while the optimized curves are all indicated in black.

(d)

Feature reconstruction

In Figure 11, the reconstruction effects of the four types of features are presented, along with the parametric and variant designs.

The experimental results illustrate that our methodology can not only convert unstructured triangular meshes into appropriate CAD features but also parameterize and customize features for variant design. This sets the stage for extracting sophisticated design details, such as construct solid geometry (CSG) trees, from unstructured manifold surfaces.

5.2. Comparative Analysis

In this section, we compare our method with representative CAD reconstruction works that produce geometric primitives, where applicable, to highlight the relative strengths of different approaches. Specifically, we focus on works that adopt the “segmentation + primitive fitting” paradigm for patch reconstruction, such as RANSAC [11], SPFN [19], ParSeNet [20], and HPNet [21].

The dataset used in this study is a subset of the ABC dataset [43]. It consists of 20,000 models for training and 3000 models for testing. To ensure fair comparisons, this dataset follows the same split as used by Sharma et al. [20]. Before analysis, all meshes undergo a data cleaning process to eliminate errors.

We utilize four metrics to evaluate the accuracy of the reconstructed CAD model compared to the ground truth (GT): (1) The Chamfer distance, a bidirectional residual measure that disregards separation into surfaces [19,20,21]. (2) The residual error, which measures the degree of alignment between each generated patch and its corresponding target segment regions, quantified using the calculation formula provided in [19,20,21]. (3) P-coverage, which measures the percentage of input vertices on the mesh surface that was covered by the predicted patches, calculated according to the formula described in [19,20,21]. (4) The patch-to-patch topology error, which quantifies the structural fidelity of the reconstructed topology by measuring its deviation from the adjacency matrix of the GT, also discussed in [19,20,21].

According to the experimental results presented in Figure 12, our method demonstrates notable advantages over other “segmentation + primitive fitting” approaches in terms of Chamfer distance, residual error, and P-coverage, which are the three primary metrics for evaluating the accuracy of geometric reconstruction. Compared to RANSAC [11], SPFN [19], ParSeNet [20], and HPNet [21], our results show a significant reduction in Chamfer distance. Additionally, our method significantly improves the P-coverage metric. This improvement is primarily due to our unified mathematical representation that categorizes four common solid CAD features as GSV, enabling us to utilize the API functions provided by the Open CASCADE kernel to perform CAD model reconstruction with enhanced geometric accuracy compared to fitting geometric primitives.

Given the importance of Boundary Representation (B-Rep) topology in assessing the consistency of CAD models, we also evaluated the topology error between different features reconstructed within a single model using the patch-to-patch topology error metric. We integrate different types of features reconstructed in various regions with the assistance of the Open CASCADE kernel to obtain a legitimate B-Rep model. As shown in Figure 12d, our method significantly outperforms the “segmentation + primitive fitting” methods in terms of topological error.

5.3. Case Studies in CAD Software

To validate the incorporation of our approach into commercial CAD software, we created a cloud-native CAD application tailored for customized 3D-printing purposes. This application is constructed on the Open CASCADE platform and is capable of direct operation within a web browser. The developmental procedure included utilizing Open CASCADE’s Python interface, PythonOCC 7.7.0 [44], and incorporating Flask 2.3.0 [45] as the web microservices framework.

We imported the triangular mesh models of the cam and sleeve into our CAD software that we developed and performed the task of mesh segmentation, depicted in Figure 13. The segmented triangular meshes are transformed into distinct features within different regions. For instance, the mechanical parts of cam and sleeve, illustrated in Figure 14, are reconstructed with extrusion features. Subsequently, the cross-sectional sketches are subjected to parametric editing, with linear segment lengths and arc radii annotated with their dimensional values. The system automatically adjusts the sketch contour according to the labeled dimensions. By iteratively applying these procedures to the remaining segmented areas, the entire CAD solid models are reconstructed. Customizing the model through sketch parametric editing enables feature deformation, aligning with variant design objectives. The 3D models post-deformation display unique personalized traits, as demonstrated in Figure 14.

The 3D models, following variant design, is printed to observe the personalized impact. Stereo Lithography Appearance (SLA) is chosen for the 3D-printing process, and the resulting mold is showcased in Figure 15. The 3D-printed parts were assessed based on their appearance and outline. The resulting models accurately reflect the design outputs generated by our CAD software, demonstrating high fidelity to the original design specifications. The outlines and external features of the printed parts align with the intended design, showcasing realistic and precise details. This preliminary evaluation indicates that our method effectively translates digital designs into physical models while maintaining the integrity of their appearance and overall geometry.

6. Conclusions

Our study presents a novel computational paradigm for reconstructing solid CAD features from segmented manifold triangular meshes. This approach makes significant contributions by introducing a unified mathematical representation that categorizes common solid CAD features as generalized swept bodies, thus facilitating efficient feature reconstruction. Through the utilization of a numerical optimization-based technique, geometric processing on the segmented meshes allows for the extraction of crucial cross-sectional sketch curves and feature paths. Demonstrating the utilization of this computational paradigm in parametric and variant designs of manifold triangular meshes, we improve their adaptability with personalized 3D-printed models, providing potential pathways for future research in the field.

In future research, there may be a shift towards consistent feature reconstruction for polygon meshes of mechanical parts, particularly emphasizing the integration of solid geometry construction (CSG) into the reconstruction process. In addition, a comprehensive accuracy analysis that considers various 3D-printing processes and parameters could be pursued in future research. Saddle points could indeed be a better choice for initial sampling; however, extracting saddle points from the surface of a discrete manifold mesh presents an interesting and challenging task. Additionally, there is a potential for investigating the high-level design semantics present in unstructured polygon meshes. The advancement of generative artificial intelligence technology provides a reliable means of extracting high-level design semantics from unstructured 3D data, encompassing point clouds and polygon meshes. This direction will steer our upcoming research efforts.