Numerical and Experimental Demonstration of a Silicon Nitride-Based Ring Resonator Structure for Refractive Index Sensing
Abstract
1. Introduction
2. Results
3. Discussion
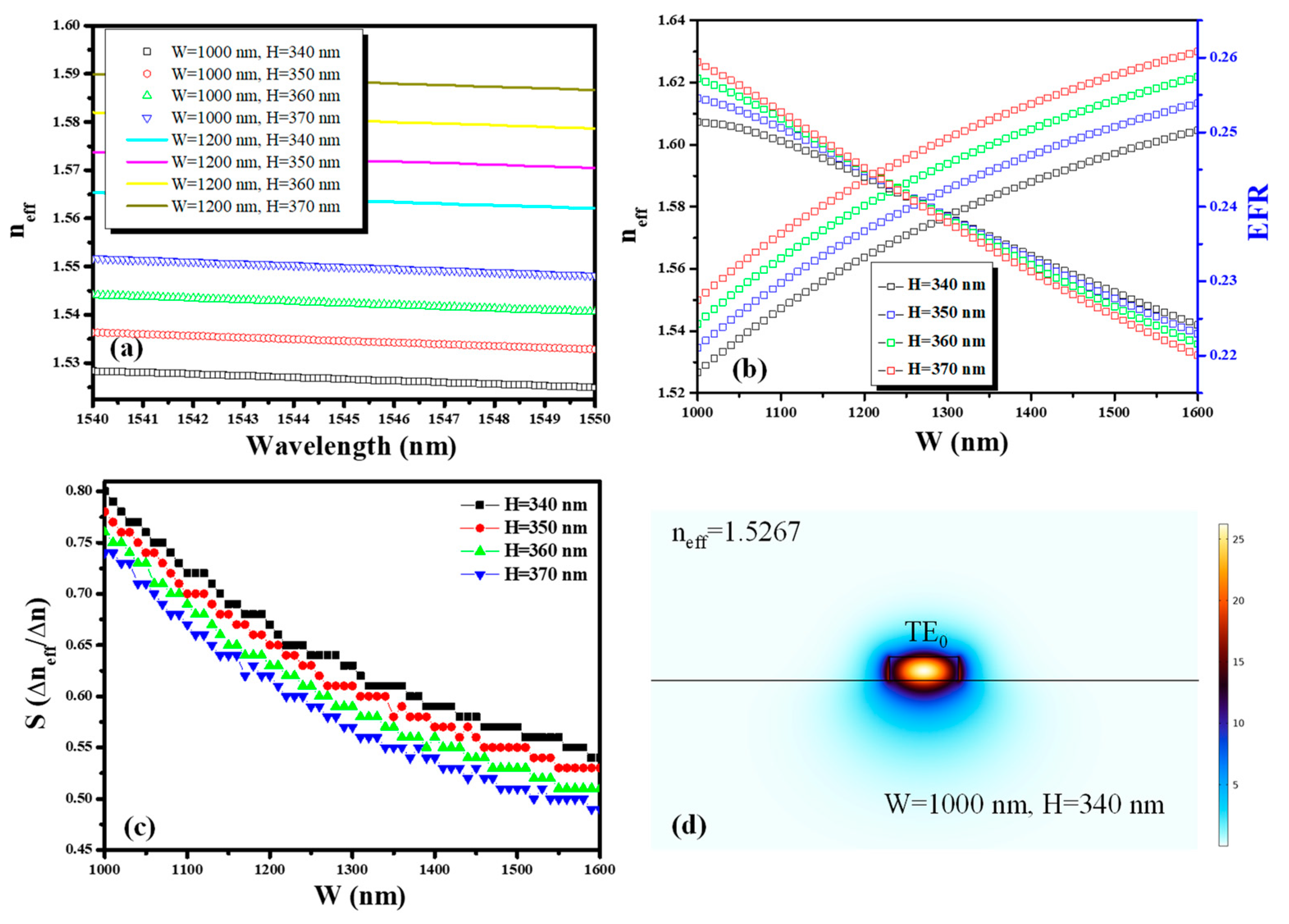
4. Numerical Simulations
5. The Fabrication Process
6. The Measurement Procedure
7. Future Directions for Ring Resonator Structure-Based Sensors
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Romero-García, S.; Merget, F.; Zhong, F.; Finkelstein, H.; Witzens, J. Silicon nitride CMOS-compatible platform for integrated photonics applications at visible wavelengths. Opt. Express 2013, 21, 14036–14046. [Google Scholar] [CrossRef] [PubMed]
- Klamkin, J.; Zhao, H.; Song, B.; Liu, Y.; Isaac, B.; Pinna, S.; Sang, F.; Coldren, L. Indium Phosphide Photonic Integrated Circuits: Technology and Applications. In Proceedings of the 2018 IEEE BiCMOS and Compound Semiconductor Integrated Circuits and Technology Symposium (BCICTS), San Diego, CA, USA, 15–17 October 2018; pp. 8–13. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of Silicon Photonics Technology and Platform Development. J. Light. Technol. 2021, 39, 4374–4389. Available online: https://ieeexplore.ieee.org/document/9380443 (accessed on 4 July 2024).
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. A Review of Photonic Sensors Based on Ring Resonator Structures: Three Widely Used Platforms and Implications of Sensing Applications. Micromachines 2023, 14, 1080. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Jin, W.; Bowers, J.E. Silicon nitride passive and active photonic integrated circuits: Trends and prospects. Photonics Res. 2022, 10, A82–A96. [Google Scholar] [CrossRef]
- Blumenthal, D.J.; Heideman, R.; Geuzebroek, D.; Leinse, A.; Roeloffzen, C. Silicon Nitride in Silicon Photonics. Proc. IEEE 2018, 106, 2209–2231. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, J.; Jin, W.; Wu, L.; Peters, J.; Xie, W.; Chang, L.; Shen, B.; Wang, H.; Yang, Q.-F.; et al. High-performance lasers for fully integrated silicon nitride photonics. Nat. Commun. 2021, 12, 6650. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Okawachi, Y.; Gil-Molina, A.; Corato-Zanarella, M.; Roberts, S.; Gaeta, A.L.; Lipson, M. Ultra-Low-Loss Silicon Nitride Photonics Based on Deposited Films Compatible with Foundries. Laser Photonics Rev. 2023, 17, 2200544. [Google Scholar] [CrossRef]
- Urs, K.M.B.; Sahoo, K.; Bhat, N.; Kamble, V. Complementary Metal Oxide Semiconductor-Compatible Top-Down Fabrication of a Ni/NiO Nanobeam Room Temperature Hydrogen Sensor Device. ACS Appl. Electron. Mater. 2022, 4, 87–91. Available online: https://pubs.acs.org/doi/abs/10.1021/acsaelm.1c00912 (accessed on 4 July 2024).
- Butt, M.A. Integrated Optics: Platforms and Fabrication Methods. Encyclopedia 2023, 3, 824–838. [Google Scholar] [CrossRef]
- Barrios, C.A.; Bañuls, M.J.; González-Pedro, V.; Gylfason, K.B.; Sánchez, B.; Griol, A.; Maquieira, A.; Sohlström, H.; Holgado, M.; Casquel, R. Label-free optical biosensing with slot-waveguides. Opt. Lett. 2008, 33, 708–710. [Google Scholar] [CrossRef] [PubMed]
- Uchida, Y.; Arakawa, T.; Higo, A.; Ishizaka, Y. Silicon Microring Resonator Biosensor for Detection of Nucleocapsid Protein of SARS-CoV-2. Sensors 2024, 24, 3250. Available online: https://www.mdpi.com/1424-8220/24/10/3250 (accessed on 4 July 2024).
- Butt, M.A. Loop-Terminated Mach-Zehnder Interferometer Integrated with Functional Polymer for CO2 Gas Sensing. Appl. Sci. 2024, 14, 4714. [Google Scholar] [CrossRef]
- Yuan, D.; Dong, Y.; Liu, Y.; Li, T. Mach-Zehnder Interferometer Biochemical Sensor Based on Silicon-on-Insulator Rib Waveguide with Large Cross Section. Sensors 2015, 15, 21500–21517. [Google Scholar] [CrossRef]
- Claes, T.; Girones Molera, J.; De Vos, K.; Schacht, E.; Baets, R.; Bienstman, P. Label-Free Biosensing With a Slot-Waveguide-Based Ring Resonator in Silicon on Insulator. IEEE Photonics J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- Muñoz, P.; Micó, G.; Bru, L.A.; Pastor, D.; Pérez, D.; Doménech, J.D.; Fernández, J.; Baños, R.; Gargallo, B.; Alemany, R.; et al. Silicon Nitride Photonic Integration Platforms for Visible, Near-Infrared and Mid-Infrared Applications. Sensors 2017, 17, 2088. [Google Scholar] [CrossRef] [PubMed]
- Ciminelli, C.; Dell’Olio, F.; Armenise, M.N.; Soares, F.M.; Passenberg, W. High performance InP ring resonator for new generation monolithically integrated optical gyroscopes. Opt. Express 2013, 21, 556–564. [Google Scholar] [CrossRef] [PubMed]
- Haas, J.; Artmann, P.; Mizaikoff, B. Mid-infrared GaAs/AlGaAs micro-ring resonators characterized via thermal tuning. RSC Adv. 2019, 9, 8594–8599. [Google Scholar] [CrossRef] [PubMed]
- Girault, P.; Lorrain, N.; Poffo, L.; Guendouz, M.; Lemaitre, J.; Carré, C.; Gadonna, M.; Bosc, D.; Vignaud, G. Integrated polymer micro-ring resonators for optical sensing applications. J. Appl. Phys. 2015, 117, 104504. [Google Scholar] [CrossRef]
- Butt, M.A. Racetrack Ring Resonator-Based on Hybrid Plasmonic Waveguide for Refractive Index Sensing. Micromachines 2024, 15, 610. [Google Scholar] [CrossRef] [PubMed]
- Bryan, M.R.; Butt, J.N.; Bucukovski, J.; Miller, B.L. Biosensing with Silicon Nitride Microring Resonators Integrated with an On-Chip Filter Bank Spectrometer. ACS Sens. 2023, 8, 739–747. Available online: https://pubs.acs.org/doi/10.1021/acssensors.2c02276 (accessed on 3 December 2023).
- Zubkova, E.; An, P.; Kovalyuk, V.; Korneev, A.; Ferrari, S.; Pernice, W.; Goltsman, G. Integrated Bragg Waveguides as an Efficient Optical Notch Filter on Silicon Nitride Platform. J. Phys. Conf. Ser. 2017, 917, 062042. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/917/6/062042 (accessed on 3 December 2023).
- Hermans, A.; Daele, M.V.; Dendooven, J.; Clemmen, S.; Detavernier, C.; Baets, R. Integrated silicon nitride electro-optic modulators with atomic layer deposited overlays. Opt. Lett. 2019, 44, 1112–1115. [Google Scholar] [CrossRef] [PubMed]
- Paik, H.; Osborn, K.D. Reducing Quantum-Regime Dielectric Loss of Silicon Nitride for Superconducting Quantum Circuits. Appl. Phys. Lett. 2010, 96, 072505. Available online: https://pubs.aip.org/aip/apl/article-abstract/96/7/072505/121275/Reducing-quantum-regime-dielectric-loss-of-silicon?redirectedFrom=fulltext (accessed on 3 December 2023).
- Kim, H.T.; Yu, M. Cascaded Ring Resonator-Based Temperature Sensor with Simultaneously Enhanced Sensitivity and Range. Opt. Express 2016, 24, 9501–9510. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-24-9-9501&id=340158 (accessed on 30 November 2023).
- de Oliveira, B.N.M.; Daniel, W.G.; Herbster, A.F. Multimode Photonic Biosensor Based on Cascaded Ring Resonator with Mach-Zehnder Interferometer for Vernier-Effect Refractive Index Sensing. In Proceedings of the 2019 SBFoton International Optics and Photonics Conference (SBFoton IOPC), Sao Paulo, Brazil, 7–9 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Butt, M.A.; Shahbaz, M.; Piramidowicz, R. Racetrack Ring Resonator Integrated with Multimode Interferometer Structure Based on Low-Cost Silica–Titania Platform for Refractive Index Sensing Application. Photonics 2023, 10, 978. [Google Scholar] [CrossRef]
- Mudumba, S.; de Alba, S.; Romero, R.; Cherwien, C.; Wu, A.; Wang, J.; Gleeson, M.A.; Iqbal, M.; Burlingame, R.W. Photonic ring resonance is a versatile platform for performing multiplex immunoassays in real time. J. Immunol. Methods 2017, 448, 34–43. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/adom.201801433 (accessed on 24 December 2023).
- Wang, F.; Wei, Y.; Han, Y. High Sensitivity and Wide Range Refractive Index Sensor Based on Surface Plasmon Resonance Photonic Crystal Fiber. Sensors 2023, 23, 6617. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N.; Voronkov, G.S.; Grakhova, E.P.; Kutluyarov, R.V. A Review on Photonic Sensing Technologies: Status and Outlook. Biosensors 2023, 13, 568. [Google Scholar] [CrossRef] [PubMed]
- Gupta, B.D.; Dodeja, H.; Tomar, A.K. Fibre-optic evanescent field absorption sensor based on a U-shaped probe. Opt. Quantum Electron. 1996, 28, 1629–1639. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Evanescent Field Ratio Enhancement of a Modified Ridge Waveguide Structure for Methane Gas Sensing Application. IEEE Sens. J. 2020, 20, 8469–8476. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, C.; Li, D.; Gao, G.; Huang, Z.; Yu, J.; Xia, J. High-quality-factor photonic crystal ring resonator. Opt. Lett. 2014, 39, 1282–1285. [Google Scholar] [CrossRef] [PubMed]
- Ali, L.; Khan, M.; Mohammed, M.U.; Yousuf, A.H.B.; Chaudhry, M.H. High Quality Silicon Photonics Optical Ring Resonator Biosensor Design. In Proceedings of the 2018 IEEE Nanotechnology Symposium (ANTS), Albany, NY, USA, 14–15 November 2018; Available online: https://ieeexplore.ieee.org/document/8653557 (accessed on 26 December 2023).
- Zhang, X.; Zhou, C.; Luo, Y.; Yang, Z.; Zhang, W.; Li, L.; Xu, P.; Zhang, P.; Xu, T. High Q-factor, ultrasensitivity slot microring resonator sensor based on chalcogenide glasses. Opt. Express 2022, 30, 3866–3875. [Google Scholar] [CrossRef] [PubMed]
- Sub-Wavelength Grating for Enhanced Ring Resonator Biosensor. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-24-14-15672&id=345275 (accessed on 1 December 2023).
- Kundal, S.; Khandelwal, A. Improving the Performance of Ring Resonator Refractive Index Sensor through Structural Modifications. Optik 2024, 296, 171555. Available online: https://www.sciencedirect.com/science/article/pii/S0030402623010537 (accessed on 25 December 2023).
- Tu, Z.; Gao, D.; Zhang, M.; Zhang, D. High-sensitivity complex refractive index sensing based on Fano resonance in the subwavelength grating waveguide micro-ring resonator. Opt. Express 2017, 25, 20911–20922. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Wang, S.; Lv, J.; Lu, Y.; Zhang, J. Refractive Index Biosensor Based on Topological Ring Resonator. Opt. Commun. 2023, 541, 129542. Available online: https://www.sciencedirect.com/science/article/pii/S0030401823002894 (accessed on 1 December 2023).
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Highly sensitive refractive index sensor based on hybrid plasmonic waveguide microring resonator. Waves Random Complex. Media 2020, 30, 292–299. [Google Scholar] [CrossRef]
- Tazawa, H.; Steier, W.H. Linearity of ring resonator-based electro-optic polymer modulator. Electron. Lett. 2005, 41, 1297–1298. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Castelló-Pedrero, L.; Gómez-Gómez, M.I.; García-Rupérez, J.; Griol, A.; Martínez, A. Performance improvement of a silicon nitride ring resonator biosensor operated in the TM mode at 1310 nm. Biomed. Opt. Express 2021, 12, 7244–7260. [Google Scholar] [CrossRef]
- Huang, W.; Luo, Y.; Zhang, W.; Li, C.; Li, L.; Yang, Z.; Xu, P. High-sensitivity refractive index sensor based on Ge–Sb–Se chalcogenide microring resonator. Infrared Phys. Technol. 2021, 116, 103792. [Google Scholar] [CrossRef]
- Ou, X.; Yang, Y.; Sun, F.; Zhang, P.; Tang, B.; Li, B.; Liu, R.; Liu, D.; Li, Z. Wide-range, ultra-compact, and high-sensitivity ring resonator biochemical sensor with CMOS-compatible hybrid plasmonic waveguide. Opt. Express 2021, 29, 19058–19067. [Google Scholar] [CrossRef] [PubMed]
- Sahraeibelverdi, T.; Guo, L.J.; Veladi, H.; Malekshahi, M.R. Polymer Ring Resonator with a Partially Tapered Waveguide for Biomedical Sensing: Computational Study. Sensors 2021, 21, 5017. [Google Scholar] [CrossRef] [PubMed]
- Lu, K.; Huang, B.; Lv, X.; Zhang, Z.; Ma, Z. Ultrasensitive Silicon Photonic Refractive Index Sensor Based on Hybrid Double Slot Subwavelength Grating Microring Resonator. Sensors 2024, 24, 1929. [Google Scholar] [CrossRef] [PubMed]
- COMSOL: Multiphysics Software for Optimizing Designs. Available online: https://www.comsol.com/ (accessed on 3 December 2023).
- Kern, W. Evolution of silicon wafer cleaning technology. Proc.—Electrochem. Soc. 1990, 90, 3–19. [Google Scholar] [CrossRef]
- Lelit, M.; Słowikowski, M.; Filipiak, M.; Juchniewicz, M.; Stonio, B.; Michalak, B.; Pavłov, K.; Myśliwiec, M.; Wiśniewski, P.; Kaźmierczak, A.; et al. Passive Photonic Integrated Circuits Elements Fabricated on a Silicon Nitride Platform. Materials 2022, 15, 1398. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, X.; Fan, D.; Wang, Y.; Chen, R.T. High quality factor subwavelength grating waveguide micro-ring resonator based on trapezoidal silicon pillars. Opt. Lett. 2016, 41, 3375–3378. [Google Scholar] [CrossRef]
- Butt, M.A.; Kozlowski, L.; Piramidowicz, R. Optimized hybrid plasmonic waveguide-based ring resonator for advanced refractive index sensing. J. Opt. 2024, 26, 075802. [Google Scholar] [CrossRef]
- Chrostowski, L.; Grist, S.; Flueckiger, J.; Shi, W.; Wang, X.; Ouellet, E.; Yun, H.; Webb, M.; Nie, B.; Liang, Z.; et al. Silicon photonic resonator sensors and devices. In Proceedings of the Laser Resonators, Microresonators, and Beam Control XIV, San Francisco, CA, USA, 22–25 January 2012; Volume 8236, pp. 387–402. [Google Scholar] [CrossRef]
- Juan-Colás, J.; Parkin, A.; Dunn, K.E.; Scullion, M.G.; Krauss, T.F.; Johnson, S.D. The electrophotonic silicon biosensor. Nat. Commun. 2016, 7, 12769. [Google Scholar] [CrossRef]






| FSR (nm) | Sensitivity (nm/RIU) | Q Factor | LOD (RIU) | |||
|---|---|---|---|---|---|---|
| Radius (µm) | 50 ± 0.02 | 75 ± 0.02 | 100 ± 0.02 | |||
| Numerical calculations | ~4.2 | ~2.8 | ~2.1 | ~110 | - | - |
| Experimental data | ~3.64 | ~2.42 | ~1.82 | ~112.5 | 1.7154 × 104 | 7.99 × 10−4 |
| Relative percent error (%) | ~15.4 | ~15.7 | ~15.3 | ~2.2 | - | - |
| Platform | Numerical/Experimental | Waveguide Configuration | Sensitivity (nm/RIU) | Q Factor | LOD | Ref. |
|---|---|---|---|---|---|---|
| Silicon nitride | Numerical and experimental | Ridge waveguide | 164.8 | 2575 | 3.65 × 10−3 | [44] |
| Ge-As-Se chalcogenide | Experimental | Ridge waveguide | 123 | 7.74 × 104 | 3.24 × 10−4 | [45] |
| Silicon | Numerical | Suspended slot hybrid plasmonic waveguide | 458.1 | - | 3.7 × 10−5 | [46] |
| Polymer | Numerical | Tapered ridge waveguide | 84.6 to 101.74 | 4.6 × 103 | - | [47] |
| Silicon | Numerical | Hybrid double-slot subwavelength grating | 1005 | 22,429 | 6.86 × 10−5 | [48] |
| Silicon nitride | Numerical and experimental | Ridge waveguide | 112.5 | 1.7154 ×104 | 7.99 × 10−4 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, M.A.; Kozłowski, Ł.; Golas, M.; Slowikowski, M.; Filipiak, M.; Juchniewicz, M.; Bieniek-Kaczorek, A.; Dudek, M.; Piramidowicz, R. Numerical and Experimental Demonstration of a Silicon Nitride-Based Ring Resonator Structure for Refractive Index Sensing. Appl. Sci. 2024, 14, 6082. https://doi.org/10.3390/app14146082
Butt MA, Kozłowski Ł, Golas M, Slowikowski M, Filipiak M, Juchniewicz M, Bieniek-Kaczorek A, Dudek M, Piramidowicz R. Numerical and Experimental Demonstration of a Silicon Nitride-Based Ring Resonator Structure for Refractive Index Sensing. Applied Sciences. 2024; 14(14):6082. https://doi.org/10.3390/app14146082
Chicago/Turabian StyleButt, Muhammad A., Łukasz Kozłowski, Michał Golas, Mateusz Slowikowski, Maciej Filipiak, Marcin Juchniewicz, Aleksandra Bieniek-Kaczorek, Michał Dudek, and Ryszard Piramidowicz. 2024. "Numerical and Experimental Demonstration of a Silicon Nitride-Based Ring Resonator Structure for Refractive Index Sensing" Applied Sciences 14, no. 14: 6082. https://doi.org/10.3390/app14146082
APA StyleButt, M. A., Kozłowski, Ł., Golas, M., Slowikowski, M., Filipiak, M., Juchniewicz, M., Bieniek-Kaczorek, A., Dudek, M., & Piramidowicz, R. (2024). Numerical and Experimental Demonstration of a Silicon Nitride-Based Ring Resonator Structure for Refractive Index Sensing. Applied Sciences, 14(14), 6082. https://doi.org/10.3390/app14146082









