Active Disturbance Rejection Control (ADRC) of Hot-Compression Molding Temperature of Bamboo-Based Fiber Composites
Abstract
1. Introduction
2. Materials and Methods
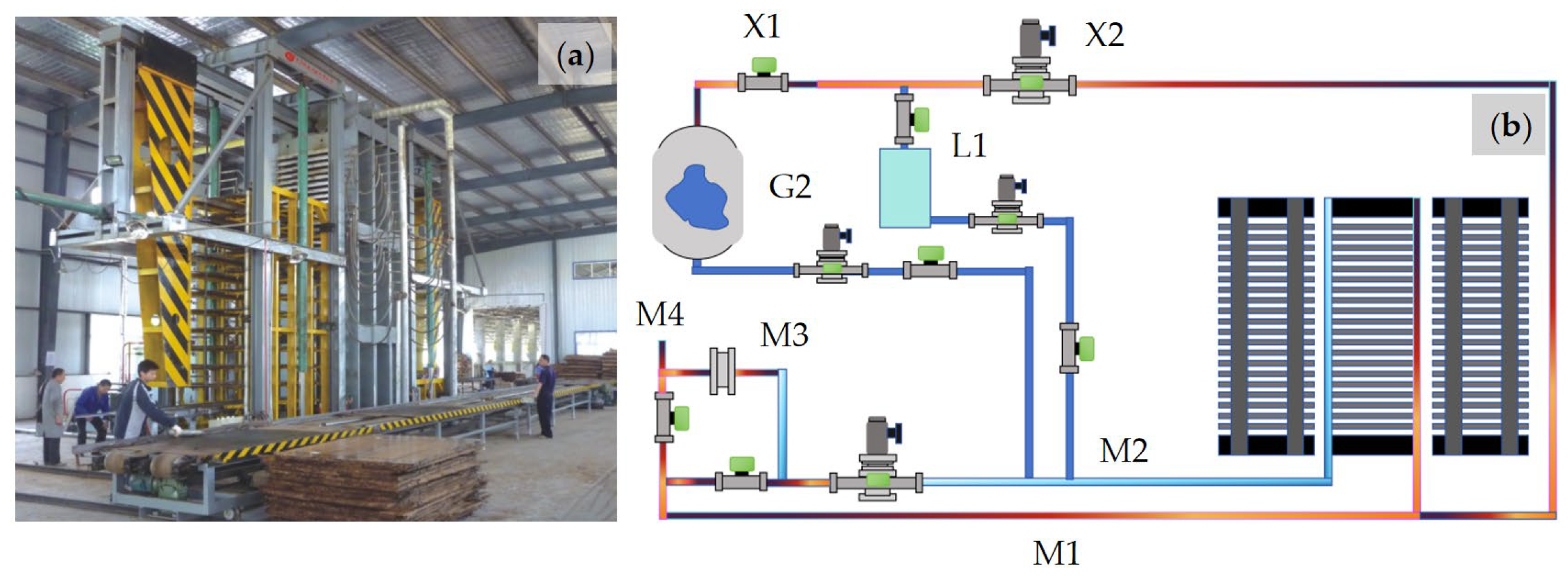
2.1. Materials
2.2. Modeling of Motor-Driven Steam Control Valve Opening Angle
2.3. Modeling of Steam-Regulating Valve Opening Angle in Terms of Heat, Pressure, and Temperature
- (1)
- Prior to commencement, establish the initial parameter estimates, the initial covariance matrix, and the initial forgetting factor. Conventionally, the covariance matrix is initialized as a larger positive number multiplied by the unit matrix, indicating a high degree of initial uncertainty. The initial values of , , and are set, and the initial data is entered accordingly.
- (2)
- Determine the ratio of the correction period to the sampling period . This signifies that the parameter estimates will undergo an update following each sampling period.
- (3)
- Increment M by 1, collect the current input u(k) and output y(k), and compute the residual using Equation (6).
- (4)
- If M is less than L, repeat the previous step; otherwise, reset M to zero and proceed with the subsequent step.
- (5)
- Preprocess the data utilizing Equations (7) and (8) to derive the values of and .
- (6)
- Input and into the fuzzy controller and determine C through control rule table reasoning.
- (7)
- Compute , P, and K by applying Equation (9) to Equation (5). At this juncture, the identification of the single parameter is completed, and the process returns to the third part for the continuation of the cycle.
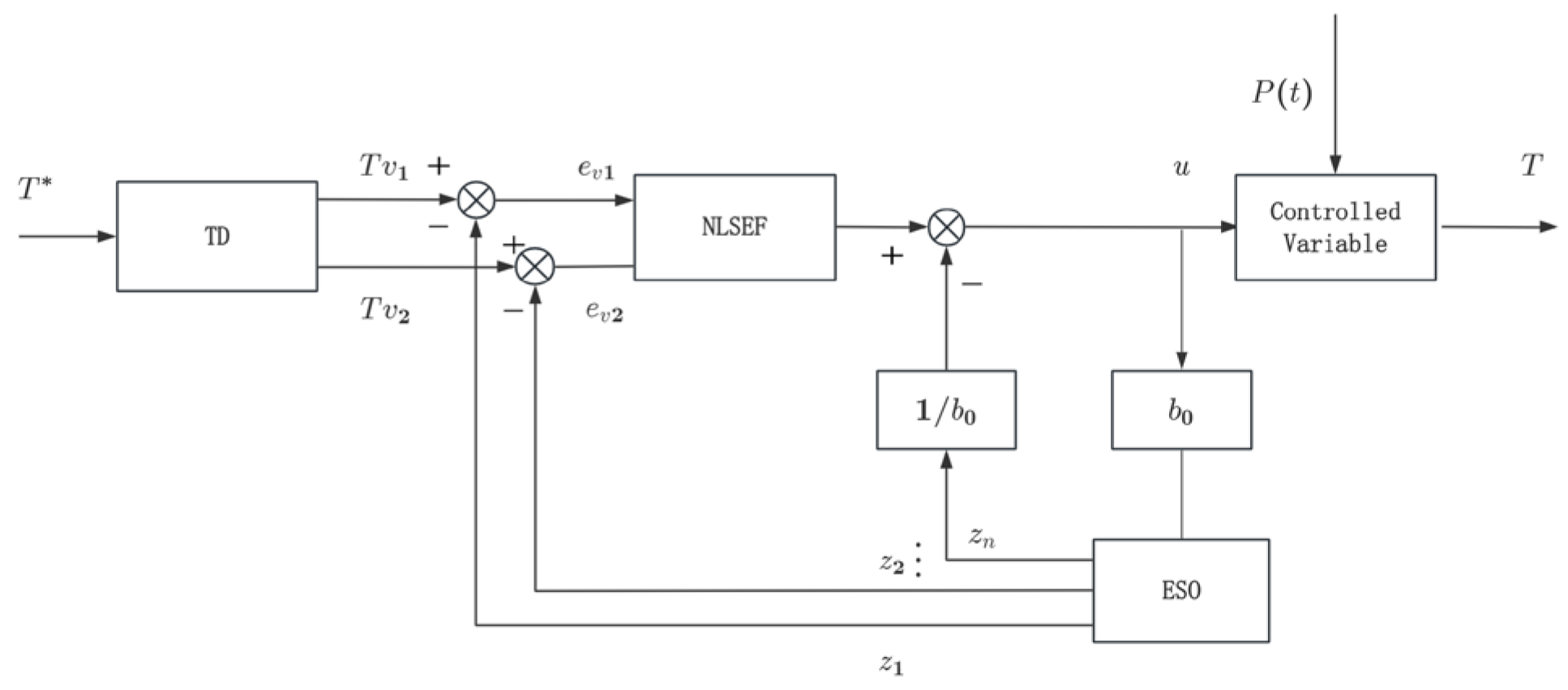
2.4. Design of ADRC
2.4.1. Tracking Differentiator
2.4.2. Expanded State Observer
2.4.3. Nonlinear State Error Feedback
3. Results and Discussion
3.1. Parameter Identification Results for Steam Regulator Valve in Terms of Heat, Pressure, and Temperature Models
3.2. ADRC Parameterization Results
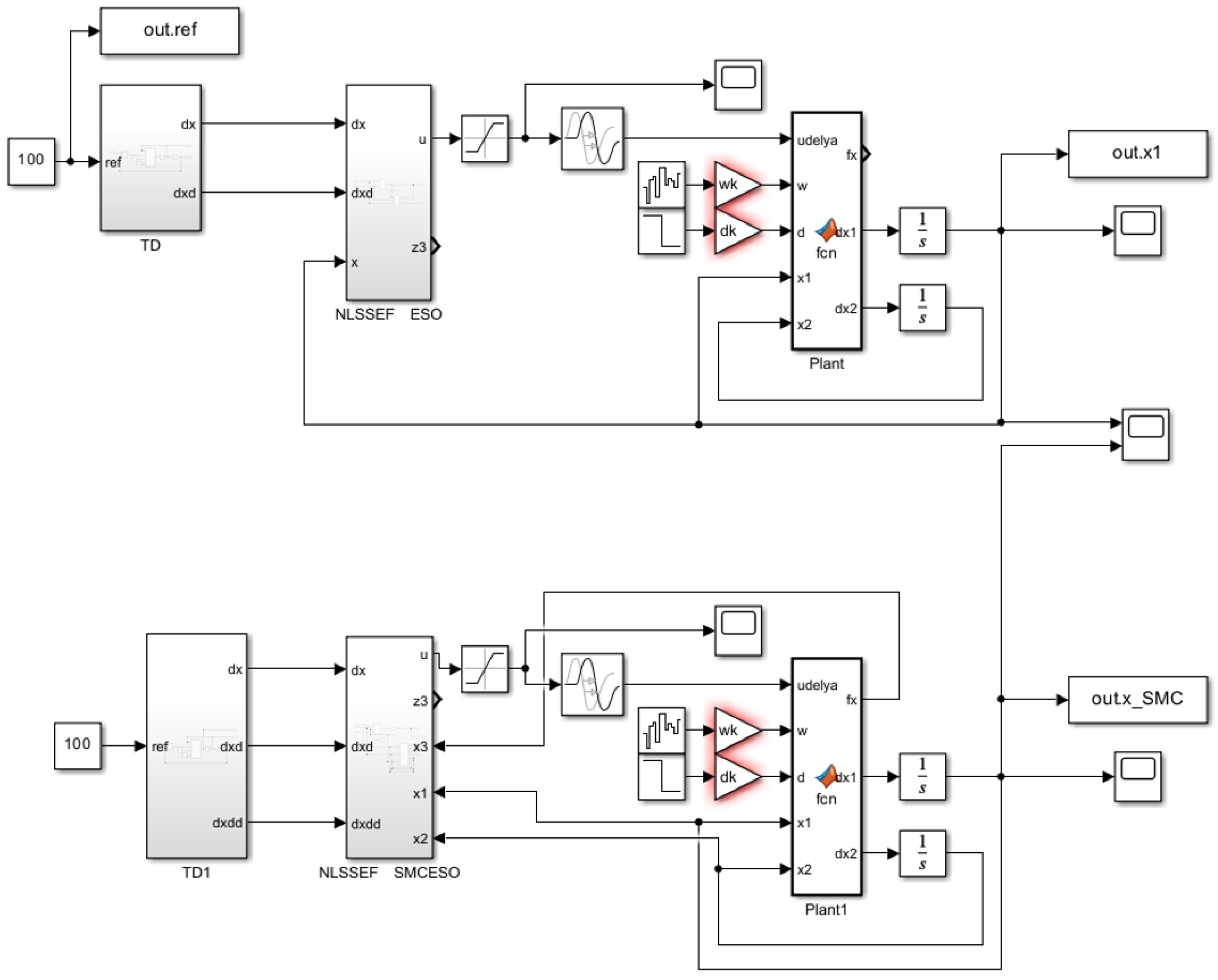
3.3. Simulation of ADRC of Hot-Compression Molding Temperature
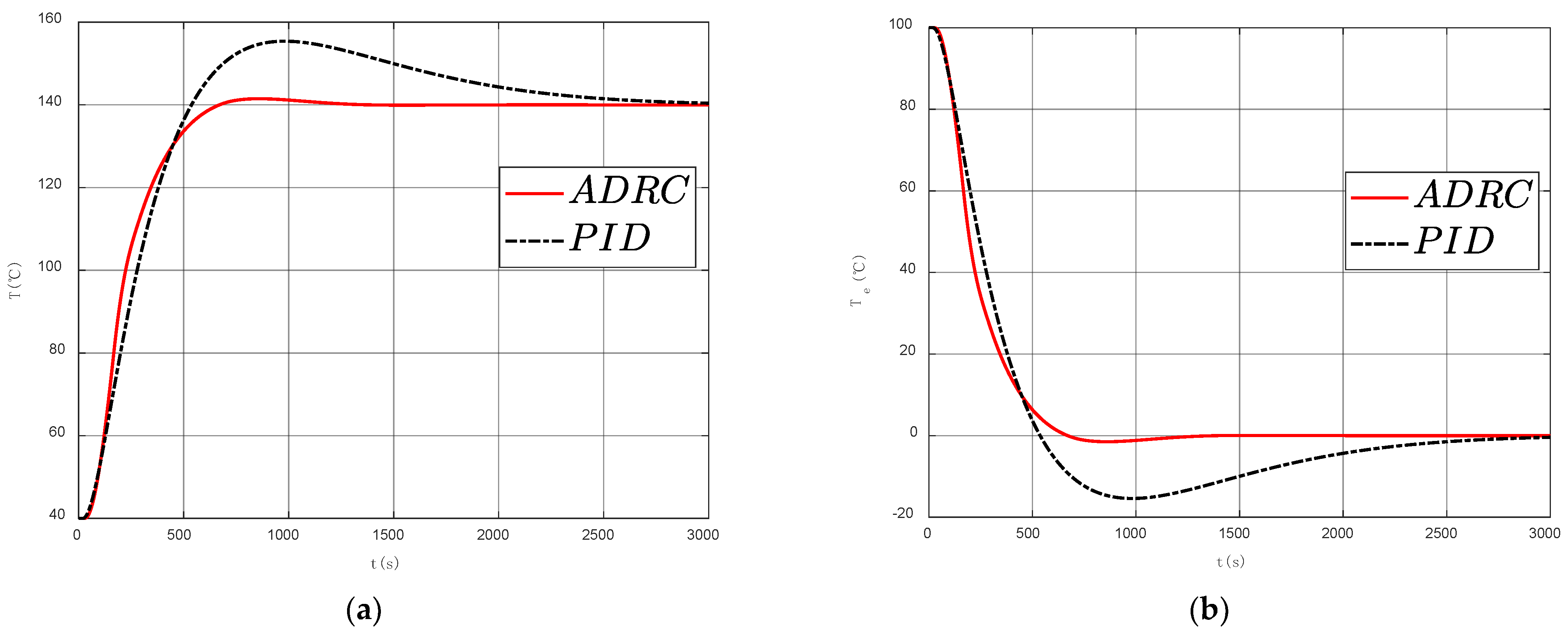
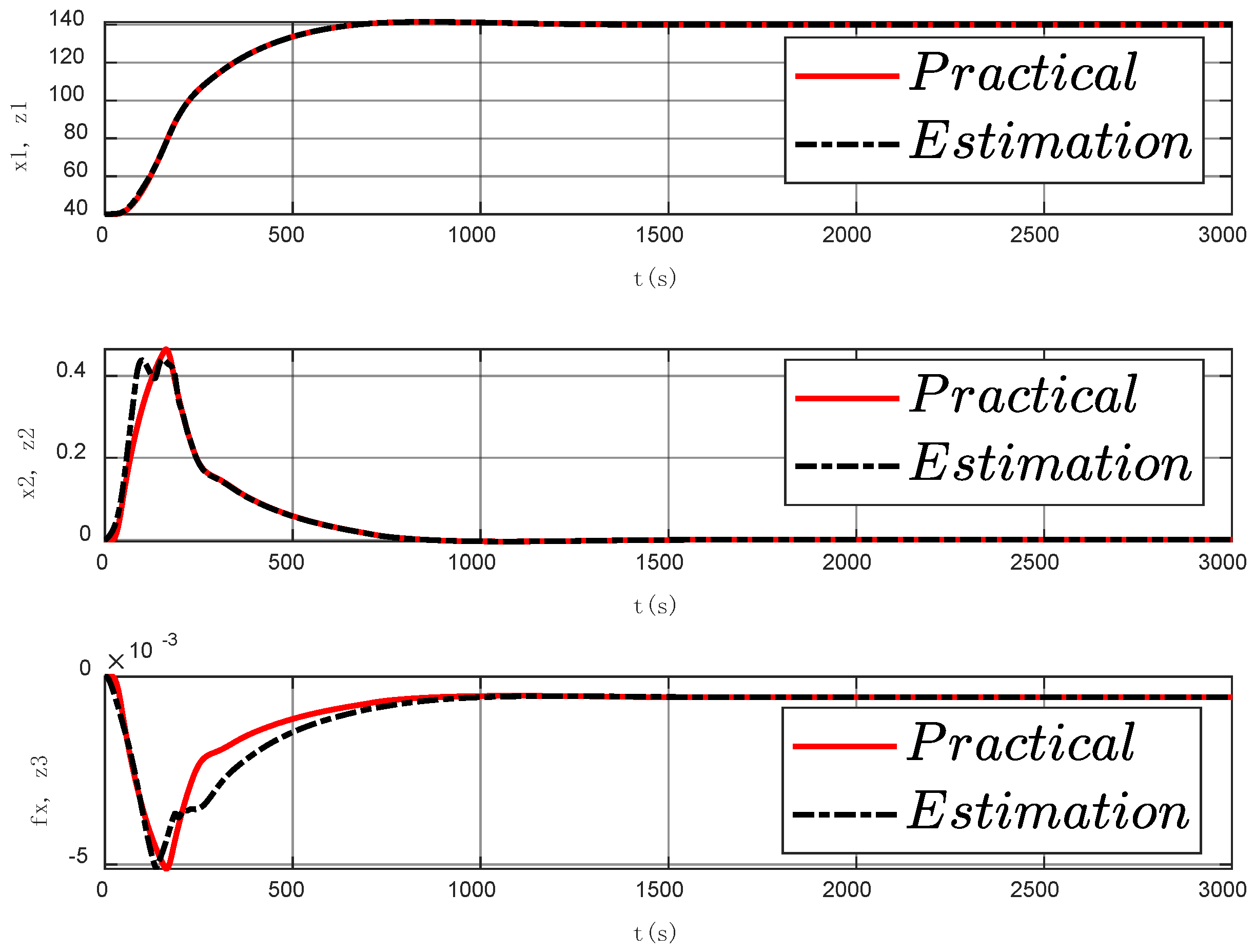
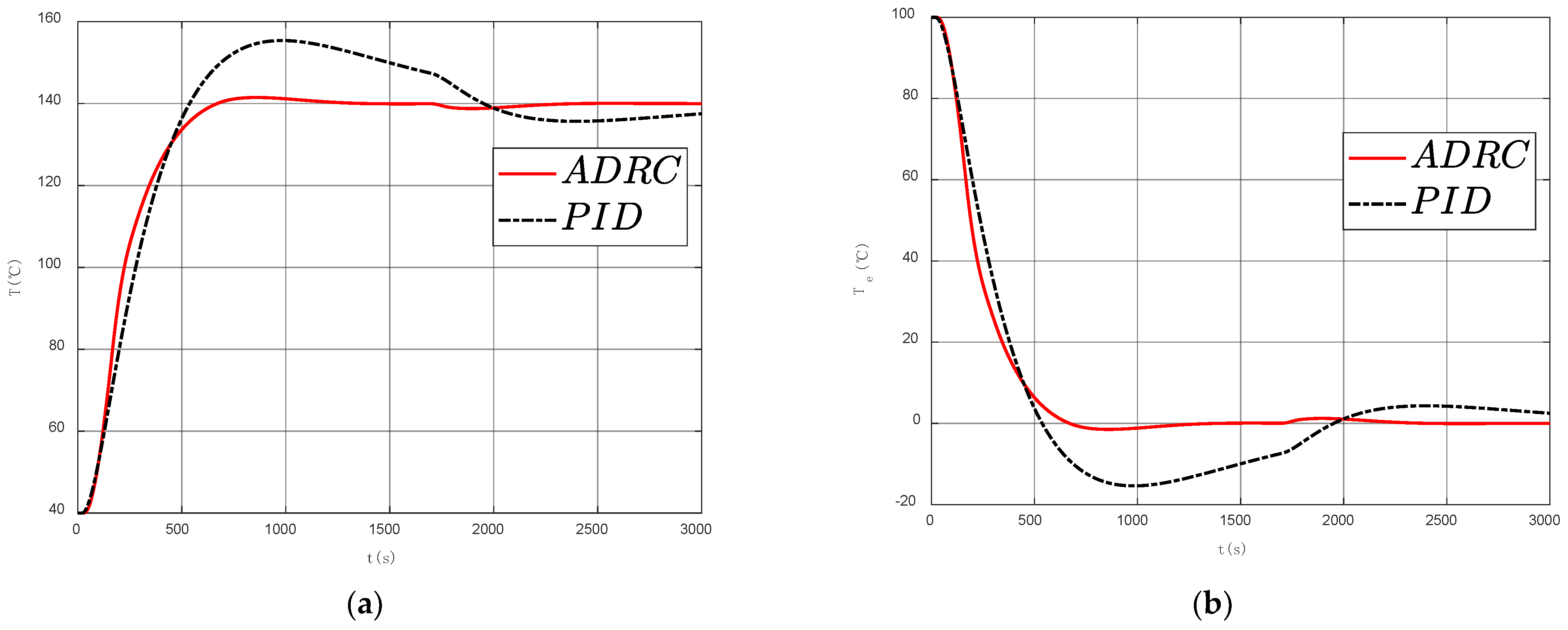
3.3.1. Simulation Results without Signal Interference
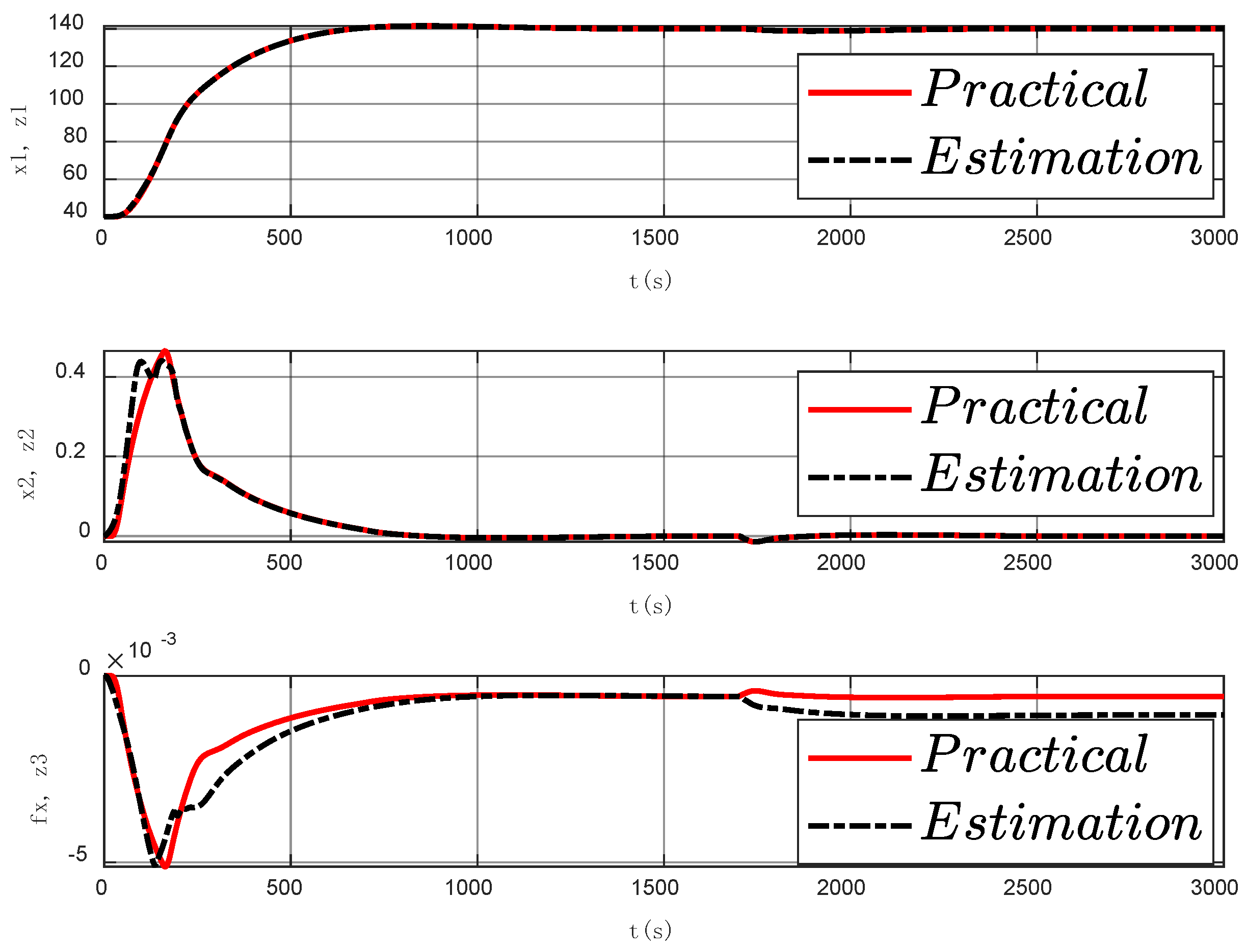
3.3.2. Simulation Results under Sinusoidal Signal Noise Interference
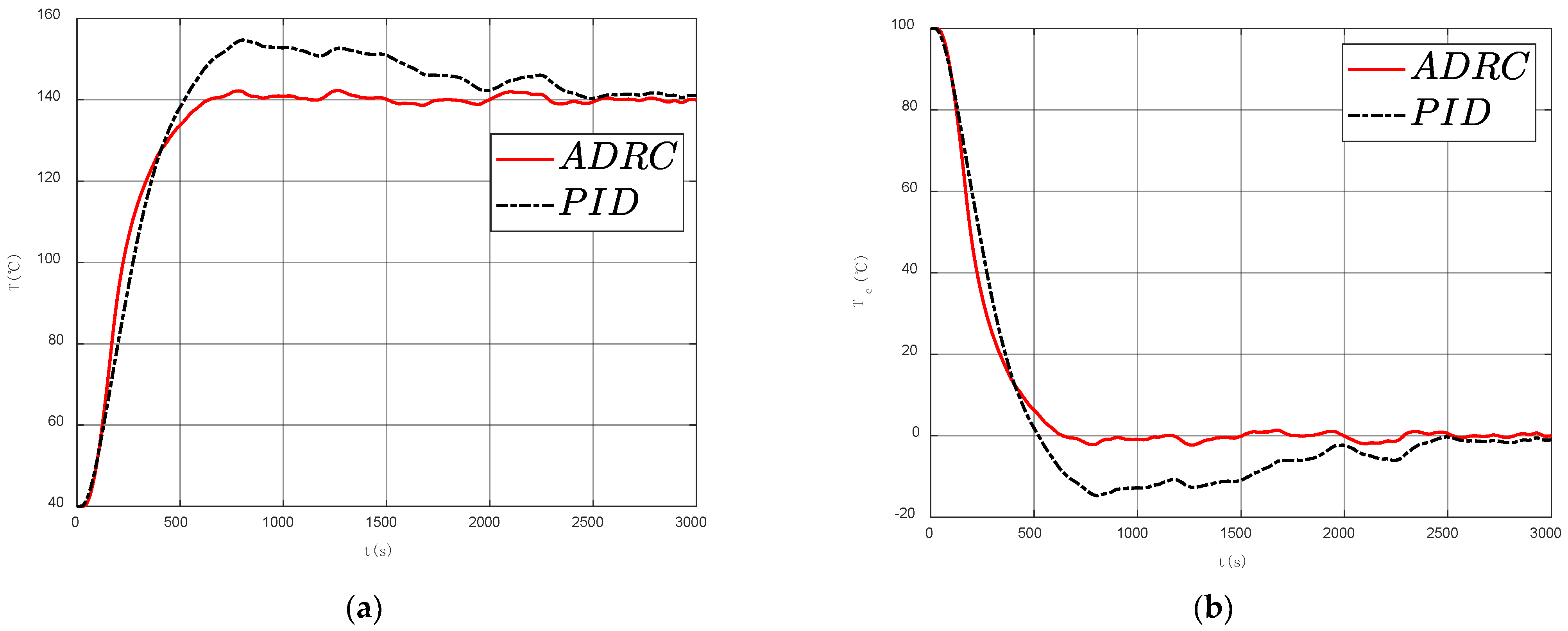
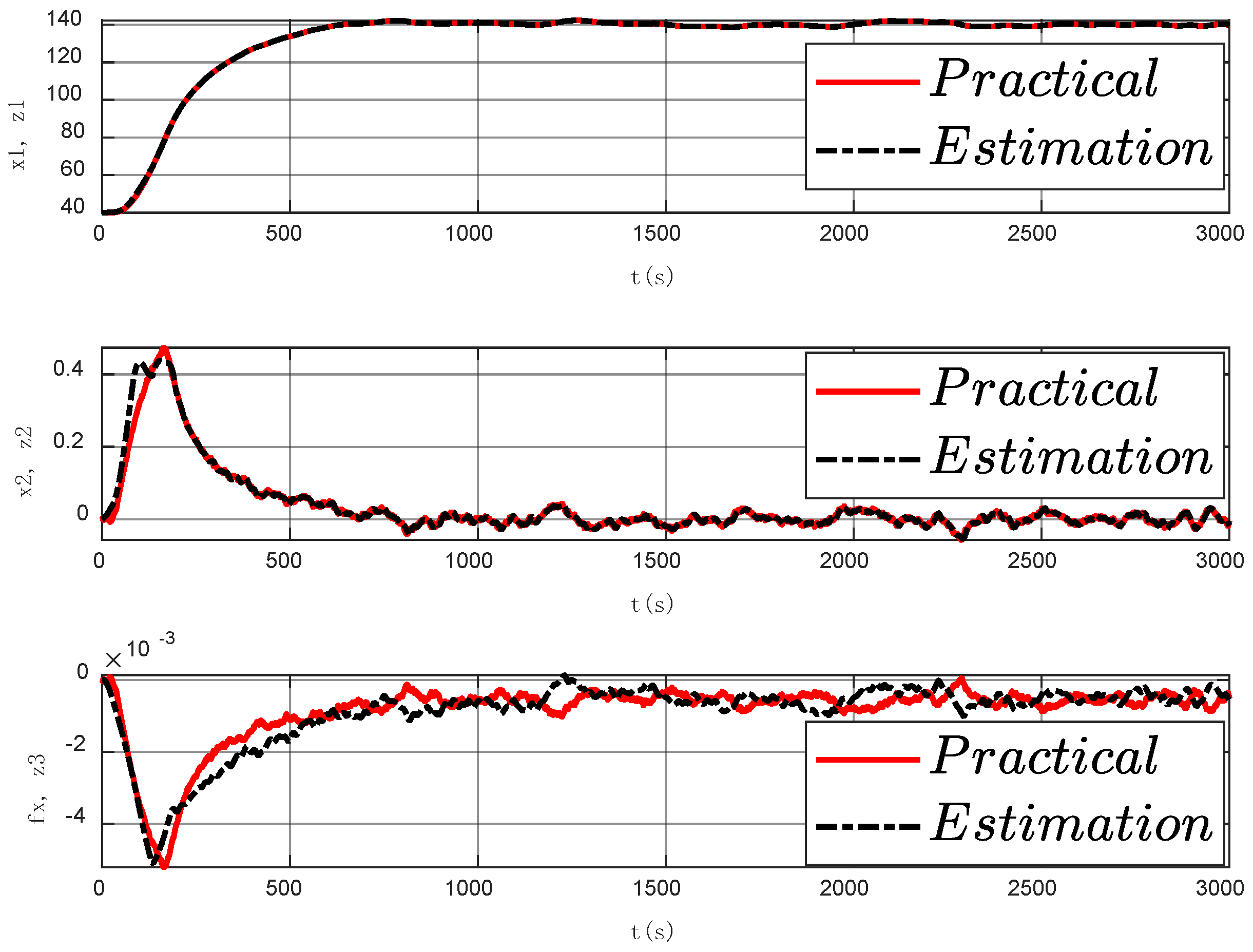
3.3.3. Simulation Results under Random Signal Noise Interference
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De, B.; Bera, M.; Bhattacharjee, D.; Ray, B.C.; Mukherjee, S. A comprehensive review on fiber-reinforced polymer composites: Raw materials to applications, recycling, and waste management. Prog. Mater. Sci. 2024, 146, 101326. [Google Scholar] [CrossRef]
- Kim, G.; Lee, H.; Arnold, K.; Rodriguez, J. Reusing uncured Fiber-reinforced thermoset composite Prepreg waste with water-soluble PVA backing film. Sustain. Mater. Technol. 2024, 41, e01016. [Google Scholar] [CrossRef]
- Liu, L.; Xiang, D.; Ma, J.; Sun, H.; Harkin-Jones, E.; Wang, M.; Zeng, S.; Wu, Y. Multifunctional basalt fiber reinforced polymer composites with in-situ damage self-sensing and temperature-sensitive behavior. Compos. Commun. 2024, 101990. [Google Scholar] [CrossRef]
- Xia, C.; Xie, W.; Meng, S.; Gao, B.; Ye, J. Preparation of integrated carbon fiber stitched fabric reinforced (SiBCN) ceramic/resin double-layered composites for ablation resistance, thermal insulation and compression resistance performance. Compos. Sci. Technol. 2024, 252, 110629. [Google Scholar] [CrossRef]
- Shu, B.; Zhang, W.; Tao, Y.; Li, C.; Zhang, S.; Xiao, Z.; Fu, N.; Yu, J.; Gu, Y.; Lu, X. Mechanical Properties and Strength Design Value of Bamboo Scrimber. J. Northwest For. Univ. 2022, 37, 216–222. [Google Scholar]
- Xu, D.; He, S.; Leng, W.; Chen, Y.; Wu, Z. Replacing Plastic with Bamboo: A Review of the Properties and Green Applications of Bamboo-Fiber-Reinforced Polymer Composites. Polymers 2023, 15, 4276. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Li, J.; Lin, J.; Song, Y.; Wang, J.; Cui, Q.; Qiu, Y.; Tang, M.; Wang, J. Design of the PID temperature controller for an alkaline electrolysis system with time delays. Int. J. Hydrog. Energy 2023, 48, 19008–19021. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Z.; Liu, J.; Wang, N. Thermal management with fast temperature convergence based on optimized fuzzy PID algorithm for electric vehicle battery. Appl. Energy 2023, 352, 121936. [Google Scholar] [CrossRef]
- Taler, D.; Sobota, T.; Jaremkiewicz, M.; Taler, J. Control of the temperature in the hot liquid tank by using a digital PID controller considering the random errors of the thermometer indications. Energy 2022, 239, 122771. [Google Scholar] [CrossRef]
- Hou, G.; Gong, L.; Wang, M.; Yu, X.; Yang, Z.; Mou, X. A novel linear active disturbance rejection controller for main steam temperature control based on the simultaneous heat transfer search. ISA Trans. 2022, 122, 357–370. [Google Scholar] [CrossRef]
- Dai, C.; Xue, Y.; Wu, Z.; Yan, G.; Li, D.; Li, Z. Active disturbance rejection control for the reheated steam temperature of a double-reheat boiler. J. Process Control 2023, 130, 103078. [Google Scholar] [CrossRef]
- Liu, S.; Huang, H.; Li, D.; Tian, B.; Xue, W.; Sun, L.; Zhu, M. A hybrid receding horizon optimization and active disturbance rejection control of boiler superheated steam temperature. Process Saf. Environ. Prot. 2023, 178, 1107–1118. [Google Scholar] [CrossRef]
- Li, Z.; Liang, S.; Guo, M.; Zhang, H.; Wang, H.; Li, Z.; Li, H. ADRC-Based Underwater Navigation Control and Parameter Tuning of an Amphibious Multirotor Vehicle. IEEE J. Ocean. Eng. 2024, 13, 4900. [Google Scholar] [CrossRef]
- Gong, R.; Sun, R.; Chen, W. Series Active Disturbance Rejection Autopilot Design for Hyper Velocity Projectiles. IEEE Access 2020, 8, 149447–149455. [Google Scholar] [CrossRef]
- He, D.; Li, Y.; Meng, X.; Si, Q. Anti-slip Control for Unmanned Underwater Tracked Bulldozer Based on Active Disturbance Rejection Control. Mechatronics 2022, 84, 102803. [Google Scholar] [CrossRef]
- Pu, C.; Wang, Z.; Wang, S. Two-stage Active Disturbance Rejection Control for Coupled Permanent Magnet Synchronous Motors System With Mismatched Disturbance. Int. J. Control Autom. Syst. 2024, 22, 1883–1892. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, Z.; Feng, F.; Xie, L. ADRC-Based Trajectory Tracking Control for a Planar Continuum Robot. J. Intell. Robot. Syst. 2023, 108, 1. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, C.; Gu, S.; Wang, T.; Zhao, L. Trajectory Tracking Control of Pneumatic Servo System: A Variable Gain ADRC Approach. IEEE Trans. Cybern. 2023, 53, 6977–6986. [Google Scholar] [CrossRef]
- Fang, Q.; Zhou, Y.; Ma, S.; Zhang, C.; Wang, Y.; Huangfu, H. Electromechanical Actuator Servo Control Technology Based on Active Disturbance Rejection Control. Electronics 2023, 12, 1934. [Google Scholar] [CrossRef]
- Liu, C.; Luo, G.; Chen, Z.; Tu, W.; Qiu, C. A linear ADRC-based robust high-dynamic double-loop servo system for aircraft electro-mechanical actuators. Chin. J. Aeronaut. 2019, 32, 2174–2187. [Google Scholar] [CrossRef]
- Ji, Y.; Kang, Z. Three-stage forgetting factor stochastic gradient parameter estimation methods for a class of nonlinear systems. Int. J. Robust Nonlinear Control 2021, 31, 971–987. [Google Scholar] [CrossRef]
- Nahri, S.N.F.; Du, S.; van Wyk, B.J. Predictive Extended State Observer-Based Active Disturbance Rejection Control for Systems with Time Delay. Machines 2023, 11, 144. [Google Scholar] [CrossRef]
- Tan, L.; Liang, S.; Su, H.; Qin, Z.; Li, L.; Huo, J. Research on Amphibious Multi-Rotor UAV Out-of-Water Control Based on ADRC. Appl. Sci. 2023, 13, 4900. [Google Scholar] [CrossRef]
- Yang, X.; Huang, Q.; Jing, S.; Zhang, M.; Zuo, Z.; Wang, S. Servo system control of satcom on the move based on improved ADRC controller. Energy Rep. 2022, 8, 1062–1070. [Google Scholar] [CrossRef]
- Yu, J.; Jin, S. Sliding Mode Tracking Differentiator With Adaptive Gains for Filtering and Derivative Estimation of Noisy Signals. IEEE Access 2021, 9, 86017–86024. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, C.; Sepehri, N. Active Disturbance Rejection Control Applied to High-order Systems with Parametric Uncertainties. Int. J. Control Autom. Syst. 2019, 17, 1483–1493. [Google Scholar] [CrossRef]
- Du, Y.; Cao, W.; She, J. Analysis and Design of Active Disturbance Rejection Control with an Improved Extended State Observer for Systems with Measurement Noise. IEEE Trans. Ind. Electron. 2023, 70, 855–865. [Google Scholar] [CrossRef]
- Dong, C.; Liu, C.; Wang, Q.; Gong, L. Switched adaptive active disturbance rejection control of variable structure near space vehicles based on adaptive dynamic programming. Chin. J. Aeronaut. 2019, 32, 1684–1694. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Z.; Qi, Z.; Li, B.; Shu, Y. Research on ADRC algorithm for longitudinal attitude of hydrofoil craft based on improved convergence law. Ocean Eng. 2024, 293, 116656. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, J.; Liu, X. Finite-Time Variable-Gain ADRC for Master-Slave Teleoperated Parallel Manipulators. IEEE Trans. Ind. Electron. 2023, 71, 9234–9243. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 10957–10968. [Google Scholar] [CrossRef]
- Ding, H.; Liu, S.; Wang, Z.; Zhang, H.; Wang, C. An ADRC Parameters Self-Tuning Controller Based on RBF Neural Network for Multi-Color Register System. Machines 2023, 11, 320. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Zhou, L.; Wang, B.; Cheng, Z.; Fan, H. Cascade ADRC with neural network-based ESO for hypersonic vehicle. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 9115–9138. [Google Scholar] [CrossRef]
- Liu, S.; Ding, H.; Wang, Z.; Li, Z.; Ma, L.e. An ADRC Parameters Self-Tuning Control Strategy of Tension System Based on RBF Neural Network. J. Renew. Mater. 2023, 11, 1991–2014. [Google Scholar] [CrossRef]


| Type | Bending Strength (Mpa) | Compressive Strength (Mpa) | Tensile Strength (Mpa) | Shear Strength (Mpa) | Flexural Modulus of Elasticity (Mpa) | Densities (g/cm3) |
|---|---|---|---|---|---|---|
| Bamboo-based fiber composites | 33.8 | 22.8 | 16.3 | 3.69 | 8300 | 1.13 |
| Larch tree | 17 | 15 | 9.5 | 1.6 | 1000 | 0.60~0.70 |
| Camphor pine | 13 | 10 | 8 | 1.4 | 9000 | 0.40~0.50 |
| Oak wood | 17 | 16 | 11 | 2.4 | 1100 | 0.80~0.90 |
| Birch | 15 | 14 | 10 | 2 | 1000 | 0.60~0.70 |
| C30 concrete | — | 14.3 | 1.43 | — | 3000 | 2.20~2.40 |
| Q235 | — | 215 | 215 | 125 | 206,000 | 7.85 |
| Time (s) | Temp (°C) | Opening Angle | Flux (L/s) | Time (s) | Temp (°C) | Opening Angle | Flux (L/s) | Time (s) | Temp (°C) | Opening Angle | Flux (L/s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 47 | 50 | 0.994 | 151.18 | 93 | 82.5 | 0.788 | 119.91 | 940 | 140 | 0.0612 | 9.302 |
| 48 | 51 | 0.989 | 150.44 | 94 | 84 | 0.784 | 119.29 | 941 | 140 | 0.0612 | 9.312 |
| 49 | 51 | 0.984 | 149.69 | 95 | 86.2 | 0.780 | 118.68 | 942 | 140 | 0.0613 | 9.323 |
| 50 | 52 | 0.979 | 148.95 | 96 | 86.3 | 0.776 | 118.07 | 943 | 140 | 0.0614 | 9.334 |
| 51 | 52.1 | 0.975 | 148.22 | 97 | 86.4 | 0.772 | 117.46 | 944 | 140.1 | 0.0614 | 9.345 |
| 52 | 52.2 | 0.970 | 147.48 | 98 | 87.7 | 0.768 | 116.86 | 945 | 140.1 | 0.0615 | 9.357 |
| 53 | 53 | 0.965 | 146.75 | 99 | 87.9 | 0.764 | 116.26 | 946 | 140.1 | 0.0616 | 9.369 |
| 54 | 54 | 0.960 | 146.03 | 100 | 89.6 | 0.760 | 115.66 | 947 | 140.1 | 0.0617 | 9.380 |
| 55 | 55 | 0.955 | 145.30 | 101 | 89.6 | 0.757 | 115.06 | 948 | 140.1 | 0.0617 | 9.393 |
| 56 | 56.1 | 0.951 | 144.58 | 102 | 89.8 | 0.753 | 114.47 | 949 | 140.2 | 0.0618 | 9.405 |
| 57 | 56.2 | 0.946 | 143.86 | 103 | 89.8 | 0.749 | 113.88 | 950 | 140.2 | 0.0619 | 9.418 |
| 58 | 58.2 | 0.941 | 143.15 | 104 | 89.8 | 0.745 | 113.29 | 951 | 140.2 | 0.0620 | 9.431 |
| 59 | 58.3 | 0.937 | 142.43 | 105 | 90.9 | 0.741 | 112.71 | 952 | 140.2 | 0.0621 | 9.444 |
| 60 | 59.8 | 0.932 | 141.73 | 106 | 91 | 0.737 | 112.12 | 953 | 140.2 | 0.0622 | 9.457 |
| 61 | 59.9 | 0.927 | 141.02 | 107 | 92.2 | 0.733 | 111.54 | 954 | 140.1 | 0.0623 | 9.471 |
| Model | Parameter | Value |
|---|---|---|
| TD | 100 | |
| 0.1 | ||
| ESO | 0.2 | |
| 0.25 | ||
| 0.5 | ||
| 0.12 | ||
| 0.0048 | ||
| 0.0000512 | ||
| NLSEF | 0.75 | |
| 1.05 | ||
| 5 | ||
| 0.05 | ||
| 0.0067 |
| Model | Parameter | Value | Unit |
|---|---|---|---|
| Spool diameter | 125 | mm | |
| Rated flow coefficient | 200 | - | |
| Nominal pressure | 6.4 | MPa | |
| Rated stroke | 60 | mm | |
| Upper temperature limit | 200 | ℃ | |
| Feedback position | 20 | mA | |
| Rated power | 2.5 | kW | |
| Rated voltage | 380 | V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Tan, S.; Liu, Z.; Liu, T.; Ma, Y.; Meng, F.; Zhang, J.; Yang, C. Active Disturbance Rejection Control (ADRC) of Hot-Compression Molding Temperature of Bamboo-Based Fiber Composites. Appl. Sci. 2024, 14, 6080. https://doi.org/10.3390/app14146080
Ding Y, Tan S, Liu Z, Liu T, Ma Y, Meng F, Zhang J, Yang C. Active Disturbance Rejection Control (ADRC) of Hot-Compression Molding Temperature of Bamboo-Based Fiber Composites. Applied Sciences. 2024; 14(14):6080. https://doi.org/10.3390/app14146080
Chicago/Turabian StyleDing, Yucheng, Shaolin Tan, Zhihao Liu, Tongbin Liu, Yaqiang Ma, Fanwei Meng, Jiawei Zhang, and Chunmei Yang. 2024. "Active Disturbance Rejection Control (ADRC) of Hot-Compression Molding Temperature of Bamboo-Based Fiber Composites" Applied Sciences 14, no. 14: 6080. https://doi.org/10.3390/app14146080
APA StyleDing, Y., Tan, S., Liu, Z., Liu, T., Ma, Y., Meng, F., Zhang, J., & Yang, C. (2024). Active Disturbance Rejection Control (ADRC) of Hot-Compression Molding Temperature of Bamboo-Based Fiber Composites. Applied Sciences, 14(14), 6080. https://doi.org/10.3390/app14146080








