Abstract
The increase in life expectancy, according to the World Health Organization, is a fact, and with it rises the incidence of age-related neurodegenerative diseases. The most recurrent symptoms are those associated with tremors resulting from Parkinson’s disease (PD) or essential tremors (ETs). The main alternatives for the treatment of these patients are medication and surgical intervention, which sometimes have restrictions and side effects. Through computer simulations in Matlab software, this work investigates the performance of adaptive algorithms based on least mean squares (LMS) to suppress tremors in upper limbs, especially in the hands. The signals resulting from pathological hand tremors, related to PD, present components at frequencies that vary between 3 Hz and 6 Hz, with the more significant energy present in the fundamental and second harmonics, while physiological hand tremors, referred to ET, vary between 4 Hz and 12 Hz. We simulated and used these signals as reference signals in adaptive algorithms, filtered-x least mean square (Fx-LMS), filtered-x normalized least mean square (Fx-NLMS), and a hybrid Fx-LMS–NLMS purpose. Our results showed that the vibration control provided by the Fx-LMS–LMS algorithm is the most suitable for physiological tremors. For pathological tremors, we used a proposed algorithm with a filtered sinusoidal input signal, Fsinx-LMS, which presented the best results in this specific case.
1. Introduction
According to the World Health Organization (WHO), people born in 2015 will have an average life expectancy of 20 years longer than people born 50 years ago in most of the world. Thus, there is also an expansion in the incidence of pathologies inherent to aging with increased longevity. In this sense, people over 60 are usually affected by neurological diseases that cause tremors—oscillatory involuntary movements in some parts of the body [1,2].
Tremors can be classified as tremors in action and tremors at rest [3]. Essential tremor (ET) is more predominantly action related and affects the upper limbs, such as the hands and head, with frequency characteristics ranging from 4 Hz to 12 Hz [4]. This type of tremor can be bilateral or symmetric [5]. ET figures as one of the most prevalent neurological diseases in the world. Luis and Ferreira [6] estimated that about 1% of the world’s population and approximately % of people over 65 years of age suffer from ET. On the other hand, tremors at rest, in most cases, are related to Parkinson’s disease, which is the second principal pathology causing involuntary tremors. It occurs when the patient’s limb is completely relaxed and there is no anti-gravitational effort. In this case, unwanted movements are produced both in the lower limbs and in the upper limbs, in the frequency range between 3 Hz and 6 Hz [5]. People who suffer from PD and ET have difficulties performing simple everyday tasks, such as eating and writing [5].
Conventional mitigating alternatives for these patients are linked to medication and surgical intervention. For treatment with the medication Levodopa, for example, it was observed that about 50% of patients, after 5 years of treatment, had some side effects, such as agitation, hallucination, mood swings, and impulsivity [7,8]. Another form of treatment is surgical intervention.
Several devices have been developed in order to apply active, passive, and semi-active control techniques to help suppress unwanted movements arising from tremors, aiming to improve the life quality of people with PD and ET. Proportional, integrative, and derivative (PID) controllers have been used in recent research on vibration suppression, in which the controller acts to minimize unwanted signal values in order to ensure that the system gain follows reference values [9]. In the proposed analysis in [10], for instance, a model of a human hand with four degrees of freedom was used, together with a piezoelectric actuator, showing the feasibility of using a PID controller to suppress PD vibrations. Such controllers can be fixed or can be updated according to some algorithms, such as adaptive techniques.
Our work brings a new contribution to discuss hand tremor suppression control with a comparison of adaptive techniques, more precisely, filtered-x based, for active vibration control applied to the suppression of movements arising from hand tremors. Among the advantages of the algorithms are faster convergence in ideal conditions and tracking capability. The comparisons take into account complexity analysis, convergence time, and mean square error (MSE) in the steady state. As is known, there are many challenges in research of this nature, especially in the difficulty of collecting and evaluating data on the intensity and frequency of tremors without the need to use invasive methods. In our analysis, we used mathematical and computational models to analyze the attenuation effect.
Therefore, tests in humans are not considered in this study. The results presented in this work enable the performance analysis of the tested statistical learning algorithms involving Monte Carlo simulations. It is important to note that simulations are not perfect representations of real-world situations, and there may be some discrepancies between the simulation and reality. Therefore, it is essential to carefully evaluate and validate simulation results before making any important decisions based on simulation outcomes [11,12].
The rest of this work is organized as follows. In Section 2, the mathematical models used to represent the hand tremor signal are presented and discussed. Section 3 presents the structure of the active vibration control and the filters used to compose the solution to the problem. Section 5 presents the results, as well as a discussion of the findings. In Section 6, final considerations and new directions for research in the area are presented.
Related Publications
Active vibration control (AVC) consists of applying a force of opposite intensity to an external source of vibration. To reduce hand tremors, Turkistani [13] developed a tremor-suppression prototype consisting of a flexible, portable glove. This prototype has a micro-electro-mechanical vibration simulation module based on an accelerometer–gyroscope embedded in the glove that mimics hand vibration. The vibration signal is collected and sent to a microcontroller so that it can be processed, and the vibration motors present in the fingers are activated to reduce the tremor in 40%.
Another method to eliminate human arm tremors was developed by Chuanasa and Songscho [14], who used the self-balancing technique. In this technique, a rotating unbalanced mass actuator was used to reproduce arm tremors with the same frequency range obtained from clinical sources. In addition to the composition of the counterbalance device designed to hold the dummy arm, a proportional derivative integral controller and an algorithm programmed in LabVIEW were used to control the rotary unbalanced mass actuator, anti-shaker, in the order to combat tremor.
The method used by Hosseini et al. [15] consists of the mathematical modeling of a system with 4 degrees of freedom of a biomechanical system that represents the human hand. Active control is performed by combining a proportional and derivative controller and tested, via MATLAB-Simulink, in three different types of actuators: piezoelectric, magnetic, and electric. Finally, the efficiency of each actuator is compared separately, with the piezoelectric actuator demonstrating greater efficiency in suppressing tremors, such as those characteristics of Parkinson’s disease.
The paper [16] describes a novel deep neural network-based motion predictor that is both user and task independent. In comparison to existing estimators and predictors, the proposed one-dimensional convolutional-multilayer perceptron (1D-CNN-MLP) model demonstrated superior performance in both simulation and experimental assessments, especially in reducing the time delay required for real-time tremor management using wearable assistive devices. The model achieved an average estimation accuracy of 99.2% and performed well in future voluntary motion prediction with up to 100 steps ahead.The proposed model also demonstrated an average tremor reduction of 93.8% ± 1.5% in real-time experimental setups, outperforming the commonly used weighted Fourier linear combiner estimator by 25%. Additionally, the proposed model achieved a prediction time as low as 1.5 ms for 100 steps ahead.
In their work, Kim and Yoon [17] introduced novel adaptive digital filtering algorithms that are based on internal model control (IMC) and aim to improve the stability, robustness, and tracking performance of active vibration and noise attenuation schemes. The proposed methods involve the use of a process model to estimate the dynamic behavior of the target plant and can be combined with an internal model controller to create a feedback control system based on IMC. The algorithms are designed to manage multi-spectral signals effectively and have been numerically verified in several cases with single sine waves and multi-spectral signals. The performance of the proposed system is evaluated in terms of time-domain tracking and estimation errors in both time and frequency domains.
Table 1 presents a comparison of techniques for passive vibration control in wearable assistive devices [13] and active vibration control [14,15,16,17], considering the last 7 years of literature. However, no evidence has been found of other publications using adaptive filters to control vibrations associated with ET and PD. Notably, in the reviewed studies, the authors worked with signal acquisition processes—which have difficult reproducibility of the results—or used mathematical models distinct from ET and PD models. Consequently, comparing algorithms that use different signal acquisition methods or specific purpose mathematical models is highly complicated unless differences between them are carefully accounted for in the evaluation process.

Table 1.
Comparative table of publications on the subject in the last 7 years.
2. Mathematical Models of Tremors in Upper Limbs
In this work, a mathematical model of hand tremor similar to signal patterns obtained by clinical means and mathematically validated is used. Thus, the need to acquire signals in humans is eliminated. There are also advantages of using mathematical models such as easy identification, good spectral frequency resolution, and convenient use in embedded systems.
2.1. Physiological Tremor Model by Time Series
The characterization method used by Jakubowski et al. [18] in the distinction between essential, physiological, and Parkinsonian tremors, consists of using higher-order statistics by Taylor series, in which third- and fourth-order cumulants are implemented to describe the behavior of tremors. Furthermore, he claims that second-order Gaussian models are not able to distinguish between the three types of vibration patterns mentioned above.
The model presented by Zhang and Chu [19] consists of the simulation of physiological tremors in an outstretched hand loaded with a weight of 2.3 to 4.5 kg, for 60 s, using an auto-regressive model of order , AR(3).
An auto-regressive process of order p, AR(p), is given by
where are the model coefficients and is a white noise with Gaussian distribution with zero mean and variance . According to [20], the order that will produce the smallest error is .
2.2. Mathematical Model of Parkinsonian Tremor
Theoretically, the Parkinsonian movement can be reconstituted by Fourier analysis with sinusoidal signals of multiple frequencies, where the amplitude and phase of the signal are determined by the spectrum [20]. In such a way, the tremor signal is given by
in which .
The collaboration of Reeke [20] rests on a simple but very similar model to the real behavior of a vibration produced by the left wrist of a patient with Parkinson’s. These models are both described by the sum of two sinusoidal and by the multiplication of two sinusoidal frequencies different from those used in the sum.
The comparison in the time domain between the models is based on summing and sinusoidal multiplication by the real tremor recorded in a patient with resting tremor in the left wrist, in which sensors capture the supinator and patient’s wrist pronator. In the representation of [20], it is possible to notice the accuracy of the mathematical model used and the representation in the frequency domain of the real tremor.
3. Vibration Active Control
Firstly, it is necessary to characterize the vibrational properties of the structure, i.e., to know how the parts of the structure vibrate, to understand and control the vibration. Thus, we enable anticipating vibration levels or determining the actions to control vibration. While passive noise control has been the predominant method used in tremor control applications, the search for ultimate vibration control has advanced to the extent that the use of active forces would be preferable to neutralize vibration. In this vibration control technique, called active vibration control (AVC), the controller coefficients are constantly updated by an adaptive algorithm.
The AVC scheme, as highlighted in Figure 1, basically consists of the plant system (coefficients that characterize the behavior of the dynamic system), actuators, sensors, and controllers. For the tests carried out, two random white Gaussian signals with zero mean and unit variance, uncorrelated, are generated. In Figure 1, they are represented by the noise generator blocks and . The signal is used to recognize the plant coefficients of the main loop (direct path) ; on the other hand, the noise generator is an anti-signal generated in the loop (or secondary path) for recognizing the coefficients of the filter . The response of the input signal into the second loop in a finite impulse response (FIR) filter is used to filter the signal, which in turn feeds the adaptive algorithm, which acts to both recognize and estimate the coefficients of the main loop and to control the noise signal through the secondary loop.
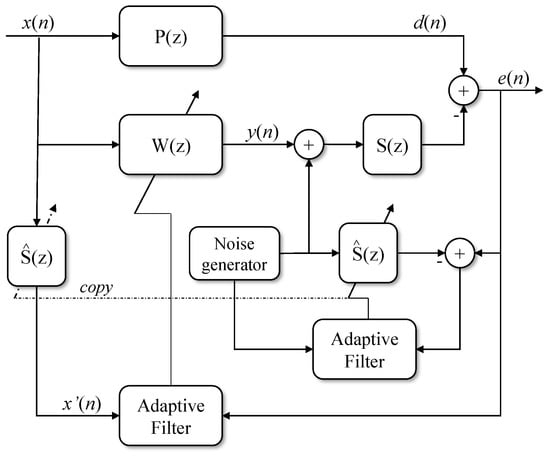
Figure 1.
Block diagram of the basic functioning of an adaptive vibration control system.
Active vibration control based on adaptive finite impulse response (FIR) filters typically introduces a conditional signal dispersion delay [21]. The reasons for these delays are geometric arrangements and computational time associated with the use of analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delays represent a phase shift in periodic signals. These delays prevent the instant feedback of signals from the least mean square (LMS) algorithm, for example. This can lead to instability and even divergence of the algorithms. Studies have presented a modification of the LMS algorithm, adjusting the underlying gradient descent algorithm [22,23,24,25] to work around this problem. The result is that any delays that occur can be fully compensated for.
Different strategies are proposed for the use of the LMS algorithm in controlling noise and vibrations, usually taking into account that the LMS alone is not capable of attenuating unpredictable signals, such as physiological tremors, for example. Active vibration control applications usually rely on the action of external elements, especially the analog-to-digital and digital-to-analog conversion processes, called here the secondary path. In the presence of those processes, traditional algorithms, such as LMS or RLS (recursive least square), should not be applied, being that the solution to this problem lies in filtering the input signal, using an estimation of the secondary path. The filtered-x least mean square (Fx-LMS) and its variations, which serve as the basis for this analysis, is an alternative proposed by Widrow et al. [26]. The strategy adopted also in [17] uses the internal model control method (IMC; the internal model control systems are characterized by a control device composed by the controller and by a simulation of the process, the internal model), together with the Fx-LMS algorithm to suppress noise and vibrations. Its results show the robustness and segment of reference values. Some variations of the Fx-LMS algorithm are widely explored in [27,28], which may serve as a basis for comparing vibration control strategies in a future research.
In this work, some adaptive algorithms based on the least mean squares for active control of variable vibration systems are evaluated. The framework also uses an auxiliary filter to improve the online estimation of the secondary path. The secondary path is represented by the transfer functions of the auxiliary filter and the controller, and its finite impulse response (FIR) model is also estimated with an adaptive strategy.
3.1. Adaptive Algorithms
The definition of an adaptive automaton, according to Widrow [29], consists of a system whose structure is adjustable in such a way that, based on a desirable value, its performance improves according to its contact with the applied environment. Thus, adaptive algorithms are employed where there is a constant change in their environment. They are usually applied in real-time systems, requiring a minimum calculation ratio per sample. These algorithms have a measurement process in order to get closer to the desired value. According to Aslam et al. [25] and Nascimento and Silva [30], adaptive filters can be seen as a disaggregating algorithm for mixing two signals and, for that, the reference values of one of the signals are essential.
3.1.1. Least-Mean Square (LMS) Algorithm
The least mean square (LMS) algorithm is one of the most commonly used adaptive filtering algorithms due to its computational simplicity, ease of proving its efficiency in stationary environments, stable behavior when implemented with finite arithmetic precision, and because it does not need to estimate the approximation gradient of values offline [29,31]. The use of adaptive learning algorithms with statistical inference allows for estimating the behavior of systems that present characteristics that can change over time, as is the case of signals from hand tremors.
Figure 2 shows a diagram that helps in understanding the LMS. The vector represents the system input values, the vector refers to the weights of the algorithm, which are updated at each iteration, and represents the output estimated by the weights and the input by
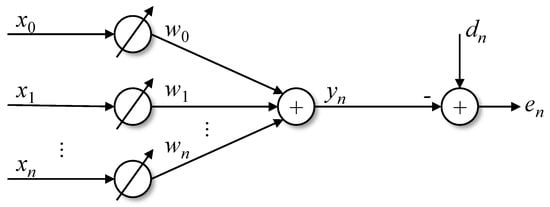
Figure 2.
Weight diagram of the LMS algorithm [26].
The signal is the signal to be approximated by the output of the system, and represents the value of the error at instant n.
Thus,
and therefore,
Taking the square value of the error (5) in order to minimize it, yields
The mean square error (MSE) is obtained from the calculation of the mean operator, , in (6),
or
where is the cross-correlation vector of input and output signals and , known as the deterministic autocorrelation matrix of the input signal.
It is observed that from (8), the MSE is given as a function of the weights, so the weights must be adjusted to reduce the error. This weight adjustment falls on a negative gradient in the decay rate of the root mean square error with respect to the weight adjustment, as shown by applying the derivative to (7),
and
The matrix is a positive definite matrix and the solution, , which minimizes the MSE, commonly known as the Wiener solution, is given by
The weight update equation for the LMS algorithm is given by
where is the adaptation step of the algorithm. The smaller this adjustment, the more precise the adaptation; however, a very small value of can result in a slower response of the adaptation system due to the high number of points.
3.1.2. Normalized Least Mean Square (NLMS) Algorithm
The normalized least mean square (NLMS) algorithm is a variation of the conventional LMS. In the LMS, the value of the learning step is a fixed value, while in the NLMS, this value is variable over time, in the form [32].
Thus, in the case of NLMS, (14) can be rewritten as
It is then necessary to define the posterior error since the adaptive step value is variable. Thus,
and substituting (15) into (16), yields
The value of , which approximates the error value to its minimum, is given by
in which is the -norm, i.e.,
Expression (19) leads to an important regulation to determine the variation of the instantaneous squared error.
Now, let us introduce a positive real scaling factor in (18) in the same way of [33]. This scaling factor is important to control the change in the tap-weight vector from one interaction to the next without changing the direction of the vector. Hence, the updating weights in the NLMS is given by
thus, we have a rate of convergence that is potentially faster than that of the LMS. Let us denote by from this moment on for simplification.
3.1.3. Filtered-X Least Mean Square (Fx-LMS) Algorithm
For real-time active noise control applications, the LMS algorithm, due to the long delay, is not the most suitable algorithm, as the noise at the system input can generate instability. As an alternative to this problem, Widrow [26] presented as a solution an algorithm that has an estimated signal input, in which the reference signal is adaptively filtered and compared with the input signal, obtaining the estimated signal. The Fx-LMS algorithm is normally used to update the adaptive filter, as shown in Figure 3.
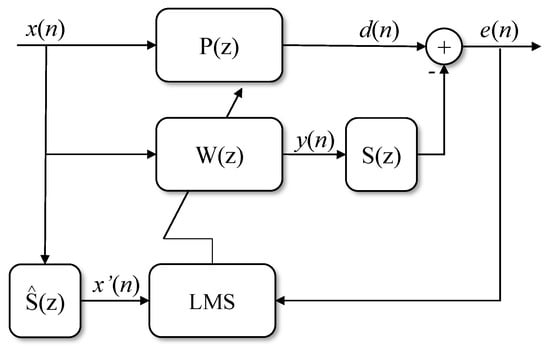
Figure 3.
Block diagram of Fx-LMS algorithm.
Analysis of the Fx-LMS convergence with stochastic signals on entry is presented in [34] considering a moving average process. In this case, is the primary path plan, and represents the estimated value of , its secondary path plan. Thus, the estimate of is given by
The equation that represents the error of the system, in the time domain, can be described as
Using a methodology analogous to Wiener’s optimal solution, an expression similar to (12) is obtained but with filtered values, given by
where denotes the optimal vector of weights, denotes the correlation matrix of filtered entries, and represents the cross-correlation between the filtered input and the desired signal.
The expression for the input is obtained by filtering using :
From (27) the weight vector that updates the Fx-LMS algorithm is
where , as in the LMS, is the convergence step of the algorithm.
4. Simulation Configurations
In this section, simulation configurations are presented for comparison of adaptive algorithms to control tremors in upper limbs. The Fx-LMS and its variations, which serve as the basis for this analysis, is an alternative to solve the problem of traditional algorithms, such as LMS and RLS [26].
Based on the results, it is possible to analyze the behavior of the Fx-LMS and Fx-NLMS algorithms in the control of physiological tremors in a mesh that considers the online adjustment of the secondary path, eliminating the need for a fitting step during the calibration period. In addition, considering the characteristics of these algorithms, the behavior for a hybrid approach is also evaluated, being titled Fx-LMS–NLMS. This is a suggestion for changing the traditional format of the algorithms mentioned above.
In a second approach, control is applied to Parkinson’s tremors. In this case, the behavior of the Fx-LMS algorithm with sinusoidal input is considered, which is denoted by Fsinx-LMS, an algorithm that is also a suggestion and adaptation of this analysis.
The design parameters (step-sizes) were defined by exhaustive trials, considering a faster fit for the secondary path for both controllers. The following value ranges were analyzed: to in steps of .
4.1. Simulation Setup for Physiological Tremors Control
The model used to simulate physiological tremors in this work is based on the study by Zhang and Chu [19], in which the weight coefficients of the model described by an AR process were obtained through filtering by the Levinson–Durbin algorithm— more details on this approach can be found in [19,35]—presented in Section 2.1. The analysis of the algorithm was performed by the minimum MSE, which presented a residual error of for a model of the third order.
The coefficients used in the AR(3) model to reproduce physiological tremor were . To control the physiological tremors signal, the plant must be a model proportional to , in this work we have used . A white Gaussian signal, with zero mean and unitary variance, was used to produce the desired signal shown in Figure 1.
The convergence step of the analyzed algorithms was maintained for all algorithms, as well as the number of interactions. After exhaustive tests, it was decided to use in the direct path and in the secondary path. In this way, the best results were obtained for both algorithms and scenarios.
4.2. Simulation Setup for Pathological Tremors Control
The model defined in Section 2.2, Equation (2)—which is a synthetic signal similar to Parkinson’s tremor—was used in order to generate the synthetic signal. This signal simulates the tremor of Parkinson’s disease, as can be seen in Figure 4. The frequency values used for the sinusoidal sum were 5.2 Hz and 4.6 Hz.
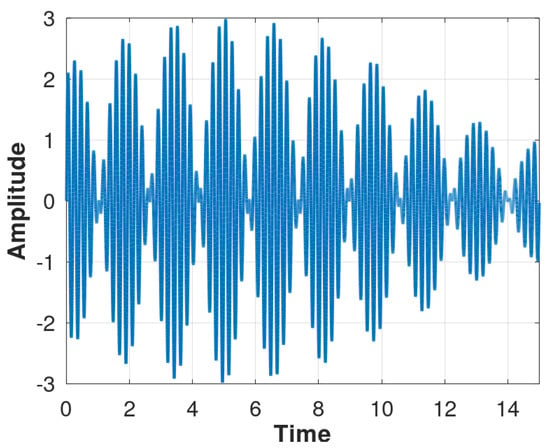
Figure 4.
Parkinson’s tremor signal in the time domain.
Figure 5 represents the Fourier transform of the synthetic Parkinson’s tremor signal shown in Figure 4. Note the occurrence of the peaks at approximately 4.5 Hz and 5.5 Hz.
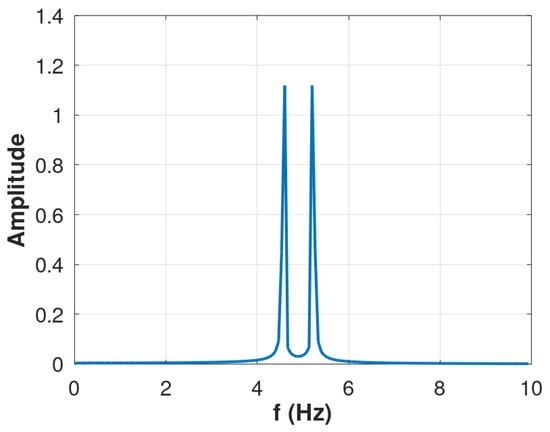
Figure 5.
Parkinson’s tremor signal in the frequency domain.
Unlike linear systems which can be uniquely identified by their impulse response, nonlinear systems need additional steps. In this way, we require nonlinear processing. Therefore, we need a transformation in input space to guarantee the modeling of the nonlinear part of the system.
The linear filter is . The desired signal was generated according (2). The input signal is the white Gaussian noise transformed by sinusoids. We clarify that, in this case, P(z) is not displayed because it is a non-linear system composed of the sum of sinusoids. The need to change the signals of the primary and secondary paths by sinusoids was due to the nonlinear characteristic of the desired signal . This is an adaptation, called here the FsinX-LMS algorithm, given that the dynamics of the Parkinson’s disease signal are non-linear and deterministic. A Gaussian white noise generator would not be able to generate a control signal for Parkinson’s tremors, given its linear nature. We used the step-size, in the primary path and in the secondary path.
5. Results
This section presents the reporting of the results of the experiments performed. First, in Section 5.1, the performance of the adaptive filter for physiological tremors (essential tremors) using Fx-LMS, Fx-NLMS and a hybrid of Fx-LMS–NLMS are shown. The second experiment comprises the results for the named Fsinx-LMS algorithm applied in the control of pathological tremors (related to Parkinson’s disease), Section 5.2.
5.1. Simulation Result of Physiological Tremors Control
The results of this research are presented by comparing the algorithms Fx-LMS, Fx-NLMS, and LMS. In the first and second scenarios, the adaptive filters (Figure 1) were updated using the Fx-LMS and Fx-NLMS algorithms, respectively. In the third scenario, a hybrid condition was considered, in which the adaptive filter corresponding to the direct path is updated by the Fx-LMS algorithm and the filter in the secondary path is updated by the Fx-NLMS algorithm. The basic difference between the three scenarios is in the normalization of the error signal of the main and secondary loops. In Scenario 1, Fx-LMS, there is no normalization of the error signal data of the algorithm loops. In Scenario 2, Fx-NLMS, there is data normalization in both the main and secondary mesh. In Scenario 3, Fx-LMS–NLMS, the normalization is done only in the secondary path.
- Scenario 1 (Fx-LMS): The behavior of the Fx-LMS algorithm (Scenario 1) in the active control of physiological tremor vibration is shown in Figure 6. The steady state is reached after approximately 4000 samples. Figure 7 presents the power spectral density (PSD) which quantifies the error distribution over the frequency spectrum.
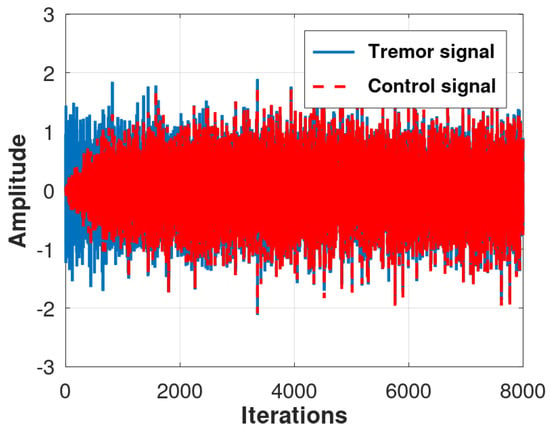 Figure 6. Control evaluation results produced by the Fx-LMS algorithm for 30 runs of a Monte Carlo simulation.
Figure 6. Control evaluation results produced by the Fx-LMS algorithm for 30 runs of a Monte Carlo simulation.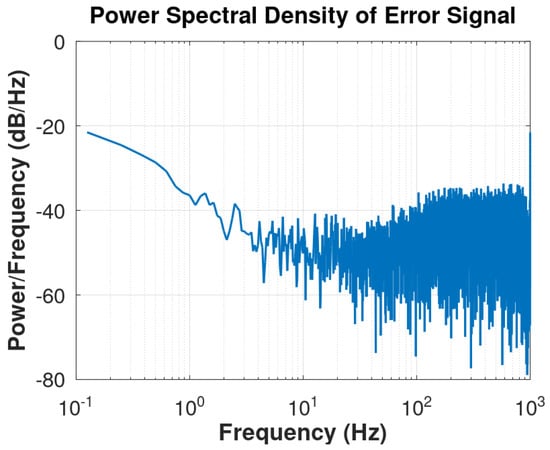 Figure 7. Behavior of the power spectral density (PSD) of the error signal by Fx-LMS.
Figure 7. Behavior of the power spectral density (PSD) of the error signal by Fx-LMS.
- Scenario 2 (Fx-NLMS): The Fx-NLMS algorithm has normalized data in both the main and secondary loops, and its result for controlling the physiological tremor signal is illustrated by Figure 8. In this case, approximately 4500 samples are needed for the control signal to converge, following the reference values, and it is enough to minimize the tremors. In Figure 9, we present the power spectral density (PSD) to quantify the error distribution over the frequency spectrum.
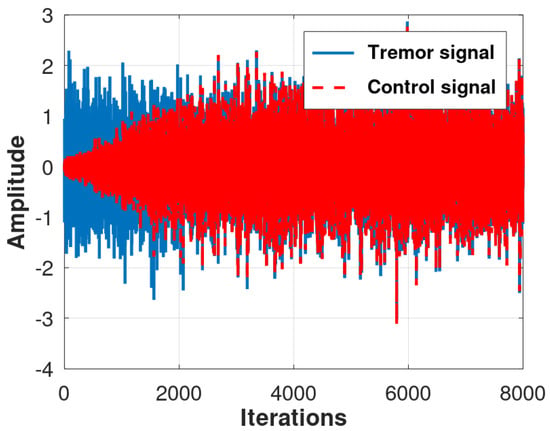 Figure 8. Control evaluation results produced by the Fx-NLMS algorithm for 30 runs of a Monte Carlo simulation.
Figure 8. Control evaluation results produced by the Fx-NLMS algorithm for 30 runs of a Monte Carlo simulation.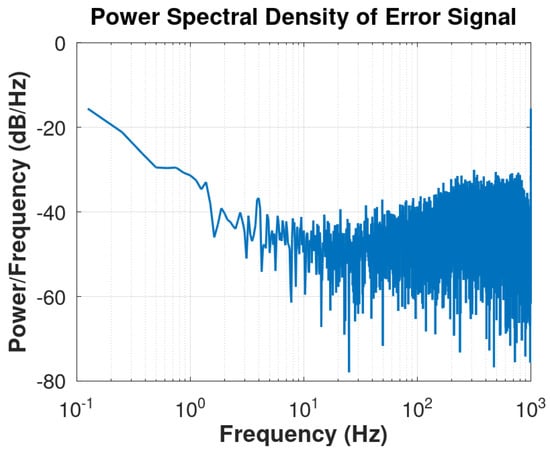 Figure 9. Behavior of the power spectral density (PSD) of the error signal by Fx-NLMS.
Figure 9. Behavior of the power spectral density (PSD) of the error signal by Fx-NLMS.
- Scenario 3 (Fx-LMS&NLMS): In Scenario 3, the hybrid, the control structure uses the Fx-LMS–NLMS algorithms, which have normalized data in the secondary loop error. This arrangement of algorithms is a suggestion of this work regarding a change in the normalization of the secondary path only. This combination enables a gain in performance. Figure 10 shows the control result of the algorithm, where the steady state is reached with approximately 4000 samples. Figure 11 provides a clear and quantitative analysis of the frequency content of the error signal.
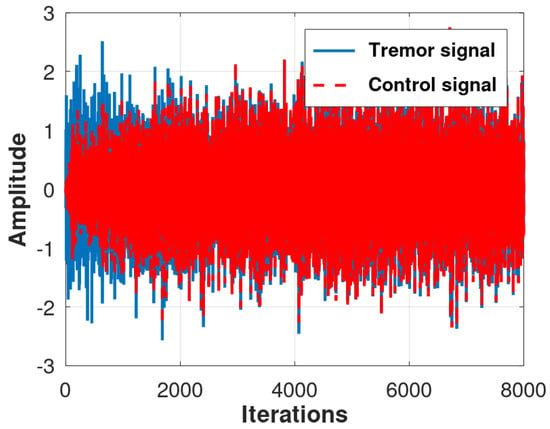 Figure 10. Control evaluation by the Fx-LMS–NLMS algorithm for 30 runs of a Monte Carlo simulation.
Figure 10. Control evaluation by the Fx-LMS–NLMS algorithm for 30 runs of a Monte Carlo simulation.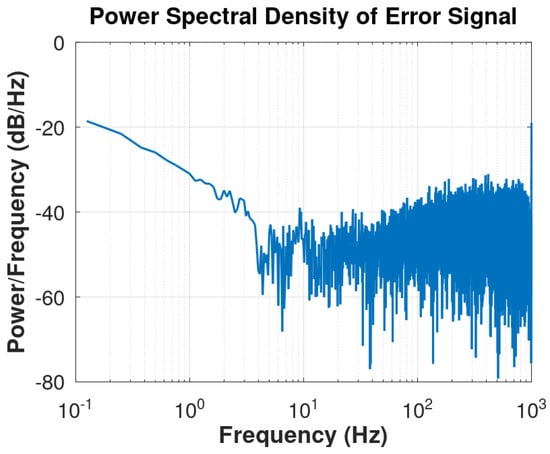 Figure 11. Behavior of the power spectral density (PSD) of the error signal by Fx-LMS–NLMS.
Figure 11. Behavior of the power spectral density (PSD) of the error signal by Fx-LMS–NLMS.
The Fx-LMS and Fx-NLMS algorithms, implemented in Scenarios 1 and 2, respectively, presented a similar mean squared error attenuation level. The most relevant difference in behavior occurred in the convergence times of each one of them. The Fx-LMS algorithm reached an error of −22 dB in 4000 samples, 500 less than the time obtained in Scenario 2.
The Fx-LMS–NLMS algorithm, implemented in Scenario 3, proved to be faster if compared to the NLMS algorithm, requiring 4000 samples to carry out the active control, a reduction of 30% compared to Scenarios 1 and 2. This result can be attributed to fast response due to normalized filtering in the modeling of the only plant of . This comparison can be seen in Figure 12.
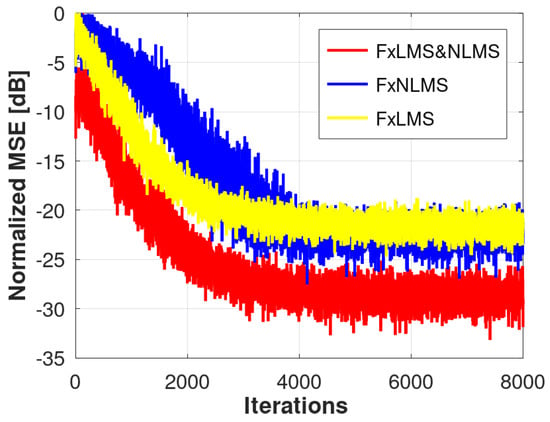
Figure 12.
Comparison of the normalized MSE behavior averaged over 30 runs. Ragged curves (yellow): Monte Carlo simulation of Fx-LMS. Ragged curves (blue): Monte Carlo simulation of Fx-NLMS. Ragged curves (red): Monte Carlo simulation of Fx-LMS–NLMS.
It is clear that an analysis in terms of computational complexity is necessary for a cost-benefit assessment. However, in a scenario where there is no complexity restriction, Fx-LMS–NLMS achieved faster convergence.
Table 2 presents more clearly the final comparison of the results in terms of the number of iterations and the amplitude and attenuation of the tremors in terms of square mean errors.

Table 2.
Comparative table of results.
5.2. Simulation Result of Pathological Tremors Control
The dynamics of Parkinsonian tremor are non-linear, deterministic, and chaotic [36]. This is a totally different way of controlling what was previously shown with algorithms based on zero-mean and unitary variance Gaussian noise signals.
The control signal generated by the Fsinx-LMS algorithm will always try to follow the non-linearity and non-stationary nature of the tremor signal similar to that produced by the Parkinson tremor signal, as illustrated in Figure 13. Analogous dynamics can be founded in [37,38]. Other solutions involving applied algorithms and other scenarios with metrics and parameters can be viewed at [39,40]. In this way, the algorithm learns the dynamics of the tremor signal until its pattern changes and the algorithm needs to re-adapt itself, converging for the new coefficients. The MSE shown in Figure 14 represents the operation of the adaptive algorithm. There is a high MSE initially, due to delay of the control system, until the error decreases drastically when the control signal follows the desired signal and the vibration pattern changes, and so the MSE increases again. This cycle repeats itself indefinitely. Unlike what happened in Section 5.1, it is not possible to obtain a steady-state error since the MSE is always trying to adapt to the behavior of the system that changes with a periodic characteristic. However, it is possible to notice that the attenuation lies around 14 dB. Figure 15 shows the PSD of the error signal plotted in log scale.
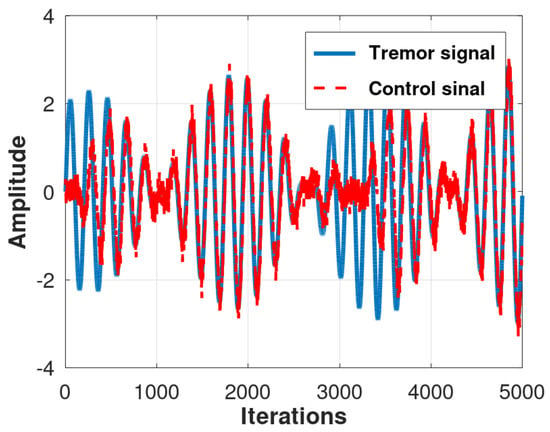
Figure 13.
Control evaluation results produced by the FsinX-LMS algorithm for 30 runs of a Monte Carlo simulation.
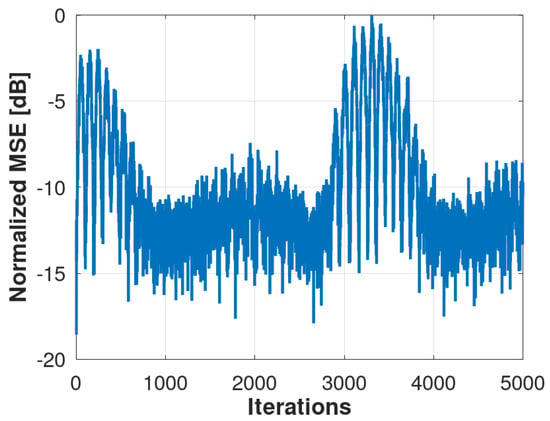
Figure 14.
Normalized-MSE results produced by the FsinX-LMS algorithm for 30 runs of a Monte Carlo simulation.
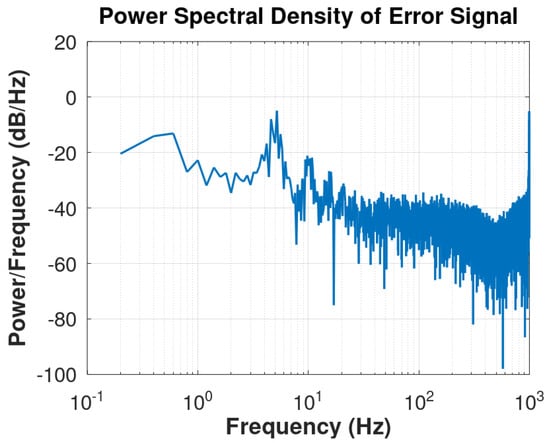
Figure 15.
Behavior of the power spectral density (PSD) of the error signal by Fx-LMS in the pathological tremor control scenario.
6. Conclusions
Adaptive algorithms usually have a complex nature, which demands a need for knowledge of statistics, mathematics, signal processing, and computing tools. This work sought to collaborate by presenting a discussion about these algorithms and a sequence of scientific tests that would allow their application in problems of mechanical, electronic, computing, and biomedical engineering. Computational modeling and simulations have been used in several areas, especially biomedical engineering to support product development and evaluation of strategies [41]. This type of approach allows methods to be evaluated prior to experiments on humans.
The bibliographic review allowed the construction and survey of the necessary concepts for the application of adaptive filtering techniques in order to actively control vibration. In addition, information about the problem to be solved and knowledge of the vibratory patterns are mentioned here. This search was based on mathematical models, avoiding the need for the invasive data collection on patients.
From the obtained results, it was noticed a great sensitivity to the model, the family of algorithms, and the parameters used. Active control of physiological and Parkinsonian tremors was presented using algorithms from the adaptive LMS family. The Fx-LMS–NLMS algorithm showed the best response among the algorithms used in this research. Its difference from the others, Fx-LMS and Fx-NLMS, is only in the number of iterations. The algorithm that obtained the slowest response was the result of non-normalization in the primary mesh, where the plant of the system is initially recognized. The Fx-LMS algorithm is traditionally used in strokes, and can, in a way, serve as a parameter in relation to its variations, per hour used in the control of physiological tremors.
To provide active control of Parkinsonian tremors, the Fsinx-LMS algorithm was presented. Derived from Fx-LMS, this algorithm has only one additional block for the non-linearization of generated random signals, producing a random phase sinusoid. This was necessary so that the non-linearities of the model could be mapped by the adaptive system. It shows that there is a way to control deterministic and non-linear tremors, such as the tremor of Parkinson’s disease, through LMS-type algorithms, provided that the generated signals are non-linear.
This study can be extended to other types of algorithms, especially for Parkinsonian tremors. In this case, kernelized algorithms can produce better results in systems with non-linear characteristics present in models that replicate this type of pathology. These algorithms have been applied by the scientific community and produced good results. Other approaches for estimating nonlinear systems can yet be considered, such as [37,38,42,43,44].
In addition, an implementation in embedded devices, DSP boards (digital signal processor) can improve the understanding of the behavior of these algorithms in a practical scenario, which would later serve as a basis for the development of an electronic prototype with the embedded technology composed of a sensor and actuator to provide active control.
Author Contributions
Conceptualization, R.S.A.A., W.D.P. and R.C.B.; methodology, R.S.A.A. and W.D.P.; analysis, R.S.A.A., J.C.T., W.D.P. and R.C.B.; writing—original draft preparation, R.S.A.A., W.D.P., R.C.B. and J.C.T.; writing—review and editing, R.S.A.A., V.R.Q.L., W.D.P., J.F.D.P.S. and R.C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Fundação para a Ciência e a Tecnologia, I.P. (Portuguese Foundation for Science and Technology) by the project UIDB/05064/2020 (VALORIZA–Research Centre for Endogenous Resource 764 Valorization), and Project UIDB/04111/2020, ILIND–Instituto Lusófono de Investigação e Desenvolvimento, under project COFAC/ILIND/ COPELABS/3/2020.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Active Vibration Control | AVC |
| Analog-to-digital converters | ADC |
| Digital Signal Processor | DSP |
| Digital-to-analog converters | DAC |
| Essential Tremors | ET |
| Filtered-x Least Mean Square | Fx-LMS |
| Filtered-x Normalized Least Mean Square | Fx-NLMS |
| Finite Impulse Response | FIR |
| Internal Model Control | IMC |
| Least Mean Square | LMS |
| Mean Square Error | MSE |
| Normalized Least Mean Square | NLMS |
| Parkinson’s Disease | PD |
| Proportional, Integrative, and Derivative | PID |
| Recursive Least Square | RSL |
| World Health Organization | WHO |
References
- Findley, L.J. Classification of tremors. J. Clin. Neurophysiol. 1996, 13, 122–132. [Google Scholar] [CrossRef] [PubMed]
- Aryal, S.; Skinner, T.; Bridges, B.; Weber, J.T. The pathology of Parkinson’s disease and potential benefit of dietary polyphenols. Molecules 2020, 25, 4382. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, K.P.; Bain, P.; Bajaj, N.; Elble, R.J.; Hallett, M.; Louis, E.D.; Raethjen, J.; Stamelou, M.; Testa, C.M.; Deuschl, G.; et al. Consensus Statement on the classification of tremors. from the task force on tremor of the International Parkinson and Movement Disorder Society. Mov. Disord. 2018, 33, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Louis, E.D.; Ottman, R. Essential tremor. In Genetics of Movement Disorders; Elsevier: Amsterdam, The Netherlands, 2003; pp. 353–363. [Google Scholar] [CrossRef]
- Lenka, A.; Jankovic, J. Tremor syndromes: An updated review. Front. Neurol. 2021, 12, 684835. [Google Scholar] [CrossRef]
- Louis, E.D.; Ferreira, J.J. How common is the most common adult movement disorder? Update on the worldwide prevalence of essential tremor. Mov. Disord. 2010, 25, 534–541. [Google Scholar] [CrossRef]
- Voon, V.; Napier, T.C.; Frank, M.J.; Sgambato-Faure, V.; Grace, A.A.; Rodriguez-Oroz, M.; Obeso, J.; Bezard, E.; Fernagut, P.O. Impulse control disorders and levodopa-induced dyskinesias in Parkinson’s disease: An update. Lancet Neurol. 2017, 16, 238–250. [Google Scholar] [CrossRef]
- Sweet, R.D.; McDowell, F. Five years’ treatment of Parkinson’s disease with levodopa: Therapeutic results and survival of 100 patients. Ann. Intern. Med. 1975, 83, 456–463. [Google Scholar] [CrossRef]
- Lekshmi, A.; Ramachandran, K. Parkinson’s tremor suppression using active vibration control method. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 577, p. 012056. [Google Scholar] [CrossRef]
- Kazi, S.; Mailah, M.; Zain, Z.M. Suppression of hand postural tremor via active force control method. Manuf. Eng. Autom. Control. Robot. 2014, 76–82. [Google Scholar]
- Hellerstein, J.L.; Gu, S.; Choi, K.; Sauro, H.M. Recent advances in biomedical simulations: A manifesto for model engineering. F1000Research 2019, 8, Rev-261. [Google Scholar] [CrossRef]
- Morrison, T.M.; Stitzel, J.D.; Levine, S.M. Modeling and Simulation in Biomedical Engineering: Regulatory Science and Innovation for Advancing Public Health. Ann. Biomed. Eng. 2022, 51, 1–5. [Google Scholar] [CrossRef]
- Turkistani, A. Development of an Effective Portable and Flexible Glove for Hand Tremor Suppression. Master’s Thesis, Western Michigan University, Kalamazoo, MI, USA, 2017. [Google Scholar]
- Chuanasa, J.; Songschon, S. Essential tremor suppression by a novel self-balancing device. Prosthetics Orthot. Int. 2015, 39, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Al-Jumaily, A.; Abboud, S.A. Active force control system for hand tremor suppression by different actuators. In Proceedings of the 2016 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA), Ras Al Khaimah, United Arab Emirates, 6–8 December 2016; pp. 1–4. [Google Scholar]
- Ibrahim, A.; Zhou, Y.; Jenkins, M.E.; Trejos, A.L.; Naish, M.D. Real-Time Voluntary Motion Prediction and Parkinson’s Tremor Reduction Using Deep Neural Networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1413–1423. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Yoon, J.Y. Modified LMS strategies using internal model control for active noise and vibration control systems. Appl. Sci. 2018, 8, 1007. [Google Scholar] [CrossRef]
- Jakubowski, J.; Kwiatos, K.; Chwaleba, A.; Osowski, S. Higher order statistics and neural network for tremor recognition. IEEE Trans. Biomed. Eng. 2002, 49, 152–159. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chu, F. Real-time modeling and prediction of physiological hand tremor. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’05), Philadelphia, PA, USA, 23 March 2005; Volume 5, p. v-645. [Google Scholar]
- Reeke, G.N.; Poznanski, R.R.; Lindsay, K.A.; Rosenberg, J.R.; Sporns, O. Modeling in the Neurosciences: From Biological Systems to Neuromimetic Robotics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Dabis, H.; Moir, T. Least mean squares as a control system. Int. J. Control. 1991, 54, 321–335. [Google Scholar] [CrossRef]
- Elliott, S.; Stothers, I.; Nelson, P. A multiple error LMS algorithm and its application to the active control of sound and vibration. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1423–1434. [Google Scholar] [CrossRef]
- Song, P.; Zhao, H. Filtered-x least mean square/fourth (FXLMS/F) algorithm for active noise control. Mech. Syst. Signal Process. 2019, 120, 69–82. [Google Scholar] [CrossRef]
- Martinek, R.; Rzidky, J.; Jaros, R.; Bilik, P.; Ladrova, M. Least mean squares and recursive least squares algorithms for total harmonic distortion reduction using shunt active power filter control. Energies 2019, 12, 1545. [Google Scholar] [CrossRef]
- Aslam, M.S.; Shi, P.; Lim, C.C. Robust Active Noise Control Design by Optimal Weighted Least Squares Approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3955–3967. [Google Scholar] [CrossRef]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Dong, J.E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Lu, L.; Yin, K.L.; de Lamare, R.C.; Zheng, Z.; Yu, Y.; Yang, X.; Chen, B. A survey on active noise control in the past decade—Part I: Linear systems. Signal Process. 2021, 183, 108039. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, S.; Zhou, Z.; Li, H. An active noise control system based on reference signal decomposition. Digit. Signal Process. 2022, 129, 103676. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Nascimento, V.H.; Silva, M.T. Adaptive filters. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 1, pp. 619–761. [Google Scholar]
- Paulo, S.D. Adaptive Filtering: Algorithms and Practical Implementation; Springer: New York, NY, USA, 2013. [Google Scholar]
- Poularikas, A.D. Adaptive Filtering: Fundamentals of Least Mean Squares with MATLAB®; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Ardekani, I.T.; Abdulla, W.H. Theoretical convergence analysis of FxLMS algorithm. Signal Process. 2010, 90, 3046–3055. [Google Scholar] [CrossRef]
- Brockwell, P.; Dahlhaus, R. Generalized Levinson–Durbin and burg algorithms. J. Econom. 2004, 118, 129–149. [Google Scholar] [CrossRef]
- Beuter, A.; Glass, L.; Mackey, M.C.; Titcombe, M.S. Nonlinear Dynamics in Physiology and Medicine; Springer: New York, NY, USA, 2003. [Google Scholar]
- Parreira, W.D.; Costa, M.H.; Bermudez, J.C. Stochastic behavior analysis of the Gaussian KLMS algorithm for a correlated input signal. Signal Process. 2018, 152, 286–291. [Google Scholar] [CrossRef]
- Dos Santos, V.A.; Parreira, W.D.; Fernandes, A.M.D.R.; Ovejero, R.G.; Leithardt, V.R.Q. Improving Speaker Recognition in Environmental Noise with Adaptive Filter. IEEE Access 2022. [Google Scholar] [CrossRef]
- Leite, M.; Parreira, W.D.; Fernandes, A.M.d.R.; Leithardt, V.R.Q. Image Segmentation for Human Skin Detection. Appl. Sci. 2022, 12, 12140. [Google Scholar] [CrossRef]
- De Freitas, M.P.; Piai, V.A.; Farias, R.H.; Fernandes, A.M.R.; de Moraes Rossetto, A.G.; Leithardt, V.R.Q. Artificial Intelligence of Things Applied to Assistive Technology: A Systematic Literature Review. Sensors 2022, 22, 8531. [Google Scholar] [CrossRef]
- Erdemir, A.; Mulugeta, L.; Ku, J.P.; Drach, A.; Horner, M.; Morrison, T.M.; Peng, G.C.; Vadigepalli, R.; Lytton, W.W.; Myers, J.G. Credible practice of modeling and simulation in healthcare: Ten rules from a multidisciplinary perspective. J. Transl. Med. 2020, 18, 1–18. [Google Scholar] [CrossRef]
- Parreira, W.D.; Bermudez, J.C.M.; Richard, C.; Tourneret, J.Y. Stochastic behavior analysis of the Gaussian kernel least-mean-square algorithm. IEEE Trans. Signal Process. 2012, 60, 2208–2222. [Google Scholar] [CrossRef]
- Dos SP Soares, A.; Parreira, W.D.; Souza, E.G.; de Almeida, S.J.; Diniz, C.M.; Nascimento, C.D.; Stigger, M.F. Energy-based voice activity detection algorithm using Gaussian and Cauchy kernels. In Proceedings of the 2018 IEEE 9th Latin American Symposium on Circuits & Systems (LASCAS), Puerto Vallarta, Mexico, 25–28 February 2018; pp. 1–4. [Google Scholar]
- Soares, A.d.S.P.; Parreira, W.D.; Souza, E.G.; Nascimento, C.d.D.d.; Almeida, S.J.M.d. Voice Activity Detection Using Generalized Exponential Kernels for Time and Frequency Domains. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2116–2123. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).















