Dynamic Characteristics of Urban Rail Train in Multivehicle Marshaling under Traction Conditions
Abstract
1. Introduction
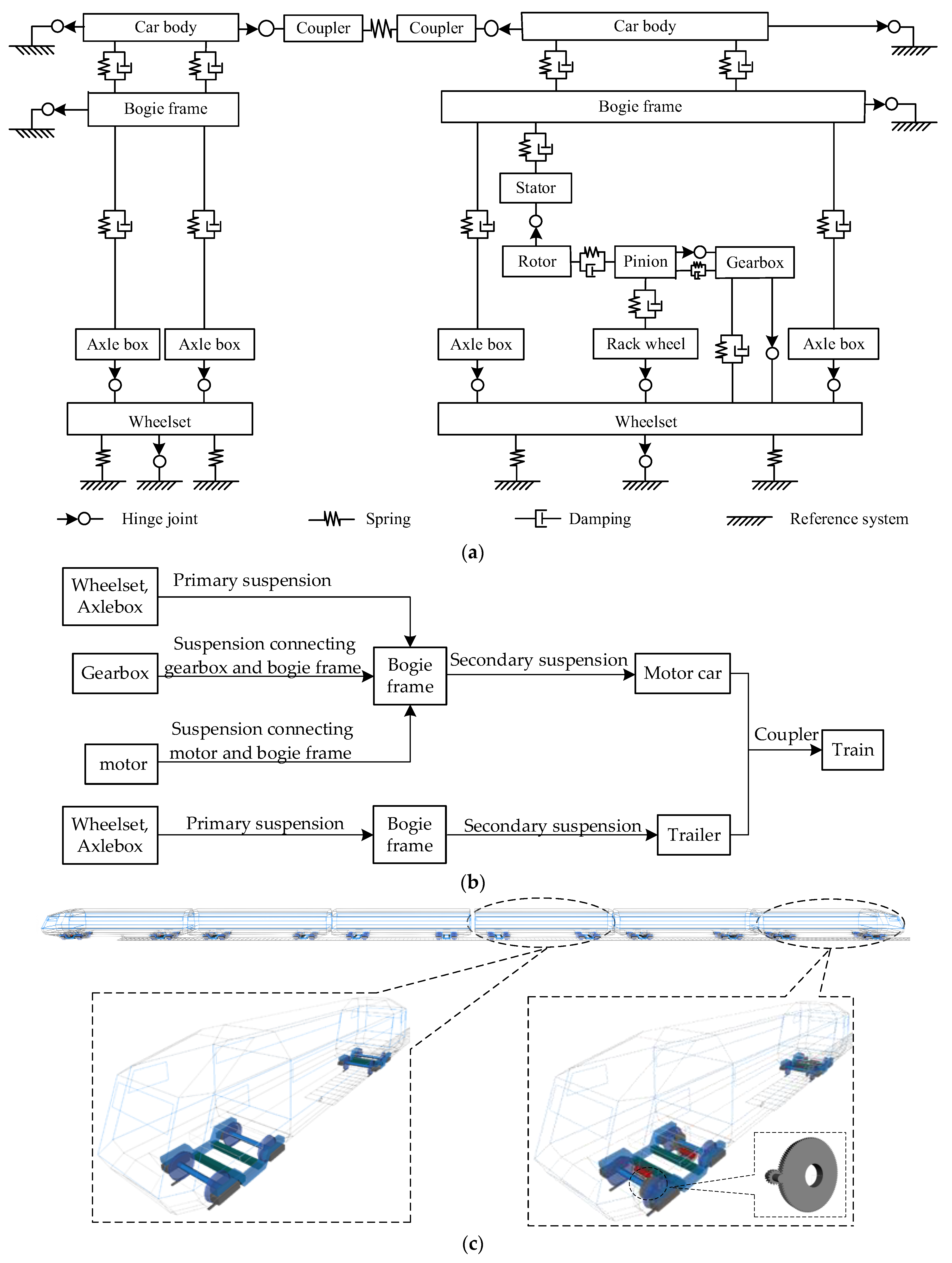
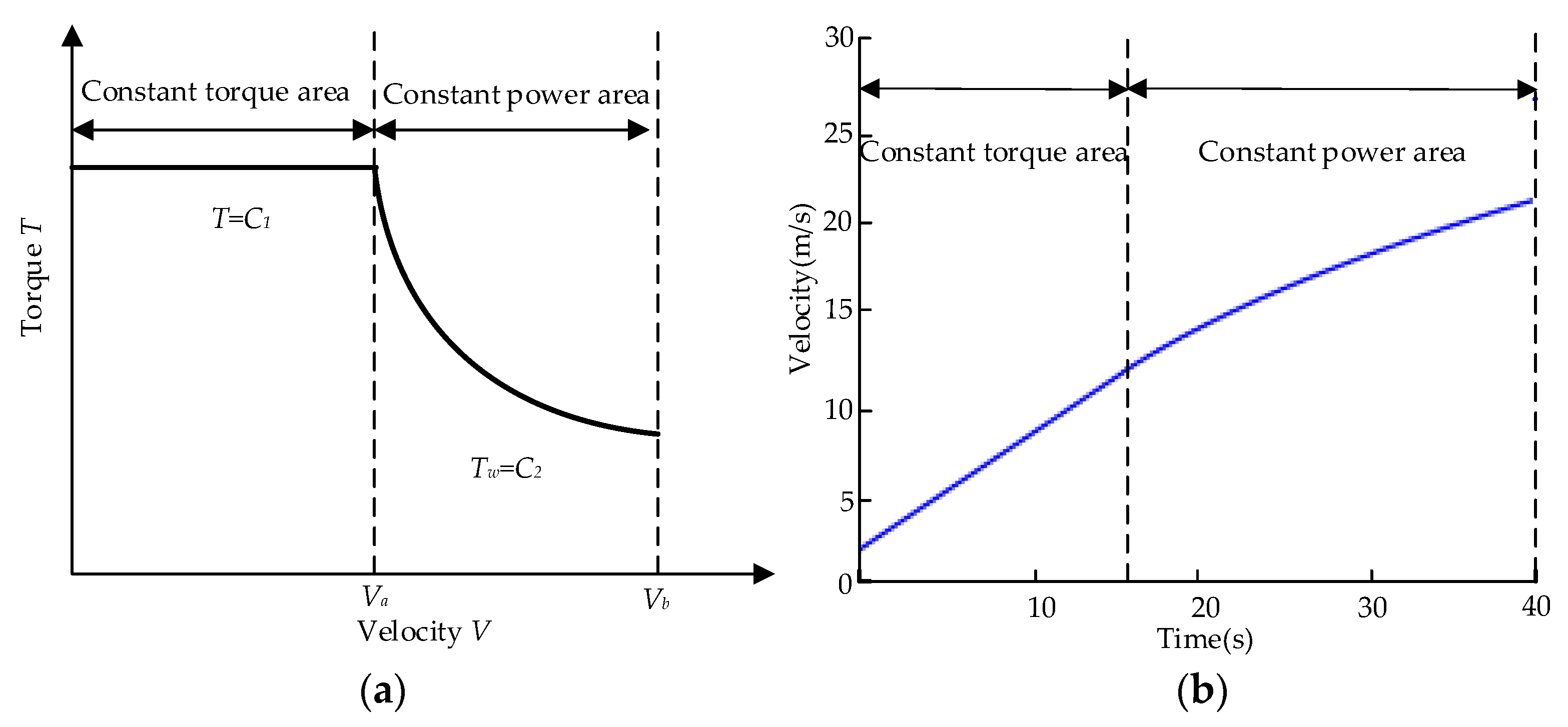
2. Dynamic Modeling
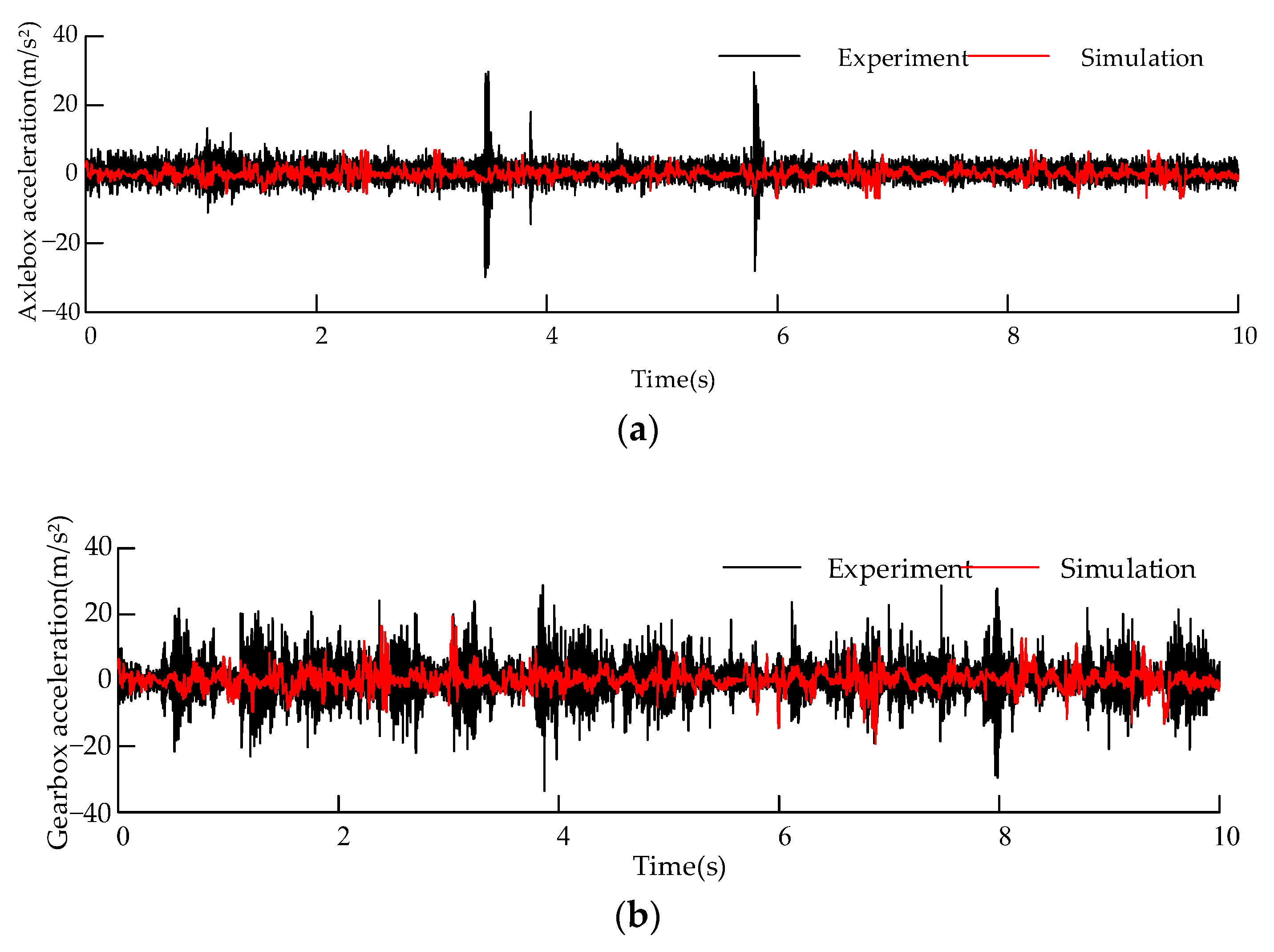
3. Model Validation
4. Analysis and Discussion
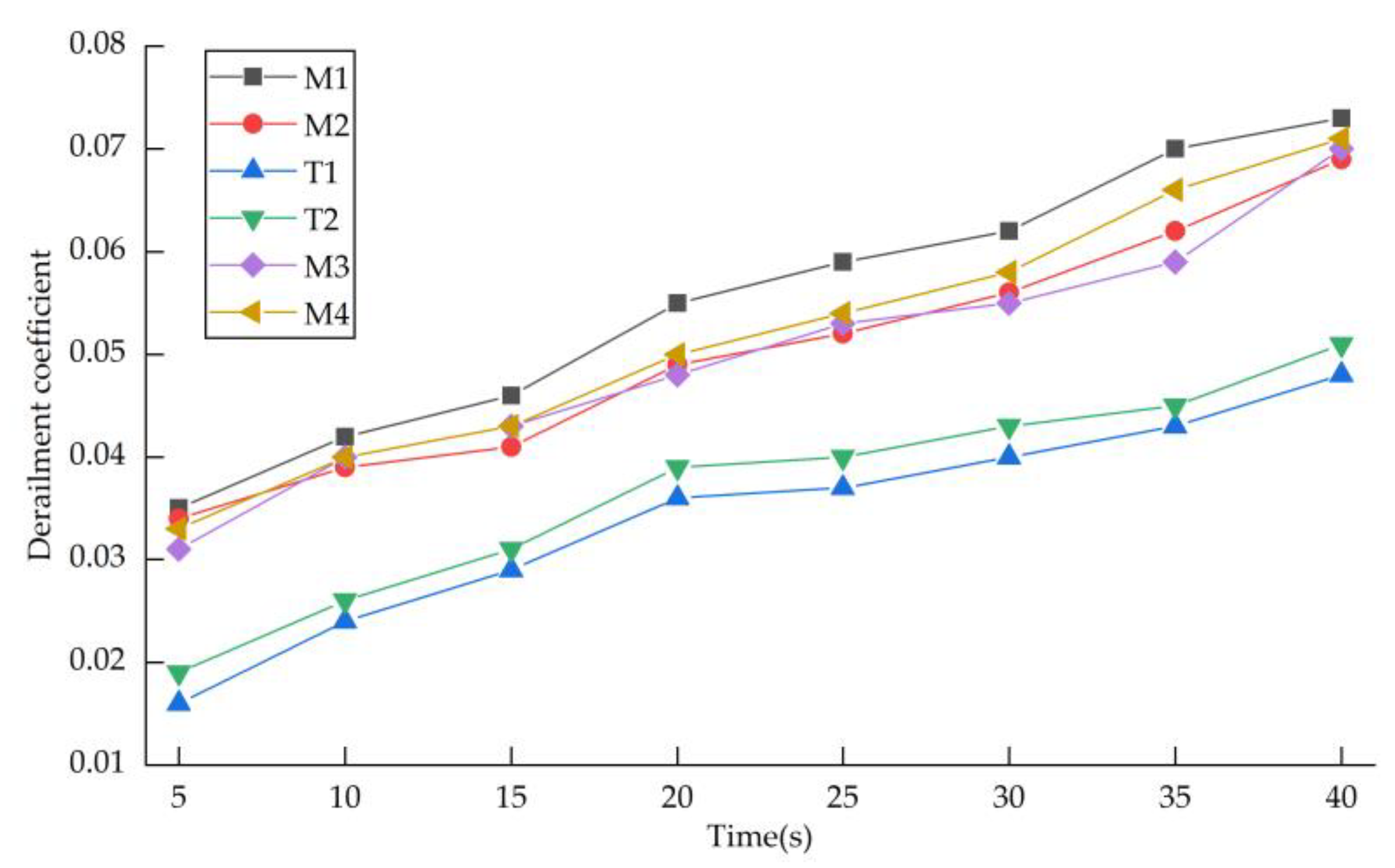
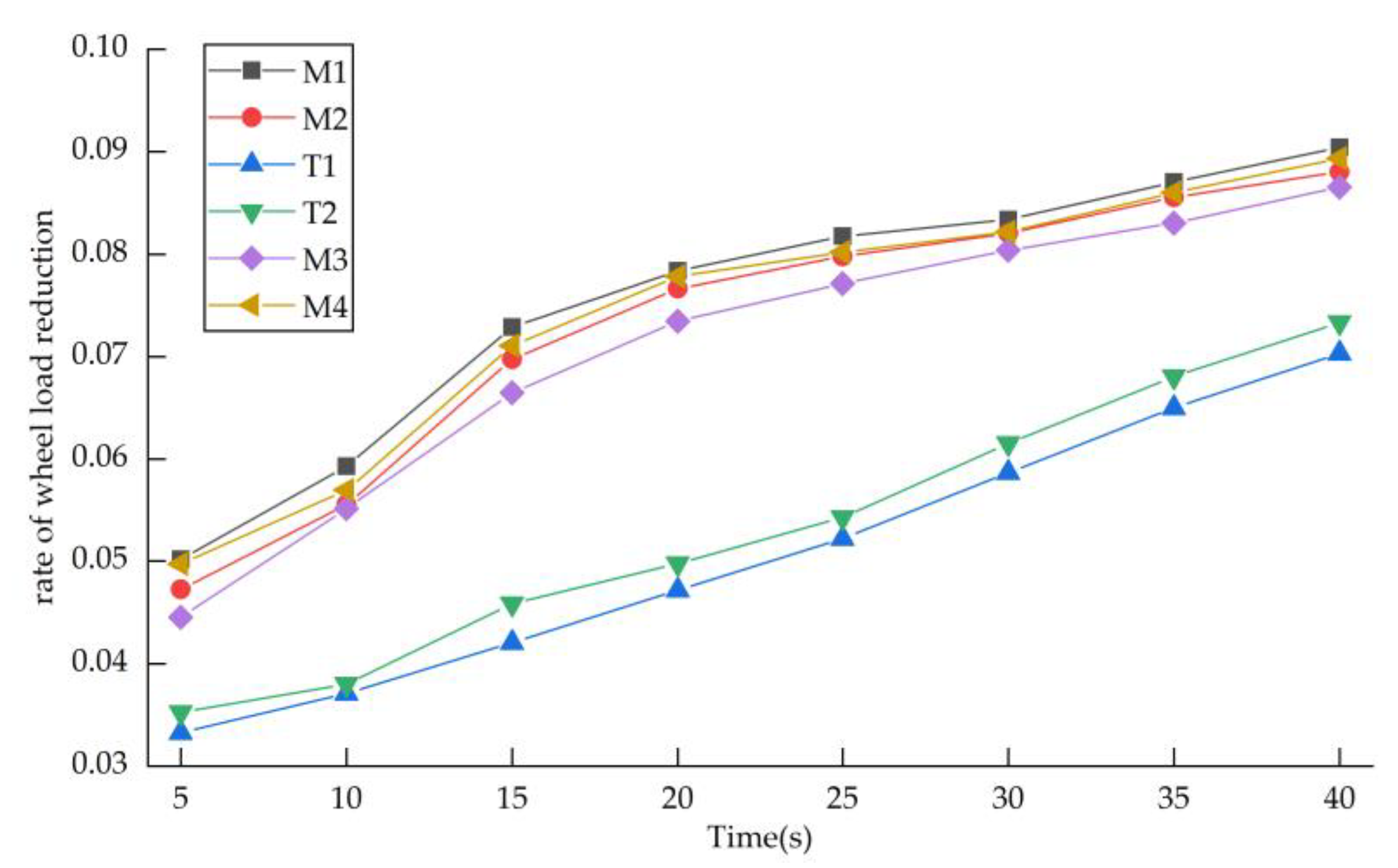
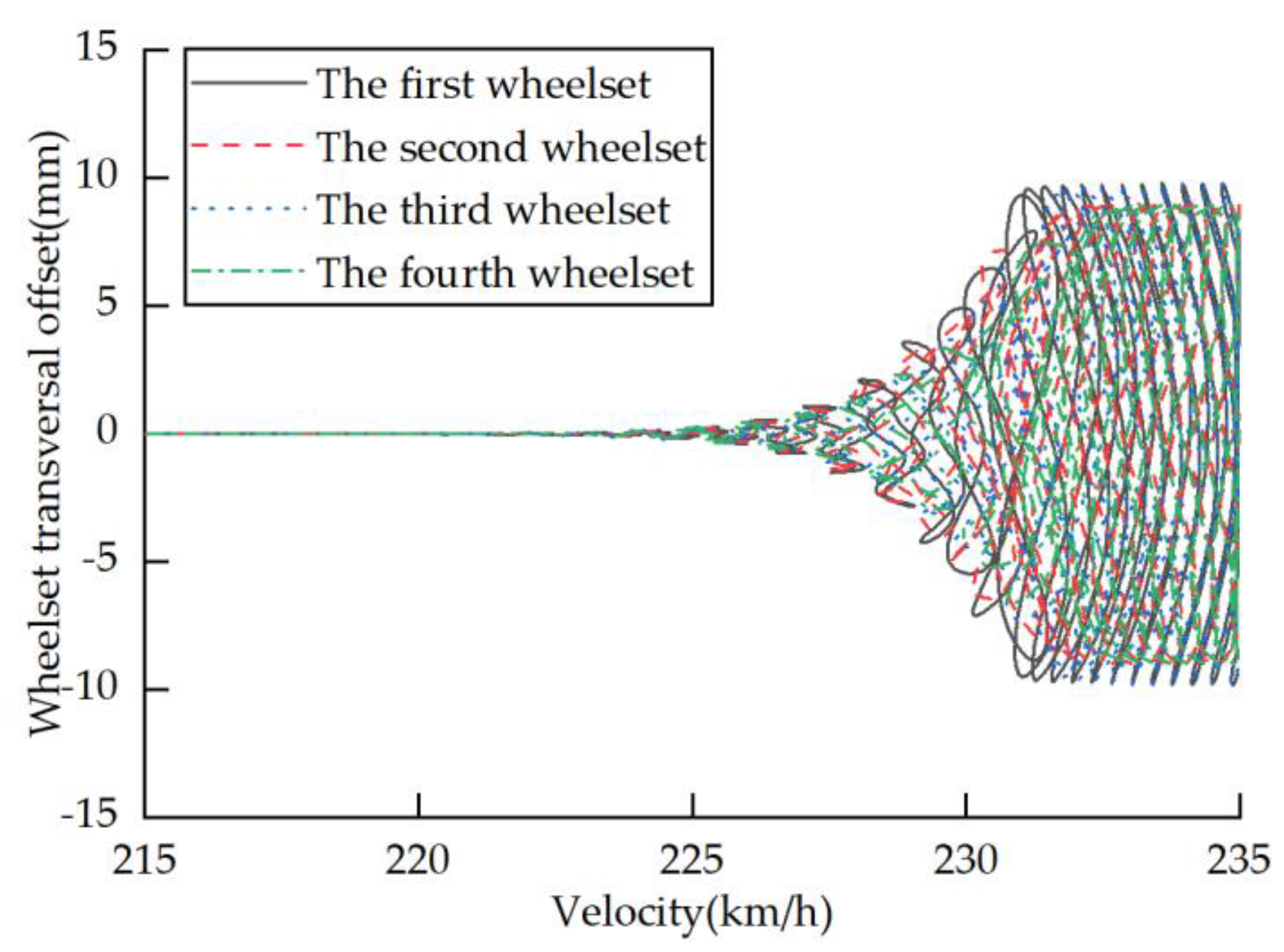
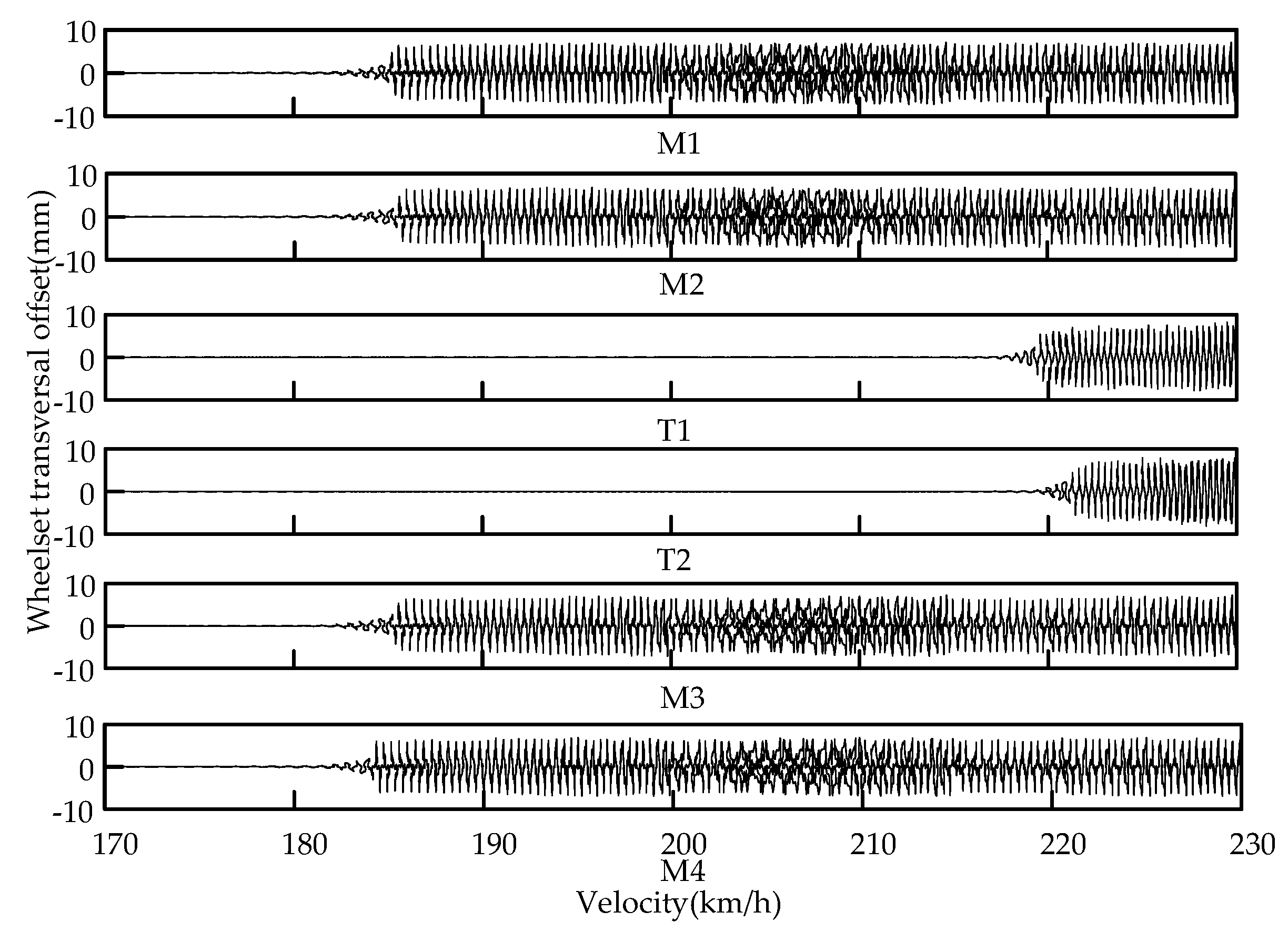
4.1. Analysis of Safety and Critical Velocity
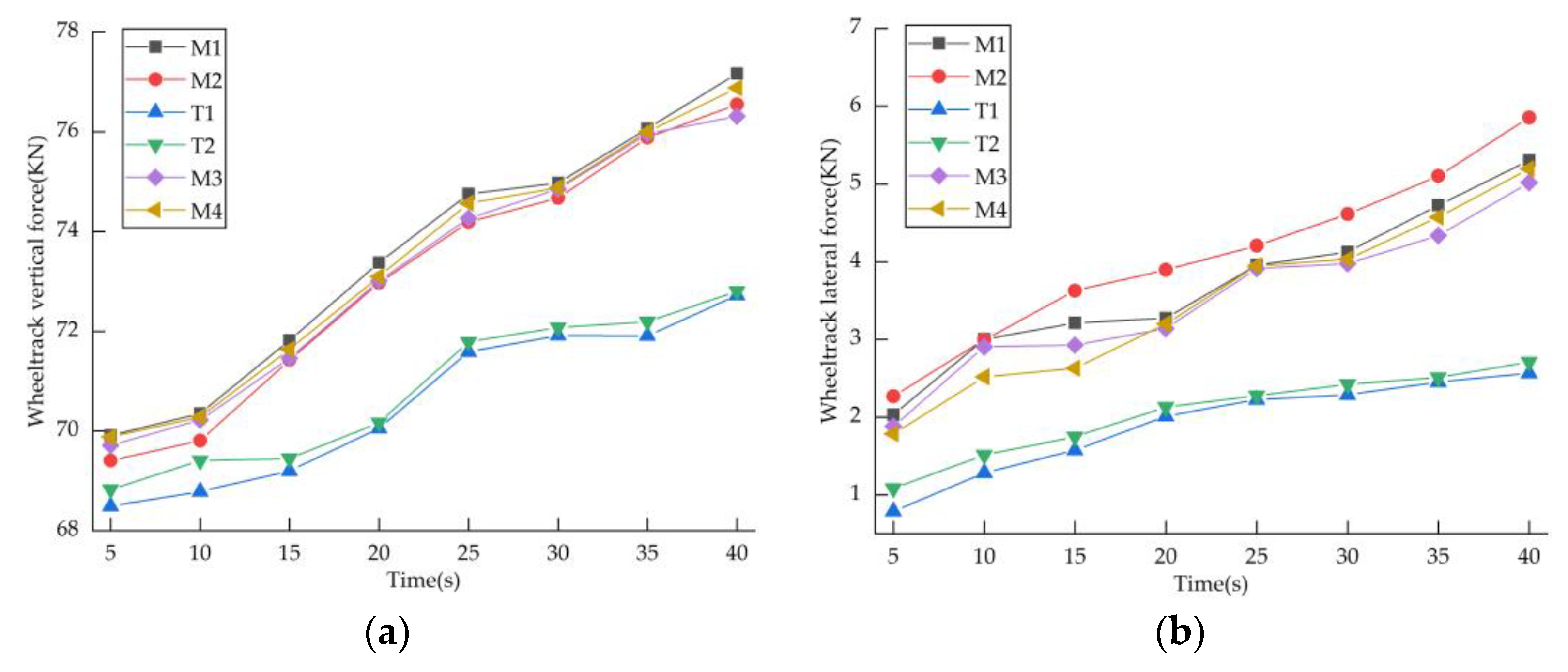
4.1.1. Security Analysis
4.1.2. Nonlinear Critical Speed Analysis
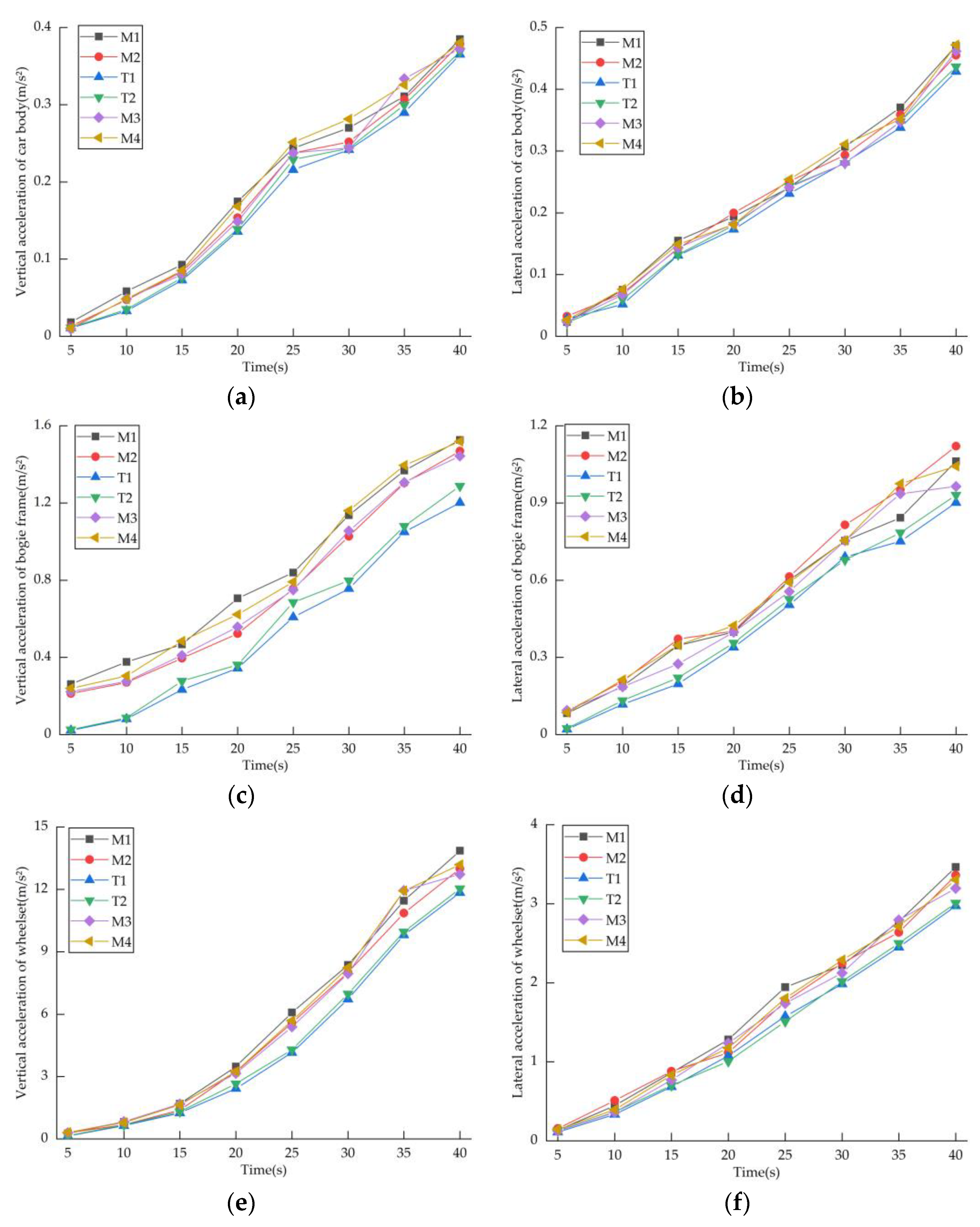
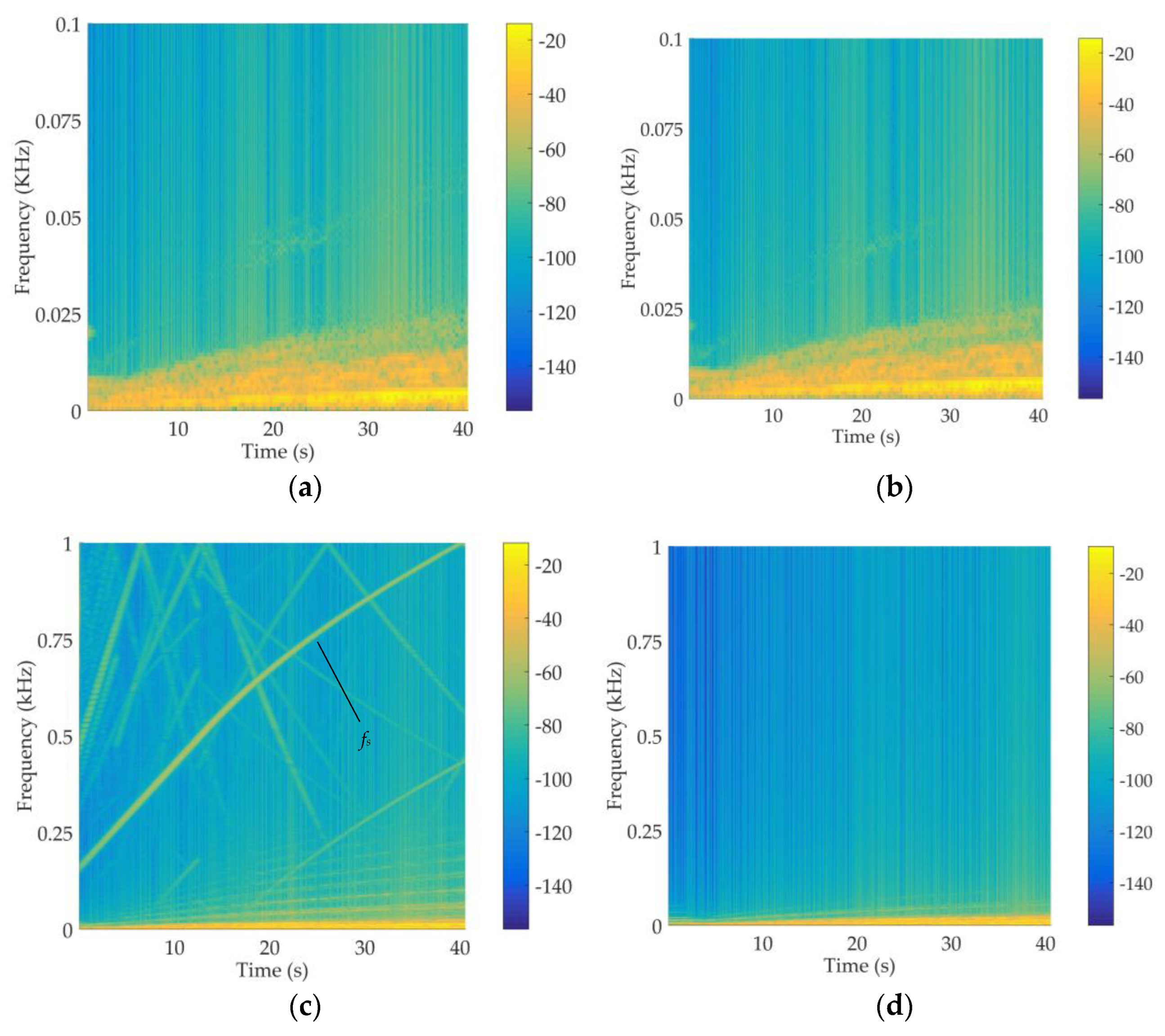
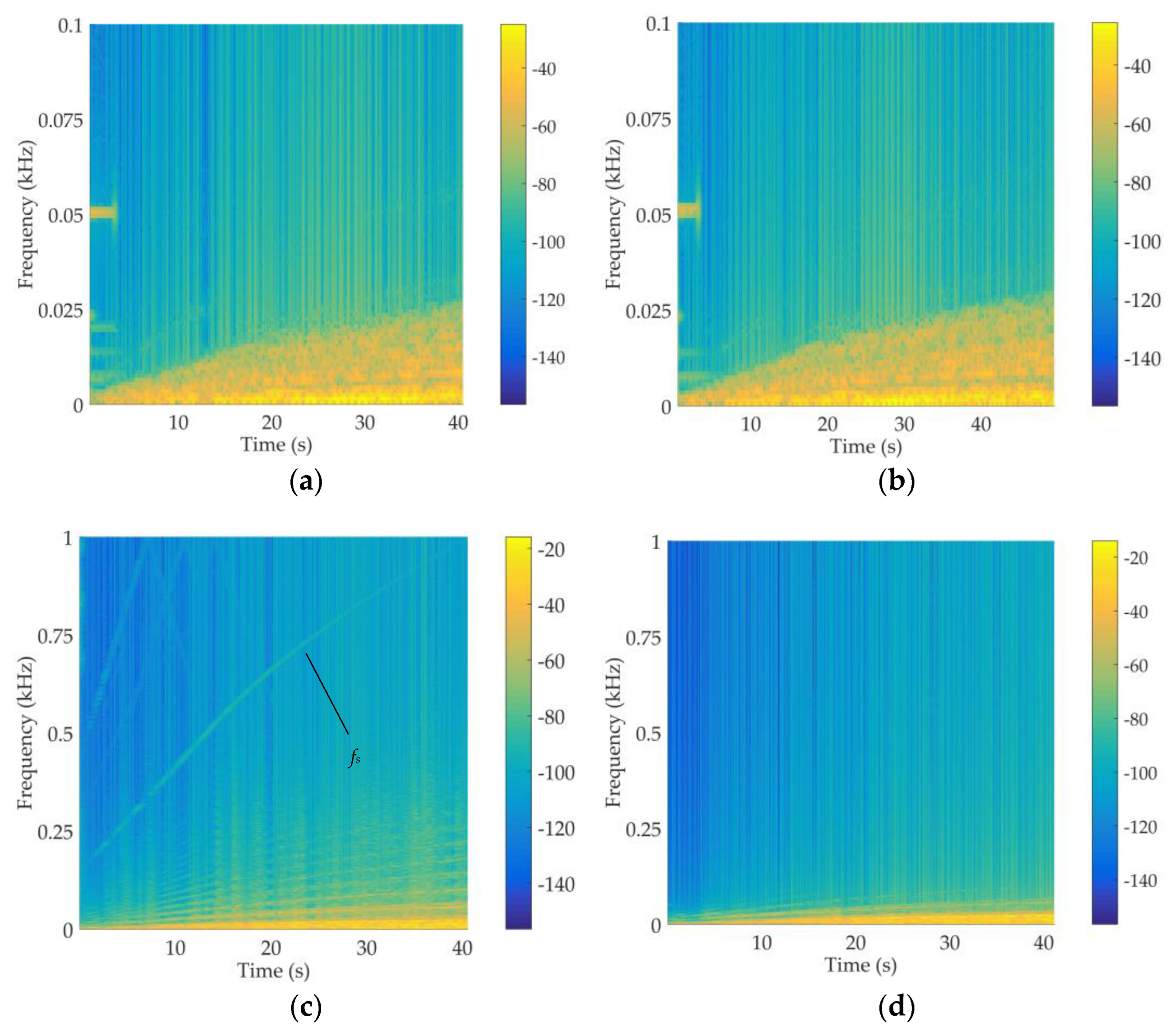
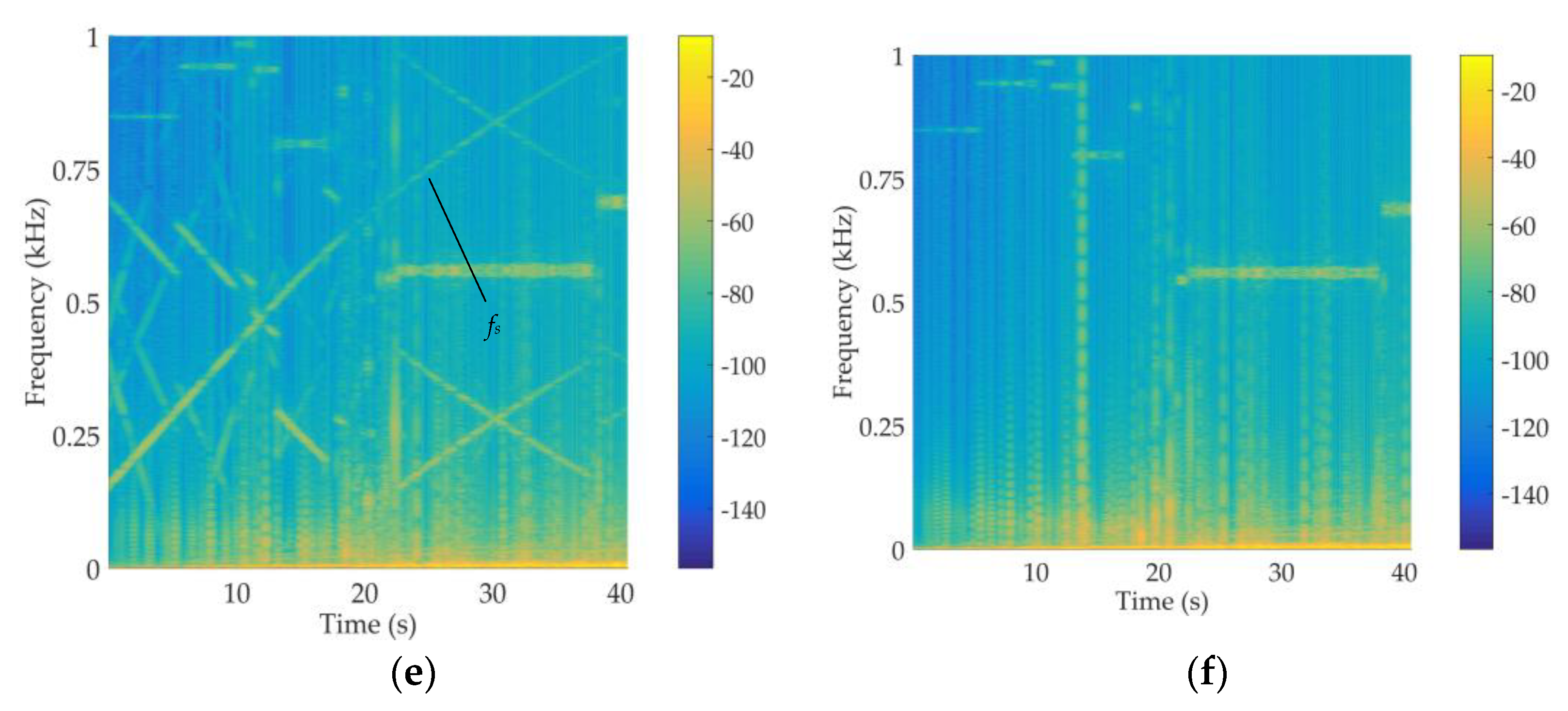
4.2. Vibration and Comfort Analysis of Urban Rail Trains
4.2.1. Vibration Response Analysis
4.2.2. Stability Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peiffer, A.; Storm, S.; Röder, A.; Maier, R.; Frank, P.G. Active vibration control for high speed train bogies. Smart Mater. Struct. 2005, 14, 1. [Google Scholar] [CrossRef]
- Simson, S.A.; Cole, C. Simulation of curving at low speed under high traction for passive steering hauling locomotives. Veh. Syst. Dyn. 2008, 46, 1107–1121. [Google Scholar] [CrossRef]
- Ribeiro, D.; Cal Ada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-element model calibration of a railway vehicle based on experimental modal parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Wang, M.Y.; Sheng, X.Z.; Li, M.X.; Li, Y.G. Estimation of vibration powers flowing to and out of a high-speed train bogie frame assisted by time-domain response reconstruction. Appl. Acoust. 2022, 185, 108390. [Google Scholar] [CrossRef]
- Ling, L.; Li, W.; Foo, E.; Wu, L.; Wen, Z.F.; Jin, X.S. Investigation into the vibration of metro bogies induced by rail corrugation. Chin. J. Mech. Eng. 2017, 30, 93–102. [Google Scholar] [CrossRef]
- Yang, J.W.; Zhao, Y.; Wang, J.H.; Liu, C.D.; Bai, Y.L. Influence of wheel flat on railway vehicle helical gear system under Traction/Braking conditions. Eng. Fail. Anal. 2022, 134, 106022. [Google Scholar] [CrossRef]
- Yang, J.W.; Sun, R.; Yao, D.C.; Wang, J.H.; Liu, C. Nonlinear Dynamic Analysis of high speed multiple units Gear Transmission System with Wear Fault. Mech. Sci. 2019, 10, 187–197. [Google Scholar] [CrossRef]
- Wang, J.H.; Yang, J.W.; Lin, Y.L.; He, Y.P. Analytical investigation of profile shifts on the mesh stiffness and dynamic characteristics of spur gears. Mech. Mach. Theory 2022, 167, 104529. [Google Scholar] [CrossRef]
- Wang, J.H.; Yang, J.W.; Li, Q. Quasi-static analysis of the nonlinear behavior of a railway vehicle gear system considering time-varying and stochastic excitation. Nonlinear Dynam. 2018, 93, 463–485. [Google Scholar] [CrossRef]
- Wang, J.H.; Yang, J.W.; Bai, Y.L.; Zhao, Y.; He, Y.P.; Yao, D.C. A comparative study of the vibration characteristics of railway vehicle axlebox bearings with inner/outer race faults. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2021, 235, 1035–1047. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, J.W.; Liu, C.D.; Wang, J.H.; Yao, D.C. Dynamic Characteristics of a Traction Drive System in High-Speed Train Based on Electromechanical Coupling Modeling under Variable Conditions. Energies 2022, 15, 1202. [Google Scholar] [CrossRef]
- Li, M.; Liu, Q.; Zhu, S.; Ai, S.; Chen, W.; Zhu, R. Contribution analysis of vibration transmission path of planetary reducer box based on velocity involvement loss. J. Low Freq. Noise Vib. Act. Control 2022, 42, 39–53. [Google Scholar] [CrossRef]
- Zhang, T.; Jin, T.M.; Zhou, Z.W.; Chen, Z.G.; Wang, K.Y. Dynamic modeling of a metro vehicle considering the motor-gearbox transmission system under traction conditions. Mech. Sci. 2022, 13, 603–617. [Google Scholar] [CrossRef]
- Wang, Z.W.; Cheng, Y.; Mei, G.M.; Zhang, W.H.; Huang, G.H.; Yin, Z.H. Torsional vibration analysis of the gear transmission system of high-speed trains with wheel defects. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2020, 234, 123–133. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhai, W.M.; Wang, K.Y. A locomotive-track coupled vertical dynamics model with gear transmissions. Veh. Syst. Dyn. 2017, 55, 244–267. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhai, W.M.; Wang, K.Y. Dynamic investigation of a locomotive with effect of gear transmissions under tractive conditions. J. Sound Vib. 2017, 408, 220–233. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhai, W.M.; Wang, K.Y. Locomotive dynamic performance under traction/braking conditions considering effect of gear transmissions. Veh. Syst. Dyn. 2018, 56, 1097–1117. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Z.G.; Zhai, W.M.; Wang, K.Y.; Wang, H. Effect of the drive system on locomotive dynamic characteristics using different dynamics models. Sci. China Technol. Sc. 2019, 62, 308–320. [Google Scholar] [CrossRef]
- Wang, J.H.; Yang, J.W.; Zhao, Y.; Bai, Y.L.; He, Y.P. Nonsmooth Dynamics of a Gear-Wheelset System of Railway Vehicles Under Traction/Braking Conditions. J. Comput. Nonlin. Dyn. 2020, 15, 081003. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Chen, Z.G.; Spiryagin, M.; Wolfs, P.; Wu, Q.; Zhai, W.M.; Cole, C. Dynamic performance of locomotive electric drive system under excitation from gear transmission and wheel-rail interaction. Veh. Syst. Dyn. 2022, 60, 1806–1828. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Chen, Z.G.; Spiryagin, M.; Arango, E.B.; Wolfs, P.; Cole, C.; Zhai, W.M. Dynamic response feature of electromechanical coupled drive subsystem in a locomotive excited by wheel flat. Eng. Fail. Anal. 2021, 122, 105248. [Google Scholar] [CrossRef]
- Wang, Z.W.; Mei, G.M.; Xiong, Q.; Yin, Z.H.; Zhang, W.H. Motor car-track spatial coupled dynamics model of a high-speed train with traction transmission systems. Mech. Mach. Theory 2019, 137, 386–403. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Z.G.; Zhai, W.M.; Wang, K.Y. Establishment and validation of a locomotive-track coupled spatial dynamics model considering dynamic effect of gear transmissions. Mech. Syst. Signal Process. 2019, 119, 328–345. [Google Scholar] [CrossRef]
- Wang, J.G.; He, G.Y.; Zhang, J.; Zhao, Y.X.; Yao, Y. Nonlinear dynamics analysis of the spur gear system for railway locomotive. Mech. Syst. Signal Process. 2017, 85, 41–55. [Google Scholar] [CrossRef]
- Huang, G.H.; Xu, S.S.; Zhang, W.H.; Yang, C.J. Super-harmonic resonance of gear transmission system under stick-slip vibration in high-speed train. J. Cent. South Univ. 2017, 24, 726–735. [Google Scholar] [CrossRef]
- Kia, S.H.; Henao, H.; Capolino, G.A. Mechanical health assessment of a railway traction system. In Proceedings of the MELECON 2008—The 14th IEEE Mediterranean Electrotechnical Conference, Ajaccio, France, 5–7 May 2008. [Google Scholar]
- Huang, G.H.; Zhou, N.; Zhang, W.H. Effect of internal dynamic excitation of the traction system on the dynamic behavior of a high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1899–1907. [Google Scholar] [CrossRef]
- Chen, Z.W.; Zhu, G. Dynamic evaluation on ride comfort of metro vehicle considering structural flexibility. Arch. Civ. Mech. Eng. 2021, 21, 162. [Google Scholar] [CrossRef]
- Pradhan, S.; Samantaray, A.K. Integrated modeling and simulation of vehicle and human multi-body dynamics for comfort assessment in railway vehicles. J. Mech. Sci. Technol. 2018, 32, 109–119. [Google Scholar] [CrossRef]
- Belforte, P.; Cheli, F.; Diana, G.; Melzi, S. Numerical and experimental approach for the evaluation of severe longitudinal dynamics of heavy freight trains. Veh. Syst. Dyn. 2008, 46, 937–955. [Google Scholar] [CrossRef]
- Tao, G.Q.; Liu, M.Q.; Xie, Q.L.; Wen, Z.F. Wheel-rail dynamic interaction caused by wheel out-of-roundness and its transmission between wheelsets. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 247–261. [Google Scholar] [CrossRef]
- Wu, Q.; Luo, S.; Wei, C.; Ma, W. Dynamics simulation models of coupler systems for freight locomotive. J. Traffic Transp. Eng. 2012, 12, 37–43. [Google Scholar]
- Ding, H.; Zhu, T.; Xiao, S.; Yang, G.; Yang, B.; Lv, R. Study on the collision characteristics of a subway coupler. Int. J. Crashworthines 2022, 1–15. [Google Scholar] [CrossRef]
- Yadav, O.P.; Vyas, N.S. Influence of slack of automatic AAR couplers on longitudinal dynamics and jerk behaviour of rail vehicles. Veh. Syst. Dyn. 2022, 1–21. [Google Scholar] [CrossRef]
- Zou, R.M.; Luo, S.H.; Ma, W.H.; Wu, Q. Dynamic Characteristics of Metro Trains under Rescue Conditions. Shock Vib. 2020, 2020, 8869605. [Google Scholar] [CrossRef]
- Lee, S.; Yu, H.; Yang, H.; Song, I.; Choi, J.; Yang, J.; Lim, G.; Kim, K.S.; Choi, B.; Kwon, J. A Study on Deep Learning Application of Vibration Data and Visualization of Defects for Predictive Maintenance of Gravity Acceleration Equipment. Appl. Sci. 2021, 11, 1564. [Google Scholar] [CrossRef]
- Patil, S.; Pardeshi, S.; Patange, A. Health Monitoring of Milling Tool Inserts Using CNN Architectures Trained by Vibration Spectrograms. Comput. Model. Eng. Sci. 2023, 136, 177–199. [Google Scholar] [CrossRef]



| Specification | Value |
|---|---|
| Car body mass (kg) | 4.08 × 104 |
| Bogie frame mass (kg) | 3188 |
| Wheelset mass (kg) | 1640 |
| Axle box mass (kg) | 85.367 |
| Gearwheel mass (kg) | 53.15 |
| Pinion mass (kg) | 5.15 |
| Gearbox mass (kg) | 149.75 |
| Rotor mass (kg) | 178..36 |
| Motor mass (kg) | 422.82 |
| Rotational inertia of car body x/y/z (t·m2) | 75.06/2277.4/2277.4 |
| Rotational inertia of bogie frame x/y/z (kg·m2) | 2040/2710/3460 |
| Rotational inertia of wheelset x/y/z (kg·m2) | 725/100/725 |
| Rotational inertia of axle box x/y/z (kg·m2) | 1.455/2.448/2.011 |
| Rotational inertia of gearwheel mass x/y/z (kg·m2) | 4.55/4.85/4.555 |
| Rotational inertia of pinion x/y/z (kg·m2) | 0.006/0.007/0.006 |
| Rotational inertia of gearbox x/y/z (kg·m2) | 4.22/10.45/8.56 |
| Rotational inertia of rotor x/y/z (kg·m2) | 24.5/1.9/24.5 |
| Rotational inertia of motor x/y/z (kg·m2) | 77.5/24.7/75.2 |
| Stiffness of primary suspension x/y/z (N/m) | 9.2 × 106/8 × 106/1.5 × 106 |
| Stiffness of secondary suspension x/y/z (N/m) | 2.06 × 105/2.06 × 105/4.41 × 105 |
| Stiffness between motor and bogie frame x/y/z (N/m) | 3 × 107/1 × 107/3 × 107 |
| Stiffness between gearbox and bogie frame x/y/z (N/m) | 3 × 106/3 × 106/3 × 106 |
| Damping coefficient of primary suspension x/y/z (N·s/m) | 5560/5560/1800 |
| Vertical damping coefficient of secondary suspension (N·s/m) | 6 × 104 |
| Damping coefficient between motor and bogie frame x/y/z (N·s/m) | 1 × 103/1 × 103/1 × 103 |
| Damping coefficient between gearbox and bogie frame x/y/z (N·s/m) | 3 × 105/2 × 105/3 × 105 |
| Specification | Value |
|---|---|
| Tooth number of pinion/gear | 16/107 |
| Modification coefficient of pinion/gear (mm) | 0.31449/−0.07614 |
| Face width of pinion/gear (mm) | 70/70 |
| Module (mm) | 85.367 |
| Pressure angle (°) | 20 |
| Helix angle (°) | 17 |
| Poisson ratio | 0.3 |
| Young modulus (GN/m) | 206 |
| Damping coefficient (kN·s/m) | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, J.; Wang, J.; Zhao, Y. Dynamic Characteristics of Urban Rail Train in Multivehicle Marshaling under Traction Conditions. Appl. Sci. 2023, 13, 3022. https://doi.org/10.3390/app13053022
Zhang Y, Yang J, Wang J, Zhao Y. Dynamic Characteristics of Urban Rail Train in Multivehicle Marshaling under Traction Conditions. Applied Sciences. 2023; 13(5):3022. https://doi.org/10.3390/app13053022
Chicago/Turabian StyleZhang, Yichao, Jianwei Yang, Jinhai Wang, and Yue Zhao. 2023. "Dynamic Characteristics of Urban Rail Train in Multivehicle Marshaling under Traction Conditions" Applied Sciences 13, no. 5: 3022. https://doi.org/10.3390/app13053022
APA StyleZhang, Y., Yang, J., Wang, J., & Zhao, Y. (2023). Dynamic Characteristics of Urban Rail Train in Multivehicle Marshaling under Traction Conditions. Applied Sciences, 13(5), 3022. https://doi.org/10.3390/app13053022






