A Feasibility Study for a Hand-Held Acoustic Imaging Camera
Abstract
:1. Introduction
2. Acoustic Imaging Concepts
2.1. Angular Resolution
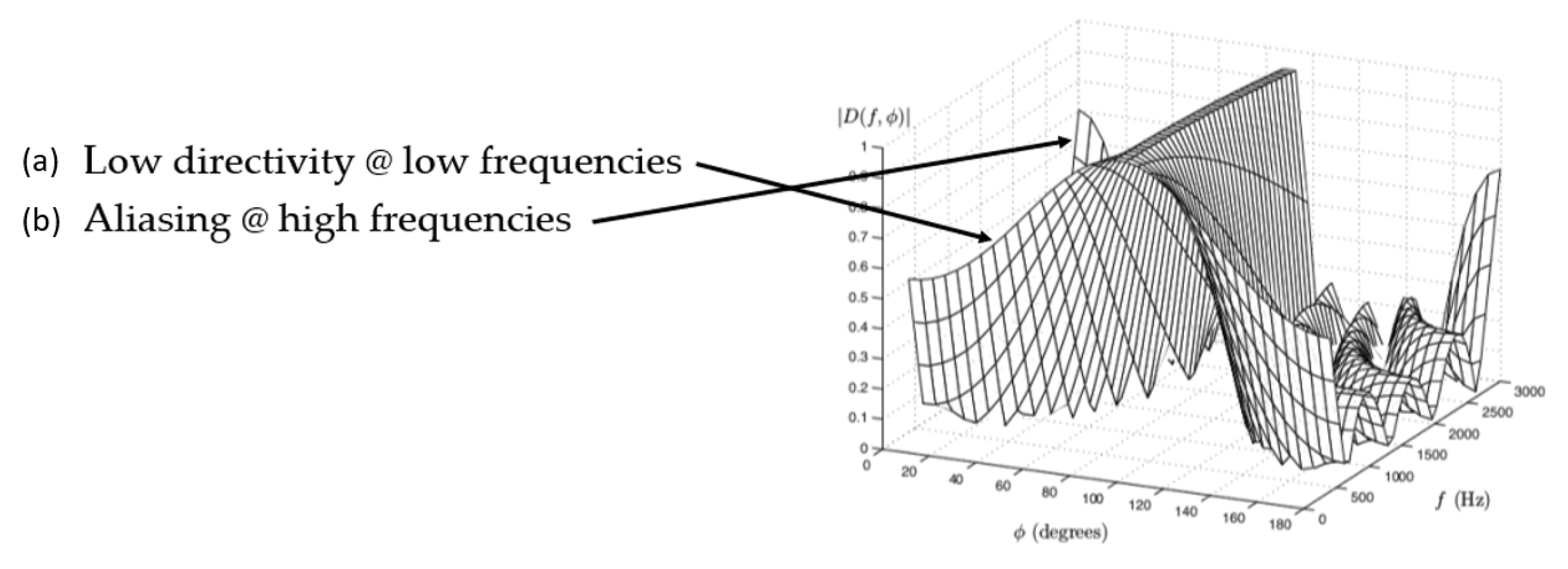
2.2. Aliasing
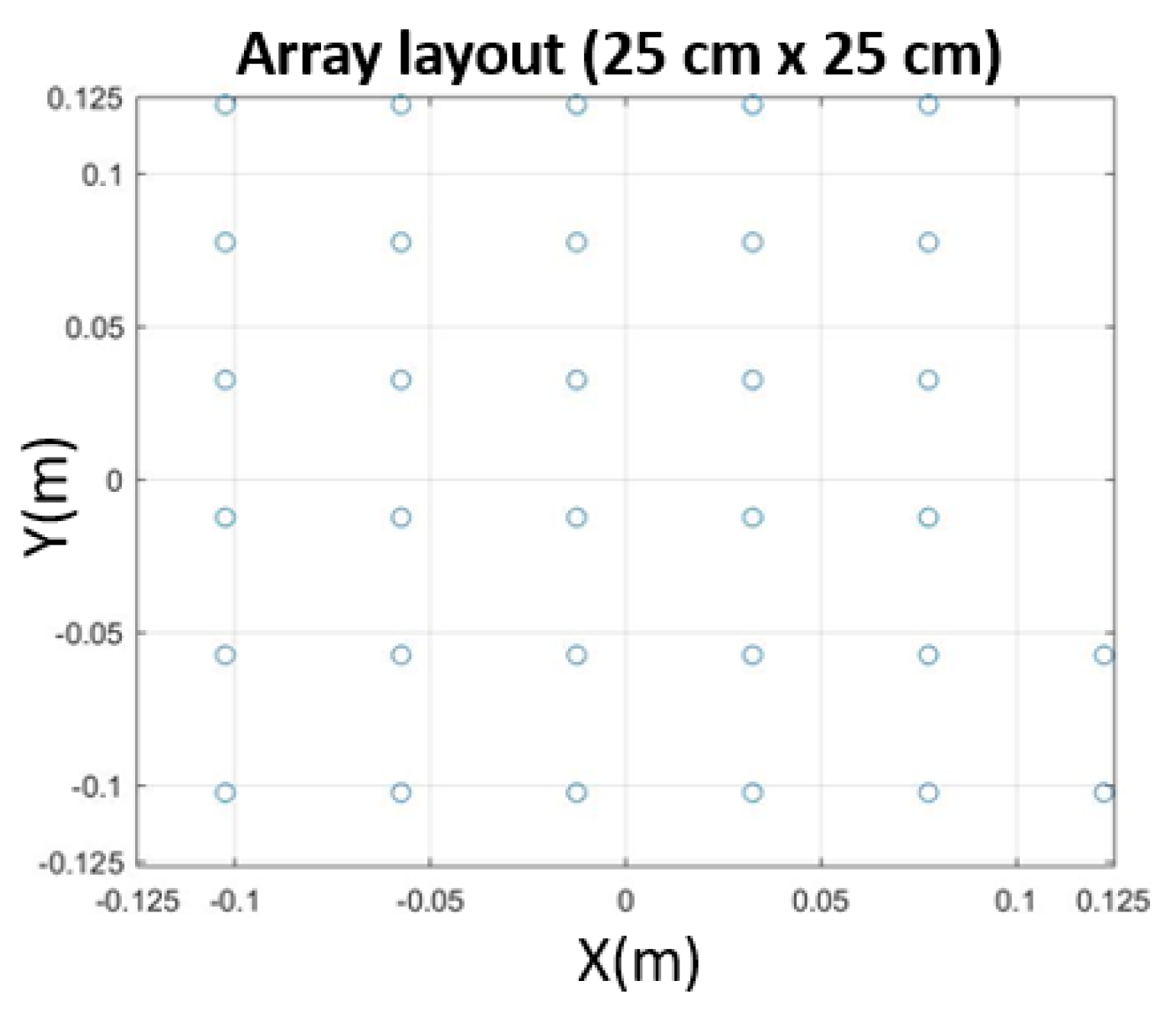
2.3. Array Geometry
- Aperture —The overall physical size determines angular resolution. Larger apertures improve discrimination.
- Number of microphones—More microphones provide enhanced spatial sampling at the cost of complexity.
- Layout—Positions within the aperture area. Uniform grids simplify analysis but suffer aliasing. Randomized arrangements help reduce lobes.
- Symmetry—Circular/spherical arrays enable uniform coverage but planar designs are easier to manufacture.
2.4. Beamforming
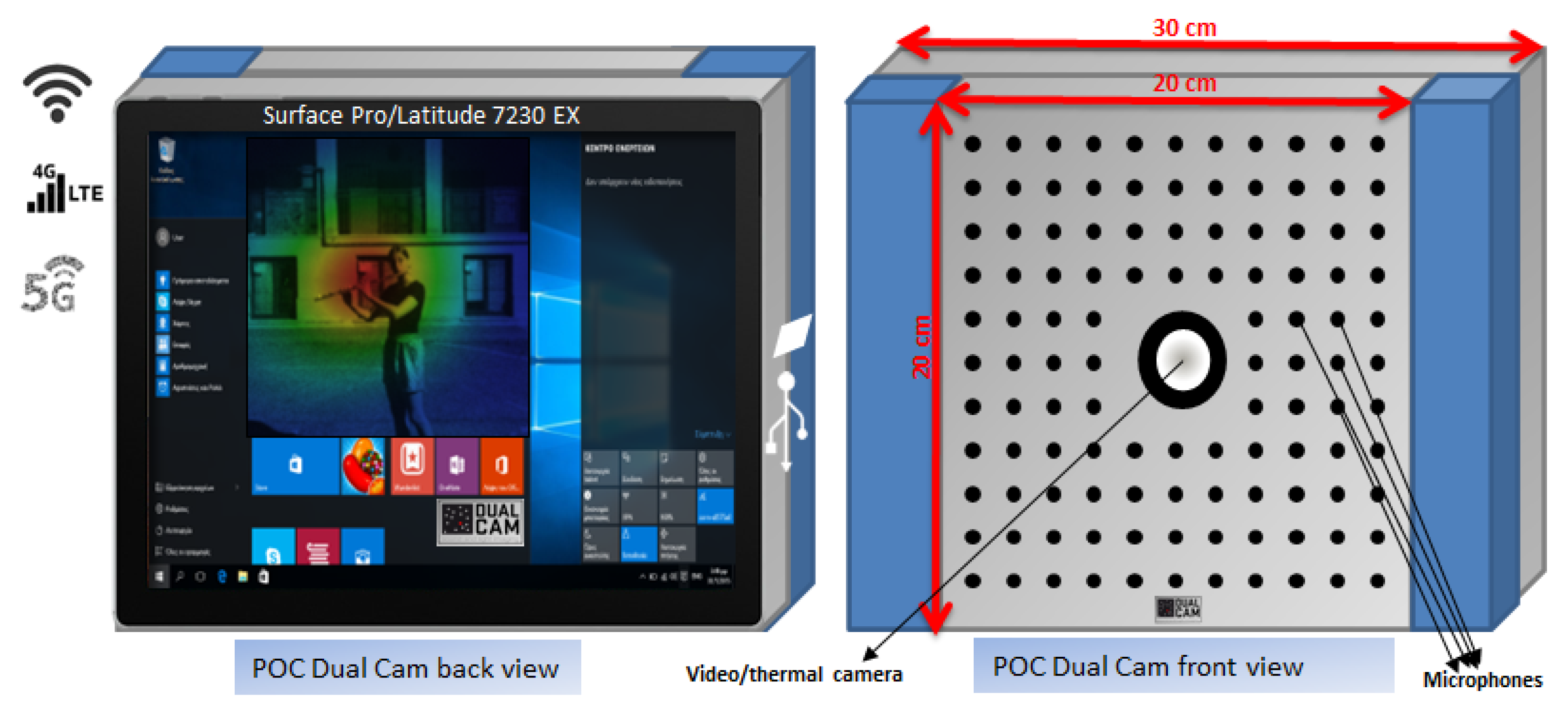
3. Dual Cam Acoustic Camera
- Digitizing microphone outputs through multichannel audio sampling.
- Partitioning the multichannel record into short time frames.
- Synthesizing beamformer filters according to designed array geometry.
- Applying filters and aligning signals for each scanning direction.
- Coherently summing aligned microphone channels to obtain beam pattern power.
- Repeating overall look directions to generate acoustic image frames registered to video.
4. Materials and Methods
- We optimize the analytic form of the cost function in order to cut the simulation computational load. This optimization of the cost function is a novel contribution beyond the existing state-of-the-art methods, improving computational efficiency.
- We include the statistical evaluation of the mismatches of the microphones that are more important in shrinking the array size. The statistical characterization of microphone mismatches enables novel array size reduction.
- We optimize the FOV (field of view) and the frequency bandwidth according to the array size reduction to explore upper harmonic reconstruction to determine whether intelligibility is retained without fundamental frequencies. The joint optimization of FOV, frequency band, and array size reduction using the upper harmonics for intelligibility preservation is an unexplored area representing a novel research direction.
5. Array Optimization Methodology
5.1. Problem Parameterization
- Directional focus. Minimizing deviation of the achieved beam pattern from the ideal unity gain pattern at the look direction over angle-frequency space. This is quantified by the integral term:
- Artefact suppression. Minimizing the beam pattern gain away from the look direction, incorporated through:
- Frequency coverage. Optimizing over the full band [fmin, fmax] through integration over f.
- Robustness. Averaging over microphone imperfections by modelling gain and phase as random variables .
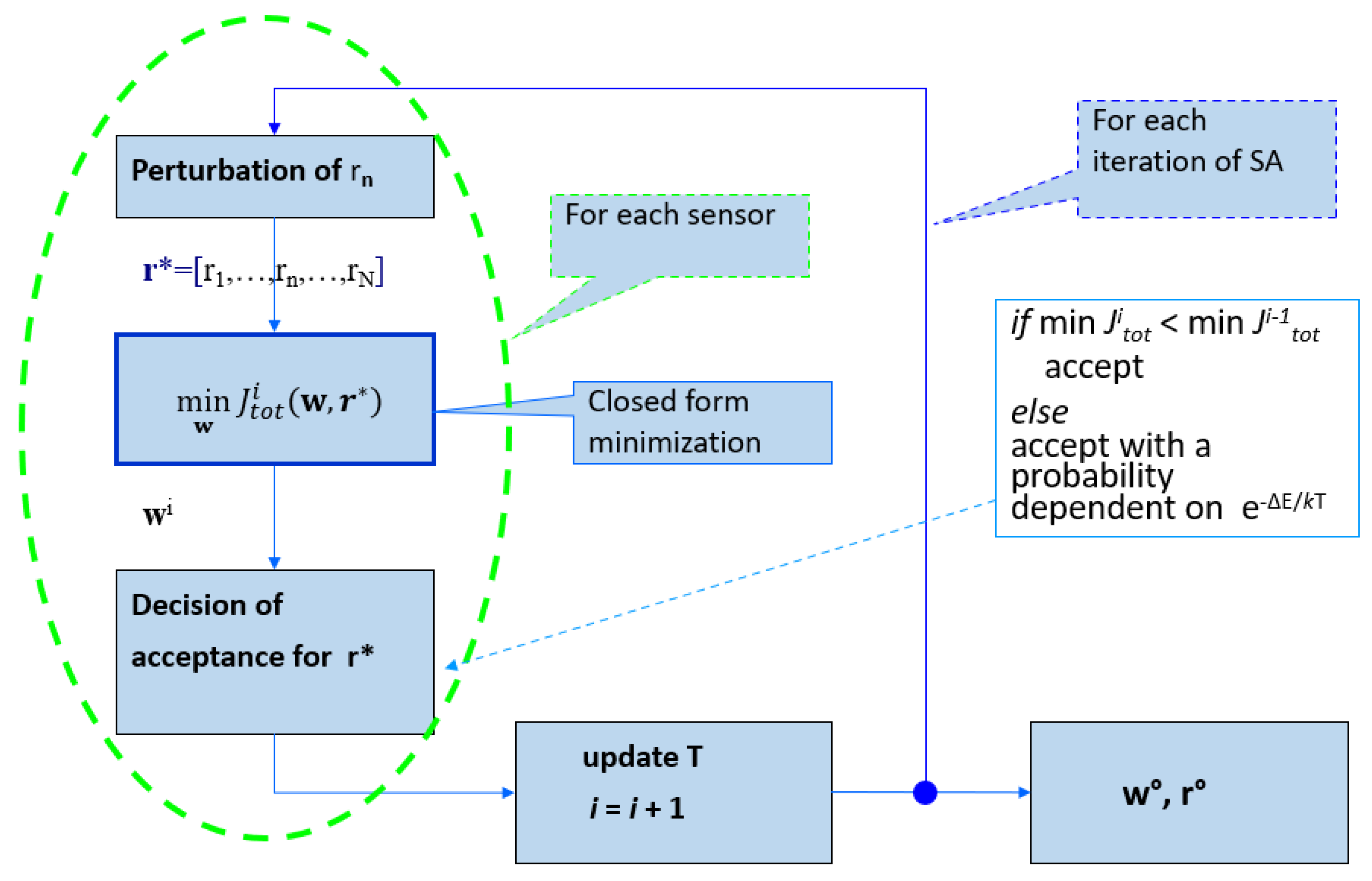
- Iterative random perturbations are applied to the microphone locations.
- New locations are accepted probabilistically based on the cost J.
- Acceptance probability is higher at higher initial “temperatures” and cooled over iterations.
- After sufficient iterations, converges to a geometry minimizing J.
5.2. Cost Function Definition
5.3. Directivity Optimization
5.4. Layout Optimization
- Iterative procedure aimed at minimizing an energy function .
- At each iteration, a random perturbation is induced in the current state .
- If the new configuration, , causes the value of the energy function to decrease, then it is accepted.
- If causes the value of the energy function to increase, it is accepted with a probability dependent on the system temperature, in accordance with the Boltzmann distribution.
- The temperature is a parameter that is gradually lowered, following the reciprocal of the logarithm of the number of iterations.
- The higher the temperature, the higher the probability of accepting a perturbation causing a cost increase and of escaping, in this way, from unsatisfactory local minima.
5.5. Robustness Constraints
6. Simulation Configuration
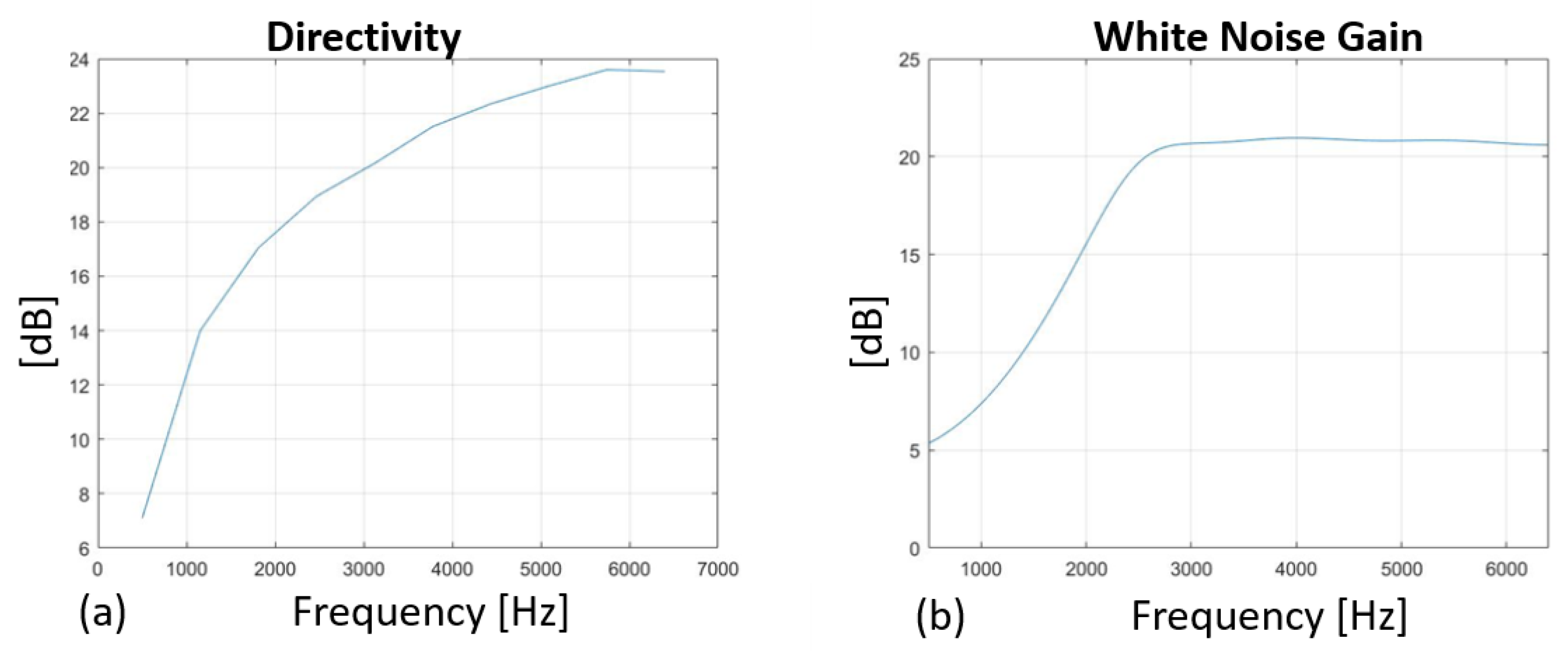
- Directivity—angular discrimination capability;
- White noise gain (WNG)—robustness to fabrication variations;
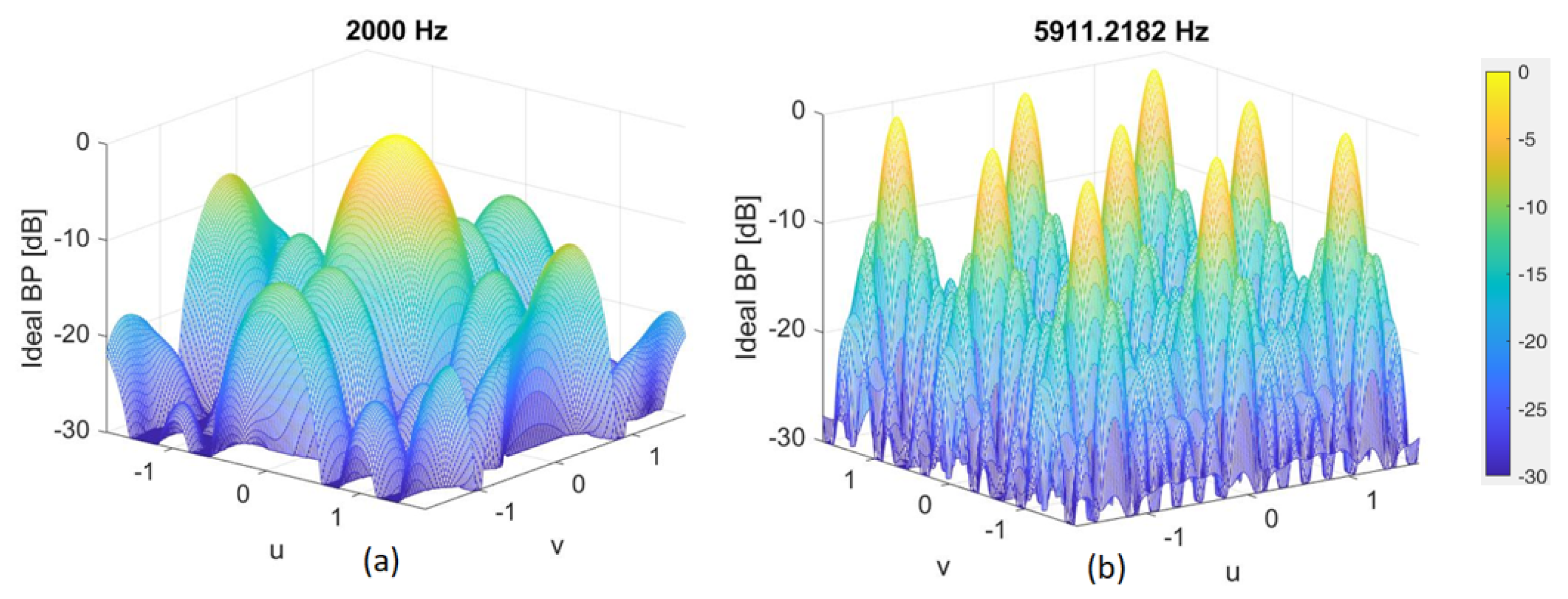
- Beam patterns and sidelobe levels—imaging artefacts.
- A 32−microphone 0.25 m square array optimized from 2 to 6.4 kHz.
- A 32−microphone 0.21 m square array optimized from 2 to 6.4 kHz.
- A 32−microphone 0.21 m square array covering [0.5, 6.4] kHz for comparison with Dual Cam specifications (128−microphone on a 0.5 m square array).
7. Miniaturized Array Optimization: Results and Discussion
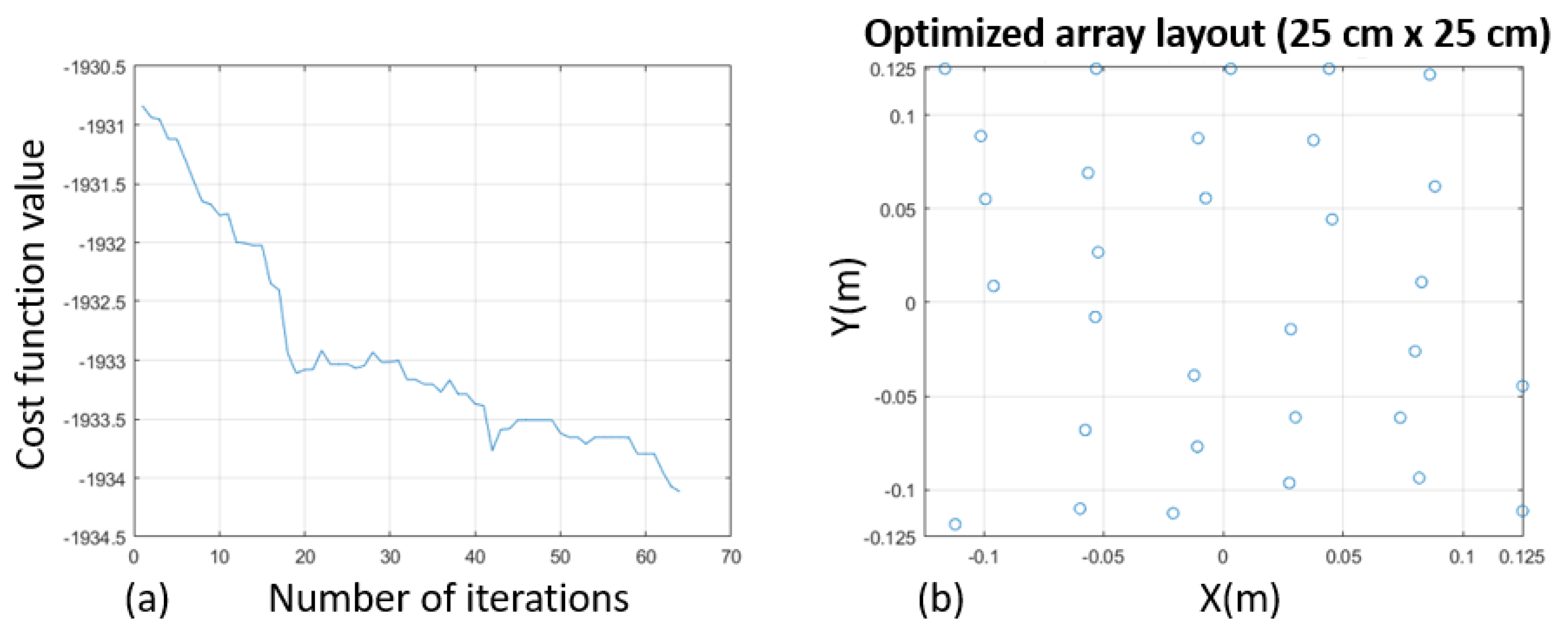
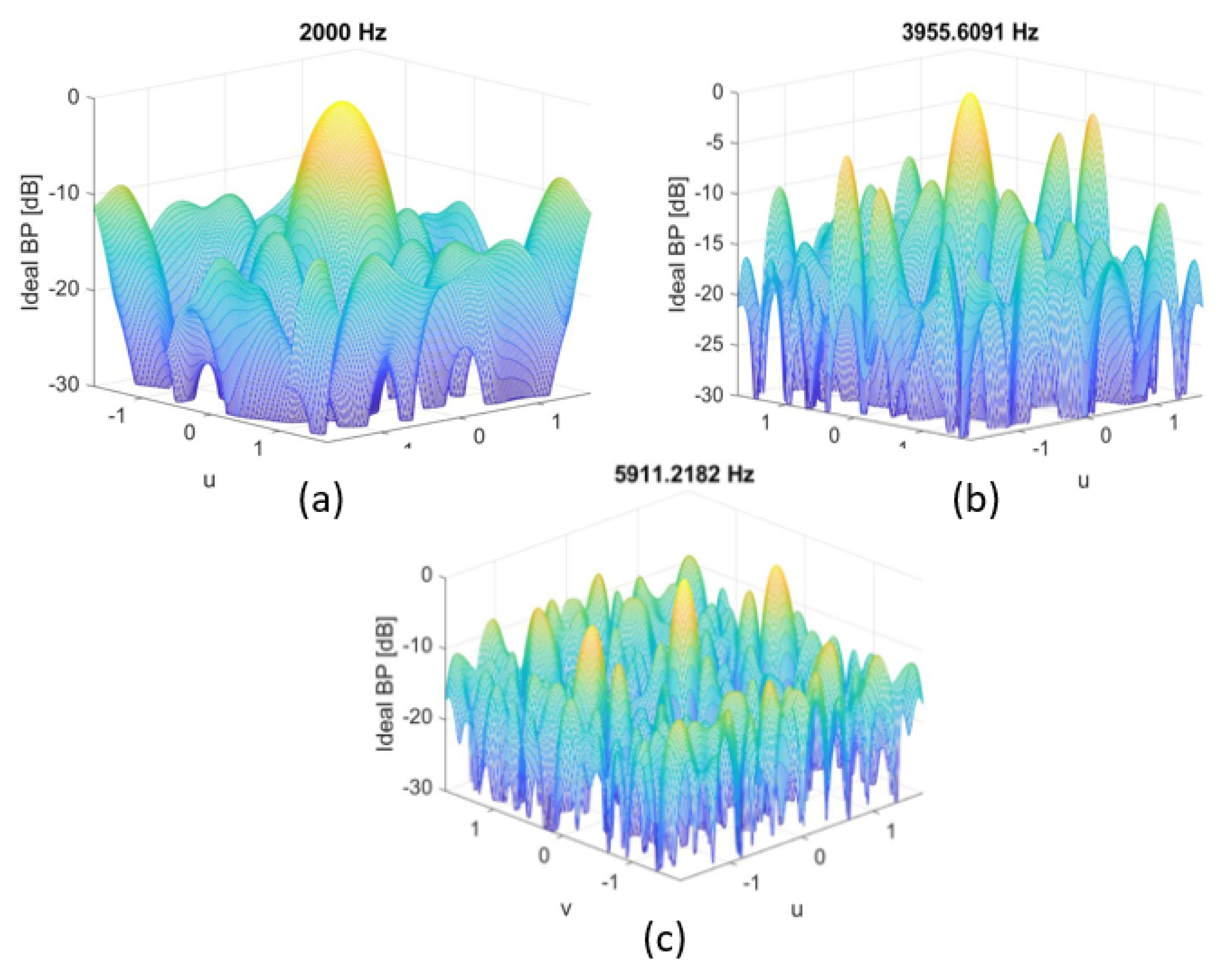
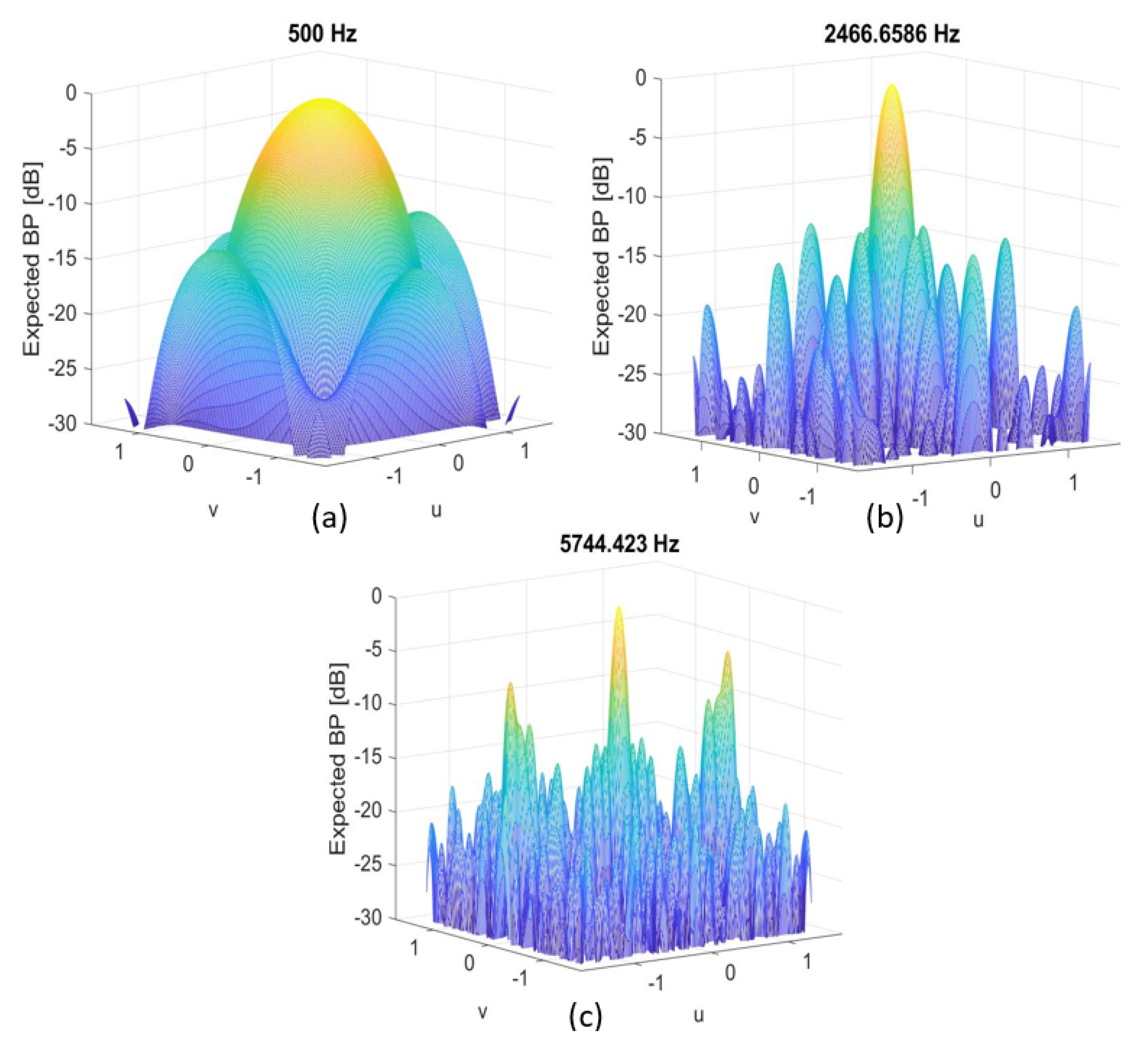
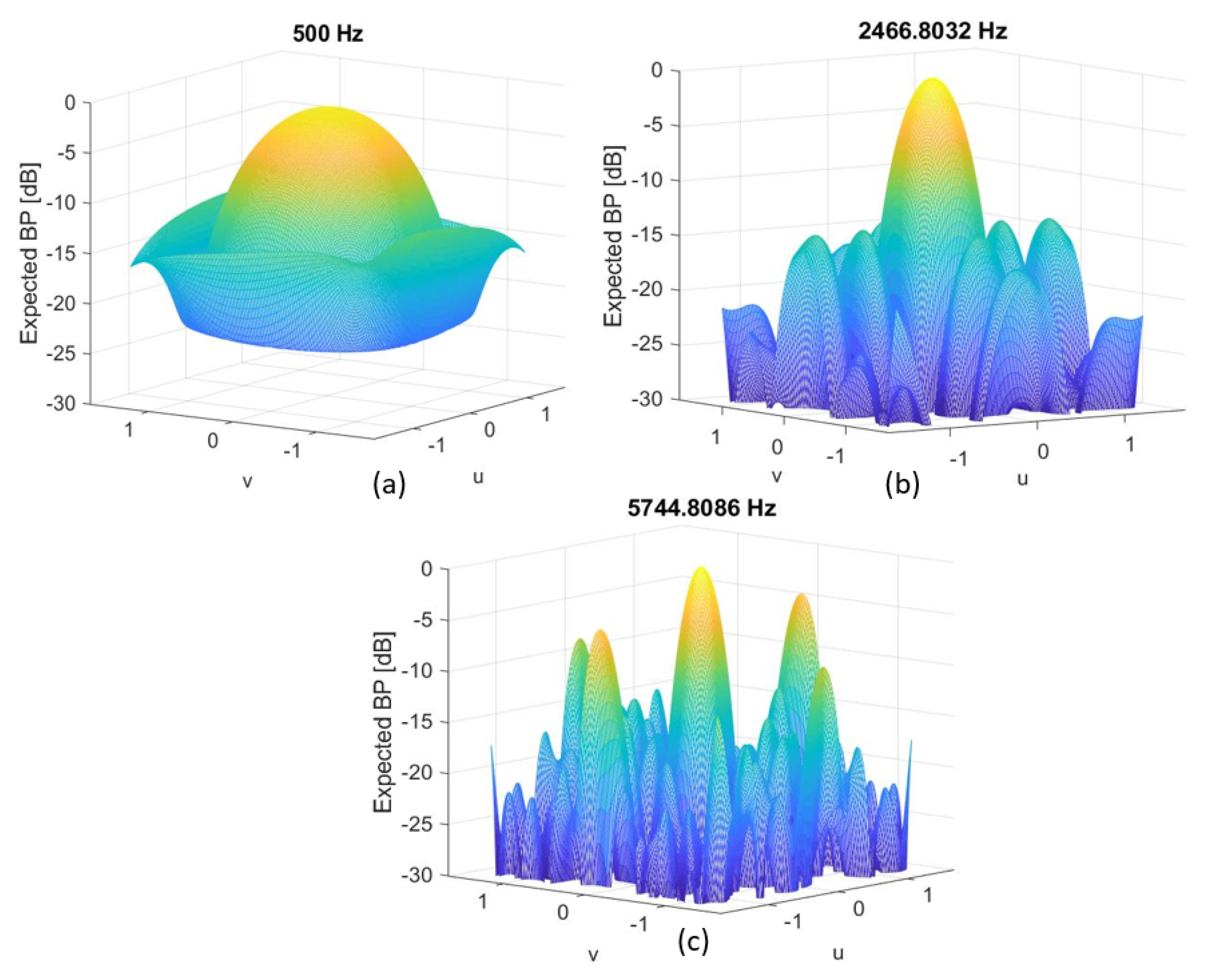
7.1. Thirty-Two-Microphones, [2, 6.4] kHz, Array 25 × 25 cm2
- L = 25 cm;
- N° of microphones = 32 mic;
- K = 31 (FIR length);
- u ∈ [−1. 5; 1.5];
- v ∈ [−1.5; 1.5];
- N° of iterations = 100;
- Bandwidth = [2000, 6400] Hz.
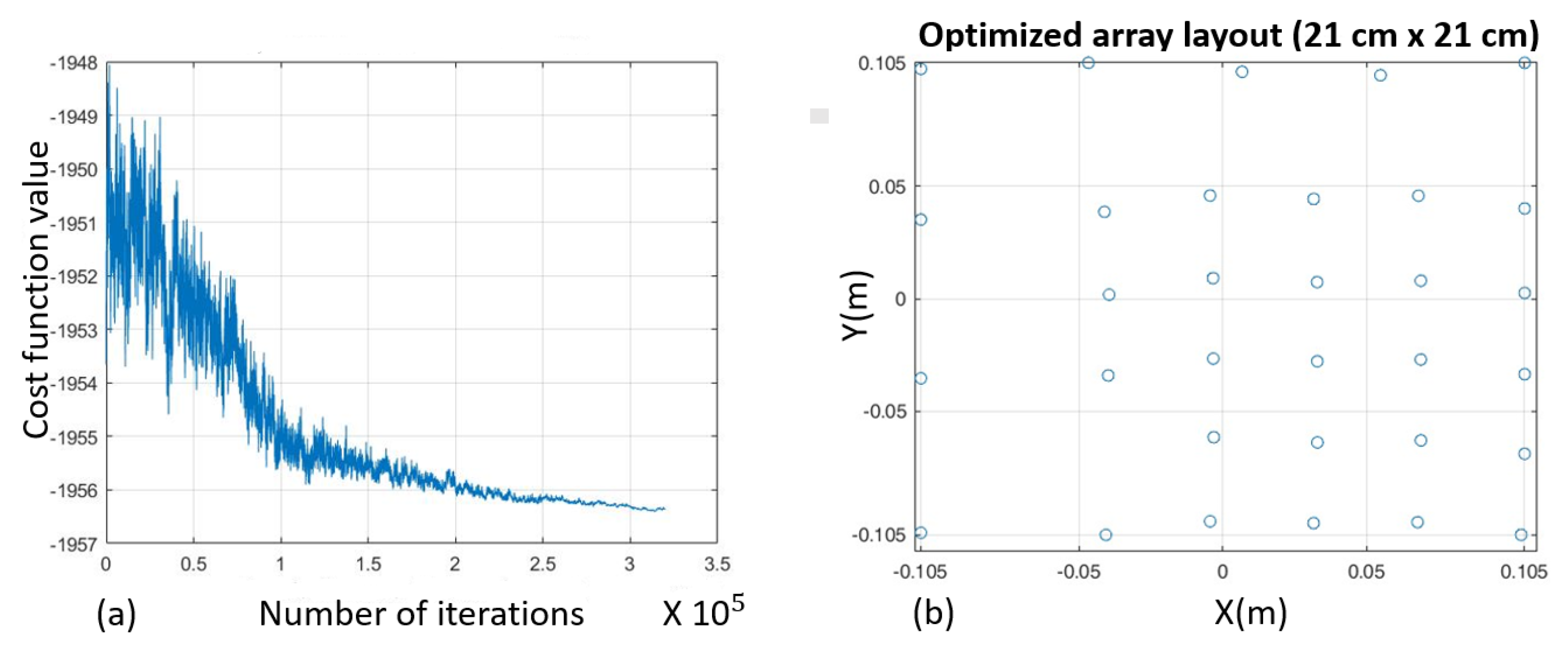
7.2. Thirty-Two-Microphones, [2, 6.4] kHz, Array 21 × 21 cm2
- L = 21 cm;
- N° of microphones = 32 mic;
- K = 31 (FIR length);
- u ∈ [−1.5; 1.5]; v ∈ [−1.41; 1.41];
- N° of iterations ≈;
- = −0.2; = 0.2;
- = −0.2; = 0.2;
- Bandwidth = [2000, 6400] Hz.
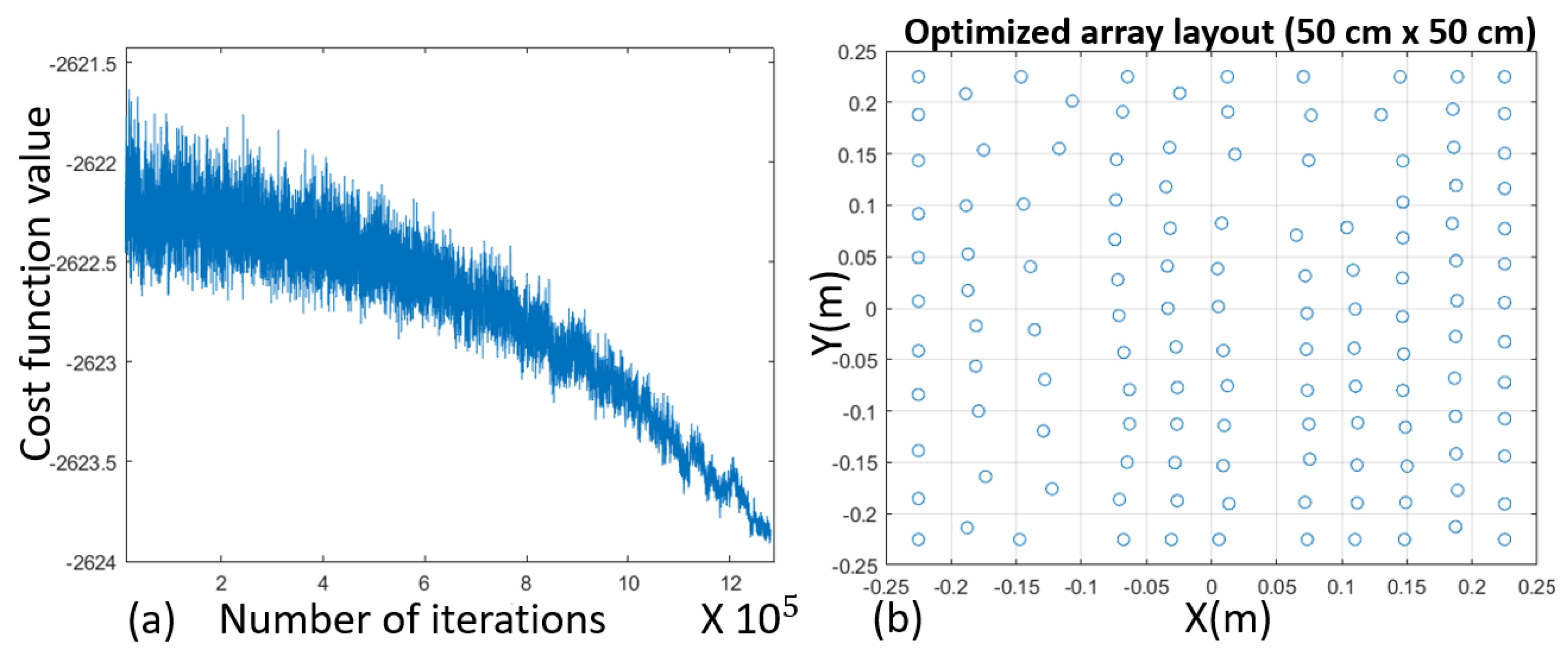
7.3. Thirty-Two-Microphones, [0.5, 6.4] kHz, 21 × 21 cm2 Array
- L = 50 cm;
- N° of microphones = 128 mic;
- K = 7 (FIR length);
- u ∈ [−1.5; 1.5]; v ∈ [−1.41; 1.41];
- N° of iterations ≈ 10;
- = −0.06; = 0.06;
- = −0.06; = 0.06;
- Bandwidth = [500, 6400] Hz.
- L = 21 cm;
- N° of microphones = 32 mic;
- K = 31 (FIR length);
- u ∈ [−1,5; 1.5]; v ∈ [−1,41; 1.41];
- N° of iterations≈ 10;
- = −0.2; = 0.2;
- = −0.2; = 0.2;
- Bandwidth = [500, 6400] Hz.
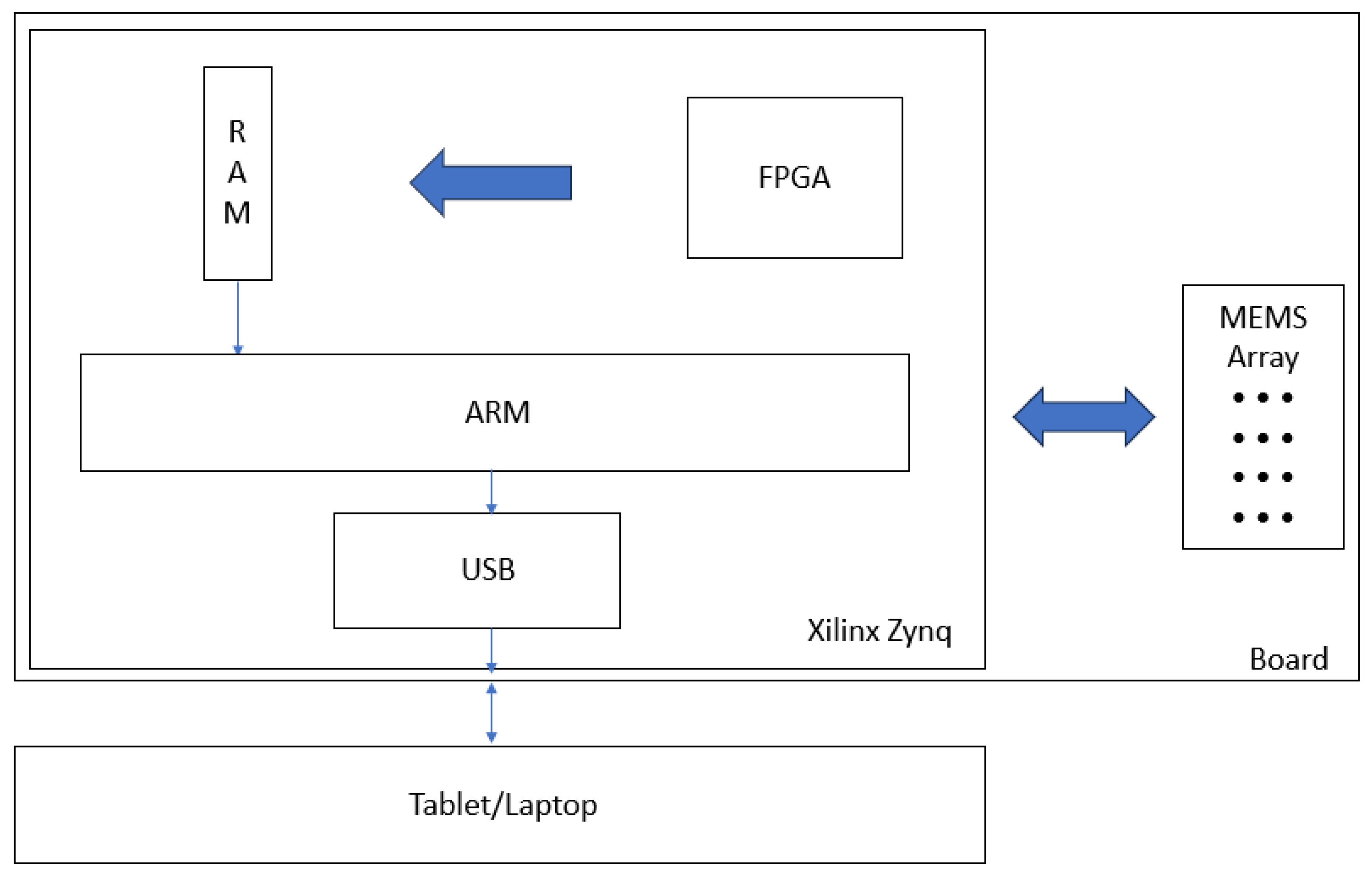
8. Hardware Development Considerations
- Fabricating irregular array geometries with a large number of elements;
- Microphone calibration and mismatch compensation;
- Embedded platform with multichannel digitization and processing;
- Robust beamforming algorithms executable in real time;
- Packaging, power, and interfacing for field deployment.
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dmochowski, J.P.; Benesty, J. Steered Beamforming Approaches for Acoustic Source Localization. In Speech Processing in Modern Communication; Cohen, I., Benesty, J., Gannot, S., Eds.; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2010; Volume 3. [Google Scholar] [CrossRef]
- Rafaely, B. Fundamentals of Spherical Array Processing; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE Assp Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Jombo, G.; Zhang, Y. Acoustic-Based Machine Condition Monitoring—Methods and Challenges. Eng 2023, 4, 47–79. [Google Scholar] [CrossRef]
- Na, Y. An Acoustic Traffic Monitoring System: Design and Implementation. In Proceedings of the 2015 IEEE 12th International Conference on Ubiquitous Intelligence and Computing and 2015 IEEE 12th International Conference on Autonomic and Trusted Computing and 2015 IEEE 15th International Conference on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14 August 2015. [Google Scholar] [CrossRef]
- António, R. On acoustic gunshot localization systems. In Proceedings of the Society for Design and Process Science SDPS-2015, Fort Worth, TX, USA, 1–5 November 2015; pp. 558–565. [Google Scholar]
- Lluís, F.; Martínez-Nuevo, P.; Møller, M.B.; Shepstone, S.E. Sound field reconstruction in rooms: Inpainting meets super-resolution. J. Acoust. Soc. Am. 2020, 148, 649–659. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Zhang, T.; Broughton-Venner, J.; Huang, P.; Tang, M.-X. Super-Resolution Ultrasound Through Sparsity-Based Deconvolution and Multi-Feature Tracking. IEEE Trans. Med. Imaging 2022, 41, 1938–1947. [Google Scholar] [CrossRef]
- Crocco, M.; Cristani, M.; Trucco, A.; Murino, V. Audio Surveillance: A Systematic Review. ACM Comput. Surv. 2016, 48, 46. [Google Scholar] [CrossRef]
- Crocco, M.; Martelli, S.; Trucco, A.; Zunino, A.; Murino, V. Audio Tracking in Noisy Environments by Acoustic Map and Spectral Signature. IEEE Trans. Cybern. 2018, 48, 1619–1632. [Google Scholar] [CrossRef]
- Worley, R.; Dewoolkar, M.; Xia, T.; Farrell, R.; Orfeo, D.; Burns, D.; Huston, D. Acoustic Emission Sensing for Crack Monitoring in Prefabricated and Prestressed Reinforced Concrete Bridge Girders. J. Bridge Eng. 2019, 24, 04019018. [Google Scholar] [CrossRef]
- Bello, J.P.; Silva, C.; Nov, O.; Dubois, R.L.; Arora, A.; Salamon, J.; Mydlarz, C.; Doraiswamy, H. SONYC: A system for monitoring, analyzing, and mitigating urban noise pollution. Commun. ACM 2019, 62, 68–77. [Google Scholar] [CrossRef]
- Sun, X. Immersive audio, capture, transport, and rendering: A review. Apsipa Trans. Signal Inf. Process. 2021, 10, e13. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Li, Z.; Li, J. Design and Implementation of Two Immersive Audio and Video Communication Systems Based on Virtual Reality. Electronics 2023, 12, 1134. [Google Scholar] [CrossRef]
- Padois, T.; St-Jacques, J.; Rouard, K.; Quaegebeur, N.; Grondin, F.; Berry, A.; Nélisse, H.; Sgard, F.; Doutres, O. Acoustic imaging with spherical microphone array and Kriging. JASA Express Lett. 2023, 3, 042801. [Google Scholar] [CrossRef]
- Chu, Z.; Yin, S.; Yang, Y.; Li, P. Filter-and-sum based high-resolution CLEAN-SC with spherical microphone arrays. Appl. Acoust. 2021, 182, 108278. [Google Scholar] [CrossRef]
- Ward, D.B.; Kennedy, R.A.; Williamson, R.C.; Brandstein, M. Microphone Arrays Signal Processing Techniques and Applications (Digital Signal Processing); Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Crocco, M.; Trucco, A. Design of Superdirective Planar Arrays With Sparse Aperiodic Layouts for Processing Broadband Signals via 3-D Beamforming. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 800–815. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. Stochastic and Analytic Optimization of Sparse Aperiodic Arrays and Broadband Beamformers WITH Robust Superdirective Patterns. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2433–2447. [Google Scholar] [CrossRef]
- Mars, R.; Reju, V.G.; Khong, A.W.H.; Hioka, Y.; Niwa, K. Chapter 12—Beamforming Techniques Using Microphone Arrays; Chellappa, R., Theodoridis, S., Eds.; Academic Press Library in Signal Processing; Academic Press: Cambridge, MA, USA, 2018; Volume 7, pp. 585–612. ISBN 9780128118870. [Google Scholar] [CrossRef]
- Hansen, R.C. Phased Array Antennas, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-40102-6. [Google Scholar]
- Cox, H.; Zeskind, R.; Kooij, T. Practical supergain. IEEE Trans. Acoust. Speech, Signal Process. 1986, 34, 393–398. [Google Scholar] [CrossRef]
- Kates, J.M. Superdirective arrays for hearing aids. J. Acoust. Soc. Am. 1993, 94, 1930–1933. [Google Scholar] [CrossRef] [PubMed]
- Bitzer, J.; Simmer, K.U. Superdirective microphone arrays. In Microphone Arrays: Signal Processing Techniques and Applications; Brandstein, M.S., Ward, D.B., Eds.; Springer: New York, NY, USA, 2001; pp. 19–38. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Ward, D.B.; Kennedy, R.A.; Williamson, R.C. Theory and design of broadband sensor arrays with frequency invariant far-field beam patterns. J. Acoust. Soc. Am. 1995, 97, 1023–1034. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. Design of Robust Superdirective Arrays With a Tunable Tradeoff Between Directivity and Frequency-Invariance. IEEE Trans. Signal Process. 2011, 59, 2169–2181. [Google Scholar] [CrossRef]
- Doclo, S. Multi-microphone noise reduction and dereverberation techniques for speech applications. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2003. Available online: ftp://ftp.esat.kuleuven.ac.be/stadius/doclo/phd/ (accessed on 14 June 2023).
- Crocco, M.; Trucco, A. The synthesis of robust broadband beamformers for equally-spaced linear arrays. J. Acoust. Soc. Am. 2010, 128, 691–701. [Google Scholar] [CrossRef]
- Mabande, E. Robust Time-Invariant Broadband Beamforming as a Convex Optimization Problem. Ph.D. Thesis, Friedrich-Alexander-Universität, Erlangen, Germany, 2015. Available online: https://opus4.kobv.de/opus4-fau/frontdoor/index/index/year/2015/docId/6138/ (accessed on 14 June 2023).
- Trucco, A.; Traverso, F.; Crocco, M. Robust superdirective end-fire arrays. In Proceedings of the 2013 MTS/IEEE OCEANS—Bergen, Bergen, Norway, 10–13 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Traverso, F.; Crocco, M.; Trucco, A. Design of frequency-invariant robust beam patterns by the oversteering of end-fire arrays. Signal Process. 2014, 99, 129–135. [Google Scholar] [CrossRef]
- Trucco, A.; Crocco, M. Design of an Optimum Superdirective Beamformer Through Generalized Directivity Maximization. IEEE Trans. Signal Process. 2014, 62, 6118–6129. [Google Scholar] [CrossRef]
- Trucco, A.; Traverso, F.; Crocco, M. Broadband performance of superdirective delay-and-sum beamformers steered to end-fire. J. Acoust. Soc. Am. 2014, 135, EL331–EL337. [Google Scholar] [CrossRef] [PubMed]
- Doclo, S.; Moonen, M. Superdirective Beamforming Robust Against Microphone Mismatch. IEEE Trans. Audio, Speech, Lang. Process. 2007, 15, 617–631. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. A Synthesis Method for Robust Frequency-Invariant Very Large Bandwidth Beamforming. In Proceedings of the 18th European Signal Processing Conference (EUSIPCO 2010), Aalborg, Denmark, 23–27 August 2010; pp. 2096–2100. [Google Scholar]
- Trucco, A.; Crocco, M.; Traverso, F. Avoiding the imposition of a desired beam pattern in superdirective frequency-invariant beamformers. In Proceedings of the 26th Annual Review of Progress in Applied Computational Electromagnetics, Tampere, Finland, 26–29 April 2010; pp. 952–957. [Google Scholar]
- Doclo, S.; Moonen, M. Design of broadband beamformers robust against gain and phase errors in the microphone array characteristics. IEEE Trans. Signal Process. 2003, 51, 2511–2526. [Google Scholar] [CrossRef]
- Mabande, E.; Schad, A.; Kellermann, W. Design of robust superdirective beamformers as a convex optimization problem. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 77–80. [Google Scholar] [CrossRef]
- Greco, D.; Trucco, A. Superdirective Robust Algorithms’ Comparison for Linear Arrays. Acoustics 2020, 2, 707–718. [Google Scholar] [CrossRef]
- Pérez, A.F.; Sanguineti, V.; Morerio, P.; Murino, V. Audio-Visual Model Distillation Using Acoustic Images. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass, CO, USA, 1–5 March 2020; pp. 2843–2852. [Google Scholar] [CrossRef]
- Sanguineti, V.; Morerio, P.; Pozzetti, N.; Greco, D.; Cristani, M.; Murino, V. Leveraging acoustic images for effective self-supervised audio representation learning. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Part XXII 16. pp. 119–135. [Google Scholar]
- Ward, D.B.; Kennedy, R.A.; Williamson, R.C. FIR filter design for frequency invariant beamformers. IEEE Signal Process. Lett. 1996, 3, 69–71. [Google Scholar] [CrossRef]
- Sanguineti, V.; Morerio, P.; Bue, A.D.; Murino, V. Unsupervised Synthetic Acoustic Image Generation for Audio-Visual Scene Understanding. IEEE Trans. Image Process. 2022, 31, 7102–7115. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Chae, M.S.; Yang, Z.; Yuce, M.R.; Hoang, L.; Liu, W. A 128-channel 6 mW wireless neural recording IC with spike feature extraction and UWB transmitter. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 312–321. [Google Scholar] [CrossRef]
- Paolo, M.; Alessandro, C.; Gianfranco, D.; Michele, B.; Francesco, C.; Davide, R.; Luigi, R.; Luca, B. Neuraghe: Exploiting CPU-FPGA synergies for efficient and flexible CNN inference acceleration on zynQ SoCs. ACM Trans. Reconfigurable Technol. Syst. 2017, 11, 1–24. [Google Scholar] [CrossRef]
- Da Silva, B.; Braeken, A.; Touhafi, A. FPGA-Based Architectures for Acoustic Beamforming with Microphone Arrays: Trends, Challenges and Research Opportunities. Computers 2018, 7, 41. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greco, D. A Feasibility Study for a Hand-Held Acoustic Imaging Camera. Appl. Sci. 2023, 13, 11110. https://doi.org/10.3390/app131911110
Greco D. A Feasibility Study for a Hand-Held Acoustic Imaging Camera. Applied Sciences. 2023; 13(19):11110. https://doi.org/10.3390/app131911110
Chicago/Turabian StyleGreco, Danilo. 2023. "A Feasibility Study for a Hand-Held Acoustic Imaging Camera" Applied Sciences 13, no. 19: 11110. https://doi.org/10.3390/app131911110
APA StyleGreco, D. (2023). A Feasibility Study for a Hand-Held Acoustic Imaging Camera. Applied Sciences, 13(19), 11110. https://doi.org/10.3390/app131911110







