TABASCO—Topology Algorithm That Benefits from Adaptation of Sorted Compliances Optimization

Abstract

Although structural topology optimization has been developing for decades, it still plays a leading role within the area of engineering design. Solving contemporary design problems coming from industry requires the implementation of efficient methods and approaches. This stimulates research progress in the development of novel and versatile topology optimization algorithms. To follow these modern trends, an original topology generator has been elaborated and finally built as a Cellular Automaton with original update rules. The motivation for building the algorithm in this way came from the idea of utilizing the benefits of local compliances sorting. This is conducted on two levels: on the global level, the monotonic function mapping local compliances distribution is defined based on their sorted values; on the local level, for each cell, the compliances are sorted within the cell neighborhood. The three largest absolute values are selected, and these are the basis from which to formulate Cellular Automata update rules. These original rules can efficiently control the generation of structural topologies. This technique is somewhat inspired by the grey wolf optimizer strategy, wherein the process of updating design variables refers to the positions of the three best fitted wolves. It is proposed that we refer to the topology algorithm that benefits from the adaptation of sorted compliances optimization as TABASCO. The developed algorithm is a modified version of the flexible Cellular Automata one presented previously. The implemented extension, regarding the local level cell sorting, allows us to improve the resulting compliance values. The advantages of the algorithm, both from numerical and practical engineering points of view, as compared to the others developed within the field, may be gathered as follows: the algorithm works based on simple update rules, i.e., its numerical implementation is not complicated; it does not require gradient computations; filtering techniques are not needed; and it can easily be combined with professional structural analysis programs which allow engineering applications. The developed topology generator has been linked with ANSYS to show that it can be incorporated into a commercial structural analysis package. This is especially important with respect to the engineering implementations.

1. Introduction

The development of structural topology optimization has already been observed for decades; nevertheless, this approach still plays a leading role in the area of engineering design. Along with the original novel concepts applied in many research and engineering fields, a variety of approaches to topology generation have been proposed over the years. Many survey papers, e.g., refs. [1,2,3,4], supported by the recently published papers of Ribeiro et al. [5] and Logo and Ismail [6], provided a broad discussion on various issues and aspects of topology optimization.

Moreover, solving contemporary design problems coming from industry requires the elaboration of novel methods and approaches, which stimulates continuous research progress in the development of efficient topology optimization algorithms. The natural consequence of this progress is that nowadays, commercial structural analysis software often also offers performing topology optimization. This easy access to topological design is very helpful for engineers but, on the other hand, the results produced by the black box systems are not necessarily the best to be found. It is definitely a step towards the engineering implementation of topological designs but working on efficient topology generators is still welcome. The present paper follows this trend, showing how to build an original efficient generator of structural topologies. Hence, it is built as a Cellular Automaton with original update rules. The rules utilize information gathered within cells’ neighborhoods and are applied to all cells/elements. The motivation for building the algorithm came from the idea of utilizing the benefits of local compliances sorting. This is conducted on two levels: first, the monotonic function mapping local compliances distribution is defined on the global level based on their sorted values; next, on the local level, for each cell, the compliances are sorted within the cell neighborhood. Among them, the three largest absolute values are selected, and this is the basis on which to formulate Cellular Automata update rules. This technique is somewhat inspired by the grey wolf optimizer [7] strategy, wherein the process of updating design variables refers to the positions of the three best fitted wolves, namely alpha, beta and delta, wolves.

It is proposed that we refer to the topology algorithm that benefits from the adaptation of sorted compliances optimization as TABASCO. The developed algorithm is a modified version of the flexible Cellular Automata model presented previously. The implemented extension, regarding local-level cell sorting, allows us to improve the resulting compliance values. The advantages of the algorithm, both from numerical and practical engineering points of view, as compared to the others developed within the field, art as follows: The algorithm works based on simple update rules; its numerical implementation is not complicated; it does not require gradient computations; it can easily be combined with professional structural analysis programs which allows engineering applications. Moreover, generated topologies are free from so-called grey elements, i.e., ones of intermediate densities, and due to the grey elements elimination, it is easier to transform obtained numerical solution to a CAD model and to prepare elements for manufacturing. One of the most important advantages of using the algorithm proposed in this paper is that the implementation of additional filtering techniques is not necessary. However, it is worth stressing that, in favor of the CA approach, the neighborhood remains the same independent of the mesh size, whereas in the case of the filtering technique, the neighborhood size has to be selected depending on the mesh size. The problem related to the above is the generation of topologies for a large number of elements. The OC method requires adjusting filtering parameters in order to obtain a solid topology. In the case of the CA-based algorithm, it is not necessary.

The formulated original rules can efficiently control the generation of structural topologies, and the topology generator built on this basis has been linked with ANSYS to show that it can be incorporated into a commercial structural analysis package. The performance of the algorithm has been illustrated by the generation of selected plane and spatial topologies using the TABASCO rules. Exemplary engineering implementation has been included.

The content of the paper is structured as follows. The structural topology optimization via heuristic methods is reviewed in Section 2. Within this subject, a Cellular Automat approach and its implementation into topology optimization are described. The TABASCO algorithm concept is introduced in Section 3, and its performance is first illustrated in Section 4 based on the generation of plane structures topologies. Next, in Section 5, the ability of the algorithm to cope with 3D structures is presented. Finally, some concluding remarks are formulated in Section 6, which ends the paper.

2. Structural Topology Optimization and Heuristic Methods

Performing topology optimization (TO) means looking for the distribution of material within a specified domain in order to minimize a chosen objective function and to satisfy imposed constraints. It is assumed that topology optimization started with Michell’s paper, published in 1904. However, intensive studies started in the 1980s, and since then, TO has become the most popular engineering tool. The growing demands drive the development of techniques and methods of TO, which can be helpful and effectively used in engineering implementations and practical problems.

Heuristic methods are becoming more popular and useful in engineering applications of topology optimization. Their simplicity of implementation and fast convergence, which does not require a large number of finite element analyses, make heuristics a useful basis for different approaches applied to the topology optimization of realistic engineering problems. Among very powerful heuristic methods are those based on physical and chemical phenomena or population intelligence. The latter are very effective, but their greatest weakness is the need to refer to computation of the objective many times, i.e., for each individual at each iteration step. This means the necessity of multiple finite element analyses of designed structures, which may be very time consuming for coarse mesh. Solving this problem efficiently is an important task for designers. Nevertheless, heuristic techniques are widely discussed and continuously applied in engineering topology optimization. As an example, they may serve topology optimization with the use of an ant colony approach [8] or a genetic algorithm [9], simulated annealing [10], or binary particle swarm optimization [11]. Less popular examples may serve a meta-heuristic using probabilistic learning [12], a heuristic algorithm mimicking a self-evolution of a structure [13], the big bang–big Crunch algorithm [14], and the recently published hunter–prey optimization algorithm [15].

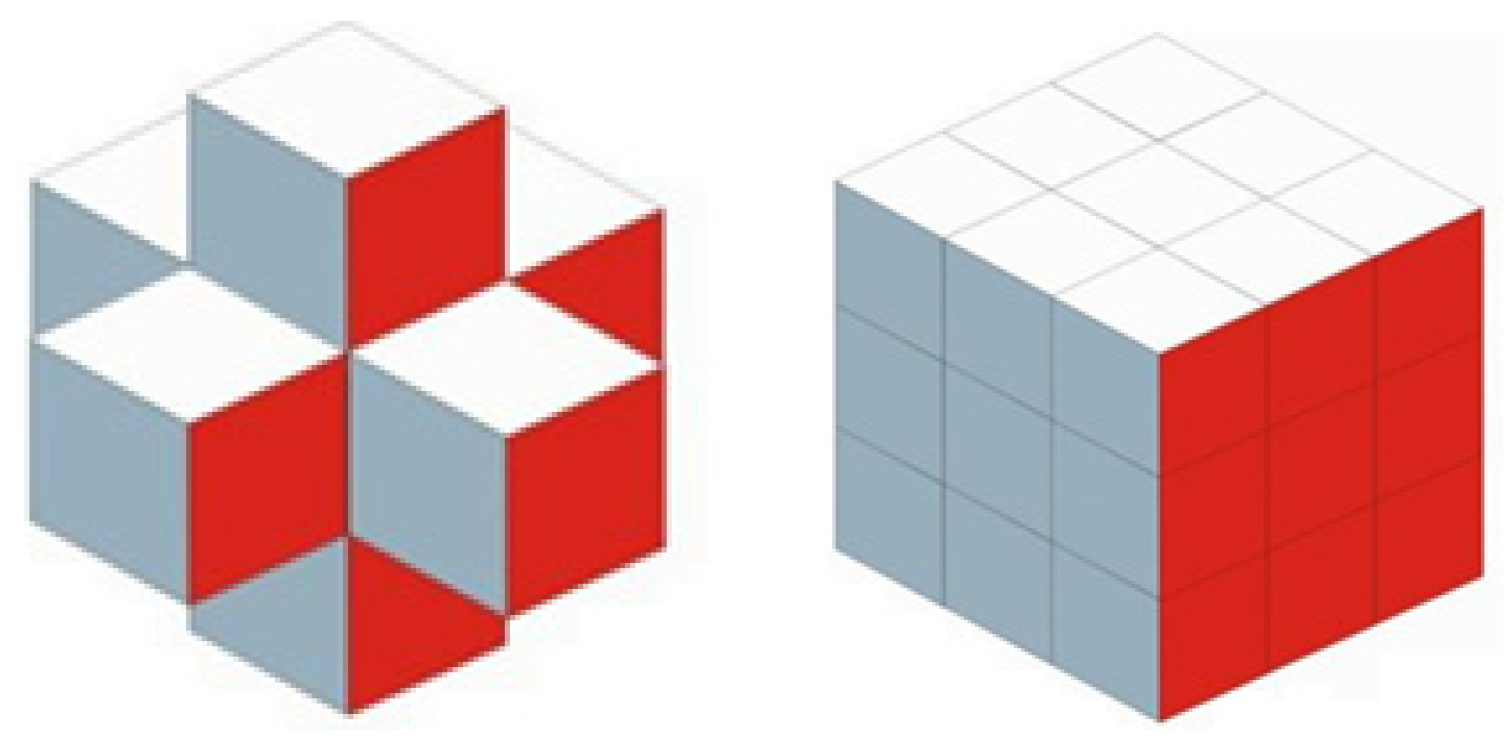
As already mentioned in the introduction, an approach based on the concept of Cellular Automata (CA) is applied in this paper. Cellular Automata mimic the behavior of complex systems in a relatively easy way. Hence, a sequence of simple decision making rules is implemented. These rules control the performance of a considered system. The engineering implementation requires the decomposition of the considered domain into a lattice of cells which usually form a uniform lattice. The examples of plane and spatial neighborhoods for regular cells are presented in Figure 1 and Figure 2, respectively:

Each cell, together with cells it is connected to, forms a neighborhood. The cells carry only local information. It is assumed that the interaction between cells is limited to their neighborhood. Local homogenous rules govern the evolution of cells state. The rules are applied simultaneously to each cell, and they are identical for all neighborhoods. The physical quantities are also updated repetitively and as a result, the process covers the global behavior of the system. Since the late 1940s when von Neumann and Ulam proposed the concept of Cellular Automata, this idea has been found interesting by researchers representing various research fields.

Cellular Automata have proved to be an effective tool in engineering optimization for both size optimization (e.g., [16,17]) and topology optimization, as started by Inou et al. [18]. The effectiveness of the CA approach in the generation of structural topologies and its versatility can be observed in various engineering problems starting from compliance minimization problems (e.g., [19]), including problems with stress and displacement constraints (e.g., [20]), through reliability-based topology optimization (e.g., [21]) or dynamic–static coupling topology optimization ([22]) to the topology optimization of energy absorbers ([23,24]) or the optimization of multi-materials structures ([25] or [26]), composites ([27]), and design of materials (e.g., [28,29]). The mentioned papers may serve only as examples of numerous applications of the Cellular Automata method. Additionally, a new trend in developing this method can be observed, namely, a hybridization of CA with other methods, pertaining to both classical methods ([19,30,31] for size optimization) and heuristics. Among hybridization CA with heuristics applied to topology optimization, the following can be mentioned: a Cellular Automaton mimicking colliding bodies [32], a hybrid evolutionary bi-directional Cellular Automaton [33], and the cuttlefish algorithm (CFA) for truss topology optimization utilizing the Cellular Automata approach [34]. The survey of combinations of CA with heuristics in broad fields of engineering computations is presented in [35,36], where, among others, the cellular grey wolf optimizer (CGWO) is proposed. In that paper, utilizing the hunting mechanism of grey wolves, the analysis steps need to be performed for each individual at each iteration, which may cause a significant increase in computation time for large engineering problems. It is worth stressing that in the present paper, which also refers to GWO, the idea is different—the analysis is performed once for each iteration and the derived rules of Cellular Automata govern the behavior of the system.

In general, the effectiveness of the population-based algorithms strongly depends on the population size. An extensive discussion of this aspect of topology optimization problems can be found, e.g., in [37]. In the optimization process at each iteration the fitness function must be calculated for each individual. As a result, the population-based methods usually require a larger number of functional calls than other non-population-based heuristics.

When considering the topology optimization problems using Cellular Automata, it is necessary to mention the valuable and groundbreaking papers of Tovar et. al, e.g., [38], where the hybrid Cellular Automata (HCA) is introduced. It must be underlined, however, that in those papers, hybridization refers to the interaction of analyses based on finite elements with the Cellular Automaton approach.

3. TABASCO Algorithm—Two-Level Sorting and Update Rules Inspired by the Grey Wolf Optimizer

Formulating the topology optimization problem, in the present stud, the attention is focused on the minimization of structural compliance c (see Equation (1)). This is the classical approach (a discussion of the problem can be found in the early paper [39]). In this paper, the approach based on finite elements has been applied and the structural topology optimization problem formulation takes the form known from the well-recognized paper by Sigmund [40]. Hence, it is assumed that only a specified volume fraction κ of a material is distributed within the final structure. This results in the constrained volume V, Equation (2):

$$\mathrm{minimize}\hspace{1em}c\left(\mathit{d}\right)={\mathbf{u}}^T\mathbf{k}\mathbf{u}={\sum }_{i=1}^N{d}_i^p{\mathbf{u}}_i^T{\mathbf{k}}_i{\mathbf{u}}_i,$$

(1)

$$\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o} V\left(\mathbf{d}\right)=\kappa V_0,$$

(2)

$$\mathbf{k} \mathbf{u}=\mathbf{f}$$

(3)

$$0<d_{min}\le d_i\le 1.$$

(4)

The following quantities have been introduced at the element level: displacement vector ${\mathit{u}}_i$, stiffness matrix ${\mathit{k}}_i,$ design variable $d_i$, defined as the relative material density, and number of elements N, as well as the global quantities: stiffness matrix $\mathbf{k}$, displacement vector $\mathit{u}$, and force vector $\mathit{f}$ from Equation (3). In order to avoid singularity, the simple bounds related to the design variables with minimal non-zero density $d_{min}$ (e.g., 10⁻⁹) have been introduced in Equation (4). In the above formulation, the convenient finite element approach has been adopted.

The broadly accepted material model SIMP—Solid Isotropic Material with Penalization [35]—has been adopted, meaning that the elasticity modulus $E_i$ for each cell/element is the function of the design variable $d_i$ as shown in Equation (5):

$$E_i=d_i^p{E}_0.$$

(5)

The quantity $E_0$ is the elasticity modulus of a solid material, whereas p, usually equal to 3, plays the role of penalization power. The SIMP approach is the most common material interpolation scheme, and it is widely discussed and exploited in literature. The majority of papers on topology optimization use SIMP (or SIMP modifications) while performing calculations, using at the same time new techniques for updating the design variables—i.e., those conventional or newly developed heuristics. It is worth mentioning here the various modifications of the SIMP method (e.g., [41,42,43] and many more) created to prevent some difficulties in the application of SIMP in selected complex problems such as multi-material topology optimization, dynamic problems, design-dependent loads, thermodynamic problems.

While performing the optimization process, the values of the design variables associated with cells are updated based on the local rules.

In order to solve the problem, a heuristic local CA update rule is proposed, utilizing the information gathered from a selected neighborhood. New values of design variables can be calculated based on the Gauss–Seidel iteration mode, i.e., a cell updates its state based on updated values found for cell neighbors in the current and previous iteration, or on the Jacobi iteration mode, i.e., a cell updates its state based on the states of the surrounding cells obtained in the previous iteration only. This scheme was chosen for this paper.

The Jacobi scheme of updating is utilized, which means that the states of neighboring cells known from the previous iteration are the basis for the update process, as in Equation (6):

$$d_i^{new}=d_i+{∆d}_i.$$

(6)

The quantity ${∆d}_i$ represents the update component implemented in each iteration. Its selection decides the effectiveness of the updating scheme; therefore, this is the important research issue. The original proposal is included in this paper. It can be treated as an extension and modification of the rule discussed in the paper [44].

The updating process consists of a few steps. First, structural analysis is performed and the compliances values for N cells are computed. Next, the compliances are sorted in ascending order and divided into three subsets: N₁ cells having the lowest values, N–N₂ cells with the largest values, and the remaining cells having intermediate values of compliances. The cells from the first subset have–C value assigned, the ones from the second subset have a value of C, whereas for cells from the intermediate interval, a function f(i) of local compliances is defined. Finally, the function mapping local compliances, which utilize results of the global sorting, take the form of Equation (7), where i denotes a cell index:

$$F\left(i\right)=\left\{\begin{array}{c}-C if i<N_1\\ f\left(i\right) if N_1\le i\le N_2\\ C if i>N_2\end{array}\right..$$

(7)

Having finished with the analysis at the global level, the local rules of design variables updating can be established. Therefore, for each cell, the neighboring cells are taken into consideration. In the former papers, in dealing with the implementation of Cellular Automata rules, in the process of topology generation, information gathered within all cells forming neighborhood has been considered.

The novel proposal, inspired by the grey wolf optimizer strategy, where the process of updating design variables refers to the positions of the three best fitted wolves, assumes that information from only three of the most influential cells is the basis for forming the update rule. Hence, on the local level, for each cell, the compliances are sorted as absolute values within the cell neighborhood. As the result of local sorting, the three values $F_1,F_2,F_3$ are chosen, and these are the basis from which to build the CA rule for the updating the design variables. The rule then takes the following final form:

$$d_i^{new}=d_i+\frac{F_1+F_2+F_3}{3}m.$$

(8)

Updating design variables results in either adding material to or removing it from a cell i. The quantity m in Equation (8) limits the possible change of the design variables’ values. The function f(i), introduced in Equation (7), is adopted here in the form of Equation (9):

$$f(i)=C\frac{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[\beta (\frac{i-N_1}{N_2-N_1}-\frac{1}{2})\right]}{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(\frac{1}{2}\beta \right)}.$$

(9)

The above form enables flexibility of the function, which is controlled by the quantity β. One can observe that β tending to zero f(i) approaches linear function, while for large values of β f(i), these are close to the step function. As mentioned above, f(i) is defined for cells from the interval [N₁, N₂]. Its width can be altered in the iteration process influencing the elimination of void cells if it is wide and forcing the elimination of cells of intermediate densities if it is narrow (for details, see [44]).

As to the move limit m, it plays in (8) the role of a multiplier. It becomes active if the updated design variable value is outside the admissible interval:

$${\mathrm{m}\mathrm{a}\mathrm{x}(d_{min},d_i-m)\le d}_i^{new}\le \min \left(1,d_i+m\right).$$

(10)

The m value is kept constant in the iteration process. The value of 0.2 is a common choice in the literature, e.g., [40,45]. The already-gathered experience from dealing with setting the move limit is that for its small values, the topology generation process slows down and the tendency of creating thin lines of generated topology can be observed. On the other hand, large values of the move limit change the structure topology and the compliance value, which may also cause the topology generation process to diverge.

4. The TABASCO Algorithm in Use

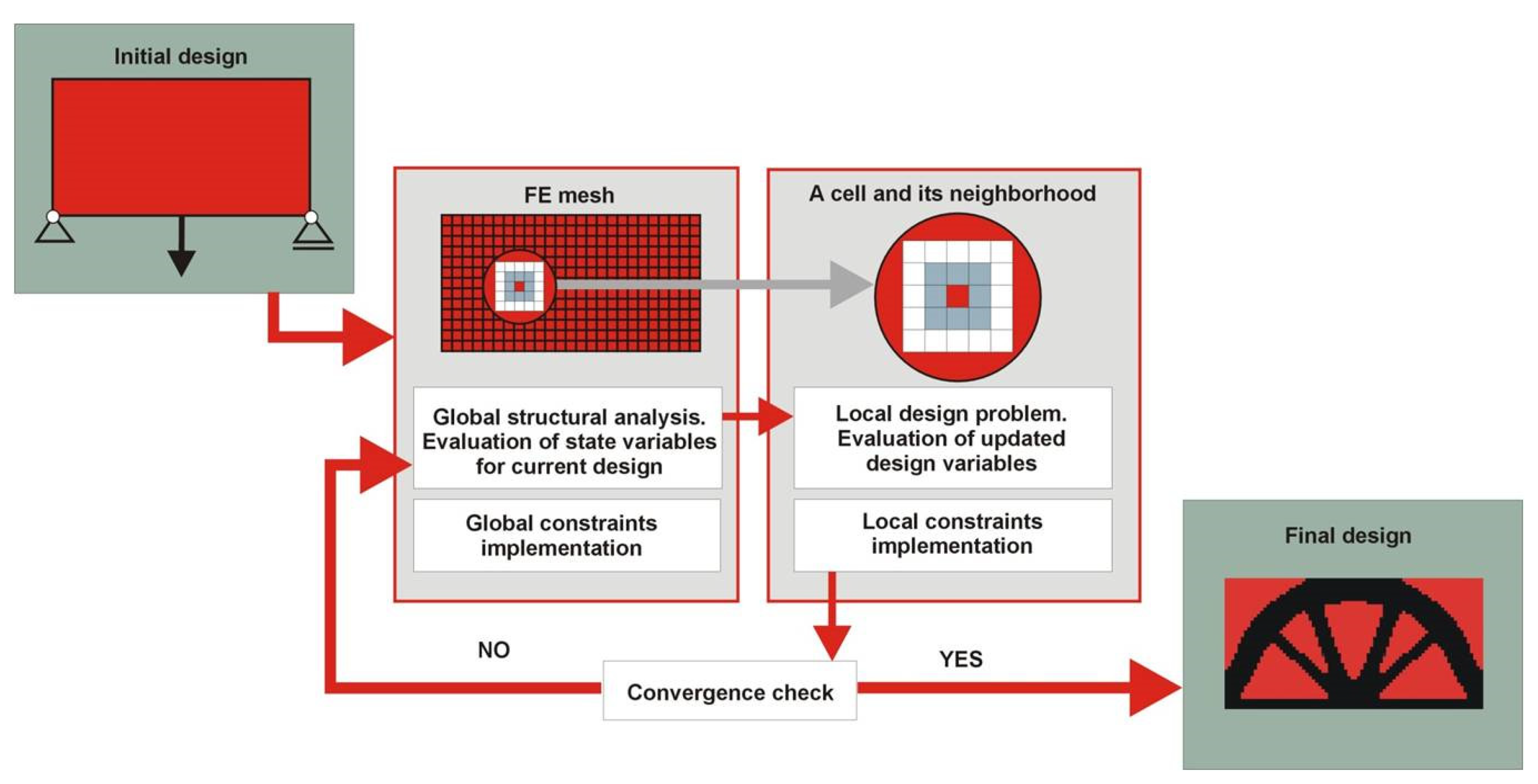
To illustrate how the TABASCO algorithm works, introductory examples have been proposed and detailed calculations are presented in this section. The Cellular Automata method allows for two approaches: simultaneous analysis and design, or the sequential approach chosen in this paper. So, the analysis using the finite element method is performed first and the design updating scheme is applied separately at each iteration. The updated value of design variable for each cell is based on the states of the neighboring cells determined in the preceding iteration, according to the Jacobi iteration scheme. The Moore-type neighborhood has been implemented. Each application of local update rules is preceded by finite element analysis performed using Matlab R2020b or Ansys 14 software. The diagram presenting the TABASCO workflow is given in Figure 3.

The stopping criterion for iteration process can be selected according to the user assumptions. The defined number of iterations was chosen in these investigations, but in general, it can be specified, for example, based on the objective function convergence rate.

The present paper proposes the new, original concept of a novel topology generator. The TABASCO algorithm utilizes some flexible local rules, discussed in earlier papers; therefore, the results of computations refer to some earlier concepts. To test the versatility of the new idea, selected 2D and 3D structures were examined.

The rectangular, plain structure has been selected as the first test example (see Figure 4).

The regular mesh of 20,000, 200 × 100 4-node elements of edge length 1 mm has been implemented to perform the FEM analysis and the process of topology generation. The value of applied load has been set to P = 100 N, while the Young modulus and Poisson ratio have been set to values of E = 10 GPa and ν = 0.3, respectively. The value of global constraint, i.e., the volume fraction 0.3, has been assumed.

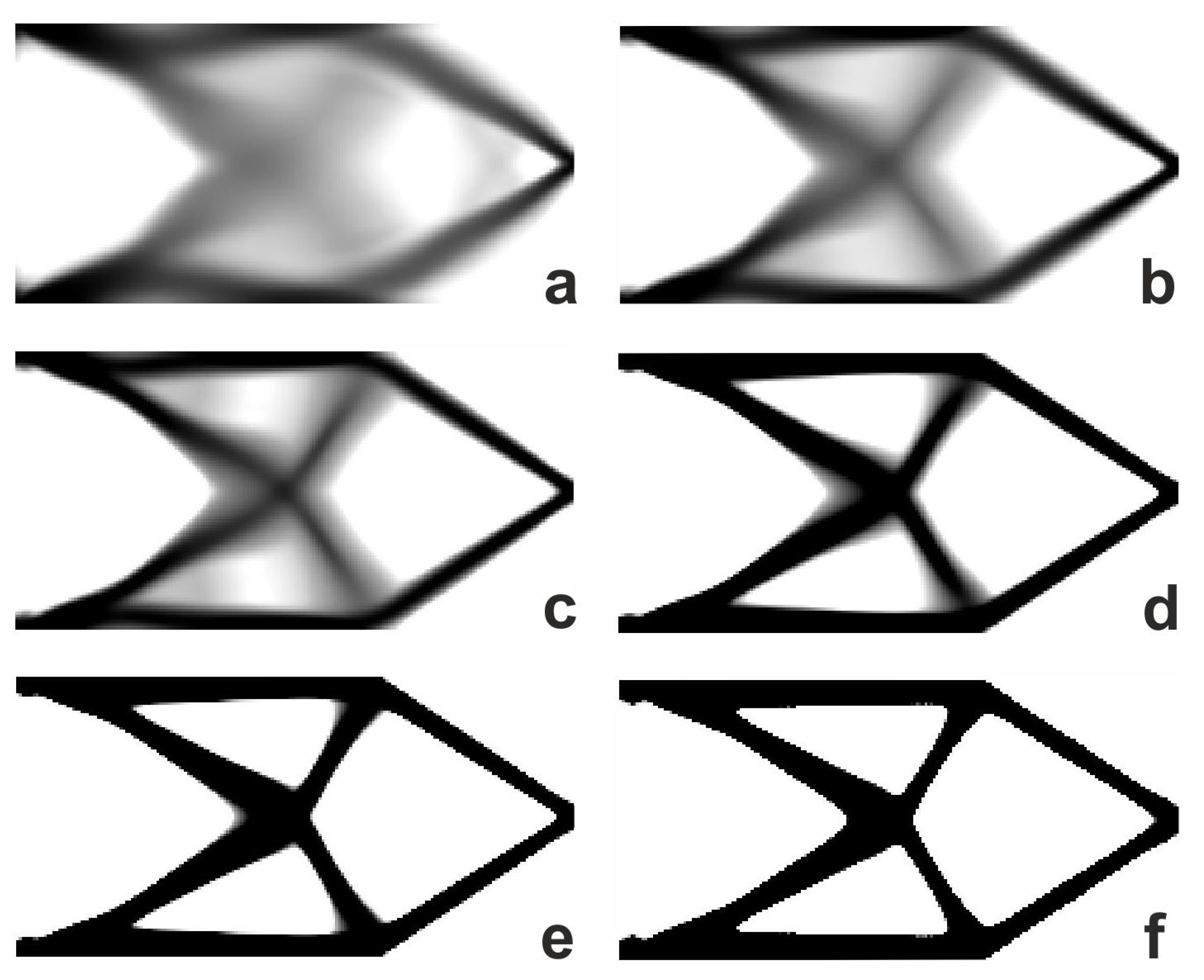
The resulting topology and the overview of the topology generation process are presented in Figure 5 and Figure 6, respectively.

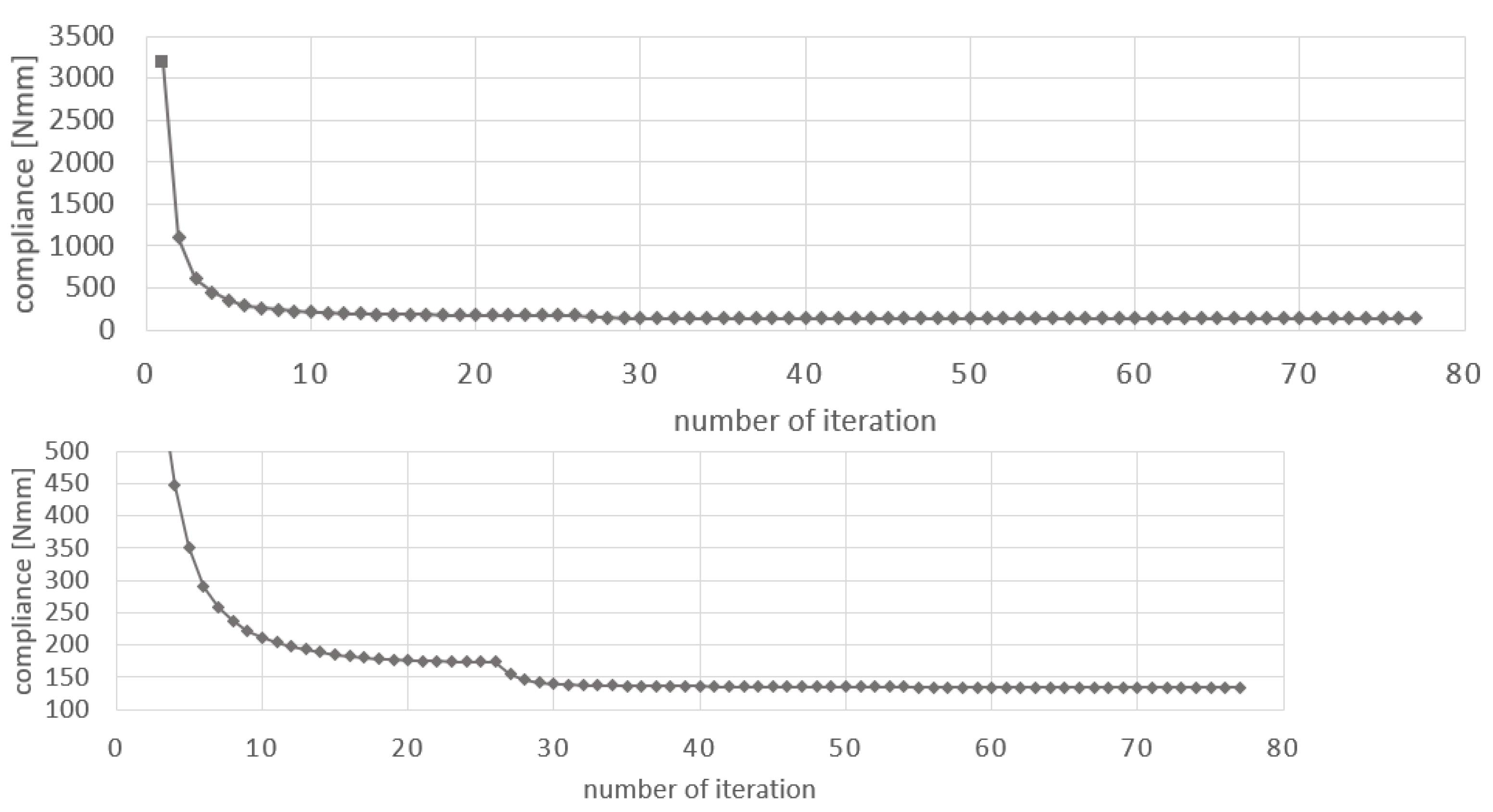
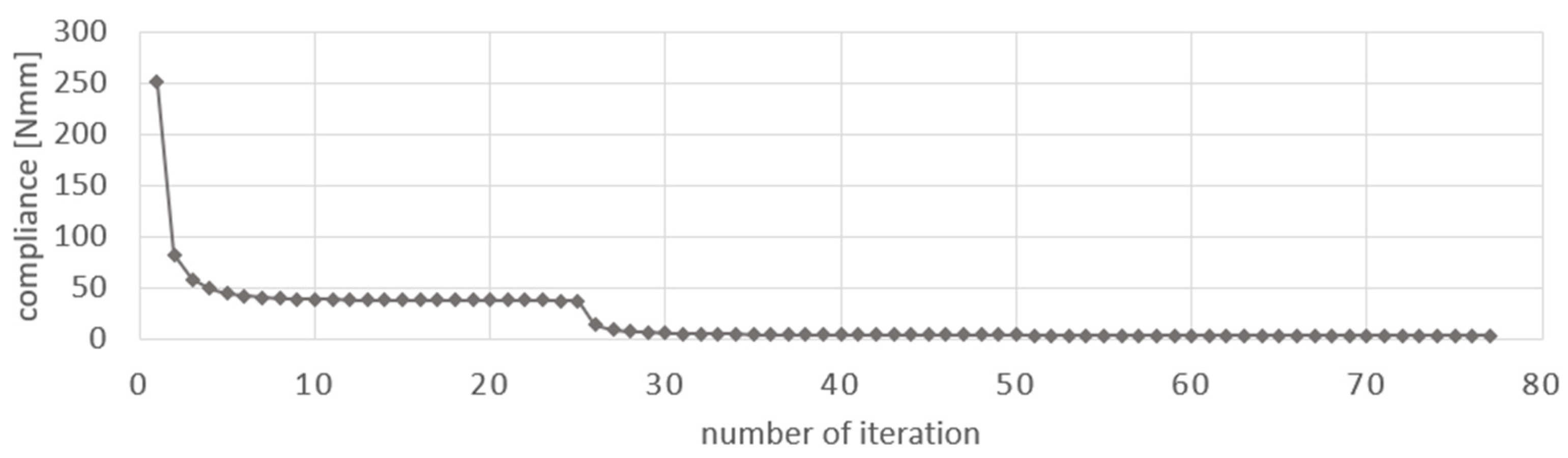
The iteration history, illustrating a good convergence to the optimized solution, is given in Figure 7.

A large number of iterations has been performed for all examples to allow comparisons of its performance for all considered problems. It is also intended to underline a fast decrease in the objective and a stable behavior when approaching minimal value. In Figure 7, presenting compliance history, the additional figure for the narrow interval of objective function values has been added, which gives us a closer look at the compliance behavior.

The resulting compliance value equals 133.22 Nmm for β = 0.1. The original FCA [44] allows us to obtain the value of 134.14 Nmm for optimized topology. It is also observed that the number of iterations needed to find the solution was reduced, i.e., it is 25 iterations, whereas FCA requires 46.

It can be noticed that the solution for this example is sensitive to the value of β, but to avoid the necessity of adjusting this control parameter, the self-adaptive technique can be implemented [46], which, in each step of the iteration process, can track the objective function’s lowest value. This technique can be realized by updating the values of design variables using, simultaneously, three values of β at each iteration, i.e., it can propose small, middle, and large ones. The algorithm selects the set of design variables created by this scheme for which the compliance has been found to be the smallest, and this set is the starting point for the next iteration.

The effectiveness of the proposed sorted compliances optimization concept (see [44]) can be controlled not only by the β parameter; the adaptive technique for the width of the interval [N₁, N₂] can be suggested. In the first exploration phase of the calculations, when the preliminary layout of the structure is being sought, the interval [N₁, N₂] is proposed to be wide. Then, in the exploitation phase, in order to guide the calculations to a black/white (solid/void) structure, the interval is successively reduced. Based on the numerous tests performed [44], the following unified strategy can be proposed: if the iteration number is lower than 25, then N₁ = 0.02 N and N₂ = 0.98 N for the second phase; while, if the iteration number is greater than 25, N₁ = 0.6 N and N₂ = 0.98 N, where N is a number of elements (cells).

As one can notice, the solution is free from the checkerboard effect, without any of the additional filtering or techniques reported in, e.g., [47]. The gray elements are absent in the solutions obtained with the proposed method, which is a great advantage compared with the OC method, for which the scale of occurrence of gray elements in the solution is dictated by additional parameters.

To complete the discussion of generating the optimized topology conducted for the test structure, the comparison with the results found using the well-known optimality criteria method [40] was prepared. The final compliance for the mentioned code was 136.55 Nmm.

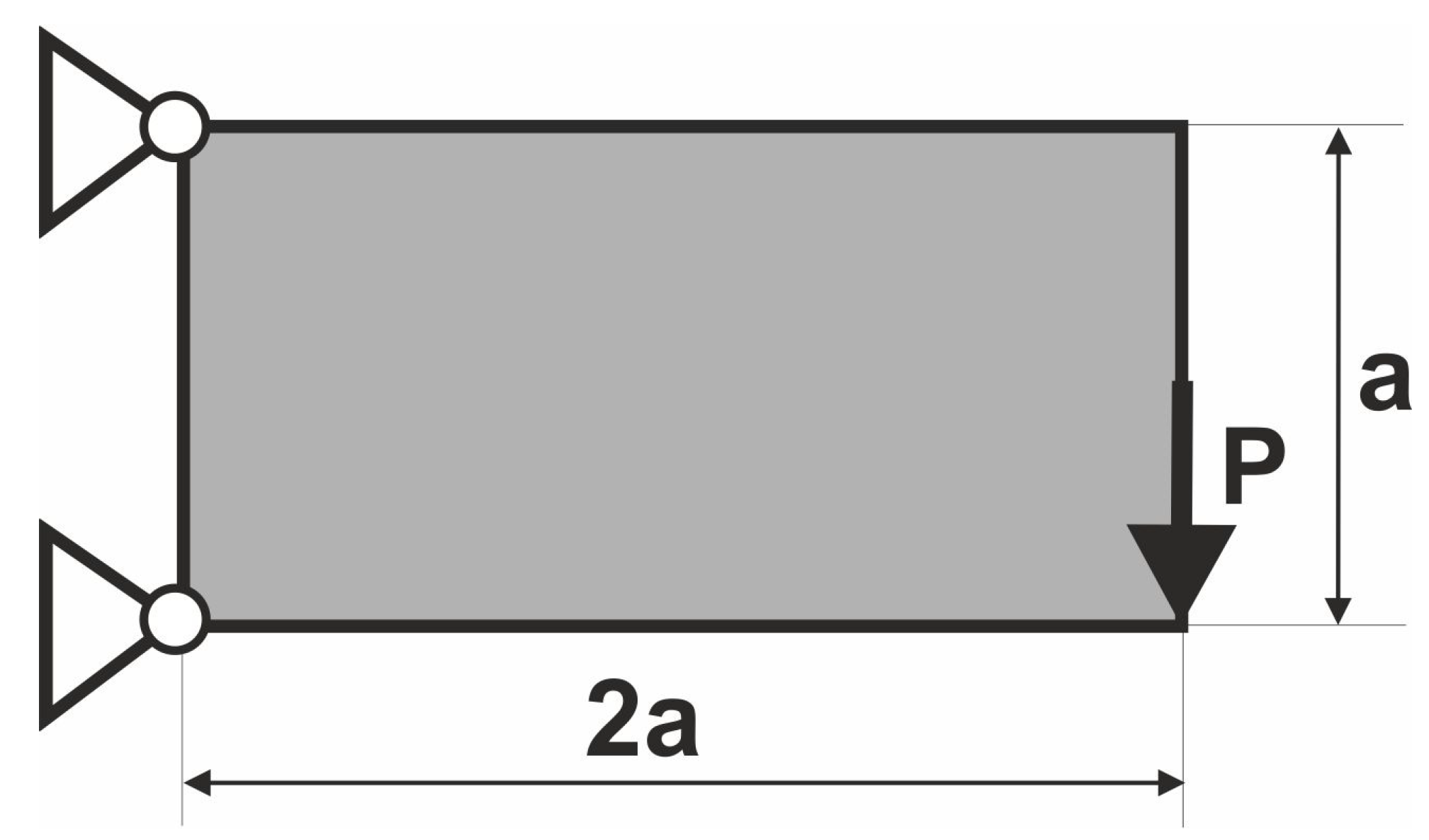
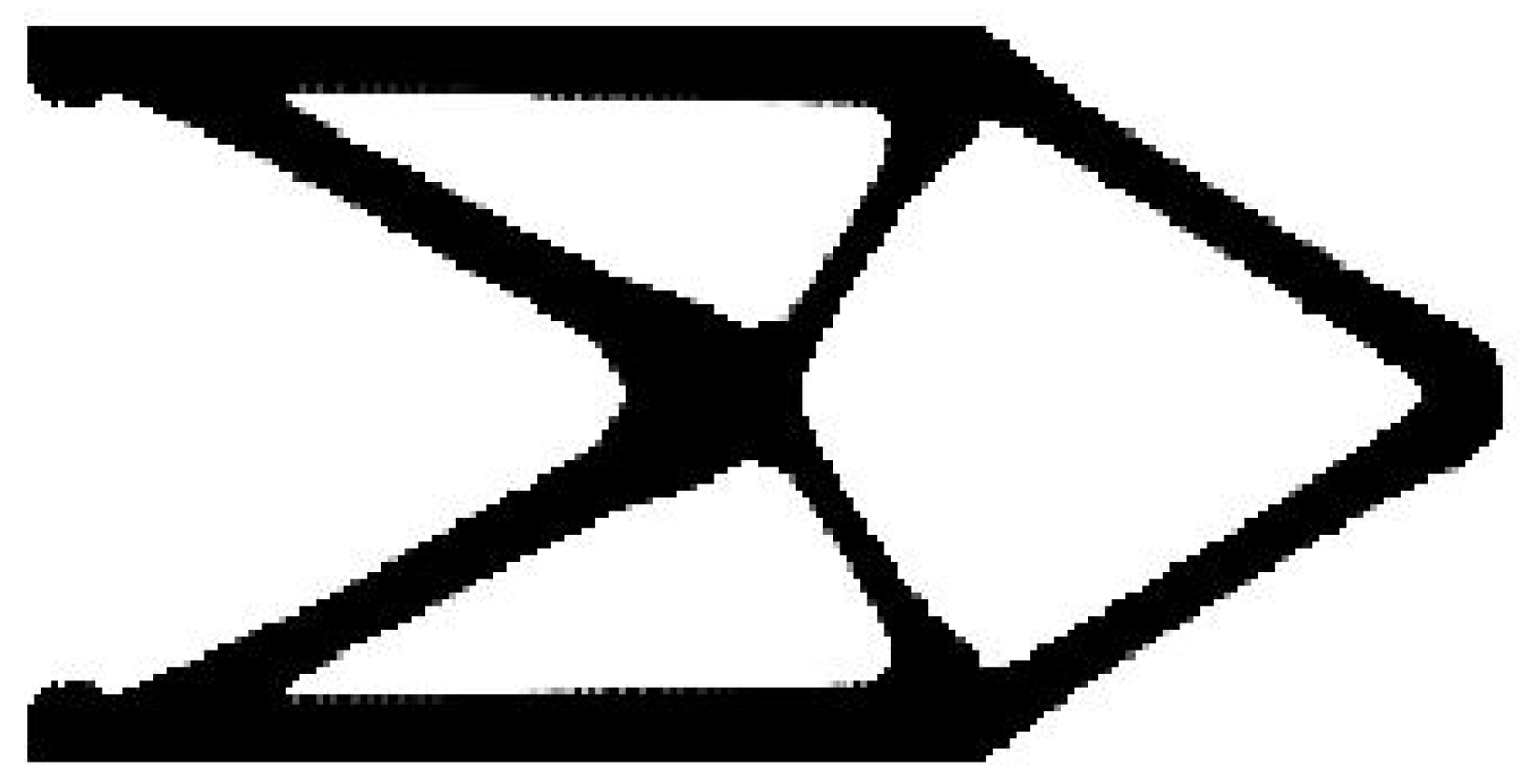
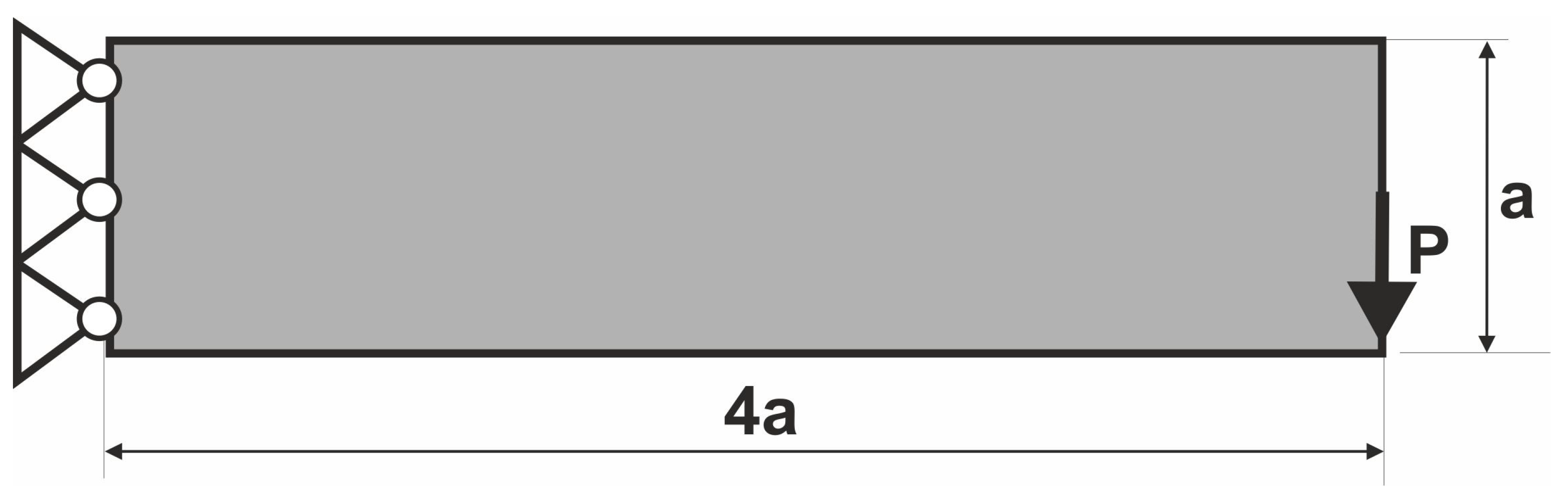
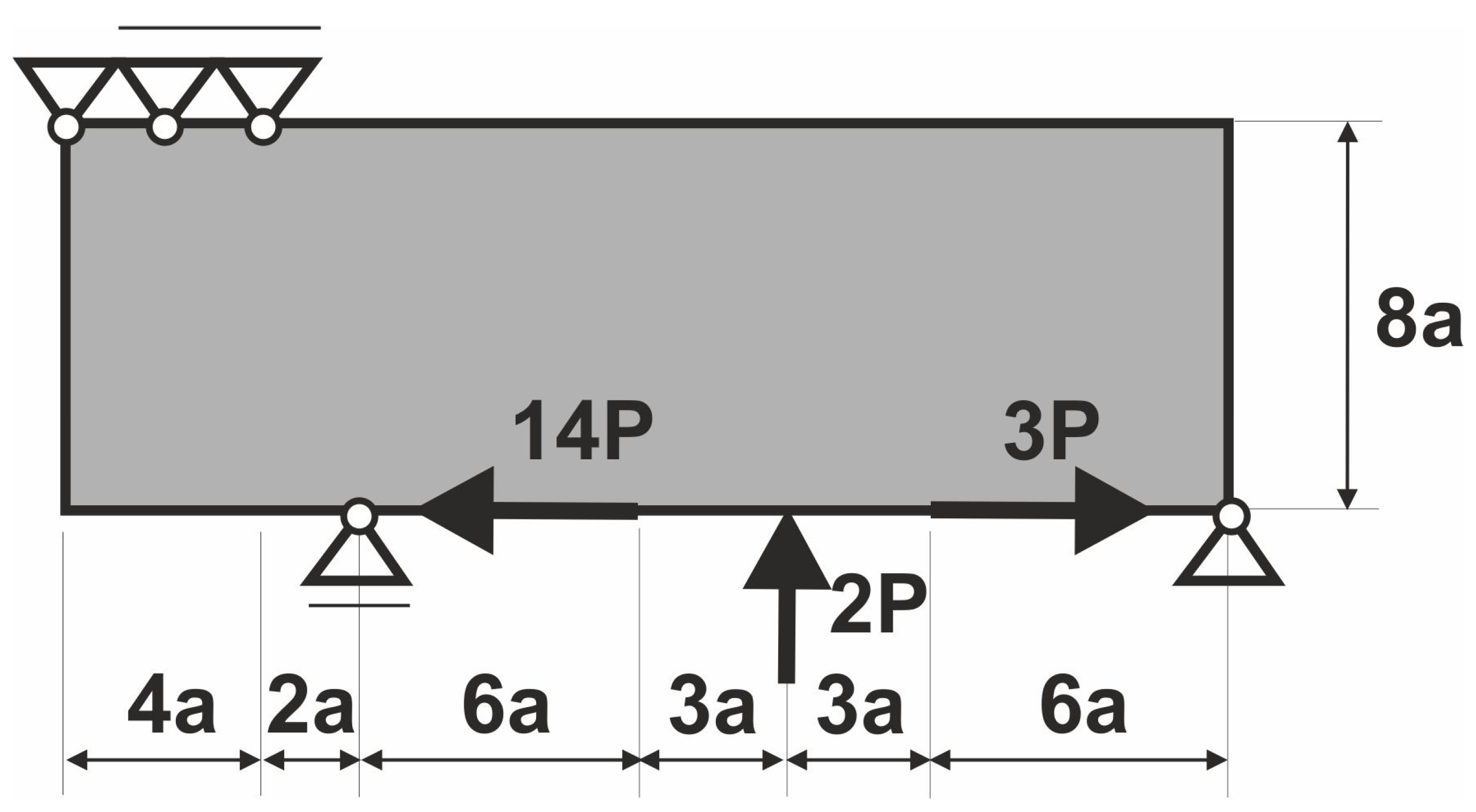
The long cantilever structure shown in Figure 8 has been chosen as the next test example.

In this example, the value of load equals P = 100 N, the parameter a is equal to a = 10 mm, while for the Young modulus and Poisson ratio, E = 10 GPa and ν = 0.3, respectively. The mesh of finite elements consists of 14,400 square elements, 240 × 60, regular mesh, 4-node elements, an element edge length 1 mm. 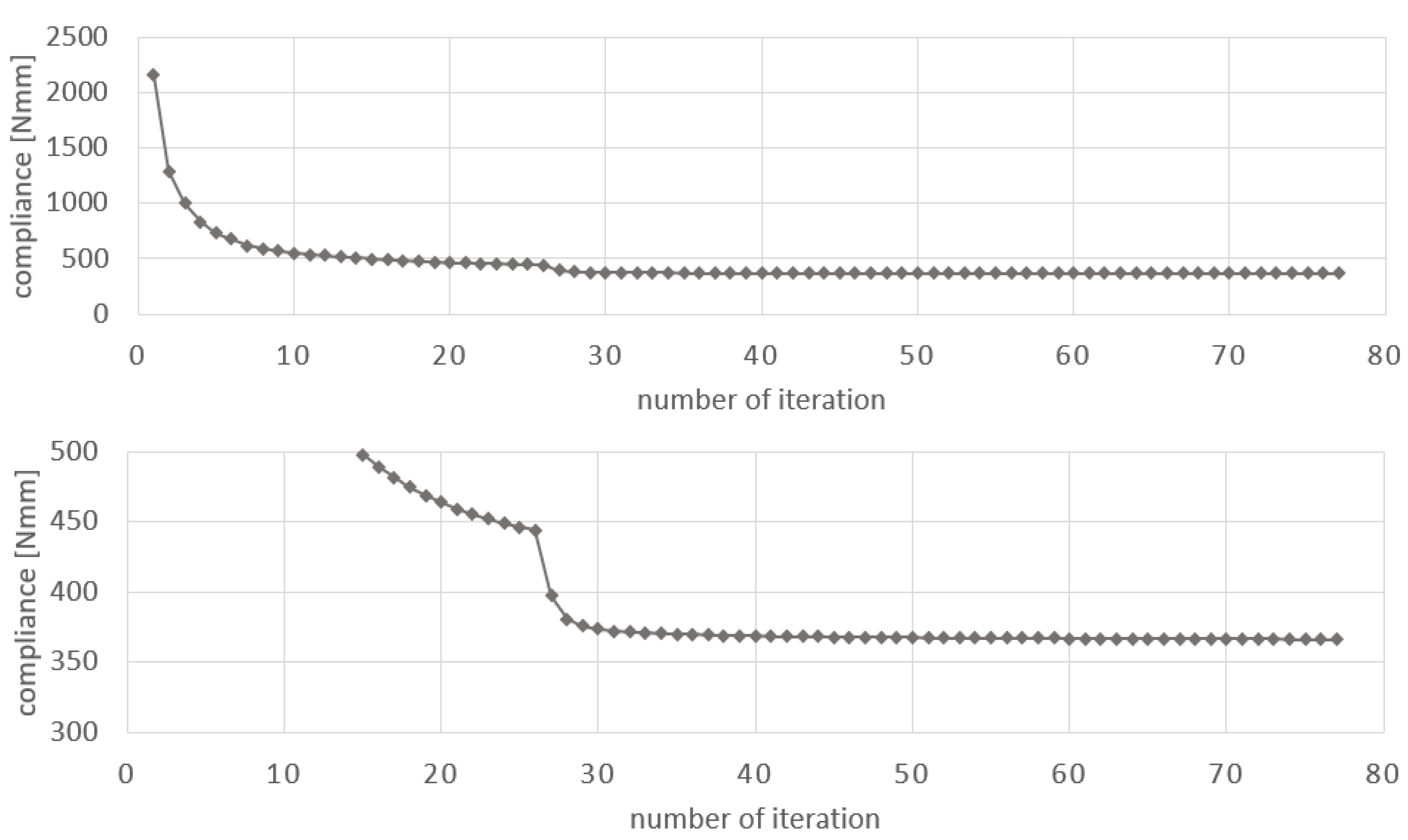The calculations were performed for the volume fraction 0.5, and the resulting topology is presented in Figure 9, while the iteration history is presented in Figure 10. For the generated topology of the second test structure, the value of the compliance equals 365.69 Nmm, and for original, former FCA [44], the value of the compliance equals 371.97 Nmm.

To sum up the investigation, the snail-like structure has been selected (see Figure 11) as the third test example.

The values of parameters P and a equal P = 100 N and a = 10 mm, while the Young modulus and Poisson ratio equal E = 10 GPa and ν = 0.3, respectively. The assumed volume fraction for this example is 0.5. The finite element mesh consists of 19,200 square elements (240 × 80, regular mesh, 4-node elements, element edge length 1 mm).

The final topology and the iteration history illustrating the fast convergence to the optimal solution are presented in Figure 12 and Figure 13, respectively.

The compliance value for the final topology of the third test structure equals 12.659 Nmm, and for original, former FCA [44], the value is 12.662 Nmm. This result has been obtained for β = 0.1.

5. Generation of 3D Topologies with TABASCO

As the first example of the design of a spatial structure using the proposed method, the tower under four concentrated loads shown in Figure 14 and Figure 15 has been selected.

The structure is discretized using 31,000 8-node elements. The quarter of a structure is considered according to symmetry. For this example, the data are selected as E = 200 GPa and ν = 0.3. Four concentrated loads values of 1000 N each are applied. The assumed volume fraction equals 0.1. The calculation was performed for β = 0.1. The final layout of the structure with the resulting compliance equal to 2.46 Nmm is illustrated in Figure 16, while the overview of the topology generation process is presented in Figure 17. The compliance history is presented in Figure 18. To make a comparison with the method reported in the literature, the optimality criteria method was employed, and the final compliance obtained in this way equals 2.76 Nmm.

One can notice a sudden decrease in the objective function values after 25 and 50 iterations; this is related to the implemented adaptive technique mentioned in Section 3 and Section 4. Due to the update rule flexibility, the interval [N₁; N₂] was reduced. The unified strategy of adjustment for implementation is as follows: if the iteration number is lower then 25, then N₁ = 0.02 N and N₂ = 0.98 N; for the second phase (iteration number greater then 25), N₁ = 0.6 N and N₂ = 0.98 N; and for the third phase (iteration number greater then 50), N₁ = 0.8 N and N₂ = 0.98 N, where N is a number of elements (cells). This extension for the third phase is applied according to the bigger number of iterations needed for 3D examples (compared to 2D examples).

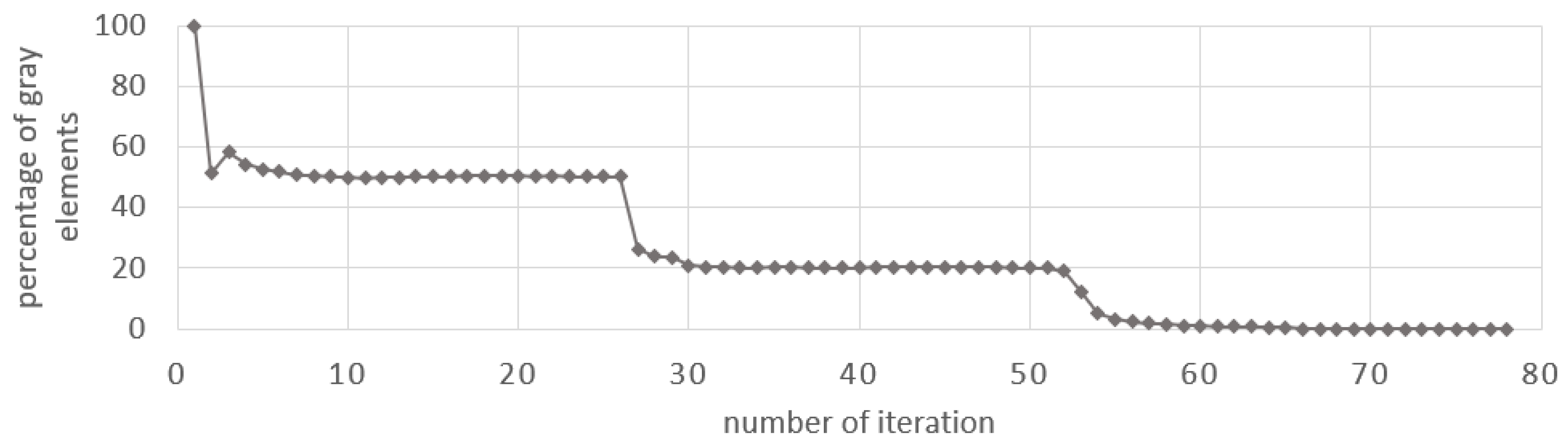
The gray elements are absent in the solution obtained with the proposed method, which is illustrated in Figure 19 by the change in the percentage of gray elements at each iteration step.

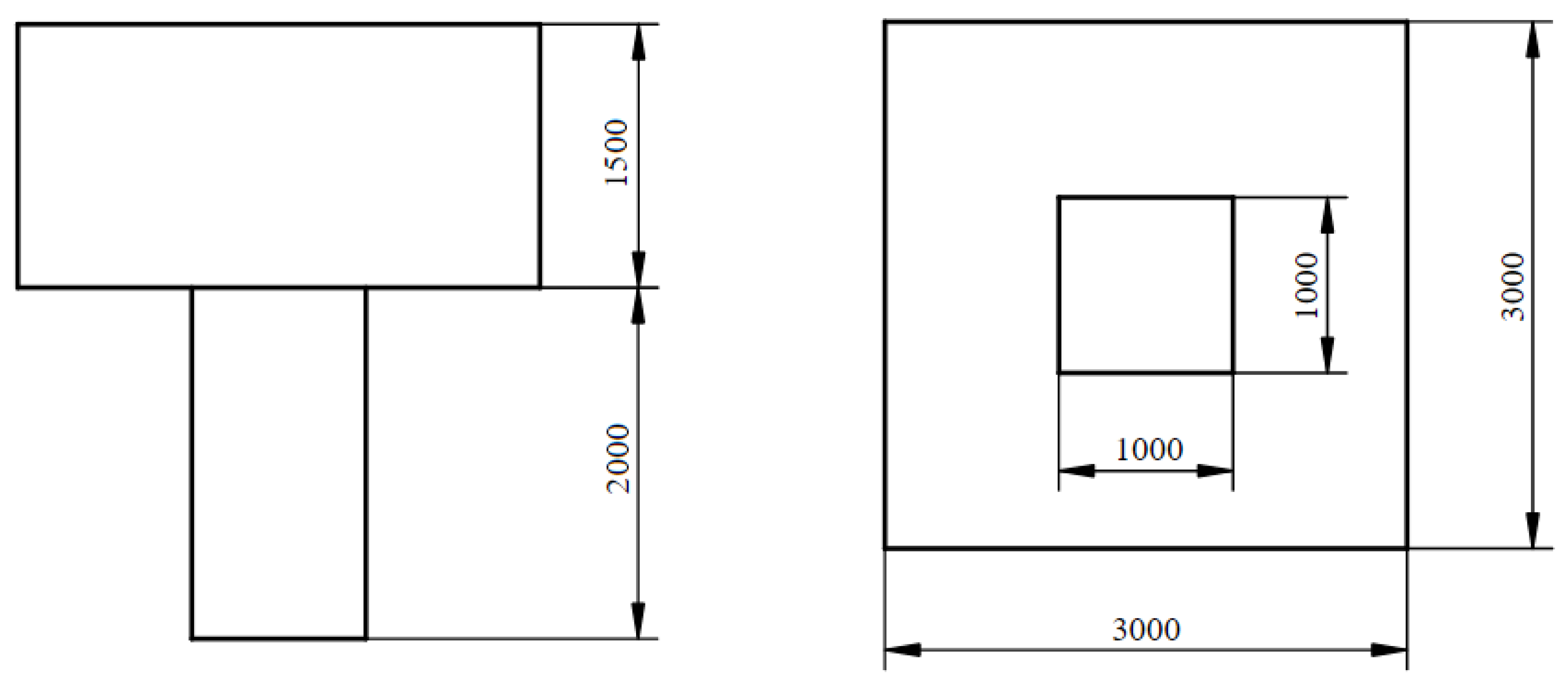
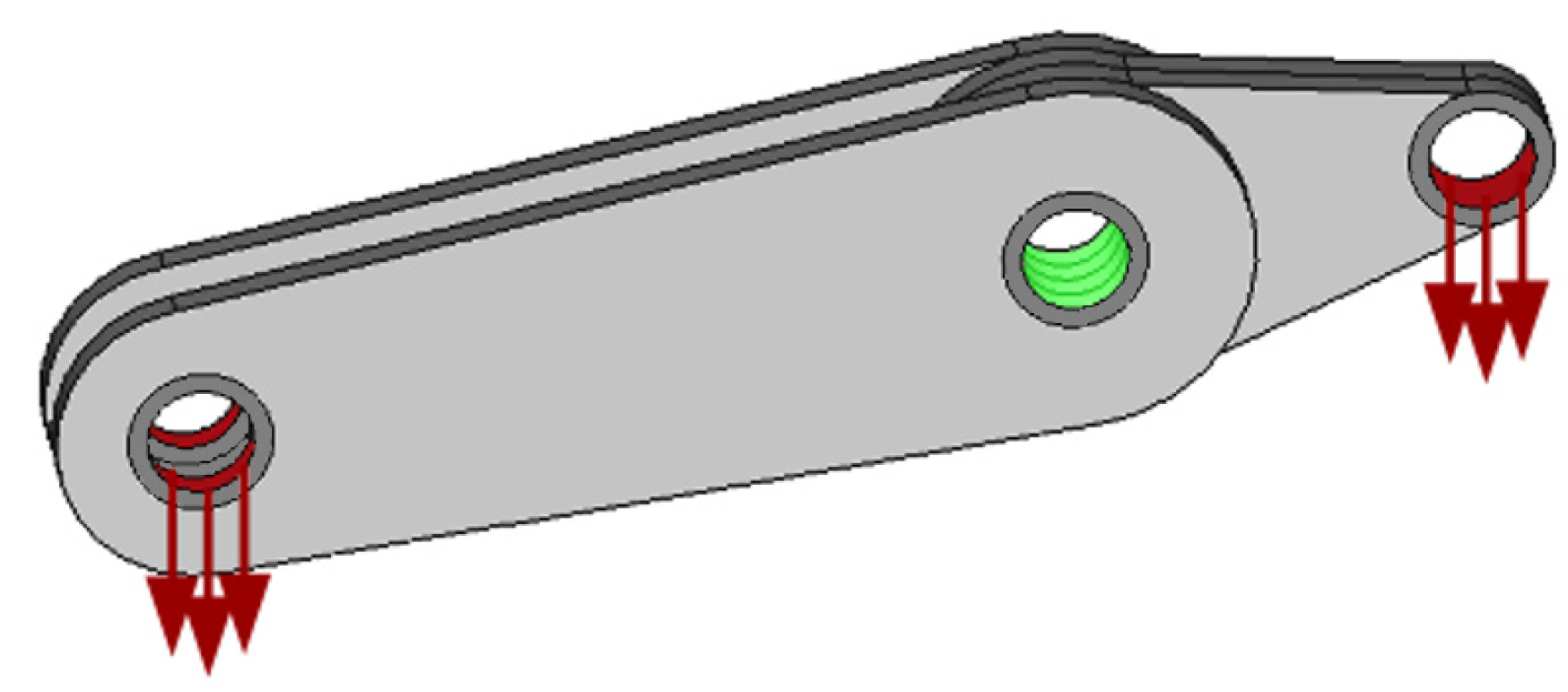
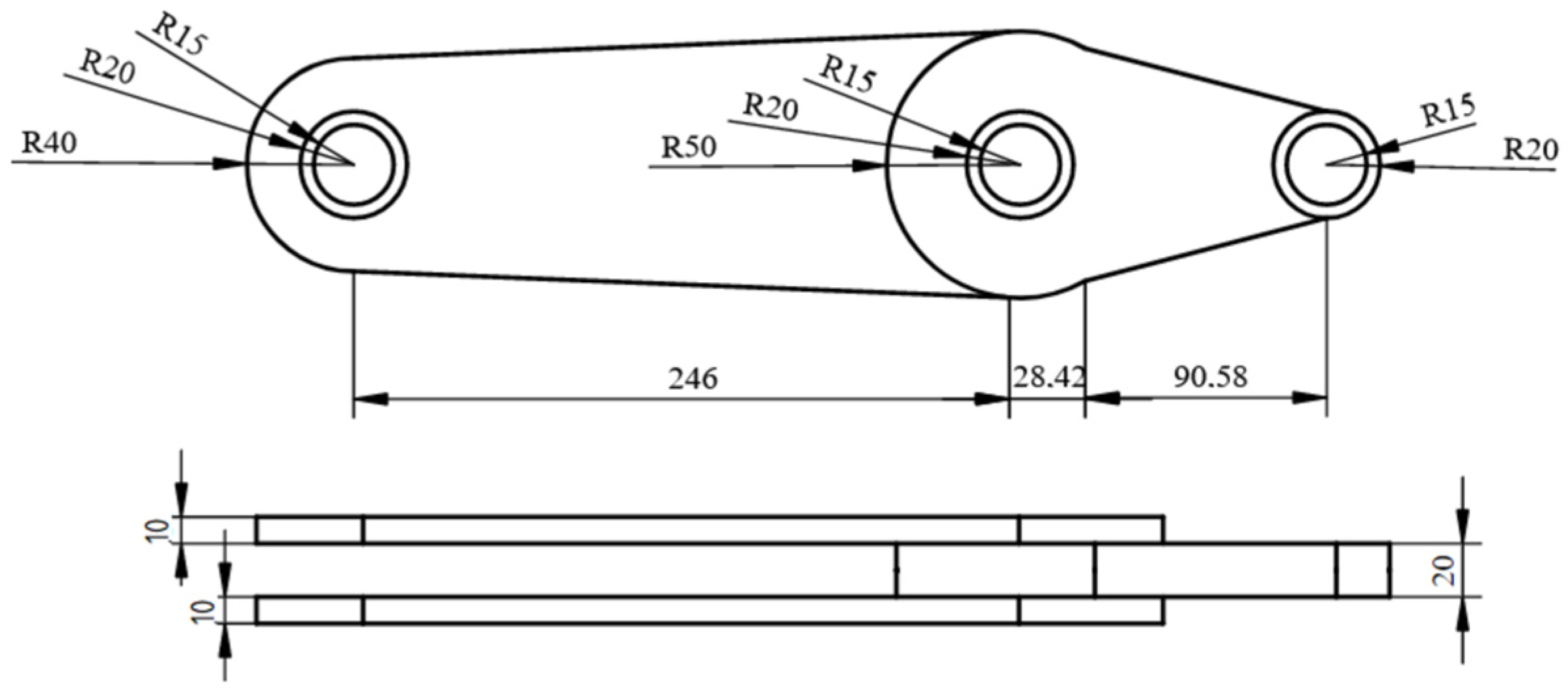
As the second example, the spatial rocker arm under bending loads shown in Figure 20 and Figure 21 has been selected.

The structure is discretized using 164,964 8-node elements. Within the structure, the non-optimized volumes are defined and marked in Figure 20 as the dark gray regions. The design domain is marked as the light gray region. The vertical load of value of 4060 N is distributed at selected nodes across the bottom edge of left cylinders (see Figure 20) and 8120 N across the bottom edge of right cylinder. The inner wall of the middle cylinder is fixed (see Figure 20, green color). The values of material properties are selected as E = 210 GPa and ν = 0.3. The calculations were performed for β = 8. The resulting topology is given in Figure 22. A final compliance for the volume fraction 0.2 equals 5212 Nmm, and the compliance history is presented in Figure 23. To attain a comparison with a method reported in the literature, the optimality criteria method was employed, and the final compliance obtained this way equals 5756 Nmm.

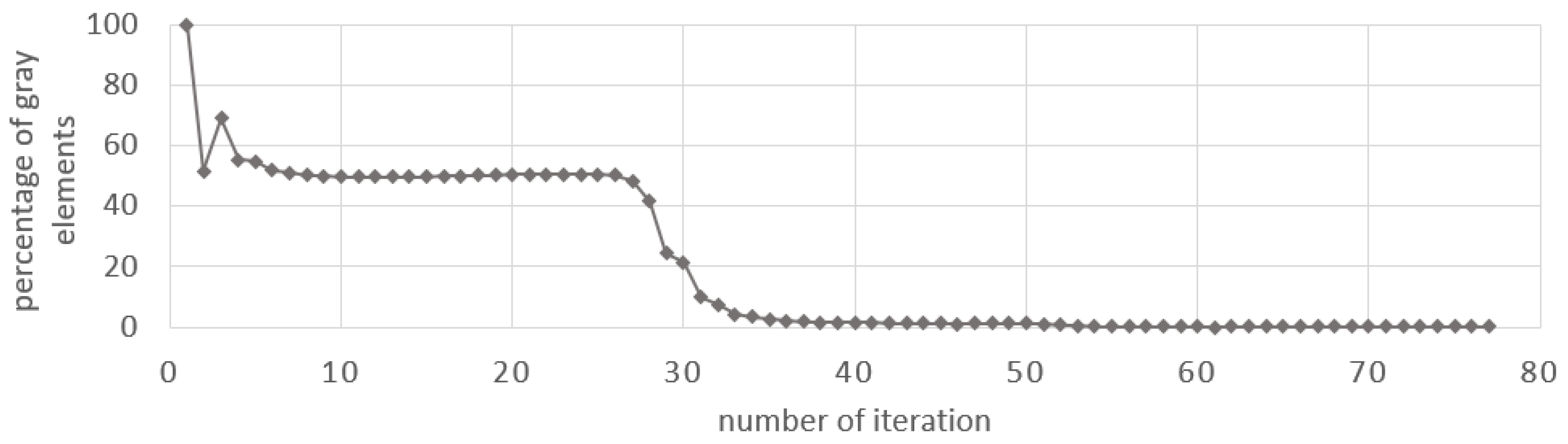
The adaptive technique mentioned in Section 3 and Section 4 was adapted. The gray elements are absent in the solution obtained with the proposed method, which is illustrated in Figure 24 by the change in the percentage of gray elements at each iteration step.

6. Concluding Remarks

The topology algorithm that benefits from the adaptation of sorted compliances optimization (TABASCO) has been developed. It is built as a Cellular Automaton with original update rules. Building the update rules, the function mapping local compliances distribution has been defined based on their sorted values on the global level, whereas on the local level, for each cell, the compliances have been additionally sorted within the cell neighborhood. The derived algorithm has successfully coped with the generation of both 2D and 3D topologies. In the latter case, a step has been made towards engineering applications by linking TABASCO with ANSYS software. The implementation of local sorting improved algorithm performance as compared with former approaches, providing results with better objective function values. Moreover, the algorithm is versatile and easy to implement. It can also be underlined that it generates distinct solid–void-resulting topologies without intermediate gray elements. This is thanks to the implementation of the CA approach with local information exchanging among cells forming a neighborhood. This approach practically eliminates the necessity of filtering techniques’ implementation. The CA approach also offers the possibility of adaptation to problems with irregular meshes (see, e.g., [48]). To conclude, the above advantages hopefully place TABASCO among other topology generators which are worthy of the attention of designers in the field of structural optimization.