Performance Evaluation of a Long-Span Cable-Stayed Bridge Using Non-Destructive Field Loading Tests
Abstract
:1. Introduction
2. Non-Destructive Field Loading Test for Pingnan Xiangsizhou Bridge
2.1. Objective of Non-Destructive Field Loading Tests
- (1)
- Defining the real load of the bridge under static load conditions;
- (2)
- Verifying the rationality of the design, and providing reference for similar bridge design;
- (3)
- Verifying the validity of the finite element model, which provides the basis for the model’s improvement and optimization;
- (4)
- Providing data for bridge monitoring and maintenance.
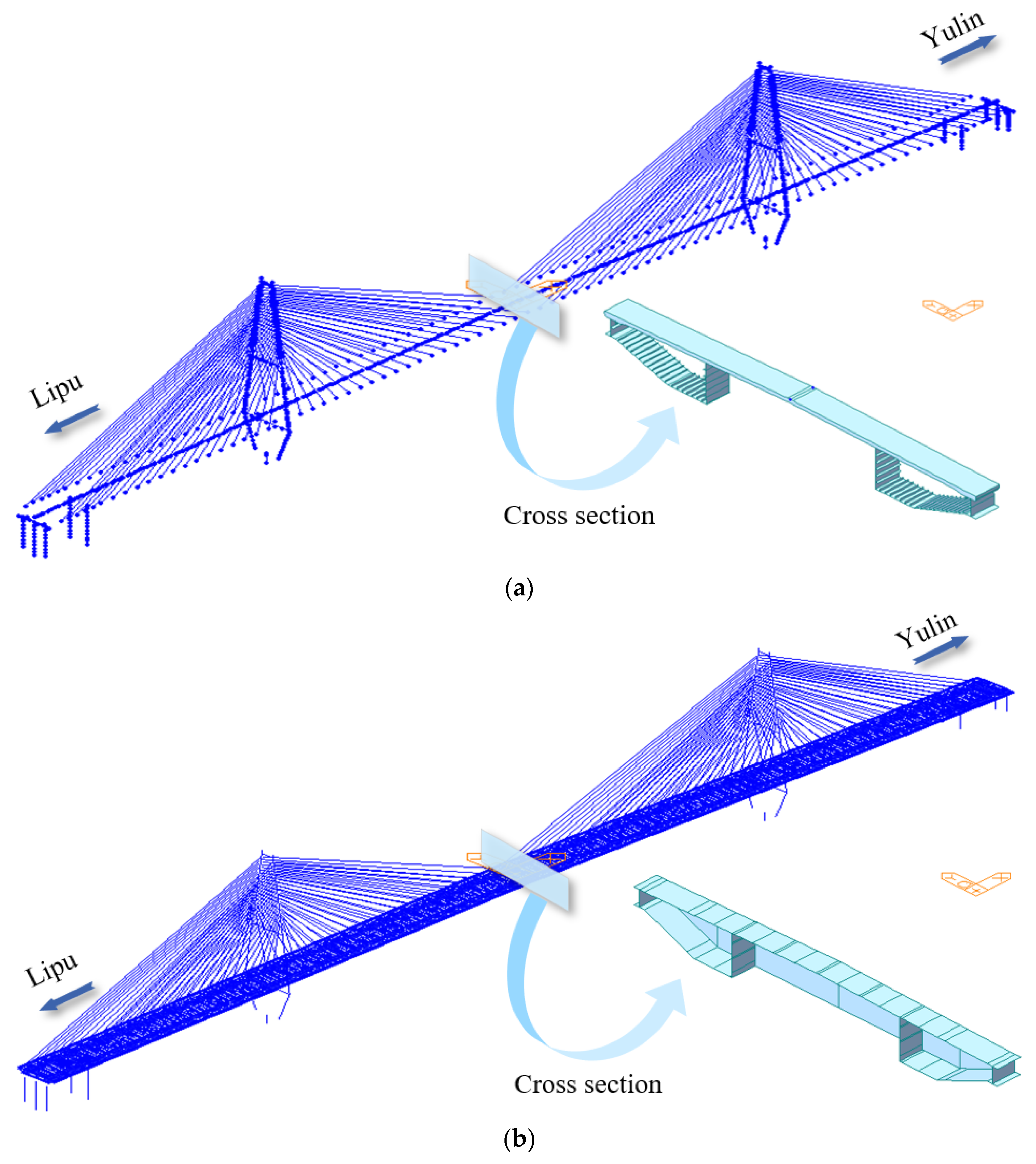
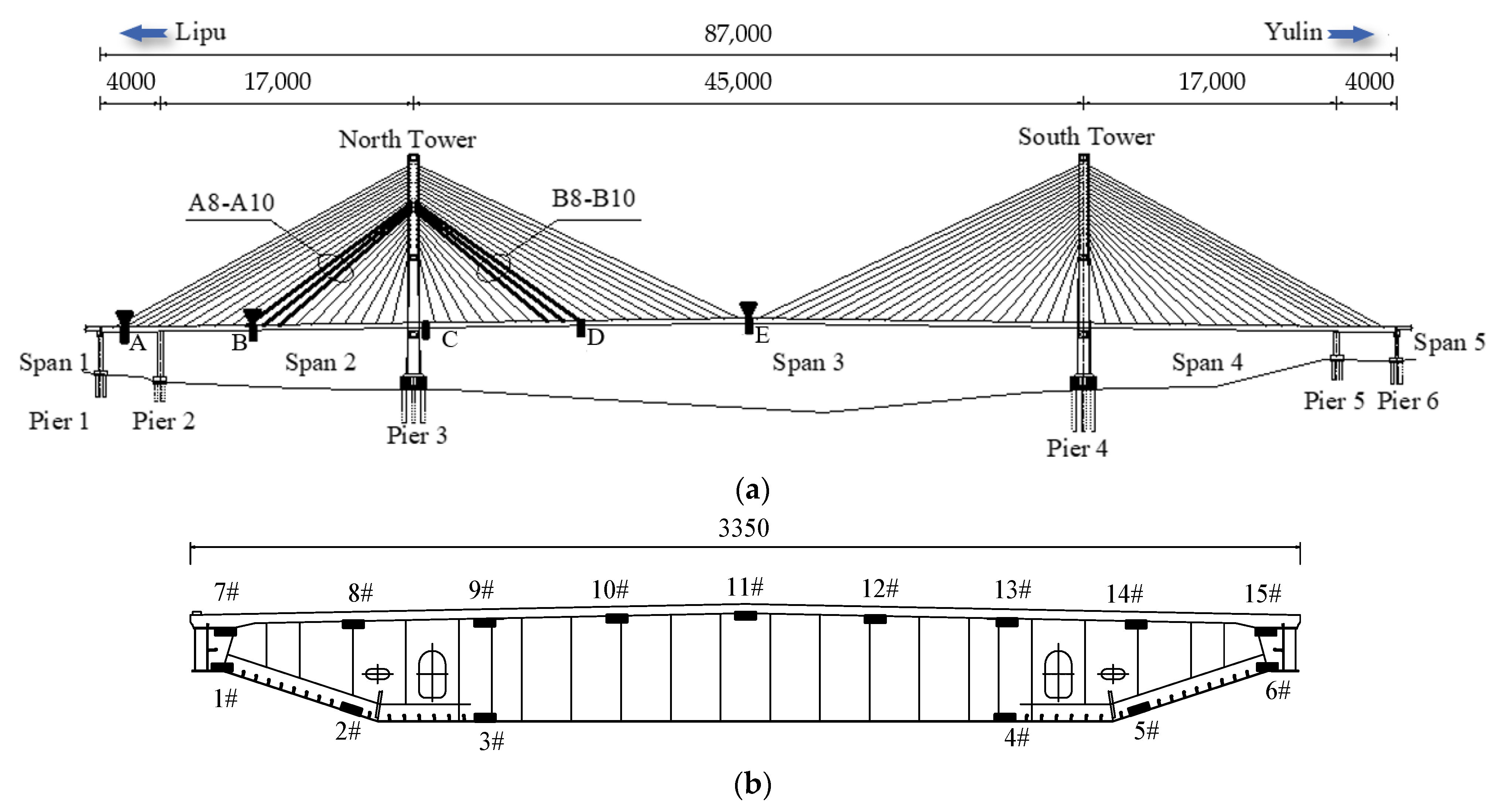
2.2. Structural Features of Pingnan Xiangsizhou Bridge
- The stay cables of the bridge are fan-shaped, with two cable planes in space; 20 pairs of cables are arranged on both sides of the main tower, with a total of 80 pairs of cables on the whole bridge. The stay cables are anchored by steel anchor beams on the towers, and by anchor plates on the beams. All stay cables are tensioned on the tower;
- The bridge tower is diamond shaped. An upper beam is set on the top of the tower connecting the two tower columns. In order to strengthen the lateral stability of the cable tower, a middle beam is set. The elevation of the top of the bearing platform is 21.20 m, the elevation of the tower base is 23.20 m, and the elevation of the top of the tower is 170.50 m. The total height of the cable tower above the tower base is 147.30 m. The heights of the lower, middle, and upper tower columns are 26.186 m, 51.375 m, and 69.739 m, respectively;
- The bridge deck is paved with asphalt concrete with a thickness of 10 cm. Column-type crash barriers are set on both sides of the carriageway. Sidewalks and maintenance railings are set on both sides of the bridge deck.
2.3. Non-Destructive Field Loading Test for Pingnan Xiangsizhou Bridge
2.3.1. Non-Destructive Field Loading Test Instrumentations
2.3.2. Cable Force Test and Principle in Non-Destructive Field Loading Test
2.4. Structural Theoretical Calculation for Pingnan Xiangsizhou Bridge
2.4.1. Geometric and Physical Parameters of Pingnan Xiangsizhou Bridge
2.4.2. Establishment of a Finite Element Model for Pingnan Xiangsizhou Bridge
- Concrete and steel are ideal elastic materials, and the elastic moduli of the concrete and steel of the new bridge are constant, being essentially consistent with the design values;
- The section deformation of the beam element conforms to the plane section assumption;
- Deformation coordination between the bridge’s concrete deck and the main beam’s steel plate, and there is no relative slip between the deck and the main beam.
2.5. Field Loading Test Conditions and Loading Arrangement
3. Experimental Results and Analysis
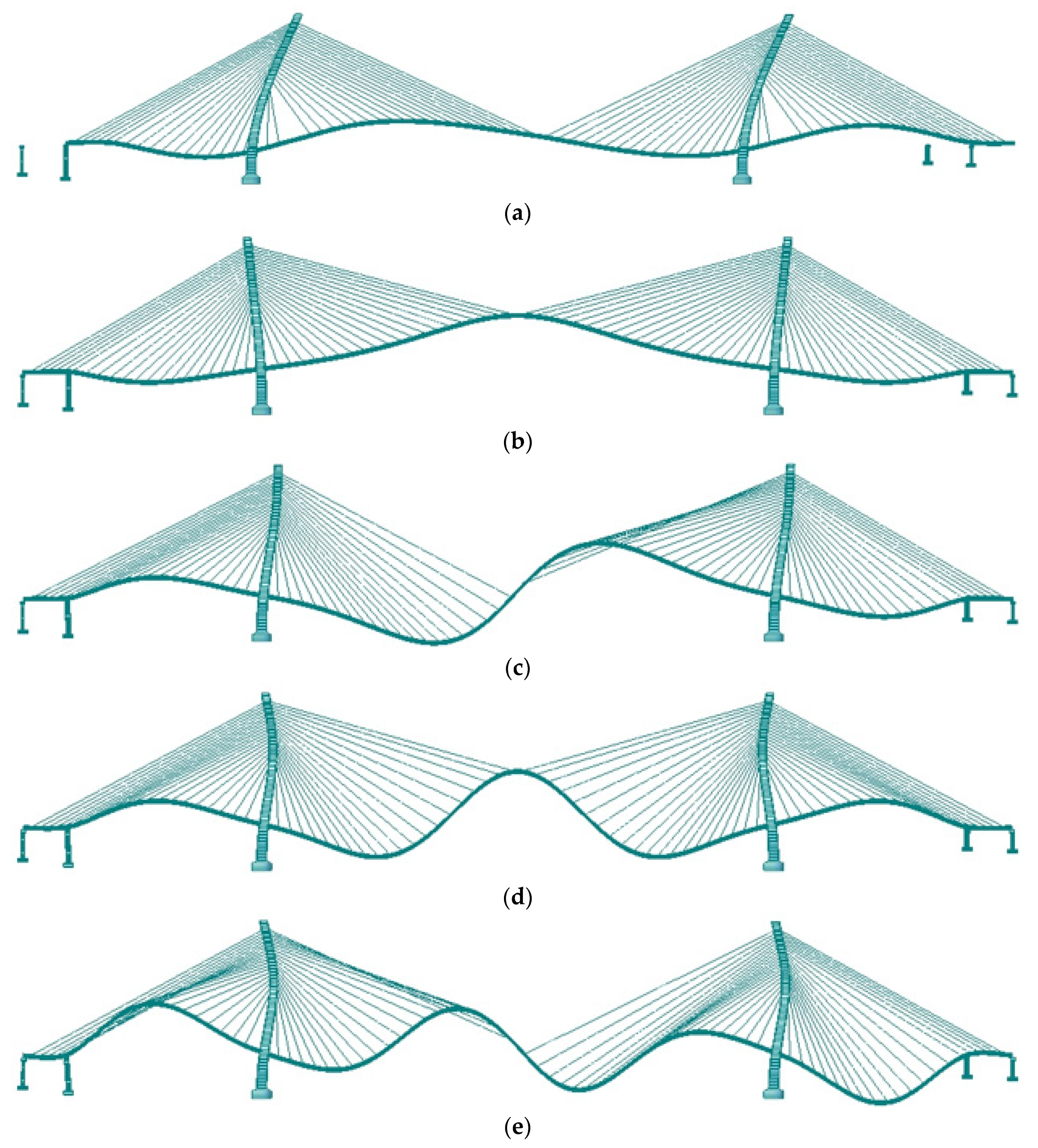
3.1. Vibration Mode and Frequency Analysis for the Field Loading Test of Pingnan Xiangsizhou Bridge
3.2. Displacement Analysis for the Field Loading Test of Pingnan Xiangsizhou Bridge
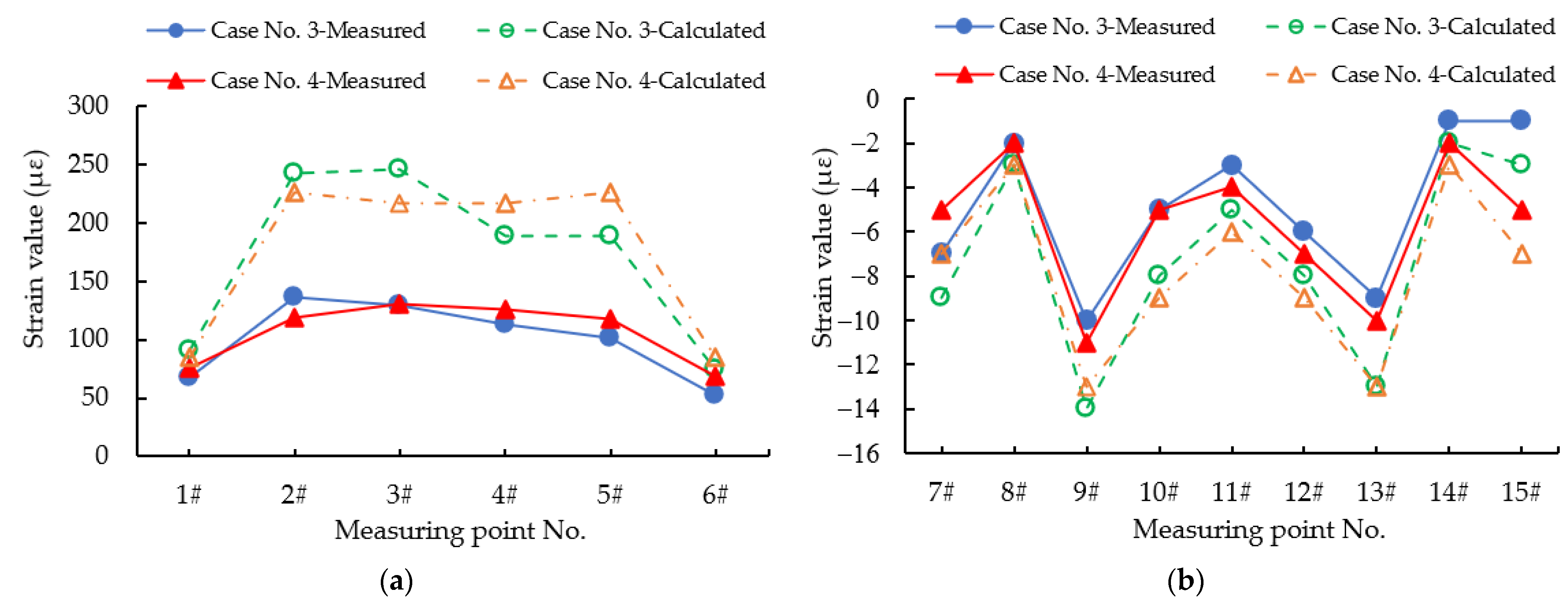
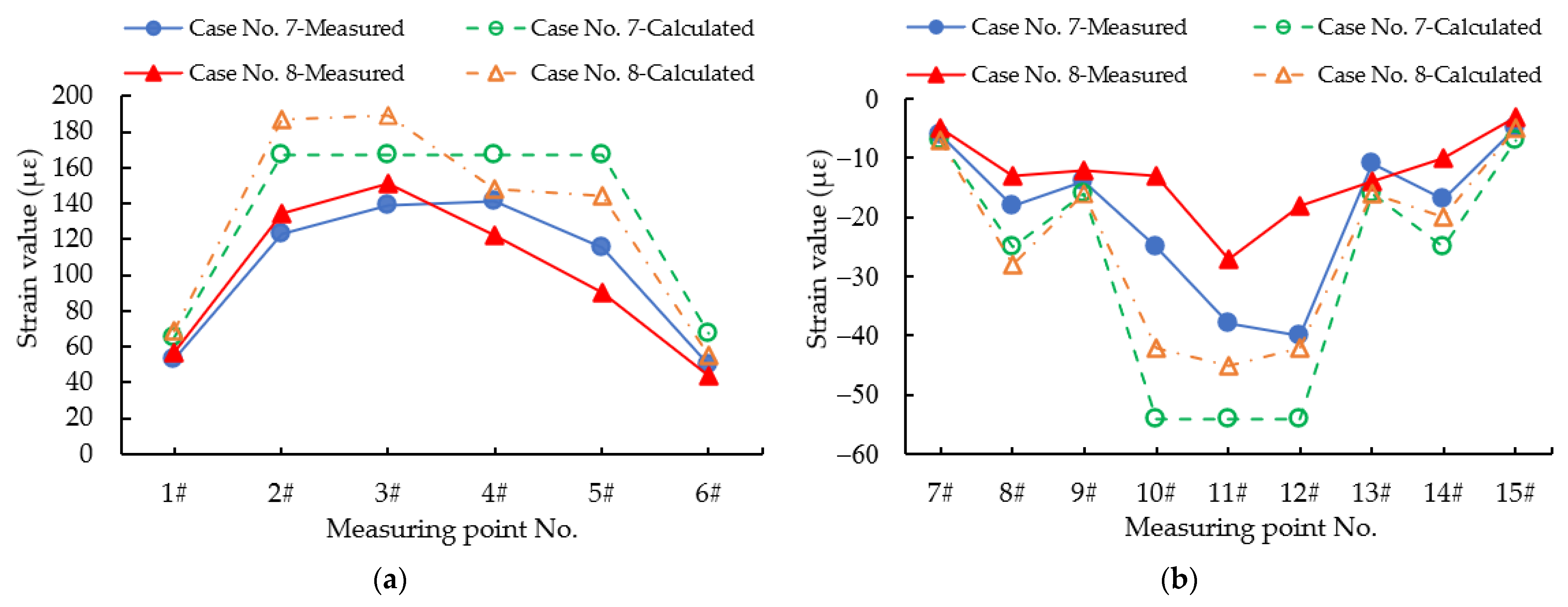
3.3. Strain Analysis for the Field Loading Test of Pingnan Xiangsizhou Bridge
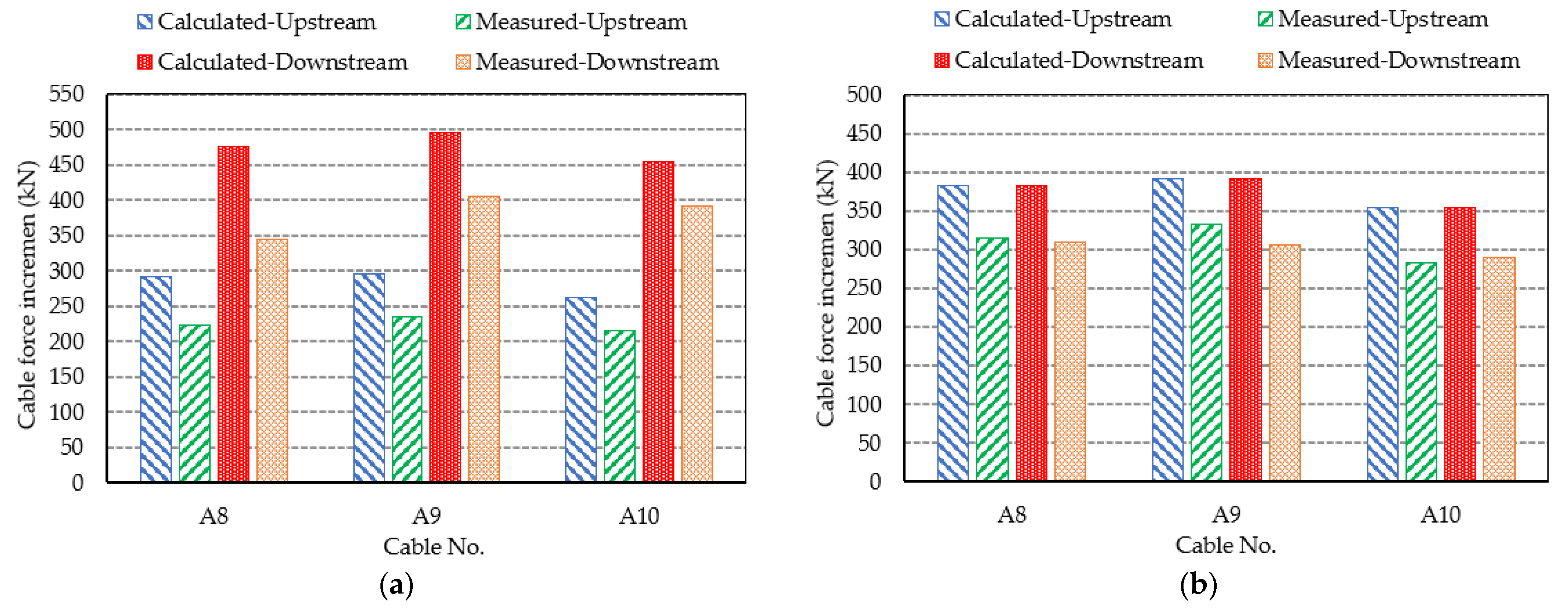
3.4. Cable Tension Increment Test Analysis for the Field Loading Test of Pingnan Xiangsizhou Bridge
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, G.; Wang, Z.; Zhu, S.; Hao, J.; Wang, J. Experimental study of mitigation of wind-induced vibration in asymmetric cable-stayed bridge using sharp wind fairings. Appl. Sci. 2021, 12, 242. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, X.; Li, J.; Xin, H.; Sun, Q.; Wang, J. Investigation of vortex-induced vibration of a cable-stayed bridge without backstays based on wind tunnel tests. Eng. Struct. 2022, 250, 113436. [Google Scholar] [CrossRef]
- Herrera, D.; Varela, G.; Tolentino, D. Reliability assessment of RC bridges subjected to seismic loadings. Appl. Sci. 2021, 12, 206. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Tan, G.; He, X. System reliability evaluation of a bridge structure based on multivariate copulas and the AHP–EW method that considers multiple failure criteria. Appl. Sci. 2020, 10, 1399. [Google Scholar] [CrossRef] [Green Version]
- Dong, F.; Shi, F.; Wang, L.; Wei, Y.; Zheng, K. Probabilistic assessment approach of the aerostatic instability of long-span symmetry cable-stayed bridges. Symmetry 2021, 13, 2413. [Google Scholar] [CrossRef]
- Liu, F.; Xu, Q.; Liu, Y. Condition diagnosis of long-span bridge pile foundations based on the spatial correlation of high-density strain measurement points. Sustainability 2021, 13, 12498. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Strauss, A.; Kim, S. Bridge reliability assessment based on monitoring. J. Bridge Eng. 2008, 13, 258–270. [Google Scholar] [CrossRef]
- Sharry, T.; Guan, H.; Nguyen, A.; Oh, E.; Hoang, N. Latest advances in finite element modelling and model updating of cable-stayed bridges. Infrastructures 2022, 7, 8. [Google Scholar] [CrossRef]
- Rizzo, P.; Enshaeian, A. Challenges in bridge health monitoring: A review. Sensors 2021, 21, 4336. [Google Scholar] [CrossRef]
- Wedel, F.; Marx, S. Application of machine learning methods on real bridge monitoring data. Eng. Struct. 2022, 250, 113365. [Google Scholar] [CrossRef]
- Yue, Z.; Ding, Y.; Zhao, H.; Wang, Z. Case Study of deep learning model of temperature-induced deflection of a cable-stayed bridge driven by data knowledge. Symmetry 2021, 13, 2293. [Google Scholar] [CrossRef]
- Okazaki, Y.; Okazaki, S.; Asamoto, S.; Chun, P. Applicability of machine learning to a crack model in concrete bridges. Comput. Civ. Infrastruct. Eng. 2020, 35, 775–792. [Google Scholar] [CrossRef]
- Ni, Y.-Q.; Xia, H.W.; Wong, K.Y.; Ko, J.M. In-service condition assessment of bridge deck using long-term monitoring data of strain response. J. Bridge Eng. 2012, 17, 876–885. [Google Scholar] [CrossRef]
- Xu, Y.-L. Making good use of structural health monitoring systems of long-span cable-supported bridges. J. Civ. Struct. Health Monit. 2018, 8, 477–497. [Google Scholar] [CrossRef]
- Carrión, F.J.; Quintana, J.A.; Crespo, S.E. SHM of a stayed bridge during a structural failure, case study: The Rio Papaloapan bridge. J. Civ. Struct. Health Monit. 2017, 7, 139–151. [Google Scholar] [CrossRef]
- Catbas, F.N.; Susoy, M.; Frangopol, D.M. Structural health monitoring and reliability estimation: Long span truss bridge application with environmental monitoring data. Eng. Struct. 2008, 30, 2347–2359. [Google Scholar] [CrossRef]
- Fan, X.P.; Liu, Y.F. New dynamic prediction approach for the reliability indexes of bridge members based on SHM data. J. Bridge Eng. 2018, 23, 06018004. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Zhao, D.-Y.; Zhang, D.-Y.; Sun, H.-B. Condition evaluation of suspension bridges for maintenance, repair and rehabilitation: A comprehensive framework. Struct. Infrastruct. Eng. 2019, 15, 555–567. [Google Scholar] [CrossRef]
- Wan, H.-P.; Ni, Y.-Q. Bayesian modeling approach for forecast of structural stress response using structural health monitoring data. J. Struct. Eng. 2018, 144, 04018130. [Google Scholar] [CrossRef]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.; Hashim, K.; Yeboah, D. Recent advancements in non-destructive testing techniques for structural health monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Ter Berg, C.J.A.; Leontaris, G.; Boomen, M.V.D.; Spaan, M.T.J.; Wolfert, A.R.M. Expert judgement based maintenance decision support method for structures with a long service-life. Struct. Infrastruct. Eng. 2019, 15, 492–503. [Google Scholar] [CrossRef] [Green Version]
- Daneshvar, M.H.; Gharighoran, A.; Zareei, S.A.; Karamodin, A. Early damage detection under massive data via innovative hybrid methods: Application to a large-scale cable-stayed bridge. Struct. Infrastruct. Eng. 2021, 17, 902–920. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Tadla, J.; Kurşun, A.; Erdiş, A. Static and dynamic field load testing of the long span nissibi cable-stayed bridge. Soil Dyn. Earthq. Eng. 2017, 94, 136–157. [Google Scholar] [CrossRef]
- Fang, I.-K.; Chen, C.-R.; Chang, I.-S. Field static load test on kao-ping-hsi cable-stayed bridge. J. Bridge Eng. 2004, 9, 531–540. [Google Scholar] [CrossRef]
- Romanova, V.; Shakhidzhanov, V.; Zinovieva, O.; Nekhorosheva, O.; Balokhonov, R. A Correlation between deformation-induced surface roughness and in-plane plastic strain in an aluminum alloy at the mesoscale. Procedia Struct. Integr. 2022, 35, 66–73. [Google Scholar] [CrossRef]
- Vásárhelyi, L.; Kónya, Z.; Kukovecz, Á.; Vajtai, R. Microcomputed tomography–based characterization of advanced materials: A review. Mater. Today Adv. 2020, 8, 100084. [Google Scholar] [CrossRef]
- Ren, W.-X.; Peng, X.-L.; Lin, Y.-Q. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge. Eng. Struct. 2005, 27, 535–548. [Google Scholar] [CrossRef]
- Ren, W.-X.; Peng, X.-L. Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration tests. Comput. Struct. 2005, 83, 536–550. [Google Scholar] [CrossRef]
- Armendariz, R.R.; Bowman, M.D. Improved load rating of an open-spandrel reinforced-concrete arch bridge. J. Perform. Constr. Facil. 2018, 32, 04018035. [Google Scholar] [CrossRef]
- Harris, D.K.; Civitillo, J.M.; Gheitasi, A. Performance and behavior of hybrid composite beam bridge in Virginia: Live load testing. J. Bridge Eng. 2016, 21, 04016022. [Google Scholar] [CrossRef]
- Ren, W.-X.; Lin, Y.-Q.; Peng, X.-L. Field load tests and numerical analysis of qingzhou cable-stayed bridge. J. Bridge Eng. 2007, 12, 261–270. [Google Scholar] [CrossRef]
- Ge, J.Y. Guide for Using Bridge Engineering Software Midas Civil; China Communications Press: Beijing, China, 2013. [Google Scholar]








| Case No. | Loading Test Arrangement | S(1 + μ) | SS | ηq |
|---|---|---|---|---|
| 1 | Symmetrical loading of the maximum positive moment (section A) of No. 1 span | 22,944.0 | 20,725.7 | 0.903 |
| 2 | Eccentric loading of the maximum negative moment (section A) of No. 1 span | −21,392.8 | −19,305.6 | 0.902 |
| 3 | Eccentric loading of the maximum positive moment (section B) of No. 2 span | 38,815.6 | 35,583.7 | 0.917 |
| 4 | Symmetrical loading of the maximum positive moment (section B) of No. 2 span | 38,782.7 | 35,533.5 | 0.916 |
| 5 | Symmetrical loading of the maximum negative bending moment (section C) of the main girder at No. 3 pier | −31,122.2 | −27,352.1 | 0.879 |
| 6 | Eccentric loading of the maximum negative bending moment (section C) of the main girder at No. 3 pier | −31,122.0 | −27,395.3 | 0.880 |
| 7 | Symmetrical loading at L/4 (section D) of No. 3 span | 28,259.2 | 29,494.4 | 1.044 |
| 8 | Eccentric loading at L/4 (section D) of No. 3 span | 28,260.9 | 29,324.4 | 1.038 |
| 9 | Symmetrical loading of the maximum positive moment (section E) of No. 3 span | 40,677.5 | 40,040.8 | 0.984 |
| 10 | Eccentric loading of the maximum negative moment (section E) of No. 3 span | 40,677.5 | 40,040.8 | 0.984 |
| Vehicle No. | Wheelbase 1 (m) | Wheelbase 2 (m) | Mass of Front Axle (kN) | Mass of Rear Axle (kN) | Total Weight of Vehicle (kN) |
|---|---|---|---|---|---|
| 1#~24# | 3.80 | 1.35 | 70 | 300 | 370 |
| Mode No. | Vibration Mode | Vibration Frequency (Hz) | ||
|---|---|---|---|---|
| Numerical | Experimental | Error (%) | ||
| 1 | 1st vertical bending | 0.303 | 0.313 | 3.30 |
| 2 | 1st transverse bending | 0.384 | 0.469 | 22.14 |
| 3 | 2nd vertical bending | 0.392 | 0.41 | 4.59 |
| 4 | 3rd vertical bending | 0.581 | 0.625 | 7.57 |
| 5 | 4th vertical bending | 0.683 | 0.85 | 24.45 |
| Case No. | Left | Right | ||||
|---|---|---|---|---|---|---|
| Measured (mm) | Calculated (mm) | Calibration Coefficient | Measured (mm) | Calculated (mm) | Calibration Coefficient | |
| 1 | 4.5 | 6.73 | 0.67 | 4.28 | 6.73 | 0.64 |
| 2 | 4.18 | 7.24 | 0.58 | 2.91 | 5.03 | 0.58 |
| 3 | 80.5 | 116.79 | 0.69 | 54.6 | 91.13 | 0.60 |
| 4 | 68.22 | 103.18 | 0.66 | 67.92 | 103.18 | 0.66 |
| 9 | 287.13 | 328.25 | 0.87 | 270.68 | 328.25 | 0.82 |
| 10 | 340.23 | 379.06 | 0.90 | 250.63 | 277.94 | 0.90 |
| Cable No. | Number per Bundle | Anchor Spacing (m) | Total Length (m) | Cable Elevation (°) | Cable Density (kg/m3) |
|---|---|---|---|---|---|
| A8 | 55 | 116.180 | 118.191 | 40.659 | 71.0 |
| A9 | 55 | 126.236 | 128.225 | 38.424 | 71.0 |
| A10 | 55 | 136.460 | 138.418 | 36.549 | 71.0 |
| B8 | 43 | 116.312 | 118.256 | 39.821 | 56.3 |
| B9 | 55 | 126.404 | 128.392 | 37.470 | 71.0 |
| B10 | 55 | 136.661 | 138.623 | 35.568 | 71.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, L.; Wang, H.; Ning, Y.; Huang, K.; Wang, W. Performance Evaluation of a Long-Span Cable-Stayed Bridge Using Non-Destructive Field Loading Tests. Appl. Sci. 2022, 12, 2367. https://doi.org/10.3390/app12052367
Wang X, Wang L, Wang H, Ning Y, Huang K, Wang W. Performance Evaluation of a Long-Span Cable-Stayed Bridge Using Non-Destructive Field Loading Tests. Applied Sciences. 2022; 12(5):2367. https://doi.org/10.3390/app12052367
Chicago/Turabian StyleWang, Xirui, Longlin Wang, Hua Wang, Yihao Ning, Kainan Huang, and Wensheng Wang. 2022. "Performance Evaluation of a Long-Span Cable-Stayed Bridge Using Non-Destructive Field Loading Tests" Applied Sciences 12, no. 5: 2367. https://doi.org/10.3390/app12052367
APA StyleWang, X., Wang, L., Wang, H., Ning, Y., Huang, K., & Wang, W. (2022). Performance Evaluation of a Long-Span Cable-Stayed Bridge Using Non-Destructive Field Loading Tests. Applied Sciences, 12(5), 2367. https://doi.org/10.3390/app12052367







