A Machine Learning Model for the Prediction of Concrete Penetration by the Ogive Nose Rigid Projectile
Abstract
:1. Introduction
1.1. Research Background
1.2. Research Motivation
1.3. Research Objectives
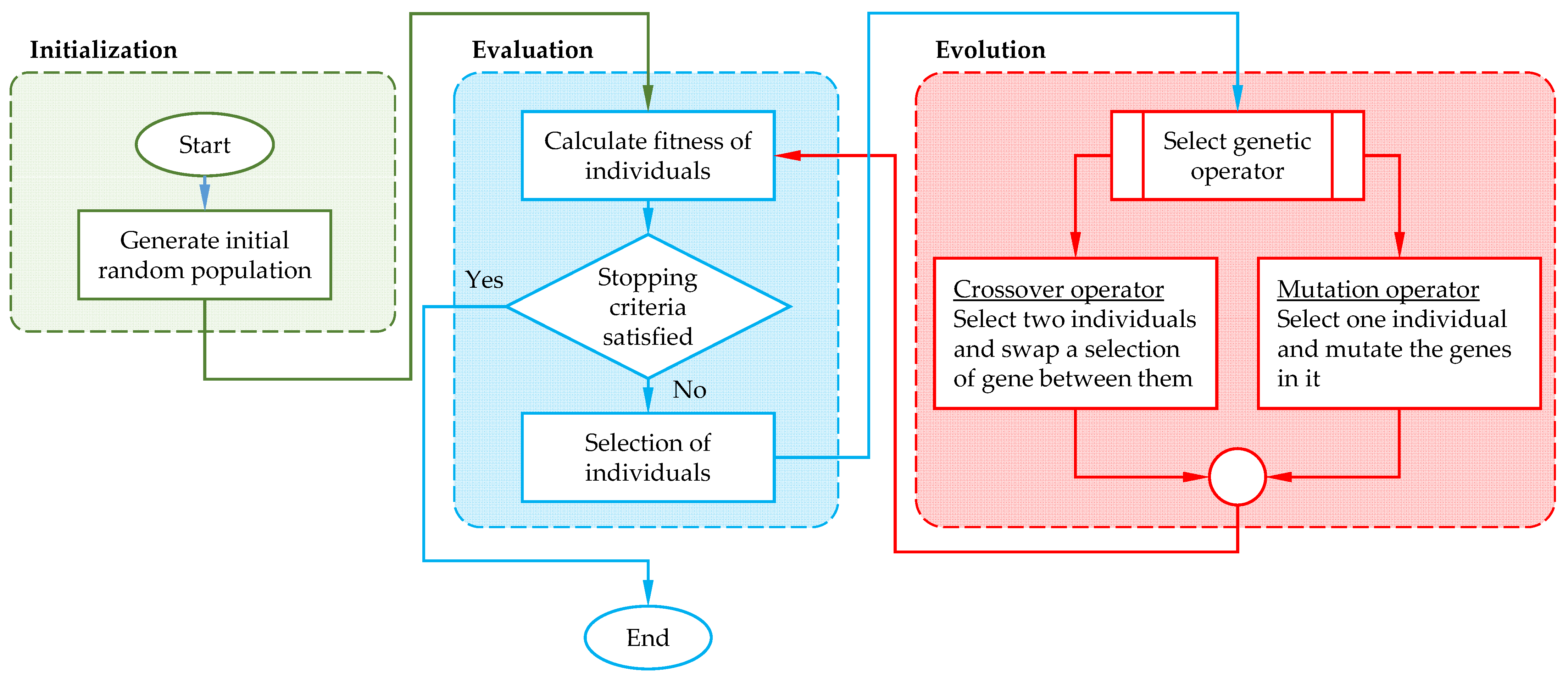
2. Machine Learning Symbolic Regression Genetic Programming Using Python
3. Data Analysis
4. Proposed Model Using Symbolic Regression in Python
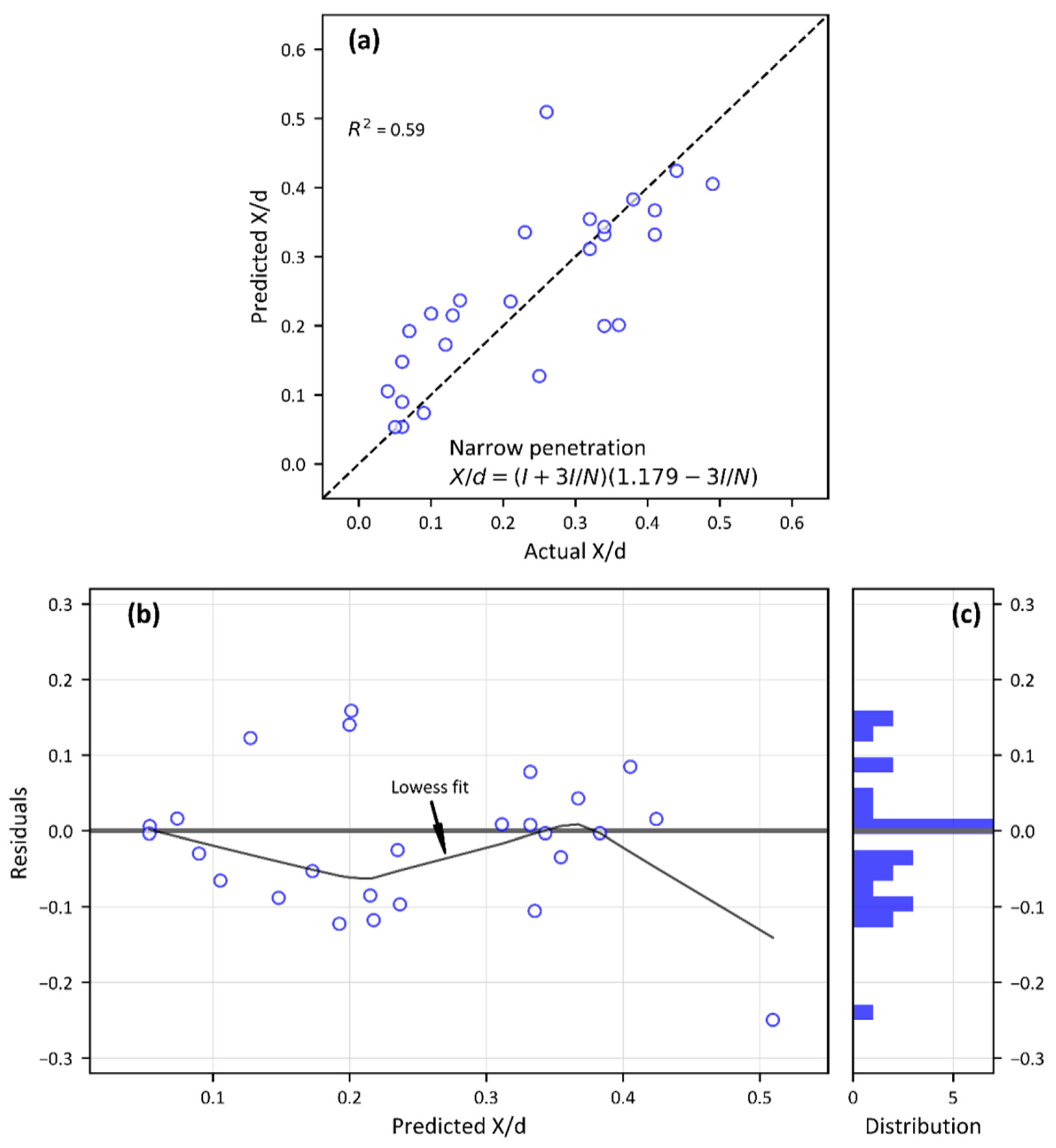
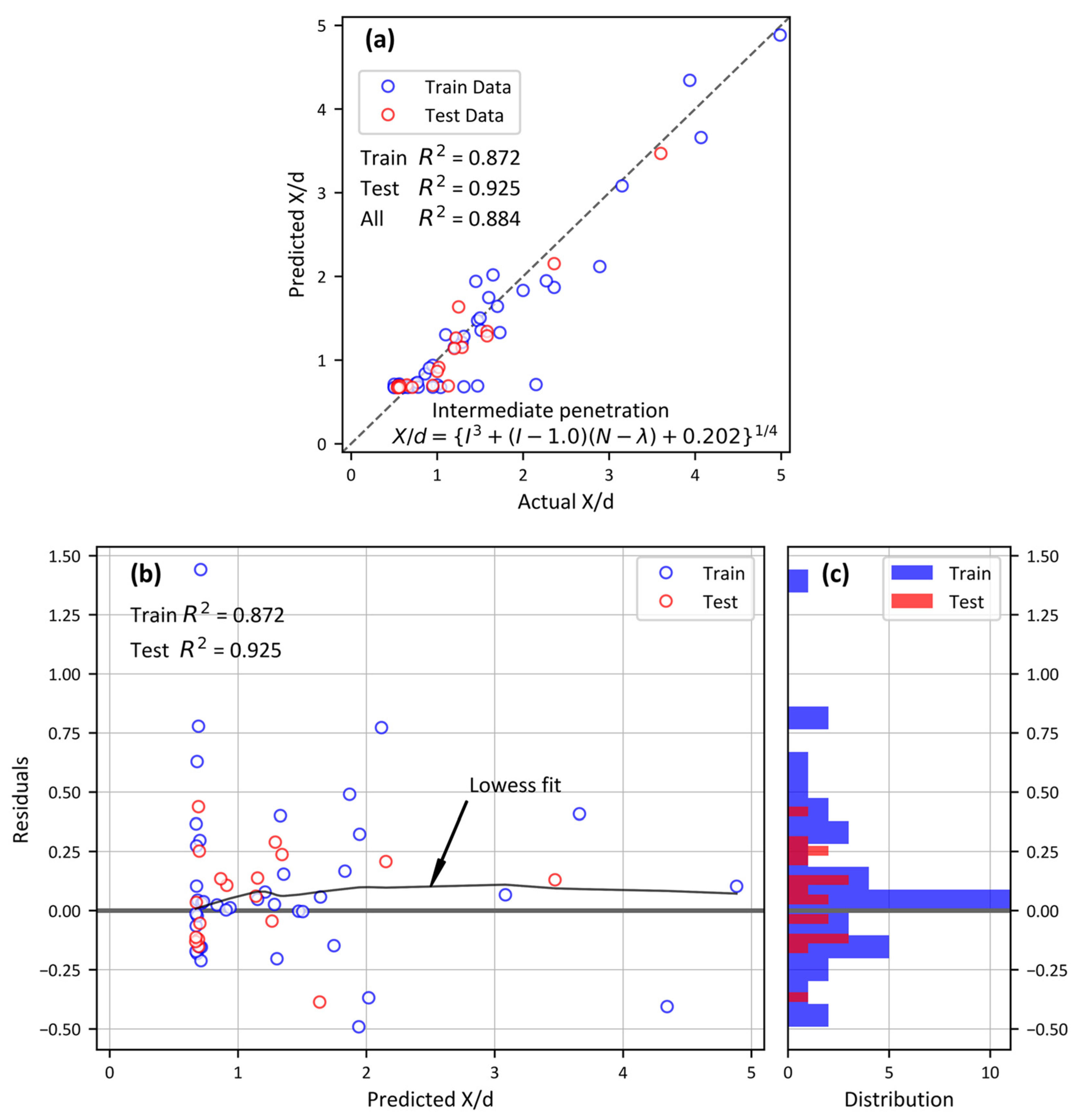
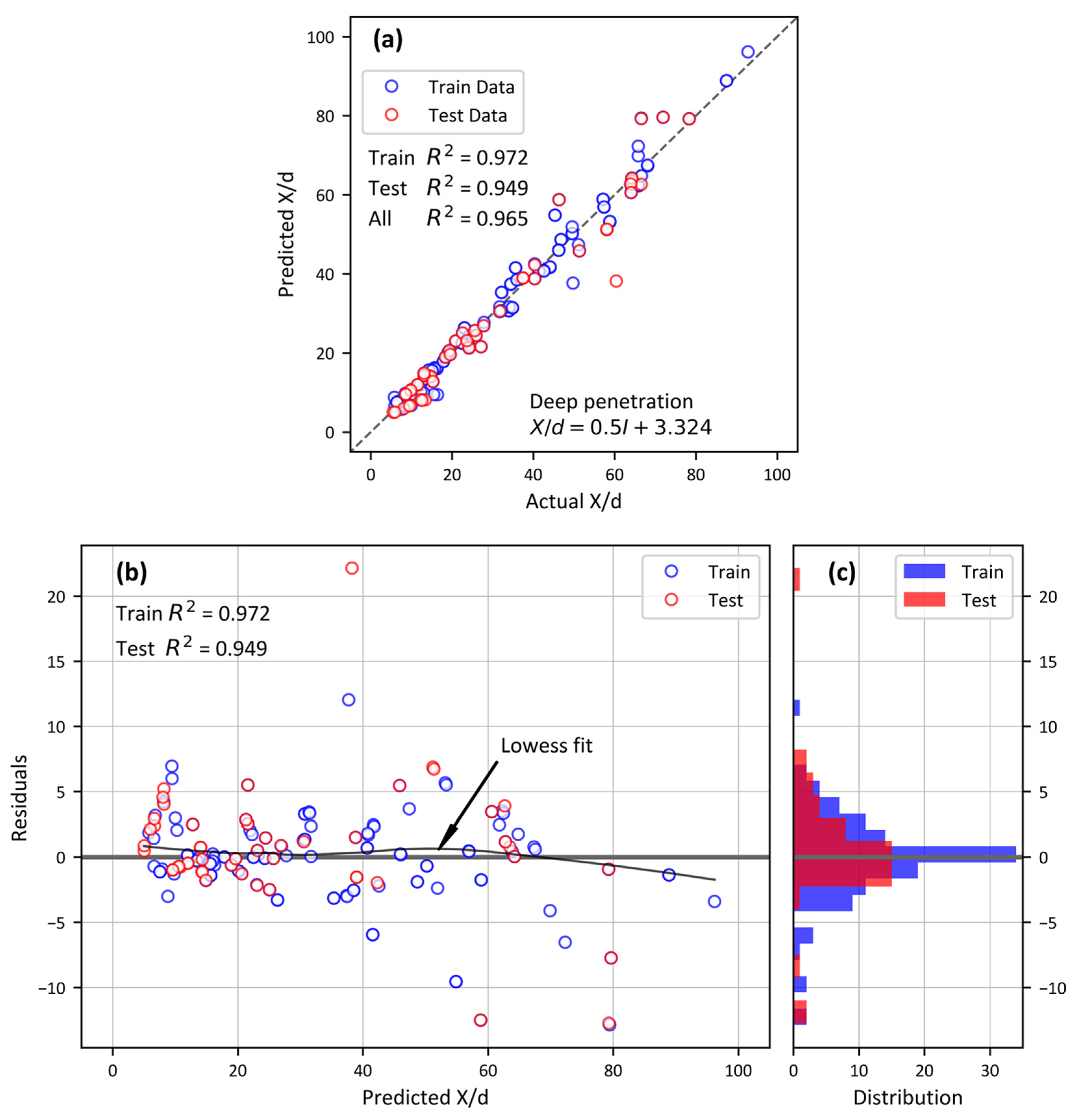
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| References | Equation in S.I. Unit | ||
|---|---|---|---|
| Petry model [1,3,5] | |||
| Ballistic Research Laboratory (BRL) Model [1,3] | |||
| Army Corp of Engineers (ACE model) [1,3,23] | |||
| National Defense Research Committee (NDRC) Model [1,3,4,24] | ≤ 2 | ||
| > 2 | |||
| G ≥ 1 | |||
| G < 1 | |||
| Ammann and Whitney model [1,3] | |||
| Whiffen model [1,3,25] | |||
| Kar Model [1,3,26,27] | G ≥ 1 | ||
| G < 1 | |||
| UKAEA model [1,3,28] | G ≤ 0.0726 | ||
| 0.0726 ≤ G ≤ 1.06 | |||
| G ≥ 1.06 | |||
| < 0.22 | |||
| ≤ 2.0 | |||
| ≥ 2.0 | |||
| Haldar and Hamieh model [1,3,6] | 0.3 ≤ Ia ≤ 4.0 | ||
| 4.0 ≤ Ia ≤ 21 | |||
| 21 ≤ Ia ≤ 455 | |||
| Adeli and Amin Model [1,3] | for 0.3 ≤ Ia ≤ 4 | ||
| 4 ≤ Ia ≤ 21 | |||
| Hughes Model [1,3,7] | Ih < 3500 | ||
| Healy and Weissman Model [1,3] | G ≥ 1 | ||
| G < 1 | |||
| CREIPI Model [1,3,29] | |||
| UMIST model [1,3] | |||
| Li and Chen Model [1,3,8,10] | ≤ 5 | ||
| > 5 | |||
| x/d < 0.5 | |||
| If N » 1 | ≤ k | ||
| > k | |||
| x/d < 0.5 | |||
| When I/N « 1 | ≤ k | ||
| > k | |||
| x/d < 0.5 | |||
References
- Li, Q.; Reid, S.; Wen, H.; Telford, A. Local impact effects of hard missiles on concrete targets. Int. J. Impact Eng. 2005, 32, 224–284. [Google Scholar] [CrossRef]
- Latif, Q.B.A.I.; Rahman, I.A.; Zaidi, A.M.A.; Latif, K. Critical impact energy for spalling, tunnelling and penetration of concrete slab impacted with hard projectile. KSCE J. Civ. Eng. 2014, 19, 265–273. [Google Scholar] [CrossRef]
- Rahman, I.A.; Ahmad Zaidi, A.M.; Imran Latif, Q.B. Review on Empirical Studies of Local Impact Effects of Hard Missile on Concrete Structures. Int. J. Sustain. Constr. Eng. Technol. (IJSCET) UTHM 2010, 1, 71–95. [Google Scholar]
- NDRC. Effects of Impact and Explosion; Summary Technical Report of Division 2; National Defence Research Committee: Washington, DC, USA, 1946; Volume 1. [Google Scholar]
- Kennedy, R.P. A review of procedures for the analysis and design of concrete structures to resist missile impact effects. Nucl. Eng. Des. 1976, 37, 183–203. [Google Scholar] [CrossRef]
- Haldar, A.; Hamieh, H.A. Local Effect of Solid Missiles on Concrete Structures. J. Struct. Eng. 1984, 110, 948–960. [Google Scholar] [CrossRef]
- Hughes, G. Hard missile impact on reinforced concrete. Nucl. Eng. Des. 1984, 77, 23–35. [Google Scholar] [CrossRef]
- Li, Q.M.; Chen, X.W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile. Int. J. Impact Eng. 2003, 28, 93–116. [Google Scholar] [CrossRef]
- Forrestal, M.; Altman, B.; Cargile, J.; Hanchak, S. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets. Int. J. Impact Eng. 1994, 15, 395–405. [Google Scholar] [CrossRef]
- Chen, X.W.; Li, Q.M. Deep penetration of a non-deformable projectile with different geometrical characteristics. Int. J. Impact Eng. 2002, 27, 619–637. [Google Scholar] [CrossRef]
- Milad, A.; Hussein, S.H.; Khekan, A.R.; Rashid, M.; Al-Msari, H.; Tran, T.H. Development of ensemble machine learning approaches for designing fiber-reinforced polymer composite strain prediction model. Eng. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Frew, D.J.; Hanchak, S.J.; Brar, N.S. Penetration of grout and concrete targets with ogive-nose steel projectiles. Int. J. Impact Eng. 1996, 18, 465–476. [Google Scholar] [CrossRef] [Green Version]
- Frew, D.; Hanchak, S.; Green, M.; Forrestal, M. Penetration of concrete targets with ogive-nose steel rods. Int. J. Impact Eng. 1998, 21, 489–497. [Google Scholar] [CrossRef]
- Forrestal, M.; Frew, D.; Hickerson, J.; Rohwer, T. Penetration of concrete targets with deceleration-time measurements. Int. J. Impact Eng. 2003, 28, 479–497. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Hanchak, S.J. Penetration Experiments with Limestone Targets and Ogive-Nose Steel Projectiles. J. Appl. Mech. 2000, 67, 841–845. [Google Scholar] [CrossRef]
- Hosseini, M.; Dalvand, A. Neural Network Approach for Estimation of Penetration Depth in Concrete Targets by Ogive-nose Steel Projectiles. Lat. Am. J. Solids Struct. 2015, 12, 492–506. [Google Scholar] [CrossRef] [Green Version]
- Thai, D.-K.; Tu, M.; Bui, Q.; Bui, T.-T. Gradient tree boosting machine learning on predicting the failure modes of the RC panels under impact loads. Eng. Comput. 2019, 1, 3. [Google Scholar] [CrossRef]
- Ahmad Zaidi, A.M.; Imran Latif, Q.B.; Rahman, I.A.; Ismail, M.Y. Development of empirical prediction formula for penetration of ogive nose hard missile into concrete targets with effect of CRH ratio. Am. J. Eng. Appl. Sci. 2010, 7, 711–716. [Google Scholar]
- Duong, T.; Hazelton, M.L. Cross-validation Bandwidth Matrices for Multivariate Kernel Density Estimation. Scand. J. Stat. 2005, 32, 485–506. [Google Scholar] [CrossRef]
- Zambom, A.Z.; Dias, R. A review of Kernel density estimation with applications to econometrics. Int. Econom. Rev. 2013, 5, 20–42. [Google Scholar]
- Afzal, W.; Torkar, R. On the application of genetic programming for software engineering predictive modeling: A systematic review. Expert Syst. Appl. 2011, 38, 11984–11997. [Google Scholar] [CrossRef]
- Chelapati, C.V.; Kennedy, R.P.; Wall, I.B. Probabilistic assessment of hazard for nuclear structures. Nucl. Eng. Des. 1972, 19, 333–364. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, R.P. Effects of an Aircraft Crash into a Concrete Reactor Containment Building; Holmes & Narver Inc.: Anaheim, CA, USA, 1966. [Google Scholar]
- Bulson, P. Explosive Loading of Engineering Structures; E & FN Spon: London, UK, 1997. [Google Scholar]
- Bangash, M.Y.H. Concrete and Concrete Structures: Numerical Modelling and Application; Elsevier Applied Science: London, UK, 1989. [Google Scholar]
- Kar, A.K. Local Effects of Tornado-Generated Missiles. J. Struct. Div. 1978, 104, 809–816. [Google Scholar] [CrossRef]
- Barr, P. Guidelines for the Design and Assessment of Concrete Structures Subjected to Impact; Report; UK Atomic Energy Authority, Safety and Reliability Directorate, HMSO: London, UK, 1990.
- Kojima, I. An experimental study on local behaviour of reinforced concrete slabs to missile impact. Nucl. Eng. Des. 1991, 130, 121–132. [Google Scholar] [CrossRef]
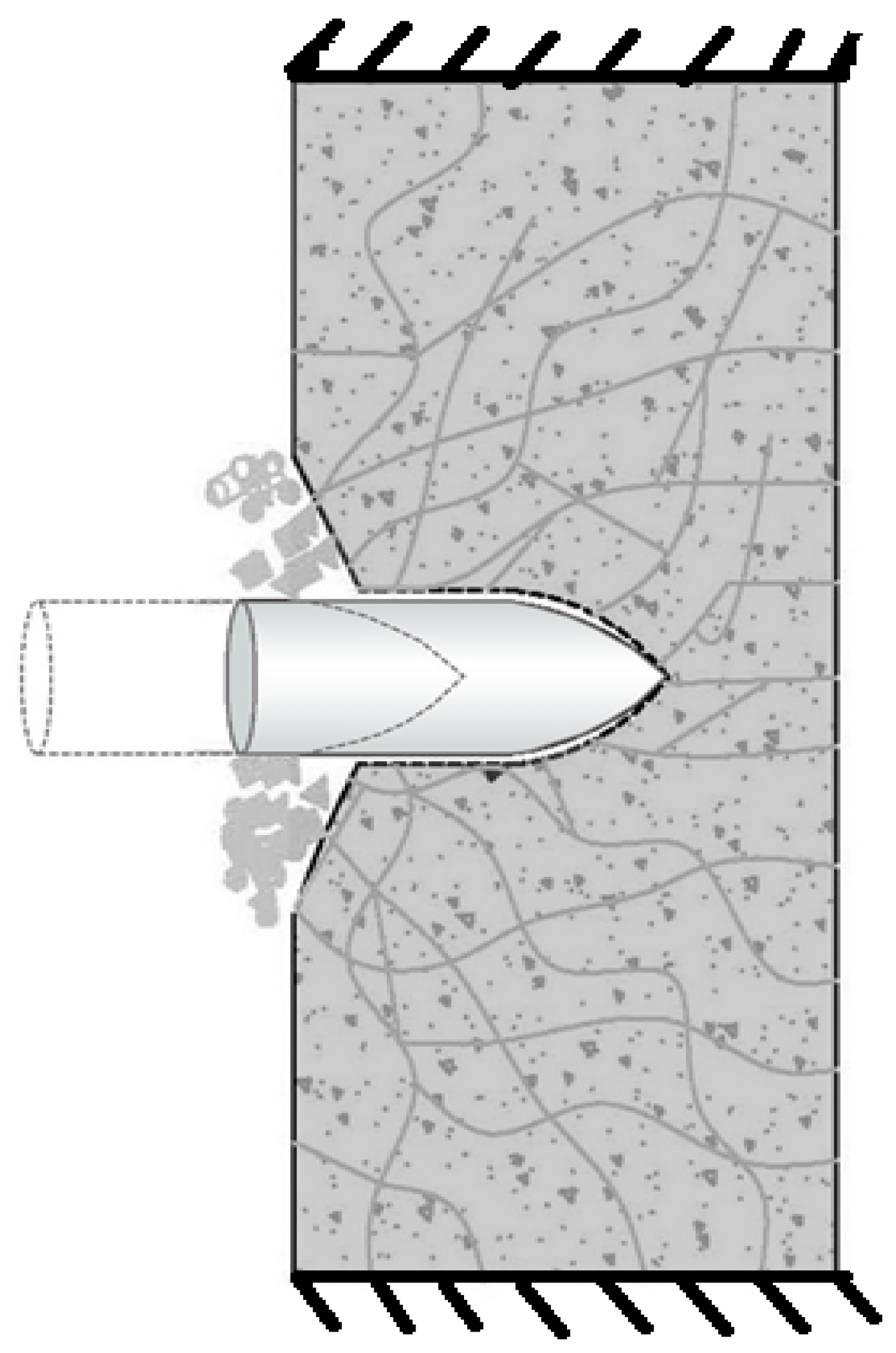
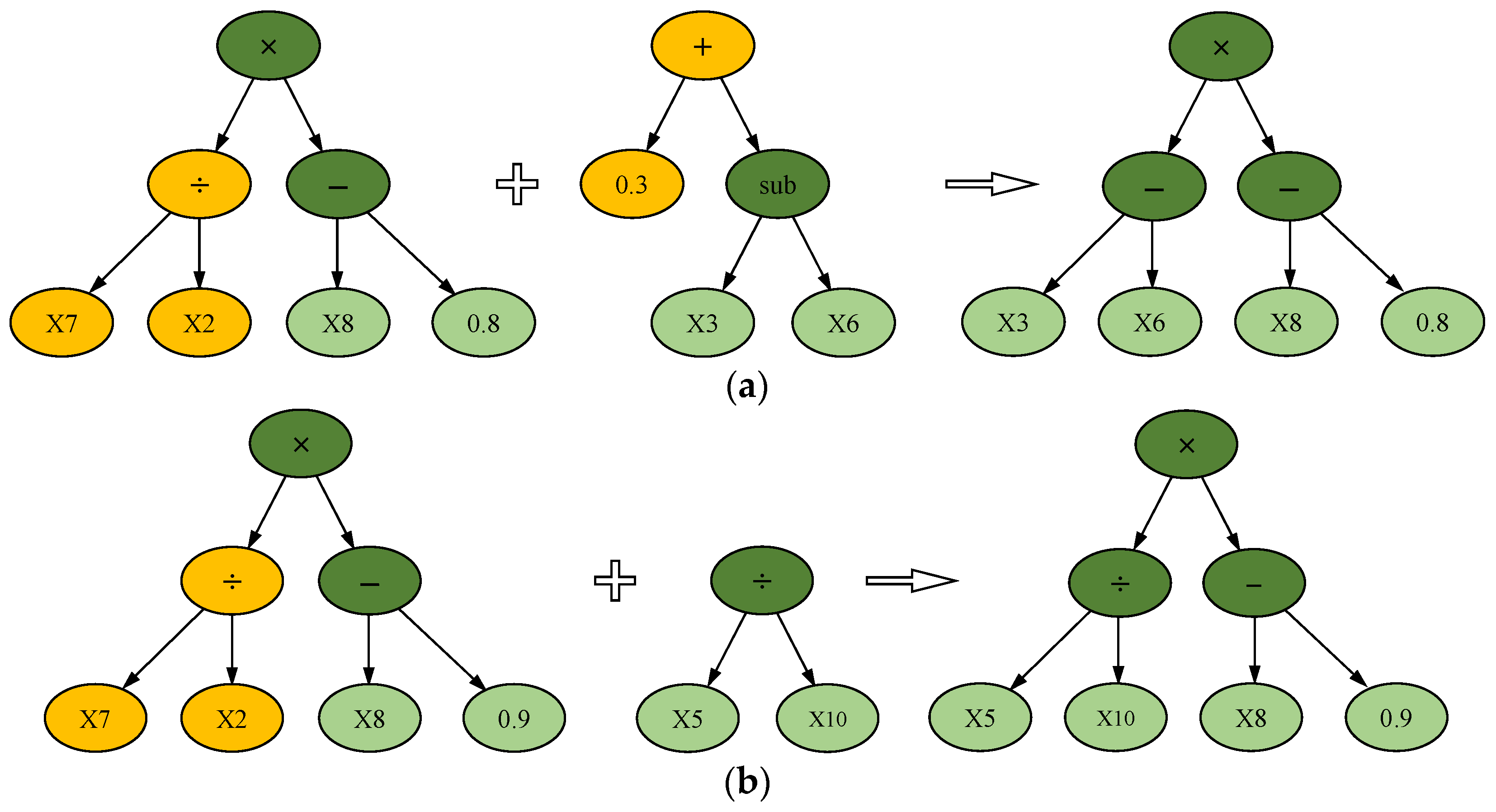
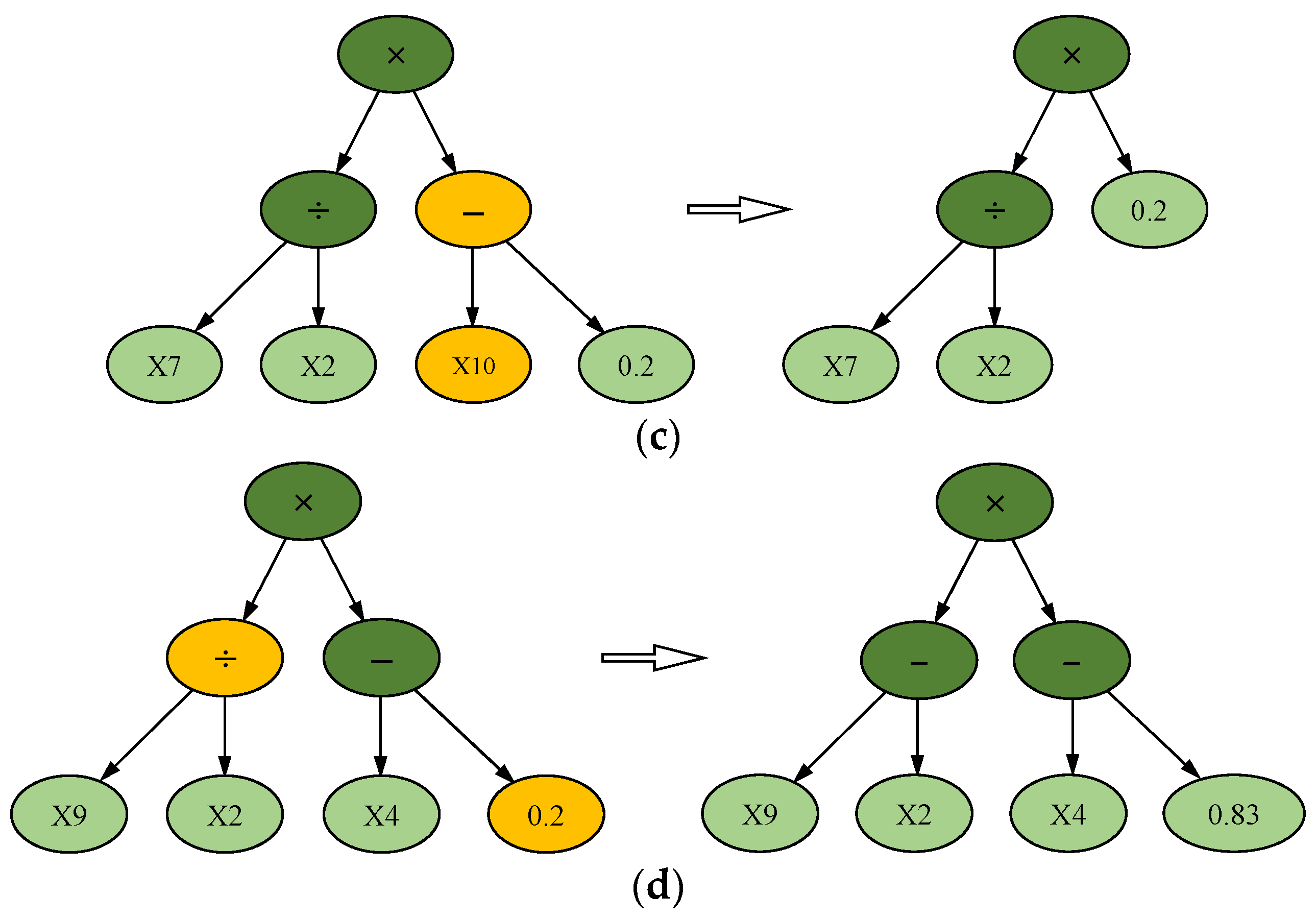
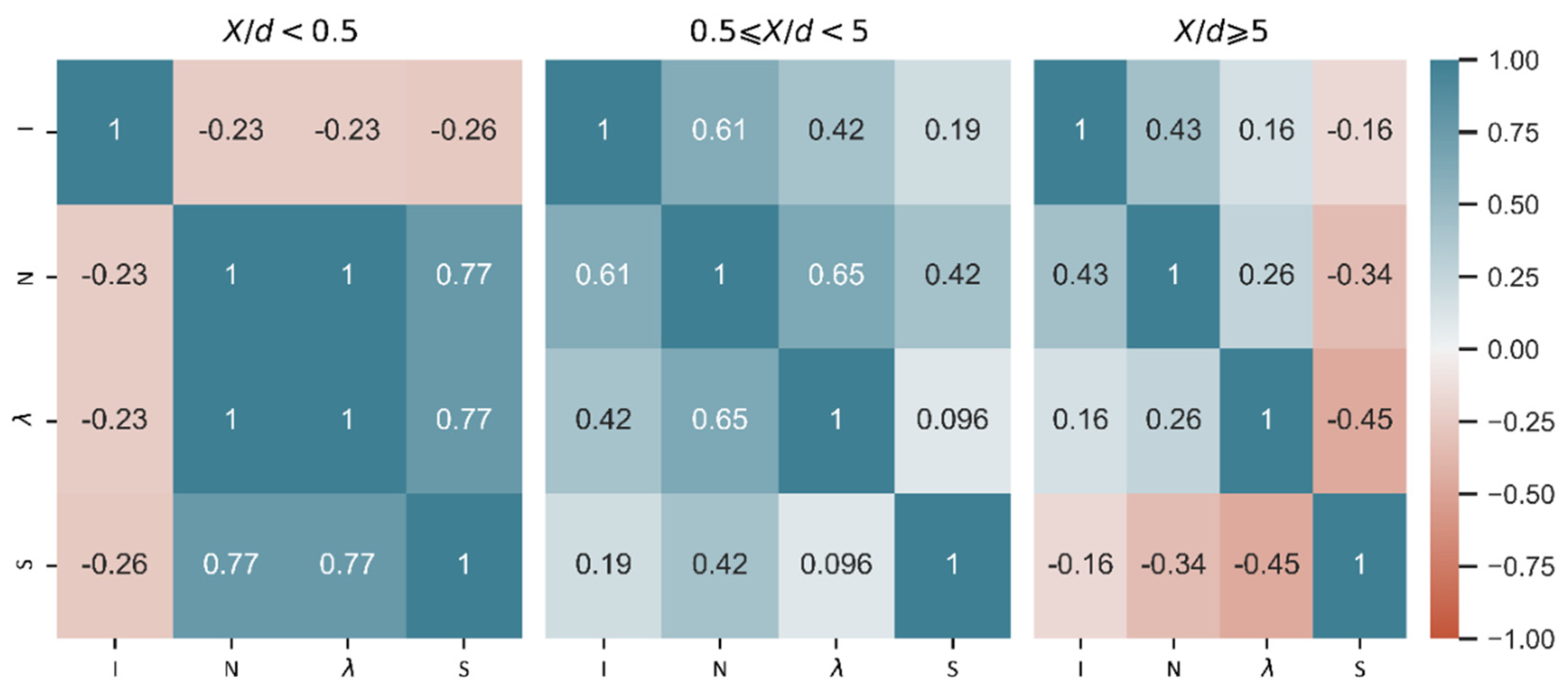
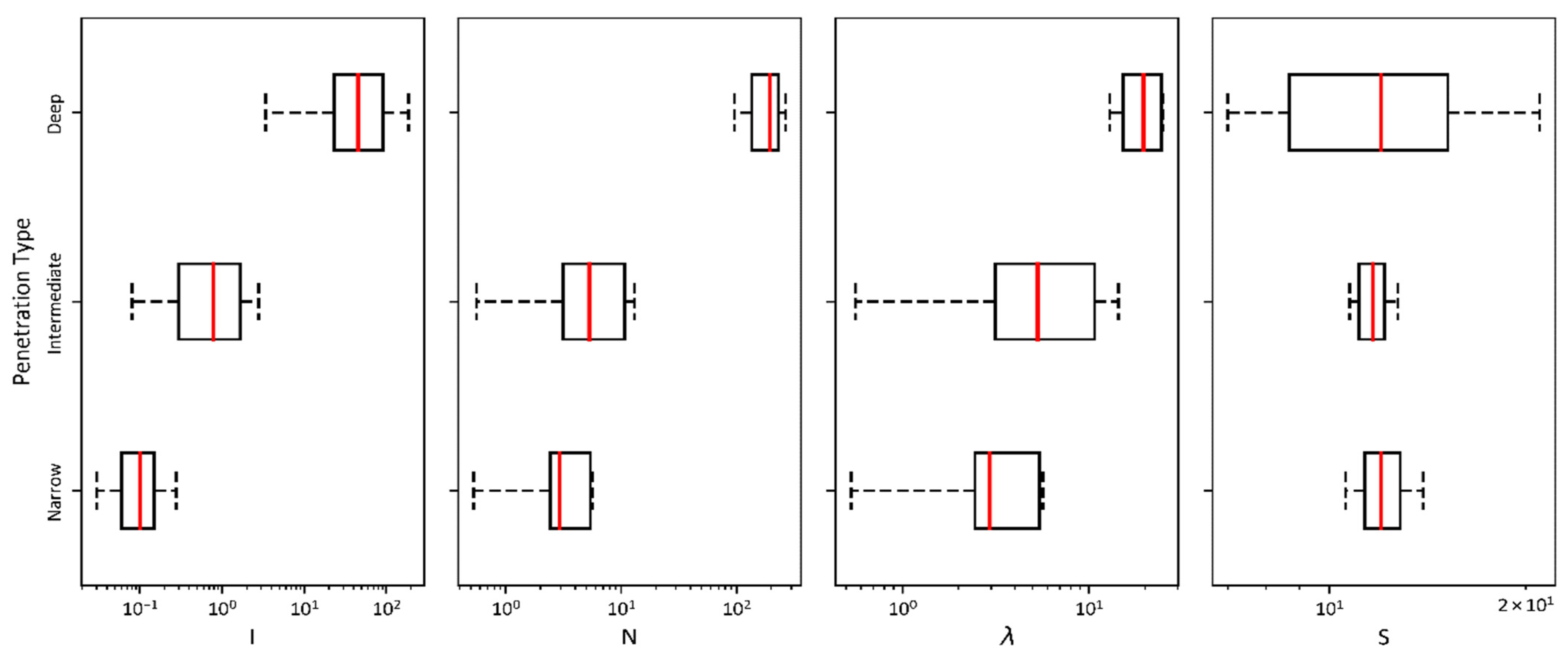
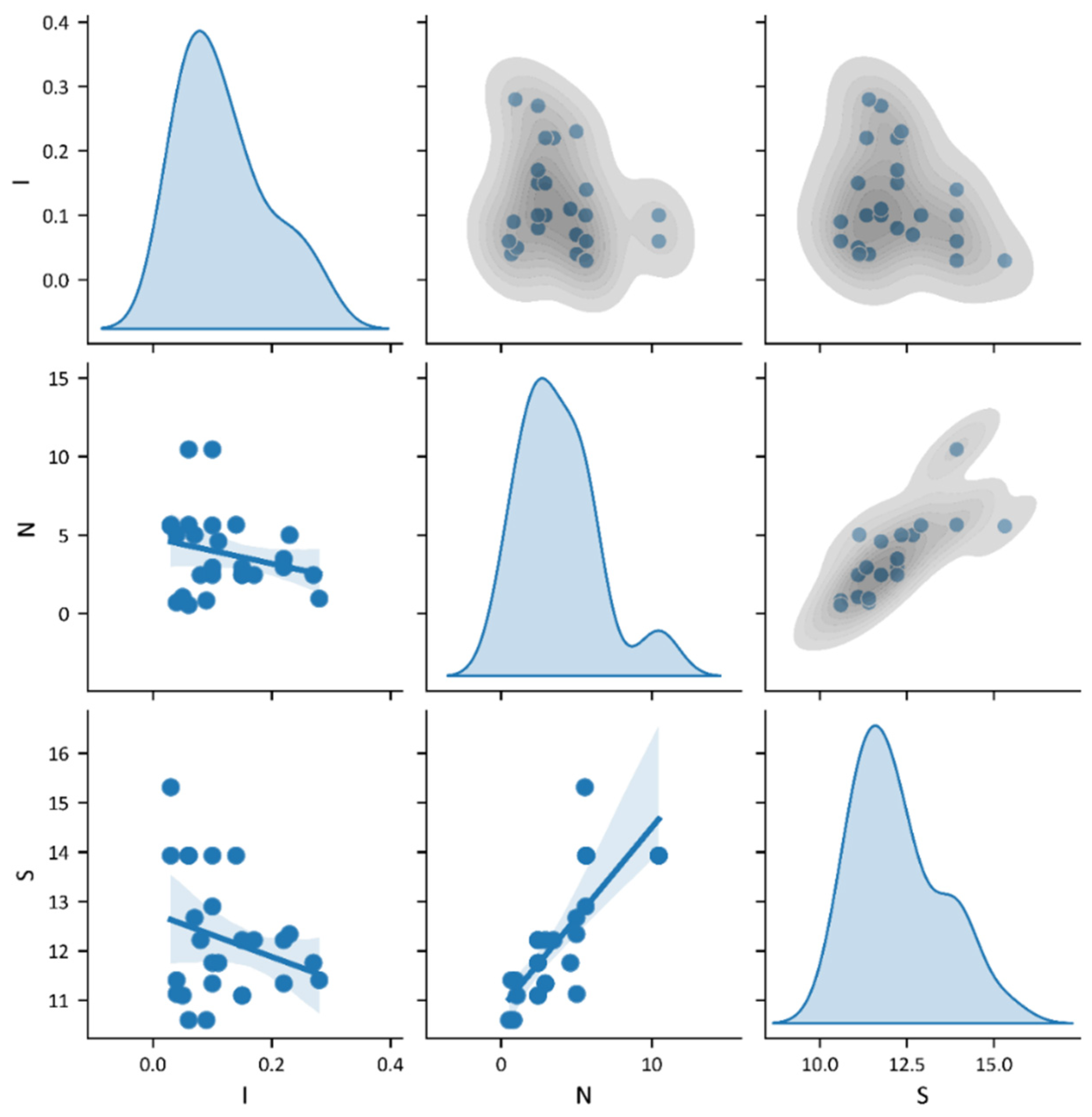
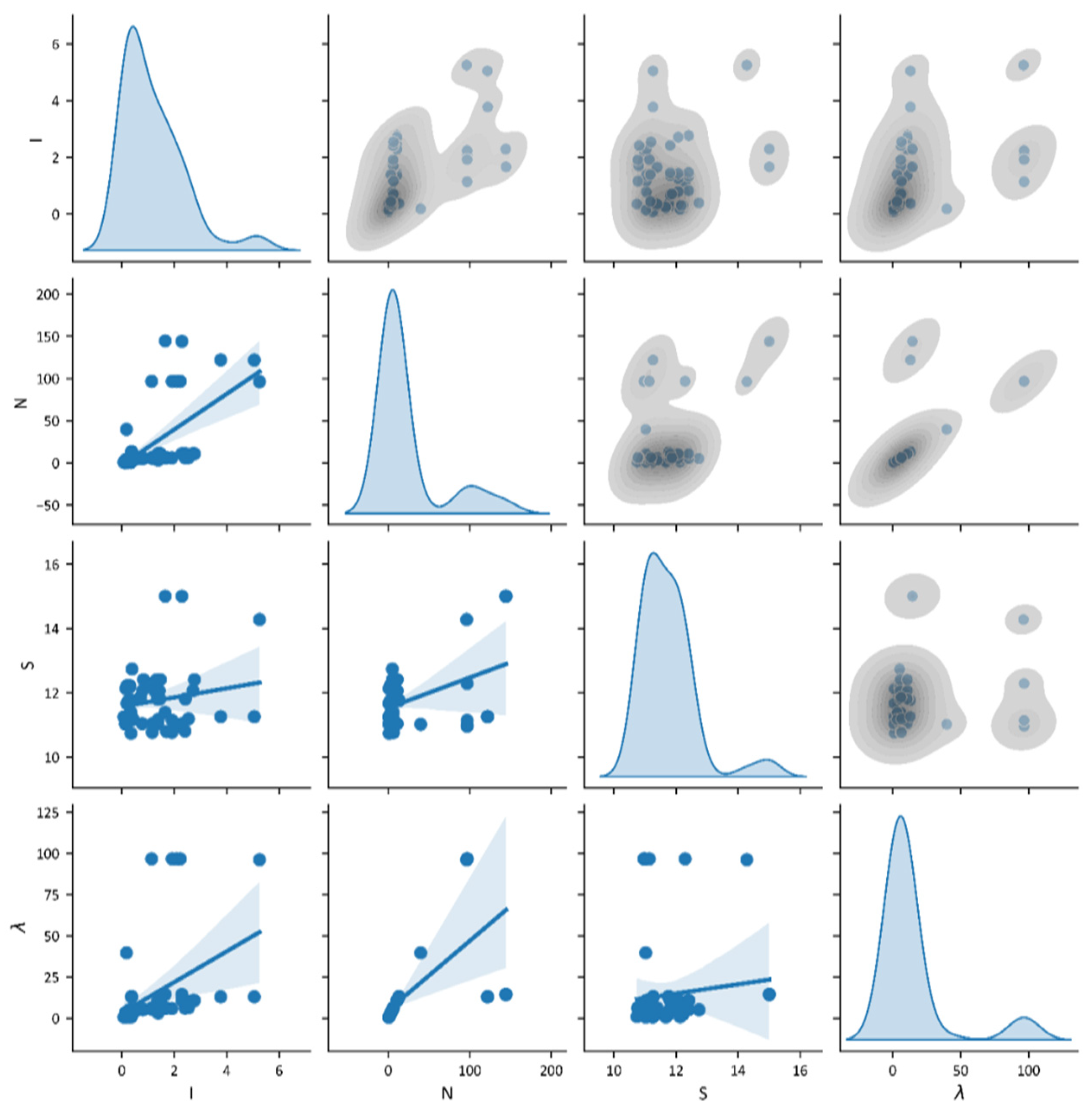
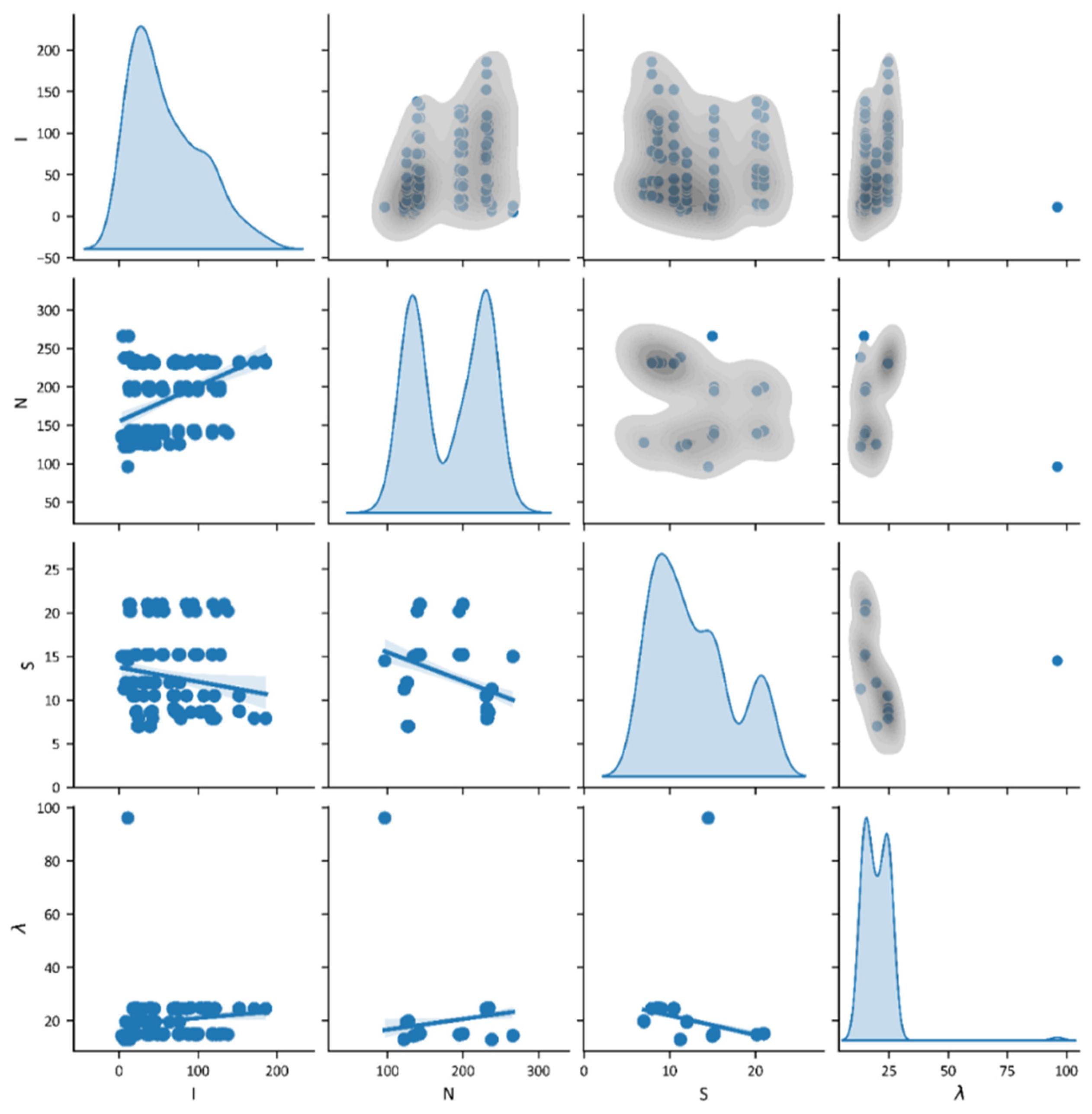
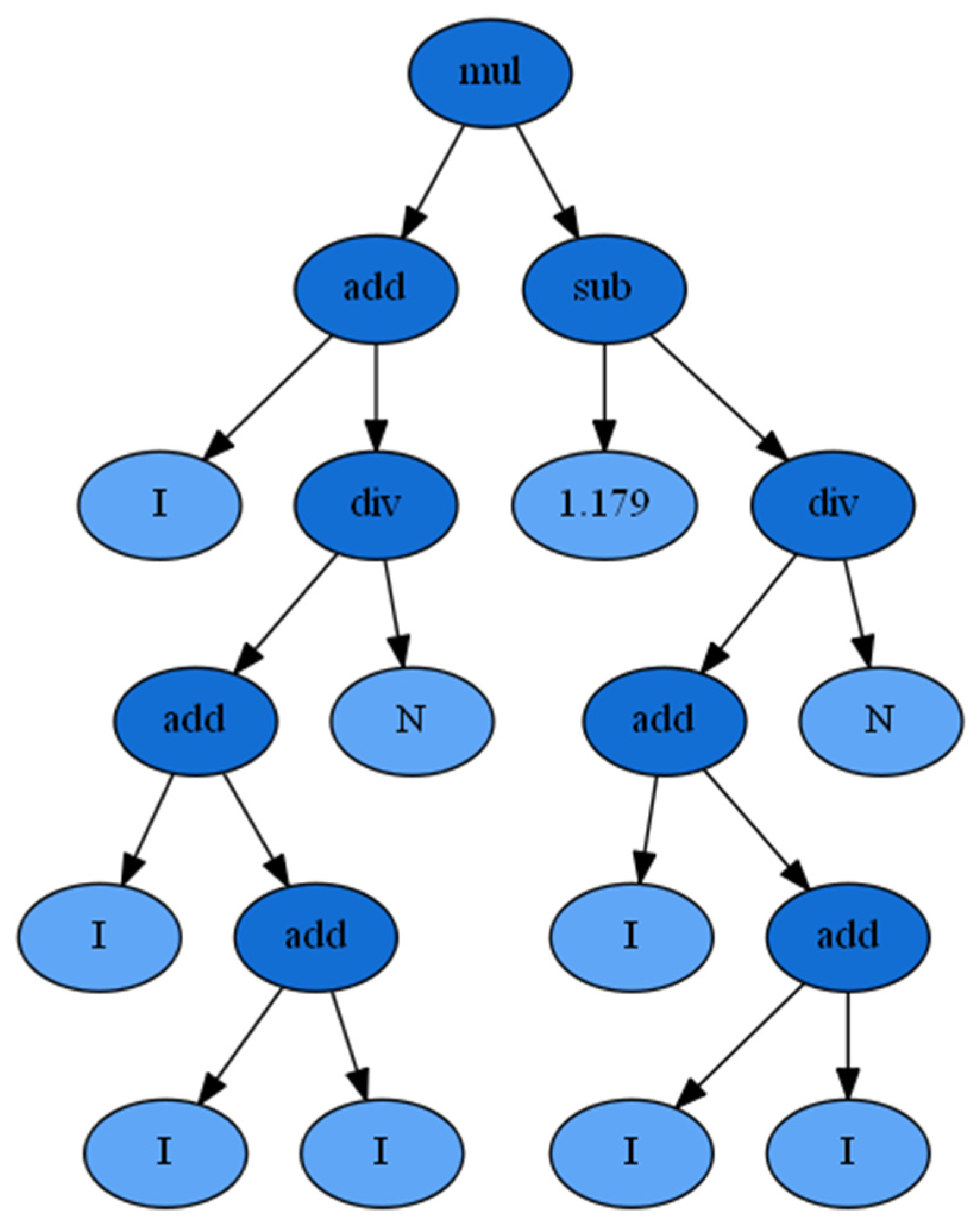

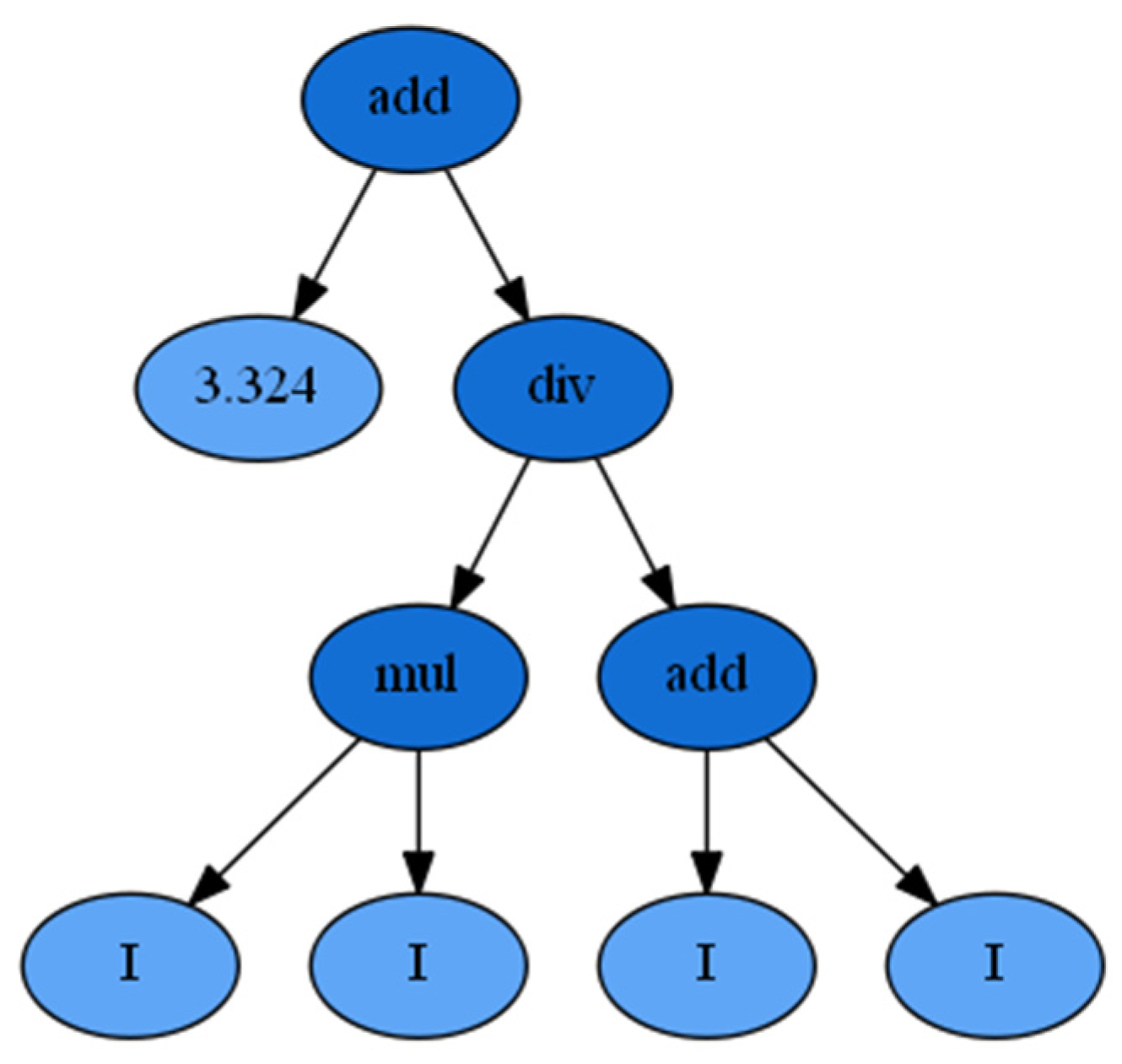

| λ | S | N | I | (X/d)test | λ | S | N | I | (X/d)test |
|---|---|---|---|---|---|---|---|---|---|
| 15.2 | 21 | 143.4 | 14.45 | 9.83 | 5.31 | 11.81 | 5.31 | 0.66 | 0.86 |
| 15.2 | 21 | 143.4 | 36.55 | 24.15 | 5.31 | 11.04 | 5.31 | 0.78 | 0.91 |
| 15.2 | 21 | 143.4 | 47.28 | 27.79 | 5.31 | 12.41 | 5.31 | 1.33 | 1.22 |
| 15.2 | 21 | 143.4 | 54.73 | 32.04 | 5.31 | 12.07 | 5.31 | 1.25 | 1.29 |
| 15.2 | 21 | 143.4 | 93.77 | 49.54 | 5.31 | 11.81 | 5.31 | 1.36 | 1.31 |
| 15.2 | 21 | 143.4 | 133.13 | 65.79 | 5.31 | 11.04 | 5.31 | 1.16 | 1.29 |
| 15.2 | 21 | 200 | 12.5 | 8.59 | 10.75 | 12.41 | 10.75 | 1.47 | 1.51 |
| 15.2 | 21 | 200 | 35.94 | 24.15 | 10.75 | 12.07 | 10.75 | 1.43 | 1.73 |
| 15.2 | 21 | 200 | 54.73 | 33.98 | 10.75 | 11.81 | 10.75 | 1.45 | 1.58 |
| 15.2 | 21 | 200 | 85.07 | 51.32 | 10.75 | 11.04 | 10.75 | 1.37 | 1.58 |
| 15.2 | 21 | 200 | 118.67 | 66.56 | 10.75 | 12.41 | 10.75 | 2.77 | 2.36 |
| 19.64 | 12 | 125.9 | 8.45 | 6.43 | 10.75 | 12.07 | 10.75 | 2.71 | 2.89 |
| 19.73 | 12 | 126.5 | 17.33 | 11.52 | 10.75 | 11.81 | 10.75 | 2.42 | 2.27 |
| 19.66 | 12 | 126 | 18.93 | 15.28 | 10.75 | 11.04 | 10.75 | 2.29 | 2.36 |
| 19.77 | 12 | 126.7 | 29.02 | 17.84 | 6.12 | 10.81 | 6.12 | 2.41 | 1.45 |
| 19.73 | 12 | 126.5 | 32.62 | 19.52 | 6.12 | 11.39 | 6.12 | 1.65 | 1.47 |
| 19.62 | 12 | 125.8 | 36.55 | 27.1 | 6.12 | 11.86 | 6.12 | 0.71 | 1 |
| 19.53 | 12 | 125.2 | 33.6 | 19.07 | 6.12 | 10.8 | 6.12 | 1.7 | 1.5 |
| 19.57 | 12 | 125.5 | 43.48 | 22.57 | 3.14 | 11.39 | 3.14 | 0.35 | 0.65 |
| 19.62 | 12 | 125.8 | 46.02 | 23.05 | 3.14 | 11.17 | 3.14 | 0.44 | 0.77 |
| 19.53 | 12 | 125.2 | 64.02 | 32.19 | 3.14 | 11.17 | 3.14 | 1.39 | 1.1 |
| 19.6 | 12 | 125.6 | 76.45 | 35.61 | 5.85 | 10.77 | 5.85 | 1.91 | 1.25 |
| 19.91 | 7 | 127.6 | 23.15 | 13.12 | 6.34 | 10.77 | 6.34 | 1.16 | 1.2 |
| 19.72 | 7 | 126.4 | 24.7 | 14.28 | 6.34 | 11.19 | 6.34 | 2.54 | 1.65 |
| 19.93 | 7 | 127.8 | 25.85 | 16.25 | |||||
| 19.87 | 7 | 127.4 | 25.34 | 15.69 | 14.45 | 15 | 144.51 | 1.66 | 3.15 |
| 19.91 | 7 | 127.6 | 39.83 | 23.42 | 14.4 | 15 | 144.03 | 2.29 | 4.07 |
| 19.76 | 7 | 126.7 | 38.35 | 22.49 | 12.98 | 11.26 | 121.91 | 3.77 | 3.94 |
| 14.44 | 15 | 135.65 | 3.42 | 5.51 | |||||
| 15.2 | 15.2 | 143.4 | 21.95 | 13.16 | 14.31 | 15 | 134.43 | 3.42 | 5.91 |
| 15.2 | 15.2 | 143.4 | 34.62 | 19.35 | 12.96 | 11.26 | 121.69 | 5.05 | 4.99 |
| 15.2 | 15.2 | 143.4 | 56.3 | 34.83 | 12.93 | 11.26 | 237.71 | 6.47 | 8.01 |
| 15.2 | 15.2 | 143.4 | 75.08 | 42.57 | 14.47 | 15 | 266.01 | 4.86 | 7.61 |
| 15.2 | 15.2 | 143.4 | 96 | 58.05 | 12.97 | 11.26 | 121.79 | 6.55 | 5.91 |
| 15.2 | 15.2 | 143.4 | 118.24 | 65.79 | 14.5 | 15 | 136.15 | 5.36 | 8.14 |
| 15.2 | 15.2 | 200 | 20.28 | 13.16 | 14.28 | 15 | 134.12 | 6.62 | 9.58 |
| 15.2 | 15.2 | 200 | 39.47 | 20.9 | 14.47 | 15 | 135.89 | 6.66 | 9.06 |
| 15.2 | 15.2 | 200 | 54.45 | 31.73 | 19.64 | 12 | 125.69 | 8.46 | 6.43 |
| 15.2 | 15.2 | 200 | 76.9 | 44.12 | 12.97 | 11.26 | 121.83 | 9.08 | 6.96 |
| 15.2 | 15.2 | 200 | 99.95 | 58.82 | 14.58 | 15 | 136.91 | 6.94 | 9.97 |
| 15.2 | 15.2 | 200 | 128.38 | 68.11 | 14.45 | 15 | 135.68 | 9.41 | 12.6 |
| 24.84 | 8.6 | 234.3 | 21.43 | 14.78 | 14.49 | 15 | 136.09 | 9.61 | 12.34 |
| 24.84 | 8.6 | 234.3 | 39.63 | 23.65 | 14.49 | 15 | 136.09 | 9.71 | 12.21 |
| 24.84 | 8.6 | 234.3 | 71.31 | 37.44 | 14.46 | 15 | 135.78 | 9.71 | 13.39 |
| 24.84 | 8.6 | 234.3 | 90.72 | 46.8 | 12.97 | 11.26 | 238.38 | 13.37 | 12.99 |
| 24.84 | 8.6 | 234.3 | 103.09 | 45.32 | 13.02 | 11.26 | 122.23 | 13.89 | 12.34 |
| 24.84 | 8.6 | 234.3 | 110.97 | 46.31 | 19.91 | 7 | 127.44 | 23.15 | 13.12 |
| 24.52 | 10.5 | 231.3 | 17.28 | 12.13 | 19.72 | 7 | 126.18 | 24.7 | 14.28 |
| 24.52 | 10.5 | 231.3 | 20.95 | 13.77 | 19.87 | 7 | 127.16 | 25.34 | 16.25 |
| 24.52 | 10.5 | 231.3 | 31.29 | 18.36 | 19.94 | 7 | 127.58 | 25.93 | 15.69 |
| 24.52 | 10.5 | 231.3 | 44.64 | 25.57 | 24.64 | 10.5 | 231.41 | 17.36 | 12.13 |
| 24.52 | 10.5 | 231.3 | 68.09 | 34.43 | 14.47 | 15 | 266.07 | 12.26 | 16.4 |
| 24.52 | 10.5 | 231.3 | 70.99 | 40.33 | 24.84 | 8.6 | 233.31 | 21.42 | 14.78 |
| 24.52 | 10.5 | 231.3 | 85.31 | 46.23 | 14.54 | 15 | 136.5 | 12.32 | 15.49 |
| 24.52 | 10.5 | 231.3 | 107.23 | 57.38 | 24.63 | 8.7 | 231.3 | 21.97 | 14.14 |
| 24.52 | 10.5 | 231.3 | 120.29 | 64.26 | 24.61 | 7.9 | 231.13 | 24.51 | 15.08 |
| 24.52 | 10.5 | 231.3 | 151.92 | 66.56 | 19.73 | 12 | 126.25 | 17.33 | 11.52 |
| 24.52 | 10.5 | 230.26 | 20.95 | 13.77 | |||||
| 24.63 | 8.7 | 232.4 | 21.97 | 14.14 | 19.66 | 12 | 125.83 | 18.93 | 15.28 |
| 24.63 | 8.7 | 232.4 | 41.92 | 24.19 | 14.84 | 20.2 | 194.91 | 12.95 | 8.51 |
| 24.63 | 8.7 | 232.4 | 74.7 | 41.38 | 15.19 | 21 | 199.51 | 12.5 | 8.59 |
| 24.63 | 8.7 | 232.4 | 114.5 | 64.04 | 19.76 | 7 | 126.46 | 38.35 | 22.49 |
| 24.63 | 8.7 | 232.4 | 151.85 | 78.33 | 19.91 | 7 | 127.44 | 39.83 | 23.42 |
| 24.63 | 8.7 | 232.4 | 70.37 | 35.96 | 14.84 | 20.2 | 139.34 | 14.98 | 10.06 |
| 24.63 | 8.7 | 232.4 | 111.12 | 57.14 | 15.19 | 21 | 142.63 | 14.45 | 9.83 |
| 24.63 | 8.7 | 232.4 | 152.64 | 71.92 | 14.84 | 15.2 | 194.91 | 20.22 | 13.16 |
| 24.61 | 7.9 | 232.2 | 24.5 | 15.08 | 24.52 | 10.5 | 230.26 | 31.28 | 18.36 |
| 24.61 | 7.9 | 232.2 | 42.21 | 25.9 | 14.84 | 15.2 | 139.34 | 21.88 | 13.16 |
| 24.61 | 7.9 | 232.2 | 77.91 | 40.33 | 24.61 | 7.9 | 231.13 | 42.21 | 25.9 |
| 24.61 | 7.9 | 232.2 | 118.85 | 63.93 | 24.84 | 8.6 | 233.31 | 39.63 | 23.65 |
| 24.61 | 7.9 | 232.2 | 121.78 | 64.26 | 19.77 | 12 | 126.52 | 29.02 | 17.84 |
| 24.61 | 7.9 | 232.2 | 171.15 | 87.54 | 24.63 | 8.7 | 231.3 | 41.85 | 24.19 |
| 19.73 | 12 | 126.25 | 32.62 | 19.52 | |||||
| 39.69 | 11.02 | 39.69 | 0.18 | 0.71 | 19.53 | 12 | 125 | 33.6 | 19.07 |
| 3.48 | 11.1 | 3.48 | 0.15 | 0.56 | 19.62 | 12 | 125.55 | 36.55 | 27.1 |
| 3.48 | 11.1 | 3.48 | 0.15 | 0.66 | 24.56 | 10.5 | 230.69 | 44.71 | 25.57 |
| 2.45 | 11.1 | 2.45 | 0.15 | 0.41 | 19.57 | 12 | 125.27 | 43.48 | 22.57 |
| 3.48 | 11.1 | 3.48 | 0.17 | 0.61 | 14.84 | 15.2 | 139.34 | 34.52 | 19.35 |
| 2.45 | 11.1 | 2.45 | 0.15 | 0.34 | 19.62 | 12 | 125.55 | 46.02 | 23.05 |
| 2.45 | 12.22 | 2.45 | 0.24 | 1.31 | 14.84 | 15.2 | 194.91 | 39.37 | 20.9 |
| 2.93 | 12.22 | 2.93 | 0.15 | 0.32 | 24.63 | 8.7 | 231.3 | 70.37 | 35.96 |
| 2.45 | 12.22 | 2.45 | 0.17 | 0.41 | 24.84 | 8.6 | 233.31 | 71.31 | 37.44 |
| 2.94 | 12.22 | 2.94 | 0.2 | 0.78 | 24.61 | 7.9 | 231.13 | 78.42 | 40.33 |
| 3.48 | 12.22 | 3.48 | 0.27 | 0.73 | 24.63 | 9.04 | 231.3 | 68.77 | 49.75 |
| 3.48 | 12.22 | 3.48 | 0.22 | 0.49 | 24.63 | 9.04 | 231.3 | 69.81 | 60.39 |
| 2.45 | 12.22 | 2.45 | 0.3 | 0.57 | 24.63 | 8.7 | 231.3 | 74.7 | 41.38 |
| 2.45 | 12.22 | 2.45 | 0.08 | 0.07 | 24.58 | 10.5 | 230.84 | 68.24 | 34.43 |
| 2.94 | 12.22 | 2.94 | 0.3 | 0.54 | 24.52 | 10.5 | 230.26 | 70.98 | 40.33 |
| 3.48 | 11.34 | 3.48 | 0.3 | 1.47 | 14.84 | 20.2 | 194.91 | 37.24 | 23.99 |
| 2.45 | 11.34 | 2.45 | 0.33 | 0.95 | 15.19 | 21 | 199.51 | 35.93 | 24.15 |
| 2.94 | 11.34 | 2.94 | 0.1 | 0.1 | 14.84 | 20.2 | 139.34 | 37.88 | 23.99 |
| 2.94 | 11.34 | 2.94 | 0.22 | 0.44 | 15.19 | 21 | 142.63 | 36.55 | 24.15 |
| 2.45 | 11.76 | 2.45 | 0.4 | 0.75 | 19.53 | 12 | 125 | 64.02 | 32.19 |
| 13.04 | 11.76 | 13.04 | 0.38 | 0.5 | 24.84 | 8.6 | 233.31 | 90.72 | 46.8 |
| 4.6 | 11.76 | 4.6 | 0.25 | 0.66 | 14.84 | 15.2 | 194.91 | 54.29 | 31.73 |
| 2.45 | 11.76 | 2.45 | 0.27 | 0.26 | 14.84 | 15.2 | 139.34 | 56.12 | 34.83 |
| 13.04 | 11.76 | 13.04 | 0.37 | 2.15 | 24.84 | 8.6 | 233.31 | 103.07 | 45.32 |
| 2.45 | 11.76 | 2.45 | 0.1 | 0.21 | 24.56 | 10.5 | 230.69 | 85.46 | 46.23 |
| 4.6 | 11.76 | 4.6 | 0.11 | 0.36 | 19.6 | 12 | 125.41 | 76.45 | 35.61 |
| 0.83 | 10.6 | 0.83 | 0.09 | 0.32 | 24.61 | 7.9 | 231.13 | 116.93 | 64.26 |
| 1.63 | 11.67 | 1.63 | 0.2 | 0.95 | 24.61 | 7.9 | 231.13 | 118.86 | 63.93 |
| 0.83 | 12.13 | 0.83 | 0.16 | 1.04 | 24.84 | 8.6 | 233.31 | 110.94 | 46.31 |
| 0.69 | 11.25 | 0.69 | 0.08 | 0.54 | 24.61 | 7.9 | 231.13 | 121.79 | 64.26 |
| 0.69 | 11.41 | 0.69 | 0.04 | 0.13 | 24.63 | 8.7 | 231.3 | 111.12 | 57.14 |
| 1.05 | 11.1 | 1.05 | 0.05 | 0.34 | 14.84 | 20.2 | 139.34 | 48.85 | 27.86 |
| 0.53 | 10.6 | 0.53 | 0.06 | 0.23 | 15.19 | 21 | 142.63 | 47.14 | 27.79 |
| 0.95 | 11.41 | 0.95 | 0.28 | 0.34 | 24.63 | 8.7 | 231.3 | 114.5 | 64.04 |
| 0.95 | 10.74 | 0.95 | 0.35 | 0.55 | 24.5 | 10.5 | 230.12 | 107.15 | 57.38 |
| 0.7 | 11.67 | 0.7 | 0.24 | 0.5 | 14.84 | 15.2 | 139.34 | 74.85 | 42.57 |
| 0.7 | 11.25 | 0.7 | 0.35 | 1 | 14.84 | 20.2 | 139.34 | 56.73 | 31.73 |
| 0.56 | 11.03 | 0.56 | 0.14 | 0.5 | 14.84 | 20.2 | 194.91 | 56.73 | 34.06 |
| 96.15 | 14.28 | 96.15 | 5.25 | 3.6 | 15.19 | 21 | 142.63 | 54.74 | 32.04 |
| 96.15 | 14.51 | 96.15 | 10.97 | 5.8 | 15.19 | 21 | 199.51 | 54.74 | 33.98 |
| 96.63 | 12.29 | 96.63 | 1.14 | 1.2 | 14.84 | 15.2 | 194.91 | 76.67 | 44.12 |
| 96.63 | 10.99 | 96.63 | 2.09 | 1.6 | 24.66 | 10.5 | 231.56 | 121.02 | 64.26 |
| 96.63 | 10.96 | 96.63 | 2.23 | 2 | 24.63 | 8.7 | 231.3 | 151.85 | 78.33 |
| 96.63 | 11.14 | 96.63 | 1.92 | 1.7 | 24.63 | 8.7 | 231.3 | 152.64 | 71.92 |
| 5.02 | 11.13 | 5.02 | 0.04 | 0.09 | 24.61 | 7.9 | 231.13 | 171.16 | 87.54 |
| 5 | 12.67 | 5 | 0.07 | 0.25 | 14.84 | 15.2 | 139.34 | 95.7 | 58.05 |
| 5 | 12.17 | 5 | 0.3 | 1.13 | 24.61 | 7.9 | 231.13 | 185.72 | 92.79 |
| 5 | 12.34 | 5 | 0.23 | 0.38 | 14.84 | 15.2 | 194.91 | 99.65 | 58.82 |
| 5.05 | 12.74 | 5.05 | 0.39 | 0.56 | 24.56 | 10.5 | 230.69 | 152.18 | 66.56 |
| 5.56 | 15.31 | 5.56 | 0.03 | 0.06 | 14.84 | 20.2 | 194.91 | 88.14 | 51.08 |
| 5.65 | 13.93 | 5.65 | 0.03 | 0.05 | 15.19 | 21 | 199.51 | 85.05 | 51.32 |
| 5.65 | 13.93 | 5.65 | 0.06 | 0.04 | 14.84 | 15.2 | 139.34 | 117.88 | 65.79 |
| 5.61 | 12.9 | 5.61 | 0.1 | 0.12 | 14.84 | 15.2 | 194.91 | 127.99 | 68.11 |
| 5.65 | 13.93 | 5.65 | 0.14 | 0.14 | 14.84 | 20.2 | 139.34 | 97.18 | 49.54 |
| 10.46 | 13.93 | 10.46 | 0.06 | 0.06 | 15.19 | 21 | 142.63 | 93.77 | 49.54 |
| 10.46 | 13.93 | 10.46 | 0.1 | 0.06 | 14.84 | 20.2 | 194.91 | 122.96 | 66.56 |
| 5.31 | 12.41 | 5.31 | 0.83 | 0.95 | 14.84 | 20.2 | 139.34 | 137.97 | 65.79 |
| 5.31 | 12.07 | 5.31 | 0.79 | 1.02 |
| Statistics | Independent Variables | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | N | λ | S | |||||||||
| Narrow | Intermediate | Deep | Narrow | Intermediate | Deep | Narrow | Intermediate | Deep | Narrow | Intermediate | Deep | |
| Count | 26 | 59 | 174 | 26 | 59 | 174 | 26 | 59 | 174 | 26 | 59 | 174 |
| Mean | 0.12 | 1.19 | 60.05 | 3.83 | 22.29 | 182.81 | 3.83 | 14.20 | 19.96 | 12.24 | 11.74 | 12.75 |
| Std | 0.074 | 1.15 | 44.29 | 2.60 | 39.85 | 47.24 | 2.60 | 25.93 | 7.30 | 1.24 | 0.89 | 4.55 |
| Cov | 0.62 | 0.97 | 0.74 | 0.68 | 1.79 | 0.26 | 0.68 | 1.83 | 0.37 | 0.10 | 0.08 | 0.36 |
| Min | 0.03 | 0.08 | 3.42 | 0.53 | 0.56 | 96.15 | 0.53 | 0.56 | 12.93 | 10.60 | 10.74 | 7.00 |
| 25% | 0.06 | 0.30 | 23.15 | 2.45 | 3.14 | 135.94 | 2.45 | 3.14 | 15.19 | 11.34 | 11.10 | 8.70 |
| 50% | 0.10 | 0.79 | 45.37 | 2.94 | 5.31 | 194.91 | 2.94 | 5.31 | 19.65 | 11.99 | 11.67 | 12.00 |
| 75% | 0.15 | 1.68 | 90.72 | 5.43 | 10.75 | 231.30 | 5.43 | 10.75 | 24.61 | 12.84 | 12.15 | 15.20 |
| Max | 0.28 | 5.25 | 185.72 | 10.46 | 144.51 | 266.07 | 10.46 | 96.63 | 96.15 | 15.31 | 15.00 | 21.00 |
| Parameter | Value | ||
|---|---|---|---|
| EQ 1 | EQ 2 | EQ 3 | |
| population size | 5000 | 5000 | 5000 |
| generations | 60 | 60 | 60 |
| stopping_criteria | 0.01 | 0.01 | 0.01 |
| p_crossover | 0.9 | 0.7 | 0.7 |
| p_subtree_mutation | 0.01 | 0.01 | 0.1 |
| p_hoist_mutation | 0.01 | 0.05 | 0.05 |
| p_point_mutation | 0.01 | 0.1 | 0.1 |
| function_set | +, −, ×, ÷ | +, −, ×, ÷, √ | +, −, ×, ÷ |
| tournament size | 25 | 25 | 25 |
| parsimony_coefficient | 0.0003 | 0.002 | 0.003 |
| metric | MAE | MAE | MAE |
| const_range | (−5, 5) | (−5, 5) | (−5, 5) |
| Metric | Comparison of Performance between Different Equations | |||
|---|---|---|---|---|
| NDRC | Barr | Li and Chen | Sym. Reg.a (Present Study) | |
| Narrow penetration (X/d < 0.5) | ||||
| R2 | −3.262 | 0.145 | −0.031 | 0.590 |
| MSE | 0.085 | 0.017 | 0.021 | 0.008 |
| MAE | 0.270 | 0.097 | 0.118 | 0.068 |
| Intermediate penetration (0.5 ≤ X/d < 5) | ||||
| R2 | 0.746 | 0.650 | 0.746 | 0.884 |
| MSE | 0.103 | 0.142 | 0.231 | 0.106 |
| MAE | 0.222 | 0.261 | 0.330 | 0.216 |
| Deep penetration (X/d ≥ 5) | ||||
| R2 | 0.565 | - | 0.963 | 0.967 |
| MSE | 199.369 | - | 16.877 | 15.087 |
| MAE | 11.295 | - | 2.799 | 2.470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran Latif, Q.B.a.; Memon, Z.A.; Mahmood, Z.; Qureshi, M.U.; Milad, A. A Machine Learning Model for the Prediction of Concrete Penetration by the Ogive Nose Rigid Projectile. Appl. Sci. 2022, 12, 2040. https://doi.org/10.3390/app12042040
Imran Latif QBa, Memon ZA, Mahmood Z, Qureshi MU, Milad A. A Machine Learning Model for the Prediction of Concrete Penetration by the Ogive Nose Rigid Projectile. Applied Sciences. 2022; 12(4):2040. https://doi.org/10.3390/app12042040
Chicago/Turabian StyleImran Latif, Qadir Bux alias, Zubair Ahmed Memon, Zafar Mahmood, Mohsin Usman Qureshi, and Abdalrhman Milad. 2022. "A Machine Learning Model for the Prediction of Concrete Penetration by the Ogive Nose Rigid Projectile" Applied Sciences 12, no. 4: 2040. https://doi.org/10.3390/app12042040
APA StyleImran Latif, Q. B. a., Memon, Z. A., Mahmood, Z., Qureshi, M. U., & Milad, A. (2022). A Machine Learning Model for the Prediction of Concrete Penetration by the Ogive Nose Rigid Projectile. Applied Sciences, 12(4), 2040. https://doi.org/10.3390/app12042040









