Abstract
Gait disorders, muscle weakness, spinal cord injuries (SCIs) and other work-related disorders have increased the need for rehabilitation exoskeletons—specifically, for the hip because a huge percentage of mechanical power comes from the hip joint. However, realising a lightweight rehabilitation hip exoskeleton for mobility and at-home use with reliable control is challenging. The devices developed are restricted by a joint actuator and energy source design and tend to have various uncertainties. Thus, this study tested the robustness of four optimal controller cases in a simulation-based environment. We sought to determine whether the most robust optimal controller consumed less energy and demonstrated better performance in tracking the desired signal. The robustness of the optimal cases was tested with the hip torque signals of healthy subjects. The number of sit-to-stand (STS) instances and the walking distance at various speeds were calculated. The results showed that the most robust case controller was more energy efficient for STS, but not for walking activity. Furthermore, this study provides compelling evidence that various optimal controllers have different degrees of robustness and effects on energy consumption.
1. Introduction
An urgent need for robotic exoskeletons has been widely observed in the military, industry, medicine and hazardous situations such as disasters and pandemics over the last few decades [1,2]. Some exoskeleton robots augment human mobility or endurance, while others are used for rehabilitation and ambulatory assistance [3]. In addition, some are used for paediatric recovery, while others serve the elderly, soldiers or athletes [4,5,6].
According to a 2019 United Nations’ report [7,8], the number of strokes and the percentage of mobility accidents are the highest among people older than 65 years and the 250,000–500,000 patients suffering from spinal cord injury (SCI) every year, increase research interest in robotic exoskeletons [9]. Additionally, more than 17% of work-related disorders are associated with lower limb activity, which also increased the need for robotic exoskeletons for mobility assistance and rehabilitation [9,10].
Thus, a lower limb exoskeleton, specifically, the rehabilitation hip exoskeleton, is the focus of this paper because 45% of the mechanical energy of lower limb movements comes from the hip joint [8,11]. Robotic exoskeletons can contribute in repetitive training of human extremities to enable patients to pursue rehabilitation sessions at home and enable therapists to focus on more specialised rehabilitation sessions [12]. Among the different rehabilitation exoskeletons are those used for sit-to-stand and walking movements. Therefore, we focus more on these activities because of their importance in daily life [13].
The rehabilitation hip exoskeleton is a mechanical structure worn to enhance gait mobility but can also be used, for instance, after hip replacement surgery or a stroke [14]. Since, in the very early stages of rehabilitation sessions, patients’ limbs are usually trained passively to track predefined trajectory motions, which vary according to the patients’ needs or limb disorders [15], different controller strategies have been used to track and control the trajectories because human extremities are intolerant of any unexpected harmful movement errors; in particular, rehabilitation exoskeletons serve people who already have some sort of limb disorder or mobility deficiency [16,17].
Some control strategies have used fuzzy hybrid controller, while others utilised Bayesian optimisation to minimise the metabolic cost of walking by adjusting various control parameters for different individuals [18,19]. Some applications were required to apply different parameters based on assistance onset timing, assistance magnitude and duration, as used in [20]. However, building a seamless controller integrated with all applications and human biological systems is still challenging. Therefore, some researchers used reinforcement learning for optimal controllers or to perform a normative range of motion and gait patterns during locomotion [21,22]. While others applied real-time optimisation control strategies based on measurements of the user, machine learning to implement various dynamic controllers, EMG-based controllers or observer-based robust controllers [23,24,25,26]. However, the most used controller is the proportional integral derivative (PID), which showed its insufficient performance in tracking a predefined trajectory and overcoming changes to model parameters and uncertainties [16,27,28]; therefore, an optimal controller, a linear quadratic regulator (LQR), is proposed to be used in this work.
However, the hip exoskeleton, like other active exoskeleton devices, contains sensors, actuators, links, batteries and electronic circuits that operate in close contact with patients; for this reason, it should operate safely and reliably. For a safe hip rehabilitation exoskeleton, a series elastic actuator (SEA) is chosen for this research, as it presents a compliant interface, accurate and stable torque control over time, low impedance and shock tolerance (elasticity), all of which afford highly confident force control and comfortable wearability and it extends the operational life time of the joint [8,16,28,29,30,31,32,33,34]. An SEA was used at the hip joint to replicate the hip torque signals of a healthy joint as desired movements in the controller.
However, the functions of the controller depend on the mathematical representation and modelling of the system. This can be a challenge because it is an approximation to a real system, which can also be affected by parametric uncertainties, variations or short-term and long-term stochastic noise disturbances (ageing) [27,35]. To the best of our knowledge, no research has validated the LQR for robustness and energy consumption. Therefore, the goal of this study is to validate the LQR controller of a rehabilitation hip exoskeleton for such variations and uncertainties and to establish the foundation of safe human–robot interactions for future research. Hence, the basic design for the exoskeleton and the SEA was introduced in [8,28,36]. Estimating the states of the system was essential for the controller; therefore, the Luenberger observer (LO) was used. The implementation and design of the LO are elaborated in [8].
Not only did the controllers attract the attention of researchers and innovators, but also the weight of such devices, as rehabilitation exoskeletons are usually attached to deficit limbs. Therefore, the energy consumption is worth studying to avoid the extra weight of additional batteries, especially when the powered hip rehabilitation exoskeleton is used outdoors and at home. The contributions of this paper are threefold: an examination of the robustness of four LQR controller cases, validation of the performance of such controllers and investigation of the energy consumption of our rehabilitation hip exoskeleton performing STS and walking movements at each control case and at various speeds. The experiments were conducted in a simulated environment as it provided insight into how an exoskeletal system behaved in a virtual environment that mimicked a real one. They assessed the performance of the model by testing various parameters that were difficult, expensive and time-consuming to reproduce using the physical model [37]. This was especially true of safety, which is a critical factor in experimental designs for human–robot interactions.
This paper is organised as follows: Section 2 presents the importance of the STS and walking activities trained by the rehabilitation hip exoskeleton, LQR strategy, concepts of robustness, performance of the controller in tracking a trajectory signal measured by root mean square errors (RMSEs), energy consumption and STS and walking power calculations. In Section 3, the methods used to test the robustness of four optimal control cases, the RMSE and a simulation energy consumption of a proposed rechargeable battery during the STS and walking movements are analysed. Finally, the results and conclusion are provided in Section 4 and Section 5, respectively.
2. Theory
The worldwide demand for rehabilitation exoskeletons is increasing along with the number of people who have partial or complete mobility disorders and SCI. Gait disorders also include people with cerebral palsy, osteoarthritis and joint replacements who need repetitive rehabilitation sessions and, usually, long-term hospitalisation.
A mobility disorder does not affect physical movement but can lead to medical complications such as osteoporosis, high blood pressure, muscle spasticity and pressure ulcers [38]. Thus, the sit-to-stand and walking activity was the main means by which our rehabilitation hip exoskeleton could provide mobility by overcoming the aforementioned clinical conditions.
2.1. Sit-to-Stand and Walking Activity
Rising from a seated position is a primary step towards pursuing gait mobility for daily activities and improving the quality of life. The STS is a crucial link between a static position and a dynamic activity, which is still a challenging aspect after a stroke [39]. In addition, the STS stimulates the circulatory and respiratory systems, reduces spasticity and increases bone density [40].
Therefore, for rehabilitation purposes, repetitive STS activities at various torque levels representing five angular speed movements were performed and analysed, followed by an analysis of walking movements at five torque levels equivalent to walking on a treadmill at various linear speeds (0.5–2.6 m/s). To control the rehabilitation hip exoskeleton, an admittance control strategy was used in which the hip torque of a healthy person, , at various torque levels was used for reference control signals. The torque signal of a healthy hip performing STS was used to control the STS activity, , whereas the torque signal of a healthy hip performing walking movements, , was applied to the walking control strategy. The torque control signals for both STS and walking are further discussed in [8,41,42] and are also shown in Figure 1 and Figure 2.
Because higher movement speeds require a higher torque, a lower torque level was selected for low-speed movement or when the patient’s joint required a small amount of torque [43]. In addition, people have different disorders and rehabilitative needs; therefore, five torque levels were used in the control strategy to fulfil the various rehabilitation sessions. Figure 1 and Figure 2 show that, if the exoskeleton was designed to train patients at a faster speed, the maximum hip torque signal of a healthy person was set at the fifth level as a reference control signal. On the other hand, the torque was set to the first level if the minimum walking speed (0.5 m/s) was needed.
Lastly, the rehabilitation hip exoskeleton aimed to restore the impaired hip torque signal to that of a healthy one by the end of the treatment program. Healthy torque signals can vary with speed, which can be assigned and modified by a physiotherapist to tackle different conditions and needs. For this reason, the hip torque signal at various speeds was controlled using an LQR. Then, the control behaviour was analysed for the robustness; RMSEs, which show the differences between the desired and measured torque signals; and the energy needed to perform repetitive sessions, which will be illustrated later.
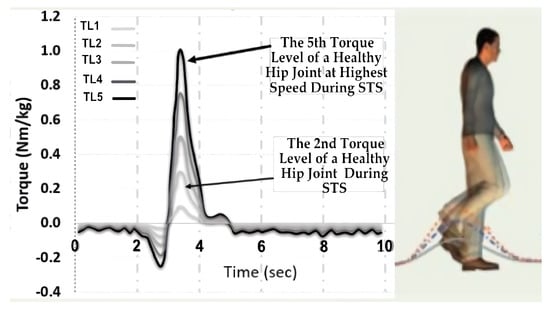
Figure 1.
The hip torque during STS activity [8,44].
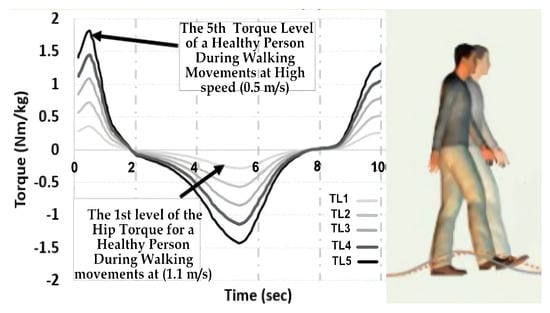
Figure 2.
The hip torque during walking activity [8,44].
2.2. The Linear Quadratic Regulator
Trajectory tracking with predefined movements is commonly used in rehabilitation exoskeletons for the lower extremities because patients can be trained passively to follow desired reference motions [8,10]. Therefore, an admittance controller based on the torque of a healthy hip joint was used for the rehabilitation exoskeleton to train the patient’s weak muscles. The controller was used with an SEA and LQR that were chosen for the reasons set out in Section 1. The SEA was used to generate the proper current for the desired torque and applications. Thus, an LQR with a Luenberger observer was used, but a mathematical model expressing the rehabilitation hip exoskeleton was needed, as illustrated in [8] and depicted based on the literature [28,36,45].
To use the LQR, the state space model of the exoskeleton was represented in the following form
where is a vector matrix representing the system states; A, B, C and D are the system’s dynamic matrices; u is the system input signal; and y is the output signal. However, the states of the system are not always accessible for sensors; thus, an observer is commonly used. Many observers are used through control systems, but the one that can increase the control system’s bandwidth and improve the disturbance response indirectly is the Luenberger observer [46], which estimates the states by using the inputs u and the outputs y of the system. Finally, it subtracts the output of the observer, , from the output of the system, y.
On the LQR controller side, the optimal placement of the system poles was based on the weights of the Q and R matrices by minimising the quadratic cost function J and finding the minimum steady-state error and the best feedback gain [47].
where Q and R are the semi-definite and positively definite design matrices, respectively. By tuning Q and R, the placement of the poles was changed, whereas the feedback gain, K, was determined from the Hamilton–Jacobi–Bellman method and solved by using the Riccati equation [8,48] that ends with
The feedback gain, K, increased or decreased depending on the values selected for Q and R. A larger weight value in R set a higher penalty on the input signal, u, which decreased the feedback gain, K and slowed the steady state and the energy needed. Conversely, the large weight values of Q meant a higher penalty on the state of the system, x, when finding the minimum cost function, J, according to (2), which increased the value of the feedback gain, K, in (3) and accelerated the system’s response accordingly.
The system states, , were necessary for the LQR algorithm, which can be inaccessible in many real systems or expensive to measure with certain sensors; thus, an LO was a suitable solution for deriving the system states [8].
The system states, , can be estimated by putting the input, u, and the system output, y, into LO. The procedures for obtaining the states and the LO diagram are discussed in more detail elsewhere [8]. Although the states are critical to finding the mathematical model of the system, which needs to be optimally controlled using the LQR, the model of the system will nevertheless include errors and imperfect model representation is more common compared to real systems. Therefore, the system robustness for the various Q and R is analysed and the energy consumption was studied regarding the sensitivity of the system to the model uncertainty.
2.3. Robustness
The control strategy depended on modelling the system, yet the mathematical model representation was based on physical components that are quite often simplified [49]. Additionally, a system may also have disturbances, stochastic noise resources or a dynamic behaviour that is hard to represent. Consequently, the mathematical representation or transfer function that describes a system is only an approximation of the real system. This means that the control system may not work in exactly the same manner on the real hardware as it does in the mathematical model. For this reason, the stability and robustness of the system in the presence of model uncertainty were simply analysed using a disk-based uncertainty (disk margin, DM) for gain (DGM) and phase (DPM) perturbation representation [50].
The DM visualises the stability of a closed-loop system for a combination of gain and phase variation. The margin shows how much uncertainty the controller can tolerate before the system becomes unstable. Another method for investigating system stability is using Nyquist’s stability criterion, which is elaborated in [51]. The stability of the system is described by how far the Nyquist curve can move away from the point (−1) before the system collapses.
After studying the Nyquist curve for all the optimal controller cases to identify the most robust optimal controller for a certain activity, the controller behaviour of the optimal cases was then studied at various speeds. The performance of the optimal controllers with various degrees of robustness was then analysed to determine the relationships among robustness, different speeds and energy consumption for different activities. The performance of a certain controller was measured by the RMSEs, comparing the torque signals with the desired torque reference signals.
2.4. The Performance and the Root Mean Square Error
The performance of the LQR case strategy was evaluated according to the RMSE between the measured torque signal, , of the LQR and the desired torque reference signal, , as deduced by
where n is the number of observation points over time. The represented in this work is the for STS and for walking at different speeds.
2.5. Energy Consumption and Power Calculation
The energy consumption of an SEA is derived from the power needed to rotate the motor with torque and angular velocity , so the power, P, is
where is the derivative of the motor angular position and the angular velocity is found by the simulation program, but can also be calculated based on the literature [42,52]. It is worth mentioning that we assumed the motor required the same energy for thrusting, and damping, . Thus, the energy, E, for each step in STS and walking achieved by the rehabilitation hip exoskeleton can be calculated as
Then, the number of steps of the STS or walking activity can be calculated as the total amount of energy stored in a battery divided by the amount of energy consumed in each step movement.
3. Methods
The simulation and design of the rehabilitation hip exoskeleton were modelled on the Denavit–Hartenberg (DH) parameters as shown in Figure 3 using the MATLAB and Autodesk Inventor software. The actuator selection was an SEA for the active hip joint. The hip rehabilitation consisted of a pelvis, four links for both legs and four joints that were active, except the knees, which were passive, ending up with a four-degree-of-freedom (DoF) prototype moving in the sagittal plane. The limitations and the range of motion (RoM) for each joint were based on the data in Table 1 [8]. The trunk and exoskeleton masses were connected to a body-weight-supported treadmill similar to the one used with the LokomatPro exoskeleton [53].
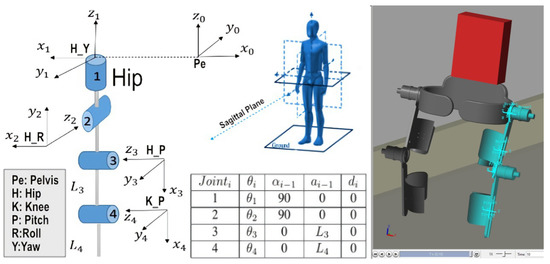
Figure 3.
The DH parameters and the rehabilitation hip exoskeleton model [8].

Table 1.
The hip and knee joints with their range of motions (RoMs) [8].
The control framework was based on a linear quadratic regulator of an SEA for a hip rehabilitation exoskeleton in which the torque control signals were the reference signals in the admittance control strategy. The control signals were five levels of torque ( to ) of STS and the walking activities for healthy subjects, as shown in Figure 1 and Figure 2 and in articles [8,41,42].
The kinematic and kinetic formulation, the system mathematical representation and the admittance control are thoroughly discussed in [8], where the modelling was based on the average height and weight of male subjects. The length of the thigh link was 52 and the shank link was 39 cm, as mentioned in [54]. The SEA was modelled based on [55,56,57,58] and the parameters used are shown in Table 2, where and are the inertia of the motor, spring and load link, respectively. and are the damping coefficients for the motor, spring and load, respectively, whereas and N are the spring stiffness and gear ratios in the SEA. Therefore, these parameters with the system links concluded with the transfer function .

Table 2.
The simulation parameters of the SEA [56].
The LQR control strategy was considered to operate in a linear time-invariant system for this study. The LQR was examined with four different values of the Q and R matrices (four cases), which were chosen empirically with different weights on Q and R to check the speed and robustness with different penalties on the input signal and states as shown in Table 3, which were the basis for finding the minimum quadratic cost function, J, regarding (2) and, consequently, the optimal controller.

Table 3.
Four controller cases with different Q and R values.
Moreover, the result of using the regulator to follow the trajectory torque signal was investigated in the form of the RMSE. Finally, the energy consumption and distance for each step activity when using the hip exoskeleton powered by a charged battery (lithium–iron 48 V, 150 Wh, with 30 LiFePO cells mounted in a battery tray) for each hip joint were simulated and studied.
4. Results and Discussion
For the robustness analyses of the system, we checked the gain () and phase margins (), as the margin is one way to specify how much uncertainty the controller design can handle before the system becomes unstable [59]. Therefore, we checked the pure gain margin/classical gain margin () and pure phase margin/classical phase margin () for all controller cases that examined the controller’s sensitivity to different uncertainties. Table 4 shows, for instance, that the controller Case 1 was still stable if the gain variations in a real system were up to 33.2 dB higher than those in our designed model. The same was valid for stability if the phase variations in the real system were up to deg higher than those in the designed model. However, this variation was valid only if there was a or only, which is uncommon in real scenarios; thus, we analysed the controller cases with a combination of both and called (see Table 4). The showed that the border of in Case 1 was within (0.2–4.5) around the nominal point 1 of the Nyquist plane, while the tolerance for phase variation was within deg. Another way to analyse the robustness of a system to uncertainty and variation was studying the Nyquist plot (see Figure 4) for each controller case.

Table 4.
Gain and phase disk margins for four different controller cases.
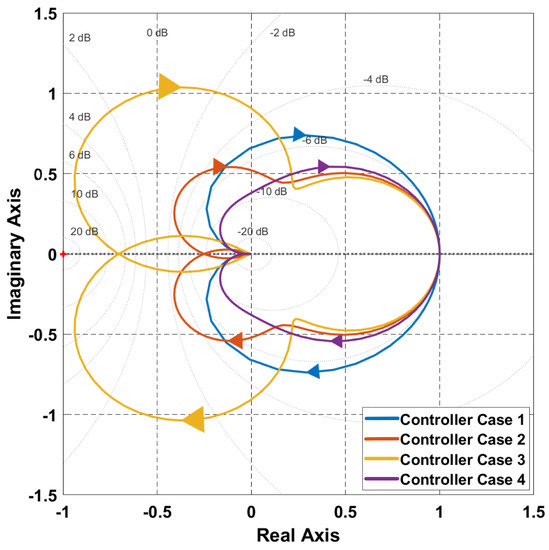
Figure 4.
The Nyquist plots of the four controller cases.
As shown in Figure 4 and Table 4, the most robust controller was Case 4 with ( = 1.4), which tolerated more uncertainties based not only on the Nyquist plot but also on the combined gain and phase disk margin dB) and disk phase margin ( deg) with respect to the other three cases as also shown in Figure 5.
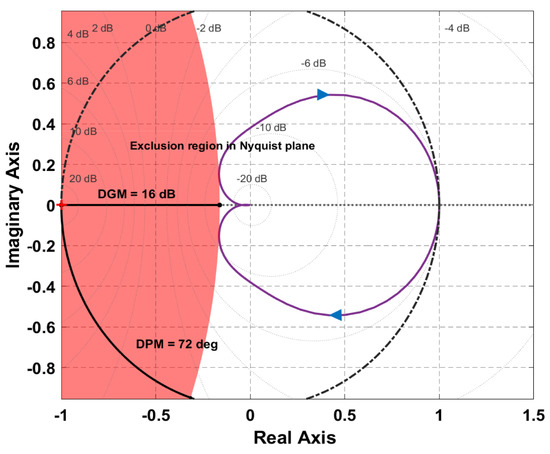
Figure 5.
The disk margin of the fourth case controller.
We then examined how each controller case tracked the hip torque reference signal for a healthy person in STS and walking activities at five torque levels, which represented various angular velocities for the joint’s movements. The energy consumption per step activity with the four controller cases and five torque levels have also been studied.
Lastly, the number of times for the rehabilitation hip exoskeleton in STS was compared with the numbers of times for different controller cases and torques. The distances reached with a fully charged battery for each hip joint in the walking activity were also calculated. The results for STS and walking activity—based on a simulation—were as follows.
4.1. Sit-to-Stand Activity
The RMSE and energy consumption for each controller case with various torques are shown in Table 5 and Table 6, while the numbers of times that each case and torque in STS could be reached are shown in Table 7. As the function of the LQR controller is based on the system states and the control signal combined at the same time, it is interesting to study the effects on each of the two criteria, but we chose the RMSE as a base of our evaluation of the control performance.

Table 5.
The RMSE for sit to stand ( Nm/kg).

Table 6.
The energy consumption for sit to stand (milliwatts).

Table 7.
The number of sit-to-stand movements with a fully charged battery (step).
4.2. Walking Activity
The RMSE, the energy consumption for the walking activity and the distance when using each controller at different torque levels are illustrated in Table 8, Table 9 and Table 10, respectively.

Table 8.
The RMSE of walking ( Nm/kg).

Table 9.
The energy consumption per walking step (milliwatts).

Table 10.
The distance of walking (kilometres).
Despite the fact that the regulator in Case 4 was the most robust controller, the RMSEs for STS and walking activity at the various torques were still not the minimum values compared with the other cases. The RMSEs were the highest for STS and walking in Case 4 at all torque levels compared with those for other cases, while the RMSEs for Case 1 were the lowest for STS and walking movements. The reason controller Case 1 had the lowest RMSE values was the longer distance of the poles on the left half of complex planes to the origin. The faster response of the controller occurred when the poles lay far away from the origin or the controller had a large input signal [60]. For this reason, controller Case 1 provided a faster response to the dynamics of the system because its poles lay on (, ) and its , compared with controller Case 4, which had its poles on (, ) with a minimum input signal due to the high penalty value of . Although Case 4 was farther away from the origin than Case 1, it still had its dominant pole at (), which was closer to the origin than the dominant pole of Case 1 at (). Consequently, the system slowed in Case 4, which affected the system’s behaviour and speed [61].
Additionally, the higher the torque/angular speed of the STS and walking activity, the higher the RMSEs. However, in analysing the energy consumption required for each step in STS and walking, we noticed that the controller Case 4, considered to be the most robust regulator, demanded less energy in STS compared with other controller cases (see Figure 6 and Table 6). Therefore, we found the highest number of times by pursuing STS using controller Case 4 at all torques.
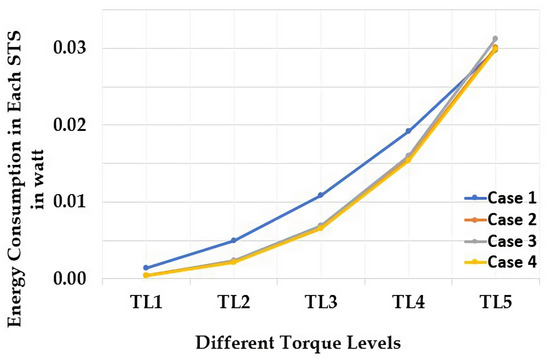
Figure 6.
The energy consumption for sit to stand with different Q and R matrices and torque levels.
Interestingly, controller Case 4 in the walking activity did not have the lowest consumed energy at all torque levels as it showed in STS. The differences are obvious in Figure 7 and Table 9; in particular, the controller Case 1 and Case 4 had the lowest energy consumption at the speed of 0.5 m/s = ) and the second-lowest energy consumption at a speed of 2.6 m/s = for Case 4; still, the controller Case 1 had the lowest energy consumption at speeds of 0.5 m/s = and 2.6 m/s = , respectively. Therefore, we obtained the longest distance for the walking activity in Case 1 at speeds of 0.5 m/s = and 2.6 m/s = , as shown in Table 10, compared to in other cases.
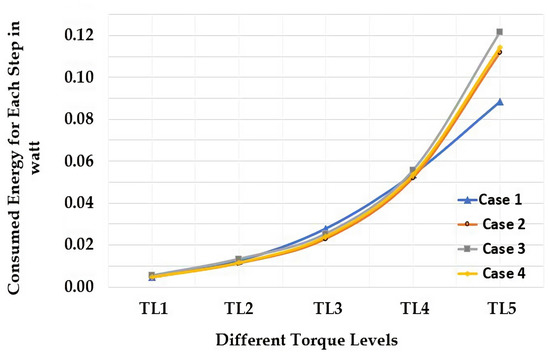
Figure 7.
The energy consumption of walking with different Q and R matrices and torque levels.
Another notable feature of the walking activity was that the most extended distances were reached in Case 2 at speeds of 1.1–2.1 m/s = – compared with the other cases for these speeds. The benefit of obtaining the longest distances was caused by the minimal energy consumed in Case 2 at these speeds (see Table 9 and Table 10). This finding supported the hypothesis that the highest penalty of the R matrix in the quadratic cost function led to instability in walking activity at certain speeds. By contrast, the STS refuted this hypothesis by the choice of the highest for controller Case 4, which was also the most robust controller case.
Thus, a possible solution is having a different mode in the operating system of the rehabilitation hip exoskeleton if the economic control strategy with the longest distance is the final target. However, this could be a solution for walking activity for certain speeds but not for STS, as the controller Case 4 in STS showed its efficient energy consumption and the number of times for achieving STS. For the walking activity, however, choosing the more energy-efficient controller cases such as Case 1 or 2 could lead to a penalty in robustness against uncertainties, as these cases were not robust cases compared with Case 4, as shown in Figure 4 and Table 4.
Subsequently, as Case 4, the most robust controller, gave the second-longest walking distance at all speeds and the highest number of times for STS, it would be the more reliable regulator choice for our rehabilitation hip exoskeleton. With the Case 4 controller, we obtain the optimal robust controller with high performance and energy efficiency.
It is worth mentioning that the controller-related energy consumption comparison between the sit-to-stand and walking activities will have differences compared to the real world as well as between the real walking on a treadmill or overground. The differences between the simulation and real world are caused by many reasons—firstly, as they depend on the modelling process, which in most cases are approximations of the real systems. Secondly, the error caused in experimental data could be affected by instruments’ errors and disturbances, which can be illuminated or processed in simulation environments. Thirdly, the simulation models are usually bounded by some assumptions. However, the simulation process can be used to verify if the errors or certain behaviour lie within the accepted domain (margin) before producing a physical system. Finally, as the linear time-invariant system was the foundation in operation of the controller cases in this research, more future study on combining the disturbance observer or a sliding mode observer is worth undertaking to overcome the non-linearity, parametric uncertainties and external disturbances [24,28,62].
5. Conclusions
Although the LQR ensured finding the optimal controller with the minimum cost function, the Q and R matrix values affected the system robustness, as it moved the system poles to various placements to stabilise the system. This study provides ample evidence that selecting appropriate Q and R influences not only the cost function but also the energy consumption and the performance of the optimal controller, specifically when the exoskeleton is restricted by certain design aspects.
The most robust optimal controller in STS showed great potential for energy consumption and the highest number of times pursuing the STS activity, while it was less efficient for walking activity. However, the most effective way to reduce the energy consumption of a rehabilitation hip exoskeleton in any activity is studying the speed required for rehabilitation and adjusting the activity to a lower torque.
This method ensured that using the exoskeleton over a longer distance when walking, and a greater number of times for STS, showed good performance when there was less choice in finding suitable Q and R matrices.
Author Contributions
Conceptualisation, R.A. and N.B.; methodology, R.A. and N.B.; software, R.A.; validation, R.A.; formal analysis, R.A. and N.B.; investigation, R.A.; resources, R.A. and N.B.; data curation, R.A.; writing—original draft preparation, R.A.; writing—review and editing, N.B.; visualisation, R.A.; supervision, N.B.; project administration, R.A.; funding acquisition, R.A. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data generated in the simulation part are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SCI | Spinal Cord Injury |
| LQR | Linear Quadratic Regulator |
| SEA | Series Elastic Actuator |
| STS | Sit To Stand |
| LO | Luenberger Observer |
| PID | Proportional Integral Derivative |
| CGM | Classical Gain Margin |
| CPM | Classical Phase Margin |
| GM&PM-C | Gain and Phase Margin Combined |
| DM | Disk Margin |
| DGM | Disk Gain Margin |
| DPM | Disk Phase Margin |
| RMSE | Root Mean Square Error |
| DH | Denavit Hartenberg Parameters |
| DoF | Degree of Freedom |
| RoM | Range of Motion |
References
- Andersson, R.; Björsell, N.; Isaksson, M. Robots Are a Promising Investment to Fight Pandemics. In Proceedings of the 8th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 26–27 August 2021; pp. 458–463. [Google Scholar]
- Buongiorno, D. Advanced Control Strategies ForNatural Human-Exoskeleton Interaction. Ph.D. Dissertation, Sant’ Anna School of Advanced Studies, Pisa, Italy, 2017. [Google Scholar]
- Pons, J.L. Wearable Robots: Biomechatronic Exoskeletons; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Turja, T.; Saurio, R.; Katila, J.; Hennala, L.; Pekkarinen, S.; Melkas, H. Intention to Use Exoskeletons in Geriatric Care Work: Need for Ergonomic and Social Design. Ergon. Des. 2020, 30, 13–16. [Google Scholar] [CrossRef]
- Patel, D.R.; Neelakantan, M.; Pandher, K.; Merrick, J. Cerebral Palsy in Children: A Clinical Overview. Transl. Pediatr. 2020, 9, S125–S135. [Google Scholar] [CrossRef] [PubMed]
- Volpicelli, G.M. Review: Sportsmate 5 Fitness Exoskeleton|WIRED. WIRED.com. Available online: https://www.wired.com/review/sportsmate-5-fitness-exoskeleton/ (accessed on 10 July 2022).
- Yuzbasioglu, N. Elderly to Make Up 22% of World Population by 2050. 2021. Available online: https://www.aa.com.tr/en/life/elderly-to-make-up-22-of-world-population-by-2050/2379462 (accessed on 10 July 2022).
- Andersson, R.; Björsell, N. The MATLAB Simulation and the Linear Quadratic Regulator Torque Control of a Series Elastic Actuator for a Rehabilitation Hip Exoskeleton. IRCE 2022, in press.
- İşcan, M.; Eken, H.; Vural, B.; Yılmaz, C. Design and Control of an Exoskeleton Robot: A Matlab Simscape Application. J. Therm. Eng. 2018, 4, 1867–1878. [Google Scholar]
- Chen, B.; Ma, H.; Qin, L.Y.; Gao, F.; Chan, K.M.; Law, S.W.; Qin, L.; Liao, W.H. Recent Developments and Challenges of Lower Extremity Exoskeletons. JOT 2016, 5, 26–37. [Google Scholar] [CrossRef] [PubMed]
- Hsu, S.H.; Changcheng, C.; Lee, H.J.; Chen, C.T. Design and Implementation of a Robotic Hip Exoskeleton for Gait Rehabilitation. Actuators 2021, 10, 212. [Google Scholar] [CrossRef]
- Budhota, A.; Chua, K.S.G.; Hussain, A.; Kager, S.; Cherpin, A.; Contu, S.; Vishwanath, D.; Kuah, C.W.K.; Ng, C.Y.; Yam, L.H.L.; et al. Robotic Assisted Upper Limb Training Post Stroke: A Randomized Control Trial Using Combinatory Approach Toward Reducing Workforce Demands. Front. Neurol. 2021, 12, 804. [Google Scholar] [CrossRef]
- Huo, W.; Mohammed, S.; Moreno, J.C.; Amirat, Y. Lower Limb Wearable Robots for Assistance and Rehabilitation: A State of the Art. IEEE Syst. J. 2016, 10, 1068–1081. [Google Scholar] [CrossRef]
- Moreno, J.C.; Brunetti, F.; Navarro, E.; Forner-Cordero, A.; Pons, J.L. Analysis of the Human Interaction with a Wearable Lower-Limb Exoskeleton. Appl. Bionics Biomech. 2009, 6, 245–256. [Google Scholar] [CrossRef]
- Long, Y.; Du, Z.J.; Wang, W.; Dong, W. Development of a Wearable Exoskeleton Rehabilitation System Based on Hybrid Control Mode. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416664847. [Google Scholar] [CrossRef]
- Ibrahim, H.A.; Ammar, H.H.; Shalaby, R. Modeling and Control of a Novel Design of Series Elastic Actuator for Upper Limb Rehabilitation. Math. Model Eng. Probl. 2022, 9, 85–93. [Google Scholar] [CrossRef]
- Yu, H.; Huang, S.; Chen, G.; Pan, Y.; Guo, Z. Human-Robot Interaction Control of Rehabilitation Robots with Series Elastic Actuators. IEEE Trans. Robot. 2015, 31, 1089–1100. [Google Scholar] [CrossRef]
- Zhang, J.F.; Yang, C.J.; Chen, Y.; Zhang, Y.; Dong, Y.M. Modeling and Control of a Curved Pneumatic Muscle Actuator for Wearable Elbow Exoskeleton. Mechatronics 2008, 18, 448–457. [Google Scholar] [CrossRef]
- Ding, Y.; Kim, M.; Kuindersma, S.; Walsh, C.J. Human-in-the-Loop Optimization of Hip Assistance with a Soft Exosuit during Walking. Sci. Robot. 2018, 3, eaar5438. [Google Scholar] [CrossRef] [PubMed]
- Kang, I.; Hsu, H.; Young, A. The Effect of Hip Assistance Levels on Human Energetic Cost Using Robotic Hip Exoskeletons. IEEE Robot. Autom. Lett. 2019, 4, 430–437. [Google Scholar] [CrossRef]
- Tu, X.; Li, M.; Liu, M.; Si, J.; Huang, H. A Data-Driven Reinforcement Learning Solution Framework for Optimal and Adaptive Personalization of a Hip Exoskeleton. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10610–10616. [Google Scholar] [CrossRef]
- Zhang, Q.; Nalam, V.; Tu, X.; Li, M.; Si, J.; Lewek, M.D.; Huang, H. Imposing Healthy Hip Motion Pattern and Range by Exoskeleton Control for Individualized Assistance. IEEE Robot. Autom. Lett. 2022, 7, 11126–11133. [Google Scholar] [CrossRef]
- He, H.; Kiguchi, K. A Study on EMG-Based Control of Exoskeleton Robots for Human Lower-Limb Motion Assist. In Proceedings of the 2007 6th International Special Topic Conference on Information Technology Applications in Biomedicine, Tokyo, Japan, 8–11 November 2007; pp. 292–295. [Google Scholar] [CrossRef]
- Mefoued, S.; Belkhiat, D.E.C. A Robust Control Scheme Based on Sliding Mode Observer to Drive a Knee-Exoskeleton. Asian J. Control 2019, 21, 439–455. [Google Scholar] [CrossRef]
- Franks, P.W.; Bryan, G.M.; Martin, R.M.; Reyes, R.; Lakmazaheri, A.C.; Collins, S.H. Comparing Optimized Exoskeleton Assistance of the Hip, Knee and Ankle in Single and Multi-Joint Configurations. Wearable Technol. 2021, 2, e16. [Google Scholar] [CrossRef]
- Mahdavian, M.; Arzanpour, S.; Park, E.J. Motion Generation of a Wearable Hip Exoskeleton Robot Using Machine Learning-Based Estimation of Ground Reaction Forces and Moments. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Tokyo, Japan, 8–11 November 2007; pp. 796–801. [Google Scholar] [CrossRef]
- Ajayi, M.O. Modelling and Control of Actuated Lower Limb Exoskeletons a Mathematical Application Using Central Pattern Generators and Nonlinear Feedback Control Techniques. Ph.D. Dissertation, Tshwane University of Technology, Pretoria, South Africa, 2016. [Google Scholar]
- Ugurlu, B.; Sariyildiz, E.; Kansizoglu, A.T.; Ozcinar, E.; Coruk, S. Benchmarking Torque Control Strategies for a Torsion-Based Series Elastic Actuator. IEEE Robot. Autom. Mag. 2021, 29, 85–96. [Google Scholar] [CrossRef]
- Pratt, G.A.; Williamson, M.M.; Dillworth, P.; Pratt, J.; Wright, A. Stiffness Isn’t Everything. In Experimental Robotics IV; Springer: Berlin/Heidelberg, Germany, 2005; pp. 253–262. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Z.; Zhang, Y.; Xiao, X.; Tan, J. A Novel Design of Serial Variable Stiffness Actuator Based on an Archimedean Spiral Relocation Mechanism. IEEE/ASME Trans. Mechatron. 2018, 23, 2121–2131. [Google Scholar] [CrossRef]
- Pratt, G.A.; Williamson, M.M. Series Elastic Actuators. IEEE Int. Conf. Intell. Robot. Syst. 1995, 1, 399–406. [Google Scholar] [CrossRef]
- Ham, V.R.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant Actuator Designs: Review of Actuators with Passive Adjustable Compliance/Controllable Stiffness for Robotic Applications. IEEE Robot. Autom. Mag. 2009, 16, 81–94. [Google Scholar] [CrossRef]
- Song, P.; Yu, Y.; Zhang, X. A Tutorial Survey and Comparison of Impedance Control on Robotic Manipulation. Robotica 2019, 37, 801–836. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, D.; Qian, W.; Xiao, X.; Guo, Z. Modeling and Control of a Cable-Driven Rotary Series Elastic Actuator for an Upper Limb Rehabilitation Robot. Front. Neurorobot. 2020, 14, 13. [Google Scholar] [CrossRef]
- Chen, J.; Fan, Y.; Sheng, M.; Zhu, M. Optimized Control for Exoskeleton for Lower Limb Rehabilitation with Uncertainty. In Proceedings of the 2019 Chinese Control And Decision Conference, Nanchang, China, 3–5 June 2019; pp. 5121–5125. [Google Scholar]
- Yildirim, M.C.; Sendur, P.; Kansizoglu, A.T.; Uras, U.; Bilgin, O.; Emre, S.; Yapici, G.G.; Arik, M.; Ugurlu, B. Design and Development of a Durable Series Elastic Actuator with an Optimized Spring Topology. J. Mech. Eng. Sci. 2021, 235, 7848–7858. [Google Scholar] [CrossRef]
- Khamar, M.; Edrisi, M.; Zahiri, M. Human-Exoskeleton Control Simulation, Kinetic and Kinematic Modeling and Parameters Extraction. MethodsX 2019, 6, 1838–1846. [Google Scholar] [CrossRef]
- Piatt, J.A.; Nagata, S.; Zahl, M.; Li, J.; Rosenbluth, J.P. Problematic Secondary Health Conditions among Adults with Spinal Cord Injury and Its Impact on Social Participation and Daily Life. J. Spinal Cord. Med. 2016, 39, 693–698. [Google Scholar] [CrossRef]
- Mao, Y.R.; Wu, X.Q.; Li Zhao, J.; Lo, W.L.A.; Chen, L.; Ding, M.H.; Xu, Z.Q.; Bian, R.H.; Huang, D.F.; Li, L. The Crucial Changes of Sit-to-Stand Phases in Subacute Stroke Survivors Identified by Movement Decomposition Analysis. Front. Neurol. 2018, 9, 185. [Google Scholar] [CrossRef]
- Chen, B.; Zhong, C.H.; Ma, H.; Guan, X.; Qin, L.Y.; Chan, K.M.; Law, S.W.; Qin, L.; Liao, W.H. Sit-to-Stand and Stand-to-Sit Assistance for Paraplegic Patients with CUHK-EXO Exoskeleton. Robotica 2018, 36, 535–551. [Google Scholar] [CrossRef]
- Mak, M.K.Y.; Levin, O.; Mizrahi, J.; Hui-Chan, C.W.Y. Joint Torques during Sit-to-Stand in Healthy Subjects and People with Parkinson’s Disease. Clin. Biomech. 2003, 18, 197–206. [Google Scholar] [CrossRef]
- Grimmer, M.; Seyfarth, A. Mimicking Human-Like Leg Function in Prosthetic Limbs. In Neuro-Robotics; Springer: Dordrecht, The Netherlands, 2014; pp. 105–155. [Google Scholar]
- Pai, Y.C.; Rogers, M.W. Speed Variation and Resultant Joint Torques during Sit-to-Stand. Achieve Med. Rehabil. 1991, 72, 881–885. [Google Scholar] [CrossRef]
- Grimmer, M. Powered Lower Limb Prostheses. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2015. [Google Scholar]
- Yildirim, M.C.; Kansizoglu, A.T.; Sendur, P.; Coruk, S.; Ugurlu, B. Development of a High Torque-to-Mass Ratio Series Elastic Actuator. In Proceedings of the 2018 International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Ellis, G.; George, H. Observers in Control Systems: A Practical Guide; Academic Press: Cambridge, CA, USA, 2002. [Google Scholar]
- Duriez, T.; Brunton, S.L.; Noack, B.R. Machine Learning Dynamics and Taming Nonlinear Control—Turbulence; Fluid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2013; Volume 33. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control—Analisys and Design. Int. J. Robust Nonlinear Control 2001, 1, 585. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Doyle, J.; Francis, B.; Tannenbaum, A. Feedback Control Theory; Macmillan Publishing Co.: London, UK, 1998. [Google Scholar]
- Åström, K.J. Model Uncertainty and Robust Control; Valencia Polytechnic University: Valencia, Spain, 2000; pp. 63–100. [Google Scholar]
- Palomba, I.; Wehrle, E.; Carabin, G.; Vidoni, R. Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements. Appl. Sci. 2020, 10, 7475. [Google Scholar] [CrossRef]
- Van Kammen, K.; Boonstra, A.; Reinders-Messelink, H.; Den Otter, R. The Combined Effects of Body Weight Support and Gait Speed on Gait Related Muscle Activity: A Comparison between Walking in the Lokomat Exoskeleton and Regular Treadmill Walking. PLoS ONE 2014, 9, e107323. [Google Scholar] [CrossRef] [PubMed]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s Segment Inertia Parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Lee, C.; Kwak, S.; Kwak, J.; Oh, S. Generalization of Series Elastic Actuator Configurations and Dynamic Behavior Comparison. Actuators 2017, 6, 26. [Google Scholar] [CrossRef]
- Malzahn, J.; Roozing, W.; Tsagarakis, N. The Compliant Joint Toolbox for MATLAB: An Introduction with Examples. IEEE Robot. Autom. Mag. 2019, 26, 52–63. [Google Scholar] [CrossRef]
- Oh, S.; Kong, K. High-Precision Robust Force Control of a Series Elastic Actuator. IEEE/Asme Trans. Mechatron. 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Munadi; Nasir, M.S.; Ariyanto, M.; Iskandar, N.; Setiawan, J.D. Design and Simulation of PID Controller for Lower Limb Exoskeleton Robot. AIP Conf. Proc. 2018, 1983, 060008. [Google Scholar] [CrossRef]
- Seiler, P.; Packard, A.; Gahinet, P. An Introduction to Disk Margins [Lecture Notes]. IEEE Control Syst. 2020, 40, 78–95. [Google Scholar] [CrossRef]
- Glad, T.; Ljung, L. Control Theory: Multivariable and Nonlinear Methods; Taylor & Francis: Abingdon, UK, 2000. [Google Scholar] [CrossRef]
- Lee, J.; Edgar, T.F. Multiloop PI/PID Control System Improvement via Adjusting the Dominant Pole or the Peak Amplitude Ratio. Chem. Eng. Sci. 2006, 61, 1658–1666. [Google Scholar] [CrossRef]
- Bergmann, L.; Liu, L.; Ngo, C.; Misgeld, B.; Leonhardt, S. Zero-Torque Control of an Exoskeleton Joint Actuator Using a Disturbance Observer. AIP Conf. Proc. 2019, 2140, 020004. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).