On the Omori Law in the Physics of Earthquakes
Abstract
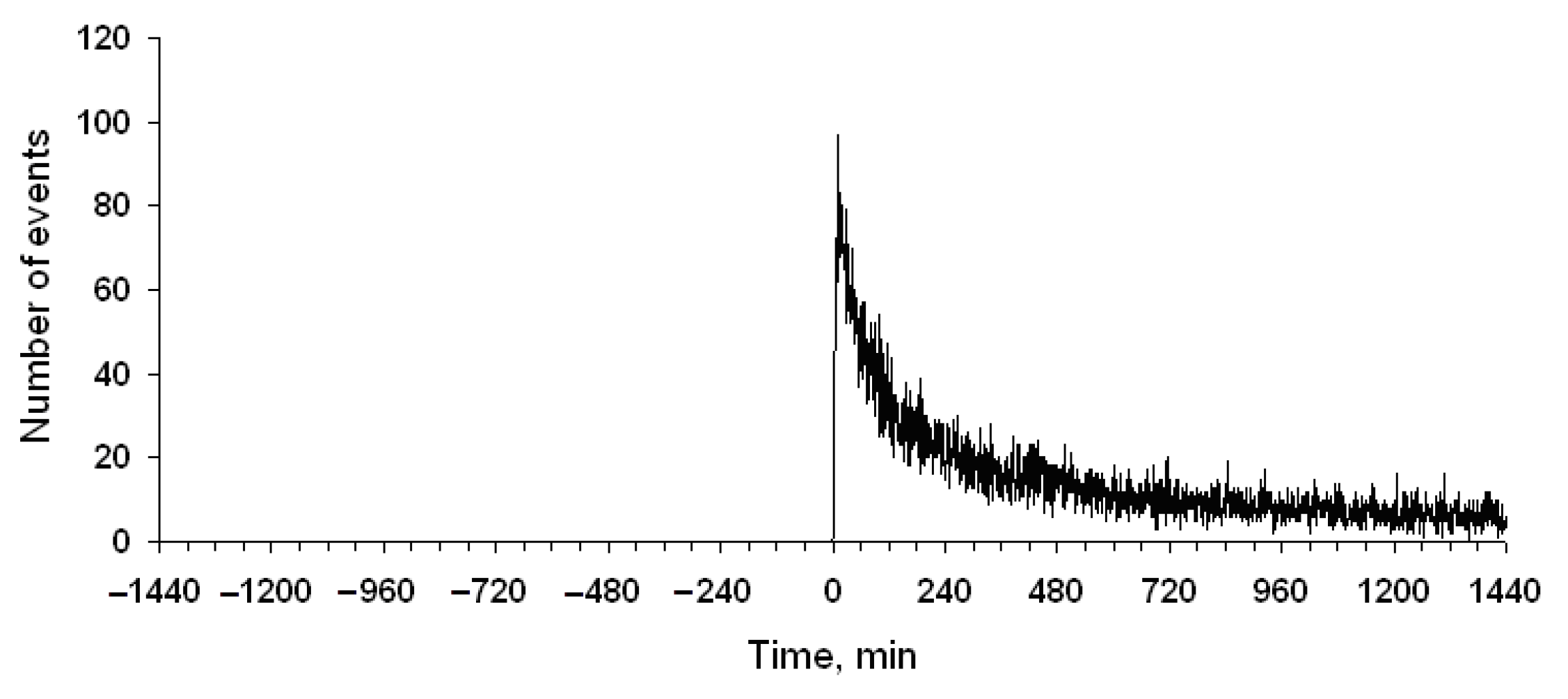
1. Introduction
2. Elementary Master Equation
3. Logistic Equation
4. Stochastic Equation
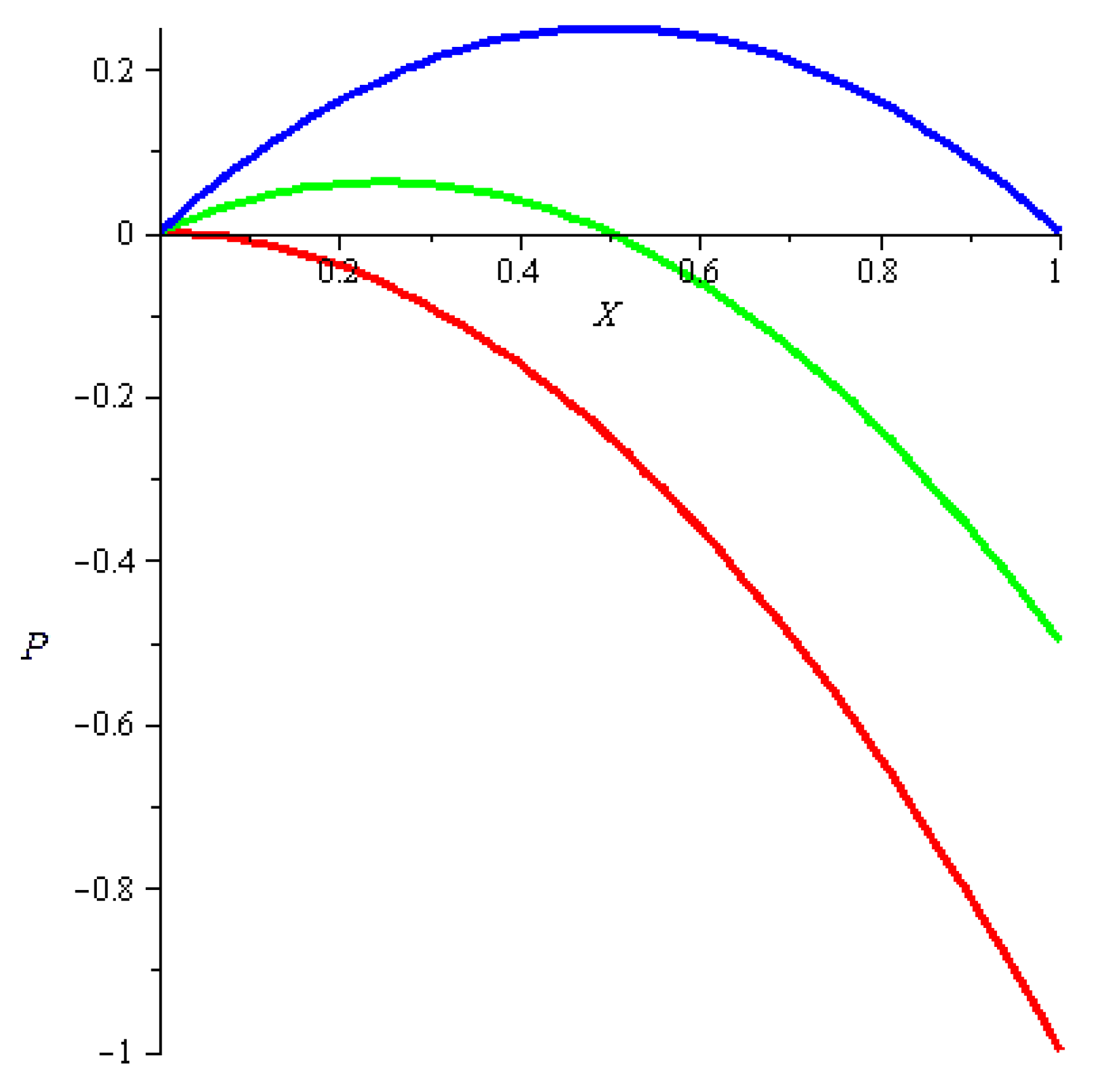
5. Nonlinear Diffusion Equation
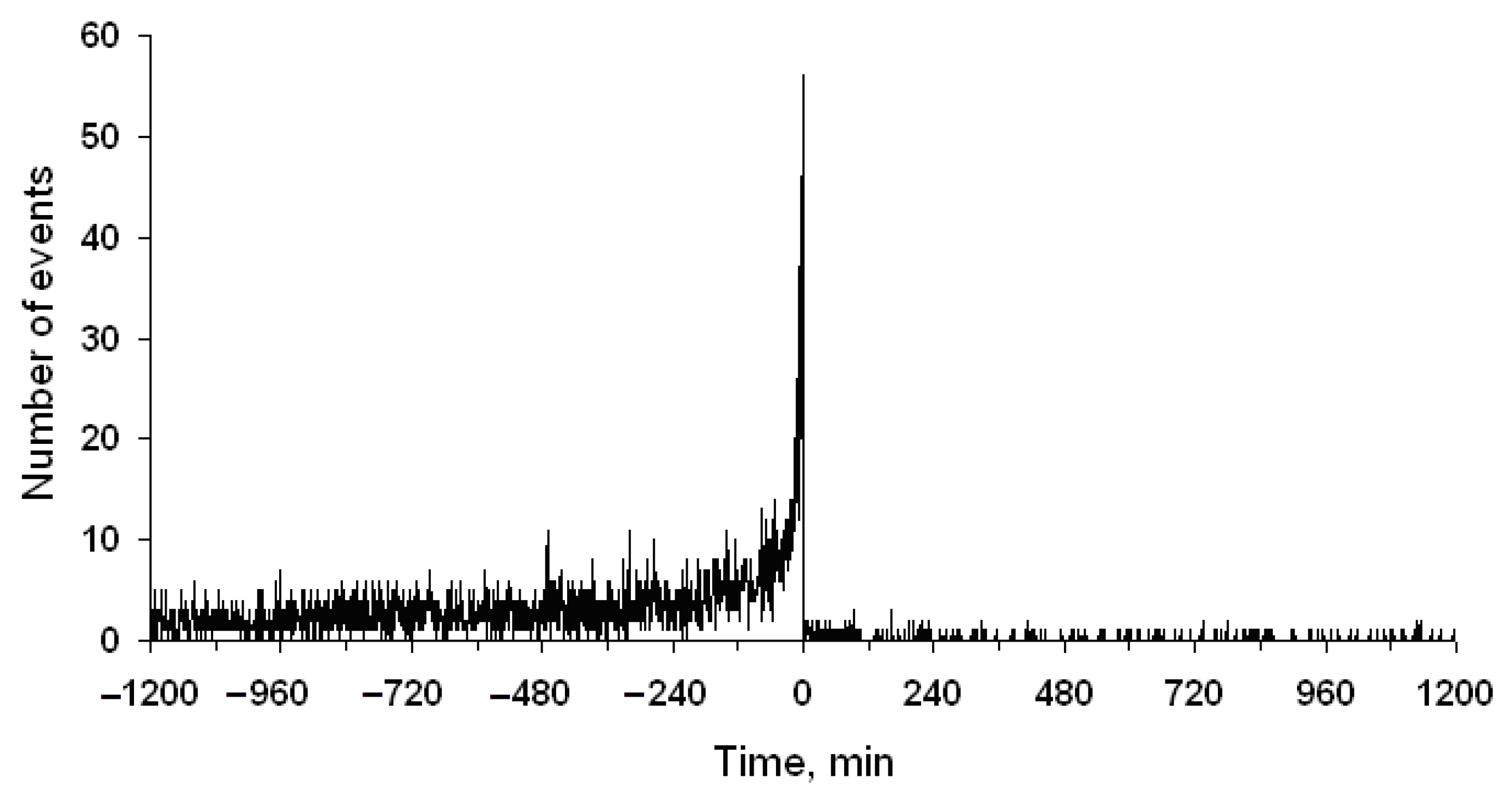
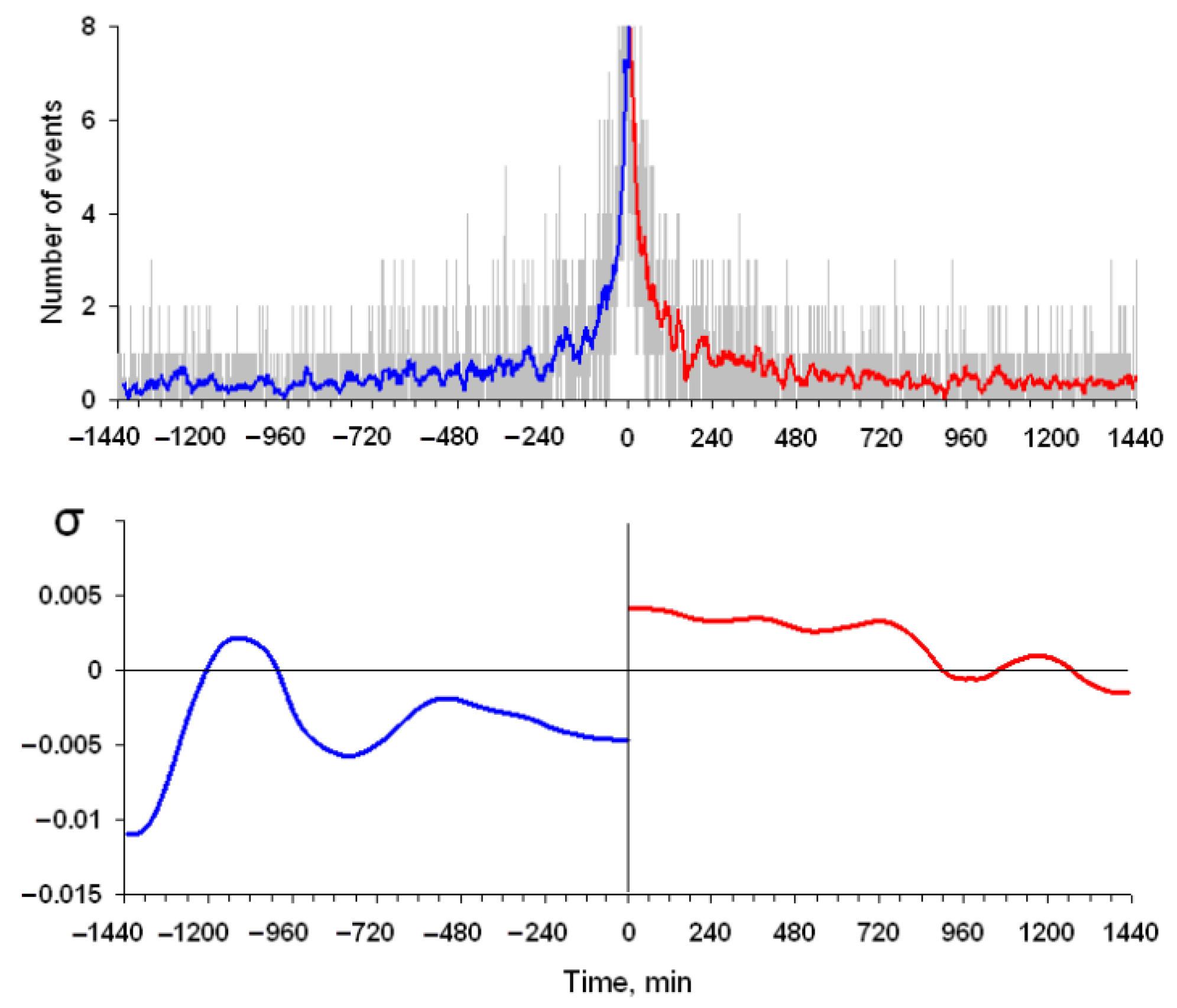
6. Discussion
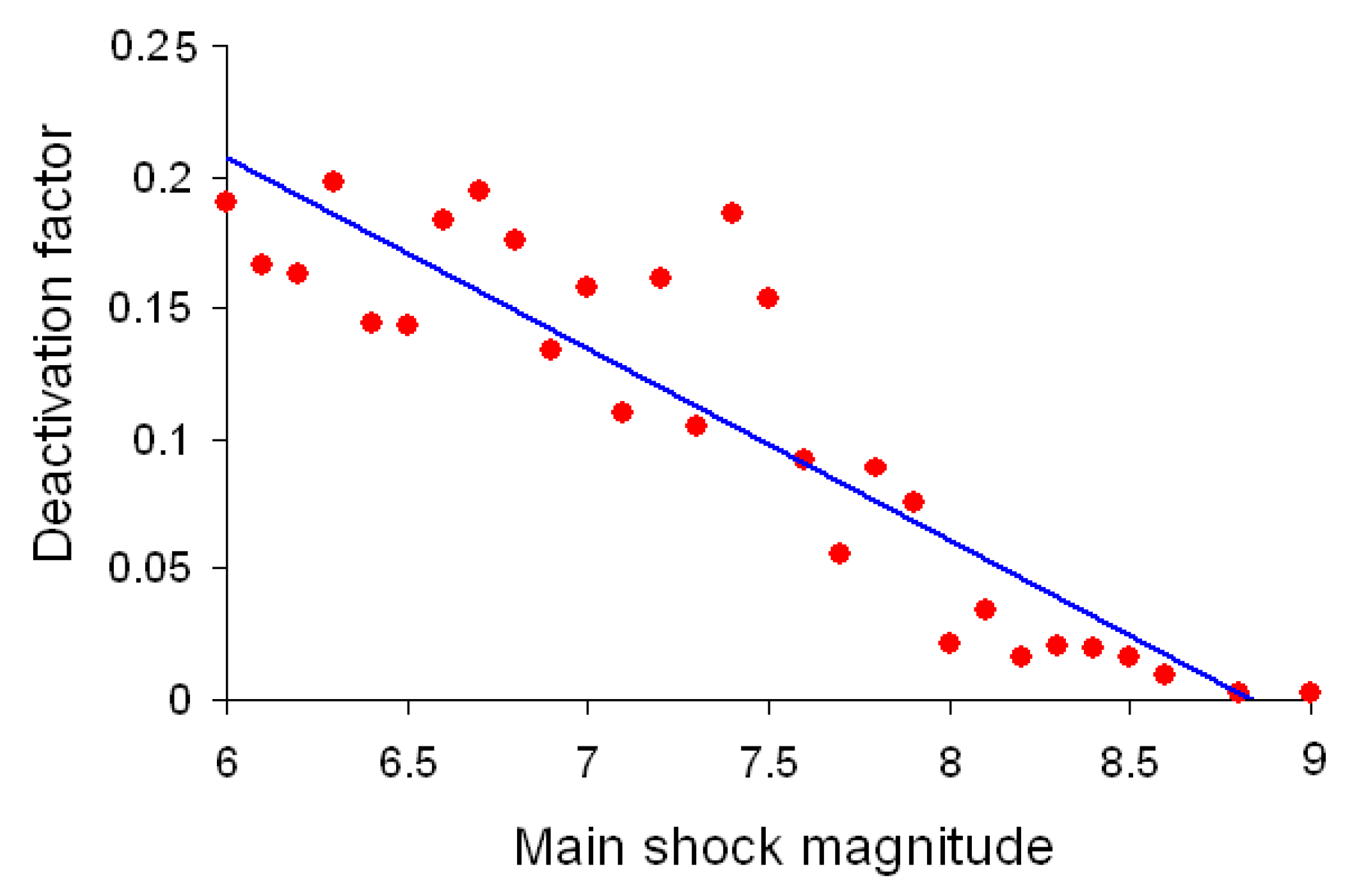
6.1. Inverse Problem
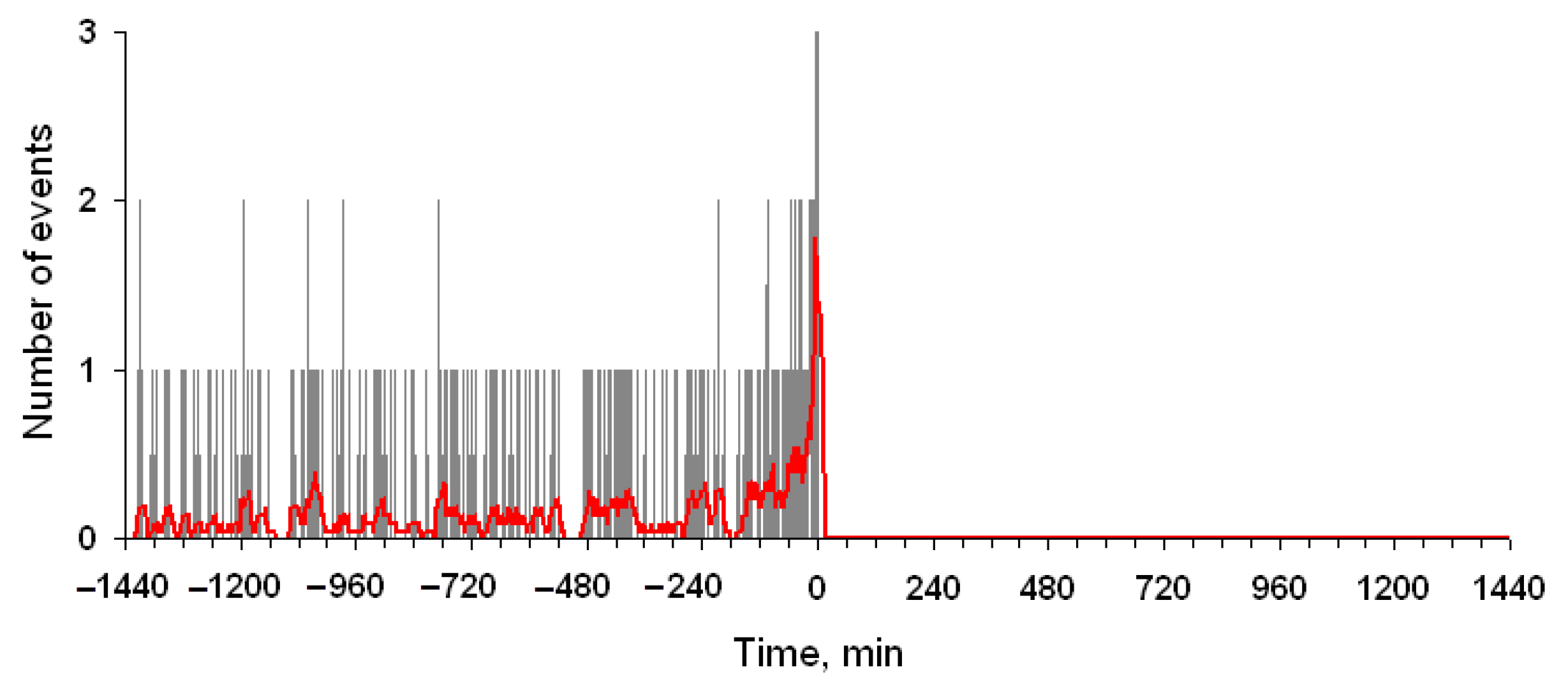
6.2. Triggers
6.3. Triads
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Omori, F. On the aftershocks of earthquake. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–200. [Google Scholar]
- Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Guglielmi, A.V. Omori’s law: A note on the history of geophysics. Phys.-Uspekhi 2017, 60, 319–324. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zavyalov, A.D. The 150th anniversary of Fusakichi Omori. J. Volcanol. Seismol. 2018, 12, 353–358. [Google Scholar] [CrossRef]
- Hirano, R. Investigation of aftershocks of the great Kanto earthquake at Kumagaya. Kishoshushi 1924, 2, 77–83. (In Japanese) [Google Scholar]
- Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Guglielmi, A.V. Interpretation of the Omori Law. Izv. Phys. Solid Earth 2016, 52, 785–786. [Google Scholar] [CrossRef][Green Version]
- Zavyalov, A.D.; Guglielmi, A.V.; Zotov, O.D. Three problems in aftershock physics. J. Volcanol. Seismol. 2020, 14, 341–352. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Klain, B.I.; Zavyalov, A.D.; Zotov, O.D. A Phenomenological theory of aftershocks following a large earthquake. J. Volcanol. Seismol. 2021, 15, 373–378. [Google Scholar] [CrossRef]
- Faraoni, V. Lagrangian formulation of Omori’s law and analogy with the cosmic Big Rip. Eur. Phys. J. C 2020, 80, 445. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Klain, B.I. The phenomenology of aftershocks. arXiv 2020, arXiv:2009.10999. [Google Scholar]
- Verhulst, P.F. Notice sur la loi que la population poursuit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Klimontovich, Y. Statistical Physics; CRC Press: Boca Raton, FL, USA, 1986; 734p. [Google Scholar]
- Kolmogorov, A.N.; Petrovsky, I.G.; Piskunov, N.S. A study of the diffusion equatio related to increase of material, and its application to a biological problem. Bull. MGU Ser. A Mat. Mekhanika 1937, 1, 1–26. [Google Scholar]
- Murray, J.D. Mathematical Biology. V.1. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002; 551p. [Google Scholar]
- Murray, J.D. Mathematical Biology. V.2. Spatial Model and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2003; 839p. [Google Scholar]
- Rodrigo, M.R. A spatio-temporal analogue of the Omori-Utsu law of aftershock sequences. arXiv 2021, arXiv:2111.02955. [Google Scholar]
- Zotov, O.D.; Zavyalov, A.D.; Klain, B.I. On the spatial-temporal structure of aftershock sequences. In Problems of Geocosmos–2018; Springer Proceedings in Earth and Environmental Sciences; Yanovskaya, T., Kosterov, A., Bobrov, N., Divin, A., Saraev, A., Zolotova, N., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations, 2nd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Guglielmi, A.V.; Zotov, O.D.; Zavyalov, A.D. A project for an Atlas of aftershocks following large earthquakes. J. Volcanol. Seismol. 2019, 13, 415–419. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zotov, O.D. Dependence of the source deactivation factor on the earthquake magnitude. arXiv 2021, arXiv:2108.02438. [Google Scholar]
- Guglielmi, A.V.; Zotov, O.D. Impact of the Earth’s oscillations on the earthquakes. arXiv 2012, arXiv:1207.0365. [Google Scholar]
- Guglielmi, A.V.; Zotov, O.D.; Zavyalov, A.D. The aftershock dynamics of the Sumatra–Andaman earthquake. Izv. Phys. Solid Earth 2014, 50, 64–72. [Google Scholar] [CrossRef]
- Zotov, O.D.; Zavyalov, A.D.; Guglielmi, A.V.; Lavrov, I.P. On the possible effect of round-the-world surface seismic waves in the dynamics of repeated shocks after strong earthquakes. Izv. Phys. Solid Earth 2018, 54, 178–191. [Google Scholar] [CrossRef]
- Zavyalov, A.D.; Guglielmi, A.V.; Zotov, O.D. Deviation from the Omori law as the result of the trigger impact of round-the-world surface seismic waves on the source of strong earthquakes. Acta Geol. Sin. 2019, 93 (Suppl. S1), 271. [Google Scholar] [CrossRef]
- Guglielmi, A.V. On self-excited oscillations of the Earth. Izv. Phys. Solid Earth 2015, 51, 920–923. [Google Scholar] [CrossRef]
- Zotov, O.D.; Guglielmi, A.V.; Sobisevich, A.L. On magnetic precursors of earthquakes. Izv. Phys. Solid Earth 2013, 49, 882–889. [Google Scholar] [CrossRef]
- Guglielmi, A.V. On the relationship between earthquakes and geomagnetic disturbances. Geophys. Res. 2020, 21, 78–83. (In Russian) [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zotov, O.D. On geoseismic noise and helioseismic oscillations. Izv. Phys. Solid Earth 2021, 57, 567–572. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Klain, B.I.; Kurazhkovskaya, N.A. On the correlation of Earthquakes with geomagnetic storms. Izv. Phys. Solid Earth 2021, 57, 994–998. [Google Scholar] [CrossRef]
- Sobolev, G.A.; Zakrzhevskaya, N.A.; Migunov, I.N.; Sobolev, D.G.; Boiko, A.N. Effect of magnetic storms on the low-frequency seismic noise. Izv. Phys. Solid Earth 2020, 56, 291–315. [Google Scholar] [CrossRef]
- Buchachenko, A.L. Magneto-plasticity and the physics of earthquakes. Can a catastrophe be prevented? Phys.-Uspekhi 2014, 57, 92–98. [Google Scholar] [CrossRef]
- Buchachenko, A.L. Magnetic control of the earthquakes. Open J. Earthq. Res. 2021, 10, 138–152. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Lavrov, I.P.; Sobisevich, A.L. Storm sudden commencements and earthquakes. Sol.-Terr. Phys. 2015, 1, 98–103. [Google Scholar] [CrossRef][Green Version]
- Guglielmi, A.V.; Klain, B.I. The solar influence on terrestrial seismicity. Sol.-Terr. Phys. 2020, 6, 111–115. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Klain, B.I.; Kurazhkovskaya, N.A. Earthquakes and geomagnetic disturbances. Sol.-Terr. Phys. 2020, 6, 80–83. [Google Scholar] [CrossRef]
- Zotov, O.D.; Guglielmi, A.V.; Silina, A.S. On possible relation of earthquakes with the sign change of the interplanetary magnetic field radial component. Sol.-Terr. Phys. 2021, 7, 59–66. [Google Scholar] [CrossRef]
- Zotov, O.D. Weekend effect in seismic activity. Izv. Phys. Solid Earth 2007, 43, 1005–1011. [Google Scholar] [CrossRef]
- Zotov, O.D.; Guglielmi, A.V. Problems of synchronism of electromagnetic and seismic events in the magnetosphere-technosphere-lithosphere dynamic system. Solnechno-Zemn. Fiz. 2010, 16, 19–25. [Google Scholar]
- Guglielmi, A.V.; Zotov, O.D. The phenomenon of synchronism in the magnetosphere-technosphere-lithosphere dynamical system. Izv. Phys. Solid Earth 2012, 48, 486–495. [Google Scholar] [CrossRef]
- Kasahara, K. Earthquake Mechanics; Cambridge University Press: Cambridge, UK, 1981; 284p. [Google Scholar]
- Mogi, K. Earthquake Prediction; Academic Press Inc.: Tokyo, Japan; Orlando, FL, USA, 1985; 355p. [Google Scholar]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Sausalito, CA, USA, 2002; 700p. [Google Scholar]
- Guglielmi, A.V. Foreshocks and aftershocks of strong earthquakes in the light of catastrophe theory. Phys.-Uspekhi 2015, 58, 384–397. [Google Scholar] [CrossRef]
- Zotov, O.D.; Guglielmi, A.V. Mirror triad of tectonic earthquakes. arXiv 2021, arXiv:2109.05015. [Google Scholar]
- Zavyalov, A.D.; Zotov, O.D. A new way to determine the characteristic size of the source zone. J. Volcanol. Seismol. 2021, 15, 19–25. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zotov, O.D.; Zavyalov, A.D.; Klain, B.I. On the Fundamental Laws of Earthquake Physics. J. Volcanol. Seismol. 2022, 16, 143–149. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shamin, R.V. Probability of the occurrence of freak waves. JETP Lett. 2010, 91, 62–65. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Kuznetsov, E.A. Solitons and collapses: Two evolution scenarios of nonlinear wave systems. Phys.-Uspekhi 2012, 182, 569–592. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavyalov, A.; Zotov, O.; Guglielmi, A.; Klain, B. On the Omori Law in the Physics of Earthquakes. Appl. Sci. 2022, 12, 9965. https://doi.org/10.3390/app12199965
Zavyalov A, Zotov O, Guglielmi A, Klain B. On the Omori Law in the Physics of Earthquakes. Applied Sciences. 2022; 12(19):9965. https://doi.org/10.3390/app12199965
Chicago/Turabian StyleZavyalov, Alexey, Oleg Zotov, Anatol Guglielmi, and Boris Klain. 2022. "On the Omori Law in the Physics of Earthquakes" Applied Sciences 12, no. 19: 9965. https://doi.org/10.3390/app12199965
APA StyleZavyalov, A., Zotov, O., Guglielmi, A., & Klain, B. (2022). On the Omori Law in the Physics of Earthquakes. Applied Sciences, 12(19), 9965. https://doi.org/10.3390/app12199965






