Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021
Abstract
1. Introduction
2. Region, Data, Method
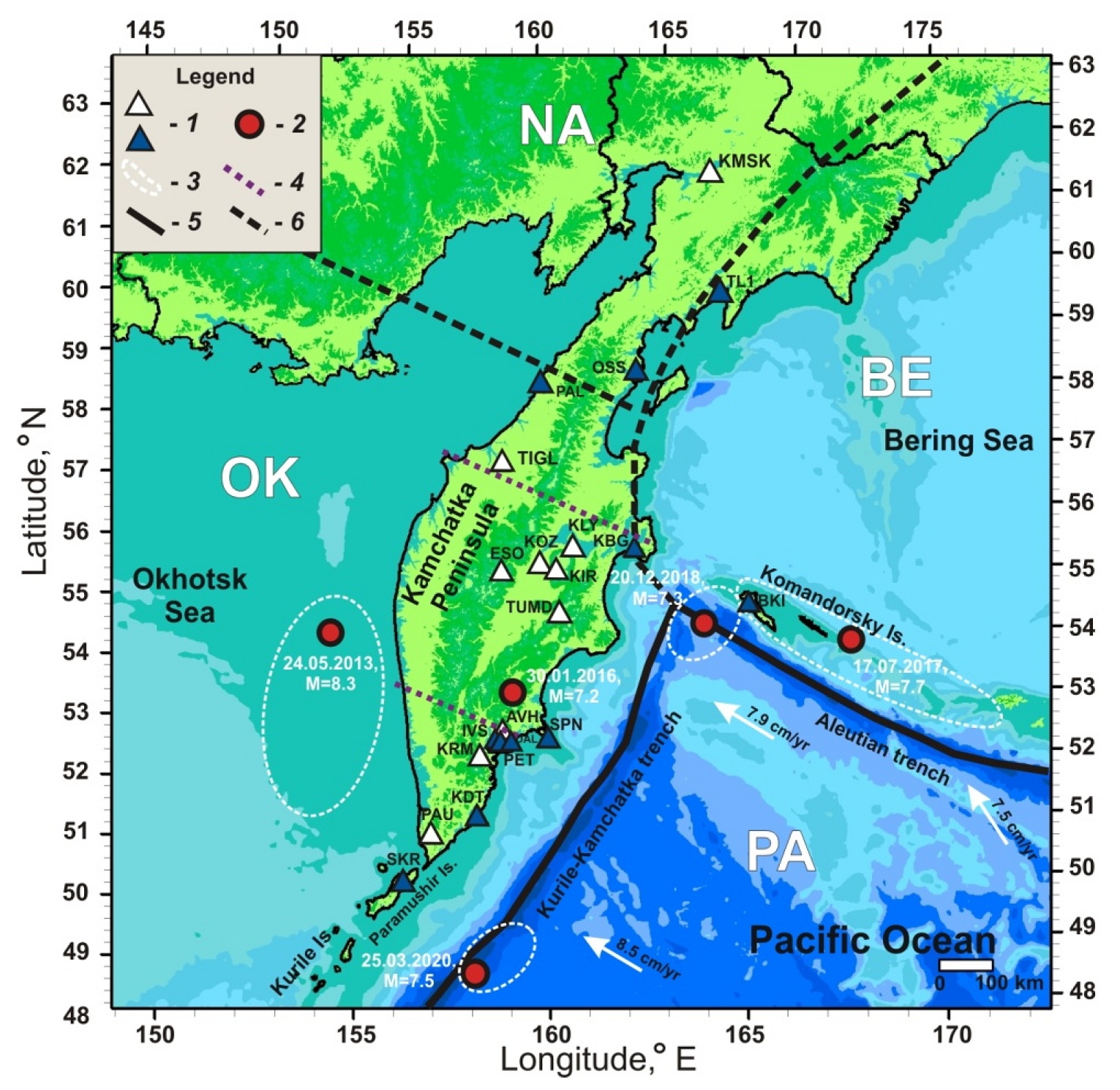
2.1. Network of Stations
2.2. Stations Identification
2.2.1. Northern, Central and Southern Groups of Station
2.2.2. Volcanic Stations
2.2.3. Coastal and Continental Stations
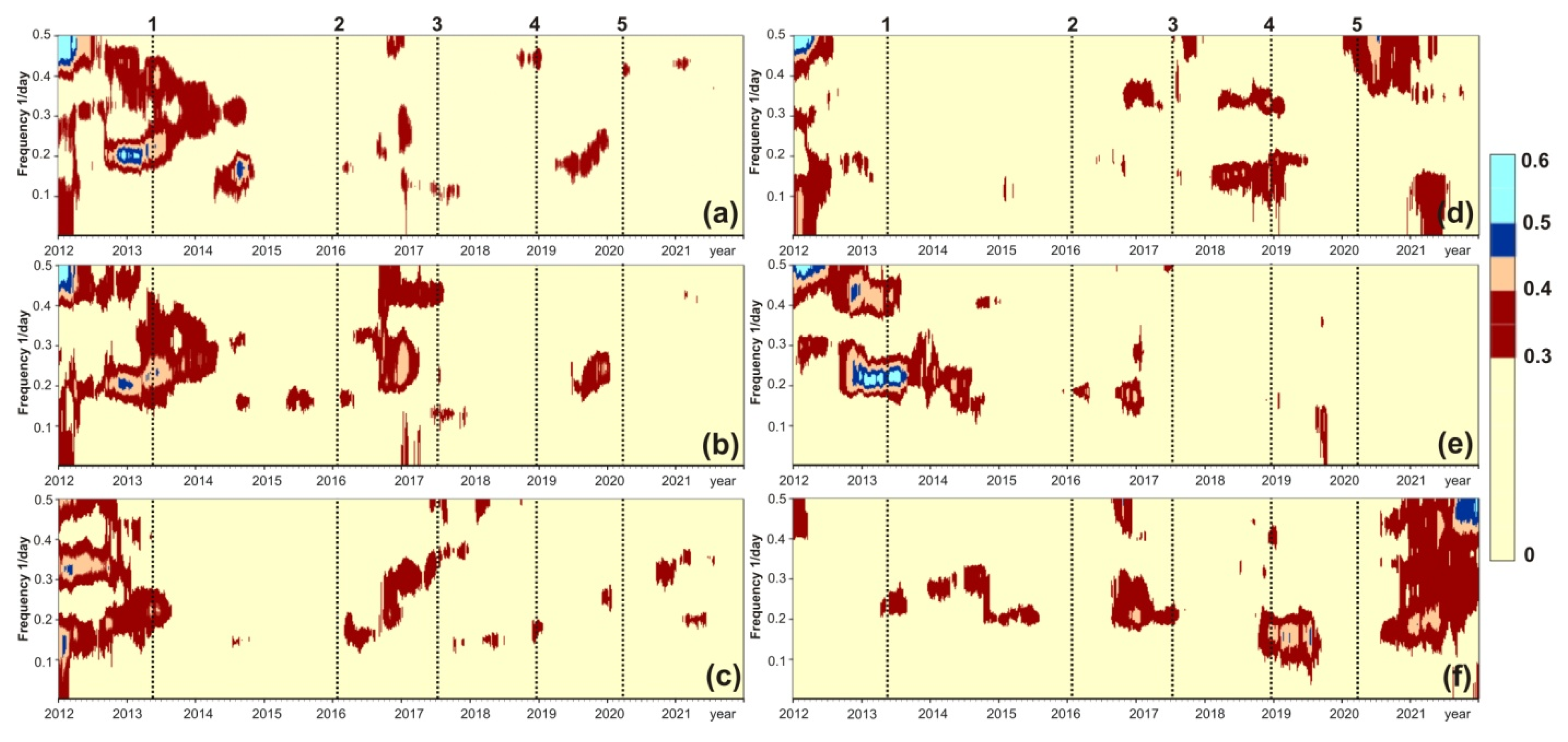
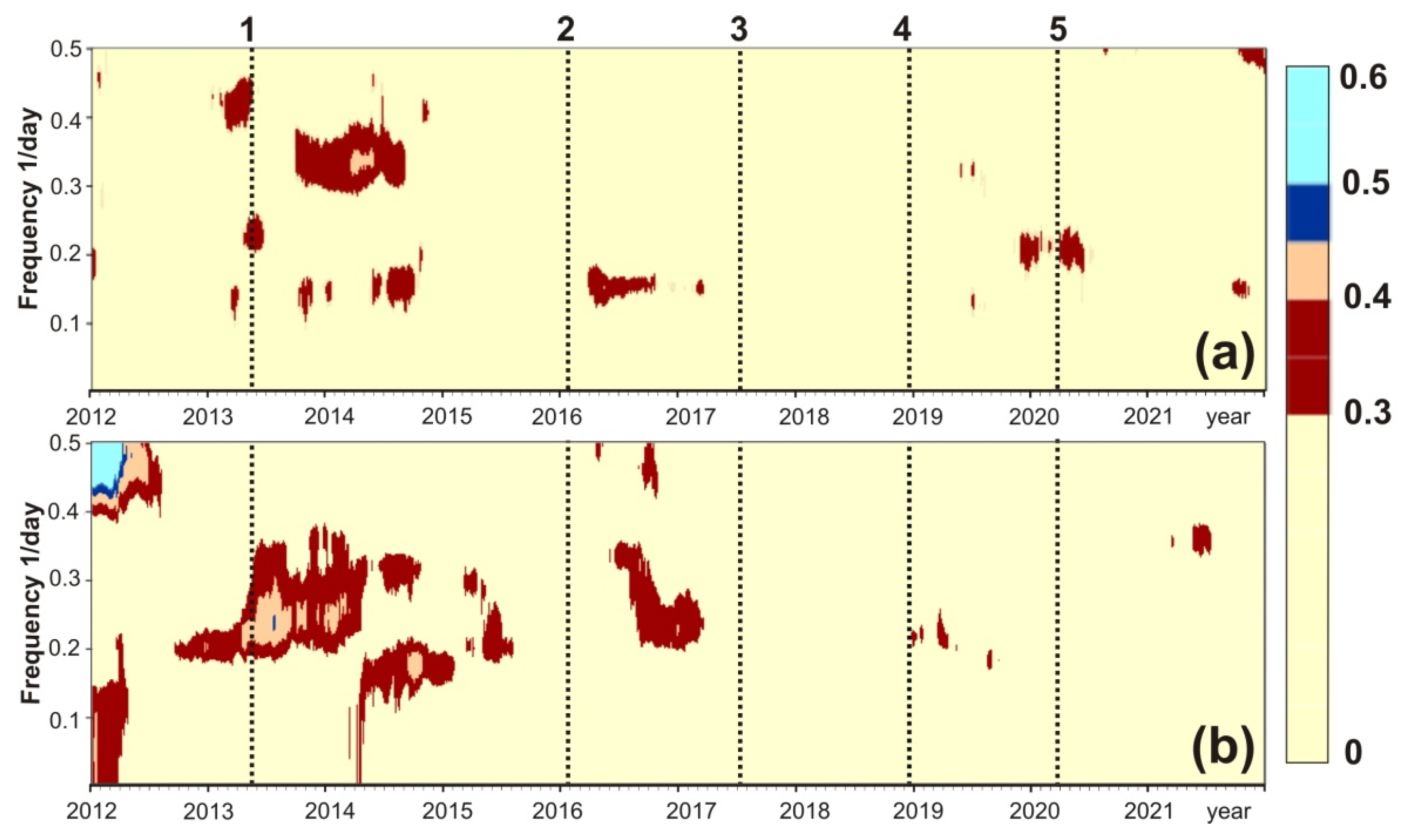
2.3. Strong Earthquakes
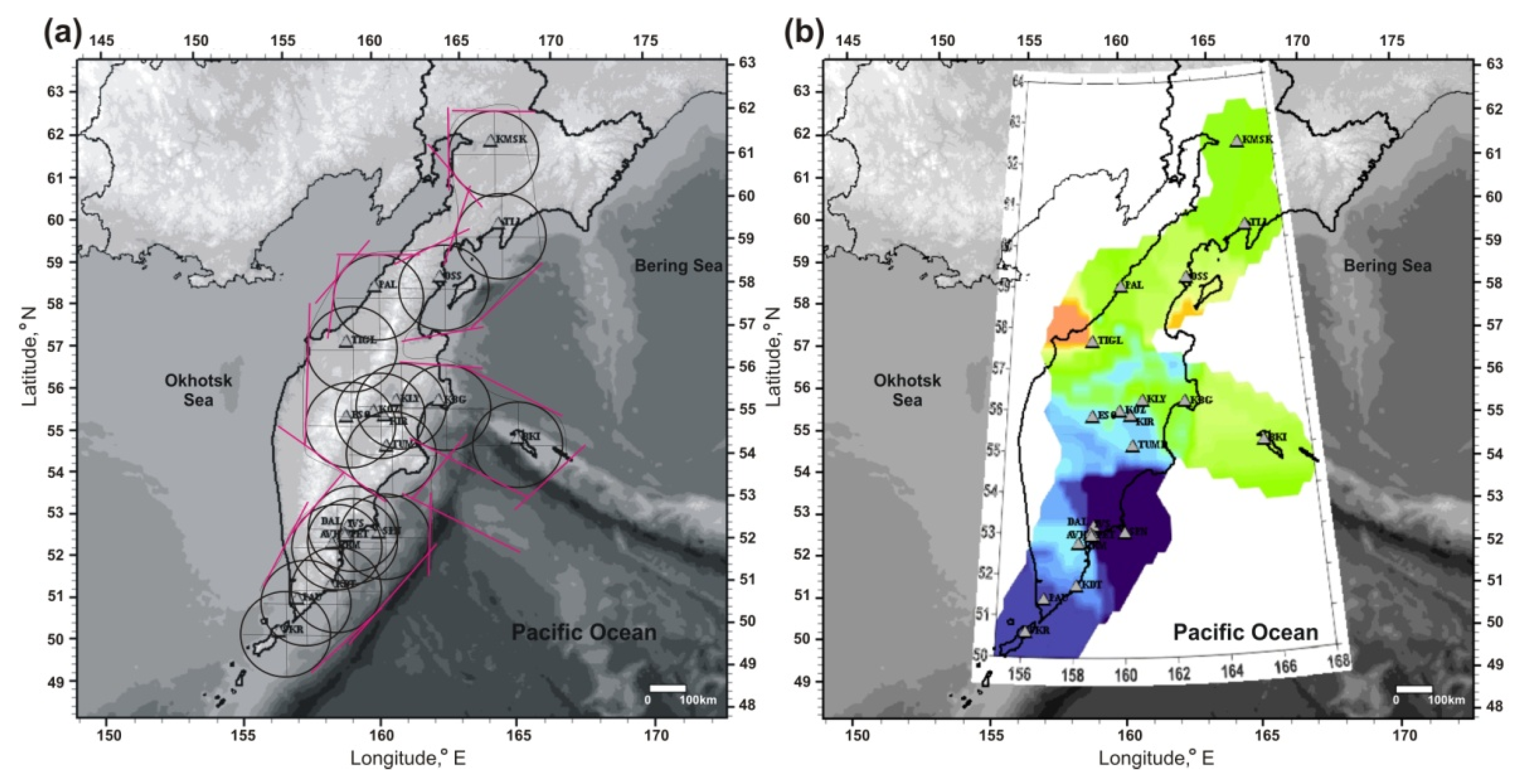
2.4. Seismic Noise Parameters
2.4.1. Minimum Normalized Entropy of Squared Orthogonal Wavelet Coefficients En
2.4.2. Visualization of the Seismic Noise Parameters Distribution
| No | Date dd.mm.yyyy Name | Time hh:mm:ss | Coordinates, deg. N° E° | H, km | Mw | M0, N∙m∙1020 |
|---|---|---|---|---|---|---|
| 1 | 24 May 2013 Sea of Okhotsk | 05:44:48 | 54.89 153.22 | 598 | 8.3 | 38.4 |
| 2 | 30 January 2016 Zhupanovskoe | 03:25:12 | 53.98 158.55 | 177 | 7.2 | 0.8 |
| 3 | 17 July 2017 Near Islands Aleutian | 23:34:13 | 54.44 168.86 | 10 | 7.7 | 5.2 |
| 4 | 20 December 2018 Uglovoye Podnyatiye | 17:01:55 | 55.10 164.70 | 17 | 7.3 | 1.0 |
| 5 | 25 March 2020 North Kuril | 02:49:21 | 48.96 158.70 | 58 | 7.5 | 2.0 |
2.5. Spectral Measure of Coherent Behavior of Seismic Noise Parameters
2.6. Conceptual Model Used in Data Interpretation
3. Data Analysis
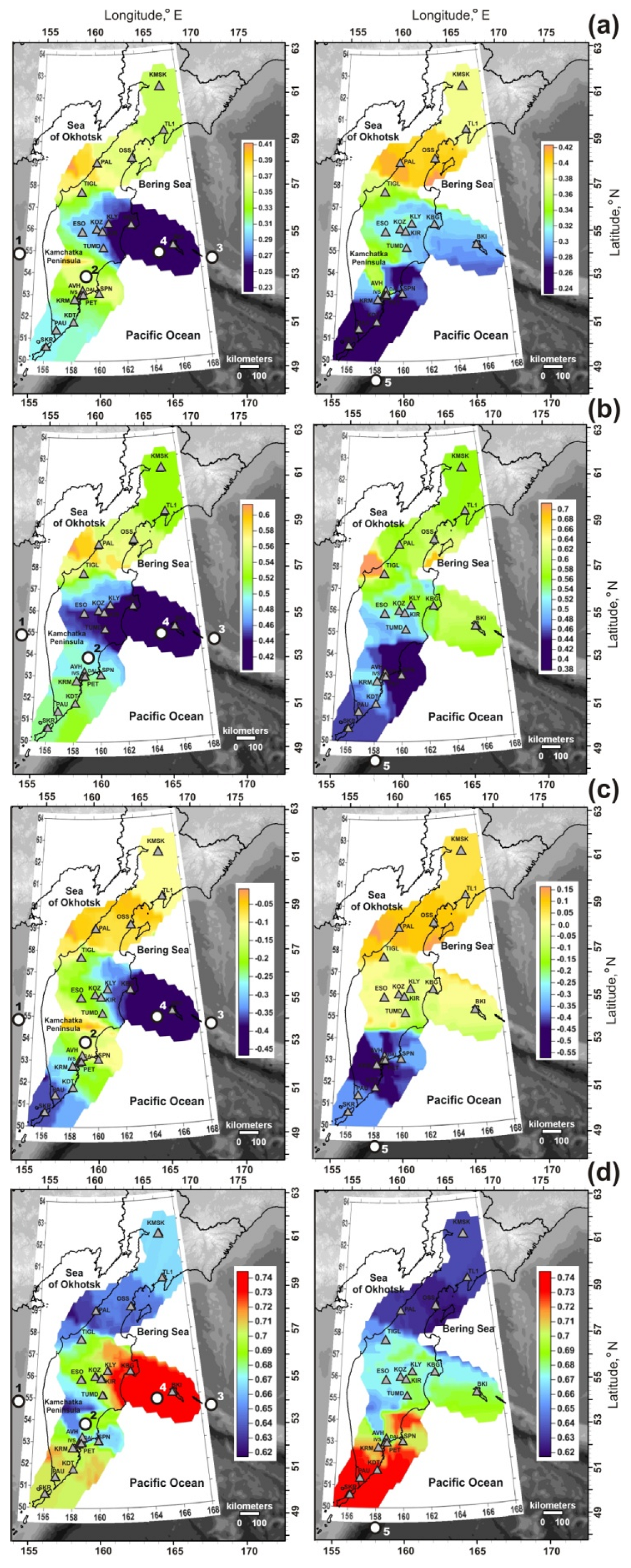
3.1. Variability of Seismic Noise Parameters’ Spatiotemporal Distribution
3.2. Synchronization Signals in Noise Parameter Changes
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tanimoto, T. The oceanic excitation hypothesis for the continuous oscillations of the Earth. Geophys. J. Int. 2005, 160, 276–288. [Google Scholar] [CrossRef]
- Tanimoto, T.; Um, J.; Nishida, K.; Kobayashi, N. Earth’s continuous oscillations observed on seismically quiet days. Geophys. Res. Lett. 1998, 25, 1553–1556. [Google Scholar] [CrossRef]
- Stehly, L.; Campillo, M.; Shapiro, N.M. A study of the seismic noise from its long-range correlation properties. J. Geophys. Res. 2006, 111, 10306. [Google Scholar] [CrossRef]
- Berger, J.; Davis, P.; Ekstrom, G. Ambient Earth Noise: A survey of the Global Seismographic Network. J. Geophys. Res. 2004, 109, 11307. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Microseismic noise in the low frequency range (periods of 1-300 min): Properties and possible prognostic features. Izvestiya. Phys. Solid Earth 2008, 44, 275–290. [Google Scholar] [CrossRef]
- Lyubushin, A.A. The statistics of the time segments of low-frequency microseisms: Trends and synchronization. Izvestiya. Phys. Solid Earth 2010, 46, 544–554. [Google Scholar] [CrossRef]
- Lyubushin, A.A. The great Japanese earthquake. Priroda 2012, 8, 23–33. (In Russian) [Google Scholar]
- Lyubushin, A.A. Mapping the properties of low-frequency microseisms for seismic hazard assessment. Izvestiya. Phys. Solid Earth 2013, 49, 9–18. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Analysis of coherence in global seismic noise for 1997–2012. Izvestiya. Phys. Solid Earth 2014, 50, 325–333. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Coherence between the fields of low-frequency seismic noise in Japan and California. Izvestiya. Phys. Solid Earth 2016, 52, 810–820. [Google Scholar] [CrossRef]
- Lyubushin, A. Synchronization of Geophysical Fields Fluctuations. In Complexity of Seismic Time Series: Measurement and Applications; Chelidze, T., Telesca, L., Vallianatos, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 161–197. [Google Scholar] [CrossRef]
- Lyubushin, A. Field of coherence of GPS-measured earth tremors. GPS Solut. 2019, 23, 120. [Google Scholar] [CrossRef]
- Lyubushin, A. Trends of Global Seismic Noise Properties in Connection to Irregularity of Earth’s Rotation. Pure Appl. Geophys. 2020, 177, 621–636. [Google Scholar] [CrossRef]
- Lyubushin, A. Connection of Seismic Noise Properties in Japan and California with Irregularity of Earth’s Rotation. Pure Appl. Geophys. 2020, 177, 4677–4689. [Google Scholar] [CrossRef]
- Lyubushin, A. Global Seismic Noise Entropy. Front. Earth Sci. 2020, 8, 611663. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Seismic Noise Wavelet-Based Entropy in Southern California. J. Seismol. 2021, 25, 25–39. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Low-Frequency Seismic Noise Properties in the Japanese Islands. Entropy 2021, 23, 474. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Exploring Complexity, an Introduction; W.H. Freedman and Co.: New York, NY, USA, 1989. [Google Scholar]
- Chelidze, T.; Matcharashvili, T.; Lursmanashvili, O.; Varamashvili, N.; Zhukova, N.; Mepariddze, E. Triggering and Synchronization of Stick-Slip: Experiments on Spring-Slider System. In Synchronization and Triggering: From Fracture to Earthquake Processes. GeoPlanet: Earth and Planetary Sciences; Rubeis, V., Czechowski, Z., Teisseyre, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 123–164. [Google Scholar] [CrossRef]
- Chebrov, V.N.; Kugayenko, Y.A.; Vikulina, S.A.; Kravchenko, N.M.; Matveenko, E.A.; Mityushkina, S.V.; Lander, A.V. Deep Mw = 8.3 sea of Okhotsk earthquake on May 24, 2013—The largest event ever recorded near Kamchatka Peninsula for the whole period of regional seismic network operation. Vestn. KRAUNTS Seriya Nauk. O Zemle 2013, 21, 17–24. (In Russian) [Google Scholar]
- Chebrov, V.N.; Kugayenko, Y.A.; Abubakirov, I.R.; Droznina, S.Y.; Ivanova, E.I.; Matveenko, E.A.; Mityushkina, S.V.; Ototyuk, D.A.; Pavlov, V.M.; Raevskaya, A.A.; et al. The 30 January 2016 earthquake with Ks = 15.7, Mw = 7.2, I = 6 in the Zhupanovsky region (Kamchatka). Vestn. KRAUNTS Seriya Nauk. O Zemle 2016, 29, 5–16. (In Russian) [Google Scholar]
- Chebrov, D.V.; Kugayenko, Y.A.; Lander, A.V.; Abubakirov, I.R.; Voropayev, P.V.; Gusev, A.A.; Droznin, D.V.; Droznina, S.Y.; Ivanova, E.I.; Kravchenko, N.M.; et al. The 29 March 2017 earthquake with Ks = 15.0, Mw = 6.6, I = 6 in Ozernoy Gulf (Kamchatka). Vestn. KRAUNTS Seriya Nauk. O Zemle 2017, 35, 7–21. (In Russian) [Google Scholar]
- Chebrov, D.V.; Kugaenko, Y.A.; Abubakirov, I.R.; Gusev, A.A.; Droznina, S.Y.; Mityushkina, S.V.; Ototyuk, D.A.; Pavlov, V.M.; Titkov, N.N. Near Islands Aleutian earthquake with Mw = 7.8 on July 17, 2017: I. Extended rupture along the Commander block of the Aleutian Island arc from observations in Kamchatka. Izv. Phys. Solid Earth 2019, 55, 576–599. [Google Scholar] [CrossRef]
- Chebrov, D.V.; Kugayenko, Y.A.; Lander, A.V.; Abubakirov, I.R.; Droznina, S.Y.; Mityushkina, S.V.; Pavlov, V.M.; Saltykov, V.A.; Serafimova, Y.K.; Titkov, N.N. The Uglovoye Podnyatiye Earthquake on 20 December 2018 (Mw = 7.3) in the Junction Zone between Kamchatka and Aleutian Oceanic Trenches. Vestn. KRAUNTs Seriya Nauk. O Zemle 2020, 45, 100–117. (In Russian) [Google Scholar] [CrossRef]
- Gordeev, E.I.; Pinegina, T.K.; Kozhurin, A.I.; Lander, A.V. Beringia: Seismic hazard and fundamental problems of geotectonics. Izv. Phys. Solid Earth 2015, 51, 512–521. [Google Scholar] [CrossRef]
- Kozhurin, A.I. Active Faulting in the Kamchatsky Peninsula, Kamchatka-Aleutian Junction. In Geophysical Monograph Series Volcanism and Subduction: The Kamchatka Region; Eichelberger, J., Gordeev, E., Kasahara, M., Lees, J., Eds.; American Geophysical Union: Washington, DC, USA, 2007; Volume 172, pp. 107–116. [Google Scholar]
- Argus, D.F.; Gordon, R.G. No-net-rotation model of current plate velocities incorporating plate motion model NUVEL-1. Geophys. Res. Lett. 1991, 18, 2039–2042. [Google Scholar] [CrossRef]
- Chebrova, A.Y.; Chemarev, A.S.; Matveenko, E.A.; Chebrov, D.V. Seismological data information system in Kamchatka branch of GS RAS: Organization principles, main elements and key functions. Geophys. Res. 2020, 21, 66–91. [Google Scholar] [CrossRef]
- Geology of the USSR. Kamchatka, the Kuril and Commander Islands. Geological Description; Nedra: Moscow, Russia, 1964; Volume 31, 733p. (In Russian) [Google Scholar]
- Gorelchik, V.I.; Garbuzova, V.T.; Storcheus, A.V. Deep-seated volcanic processes beneath Klyuchevskoi volcano as inferred from seismological data. J. Volcanol. Seismol. 2004, 6, 21–34. [Google Scholar]
- Thompson, G. Seismic Monitoring of Volcanoes. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, I.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Kotenko, T.A.; Sandimirova, E.I.; Kotenko, L.V. The 2016–2017 eruptions of Ebeko Volcano (Kuriles Islands). Vestn. KRAUNTs Seriya Nauk. O Zemle 2018, 37, 32–42. (In Russian) [Google Scholar]
- Belousov, A.; Belousova, M.; Auer, A.; Walter, T.; Kotenko, T.; Belousova, M.; Auer, A.; Walter, T.; Kotenko, T. Mechanism of the historical and the ongoing Vulcanian eruptions of Ebeko volcano, Northern Kuriles. Bull. Volcanol. 2021, 83, 4. [Google Scholar] [CrossRef]
- Walter, T.; Belousov, A.; Belousova, M.; Kotenko, T.; Auer, A. The 2019 Eruption Dynamics and Morphology at Ebeko Volcano Monitored by Unoccupied Aircraft Systems (UAS) and Field Stations. Remote Sens. 2020, 12, 1961. [Google Scholar] [CrossRef]
- Lyubushin, A.A.; Kopylova, G.N.; Kasimova, V.A.; Taranova, L.N. The Properties of Fields of Low Frequency Noise from the Network of Broadband Seismic Stations in Kamchatka. Bull. Kamchatka Reg. Assoc. Educ. Sci. Cent. Earth Sci. 2015, 26, 20–36. (In Russian) [Google Scholar]
- Kasimova, V.A.; Kopylova, G.N.; Lyubushin, A.A. Variations in the parameters of background seismic noise during the preparation stages of strong earthquakes in the Kamchatka region. Izv. Phys. Solid Earth 2018, 54, 269–283. [Google Scholar] [CrossRef]
- Riznichenko, Y.V. The source dimensions of the crustal earthquakes and the seismic moment. In Issledovaniya po Fizike Zemletryasenii (Studies in Earthquake Physics); Nauka: Moscow, Russia, 1976; pp. 9–27. (In Russian) [Google Scholar]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pageoph 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Kopylova, G.N.; Lyubushin, A.A.; Taranova, L.N. New prognostic technology for analysis of low-frequency seismic noise variations (on the example of the Russian Far East). Russ. J. Seismol. 2021, 3, 75–91. (In Russian) [Google Scholar] [CrossRef]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988; 254p. [Google Scholar]
- Kantelhard, J.W.; Zschiegner, S.A.; Konscienly-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: San Diego, CA, USA, 1998; 671p. [Google Scholar]
- Lyubushin, A.; Yakovlev, P. Properties of GPS noise at Japan islands before and after Tohoku mega-earthquake. Springer Plus Open Access J. 2014, 3, 364. [Google Scholar] [CrossRef][Green Version]
- Kopylova, G.N.; Ivanov, V.Y.; Kasimova, V.A. The implementation of information system elements for interpreting integrated geophysical observations in Kamchatka. Russ. J. Earth Sci. 2009, 11, ES1006. [Google Scholar] [CrossRef]
- Fedotov, S.A. Dolgosrochnyy Seysmicheskiy Prognoz Dlya Kurilo-Kamchatskoy Dugi (Long-Term Seismic Forecast for Kurilo-Kamchatka Arcs); Nauka Publ.: Moscow, Russia, 2005; 302p. (in Russian) [Google Scholar]
- Mogi, K. Earthquake Prediction; Mir: Moscow, Russia, 1988; 382p. (In Russian) [Google Scholar]
| Seismic Station | Station Code | Coordinates | Equipment | Frequency Range/ Registration Frequency, Hz | Belonging to Dedicated Groups of Stations | ||||
|---|---|---|---|---|---|---|---|---|---|
| N ° | E ° | h asl, m | |||||||
| Avacha | AVH | 53.264 | 158.740 | 942 | CMG-6TD | 0.033–40/100 | southern | continental | volcanic |
| Bering | BKI | 55.194 | 165.984 | 12 | CMG-3TB | 0.0083–40/100 | central | coastal | non-volcanic |
| Dal’niy | DAL | 53.031 | 158.754 | 57 | CMG-6TD | 0.033–40/100 | southern | coastal | non-volcanic |
| Institut | IVS | 53.066 | 158.608 | 160 | CMG-3TB | 0.0083–40/100 | southern | coastal | non-volcanic |
| Kamenskaya | KMSK | 62.467 | 166.206 | 40 | CMG-6TD | 0.033–40/100 | northern | continental | non-volcanic |
| Karymshina | KRM | 52.828 | 158.131 | 100 | CMG-3TB | 0.033–40/100 | southern | continental | non-volcanic |
| Kirisheva | KIR | 55.953 | 160.342 | 1470 | CMG-6TD | 0.033–40/100 | central | continental | volcanic |
| Klyuchi | KLY | 56.317 | 160.857 | 35 | KS2000 | 0.01–40/100 | central | continental | volcanic |
| Kozyrevsk | KOZ | 56.058 | 159.872 | 60 | CMG-6TD | 0.033–40/100 | central | continental | volcanic |
| Krutoberegovo | KBG | 56.258 | 162.713 | 30 | CMG-3TB | 0.0083–40/100 | central | coastal | non-volcanic |
| Ossora | OSS | 59.262 | 163.072 | 35 | CMG-6TD | 0.033–40/100 | northern | coastal | non-volcanic |
| Palana | PAL | 59.094 | 159.968 | 70 | STS-2 | 0.0083–40/100 | northern | coastal | non-volcanic |
| Pauzhetka | PAU | 51.468 | 156.815 | 130 | CMG-6TD | 0.033–40/100 | southern | continental | non-volcanic |
| Petropavlovsk | PET | 53.023 | 158.650 | 100 | STS-1 | 0.0027–10/20 | southern | coastal | non-volcanic |
| Severo-Kuril’sk | SKR | 50.670 | 156.116 | 30 | CMG-3TB | 0.0083–40/100 | southern | coastal | volcanic |
| Tigil | TIGL | 57.765 | 158.671 | 115 | CMG-6TD | 0.033–40/100 | northern | continental | non-volcanic |
| Tilichiki | TL1 | 60.446 | 166.145 | 25 | CMG-3TB | 0.0083–40/100 | northern | coastal | non-volcanic |
| Tumrok | TUMD | 55.203 | 160.399 | 478 | CMG-6TD | 0.033–40/100 | central | continental | volcanic |
| Khodutka | KDT | 51.809 | 158.077 | 22 | CMG-6TD | 0.033–40/100 | southern | coastal | non-volcanic |
| Shipunskiy | SPN | 55.106 | 160.011 | 95 | CMG-6TD | 0.033–40/100 | southern | coastal | non-volcanic |
| Esso | ESO | 55.932 | 158.695 | 490 | CMG-6TD | 0.033–40/100 | central | continental | non-volcanic |
| Station Groups Influence Factors * | All Stations, N= 21 (100%) | Northern, N = 5 (100%) | Central, N = 7 (100%) | Southern, N = 9 (100%) | Non-Volcanic, N = 15 (100%) |
|---|---|---|---|---|---|
| coastal, n (%) | 11 (52%) | 3 (60%) | 2 (29%) | 6 (67%) | 10 (67%) |
| volcanic, n (%) | 6 (29%) | – | 4 (57%) | 2 (22%) | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopylova, G.; Kasimova, V.; Lyubushin, A.; Boldina, S. Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021. Appl. Sci. 2022, 12, 8658. https://doi.org/10.3390/app12178658
Kopylova G, Kasimova V, Lyubushin A, Boldina S. Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021. Applied Sciences. 2022; 12(17):8658. https://doi.org/10.3390/app12178658
Chicago/Turabian StyleKopylova, Galina, Victoriya Kasimova, Alexey Lyubushin, and Svetlana Boldina. 2022. "Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021" Applied Sciences 12, no. 17: 8658. https://doi.org/10.3390/app12178658
APA StyleKopylova, G., Kasimova, V., Lyubushin, A., & Boldina, S. (2022). Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021. Applied Sciences, 12(17), 8658. https://doi.org/10.3390/app12178658









