Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models
Abstract
1. Introduction
- (1)
- The superiority of using DBSAN algorithms on the nonlinearly-inseparable data: DBSCAN is one of the typical density-based algorithms which group data points of dense regions, and separate regions of low density [14]. It has advantages at solving nonlinear inseparable issues by discovering clusters with arbitrary shapes, namely applicable on spatial data clustering. The second advantage of DBSCAN compared to other methods is the ignorance of expert knowledge on parameter setting, which is helpful to reduce human interference.
- (2)
- The usage of granular models in data description and rule-based modeling: according to human beings’ knowledge, GrC divides an object into information granules, and builds granular models for description [20]. By making use of granular models, the shaped clusters in DBSCAN could be broken up into granules which slip the shape’s influence. Moreover, granules could reconstruct a cluster with arbitrary shapes. With the information carried in each granule, it is easy to satisfy the expression of new data and complete their online clustering.
- (3)
- The proposed method has an advantage in reducing the computation cost in online clustering. Compared with other clustering algorithms, DBSCAN has a relatively acceptable computation complexity, and even has good efficiency on large data sets [21,22]. Additionally, by using a limited number of granules and rules to guide the online clustering, the time of new data clustering can be significantly reduced.
2. Related Work on DBSCAN Variants
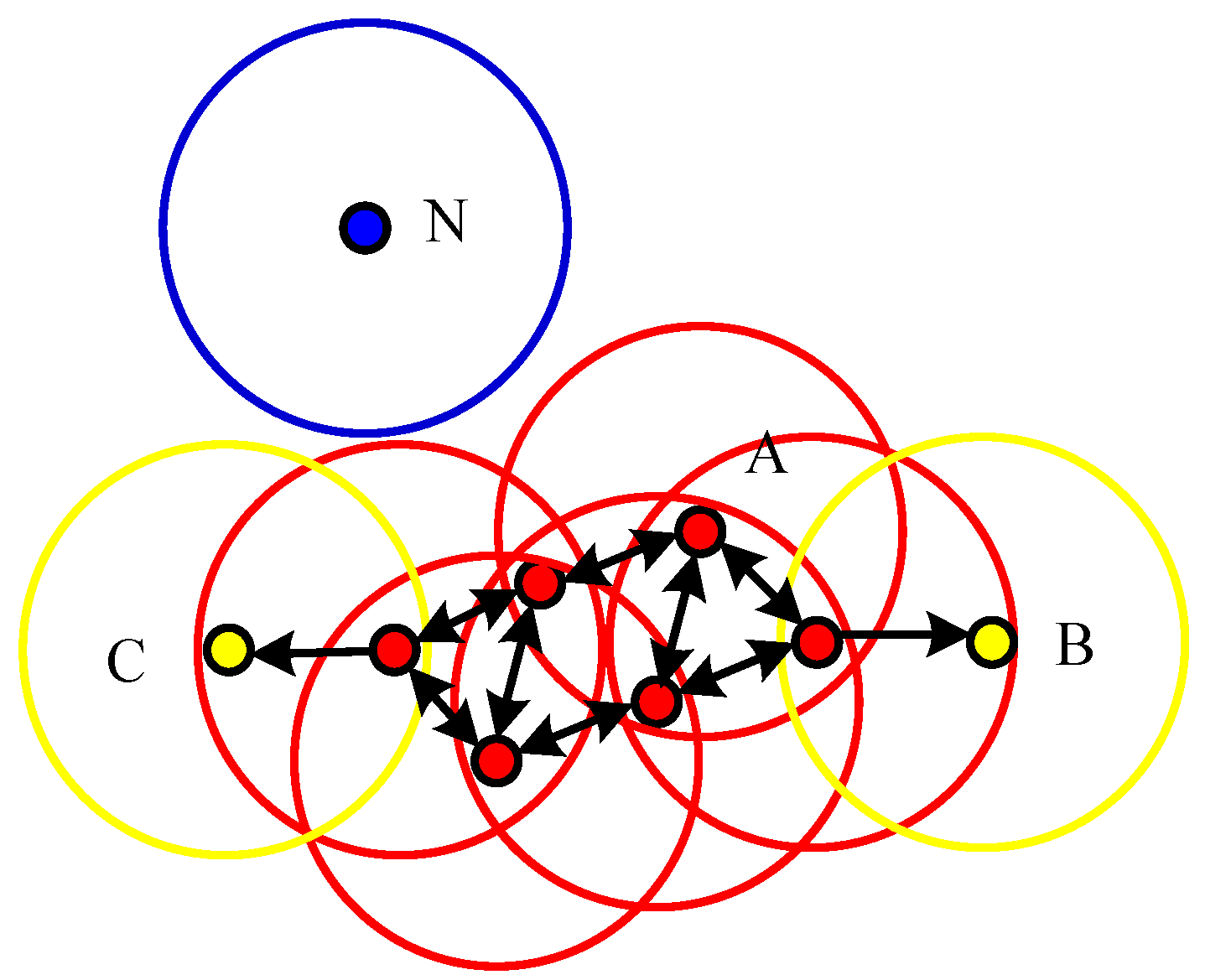
2.1. Basic DBSCAN Algorithm
2.2. Extensions of DBSCAN Algorithms
2.3. Incremental DBSCAN Variants
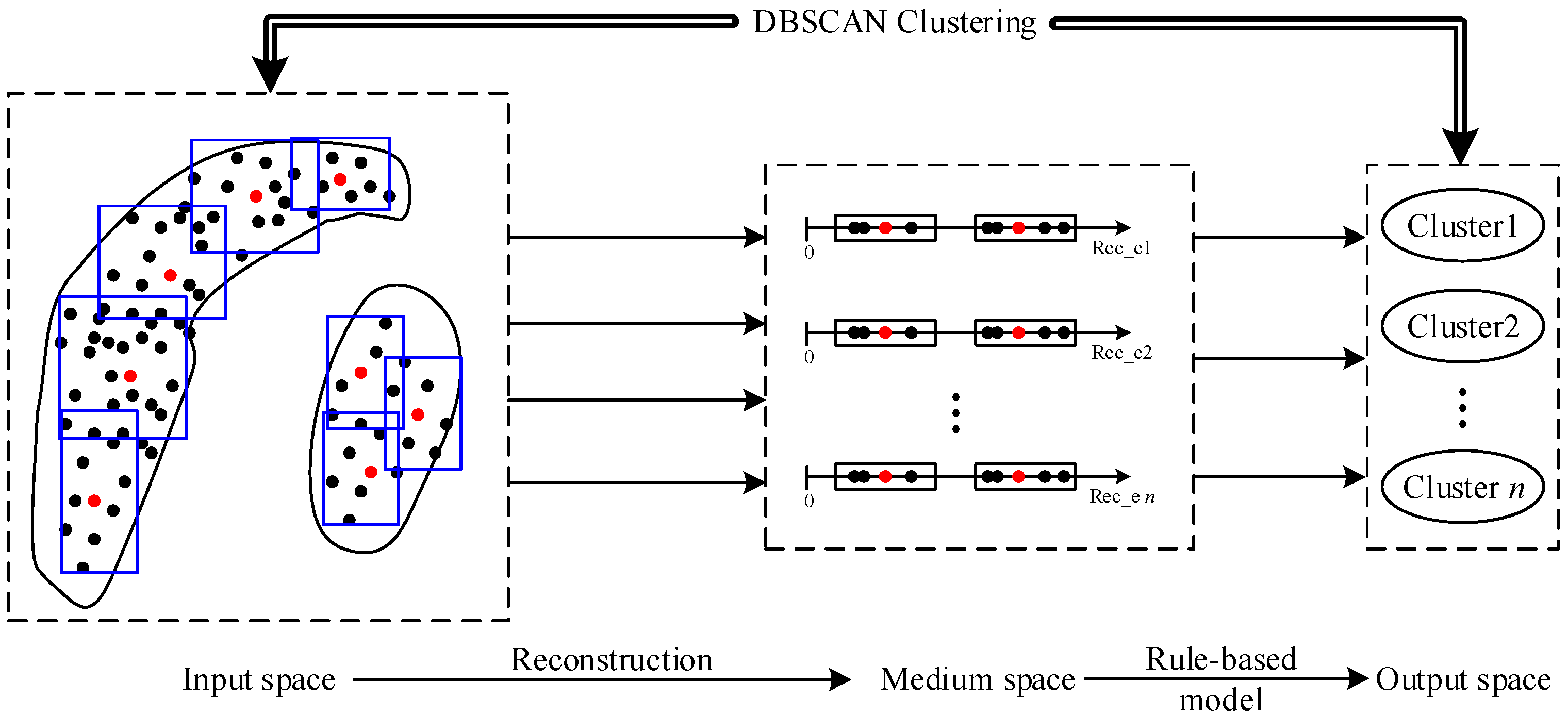
3. Framework and Necessary Preparation
3.1. Data Preprocessing
3.2. Implementation of DBSCAN Algorithm
4. Methodology of the Proposed Three-Layer Granule Models
4.1. Granulating in the Input Space
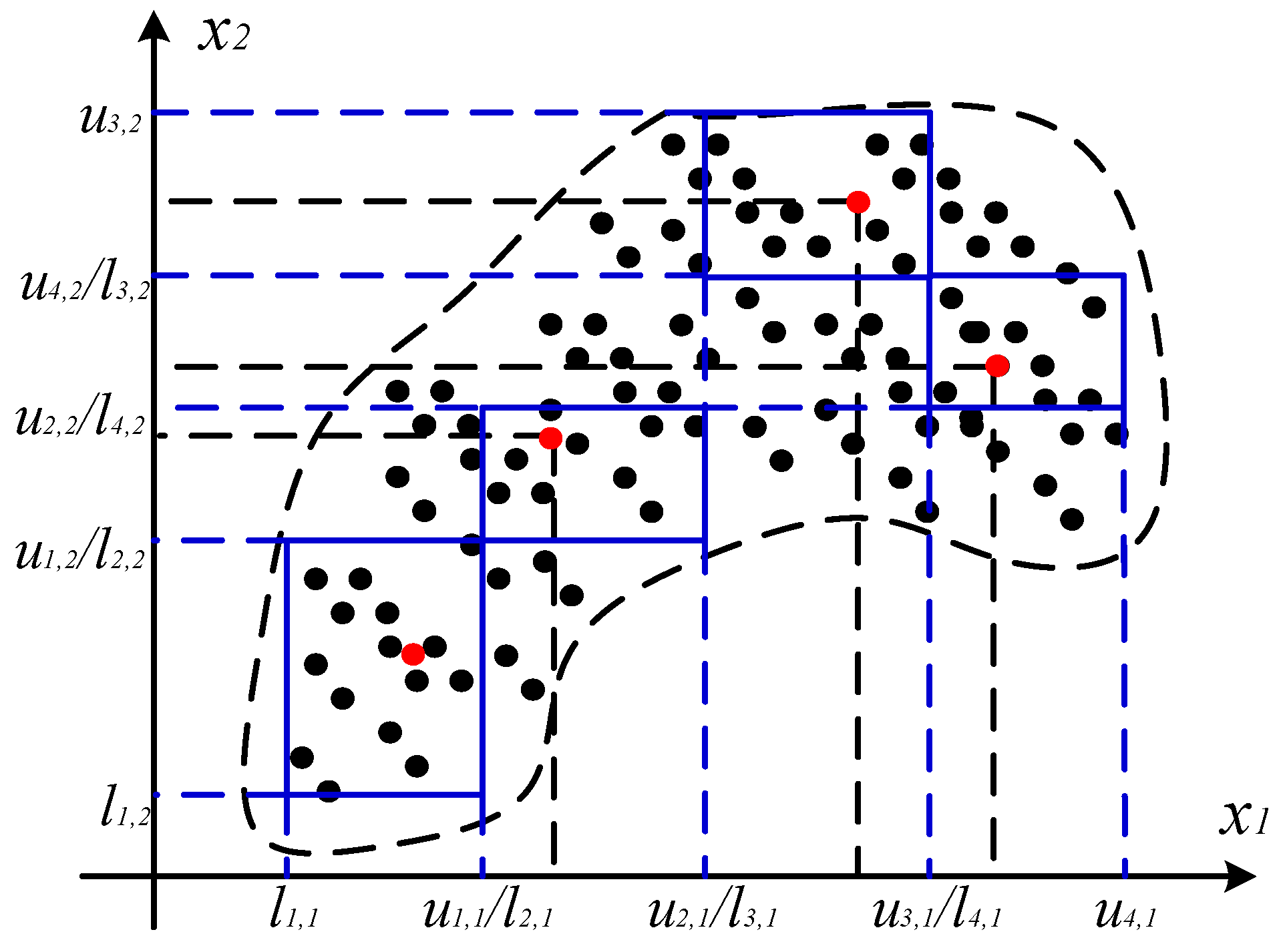
4.1.1. Construction of Information Granules (IGs)
4.1.2. Determination of the Granule Size
4.2. Granulating in the Medium Space
4.2.1. Construction of the Medium Space
4.2.2. Justifiable Granulating
4.3. Online Clustering via Rule-Based Models
5. Experiment and Discussion
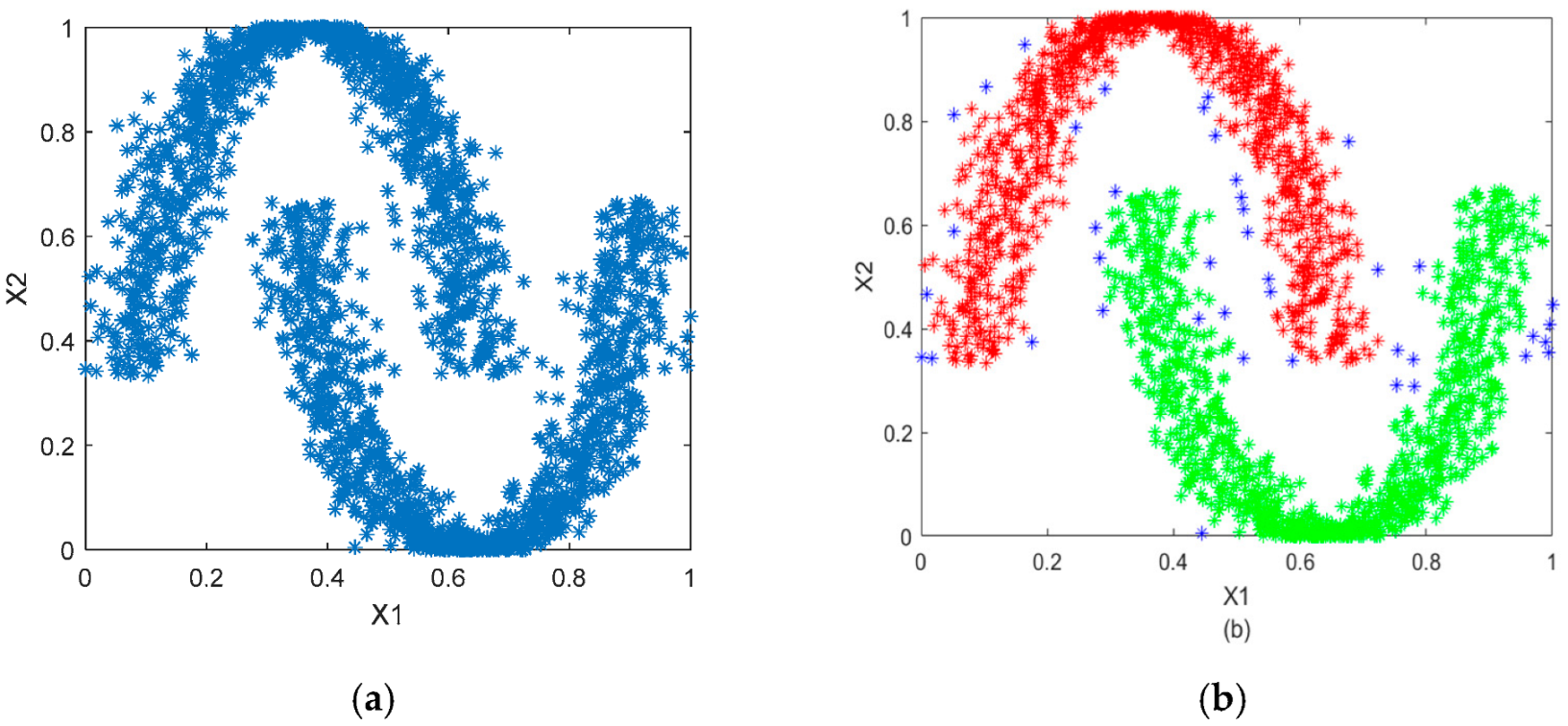
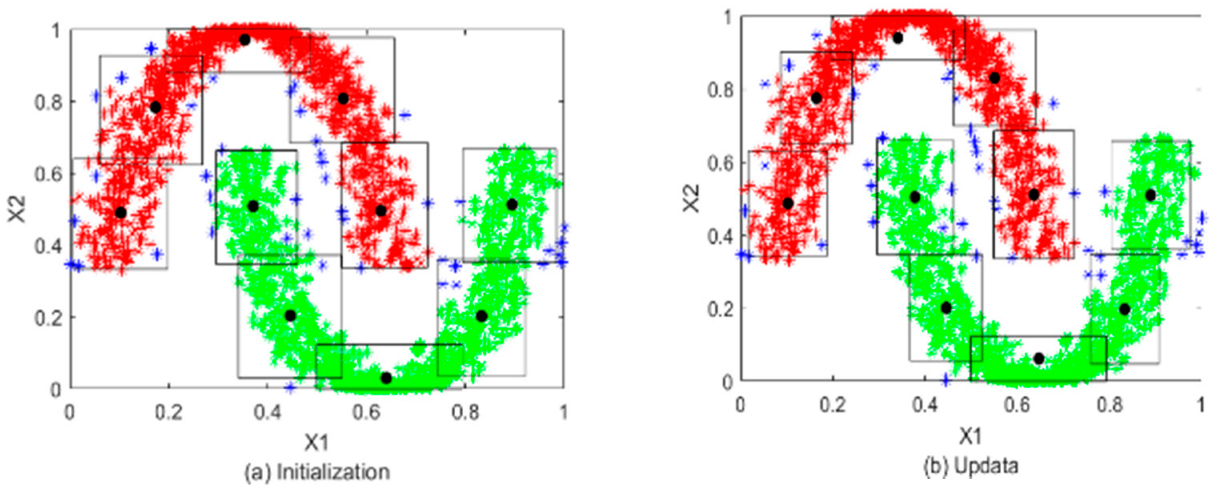
5.1. Synthetic Data
5.1.1. Optimal Prototypes and Granules Construction of Input Space
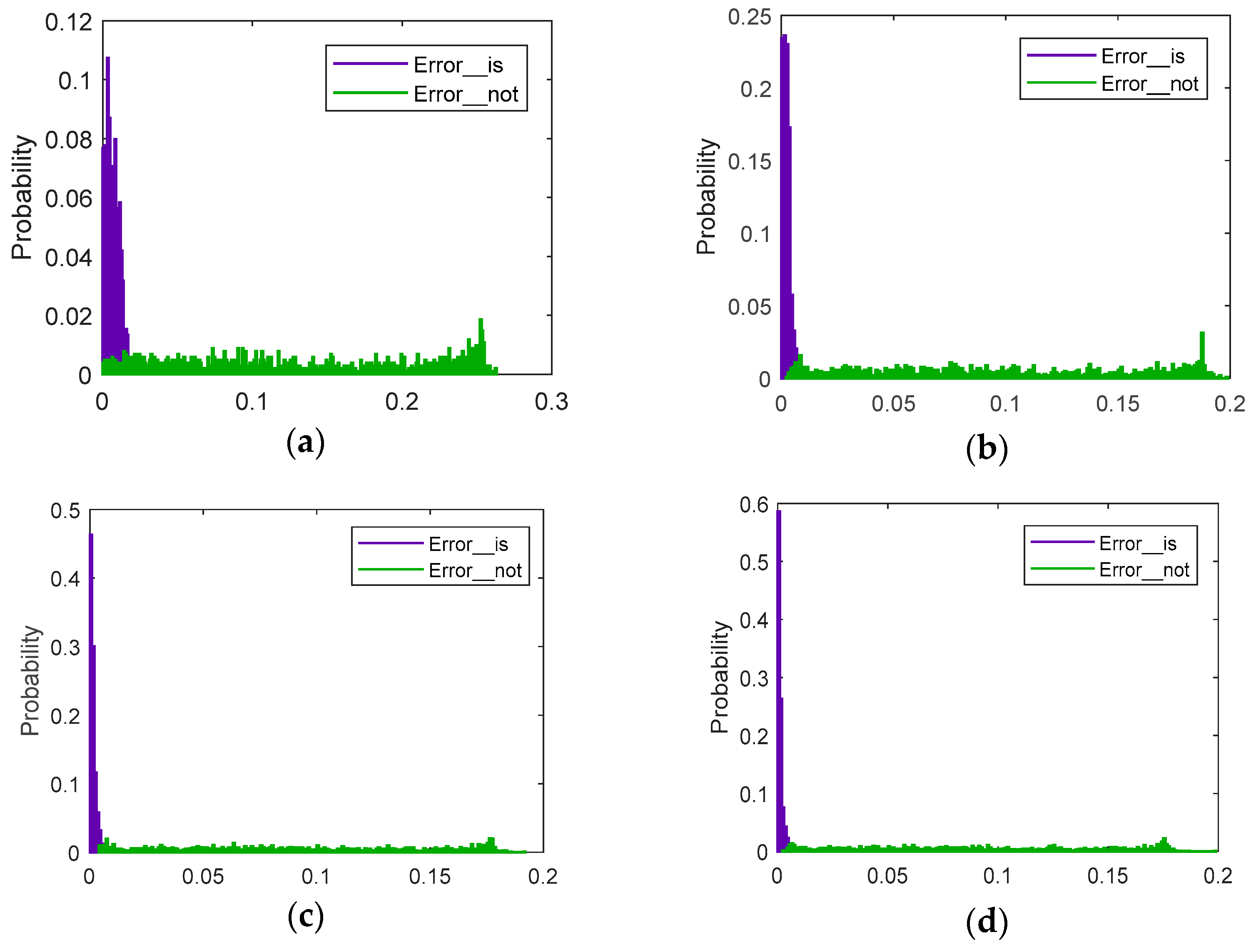
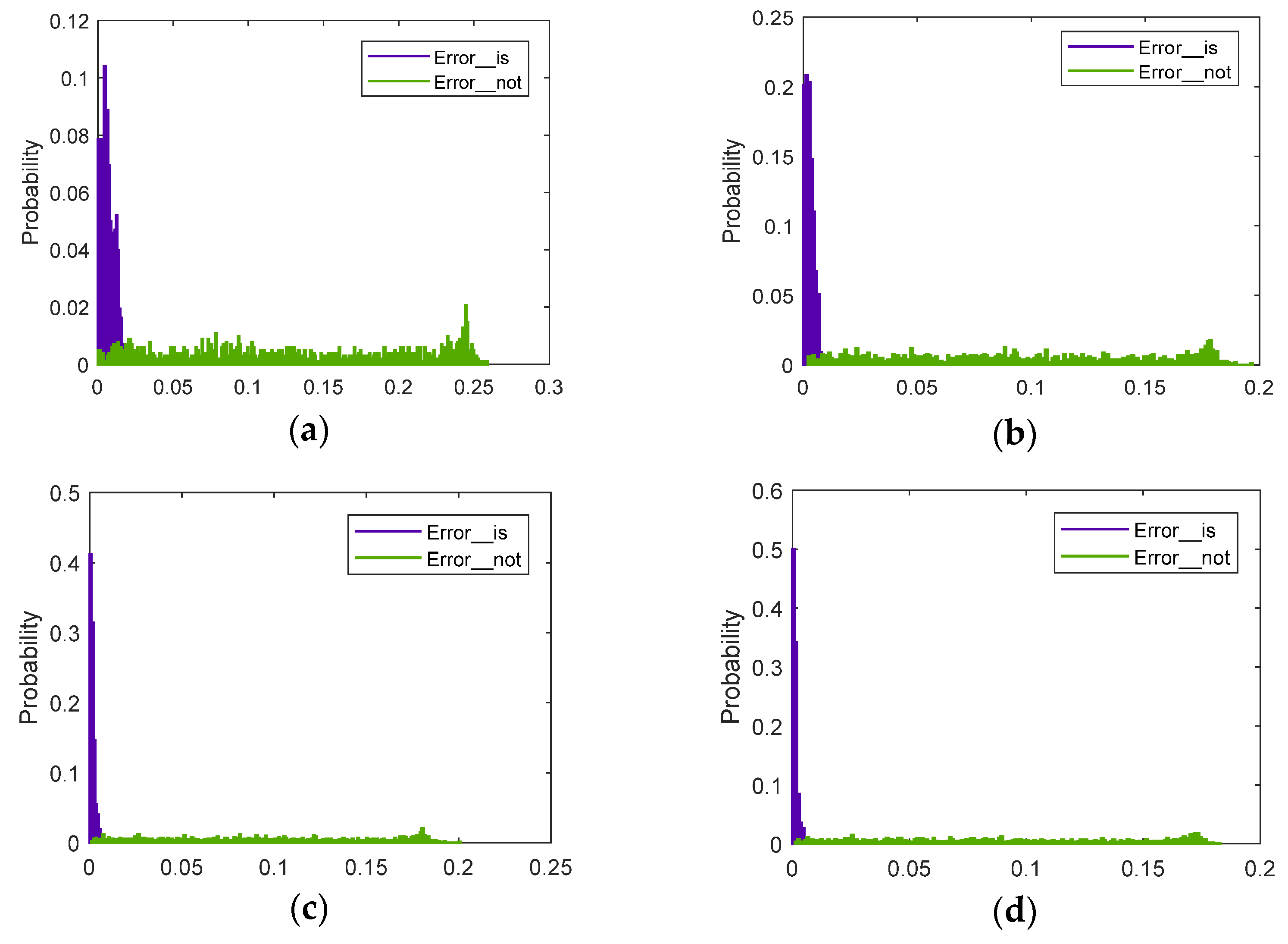
5.1.2. Construction on Interval Granules in Medium Space
5.1.3. Online Testing and Evaluation
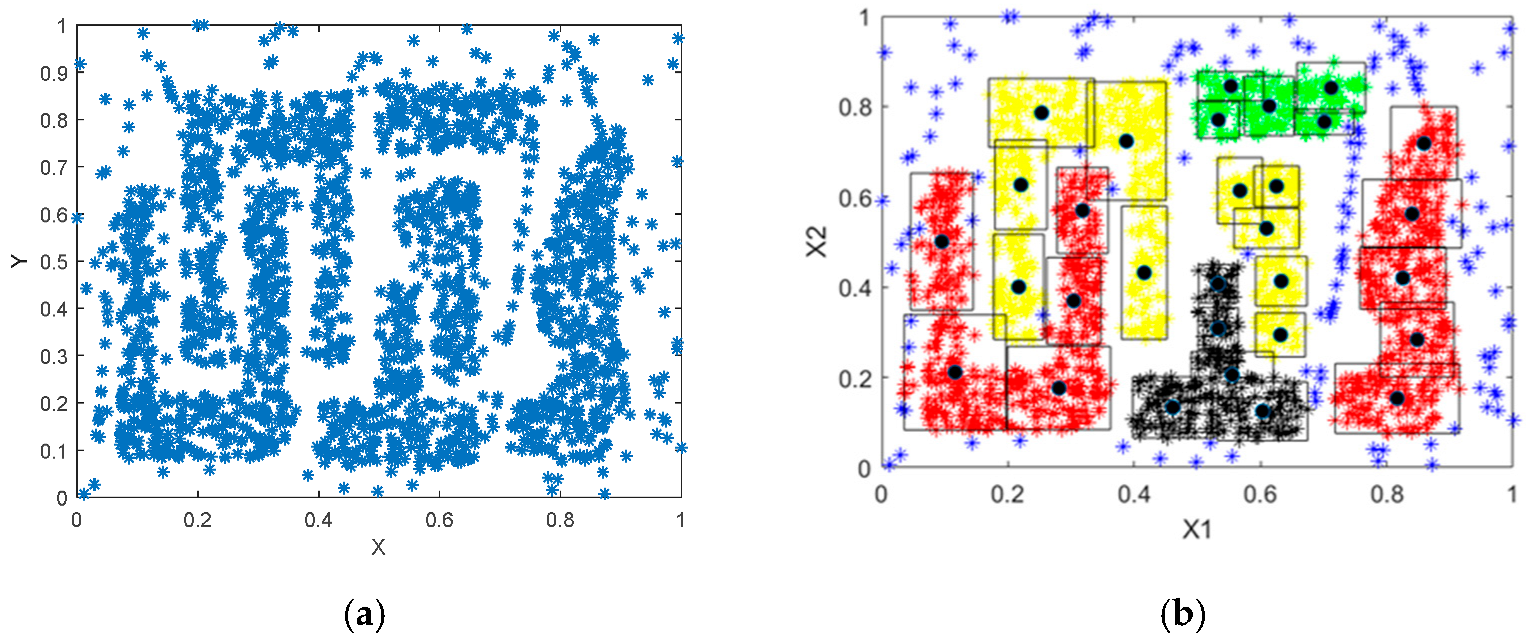
5.2. Spatial Benchmark Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yoseph, F.; Ahamed Hassain Malim, N.H.; Heikkilä, M.; Brezulianu, A.; Geman, O.; Paskhal Rostam, N.A. The impact of big data market segmentation using data mining and clustering techniques. J. Intell. Fuzzy Syst. 2020, 38, 6159–6173. [Google Scholar] [CrossRef]
- Ping, W. Data mining and XBRL integration in management accounting information based on artificial intelligence. J. Intell. Fuzzy Syst. 2021, 40, 6755–6766. [Google Scholar] [CrossRef]
- Vidhya, K.A.; Geetha, T.V. Rough set theory for document clustering: A review. J. Intell. Fuzzy Syst. 2017, 32, 2165–2185. [Google Scholar] [CrossRef]
- Goyal, N.; Gupta, K. A hierarchical laplacian TWSVM using similarity clustering for leaf classification. Clust. Comput. 2022, 25, 1541–1560. [Google Scholar] [CrossRef]
- Li, C.; Cerrada, M.; Cabrera, D.; Sanchez, R.V.; Pacheco, F.; Ulutagay, G.; Valente de Oliveira, J. A comparison of fuzzy clustering algorithms for bearing fault diagnosis. J. Intell. Fuzzy Syst. 2018, 34, 3565–3580. [Google Scholar] [CrossRef]
- Thao, N.X.; Ali, M.; Smarandache, F. An intuitionistic fuzzy clustering algorithm based on a new correlation coefficient with application in medical diagnosis. J. Intell. Fuzzy Syst. 2019, 36, 189–198. [Google Scholar] [CrossRef]
- Majhi, S.K.; Bhatachharya, S.; Pradhan, R.; Biswal, S. Fuzzy clustering using salp swarm algorithm for automobile insurance fraud detection. J. Intell. Fuzzy Syst. 2019, 36, 2333–2344. [Google Scholar] [CrossRef]
- Soni, N.; Ganatra, A. Categorization of several clustering algorithms from different perspective: A review. Int. J. Adv. Comput. Res. 2012, 2, 2249–7277. [Google Scholar]
- Gong, X. Big Data Clustering Algorithm Based on Computer Cloud Platform. Lecture Notes on Data Engineering and Communications Technologies. In Proceedings of the 2021 International Conference on Machine Learning and Big Data Analytics for IoT Security and Privacy, Shanghai, China, 6–8 November 2021; Volume 98, pp. 254–262. [Google Scholar] [CrossRef]
- Schubert, E.; Rousseeuw, P.J. Faster k-Medoids Clustering: Improving the PAM, CLARA, and CLARANS Algorithms. In International Conference on Similarity Search and Applications; Springer: Cham, Switzerland, 2019; pp. 171–187. [Google Scholar]
- Schubert, E.; Rousseeuw, P.J. Fast and eager k-medoids clustering: O (k) runtime improvement of the PAM, CLARA, and CLARANS algorithms. Inf. Syst. 2021, 101, 101804. [Google Scholar] [CrossRef]
- Kashtiban, A.M.; Khanmohammadi, S. A genetic algorithm with SOM neural network clustering for multimodal function optimization. J. Intell. Fuzzy Syst. 2018, 35, 4543–4556. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, X.; Chang, Q. Spatial clustering analysis of green economy based on knowledge graph. J. Intell. Fuzzy Syst. 2021, 1–10, preprint. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. Density-based spatial clustering of applications with noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 240, p. 6. [Google Scholar]
- Unver, M.; Erginel, N. Clustering applications of IFDBSCAN algorithm with comparative analysis. J. Intell. Fuzzy Syst. 2020, 39, 6099–6108. [Google Scholar] [CrossRef]
- Ouyang, T.; Pedrycz, W.; Pizzi, N.J. Record linkage based on a three-way decision with the use of granular descriptors. Expert Syst. Appl. 2019, 122, 16–26. [Google Scholar] [CrossRef]
- Jakobsson, M.; Johansson, K.A. Practical and secure software-based attestation. In Proceedings of the 2011 Workshop on Lightweight Security & Privacy: Devices, Protocols, and Applications, Istanbul, Turkey, 14–15 March 2011; pp. 1–9. [Google Scholar]
- Amruthnath, N.; Gupta, T. Fault class prediction in unsupervised learning using model-based clustering approach. In Proceedings of the 2018 International Conference on Information and Computer Technologies (ICICT), DeKalb, IL, USA, 23–25 March 2018; pp. 5–12. [Google Scholar]
- Ouyang, T.; Pedrycz, W.; Reyes-Galaviz, O.F.; Pizzi, N.J. Granular description of data structures: A two-phase design. IEEE Trans. Cybern. 2019, 51, 1902–1912. [Google Scholar] [CrossRef]
- Bargiela, A.; Pedrycz, W. Granular computing. In Handbook on Computational Intelligence: Volume 1: Fuzzy Logic, Systems, Artificial Neural Networks, and Learning Systems; World Scientific: Singapore, 2016; pp. 43–66. [Google Scholar]
- Ouyang, T. Structural rule-based modeling with granular computing. Appl. Soft Comput. 2022, 128, 109519. [Google Scholar] [CrossRef]
- Ouyang, T.; Pedrycz, W.; Pizzi, N.J. Rule-based modeling with DBSCAN-based information granules. IEEE Trans. Cybern. 2019, 51, 3653–3663. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, D.P.; Garrett, J.H., Jr.; Soibelman, L. A density-based spatial clustering approach for defining local indicators of drinking water distribution pipe breakage. Adv. Eng. Inform. 2011, 25, 380–389. [Google Scholar] [CrossRef]
- Panahandeh, G.; Åkerblom, N. Clustering driving destinations using a modified dbscan algorithm with locally-defined map-based thresholds. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering, Porto, Portugal, 18–20 October 2015; Springer: Cham, Switzerland, 2015; pp. 97–103. [Google Scholar]
- Dey, R.; Chakraborty, S. Convex-hull & DBSCAN clustering to predict future weather. In Proceedings of the 2015 International Conference and Workshop on Computing and Communication (IEMCON), Vancouver, BC, Canada, 15–17 October 2015; pp. 1–8. [Google Scholar]
- Sharma, A.; Chaturvedi, S.; Gour, B. A semi-supervised technique for weather condition prediction using DBSCAN and KNN. Int. J. Comput. Appl. 2014, 95, 21–26. [Google Scholar] [CrossRef]
- Zhou, L.; Hopke, P.K.; Venkatachari, P. Cluster analysis of single particle mass spectra measured at Flushing, NY. Anal. Chim. Acta 2006, 555, 47–56. [Google Scholar] [CrossRef]
- Chauhan, R.; Kaur, H.; Puri, R. An Empirical Analysis of Unsupervised Learning Approach on Medical Databases. In Emerging Trends in Electrical, Communications and Information Technologies; Springer: Singapore, 2017; pp. 63–70. [Google Scholar]
- Plant, C.; Teipel, S.J.; Oswald, A.; Böhm, C.; Meindl, T.; Mourao-Miranda, J.; Bokde, A.W.; Hampel, H.; Ewers, M. Automated detection of brain atrophy patterns based on MRI for the prediction of Alzheimer’s disease. Neuroimage 2010, 50, 162–174. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.K.; Paul, T.U. Segmentation of brain tumour from MRI image analysis of k-means and dbscan clustering. Int. J. Res. Eng. Sci. 2013, 1, 48–57. [Google Scholar]
- Guo, Z.; Liu, H.; Pang, L.; Fang, L.; Dou, W. DBSCAN-based point cloud extraction for Tomographic synthetic aperture radar (TomoSAR) three-dimensional (3D) building reconstruction. Int. J. Remote Sens. 2021, 42, 2327–2349. [Google Scholar] [CrossRef]
- Lou, J.; Cao, H.; Zheng, H.; Xiao, J. Anomaly Monitoring of Power Characteristic of Wind Turbine based on Multi-Dimensional Clustering Method. Adv. Sci. Technol. Lett. 2016, 139, 433–438. [Google Scholar]
- Khan, K.; Rehman, S.U.; Aziz, K.; Fong, S.; Sarasvady, S. DBSCAN: Past, present and future. In Proceedings of the Fifth International Conference on the Applications of Digital Information and Web Technologies (ICADIWT 2014), Chennai, India, 17–19 February 2014; pp. 232–238. [Google Scholar]
- Li, H.; Liu, J.; Wu, K.; Yang, Z.; Liu, R.W.; Xiong, N. Spatio-temporal vessel trajectory clustering based on data mapping and density. IEEE Access 2018, 6, 58939–58954. [Google Scholar] [CrossRef]
- Ienco, D.; Bordogna, G. Fuzzy extensions of the DBScan clustering algorithm. Soft Comput. 2018, 22, 1719–1730. [Google Scholar] [CrossRef]
- Bordogna, G.; Ienco, D. Fuzzy core dbscan clustering algorithm. In Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Montpellier, France, 15–19 July 2014; Springer: Cham, Switzerland, 2014; pp. 100–109. [Google Scholar]
- Smiti, A.; Eloudi, Z. Soft dbscan: Improving dbscan clustering method using fuzzy set theory. In Proceedings of the 2013 6th International Conference on Human System Interactions (HSI), Sopot, Poland, 6–8 June 2013; pp. 380–385. [Google Scholar]
- Ma, L.; Gu, L.; Li, B.; Qiao, S.; Wang, J. G-dbscan: An improved dbscan clustering method based on grid. Adv. Sci. Technol. Lett. 2014, 74, 23–28. [Google Scholar]
- Ren, F.; Hu, L.; Liang, H.; Liu, X.; Ren, W. Using density-based incremental clustering for anomaly detection. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Washington, DC, USA, 12–14 December 2008; Volume 3, pp. 986–989. [Google Scholar]
- Chen, N.; Chen, A.Z.; Zhou, L.X. An incremental grid density-based clustering algorithm. J. Softw. 2002, 13, 1–7. [Google Scholar]
- Ouyang, T.; Shen, X. Online Structural Clustering Based on DBSCAN Extension with Granular Descriptors. Inf. Sci. 2022, 607, 688–704. [Google Scholar] [CrossRef]
- Chakraborty, S.; Nagwani, N.K. Analysis and study of Incremental DBSCAN clustering algorithm. arXiv 2014, arXiv:1406.4754, 2014. [Google Scholar]
- Bakr, A.M.; Ghanem, N.M.; Ismail, M.A. Efficient incremental density-based algorithm for clustering large datasets. Alex. Eng. J. 2015, 54, 1147–1154. [Google Scholar] [CrossRef]
- Jo, J.M. Effectiveness of normalization pre-processing of big data to the machine learning performance. J. Korea Inst. Electron. Commun. Sci. 2019, 14, 547–552. [Google Scholar]
- Panda, S.; Sahu, S.; Jena, P.; Chattopadhyay, S. Comparing fuzzy-C means and K-means clustering techniques: A comprehensive study. In Advances in Computer Science, Engineering & Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 451–460. [Google Scholar]
- Pedrycz, W.; Al-Hmouz, R.; Morfeq, A.; Balamash, A. The design of free structure granular mappings: The use of the principle of justifiable granularity. IEEE Trans. Cybern. 2013, 43, 2105–2113. [Google Scholar] [CrossRef] [PubMed]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Ouyang, T.; Shen, X. Representation learning based on hybrid polynomial approximated extreme learning machine. Appl. Intell. 2022, 52, 8321–8336. [Google Scholar] [CrossRef]
- Barbakh, W.; Fyfe, C. Online clustering algorithms. Int. J. Neural Syst. 2008, 18, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Barton, T.; Bruna, T.; Kordik, P. Chameleon 2: An improved graph-based clustering algorithm. ACM Trans. Knowl. Discov. Data 2019, 13, 1–27. [Google Scholar] [CrossRef]


| z1 | z2 | z3 | |
|---|---|---|---|
| Cluster1 | (0.5507, 0.8299) | (0.1020, 0.4865) | (0.6361, 0.5103) |
| Cluster2 | (0.4456, 0.2005) | (0.8895, 0.5088) | (0.8331, 0.1971) |
| G1 | G2 | G3 | |
| Cluster1 | [0.4606, 0.6408] × [0.6993, 0.9605] | [0.0160, 0.1881] × [0.3429, 0.6302] | [0.5487, 0.7236] × [0.3354, 0.6852] |
| Cluster2 | [0.3668, 0.5244] × [0.0557, 0.3452] | [0.8040, 0.9750] × [0.3605, 0.6572] | [0.7584, 0.9078] × [0.0471, 0.3471] |
| z4 | z5 | ||
| Cluster1 | (0.3409, 0.9394) | (0.1640, 0.7746) | |
| Cluster2 | (0.3778, 0.5040) | (0.6467, 0.0618) | |
| G4 | G5 | ||
| Cluster1 | [0.1948, 0.4869] × [0.8788, 1.0000] | [0.0861, 0.2420] × [0.6489, 0.9004] | |
| Cluster2 | [0.2959, 0.4598] × [0.3455, 0.6625] | [0.4993, 0.7941] × [0, 0.1237] |
| c = 5 | c = 10 | |
|---|---|---|
| Cluster1 | IGy: [0, 0.0260]; IGn: [0.0011, 0.2591]; | IGy: [0, 0.0090]; IGn: [0.0034, 0.1914]; |
| Cluster2 | IGy: [0, 0.0270]; IGn: [0.0046,0.2526]; | IGy: [0, 0.0080]; IGn: [0.0055,0.1875]; |
| c =15 | c =20 | |
| Cluster1 | IGy: [0, 0.0090]; IGn: [0.0044,0.1804]; | IGy: [0, 0.0070]; IGn: [0.0036,0.1796]; |
| Cluster2 | IGy: [0, 0.0070]; IGn: [0.0047,0.1887]; | IGy: [0, 0.0070]; IGn: [0.0029,0.1789]; |
| c = 5 | c = 10 | c = 15 | c = 20 | |
|---|---|---|---|---|
| Acc. | 0.8920 | 0.9350 | 0.9400 | 0.9520 |
| Time | 0.0316 | 0.0438 | 0.0908 | 0.0927 |
| C-DBSCAN | G-DBSCAN | Proposed Approach | Online k-Means | Online W-k-Means | |
|---|---|---|---|---|---|
| Acc. | 0.9450 | 0.9330 | 0.9520 | 0.8947 | 0.9058 |
| Time | 0.2279 | 0.1712 | 0.0927 | 0.0632 | 0.0675 |
| z1 | z2 | z3 | z4 | z5 | |
|---|---|---|---|---|---|
| C1 | (0.0953, 0.5005) | (0.3181, 0.5696) | (0.2808, 0.1761) | (0.3042, 0.3694) | (0.1163, 0.2112) |
| C2 | (0.5333, 0.7704) | (0.7013, 0.7656) | (0.712, 0.841) | (0.6139, 0.8009) | (0.553, 0.8449) |
| C3 | (0.5329, 0.3078) | (0.6032, 0.1249) | (0.5328, 0.4072) | (0.4611, 0.1334) | (0.5553, 0.2053) |
| C4 | (0.2533, 0.7857) | (0.217, 0.4002) | (0.4159, 0.4317) | (0.2205, 0.6264) | (0.3876, 0.7231) |
| C5 | (0.6318, 0.294) | (0.6254, 0.6233) | (0.6097, 0.5299) | (0.5676, 0.6134) | (0.6329, 0.4129) |
| C6 | (0.8482, 0.2836) | (0.8402, 0.5621) | (0.8256, 0.4199) | (0.8166, 0.1532) | (0.8591, 0.7181) |
| Cluster 1 | Cluster 2 | Cluster 3 | |
|---|---|---|---|
| IGy | [0, 0.022] | [0, 0.003] | [0, 0.006] |
| IGn | [0.0018, 0.3038] | [0.0387, 0.4747] | [0.0039, 0.2559] |
| Cluster 4 | Cluster 5 | Cluster 6 | |
| IGy | [0, 0.021] | [0, 0.005] | [0, 0.01] |
| IGn | [0.0300, 0.2203] | [0.0037, 0.2137] | [0.0509, 0.4409] |
| Granule-Based | C-DBSCAN | G-DBSCAN | k-Means | W-k-Means | ||||
|---|---|---|---|---|---|---|---|---|
| c = 5 | c = 10 | c = 15 | c = 20 | |||||
| Acc. | 0.7550 | 0.8760 | 0.8990 | 0.9134 | 0.8979 | 0.8754 | 0.5218 | 0.5854 |
| Time | 0.0671 | 0.1185 | 0.1861 | 0.1907 | 0.4347 | 0.3924 | 0.1419 | 0.1576 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Shen, X.; Ouyang, T. Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models. Appl. Sci. 2022, 12, 9402. https://doi.org/10.3390/app12199402
Zhang X, Shen X, Ouyang T. Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models. Applied Sciences. 2022; 12(19):9402. https://doi.org/10.3390/app12199402
Chicago/Turabian StyleZhang, Xinhui, Xun Shen, and Tinghui Ouyang. 2022. "Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models" Applied Sciences 12, no. 19: 9402. https://doi.org/10.3390/app12199402
APA StyleZhang, X., Shen, X., & Ouyang, T. (2022). Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models. Applied Sciences, 12(19), 9402. https://doi.org/10.3390/app12199402








