1. Introduction
Visual Question Answering (VQA) [
1,
2] is a cross-domain task of computer vision and natural language processing, and it has become increasingly important in the research and application of multimodal machine learning. In the past few decades, significant advances have been made in computer vision and natural language processing, with an explosion of visual and textual data to acquire and process. The most common VQA consists of an image and a question to be answered by the machine. Compared with other computer vision tasks, this model answers in real-time, not in advance. Moreover, the VQA model is required to comprehend the multimodal information of images and texts in a more artificially intelligent [
3] way, leading to an in-depth understanding of vision and language.
VQA remains a challenging and open research topic. Recent research has focused on how to solve language bias. Language bias [
4,
5,
6,
7,
8] threatens the implementation of VQA, which indicates that the current VQA model has an inadequate understanding of multimodal information. Language bias seems to be caused by the uneven distribution of datasets, a common problem in the real world. For example, if 90 percent of the bananas in the training set are yellow, the model would ask, “what color the banana is” and answer, “yellow” all the time, based on language bias. As shown in
Figure 1, many VQA models tend to answer “yes” or “no” directly. Take another typical example. For the question “what color is the banana in the image?”, although the banana is green, the model still tends to predict “yellow”.
With language bias, the model overly relies on the correlation between the question and the answer while it ignores the information in the image. In essence, language bias arises from data imbalance, which leads to over-fitting of the model; that is, the model fits the head samples in the dataset [
8]. The over-fitting of the model is an inherent problem of the model itself. The deep neural network has a variance in the case of an individual model, and the variance can be reduced by an ensemble or knowledge distillation [
9,
10,
11,
12] (Over-fitting to the label imbalance may lead to some models not training very well). At the feature level, the variance is caused by the incompleteness of the feature subgraph [
12], so it is easy to produce over-fitting. Recently, knowledge [
13,
14] distillation and self-knowledge distillation [
15,
16] have been proven to be able to learn multi-view features and reduce over-fitting [
12,
17,
18].
Neural network analysis of information is multi-view; for the same object, its different views have semantic consistency [
19,
20,
21], and the multi-view structure can be ubiquitous in the dataset and feature level [
12]. Therefore, the model can give the prediction based on a learned subgraph. However, if the subgraph is not comprehensive, the prediction can be biased. As shown in
Figure 2, for the same question, “what color is the banana?”, the model learns the feature of yellow bananas while it ignores the feature of green bananas, which are less frequent in the training set. In other words, the model ignores the view of green bananas, causing visual bias, which further leads to language bias. Therefore, the model needs to focus on the feature of the less distributed samples in the training set and learn a comprehensive set of multi-view features so as to overcome VQA language bias and over-fitting.
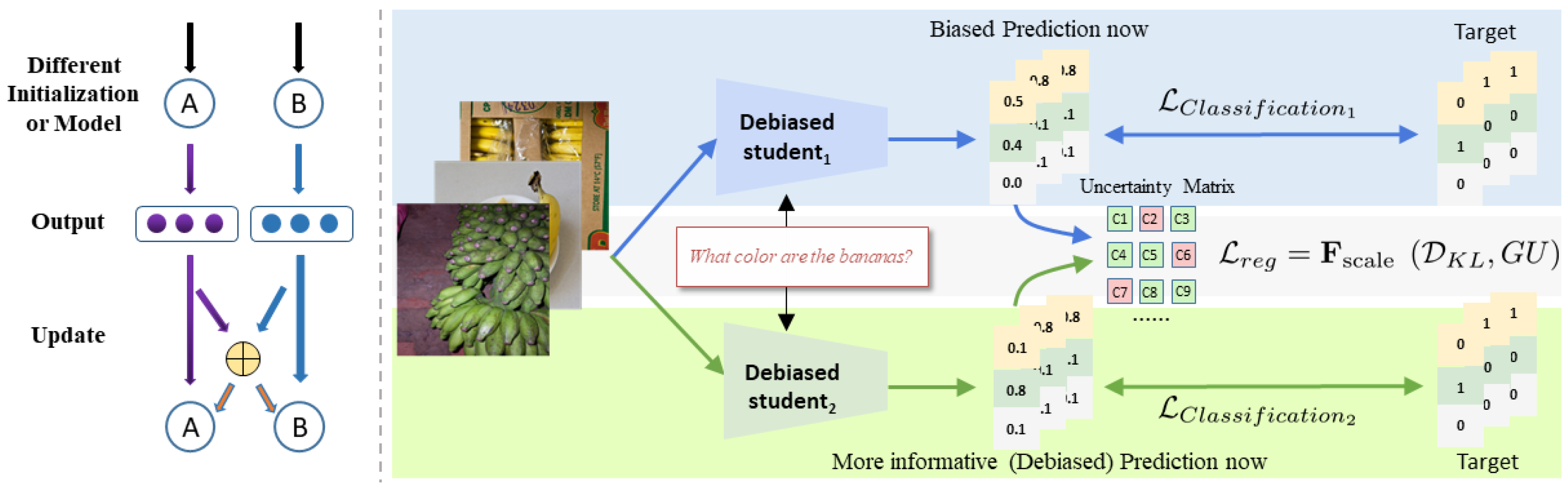
The paper discusses how to reduce the language bias of the VQA model via self-knowledge distillation and proposes a new online learning framework, “language bias-driven self-knowledge distillation (LBSD)”, for implicit learning of multi-view visual features. Self-knowledge distillation enables the model to acquire more dark knowledge and improves its generalization ability. In short, with self-knowledge distillation, the model can have a more comprehensive understanding of view features. Online knowledge distillation no longer uses teacher models but allows student models to learn from each other by using KL divergence to uniformly constrain the output. It is worth mentioning that the student network is actually equal to the teacher network; the two networks are the same. However, the learning degree of student models cannot be described by using KL divergence alone [
22,
23]. Therefore, the authors of this paper put forward the concept of generalization uncertainty to help the model learn unbiased knowledge.
LBSD enables two debiased models to distill knowledge from each other to learn more complete visual features. It distinguishes between debiased students and biased students by calculating the generalization uncertainty of the prediction of student models and reinforces the mutual learning of the two models about unbiased knowledge. The paper also finds that heterogeneous student models can be used to reduce language bias. LBSD enables the model to learn a more complete set of visual features and to focus on the features of the less distributed samples in the training set by utilizing generalization uncertainty, thus reducing the language bias of the model and improving the robustness of the VQA model.
Contribution. In summary, the contributions of this paper are as follows:
(1) The authors of this paper propose a training framework (LBSD) based on online self-knowledge distillation, which can considerably reduce the VQA language bias. Moreover, the authors of this paper explore the different cases of student models (heterogeneous networks). The authors of this paper verify the effectiveness of the LBSD method and analyze the theory behind it.
(2) The authors of this paper propose a method to measure generalization uncertainty based on Top-k information entropy, and use it to distinguish between debiased students and biased students, so as to force the model to focus on the samples that cannot be directly answered by language bias in the VQA datasets. The authors of this paper also prove the proportional relationship between the generalized uncertainty and the expected test error.
3. Methods
In order to reduce VQA language bias, the authors of this paper consider making the model focus on the less distributed samples in the training set to learn a more complete set of multi-view features. To this end, the authors of this paper propose a new online self-knowledge distillation learning framework (LBSD) for implicit learning of multi-view visual feature sets to alleviate language bias. The methods are divided into: (1) language bias-driven self-knowledge distillation and (2) using generalization uncertainty to help student models learn unbiased visual knowledge. In the following sections, the authors of this paper explain the workflow of LBSD and analyze the theory behind it. The block diagram of the method presented in this paper is shown in
Figure 3 and Algorithm 1.
| Algorithm 1: Language Bias-Driven Self-Distillation |
| Input: Training set , (), label set (), learning rate and |
| . |
| Initialize: Debiased Models and (different initial conditions |
| or models). |
| Repeat : |
| |
| Randomly sample data from ,. |
| 1: Update the predictions and of
for the current |
| mini-batch |
| 2: Compute the stochastic gradient and update by Equation (13) : |
|
3: Update the predictions of . |
| 4: Compute the stochastic gradient and update : |
|
5: Update the predictions of . |
| Until : convergence |
3.1. Preliminaries
To tackle the multi-class classification problem in VQA field, the general form of VQA is: A dataset is given containing N triplets of images , questions and answers .
The aim of the VQA task is to learn a mapping function :, which generates the answer distributions for any given image-question pair. The authors of this paper omit subscript i in the following.
For each question
Q and image
I, the Bottom-Up Top-Down (UpDn) [
56] model uses a question encoder
and an object detector separately
to extract a set of word embeddings
Q and a set of visual object embeddings
V. The model is fed both
V and
Q to get the joint feature
. Then, the joint features are fed into the classifier
C to get the final predictions.
For fair comparisons, the authors of this paper use the Bottom-Up Top-Down (UpDn) model [
56], which is mainly used by many researchers as the backbone network.
3.2. Language Bias-Driven Self-Distillation
The method aims to learn unbiased visual knowledge via the mutual learning of two debiased models so as to reduce VQA language bias. The training strategy, which can be integrated with the current debiased methods, consists of the mutual learning of two debiased models. A dataset is given
containing N triplets of images
, questions
and answers
, it can be input into two identical models with different random initializations,
and
, and two probability vectors
p can be predicted by the model,
z means Softmax output.
where
k represents the number of outputs or classes of the neural network.
At the same time, the VQA model is generally defined as multi-type. Therefore, for multiple types, the objective function of the training network
is defined as the cross-entropy error between the prediction and the correct label, as shown as follows,
K means samples,
M means classes and
means the cross entropy error:
In order to allow the two student models to learn unbiased visual features from each other (similar to self-knowledge distillation), the authors of this paper use KL divergence to constrain all the predictions, thus distilling the unbiased knowledge of the two models. The formula of KL divergence between
and
is shown as follows:
The two student models simultaneously start parameter optimization, and the optimization loss is shown as follows. The consistency constraint of the predictions of the two models can realize the mutual learning of unbiased knowledge between the two models.
Since KL divergence is asymmetric, it can be replaced by Jensen–Shannon (JS) divergence (a variation of KL divergence) to ensure the consistency constraint between the two student models. Such replacement will not affect the final precision of the model.
Moreover, all the current self-knowledge distillation models use student models with different random initializations. The strategy is effective because the model learns more complete sets of multi-view features. The authors of this paper also explore the case where two heterogeneous student networks serve as the student models. The heterogeneous networks have the same feature extraction structure, but they have different loss functions and network branches.
3.3. Debiased Mutual Students
As mentioned above, the language bias of datasets is, in essence, the distribution bias of image samples. For the same input image/text sample pair, the two student networks may have different outputs because of an inconsistent random seed, order of data reading or even network structure.
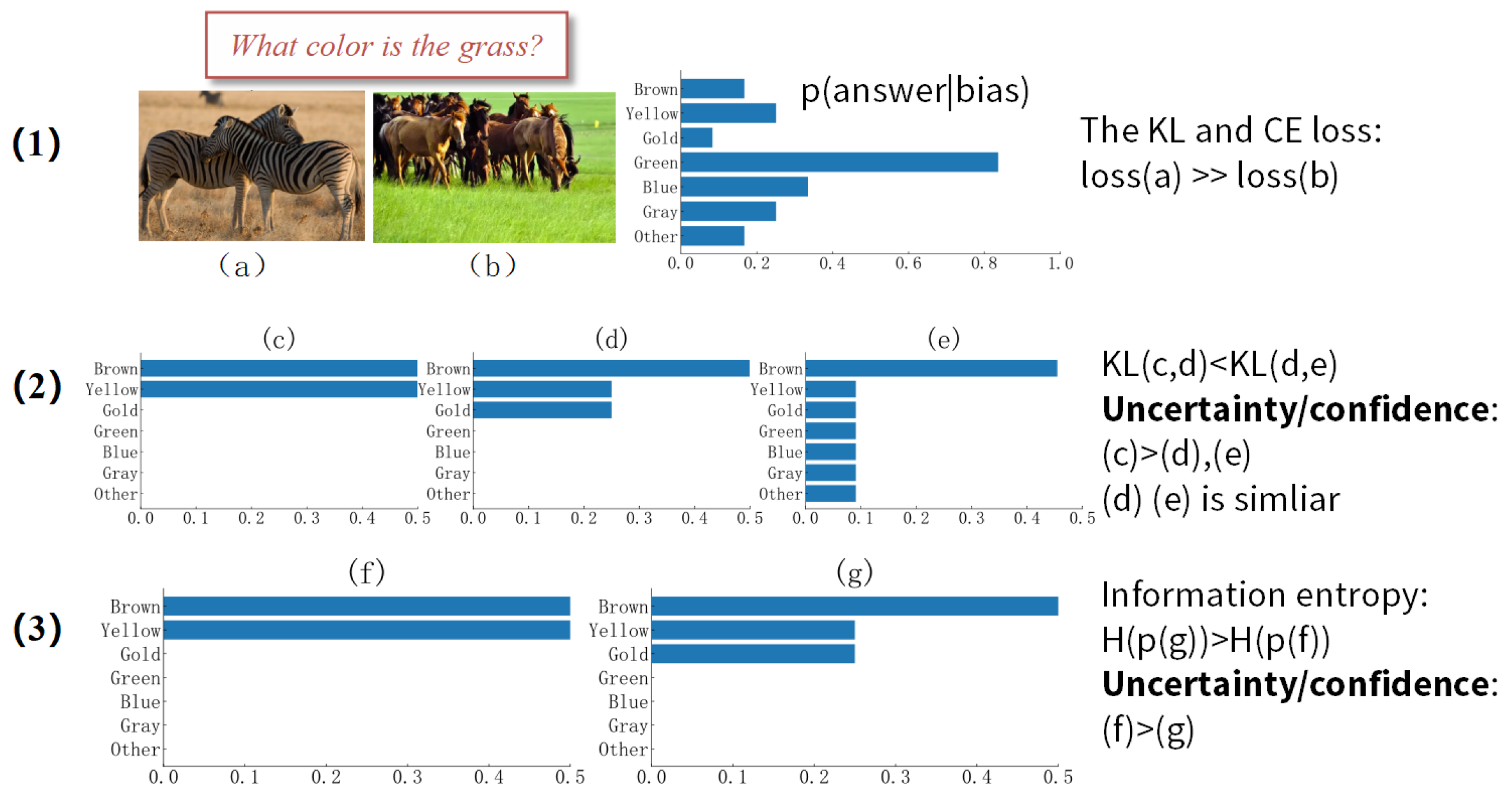
As shown in
Figure 4, for more-distributed image/text sample pairs in the dataset, the model can simply answer the question through language bias, and the confidence of the answer is very high. The different student models tend to have the same answer. For the gradient update of neural networks, the cross-entropy loss and KL divergence loss of image/text samples that can answer the question by language bias are minimal. However, for the less-distributed samples, the model is more likely to have different answers. Therefore, the different answers can be measured and analyzed to help the model focus more on the samples that cannot be directly answered by language bias so as to reduce language bias.
In general, the current self-distillation methods only use KL divergence for the mutual distillation of knowledge. As KL divergence is not commutative, it cannot be understood as “distance”, which measures the information loss between two distributions. Simply constraining the KL divergence of the two student models cannot figure out the difference between the output and help the two models learn from each other with more precision. As shown in
Figure 4, KL divergence for different distributions and consistency constraints is not always consistent with our expectations. For this reason, the authors of this paper consider using information entropy to evaluate the output uncertainty of the two models and evaluate the output difference based on the uncertainty.
As shown in
Figure 4, although information entropy
H is a common method to measure information uncertainty, the output is not always consistent with our understanding. For
= [0.5, 0.25, 0.25] and
= [0.5, 0.5, 0], the formula leads to
>
. For general classification scenarios, it is clear that
is less certain than
, and the confidence of predictions is extremely low. Therefore, in order to describe the prediction uncertainty, the authors of this paper adopt a simple and improved version: Top-k information entropy.
Suppose that
,
, …,
are
k values with the highest probability, the following formula can be obtained:
By using the above formula, the authors of this paper can get a result in the range of 0 to 1 and take C as the final uncertainty measure.
In order to measure the output difference between the two student models, for the uncertainty
and
, the output difference can be defined as
. In order to enhance the mutual learning of the two student models in the case of output difference (questions that cannot be answered directly with language bias), the authors of this paper define a generalization uncertainty index
to represent the intensity. The formula is
, and the final loss function of the generalization uncertainty index can be obtained. The formula is as follows:
In the next section, the authors of this paper will prove that the generalization uncertainty index of the two student models can be used to estimate the test error of the model.
3.4. Theoretical Analysis
3.4.1. Theoretical Analysis of Generalization Uncertainty (GU)
In this section, the authors of this paper demonstrate that the generalized uncertainty index between two student models can be used to estimate the model test error on image-text sample pairs. Thus, generalized uncertainty is used in the training process to help students learn unbiased knowledge. Following the research of Nakkiran and Bansal [
57], Jiang et al. [
58] and others [
59,
60,
61], the authors of this paper use class-segregated calibration (or class-wise calibration) [
58,
62,
63,
64,
65,
66] to prove the proportional relationship between the generalized uncertainty and the test error.
Notation 1. The authors in this paper define two neural networks trained from different random seeds as n, . The data of this model include K categories with input and label (Y). The model is parameterized by stochastic learning. The probability expression of the predicted output of the model is . is the distribution map from , and is the sample estimate for the different parameter distribution of models. The parameters of the model can be defined as Ω. The function is the indicator function, which means the prediction is true or otherwise.
Definition 1. The model N () satisfies the generalization uncertainty proportional (GUP) on the distribution if: Definition 2. The self-knowledge distillation model N () satisfies class-wise calibration (or class-segregated calibration) on if any kind of confidence value q falls in and for any class k falls in , Theorem 1. If the self-knowledge distillation model N () satisfies class-wise calibration (or class-segregated calibration) on , then N satisfies the generalization uncertainty proportional (GUP) on . Proof. The authors in this paper define the Expected Test error as TE (Test error). The TOP-K error of the two-student model with generalized uncertainty is fixed at GUE. By simplifying the two errors, the following results can be obtained, and the proportional relationship (GUP) between them can be obtained. Since
K previously represented the number of categories, for this reason, the authors of this paper represent
J as the
K term in TOP-K,
i as the corresponding prediction at the sample of
J-th value.
The detailed proof of generalization uncertainty can be found in
Appendix A. □
3.4.2. Theoretical Analysis of Debiased Self-Distillation
In this section, the authors of this paper demonstrate that self-knowledge distillation and generalized uncertainty can enable models to learn more complete multi-view feature sets and reduce language bias in VQA. The authors of this paper followed the research of Allen Zhu and Zhiyuan Li [
12,
19].
Notation 2. Let us set up a model whose dataset contains K categories, p-input patch s and the ReLU function. The model input is and the label is . To simplify the problem, the authors of this paper assume that each category contains related features that are orthogonal to each other. The authors of this paper define these features as vectors of , .
Following the settings of Zhu et al.’s research. The authors of this paper get the definitions as follows. The set of all features:
Definition 3. (Data distribution) The authors of this paper define the multi-view and single-view distribution and , D∈, and . Sample features with probability , . The coefficients , is the feature noise, is the random Gaussian noise. For each , the authors of this paper set: Definition 4. (The final data distribution D and the training dataset . Suppose D contains and μ . For N samples in D, the training dataset = ∪. random sampling from the set . , and .
Definition 5. The authors of this paper define a network with a cross-entropy loss function using a stochastic learning algorithm as follows: The logits function of the single model (,) can be defined as The logits function of the model using knowledge distillation can be defined as Theorem 2. For the single model, the authors of this paper use the prediction error as follows, : Theorem 3. For self-knowledge distillation with the generalization uncertainty model, λ (λ > 1) is the gain from generalized uncertainty. The authors of this paper use the prediction error as follows, :The authors of this paper find that when comparing Theorems 2 and 3, the prediction error of the model decreased. That means the LBSD method can reduce language bias. The detailed proof can be found in Appendix A.