Abstract
The current study presents an adaptive control approach to solve the tracking trajectory problem for a robotic manipulator that uses a gripper based on bimorph piezoelectric actuators. The development of an adaptive gain state feedback form that considers the state restrictions is proposed using a novel class of barrier Lyapunov function that drives the effective control of joints and piezoelectric actuators. The proposed method allows for the inclusion of complex combinations of state restrictions in the Lyapunov function, yielding the construction of differential forms for the gains in the controller that can handle the evolution of trajectories of the robotic arm inside the restricted region. The proposed control design successfully tracks reference trajectories for both joints of the robotic arm as well as the motion of the piezoelectric device during several operative scenarios. A comprehensive experimental study evaluates the effect of introducing state-dependent gain considering state restrictions of the ellipsoidal type. The comparison of the mean square error confirms the contributions of the developed control action, showing better tracking quality for less control power with the same evaluation, which is a desirable characteristic in the controlled motion of micromanipulators. The proposed controller solves the tracking trajectory problem for the micromanipulation system, satisfies the motion restrictions, and allows better tracking performance to be enforced. Furthermore, comparison of the obtained trajectories seems to validate the proposed controller’s contribution concerning a feedback form with fixed gains.
1. Introduction
Piezoelectric materials are suitable for developing automatized systems on millimetric or microscopic scales, including roboticized grippers, thanks to their fast reaction time and potential for miniaturization [1]. Due to their unique reversible electrical and mechanical properties, piezoelectric actuators have been used as sensor and actuator components in various robotic devices. The applications of piezoelectric materials range from buzzers to diesel engines, fuel injectors, sonar, ultrasound, and nanopositioners in scanning microscopes [2,3]. As actuators, piezoelectric materials are increasingly important in the latest positioning technologies thanks to their precise displacement [4] as well as several other advantages, such as quick response, large generative force, and high electromechanical coupling [5].
Piezoelectric actuators are categorized into stack actuators and bending actuators, characterized by the diversity of layers forming the actuator. The multilayers can either be double mounted or single-ended as a cantilever [6,7]. A particular case of multilayer bending actuators is a piezoelectric bimorph actuator, which consists of two layers of piezoelectric material connected over their length surfaces [5]. The resultant bending motion becomes the working principle in micromechanical applications. Consequently, piezoelectric bimorphs have been involved in areas related to precise position control, among others [3,5]. An essential characteristic of bending piezoelectric bimorphs is that the deflection of the bender’s tip is dependent on an alternating driving voltage. Many studies have investigated the behavior of piezoelectric actuators. Other studies have investigated the nonlinear behavior of bending piezoelectric bimorphs structures under exposure to high electric fields, modeling asymmetrical bending piezoelectric bimorph structures and the static behavior of the expected bending moment, and providing analytical description of the bending piezoelectric bimorphs’ free tip deflection by matrix calculus. The universal deformation state equations have been further extended to trimorph bending structures. The free tip deflection of piezoelectric multilayer beam bending actuators under the influence of an electric load was presented by DeVoe and Pisano [8]. The dynamic behavior of a bimorph bending structure excited to bending vibrations by external harmonic forces, bending moments, pressure loads, and electrical driving voltages, including a flexible plate attached at the free bender’s tip, was established as well, and a system of differential equations describing the dynamics of a bimorph was formulated. These establishments of piezoelectric responses have contributed to its application as a micro-manipulating system [9]. Piezoelectric actuators have been implemented in industrial, automotive, aviation, aerospace, medical, and consumer electronics applications. Their quiet drive settings make piezoelectric actuators an auto-focusing mechanism in microphone-equipped video cameras and mobile phones. In addition, as piezo actuators require no lubrication, they can be used in cryogenic and vacuum environments, among others. Using a stack actuator, extremely fine control is possible, with controlled voltages corresponding to slow expansion motions. As a result, a piezoelectric actuator can operate billions of times without wear or deterioration. The motion speed is exceptional, and is limited only by the object’s inertia, movement, and the output capability of the electronic driver. When operating in an energized condition, a piezoelectric actuator consumes a small amount of electrical power and produces limited heat [10,11,12].
Grasping and moving small objects from one location to another depends on the shape and weight of the object and whether it is fragile or firm. The essential operation of the micro-gripper relies on the mechanism of the specific type of actuators employed, such as a thermo-piezoelectric actuator. Micro-grippers have been developed using two parallel lead zirconate titanate (PZT) layers with a fixed range of displacement [13,14]. Other micro-manipulation mechanisms have been designed to enable the tip of the micro-gripper to move in parallel. Static characteristics, control of the micro-manipulator, and variation of deflection with the frequency have all been reported. This work aims to extend the investigation of parallel micro-gripping in terms of the effect of the sandwiched supporting layer on the deflection of the piezoelectric bimorph actuator. This fact allows us to understand to what extent the rigidity of the bimorph varies due to the brass layer between both piezoceramic layers. The second aim involves the implementation of a parallel micro-gripper by utilizing the piezoelectric bimorph itself to grasp soft objects instead of attaching an additional flexible cantilever. It has been well reported that piezoelectric actuators have been used to drive the micro-manipulation of micro-objects. A piezoelectric actuator can be used to provide movement to the flexible amplification mechanism of the micro-gripper. While this may deliver a large force, its size is significant and it has a complex structure. This study aims to achieve the grasping action directly from the piezoelectric bimorph in order to minimize the weight and complexity of the micro-gripper [15]. In addition, we aim to establish the supporting brass layer’s essential role in providing the micro-gripper’s basic behavior and increasing its life cycle.
Usually, the integration of piezoelectric-based grippers into a robotic arm to construct micromanipulators requires the implementation of efficient electrical instrumentation. This electronic configuration should be able to handle the high voltages required by the actuators while providing precise power transfer to motorized actuators which can mobilize the gripper towards the position where the object to be manipulated is placed [16,17,18]. The instrumentation development must be completed with effective control actions able to drive the robotic manipulator. The application of such a controller may solve the reference trajectory tracking problem. At the same time, the motion satisfies the state restrictions related to the joint limits and the limited piezoelectric range of motion. The compatibility of these two problems is commonly a control design challenge, because while the tracking error must be stabilized while satisfying the restrictions. This fact restricts the application of the traditional barrier Lyapunov function, for example, as well as other equivalent techniques that can handle the state restrictions. Recently, several control design variants have attempted to aggregate both problems using safe operating conditions or the application of positive functions in the design. Based on this problem, there is a clear motivation to design new controllers that can drive the motion of the robotic manipulator and the actuators associated with the gripping device. This study aims to provide a new option by designing a novel control that can integrate both problems using a modified class of barrier Lyapunov function which uses state-dependent parameters that depend on the distance between the current state and the sets of restrictions.
The main contributions of this study are: (a) A novel state constraint adaptive controller that solves position tracking for a robotic manipulator holding a gripper based on parallel bimorph piezoelectric actuators; and (b) the formal manner of constructing the state-dependent gain, taking into account both the effect of tracking error and the presence of state restrictions in the manipulator.
2. Design of the Micromanipulation Device Using Piezoelectric Actuators
The proposed micromanipulation device requires an ensemble of electromechanical devices synchronized with the piezoelectric actuator, an effective instrumentation strategy, and control design and implementation that can solve the tracking problem while satisfying the state restrictions. For this particular problem, the robotic arm device uses a three degrees of freedom (DOF) configuration, with the end effector defined by a pair of parallel bimorph piezoelectric actuators forming the gripper for grasping objects at a micrometric scale. This section details these two elements.
2.1. Design of the Piezolectric Actuator-Based Robotic Manipulator
The selected robotic arm is an electromechanical device consisting of three joints and their corresponding links made of aluminum, driven by direct current motors (a 90 RPM Precision Spur Gear Motor Servocity SKU 638238 for the first joint and 32 RPM Premium Planetary Gear Motor Servocity SKU 638290 for the other two joints). The proposed device includes motion sensors based on relative encoders (Relative, Quadrature, Magnetic Hall Effect, and 1,245.768 Countable Events Per Revolution) placed at the shaft extension of the motors. In addition, an individual encoder is fixed at each joint of the device. The proposed controller is implemented in a programmable microcontroller (Arduino Mega2556), which runs the dynamic evolution of gains and the control structure.
The proposed robotic manipulator with a piezoelectric actuator is shown in Figure 1 with the three DOFs highlighted. The first DOF is found in the basement (), exerting an axial movement. The other two degrees are at the vertical revolutes ( and ). This structure can support the gripper design, including the piezoelectric actuators.
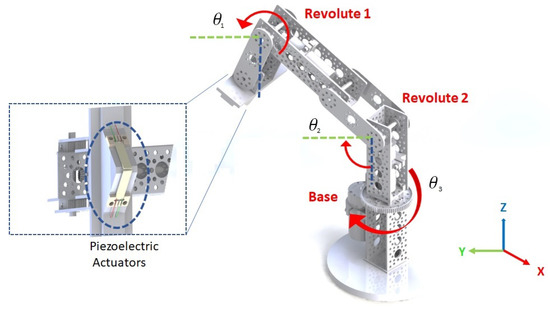
Figure 1.
Description of the robotic arm and the gripping device based on bimorph piezoelectric ctuators.
The mathematical model of the multibody robotic manipulator can be represented using the Euler–Lagrange equations and taking into account the effect of uncertainties and external perturbations, as follows:
The state vector , , defines the set of joint coordinates for the robotic arm. Here, is the drift term of the robotic manipulator, while is the matrix that characterizes the input effect on the robotic dynamics. The term represents the effect of external perturbations and internal modeling uncertainties, which are assumed to belong to the set defined in Assumption 2.
Assumption 1.
The drift term of the robotic model defined by (with and ) satisfies the inequality with and positive scalars.
Assumption 2.
The admissible class of mechanical perturbations ξ is defined by the following set ():
2.2. Gripper Based on Parallel Arrange of Piezoelectric Actuators
The proposed gripping system is constructed using a self-designed support structure that carries a pair of piezoelectric actuators in a parallel arrangement. The holding support device uses an additive manufacturing strategy based on the 3D printing technique. This strategy reduces the weight of the gripping support. The selected actuators attached to the support are bimorph-shaped devices that can bend unilaterally or bilaterally. Each actuator is controlled using a voltage source ranging from 0 to 150 volts, which is controlled using a pulse-width modulation strategy (Figure 2).

Figure 2.
Gripper side view .
The prefabricated piezoelectric actuators were obtained from Thor Labs Company, and have the following characteristics: a displacement range of 450 microns, a hysteresis effect larger than 15%, and a curie temperature of 230 C. Although in this study the actuator motion is usually ruled by a single oscillating mode [19,20,21], this is commonly used as a simplified form of mathematical representation, typically presented as a partial differential equation. This simplified form satisfies an ordinary differential equation based on applying a spatial discretization method, which is obtained using Galerkin’s method [22,23,24]. Based on this technique, the temporal–spatial motion of the actuator, , can be represented as . Here, represents the deflection of the actuator’s distal element with respect to its resting position, while is a unitary normalized function, that is, .
The dynamics of the piezoelectric actuator are defined by the following two differential equations that aggregate the actuator’s mechanical section and the device’s electrical dependence. The proposed mechanical equation integrates the effect of the acceleration related to the end-effector of the robotic arm.
In expression (3), the dynamic actuation mode for the actuator is represented by coupled mechanical–electrical forms. In this lumped parameters model, the mechanical dynamics characterized by the lumped displacement, x, are driven by the voltage signal, V, which turns out to be regulated by the input current, , based on Ohm’s law. This current is supplied by the external source, which is the actual controller of the system under study. The parameter m represents the mass of the actuator, is the parameter related to the motion direction corresponding to the hysteresis effect depending on the motion, represents the hysteresis effect concerning the motion displacement and velocity, and and are the constants defining the dependence of x and , respectively, on the motion dynamics. Similarly, and represent the time-dependence including the internal voltage relationship. Considering that the gripper is attached to the distal section of the robotic arm, the mechanical effect is taken into consideration, here with the acceleration enforced by this interconnected motion, , where is the mass of the last link in the arm and is the acceleration of the same section. The parameter C represents the capacitance of the sections making up the bimorph configuration, while is the back mechanical-electrical section.
2.3. State Constraints for the Robotic Arm and the Microgripping Device
The mechanical design of the robotic arm introduces state restrictions for at least and . For the sake of simplicity, and without loss of generality, this study considers the following class of restrictions in the normative sense, defined by the following sets:
Notice that the considered restrictions presented in (4) are mainly related to the variables of the robotic manipulator. For this study, these constraints are considered, without loss of generality, in light of the proposed technique being easily able to aggregate the presence of other restrictions for the piezoelectric actuator.
3. Problem Statement
The problem considered in this study corresponds to the design of a controller that can simultaneously enforce the tracking of reference trajectories for the robotic arm and the microgripper. The set of reference trajectories is provided by applying inverse kinematics based on the motions needed for the arm’s articulations and the end-effector. The corresponding time-dependent vector for the arm is characterized by the variable , which is twice differentiable. Each trajectory should correspond to the motion requested for the arm and the parallel configuration of the gripper using the piezoelectric actuators, the trajectories of which are defined by . The temporal evolution of these reference angles is calculated considering a motion based on path planning that allows the gripper to approach the position where the object must be manipulated. It is desirable that these motions be completed in a predefined period to at least an invariant region depending on non-matched perturbations. Hence, asymptotic convergence to an invariant zone is expected, considering that reference trajectories must be tracked as long as the time tends to infinity. Formally, the control design must solve the following tracking problem for both, which is defined as .
where is a non-negative scalar proportional to the level of non-matched uncertainties and noises affecting the dynamics of the robotic arm and the gripper and is a reference variable.
This is a proposed contribution to the control design presented in this study regarding the application of adaptive automatic controllers able to regulate the motion of the microgripper attached to the robotic arm while satisfying the state restrictions for both the robotic arm and piezoelectric actuator. Moreover, the feasible control design must consider that only the position measurements can be used, as velocity data are not available.
4. Main Contribution of the Control Design
The main goal of the proposed controller is to ensure that the origin is an asymptotic practical stable equilibrium point for the tracking error dynamics . This section presents the control challenge, a brief description of the reference trajectories design, and the corresponding state feedback formed with the estimated derivative of that error.
The Control Challenge
The problem considered in this paper consists of solving the design of a controller that ensures convergence between the variables considered in (1) and (3) and the states of the reference model inside of an invariant zone with a size proportional to the power of the non-matched perturbations of the arm. This statement can be reformulated to design an output feedback controller such that as long as t tends to infinity. By design, the reference trajectory can be obtained by implementing the inverse kinematics (a twice differentiable time-dependent function) of the robotic arm. The same option can be used to drive the position dynamics of the piezoelectric actuator:
where the the reference trajectory is represented by . In (6), the initial conditions and are given vectors with bounded components. The function h is a local Lipschitz function, which ensures the existence and uniqueness of the reference trajectories.
The dynamics of the reference trajectories presented in (6) have a stable equilibrium point and, by the converse Lyapunov theorem, it can be ensured that the system in the new coordinates satisfies
Due to the assumption that the inequality presented in (7) is considered valid and taking into consideration that both vector fields f and h are continuous, the following inequality can be straightforwardly verified. There is a positive constant such that the following inequality is valid:
Considering the inclusion of a pair of auxiliary state variables, and , for the tracking error, its dynamics then satisfy
where the function can be derived straightforwardly from (1) and (3). The extended state-dependent function related to the extended controller is provided in , which is left invertible according to the nature of the mechanical system and the piezoelectric device.
The controller proposal presented in this study satisfies the following structure, which coincides with a state feedback structure having adaptive gains depending on the tracking error and its derivative:
where , with and being the time varying matrix gains for the sections of the controller proportional to the tracking error and derivative, respectively.
The gain deviation term can be found as a solution to the following differential equation:
where , , when is selected such that is a Hurwitz matrix and with the matrix B can be obtained once more with the models of the robotic arm and piezolectric actuators. Here, is a positive definite matrix, described below. Matrices A and B accept the following definitions:
The state dependent is used to include the effect of state restrictions in the following manner:
Notice that in (11), the time derivative of should be estimated considering the evolution of and . The online estimate of could be calculated using traditional derivatives, or it can alternatively be solved using robust exact differentiators such as the super-twisting algorithm (STA). Hence, the algorithm used to adjust the gain can be solved using the variables of the robotic arm carrying the piezoelectric actuator.
Theorem 1.
Consider the dynamics of the robotic arm (1) together with the gripper armed with two parallel piezolectric grippers with the dynamics provided in (3) and with the state restrictions in (4), the dynamics of which are affected by the class of perturbations described in (2). Assume that the state variables of the robotic arm must track the corresponding reference trajectories for the entire robotic manipulator provided by (6). Taking into consideration the proposed controller τ structure in (10) has a state-dependent gain defined in (11) that includes the effect of state constraints, if there is a positive definite and symmetric matrix Q such that the matrix equationhas a positive definite solution where
withandpositive definite matrices. Then, the tracking errorhas a practical asymptotic equilibrium point in a positively invariant ball around the origin delimited with the radius defined by
Proof.
For the proof, the dynamics of state tracking with can be obtained from the evolution shown in (9), which yields
Using the selected controller in (10) and considering that functions F, G, and h are known, the application of the proposed controller in (10) simplifies the dynamics of to
Consider the following time-dependent Lyapunov candidate function related to the acceleration tracking error as well as the state-dependent gains used to insert the position and velocity restrictions:
According to the Laypunov stability theory for non-autonomous systems [25], it is necessary to prove the following properties for the proposed Lyapunov candidate function : (a) , with and being continuous positive definite functions; and (b) the time derivative of must be negative definite. For this case, and . The time derivative of satisfies the following differential equation:
The term admits the following equivalent form:
The application of the Young’s inequality (that is, for any matrices , there exists a positive definite matrix such that ) to the term containing uncertainties and perturbations () in (19) leads to the following form for the right-hand side of :
Using the results corresponding to the upper bound of leads to
The application of the result derived in (19) to the expression of (18) leads to the following description of the derivative of :
where .
Taking into account the assumption in the theorem statement about as well as the adjustment law for leads to
Taking into account the case when , yielding to
in view of the description of the function the expression in (24) can be presented as
Consider the following lemma.
Lemma 1.
For any constant ρ such that , the following inequality is satisfied:
Using the inequality in the previous lemma for the logarithmic function, the differential inequality for the first Lyapunov candidate function can be transformed to
This expression is equivalent to , which implies that if , then .
This expression implies the origin is an asymptotic stable equilibrium point of . □
5. Experimental Validations of the Proposed Controller
An experimental prototype was designed, constructed, instrumented, and controlled to confirm the proposed controller’s effectiveness. The proposed technique considers the inclusion of the experimental robotic manipulator carrying the gripper. The proposed methodology for testing the developed controller includes the practical realization of the distributed parameter representation for the manipulator, considering the application of the selected constructive strategy, the instrumentation using DC motors as actuators, and optical encoders for detecting an angular position at the joints.
The engines selected for performing the movement used a 12 volt DC motor (Servocity), including an encoder (32 RPM). The encoder information was used to close the loop in position control.
Figure 3 shows the entire structure of the developed micromanipulator with all the components considered in the design, including the DC motors, the piezoelectric actuators, and the mechanical sections as well as the image processing element to detect the current microgripper configuration.

Figure 3.
Entire structure of the micromanipulator using the piezoelectric actuators.
This discretized form of the controller was implemented on an ATMega microcontroller 2560, allowing the development of the proposed controller for the dynamics of the piezoelectric actuator. This board has 54 digital I/O pins (of which 15 provide PWM output that can be used for controlling DC motors), 16 analog input pins, and 40 mA current per I/O pin.
The presence of perturbations, modeling uncertainties, and measurement noise appear as part of device operation under the selected conditions. The perturbations and uncertainties result from the mechanical configuration and the unconsidered dynamics of the actuators.
This study used a PID controller for comparison, considering that this is the controller which is mainly used for robotic manipulators. The comparative study evaluated the application of PID control in general, and did not consider the independent effect of each gain in its structure. These parameters were adjusted using the self-tunning process inserted in the PID formulation proposed in the Matlab algorithm. This algorithm performs a frequency-response estimation experiment that injects signals into the plant and measures the plant output with a closed or open feedback loop. The method uses the resulting estimated frequency response to tune PID gains for the plant. The application of such an algorithm allowed us to create a fair comparison with the controller proposed as the main contribution of this study. Even when other parameters produce lesser mean square errors, they may increase the power related to the controller’s application.
The selected gains for the PID controller and the initial conditions for the adaptive control considering the state restrictions are presented in Table 1, with .

Table 1.
Selected values of the PID controller and initial conditions for the adaptive controller.
Figure 4a, Figure 5a, and Figure 6a show the structural and motion components at all joints of the manipulator carrying the piezoelectric manipulator. These photographs demonstrate the composition of the mechanical structure and the DC motors as well as the relative distribution of the encoders. In addition, the mechanical engines located at each joint are depicted in order to demonstrate how the relative motion at each joint is obtained.
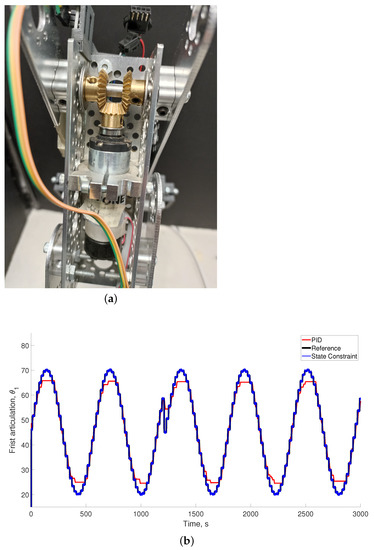
Figure 4.
(a) Photograph of the electromechanical configuration for the first articulation ; (b) comparison of the controlled motion for the first articulation () when the PID and adaptive control with state constraints are considered.
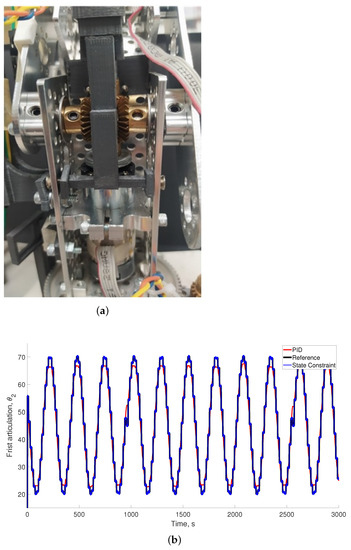
Figure 5.
(a) Photograph of the electromechanical configuration for the second articulation ; (b) comparison of the controlled motion for the second articulation () when the PID and adaptive control with state constraints are considered.
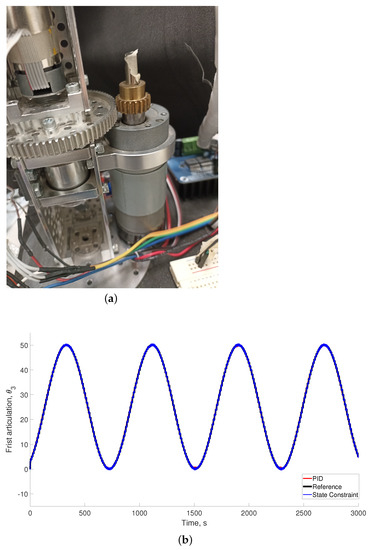
Figure 6.
(a) Photograph of the electromechanical configuration for the third articulation ; (b) comparison of the controlled motion for the third articulation () when the PID and adaptive control with state constraints are considered.
Figure 4b, Figure 5b, and Figure 6b depict the reference and the experimental trajectories for all the articulations in the robotic arm. All figures show the angular motion in degrees. The comparison demonstrates that the proposed controller allowed the references to be tracked with better quality and with oscillations with smaller amplitudes compared to the traditional constant gain controller. The same characteristic was observed for all the trajectories proposed, which had the aim of forcing the controller to track more quickly-changing references.
The comparison of tracking errors using the mean square evaluation confirms the benefits of using the proposed controller, exhibiting faster convergence to the invariant zone characterized in the theorem presented in this study. In addition, the averaged value obtained at the steady state period of time is smaller with the state constraint controller (Figure 7).
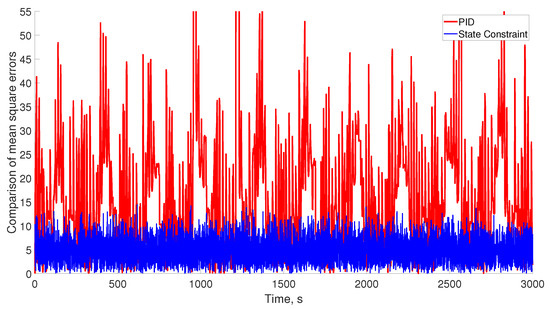
Figure 7.
Comparison of the mean square error between the proposed state constraint and the traditional state feedback control form.
The control action produced with the implemented controller exhibits different behavior compared to that generated with the constant gains variant. The obtained control action with the restricted controller has a smaller amplitude. Nonetheless, when the trajectories grow closer to the boundaries, the control action increases its amplitude, as predicted by the gains laws presented in Expression (11). Figure 8 compares the evolution of the control actions using the proposed laws for the state constraint variant and its comparison with constant values. This comparison confirms that the obtained controllers produce smaller amplitudes for the control action, which consumes less power during trajectory tracking of the reference states.
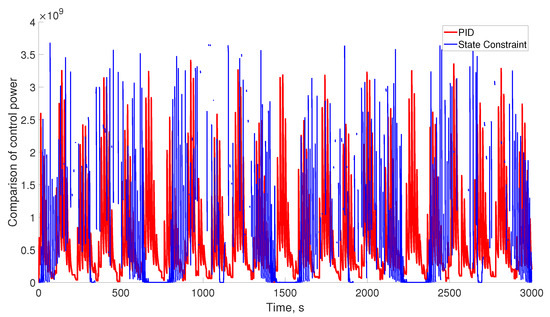
Figure 8.
Comparison of control action between the proposed state constraint and the traditional state feedback control form.
The proposed controller demonstrates significant advantages concerning similar state feedback options. The set of benefits can be observed for both the effectiveness of the tracking trajectory and for the motion produced for the end effector using the controlled action of all the joints simultaneously. This study calculated the averaged integral for the norm of the control actions both using the proposed barrier-based control and traditional state feedback (PID control). The integral of the control action is presented when the number of samples corresponding to the end of the experimental evaluation was 3000. After carrying out averaged integration, we estimated the state feedback formulation as , while that obtained with the barrier-based controllers was . Moreover, we calculated the ratio of the average mean square error obtained with both controllers (estimated with the information presented in Figure 8) concerning the corresponding averaged value of the integral for the norm of the control actions. These values evaluate a measure of efficiency in tracking performance for the control power invested in attaining such tracking. For the PID controller, the proposed ratio was , while the value with the barrier controller was . This comparison explains the benefit of introducing the proposed controller with respect to traditional formulations.
Figure 9a demonstrates a detailed view of the gripper structure based on the selected piezoelectric actuators. The design of the gripper structure allows the gripping structures to be moved with the possibility of reaching an opening range of 120 μm. In contrast, the closing range is 80 μm with the selected handling configuration. Figure 9b shows a sequence of motions for the gripping structure when moving towards the handling of a 150 μm spherical object. This sequence demonstrates the relative motion of the gripper device using the controlled actuation of the piezoelectric actuators under the selected control action and based on the algorithm that considers the joints restrictions in the manipulator section of the proposed device.
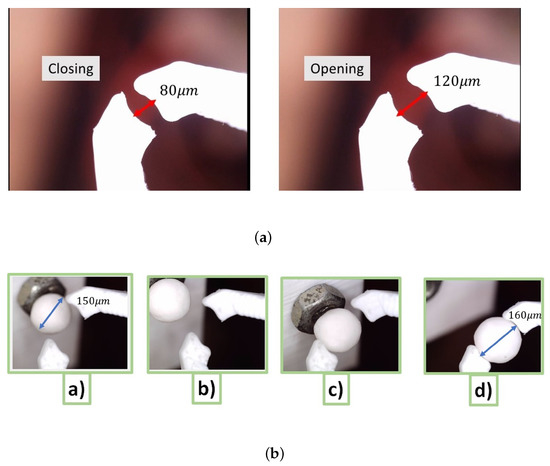
Figure 9.
(a) Direct visualization of the gripper section attached to the piezolectric actuators; (b) manipulation of a 160 m polystyrene sphere using the gripping device made with the piezoelectric actuators.
6. Conclusions
This study presents the design of a feedback controller with state-dependent gains for regulating the position of a robotic manipulator carrying a piezoelectric actuator-based gripper. The control method considers the effect of perturbations, uncertain modeling elements, and the presence of state restrictions in an ellipsoid form. The application of an adaptive control ensures asymptotic convergence of the states to an invariant zone with a size that depends on the power of the uncertainties and perturbations. In addition, the proposed controller’s significant characteristics are evidenced by experimental evaluations for a particular developed robotic manipulator. Comparative analysis of the suggested controller concerning the traditional state feedback justifies the benefits of the proposed methodology. This comparison demonstrated a minor mean square tracking error with a smaller power associated with the control action. The experimental results show the effective handling of microscopic objects using the developed robotic device. The controller’s application overcame all of the main difficulties, including the necessity of implementing a state-dependent controller using a barrier-based design.
Author Contributions
Conceptualization, I.S. and I.C.; methodology, F.M.-G. and D.C.-O.; software, F.M.-G.; validation, F.M.-G., D.C.-O. and I.C.; formal analysis, I.C.; investigation, I.S. and D.C.-O.; resources, I.S., D.C.-O. and I.C.; data curation, F.M.-G. and I.C.; writing—original draft preparation, F.M.-G. and I.C.; writing—review and editing, F.M.-G. and I.C.; visualization, F.M.-G. and D.C.-O.; supervision, I.C.; project administration, F.M.-G., D.C.-O. and I.S.; funding acquisition, I.S., D.C.-O. and I.C. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the National Polytechnic Institute for the financial support provided through their research grants with references SIP-2022-1150, SIP-2022-0916, SIP-2022-1503, and SIP-2022-1151.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of Open Access Journals |
| TLA | Three-Letter Acronym |
| LD | Linear Dichroism |
References
- Near, C.D. Piezoelectric actuator technology. Smart Structures and Materials 1996: Smart Structures and Integrated Systems. SPIE 1996, 2717, 246–258. [Google Scholar]
- Tzen, J.J.; Jeng, S.L.; Chieng, W.H. Modeling of piezoelectric actuator for compensation and controller design. Precis. Eng. 2003, 27, 70–86. [Google Scholar] [CrossRef]
- Richter, H.; Misawa, E.A.; Lucca, D.; Lu, H. Modeling nonlinear behavior in a piezoelectric actuator. Precis. Eng. 2001, 25, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Lining, S.; Changhai, R.; Weibin, R.; Liguo, C.; Minxiu, K. Tracking control of piezoelectric actuator based on a new mathematical model. J. Micromechan. Microeng. 2004, 14, 1439. [Google Scholar] [CrossRef]
- Ru, C.; Chen, L.; Shao, B.; Rong, W.; Sun, L. A hysteresis compensation method of piezoelectric actuator: Model, identification and control. Control. Eng. Pract. 2009, 17, 1107–1114. [Google Scholar] [CrossRef]
- Yi, J.; Chang, S.; Shen, Y. Disturbance-observer-based hysteresis compensation for piezoelectric actuators. IEEE/ASME Trans. Mechatronics 2009, 14, 456–464. [Google Scholar]
- Zheng, Z.; Kumar, P.; Chen, Y.; Cheng, H.; Wagner, S.; Chen, M.; Verma, N.; Sturm, J.C. Piezoelectric Soft Robot Inchworm Motion by Controlling Ground Friction through Robot Shape. arXiv 2021, arXiv:2111.00944. [Google Scholar]
- DeVoe, D.L.; Pisano, A.P. Modeling and optimal design of piezoelectric cantilever microactuators. J. Microelectromechanical Syst. 1997, 6, 266–270. [Google Scholar] [CrossRef]
- Čeponis, A.; Jūrėnas, V.; Mažeika, D. Development of 5-DOF piezoelectric actuator for planar—Angular positioning. Appl. Sci. 2022, 12, 1033. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B.; Thielager, J.; Stiebel, C. A novel drive and control method for piezoelectric motors in microscopy stages. In Proceedings of the Euspen’s 21st International Conference & Exhibition, Copenhagen, Denmark, 12–16 June 2021; pp. 7–10. [Google Scholar]
- Gao, X.; Yang, J.; Wu, J.; Xin, X.; Li, Z.; Yuan, X.; Shen, X.; Dong, S. Piezoelectric actuators and motors: Materials, designs, and applications. Adv. Mater. Technol. 2020, 5, 1900716. [Google Scholar] [CrossRef]
- Touairi, S.; Khouya, Y.; Bahanni, C.; Khaouch, Z.; Mabrouki, M. Mechatronic control and modeling of a piezoelectric actuator. In Proceedings of the 2019 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 3–4 April 2019; pp. 1–6. [Google Scholar]
- Liu, R.; Wang, L.; Jin, J.; Zhao, H.; Zhang, A.; Chen, D. A novel 3-DoF piezoelectric robotic pectoral fin: Design, simulation, and experimental investigation. Smart Mater. Struct. 2022, 31, 65003. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, W.L.; Zhu, Z.; Zhu, L.M. Design, assessment, and trajectory control of a novel decoupled robotic nanomanipulator. IEEE/ASME Trans. Mechatronics 2022. [Google Scholar] [CrossRef]
- Flores, G.; Aldana, N.; Rakotondrabe, M. Model predictive control based on the generalized Bouc-Wen model for piezoelectric actuators in robotic hand with only position measurements. IEEE Control. Syst. Lett. 2021, 6, 2186–2191. [Google Scholar] [CrossRef]
- AbuZaiter, A.; Nafea, M.; Ali, M.S.M. Development of a shape-memory-alloy micromanipulator based on integrated bimorph microactuators. Mechatronics 2016, 38, 16–28. [Google Scholar] [CrossRef]
- Flores, G.; Rakotondrabe, M. Robust nonlinear control for a piezoelectric actuator in a robotic hand using only position measurements. IEEE Control. Syst. Lett. 2021, 6, 872–877. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Liu, J.; Dai, C.; Sun, Y. Robotic micromanipulation: Fundamentals and applications. Annu. Rev. Control. Robot. Auton. Syst. 2019, 2, 181–203. [Google Scholar] [CrossRef]
- Yuan, S.; Zhu, C.; Chu, X.; Zhao, Y.; Amin, M.; Fan, Y. A novel linear piezoelectric actuator with two working principles of standing and traveling wave vibration mode. AIP Adv. 2015, 5, 107213. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Liu, Y.; Zhao, L.; Xu, D.; Chen, W.; Deng, J. Design and experiments of a single-foot linear piezoelectric actuator operated in a stepping mode. IEEE Trans. Ind. Electron. 2018, 65, 8063–8071. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Z.; Jian, Y.; Zhang, B. Characteristics analysis of a plate type linear piezoelectric actuator based on a point contact model. Smart Mater. Struct. 2018, 27, 115031. [Google Scholar] [CrossRef]
- Moghaddam, S.M.F.; Ahmadi, H. Active vibration control of truncated conical shell under harmonic excitation using piezoelectric actuator. Thin-Walled Struct. 2020, 151, 106642. [Google Scholar] [CrossRef]
- Shirazi, M.J.; Salarieh, H.; Alasty, A.; Shabani, R. Tip tracking control of a micro-cantilever Timoshenko beam via piezoelectric actuator. J. Vib. Control. 2013, 19, 1561–1574. [Google Scholar] [CrossRef]
- Bahrami, M.N.; Yousefi-Koma, A.; Raeisifard, H. Modeling and nonlinear analysis of a micro-switch under electrostatic and piezoelectric excitations with curvature and piezoelectric nonlinearities. J. Mech. Sci. Technol. 2014, 28, 263–272. [Google Scholar] [CrossRef]
- Legnani, W.; Moschandreou, T.E.; Reyhanoglu, M. Nonlinear Systems: Theoretical Aspects and Recent Applications; IntechOpen: London, UK, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).