Effect of Buildings on the Radiation Characteristics of MF Broadcast Antennas
Abstract
:1. Introduction
2. Materials and Methods
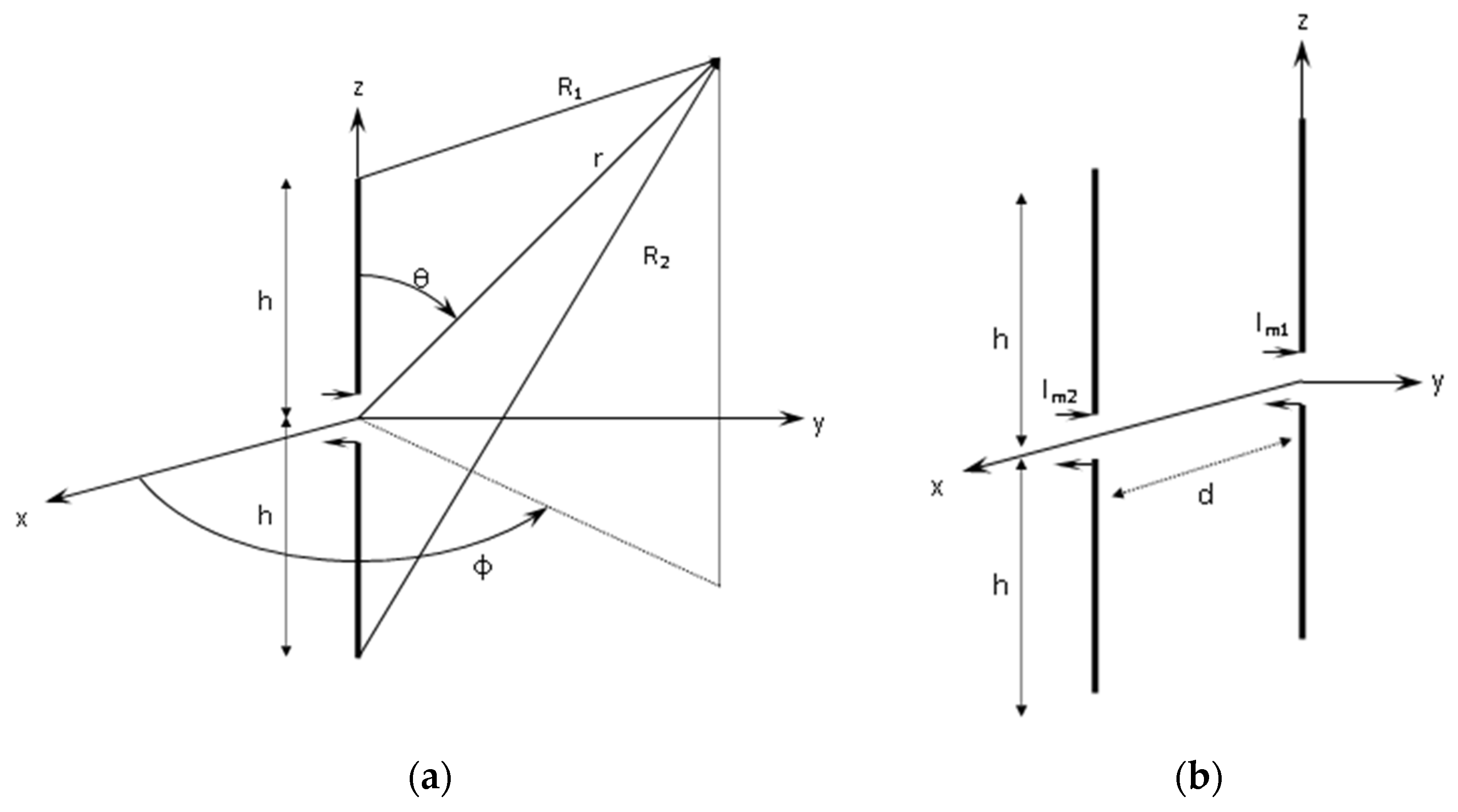
2.1. Antenna and Ground Modeling
2.2. Current Distribution
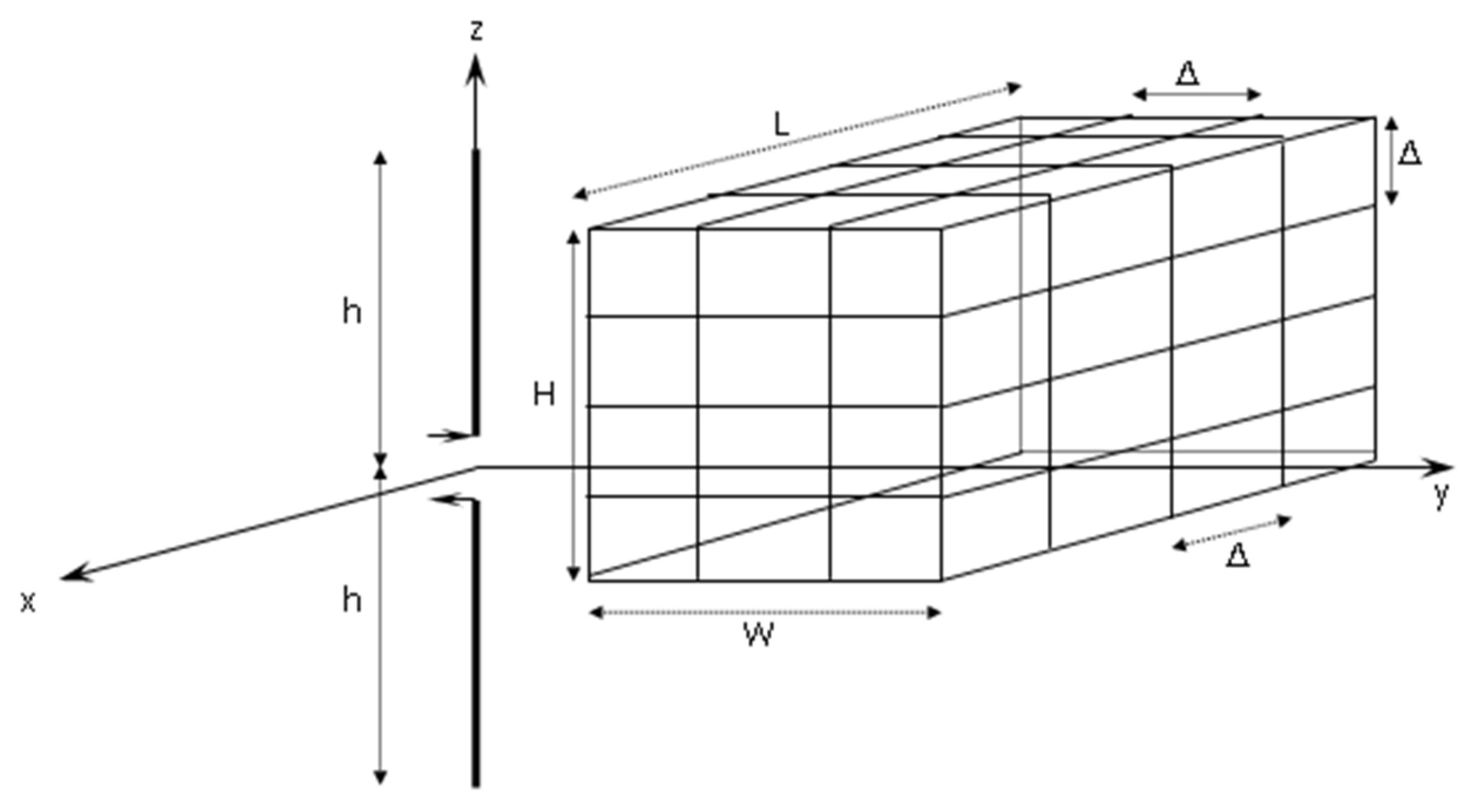
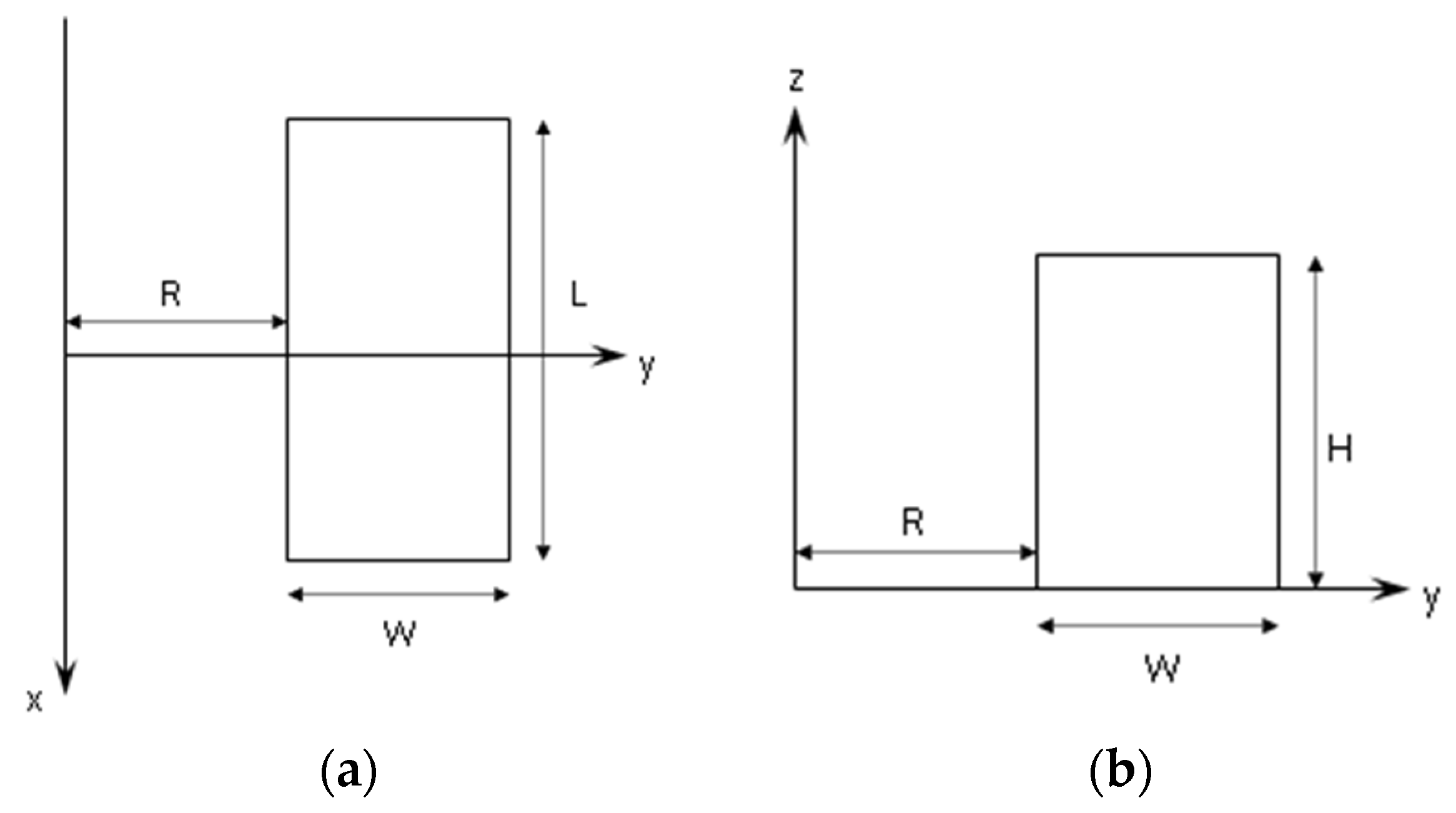
2.3. Building Modeling
2.4. Scattering from a Wire Grid
2.5. Radiation of the Antennas in the Presence of Buildings
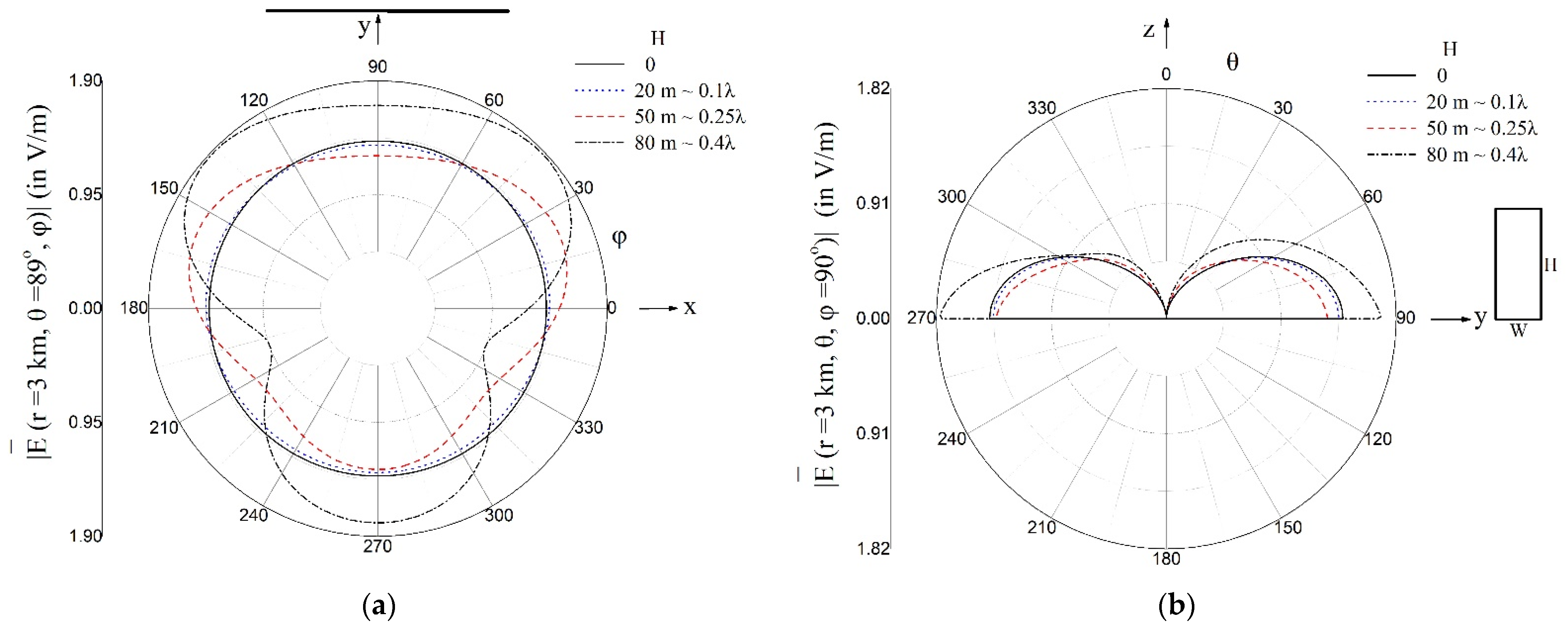
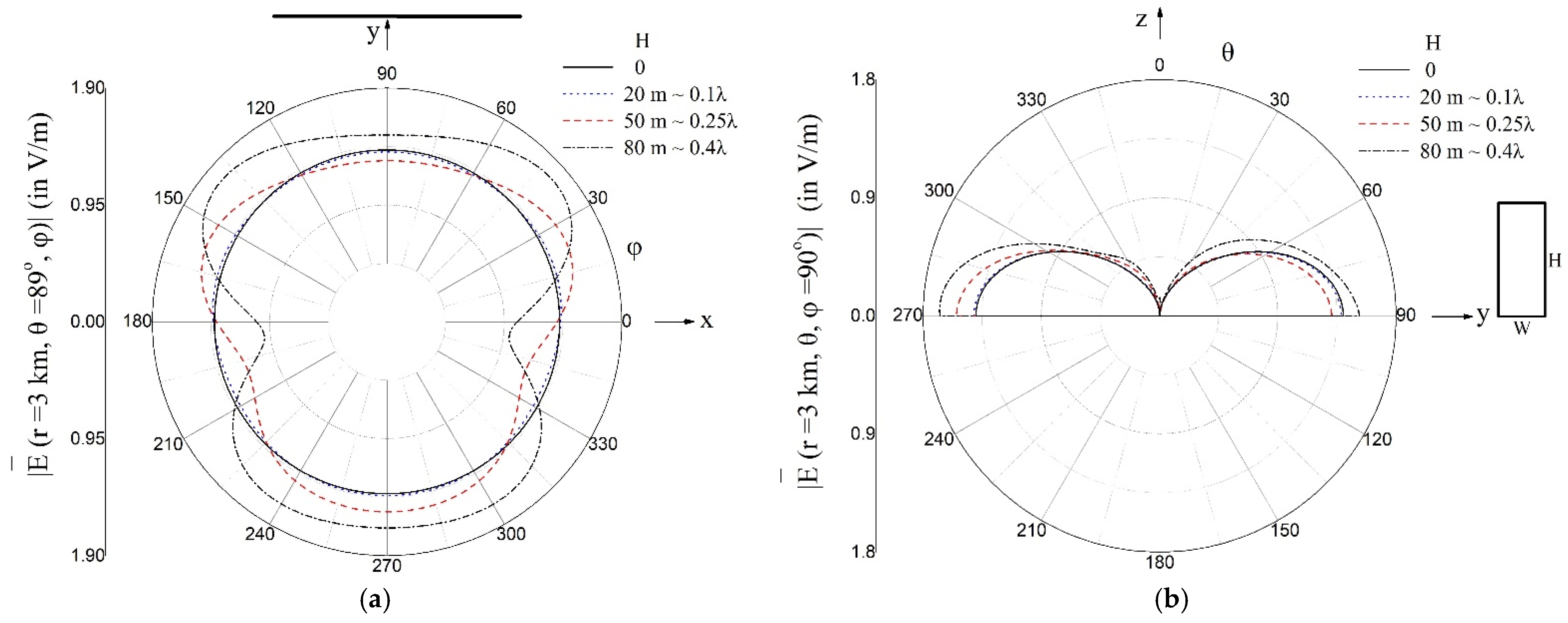
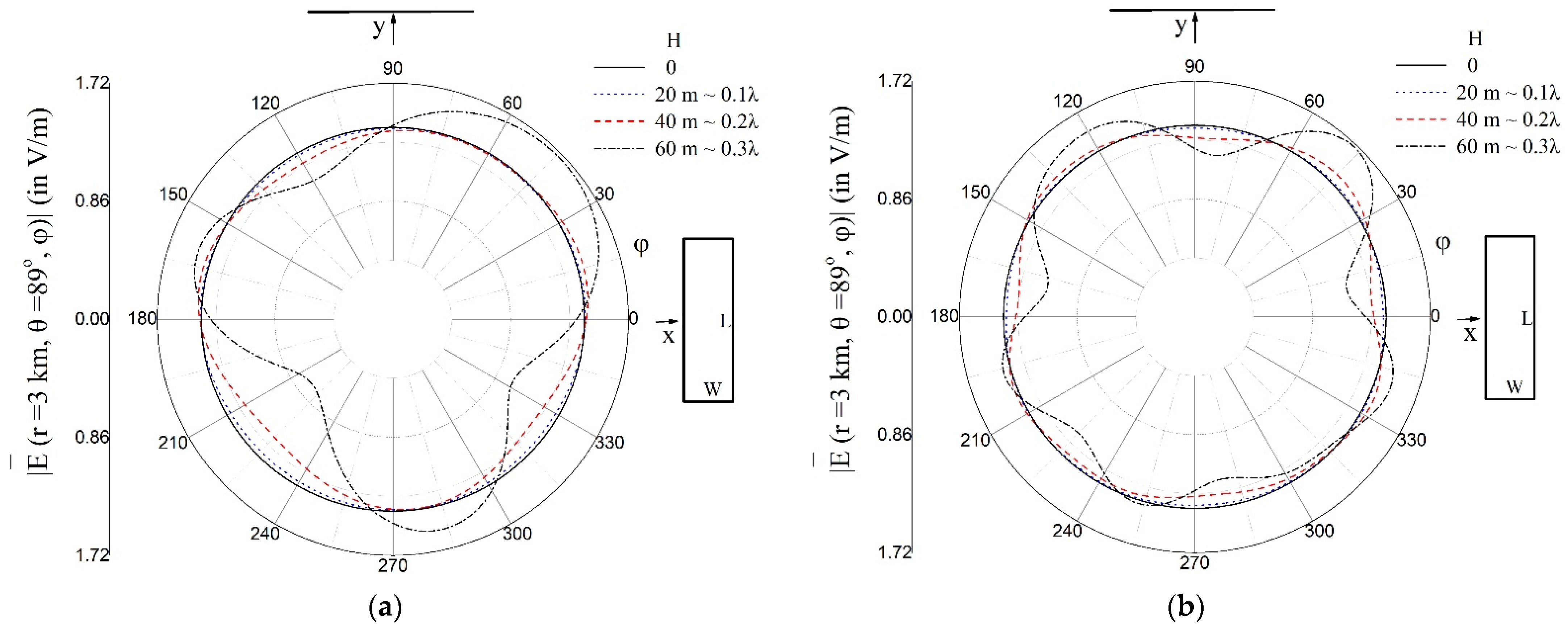
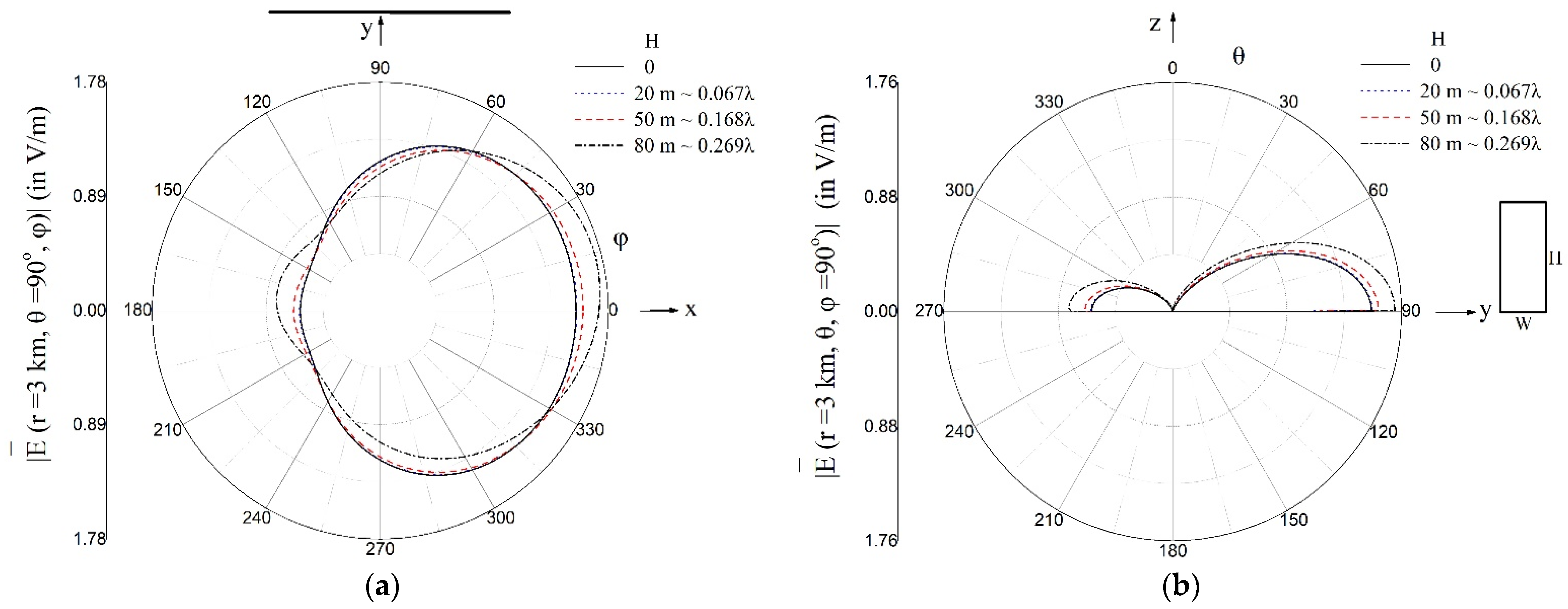
3. Results
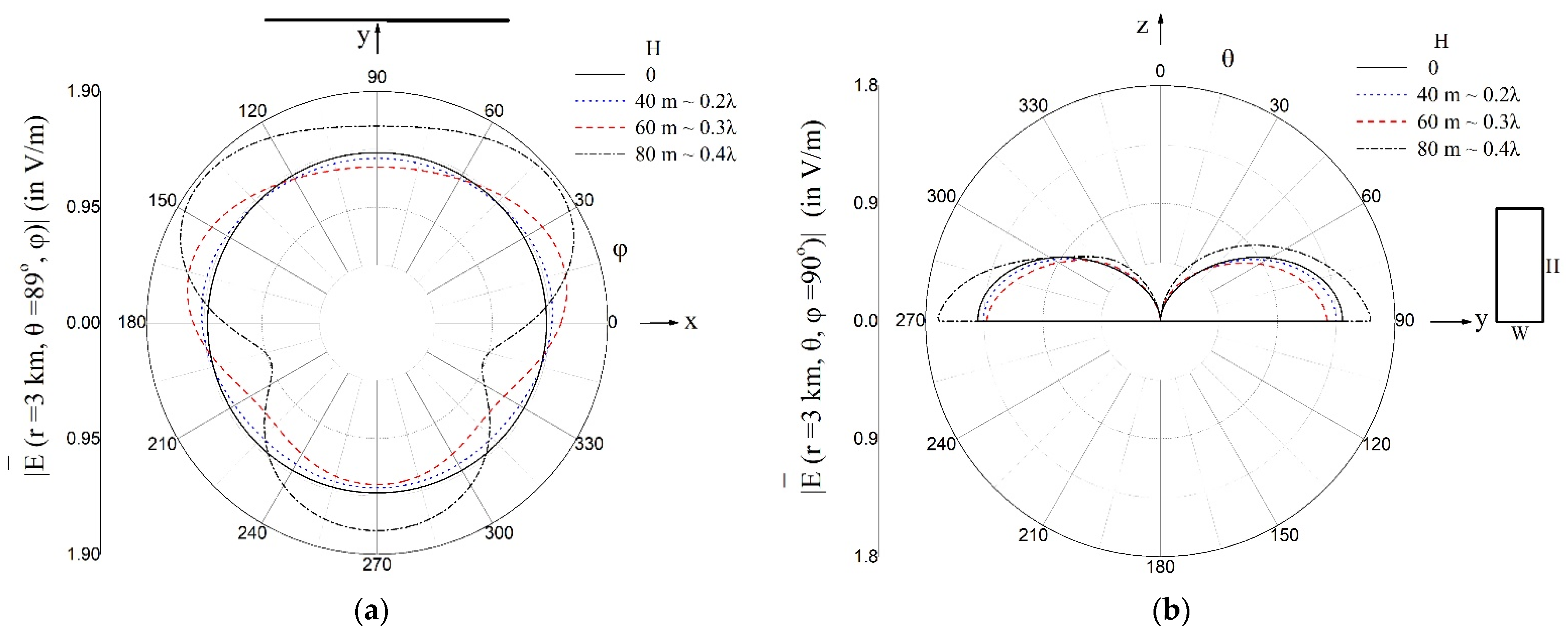
3.1. Radiation Patterns of the Monopole
3.2. Radiation Patterns of the Array
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Causebrook, J.H. Medium-wave propagation in built-up areas. Proc. IEE 1978, 125, 804–808. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, L.; He, S. Research on HF antenna blockage effects and their alleviation. J. Electromagn. Waves Appl. 2022, 36, 1544–1558. [Google Scholar] [CrossRef]
- Dagdeviren, A.; Cerezci, O.; Turetken, B. A study of the blockage effects on the pattern of ship mounted X-band communication antennas. In Proceedings of the of the 2006 International Conference on Mathematical Methods in Electromagnetic Theory (MMET), Kharkiv, Ukraine, 26–29 June 2006; pp. 353–355. [Google Scholar]
- Alitalo, P.; Valagiannopoulos, C.A.; Tretyakov, S.A. Simple cloak for antenna blockage reduction. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APS-URSI), Spokane, WA, USA, 3–8 July 2011; pp. 669–672. [Google Scholar]
- Rodriguez-Cano, R.; Zhao, K.; Zhang, S.; Pedersen, G.F. Handset frame blockage reduction of 5G mm-wave phased arrays using hard surface inspired structure. IEEE Trans. Veh. Technol. 2020, 69, 8132–8139. [Google Scholar] [CrossRef]
- Goh, Y.Z.; Neve, M.J.; Rowe, G.B. Effects of complex wall structures on antenna radiation characteristics. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 2485–2486. [Google Scholar]
- Wait, J.; Spies, K. Radio propagation over a cylindrical hill including the effect of a surmounted obstacle. IEEE Trans. Antennas Propagat. 1968, 16, 700–705. [Google Scholar] [CrossRef]
- Lichum, L. A new MF and HF ground-wave model for urban areas. IEEE Trans. Antennas Propagat. Mag. 2000, 42, 21–33. [Google Scholar] [CrossRef]
- Pedersen, J.; Chabra, J. Measured results of an efficient broadband HF antenna system for reliable all terrain communication between unattended ground sensors. Proc. SPIE 2002, 4741, 144–155. [Google Scholar]
- Lopez, S.; de la Vega, D.; Guerra, D.; Prieto, G.; Velez, M.; Angueira, P. Estimation of the single obstacle attenuation in MF band from field data. In Proceedings of the 2007 Loughborough Antennas and Propagation Conference, Loughborough, UK, 2–3 April 2007; pp. 165–168. [Google Scholar]
- Zhang, W.; Kong, F.; Zheng, W. Investigation into effects of buildings near broadcasting antenna on far fields using a Finite-Difference method. J. Shanghai Univ. 1998, 2, 139–143. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.; Sun, N. The effect of high buildings on radiation characteristics of nearby antenna. Sci. Sin. 1981, XXIV, 1753–1762. [Google Scholar]
- Chen, H.K.; Sun, N.H.; Li, M.Y. A study of the effect of buildings on the radiation patterns of simple antenna arrays. IEEE Trans. Antennas Propagat. 1983, 31, 689–692. [Google Scholar] [CrossRef]
- Fu, Y.; Langley, R.J.; Rigelsford, J.M.; Hate, M.; McCalla, J. The effects of local terrain topology and antenna infrastructure on simulated near-field characteristics for HF broadcast antennas. In Proceedings of the 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 1218–1221. [Google Scholar]
- Moon, C.M.; An, D.J.; Lee, J.H. A study on the effect of building on the HF direction finding. In Proceedings of the 7th IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies (MAPE), Xi’an, China, 25–27 October 2017; pp. 540–542. [Google Scholar]
- Sun, X.; Yang, P.; Li, R.; Ye, J. Analysis of the influence of buildings on localizer’s course structure. In Proceedings of the 2021 International Conference on Big data Analysis and Computer Science (BDACS), Kunming, China, 25–27 June 2021; pp. 258–263. [Google Scholar]
- Xu, J.; Ye, J.; Liang, F.; Li, Y.; Yuan, B. Simulation analysis and research on the influence of buildings on a DVOR station. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 1291–1294. [Google Scholar]
- Xu, J.; Ye, J.; Liang, F.; Li, Y.; Lin, H. Simulation analysis and research on the influence of buildings on a glide path antenna. In Proceedings of the 2021 International Conference on Computer Technology and Media Convergence Design (CTMCD), Sanya, China, 23–25 April 2021; pp. 63–66. [Google Scholar]
- Zhang, J.; Glazunov, A.A.; Zhang, J. Wireless energy efficiency evaluation for buildings under design based on analysis of interference gain. IEEE Trans. Veh. Technol. 2020, 69, 6310–6324. [Google Scholar] [CrossRef]
- Zhang, J.; Glazunov, A.A.; Zhang, J. Wireless performance evaluation of building layouts: Closed-form computation of figures of merit. IEEE Trans. Commun. 2021, 69, 4890–4906. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, J.; Song, H.; Zhang, J. Partition-based analytic evaluation of building wireless performance. IEEE Trans. Veh. Technol. 2021, 70, 9036–9049. [Google Scholar] [CrossRef]
- Zhou, Y.; Shao, Y.; Zhang, J.; Zhang, J. Wireless performance evaluation of building materials integrated with antenna arrays. IEEE Commun. Lett. 2022, 26, 942–946. [Google Scholar] [CrossRef]
- Zhang, J.; Glazunov, A.A.; Yang, W.; Zhang, J. Fundamental wireless performance of a building. IEEE Wirel. Commun. 2022, 29, 186–193. [Google Scholar] [CrossRef]
- Tan, J.; Shao, Y.; Zhang, J.; Zhang, J. Artificial neural network application in prediction of concrete embedded antenna performance. In Proceedings of the 15th European Conference on Antennas and Propagation (EUCAP), Dusseldorf, Germany, 22–26 March 2021. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory Analysis and Design, 3rd ed.; Wiley Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Furse, C.M.; Gandhi, O.P.; Lazzi, G. Wire Elements: Dipoles, Monopoles and Loops. In Modern Antenna Handbook; Balanis, C.A., Ed.; Wiley: Hoboken, NJ, USA, 2008; pp. 59–95. [Google Scholar]
- Richmond, J.H. A wire-grid model for scattering by conducting bodies. IEEE Trans. Antennas Propagat. 1966, 14, 782–786. [Google Scholar] [CrossRef]
- Lin, J.L.; Curtis, W.L.; Vincent, M.C. Radar cross section of a rectangular conducting plate by wire mesh modeling. IEEE Trans. Antennas Propagat. 1974, 22, 718–720. [Google Scholar]
- Maeda, Y.; Murakawa, K.; Yamane, H.; Tokuda, M. technique for estimating Electromagnetic field distributions in and around buildings using wire-grid approximation. Electron. Commun. Jpn. 1995, 78, 110–118. [Google Scholar] [CrossRef]

| Study | Frequency Range | Antenna Model | Building Model | Method | Purpose | Main Results-Conclusions |
|---|---|---|---|---|---|---|
| [12] | MF (990 kHz) | T-type, 60 m in height | λ/4 parasitic monopole or infinite-long PEC cylinder | Reciprocity or dyadic Green’s function technique | Impact of building on radiation pattern and field intensity | Decrease in field intensity up to 2.3 dB. The radiation pattern is mostly affected by the height of the building. |
| [11] | MF (990 kHz) | λ/2 dipole | PEC, three different heights considered | Finite difference method | Impact of buildings on the far field | The reduction in field intensity around a building may be up to 8.4 dB (building 30 m high, 100 m from the antenna), while the field variation becomes negligible 400 m from the antenna. |
| [2] | HF (2–30 MHz) | Logical periodic dipole antenna (LPDA) | Rectangular parallelepiped (mesh of metallic wire segments and triangles) | Full-wave simulation software package (FEKO) | Impact of buildings on radiation pattern, gain, VSWR. | Only the radiation pattern (among gain, VSWR, impedance) is affected by building blockage. The impact on patterns is greater if the size or height of the blockage is larger than λ/2. |
| [15] | HF | 12-element (cross-loop antenna) circular array | Actual buildings (bodies of concrete or wood of appropriate size/shape) | Commercially available software (FEKO) | Impact of buildings on direction finding (DF) | The antenna response changes due to the presence of buildings, resulting in estimation error of the DF system (up to 1° for the azimuth and 7° for the elevation). |
| [13] | - | 2-element broadside or endfire array | Infinite-long conductive or dielectric, rectangular cylinder | MoM and unimoment method | Impact of building on radiation pattern and field intensity | Deviation of the direction of the principal radiation lobe and production of side lobes, depending on the distance between the antenna and the building and the permittivity and size of the building. |
| [6] | 2.45 GHz | Rectangular patch antenna | Complex wall structures | Commercially available software (CST Microwave Studio) | Impact of walls on the radiation characteristics of access-point antennas | The radiation pattern is distorted (compared to the free-space pattern) when the antenna is mounted on complex wall structures, especially corners. |
| [29] | 30 MHz–1 GHz | Electric dipole inside the building | Wire-grid body | MoM | Derivation of EM field distribution in and around buildings | The calculated results were validated through measurements and the resonant characteristics of the building were determined. |
| [4] | 0.75–5 GHz | Horn antenna | Single solid-metal cylinder or a set of such cylinders | Numerical simulation (by using the tool Ansoft HFSS) | Design of the appropriate cloak to reduce the blockage | The (uncloaked) objects produce strong sidelobes to the antenna’s radiation pattern (compared to free space) and decrease its directivity. |
| Current study | MF (1494 kHz & 1008 kHz) | Monopole and 2-element array | Rectangular parallelepiped (wire-grid body) | Point-matching solution and custom computer code | Impact of buildings on radiation pattern | The height is the most important parameter that determines whether other parameters of the buildings affect the radiation pattern considerably. The impact on the radiation pattern is significant if the height of the building is greater than . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liodakis, G.S.; Ioannidou, M.P.; Petrakis, N.S.; Baklezos, A.T.; Kapetanakis, T.N.; Nikolopoulos, C.D.; Vardiambasis, I.O. Effect of Buildings on the Radiation Characteristics of MF Broadcast Antennas. Appl. Sci. 2022, 12, 6525. https://doi.org/10.3390/app12136525
Liodakis GS, Ioannidou MP, Petrakis NS, Baklezos AT, Kapetanakis TN, Nikolopoulos CD, Vardiambasis IO. Effect of Buildings on the Radiation Characteristics of MF Broadcast Antennas. Applied Sciences. 2022; 12(13):6525. https://doi.org/10.3390/app12136525
Chicago/Turabian StyleLiodakis, George S., Melina P. Ioannidou, Nikolaos S. Petrakis, Anargyros T. Baklezos, Theodoros N. Kapetanakis, Christos D. Nikolopoulos, and Ioannis O. Vardiambasis. 2022. "Effect of Buildings on the Radiation Characteristics of MF Broadcast Antennas" Applied Sciences 12, no. 13: 6525. https://doi.org/10.3390/app12136525
APA StyleLiodakis, G. S., Ioannidou, M. P., Petrakis, N. S., Baklezos, A. T., Kapetanakis, T. N., Nikolopoulos, C. D., & Vardiambasis, I. O. (2022). Effect of Buildings on the Radiation Characteristics of MF Broadcast Antennas. Applied Sciences, 12(13), 6525. https://doi.org/10.3390/app12136525








