Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle
Abstract
1. Introduction
- It is valid even if a given non-linear problem does not contain any small perturbation parameters at all;
- It controls effectively the convergence of approximation series and adjusts convergence regions when necessary;
- It efficiently approximates a non-linear problem by choosing different sets of base functions.
2. Improved Homotopy Analysis Method
2.1. Formulations
2.2. Traditional Homotopy Analysis Method
2.2.1. Zero-Order Deformation Equation
2.2.2. High-Order Deformation Equation
2.3. Improved Homotopy Analysis Method
2.3.1. Construction of a New Nonlinear Homotopy Differential Equation
2.3.2. Construction of High-Order Homotopy Equation
2.3.3. Convergence Theorem
3. Explicit Solution to Rotation Angle for Large Deformation of Cantilever Beams by IHAM
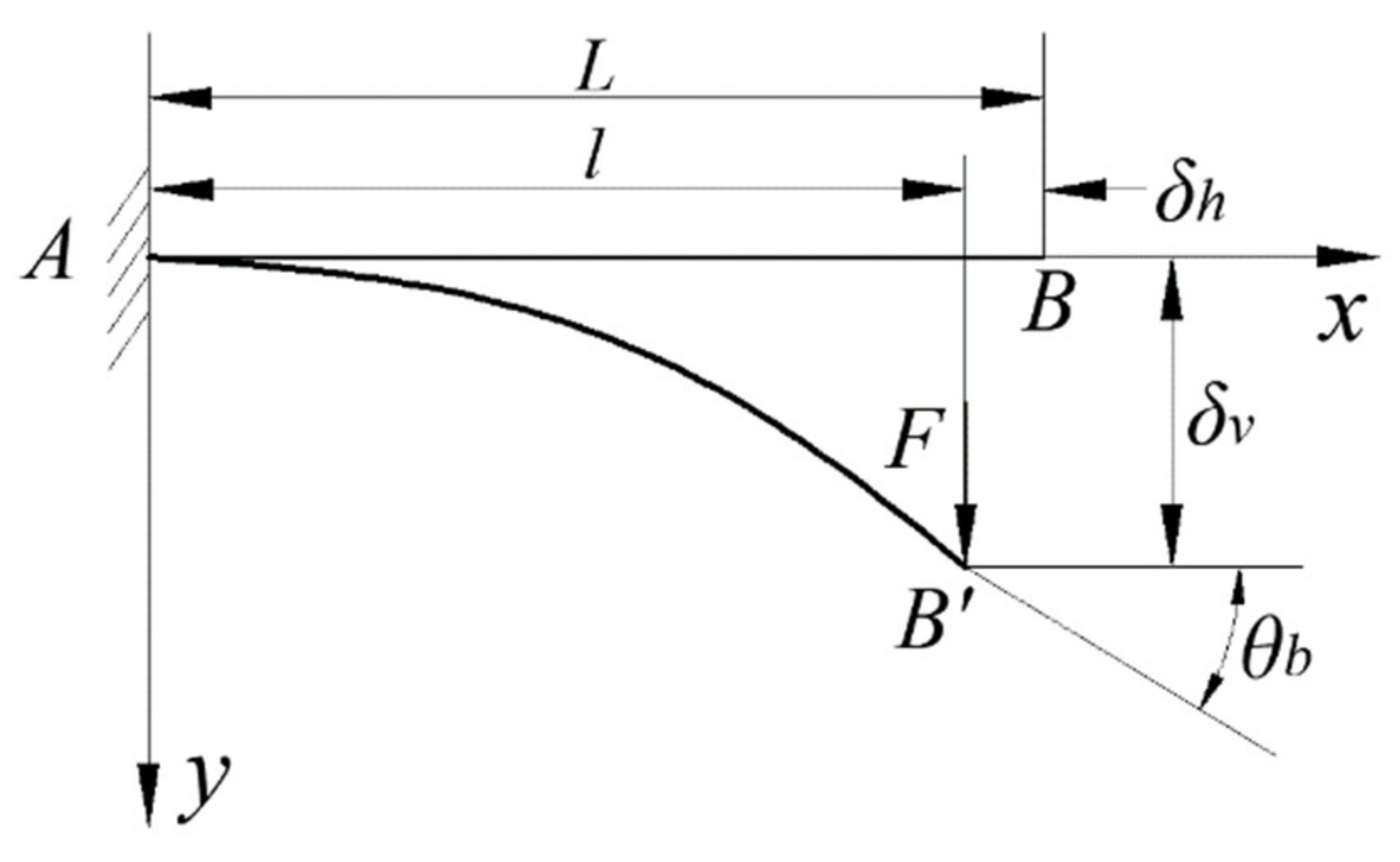
3.1. Problem Description
3.2. Zero Order Deformation Equation
3.3. High-Order Deformation Equations
4. Calculation Results
4.1. Exact Solution to Rotation Angle
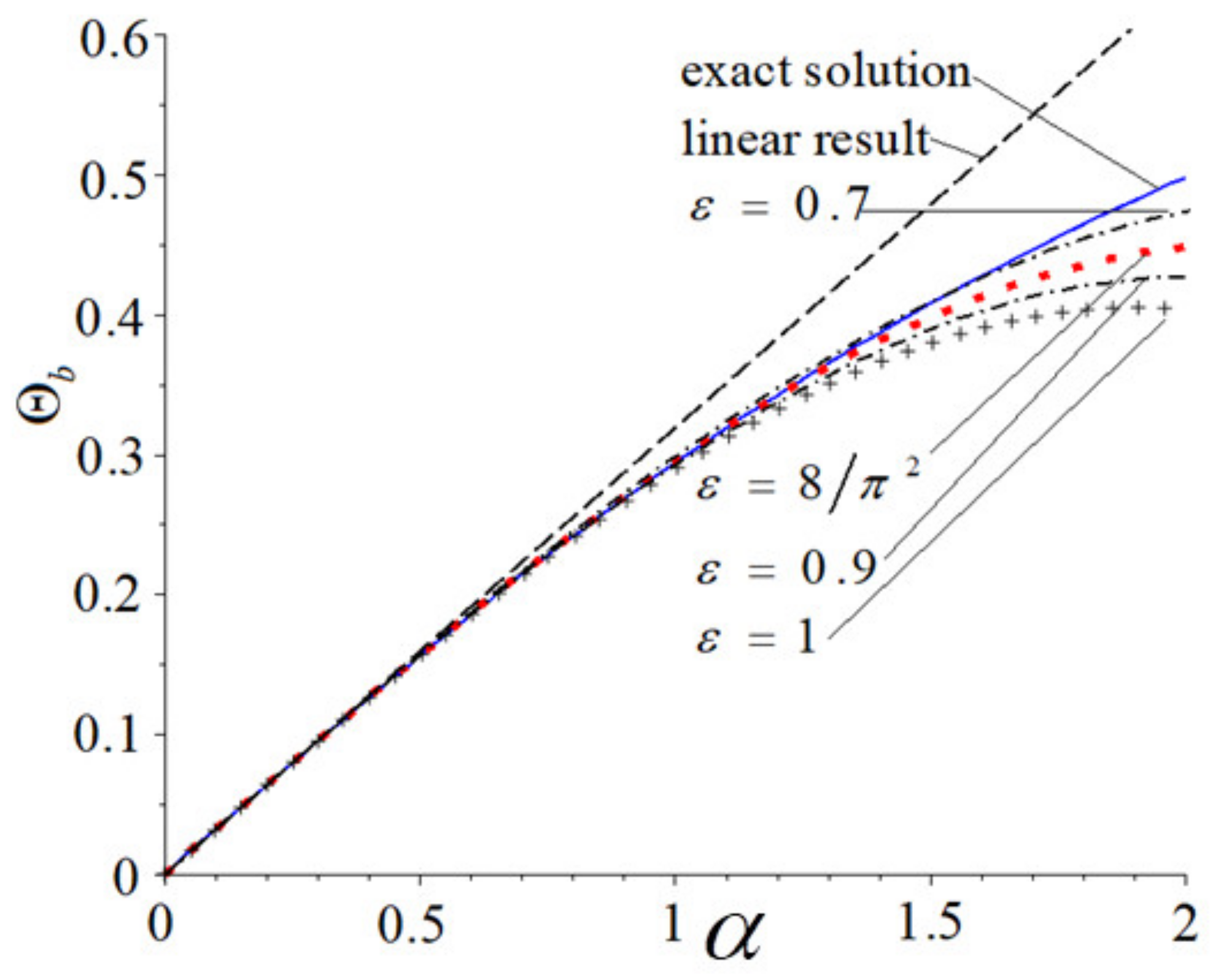
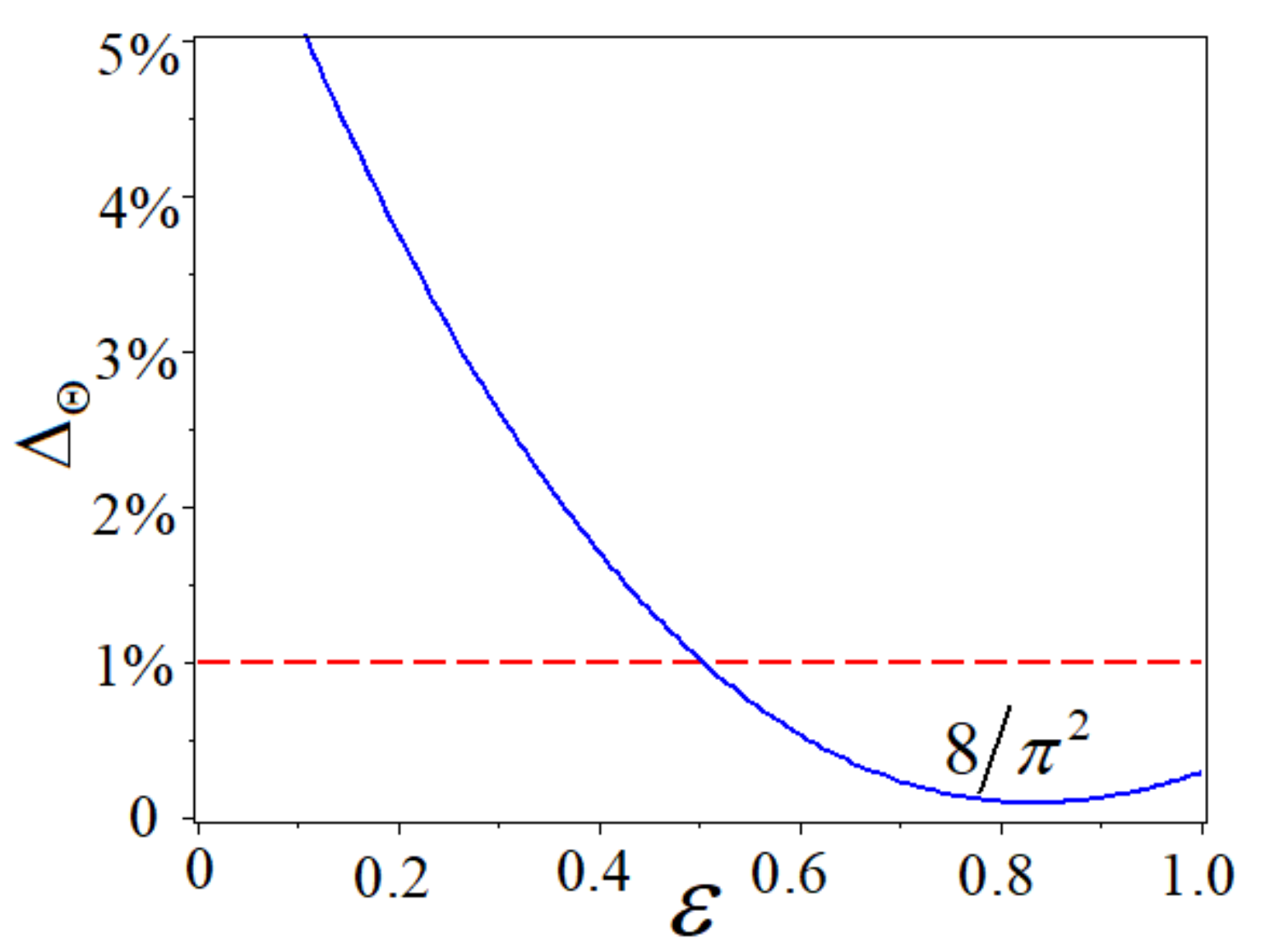
4.2. Effect of Auxiliary Parameter on Convergence
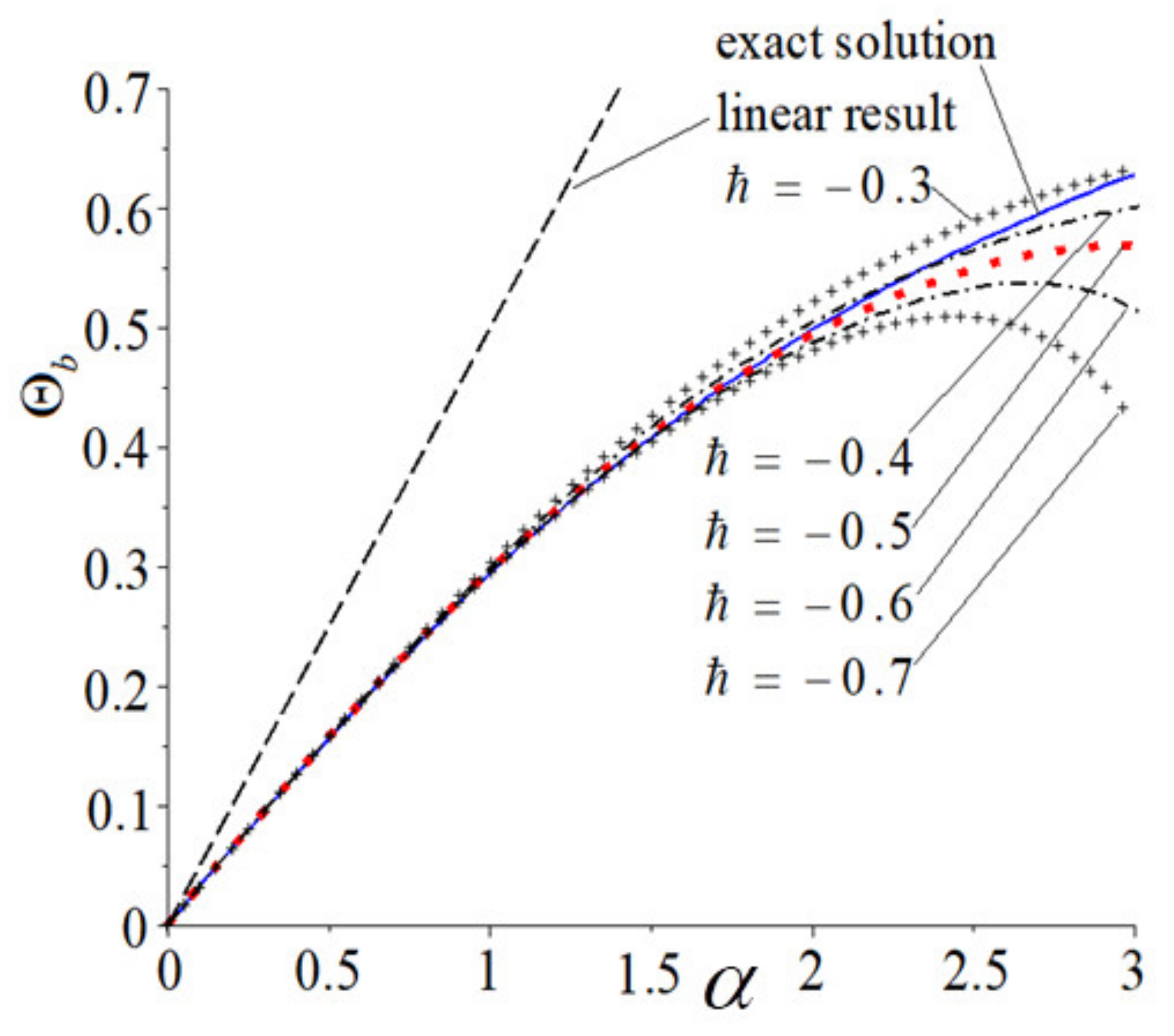
4.3. Effect of Auxiliary Parameter on Convergence
4.4. Comparison between IHAM and HAM
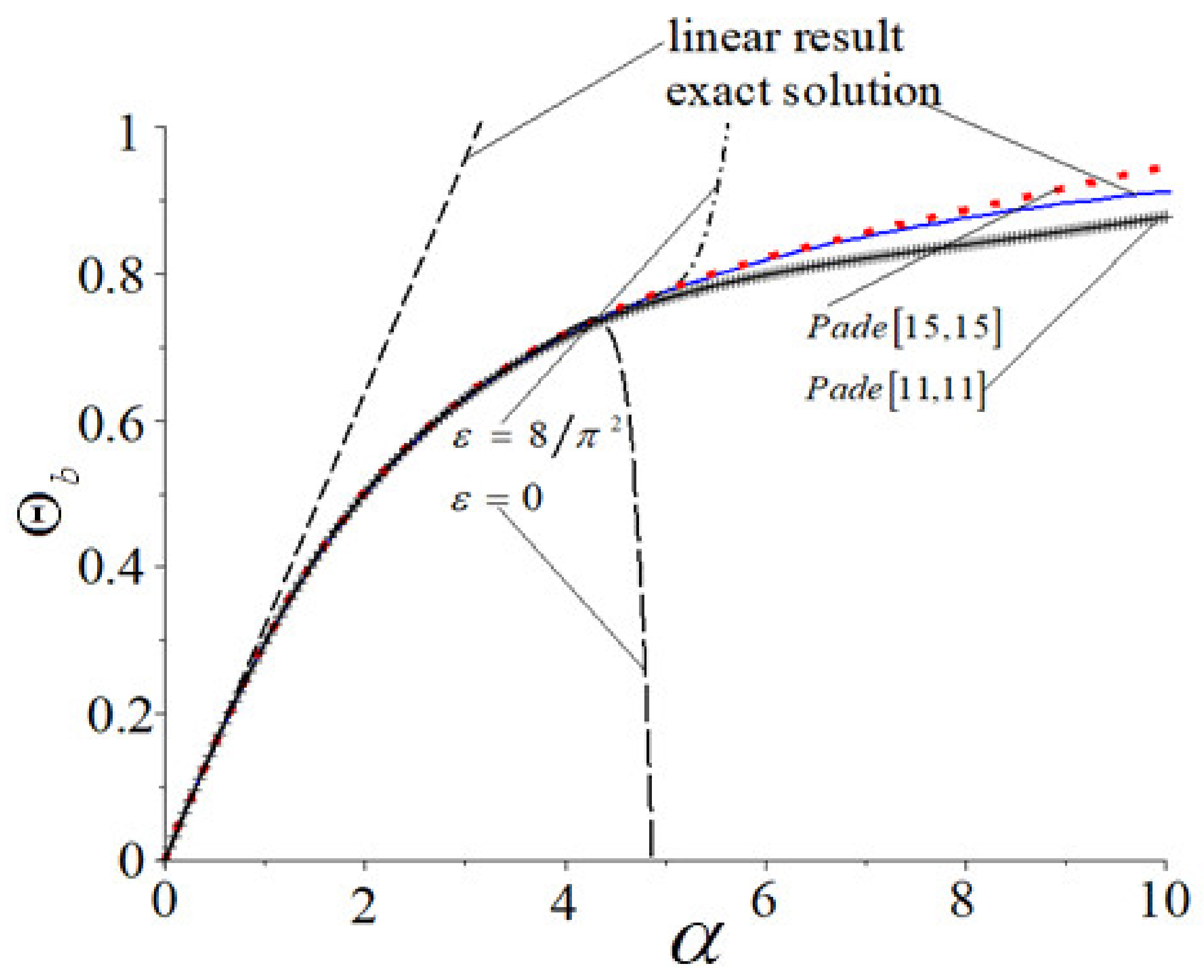
4.5. Homotopy–Páde Approximation
- Discrepancy between the linear solution and the exact solution is very large;
- Thirtieth-order solution by IHAM with approaches the exact solution much closer than the 30th-order solution does by HAM with ;
- The convergence region and rate have been substantially improved by homotopy-Páde approximation;
- And again the Páde approximation solution by IHAM is closer to the exact solution than is the Páde approximation solution by HAM.
5. Discussion about the Relative Errors
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Xiang, H.F. Prospect of world bridge engineering in the 21st century. J. Civ. Eng. 2000, 33, 1–6. (In Chinese) [Google Scholar]
- Qin, R. Long-Span Bridge Structure; Science Publishing House: Beijing, China, 2008. (In Chinese) [Google Scholar]
- He, G.K. High-rise building structure facing the 21st century. Build. Sci. 2002, 11, 1–4. (In Chinese) [Google Scholar]
- Hu, S.D.; Fang, E.H. Analysis of the world’s tallest 100 buildings. Constr. Technol. 2004, 35, 540–542. (In Chinese) [Google Scholar]
- Cole, J.D. Perturbation Methods in Applied Mathematics; Blaisdell Publishing Company: Waltham, MA, USA, 1968. [Google Scholar]
- Nayfeh, A.H. Problems in Perturbation; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Bush, A.W. Perturbation Methods For Engineers and Scientists; CRC Press Library of Engineering Mathematics; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Nayfeh, A.H. Perturbation Methods; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Liao, S.J. An analytic approximation of the drag coefficient for the viscous 5ow past a sphere. Int. J. Non-Linear Mech. 2002, 37, 1–18. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Lyapunov, A.M. General Problem on Stability of Motion; Taylor & Francis: London, UK, 1992; 1892 (English translation). [Google Scholar]
- Karmishin, A.V.; Zhukov, A.I.; Kolosov, V.G. Methods of Dynamics Calculation and Testing for Thin-Walled Structures; Mashinostroyenie: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Hilton, P.J. An Introduction to Homotopy Theory; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- Sen, S. Topology and Geometry for Physicists; Academic Press: Orlando, FL, USA, 1983. [Google Scholar]
- Grigolyuk, E.I.; Shalashilin, V.I. Problems of Non-Linear Deformation: The Continuation Method Applied to Non-Linear Problems in Solid Mechanics; Hardbound; Kluwer Academic Publishers: Dordrecht, The Netherland, 1991. [Google Scholar]
- Alexander, J.C.; Yorke, J.A. The homotopy continuation method: Numerically implementable topological procedures. Trans. Amer. Math. Soc. 1978, 242, 271–284. [Google Scholar] [CrossRef]
- Li, T.Y. Numerical solution of multivariate polynomial systems by homotopy continuation methods. Acta Numer. 1997, 6, 399–436. [Google Scholar] [CrossRef]
- Li, T.Y. Solving polynomial systems by the homotopy continuation method. In Handbook of Numerical Analysis; Ciarlet, P.G., Ed.; North-Holland: Amsterdam, The Netherlands, 2003; Volume XI, pp. 209–304. [Google Scholar]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. (In Chinese). [Google Scholar]
- Hayat, T.; Sajid, M. On analytic solution for thin film flow of a forth grade fluid down a vertical cylinder. Phys. Lett. A 2007, 361, 316–322. (In Chinese) [Google Scholar] [CrossRef]
- Liao, S.J. A new branch of solutions of boundary-layer flows over a permeable stretching plate. Int. J. Non-Linear Mech. 2007, 42, 819–830. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of homotopy analysis method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 360, 109–113. [Google Scholar] [CrossRef]
- Hayat, T.; Ellahi, R.; Ariel, P.D.; Asghar, S. Homotopy solution for the channel flow of a third grade fluid. Nonlinear Dyn. 2006, 45, 55–64. [Google Scholar] [CrossRef]
- Liang, S.; Jeffrey, D.J. Approximate solutions to a parameterized sixth order boundary value problem. Comp. Math. App. 2010, 59, 247–253. [Google Scholar] [CrossRef][Green Version]
- Ghotbi, A.R.; Omidvar, M.; Barari, A. Infiltration in unsaturated soils—An analytical approach. Comp. Geotech. 2011, 38, 777–782. [Google Scholar] [CrossRef]
- Nassar, C.J.; Revelli, J.F.; Bowman, R.J. Application of the homotopy analysis method to the Poisson–Boltzmann equation for semiconductor devices. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 2501–2512. [Google Scholar] [CrossRef]
- Mastroberardino, A. Homotopy analysis method applied to electrohydro dynamic flow. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 2730–2736. [Google Scholar] [CrossRef]
- Aureli, M. A framework for iterative analysis of non-classically damped dynamical systems. J. Sound Vib. 2014, 333, 6688–6705. [Google Scholar] [CrossRef]
- Sardanyés, J.; Rodrigues, C.; Januário, C.; Martins, N.; Gil-Gómez, G.; Duarte, J. Activation of effector immune cells promotes tumor stochastic extinction: A homotopy analysis approach. Appl. Math. Comput. 2015, 252, 484–495. [Google Scholar] [CrossRef][Green Version]
- Zou, K.; Nagarajaiah, S. An analytical method for analyzing symmetry-breaking bifurcation and period-doubling bifurcation. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 780–792. [Google Scholar] [CrossRef]
- Van Gorder, R.A. Analytical method for the construction of solutions to the Föppl–Von Kármán equations governing deflections of a thin flat plate. Int. J. Non-Linear Mech. 2012, 47, 1–6. [Google Scholar] [CrossRef]
- Liao, S.J.; Xu, D.L.; Stiassnie, M. On the steady-state nearly resonant waves. J. Fluid Mech. 2016, 794, 175–199. [Google Scholar] [CrossRef]
- Wu, W.; Liao, S.J. Solving solitary waves with discontinuity by means of the homotopy analysis method. Chaos Solitons Fractals 2005, 26, 177–185. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Liao, S.J. Solving the one-loop soliton solution of the Vakhnenko equation by means of the Homotopy Analysis Method. Chaos Solitons Fractals 2005, 23, 1733–1740. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.Y.; Wu, W. Solving the nonlinear periodic wave problems with the homotopy analysis method. Wave Motion 2004, 41, 329–337. [Google Scholar] [CrossRef]
- Abbasbandy, S. Soliton solutions for the 5th-order KdV equation with the homotopy analysis method. Nonlinear Dyn. 2008, 51, 83–87. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of the homotopy analysis method to solve a generalized Hirota-Satsuma coupled KdV equation. Phys. Lett. A 2007, 361, 478–483. [Google Scholar] [CrossRef]
- Wand, Z.; Zou, L.; Zhang, H. Applying homotopy analysis method for solving differential-difference equation. Phys. Lett. A 2007, 370, 287–294. [Google Scholar]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; PWS Publishing Company: Boston, MA, USA, 1997. [Google Scholar]
- Love, A.E.H. The Mathematics Theory of Elasticicy, 4th ed.; Dover Publications: New York, NY, USA, 1944. [Google Scholar]
- Frisch-Fay, R. Flexible Bars; Butterworths: London, UK, 1962. [Google Scholar]
- Yu, T.X.; Zhang, L.Z. Theory of Plastic Bending and Its Applications; Science Publishing House: Beijing, China, 1992. [Google Scholar]
- Lin, X.; Huang, Y.X.; Zhao, Y.; Wang, T. Large deformation analysis of a cantilever beam made of axially functionally graded material by homotopy analysis method. Appl. Math. Mech. 2019, 40, 1375–1386. [Google Scholar] [CrossRef]
- Kimiaeifar, A.; Domairry, G.; Mohebpour, S.R.; Sohouli, A.R.; Davodi, A.G. Analytical solution for large deflections of a cantilever beam under nonconservative load based on homotopy analysis method. Numer. Methods Partial. Differ. Equ. 2011, 27, 541–553. [Google Scholar] [CrossRef]
- Doeva, O.; Masjedi, P.K.; Weaver Paul, M. Static analysis of composite beams on variable stiffness elastic foundations by the Homotopy Analysis Method. Acta Mech. 2021, 232, 4169–4188. [Google Scholar] [CrossRef]
- Masjedi, P.K.; Weaver Paul, M. Analytical solution for arbitrary large deflection of geometrically exact beams using the homotopy analysis method. Appl. Math. Model. 2022, 103, 516–542. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.-K.; Liao, S. An explicit solution of the large deformation of a cantilever beam under point load at the free end. J. Comput. Appl. Math. 2008, 212, 320–330. [Google Scholar] [CrossRef]

| HAM | IHAM |
|---|---|
| and | |
| and |
| Exact Solution | (HAM [48]) | (IHAM) | (IHAM) | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.031802 | 0.031831 | 0.0916% | 0.031807 | 0.0172% | 0.031802 | 0.000178% |
| 0.2 | 0.063430 | 0.063662 | 0.365% | 0.063473 | 0.0669% | 0.063429 | 0.00284% |
| 0.3 | 0.094719 | 0.095493 | 0.817% | 0.094854 | 0.143% | 0.094705 | 0.0143% |
| 0.4 | 0.12551 | 0.12732 | 1.44% | 0.12581 | 0.237% | 0.12546 | 0.0446% |
| 0.5 | 0.15567 | 0.15915 | 2.24% | 0.15620 | 0.336% | 0.15551 | 0.107% |
| 0.6 | 0.18509 | 0.19099 | 3.19% | 0.18588 | 0.426% | 0.18468 | 0.219% |
| 0.7 | 0.21366 | 0.22282 | 4.29% | 0.21470 | 0.488% | 0.21281 | 0.399% |
| 0.8 | 0.24132 | 0.25465 | 5.52% | 0.24254 | 0.505% | 0.23971 | 0.667% |
| 0.9 | 0.26801 | 0.28648 | 6.89% | 0.26924 | 0.458% | 0.26521 | 1.05% |
| 1.0 | 0.29371 | 0.31831 | 8.38% | 0.29466 | 0.324% | 0.28913 | 1.56% |
| 1.1 | 0.31839 | 0.35014 | 9.97% | 0.31866 | 0.0857% | 0.31130 | 2.22% |
| 1.2 | 0.34206 | 0.38197 | 11.7% | 0.34110 | 0.279% | 0.33155 | 3.07% |
| 1.3 | 0.36473 | 0.41380 | 13.5% | 0.36184 | 0.791% | 0.34970 | 4.12% |
| 1.4 | 0.38641 | 0.44563 | 15.3% | 0.38074 | 1.47% | 0.36557 | 5.39% |
| 1.5 | 0.40714 | 0.47746 | 17.3% | 0.39764 | 2.33% | 0.37899 | 6.92% |
| 1.6 | 0.42685 | 0.50930 | 19.2% | 0.41242 | 3.40% | 0.38978 | 8.71% |
| 1.7 | 0.44587 | 0.54113 | 21.4% | 0.42493 | 4.70% | 0.39777 | 10.8% |
| 1.8 | 0.46394 | 0.57296 | 23.5% | 0.43502 | 6.23% | 0.40279 | 13.2% |
| 1.9 | 0.48120 | 0.60479 | 25.7% | 0.44257 | 8.03% | 0.40465 | 15.9% |
| 2 | 0.49768 | 0.63662 | 27.9% | 0.44741 | 10.1% | 0.40319 | 19.0% |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | |
| Exact Solution | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.2 | 0.063430 | 0.063459 | 0.0452% | 0.063475 | 0.0702% | 0.063496 | 0.104% |
| 0.4 | 0.12551 | 0.12572 | 0.163% | 0.12584 | 0.261% | 0.12601 | 0.395% |
| 0.6 | 0.18509 | 0.18566 | 0.306% | 0.18605 | 0.518% | 0.18660 | 0.814% |
| 0.8 | 0.24132 | 0.24231 | 0.411% | 0.24318 | 0.771% | 0.24441 | 1.28% |
| 1.0 | 0.29371 | 0.29493 | 0.416% | 0.29648 | 0.943% | 0.29871 | 1.71% |
| 1.2 | 0.34206 | 0.34300 | 0.275% | 0.34539 | 0.975% | 0.34895 | 2.01% |
| 1.4 | 0.38641 | 0.38626 | 0.0408% | 0.38961 | 0.827% | 0.39472 | 2.14% |
| 1.6 | 0.42685 | 0.42461 | 0.547% | 0.42900 | 0.479% | 0.43580 | 2.07% |
| 1.8 | 0.46394 | 0.45810 | 1.26% | 0.46362 | 0.0691% | 0.47216 | 1.77% |
| 2.0 | 0.49768 | 0.48666 | 2.21% | 0.49362 | 0.815% | 0.50391 | 1.25% |
| 2.2 | 0.52847 | 0.50998 | 3.50% | 0.51913 | 1.77% | 0.53127 | 0.530% |
| 2.4 | 0.55661 | 0.52714 | 5.29% | 0.54011 | 2.96% | 0.55449 | 0.382% |
| 2.6 | 0.58237 | 0.53627 | 7.92% | 0.55613 | 4.51% | 0.57375 | 1.48% |
| 2.8 | 0.60600 | 0.53404 | 11.9% | 0.56612 | 6.58% | 0.58908 | 2.79% |
| 3 | 0.62772 | 0.51507 | 17.9% | 0.56805 | 9.50% | 0.60016 | 4.39% |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | |
| Exact Solution | (HAM [48]) | (IHAM) | |||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0.3 | 0.094719 | 0.094757 | 0.0403% | 0.094782 | 0.0664% |
| 0.6 | 0.18509 | 0.18533 | 0.131% | 0.18551 | 0.229% |
| 0.9 | 0.26801 | 0.34295 | 0.217% | 0.26911 | 0.411% |
| 1.2 | 0.34206 | 0.29440 | 0.262% | 0.29507 | 0.554% |
| 1.5 | 0.40714 | 0.40824 | 0.268% | 0.40974 | 0.637% |
| 1.8 | 0.46394 | 0.46512 | 0.253% | 0.46705 | 0.670% |
| 2.1 | 0.51342 | 0.51462 | 0.233% | 0.51685 | 0.668% |
| 2.4 | 0.55661 | 0.55780 | 0.214% | 0.56021 | 0.647% |
| 2.7 | 0.59444 | 0.59563 | 0.200% | 0.59809 | 0.615% |
| 3 | 0.62772 | 0.62892 | 0.191% | 0.63134 | 0.577% |
| 3.3 | 0.65714 | 0.65838 | 0.189% | 0.66067 | 0.538% |
| 3.6 | 0.68327 | 0.68494 | 0.244% | 0.68669 | 0.500% |
| 3.9 | 0.70659 | 0.71070 | 0.584% | 0.70987 | 0.464% |
| 4.2 | 0.72749 | 0.73465 | 0.985% | 0.73053 | 0.418% |
| 4.5 | 0.74630 | 0.70350 | 5.73% | 0.74859 | 0.307% |
| 4.8 | 0.76329 | 0.28076 | 63.2% | 0.76402 | 0.0959% |
| 5.1 | 0.77870 | — | — | 0.78403 | 0.684% |
| 5.4 | 0.79272 | — | — | 0.84973 | 7.19% |
| 5.7 | 0.80552 | — | — | — | — |
| 6 | 0.81723 | — | — | — | — |
| 1 | 1 | 0 | 1 | 0 | |
| Exact Solution | (HAM [48]) | (IHAM) | |||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0.15567 | 0.15583 | 0.0991% | 0.15594 | 0.173% |
| 1 | 0.29371 | 0.29440 | 0.237% | 0.29507 | 0.463% |
| 1.5 | 0.40714 | 0.40824 | 0.268% | 0.40974 | 0.639% |
| 2 | 0.49768 | 0.49887 | 0.239% | 0.50102 | 0.671% |
| 2.5 | 0.56977 | 0.57095 | 0.206% | 0.57340 | 0.637% |
| 3 | 0.62772 | 0.62875 | 0.165% | 0.63134 | 0.577% |
| 3.5 | 0.67489 | 0.67527 | 0.0565% | 0.67834 | 0.511% |
| 4 | 0.71380 | 0.71244 | 0.192% | 0.71700 | 0.448% |
| 4.5 | 0.74630 | 0.74176 | 0.608% | 0.74920 | 0.389% |
| 5 | 0.77373 | 0.76472 | 1.16% | 0.77639 | 0.344% |
| 5.5 | 0.79711 | 0.78279 | 1.80% | 0.79971 | 0.326% |
| 6 | 0.81723 | 0.79728 | 2.44% | 0.82010 | 0.351% |
| 6.5 | 0.83466 | 0.80932 | 3.04% | 0.83834 | 0.441% |
| 7 | 0.84986 | 0.81979 | 3.53% | 0.85507 | 0.613% |
| 7.5 | 0.86321 | 0.82935 | 3.92% | 0.87080 | 0.879% |
| 8 | 0.87499 | 0.83850 | 4.17% | 0.88594 | 1.25% |
| 8.5 | 0.88544 | 0.84758 | 4.27% | 0.90079 | 1.73% |
| 9 | 0.89475 | 0.85684 | 4.24% | 0.91557 | 2.33% |
| 9.5 | 0.90307 | 0.86644 | 4.06% | 0.93046 | 3.03% |
| 10 | 0.91055 | 0.87648 | 3.74% | 0.94558 | 3.85% |
| 1 | 1 | 0 | 1 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, X.; Huo, S.; Xie, C. Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle. Appl. Sci. 2022, 12, 6400. https://doi.org/10.3390/app12136400
Li Y, Li X, Huo S, Xie C. Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle. Applied Sciences. 2022; 12(13):6400. https://doi.org/10.3390/app12136400
Chicago/Turabian StyleLi, Yinshan, Xinye Li, Shuhao Huo, and Chen Xie. 2022. "Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle" Applied Sciences 12, no. 13: 6400. https://doi.org/10.3390/app12136400
APA StyleLi, Y., Li, X., Huo, S., & Xie, C. (2022). Explicit Solutions to Large Deformation of Cantilever Beams by Improved Homotopy Analysis Method I: Rotation Angle. Applied Sciences, 12(13), 6400. https://doi.org/10.3390/app12136400





