1. Introduction
Historically, hydropower was used as a source of baseload generation for electric power, but now it is increasingly used for grid balancing. Among dispatchable renewable energy sources, hydropower plants are the most often used [
1], achieving up to 15 s response times [
2] for 90% of the total power response. The future potential of hydropower is shifting towards grid regulation tasks. Including nondispatchable renewable energy sources, e.g., inter alia wind and photovoltaics, and market deregulation, creates the requirement for rapid power generation fluctuations and power increase in the afternoon [
3,
4,
5]. Any new hydraulic turbine design should therefore enable this type of operation and reach high efficiency and stable operation outside its optimal operating interval. Besides stable continuous turbine operation away from the best efficiency point, new designs will also need to function sufficiently in transient operation. Bulb turbines face challenges for such operation; designers will have to overcome the detrimental effects that flow fluctuations and cavitation have on turbine operation, while still ensuring adequate performance over a broad interval of operating points and in transient operation [
3].
At the best efficiency point, an optimal combination of the runner frequency of the rotation, head, and discharge is available. At such an operating point, flow separation is usually low, and no cavitation is observed. For operation away from the optimum efficiency point, bulb turbines, as compared e.g., to Francis turbines [
4], feature double regulation and may operate in a wide interval of operating conditions with reasonably high efficiency. Although all hydraulic turbine types are constantly improved, the gains in efficiency are in the per mille range and the cavitation in hydraulic turbines remains an issue. The cavitation in the hydraulic turbines [
4,
6,
7] decreases efficiency and increases vibrations and erosion, thereby reducing the service life.
The procedures optimizing the performance of turbine hydraulics are most often based on the use of so-called inverse design methods [
8] and computational fluid dynamics (CFD) [
9].
Inverse design methods have been in use for decades, with the first 3D methods emerging around 30 years ago. These methods are based on the a priori specification of the pressure or blade loading distribution. Such distribution along the runner blade in the radial and meridional directions facilitates the calculation of the runner blade’s angle. This reduces the computational CFD work required when insufficient information on the runner geometry is known in advance. Zangeneh [
10] proposed a three-dimensional design method for radial and mixed turbines for the compressible case. Today his method is still often used for designing radial turbine machinery. Zhu et al. performed inverse design optimization of the reversible pump-turbine [
11], while also considering cavitation characteristics. Leguizamón and Avellan [
12] very recently provided an open-source implementation of an inverse Francis turbine design, together with a validation study confirming the approach’s appropriateness. Cavitation is not often studied using inverse design methods; among the available studies, Daneshkah and Zangeneh [
13] linked the blade loading and blade stacking to the efficiency and cavitation characteristics of a Francis runner, providing a valuable physical understanding and useful design guidelines.
The 3D design of the runners and the guide apparatus may be determined by performing consecutive CFD calculations, while constantly varying 3D geometry and design parameters [
9,
14]. Unfortunately, CFD alone is unable to establish an optimized 3D design. A 3D design study using CFD was performed by Xue et al. [
15], considering the efficiency, stability of design, and cavitation of a pump turbine during pumping mode. A comprehensive hydraulic and parametric analysis of a Francis turbine runner was performed by Ma et al. [
16]. They [
16] performed a multipoint and multiobjective optimization design procedure, achieving efficiency improvements up to 0.91%. The optimization procedure included the 3D inverse design method, CFD analysis, and multipoint and multiobjective optimization technology.
Runner blades are central turbine elements, where energy is transferred from the fluid to the generator shaft. Blade sizes and angles, including hydrofoil selection, contribute to the blade design. The blade design is often a trade-off between efficiency, cavitation development, and cavitation erosion. A pressure difference between the suction and pressure sides is limited by cavitation, while at the same time the high pressure difference enables energy transfer from water to the generator. If the turbine is at full load and the water level is low in the reservoir, the pressure on the suction side may decrease and locally drop below the vapor pressure. Cavitation on the runner blades may appear in several locations. These are the turbine blade leading edge, the tip, the pivot, the gap between the blade tip and the discharge ring, the blade suction side close to the trailing edge, and the cavitation near the draft tube cone [
7,
17]. For the abovementioned cavitation types, the root causes are suboptimal runner blade design and hydrofoil selection for the selected operating conditions. Cavitation is extensively studied in hydraulic turbine machinery; among these, few studies have employed the visualization method [
6,
7].
On bulb turbines’ blades, the initial cavitation most often appears at the location with the highest local speed i.e., at the blade tip [
18]. We show an experimental analysis of a modification to the hydrofoil design of bulb turbine blades so as to resist cavitation during continuous operating conditions at high flows. The paper shows the cavitation characteristics of two bulb turbine hydrofoils. The improvement from the existing to modified hydrofoil is discussed based on visualization analysis in the cavitation channel. Furthermore, we show a comparison of the modified runner blades with the unmodified blades in terms of the turbine output. The paper shows marked improvement in cavitation occurrence between existing and modified hydrofoils, and a confirmed regression model of the void fraction.
2. Hydrofoil
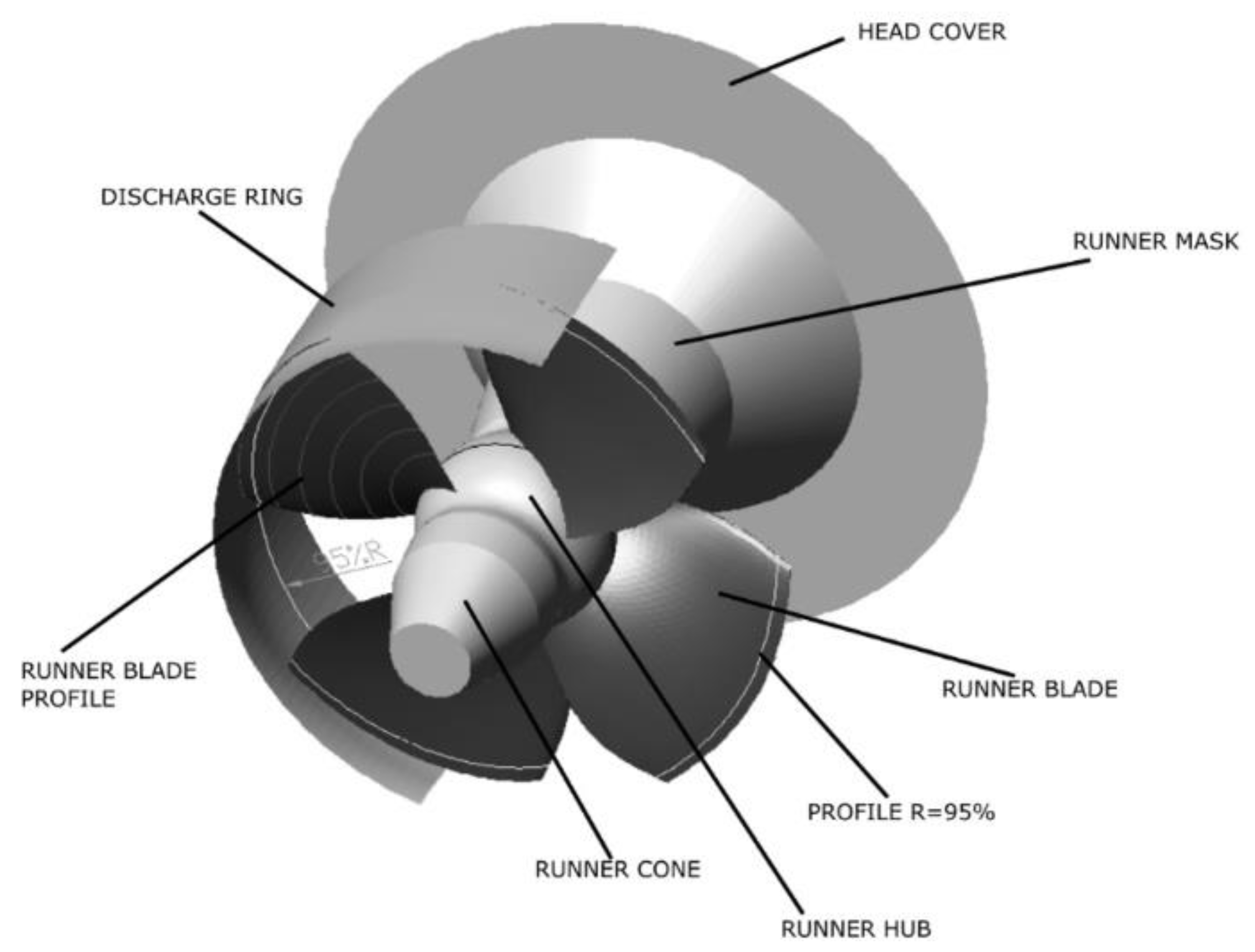
Bulb turbine (
Figure 1) blade hydrofoils are optimized for a mix of parameters, among which are maximum hydraulic efficiency, high output power, minimum turbine vibrations, high strength, reduced fatigue, and reduced cavitation phenomena. Reduced cavitation enables operators to reduce the service intervals required for cavitation damage repair and welding costs, as well as loss of money for nonoperation.
In this study, we focus on a range of volumetric flows, which appear on a bulb turbine at a 25° blade angle (
Figure 2). Here cavitation frequently occurs at approximately 15% higher volumetric flows than at the best efficiency point [
6]. The 25° blade angle was chosen because it lies in the middle of the angle interval usually agreed between the producers and customers of bulb turbines. The blade angle 25° is often reinforced during performance or acceptance tests [
18], because it corresponds to both common operating conditions and features increased probability for cavitation.
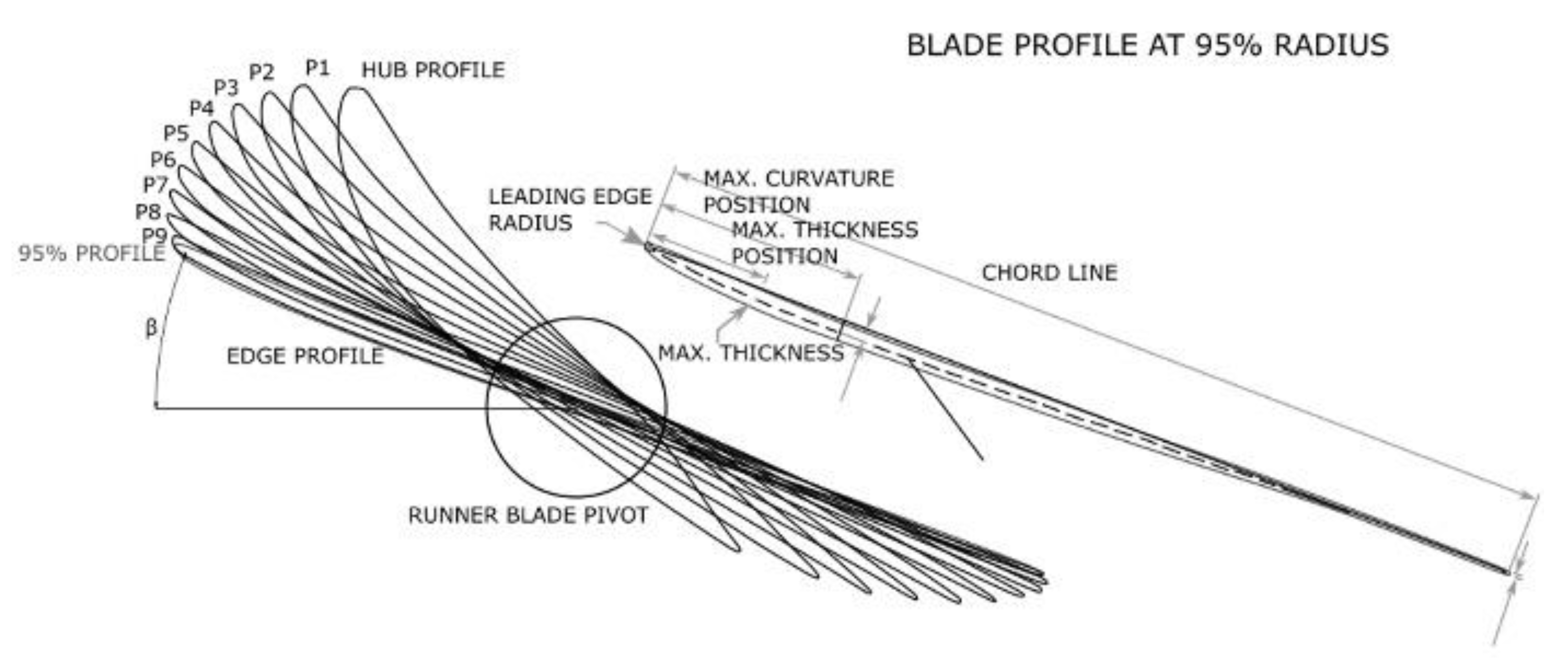
The bulb runner blade hydrofoil’s shape determines the flow conditions in the runner. Well-shaped 3D blade hydrofoils reduce the inception and the growth of cavitation on the bulb turbine runner hydrofoils. Turbine hydrofoil profiles were used in designing the bulb runner blade’s 3D shape, spanning from the runner hub toward the blade tip (
Figure 2). For reliable 3D characterization of the turbine runner blade, and thus the entire bulb runner, several hydrofoils are usually selected. Later, a smooth surface is drawn over all hydrofoils to form the entire 3D geometry of the runner blade, further enabling CFD or experimental analysis.
Although the bulb turbine blade can consist of many hydrofoils as explained above, in this paper we focus on a single hydrofoil. The most potential for energy conversion in bulb turbines is available near the tip, where tangential blade velocity and flow velocities are high. Due to high velocities, large pressure gradients, and the vicinity of the tip gap flow, this region is highly susceptible to cavitation occurrence and surface erosion. Here, several cavitation structures are usually found during acceptance tests. To focus on the cavitation properties of the hydrofoils, we have selected for further analysis the hydrofoil at 95% bulb turbine diameter D, measured from the runner rotation axis to the blade tip. The selected hydrofoil is thus located near the tip as shown in
Figure 2 and
Figure 3. We made this selection on the basis of the energy transfer. Most of the energy is transferred where the turbine blade has a large diameter and the blade has a high surface area, and where the blade and flow velocities are high.
Hydrofoils have been studied extensively, including profile families such as NACA (among them 4–8 series), Göttingen, Munk, NPL, and others [
19,
20,
21]. The available families of hydrofoils facilitate the turbine engineer’s selection of the blade’s hydrofoil to suit the required operating intervals and conditions, inter alia, for operation at high volumetric flows and runner blade angles. To enable operation in specific operating conditions, including cavitation properties, the turbine designer selects hydrofoil properties like leading edge radius, camber, location of maximum thickness, maximum curvature, and trailing edge design.
The locations of cavitation occurrence on bulb turbine blades are well documented in [
22]. In the hill diagram, we will focus on the high discharge region. Here, the cavitation is found in four regions [
22]: the blade suction side, blade pressure side, fillet, and tip gap. The flow properties in and near the gap are dominated by turbulence and may appear in the entire hill diagram. The hydrofoil properties that most affect the cavitation on the blade suction and pressure side are the leading edge radius, the location of maximum thickness, and the curvature; we may also assume that the blade angle in bulb turbines is always optimal due to the turbine’s dual regulation. We want to design a leading edge such that the flow around it is smooth so as to prevent any flow separation. As discussed above, we will focus on the hydrofoil at 95% of the blade radius, where we assume that in addition to the mentioned leading edge, maximum thickness and curvature influence, the cavitation properties are also influenced also by the presence of the gap flow. At 95% of the blade radius, the flow properties (velocity and pressure) are more pronounced because of higher blade velocity than near the hub. The sharp leading edges may introduce flow separation [
23] and deteriorate the flow properties further downstream from the leading edge. Downstream from the leading edge the flow is determined by the camber shape, the position of maximum curvature, maximum thickness, etc. These parameters, among others, determine the velocity distribution in the blade channel from the pressure to the suction side. Velocity is related to absolute pressure; an increase in flow velocity decreases the local pressure [
7], thus, the velocity distribution affects the cavitation properties. The pressure distribution may cause local cavitation inception, and both can influence boundary layer separation.
The hydrofoils in the bulb or any other water turbines are the base elements of the turbine runner blades and are thus rotating. The bulb turbine features pressure distribution with the pressure normally decreasing from the leading edge towards the trailing edge. According to the bulb turbine’s triangles of velocity, downstream from the hydrofoil the relative velocity increases and reaches its maximum near the trailing edge [
7], and the situation is remarkably different in comparison with the single hydrofoil in the water tunnel. Furthermore, the pressure distribution around the hydrofoil in the cavitation tunnel cannot fully represent the pressure properties around the bulb turbine blade. The situation in the bulb turbines is therefore very complex and the flow properties around individual hydrofoils cannot be directly correlated around the bulb turbine runner blades. Nevertheless, we will assume [
6] that bulb runner cavitation can be related to the cavitation analysis of a single hydrofoil in the water tunnel.
Hydrofoil Modifications
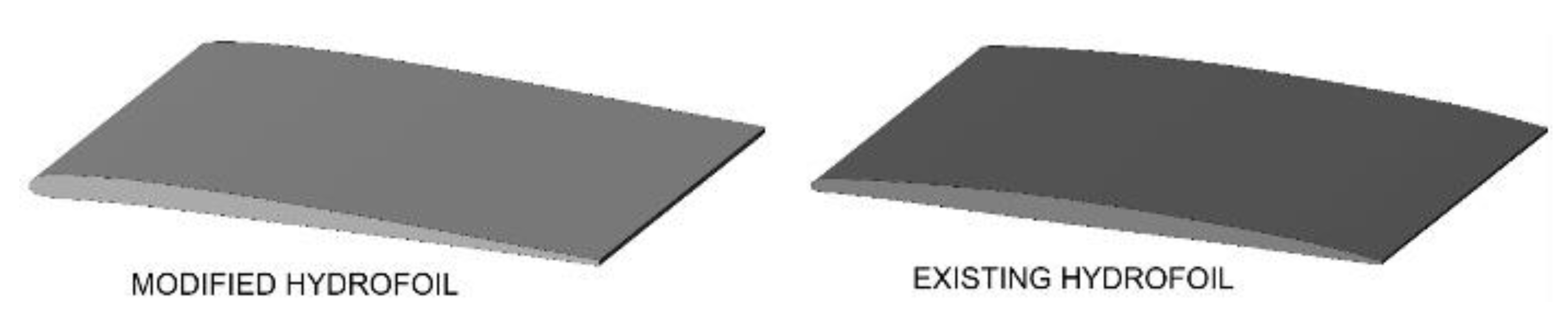
The turbine blade hydrofoils are the primary component of the turbine blades. To improve performance, the turbine hydrofoil profiles should be smoothly and consistently remodelled in a spatial 3D redesign of the entire bulb turbine runner blade. The new blade differs from the old in the following parameters: the leading-edge radius has increased, the maximum thickness location has moved forward, and the location of the maximum hydrofoil curvature has moved forward. The characteristics of both turbine hydrofoils are shown in
Table 1.
The modified hydrofoil as compared to the unmodified one features reduced absolute velocity in a section from the location of the maximum hydrofoil thickness and curvature to the trailing edge. The cavitation properties of the modified hydrofoil as compared to the unmodified one are in this section favorable. Because the points of maximum thickness and curvature for the modified hydrofoil profile were moved forward towards the leading edge, this section is relatively long.
The unmodified hydrofoil in a region from the leading edge to the location of the maximum thickness is very sensitive to the optimum angle of attack due to its sharp leading edge. Away from the optimum attack angle, the unmodified hydrofoil has disadvantageous cavitation characteristics in comparison with the modified one [
6]. Contemporary water turbines often operate away from the best efficiency points due to the introduction of renewable energy sources and environmental changes. This trend will most probably increase in the future.
Two dimensional hydrofoils (
Figure 4) were created from the 3D spatial bulb turbine blade hydrofoils (
Figure 2 and
Figure 3). The 3D turbine blade hydrofoil was transformed from the cylindrical coordinate system of a turbine blade to a planar Cartesian x–y coordinate system as shown in
Figure 3.
As shown previously, both hydrofoils correspond to the runner blades’ profiles at 95% R (
Figure 3). The properties of both bulb runners are given in [
4]. The turbine runners and both 2D hydrofoils were manufactured from brass using the same manufacturing techniques and both were given the same surface processing. The hydrofoils were later subjected to flow and image analysis in a cavitation tunnel and regression modelling.
The hydrofoil parameters for the experiment in the cavitation tunnel are shown in
Table 2. The same manufacturing method as for the hydrofoils on the bulb turbine was used for the manufacture of the hydrofoils used in the cavitation tunnel.
3. Experiment
Experiments were performed on the turbine measuring station for both bulb turbine runners and in the cavitation tunnel for both hydrofoils. A turbine measuring station was used to determine efficiency for a single runner blade angle. In the cavitation tunnel, cavitation properties were measured for analogous operating points.
3.1. Turbine Measurements
Measurements of efficiency were performed on a low-head axial and bulb turbines measuring station for low-head bulb turbines (
Figure 5) in Kolektor Turboinštitut (Ljubljana, Slovenia). The measuring station was built according to standard [
18] and was used for the model, witness, and acceptance tests. In agreement with standard [
18], all measurements and data acquisitions were automatic. The nominal runner diameter of the test rig is 350 mm, and the recirculating flow is generated using two radial pumps with frequency regulation. The flow measurement was performed by using an electromagnetic flowmeter with a diameter of DN 400 and an accuracy of ±0.15%. The static pressure was measured using a differential pressure transducer (accuracy of ±0.025%), with the measuring taps located on the inlet and the outlet. Absolute suction pressure was measured using an absolute pressure transducer with an accuracy of ±0.025% to assure that the measuring station operated well above the incipient cavitation number. An electromagnetic incremental sensor was used to measure the rotational speed; the output was processed by a counter-timer module with an accuracy of ±0.01%. The shaft torque was measured on a horizontal shaft using a rotating torque transducer with an accuracy of ±0.01%. The friction torque was estimated by operation with air.
Both bulb turbine runners were tested under similar conditions at six operating points. The blade angle was cases set to 25° in all cases (
Figure 6). The blade angle was set using a control template. For comparison, both runners operated at the same specific energy E (J/kg) and the corresponding nondimensional energy numbers
were recorded. E was determined from the total specific energy at the turbine inlet and the outlet cross-sections [
7]. Energy numbers
were determined using the equation:
Here N (min
−1) is the rotational frequency, while D (m) is the discharge ring diameter of the bulb turbine. The turbine rotational frequency N (1000 min
−1) was the same for all measuring points. Both runners had the same nominal diameter D (m). The guide vane opening coefficient A
0 was the same for each pair of measuring points used in the comparison:
av (mm) is the guide vane’s opening and z (/) is the number of guide vanes. Dv (mm) is the guide vane pivot diameter. Important manufacturing methods and characteristics were kept the same for reliable comparison between both runners. Control of runner tip gaps to the discharge ring and clearances of guide vanes to the guide vane pressure rings are very important for reliably estimating model turbine runners. Both runners were manufactured from the same material and using the same production methods and procedures. As such, for both runners, the tip gaps, guide vane clearances, and surface finishes were the same.
The measuring station was of a closed type. To maintain the ψ fixed, the main water circulation pump’s frequency was controlled. The volumetric flow Q (m
3/s) represented in its nondimensional form as flow number φ [
18] is:
The results from a previous study show that the increase in efficiency amounts to around 1% for the same runner geometry. Most of the increase according to the hill diagram is due to the small shift of the operating points towards low flow numbers and higher efficiency [
6].
3.2. Cavitation Tunnel Measurements
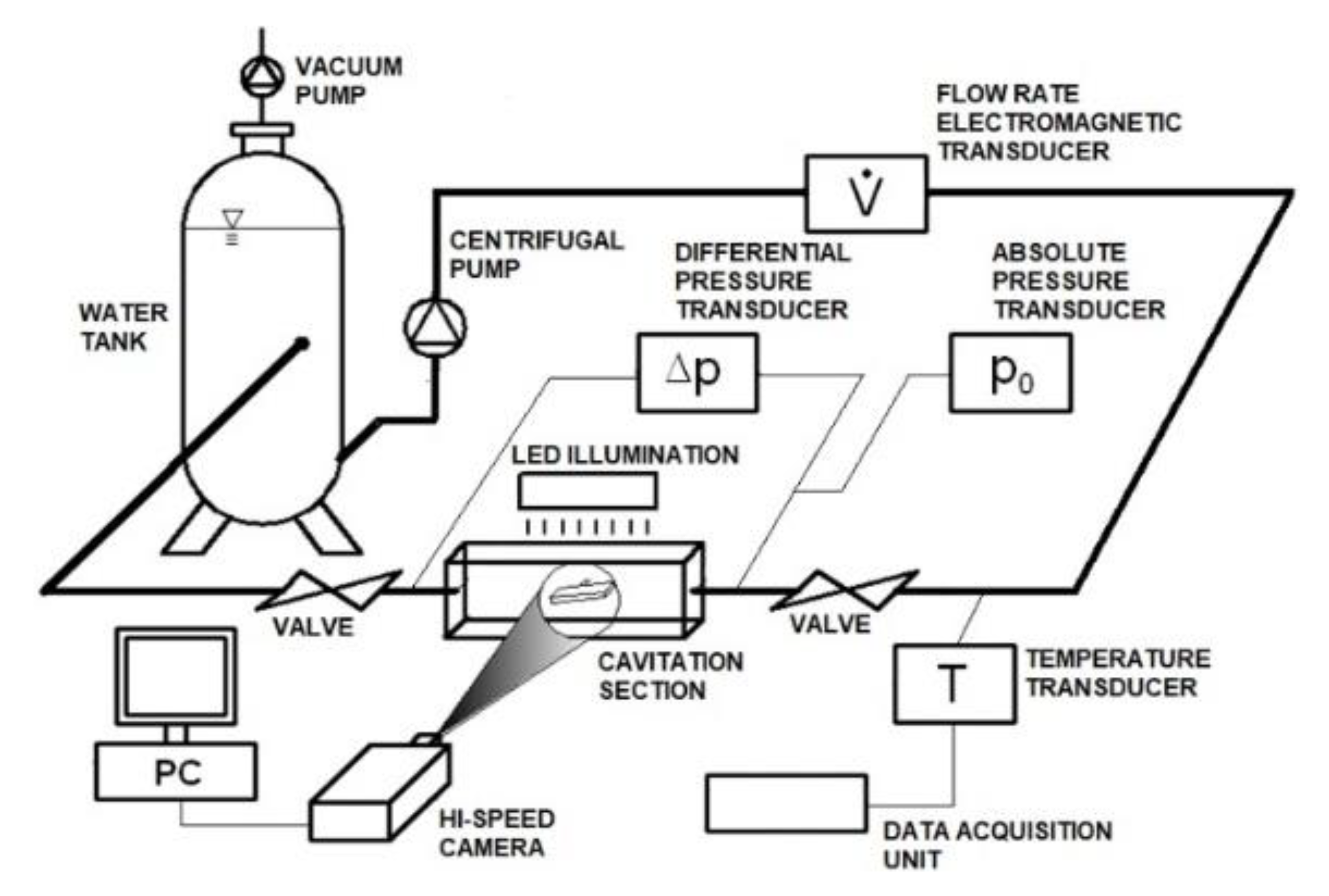
The flow visualization measurements were taken on the cavitation measuring station. The approach to investigating the turbine blade flow properties in a separate tunnel experiment was similar to that used in [
24]. A closed-type cavitation measuring station was used as shown in
Figure 7. The flow was provided by a centrifugal pump driven by a frequency variable drive. The volumetric flow measurement was performed using an electromagnetic transducer ABB COPA-XL. Absolute pressure p
abs was measured on the suction side using an ABB 2600T 264NS pressure transducer. The temperature was measured by a Pt-100 4 wire temperature transducer, connected to the Agilent 34970A data acquisition unit. Valves in front of and behind the test section were fully open during experiments and they were only used during installation. Suction pressure was set using a vacuum pump, located on the top of a tank with a free water surface.
The cavitation tunnel test section cross-section was 50 cm × 100 cm. Hydrofoil width was 50 mm and chord length was l = 60 mm. The hydrofoil was installed at the angle of attack 8°.
A high-speed Photron SA-Z camera was used together with a Nikkor 105 mm 1:2.8 lens to visualize the cavitation in the cavitation section. The camera was mounted from the side. The camera was operated in a free-running mode. Images were recorded using PFV software in 8-bit BMP black and white mode at a resolution of 640 × 280. The framerate used was 25,000 frames/s. Shutter speed was equal to 10 µs. For each operating point, 2000 frames were recorded. For all experiments, all other camera settings were the same. A high intensity continuous LED illumination was provided by many CREE XLamp XM-L LED modules. LED modules were powered by an Instek DC power supply. Illumination was provided from the top of the test section above the hydrofoil on its suction side and arranged such that as few reflections as possible were present in the recorded sequences. Illumination intensity was not the same for all experiments; with the modified hydrofoil it was necessary to increase illumination intensity to visualize weaker cavitation structures. Keeping the illumination constant was impossible due to the low 8-bit depth of recorded images.
We have selected two dimensionless numbers to describe the cavitation in the cavitation tunnel, namely the Reynolds number Re and cavitation number σ. In Reynolds number Re
L is hydrofoil length, v (m/s) is flow velocity in front of the hydrofoil and ν is the kinematic viscosity of water. To obtain the hydrofoil cavitation characteristics, the cavitation numbers σ were evaluated. Cavitation number σ was calculated according
where p
v (N/m
2) is the water evaporation pressure and p
abs (N/m
2) is absolute pressure. Water evaporation pressure was estimate using the Equation
where T
w (°C) is water temperature. Equation (6) provides for a maximum difference of 0.2%, with a negligible influence on the measurements.
The cavitation σ-η curve is used to estimate the cavitation properties of bulb turbines. The cavitation point for the highest cavitation numbers is measured at ambient pressure, while for subsequent cavitation points suction pressure is decreased. For the tunnel measurements the cavitation number σ was used to observe the cavitation’s development on both hydrofoils. For each experiment, the absolute pressure pabs was set as constant at the inlet of the cavitation tunnel. To decrease the cavitation number σ we increased the flow Q (m3/s) and flow velocity. Several such operating points were measured for increasingly lower absolute pressure pabs in the test section. This enabled comparison between both hydrofoils and among different absolute pressures.
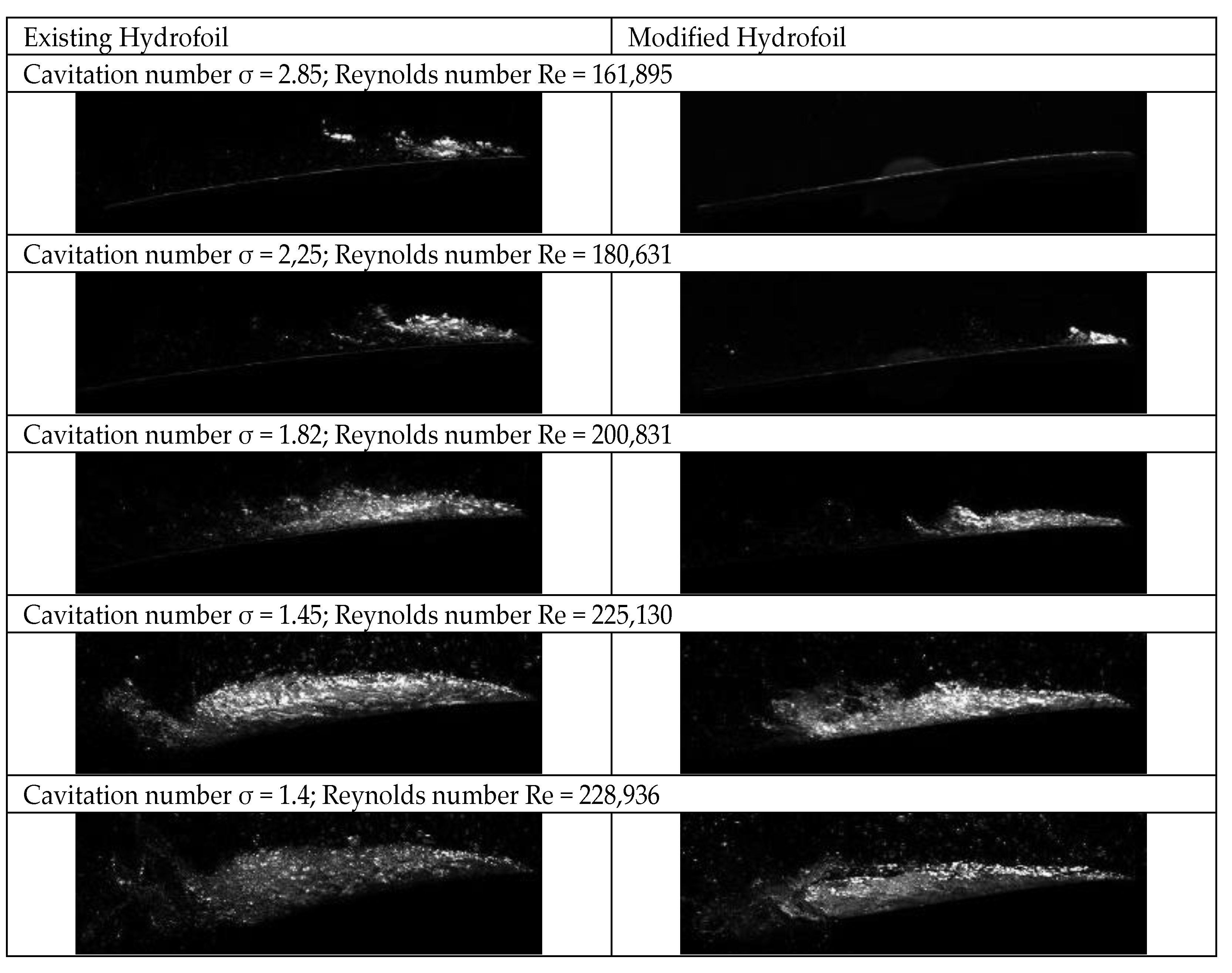
The measuring points for both hydrofoils were selected according to cavitation structures sizes, shapes, and intensities. In general, cavitation intensity increased as cavitation number σ decreased. Instantaneous cavitation numbers σ were selected manually; we wanted to capture significant visible structural changes in cavitation. Such a procedure captured all important structures, starting with incipient cavitation on the leading edge, then sheet cavitation, cloud cavitation, and supercavitation across the entire hydrofoil [
25,
26]. Cavitation structure formation on both hydrofoils emerged at different cavitation numbers σ and, thus, the selection of cavitation number σ and corresponding measuring points for both hydrofoils was not the same.
3.3. Cavitation Image Analysis
Illuminated cavitation structures on the hydrofoils were recorded in a set of black and white images using the experimental setup from
Section 3.2. The cavitation structures in the image have elevated grey level intensities, with vapor phase forming time and 2D space-dependent structures [
22,
27]. With computer-aided visualization of the process, the simultaneous time series of images were recorded. An assumption was made that the intensity of the illumination is proportional to the amount and intensity of the void fraction, being further proportional to the intensity of the cavitation structures in the observed regions [
23]. This assumption is credible for cavitation intensity, low void fractions, and corresponding ratios of the intensity of the void fraction and grey level.
The time series of images from high-speed visualization in the cavitation tunnel were analyzed such that individual traveling bubbles were first filtered out. All bright objects in the individual image were deleted whenever they were very small. All other objects, like the attached cavitation or cavitation clouds, were retained. From these filtered images, the average grey level Eg (i,j,t) and standard deviation were calculated as explained below.
The grey level variable E
g (i,j,t) was acquired by processing intervals of 256 grey levels (8-bit camera image depth) from black (intensity = 0) to white (intensity = 255). The averaged grey level series were calculated in observation region. The standard deviation was estimated using the equation below:
Here 〈E
g (i,j)〉 is time and spatially averaged grey level, which is proportional to the average void fraction of the cavitation structure’s.
The time interval t in Equations (7) and (8) is set from the duration and frequency of acquisition.
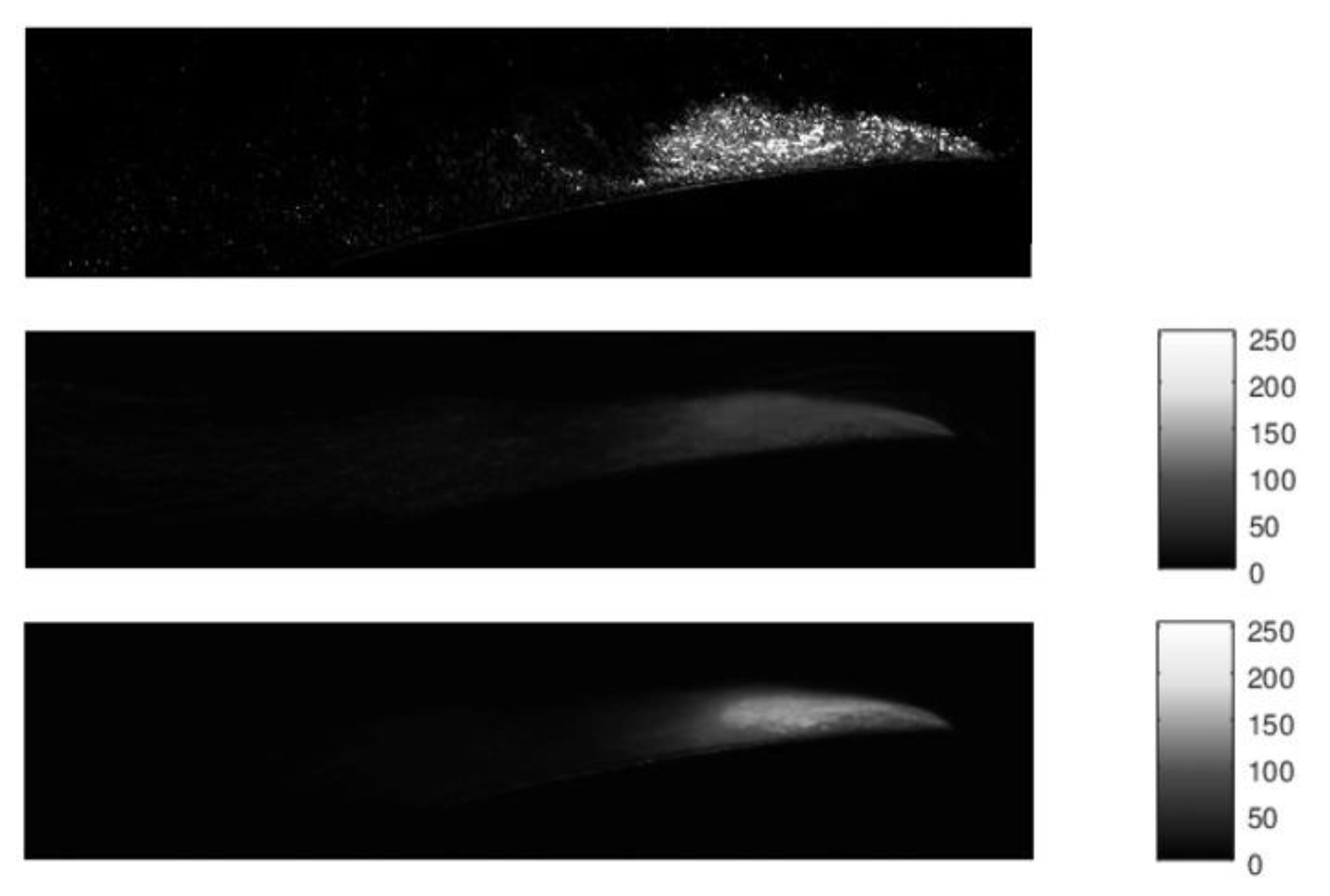
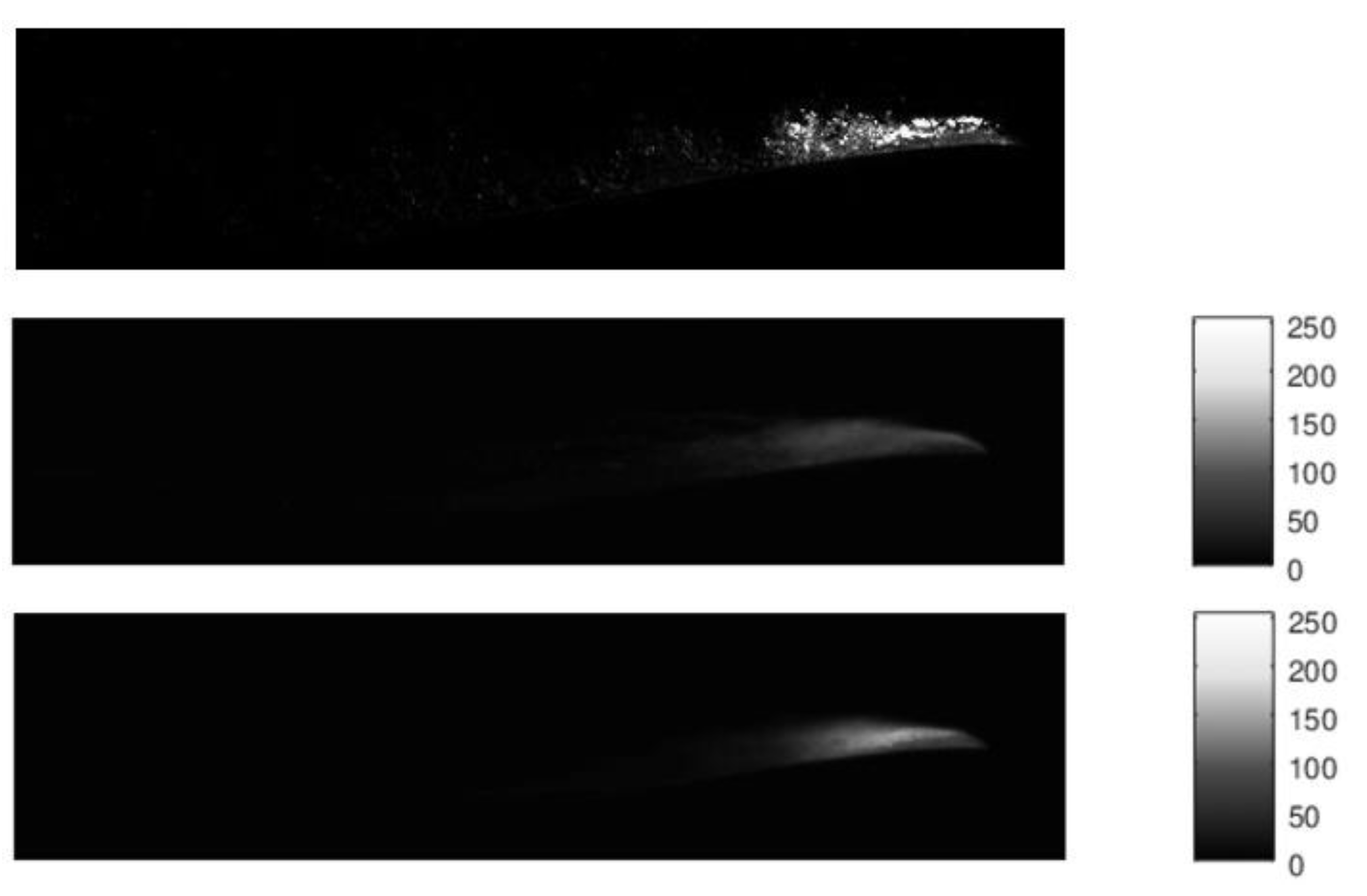
A sample of image analysis is shown in
Figure 8 for the existing hydrofoil (p = 0.15 bar; Q = 61.7 m
3/h; σ = 2.27) and in
Figure 9 for the modified hydrofoil (p = 0.15 bar; Q = 61.7 m
3/h; σ = 2.27). Cavitation length for the selected operating points was estimated to L = 22.74 mm for existing hydrofoil and L = 11.27 mm for modified hydrofoil. Such a method of estimating cavitation length was used for all operating points for both hydrofoils and later for regression cavitation length modelling.
3.4. Regression Cavitation Length Model
Cavitation properties are a consequence of flow parameters, which are best described using Reynolds number Re and cavitation number σ. We will show that cavitation length on a hydrofoil in a cavitation tunnel may be well predicted based on these two dimensionless numbers. A good correlation is expected between the measured and calculated cavitation lengths. For this, we will use the following power-law regression model for cavitation length L
Model parameters β0, β1, and β2 were calculated using the minimum mean square error method.
5. Conclusions
In future power grids, waterpower flexibility will be an important parameter for ensuring network stability. Water turbines will need to operate at wide flow intervals and in transient regimes, and also allow for fast response times. For this reason, among others, further research on cavitation is required.
The goal of this research was to demonstrate the relation between the hydrofoil shape and cavitation phenomena. Existing and modified hydrofoils were extracted from runner blades on the 95% runner blade radius and modified. The modifications were made on the hydrofoil’s leading edge, as well as at the points of maximum thickness and curvature. The leading-edge radius was enlarged to avoid flow separation. Maximum thickness and curvature were moved in the direction of the leading edge to stabilize the flow around the hydrofoil towards the trailing edge. Both hydrofoils were implemented in a bulb turbine and measured under equal energy numbers. Measurements of both turbine runners were performed on the measuring station according to the standard for acceptance tests of water turbines.
The results of this study show improved cavitation characteristics. However, we show here only a single modification of the hydrofoil and the results only demonstrate the efficiency of this modification. Of particular benefit for future design would be a comprehensive study, providing for a hydrofoil and runner shape optimization algorithm, based on selection and later minimization of the objective functions, including the manufacture and measurements of a selection of hydrofoils and runners.
To evaluate the cavitation properties, the flow was visualized in the cavitation tunnel on the suction side. The modified hydrofoil exhibited improved cavitation properties and we chose to evaluate the intensity of the cavitation using the cavitation cloud length. A regression model prediction of the cavitation length shows that modified hydrofoil features improved cavitation characteristics in comparison with the existing hydrofoil.
The primary goal of this study was to provide for improved cavitation characteristics on the modified hydrofoil. Using the modified hydrofoil invariably changes runner characteristics and this resulted in operating points shifting to the left in the hill diagram. This leftward shift resulted in increased efficiency as shown in [
6].
We believe that future requirements for water turbines will emphasize flexibility. For this reason, the future research on cavitation in water turbines will focus on the minimization of cavitation occurrence and erosion, while at the same time providing adequate energy output and efficiency.