Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps
Abstract
1. Introduction
2. Methods and Materials
2.1. DFT+U
2.2. Materials
3. Technical Details
4. Results and Discussion
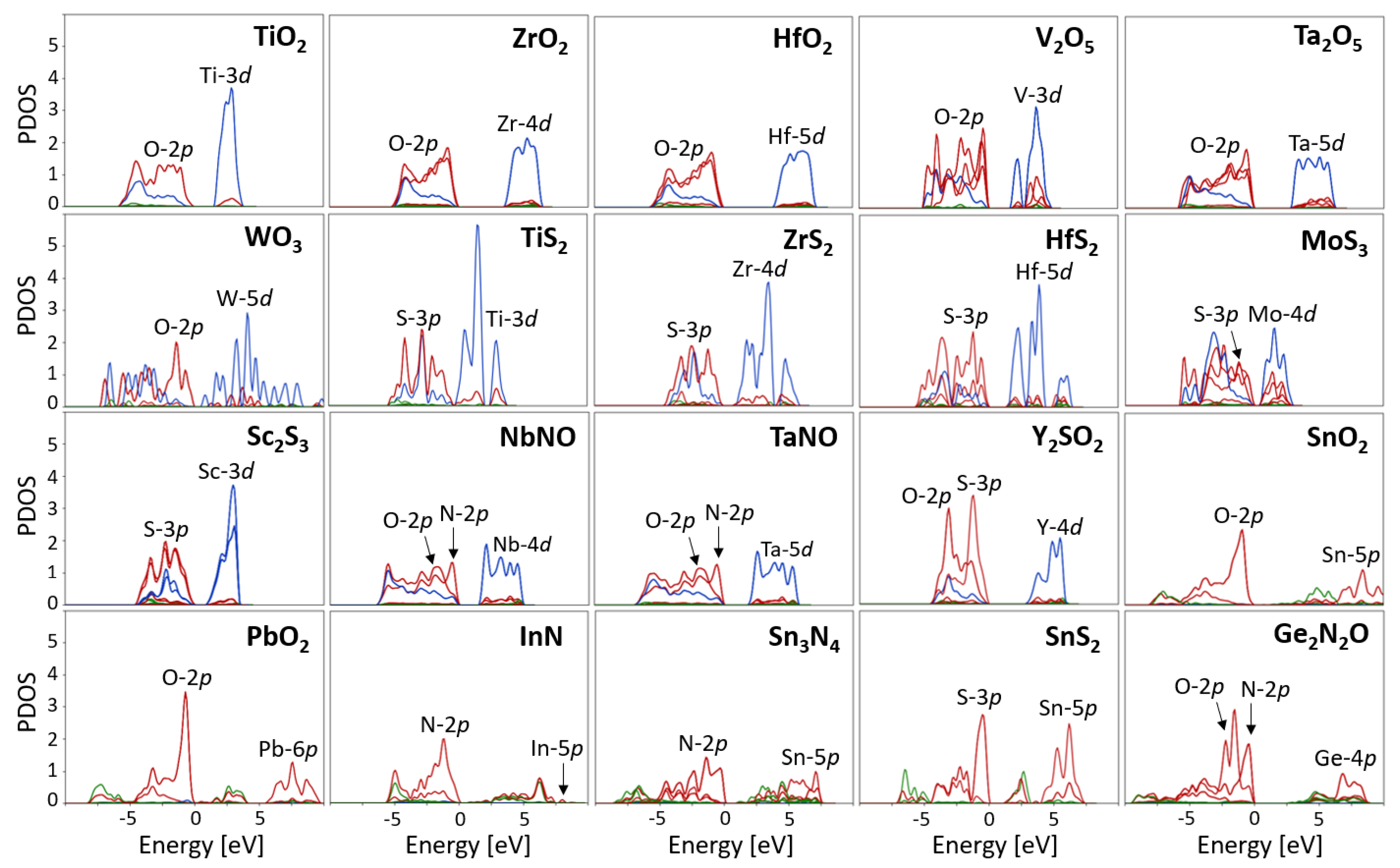
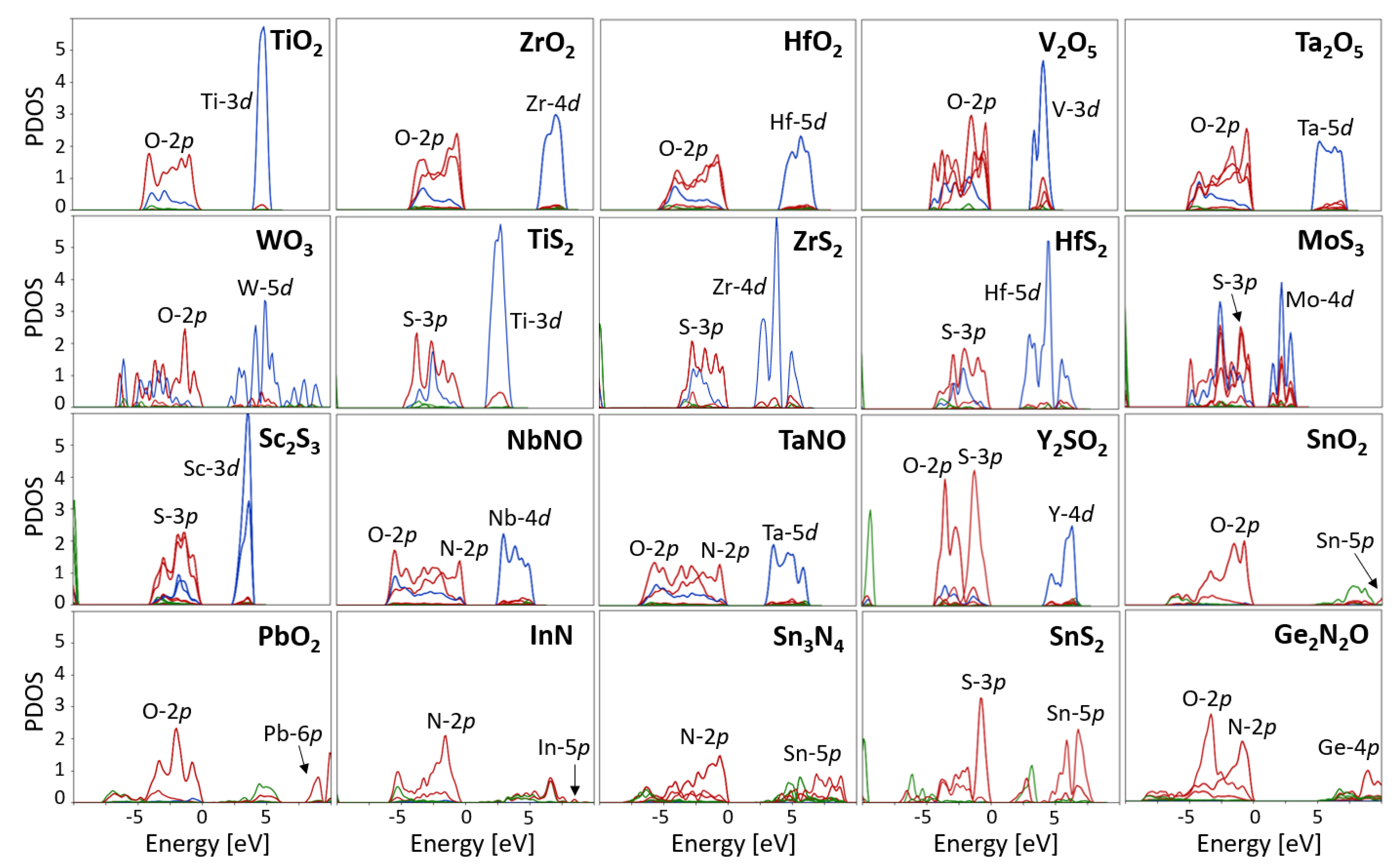
4.1. Determination of the States Requiring Hubbard Corrections
4.2. Hubbard U Parameters from First Principles
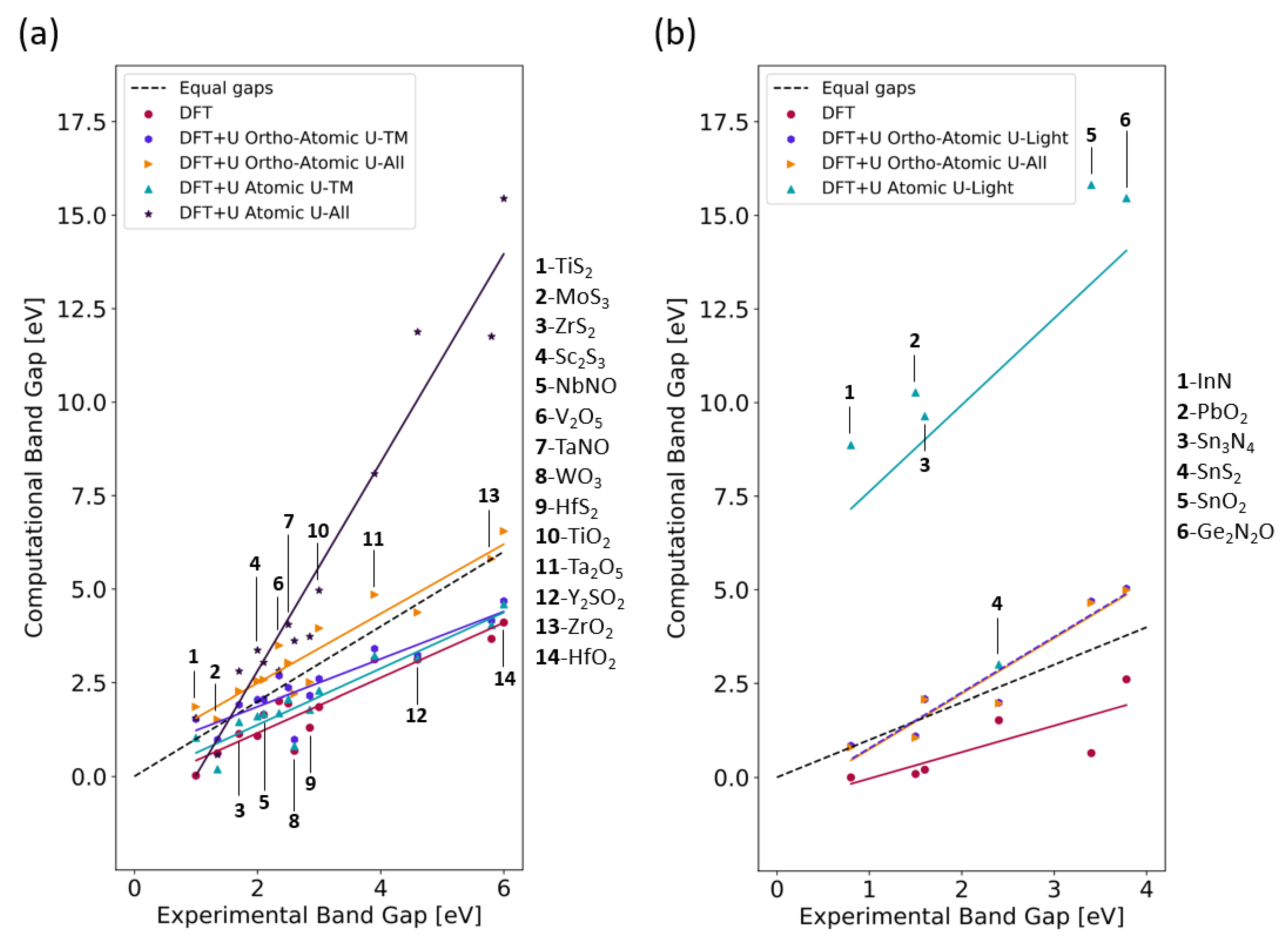
4.3. Band Gaps from DFT+U Calculations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Convergence Tests for the Self-Consistent Calculation of Hubbard Parameters
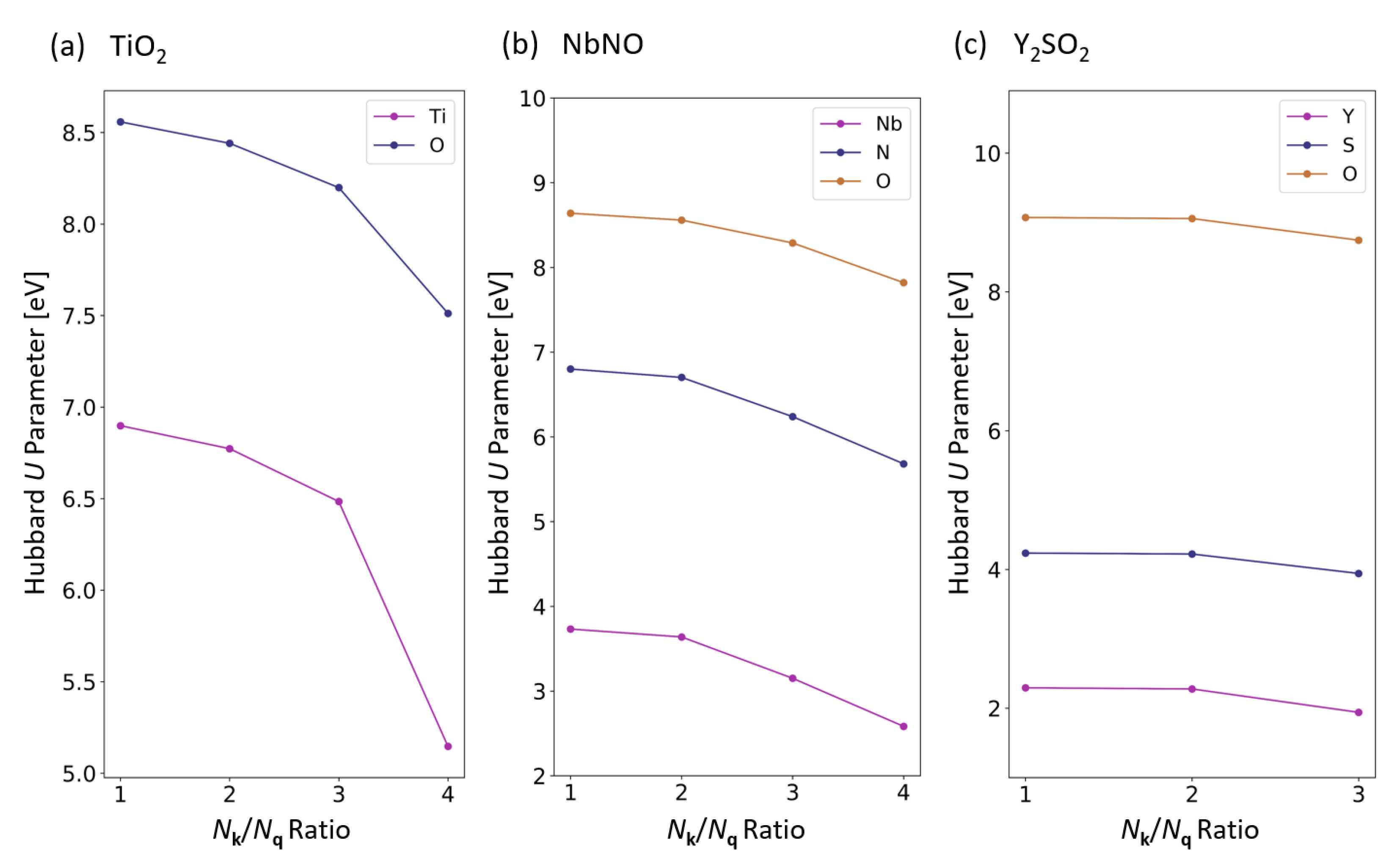

| Formula | k-Point | Ratio | |||
|---|---|---|---|---|---|
| Mesh | 1 | 2 | 3 | 4 | |
| TiO | |||||
| NbNO | |||||
| YSO | |||||
Appendix B. Computational Cost Comparison of HSE06 and Hubbard Parameter Calculations
| Formula | No. of Atoms | k-Points | U Calculation | HSE06 Calculation | Ratio | |||
|---|---|---|---|---|---|---|---|---|
| per Unit Cell | Mesh | q-Points | q-Points | |||||
| TiO | 6 | 3 h 46 m | 3.30 | 10 h 1 m | 2.7 | |||
| NbNO | 12 | 7 h 35 m | 2.68 | 61 h 52 m | 8.2 | |||
References and Notes
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Perdew, J.; Levy, M. Physical content of the exact Kohn-Sham orbital energies: Band gaps and derivative discontinuities. Phys. Rev. Lett. 1983, 51, 1884–1887. [Google Scholar] [CrossRef]
- Perdew, J.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Cohen, A.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of Density Functional Theory. Science 2008, 321, 792. [Google Scholar] [CrossRef]
- De P.R. Moreira, I.; Illas, F.; Martin, R. Effect of Fock exchange on the electronic structure and magnetic coupling in NiO. Phys. Rev. B 2002, 65, 155102. [Google Scholar]
- Corà, F.; Alfredsson, M.; Mallia, G.; Middlemiss, D.; Mackrodt, W.; Dovesi, R.; Orlando, R. The performance of hybrid density functionals in solid state chemistry. Struct. Bonding 2004, 113, 171. [Google Scholar]
- Feng, X.B.; Harrison, N. Metal-insulator and magnetic transition of NiO at high pressures. Phys. Rev. B 2004, 69, 035114. [Google Scholar] [CrossRef]
- Alfredsson, M.; Price, G.; Catlow, C.; Parker, S.; Orlando, R.; Brodholt, J. Electronic structure of the antiferromagnetic B1-structured FeO. Phys. Rev. B 2004, 70, 165111. [Google Scholar] [CrossRef]
- Chevrier, V.; Ong, S.; Armiento, R.; Chan, M.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B 2010, 82, 075122. [Google Scholar] [CrossRef]
- Seo, D.H.; Urban, A.; Ceder, G. Calibrating transition-metal energy levels and oxygen bands in first-principles calculations: Accurate prediction of redox potentials and charge transfer in lithium transition-metal oxides. Phys. Rev. B 2015, 92, 115118. [Google Scholar] [CrossRef]
- Tolba, S.; Gameel, K.; Ali, B.; Almossalami, H.; Allam, N. Density Functional Calculations-Recent Progresses of Theory and Application; IntechOpen: London, UK, 2018. [Google Scholar]
- Skone, J.; Govoni, M.; Galli, G. Self-consistent hybrid functional for condensed systems. Phys. Rev. B 2014, 89, 195112. [Google Scholar] [CrossRef]
- Skone, J.; Govoni, M.; Galli, G. Nonempirical range-separated hybrid functionals for solids and molecules. Phys. Rev. B 2016, 93, 235106. [Google Scholar] [CrossRef]
- Bischoff, T.; Wiktor, J.; Chen, W.; Pasquarello, A. Nonempirical hybrid functionals for band gaps of inorganic metal-halide perovskites. Phys. Rev. Mater. 2019, 3, 123802. [Google Scholar] [CrossRef]
- Kronik, L.; Stein, T.; Refaely-Abramson, S.; Baer, R. Excitation gaps of finite-sized systems from optimally tuned range-separated hybrid functionals. J. Chem. Theory Comput. 2012, 8, 1515–1531. [Google Scholar] [CrossRef] [PubMed]
- Wing, D.; Ohad, G.; Haber, J.; Filip, M.; Gant, S.; Neaton, J.; Kronik, L. Band gaps of crystalline solids from Wannier-localization based optimal tuning of a screened range-separated hybrid functional. arXiv 2020, arXiv:2012.03278. [Google Scholar]
- Lorke, M.; Deák, P.; Frauenheim, T. Koopmans-compliant screened exchange potential with correct asymptotic behavior for semiconductors. Phys. Rev. B 2020, 102, 235168. [Google Scholar] [CrossRef]
- Perdew, J.; Kurth, S.; Zupan, A.; Blaha, P. Accurate Density Functional with Correct Formal Properties: A Step Beyond the Generalized Gradient Approximation. Rev. Phys. Lett. 1999, 82, 2544. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Kitchaev, D.; Peng, H.; Liu, Y.; Sun, J.; Perdew, J.; Ceder, G. Energetics of MnO2 polymorphs in density functional theory. Phys. Rev. B 2016, 93, 045132. [Google Scholar] [CrossRef]
- Hinuma, Y.; Hayashi, H.; Kumagai, Y.; Tanaka, I.; Oba, F. Comparison of approximations in density functional theory calculations: Energetics and structure of binary oxides. Phys. Rev. B 2017, 96, 094102. [Google Scholar] [CrossRef]
- Ekholm, M.; Gambino, D.; Jönsson, H.; Tasnádi, F.; Alling, B.; Abrikosov, I. Assessing the SCAN functional for itinerant electron ferromagnets. Phys. Rev. B 2018, 98, 094413. [Google Scholar] [CrossRef]
- Tran, F.; Baudesson, G.; Carrete, J.; Madsen, G.; Blaha, P.; Schwarz, K.; Singh, D. Shortcomings of meta-GGA functionals when describing magnetism. Phys. Rev. B 2020, 102, 024407. [Google Scholar] [CrossRef]
- Dabo, I.; Ferretti, A.; Poilvert, N.; Li, Y.; Marzari, N.; Cococcioni, M. Koopmans’ condition for density-functional theory. Phys. Rev. B 2010, 82, 115121. [Google Scholar] [CrossRef]
- Ferretti, A.; Dabo, I.; Cococcioni, M.; Marzari, N. Bridging density-functional and many-body perturbation theory: Orbital-density dependence in electronic-structure functionals. Phys. Rev. B 2014, 89, 195134. [Google Scholar] [CrossRef]
- Borghi, G.; Ferretti, A.; Nguyen, N.; Dabo, I.; Marzari, N. Koopmans-compliant functionals and their performance against reference molecular data. Phys. Rev. B 2014, 90, 075135. [Google Scholar] [CrossRef]
- Nguyen, N.; Colonna, N.; Ferretti, A.; Marzari, N. Koopmans-compliant spectral functionals for extended systems. Phys. Rev. X 2018, 8, 021051. [Google Scholar] [CrossRef]
- Colonna, N.; Nguyen, N.; Ferretti, A.; Marzari, N. Koopmans-Compliant Functionals and Potentials and Their Application to the GW100 Test Set. J. Chem. Theory Comput. 2019, 15, 1905. [Google Scholar] [CrossRef]
- Colonna, N. Paul Scherrer Institute, Villigen, Switzerland; Marzari, N., Ed.; École Polytechnique Fédérale de Lausanne: Lausanne, Switzerland, Private communication; 2021. [Google Scholar]
- Anisimov, V.; Zaanen, J.; Andersen, O. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.; Aryasetiawan, F.; Liechtenstein, A. First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+U method. J. Phys. Condens. Matter 1997, 9, 767. [Google Scholar] [CrossRef]
- Dudarev, S.; Botton, G.; Savrasov, S.; Humphreys, C.; Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Campo, V.L., Jr.; Cococcioni, M. Extended DFT+U+V method with on-site and inter-site electronic interactions. J. Phys. Condens Matter 2010, 22, 055602. [Google Scholar]
- Ricca, C.; Timrov, I.; Cococcioni, M.; Marzari, N.; Aschauer, U. Self-consistent DFT+U+V study of oxygen vacancies in SrTiO3. Phys. Rev. Res. 2020, 2, 023313. [Google Scholar] [CrossRef]
- Timrov, I.; Agrawal, P.; Zhang, X.; Erat, S.; Liu, R.; Braun, A.; Cococcioni, M.; Calandra, M.; Marzari, N.; Passerone, D. Electronic structure of Ni-substituted LaFeO3 from near edge X-ray absorption fine structure experiments and first-principles simulations. Phys. Rev. Res. 2020, 2, 033265. [Google Scholar] [CrossRef]
- Timrov, I.; Marzari, N.; Cococcioni, M. Self-consistent Hubbard parameters from density-functional perturbation theory in the ultrasoft and projector-augmented wave formulations. Phys. Rev. B 2021, 103, 045141. [Google Scholar] [CrossRef]
- Cococcioni, M.; Marzari, N. Energetics and cathode voltages of LiMPO4 olivines (M = Fe, Mn) from extended Hubbard functionals. Phys. Rev. Mater. 2019, 3, 033801. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Rubio, A. Parameter-free hybridlike functional based on an extended Hubbard model: DFT+U+V. Phys. Rev. B 2020, 102, 155117. [Google Scholar] [CrossRef]
- Lee, S.H.; Son, Y.W. First-principles approach with a pseudohybrid density functional for extended Hubbard interactions. Phys. Rev. Res. 2020, 2, 043410. [Google Scholar] [CrossRef]
- Grüning, M.; Marini, A.; Rubio, A. Density functionals from many-body perturbation theory: The band gap for semiconductors and insulators. J. Chem. Phys. 2006, 124, 154108. [Google Scholar] [CrossRef] [PubMed]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 1965, 139, A796. [Google Scholar] [CrossRef]
- Caruso, F.; Rinke, P.; Ren, X.; Scheffler, M.; Rubio, A. Unified description of ground and excited states of finite systems: The self-consistent GW approach. Phys. Rev. B 2012, 86, 081102. [Google Scholar] [CrossRef]
- Ren, X.; Marom, N.; Caruso, F.; Scheffler, M.; Rinke, P. Beyond the GW approximation: A second-order screened exchange correction. Phys. Rev. B 2015, 92, 081104. [Google Scholar] [CrossRef]
- Caruso, F.; Dauth, M.; van Setten, M.; Rinke, P. Benchmark of GW approaches for the GW100 test set. J. Chem. Theory Comput. 2016, 12, 5076–5087. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G. Hubbard model in infinite dimensions. Phys. Rev. B 1992, 45, 6479. [Google Scholar] [CrossRef] [PubMed]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Anisimov, V.; Poteryaev, A.; Korotin, M.; Anokhin, A.; Kotliar, G. First-principles calculations of the electronic structure and spectra of strongly correlated systems: Dynamical mean-field theory. J. Phys. Condens. Matter 1997, 9, 7359. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Katsnelson, M. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 1998, 57, 6884. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.; Haule, K.; Oudovenko, V.; Porcollet, O.; Marianetti, C. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865. [Google Scholar] [CrossRef]
- Perdew, J.; Yang, W.; Burke, K.; Yang, Z.; Gross, E.; Scheffler, M.; Scuseria, G.; Henderson, T.; Zhang, I.; Ruzsinszky, A.; et al. Understanding band gaps of solids in generalized Kohn-Sham Theory. Proc. Natl. Acad. Sci. USA 2017, 114, 2801–2806. [Google Scholar] [CrossRef] [PubMed]
- Gaspari, R.; Labat, F.; Manna, L.; Adamo, C.; Cavalli, A. Semiconducting and optical properties of selected binary compounds by linear response DFT+U and hybrid functional methods. Theor. Chem. Acc. 2016, 135, 73. [Google Scholar] [CrossRef]
- Ozkilinc, O.; Kayi, H. Effect of chalcogen atoms on the electronic band gaps of donor-acceptor-donor type semiconducting polymers: A systematic DFT investigation. J. Mol. Modeling 2019, 25, 167. [Google Scholar] [CrossRef] [PubMed]
- Paudel, T.; Lambrecht, W. First-principles calculation of the O vacancy in ZnO: A self-consistent gap-corrected approach. Phys. Rev. B 2008, 77, 205202. [Google Scholar] [CrossRef]
- Lalitha, S.; Karazhanov, S.; Ravindran, P.; Senthilarasu, S.; Sathyamoorthy, R.; Janabergenov, J. Electronic structure, structural and optical properties of thermally evaporated CdTe thin films. Phys. B 2007, 387, 227–238. [Google Scholar] [CrossRef]
- Gautam, G.; Carter, E. Evaluating transistion metal oxides within DFT-SCAN and SCAN+U frameworks for solar thermochemical applications. Phys. Rev. Mater. 2018, 2, 095401. [Google Scholar] [CrossRef]
- Long, O.; Gautam, G.; Carter, E. Evaluating optimal U for 3d transition-metal oxides within the SCAN+U framework. Phys. Rev. Mater. 2020, 4, 045401. [Google Scholar] [CrossRef]
- Dederichs, P.; Blügel, S.; Zeller, R.; Akai, H. Ground states of condensed systems: Application to cerium impurities. Phys. Rev. Lett. 1984, 53, 2512. [Google Scholar] [CrossRef]
- McMahan, A.; Martin, R.; Satpathy, S. Calculated Hamiltonian for La2CuO4 and solution in the impurity Anderson approximation. Phys. Rev. B 1988, 38, 6650. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Andersen, O.; Jepsen, O.; Zaanen, J. Density-functional calculation of the parameters in the Anderson model: Application to Mn in CdTe. Phys. Rev. B 1989, 39, 1708. [Google Scholar] [CrossRef] [PubMed]
- Hybertsen, M.; Schlüter, M.; Christensen, N. Calculation of Coulomb-interaction parameters for La2CuO4 using a constrained-density-functional approach. Phys. Rev. B 1989, 39, 9028. [Google Scholar] [CrossRef] [PubMed]
- Gunnarsson, O. Calculations of parameters in model Hamiltonians. Phys. Rev. B 1990, 41, 514. [Google Scholar] [CrossRef]
- Pickett, W.; Erwin, S.; Ethridge, E. Reformation of the LDA+U method for a local-orbital basis. Phys. Rev. B 1998, 58, 1201. [Google Scholar] [CrossRef]
- Solovyev, I.; Imada, M. Screening of Coulomb interactions in transition metals. Phys. Rev. B 2005, 71, 045103. [Google Scholar] [CrossRef]
- Nakamura, K.; Arita, R.; Yoshimoto, Y.; Tsuneyuki, S. First-principles calculation of effective onsite Coulomb interactions of 3d transition metals: Constrained local density functional approach with maximally localized Wannier functions. Phys. Rev. B 2006, 74, 235113. [Google Scholar] [CrossRef]
- Shishkin, M.; Sato, H. Self-consistent parametrization of DFT+U framework using linear response approach: Application to evaluation of redox potentials of battery cathodes. Phys. Rev. B 2016, 93, 085135. [Google Scholar] [CrossRef]
- Springer, M.; Aryasetiawan, F. Frequency-dependent screened interaction in Ni within the random-phase approximation. Phys. Rev. B 1998, 57, 4364. [Google Scholar] [CrossRef]
- Kotani, T. Ab initio random-phase-approximation calculation of the frequency-dependent effective interaction between 3d electrons: Ni, Fe, and MnO. J. Phys. Condens. Matter 2000, 12, 2413. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Imada, M.; Georges, A.; Kotliar, G.; Biermann, S.; Lichtenstein, A. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 2004, 70, 195104. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Karlsson, K.; Jepsen, O.; Scönberger, U. Calculations of Hubbard U from first-principles. Phys. Rev. B 2006, 74, 125106. [Google Scholar] [CrossRef]
- Sasioglu, E.; Friedrich, C.; Blügel, S. Effective Coulomb interaction in transition metals from constrained random-phase approximation. Phys. Rev. B 2011, 83, 121101(R). [Google Scholar] [CrossRef]
- Vaugier, L.; Jiang, H.; Biermann, S. Hubbard U and Hund exchange J in transition metal oxides: Screening versus localization trends from constrained random phase approximation. Phys. Rev. B 2012, 86, 165105. [Google Scholar] [CrossRef]
- Amadon, B.; Applencourt, T.; Bruneval, F. Screened Coulomb interaction calculations: cRPA implementation and applications to dynamical screening and self-consistency in uranium dioxide and cerium. Phys. Rev. B 2014, 89, 125110. [Google Scholar] [CrossRef]
- Mosey, N.; Carter, E. Abinitio evaluation of Coulomb and exchange parameters for DFT+U calculations. Phys. Rev. B 2007, 76, 155123. [Google Scholar] [CrossRef]
- Mosey, N.; Liao, P.; Carter, E. Rotationally invariant ab initio evaluation of Coulomb and exchange parameters for DFT+U calculations. J. Chem. Phys. 2008, 129, 014103. [Google Scholar] [CrossRef] [PubMed]
- Andriotis, A.; Sheetz, R.; Menon, M. LSDA+U method: A calculation of the U values at the Hartree-Fock level of approximation. Phys. Rev. B 2010, 81, 245103. [Google Scholar] [CrossRef]
- Agapito, L.; Curtarolo, S.; Buongiorno Nardelli, M. Reformation of DFT+U as a pseudohybird density functional for accelerated materials discovery. Phys. Rev. X 2015, 5, 011006. [Google Scholar]
- Timrov, I.; Marzari, N.; Cococcioni, M. Hubbard parameters from density-functional perturbation theory. Phys. Rev. B 2018, 98, 085127. [Google Scholar] [CrossRef]
- Tablero, C. Representations of the occupation number matrix on the LDA/GGA+U method. J. Phys. Condens. Matter 2008, 20, 325205. [Google Scholar] [CrossRef]
- Amadon, B.; Jollet, F.; Torrent, M. γ and β cerium: LDA+U calculations of ground-state parameters. Phys. Rev. B 2008, 77, 155104. [Google Scholar] [CrossRef]
- Ricca, C.; Timrov, I.; Cococcioni, M.; Marzari, N.; Aschauer, U. Self-consistent site-dependent DFT+U study of stoichiometric and defective SrMnO3. Phys. Rev. B 2019, 99, 094102. [Google Scholar] [CrossRef]
- Floris, A.; Timrov, I.; Himmetoglu, B.; Marzari, N.; de Gironcoli, S.; Cococcioni, M. Hubbard-corrected density functional perturbation theory with ultrasoft pseudopotentials. Phys. Rev. B 2020, 101, 064305. [Google Scholar] [CrossRef]
- Timrov, I.; Aquilante, F.; Binci, L.; Cococcioni, M.; Marzari, N. Pulay forces in density-functional theory with extended Hubbard functionals: From nonorthogonalized to orthogonalized manifolds. Phys. Rev. B 2020, 102, 235159. [Google Scholar] [CrossRef]
- O’Regan, D.; Hine, N.; Payne, M.; Mostofi, A. Projector self-consistent DFT+U using nonorthogonal generalized Wannier functions. Phys. Rev. B 2010, 82, 081102(R). [Google Scholar] [CrossRef]
- Korotin, D.; Kukolev, V.; Kozhevnikov, A.; Novoselov, D.; Anisimov, V. Electronic correlations and crystal structure distortions in BaBiO3. J. Phys. Condens. Matter 2012, 24, 415603. [Google Scholar] [CrossRef]
- Shick, A.B.; Liechtenstein, A.I.; Pickett, W.E. Implementation of the LDA+U method using the full-potential linearized augmented plane-wave basis. Phys. Rev. B 1999, 60, 10763. [Google Scholar] [CrossRef]
- Bengone, O.; Alouani, M.; Blöchl, P.; Hugel, J. Implementation of the projector augmented-wave LDA+U method: Application to the electronic structure of NiO. Phys. Rev. B 2000, 62, 16392. [Google Scholar] [CrossRef]
- Rohrbach, A.; Hafner, J.; Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys. Condens. Matter 2003, 15, 979. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, Z.H.; Jiang, H. The local projection in the density functional theory plus U approach: A critical assessment. J. Chem. Phys. 2016, 144, 144106. [Google Scholar] [CrossRef] [PubMed]
- Kulik, H.; Cococcioni, M.; Scherlis, D.; Marzari, N. Density Functional Theory in transition-metal chemistry: A self-consistent Hubbard U approach. Phys. Rev. Lett. 2006, 97, 103001. [Google Scholar] [CrossRef]
- Kulik, H.; Marzari, N. A self-consistent Hubbard U density-functional theory approach to the addition-elimination reactions of hydrocarbons on bare FeO+. J. Chem. Phys. 2008, 129, 134314. [Google Scholar] [CrossRef]
- Yu, M.; Yang, S.; Wu, C.; Marom, N. Machine learning the Hubbard U parameter in DFT+U using Bayesian optimization. NPJ Comp. Mat. 2020, 6, 180. [Google Scholar] [CrossRef]
- Kulik, H.; Marzari, N. Systematic study of first-row transition-metal diatomic molecules: A self-consistent DFT+U approach. J. Chem. Phys. 2010, 133, 114103. [Google Scholar] [CrossRef]
- Löwdin, P.O. On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals. J. Chem. Phys. 1950, 18, 365. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.; Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 2006, 124, 219906. [Google Scholar] [CrossRef]
- Xiong, Y.; Campbell, Q.; Fanghanel, J.; Badding, C.; Wang, H.; Kirchner-Hall, N.; Theibault, M.; Timrov, I.; Mondschein, J.; Seth, K.; et al. Optimizing accuracy and efficacy in data-driven materials discovery for the solar production of hydrogen. arXiv 2021, arXiv:2102.01154. [Google Scholar]
- Wu, Y.; Lazic, P.; Hautier, G.; Persson, K.; Ceder, G. First principles high throughput screening of oxynitrides for water-splitting photocatalysts. Energy Environ. Sci. 2012, 6, 157. [Google Scholar] [CrossRef]
- Huo, Z.; Wei, S.; Yin, W. High-throughput screening of chalcogenide single perovskites by first-principles calculations for photovoltaics. J. Phys. D Appl. Phys. 2018, 51, 474003. [Google Scholar] [CrossRef]
- Kar, M.; Körzdörfer, T. Computational high throughput screening of inorganic cation based halide perovskites for perovskite only tandem solar cells. Mater. Res. Express 2020, 7, 055502. [Google Scholar] [CrossRef]
- Varley, J.; Miglio, A.; Ha, V.; van Setten, M.; Rignanese, G.; Hautier, G. High-throughput design of non-oxide p-type transparent conducting materials: Data mining, search strategy, and identification of boron phosphide. Chem. Mater. 2017, 29, 2568–2573. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.; Hautier, G.; Chen, W.; Richards, W.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Garrity, K.; Bennett, J.; Rabe, K.; Vanderbilt, D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446. [Google Scholar] [CrossRef]
- We used pseudopotentials from the GBRV library of the form: X_pbe_v1.uspp.F.UPF, where X is the atomic symbol.
- Marzari, N.; Vanderbilt, D.; De Vita, A.; Payne, M. Thermal contraction and disordering of the Al(110) surface. Phys. Rev. Lett. 1999, 82, 3296. [Google Scholar] [CrossRef]
- Dhoundiyal, H.; Das, P.; Bhatnagar, M. Electrical and magnetic properties of V2O5 microstructure formed by self-assembled nanorods. Phys. B Condens. Matter 2021, 603, 412622. [Google Scholar] [CrossRef]
- Mehraj, S.; Ansari, M.S. Annealed SnO2 thin films: Structural, electrical and their magnetic properties. Thin Solid Films 2015, 589, 57–65. [Google Scholar] [CrossRef]
- Joseph, A.; Anjitha, C.; Aravind, A.; Aneesh, P. Structural, optical and magnetic properties of SnS2 nanoparticles and photo response of p-Si/n-SnS2 heterojunction diode. Appl. Surface Sci. 2020, 528, 146977. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039. [Google Scholar] [CrossRef]
- We note that in this case we decided to apply the Hubbard U correction only to p states and not to s states of the group III-IV elements at the CBM. The reason is that the current implementation of the DFT+U approach that we use does not support multi-channel Hubbard corrections for the same element. In any case, since s states are very delocalized, we do not expect that the U correction for these states will be very important; however, this assumption requires verification.
- Yu, K.; Carter, E. Communication: Comparing ab initio methods of obtaining effective U parameters for closed-shell materials. J. Chem. Phys. 2014, 140, 121105. [Google Scholar] [CrossRef] [PubMed]
- Bennett, J.; Hudson, B.; Metz, I.; Liang, D.; Spurgeon, S.; Cui, Q.; Mason, S. A systematic determination of hubbard U using the GBRV ultrasoft pseudopotential set. Comput. Mater. Sci. 2019, 170, 109137. [Google Scholar] [CrossRef]
- Mo, S.; Ching, W. Electronic and optical properties of three phases of titanium dioxide: Rutile, anatase, and brookite. Phys. Rev. B 1995, 51, 13023. [Google Scholar] [CrossRef]
- Robertson, J. Band offsets of wide-band-gap oxides and implications for future electronic devices. J. Vac. Sci. Tech. B 2000, 18, 1785. [Google Scholar] [CrossRef]
- Xiong, K.; Robertson, J. Point defects in HfO2 high K gate oxide. Microelectron. Eng. 2005, 80, 408–411. [Google Scholar] [CrossRef]
- Hieu, N.V.; Lichtman, D. Bandgap radiation induced photodesorption from V2O5 powder and vanadium oxide surfaces. J. Vac. Sci. Technol. 1981, 18, 49–53. [Google Scholar] [CrossRef]
- Chun, W.; Ishikawa, A. Conduction and valence band positions of Ta2O5, TaON, and Ta3N5 by UPS and electrochemical methods. J. Phys. Chem. 2003, 107, 1798–1803. [Google Scholar] [CrossRef]
- Granqvist, C. Electrochromic tungsten oxide films: Review of progress 1993-1998. Solar Energy Mat. Solar Cells 2000, 60, 201–262. [Google Scholar] [CrossRef]
- Fang, C.; de Groot, R.; Haas, C. Bulk and surface electronic stucture of 1T-TiS2 and 1T-TiSe2. Phys. Rev. B 1997, 56, 4455. [Google Scholar] [CrossRef]
- Moustafa, M.; Zandt, T.; Janowitz, C.; Manzke, R. Growth and band gap determination of the ZrSxSe2-x single crystal series. Phys. Rev. B 2009, 80, 035206. [Google Scholar] [CrossRef]
- Traving, M.; Seydel, T.; Kipp, L.; Skibowski, M.; Starrost, F.; Krasovskii, E.; Perlov, A.; Schattke, W. Combined photoemission and inverse photoemission study of HfS2. Phys. Rev. B 2001, 63, 035107. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Lee, C.; Pollak, F.; Schleich, D. Optical study of amorphous MoS3: Determination of the fundamental energy gap. J. Non-Crystalline Solids 1987, 91, 235–242. [Google Scholar] [CrossRef]
- Dismukes, J.; White, J. The preparation, properties, and crystal structures of some scandium sulfides in the range Sc2S3-ScS. Inorg. Chem. 1964, 3, 1220–1228. [Google Scholar] [CrossRef]
- Tamura, S.; Ueno, K.; Hato, K. Niobium oxynitride prepared by thermal NH3 nitridation as a photoanode materials for solar water splitting. Mater. Res. Bull. 2019, 112, 221–225. [Google Scholar] [CrossRef]
- Mikami, M.; Nakamura, S.; Itoh, M.; Nakajima, K.; Shishido, T. Lattice dynamics and optical properties of yttrium oxysulfide. J. Lumin. 2003, 102-103, 7–12. [Google Scholar] [CrossRef]
- Park, Y.; Kim, K. Sputtering growth and optical properties of [100]-oriented tetragonal SnO2 and its Mn alloy films. J. Appl. Phys. 2003, 94, 6401. [Google Scholar] [CrossRef]
- Ma, F.; Jiao, Y.; Gao, G.; Gu, Y.; Bilic, A.; Sanvito, S. Substantial band-gap tuning and a strain-controlled semiconductor to gapless/band-inverted semimetal transition in rutile lead/stannic dioxide. ACS Appl. Mater. Intefaces 2016, 39, 25667–25673. [Google Scholar] [CrossRef]
- Nanishi, Y.; Saito, Y.; Yamaguchi, T. RF-molecular beam epitaxy growth and properties of InN and related alloys. Jpn. J. Appl. Phys. 2003, 42, 2549. [Google Scholar] [CrossRef]
- Boyko, T.; Hunt, A.; Zerr, A.; Moewes, A. Electronic structure of spinel-type nitride compounds Si3N4, Ge3N4, and Sn3N4 with tunable band gaps: Application to light emitting diodes. Phys. Rev. Lett. 2013, 111, 097402. [Google Scholar] [CrossRef]
- Ray, S.; Karanjai, M.; DasGupta, D. Structure and photoconductive properties of dip-deposited SnS and SnS2 thin films and their conversion to tin dioxide by annealing in air. Thin Solid Films 1999, 350, 72–78. [Google Scholar] [CrossRef]
- Ching, W.; Ren, S. Electronic structures of Si2N2O and Ge2N2O crystals. Phys. Rev. B 1981, 24, 5788. [Google Scholar] [CrossRef]
- Kirchner-Hall, N.; Zhao, W.; Xiong, Y.; Timrov, I.; Dabo, I. Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps. Mater. Cloud Arch. 2021. [Google Scholar] [CrossRef]
- The computational cost of DFT+U calculations is negligible with respect to the cost of linear-response calculations of Hubbard parameters. Therefore, here we neglect the former, and compare only the latter with respect to the cost of HSE06 calculations.
- Yan, Q.; Yu, J.; Suram, S.; Zhou, L.; Shinde, Z.; Newhouse, P.; Chen, W.; Li, G.; Persson, K.; Gregoire, J.; et al. Solar fuels photoanode materials discovery by integrating high-throughput theory and experiment. Proc. Natl. Acad. Sci. USA 2017, 114, 3040. [Google Scholar] [CrossRef] [PubMed]
- The k-points sampling of NbNO was slightly adjusted from 6 × 5 × 5 to 6 × 6 × 6 for the HSE06 calculations to make it divisible by 3.
| Formula | Space Group | |
|---|---|---|
| 1 | TiO | |
| 2 | ZrO | |
| 3 | HfO | |
| 4 | VO | |
| 5 | TaO | |
| 6 | WO | |
| 7 | SnO | |
| 8 | PbO | |
| 9 | InN | |
| 10 | SnN | |
| 11 | TiS | |
| 12 | ZrS | |
| 13 | HfS | |
| 14 | MoS | |
| 15 | ScS | |
| 16 | SnS | |
| 17 | NbNO | |
| 18 | TaNO | |
| 19 | GeNO | |
| 20 | YSO |
| Formula | Hubbard U (Ortho-Atomic) [eV] | Hubbard U (Atomic) [eV] | ||||
|---|---|---|---|---|---|---|
| TiO | Ti(): 6.10, | O(): 8.23 | Ti(): 3.81, | O(): 15.89 | ||
| ZrO | Zr(): 2.72, | O1(): 9.20, | O2(): 8.79 | Zr(): 1.07, | O1(): 33.67, | O2(): 27.20 |
| HfO | Hf(): 2.74, | O1(): 9.58, | O2(): 9.41 | Hf(): 1.14, | O1(): 47.79, | O2(): 38.18 |
| VO | V(): 5.37, | O1(): 7.42, | O2(): 7.65, | V(): 3.70, | O1(): 12.96, | O2(): 10.09, |
| O3(): 7.06 | O3(): 11.12 | |||||
| TaO | Ta1(): 3.06, | Ta2(): 3.07, | O1(): 8.99, | Ta1(): 1.54, | Ta2(): 1.55, | O1(): 30.11, |
| O2(): 8.36, | O3(): 8.20 | O2(): 30.10, | O3(): 19.03, | O4(): 17.79 | ||
| WO | W(): 3.99, | O(): 8.27 | W(): 2.80, | O(): 15.18 | ||
| TiS | Ti(): 5.61, | S(): 3.85 | Ti(): 4.45, | S(): 6.39 | ||
| ZrS | Zr(): 2.61, | S(): 3.96 | Zr(): 1.62, | S(): 8.36 | ||
| HfS | Hf(): 2.61, | S(): 3.75 | Hf(): 1.81, | S(): 9.65 | ||
| MoS | Mo(): 3.28, | S1(): 3.31, | S2(): 4.61, | Mo(): 3.87, | S1(): 6.08, | S2(): 5.62, |
| S3(): 4.62 | S3(): 5.53 | |||||
| ScS | Sc1(): 3.28, | Sc2(): 3.37, | S1(): 3.83, | Sc1(): 1.69, | Sc2(): 1.77, | S1(): 8.72, |
| S2(): 3.88 | S2(): 9.15, | S3(): 9.17 | ||||
| NbNO | Nb(): 3.48, | N(): 6.47, | O(): 8.51 | Nb(): 2.17, | N(): 9.85, | O(): 19.94 |
| TaNO | Ta(): 3.10, | N(): 6.66, | O(): 8.87 | Ta(): 1.88, | N(): 11.51, | O(): 26.04 |
| YSO | Y(): 1.98, | S(): 4.16, | O(): 9.17 | Y(): 0.59, | S(): 28.16, | O(): 47.87 |
| SnO | O(): 10.19, | Sn(): 1.26 | O(): 95.85, | Sn(): 0.67 | ||
| PbO | O(): 9.58, | Pb(): 1.20 | O(): 39.60, | Pb(): 0.58 | ||
| InN | N(): 6.52, | In(): 1.17 | N(): 28.91, | In(): 0.62 | ||
| SnN | N(): 6.56, | Sn1(): 1.43, | Sn2(): 1.23 | N(): 24.14, | Sn1(): 1.01, | Sn2(): 0.81 |
| SnS | S(): 3.88, | Sn(): 1.37 | S(): 7.66, | Sn(): 1.16 | ||
| GeNO | O(): 10.35, | N(): 6.62, | Ge(): 1.18 | O(): 103.08, | N(): 31.57, | Ge(): 0.72 |
| Formula | Expt. | DFT | DFT+U (Ortho-Atomic) | DFT+U (Atomic) | ||
|---|---|---|---|---|---|---|
| U-TM | U-All | U-TM | U-All | |||
| TiO | 3 [118] | 1.85 | 2.60 | 3.95 | 2.28 | 4.96 |
| ZrO | 5.8 [119] | 3.67 | 4.16 | 5.81 | 4.04 | 11.75 |
| HfO | 6 [120] | 4.11 | 4.68 | 6.55 | 4.59 | 15.44 |
| VO | 2.35 [121] | 2.01 | 2.69 | 3.50 | 1.69 | 2.82 |
| TaO | 3.9 [122] | 3.12 | 3.41 | 4.85 | 3.22 | 8.08 |
| WO | 2.6 [123] | 0.69 | 0.99 | 2.20 | 0.81 | 3.62 |
| TiS | 1 [124] | 0.02 | 1.53 | 1.86 | 1.03 | 1.56 |
| ZrS | 1.7 [125] | 1.13 | 1.92 | 2.27 | 1.45 | 2.81 |
| HfS | 2.85 [126] | 1.30 | 2.16 | 2.51 | 1.78 | 3.73 |
| MoS | 1.35 [127] | 0.62 | 0.98 | 1.52 | 0.19 | 0.58 |
| ScS | 2 [128] | 1.08 | 2.04 | 2.55 | 1.61 | 3.36 |
| NbNO | 2.1 [129] | 1.65 | 2.05 | 2.58 | 1.67 | 3.04 |
| TaNO | 2.5 [129] | 1.95 | 2.36 | 3.03 | 2.07 | 4.05 |
| YSO | 4.6 [130] | 3.11 | 3.23 | 4.38 | 3.14 | 11.88 |
| MAE | 1.10 | 0.66 | 0.55 | 0.87 | 2.68 | |
| Formula | Expt. | DFT | DFT+U (Ortho-Atomic) | DFT+U (Atomic) | |
|---|---|---|---|---|---|
| U-Light | U-All | U-Light | |||
| SnO | 3.4 [131] | 0.65 | 4.69 | 4.65 | 15.81 |
| PbO | 1.5 [132] | 0.09 | 1.10 | 1.06 | 10.27 |
| InN | 0.8 [133] | 0 | 0.85 | 0.80 | 8.87 |
| SnN | 1.6 [134] | 0.21 | 2.09 | 2.08 | 9.63 |
| SnS | 2.4 [135] | 1.53 | 2.00 | 1.98 | 3.00 |
| GeNO | 3.78 [136] | 2.61 | 5.03 | 4.99 | 15.46 |
| MAE | 1.40 | 0.65 | 0.63 | 8.26 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirchner-Hall, N.E.; Zhao, W.; Xiong, Y.; Timrov, I.; Dabo, I. Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps. Appl. Sci. 2021, 11, 2395. https://doi.org/10.3390/app11052395
Kirchner-Hall NE, Zhao W, Xiong Y, Timrov I, Dabo I. Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps. Applied Sciences. 2021; 11(5):2395. https://doi.org/10.3390/app11052395
Chicago/Turabian StyleKirchner-Hall, Nicole E., Wayne Zhao, Yihuang Xiong, Iurii Timrov, and Ismaila Dabo. 2021. "Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps" Applied Sciences 11, no. 5: 2395. https://doi.org/10.3390/app11052395
APA StyleKirchner-Hall, N. E., Zhao, W., Xiong, Y., Timrov, I., & Dabo, I. (2021). Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps. Applied Sciences, 11(5), 2395. https://doi.org/10.3390/app11052395







