Dirac Equation-Based Formulation for the Quantum Conductivity in 2D-Nanomaterials

Abstract

Starting from the four component-Dirac equation for free, ballistic electrons with finite mass, driven by a constant d.c. field, we derive a basic model of scalar quantum conductivity, capable of yielding simple analytic forms, also in the presence of magnetic and polarization effects. The classical Drude conductivity is recovered as a limit case. A quantum-mechanical evaluation is provided for parabolic and linear dispersion, as in graphene, recovering currently used expressions as particular cases. Numerical values are compared with the ones from the literature in the case of graphene under d.c. applied field. In particular, the effect of the sample length and field strength on the conductivity are highlighted.

1. Introduction

Graphene has recently attracted intense attention in the research community due to its extraordinary mechanical, electronic and optical properties [1,2,3,4,5]. The advent of graphene as well as of other 2D-materials on one hand, the drive towards circuit miniaturization on the other hand, have led the analysis of carrier transport in low-dimensional systems as the key-development for the analysis and design of nanomaterials-based technological platform [6].

This area of research is at the intersection of electrodynamics and quantum transport, ranging from nanoscopic to mesoscopic dimensions [7].

Quantum currents and conductivity in nanostrcutures (graphene in particular) presents novel and intriguing aspects that have been the object of much interest in the last years [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

For instance, in ref. [32] is found a useful synthesis of the peculiar features of currents at the nanoscale.

In evaluating this kind of situations with finite electron mass, use is currently made of Schrödinger equation from quantum mechanics in the framework of a free electron model, where the electron is described by a scalar wave-function. It is well appreciated, however, that such description is incomplete when polarization/magnetization aspects become important, e.g., in the very practical situation of applied electromagnetic fields, where using a four-component spinor description becomes necessary.

Moreover, in a conductor, the scalar ratio between the first pair of components of the spinor and the second pair plays the role of a characteristic impedance in a transmission line. The ratio of source impedance to load impedance is, in fact, an essential part of the correct definition of transmittivity.

In this work, we introduce a Dirac equation- based, free electron, ballistic model with finite mass under the action of a d.c. electric field in a highly idealized 2D-geometry. Electromagnetic boundary conditions of the field as well as the tensor character of the conductance are neglected. All real life loss mechanisms, such as intra-band transitions, interaction with the substrate, etc., are subsumed by a global finite life-time.

Considering just one–dimensional motion under the influence of a constant field, we then derive analytically the eigenvectors of the Dirac equation and find the resulting quantum current.

A Kubo-type approach is followed, including density of states and Fermi distribution, and obtain relatively simple analytical expressions valid for fields of moderate strength.

Numerical results are provided for the case of graphene conductivity, under d.c. condition.

We first consider the case of applying a constant bias, that is $V\left(x\right)=V_0$, in order to compare the numerical results from the present method with respect the ones obtained by implementing the Kubo–Drude (KD) formulation [33,34]. The comparison shows excellent agreement, thus confirming the robustness of the present formulation.

We then analyze the case of applying an electric field superposing the uniform bias, $V\left(x\right)=V_0+\overline{E}x$, as shown in Figure 1. The latter situation can be analyzed only by using the present Dirac-based formulation (DF); in fact, the KD formulation can only deal with the case of applying a constant bias along the structure. Moreover, the KD formula is based on a scalar wave function, and does not provide, e.g., any information about the particles spin. Indeed, the present formulation relies on a rigorous four-component spinor description, that can be used to provide, depending on the kind of problems (electric/magnetic polarization) a proper formulation for the spin wave propagation.

2. Dirac Equation-Based Model

We consider the 2-D problem of Figure 2, where a constant electric field $\overline{E}$ is applied in the negative x-direction over a strip of dimensions $L_x\times L_y$. We assume motion in the x-direction and uniformity in y.

In writing Dirac equation applicable to the structure of Figure 2, Fermi velocity, $v_F$, effective mass, $m_e$, and lifetime in the band, $\tau$, are given constants in the band of interest. The loss per unit length

$$\frac{1}{v_F\tau }=\frac{1}{L_F}(L_F>L_x)$$

subsumes all mechanism, such as intraband transition, interaction with the substrate, etc. $L_f$ indicates the compound mean free path due to all loss mechanisms, $L_X$ is the actual sample length. The condition $L_F>L_x$ means that the current, with some attenuation, reaches the output end of the sample. The condition $L_F>L_x$ means that the current, with some attenuation, reaches the output end of the sample.

The only potential appearing in the Dirac equation is the d.c. potential $V\left(x\right)=V_0+E_{x}x$, where $V_0$ is the constant bias.

Our aim is to be able to compare with the results of current Schrödinger-based formulas at a given energy $E^{\prime }$ in the interval $k_{B}T\le E^{\prime }\le \mu$, where $k_B$ is the Boltzmann constant, T the absolute temperature ($k_{B}T=25$ meV) and $\mu$ is the chemical potential, that is, the upper energy level we consider still occupied. The latter can be considered as the superposition of the initial chemical potential, say the intrinsic Fermi level ${\mu }_0=2E_F$, and the applied external potential $E_V$, leading to $\mu ={\mu }_0+E_V$.

Now, in the Dirac equation we separate out the energy $m_e{v}_F^2=2E_F$ ($E_F$ indicates the energy at the Fermi surface) and set

$$i\hslash \partial t=m_e{v}^2+E^{\prime }$$

in absence of losses ($L_F\to \infty$), Dirac equation is

$$-i\hslash v_F{\mathit{\alpha }}_x{\partial }_x\overline{\mathit{\psi }}+\mathit{\beta }{m}_e{v}_F^2\overline{\mathit{\psi }}=[m_e{v}_F^2+E^{\prime }+\left|e\right|V]\overline{\mathit{\psi }}$$

(1)

The $4\times 4$ Dirac Matrices $\mathit{\alpha }$, $\mathit{\beta }$ appearing above are defined as

$${\mathit{\alpha }}_x=\left[\begin{array}{cc}\mathbf{0}& {\mathit{\sigma }}_x\\ {\mathit{\sigma }}_x& \mathbf{0}\end{array}\right];{\mathit{\beta }}_x=\left[\begin{array}{cc}\mathit{I}& {\mathbf{0}}_x\\ {\mathbf{0}}_x& -\mathit{I}\end{array}\right];\mathrm{where}{\mathit{\sigma }}_x=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$

and are endowed with the following properties

$$\mathit{\alpha }·\mathit{\alpha }=3{\mathit{\beta }}^2=3{\mathbf{I}}_{\mathbf{4}\times \mathbf{4}}\mathit{\alpha }\mathit{\beta }=-\mathit{\beta }\mathit{\alpha }$$

After pre-multiplying (1) by ${\mathit{\alpha }}_x$, we re-arrange in the form of an homogeneus system of four firs order differential equations over the semi-infinite interval $0\le x$ with given boundary condition $\overline{\mathit{\psi }}\left(0\right)$:

$$\partial \overline{\mathit{\psi }}=i\mathit{K}\left(x\right)\overline{\mathit{\psi }}$$

(2)

with $\mathit{K}\left(x\right)\equiv \frac{1}{\hslash v_F}(2E_F+E^{\prime }+\left|e\right|V){\mathit{\alpha }}_x+\frac{1}{\hslash v_F}2E_F\mathit{\beta }{\mathit{\alpha }}_x$.

Considerable simplification in the following is obtained if $\left|e\right|V$ is replaced by its average value over the interval $x_0$ ($x_0$ is the length of an appropriate segmentation of the sample length $L_x$), $E_V=\left|e\right|(V_0+\overline{E}\frac{x_0}{2})$ so that $\mathit{K}$ is now a constant matrix.

Using the specific properties of the Dirac matrices in the general solution of the linear system (2) (as given in ref. [35] for instance), the following useful result can be shown to hold.

$$\overline{\mathit{\psi }}\left(x\right)=expi\mathit{K}x\overline{\mathit{\psi }}\left(0\right)=[cos\left(kx\right)\mathit{I}+i\frac{sin\left(kx\right)}{k}\mathit{K}]\overline{\mathit{\psi }}\left(0\right)$$

(3)

Eigenvalues of K are given by:

$$k=\pm \frac{1}{\hslash v_F}\sqrt{{(2E_F+E^{\prime }+E_V)}^2-{\left(2E_F\right)}^2}$$

and $\pm k$ represents the forward and backward propagation constants, respectively, with real k if $E^{\prime }+E_V\ge 0$.

The eigenvectors (4-spinors) of $\mathit{K}$ corresponding to $\pm k$ are of the form

$${\mathit{\psi }}_a=\left[\begin{array}{c}\mathit{a}\\ \eta {\mathit{\sigma }}_x\mathit{a}\end{array}\right]e^{ikx}{\mathit{\psi }}_b=\left[\begin{array}{c}\mathit{b}\\ -\eta {\mathit{\sigma }}_x\mathit{b}\end{array}\right]e^{-ikx}$$

(4)

with

$$\eta =\sqrt{\frac{E^{\prime }+E_V}{E^{\prime }+E_V+2E_F}}$$

Since $E^{\prime }$,$E_F$ are real and positive, if $E^{\prime }+E_V\ge 0$,$\eta$ is real; it becomes purely imaginary if $E^{\prime }+E_V\le 0$ and $E^{\prime }+E_V+4E_F>0$, becoming real again when also $E^{\prime }+E_V+4E_F<0$, as summarized in Figure 3.

When $E^{\prime }+E_V<0$, k is pure imaginary and (4) is modified as follows:

$${\mathit{\psi }}_a=\left[\begin{array}{c}\mathit{a}\\ \eta {\mathit{\sigma }}_x\mathit{a}\end{array}\right]e^{-\gamma x}{\mathit{\psi }}_b=\left[\begin{array}{c}\mathit{b}\\ -\eta {\mathit{\sigma }}_x\mathit{b}\end{array}\right]e^{\gamma x}$$

(5)

with

$$\gamma =\frac{1}{\hslash v_F}\sqrt{{\left(2E_F\right)}^2-{(2E_F+E^{\prime }+E_V)}^2}$$

real, positive and $\eta$ either real or pure imaginary.

Such modification is important in the definition of current.

The above spinors are orthogonal with weight ${\mathit{\alpha }}_{\mathbf{x}}$; $a,b$ are constant 2D vectors determined by boundary conditions and normalization. In absence of y-dependence, these may be assumed as

$$\mathit{a}=\frac{a}{\sqrt{2}}\left[\begin{array}{c}1\\ 1\end{array}\right]\mathit{b}=\frac{b}{\sqrt{2}}\left[\begin{array}{c}1\\ -1\end{array}\right]$$

The general solution (3) may be expressed as a linear combination of the above eigenvectors as a travelling wave or a standing wave with boundary condition $\overline{\mathit{\psi }}\left(0\right)$. Let us now consider the case of constant, low loss that assumes negligible coupling due to loss between progressive and regressive waves. We may introduce this constant propagation loss in (2), by writing:

$${\partial }_x\mathit{\psi }=\left[\mp \frac{1}{L_F}+i\mathit{K}\right]\mathit{\psi }$$

(6)

The upper/lower sign refers to the progressive/regressive wave, respectively. We have

$$\mathit{\psi }=exp\mp \frac{x}{L_F}\overline{\mathit{\psi }}\left(x\right)$$

The solution of (6) is their linear combination weighted by the exponentials:

$$\mathit{\psi }\left(x\right)=exp-\frac{x}{L_F}{\mathit{\psi }}_a+exp\frac{x}{L_F}{\mathit{\psi }}_b$$

It is noted that the above two spinors modified by the exponentials are still orthogonal with weight ${\alpha }_x$, consistently with the original low loss assumption, that considers the original lossless wavefunction attenuated without altering their shape

3. Current: The Classical Drude Limit

At a fixed energy, the general definition of quantum current density from Dirac equation is

$$J\left(x\right)=-\left|e\right|N{v}_F{\mathit{\psi }}^{⊺}{\mathit{\alpha }}_x\mathit{\psi }$$

For $E^{\prime }+E_V\ge 0$, we have

$$J\left(x\right)=J_a-J_b=-2\left|e\right|N{v}_F\sqrt{\frac{E^{\prime }+E_V}{E^{\prime }+E_V+4E_F}}\left({\left|\mathit{a}\right|}^{2}exp-\frac{2x}{L_F}-{\left|\mathit{b}\right|}^{2}exp\frac{2x}{L_F}\right)$$

(7)

where N is the charge density per unit area. For $E^{\prime }+E_V<0$ and $E^{\prime }+E_V+4E_F>0$, we have instead

$$J\left(x\right)=-4\left|e\right|N{v}_F\sqrt{\frac{E^{\prime }+E_V}{E^{\prime }+E_V+4E_F}}Im\left(a{b}^{*}\right)$$

(8)

Furthermore, finally for $E^{\prime }+E_V<0$ and $E^{\prime }+E_V+4E_F<0$,

$$J\left(x\right)=-2\left|e\right|N{v}_F\sqrt{\frac{E^{\prime }+E_V}{E^{\prime }+E_V+4E_F}}\left({\left|\mathit{a}\right|}^{2}exp-\frac{2x}{L_F}-2\gamma x-{\left|\mathit{b}\right|}^{2}exp\frac{2x}{L_F}+2\gamma x\right)$$

(9)

According to (7), the current entering the junction from the left is

$$J_a\left(0\right)=-2\left|e\right|N{v}_F{\left|a\left(0\right)\right|}^2\sqrt{\frac{E^{\prime }+\left|e\right|V_0}{E^{\prime }+\left|e\right|V_0+4E_F}}$$

With a view to deriving an expression for conductivity under travelling wave condition, in (7) we only retain the progressive wave term.

Moreover, in order to recover the classic Drude formula, the normalization |a(0)|${}^2$ is fixed so that

$$J_a\left(0\right)=-\left|e\right|N{v}_F{\mathrm{Am}}^{-1}.$$

We have then

$$J\left(x\right)=-\left|e\right|N{v}_F{e}^{-\frac{2x}{L_F}}{\left[\frac{1+\frac{ϵ}{E^{\prime }+\left|e\right|V_0}}{1+\frac{ϵ}{4E_F+E^{\prime }+\left|e\right|V_0}}\right]}^{\frac{1}{2}}.$$

(10)

with $ϵ\equiv \left|e\right|\overline{E}\frac{L_x}{2}$.

The “weak applied field” condition means $\frac{ϵ}{E^{\prime }+\left|e\right|V_0}\ll 1$ Even in absence of bias applied to the sample, the minimum value of $E^{\prime }$ is $kBT$ at room temperature, which corresponds for a moderate field of, say, 400 ${\mathrm{Vm}}^{-1}$, to a length of 125 $\mu \mathrm{m}$. Consequently, it is usually justified to expand (10) in series of $\frac{ϵ}{E^{\prime }+\left|e\right|V_0}$. To first order we find (the following equation has been corrected)

$$J\left(x\right)=-\left|e\right|N{v}_F{e}^{-\frac{2x}{L_F}}\left({1}+\frac{{1}}{{2}}\frac{ϵ}{{4}(E^{\prime }+|e\left|V_0\right)}\right).$$

With a review to recovering the classical Drude conductivity as a limit case, we set $x=v_F{\tau }_c=L_c$, where ${\tau }_c$ is the classical mean time between collisions $({\tau }_c<\tau )$. This yields a conductivity at the energy $E^{\prime }$: (the following equation has been corrected)

$$\sigma =-\frac{dJ}{d\overline{E}}=e^{2}N{v}_F{e}^{-\frac{2L_c}{L_F}}\frac{L_x}{{4}(E^{\prime }+|e\left|V_0\right)}{{\Omega }}^{-1}$$

(11)

If we now choose a value of $E^{\prime }$ in the middle of the Fermi sphere, that is

$$E^{\prime }=\frac{{1}}{{2}}{E}_F=\frac{{1}}{{4}}{m}_e{v}_F^2\gg \left|e\right|V_0$$

together with $v_F{\tau }_c=L_c$ and consider $L_c\ll L_F$, we recover the classical Drude result:

$$\sigma =\frac{e^{2}N}{m_e}{\tau }_c.$$

After this verification, it is required to obtain full quantum-mechanical expression of the Kubo-type [32] that can be compared with theoretical and experimental results in the current literature.

4. Full Quantum-Mechanical Calculation

Returning now to a ballistic regime with flow in the x-direction, uniform in y, the distance x in (10) is to be replaced by $L_x$. Moreover, for a band of energies, the classical electron density N is to be replaced by a density of states, weighted over allowed energies, by the occupation probability and integrated from the thermal energy level, $k_{B}T$ at room temperature, up to the chemical potential $\mu$. This means:

$$J=-2\left|e\right|v_F\frac{1}{L_x{L}_y}exp-\frac{2x}{L_F}{\int }_{k_{B}T}^{\mu }D\left(E^{\prime }\right)f\left(E^{\prime }\right){\left[\frac{1+\frac{ϵ}{E^{\prime }+\left|e\right|V_0}}{1+\frac{ϵ}{4E_F+E^{\prime }+\left|e\right|V_0}}\right]}^{\frac{1}{2}}d{E}^{\prime }$$

(12)

The pre-factor 2 in the above expression is due to two electrons of opposite spins finding place in a state.

Since we are considering a ribbon configuration, we assume the density of states of a two-dimensional system with parabolic $E-k$ characteristic first. The particular case of graphene will be considered later. In (12)

$$N_S=\frac{\pi k^2}{\frac{{\left(2\pi \right)}^2}{L_x{L}_y}}\mathrm{is}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{states}\mathrm{in}k-\mathrm{space},E^{\prime }=\frac{{\left(\hslash k\right)}^2}{2m_e}$$

$$D\left(E^{\prime }\right)=\frac{d{N}_S}{dk}\frac{dk}{d{E}^{\prime }}=\frac{k}{2\pi }{L}_x{L}_y\frac{m_e}{{\hslash }^{2}k}=L_x{L}_y\frac{m_e}{2\pi {\hslash }^2}=const.$$

The probability of occupation, shifted for the presence of bias, is [32]:

$$f=\frac{1}{1+exp\frac{E^{\prime }-(\mu -{\mu }_0)}{k_{B}T}}$$

where it is recalled $E_V=\left|e\right|(V_0+\overline{E}\frac{L_x}{2})$, and $\mu ={\mu }_0+E_V$. Again in the limit of weak fields, we find from (12):

$$J=-\left|e\right|\frac{2E_F}{\pi {\hslash }^2{v}_F}exp-\frac{2L_x}{L_F}{\int }_{k_{B}T}^{\mu }f\left(E^{\prime }\right)\left(1+\frac{1}{4}\frac{\left|e\right|\overline{E}{L}_x}{E^{\prime }+\left|e\right|V_0}\right)d{E}^{\prime },$$

and the conductivity is:

$$\sigma =-\frac{dJ}{d\overline{E}}=\frac{e^2{E}_F{\tau }^{\prime }}{2\pi {\hslash }^2}exp-\frac{2L_x}{L_F}{\int }_{k_{B}T}^{\mu }f\left(E^{\prime }\right)\frac{1}{E^{\prime }+\left|e\right|V_0}d{E}^{\prime }{{\Omega }}^{-1},$$

(13)

where ${\tau }^{\prime }\equiv \frac{L_x}{v_F}$ is the “transit” time through the sample. At low temperatures, $\mu \to E_F$, $f\left(E^{\prime }\right)\to 1$; considering $L_x\ll L_F$, the exponential is close to unity and (13) reduces to:

$$\sigma =\frac{e^2{E}_F{\tau }^{\prime }}{2\pi {\hslash }^2}{\int }_{k_{B}T}^{\mu }\frac{1}{E^{\prime }+\left|e\right|V_0}d{E}^{\prime }.$$

(14)

Approximating the integral by the average value of its argument $(E^{\prime }=E_F)\times$ the interval, we get

$$\sigma =\frac{e^2{\tau }^{\prime }\mu }{2\pi {\hslash }^2}\frac{E_F}{E_F+\left|e\right|V_0}.$$

(15)

If, moreover, $\left|e\right|V_0\ll E_F$, that is usually the case, (15) reduces to Equation (18) of ref. [36]. Equation (13) above, however, provides a more realistic ballistic model under more general conditions of room temperature, non negligible bias and finite lifetime in the band for parabolic $E-k$ characteristics.

5. Graphene

Graphene provides an important particular case, since the dispersion relation is assumed linear of the type:

$$E^{\prime }\left(k\right)=\hslash k\frac{m_e{v}_F}{2m_e}=v_F\frac{\hslash k}{2},$$

that implies a density of states:

$$D\left(E^{\prime }\right)=\frac{d{N}_S}{dk}\frac{dk}{d{E}^{\prime }}=\frac{k}{2\pi }{L}_x{L}_y\frac{2}{\hslash v_F}=\frac{2E^{\prime }}{\pi {\left(\hslash v_F\right)}^2}{L}_x{L}_y.$$

The current density (12) is replaced by:

$$J=-4\left|e\right|\frac{1}{\pi {\hslash }^2{v}_F}exp-\frac{2L_x}{L_F}{\int }_{k_{B}T}^{\mu }{E}^{\prime }f\left(E^{\prime }\right){\left[\frac{1+\frac{ϵ}{E^{\prime }+\left|e\right|V_0}}{1+\frac{ϵ}{4E_F+E^{\prime }+\left|e\right|V_0}}\right]}^{\frac{1}{2}}d{E}^{\prime }.$$

(16)

Consequently, in the weak field limit condition, the (differential) conductivity is given by:

$$\sigma =-\frac{dJ}{d\overline{E}}=\frac{e^2{\tau }^{\prime }}{\pi {\hslash }^2}exp-\frac{2L_x}{L_F}{\int }_{k_{B}T}^{\mu }f\left(E^{\prime }\right)\frac{E^{\prime }}{E^{\prime }+\left|e\right|V_0}d{E}^{\prime }{{\Omega }}^{-1}$$

(17)

Approximating the integral as above, the limit value of (17) at low temperature is still (15), but differences appear at room temperature and in presence of non-negligible bias.

6. Results

In this section, we deal with the graphene conductivity calculation. We (i) first consider the case of applying a constant bias, that is $V\left(x\right)=V_0$, in order to compare the numerical results derived from the present method, from Equation (17), and the ones obtained by implementing the well known Kubo–Drude formulation [33,34]. Then, we (ii) analyze the case of applying an electric field superposing the uniform bias (along the domain), $V\left(x\right)=V_0+\overline{E}x$. It has to be remarked that the Kubo–Drude formulation can only deal with the case of a constant applied voltage (i), whereas the present method is quite more general and deals with a potential varying along the graphene domain.

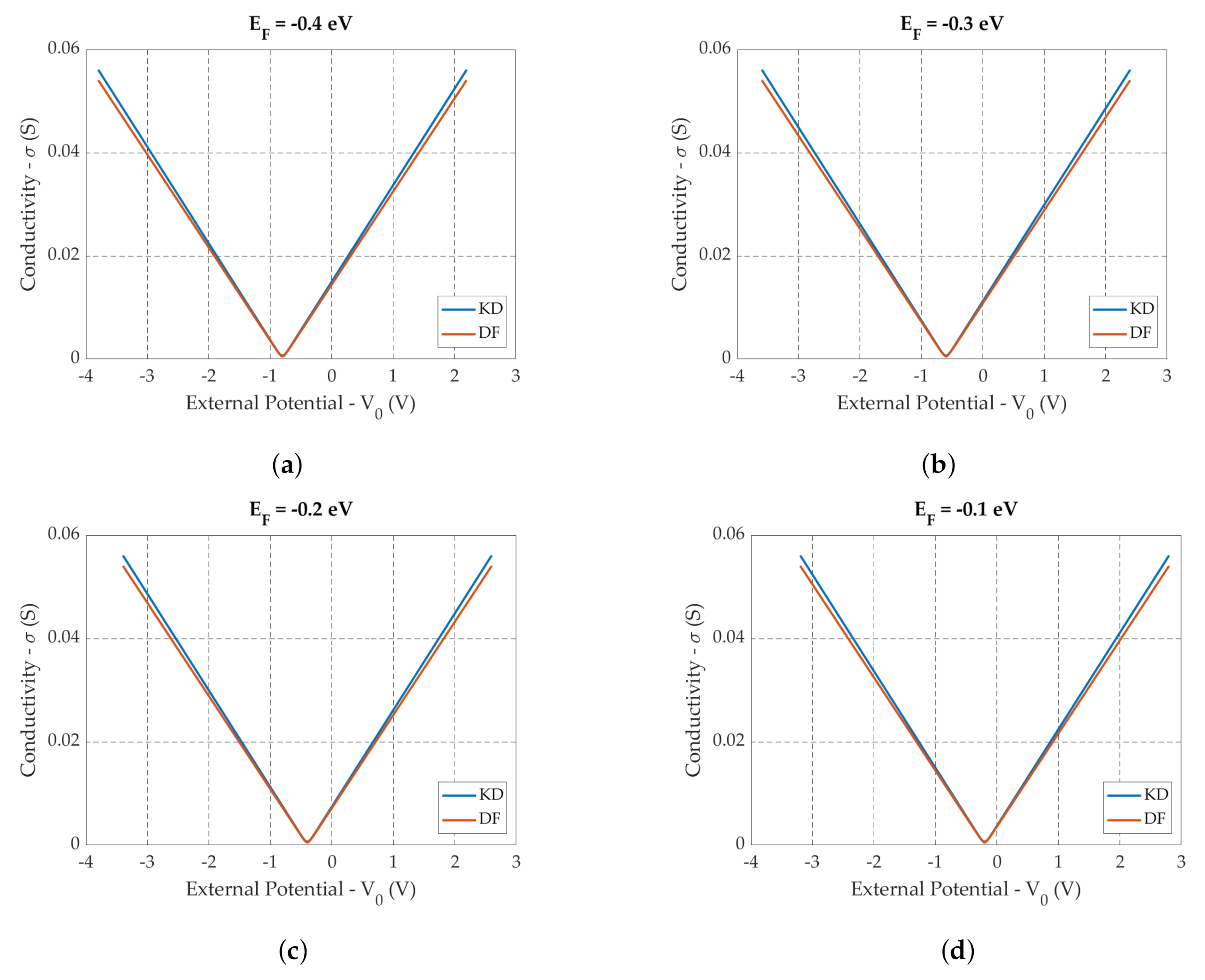
6.1. Graphene Conductivity under a Uniform Bias Potential

We consider the application of a uniform bias voltage $V\left(x\right)=V_0$, ($\overline{E}=0$), with $V_0\in [-3,3]$ V. This comparison is a core issue in order to have a robust estimate and calibration of the present method. The present Dirac-based formulation is developed for a progressive 4-components spinor wave, excited from the x-axis left-side (see Figure 2), travelling to the right-side, where it is considered matched for x increasing to plus infinity, with the electric field increasing in the same direction. Then, for the range $V_0\in [0,3]$ V, we use Equation (17). The range $V_0\in [-3,0]$ V leads to a symmetrical problem, corresponding to a wave excited on the right side and travelling to the left-side, matched for x decreasing to minus infinity, with the electric field increasing in the same direction.

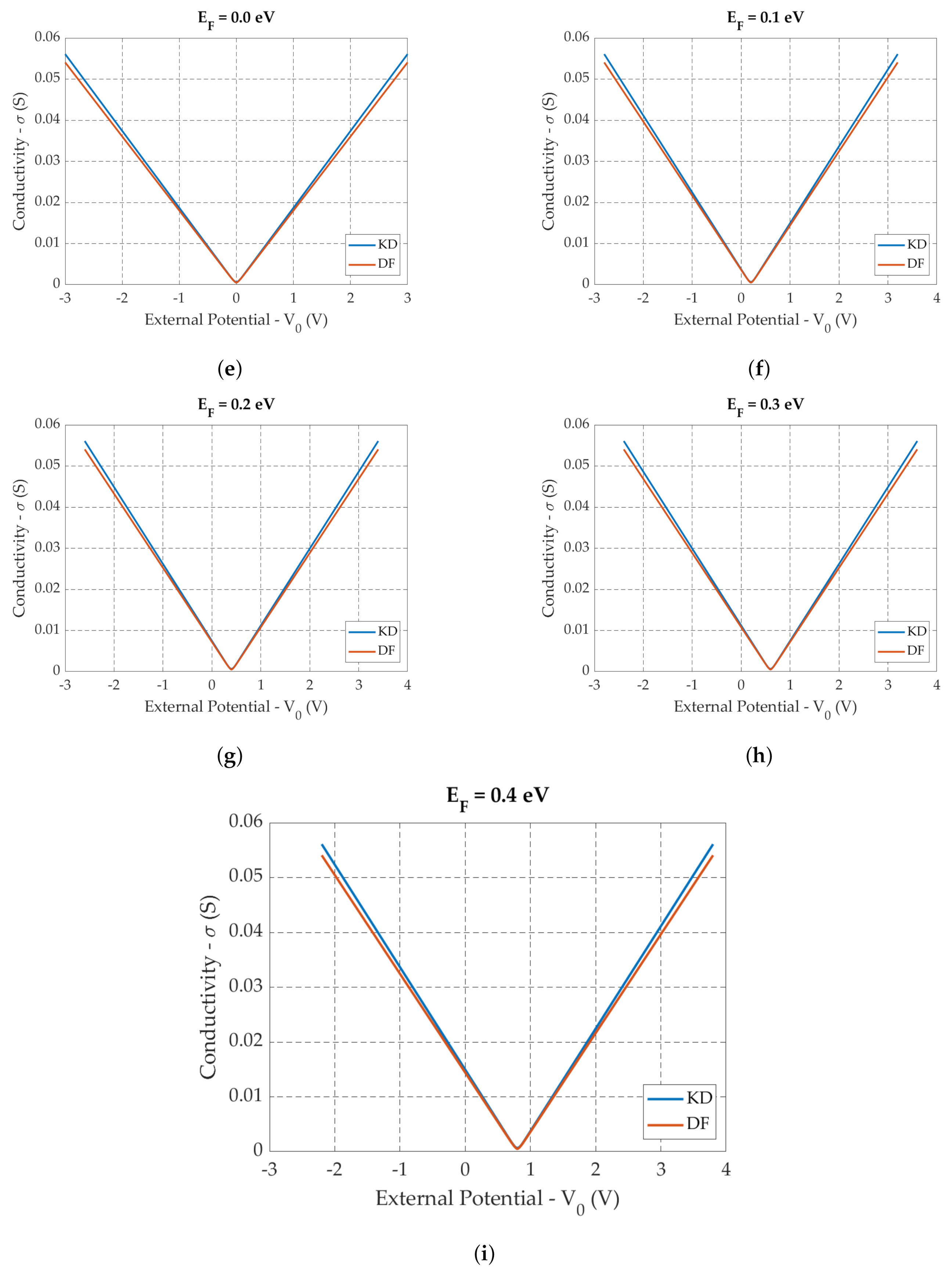
6.1.1. Conductivity in Function of the Chemical Potential $\mu$

The comparison is performed, for both Equation (17) and the Kubo formula of ref. [33] in terms of (i) the same lifetime (scattering time) $\tau$ in the band, (ii) the same intrinsic chemical potential (pre-doping) ${\mu }_0$, and for $V_0\in [-3,3]$ V; We recall that the intrinsic Fermi level is the initial Dirac point of the energy: it can be set to zero, but, realistically, under operative conditions there is a level shift caused by the doping (or gating), [34].

The plots shown in Figure 4 depict the conductivity in function of the applied external voltage for different values of the pre-doping Fermi level, $\mu$. We can observe an excellent agreement among the curves, namely, the Kubo–Drude (blue) and Dirac formulation (red) curves. Moreover, the two sets of curves are symmetric with respect to ${\mu }_0$, thus confirming the ambipolar behaviour, one of the main properties of graphene as nano-structured material.

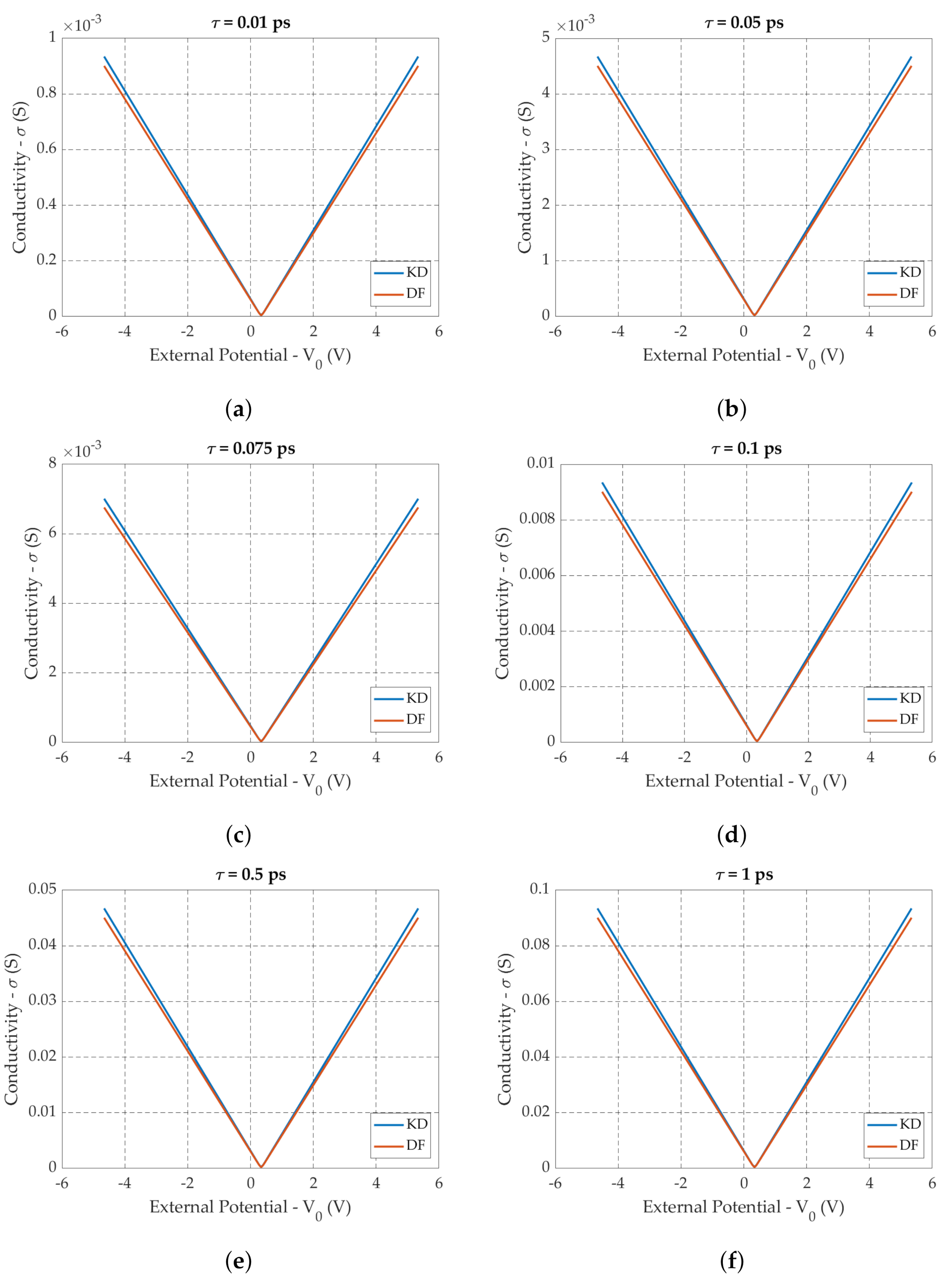
6.1.2. Conductivity in Function of the Scattering Time

Again, the comparison shows and excellent agreement. In particular, we observe, from Figure 5, that if the scattering time increases, the conductivity linearly increases accordingly. All the calculations have been performed by setting ${\mu }_0=2E_F=0.34$ eV, a typical values in the experimental environments.

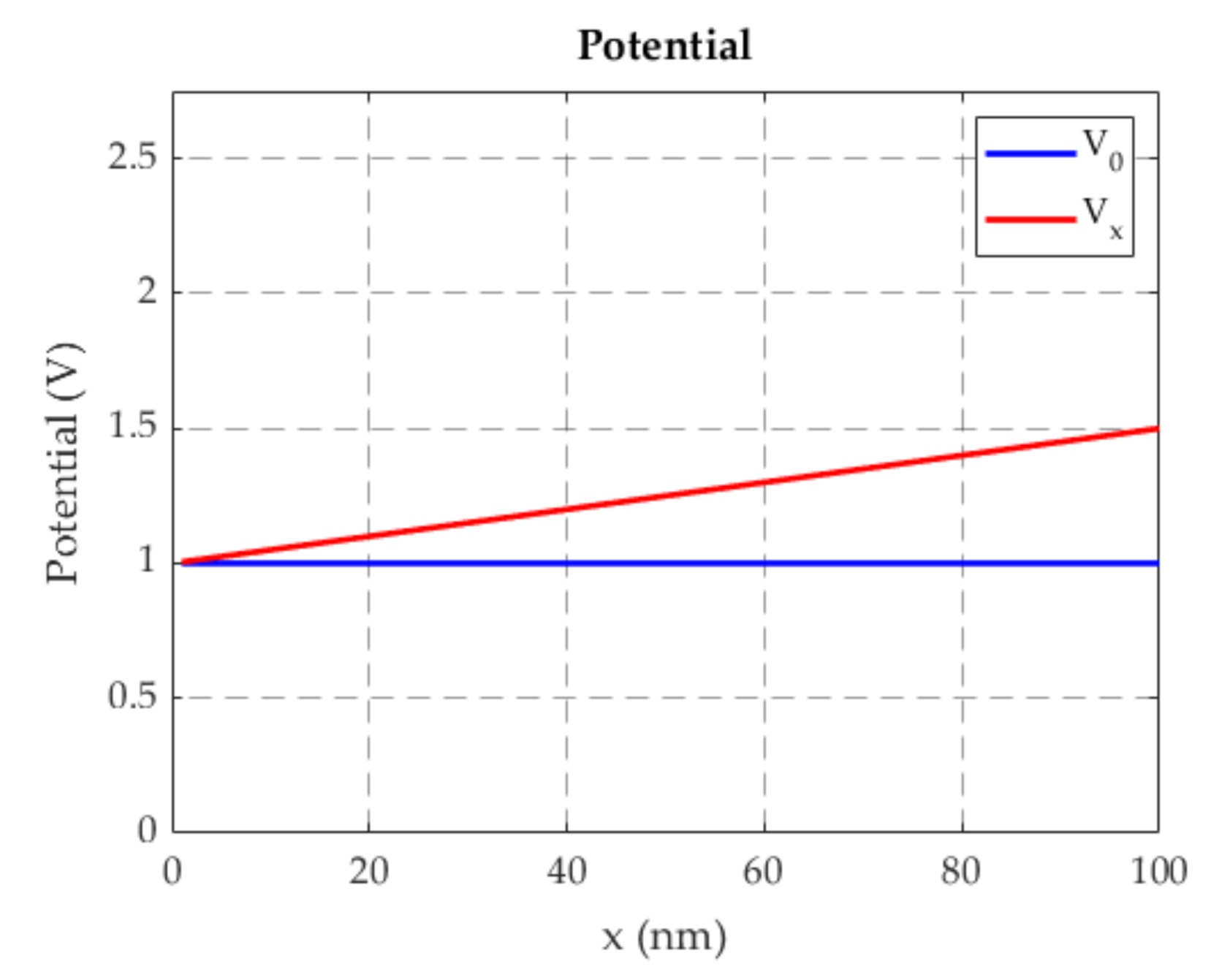
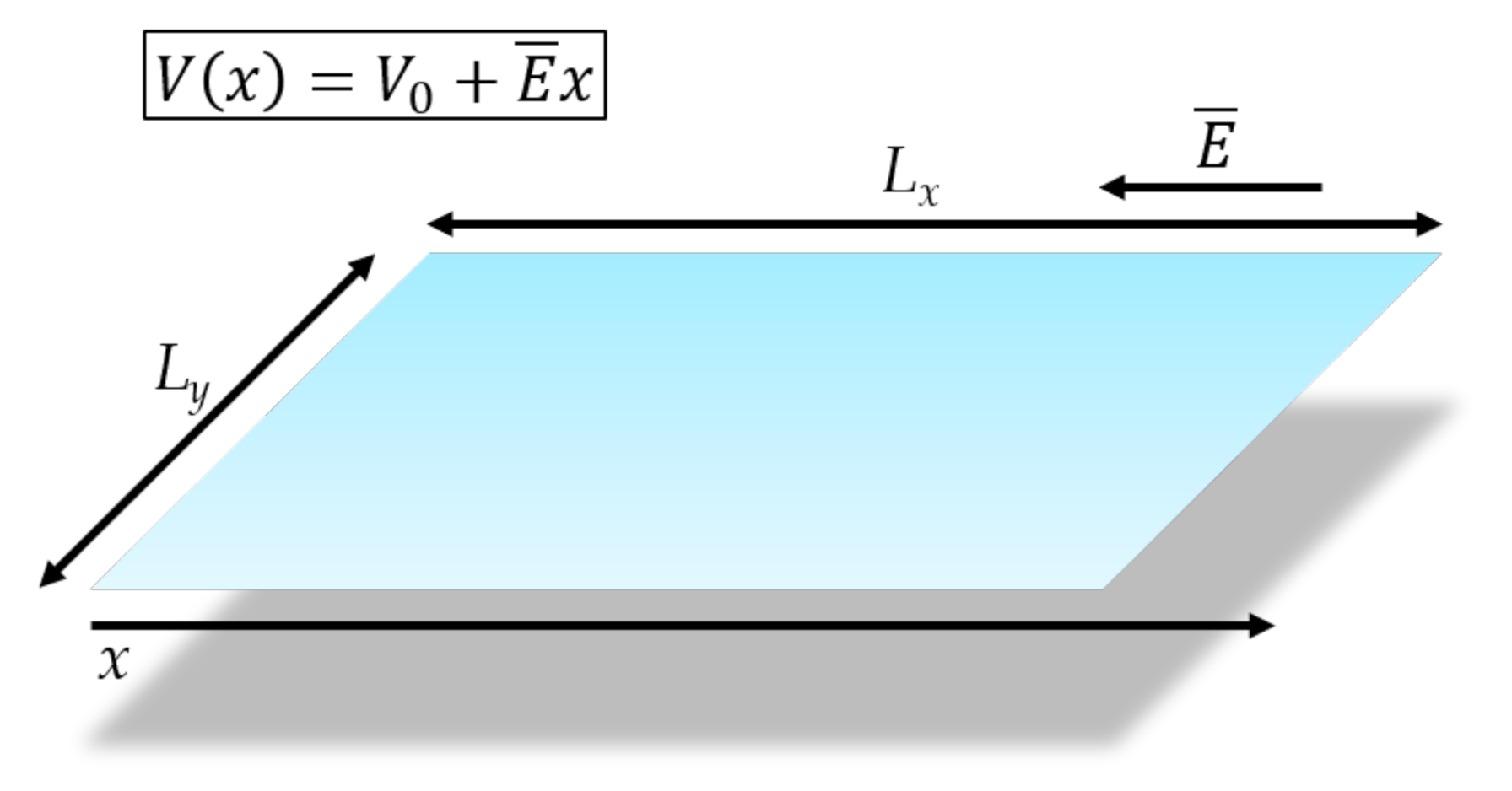
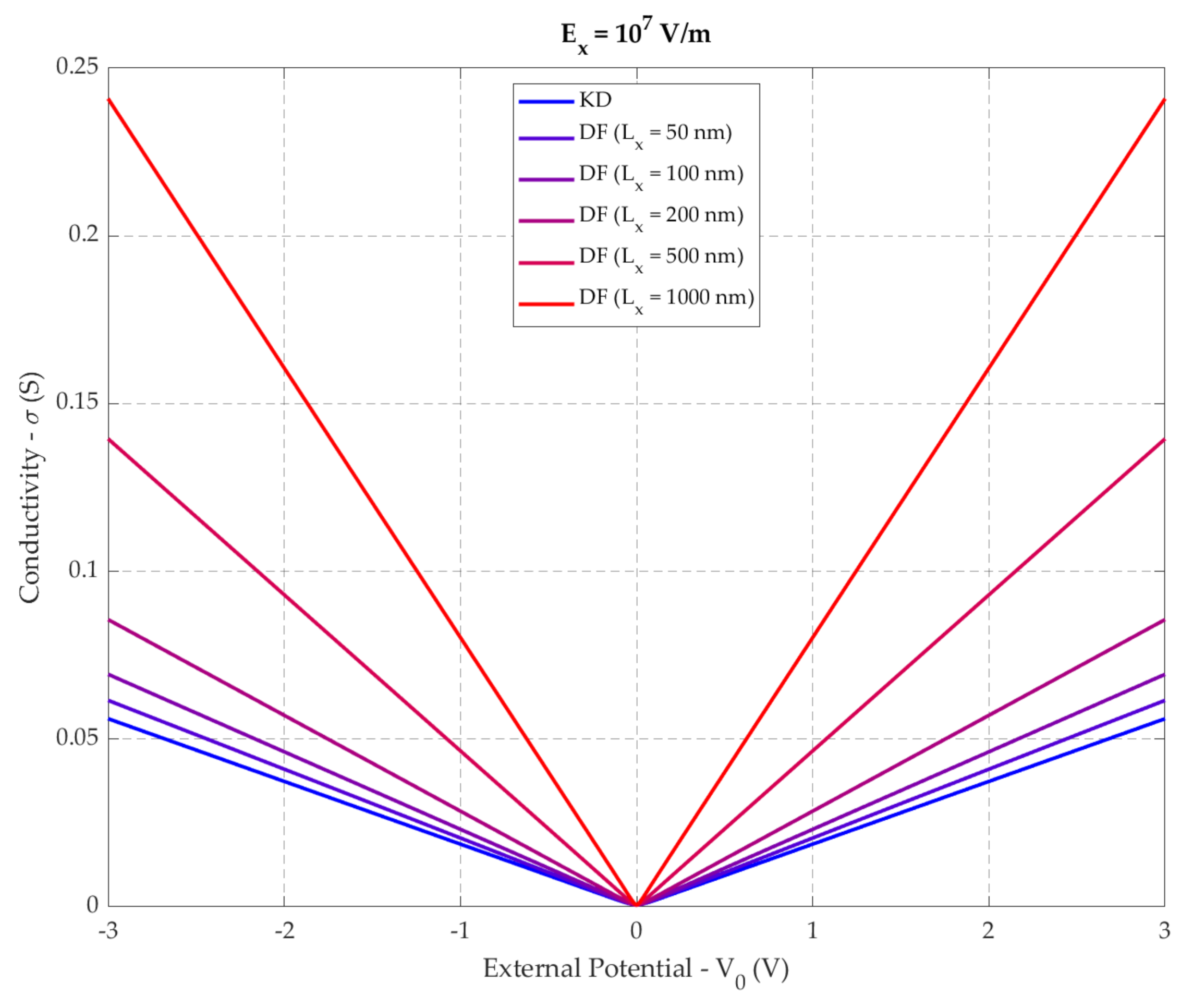
6.2. Graphene Conductivity by Applying a Longitudinal Electric Field $E_x$

In this section, we analyze the behavior of the graphene conductivity in the realistic case of applying a longitudinal (x-direction in Figure 2) electric field, that superposes the bias potential, $V\left(x\right)=V_0+\overline{E}x$. This situation cannot be addressed by the Kubo–Drude formulation. In Equation (17), we set $\overline{E}=E_x\widehat{x}$, with $\overline{E}={10}^7$ (V/m) and, for sake of simplicity, consider ${\mu }_0=2E_F=0$ eV. We then calculate the conductivity for different values of $L_x$ lengths of the graphene domain, as shown in Figure 6. As a matter of fact, by increasing the length of the graphene sample, but still considering quantum transport in the ballistic regime (reasonably up to $L_x<1$ µm), we progressively increase the energy transferred to the material. This energy doping (shift of the Fermi level) corresponds to an increase of charge concentration, and, in turn, of conductivity. The behavior of the conductivity curves will then tend to flatten (saturation), further increasing the length of the sample and of the applied field (non-ballistic regime). The latter phenomen will be the object of future work. In Figure 6 is also reported the conductivity calculated from the Kubo–Drude formulation [33,34] that can only take into account the bias potential.

7. Conclusions

Starting from the Dirac equation mathematical model, based on a four-component spinor description, we derive a rigorous formulation of the scalar quantum conductivity for particles with finite mass, driven by a constant d.c. field. A quantum-mechanical evaluation is then provided in the case of parabolic and linear dispersion. The graphene conductivity is then analyzed. To this aim, numerical values derived from the present method are compared with the ones from the literature (Kubo formula), in the case of $V\left(x\right)=V_0$, with excellent agreement. We then analyze the case of applying a uniform) electric field $V\left(x\right)=V_0+\overline{E}x$. The present formulation of the conductivity can be inserted into full-wave solver for the analysis and design of graphene-based devices in the ballistic regime [37], and in the quasi-ballistic regime, e.g., in geometrical diodes, [38].

The present method is as rigorous as it is flexible, and can be used to provide, depending on the particular problem (electric/magnetic polarization, d.c./a.c. conditions) proper formulation for charged particles wave propagation, e.g., spin waves, matter waves, electromagnetic waves.