Time Series Clustering of Online Gambling Activities for Addicted Users’ Detection
Abstract
1. Introduction
2. Literature Review
3. Experimental Phase
3.1. Data
- player_id: unique identifier of the player in the operator system.
- player_logon: username of the player in the operator system.
- cod_ficha: unique identifier for a bet.
- cod_ficha_jog: gambling external code attributed by the online gambling operator.
- cod_aptr_jog: betting code used by the online gambling operator.
- timestp_ini: start time of betting event.
- timestp_fim: end time of betting event.
- timestp: timestamp of the betting operation placed by a user.
- a_saldo_ini: balance before the betting start.
- a_valor: value of the bet.
- a_saldo_fim: balance after betting close.
- a_bonus_ini: player bonus before betting start.
- a_bonus: bet bonus.
- a_bonus_fim: player bonus after betting close.
- g_ganho: amount won from the bet.
- N: number of gamblers.
- : number of bets placed by the player .
- instants of bets for player i.
- balance of the bet placed in .
- player_id
- player_logon
- cod_ficha
- cod_ficha_jog
- cod_aptr_jog
- timestp: the instant of the bet.
- a_valor: value of the bet, including bonuses.
- g_ganho: balance of the bet.
- player_id
- time_stamp: sequence of timestp in which the bets are placed.
- player_logon
- cod_ficha: sequence of cod_ficha, useful to identify the single bets.
- cod_aptr_jog sequence of cod_aptr_jog.
- cod_fichajog: sequence of cod_fichajog.
- g_ganho: time series of the balances of player’s bets.
- a_valor: sequence of a_valor.
- g_ganho_tot: sum of the balances of the player.
- a_saldo_tot: sum of the bets’ value of the player.
3.2. Experimental Settings
- Model: Lenovo NeXtScale
- Architecture: Linux Infiniband Cluster
- Nodes: 1022
- Processors: 2 × 18-cores Intel Xeon E5-2697 v4 (Broadwell) at 2.30 GHz
- Cores: 36 cores/node
- RAM: 128 GB/node, 3.5 GB/core
- Internal Network: Intel OmniPath, 100 Gb/s
- Peak performance single node: 1.3 TFlop/s
- Peak Performance: 1.5 PFlop/s
- Accelerators: 60 nodes equipped with 1 Nvidia K80 GPU and 2 nodes equipped with 1 Nvidia V100 GPU
- multiple calls to a data preparation function.
- part of the computation of the algorithm does not take place in parallel.
- _mm_assignment: computes item assignment based on DTW alignments and returns cost as a bonus.
- _mm_valence_warping: computes valence and warping matrices from paths, returning the sum of diagonals and a list of matrices.
- _mm_update_barycenter: updates the barycenters.
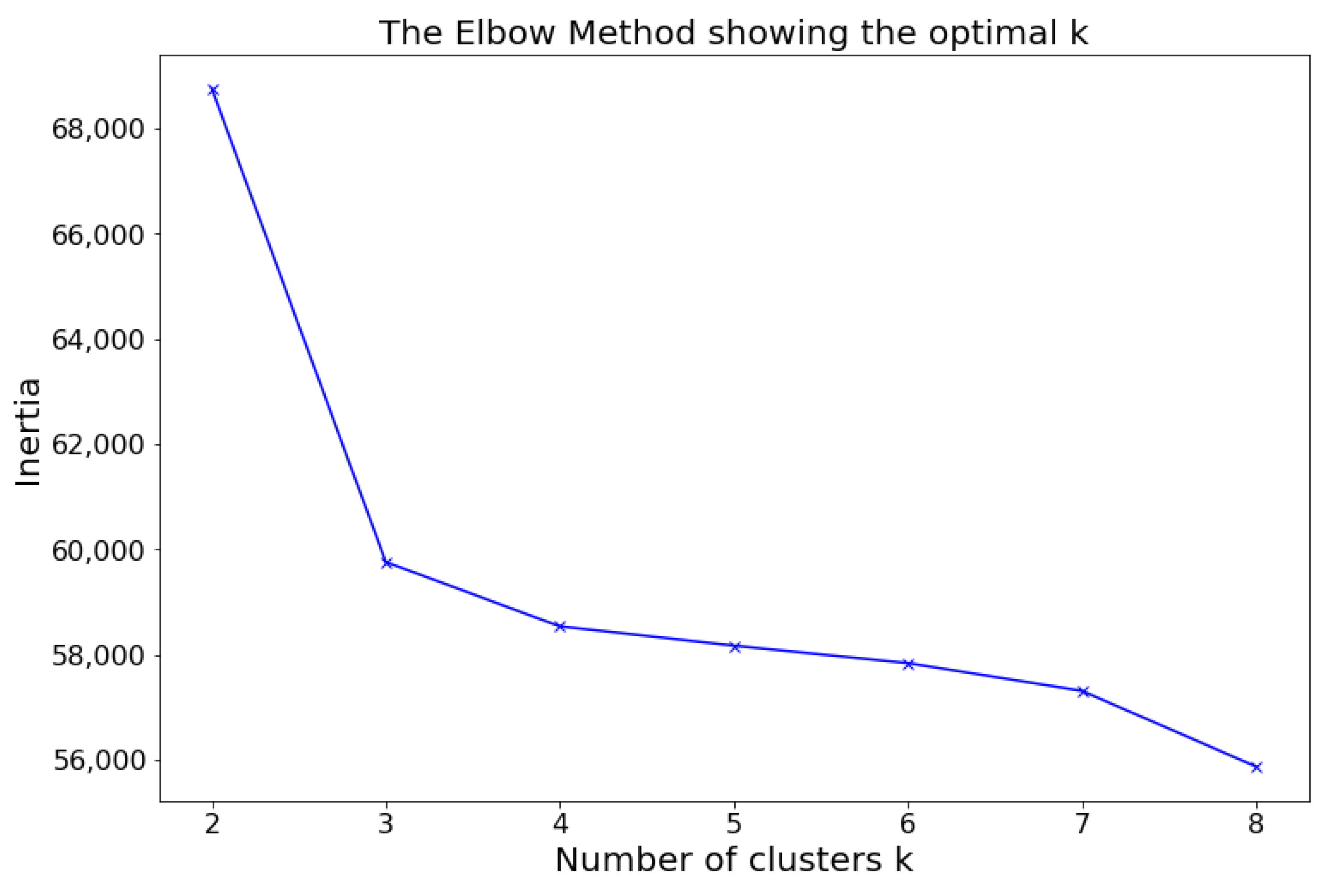
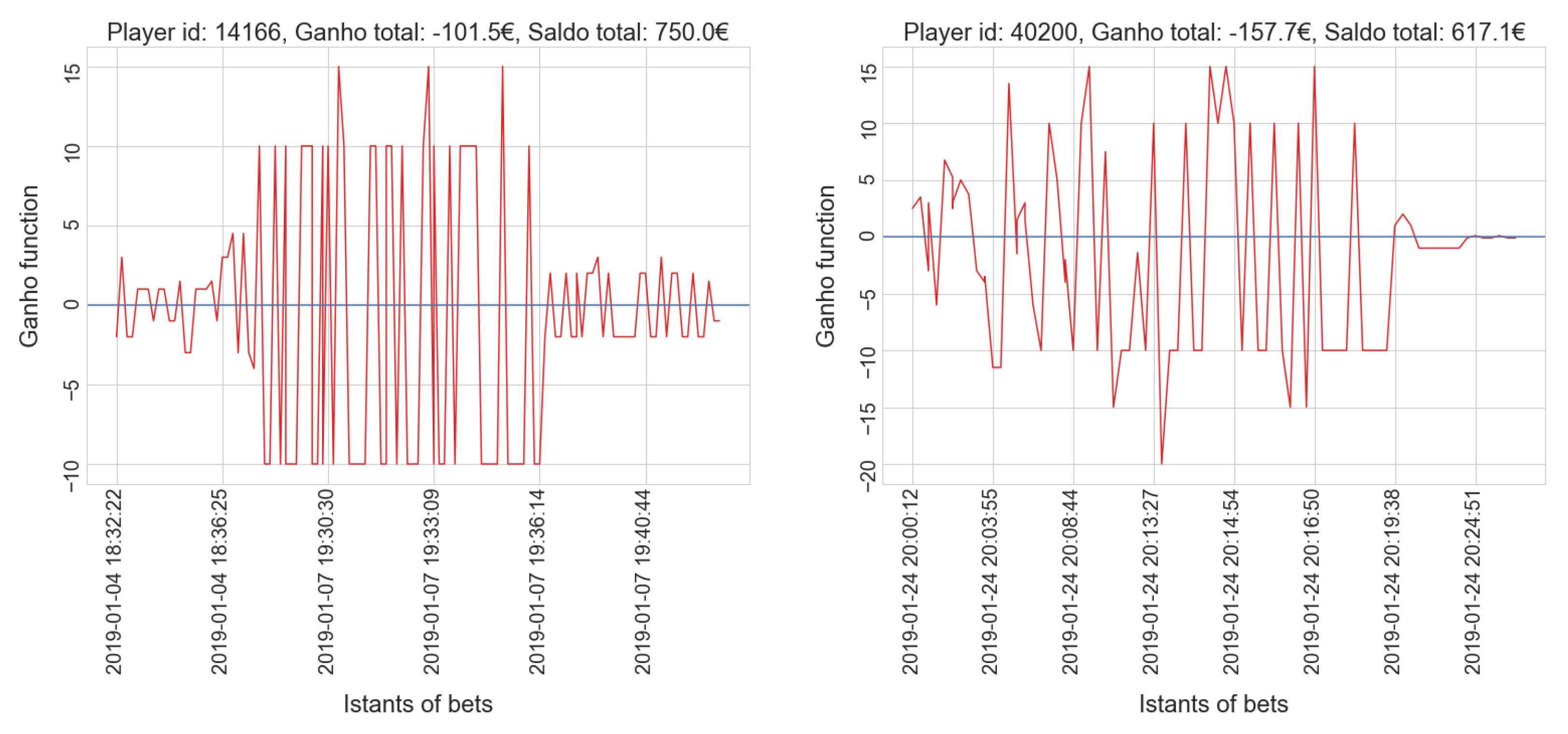
4. Results and Discussion
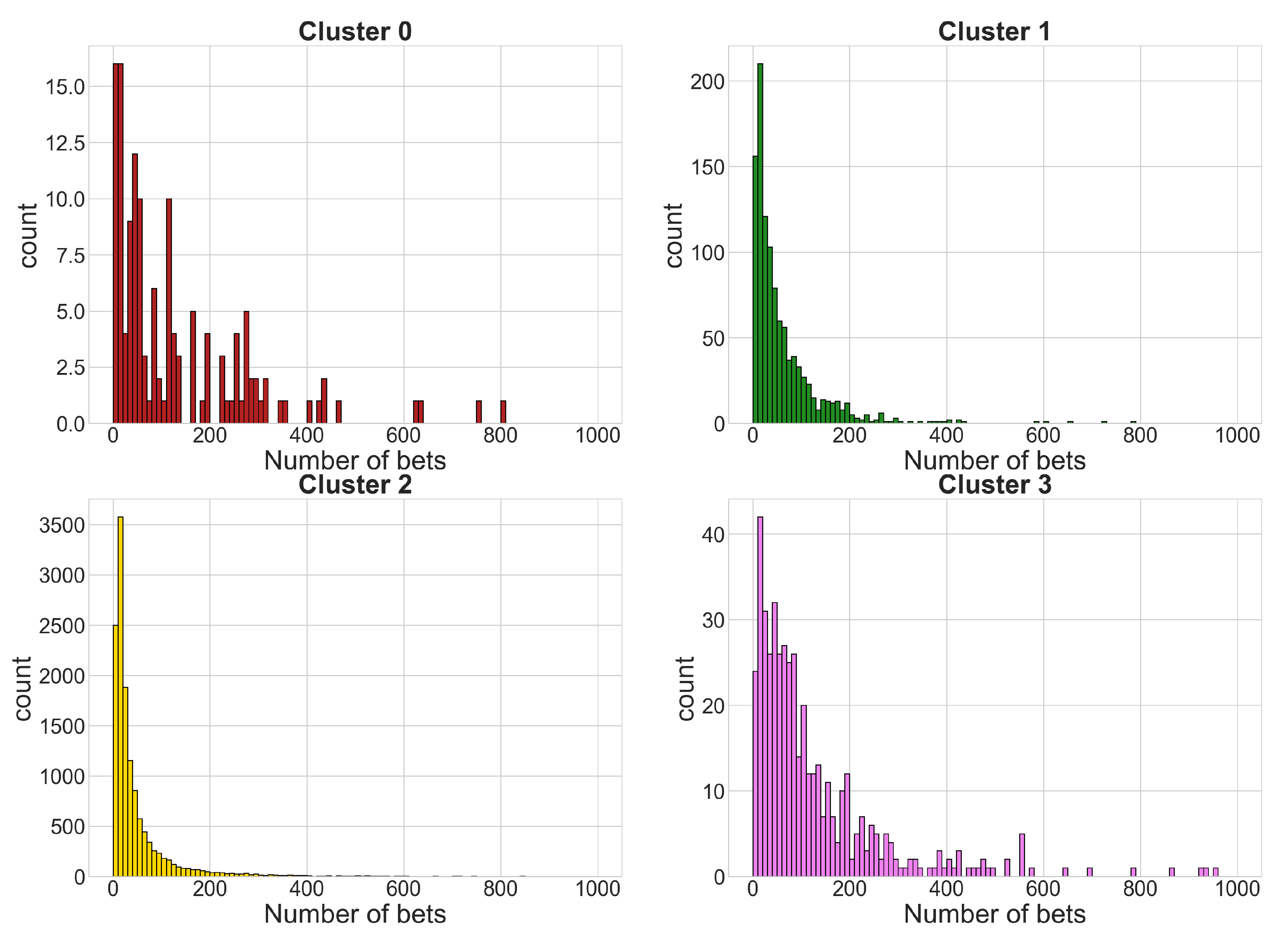
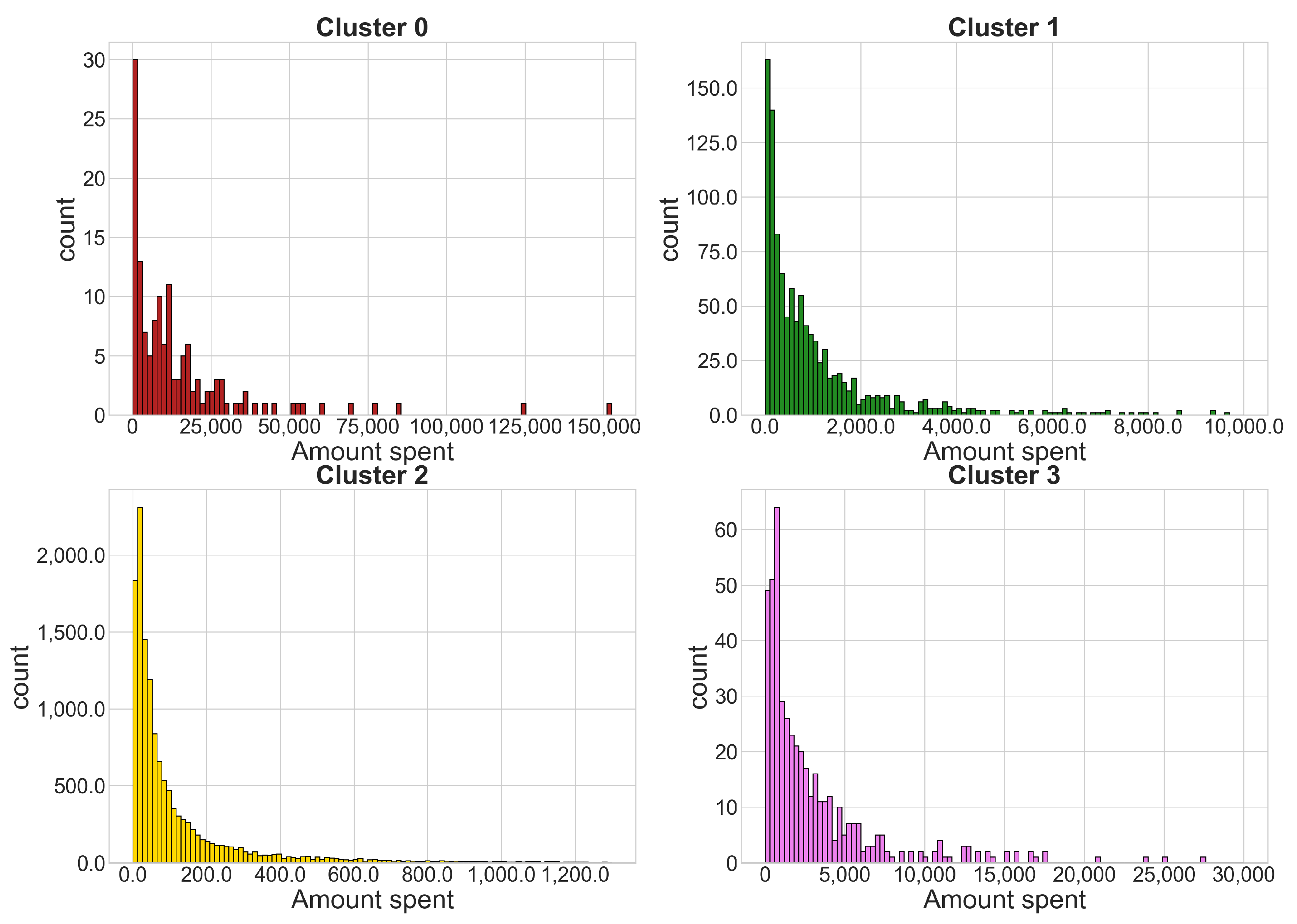
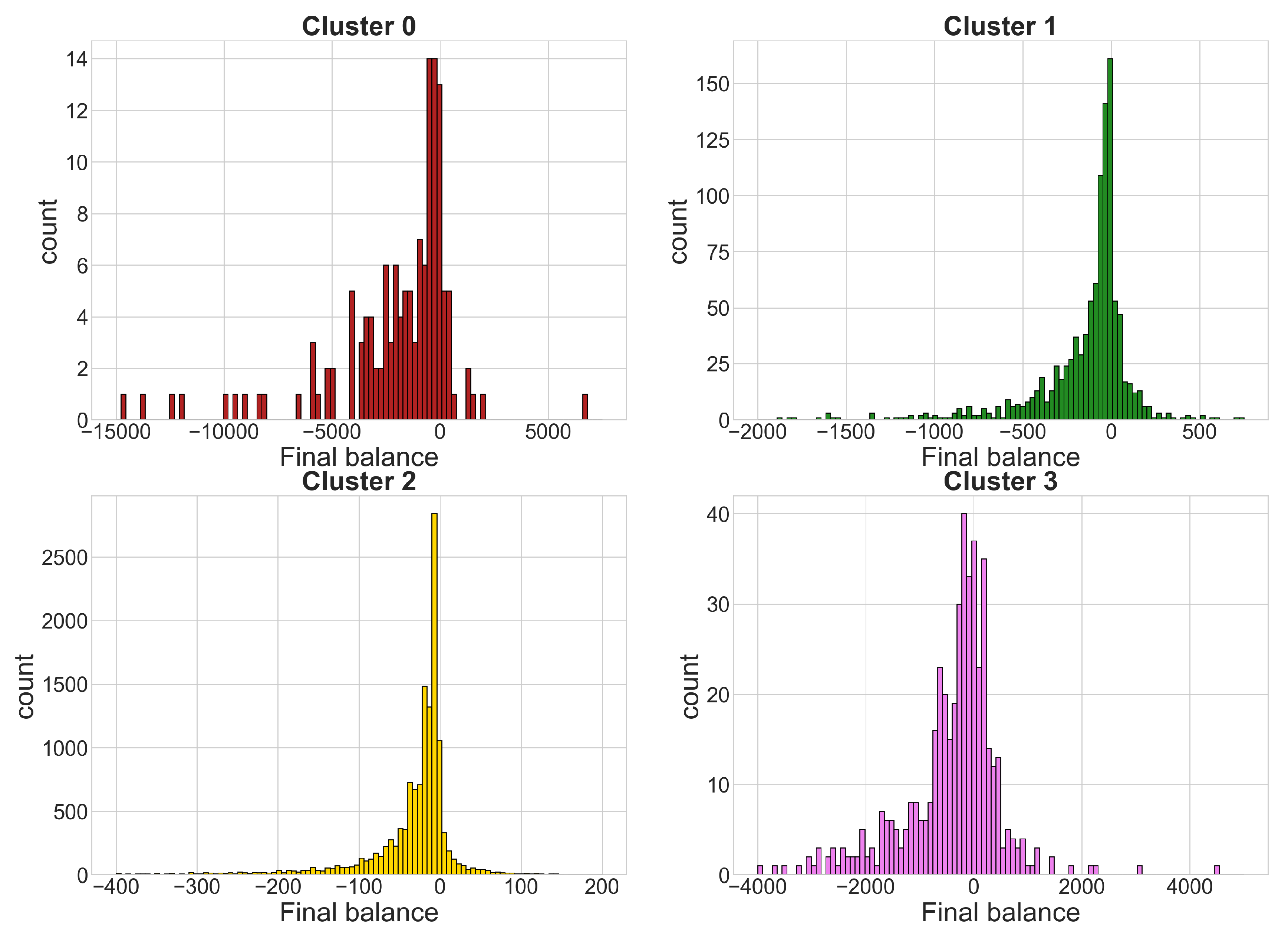
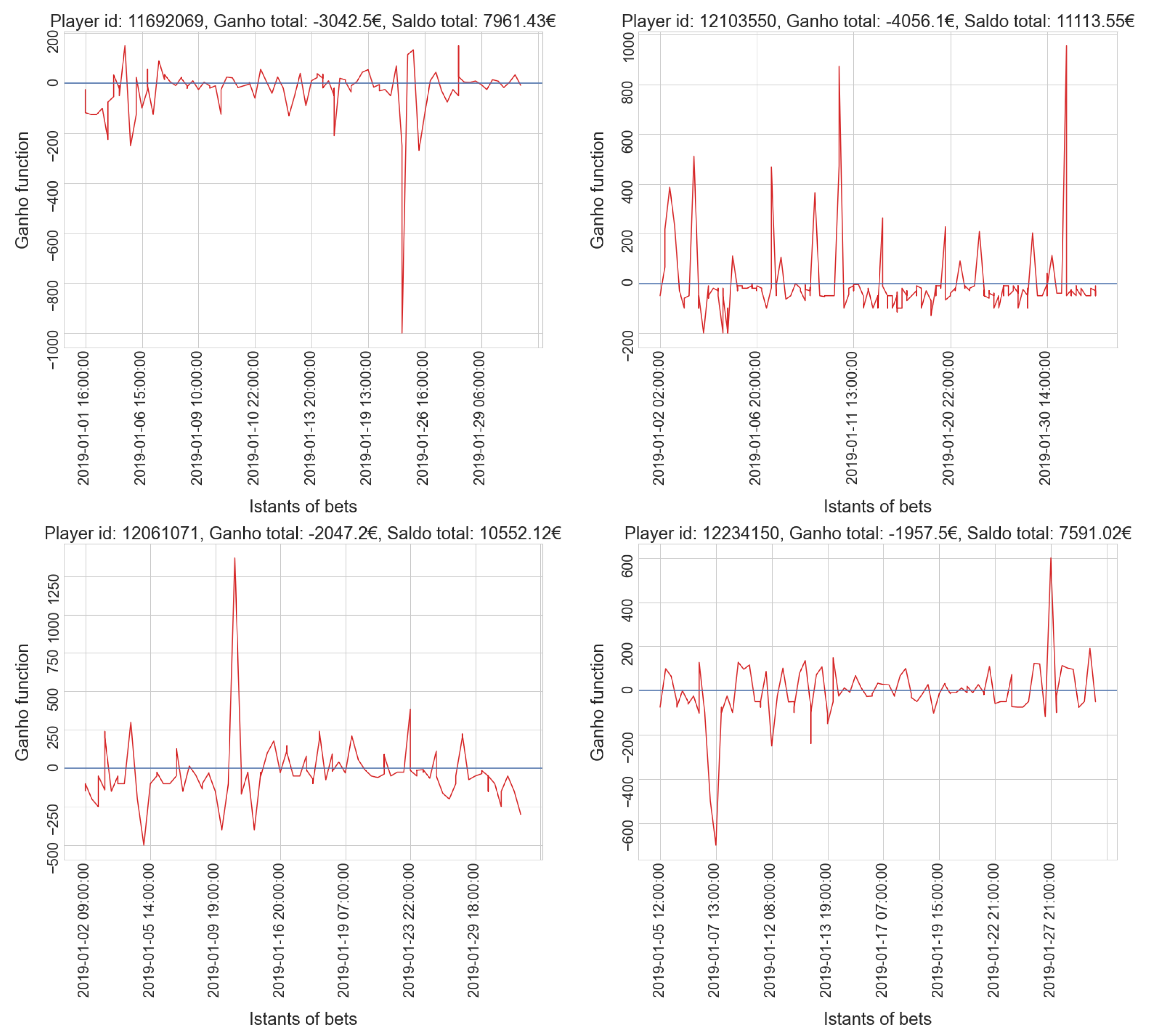
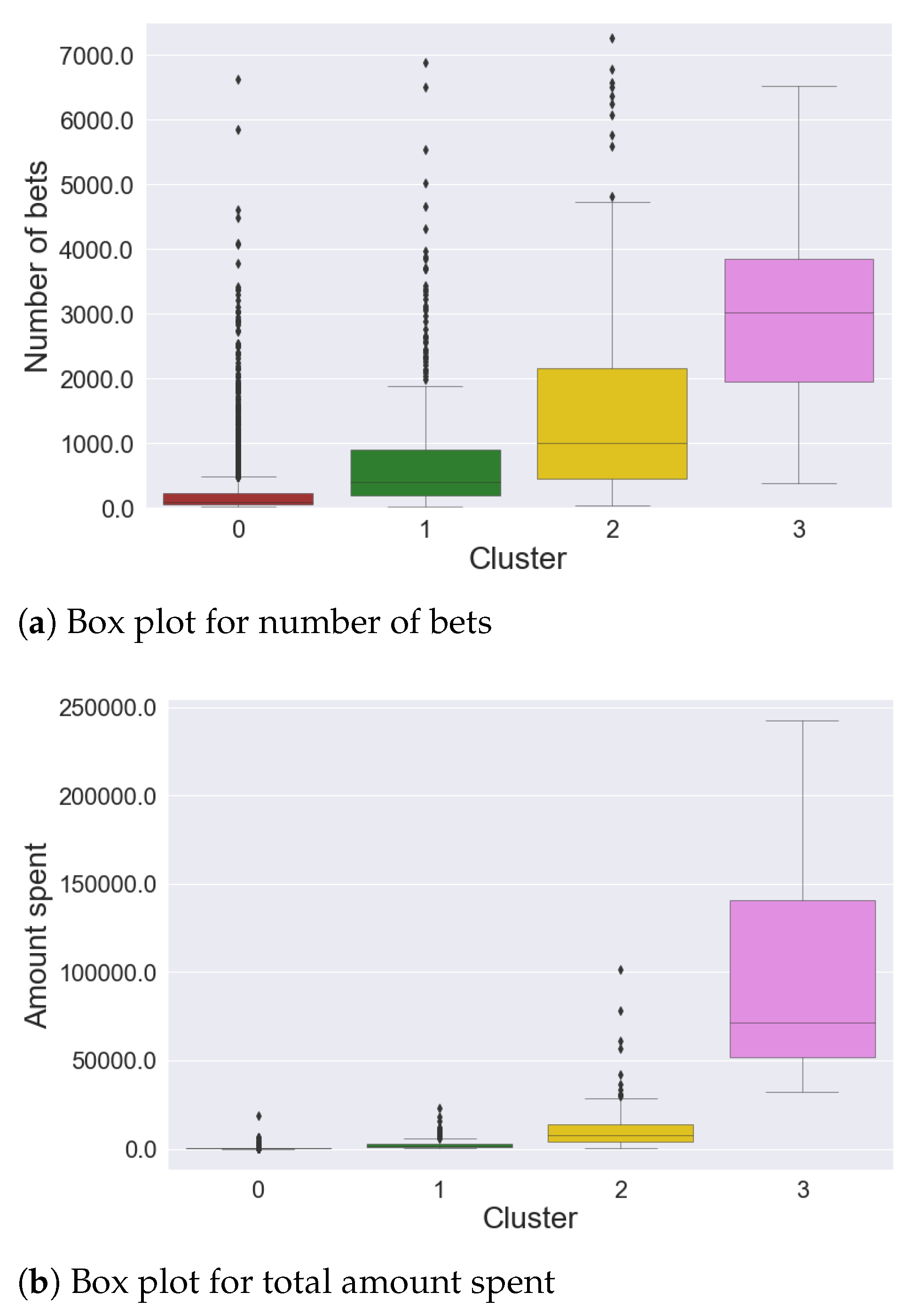
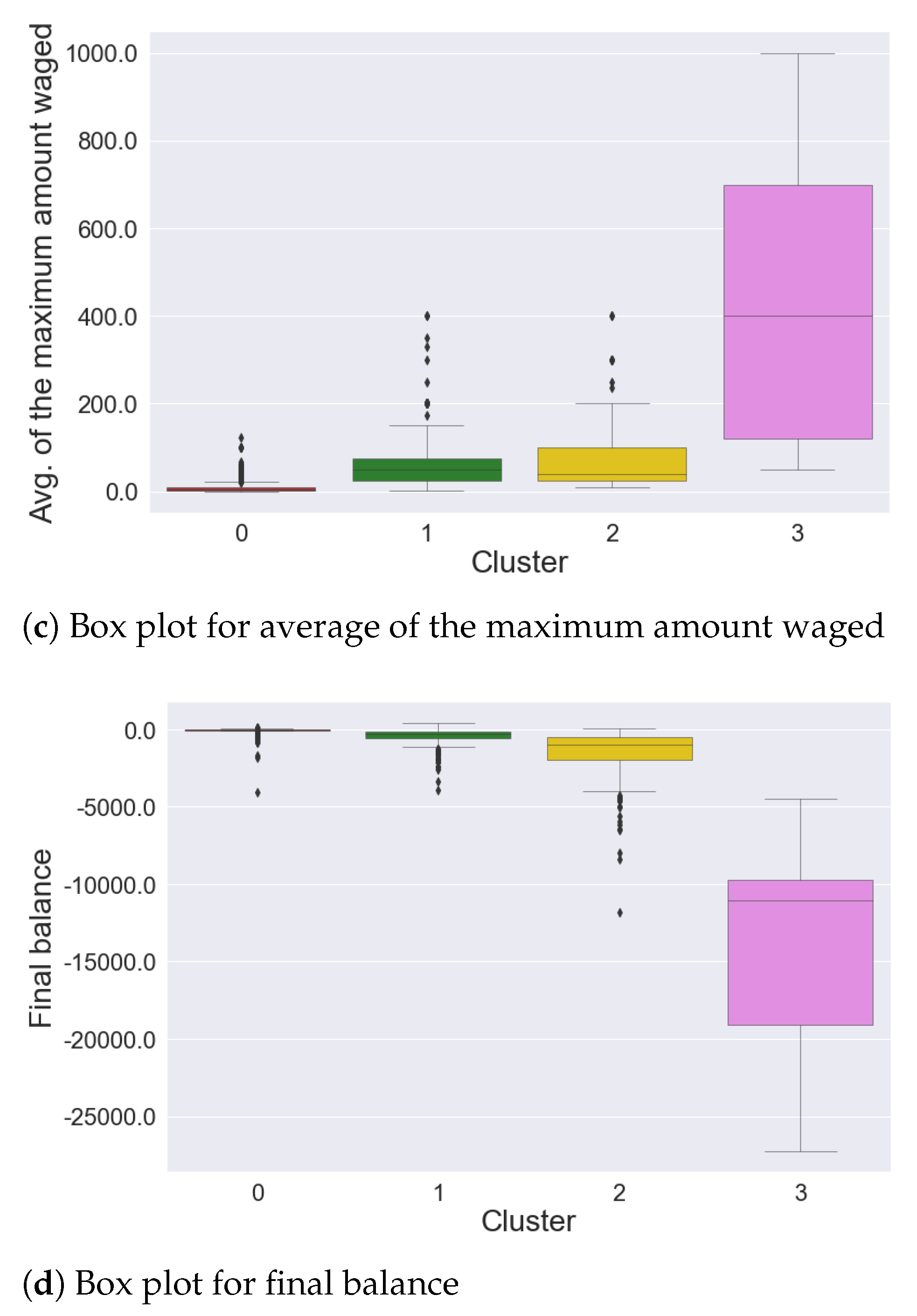
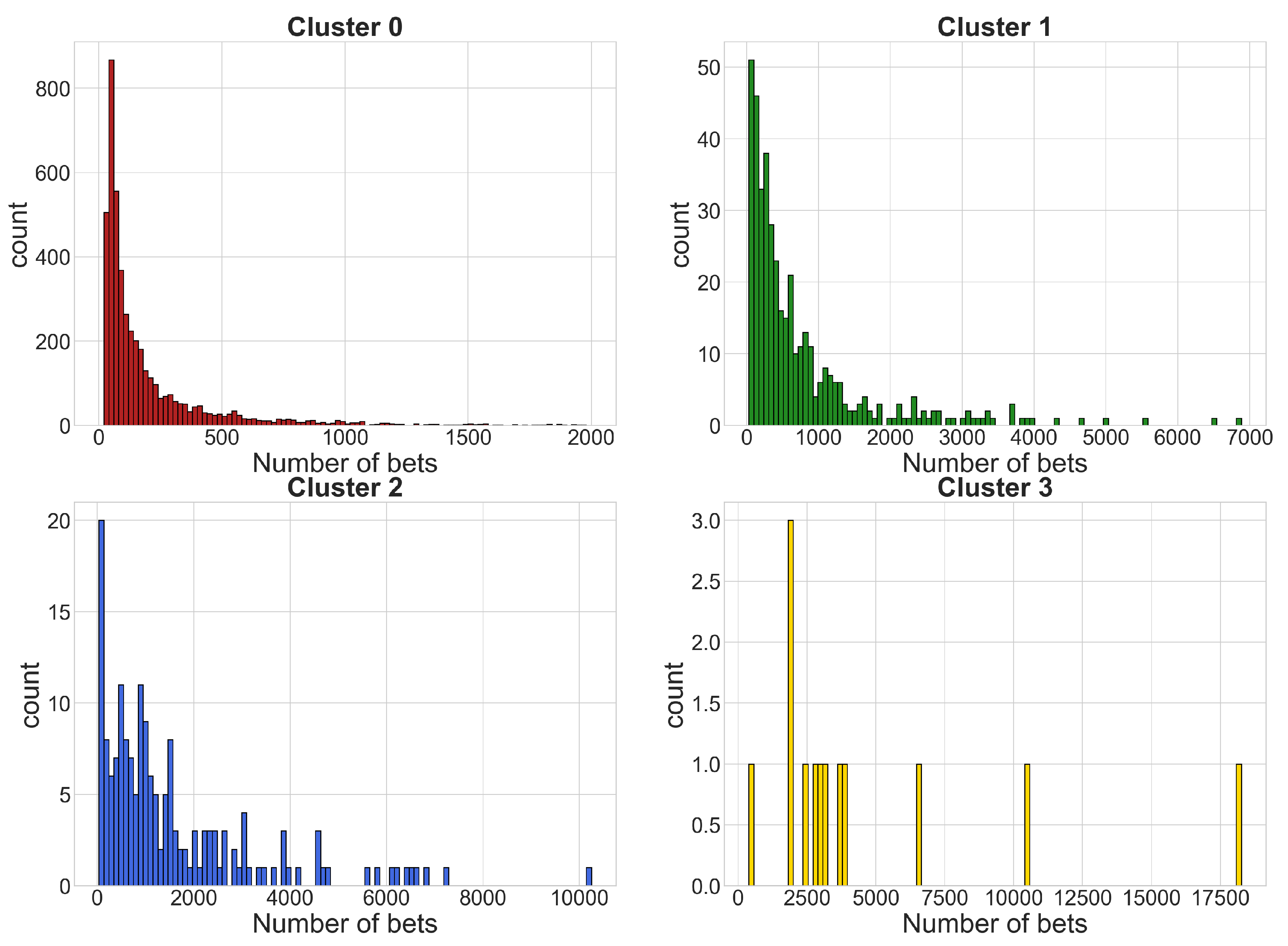
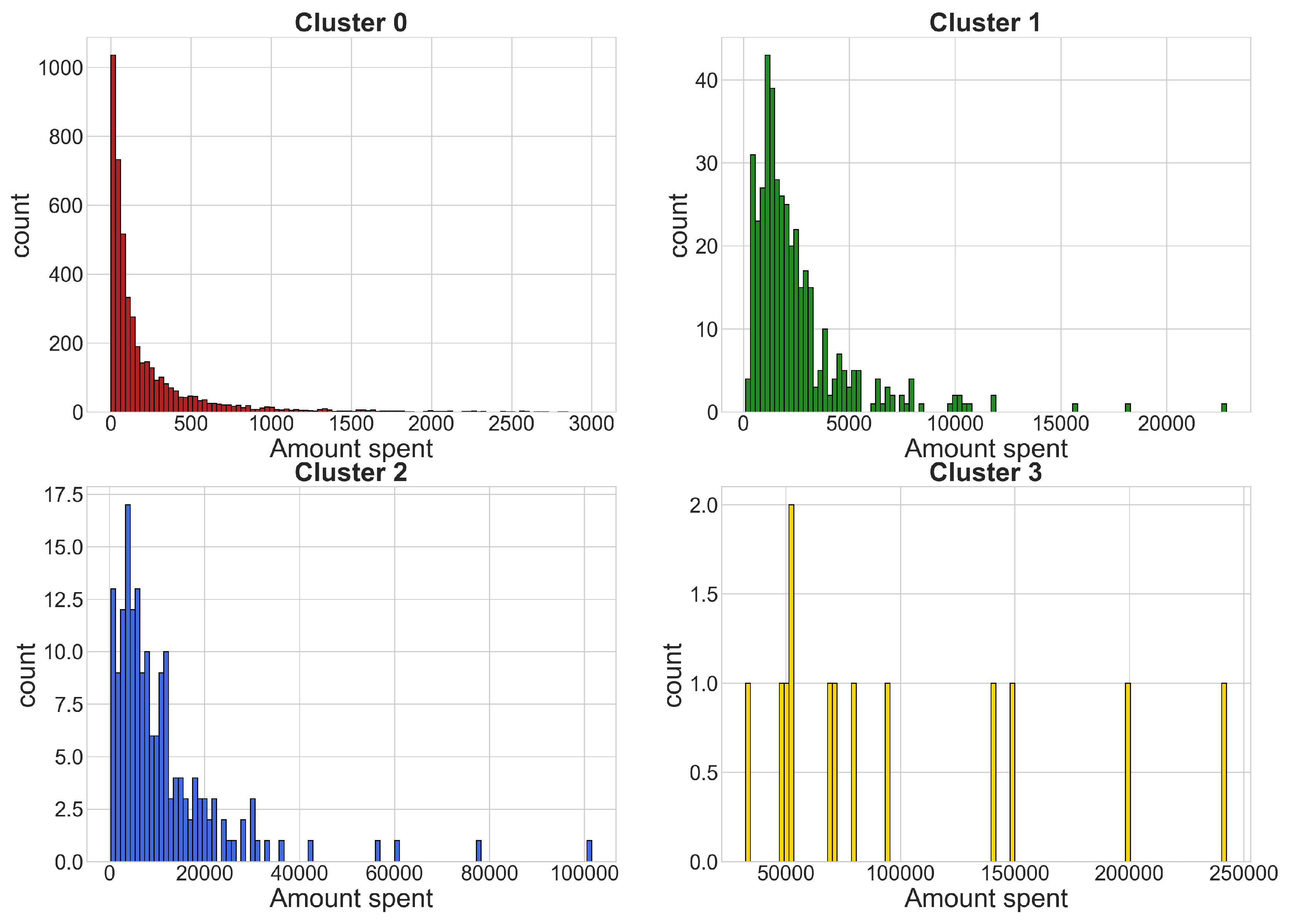
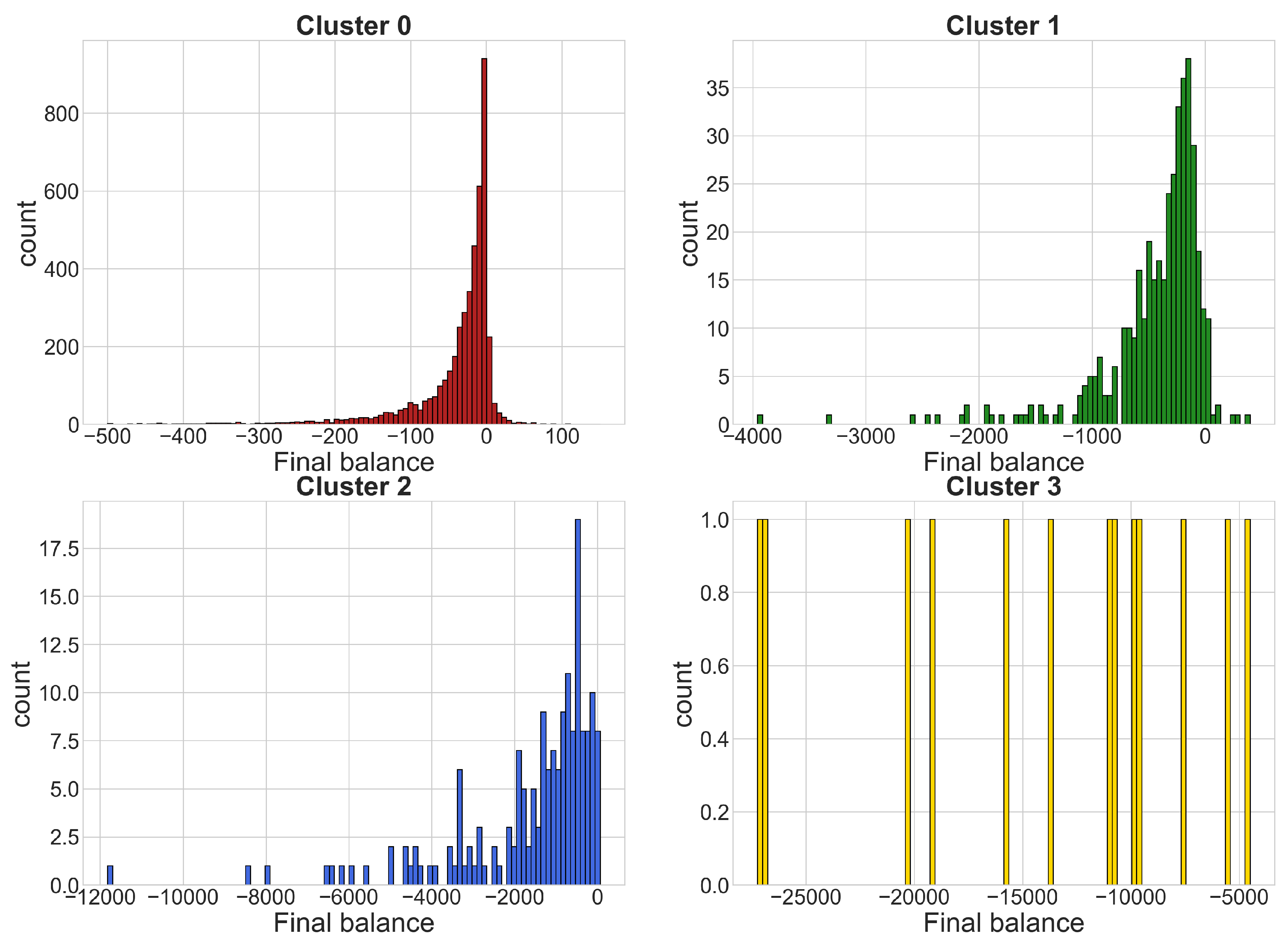
4.1. Sports Dataset
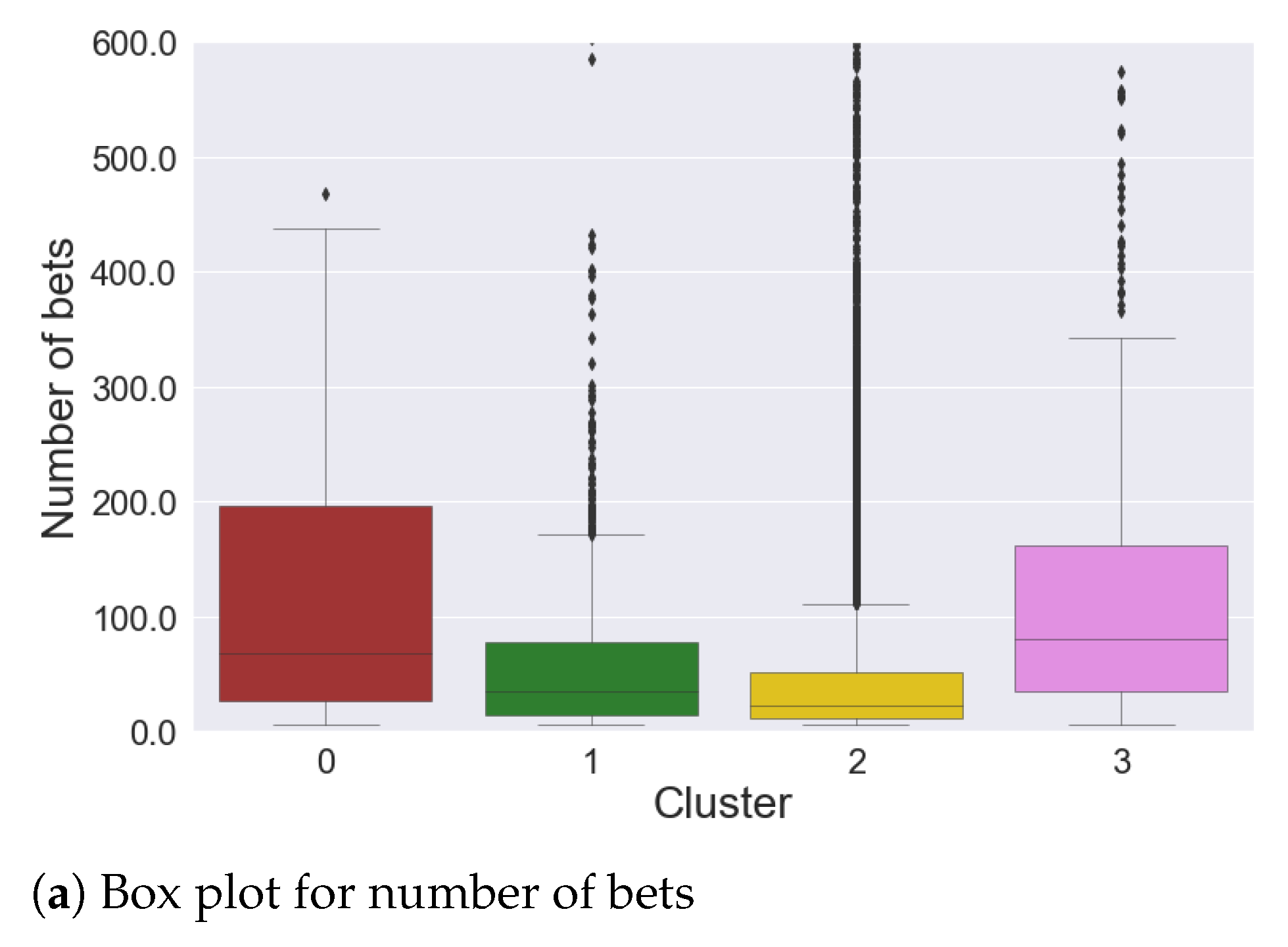
- Cluster 0: 140 time series
- Cluster 1: 1086 time series
- Cluster 2: 13,390 time series
- Cluster 3: 467 time series
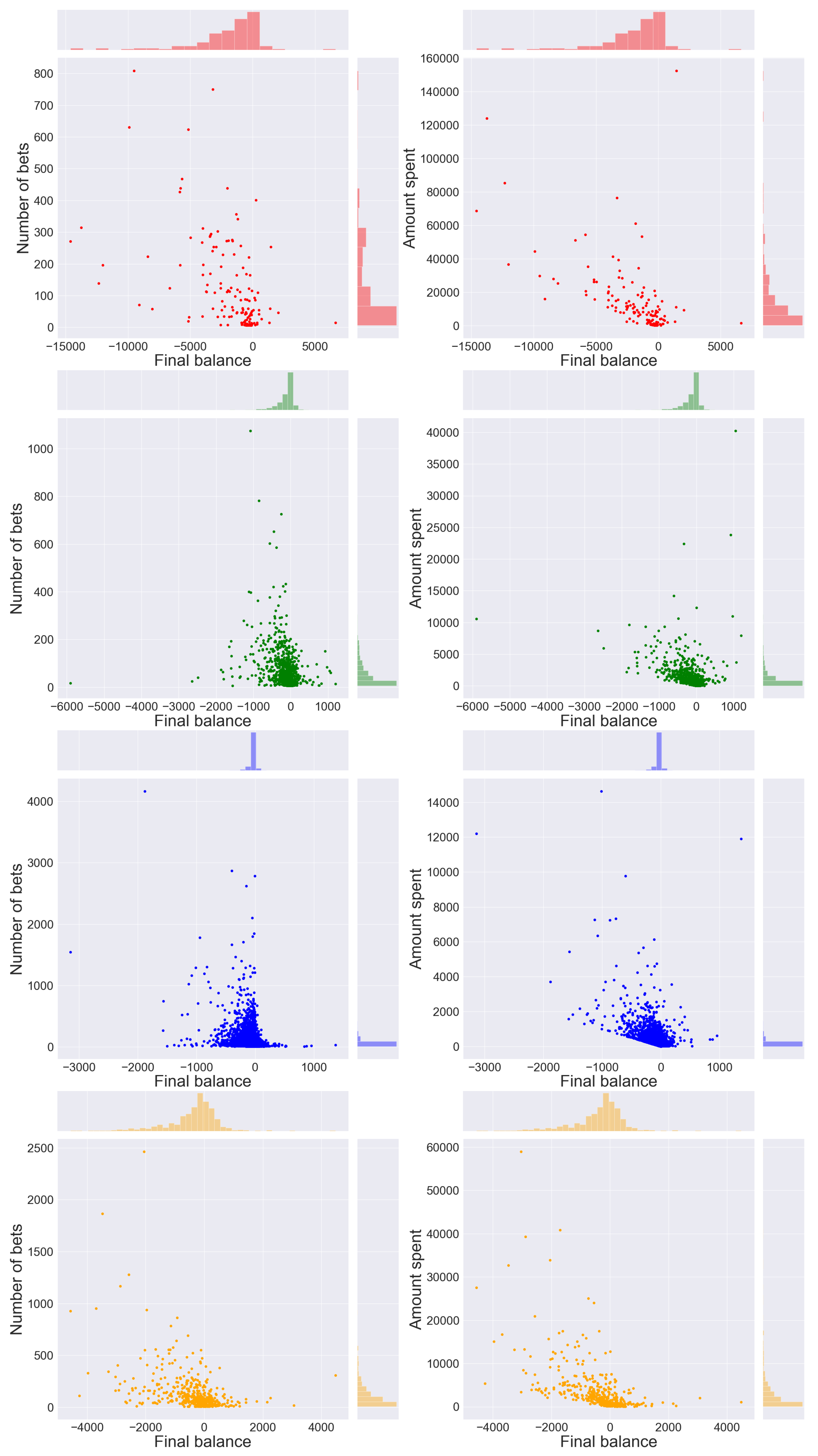
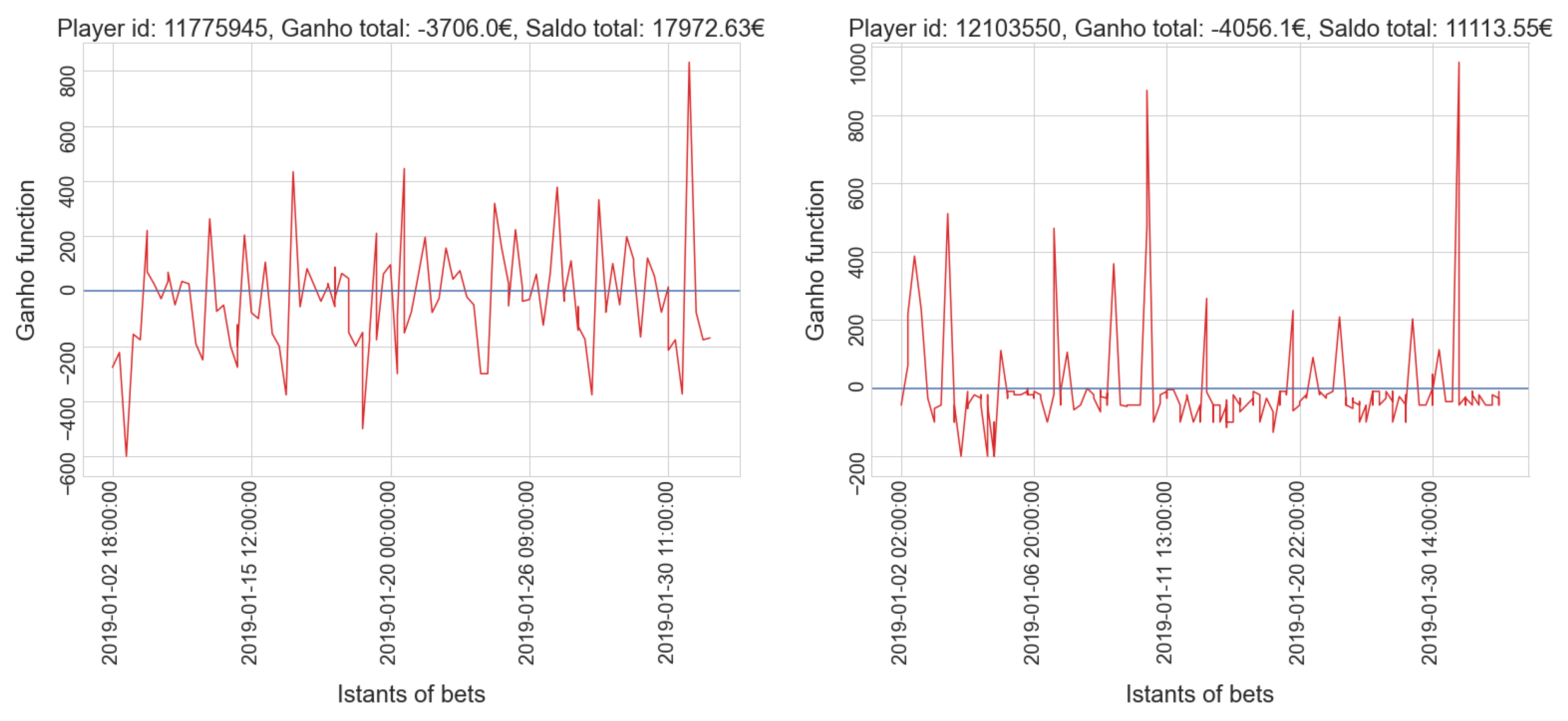
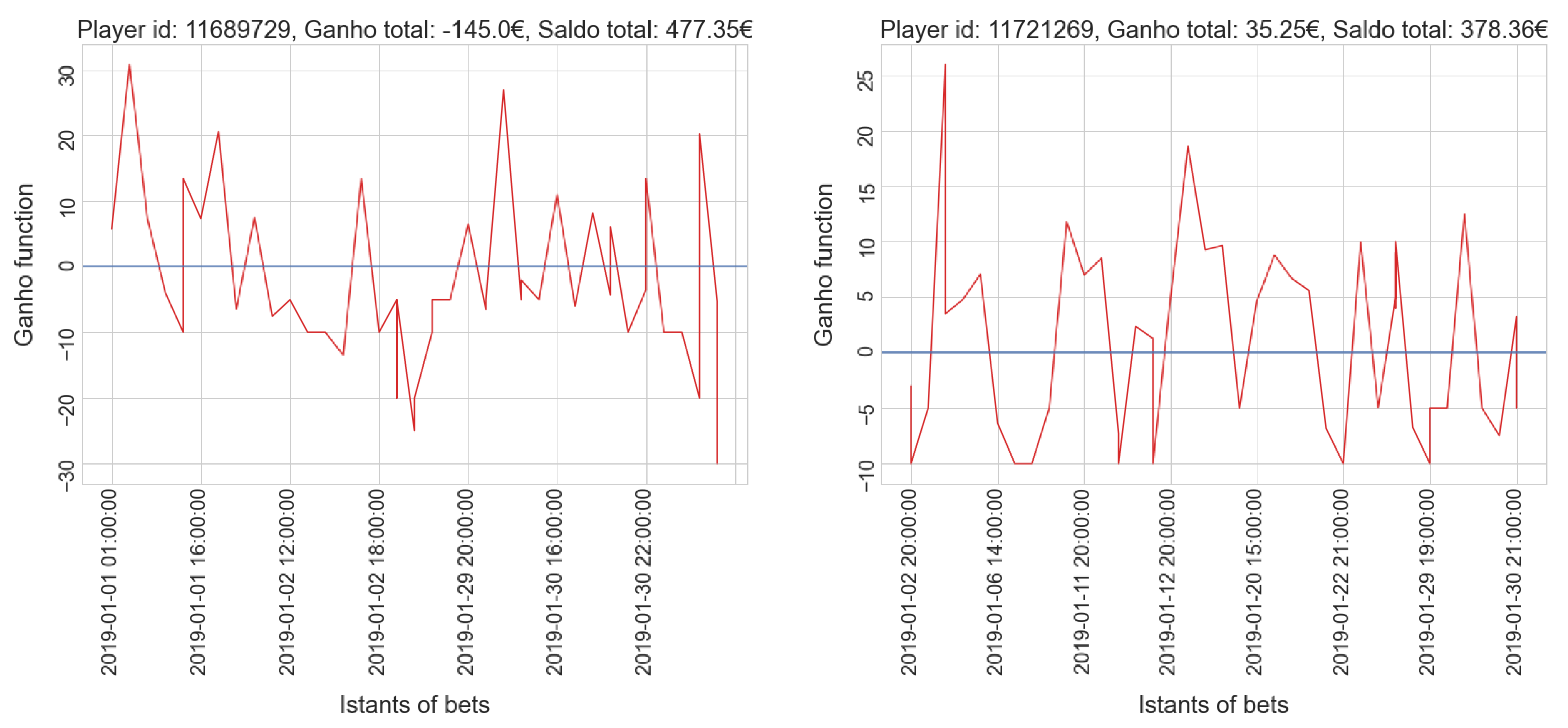
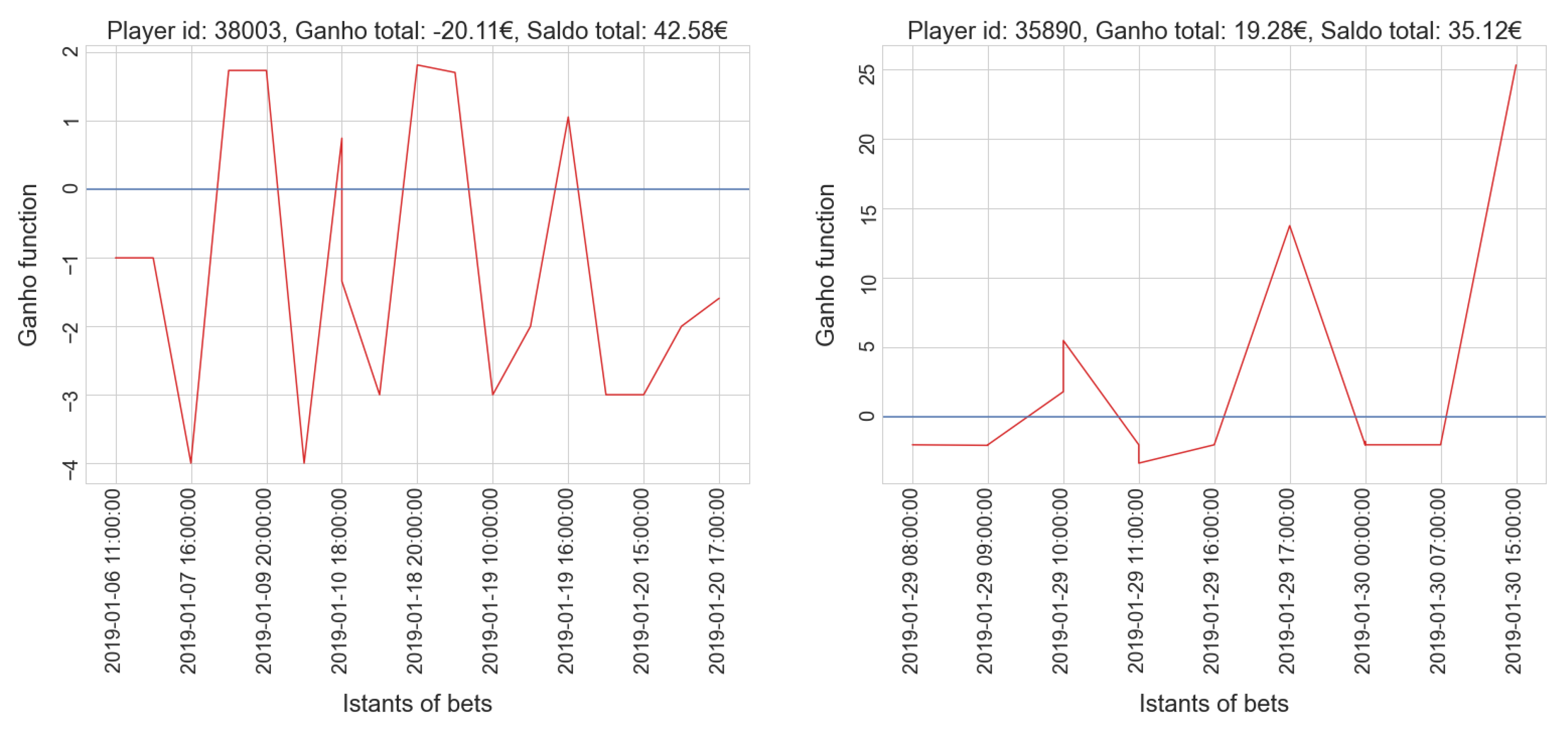
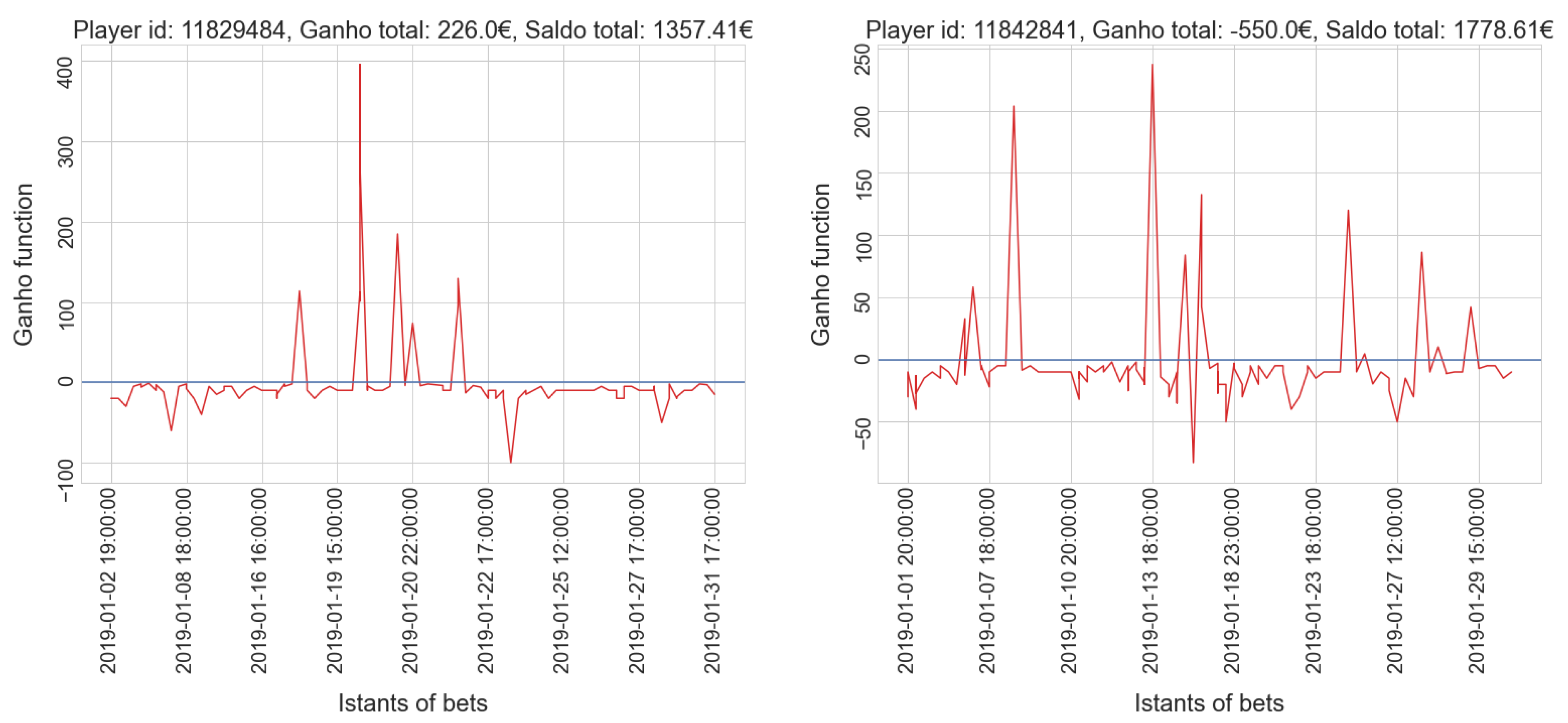
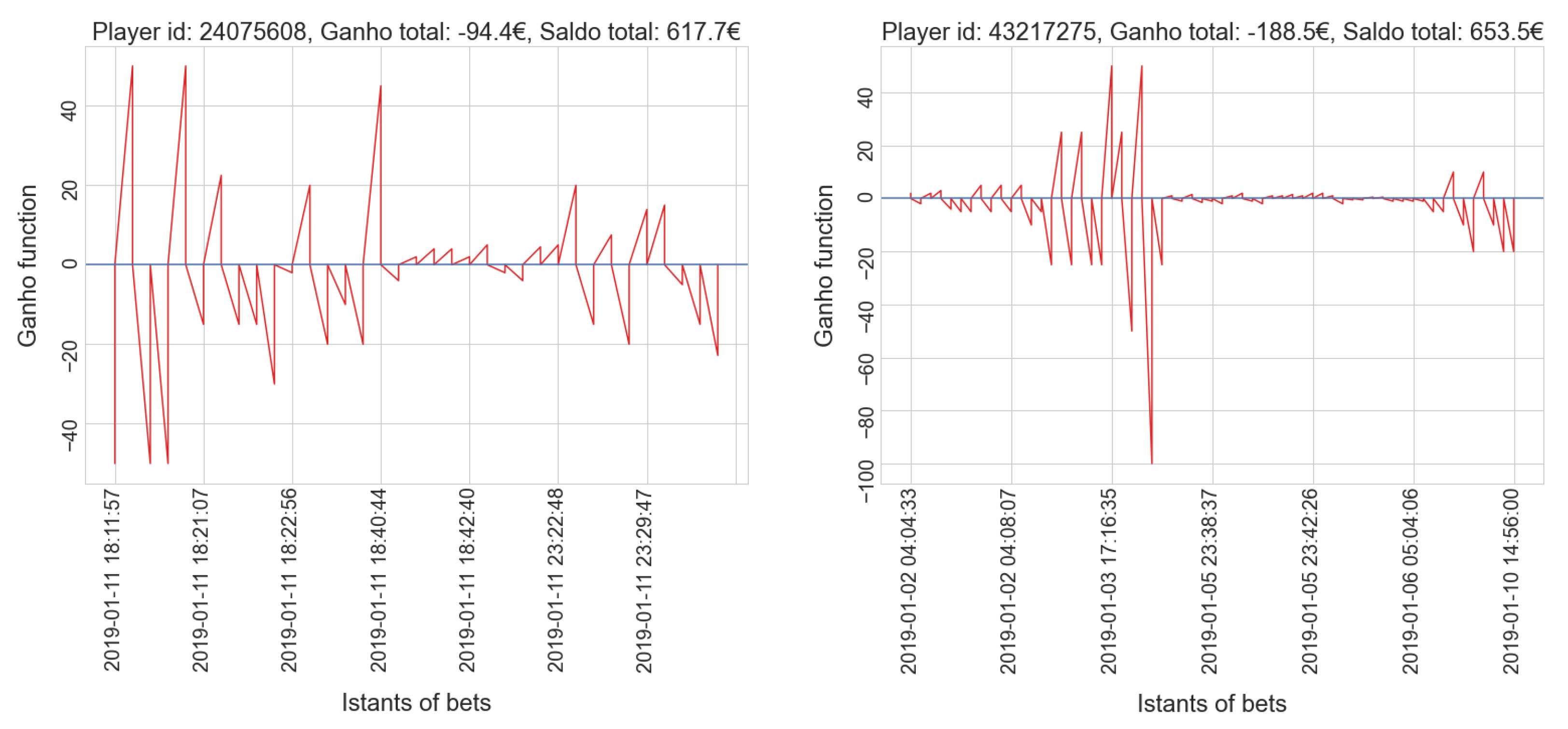
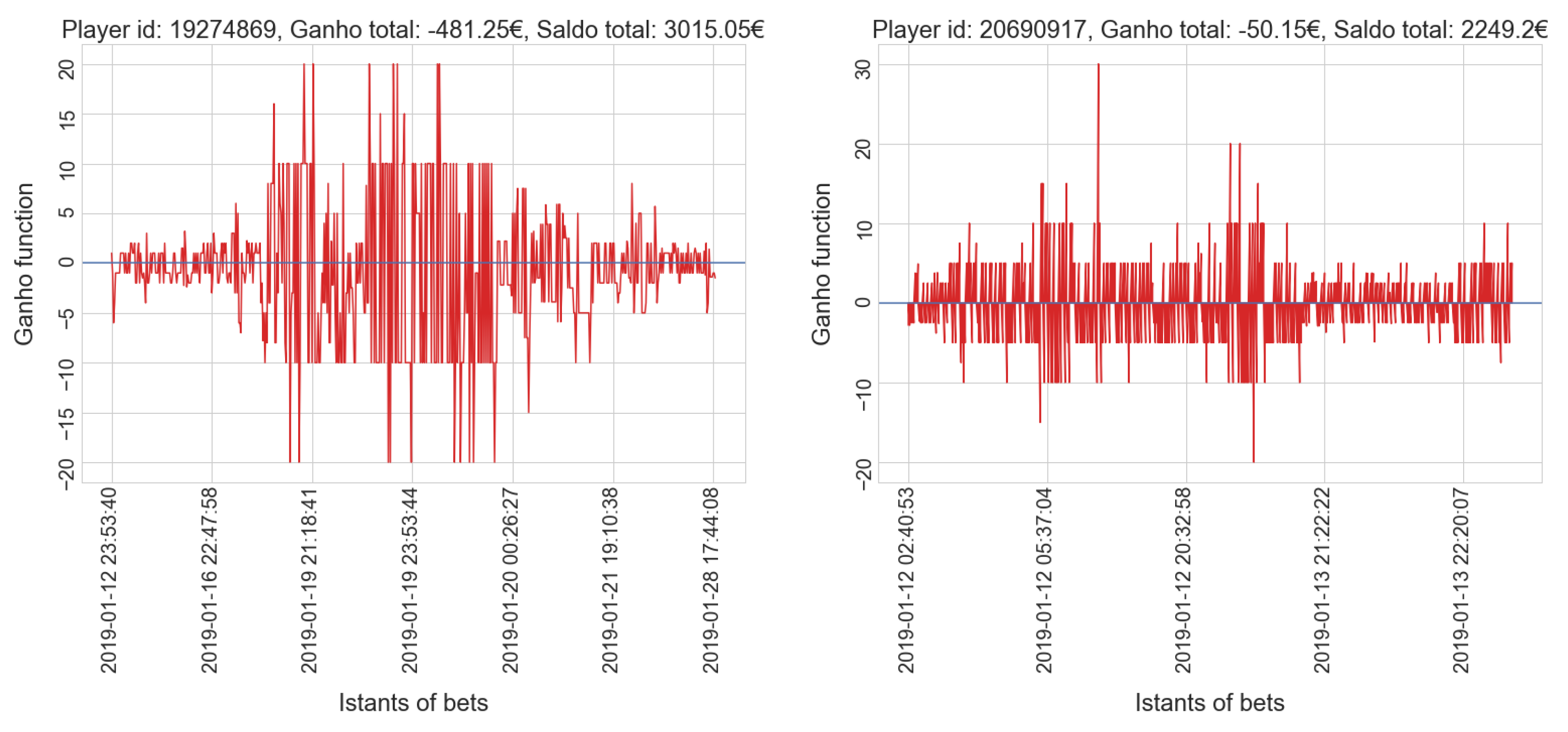
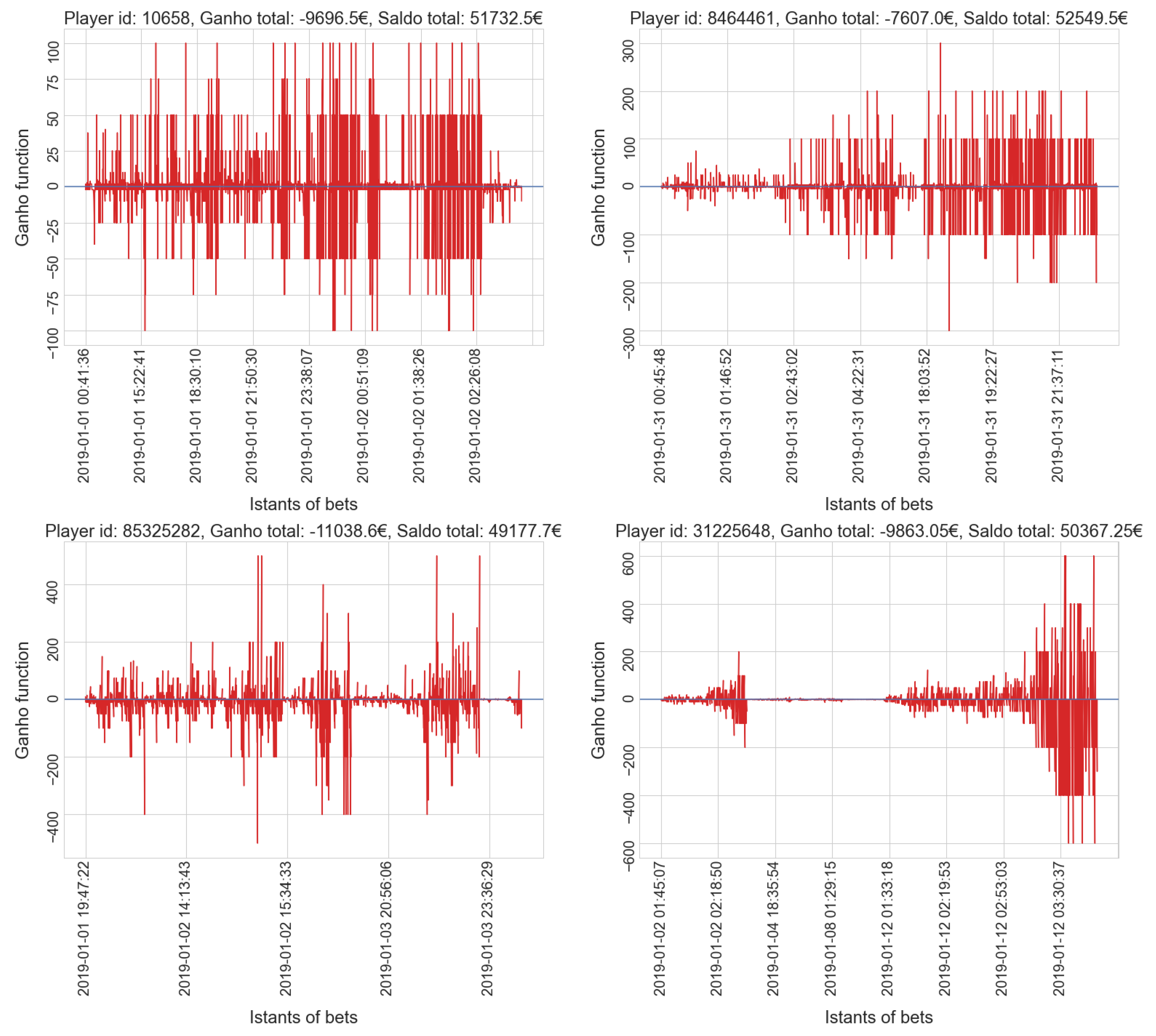
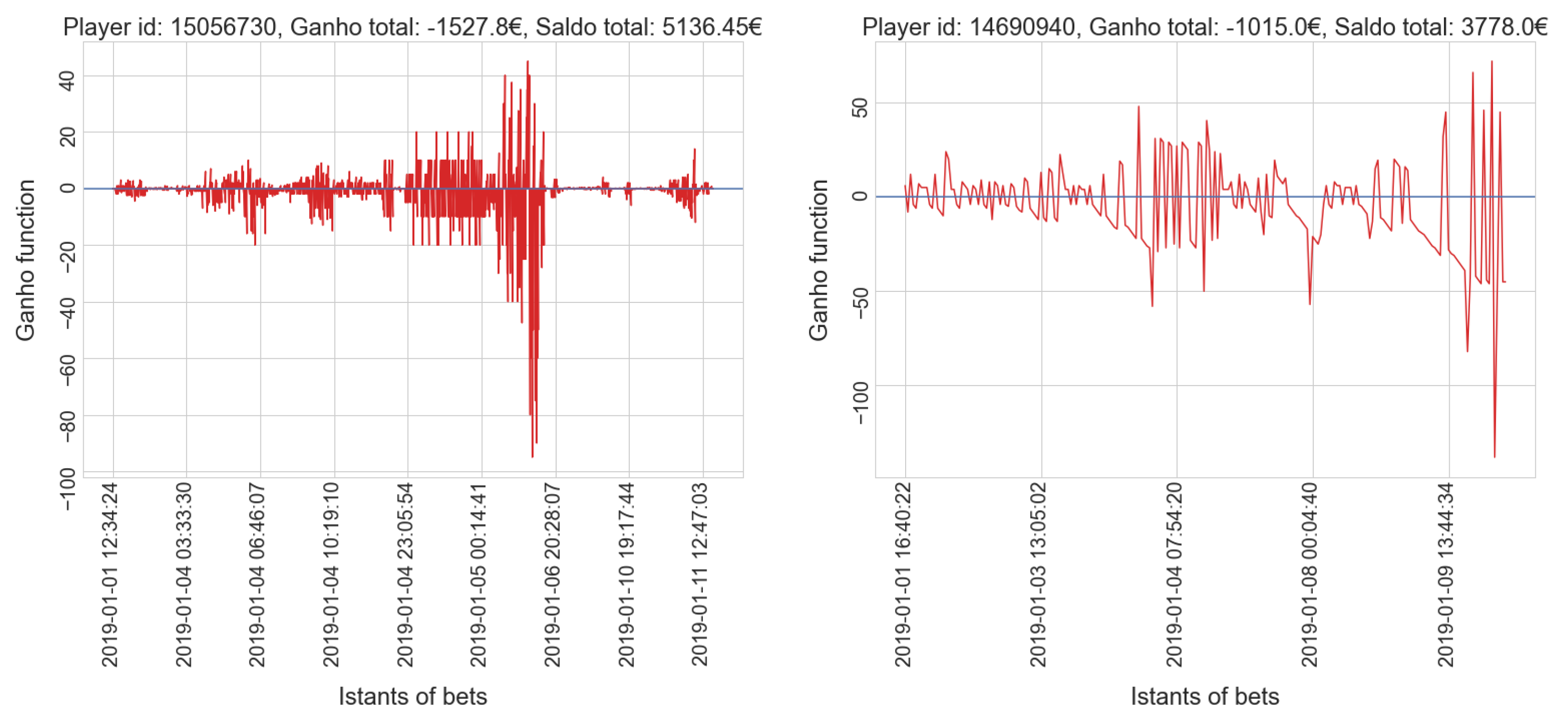
- gamblers who have a positive balance tend to have a low number of placed bets, while only a few players who place many bets actually win.
- gamblers who have a positive balance tend to have a lower amount spent compared to most players in the same cluster; only a few players who invest much money get a positive balance, which is usually very high.
4.2. Black Jack
- Cluster 0: 4575
- Cluster 1: 415
- Cluster 2: 174
- Cluster 3: 13
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Time Series Analysis
Appendix A.1. Dynamic Time Warping
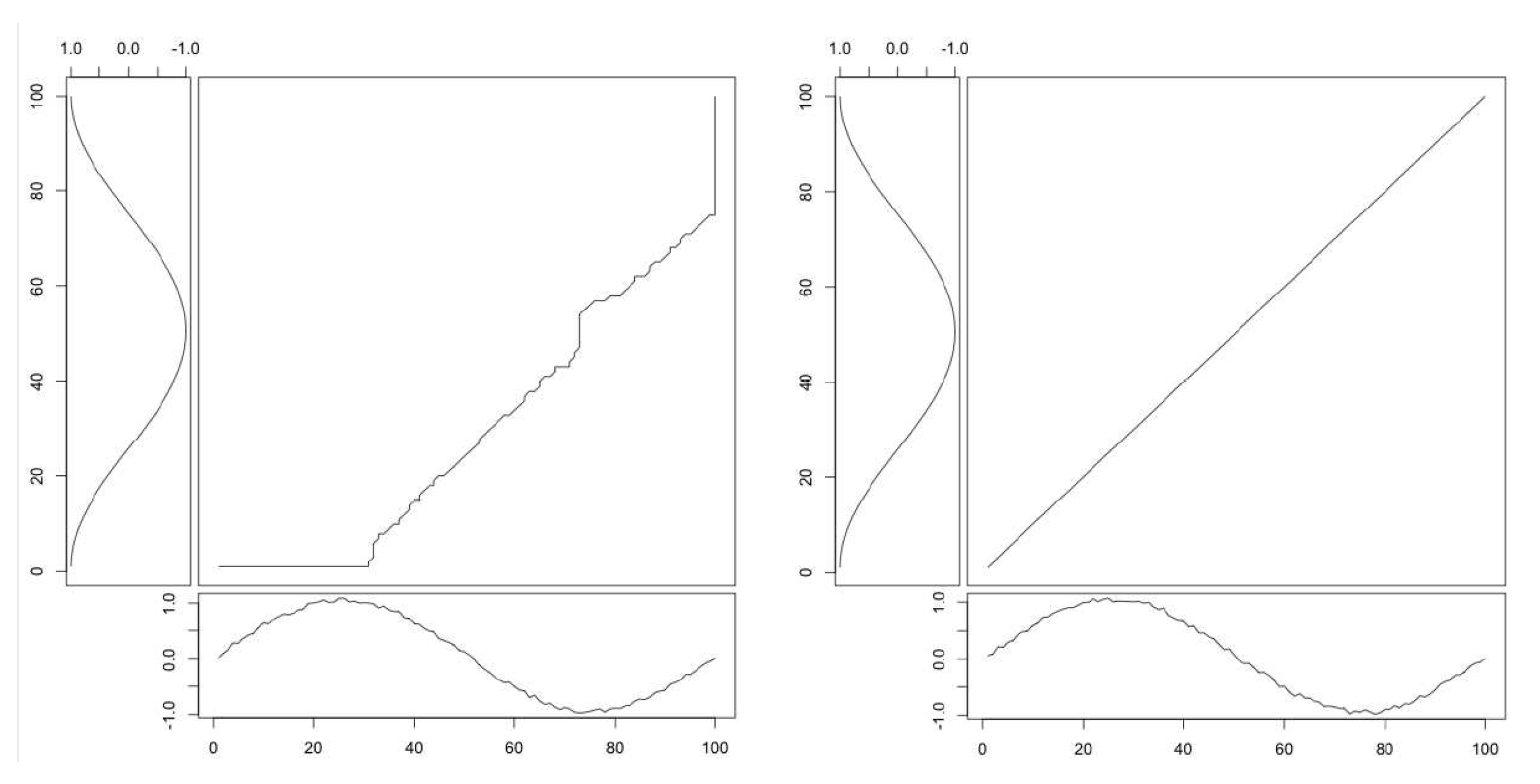
Appendix A.2. Constrained DTW
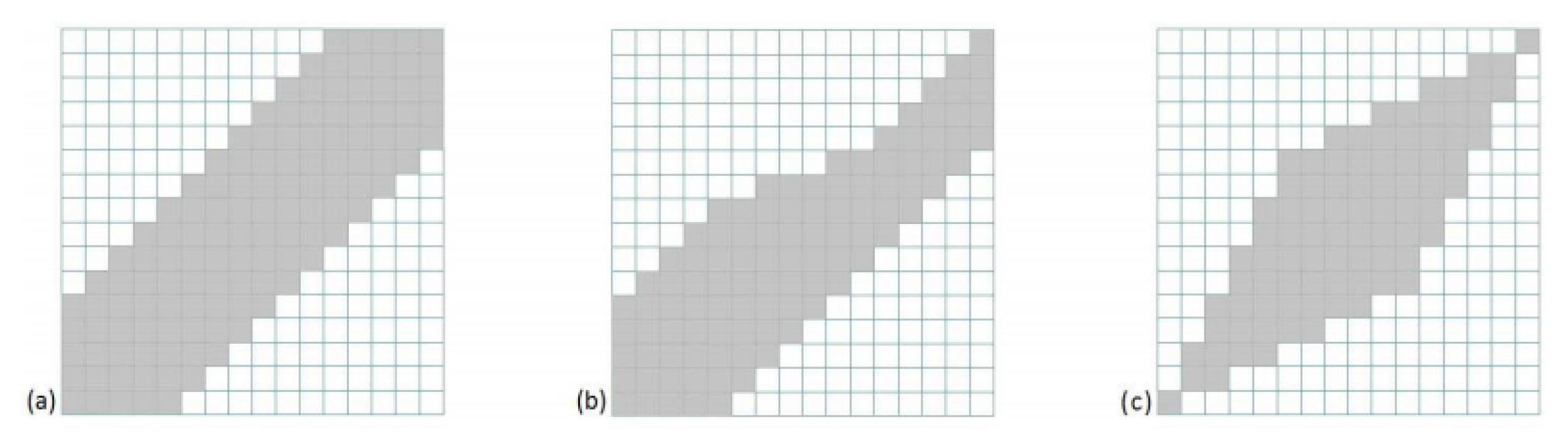
Appendix A.3. Time Series Averaging and Centroid Estimation
Appendix A.4. DTW Barycenter Averaging
- Computing DTW between each individual sequence and the temporary average sequence to be refined, in order to find associations between coordinates of the average sequence and coordinates of the set of sequences.
- Updating each coordinate of the average sequence as the barycenter of coordinates associated with it during the first step.
| Algorithm A1: DBA. |
 |
Appendix A.5. K-Means for Time Series under DTW
| Algorithm A2: k-means clustering. |
 |
| Algorithm A3: Time series k-means. |
 |
References
- Schneider, S. Towards a comprehensive European framework on online gaming. Gaming Law Rev. Econ. 2013, 17, 6–7. [Google Scholar] [CrossRef]
- European Gambling and Betting Association. Market Reality; EGBA: Brussels, Belgium, 2016. [Google Scholar]
- Jensen, C. Money over misery: Restrictive gambling legislation in an era of liberalization. J. Eur. Public Policy 2017, 24, 119–134. [Google Scholar] [CrossRef]
- Cowlishaw, S.; Kessler, D. Problem gambling in the UK: Implications for health, psychosocial adjustment and health care utilization. Eur. Addict. Res. 2016, 22, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Browne, M.; Greer, N.; Armstrong, T.; Doran, C.; Kinchin, I.; Langham, E.; Rockloff, M. The Social Cost of Gambling to Victoria; Victorian Responsible Gambling Foundation: North Melbourne, Australia, 2017.
- Coussement, K.; De Bock, K.W. Customer churn prediction in the online gambling industry: The beneficial effect of ensemble learning. J. Bus. Res. 2013, 66, 1629–1636. [Google Scholar] [CrossRef]
- Percy, C.; França, M.; Dragičević, S.; d’Avila Garcez, A. Predicting online gambling self-exclusion: An analysis of the performance of supervised machine learning models. Int. Gambl. Stud. 2016, 16, 193–210. [Google Scholar] [CrossRef]
- Ladouceur, R.; Shaffer, P.; Blaszczynski, A.; Shaffer, H.J. Responsible gambling: A synthesis of the empirical evidence. Addict. Res. Theory 2017, 25, 225–235. [Google Scholar] [CrossRef]
- Haeusler, J. Follow the money: Using payment behavior as predictor for future self-exclusion. Int. Gambl. Stud. 2016, 16, 246–262. [Google Scholar] [CrossRef]
- Philander, K.S. Identifying high-risk online gamblers: A comparison of data mining procedures. Int. Gambl. Stud. 2014, 14, 53–63. [Google Scholar] [CrossRef]
- Wood, R.T.; Wohl, M.J. Assessing the effectiveness of a responsible gambling behavioral feedback tool for reducing the gambling expenditure of at-risk players. Int. Gambl. Stud. 2015, 15, 1–16. [Google Scholar] [CrossRef]
- Auer, M.; Griffiths, M.D. An empirical investigation of theoretical loss and gambling intensity. J. Gambl. Stud. 2014, 30, 879–887. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gustafson, J. Using Machine Learning to Identify Potential Problem Gamblers. Master’s Thesis, Umeå University, Umeå, Sweden, 2019. [Google Scholar]
- Auer, M.; Griffiths, M.D. Predicting limit-setting behavior of gamblers using machine learning algorithms: A real-world study of Norwegian gamblers using account data. Int. J. Ment. Health Addict. 2019, 1–18. [Google Scholar] [CrossRef]
- Rabiner, L.; Juang, B.H.; Lee, C.H. An overview of automatic speech recognition. In Automatic Speech and Speaker Recognition; Springer: Boston, MA, USA, 1996; pp. 1–30. [Google Scholar]
- Itakura, F. Minimum prediction residual principle applied to speech recognition. IEEE Trans. Acoust. Speech Signal Process. 1975, 23, 67–72. [Google Scholar] [CrossRef]
- Kruskal, J.B.; Liberman, M. The Symmetric Time-Warping Problem: From Continuous to Discrete. In Time Warps, String Edits, and Macromolecules—The Theory and Practice of Sequence Comparison; Sankoff, D., Kruskal, J.B., Eds.; CSLI Publications: Stanford, CA, USA, 1999; Chapter 4. [Google Scholar]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Cassisi, C.; Montalto, P.; Aliotta, M.; Cannata, A.; Pulvirenti, A. Similarity measures and dimensionality reduction techniques for time series data mining. Adv. Data Min. Knowl. Discov. Appl. 2012, 71–96. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. Scaling up dynamic time warping for datamining applications. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 285–289. [Google Scholar]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Andrade-Cetto, L. Constrained Dynamic Time Warping. U.S. Patent 7,904,410, 8 March 2011. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]




| Data Preparation | ||||
|---|---|---|---|---|
| Type of Game | # of Raw Datasets | Total Size Raw Datasets | Size Final Dataset | # of Time Series |
| Sports | 7 | 5.40 GB | 101 MB | 15,081 |
| Black Jack | 5 | 481 MB | 72.6 MB | 5177 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peres, F.; Fallacara, E.; Manzoni, L.; Castelli, M.; Popovič, A.; Rodrigues, M.; Estevens, P. Time Series Clustering of Online Gambling Activities for Addicted Users’ Detection. Appl. Sci. 2021, 11, 2397. https://doi.org/10.3390/app11052397
Peres F, Fallacara E, Manzoni L, Castelli M, Popovič A, Rodrigues M, Estevens P. Time Series Clustering of Online Gambling Activities for Addicted Users’ Detection. Applied Sciences. 2021; 11(5):2397. https://doi.org/10.3390/app11052397
Chicago/Turabian StylePeres, Fernando, Enrico Fallacara, Luca Manzoni, Mauro Castelli, Aleš Popovič, Miguel Rodrigues, and Pedro Estevens. 2021. "Time Series Clustering of Online Gambling Activities for Addicted Users’ Detection" Applied Sciences 11, no. 5: 2397. https://doi.org/10.3390/app11052397
APA StylePeres, F., Fallacara, E., Manzoni, L., Castelli, M., Popovič, A., Rodrigues, M., & Estevens, P. (2021). Time Series Clustering of Online Gambling Activities for Addicted Users’ Detection. Applied Sciences, 11(5), 2397. https://doi.org/10.3390/app11052397










