A Dual-Mass Resonant MEMS Gyroscope Design with Electrostatic Tuning for Frequency Mismatch Compensation
Abstract
1. Introduction
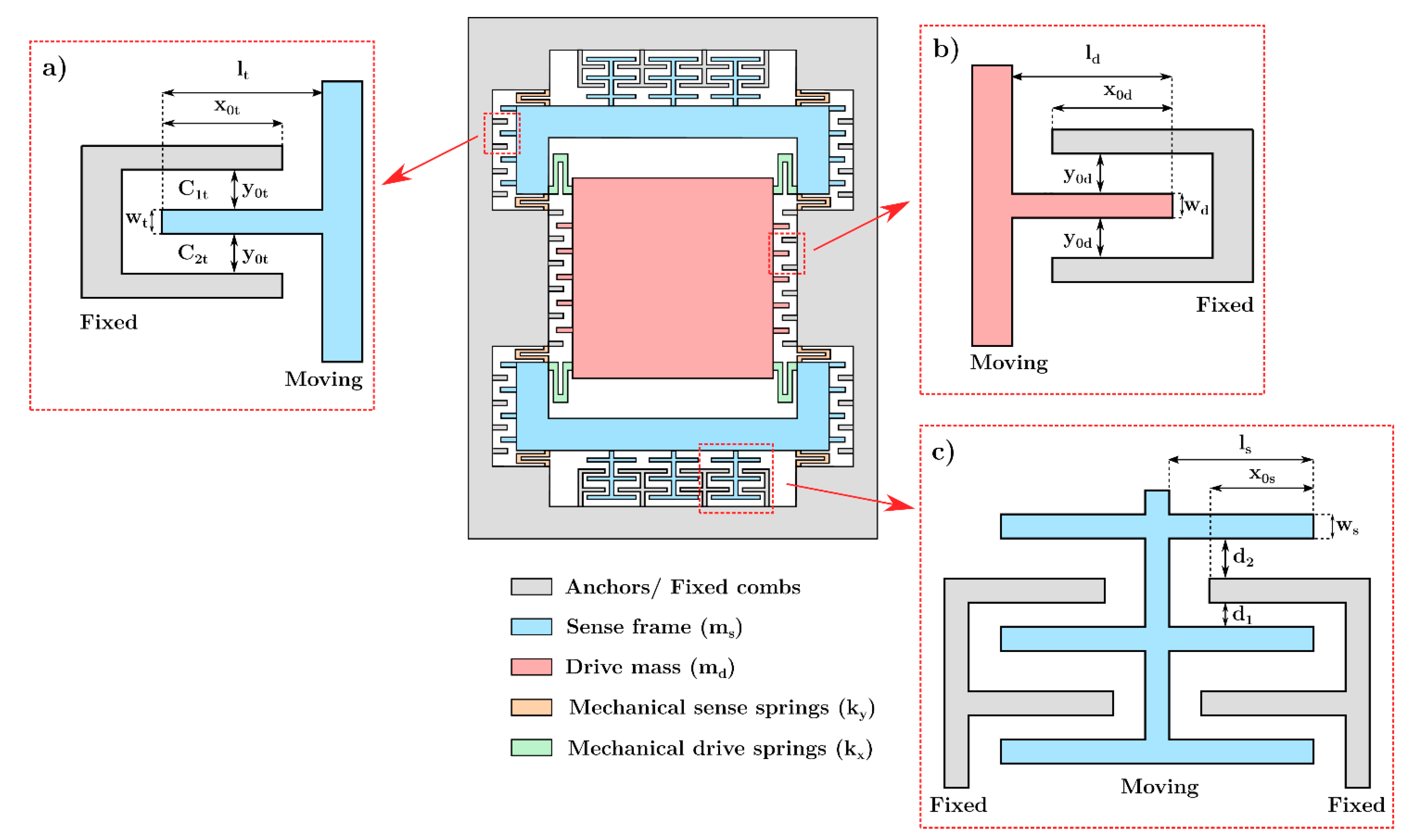
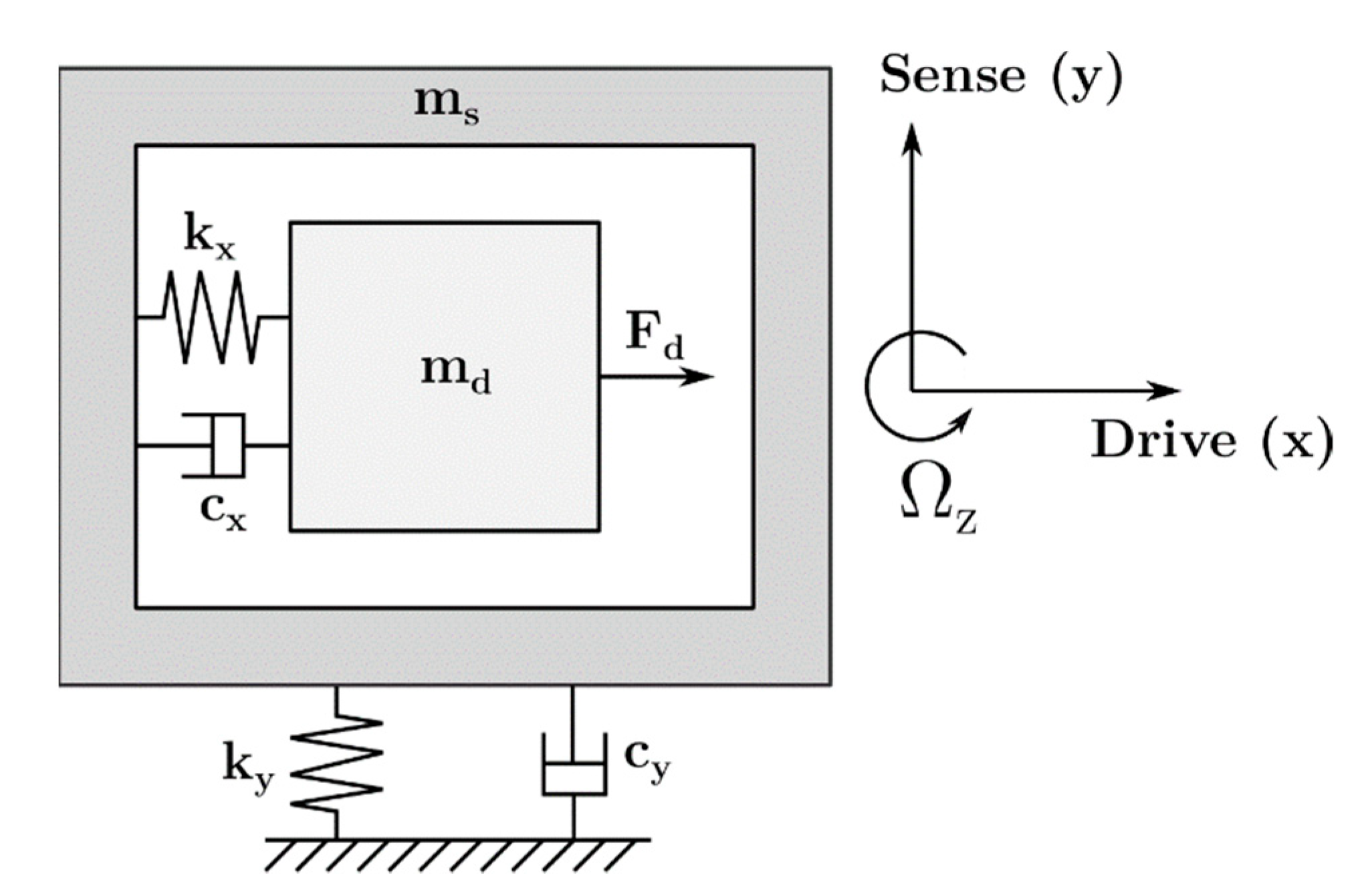
2. Mechanical Design and Working Principle
3. Mathematical Model of the Proposed MEMS Gyroscope
3.1. Stiffness Calculation for the Mechanical Beams
3.2. Electrostatic Tuning for Mode-Matching
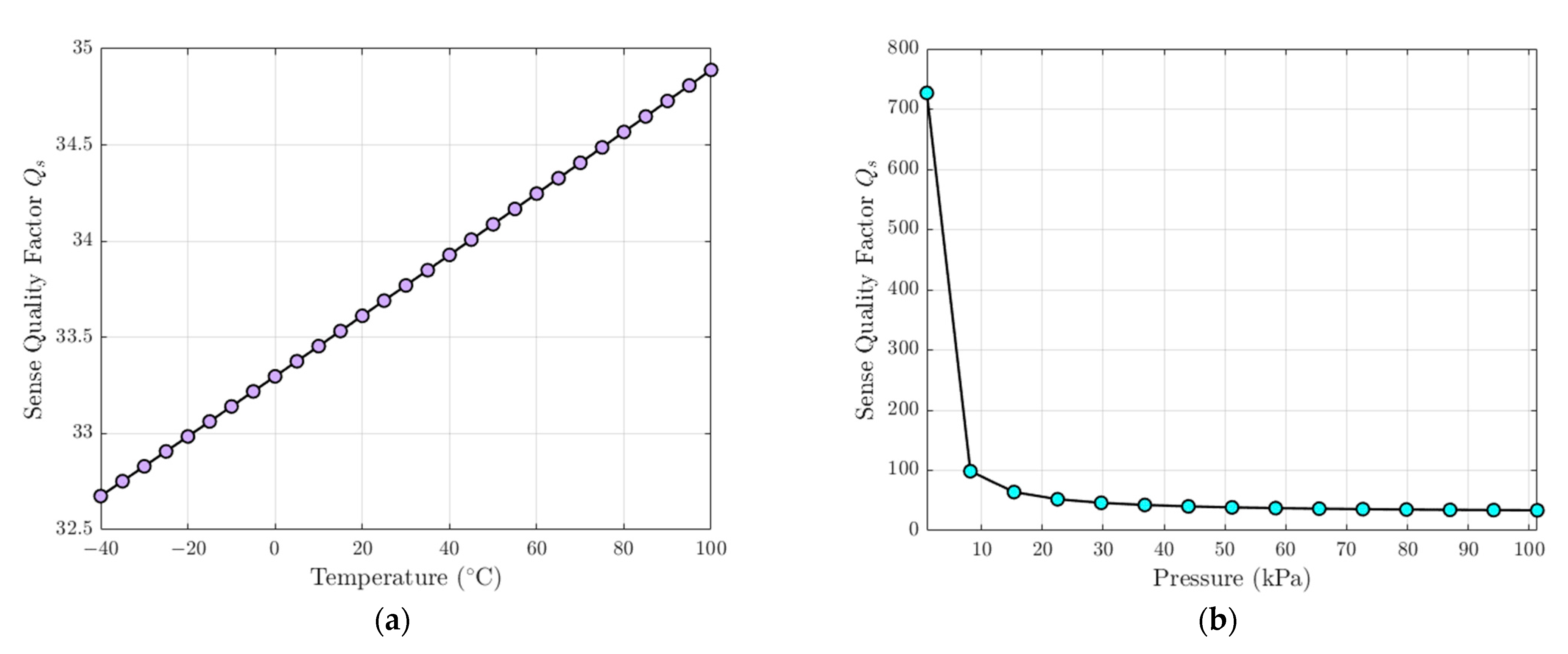
3.3. Air Damping Model for MEMS Gyroscope
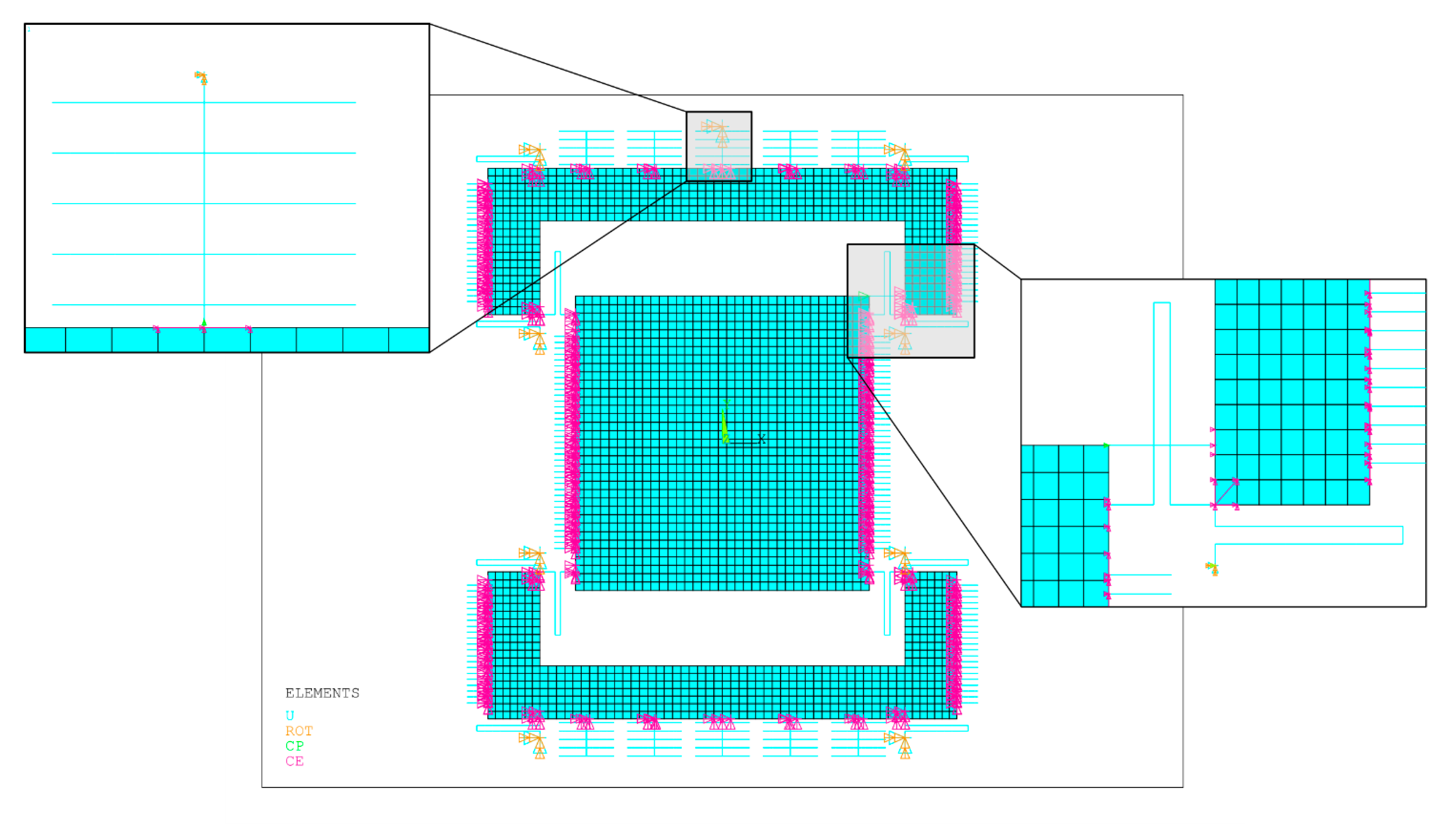
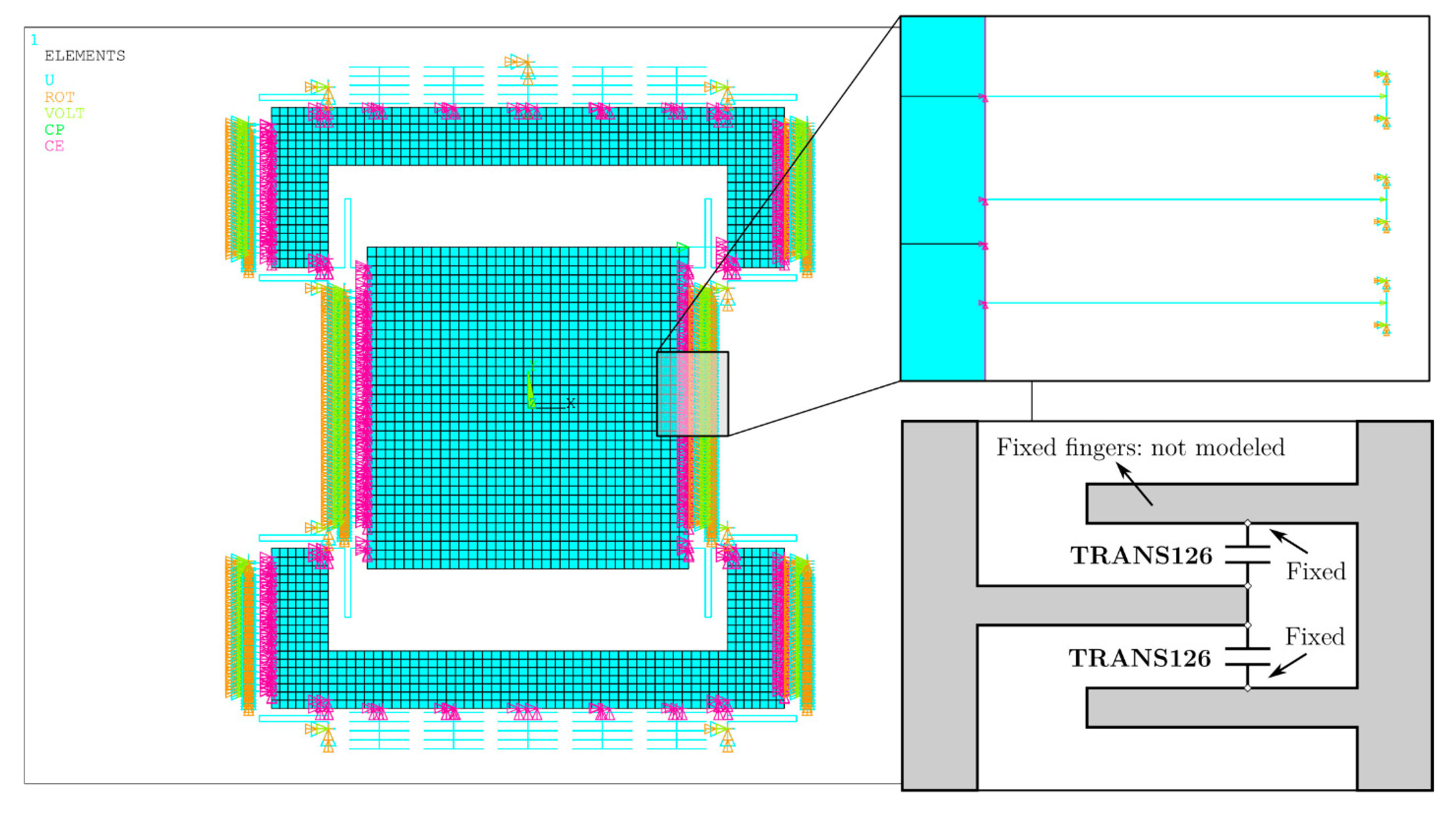
4. Multiphysics FEM Model of the Proposed MEMS Gyroscope
5. FEM Simulations
5.1. Static Analysis
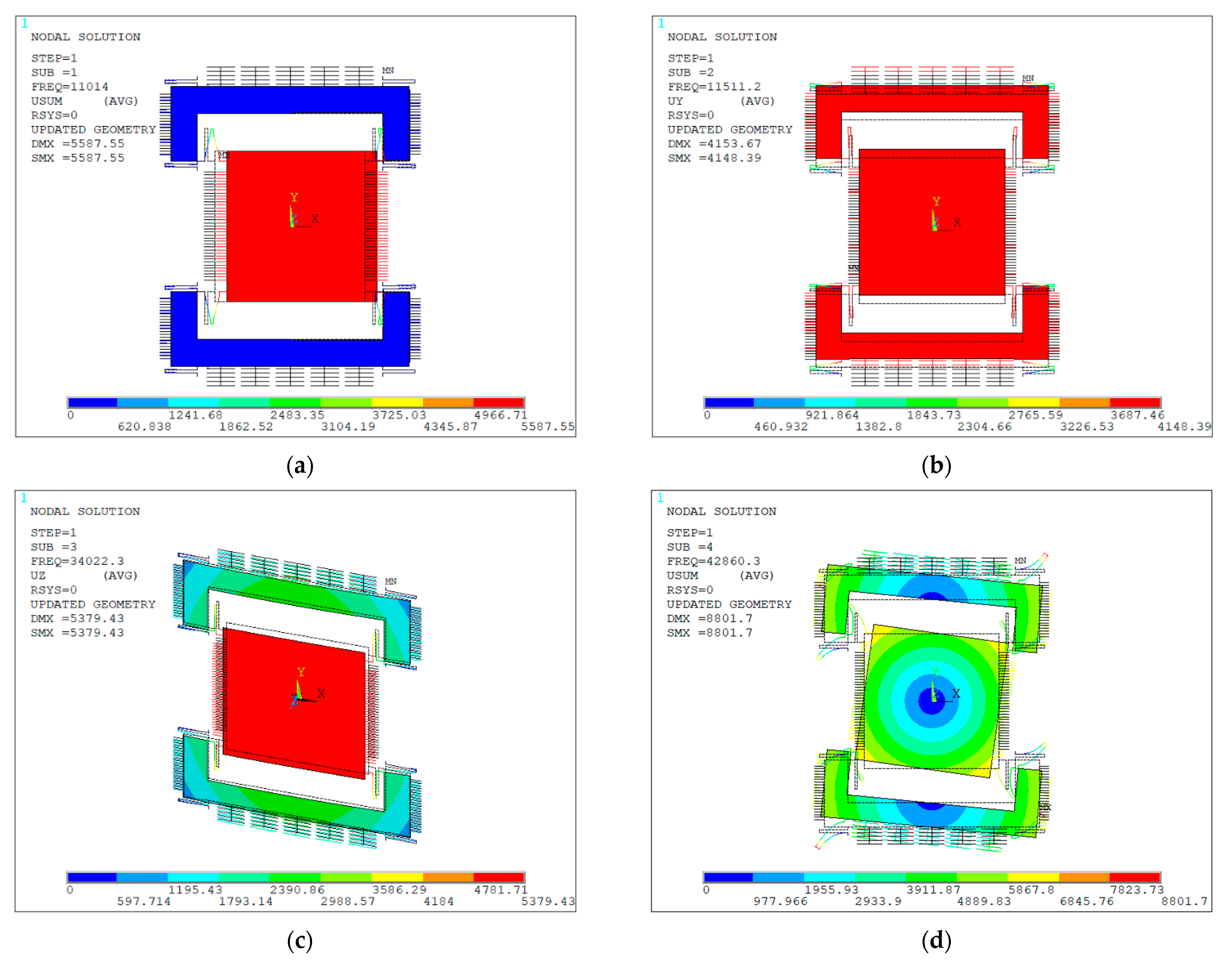
5.2. Modal Analysis
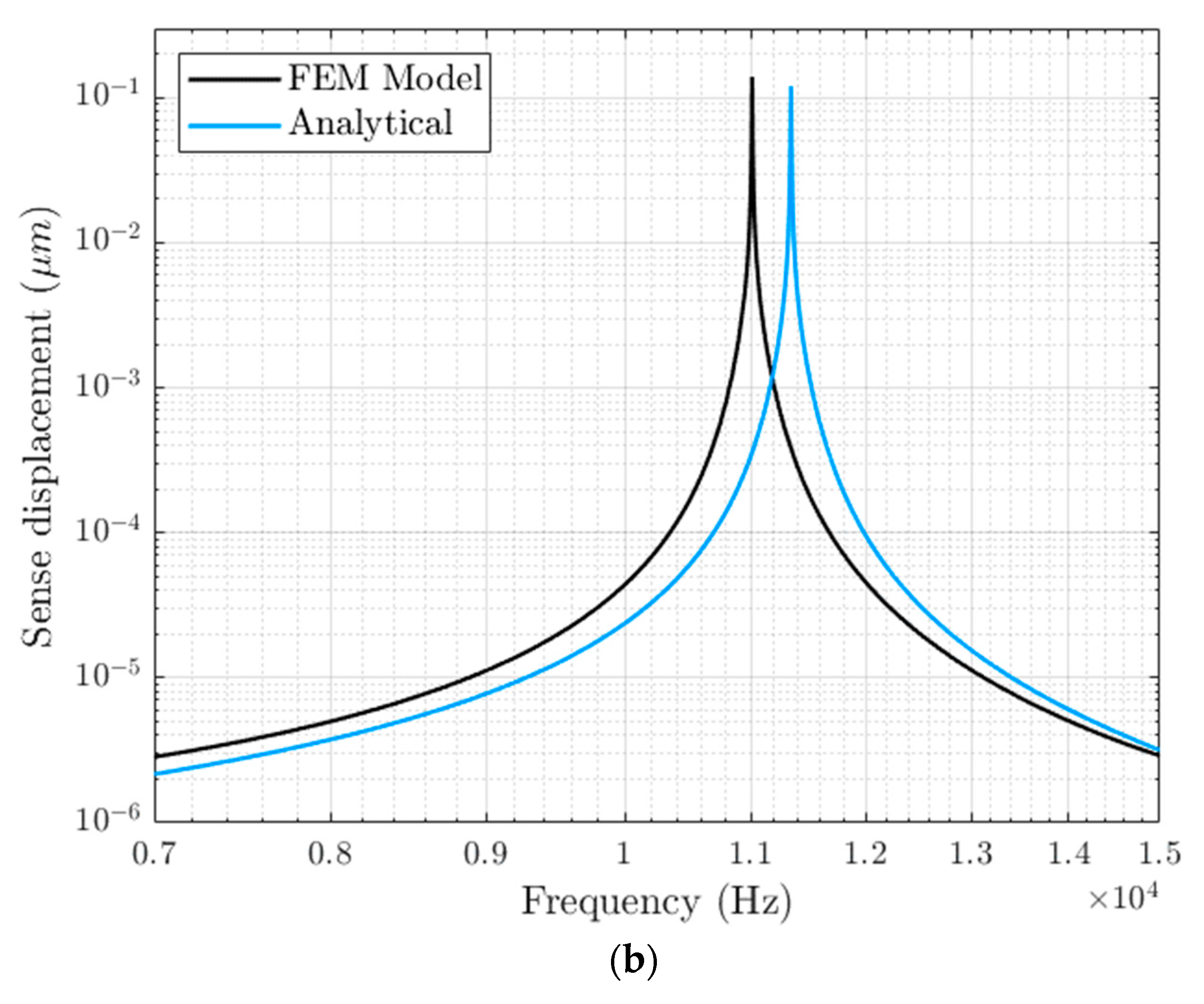
5.3. Dynamic Analysis
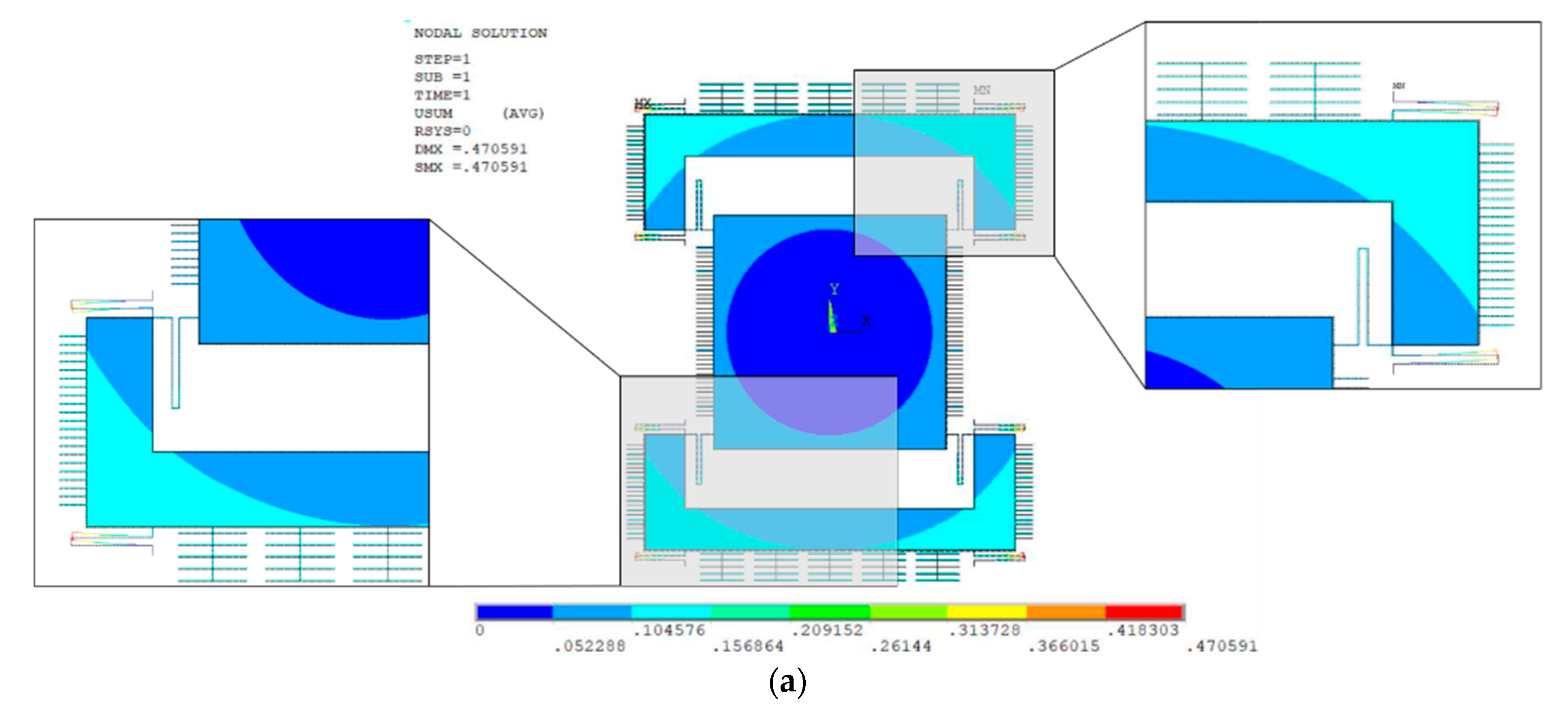
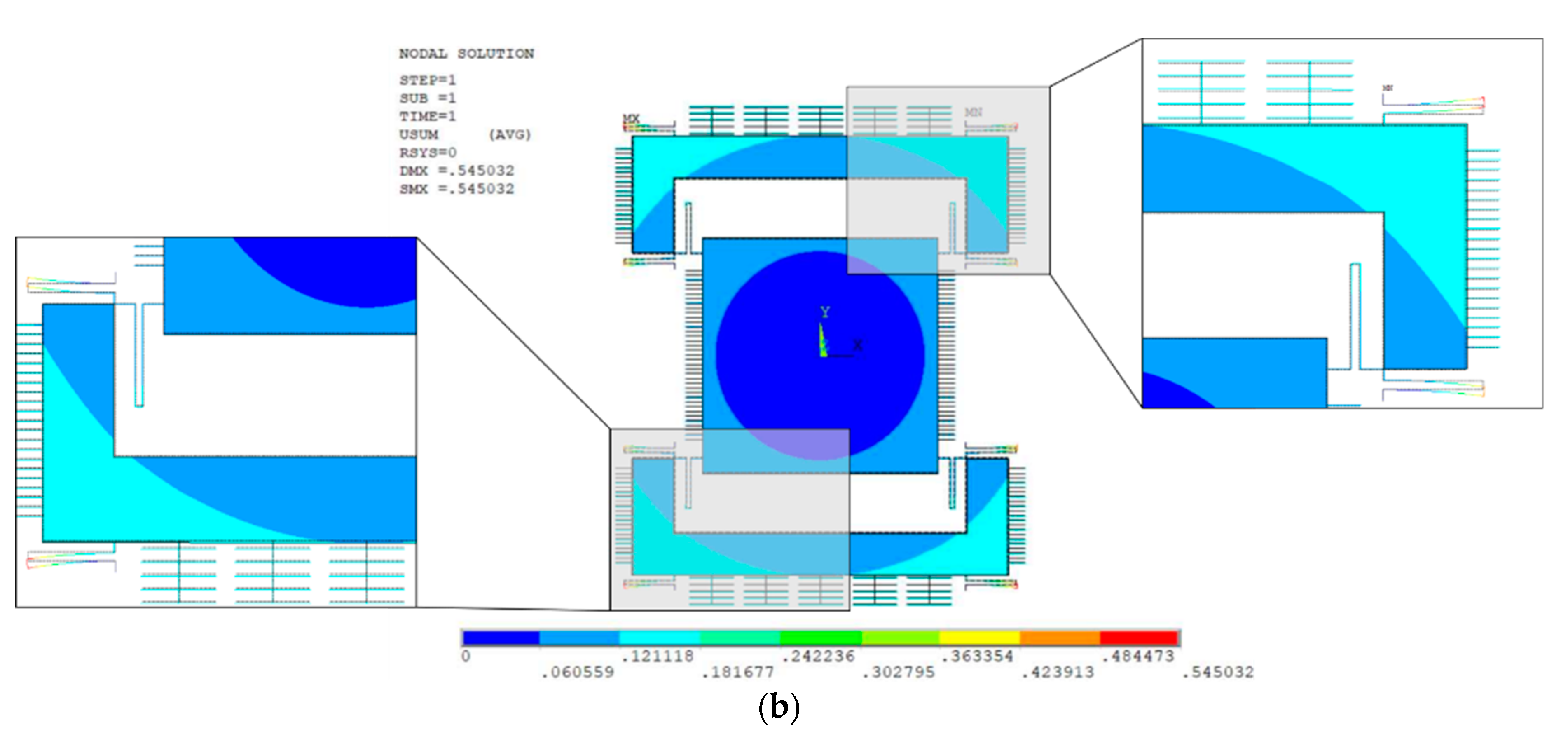
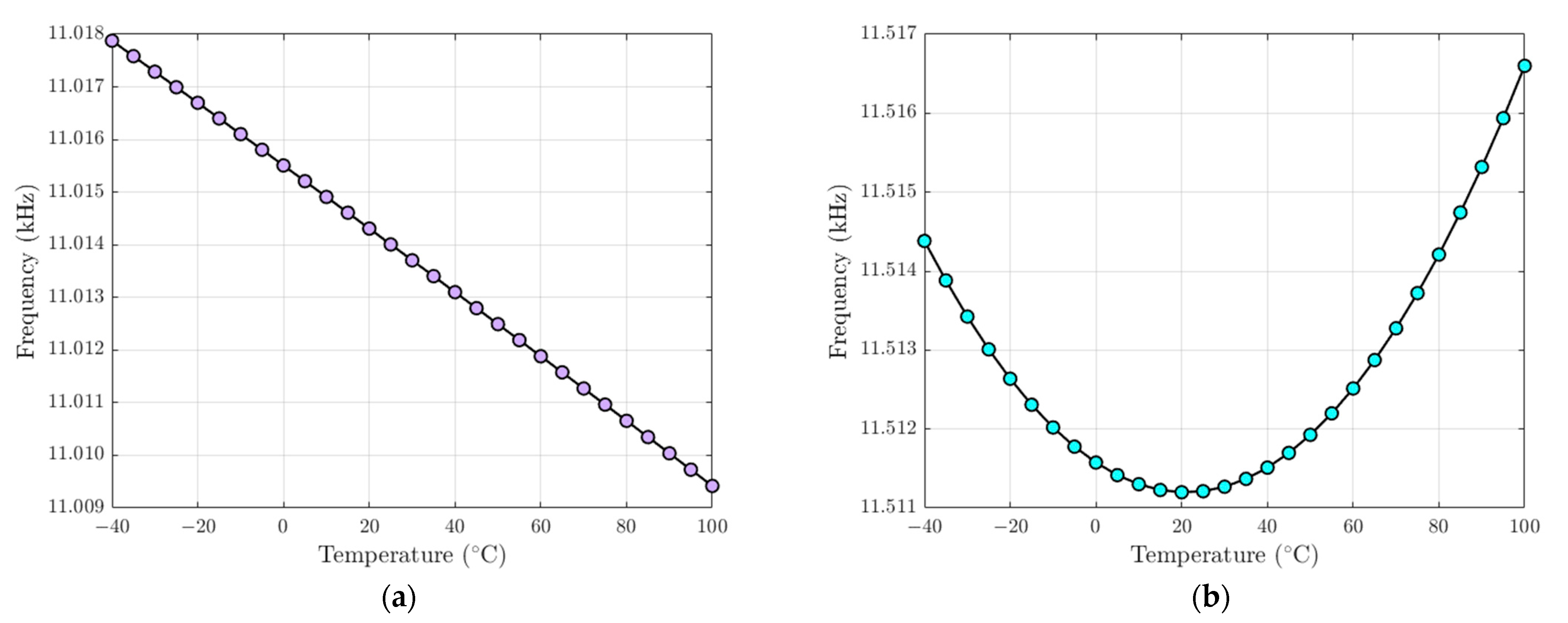
5.4. FEM Analysis of Temperature Variations on Structural Stability
5.5. FEM Analysis of Fabrication Process Tolerances on Structural Stability
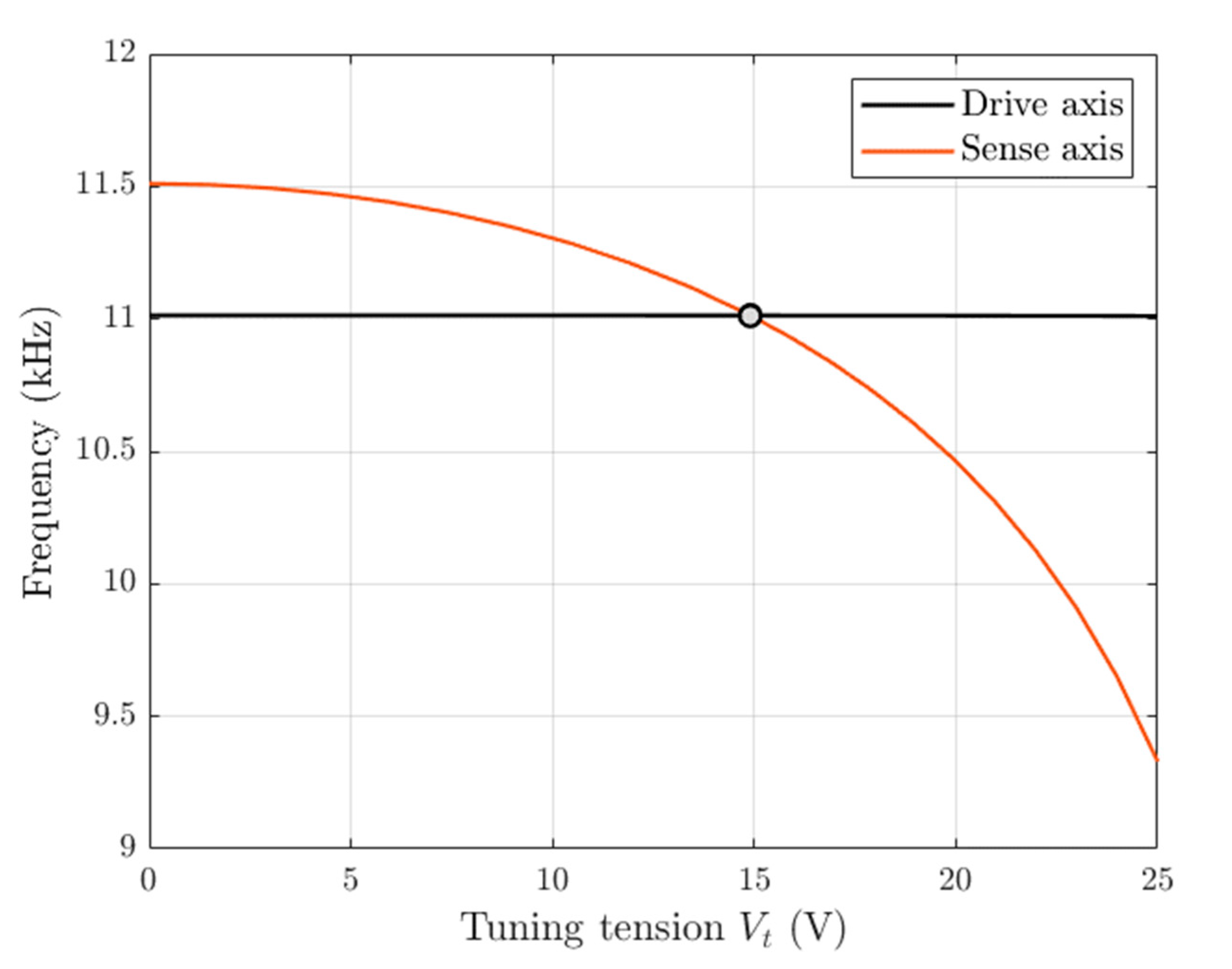
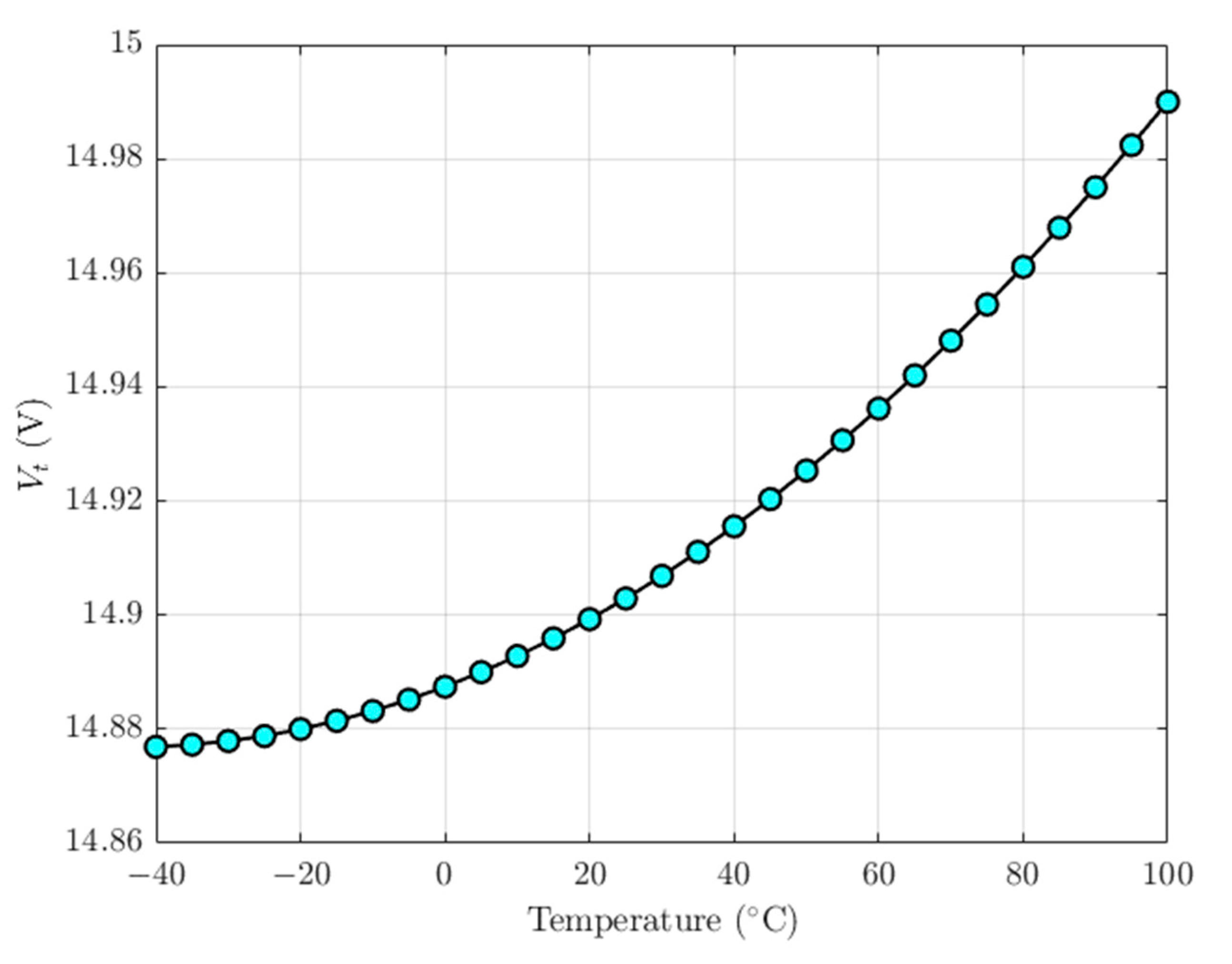
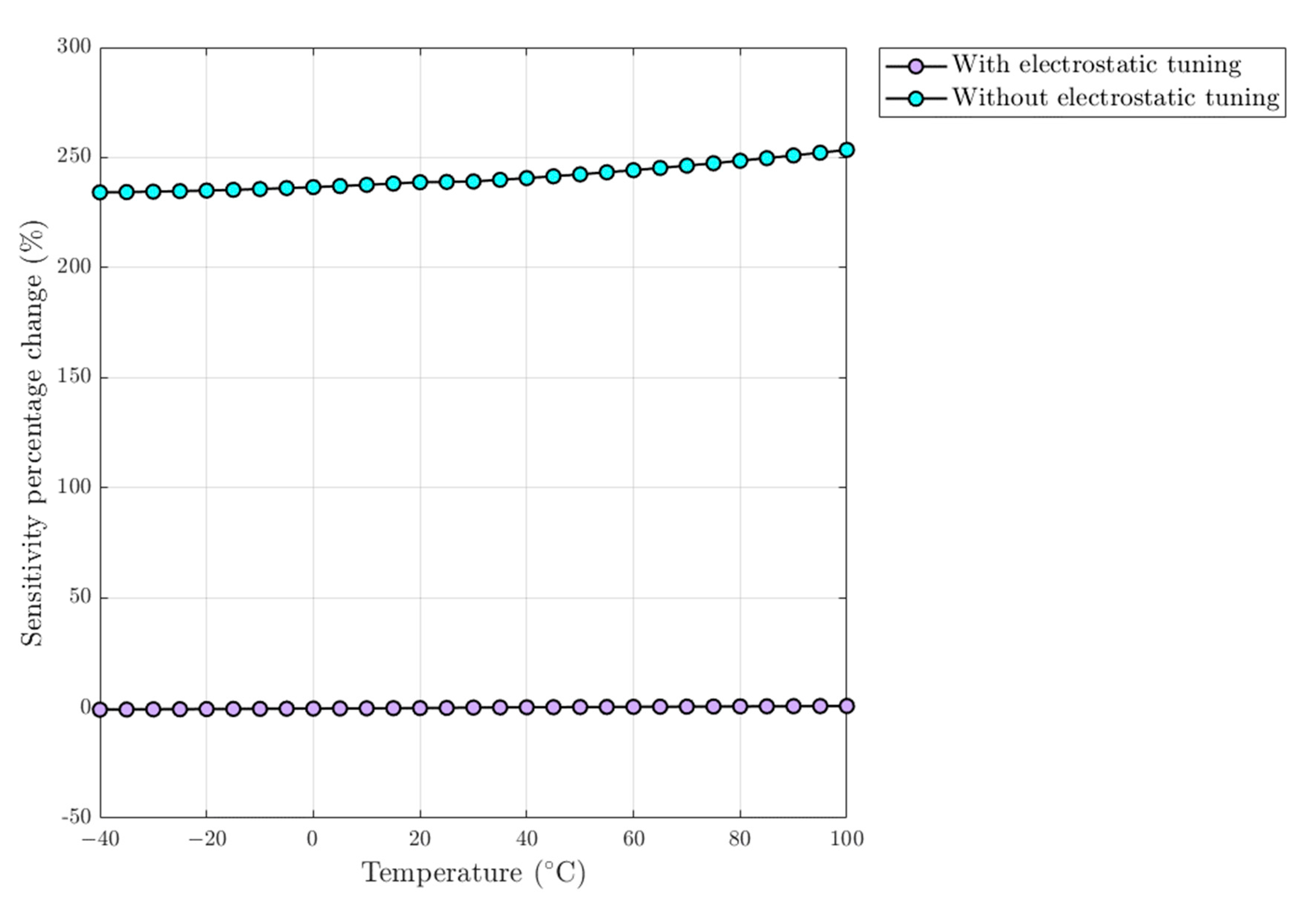
5.6. Compensation of Thermally Induced Frequency Mismatch through Electrostatic Tuning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef]
- Tian, L.; Niu, Y.; Cai, X.; Yang, Y. A cosine-fitting self-alignment method of MEMS-based inertial navigation system consisting of a skew FOG. IEEE Sens. J. 2020, 20, 1350–11356. [Google Scholar] [CrossRef]
- Botero-Valencia, J.; Marquez-Viloria, D.; Castano-Londono, L.; Morantes-Guzmán, L. A low-cost platform based on a robotic arm for parameters estimation of Inertial Measurement Units. Measurement 2017, 110, 257–262. [Google Scholar] [CrossRef]
- Xiao, D.; Zhou, X.; Li, Q.; Hou, Z.; Xi, X.; Wu, Y.; Wu, X. Design of a disk resonator gyroscope with high mechanical sensitivity by optimizing the ring thickness distribution. J. Microelectromech. Syst. 2016, 25, 606–616. [Google Scholar] [CrossRef]
- Hiller, T.; Pentek, Z.; Liewald, J.; Buhmann, A.; Roth, H. Origins and mechanisms of bias instability noise in a three-axis mode-matched MEMS gyroscope. J. Microelectromech. Syst. 2019, 28, 586–596. [Google Scholar] [CrossRef]
- Sharma, A.; Zaman, F.; Ayazi, F. A Sub-0.2°/hr Bias Drift Micromechanical Silicon Gyroscope with Automatic CMOS Mode-Matching. IEEE J. Solid-State Circ. 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Performance characterization of a new temperature-robust gain-bandwidth improved MEMS gyroscope operated in air. Sens. Actuators A Phys. 2009, 155, 16–22. [Google Scholar] [CrossRef]
- Verma, P.; Khan, K.Z.; Khonina, S.N.; Kazanskiy, N.L.; Gopal, R. Ultraviolet-LIGA-based fabrication and characterization of a nonresonant drive-mode vibratory gyro/accelerometer. J. Micro-NanoLith. MEM 2016, 15, 035001. [Google Scholar] [CrossRef]
- Saqib, M.; Mubasher Saleem, M.; Mazhar, N.; Awan, S.U.; Shahbaz Khan, U. Design and analysis of a high-gain and robust multi-DOF electro-thermally actuated MEMS gyroscope. Micromachines 2018, 9, 577. [Google Scholar] [CrossRef]
- Ding, X.; Jia, J.; Gao, Y.; Li, H. Mechanical and electrical noise in sense channel of MEMS vibratory gyroscopes. Sensors 2017, 17, 2306. [Google Scholar] [CrossRef] [PubMed]
- Balachandran, G.K.; Petkov, V.P.; Mayer, T.; Balslink, T. A 3-axis gyroscope for electronic stability control with continuous self-test. IEEE J. Solid-State Circ. 2015, 51, 177–186. [Google Scholar]
- Jia, J.; Ding, X.; Gao, Y.; Li, H. Automatic Frequency tuning technology for dual-mass MEMS gyroscope based on a quadrature modulation signal. Micromachines 2018, 9, 511. [Google Scholar] [CrossRef]
- Xu, L.; Li, H.; Ni, Y.; Liu, J.; Huang, L. Frequency tuning of work modes in z-axis dual-mass silicon microgyroscope. J. Sens. 2014, 2014, 891735. [Google Scholar] [CrossRef]
- Sharma, M.; Sarraf, E.H.; Cretu, E. A novel dynamic pull-in MEMS gyroscope. Procedia Eng. 2011, 25, 55–58. [Google Scholar] [CrossRef]
- Alper, S.E.; Azgin, K.; Akin, T. A high-performance silicon-on-insulator MEMS gyroscope operating at atmospheric pressure. Sens. Actuators A Phys. 2007, 135, 34–42. [Google Scholar] [CrossRef]
- Giner, J.; Maeda, D.; Ono, K.; Shkel, A.M.; Sekiguchi, T. MEMS gyroscope with concentrated springs suspensions demonstrating single digit frequency split and temperature robustness. J. Microelectromech. Syst. 2018, 28, 25–35. [Google Scholar] [CrossRef]
- Giannini, D.; Bonaccorsi, G.; Braghin, F. Size optimization of MEMS gyroscopes using substructuring. Eur. J. Mech. A Solids 2020, 84, 104045. [Google Scholar] [CrossRef]
- Iqbal, F.; Din, H.; Lee, B. Single Drive Multi-Axis Gyroscope with High Dynamic Range, High Linearity and Wide Bandwidth. Micromachines 2019, 10, 410. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook (Revision 8.0.). Available online: http://www.memscap.com (accessed on 30 November 2020).
- Somà, A.; De Pasquale, G. Numerical and experimental comparison of MEMS suspended plates dynamic behaviour under squeeze film damping effect. Analog Integr. Circuits Signal Process. 2008, 57, 213–224. [Google Scholar] [CrossRef]
- Veijola, T.; Turowski, M. Compact damping models for laterally moving microsctructures with gas-rarefaction effects. J. Microelectromech. Syst. 2001, 10, 263–273. [Google Scholar] [CrossRef]
- De Pasquale, G.; Veijola, T.; Somà, A. Modelling and validation of air damping in perforated gold and silicon MEMS plates. J. Micromech. Microeng. 2010, 20, 015010. [Google Scholar] [CrossRef]
- Mol, L.; Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Squeezed film damping measurements on a parallel-plate MEMS in the free molecule regime. J. Micromech. Microeng. 2009, 19, 074021. [Google Scholar] [CrossRef]
- Somà, A.; Saleem, M.M. Modeling and experimental verification of thermally induced residual stress in RF-MEMS. J. Micromech. Microeng. 2015, 25, 055007. [Google Scholar] [CrossRef]
- Ballestra, A.; Somà, A.; Pavanello, R. Experimental-Numerical Comparison of the Cantilever MEMS Frequency Shift in presence of a Residual Stress Gradient. Sensors 2008, 8, 767–783. [Google Scholar] [CrossRef] [PubMed]
- Somà, A.; De Pasquale, G.; Brusa, E.; Ballestra, A. Effect of residual stress on the mechanical behavior of microswitches at Pull-In. Strain 2010, 46, 358–373. [Google Scholar] [CrossRef]
- Bukhari, S.A.R.; Saleem, M.M.; Khan, U.S.; Hamza, A.; Iqbal, J.; Shakoor, R.I. Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines 2020, 11, 862. [Google Scholar] [CrossRef] [PubMed]





| Parameters | Value | Unit |
|---|---|---|
| Device size | ||
| Structural layer thickness | 25 | |
| Mass value of the drive mass ) | kg | |
| Mass value of the sense frame | kg | |
| Sensing plates length | 65 | |
| Sensing plates width | 4 | |
| Number of sensing plates pairs | 100 | - |
| Moving and fixed sensing plates overlap length | 55 | |
| Smaller sense gap size | 3 | |
| Larger sense gap size | 9 | |
| Drive comb pairs | 74 | - |
| Drive combs width | 4 | |
| Drive combs length | 50 | |
| Moving and fixed drive combs fingers overlap length | 40 | |
| Gap between drive combs | 3 | |
| Drive tuning comb pairs | 84 | - |
| Width of tuning combs | 4 | |
| Length of tuning combs | 50 | |
| Overlap length between the moving and fixed tuning combs fingers | 40 | |
| Gap between tuning combs | 3 |
| Mechanical Stiffness | Analytical Model (N/m) | FEM Model (N/m) |
|---|---|---|
| Drive mode () | 160.2 | 153.2 |
| Sense mode () | 320.5 | 298.6 |
| Mode Shape | Analytical Model (Hz) | FEM Model (Hz) | Error (%) |
|---|---|---|---|
| Drive axis | 11,348 | 11,014 | −2.94 |
| Sense axis | 11,757 | 11,511 | −2.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pistorio, F.; Saleem, M.M.; Somà, A. A Dual-Mass Resonant MEMS Gyroscope Design with Electrostatic Tuning for Frequency Mismatch Compensation. Appl. Sci. 2021, 11, 1129. https://doi.org/10.3390/app11031129
Pistorio F, Saleem MM, Somà A. A Dual-Mass Resonant MEMS Gyroscope Design with Electrostatic Tuning for Frequency Mismatch Compensation. Applied Sciences. 2021; 11(3):1129. https://doi.org/10.3390/app11031129
Chicago/Turabian StylePistorio, Francesca, Muhammad Mubasher Saleem, and Aurelio Somà. 2021. "A Dual-Mass Resonant MEMS Gyroscope Design with Electrostatic Tuning for Frequency Mismatch Compensation" Applied Sciences 11, no. 3: 1129. https://doi.org/10.3390/app11031129
APA StylePistorio, F., Saleem, M. M., & Somà, A. (2021). A Dual-Mass Resonant MEMS Gyroscope Design with Electrostatic Tuning for Frequency Mismatch Compensation. Applied Sciences, 11(3), 1129. https://doi.org/10.3390/app11031129







