Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances
Abstract
:1. Introduction
2. Related Work
3. Preliminaries
3.1. Notation
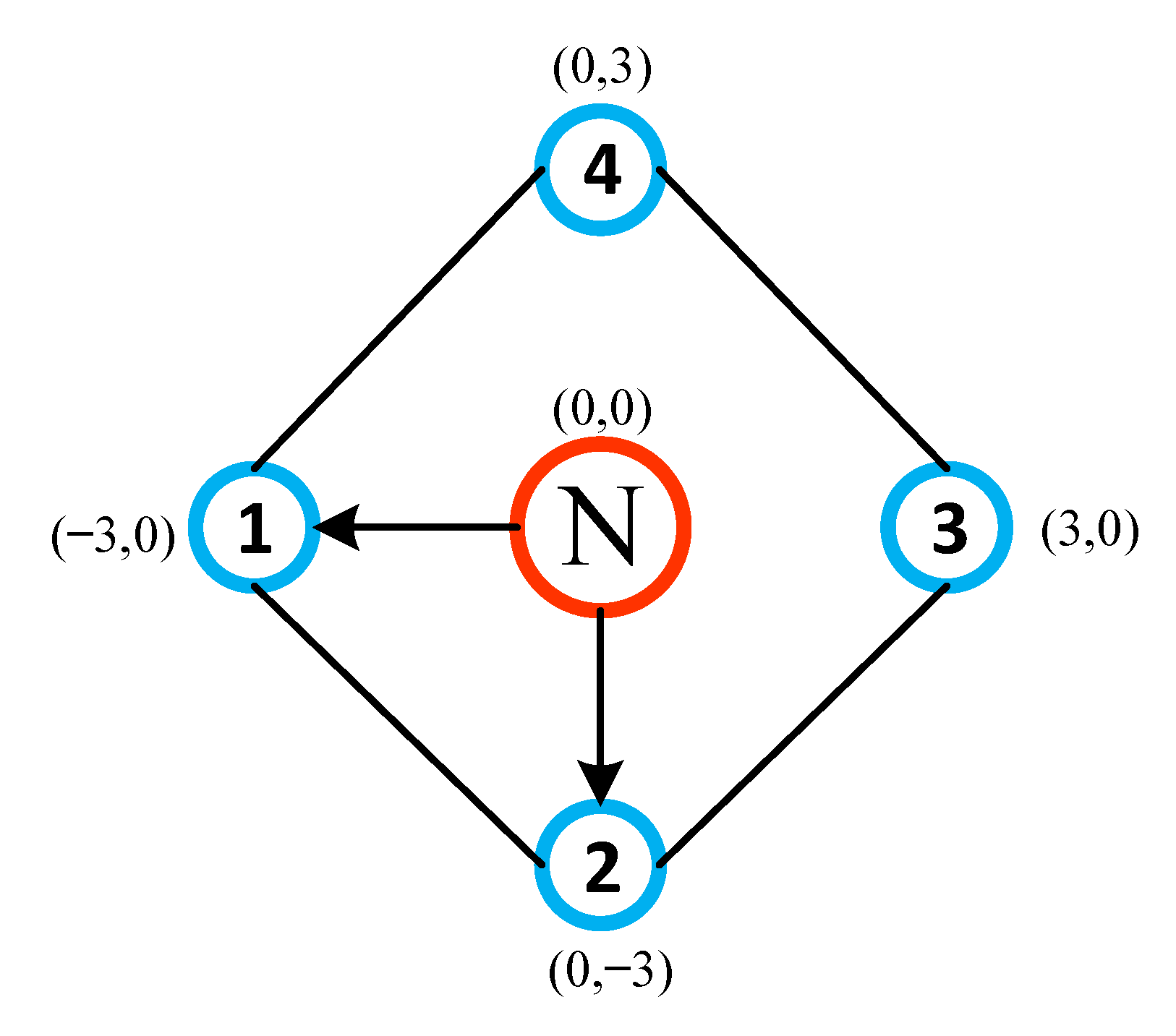
3.2. Graph Theory
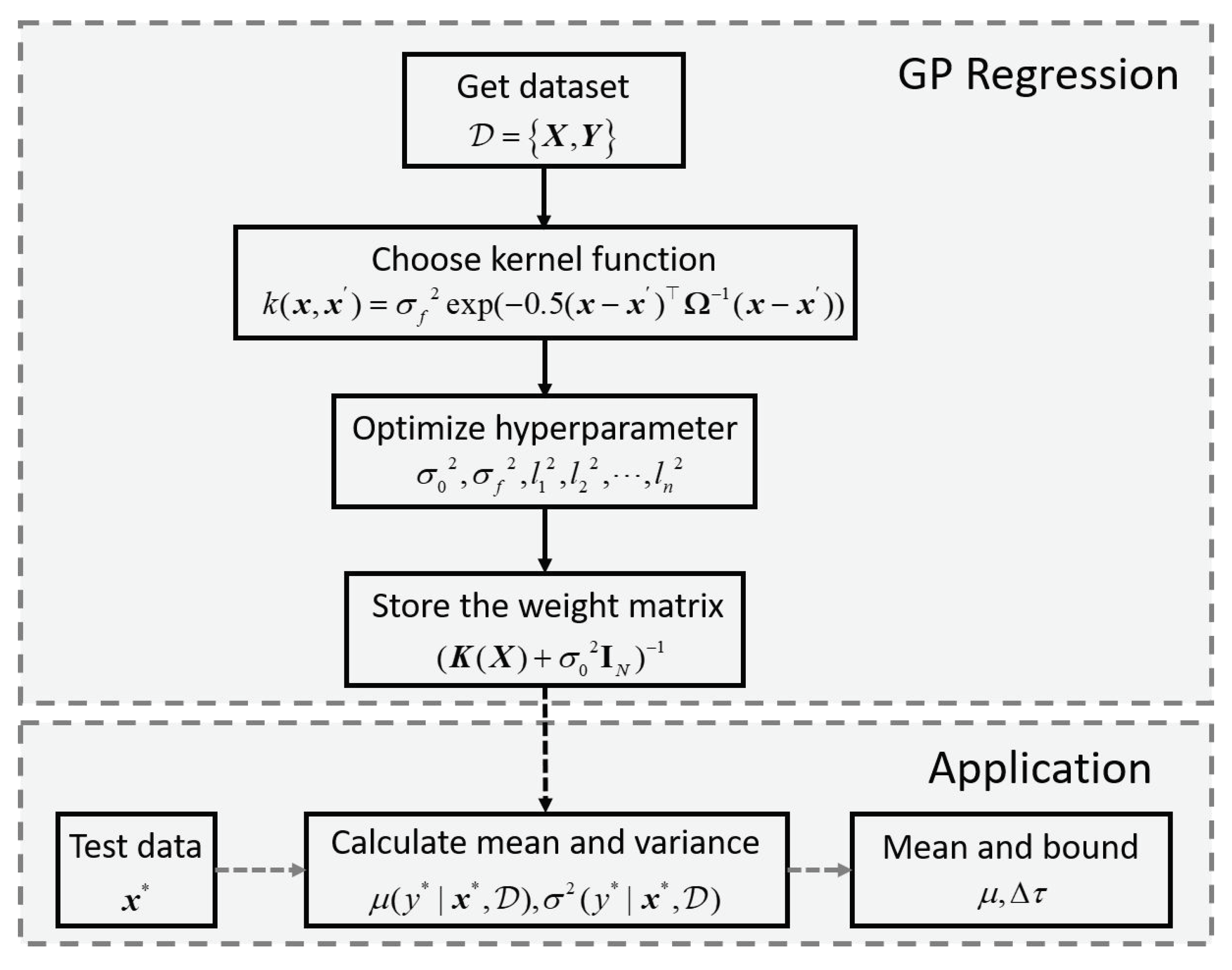
3.3. Gaussian Process Regression
4. Problem Formulation
4.1. Models of Fixed-Wing UAVs
4.2. Definition of Consensus Tracking Errors
5. Main Results
5.1. Offline Regression for Unknown Dynamics of UAVs
5.2. Learning-Based Control Law
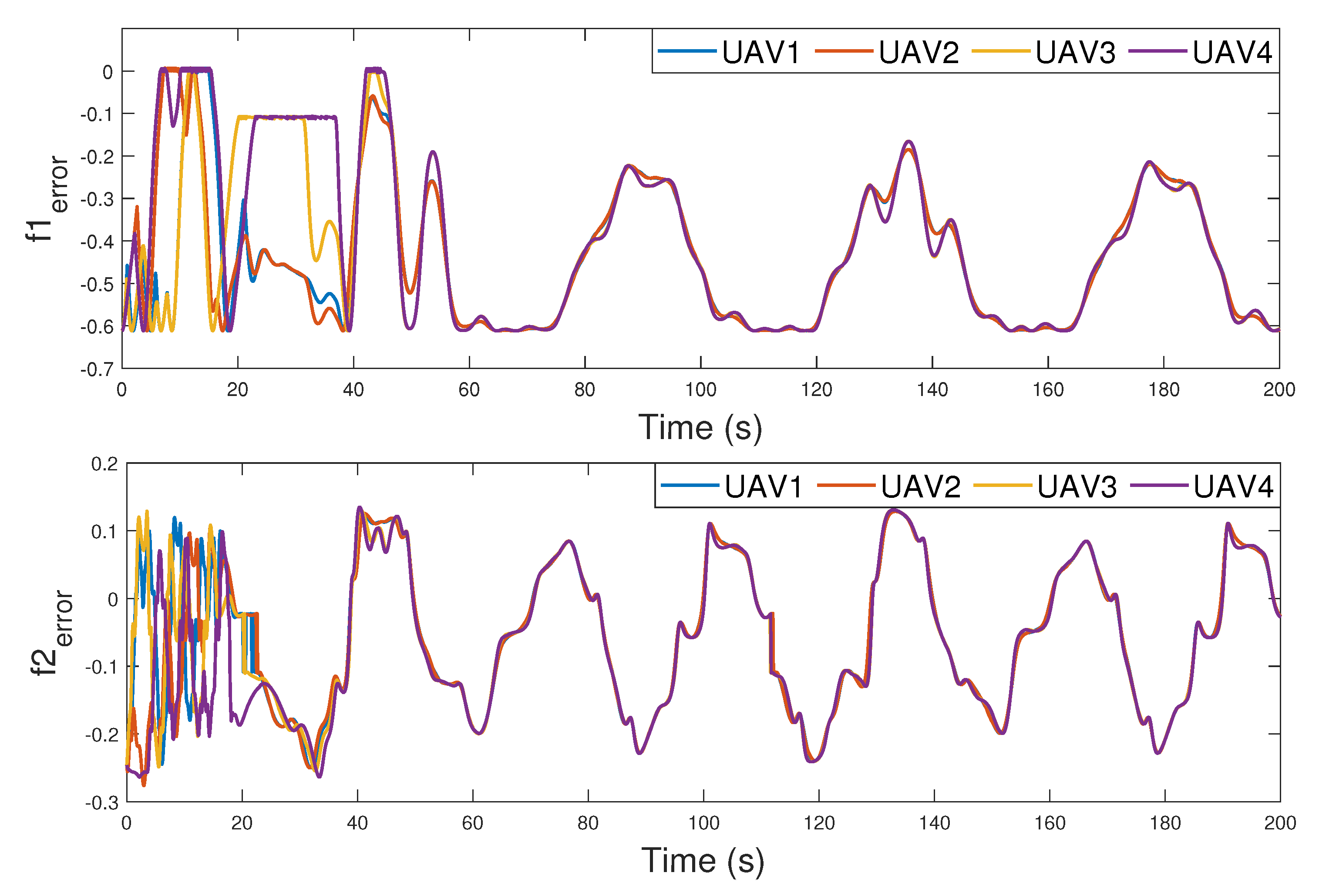
6. Simulation Results
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| x position of i-th UAV in the inertial frame | |
| y position of i-th UAV in the inertial frame | |
| x position of the target in the inertial frame | |
| y position of the target in the inertial frame | |
| heading angle of i-th UAV in the inertial frame | |
| velocity of i-th UAV in the inertial frame | |
| undirected graph to describe the interactions among UAVs | |
| GP | Gaussian process |
| GPR | Gaussian process regression |
| NNs | neural networks |
| UAV | unmanned aerial vehicle |
| DOF | degree of freedom |
| MAS | multi-agent systems |
| RMSE | root mean squared error |
References
- Wang, X.; Shen, L.; Liu, Z.; Zhao, S.; Cong, Y.; Li, Z.; Jia, S.; Chen, H.; Yu, Y.; Chang, Y.; et al. Coordinated flight control of miniature fixed-wing UAV swarms: Methods and experiments. Sci. China Inf. Sci. 2019, 62, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zeng, Z.; Cong, Y. Multi-agent distributed coordination control: Developments and directions via graph viewpoint. Neurocomputing 2016, 199, 204–218. [Google Scholar] [CrossRef]
- Nichols, J.W.; Sun, L.; Beard, R.W.; McLain, T. Aerial rendezvous of small unmanned aircraft using a passive towed cable system. J. Guid. Control Dyn. 2014, 37, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Lellis, E.D.; Vito, V.D.; Ruby, M.; Salbego, N. Adaptive Algorithm for Fixed Wing Uav Autolanding on Aircraft Carrier, AIAA. 2013. Available online: https://arc.aiaa.org/doi/abs/10.2514/6.2013-4585 (accessed on 15 August 2013).
- Zhao, S.; Wang, X.; Chen, H.; Wang, Y. Cooperative Path Following Control of Fixed-wing Unmanned Aerial Vehicles with Collision Avoidance. J. Intell. Robot. Syst. 2020, 100, 1569–1581. [Google Scholar] [CrossRef]
- Gerardo, F.; Alejandro, F.; Andre, M. A full controller for a fixed-wing UAV. arXiv 2019, arXiv:1903.03945. Available online: https://arxiv.org/abs/1903.03945 (accessed on 10 March 2019).
- Su, C.; Wang, X.; Shen, L.; Yu, H. Adaptive uav maneuvering control system based on dynamic inversion and long-short-term memory network. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 6880–6885. [Google Scholar]
- Ghommam, J.; Saad, M. Coordinated 3d path following control for a team of uavs with reference velocity recovery. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3008–3014. [Google Scholar]
- Tang, Y.; Lin, D.; Cao, L.J.; Liu, Y.C. Attitude Control of Fixed-Wing UAV Under Model Uncertainty and Disturbances. Electron. Opt. Control 2020, 27, 85–89. [Google Scholar]
- Roza, A.; Maggiore, M.; Scardovi, L. A smooth distributed feedback for formation control of unicycles. IEEE Trans. Autom. Control 2019, 64, 4998–5011. [Google Scholar] [CrossRef]
- Seyboth, G.S.; Wu, J.; Qin, J.; Yu, C.; Allgower, F. Collective circular motion of unicycle type vehicles with nonidentical constant velocities. IEEE Trans. Control Netw. Syst. 2014, 1, 167–176. [Google Scholar] [CrossRef]
- Hemakumara, P.; Sukkarieh, S. Non-parametric uav system identification with dependent gaussian processes. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4435–4441. [Google Scholar]
- Beckers, T.; Umlauft, J.; Hirche, S. Stable model-based control with gaussian process regression for robot manipulators. IFAC-PapersOnLine 2017, 50, 3877–3884. [Google Scholar] [CrossRef]
- Maiworm, M.; Limon, D.; Findeisen, R. Online learning-based model predictive control with gaussian process models and stability guarantees. Int. J. Robust Nonlinear Control 2021. Available online: https://doi.org/10.1002/rnc.5361 (accessed on 27 September 2021).
- Deisenroth, M.P.; Fox, D.; Rasmussen, C.E. Gaussian processes for data-efficient learning in robotics and contro. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 408–423. [Google Scholar] [CrossRef] [Green Version]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M.W. Information-theoretic regret bounds for gaussian process optimization in the bandit setting. IEEE Trans. Inf. Theory 2012, 58, 3250–3265. [Google Scholar] [CrossRef] [Green Version]
- Lederer, A.; Umlauft, J.; Hirche, S. Uniform error bounds for gaussian process regression with application to safe control. In Proceedings of the 33rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Yang, Z.; Sosnowski, S.; Liu, Q.; Jiao, J.; Lederer, A.; Hirche, S. Distributed learning consensus control for unknown nonlinear multi-agent systems based on gaussian processes. arXiv 2021, arXiv:2103.15929. Available online: https://arxiv.org/abs/2103.15929 (accessed on 27 September 2021).
- O’Callaghan, S.; Ramos, F.T.; Durrant-Whyte, H. Contextual Occupancy Maps using Gaussian Processes. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Khansari-Zadeh; Kim, H.J.; Johansson, K.H. Path planning for remotely controlled UAVs using Gaussian process filter. In Proceedings of the 2017 17th International Conference on Control, Automation and Systems (ICCAS 2017), Jeju, Korea, 18–21 October 2017. [Google Scholar]
- Cai, L.; Liu, X.; Ding, H.; Chen, F. Human Action Recognition Using Improved Sparse Gaussian Process Latent Variable Model and Hidden Conditional Random Filed. IEEE Access 2018, 6, 20047–20057. [Google Scholar] [CrossRef]
- Ghasrodashti, E.K.; Helfroush, M.S.; Danyali, H. Sparse-Based Classification of Hyperspectral Images Using Extended Hidden Markov Random Fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4101–4112. [Google Scholar] [CrossRef]
- Kordi Ghasrodashti, E.; Helfroush, M.S.; Danyali, H. Spectral-spatial classification of hyperspectral images using wavelet transform and hidden Markov random fields. Geocarto Int. 2018, 33, 771–790. [Google Scholar] [CrossRef]
- Lee, J.; Muskardin, T.; Paez, C.R.; Oettershagen, P.; Stastny, T.; Sa, I. Roland Siegwart and Konstantin Kondak, Towards Autonomous Stratospheric Flight: A Generic Global System Identification Framework for Fixed-Wing Platforms. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Yoo, J.; Mohammad, S.; Billard, A. Learning Stable Nonlinear Dynamical Systems With Gaussian Mixture Models. IEEE Trans. Robot. 2011, 27, 943–957. [Google Scholar]
- Hemakumara, P.; Sukkarieh, S. Learning UAV Stability and Control Derivatives Using Gaussian Processes. IEEE Trans. Robot. 2013, 29, 813–824. [Google Scholar] [CrossRef]
- Park, S.; Mustafa, S.K.; Shimada, K. Learning-Based Robot Control with Localized Sparse Online Gaussian Process. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Umlauft, J.; Pohler, L.; Hirche, S. An uncertainty-based control lyapunov approach for control-affine systems modeled by gaussian process. IEEE Control Syst. Lett. 2018, 2, 483–488. [Google Scholar] [CrossRef]
- Maiworm, M.; Limon, D.; Manzano, J.M.; Findeisen, R. Stability of gaussian process learning based output feedback model predictive control. In Proceedings of the 6th IFAC Conference on Nonlinear Model Predictive Control NMPC 2018, Madison, WI, USA, 19–22 August 2018; pp. 455–461. [Google Scholar]
- Wang, P.; Luo, Y.; Yu, J.J. Coordinated Formation for multiple UAVs Based on H∞ Control, 2020. (In Chinese). Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=7102783600 (accessed on 27 September 2021).
- Defoort, M.; Floquet, T.; Kokosy, A.; Perruquetti, W. Sliding-Mode Formation Control for Cooperative Autonomous Mobile Robots. IEEE Trans. Ind. Electron. 2008, 55, 3944–3953. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Atkins, E. Distributed multi-vehicle coordinated controlvia local information exchange. Int. J. Robust Nonlinear Control 2007, 17, 1002–1033. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Umlauft, J.; Beckers, T.; Kimmel, M.; Hirche, S. Feedback linearization using gaussian processes. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5249–5255. [Google Scholar]
- Beckers, T.; Colombo, L.; Hirche, S. Online learning-based trajectory tracking for underactuated vehicles with uncertain dynamics. arXiv 2020. Available online: https://arxiv.org/abs/2009.06689 (accessed on 27 September 2021).
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]



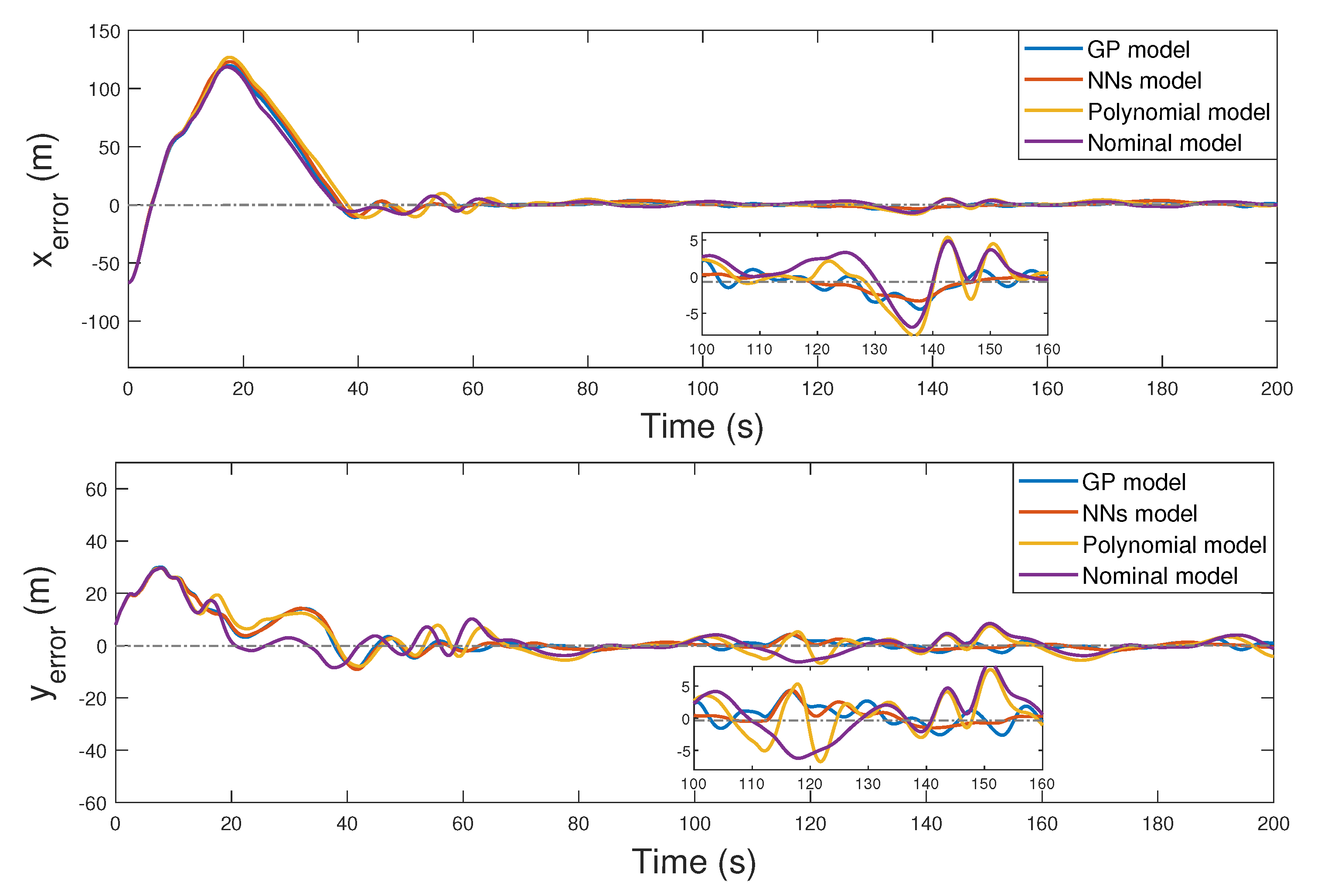
| GP model | ||
| NNs model | ||
| Polynomial model |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhao, S.; Wang, X. Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances. Appl. Sci. 2021, 11, 9830. https://doi.org/10.3390/app11219830
Wang Q, Zhao S, Wang X. Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances. Applied Sciences. 2021; 11(21):9830. https://doi.org/10.3390/app11219830
Chicago/Turabian StyleWang, Qipeng, Shulong Zhao, and Xiangke Wang. 2021. "Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances" Applied Sciences 11, no. 21: 9830. https://doi.org/10.3390/app11219830
APA StyleWang, Q., Zhao, S., & Wang, X. (2021). Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances. Applied Sciences, 11(21), 9830. https://doi.org/10.3390/app11219830






