Abstract
This paper presents the simulation and calculation-based aspect of constructing a dynamically stable, self-balancing electric monowheel from first principles. It further goes on to formulate a reference model-based adaptive control structure in order to maintain balance as well as the desired output. First, a mathematical model of the nonlinear system analyzes the vehicle dynamics, followed by an appropriate linearization technique. Suitable parameters for real-time vehicle design are calculated based on specific constraints followed by a proper motor selection. Various control methods are tested and implemented on the state-space model of this system. Initially, classical pole placement control is carried out in MATLAB to observe the responses. The LQR control method is also implemented in MATLAB and Simulink, demonstrating the dynamic stability and self-balancing system property. Subsequently, the system considers an extensive range of rider masses and external disturbances by introducing white noise. The parameter estimation of rider position has been implemented using Kalman Filter estimation, followed by developing an LQG controller for the system, in order to mitigate the disturbances caused by factors such as wind. A comparison between LQR and LQG controllers has been conducted. Finally, a reference model-assisted adaptive control structure has been established for the system to account for sudden parameter changes such as rider mass. A reference model stabilizer has been established for the same purpose, and all results have been obtained by running simulations on MATLAB Simulink.
1. Introduction
The invention of the wheel was a path-breaking event in the history of humankind. Since then, man has used the concept of the wheel to construct various vehicles that have revolutionized transportation. Over the years, transport vehicles have evolved from having multiple wheels to four wheels, to the most widely used domestic transport mode of the two-wheeled vehicle. In this paper, we have decided to take this evolution a step further by physically constructing, from first principles, a self-balancing single-wheeled vehicle, also known as the monowheel, as shown in Figure 1. The electric vehicle concept is emerging because of increased awareness about ongoing pollution and the energy shortage crisis. Today, automobiles and motorcycles are no longer the best forms of transportation. With the ever-increasing prices of petroleum products, there is a need for a form of transport that is cheaper and more efficient. Saving energy to mitigate the problem of fuel depletion is of prime importance. Such demands are causing a surge in research on eco-friendly transportation. Electrical vehicle technology is a step towards fulfilling these goals, and so the idea of an electric unicycle or monowheel is attractive [1].
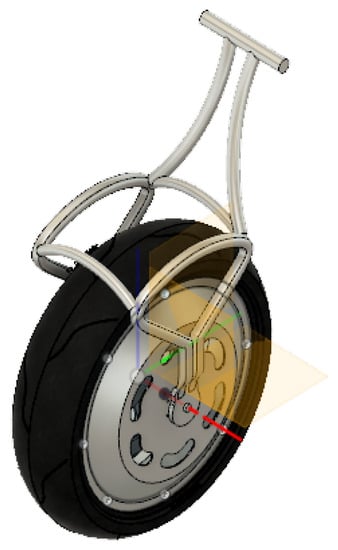
Figure 1.
Basic design sketch of the monowheel.
Many cities are now allowing personal mobility vehicles to mix with pedestrian traffic to de-congest modern roads. The electric monowheel is ideal for such a situation owing to its compactness in structure. It is a transitional vehicle that goes to most places where a person can walk or ride a bike, and it is easy to carry around due to its light weight. Typically, in conventional two-wheeled transportation, one wheel provides the force for speed control, while the other wheel deals with changes in direction and steering. However, in a monowheel, both the speed as well as direction are controlled through the single physical machinery.
The electric monowheel has attracted a great deal of attention from both academia as well as the industry [2,3,4]. These vehicles are available as fun vehicles for children, people who are style-conscious, and creative workers in many domains. The monowheel is derived initially from the unicycle concept, upon which various research works have been conducted. Kim et al. presented an optimal minimum energy control solution for the same through Jacobi Elliptic Functions [5]. Chen et al. [6] proposed a schematic design of a unicycle. Similar to a Segway device, it comes with a handling rod for maneuvering and a supportive seat for the rider. They then conducted a dynamic analysis and proposed a robust control law for their schematic design. Muthukumar et al. [7] developed and conceptualized the ergonomic study of a typical unicycle. Based on a dynamic model, Jin et al. [8] proposed a steering control method for the torque applied on an underactuated unicycle robot.
Many researchers believe that the monowheel can be a serious vehicle for transportation in the future. It is a pollution-free vehicle that needs only one DC motor to drive it. A few researchers developed an electric unicycle made from inexpensive components, such as an DC brush motor, with an inexpensive gearbox, an accelerator, an eight-bit micro-controller, a rubber wheel, a rate gyro, a PWM motor driver, and nickel–metal hydride (NiMH) batteries. Also, it is important to ensure an economical, eco-friendly means of short-distance transportation due to rising fuel prices. The electric unicycle has not been a commercial success. However, we trust that it can become a popular single-wheeled vehicle that satisfies the parameters of being low cost, economical, and ecologically friendly. The design and implementation of a practical and logistically safe self-balancing monowheel have garnered attention in modern times. Since the late 1800s, many different kinds of single-wheeled vehicles have been proposed with a similar design, drive mechanism, and power source. In some cases, propellers were the prime movers, while in others gas engines or electric motors were used. In 1869, the first monowheel was constructed, which used a mechanism analogous to a bike to pedal the inner wheel, which became the standard structure for the many designs of unicycles that were to follow. A pedal force was used to drive an outer wheel directly using a gear in an unicycle patented in 1893. After that, a gear-driven chain coupe was used to give traction to the unicycle. The system is nonlinear and highly unstable, thus requiring a complicated and robust control design. Hofer et al. designed an observer-based cascade stabilizer, and a fuzzy controller for a similar system [9]. Various techniques were proposed by Caldecott et al. for the PD control of an electric unicycle [10]. A modeling approach was undertaken by Huang et al., along with a controller for self-balance [11]. Many developed system designs and nonlinear electric unicycle control methods have been proposed, such as those in [12,13].
However, none of these have been implemented in the real world, and they do not account for friction. The LQR method, or the Linear Quadratic Method, has been a control branch for various such model-based systems, which over time minimizes an integral function as well as giving a quadratic measure of the states along with the control actions’ quadratic measures. The LQR solution finally produces a set of constants, which at each point in time gives a control action that is optimal when multiplied by each of the states. LQR provides robustness in performance. Based on the sub-optimal approach for an AC servo motor, Ou et al. develope a controller design scheme based on the discrete sliding mode [14]. Lin et al. implemented this method to design a robust PI controller for a one-link robot by integrating it with a reduced parameter sensitivity technique [15]. This control method has been used in single-wheeled mobile robots [16], as well as to develop a state feedback controller, as in [17]. For establishing self-balancing, an adaptive friction compensation method was integrated by Li et al. along with this LQR method. It also included the speed tracking of the system while considering variable rider weights along with varying friction coefficients [18].
Blackwell presented a working self-balancing unicycle, while using an existing control mechanism [19]. Bombardier worked on the monowheel as a sports vehicle powered by a hydrogen cell [20]. Ryno motors [21] demonstrated a prototype of the Ryno bike monowheel. Janick et al. introduced a motorized transport vehicle for pedestrians, and they filed a US patent for the vehicle. A “self-propelled unicycle engaged with vehicle” was patented by Ford Motor Company [22], which was used only for independent use. This included a hub and a coupled wheel [23]. Shelke et al. thought of a compact folding bicycle which would lead to easy parking and transportation. The mechanism of folding could vary, with each offering various combinations of folding speed and folding ease, durability, compactness of frame, weight, ride, and variations of prices with changes in the internal material [24]. Park et al. designed a self-balancing mobile robot on two wheels, which primarily used a control moment gyroscope module. The robot is capable of achieving improved rotation in more confined spaces and has more speed than regular legged robots, Because of this, it is mostly used as a mobile robot platform [25]. Kadis et al. proposed the Micycle system, involving an analysis of the components of the system. The automatic steering mechanism helps the rider to balance in the rolling direction.This was followed by developing the dynamics of the unicycle in the pitch direction through the Lagrangian formulation. The plant was stabilized in the pitch direction using a linear PD controller, and the system was simulated on MATLAB Simulink. The controller helped in the implementation of the simulated and physical system, and data helped to quantitatively assess the control system [10].
The study of the monowheel is relatively recent, with noticeable research work in this field. Although some concepts of self-stabilizing monowheel robots already exist, most of them are structurally quite different from our approach, and their stabilization methods lead to some restrictions which we wish to overcome. Ozaka’s robot possesses a single wheel with an extended arm, which is stretched out to the left and right to maintain the roll balance. Although not many positive experimental results were obtained, this robot was speculated to be the the first self-balancing unicycle robot [20]. In [26], the authors describe one of the most similar versions to our system. Another such version with a constructed model is known as Gyrover [3], which implements a mechanical gyroscope inside the wheel in order to stabilize the vehicle while stationary or when moving at very low velocities. The gyroscope’s axis is altered using a tilt mechanism to enable the turning of the robot through the precision effect. This is similar to the design proposed by Bauer [27]. A robotic self-balancing unicycle was proposed by Schoonwinkel, which implements a horizontal flywheel that mimics the twisting of an arm and torso movement to establish balance as well as the motion control of the robot [19]. An LQG controller action was proposed by Vos et al. in 1990 in order to obtain control stability over Schoonwinkel’s robot [21]. In 2007, the University of California, San Diego developed the UniBot, which combined the ideas of the “inertia wheel pendulum” along with the “wheeled inverted pendulum” and achieved lateral balance with the help of vertical flywheel control [23]. In 2005, Dao et al. developed a self-balancing unicycle robot that achieved lateral stability with the help of two gyroscopes that acted as actuators [22]. In 2009, Guo et al. developed a dynamic nonlinear model with a vertical flywheel for a unicycle robot and simulated the model [25]. With the sliding mode control of a single-wheeled robotic vehicle, Ruan et al. developed a similar robot that utilized a flywheel that was vertical, which was then verified through simulations [24].
There are numerous ongoing research works about this system in the fields of robotics and automation. However, what is noticeable is the limited work aimed towards a physical application that considers a rider. Furthermore, while various control systems for this system are available in the literature, a sufficient focus has not been placed on the LQR control of such systems with varying load masses. Constructing laboratory-grade dynamic self-stabilizing robots has been a research topic for a while in the field of automation. We aim to take this a level further so that the monowheel becomes a viable mode of future transport. We wish to build a more realistic system, considering the rider’s necessities, that adapts to an extensive range of rider masses and external disturbances such as wind, friction, bumpy roads, etc. Further, it is very much possible that the monowheel may be subjected to sudden parameter changes, such as a change in the rider mass. This is possible if the rider uses the monowheel as a means to deliver goods. There will be an increase in load mass as he picks up or drops the delivery goods at certain points in time. In order to make the monowheel robust to these sudden parameter changes, we also aim to develop an adaptive control strategy that accounts for this. There are many adaptive control techniques available in the literature [28,29,30].
In this paper, we have aimed to achieve the following:
- Establish the dynamic stability of the system and make it self-balanced in the linear direction (forward and backward movement), with variations in rider input velocity, using the method of LQR control, and for a wide range of rider masses;
- Establish an LQG control mechanism to account for wind disturbances and perform a comparison with regular LQR controlled output by considering external disturbances such as wind and friction as noise to maintain dynamic stability in such conditions;
- Estimate position state output through Kalman Filter estimation;
- Develop a nonlinear reference model for the monowheel system to deal with higher-order uncertain dynamics in terms of the model parameters (rider mass, rider upper body height);
- Obtain adaptive control laws and adaptive parameter update laws [31,32], develop a novel reference stabilizer for the nonlinear and unstable reference model using the LQR control method, and establish the real-time adaptation of the system with a 25% increase in load mass.
2. Problem Statements
Our objective is to design a functional, scaled model of a dynamically stable, self-balancing monowheel, the electrical/mechanical architecture of which is balanced and propelled electrically with the help of batteries and a motor-driven system. The control system for self-balancing should be designed for a large range of masses while factoring in all external disturbances, and an adaptive control structure should be formulated to ensure robustness even under sudden parameter change conditions.
2.1. Control Objectives and Design Objectives
The primary objective in a monowheel is to maintain the rider at his mean, stable position, despite parameter variations such as increasing vehicle velocity, acceleration, etc., as well as braking and external disturbances. The main control objective is to regulate the monowheel’s speed within safe limits by directing the controller to follow a reference velocity, as well as to design an adaptive control structure which can ensure that the controller continues to follow the given reference velocity despite sudden changes in parameters. A monowheel system design that is suitable for handling and control by a single person, even in a resting position, is associated with some significant constraints, such as the height of the person riding the vehicle, the maximum weights that the vehicle can withstand, power, and transmission. The following are the fundamental aspects of designing the system:
- Vehicle dynamics: This is the analysis of the reaction of the vehicle to driver inputs on a given solid surface. This part of engineering is predominantly based on classical mechanics. Aerodynamics, drive train and braking, mass distribution, suspension and steering, and tires are some of the factors that govern vehicle dynamics.
- Chassis designing: The outer frame supporting the driver should be robust and carry heavy loads without failure.
- Wheel mechanics: The calculation of forces acting on the wheel during the response using sensors such as the gyro sensor and accelerometer is required.
- Wheel hub design: This is where the real hardware comes together, requiring free movement between the wheel and driving systems.
2.2. Selection of Parameters and Calculations
After a significant amount of market research and study of motor vehicle laws, the basic parameters of the system were set as shown in Table 1.

Table 1.
Nominal values of simulation parameters.
We calculate the various forces, torque, and power associated with the system based on these parameters. Different environmental coefficients at nominal conditions are shown in Table 2.

Table 2.
Nominal values of physical parameters.
2.3. Selection of Motor
A pair of 350 W, 24 V brush-DC motors was considered most suitable for this system due to its low overall construction cost and high ratio of torque to inertia. These motors require a straightforward and inexpensive controller that is operational in extreme environments, possesses a suitable maximum RPM, and that is feasible to rebuild for extended life compared to brushless DC motors. On the downside, brushes have lower life, provide poor heat dissipation due to the rotor’s limitations, have high rotor inertia, and exhibit electromagnetic interference (EMI) generated by brush arcing.
3. Kinematics and Dynamics
An an inverted pendulum is a highly unstable, open-loop system [33], the present system is analogous to that of an inverted pendulum. It is implemented as an inverted pendulum pivoted on a cart that can move horizontally under the control of an electronic system, as shown in Figure 2.
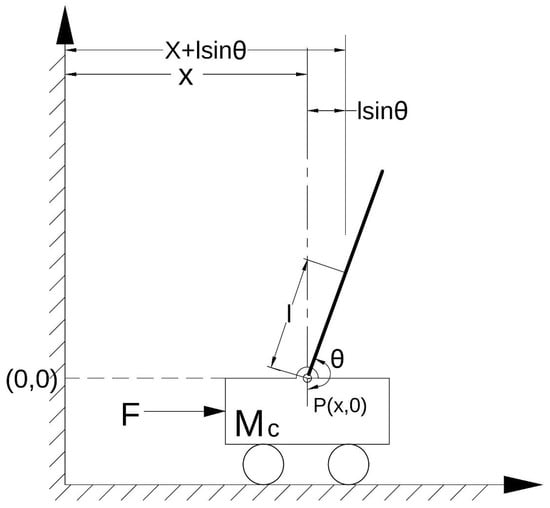
Figure 2.
Pendulum cart system—analogous to the monowheel system.
The cart is analogous to the monowheel itself, while the mounted pendulum is analogous to the rider. All model parameters are mentioned in Table 3.

Table 3.
Nominal values of model parameters.
The kinematics of the system are defined as
The Lagrangian for a system of particles is defined by
where is the total potential energy of the system, and T is the total kinetic energy, which is the sum of the translational () and rotational kinetic energy (). The total translational () kinetic energy includes the kinetic energy of both the cart and pendulum; i.e., . The translational kinetic energy cart is given by
The rotational kinetic energy () cart is given by
From (1)–(4), we get
Since the system has 2 DOF, it possesses two Lagrangian equations of motion, as given below:
3.1. Linearization
Linearization is a method used to calculate the linear approximations of a nonlinear system function that are valid within a small range of values around an operating point. The linear approximation is assessed using the first-order Taylor series expansion, thereby ensuring the system’s local stability and steady-state condition at an equilibrium point. This helps in analyzing a system’s stability and disturbance rejection property. For a system or a function defined as , the linearized system is expressed as , where a is the operating point and is the first-order differentiation at point a.
By the substitution of variables such as , from (8) and (9), we get
Writing Equations (10) and (11) in matrix form,
Now, considering the operating point as for linearization, we obtain our state space matrix as
where . The force applied F is generated by the PM DC motor, and the relation between F and the applied voltage is
By substituting the values of constants, we get
Upon analysis, it has been found that rank of state matrix A is 3, and the ranks of both the controllability as well as observability matrices are also 3. Hence, it can concluded be that the system is both controllable as well as observable, as the ranks are the same as that of matrix A.
4. Control Analysis
Various full-state feedback control methods—mainly pole placement and LQR control methods—were implemented and analyzed for this system, as shown in Figure 3.
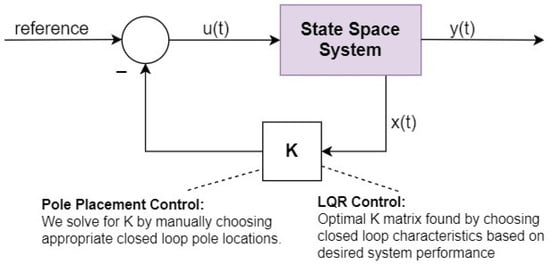
Figure 3.
Full state feedback control—pole placement and LQR.
Both the methods have exactly the same physical structure, and we can implement our results using either of these controllers. What sets them apart from each other is that, while the implementation of K in both is the same, the method of choosing the value of K is different. For pole placement, we solve for K by choosing closed-loop pole locations. However, the issue here is the determination of the most optimal location for those poles, especially for higher-order systems. On the other hand, with LQR, instead of picking pole locations, we find the optimal K matrix by choosing closed-loop characteristics based on the desired performance and efficiency of the system.
4.1. Pole Placement Control
The open-loop poles are in the unstable region, as discussed in the root locus section. The poles are required to be in the stable region. For the same region, the pole placement method is implemented, where the open-loop poles are chosen as . The response is shown in Figure 4.
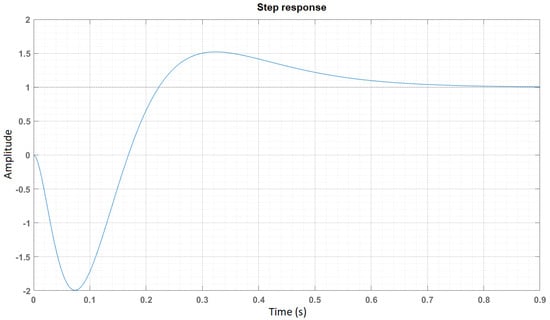
Figure 4.
Pole placement control.
However, these results are not realistic, as with such a trajectory, the vehicle will have high chances of toppling over. Moreover, instead of choosing arbitrary poles for pole placement control, a more systematic approach would be the LQR method.
4.2. LQR Control
For this system, we utilize an LQR method with an optimal control regulator that tracks a reference trajectory better than traditional controllers such as PID. This method is beneficial when we linearize nonlinear systems about defined equilibrium points. While the LQR method may be limited to linear systems, they can be highly effective tools for realizing exponentially stable controllers used in linearized nonlinear systems. LQR, by definition, gives the optimal state-feedback law that minimizes particular quadratic objective functions.
A basic LQR control system model for the monowheel has been implemented by writing code in the MATLAB environment, along with implementing that code on the model developed on MATLAB Simulink with and R = 0.05; the step response is shown in Figure 5 with s, s.
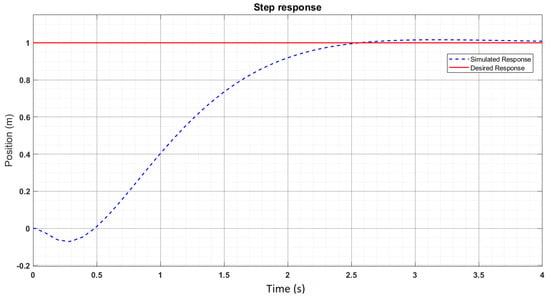
Figure 5.
Step response for LQR control.
It is important to note that the monowheel would be subjected to a wide range of masses when used for real-world applications, as well as when different people try to ride it. The system needs to maintain dynamic stability and self-balancing properties for a wide variation in masses. The previously established LQR control model is accordingly altered, which was also performed in the MATLAB program. The current model can sustain riders with weights ranging from 12 kg to 180 kg while in motion. However, the very smooth responses are available in the range of 30 kg to 180 kg, assuming the frame can sustain such weights. The step responses for different weights are shown in Figure 6a–d.
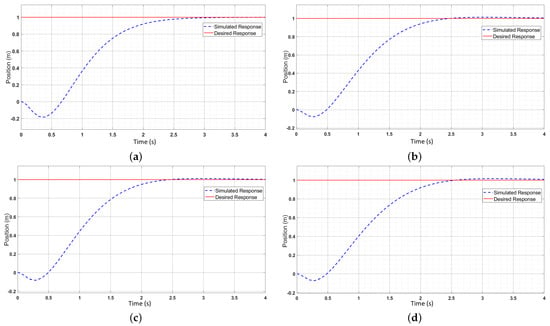
Figure 6.
Step responses at various masses. (a) Weight = 10 kg. (b) Weight = 40 kg. (c) Weight = 120 kg. (d) Weight = 180 kg.
The plant model in MATLAB Simulink represents the state-space equations as blocks. Likewise, the controller and sensor designs were developed from first principles without the use of any predefined blocks. This system accepts position x as its reference input. Figure 7 shows the responses of all four states of the system. Only one of the states (x) contributes to making the system controllable.
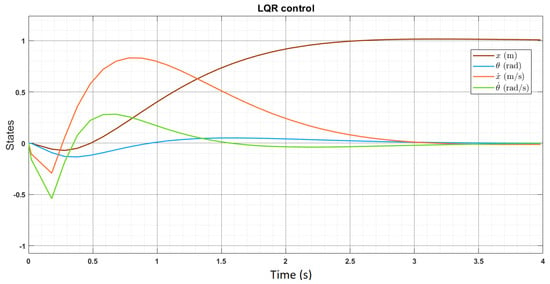
Figure 7.
State responses, where x is position, is angle of pendulum from cart, is velocity, and is angular velocity.
5. Kalman Filter Estimation and LQG Control
The Kalman Filter is an algorithm that helps in the determination of the estimated values of unknown variables using known measurements observed over some time. It is an optimal predictor–corrector type estimator. Observed over time, using a series of realistic measurements involving disturbances such as statistical noise, the Kalman Filter essentially minimizes the estimated error covariance while the initially assumed conditions are satisfied. Over each time interval, estimating a joint probability distribution gives the approximations of unknown variables [34,35]. These estimates are a great deal more accurate than those derived with only a single measurement. Since the mean-squared errors of estimated values are minimized for linear stochastic systems, the approach is also called the linear least mean squares estimator (LSME). The Kalman filter determines the monowheel position state vector because both the velocity and angle can be measured using predefined sensors. At the same time, it is challenging to find out the exact value of position using this approach. However, it is possible to estimate position values accurately since this state is both controllable and observable, as already established earlier. Kalman filters estimate states based on linear dynamical systems. The mathematical equation that represents the evolution of the state from time to k is given by the following process model:
Here, the state transition matrix is given by A. This matrix is then applied to , which is the vector of the state in the previous time interval. The control-input matrix is given by B, where is the input. represents the process noise, which has covariance Q and is assumed to be zero-mean Gaussian. The relationship between the state and the measurement is shown by the coupling of the process and measurement models together. At a time step k, it is given as
Here, the measurement vector is given as , while the measurement matrix is given as H. The measurement noise vector is given by , and it is assumed to be zero-mean Gaussian with covariance R. At time k, the Kalman filter provides an estimate of states , when —i.e., the initial condition is known—as well as values such as the series of measurement , , and system information, represented by and R, are known. In our case, assuming a rider mass kg, ,
The two stages of Kalman filter algorithm are prediction and update. Appropriate code was formulated in MATLAB and tested on the Simulink model to implement the stages. Figure 8 and Figure 9 show a comparison between the estimated value and the measured value of vehicle position and velocity, respectively.
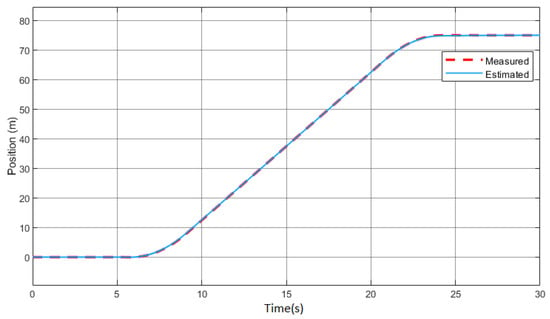
Figure 8.
Position estimation.
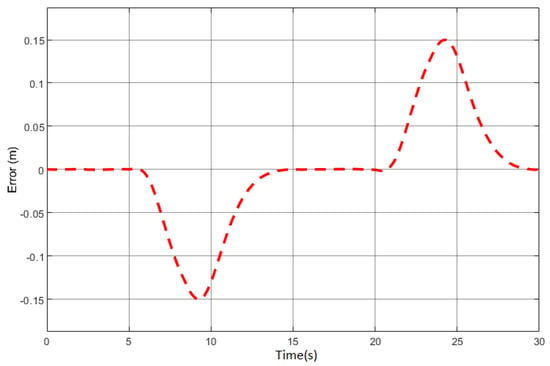
Figure 9.
Position error.
Subsequently, Figure 10 and Figure 11 give the estimation errors corresponding to position and velocity, respectively. The red dotted line is the estimated value in the estimation graphs, and the blue line represents the actual value.
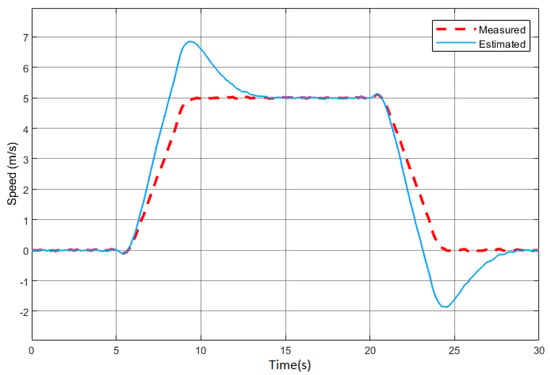
Figure 10.
Velocity estimation.
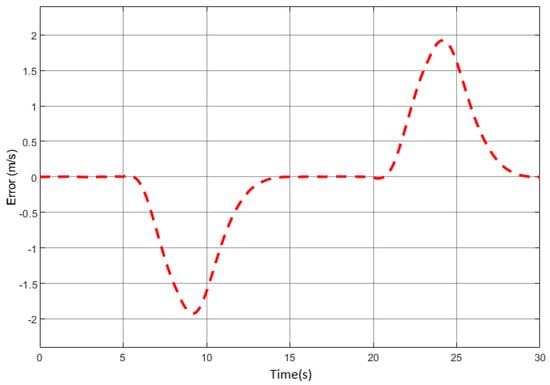
Figure 11.
Velocity error.
With a steady increment in velocity, the estimated value of position is close to the true value; i.e., the error is minimum. In the velocity estimate, upon a sudden change in velocity, there is a significant difference between the actual value and the estimated value for that particular instance. This estimation analysis considers the rider’s mass to be 80 kg. With a change in weight, the estimation would also change. For this, a mass-adaptive system is under formulation.
Since the system has some noise in it, a second approach is explored using LQG control. The aim is to provide control with minimum noise. LQG control, a combination of LQR control and the Kalman Filter, is an optimal control solution where white Gaussian noise drives the linear systems. A standard LQG controller is robust to significant variations in system parameters due to its dependence on the standard Kalman filter. LQR control and Kalman filter estimation responses are shown, followed by the responses with the LQG control. Figure 12a shows the velocity response of the noisy system with LQR control. Figure 12b compares the LQR-controlled velocity response with the Kalman filter estimation of the velocity state. Figure 12c shows the velocity response of the noisy system with LQG control. Figure 12 compares the LQG controlled velocity response with the Kalman filter estimation of the velocity state under LQG controlled action.
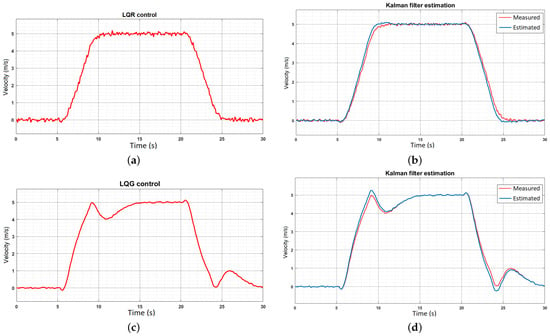
Figure 12.
Velocity responses with LQR and LQG control. (a) Velocity response with LQR control. (b) Velocity estimation during LQR control. (c) Velocity response with LQG control. (d) Velocity estimation during LQG control.
5.1. Factoring in Velocity
The previous model showed the precise representation of the pendulum cart system. Although the monowheel system is analogous to the pendulum cart system, it is not precisely the same. The pendulum cart system gives the state x (position) as the primary output. In contrast, for the monowheel system, we require the velocity to be the system output, and the reference input is a velocity that the rider provides manually. The reference point x (position state) of all other states is controllable and observable in the pendulum cart system, which is in the continuous-time domain. However, the monowheel system works in discrete time. In reality, the input is not bounded, and hence manual constraints are needed. Converting the original LQR model into a more realistic system by replacing the initial position reference input with a joystick’s velocity input overcomes such challenges. A saturation block is introduced to bound the intake within practical limits, followed by a rate limiter to bound the acceleration. The velocity input is then passed through an integrator to generate a corresponding position signal, which is fed into the plant. The entire model is converted into a discrete time-domain system to enable the smooth functioning of sensors and micro-controllers while working on the hardware. Figure 13 and Figure 14 provide real-time velocity responses. The light-blue plot shows the controlled input after the action of LQR control. The green plot represents the vehicle’s final velocity output after factoring in self-balancing control action and dynamic stability. The orange plot shows the rider’s velocity as an input in real time, within 30 s.
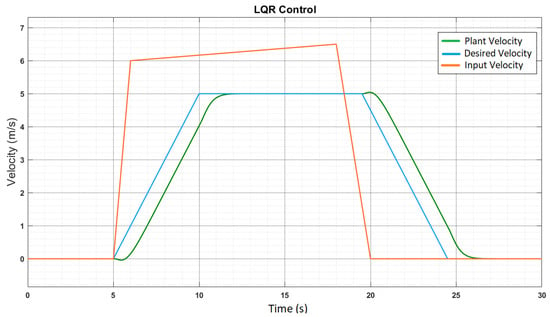
Figure 13.
Input-regulated output speed.
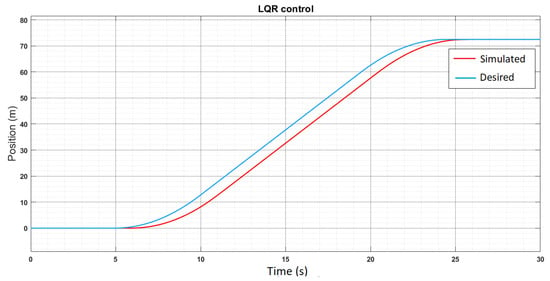
Figure 14.
Reference point.
Figure 15 demonstrates the velocity response of the system (with noise) when a step reference input is given. The system takes about s to stabilize.
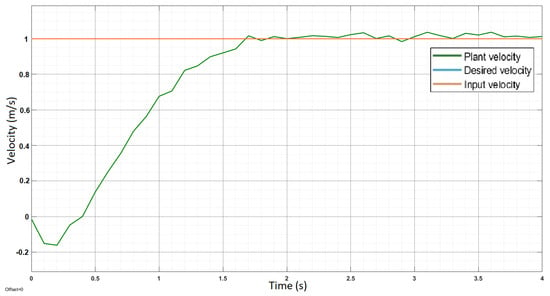
Figure 15.
Step response of system with a weight of 80 kg.
5.2. Disturbance Adaptation
Next, we must understand that, for any vehicle, the real-life application is significantly different from simulations that are made considering ideal conditions, merely because of the external disturbances, such as wind, friction, gradient, etc., that are associated with the real world. To adapt to such uncertainties, a certain degree of white noise is introduced in the Simulink model, mimicking these disturbances. The white noise power is assumed to be s, which is a fair representation. The responses for different weights are shown in Figure 16. The response output becomes smoother as the rider’s mass increases due to the greater inertia associated with increased mass.
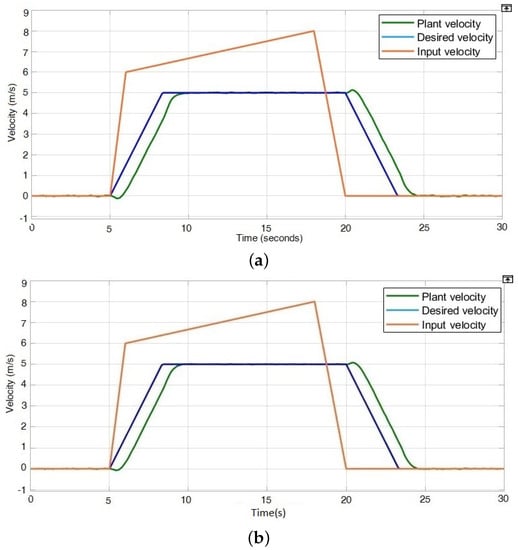
Figure 16.
Velocity response of the system at different masses. (a) Weight = 30 kg. (b) Weight = 180 kg.
6. Reference Model Assisted Adaptive Control
Adaptive control law and adaptive laws [36,37] are formulated using a reference model-assisted adaptive control structure to make the system adaptive to various changes in parameters. The dynamic equations [38] of our system are
where B is the constant coefficient of friction, M is the mass of the monowheel, and g is the acceleration due to gravity. and are the variable parameters, where , and . Here, m represents the rider mass and l represents the rider height, which will vary from person to person. Equations (14) and (15) have been derived in [38] through analyses similar to those mentioned in Section 3 and Section 3.1.
For ease of analysis, certain mathematical adjustments have been made. Let us define
and so through differentiation on both sides, we get
Our nominal model is thus chosen as
Expressing in state-space format,. We are only interested in the velocity and angle response; i.e., the states and . Since the state does not directly govern any of the other states, as well as being irrelevant to our further analysis, it has been eliminated in order to reduce redundancy. Hence, the new state space equations after re-writing states as are given as
The corresponding reference model has been chosen as follows:
The state error is defined as , where for this system. The tracking error dynamics corresponding to each state are formulated as follows
where From these tracking errors, the adaptive update laws are
where are adaptation gains to provide desired control authority over the transient behavior. Coefficients are chosen to provide a constrained solution such that the suffix pertains to the error dynamics in which the parameter error term appears. The adaptive control law is chosen as
6.1. Lyapunov Stability Analysis
Let our Lyapunov candidate function be
By differentiating V with respect to time, we get
Substituting the error dynamics, adaptive update laws, and adaptive control laws (, , u) in order to cancel out all , we finally arrive at
For the function to be Lyapunov stable, must be negative definite. The term is a negative definite term. If , then, is negative definite. When , we must find a range of values of and for which is negative at all times.
If > 0, then
If < 0, then
Thus, the proposed adaptive control structure with the constraints derived in Equations (33) and (34) guarantees , which implies that which from Equation (30) implies that , = and so . The control signal u(t) as given by Equation (29) is also bounded; that is, . Next, from Equations (26) and (28), we find that because all the signals which are part of those equations are bounded. Additionally, since is lower-bounded by the negative of the squared error signals, the error signals also satisfy the following property: . Note that such a property is not applicable to the parameter error signals in general. In conclusion, since and , the corollary of the Barbalet lemma implies that
The reference model stabilizer is built using LQR control techniques with a structure
where and are 3 x 1 and 1 x 3 state control and reference control gain matrices, respectively, as mentioned in Table 4, meaning that the reference signal stabilizes at the desired velocity value inputted by the rider.

Table 4.
Nominal values of parameters and feedback gains.
6.2. Building the Adaptive Controlled System
The system was built according to the following block diagram as shown in Figure 17.
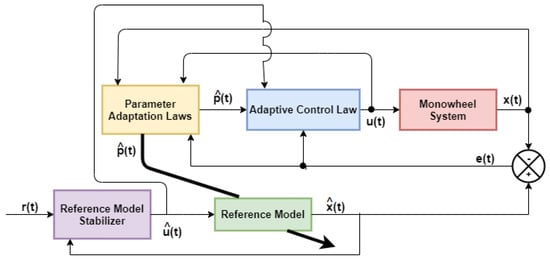
Figure 17.
Model assisted adaptive control structure for Monowheel System.
6.3. Simulation Results and Discussion
Next, we carry out a simulation for the proposed adaptive control environment in the monowheel system. Parameter is varied from 80 kg to 110 kg at 50 s of the simulation; i.e., the load mass is increased by 30 kg. Figure 18 shows a comparison between the graph of the reference model and the corresponding nominal model outputs.
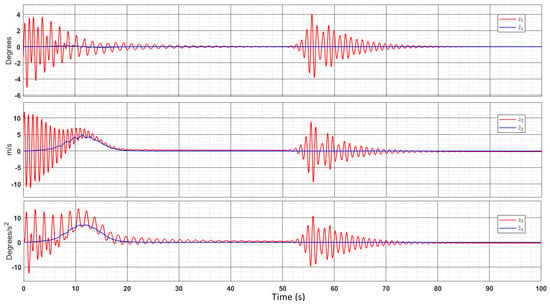
Figure 18.
The reference and the nominal states.
It is to be noted that the reference and nominal models were set at different initial conditions. The initial conditions of reference model are considered to be and The values of the nominal parameters are as mentioned in Table 4. Due to the unequal initial conditions, the nominal system state responses take around 30 s to completely stabilize into the values of the reference system state response. Due to the introduction of disturbance in parameter at 50 s, we observe a spike in the nominal state responses, which takes around 20 s to stabilize completely at s. The corresponding state errors are shown in Figure 19.
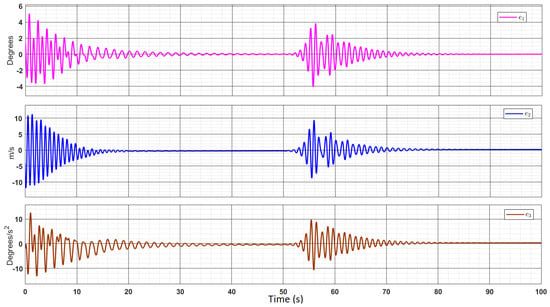
Figure 19.
State errors.
Once the reference system is stabilized, the next task is to develop the adaptation laws. This mechanism consists of the tracking-error dynamics , parameter estimation dynamics , and adaptive control law for , as established in Equations (24)–(30), respectively. This mechanism is designed such that all the tracking errors converge to zero asymptotically. In addition, the parameter estimates converge to the steady-state values within the bounds mentioned in Table 4 and satisfy the constraints obtained in Equations (33) and (34). The Lyapunov stability analysis is utilized to obtain the parameter constraints and to choose the tuning parameters (i.e., The chosen values of such tuning parameters are presented in Table 5.

Table 5.
Adaptation gains.
Based on these adaptation gain values, Equations (32)–(34) were implemented on MATLAB Simulink, and the corresponding responses were obtained. Figure 20 demonstrates that for the chosen values of adaptation gain values, the derivative of the Lyapunov candidate function is always negative definite, as it satisfies the condition in Equation (33). Using these values, the tracking-error dynamics are stabilized around zero as shown in Figure 19. The proposed controller can adapt to the change, which is introduced at 50 s and ensures the convergence of the error between the two responses to zero within a short time of 20 s. The error, which was already zero before the change in parameters, re-converges to zero after short transience, thereby demonstrating the controller’s robustness, as shown in Figure 19; that is, the tracking error is dynamically stable around and it is at zero except for a brief period of transience immediately following the change in a parameter.
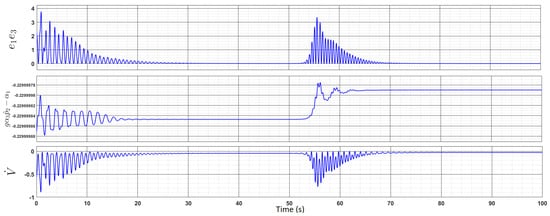
Figure 20.
Validation of negative-definite derivative of Lyapunov candidate function.
It is equally important to obtain the bounded steady-state response of the estimated parameters () of the reference model. Hence, using the heuristic approach and the knowledge of the monowheel system, the parametric update laws in Equation (28) and the control law in Equation (29) have been tuned. The response of estimated parameters is shown in Figure 21, and the corresponding parameter errors are as shown in Figure 22. The oscillations and damping are observed in the response of due to the presence of tracking errors in the dynamics of the parameter update laws in Equation (28).
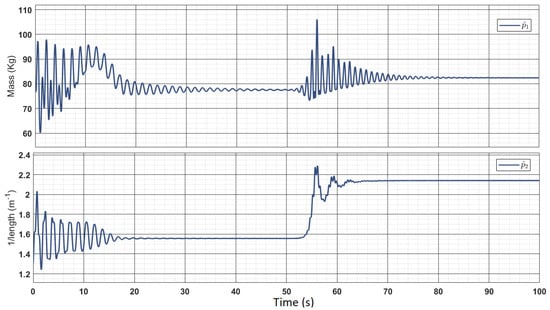
Figure 21.
Parameter estimates.
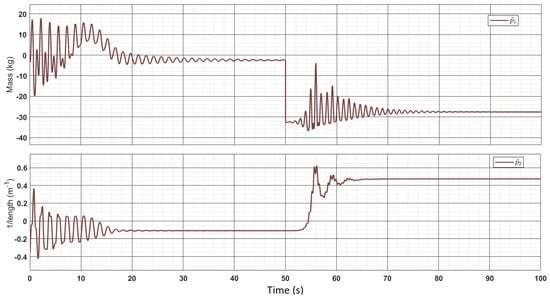
Figure 22.
Parameter errors.
It is necessary to obtain the regulatory response of the monowheel system in the presence of parametric violation. During this process, the gains (i.e. ) of the adaptive control law are required to be tuned around their optimal values to satisfy the constraint in Equation (33). The responses of state variables and the control action around the signal under parametric uncertainties introduced from are shown in Figure 23. Note that all the variables are asymptotically stabilized within their respective safe limits prescribed as per the control objectives. The monowheel has shown an over-damped velocity response after introducing the uncertainties at 50 s, which may be the prime source of the oscillatory behavior of estimated parameters and tracking-error dynamics.
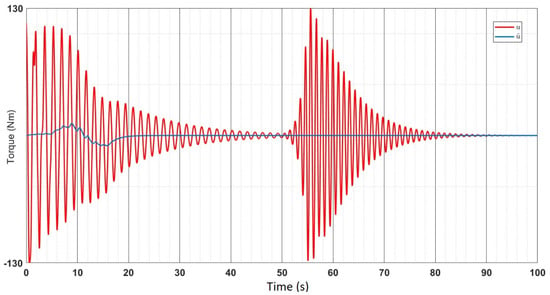
Figure 23.
Comparing stabilized input and Adaptive Control Law.
It is to be noted that for the given system, the final velocity output indeed comes close to the actual reference input that is inputted by the rider in real time as he rides. Figure 24 shows this. The entire adaptive control structure is implemented in MATLAB Simulink to obtain simulation-based results.
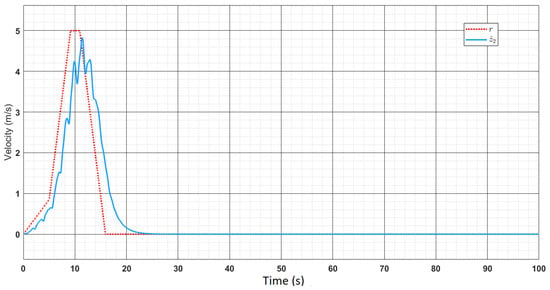
Figure 24.
Comparing reference input velocity and actual velocity output.
All tracking errors converge to 0 by 30 s, and upon further parameter disturbance, the responses take 20 s to settle back to zero. The controller gives a robust controlled output for over 30 kg ( loading) of load disturbance. It also provides a similar kind of controlled output when there is a change in the second parameter; i.e., the upper body height of the rider. However, this paper has not discussed the fact that it is impractical for the rider’s height to change while riding a moving vehicle. All parameter estimates also stabilize at a finite point, both before the disturbance as well as after disturbance. The control input is such that it ensures that the nominal system model mimics the reference model. At certain times, the input torque goes as high as 100 Nm—a permissible value, as motor selection can be performed accordingly.
7. Concluding Remarks
In this paper, a complete analysis of the monowheel system is carried out, along with different control methods for dynamic stability and self-balancing, followed by the formulation of a reference model-assisted adaptive control structure that helps the system to adapt to sudden disturbances in parameters. A realistic estimate of the monowheel’s physical parameters was made by referring to Ryno Motor’s patent US20120217072A1. Based on that, all other system parameters were calculated, followed by an analysis of the kinematics and the system’s dynamics using the Lagrangian dynamic formulation and representing the system in its state-space form. Both pole placement and LQR control methods were explored using a MATLAB Simulink model to mimic the system. Various modifications were made to allow the system to withstand a wide range of rider masses with weights ranging from 12–180 kg while in motion. However, very smooth responses are available in a range of 30–180 kg, under the assumption that the frame would withstand such masses. More modifications were made to consider the self-balancing property under a wide variation of velocity changes and account for external disturbances introduced as white noise. Next, an LQG controller was designed to account for any additional wind disturbances. The results were compared with that of the regular LQR controller, followed by implementing a Kalman filter to estimate the position state of the monowheel based on all other available measured parameters. The maximum rider speed is reached at 20 km/h, and all analysis is performed within the range of 0–20 km/h. However, higher speeds are achievable by changing the calculations accordingly.
Next, we moved on to designing a reference model-assisted adaptive control structure for the system so that the system output responses can adapt to a sudden change in parameters and maintain a favorable outcome. For this structure, nominal and reference models were designed, followed by the formulation of error dynamics and adaptive update and control laws. The Lyapunov stability analysis of this system was carried out. A reference model stabilizer was formulated using the standard LQR control method. Although the self-balancing property was achieved for a wide range of masses using LQR control and the system has been made adaptive to load disturbances, the system still has a few shortcomings:
- Self-balancing and stability have not been analyzed for cases with sudden braking;
- All analysis was conducted under the assumption that the frame’s mass is 35 kg and the maximum velocity to be attained is 20 km/h;
- A standard incline gradient ratio of 1:4000 feet is assumed. For inclinations greater than that, there will be a change in the calculations and analysis;
- After introducing a load disturbance, the system takes around 20 s to stabilize at the desired value.;
- The system is adaptively controllable only within the parameter ranges given in Table 4.
Upgraded designs to account for such shortcomings and attempt to implement these control methods in a physical model will be our primary focus of research in the future.
Author Contributions
Conceptualization, I.S. and S.G.; methodology, I.S., S.G., and D.D.; software, I.S. and S.G.; validation, I.S. and S.G.; formal analysis, I.S., S.G. and D.D.; writing—original draft preparation, I.S. and S.G.; writing—review and editing, D.D. and S.O.; supervision, D.D.; funding acquisition, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the European Regional Development Fund in “A Research Platform focused on Industry 4.0 and Robotics in Ostrava Agglomeration” project, Reg. No. CZ.02.1.01/0.0/0.0/17_049/0008425 within the Operational Programme Research, Development and Education.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cardini, S.B. A history of the monocycle stability and control from inside the wheel. IEEE Control. Syst. Mag. 2006, 26, 22–26. [Google Scholar] [CrossRef]
- Aicardi, M.; Casalino, G.; Bicchi, A.; Balestrino, A. Closed loop steering of unicycle like vehicles via Lyapunov techniques. IEEE Robot. Autom. Mag. 1995, 2, 27–35. [Google Scholar] [CrossRef]
- Brown, H.B.; Xu, Y. A single-wheel, gyroscopically stabilized robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3658–3663. [Google Scholar]
- Sheng, Z.; Yamafuji, K. Postural stability of a human riding a unicycle and its emulation by a robot. IEEE Trans. Robot. Autom. 1997, 13, 709–720. [Google Scholar] [CrossRef]
- Kim, Y.; Singh, T. Minimum Energy Control of a Unicycle Model Robot. J. Dyn. Syst. Meas. Control. 2021, 143, 101003. [Google Scholar] [CrossRef]
- Chen, P.C.; Pan, S.M.; Chuang, H.S.; Chiang, C.H. Dynamics analysis and robust control for electric unicycles under constrained control force. Arab. J. Sci. Eng. 2016, 41, 4487–4507. [Google Scholar] [CrossRef]
- M V, M.; Ramadass, R.; R, A. Conceptualization and Ergonomic Analysis of a Typical Unicycle. Int. J. Sci. Eng. Res. 2015, 6, 909–920. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, Y.; Zhang, H.; Liu, Z.; Liu, Y.; Zhu, Y.; Zhao, J. Steering Control Method for an Underactuated Unicycle Robot Based on Dynamic Model. Math. Probl. Eng. 2018, 2018, 5240594. [Google Scholar] [CrossRef]
- Hofer, K. Electric vehicle on one wheel. In Proceedings of the 2005 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 7 September 2005; pp. 517–521. [Google Scholar]
- Caldecott, D.; Edwards, A.; Haynes, M.; Jerbic, M.; Kadis, A.; Madigan, R.; Prime, Z.; Cazzolato, B. Modelling, simulation and control of an electric unicycle. In Proceedings of the Australasian Conference on Robotics and Automation, Brisbane, QLD, Australia, 1–3 December 2010. [Google Scholar]
- Huang, C.N. The development of self-balancing controller for one-wheeled vehicles. Engineering 2010, 2, 212–219. [Google Scholar] [CrossRef][Green Version]
- Tsai, C.C.; Chan, C.K.; Shih, S.C.; Lin, S.C. Adaptive nonlinear control using RBFNN for an electric unicycle. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 2343–2348. [Google Scholar]
- Liao, C.; Tsai, C. Adaptive hierarchical decoupling slidingmode control of a electric unicycle. In Proceedings of the 2009 International Conference on Service and Interactive Robots, Taipei, Taiwan, 6–7 August 2009. [Google Scholar]
- Ou, Y.; Xu, Y. Balance control of a single wheel robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 2, pp. 2043–2048. [Google Scholar]
- Lin, S.; Tsai, C.; Shi, X. System design and nonlinear control of an electric unicycle. In Proceedings of the 2008 National Conference on Intelligent Living Technology (ILT), Taichung, Taiwan, 6 June 2008. [Google Scholar]
- Lauwers, T.B.; Kantor, G.A.; Hollis, R.L. A dynamically stable single-wheeled mobile robot with inverse mouse-ball drive. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 2884–2889. [Google Scholar]
- Li, Y.; Tsai, C.; Ho, K. Adaptive Throttle based Steering Control of an Electric Unicycle with a Steering Mechanism. In Proceedings of the 2011 International Conference on Service and Interactive Robots, Taichung, Taiwan, 25–27 November 2011; pp. 538–543. [Google Scholar]
- Li, Y.Y.; Tsai, C.C.; Tai, F.C. Adaptive steering control of an electric unicycle. J. Chin. Inst. Eng. 2014, 37, 771–783. [Google Scholar] [CrossRef]
- Schoonwinkel, A. Design and Test of a Computer Stabilized Unicycle. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1987. [Google Scholar]
- Osaka, C.; Kanoh, H.; Masubuchi, M.; Hayasbi, S. Stabilization of Unicycle. Syst. Control 1981, 25, 159–166. [Google Scholar]
- Vos, D.W.; Von Flotow, A.H. Dynamics and nonlinear adaptive control of an autonomous unicycle: Theory and experiment. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 182–187. [Google Scholar]
- Dao, M.Q.; Liu, K.Z. Gain-scheduled stabilization control of a unicycle robot. JSME Int. J. Ser. Mech. Syst. Mach. Elem. Manuf. 2005, 48, 649–656. [Google Scholar] [CrossRef]
- Pommeren, J. 3D control of the robot successful [EB/OL]. J. Syst. Des. Dyn. 2007. Available online: http://hackedgadgets.com/2007/10/08/unibot-3dstabilization (accessed on 25 August 2021).
- Ruan, X.; Hu, J.; Wang, Q. Modeling with Euler-Lagrang equation and cybernetical analysis for a unicycle robot. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–1 October 2009; Volume 2, pp. 108–111. [Google Scholar]
- Guo, L.; Liao, Q.; Wei, S.; CUI, J.w. Dynamical modeling of unicycle robot and nonlinear control. J. Syst. Simul. 2009, 21, 2730–2733. [Google Scholar]
- Cieslak, P.; Buratowski, T.; Uhl, T.; Giergiel, M. The mono-wheel robot with dynamic stabilisation. Robot. Auton. Syst. 2011, 59, 611–619. [Google Scholar] [CrossRef]
- Bauer, R.J. Kinematics and dynamics of a double-gimbaled control moment gyroscope. Mech. Mach. Theory 2002, 37, 1513–1529. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D.; Modi, H.; Shah, S. Adaptive backstepping control scheme with integral action for quanser 2-dof helicopter. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017. [Google Scholar] [CrossRef]
- Kapoor, D.; Sodhi, P.; Deb, D. Solar panel simulation using adaptive control. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012. [Google Scholar] [CrossRef]
- Kapoor, D.; Deb, D.; Sahai, A.; Bangar, H. Adaptive failure compensation for coaxial rotor helicopter under propeller failure. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012. [Google Scholar] [CrossRef]
- Nath, A.; Deb, D.; Dey, R. Robust observer-based adaptive control of blood glucose in diabetic patients. Int. J. Control 2020, 1–14. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D.; Dey, R.; Balas, V.E. Model Reference Adaptive Control of Microbial Fuel Cells. In Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2019; pp. 109–121. [Google Scholar] [CrossRef]
- Spong, M.W. The swing up control problem for the acrobot. IEEE Control Syst. Mag. 1995, 15, 49–55. [Google Scholar]
- Gupta, S.; Singh, A.P.; Deb, D.; Ozana, S. Kalman Filter and Variants for Estimation in 2DOF Serial Flexible Link and Joint Using Fractional Order PID Controller. Appl. Sci. 2021, 11, 6693. [Google Scholar] [CrossRef]
- Rajkumar, S.M.; Chakraborty, S.; Dey, R.; Deb, D. Online Delay Estimation and Adaptive Compensation in Wireless Networked System: An Embedded Control Design. Int. J. Control Autom. Syst. 2019, 18, 856–866. [Google Scholar] [CrossRef]
- Deb, D.; Tao, G.; Burkholder, J.O. An adaptive inverse compensation scheme for signal-dependent actuator nonlinearities. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar] [CrossRef]
- Nath, A.; Deb, D.; Dey, R. An augmented subcutaneous type 1 diabetic patient modelling and design of adaptive glucose control. J. Process. Control 2020, 86, 94–105. [Google Scholar] [CrossRef]
- Singh, A.P.; Deb, D.; Agrawal, H.; Balas, V.E. Fractional Modeling and Controller Design of Robotic Manipulators: With Hardware Validation; Springer Nature: Cham, Switzerland, 2020; Volume 194. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).