Abstract
This paper analyzes the influence of inverter-interfaced distributed generations’ (IIDGs) response during transmission network faults. The simplest and safest solution is to switch IIDGs off during network faults without impacting the network voltages. A more elaborate and efficient concept, required by national grid codes, is based on controlling the IIDGs’ currents, involving positive- and negative-sequence voltage measured at the connection point. In this way the magnitude and phase of the injected currents can be adjusted, although the generated power will depend on the actual line voltages at the connection point. Therefore, an improved concept is proposed to adjust IIDGs’ fault current injection through the required active and reactive power, employing the same voltage characteristics. The proposed, i.e., power-based concept, is more definite than the current-based one, since the required power will always be generated. The discussed concepts for the fault current injection by IIDGs were tested in different 110-kV networks with loop and radial topologies, and for different short-circuit capabilities of the aggregated network supply. Based on extensive numerical calculations, the power-based concept during transmission networks faults generates more reactive power compared to the current-based concept. However, the voltage support by IIDGs during transmission networks faults, regardless of the concept being used, is influenced mainly by the short-circuit capability of the aggregated network supply. As regards distance protection operation, it is influenced additionally by the network topology, i.e., in radial network topology, the remote relay’s operation can be delayed due to a largely seen impedance.
1. Introduction
1.1. Motivation and Literature Review
The system operator can specify that inverter-interfaced distributed generation (IIDG) should provide a fast fault current (FFC) during network faults. The main idea behind this requirement is to generate a predominantly reactive current to identify a fault by network protection, and to support the network voltages [1]. All the static and dynamic FFC requirements have already been implemented in national grid codes, e.g., the Slovenian requirements are similar to the German ones [2]. However, the inverter currents are limited, typically to 120% of its rated value, which impacts the operation of the network protection. Thus, FFC injection by IIDGs raises questions, not only on inverter control during network faults, but also on the network protection operation. The motivation for this paper is to evaluate the impact of IIDGs with FFC injection on the voltage support and distance protection operation during transmission network faults.
New generations of generic IIDG models incorporate balanced FFC (BFFC) injection based on a voltage sag logic [3,4,5]. Improved BFFC is proposed in [6] by an inverter’s DC-link compensation term, which reduces active power during network faults. However, a large body of literature proposes control approaches for unbalanced FFC (UFFC) injection during asymmetrical network faults [7,8,9,10,11,12,13,14,15,16,17,18,19,20]; a comprehensive review is given in [7]. These control approaches all have several objectives, i.e., the quality and limitation of the injected FFC, mitigation of the inverter’s DC-link voltage ripple, damping of instantaneous power oscillations, control of phase voltages within predefined safety limits, and computation of the reactive power reference, depending on the resistive–inductive network impedance model and reference voltage sequences. A commonly used flexible voltage support during network faults is proposed in [8], applying instantaneous symmetrical component-based FFC injection. Ref. [9] investigates an FFC dynamic response, which can reach up to five times the nominal current in cases of sub-optimal control parameters. To prevent the inverter’s transient overcurrents, Ref. [10] proposes a model-predictive control, whereas [11,12] propose flexible power control. The approach proposed in [13] can balance positive and negative-sequence active and reactive powers while keeping the injected FFC to a predefined maximum value. The FFC injection proposed in [14] uses a mixed-potential function to control the DC-link voltage compensation term to reduce power oscillations. Ref. [15] proposes an approach for controlling phase voltages within predefined safety limits by setting the positive and negative reactive power references based on an equivalent impedance network model. The IIDG control proposed in [16] boosts short-term voltage stability based on the negative-sequence voltage at the point of common coupling, and controls the phase voltages within predefined safety limits. Ref. [17] adjusts the FFC injection to network conditions, whereas [18] proposes unified reactive power support with an active power curtailment controller, which can distinguish between islanding and voltage transient events, and provides effective voltage unbalance compensation along with zero active power oscillations and FFC with a controlled peak. Another flexible control approach is proposed in [19], where the FFC reference is determined by the fault condition and predefined constants from the grid code. Furthermore, the approach proposed in [20] guarantees safe operation of the inverter during voltage sags by calculating the appropriate reference FFC according to the equivalent impedance and the voltage sag characteristics, avoiding active power oscillations, and limiting FFC to the maximum value allowed by the inverter.
The IIDG models discussed in [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] are too complicated for protection studies in large networks. Therefore, IIDGs are, typically, modeled simply as a constant current source, showing the impact of their capacity and location on the coordination of overcurrent relays in distribution networks and micro-grids with different topologies [21,22,23,24,25]. More elaborate is the BFFC-based model proposed in [26], as a current limiting element in parallel with the filter capacitor. Ref. [27] uses this model to develop a protection strategy for microgrids. Furthermore, Ref. [28] uses current-limiting characteristics for grid-following and grid-forming IIDGs as constraints for the protection coordination in microgrids. Other protection studies [29,30,31,32,33] incorporate IIDG models with instantaneous FFCs. A BFFC injection, required by the Spanish grid code, is used in [29], presenting a communication-based directional relay system. Ref. [30] discussed protection coordination in distribution networks while considering UFFC injection. Ref. [31] enhances overcurrent protection coordination using the IIDG model that provides limited power by using orthogonal components of the grid voltages, while a current limitation approach has been proposed in [32] to restrict FFC injection. Ref. [33] uses an IIDG model that complies fully with the network code requirements for BFFC injection, to perform a sensitivity analysis of a test network’s transient short circuit current response. Furthermore, Ref. [34] summarizes the FFC contribution by IIDGs and the network protection operation.
1.2. Contribution and Structure of the Paper
This paper analyzes two FFC concepts for IIDGs based on voltage characteristics for positive and negative sequence components, as required in [2]. The standard, i.e., current-based concept adjusts the magnitude and phase of the line currents injected by an IIDG. The proposed concept adjusts FFC through active and reactive power employing the same voltage characteristics, which is the first contribution of this paper. Both FFC concepts, i.e., current- and power-based, are formulated in the phasor-domain, which is the second contribution of this paper. Thus, a simple IIDG model is obtained that complies with grid codes and is suitable for protection studies in large networks; moreover, BFFC and UFFC are both possible. The gap between complicated instantaneous-based FFC calculation approaches and the simplified constant current approach is filled in this way. Furthermore, several protection studies have already reported the impact of IIDGs on protection operation in distribution networks and microgrids, focusing on overcurrent protection coordination. However, a comprehensive analysis of the operation of transmission-network protection impacted by IIDGs is missing. Analysis of IIDG responses and distance protection operation during transmission-network faults is another contribution of this paper.
The rest of this paper is organized as follows. Section 2 proposes the phasor-based IIDG model and describes the discussed FFC concepts based on reference current and power. The test network is presented in Section 3, including relevant data, topologies, and the different SSC of an aggregated network supply. The active and reactive power of all the IIDGs during the network faults are analyzed, together with the voltages at the connection point and distance protection operation. Section 4 presents a case study, i.e., a transmission network related to the 110-kV northeastern part of the Slovenian power system, considering the expected IIDG’s capacities. The power generated by IIDGs, voltage profiles, and distance protection operation are analyzed for different topologies during the faults at different locations. Section 5 raises a discussion on IIDG models for FFC injection, and indicates future work on protection studies, while Section 6 concludes the paper.
2. IIDG Model for FFC Injection
A phasor-based model is proposed; Figure 1 shows the basic model structure. Two concepts are used to calculate references for line current phasors, which involve voltage characteristics, whereas the model also enables selection between BFFC and UFFC injection. Ideal three-phase star-connected current sources were used, which can also operate as a sink, enabling the simulation of a battery energy storage (BES) unit in the discharging and charging regime. Thus, the dynamics of current controllers and an inverter were neglected, which is suitable for protection studies in large networks.
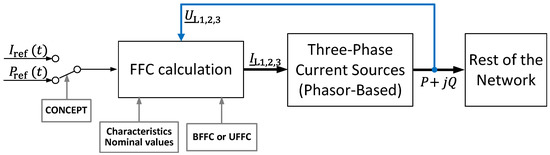
Figure 1.
Structure of an IIDG model for FFC injection.
2.1. Voltage Characteristics
The proposed characteristics are shown in Figure 2, where , , and denote functions for the positive and negative sequence components. , , and are, respectively, positive and negative sequence voltage magnitudes and nominal line voltage. Three independent parameters describe each characteristic, i.e., a voltage dead-band, a slope, and the maximal value. The parameter limits proposed by the grid code [2] are ±20% for the voltage dead-band, a slope [2, 6] pu/pu, whereas the maximal value should not exceed 80% of the IIDG’s overcurrent protection setting. Furthermore, a reactive current is prioritized, while an active current should be readjusted continually.
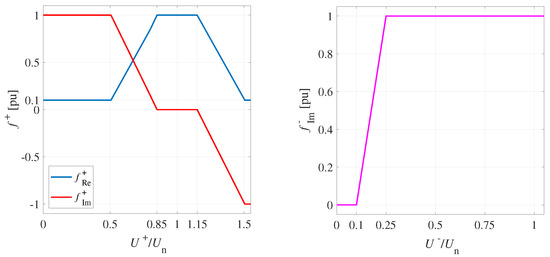
Figure 2.
Voltage characteristics for positive and negative sequence components.
2.2. Current- and Power-Based Concept
Applying the standard, i.e., current-based concept, is the reference line current phasor calculated as
where refers to the time-dependent normalized reference current, is the IIDG’s nominal line current, and stands for the complex conjugate. Note that this concept complies with the requirements given in [2]. Figure 3 shows the functional scheme for the current-based concept, where denote line voltage phasors at the IIDG’s connection point, , denote positive and negative sequence voltage phasors, while ,, and are real and imaginary parts of the positive and negative sequence current phasors. Furthermore, the magnitude of the line current phasors is limited as . Moreover, the voltage at the connection point is a nonlinear function of operating conditions and reference currents, which are also a function of voltages at the same connection point. A delay is introduced in the calculation by a first-order system with a time constant of 1 ms to break the algebraic loop.
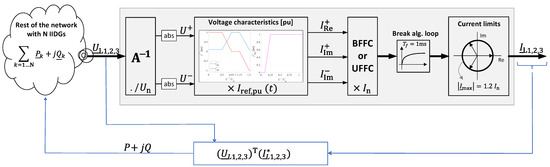
Figure 3.
Functional scheme for calculating IIDG’s reference line current phasors—current-based concept.
The limitation of the current-based concept is that the generated power will depend on actual line voltages at the connection point. Therefore, active and reactive power are introduced using the same voltage characteristics instead of currents. Thus, applying the proposed, i.e., power-based concept is the reference line current phasor calculated as
where refers to the time-dependent normalized reference power, is the IIDG’s nominal capacity, and stands for the complex conjugate. Furthermore, the functional scheme for the reference phasor currents calculation (Figure 3) should be modified according to the power-based concept (2) and (3). Note that this concept also complies with the requirements given in [2]; however, its behavior is more definite than the current-based.
2.3. BFFC and UFFC
Selection between BFFC and UFFC affects the calculation of line current phasors and . When using the BFFC, they are calculated as and . When using the UFFC are line current phasors and calculated by the transformation matrix for symmetrical components .
3. Test Network
A 4-bus test network with a loop topology was considered, as is shown in Figure 4. The IIDGs were connected at substations B, C, and D. The nominal power of each IIDG was set to 10 MW, which covers local loads at each of the substations. Both concepts were tested, i.e., current- and power-based, while injecting only BFFC.
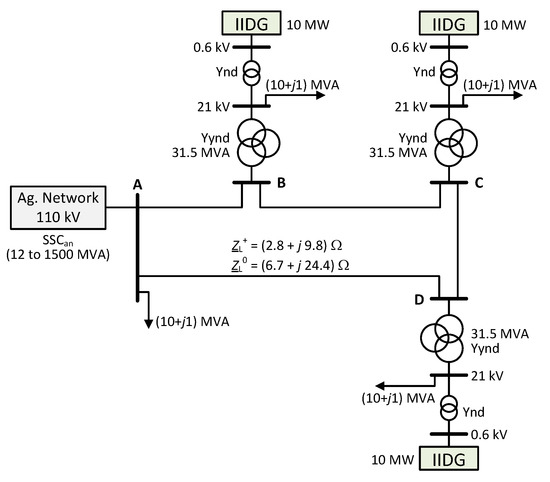
Figure 4.
Single line diagram of the test network with relevant data.
3.1. Reference Tracking
Arbitrary time-profiles of IIDGs were assumed during normal voltage conditions, where IIDG D was assumed to operate as a BES unit. Note that normalized references and were changed in the same way, separately for each of the discussed concepts; Figure 5a shows almost perfect active power reference tracking for the power-based concept, especially for a BES unit during the transition between charging and discharging operating regimes. Furthermore, a small amount of reactive power was generated during a time interval when the voltages deviated from the voltage dead-band. The current-based concept showed exact tracking of the reference current; however, the resulting active power was lower when compared with the power-based concept, as shown in Figure 5b. The power reduction was due to the off-nominal initial voltages that were approximately 0.93 pu. The obtained results show that the power-based concept is more definite, since the required power will be generated.
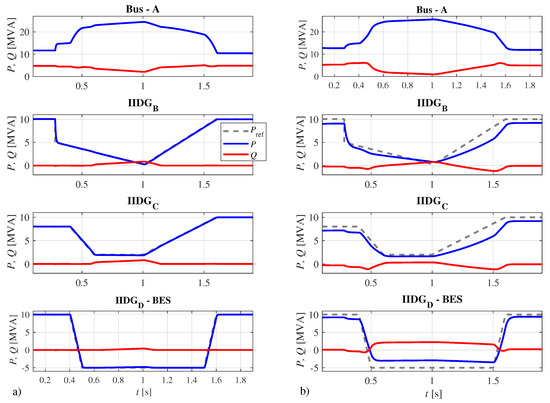
Figure 5.
Comparison in power generation assuming reference tracking of the power-based FFC (a), and current-based FFC (b).
3.2. Responses during Network Faults
The next test assumes a phase-to-phase (Ph-Ph) fault with a fault resistance of 2 in the middle of the C-D line. The fault was incepted at a simulation time of 1 s, while at 1.2 s, the faulted line was disconnected. All IIDGs operated with a nominal power of 10 MW, while the Short-Circuit Capability (SSC) of an aggregated network supply was set as 50 MVA. Figure 6 shows power generation for both the discussed FFC concepts. More reactive power was generated when using the power-based concept, which is a consequence of considering actual voltages (positive and negative components) at the IIDG’s connection points to calculate generated line currents. Consequently, a larger reduction in the active power was noticed when using the power-based concept.
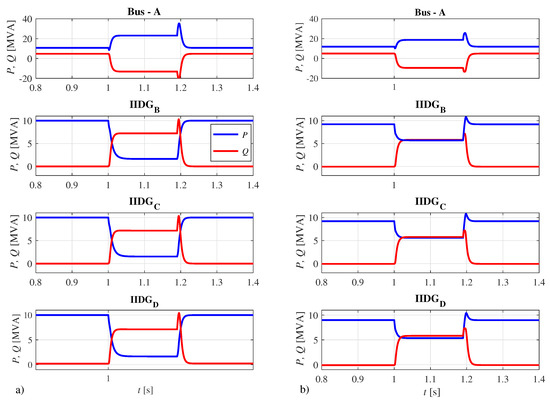
Figure 6.
Comparison in power generation during a Ph-Ph fault (L2-L3) in the middle of the C-D line, employing the power-based FFC (a), and current-based FFC (b).
Figure 7 shows steady-state line voltages at the IIDGs’ connection point during the fault. Along with both FFC concepts, a concept was also considered where the IIDGs were switched off during the fault. The current-based concept resulted in higher line voltages in all three phases, but the differences were minimal compared to the power-based concept. However, when the IIDG’s were switched off during a fault, the voltages were considerably lower than when employing the FFC.
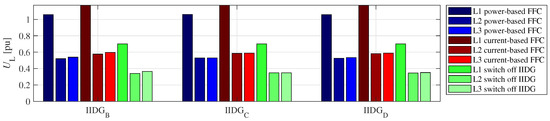
Figure 7.
Comparison of line voltages during a Ph-Ph fault (L2-L3) in the middle of the C-D line, employing the power-based FFC, current-based FFC, and when switching-off IIDGs.
3.3. Impact of SSC of an Aggregated Network Supply
Additional tests were performed for a phase-to-phase (Ph-Ph) fault with a fault resistance of 2 in the middle of the C-D line for different SSC values of an aggregated network supply. Table 1 and Table 2 give the steady-state values during the fault for the generated power and line voltages. The obtained results show that an increase in the aggregated network SSC decreased the differences in generated power between both FFC concepts. The generated reactive power was not affected significantly by an aggregated network SSC when using the power-based FFC concept. Compared with the current-based concept, the power-based concept also generated more reactive power and less active power. Furthermore, the generated apparent power was approximately equal for both the discussed FFC concepts. Minor differences in voltage support by both FFC concepts were seen only for small values of an aggregated network SSC.

Table 1.
Steady-state results during a Ph-Ph fault (L2-L3) in the middle of the C-D line, employing the power-based FFC.

Table 2.
Steady-state results during a Ph-Ph fault (L2-L3) in the middle of the C-D line, employing the current-based FFC.
3.4. Distance Protection Operation
Only distance protection was analyzed, since it is the primary protection for 110-kV networks. The criterion for the operation of distance protection is the positive-sequence impedance, which was calculated using line voltage and current phasors measured on both sides of the faulted line [35]. The cases discussed in the previous section show a small error in calculated impedance from both sides of the faulted line, regardless of which FFC concept was employed. The error in calculated impedance was up to 20% in the R-direction and only up to 2.5% in the X-direction. Consequently, the correct operation of distance protection was expected, because the fault was supplied equally from both sides of the line.
To test distance protection operation properly, two more challenging tests were assumed. In the first test, the SSC of the aggregated network supply was reduced to only 12 MVA and the line A-D was out of service, thus leading to the radial topology. Different fault types, i.e., three-phase (3-Ph), phase-to-phase (Ph-Ph), and phase-to-ground (Ph-G), were considered on the line C-D at the distances that correspond to 20% and 80% from the bus C. Furthermore, fault resistance of 2 was considered. Figure 8 shows the impedances seen by the relays C and D, i.e., and , respectively. Furthermore, line impedance is also shown, together with protection zones. Note that the first zone covers 85% of the line length, while the second zone is extended to the next line by covering 120% of the protected line length. The protection operation for faults in the first zone is instantaneous, while it is delayed for faults in the second zone to achieve selectivity [35]. As shown in Figure 8, the distance relay at side C would operate correctly in all cases, since the impedance was seen in the first zone. The operation of the relay at side D would be delayed in some situations, due to the impedance seen in the second zone. However, after the faulted line was disconnected from side C, the measured impedance of the relay at side D moved into the first operating zone in all cases, as indicated by the dotted arrow line. To avoid delays in distance protection operation, the introduction of communication with the appropriate logic scheme (tripping or blocking) is necessary [36].
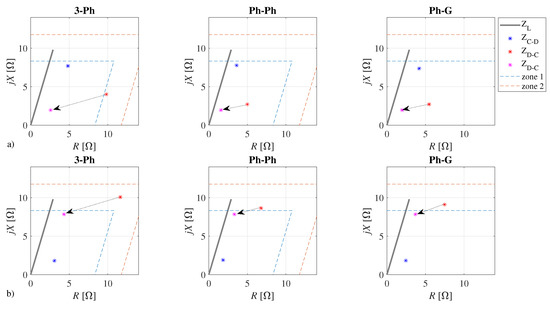
Figure 8.
Distance protection operation in radial topology for different fault types on the C-D line at 20% from bus C (a), and at 80% from bus C (b), where = 12 MVA (the dotted arrow line indicates disconnection at the side C).
In the last test, the SSC of an aggregated network was increased significantly to 1500 MVA. Again, the line A-D was out of service, representing the typical situation of a strong network that operates against a weak network with a significant impact on distance protection. Different fault types were assumed on line C-D at a distance of 20% from bus D. Again, fault resistance of 2 was considered. The distance protection relay at side D would fail to operate in cases of 3-Ph and Ph-Ph faults, as is shown in Figure 9, since the seen impedance was out of all the protection zones. Only after the faulted line was disconnected from side C, the relay at side D calculated short-circuit impedance correctly, as indicated by the dotted arrow line. This would cause some unacceptable delay in the fault clearance; therefore, the build-in function “Echo and Tripping in the Event of Weak Infeed” should be implemented in such cases [36].
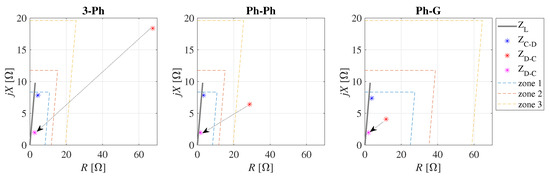
Figure 9.
Distance protection operation in radial topology for different fault types on the C-D line at 20% from bus D, where = 1500 MVA (the dotted arrow line indicates disconnection at the side C).
4. Case Study: The Northeast Part of the Slovenian Transmission System
The northeast part of the Slovenian transmission system is discussed, as shown in Figure 10. An individual substation (SS) was modeled by a TR 110 kV/X, an aggregated constant load, and an aggregated PV unit with the discussed FFC concepts. Furthermore, two BES units with the discussed FFC concepts and two hydropower plants (HPPs) were also considered in the network, along with five different aggregated network supplies. The main data of all discussed SSs are given in Table 3. Maximal load was calculated according to the measurements for a period of three months during the summer, considering only the day-time. Furthermore, according to realistic plans, the PV and BES units’ capacity will increase approximately up to four times by 2030. All PVs and BESs were assumed to operate with their maximal capacity expected by 2030, except the PVs in SSs Sobota and Mackovci and BES in Kidricevo.
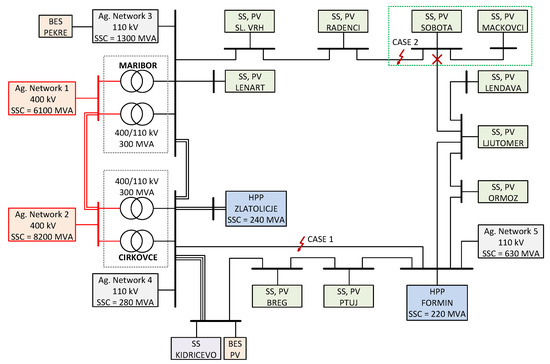
Figure 10.
Single line diagram of the Slovenian northeast transmission network.

Table 3.
Main substation data with current capacities of the PV and BES units.
Numerous short-circuit analyses were performed for different fault types and locations on different 110-kV lines. The faults were incepted at a simulation time of 0.3 s, while at 0.42 s, the faulted line was disconnected. Three states were observed, i.e., normal operation (State 1), fault (State 2), and disconnection of the faulted line (State 3). Only two cases are presented, with the most indicative results.
4.1. Case 1—Faults in Loop Topology with a Strong Network Supply
In the first case, faults were assumed on the Formin–Cirkovce line, as shown in Figure 10. Power generation of IIDGs and line voltage magnitudes at the 110-kV level are shown in Figure 11 and Figure 12 for a Ph-Ph fault. Due to the loop-network topology, all PVs and BESs changed their power during the fault, i.e., active power was reduced, while reactive power was increased. Minor responses were noticed by BES Pekre and by PVs Lenart and Sl. Vrh, since they were the more distant from the fault location, but close to the SS 400/110 kV Maribor. The largest responses were noticed by PVs Lendava, Ljutomer, and Ormoz, which were the more distant from both SSs 400/110 kV. Other PVs show moderate responses in generated power. PVs Ptuj, Breg and BES Kidricevo also showed moderate responses, even though they are the closest to the fault location; however, they are also electrically close to the SS 400/110 kV Maribor. Voltages during the fault were less reduced at PV and BES locations with smaller changes in the generated power, which shows the dominant impact of the aggregated network supplies. Moreover, compared to the concept when PV and BES units would be switched off during the fault, the voltage profile was slightly improved by the FFC-based IIDGs at the buses near the fault location. Regarding the distance protection operation for different fault types, no issues were observed, regardless of the IIDG concept (FFC or switching off), which is entirely due to the dominant SSC of aggregated network supplies.
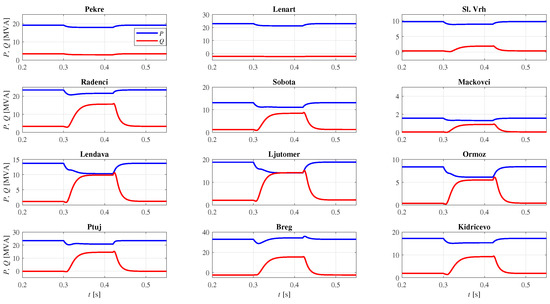
Figure 11.
Generated power for case 1 during normal operation, Ph-Ph fault, and after the faulted line was disconnected.
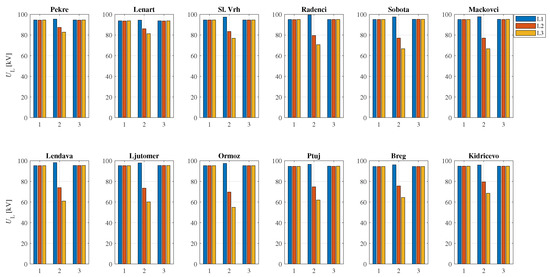
Figure 12.
Line voltage magnitudes for case 1 during normal operation (State 1), Ph-Ph fault L2-L3 (State 2), and after the faulted line was disconnected (State 3).
4.2. Case 2—Faults in Radial Topology with Weak IIDGs
The second case assumes faults on the Radenci–Sobota line, while the Sobota–Ljutomer line was out of service, leading to a radial topology between Maribor and Mackovci, as shown in Figure 10. Consequently, a typical situation was obtained, where a strong network (SS 400/110 kV Maribor) operates against a weak network (PVs Sobota and Mackovci) during the faults. Furthermore, when the faulted line was disconnected, the SSs Sobota and Mackovci operated as an island. Figure 13 and Figure 14 show the power generation of the PV and BES units and line voltage magnitudes at the 110-kV level for a Ph-Ph fault. Since the loop was opened between SSs Sobota and Ljutomer, the PVs Lendava, Ljutomer, Ormoz, Ptuj, Breg, and BES Kidricevo showed minor changes in generated power. Consequently, the voltages during the fault at these locations practically did not change. PVs Lenart, Sl. Vrh and BES Pekre showed minor responses in the generated power, since the fault was supplied mainly from the SS 400/110 kV Maribor. The largest repose in generated power was shown by PVs Radenci, Sobota, and Mackovci, which were very close to the fault location. Voltages at those PVs were reduced by approximately 50% during the fault; however, the reduction in voltages at PVs closer to the SS 400/110 kV Maribor (PVs Sl. Vrh and Lenart) was smaller. Furthermore, it can be observed that the voltages at Mackovci and Sobota increased slightly after the disconnection of the faulted Radenci–Sobota line, since these SSs operate as an island. The distance relay at the side of the strong network (SS Radenci) operated correctly for all fault types and admissible locations. On the other hand, the distance relay from the weak side (SS Sobota) failed to operate in all cases, due to the limited PV currents in Sobota and Mackovci.
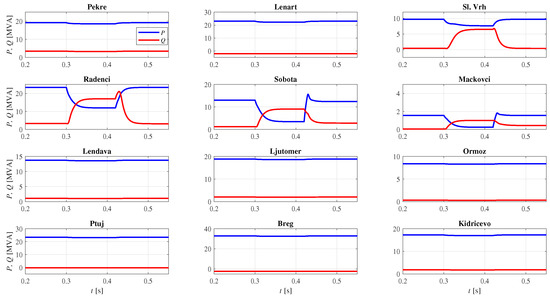
Figure 13.
Generated power for case 2 during normal operation, Ph-Ph fault, and after the faulted line was disconnected.
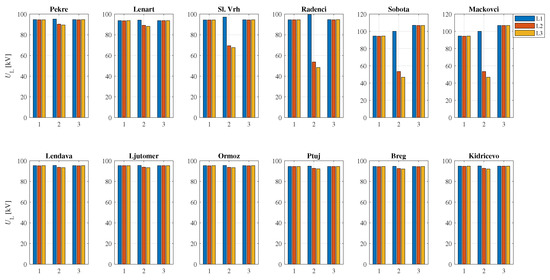
Figure 14.
Line voltage magnitudes for case 2 during normal operation (State 1), Ph-Ph fault L2-L3 (State 2), and after the faulted line was disconnected (State 3).
5. Discussion and Future Work
An increased share of the IIDGs will undoubtedly influence the operation of a power system protection. Therefore, a simple phasor-based IIDG model that complies with grid codes is proposed, which can be used to perform protection studies in large networks. Moreover, the proposed model offers flexibility in choosing between the power- and current-based concept, and between the BFFC and UFFC injection. A comparison of relevant IIDG models is given in Table 4. A natural extension of this work would be implementing the proposed IIDG model for FFC injection in overcurrent protection coordination in medium voltage distribution networks and microgrids.

Table 4.
Comparison of relevant IIDG models suitable for protection studies.
6. Conclusions
This paper proposes a phasor-based IIDG model for FFC injection, which is suitable for protection studies in large networks. A comparison is made between the power- and current-based FFC concepts for a testing network with three IIDGs and a case study, i.e., the northeast part of the Slovenian transmission system. The obtained results show that both the discussed FFC concepts during network faults increased generated reactive power while decreasing the active power. The responses of generated power were more expressed when using the power-based FFC concept. Furthermore, reactive power generation was not affected considerably by the SSC of an aggregated network supply, and was more significant when using the power-based concept. Moreover, the largest reactive power generation is noticeable at IIDGs electrically close to the fault location and IIDGs distant from the strong network supplies.
Regarding overall voltage support during network faults, a minor impact of FFC injection was noticed only when the IIDGs’ overall capacity was comparable to the SSC of the aggregated network supply. IIDGs might also influence the operation of distance protection in combination with special cases of network topology and the SSC of an aggregated network supply. When the capacity of IIDGs is comparable to the SSC of the aggregated network supply, then an impact could be expected on distance protection operation. However, the most critical situation in radial network topologies will occur when a strong network operates against a weak network during the faults.
Author Contributions
Supervision, B.P. and J.R.; Writing—original draft, B.P. and B.G.; Writing—review and editing, B.P. and J.Č. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by ARRS under Projects P2-0115 and J2-1742.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not report any data.
Acknowledgments
The authors would like to thank ELES, Ltd., Electricity Transmission System Operator.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IIDG | Inverter-Interfaced Distributed Generation |
| FFC | Fast Fault Current |
| BFFC | Balanced FFC |
| UFFC | Unbalanced FFC |
| SSC | Short-Circuit Capability |
| BES | Battery Energy Storage |
| PV | Photovoltaic |
| SS | Substation |
| 3-Ph | Three-Phase |
| Ph-Ph | Phase-to-Phase |
| Ph-G | Phase-to-Ground |
References
- EUR-Lex. Establishing a Network Code on Requirements for Grid Connection of Generators; Commission Regulation (EU) 2016/631; European Union: Brussels, Belgium, 2016. [Google Scholar]
- VDE-AR-N 4120:2017-05, Technical Requirements for the Connection and Operation of Customer Installations to the High-voltage Network (TCC High-Voltage); VDE Verlag GmbH: Berlin, Germany, 2017.
- Modeling and Validation Work Group; Renewable Energy Modeling Task Force. WECC Wind Plant Dynamic Modeling Guidelines; WECC: Salt Lake City, UT, USA, 2014. [Google Scholar]
- WECC Modeling and Validation Work Group. Solar Photovoltaic Power Plant Modeling and Validation Guideline; WECC: Salt Lake City, UT, USA, 2019. [Google Scholar]
- Farantatos, E. Model User Guide for Generic Renewable Energy System Models; Technical Update 3002014083; EPRI: Palo Alto, CA, USA, 2018. [Google Scholar]
- Mirhosseini, M.; Pou, J.; Agelidis, V.G. Single- and Two-Stage Inverter-Based Grid-Connected Photovoltaic Power Plants with Ride-Through Capability under Grid Faults. IEEE Trans. Sustain. Energy 2015, 6, 1150–1159. [Google Scholar] [CrossRef]
- Celik, D.; Meral, M.E. Voltage Support Control Strategy of Grid-Connected Inverter System under Unbalanced Grid Faults to Meet Fault Ride through Tequirements. IET Gener. Transm. Distrib. 2020, 14, 3198–3210. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.C.; Alarcon-Gallo, E. Flexible Voltage Support Control for Three-Phase Distributed Generation Inverters under Grid Fault. IEEE Trans. Power Electron. 2013, 60, 1429–1441. [Google Scholar] [CrossRef]
- Popadic, B.; Dumnic, B.; Strezoski, L. Modeling of Initial Fault Response of Inverter-Based Distributed Energy Resources for Future Power System Planning. Int. J. Electr. Power Energy Syst. 2020, 117, 105722. [Google Scholar] [CrossRef]
- Meyer, R.; Zlotnik, A.; Mertens, A. Fault Ride-Through Control of Medium-Voltage Converters with LCL Filter in Distributed Generation Systems. IEEE Trans. Ind. Appl. 2014, 50, 3448–3456. [Google Scholar] [CrossRef]
- Guo, X.; Liu, W.; Lu, Z. Flexible Power Regulation and Current-Limited Control of the Grid-Connected Inverter under Unbalanced Grid Voltage Faults. IEEE Trans. Ind. Electron. 2017, 64, 7425–7432. [Google Scholar] [CrossRef]
- Afshari, E.; Moradi, G.R.; Rahimi, R.; Farhangi, B.; Yang, Y.; Blaabjerg, F.; Farhangi, S. Control Strategy for Three-Phase Grid-Connected PV Inverters Enabling Current Limitation Under Unbalanced Faults. IEEE Trans. Ind. Electron. 2017, 64, 8908–8918. [Google Scholar] [CrossRef] [Green Version]
- Camacho, A.; Castilla, M.; Miret, J.; Borrell, A.; Garcia de Vicuna, L. Active and Reactive Power Strategies with Peak Current Limitation for Distributed Generation Inverters during Unbalanced Grid Faults. IEEE Trans. Ind. Electron. 2015, 62, 1515–1525. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Fazeli, M. A Low-Voltage Ride-Through Strategy Using Mixed Potential Function for Three-Phase Grid-Connected PV Systems. Electr. Power Syst. Res. 2019, 173, 271–280. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Guzman, R.; Borrell, A. Reactive Power Control for Distributed Generation Power Plants to Comply with Voltage Limits During Grid Faults. IEEE Trans. Power Electron. 2014, 29, 6224–6234. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.; Nadarajah, M.; Hossain, M.J. A Grid-Support Strategy with PV Units to Boost Short-Term Voltage Stability under Asymmetrical Faults. IEEE Trans. Power Syst. 2020, 35, 1120–1131. [Google Scholar] [CrossRef]
- Shuvra, M.A.; Chowdhury, B. Distributed Dynamic Grid Support Using Smart PV Inverters during Unbalanced Grid Faults. IET Renew. Power. Gener. 2019, 13, 598–608. [Google Scholar] [CrossRef]
- Khan, H.; Chacko, S.J.; Fernandes, B.G.; Kulkarni, A. Reliable and Effective Ride-Through Controller Operation for Smart PV Systems Connected to LV Distribution Grid under Abnormal Voltages. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2371–2384. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current Reference Generation Based on Next-Generation Grid Code Requirements of Grid-Tied Converters during Asymmetrical Faults. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3784–3797. [Google Scholar] [CrossRef] [Green Version]
- Garnica, M.; Garcia de Vicuna, L.; Miret, J.; Castilla, M.; Guzman, R. Optimal Voltage-Support Control for Distributed Generation Inverters in RL Grid-Faulty Networks. IEEE Trans. Power Electron. 2020, 67, 8405–8415. [Google Scholar] [CrossRef] [Green Version]
- Zeineldin, H.H.; Sharaf, H.M.; Ibrahim, D.K.; El-Zahab, E.E.-D.A. Optimal Protection Coordination for Meshed Distribution Dystems with DG Using Dual Setting Directional Over-Current Relays. IEEE Trans. Smart Grid 2015, 6, 115–123. [Google Scholar] [CrossRef]
- Huchel, L.; Zeineldin, H.H. Planning the Coordination of Directional Overcurrent Relays for Distribution Systems Considering DG. IEEE Trans. Smart Grid 2016, 7, 1642–1649. [Google Scholar] [CrossRef]
- Pereira, K.; Pereira, B.R.; Contreras, J.; Mantovani, J.R.S. A Multiobjective Optimization Technique to Develop Protection Systems of Distribution Networks with Distributed Generation. IEEE Trans. Power Syst. 2018, 33, 7064–7075. [Google Scholar] [CrossRef] [Green Version]
- Katyara, S.; Staszewski, L.; Leonowicz, Z. Protection Coordination of Properly Sized and Placed Distributed Generations-Methods, Applications and Future Scope. Energies 2018, 11, 2627. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.M.; Le, P.D.; Nguyen, T.P.; Nguyen, H. An adaptive and scalable protection coordination system of overcurrent relays in distributed-generator-integrated distribution networks. Appl. Sci. 2021, 11, 8454. [Google Scholar] [CrossRef]
- Plet, C.A.; Green, T.C. Fault Response of Inverter Interfaced Distributed Generators in Grid-Connected Applications. Electr. Power Syst. Res. 2014, 106, 21–28. [Google Scholar] [CrossRef]
- Pinto, J.O.C.P.; Moreto, M. rotection Strategy for Fault Detection in Inverter-Dominated Low Voltage AC Microgrid. Electr. Power Syst. Res. 2021, 190, 106572. [Google Scholar] [CrossRef]
- Barnes, A.K.; Tabarez, J.E.; Mate, A.; Bent, R.W. Optimization-Based Formulations for Short-Circuit Studies with Inverter-Interfaced Generation in PowerModelsProtection.jl. Energies 2021, 14, 2160. [Google Scholar] [CrossRef]
- Bakkar, M.; Bogarra, S.; Corcoles, F.; Iglesias, J. Overcurrent Protection Based on ANNs for Smart Distribution Networks with Grid-Connected VSIs. IET Gener. Transm. Distrib. 2020, 15, 1159–1174. [Google Scholar] [CrossRef]
- Zarei, S.F.; Khankalantary, S. Protection of Active Distribution Networks with Conventional and Inverter-Based Distributed Generators. Int. J. Electr. Power Energy Syst. 2021, 129, 106746. [Google Scholar] [CrossRef]
- Salem, M.M.; Elkalashy, N.I.; Atia, Y.; Kawady, T.A. Modified Inverter Control of Distributed Generation for Enhanced Relaying Coordination in Distribution Networks. IEEE Trans. Power Deliv. 2017, 32, 78–87. [Google Scholar] [CrossRef]
- Yousaf, M.; Muttaqi, K.M.; Sutanto, D. A Control Strategy to Mitigate the Sensitivity Deterioration of Overcurrent Protection in Distribution Networks with the Higher Concentration of the Synchronous and Inverter-Based DG Units. IEEE Trans. Ind. Appl. 2021, 57, 2298–2306. [Google Scholar] [CrossRef]
- Aljarrah, R.; Marzooghi, H.; Yu, J.; Terzija, V. Sensitivity Analysis of Transient Short Circuit Current Response to the Penetration Level of Non-Synchronous Generation. Int. J. Electr. Power Energy Syst. 2021, 125, 106556. [Google Scholar] [CrossRef]
- ENTSO-E. Short Circuit Contribution of New Generating Units Connected with Power Electronics and Protection Behaviour; ENTSO-E: Brussels, Belgium, 2019. [Google Scholar]
- Ziegler, G. Numerical Distance Protection: Principles and Applications, 4th ed.; Publicis Publishing: Erlangen, Germany, 2011. [Google Scholar]
- Werstiuk, C. The Relay Testing Handbook: Principles and Practice; Valence Electrical Training Services: Littleton, CO, USA, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).