A Study on the Anomaly Detection of Engine Clutch Engagement/Disengagement Using Machine Learning for Transmission Mounted Electric Drive Type Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Target Vehicle and Data
2.1. Target Vehicle
2.2. Target Data
- Cranking an engine using MG1 or MG2;
- Speed synchronization of both sides of the engine clutch (engine and traction motor speed synchronization);
- Engine clutch engagement and transition to HEV mode.
3. Data Preprocessing for Model Training and Test
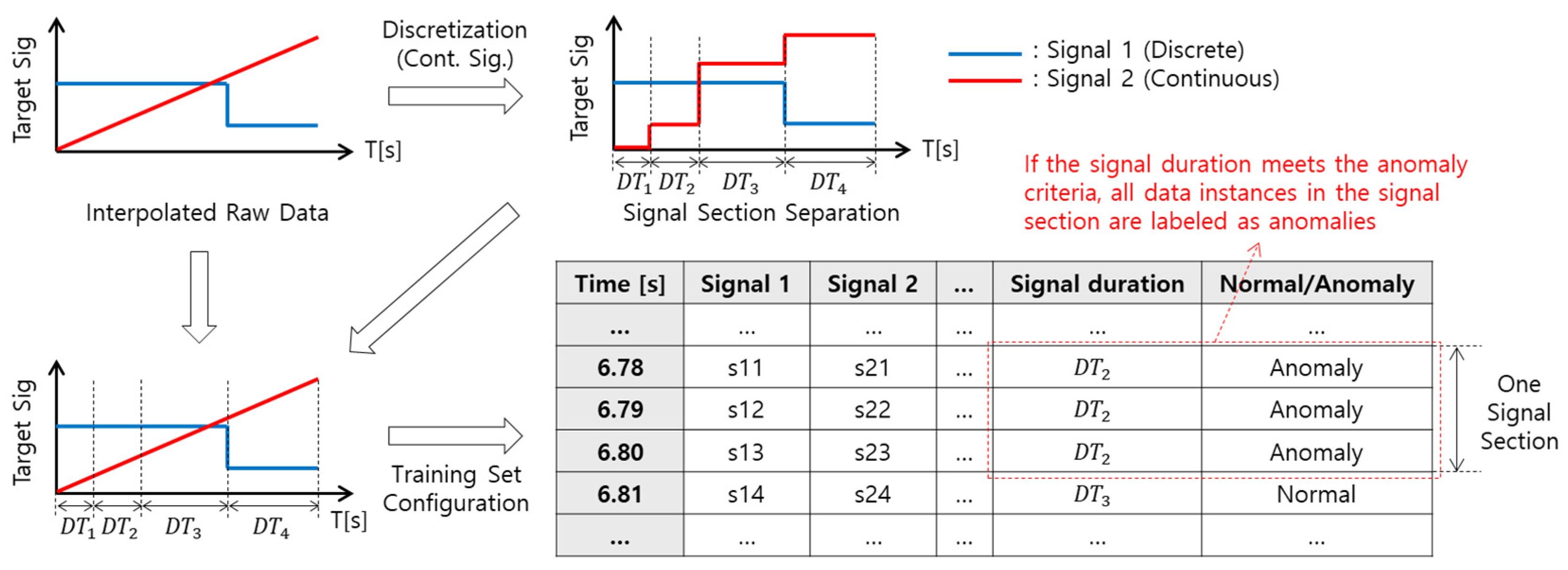
3.1. Data Interpolation
3.2. Target Data Section Extraction (Pattern Extraction)
4. Anomaly Detection Model Training
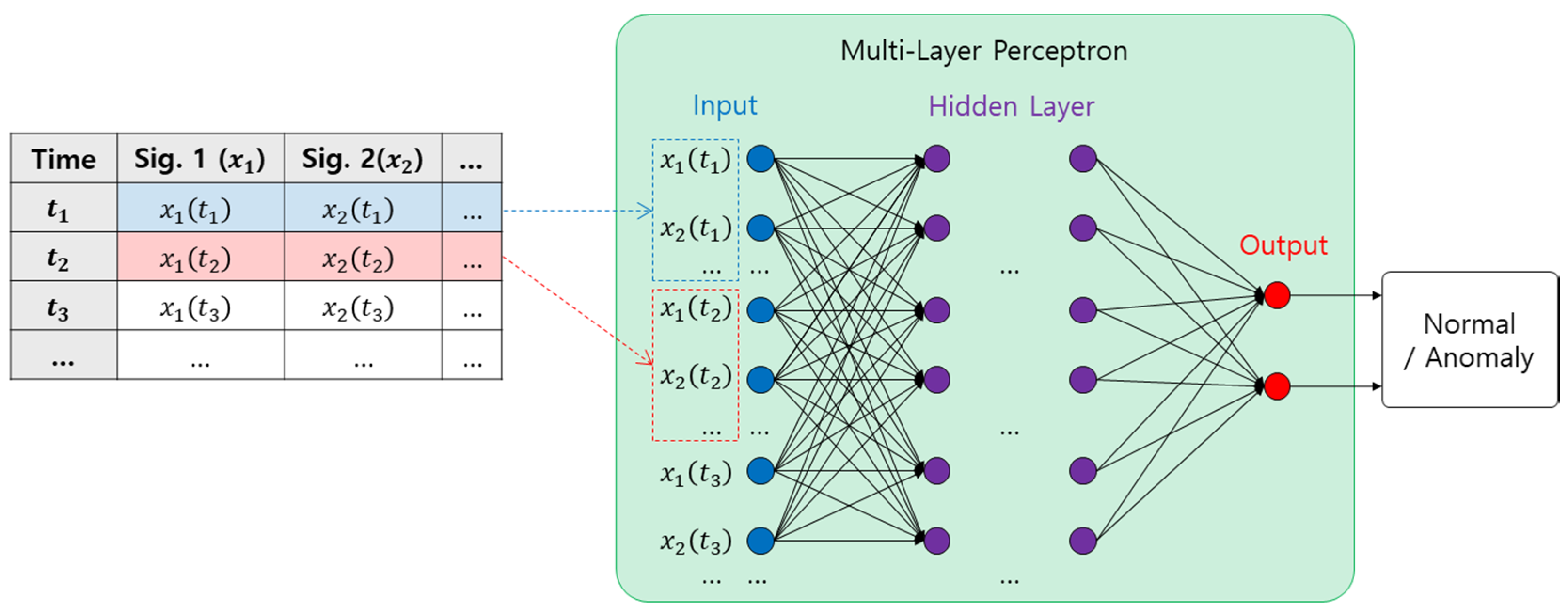
4.1. Multi-Layer Perceptron (MLP)
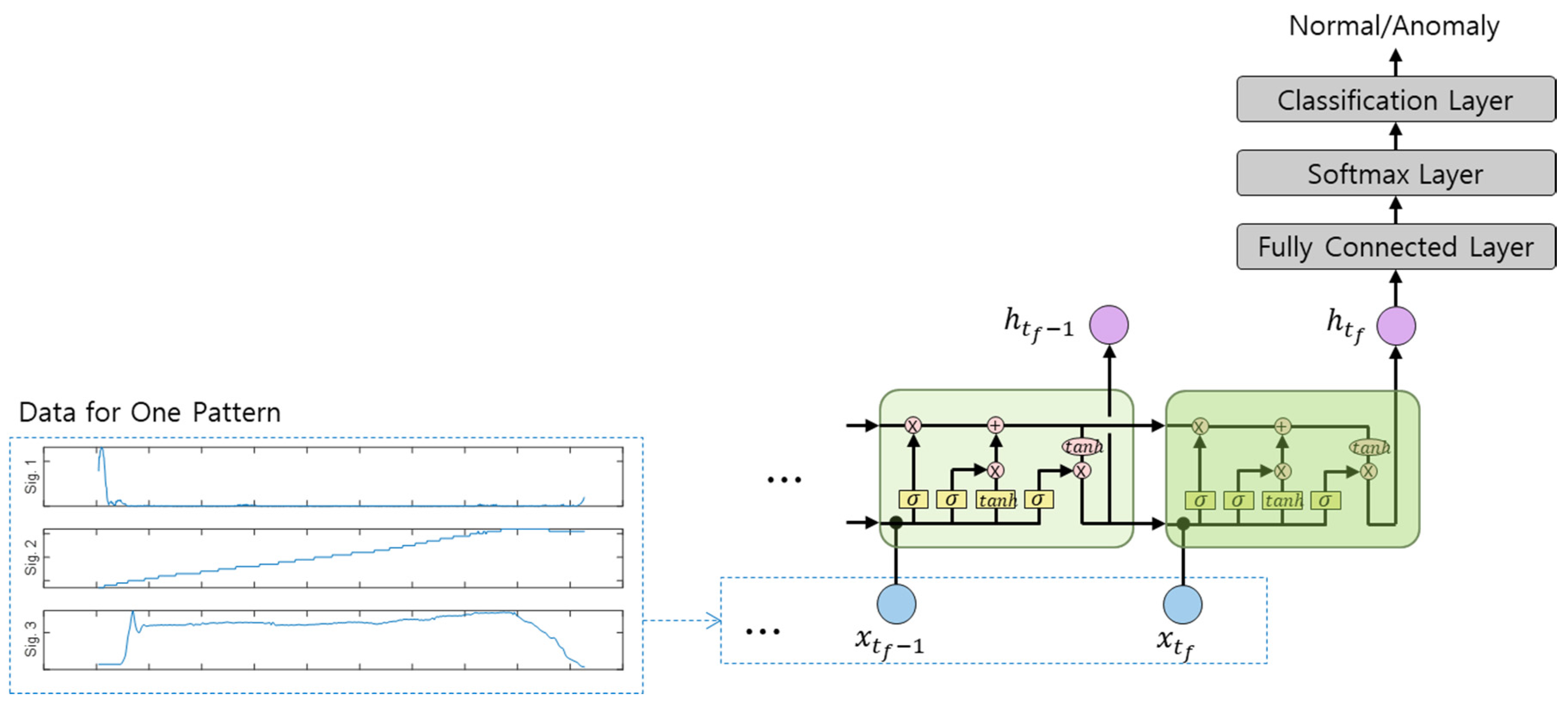
4.2. Long Short-Term Memory (LSTM)
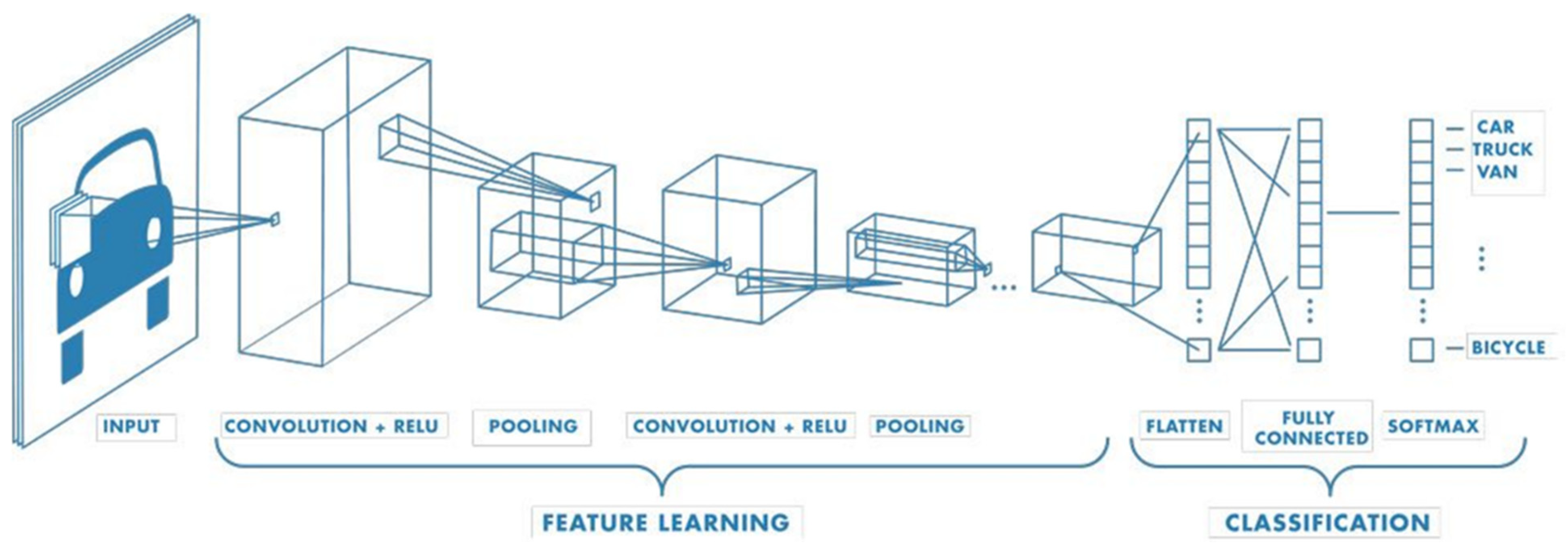
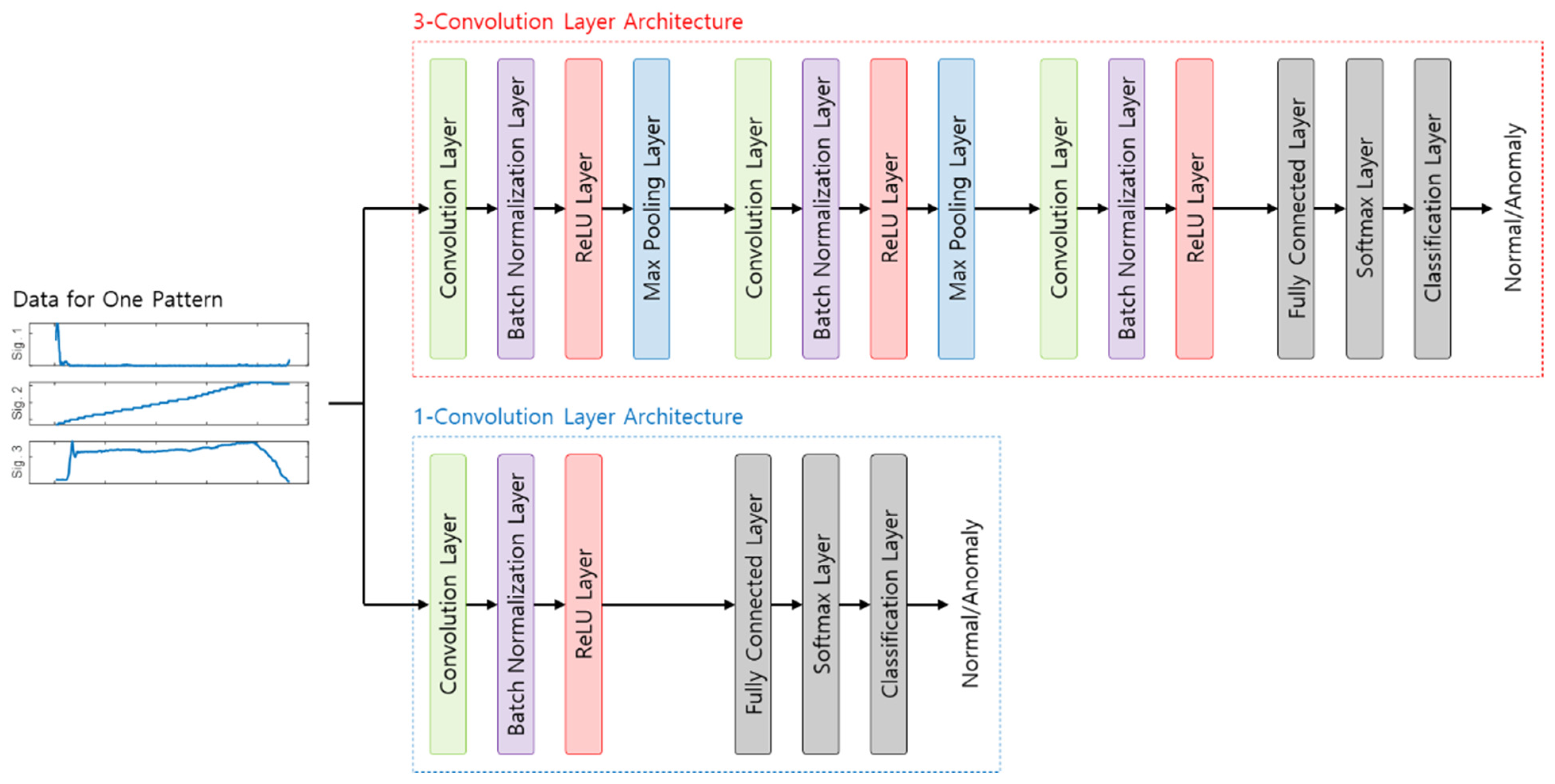
4.3. Convolutional Neural Network (CNN)
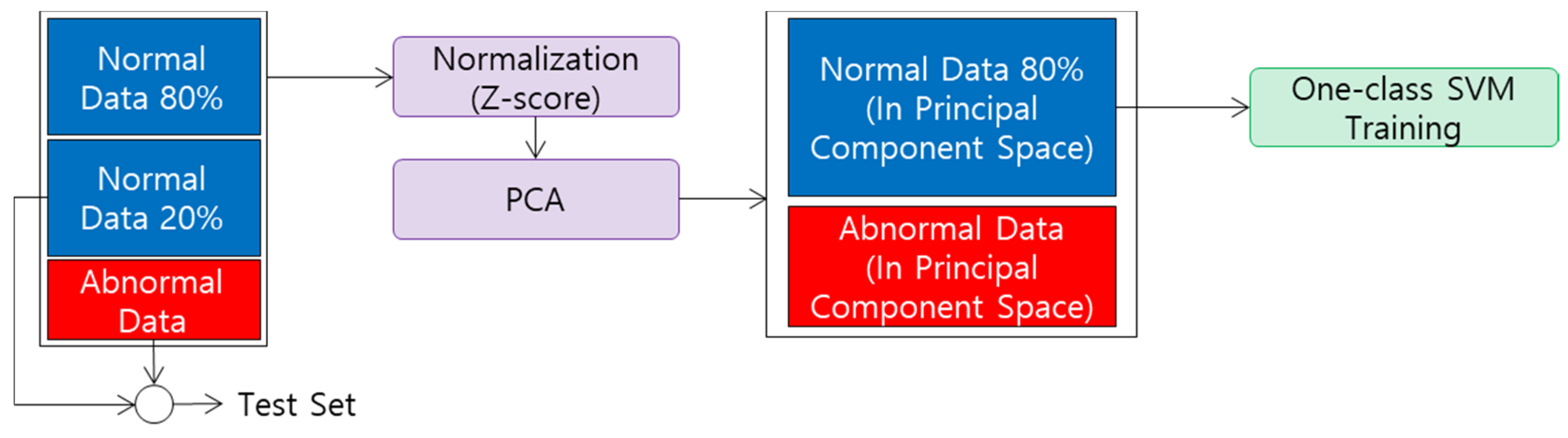
4.4. One-Class SVM
5. Anomaly Detection Model Test Results
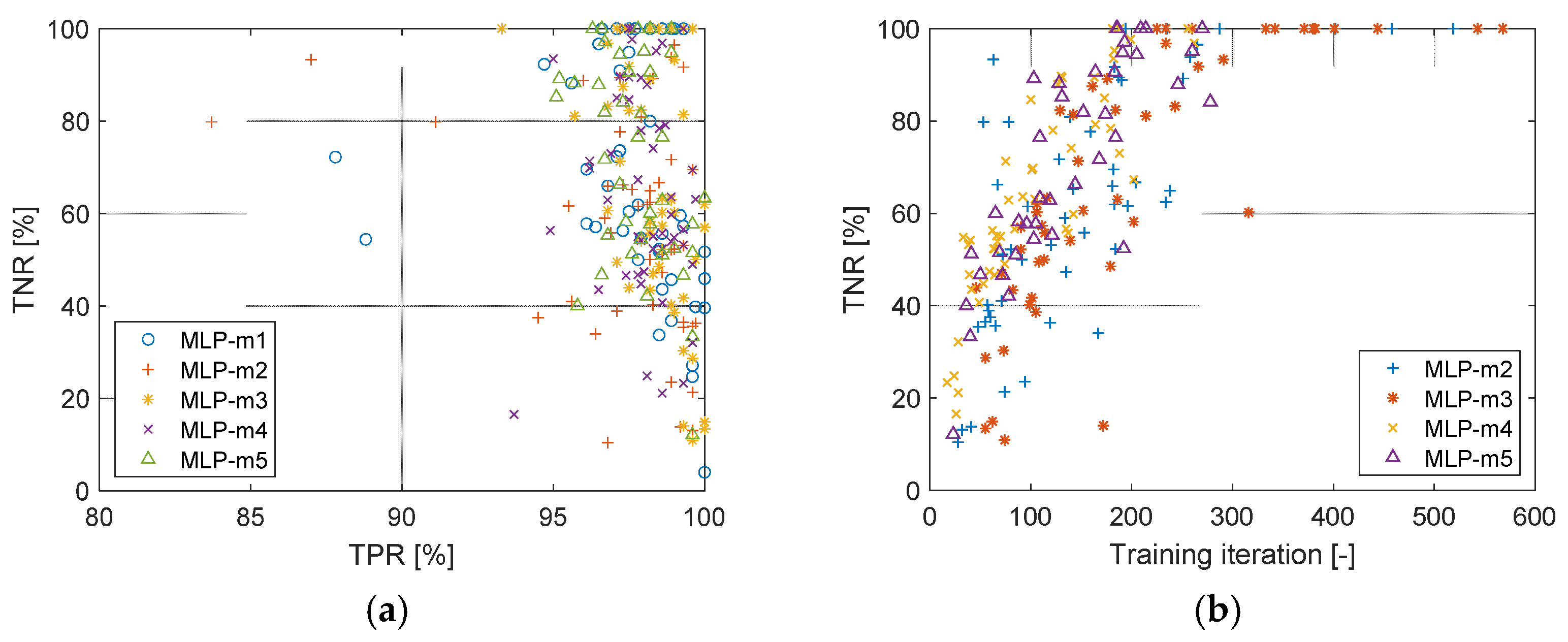
5.1. Multi-Layer Perceptron (MLP)
5.2. Long Short-Term Memory (LSTM)
5.3. Convolutional Neural Network (CNN)
5.4. One-Class SVM
6. Discussion
- For engine clutch engagement/disengagement data, constructing training architecture to determine normal/anomaly by data instance and performing one-class classification are advantageous for anomaly detection.
- The structure of determining normal/anomaly per pattern cannot learn characteristics of engine clutch engagement/disengagement data properly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, Y.S.; Park, J.; Park, T.W.; Bang, J.S.; Sim, H.S. Anti-jerk controller design with a cooperative control strategy in hybrid electric vehicle. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011. [Google Scholar]
- Anselma, P.G.; Del Prete, M.; Belingardi, G. Battery High Temperature Sensitive Optimization-Based Calibration of Energy and Thermal Management for a Parallel-through-the-Road Plug-in Hybrid Electric Vehicle. Appl. Sci. 2021, 11, 8593. [Google Scholar] [CrossRef]
- Sim, K.; Oh, S.-M.; Kang, K.-Y.; Hwang, S.-H. A Control Strategy for Mode Transition with Gear Shifting in a Plug-In Hybrid Electric Vehicle. Energies 2017, 10, 1043. [Google Scholar] [CrossRef] [Green Version]
- Xiao, R.; Liu, B.; Shen, J.; Guo, N.; Yan, W.; Chen, Z. Comparisons of Energy Management Methods for a Parallel Plug-In Hybrid Electric Vehicle between the Convex Optimization and Dynamic Programming. Appl. Sci. 2018, 8, 218. [Google Scholar] [CrossRef] [Green Version]
- Maddumage, W.; Perera, M.; Attalage, R.; Kelly, P. Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction. Energies 2021, 14, 1833. [Google Scholar] [CrossRef]
- Zhang, Y.; Gantt, G.W.; Rychlinski, M.J.; Edwards, R.M.; Correia, J.J.; Wolf, C.E. Connected Vehicle Diagnostics and Prognostics, Concept, and Initial Practice. IEEE Trans. Reliab. 2009, 58, 286–294. [Google Scholar] [CrossRef]
- Chen, H.; Peng, Y.; Zeng, X.; Shang, M.; Song, D.; Wang, Q. Fault Detection and Confirmation for Hybrid Electric Vehicle. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar]
- Song, Y.; Wang, B. Analysis and Experimental Verification of a Fault-Tolerant HEV Powertrain. IEEE Trans. Power Electron. 2013, 28, 5854–5864. [Google Scholar] [CrossRef]
- Yang, N.; Shang, M. Common Fault Detection and Diagnosis of Santana Clutch. In Proceedings of the 2016 International Conference on Education, Management, Computer and Society, Shenyang, China, 1–3 January 2016; Atlantis Press: Shenyang, China, 2016. [Google Scholar]
- Ferreira, D.R.; Scholz, T.; Prytz, R. Importance Weighting of Diagnostic Trouble Codes for Anomaly Detection. In Proceedings of the Machine Learning, Optimization, and Data Science, Siena-Tuscany, Italy, 19–23 July 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 410–421. [Google Scholar]
- Pan, Y.; Feng, X.; Zhang, M.; Han, X.; Lu, L.; Ouyang, M. Internal Short Circuit Detection for Lithium-Ion Battery Pack with Parallel-Series Hybrid Connections. J. Clean. Prod. 2020, 255, 120277. [Google Scholar] [CrossRef]
- Algredo-Badillo, I.; Ramírez-Gutiérrez, K.A.; Morales-Rosales, L.A.; Pacheco Bautista, D.; Feregrino-Uribe, C. Hybrid Pipeline Hardware Architecture Based on Error Detection and Correction for AES. Sensors 2021, 21, 5655. [Google Scholar] [CrossRef]
- Qin, G.; Ge, A.; Li, H. On-Board Fault Diagnosis of Automated Manual Transmission Control System. IEEE Trans. Control Syst. Technol. 2004, 12, 564–568. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Ouyang, M.; Hua, J.; Li, X. Active Fault Tolerance Control System of Fuel Cell Hybrid City Bus. Int. J. Hydrog. Energy 2010, 35, 12510–12520. [Google Scholar] [CrossRef]
- Tabbache, B.; Benbouzid, M.E.H.; Kheloui, A.; Bourgeot, J. Virtual-Sensor-Based Maximum-Likelihood Voting Approach for Fault-Tolerant Control of Electric Vehicle Powertrains. IEEE Trans. Veh. Technol. 2013, 62, 1075–1083. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gao, B.; Chen, H. Data-Driven Design of Parity Space-Based FDI System for AMT Vehicles. IEEE/ASME Trans. Mechatron. 2015, 20, 405–415. [Google Scholar] [CrossRef]
- Roubache, T.; Chaouch, S.; Naït-Saïd, M.-S. Backstepping Design for Fault Detection and FTC of an Induction Motor Drives-Based EVs. Automatika 2016, 57, 736–748. [Google Scholar] [CrossRef] [Green Version]
- Trask, S.J.H.; Jankord, G.J.; Modak, A.A.; Rahman, B.M.; Rizzoni, G.; Midlam-Mohler, S.W.; Guercioni, G.R. System Diagnosis and Fault Mitigation Strategies for an Automated Manual Transmission. In Proceedings of the ASME 2017 Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017; Volume 2, p. V002T19A001. [Google Scholar]
- Meyer, R.T.; Johnson, S.C.; DeCarlo, R.A.; Pekarek, S.; Sudhoff, S.D. Hybrid Electric Vehicle Fault Tolerant Control. J. Dyn. Syst. Meas. Control 2018, 140, 021002. [Google Scholar] [CrossRef] [Green Version]
- Kersten, A.; Oberdieck, K.; Bubert, A.; Neubert, M.; Grunditz, E.A.; Thiringer, T.; Doncker, R.W.D. Fault Detection and Localization for Limp Home Functionality of Three-Level NPC Inverters with Connected Neutral Point for Electric Vehicles. IEEE Trans. Transp. Electrif. 2019, 5, 416–432. [Google Scholar] [CrossRef]
- Fill, A.; Koch, S.; Birke, K.P. Algorithm for the Detection of a Single Cell Contact Loss within Parallel-Connected Cells Based on Continuous Resistance Ratio Estimation. J. Energy Storage 2020, 27, 101049. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Li, S.; Cao, B. A Method to Simultaneously Detect the Current Sensor Fault and Estimate the State of Energy for Batteries in Electric Vehicles. Sensors 2016, 16, 1328. [Google Scholar] [CrossRef] [Green Version]
- Jeon, N.; Lee, H. Integrated Fault Diagnosis Algorithm for Motor Sensors of In-Wheel Independent Drive Electric Vehicles. Sensors 2016, 16, 2106. [Google Scholar] [CrossRef] [Green Version]
- Na, W.; Park, C.; Lee, S.; Yu, S.; Lee, H. Sensitivity-Based Fault Detection and Isolation Algorithm for Road Vehicle Chassis Sensors. Sensors 2018, 18, 2720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Q.; Tian, W.; Chen, W.; Ahmed, Q.; Wu, Y. Model-Based Fault Diagnosis of an Anti-Lock Braking System via Structural Analysis. Sensors 2018, 18, 4468. [Google Scholar] [CrossRef] [Green Version]
- Byun, Y.-S.; Kim, B.-H.; Jeong, R.-G. Sensor Fault Detection and Signal Restoration in Intelligent Vehicles. Sensors 2019, 19, 3306. [Google Scholar] [CrossRef] [Green Version]
- Akin, B.; Ozturk, S.B.; Toliyat, H.A.; Rayner, M. DSP-Based Sensorless Electric Motor Fault-Diagnosis Tools for Electric and Hybrid Electric Vehicle Powertrain Applications. IEEE Trans. Veh. Technol. 2009, 58, 2679–2688. [Google Scholar] [CrossRef]
- Olsson, T.; Kallstrom, E.; Gillblad, D.; Funk, P. Fault Diagnosis of Heavy Duty Machines: Automatic Transmission Clutches. In Proceedings of the International Conference on Case-Based Reasoning: Workshop on Synergies between CBR and Data Mining, Cork, Ireland, 29 September–1 October 2014. [Google Scholar]
- Sankavaram, C.; Kodali, A.; Pattipati, K.R.; Singh, S. Incremental Classifiers for Data-Driven Fault Diagnosis Applied to Automotive Systems. IEEE Access 2015, 3, 407–419. [Google Scholar] [CrossRef]
- Choi, S.D.; Akin, B.; Kwak, S.; Toliyat, H.A. A Compact Error Management Algorithm to Minimize False-Alarm Rate of Motor/Generator Faults in (Hybrid) Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 618–626. [Google Scholar] [CrossRef]
- Källström, E.; Lindström, J.; Håkansson, L.; Karlberg, M.; Bellgran, D.; Frenne, N.; Renderstedt, R.; Lundin, J.; Larsson, J. Analysis of Automatic Transmission Vibration for Clutch Slippage Detection. In Proceedings of the the 22th International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015; p. 8. [Google Scholar]
- Theissler, A. Detecting Known and Unknown Faults in Automotive Systems Using Ensemble-Based Anomaly Detection. Knowl. Based Syst. 2017, 123, 163–173. [Google Scholar] [CrossRef]
- Nair, V.V.; Koustubh, B.P. Data Analysis Techniques for Fault Detection in Hybrid/Electric Vehicles. In Proceedings of the 2017 IEEE Transportation Electrification Conference (ITEC-India), Pune, India, 13–15 December 2017; pp. 1–5. [Google Scholar]
- Moosavian, A.; Najafi, G.; Ghobadian, B.; Mirsalim, M. The Effect of Piston Scratching Fault on the Vibration Behavior of an IC Engine. Appl. Acoust. 2017, 126, 91–100. [Google Scholar] [CrossRef]
- Becherif, M.; Péra, M.-C.; Hissel, D.; Zheng, Z. Determination of the Health State of Fuel Cell Vehicle for a Clean Transportation. J. Clean. Prod. 2018, 171, 1510–1519. [Google Scholar] [CrossRef] [Green Version]
- Kordes, A.; Wurm, S.; Hozhabrpour, H.; Wismüller, R. Automatic Fault Detection Using Cause and Effect Rules for In-Vehicle Networks. In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems, Funchal, Portugal, 16–18 March 2018; pp. 537–544. [Google Scholar]
- Yu, H.; Langari, R. A Neural Network-Based Detection and Mitigation System for Unintended Acceleration. J. Frankl. Inst. 2018, 355, 4315–4335. [Google Scholar] [CrossRef]
- Ostapenko, D.I.; Fisch, J. Predictive Maintenance Using MATLAB: Pattern Matching for Time Series Data. Available online: https://www.matlabexpo.com/content/dam/mathworks/mathworks-dot-com/images/events/matlabexpo/de/2018/predictive-maintenance-with-matlab--time-series-production-data-analysis.pdf (accessed on 29 October 2021).
- Ginzarly, R.; Hoblos, G.; Moubayed, N. From Modeling to Failure Prognosis of Permanent Magnet Synchronous Machine. Appl. Sci. 2020, 10, 691. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Huang, B.; Yun, Y.; Cattley, R.; Gu, F.; Ball, A.D. Model Based IAS Analysis for Fault Detection and Diagnosis of IC Engine Powertrains. Energies 2020, 13, 565. [Google Scholar] [CrossRef] [Green Version]
- Ewert, P.; Orlowska-Kowalska, T.; Jankowska, K. Effectiveness Analysis of PMSM Motor Rolling Bearing Fault Detectors Based on Vibration Analysis and Shallow Neural Networks. Energies 2021, 14, 712. [Google Scholar] [CrossRef]
- Jiang, J.; Cong, X.; Li, S.; Zhang, C.; Zhang, W.; Jiang, Y. A Hybrid Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. IEEE Access 2021, 9, 19175–19186. [Google Scholar] [CrossRef]
- Ding, N.; Ma, H.; Zhao, C.; Ma, Y.; Ge, H. Data Anomaly Detection for Internet of Vehicles Based on Traffic Cellular Automata and Driving Style. Sensors 2019, 19, 4926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moavenian, M. Fault Detection and Isolation of Vehicle Driveline System. Int. J. Automot. Eng. 2012, 2, 11. [Google Scholar]
- Xue, Q.; Zhang, X.; Teng, T.; Zhang, J.; Feng, Z.; Lv, Q. A Comprehensive Review on Classification, Energy Management Strategy, and Control Algorithm for Hybrid Electric Vehicles. Energies 2020, 13, 5355. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Lee, H. Mode Transition Control Using Disturbance Compensation for a Parallel Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 150–166. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial Neural Networks (the Multilayer Perceptron)—a Review of Applications in the Atmospheric Sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Widiasari, I.R.; Nugroho, L.E. Deep Learning Multilayer Perceptron (MLP) for Flood Prediction Model Using Wireless Sensor Network Based Hydrology Time Series Data Mining. In Proceedings of the 2017 International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 2–4 November 2017; pp. 1–5. [Google Scholar]
- Kanchymalay, K.; Salim, N.; Sukprasert, A.; Krishnan, R.; Hashim, U.R. Multivariate Time Series Forecasting of Crude Palm Oil Price Using Machine Learning Techniques. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012117. [Google Scholar] [CrossRef]
- Gulli, A.; Kapoor, A.; Pal, S. Deep Learning with TensorFlow 2 and Keras Regression, ConvNets, GANs, RNNs, NLP, and More with TensorFlow 2 and the Keras API, 2nd ed.; Packt Publishing Ltd.: Birmingham, UK, 2019; ISBN 978-1-83882-341-2. [Google Scholar]
- Ma, Y.; Chang, Q.; Lu, H.; Liu, J. Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification. Appl. Sci. 2018, 8, 630. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Xu, Y. VS-GRU: A Variable Sensitive Gated Recurrent Neural Network for Multivariate Time Series with Massive Missing Values. Appl. Sci. 2019, 9, 3041. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, M.; Dong, R. Time-Series Prediction of Environmental Noise for Urban IoT Based on Long Short-Term Memory Recurrent Neural Network. Appl. Sci. 2020, 10, 1144. [Google Scholar] [CrossRef] [Green Version]
- Elsaraiti, M.; Merabet, A. Application of Long-Short-Term-Memory Recurrent Neural Networks to Forecast Wind Speed. Appl. Sci. 2021, 11, 2387. [Google Scholar] [CrossRef]
- Ye, F.; Yang, J. A Deep Neural Network Model for Speaker Identification. Appl. Sci. 2021, 11, 3603. [Google Scholar] [CrossRef]
- Zhang, X.; Kuehnelt, H.; De Roeck, W. Traffic Noise Prediction Applying Multivariate Bi-Directional Recurrent Neural Network. Appl. Sci. 2021, 11, 2714. [Google Scholar] [CrossRef]
- Ramos, R.G.; Domingo, J.D.; Zalama, E.; Gómez-García-Bermejo, J. Daily Human Activity Recognition Using Non-Intrusive Sensors. Sensors 2021, 21, 5270. [Google Scholar] [CrossRef]
- Ankita; Rani, S.; Babbar, H.; Coleman, S.; Singh, A.; Aljahdali, H.M. An Efficient and Lightweight Deep Learning Model for Human Activity Recognition Using Smartphones. Sensors 2021, 21, 3845. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, Y. Early-Stage Gas Identification Using Convolutional Long Short-Term Neural Network with Sensor Array Time Series Data. Sensors 2021, 21, 4826. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Unc. Fuzz. Knowl. Based Syst. 1998, 06, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Understanding LSTM Networks—Colah’s Blog. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 11 June 2021).
- Long Short-Term Memory. Wikipedia 2021. Available online: https://en.wikipedia.org/wiki/Long_short-term_memory (accessed on 29 October 2021).
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Convolutional Neural Network. Available online: https://ww2.mathworks.cn/en/discovery/convolutional-neural-network-matlab.html (accessed on 7 May 2021).
- Lee, S.; Lee, Y.-S.; Son, Y. Forecasting Daily Temperatures with Different Time Interval Data Using Deep Neural Networks. Appl. Sci. 2020, 10, 1609. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Zi, Y.; Xie, J.; Chen, J.; An, T. The Next Failure Time Prediction of Escalators via Deep Neural Network with Dynamic Time Warping Preprocessing. Appl. Sci. 2020, 10, 5622. [Google Scholar] [CrossRef]
- Nam, J.; Kang, J. Classification of Chaotic Signals of the Recurrence Matrix Using a Convolutional Neural Network and Verification through the Lyapunov Exponent. Appl. Sci. 2021, 11, 77. [Google Scholar] [CrossRef]
- Wang, C.; Sun, H.; Zhao, R.; Cao, X. Research on Bearing Fault Diagnosis Method Based on an Adaptive Anti-Noise Network under Long Time Series. Sensors 2020, 20, 7031. [Google Scholar] [CrossRef]
- Li, J.; Hu, D.; Chen, W.; Li, Y.; Zhang, M.; Peng, L. CNN-Based Volume Flow Rate Prediction of Oil–Gas–Water Three-Phase Intermittent Flow from Multiple Sensors. Sensors 2021, 21, 1245. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Huang, G.; Hao, X.; Yang, Y.; Li, Z. A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process. Sensors 2021, 21, 4284. [Google Scholar] [CrossRef]
- Al-Qershi, F.; Al-Qurishi, M.; Aksoy, M.S.; Faisal, M.; Algabri, M. A Time-Series-Based New Behavior Trace Model for Crowd Workers That Ensures Quality Annotation. Sensors 2021, 21, 5007. [Google Scholar] [CrossRef] [PubMed]
- Theodoropoulos, P.; Spandonidis, C.C.; Giannopoulos, F.; Fassois, S. A Deep Learning-Based Fault Detection Model for Optimization of Shipping Operations and Enhancement of Maritime Safety. Sensors 2021, 21, 5658. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional Neural Networks for Time Series Classification. J. Syst. Eng. Electron. 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Khan, S.S.; Madden, M.G. One-Class Classification: Taxonomy of Study and Review of Techniques. Knowl. Eng. Rev. 2014, 29, 345–374. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.S.; Madden, M.G. A Survey of Recent Trends in One Class Classification. In Proceedings of the Artificial Intelligence and Cognitive Science, Dublin, Ireland, 19–21 August 2009; Coyle, L., Freyne, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 188–197. [Google Scholar]
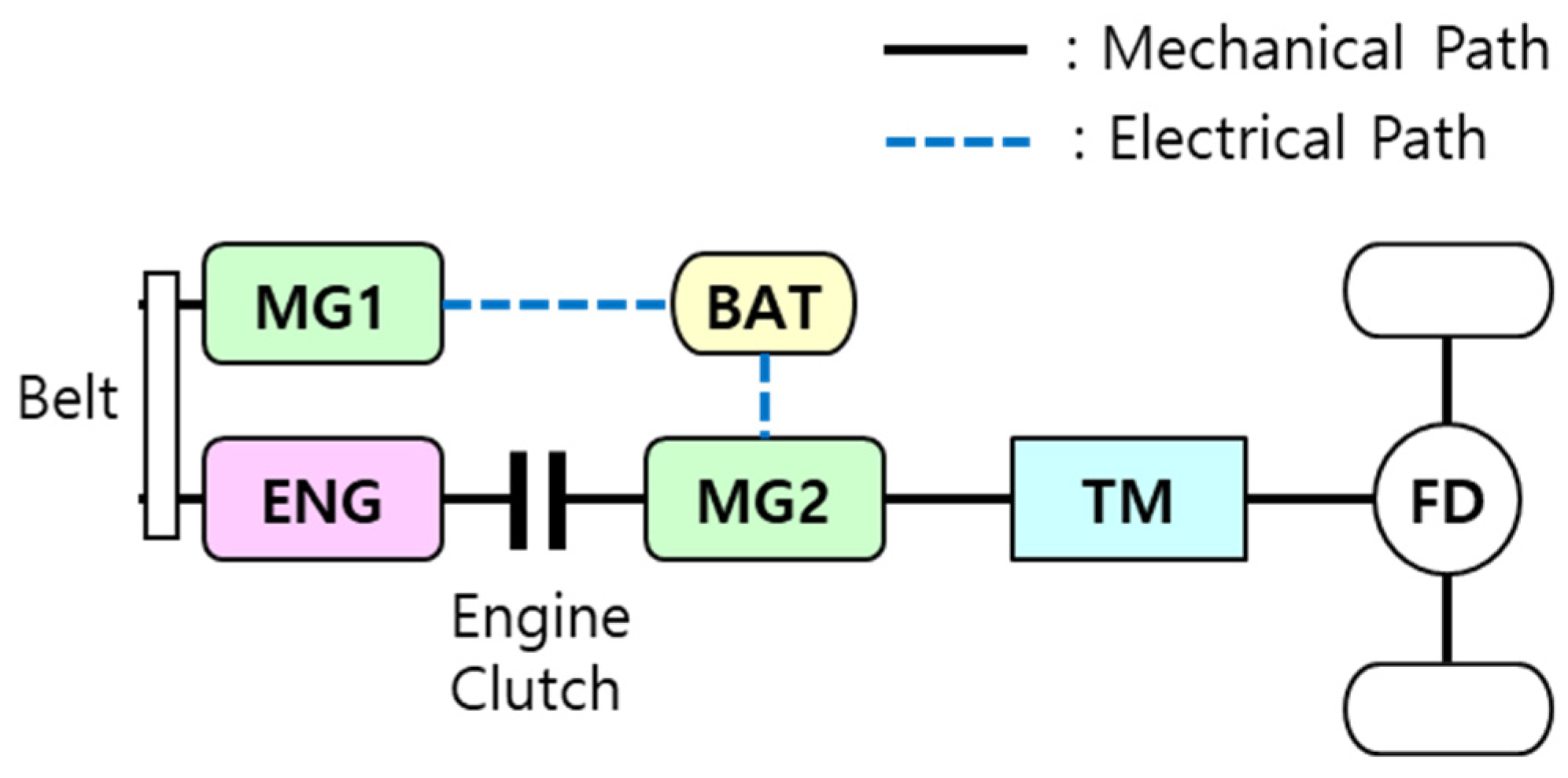
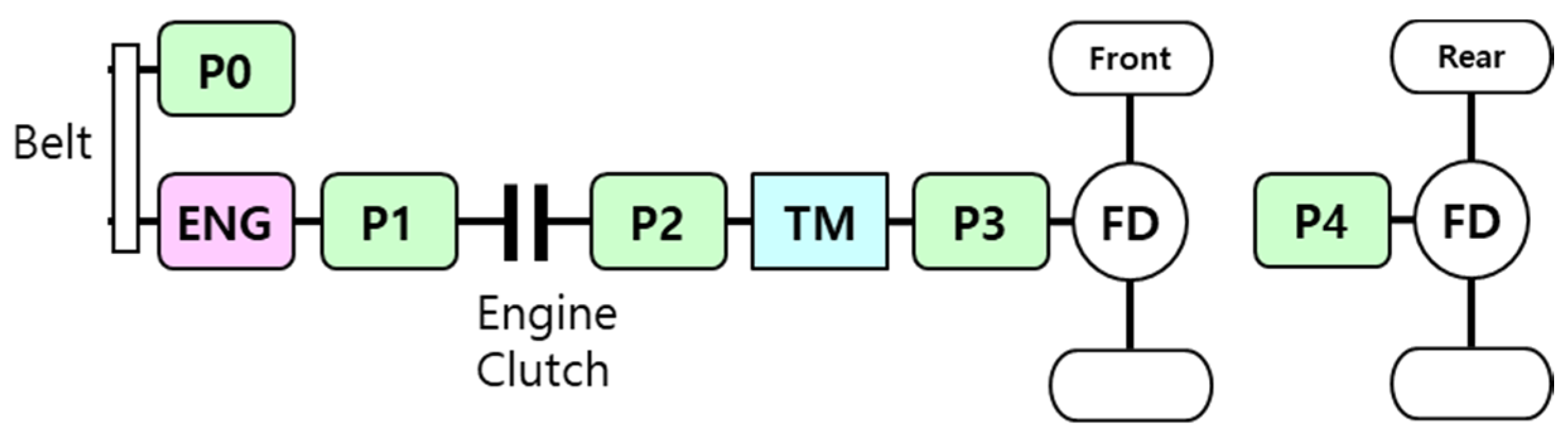
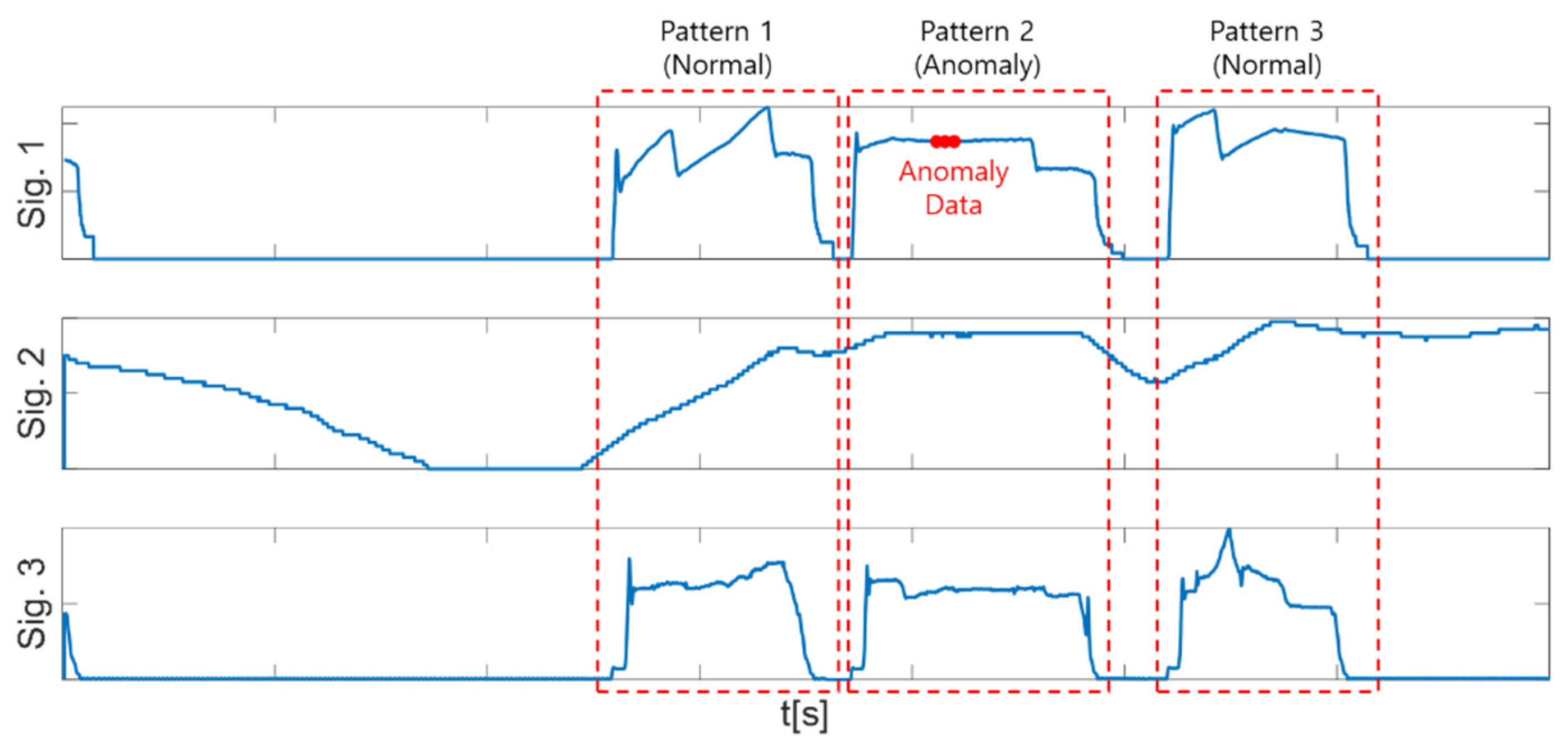
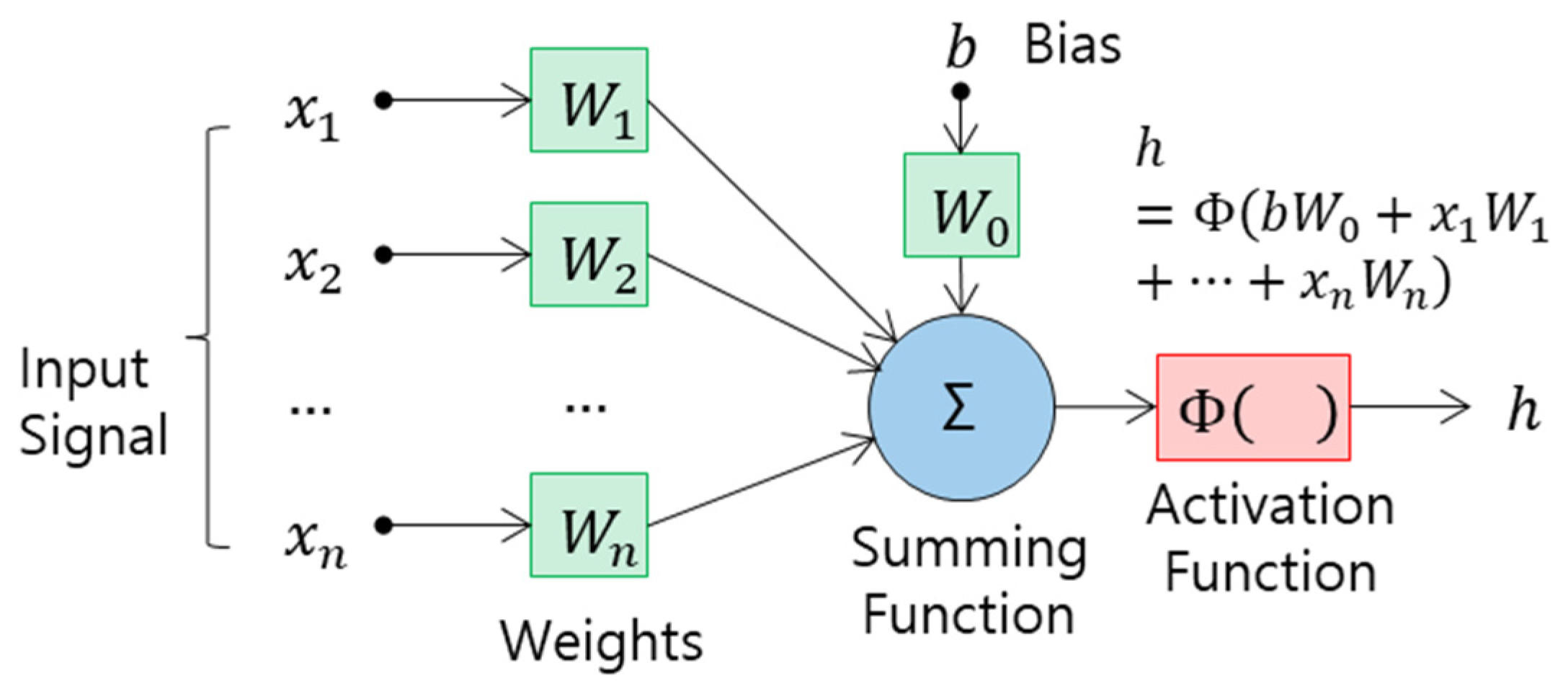
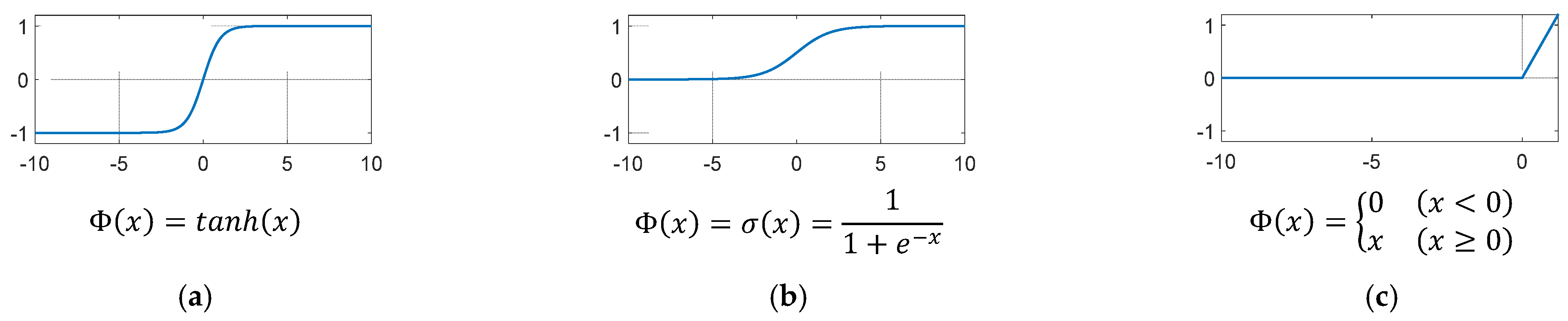




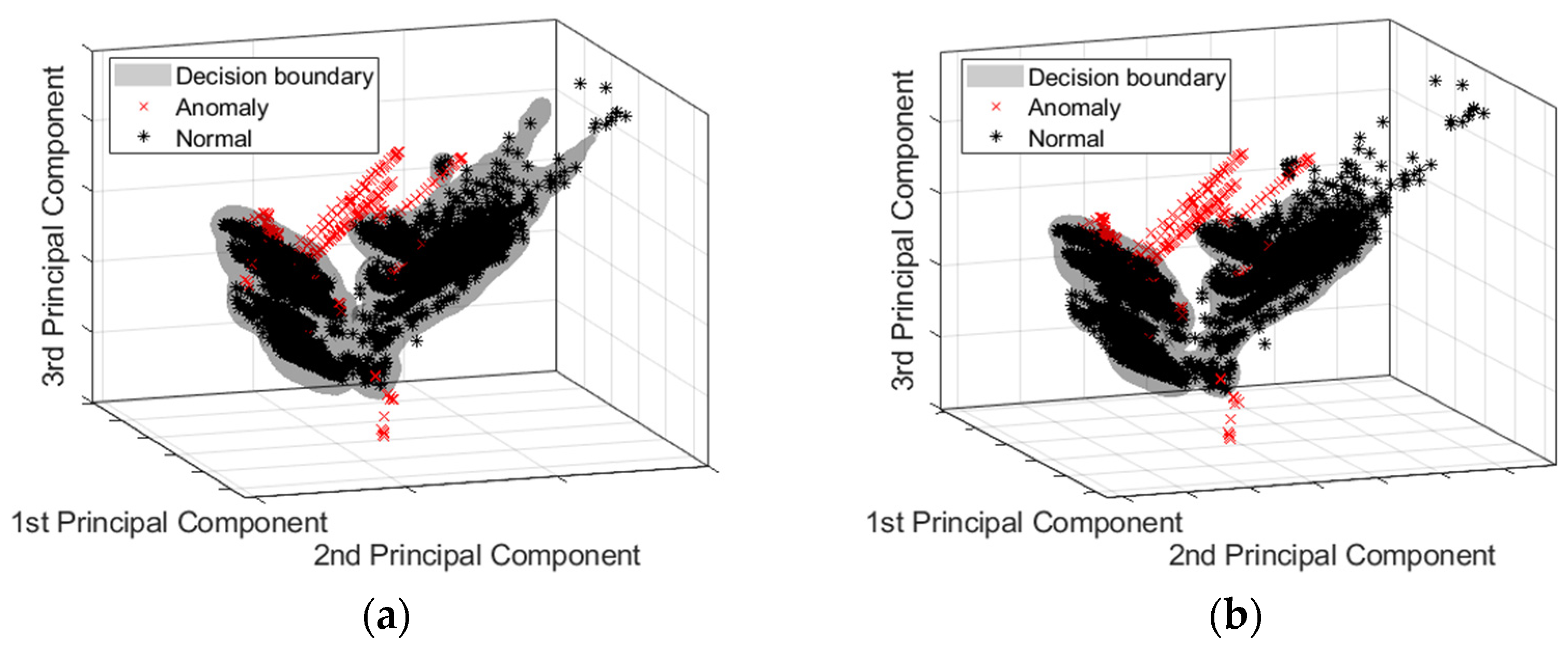
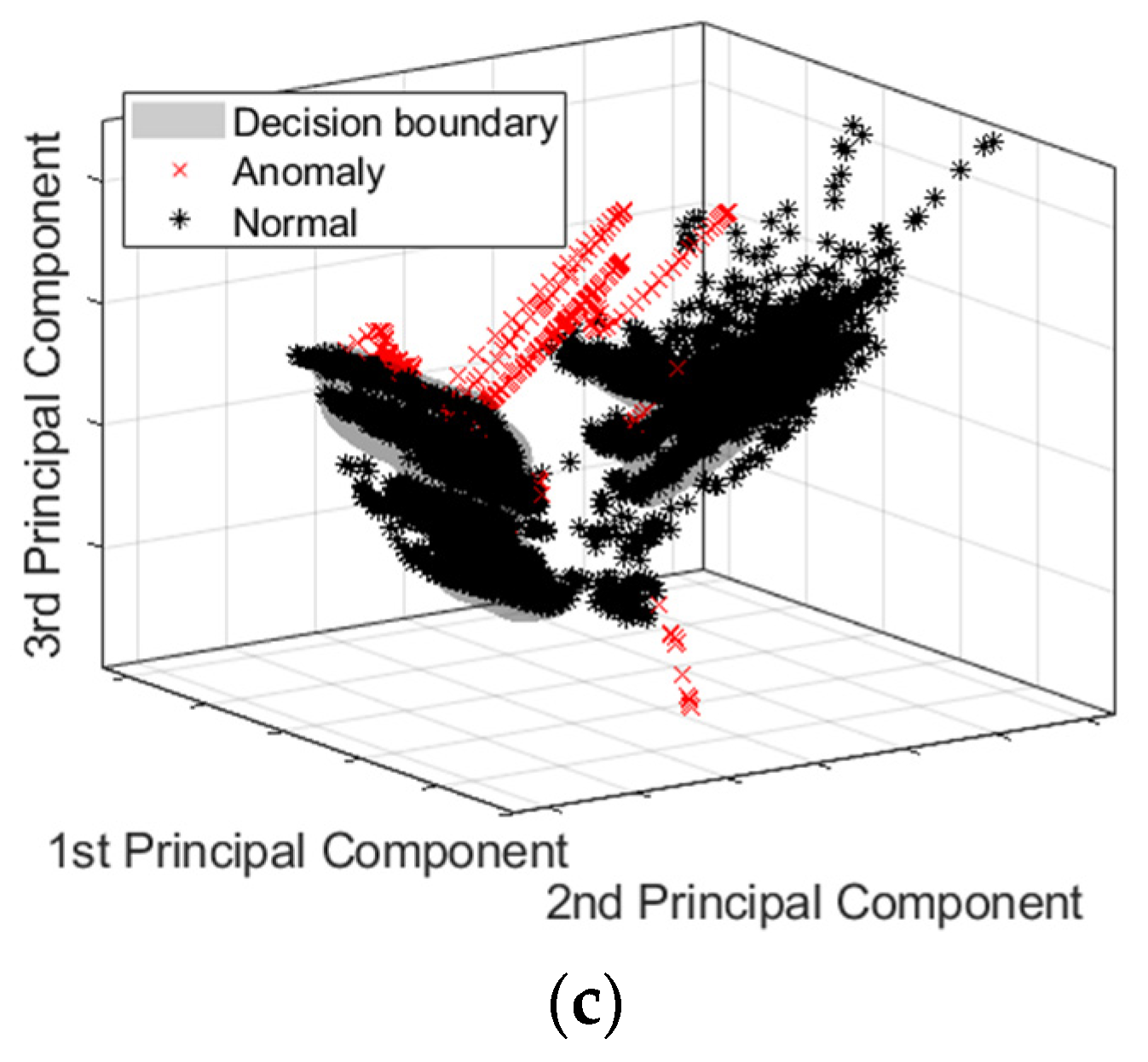
| Case | Description |
|---|---|
| Engine clutch engagement failure | The speed difference between an engine and a motor exceeds a certain level, although an HCU applies an engine clutch command to be fully engaged. (This case is that the engine clutch is not fully engaged as intended. For the target vehicle, as the engine clutch connects the engine and the motor, there should be no speed difference between the engine and the motor when HCU commands the engine clutch as full engagement in normal conditions.) |
| Engine clutch disengagement failure | The speed difference between an engine and a motor is less than a certain level over a certain time, although an HCU applies an engine clutch command to be released/open and an engine operating mode command to be off for EV mode. (This case is that the engine clutch is not released as intended in EV mode. As a result, the speed difference is small as the engine clutch still connects the engine and the motor. In normal conditions, there should be a speed difference between the engine and the motor because the motor has speed according to the vehicle speed and the engine speed is zero due to the engine off command.) |
| Clutch pressure command following failure | The difference between a clutch pressure command value and a clutch pressure sensor value exceeds a certain level over a certain time. (This case is that the engine clutch pressure does not follow a command. In normal conditions, the difference between the pressure command and pressure sensor value should be small enough. When the pressure command changes significantly, hydraulic generation delay can slightly increase this difference, but the duration should not be long.) |
| Normal Patterns | Anomaly Patterns | |
|---|---|---|
| Number of data | 1878 | 25 |
| Normal Patterns | Anomaly Patterns | |
|---|---|---|
| Number of data | 1878 | 625 |
| Model | The Number of Hidden Layers | The Number of Hidden Units per Hidden Layer |
|---|---|---|
| MLP-m1 | 1 | 10 |
| MLP-m2 | 2 | 10 |
| MLP-m3 | 3 | 10 |
| MLP-m4 | 1 | 100 |
| MLP-m5 | 3 | 100 |
| Model | The Number of LSTM Layers | The Number of Hidden Units per LSTM Layer |
|---|---|---|
| LSTM-m1 | 1 | 200 |
| LSTM-m2 | 1 | 400 |
| LSTM-m3 | 3 | 100 |
| 3-Convolution Layer Architecture | |||
| Hyperparameter | 1st convolutional layer | 2nd convolutional layer | 3rd convolutional layer |
| Filter size | (1, 50) | (1, 50) | (1, 50) |
| The number of filters | 64 | 128 | 256 |
| Stride | (1, 1) | (1, 1) | (1, 1) |
| 1-Convolution Layer Architecture | |||
| Hyperparameter | 1st convolutional layer | - | - |
| Filter size | (1, 50) | - | - |
| The number of filters | 64 | - | - |
| Stride | (1, 1) | - | - |
| Model | The Number of Convolution Layers |
|---|---|
| CNN-m1 | 1 |
| CNN-m2 | 3 |
| Model | Model Input/Output | Discretization | Outlier Fraction [%] |
|---|---|---|---|
| One-class SVM-m1 | Type 1 | - | 0.1 |
| One-class SVM-m2 | Type 2 | Using domain knowledge | 0.1 |
| One-class SVM-m3 | Type 2 | Densely | 0.01 |
| One-class SVM-m4 | Type 2 | Densely | 0.1 |
| One-class SVM-m5 | Type 2 | Densely | 1 |
| Model | TPR (Average) | TNR (Average) | Accuracy (Average) |
|---|---|---|---|
| MLP-m1 | 97.6 | 70.1 | 90.5 |
| MLP-m2 | 97.5 | 62.3 | 87.9 |
| MLP-m3 | 98.4 | 67.2 | 90.5 |
| MLP-m4 | 98.0 | 67.2 | 90.5 |
| MLP-m5 | 97.8 | 72.0 | 91.0 |
| Model | TPR [%] | TNR [%] | Accuracy [%] |
|---|---|---|---|
| LSTM-m1 | 98.9 | 28.4 | 79.6 |
| LSTM-m2 | 90.5 | 28.2 | 75.7 |
| LSTM-m3 | 100 | 4.0 | 74.6 |
| Model | TPR [%] | TNR [%] | Accuracy [%] |
|---|---|---|---|
| CNN-m1 | 100 | 19.8 | 80.6 |
| CNN-m2 | 100 | 29.8 | 83.0 |
| Model | TPR [%] | TNR [%] | Accuracy [%] |
|---|---|---|---|
| One-class SVM-m1 | 56.0 | 83.5 | 66.3 |
| One-class SVM-m2 | 93.3 | 99.9 | 97.9 |
| One-class SVM-m3 | 96.8 | 100 | 99.0 |
| One-class SVM-m4 | 97.2 | 99.9 | 99.0 |
| One-class SVM-m5 | 98.2 | 99.0 | 98.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Jeong, S.; Cho, Y.; Seo, H.; Bang, J.; Kim, J.; Lee, H. A Study on the Anomaly Detection of Engine Clutch Engagement/Disengagement Using Machine Learning for Transmission Mounted Electric Drive Type Hybrid Electric Vehicles. Appl. Sci. 2021, 11, 10187. https://doi.org/10.3390/app112110187
Ji Y, Jeong S, Cho Y, Seo H, Bang J, Kim J, Lee H. A Study on the Anomaly Detection of Engine Clutch Engagement/Disengagement Using Machine Learning for Transmission Mounted Electric Drive Type Hybrid Electric Vehicles. Applied Sciences. 2021; 11(21):10187. https://doi.org/10.3390/app112110187
Chicago/Turabian StyleJi, Yonghyeok, Seongyong Jeong, Yeongjin Cho, Howon Seo, Jaesung Bang, Jihwan Kim, and Hyeongcheol Lee. 2021. "A Study on the Anomaly Detection of Engine Clutch Engagement/Disengagement Using Machine Learning for Transmission Mounted Electric Drive Type Hybrid Electric Vehicles" Applied Sciences 11, no. 21: 10187. https://doi.org/10.3390/app112110187
APA StyleJi, Y., Jeong, S., Cho, Y., Seo, H., Bang, J., Kim, J., & Lee, H. (2021). A Study on the Anomaly Detection of Engine Clutch Engagement/Disengagement Using Machine Learning for Transmission Mounted Electric Drive Type Hybrid Electric Vehicles. Applied Sciences, 11(21), 10187. https://doi.org/10.3390/app112110187






