1. Introduction
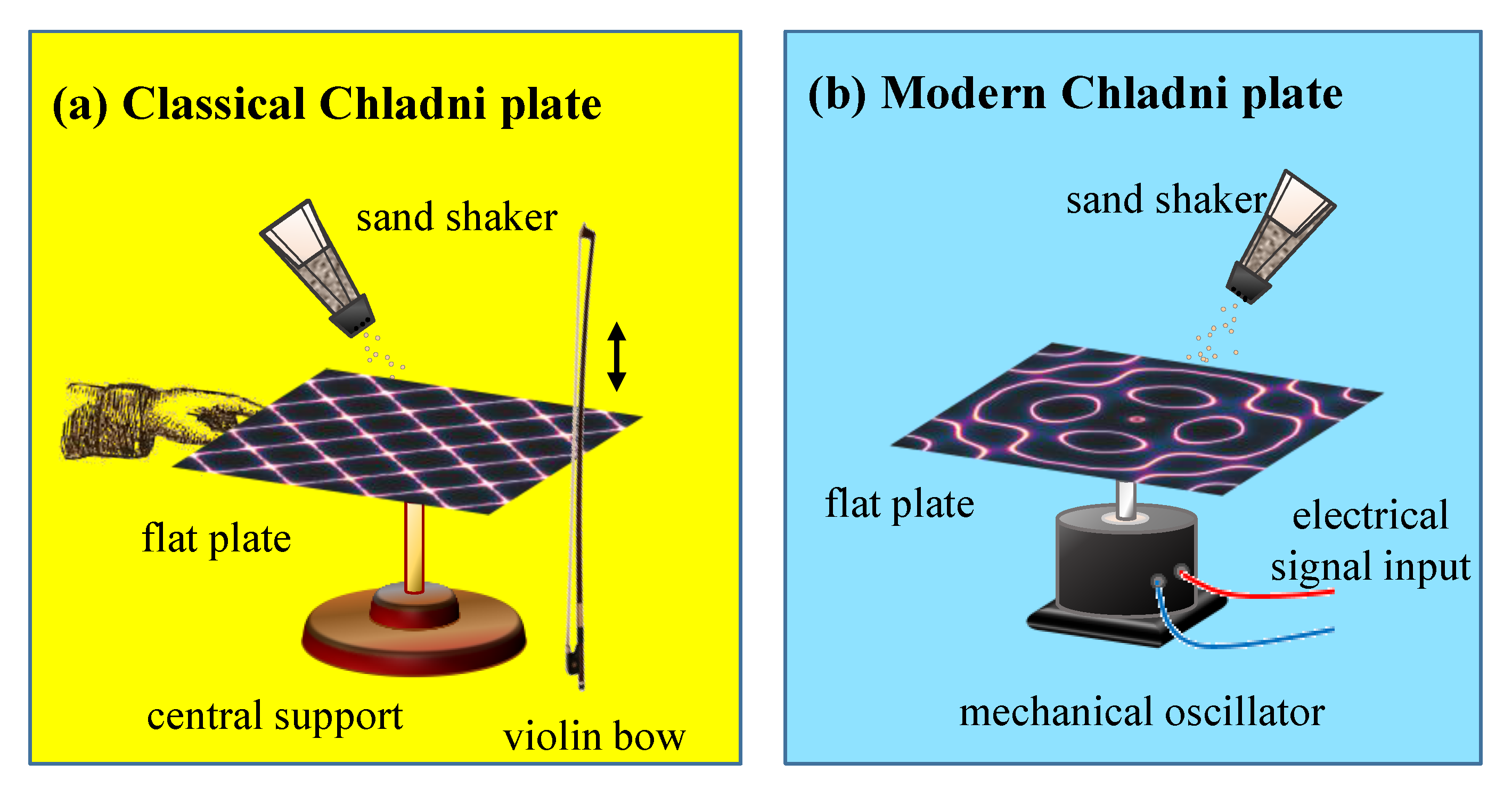
In the 18th century, Ernst Chladni employed a bow to excite a thin plate, and used small particles to visualize the nodal lines of the resonance [
1,
2], as shown in
Figure 1a. Chladni’s work is the first real attempt to explore acoustic properties through experiments [
3,
4,
5,
6]. The resonant modes excited by a bow are usually the eigenmodes of the plate. Nowadays, the modern Chladni plate, as shown in
Figure 1b, is excited by an electronically controlled point oscillator to generate the resonant modes systematically. Owing to the point interaction between the plate and the driving source, the nodal patterns observed in the modern Chladni plate have been observed to be entirely different from the eigenmodes of the free plate [
7]. The formation of modern Chladni patterns has been explored via Helmholtz equation, RLC networks, and Kirchhoff–Love equation [
7,
8,
9,
10,
11]. However, there is no theoretical model that includes the action of the point interaction between the plate and the driving source.
The point interaction in terms of the Dirac d-function potential has attracted great interest in the development and advancement of quantum mechanics [
12,
13,
14]. The delta-function potential in two or three dimensions has been widely considered in the literature because of its usefulness in nuclear [
15], atomic [
16], solid-state [
17], and particle physics [
18]. Šeba [
19] firstly explored the coupling interaction between a two-dimensional integrable billiard and a d-function potential. The strong coupling in quantum billiards might cause the transition from integrable to chaotic features [
20,
21,
22,
23,
24,
25]. As the two- or three-dimensional delta-function potential is plagued with the presence of ultraviolet divergences, renormalization analyses and cutoff regularization [
26,
27,
28,
29,
30] are usually used to deal with infinities. An alternative approach to remove the difficulty of the divergence is to utilize a truncated basis for expressing the point interaction [
31]. From the viewpoint of physical perspectives, the truncation of the basis can be linked to the real systems in which the interaction ordinarily originates from a point-like scatterer with a small, but finite size. So far, the explorations regarding to the point interaction almost all focus on the variation of eigenvalues, and rarely on the structure of eigenfunctions. It is scientifically important to verify the influence of the point interaction on the pattern formation of eigenfunctions through experiment.
In this work, we study the influence of point interaction on the resonant modes in modern Chladni plates. The structure of the paper is as follows.
Section 2 presents the theoretical model for point interaction. We employ a truncated basis to explore the point interaction in quantum billiards. Numerical analyses reveal that the point interaction gives rise to the shift of the eigenvalue that causes the superposition of the unperturbed eigenfunctions to form the eigenfunction. The variation in the amplitude patterns with the coupling strength is confirmed to be very significant, as with the nodal-line patterns.
Section 3 presents our findings in modern Chladni plates, followed by applications in
Section 4 and conclusions in
Section 5. We systematically verify that the perceptible dependence of the nodal-line pattern on the coupling strength can be analogously manifested from the point-driven Chladni plates. Furthermore, the dispersion relation between the frequency and the wave number for the flexural wave can be precisely determined in using the point-interaction model to analyze the modern Chladni patterns. Since the dispersion relation contains the information of the flexural rigidity and the Young modulus, the proposed model is believed to be not only pedagogically beneficial to understanding the point interaction in quantum systems but also practically useful for measuring the acoustic properties of plates.
2. Theoretical Model for the Point Interaction
The present analysis follows the model developed by Šeba [
19]. The two-dimensional Helmholtz equation for the domain Ω with boundary shape δΩ is given by
where
and
and
, with the indices of
, are the eigenvalues and eigenfunctions, respectively. The issue of quantum billiards is associated with the Dirichlet boundary conditions with
. Considering a d-function potential at
inside the domain, the Helmholtz equation in Equation (1) can be expressed as
where the parameter
α is a real number and its absolute value is directly related to the coupling strength. Although the singular potential is not an ordinary function, Equation (3) can be physically analyzed using a truncated basis. The truncation of a basis certainly leads the effective potential to be equivalent to a scatterer with small finite size accompanied with Gibbs-like oscillations. Nevertheless, the finiteness of the scatterer size should be applicable to realistic systems from a physical perspective. In terms of a truncated basis
(
), the functions
and
in Equation (3) can be approximately expressed as
Substituting Equations (4) and (5) into Equation (3) and using Equation (1), the eigenfunction of Equation (3) can be derived as
where
is the Green function given by
The identification
was used in deriving Equation (6). Setting
in both sides of Equation (6), the transcendental equation for solving the eigenvalues
k is given by
, where
is a meromorphic function. It has been discussed [
30,
31] that a d-function potential in the Helmholtz equation is problematic in the limit of
for a complete basis. The renormalization process from the self-adjoint extension theory [
30,
31] is employed to treat short-range singularities in a proper manner. Based on the renormalization process, the eigenvalues are determined by
where
is called the renormalized coupling constant. It has been fully discussed [
30] that
can be related to the physical coupling constant
α defined in Equation (3) with a truncated basis.
We use a square-shape quantum billiard to illustrate the relationship between the coupling parameter
α and the spectrum of eigenvalues. For a free square-shape billiard with the region in
, the eigenfunctions are given by
where
n = 1,2,3··· and
m = 1,2,3···. Using Equation (9), the meromorphic function
for a Dirac’s delta potential at
can be expressed as
The index
N is chosen by the criterion that the eigenvalue
k is less than
. Under this criterion, the eigenvalues
k are numerically confirmed to approach some asymptote.
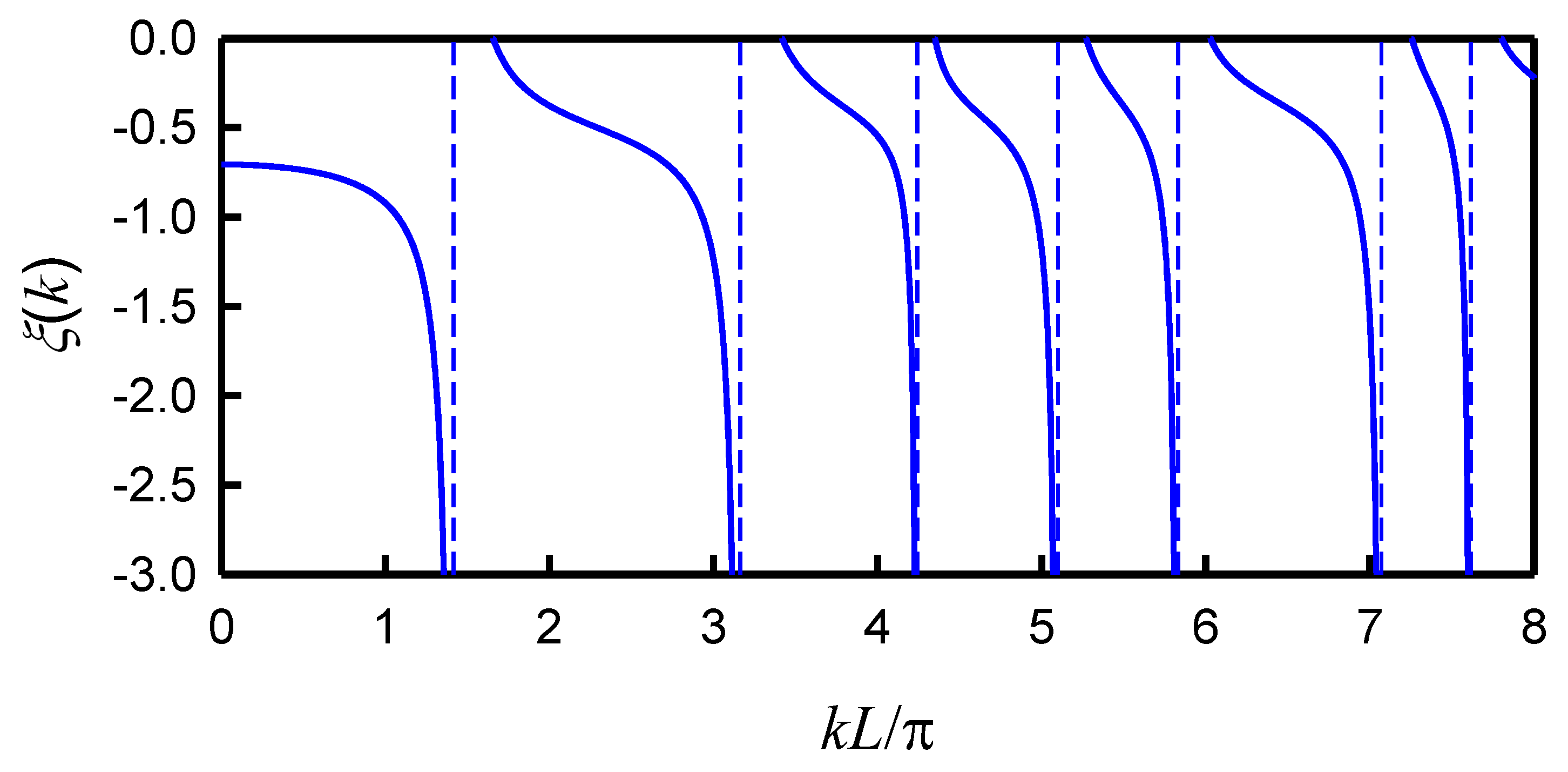
Figure 2 shows the calculated result for
in Equation (10) as a function of
k with
. For a given
α, the eigenvalues are determined by the condition of
. In the case of
, the spectrum of eigenvalues corresponds to the zeros
of the function
, while the spectrum of the free system is given by the poles
of
. The poles
for the square billiard are given by
. For a positive
α increasing from zero to infinity, the eigenvalue can be seen to shift from a pole to a zero by decreasing.
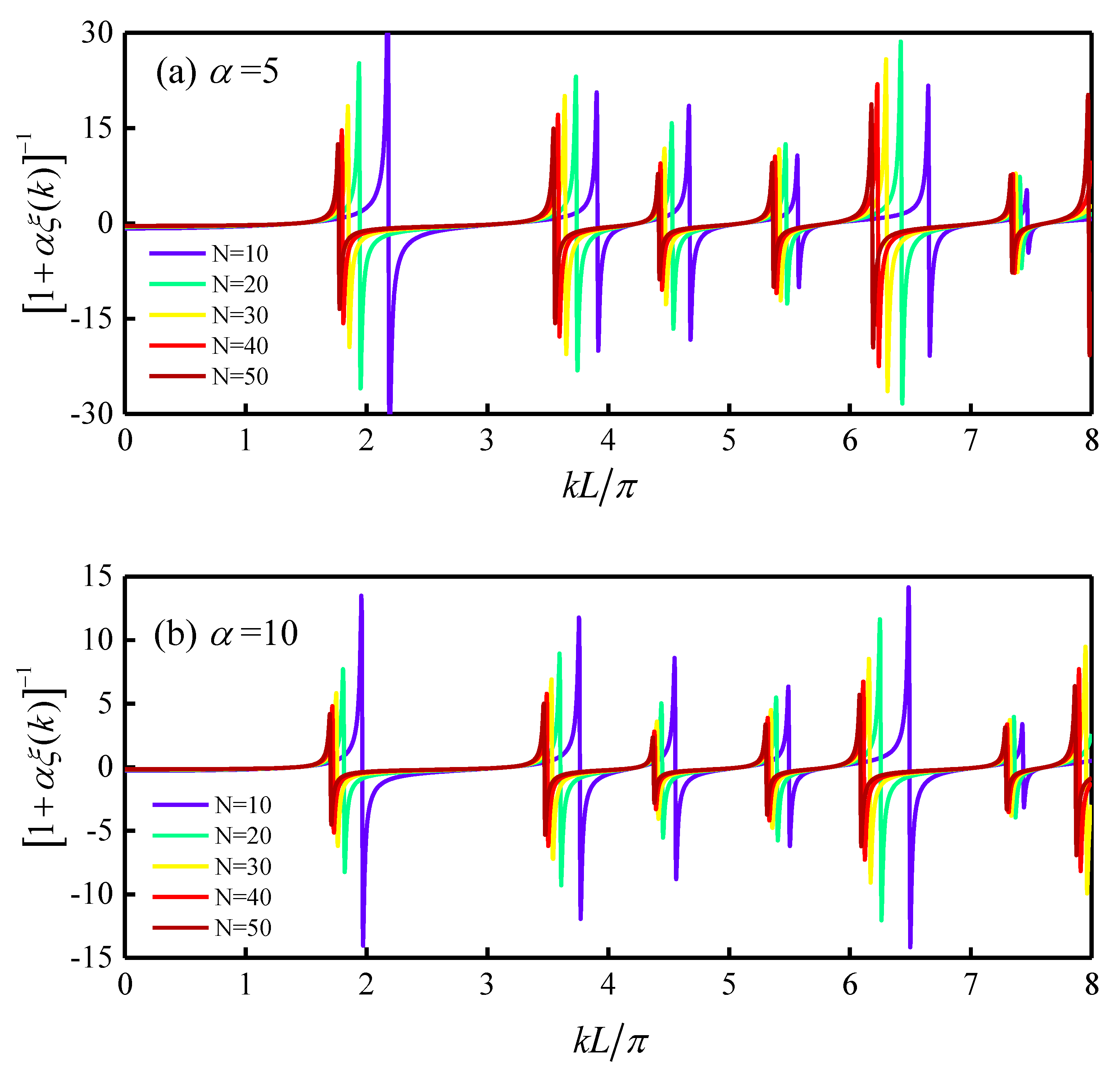
To demonstrate the trend of approach for computing eigenvalues with respect to the index
N, the calculated results for
as a function of
k for different
N increasing from 10 to 50 are shown in
Figure 3a for a given
and
Figure 3b for a given
. The eigenvalues
k can be found to be located at the abrupt changes of the spectrum
. The convergence of the numerical eigenvalues can be clearly seen as the value of the index
N increases from 10 to 50 in the range of
. Furthermore, the redshift of the eigenvalue subject to the increasing of the coupling strength
α can be observed by comparing the results shown in
Figure 3a,b for
and
, respectively. We also investigated the influence of the spreading function for the interaction by considering a Gaussian-type function
. The numerical results revealed that the results obtained with Gaussian-type function are almost the same as those obtained with d function for
.
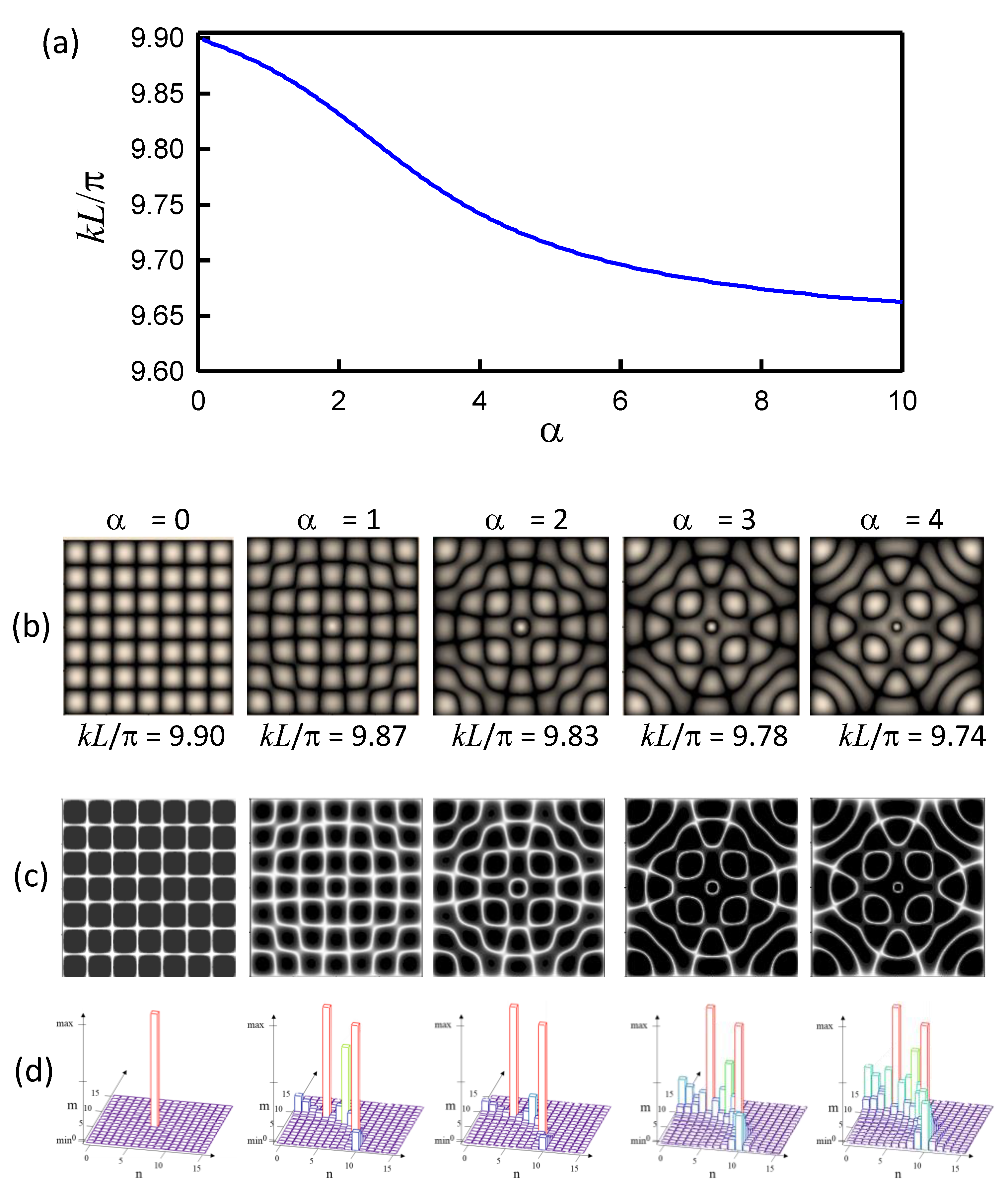
Figure 4a shows the shift in the eigenvalue with the coupling parameter
α for a specific case of
. The dependence of the wave pattern of the eigenfunction
on the parameter
α is shown in
Figure 4b. The structure of the nodal line corresponding to the eigenfunction is illustrated in
Figure 4c. The wave pattern
at
can be seen to be the feature of the square array, corresponding to the original eigenfunction
; its nodal-line pattern displays the characteristic of the square lattice. The increase in the coupling strength
α causes the red shift of the eigenvalue, leading the eigenfunction to be the superposition of the original eigenfunctions
. The weighting coefficient for the state
is inversely proportional to
. The closer the value of
to the eigenvalue
k, the larger the contribution of the state
. The eigenvalue can be seen to be significantly decreasing for
and to gradually saturate for
. As shown in
Figure 4b,c, the variation in the amplitude patterns with the coupling strength is very conspicuous, as with the nodal-line patterns.
Figure 4d shows the contribution of original eigenfunctions
in the perturbed eigenfunction
shown in
Figure 4c. The number of contributed eigenfunctions
in the perturbed eigenfunction
can be clearly seen to increase with the increasing coupling strength
α. In the following, we will verify that the perceptible dependence of the nodal-line pattern on the coupling strength can be analogously manifested from the point-driven modern Chladni plates.
3. Exploring the Point Interactions in Modern Chladni Plates
The transverse vibration of a plate is governed by the biharmonic equation [
32]
where
is the biharmonic operator given by
Equation (11) can be factorized as
in which the first factor describes propagating dispersive waves, whereas the second one describes evanescent waves. As the aspect ratio of the thickness to the lateral dimension for the studied plate is generally less than 0.02, the vibrating eigenmodes can be approximated with the 2D Helmholtz equation [
33]. Even so, the free edge boundary conditions make the problem particularly difficult, as noted by Rayleigh [
34]. As a first approximation, one can model the plate as a tightly stretched thin elastic membrane by assuming the constant
μ (the ratio of lateral contraction to longitudinal elongation) to be zero, i.e., every point of the circumference is free to move along lines perpendicular to the plane of the plate. Under this approximation, the boundary condition can be simplified as the Neumann boundary conditions with
on δΩ. Strictly, the Neumann boundary condition is practically applicable to a stretched membrane, but not to a plate vibrating in virtue of rigidity. Nevertheless, it has been demonstrated [
35] that a hypothetical free membrane can be used to deduce some of classical Chladni figures successfully. Based on this confirmation, a free membrane with a point scatter is proposed to model the modern Chladni figures.
A square-shaped aluminum plate with a side length of
L = 32 cm and a thickness of
h = 1.0 mm was used to perform the modern Chladni experiment. The frequency response was measured by a sine function generator with an automatic scanning system with a resolution of 0.1 Hz. As the conductance of the vibrating system displayed a sharp drop at each resonant frequency, we accurately measured the resonant frequency by exceeding the change in conductance of the system [
36]. Chladni patterns at resonant frequencies were exhibited with silica sand of 0.3 mm grain size and were stored with a digital camera. Fixing the center of the plate on the mechanical oscillator, several resonant patterns could be precisely observed by scanning the frequency between 200 and 3000 Hz, as shown in
Figure 5a for the nodal-line patterns. All the observed nodal-line patterns are obviously different from the characteristics of eigenfunctions of free plate.
From Equations (6) and (7), the eigenfunctions of the square plate with the point interaction at
can be directly expressed as the Green function:
where the free eigenfunctions
are given by
where
n = 0,1,2,3··· and
m = 0,1,2,3···. The eigenvalues are determined from the transcendental equation
with
. For a given
α, the eigenvalue
k can be solved to one-to-one correspond to the free eigenvalue of
. We numerically confirmed that all experimental nodal-line patterns can be excellently reconstructed by scanning the value of
a for the best fit and using
.
Figure 5b shows the numerical nodal-line patterns corresponding to the experimental results shown in
Figure 5a. The value of
α for the best reconstruction and the eigenvalue
k are specified for each case in
Figure 5b. The excellent agreement not only confirms the point-interaction model, but also validates the present analysis for explaining the coupling strength of the modern Chladni figure.
The square plate was experimentally driven by a mechanical oscillator located at
instead of the center to further confirm the theoretical model. Using Equations (14) and (15), numerical calculations were performed under the same procedure of finding the value of
α and the corresponding
k to make the best reconstruction for the experimental results.
Figure 6a,b show experimental and numerical nodal-line patterns, respectively. The off-center excitation can be found to introduce the effect of symmetry breaking into the driven system, leading the nodal-line structure to be more intricate. Numerical patterns can be found to be similar to the experimental results for global structures, except for some differences in the crossing and anti-crossing of nodal lines. Nevertheless, the overall theoretical nodal-line patterns are rather in agreement with the counterparts of experimental figures. This agreement indicates that the proposed model can be universally applied to an arbitrary location for the point interaction.
Figure 7 depicts the dependence of the coupling strength
α on the resonant frequency
f by means of the best reconstruction of experimental patterns. The coupling strength
α can be seen to be linearly proportional to the resonant frequency. The value of
α is significantly greater than 5 for the frequency higher than 1000 Hz. This result indicates that the point interaction in modern Chladni plate generally approaches the strong-coupling regime. Based on the quantum-acoustic analogy, it has been outlined [
37] that the interpretation of Chladni figures of irregularly shaped plates is intimately connected with the quantum mechanics of chaotic billiards. In this work, we originally demonstrate that the modern Chladni plate can be employed to analogously manifest the point interaction in quantum billiards.
4. Applications
More importantly, the point-interaction model can be exploited to precisely determine the dispersion relation between the frequency and the wave number for the flexural wave. From the Kirchhoff–Love plate theory, the dispersion relation between the frequency and the wave number is given by [
38]
where
,
D is the flexural rigidity given by
where
E is the Young modulus,
ν is the Poisson ratio,
ρ is the mass density, and
h is the thickness of the plate. The material properties for aluminum are as follows:
E = 70 GPa,
ν = 0.33, and
ρ = 2700 kg/m
3 [
38]. Using these material properties and
h = 1 mm, the theoretical coefficient
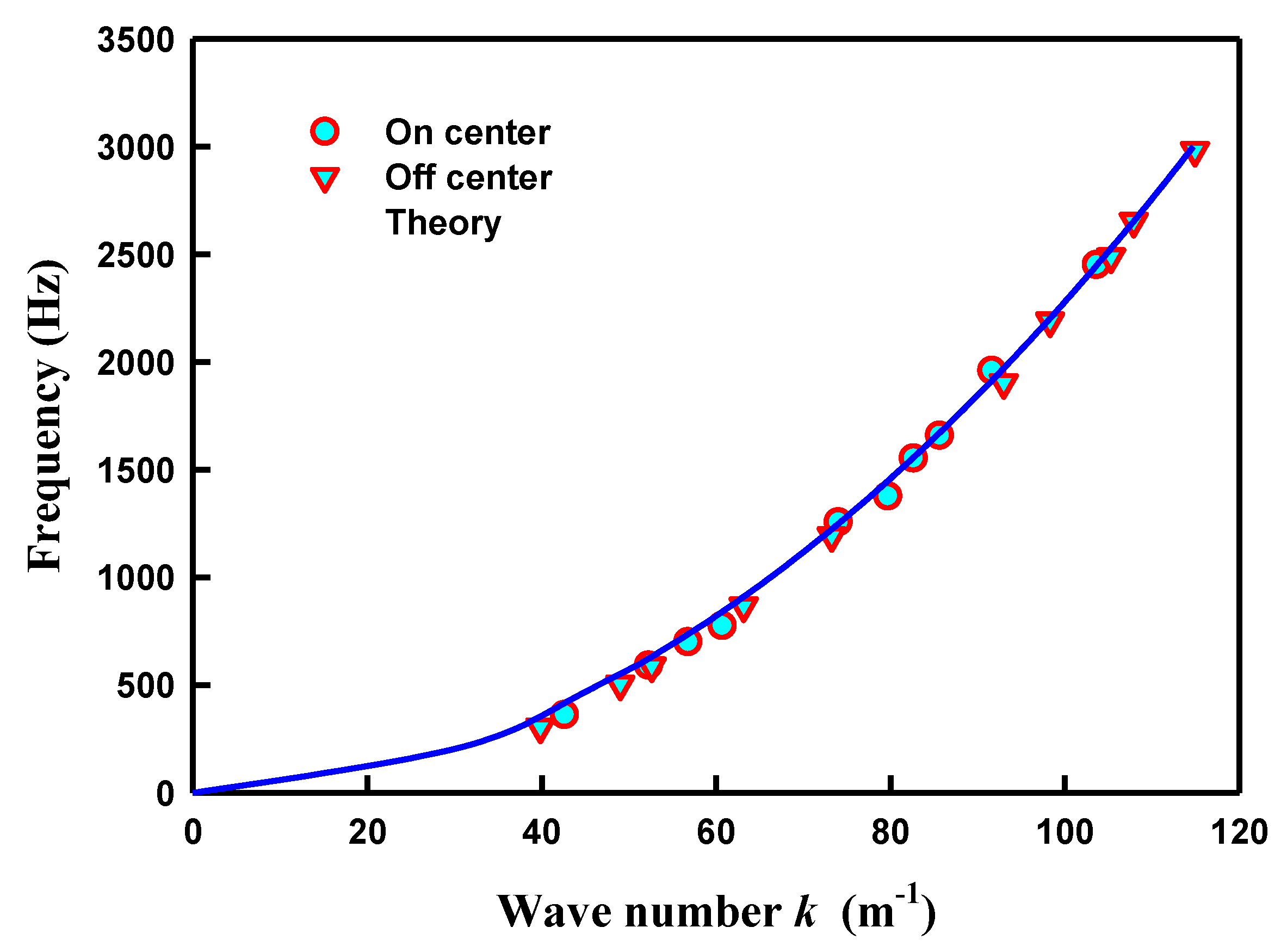
can be calculated to be 0.248. We employed the parabolic formula in Equation (16) to make the best fit to the experimental results obtained in
Figure 5 and
Figure 6. The fitting coefficient
is approximately 0.228, as shown in
Figure 8. The experimentally determined coefficient
can be found to agree with the theoretical value very well. This good agreement validates that the point-interaction model can be utilized not only to explore the formation of modern Chladni patterns, but also to determine the dispersion relation between the resonant frequency and the wave number for the vibration of plates. As the dispersion relation in Equation (16) includes the information of the flexural rigidity
D as well as the Young modulus
E, the proposed theoretical model is believed to be practically useful for measuring the acoustic properties of plates.