Assessment of Lightweight Concrete Thermal Properties at Elevated Temperatures
Abstract
:1. Introduction
2. Materials and Methods
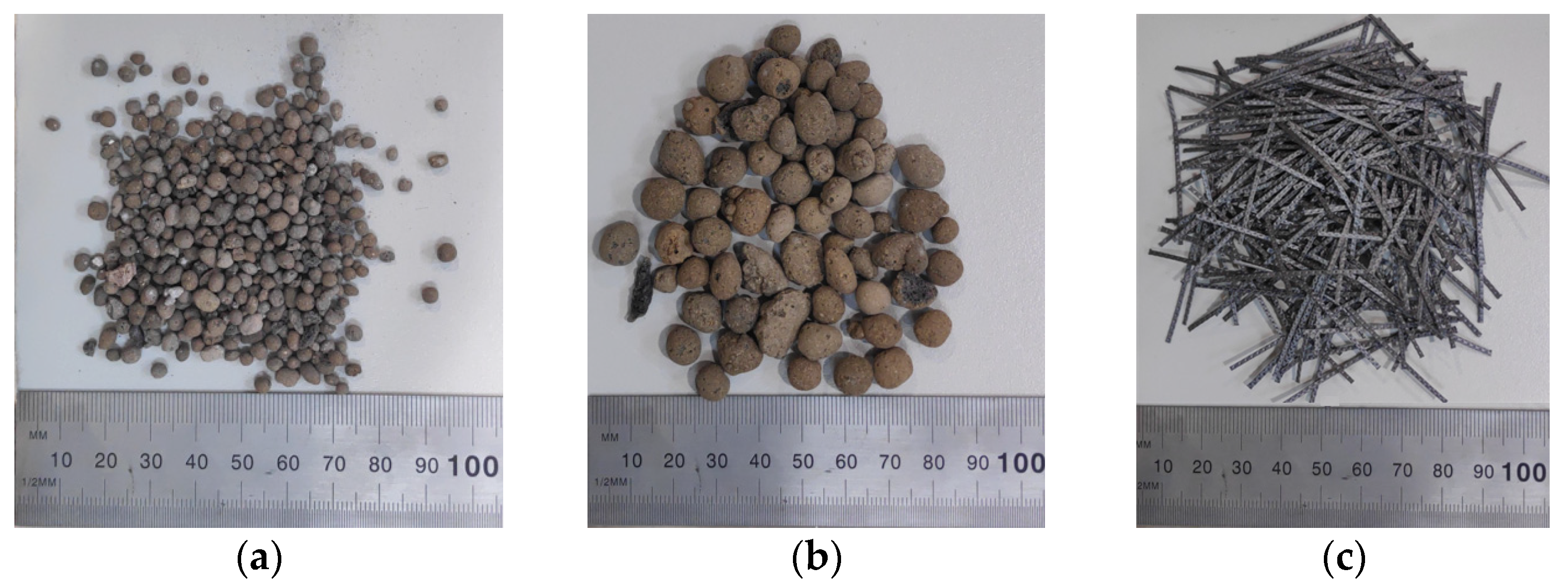
2.1. Materials
2.2. Mix Proportions
2.3. Methodology
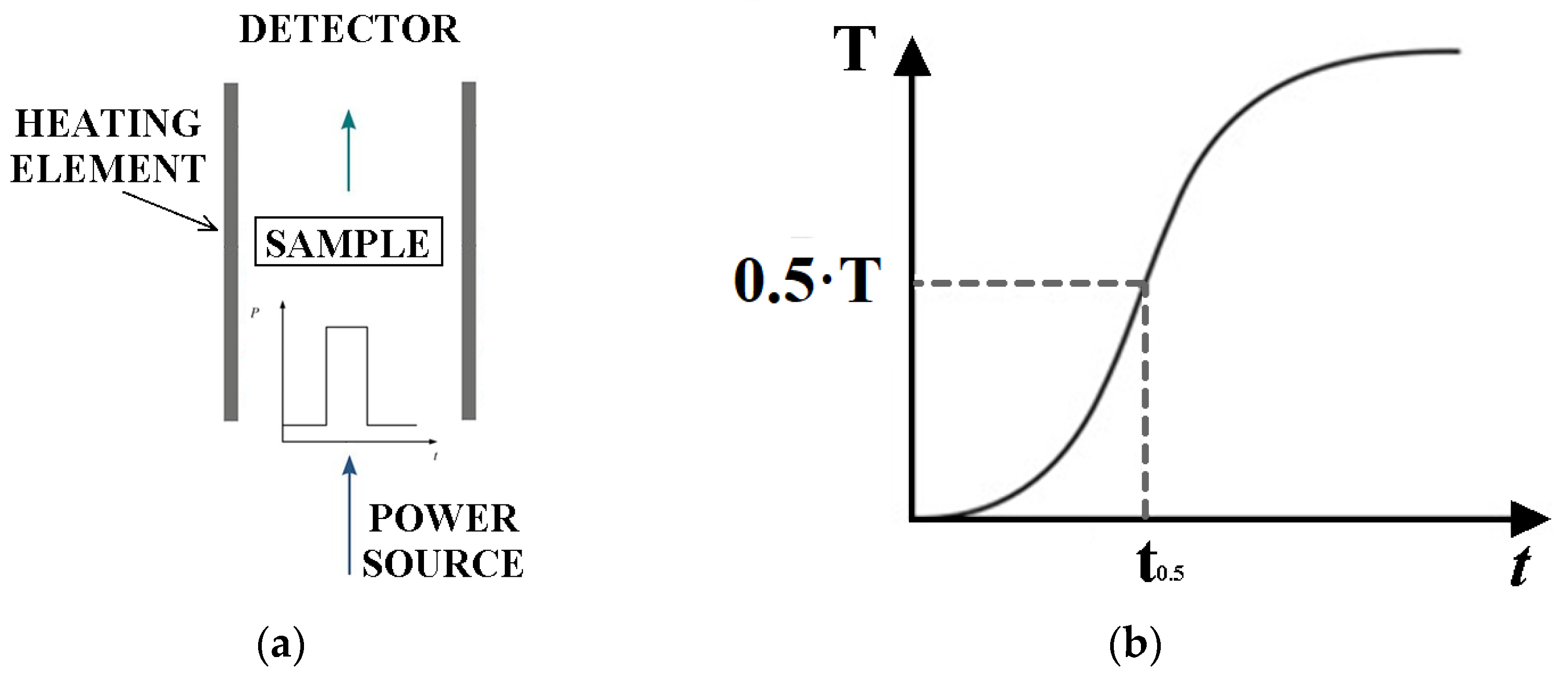
2.3.1. LFA Method
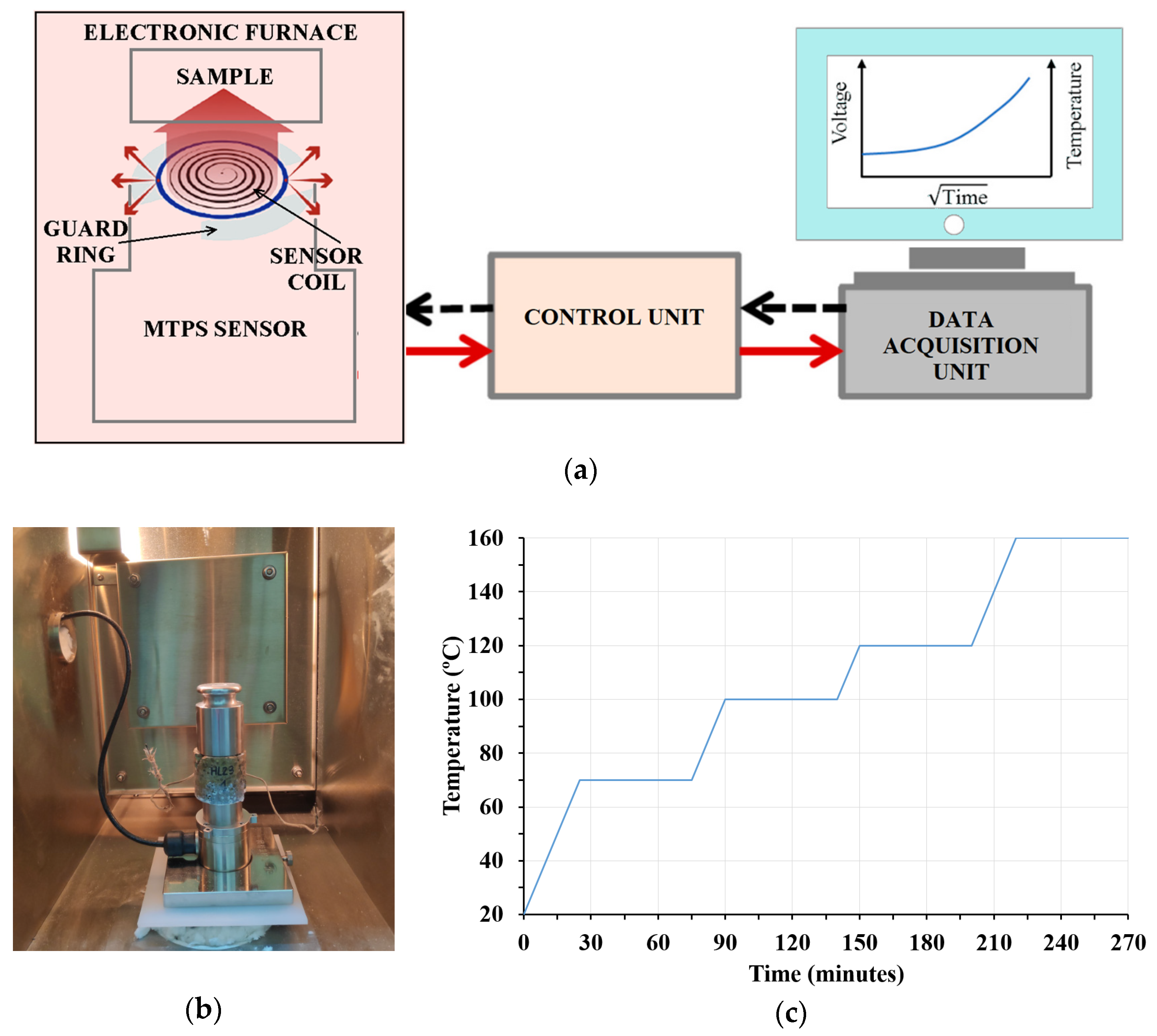
2.3.2. MTPS Technique
2.3.3. DSC Technique
3. Results and Discussion
3.1. LFA Results
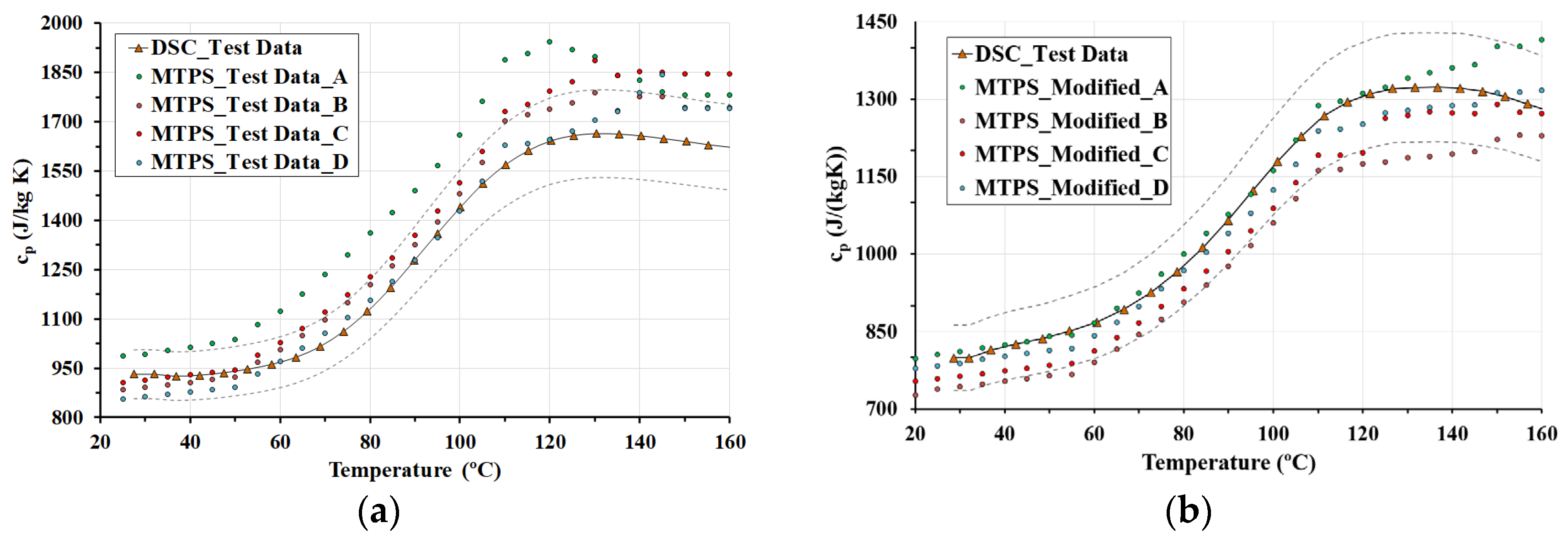
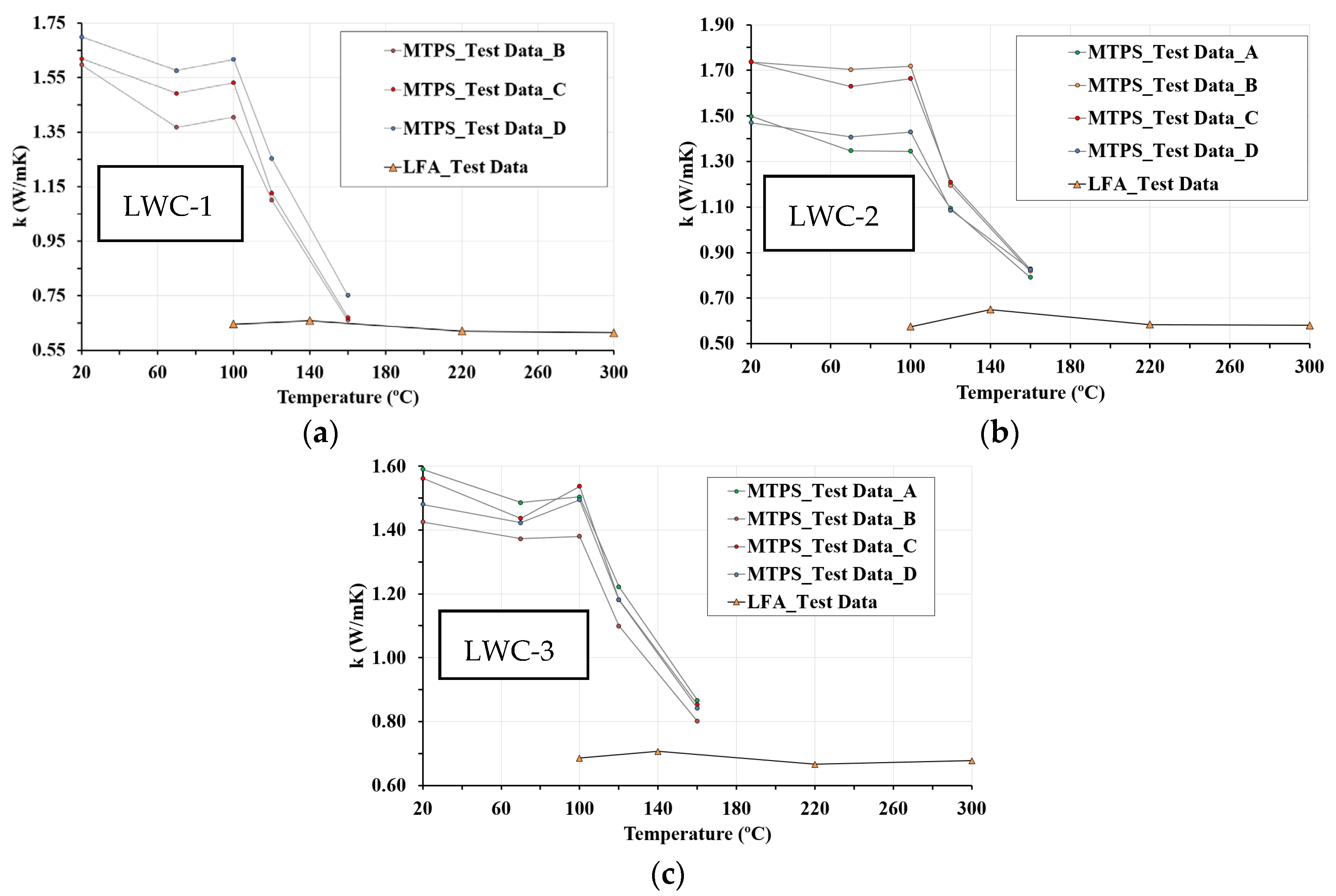
3.2. MTPS Results
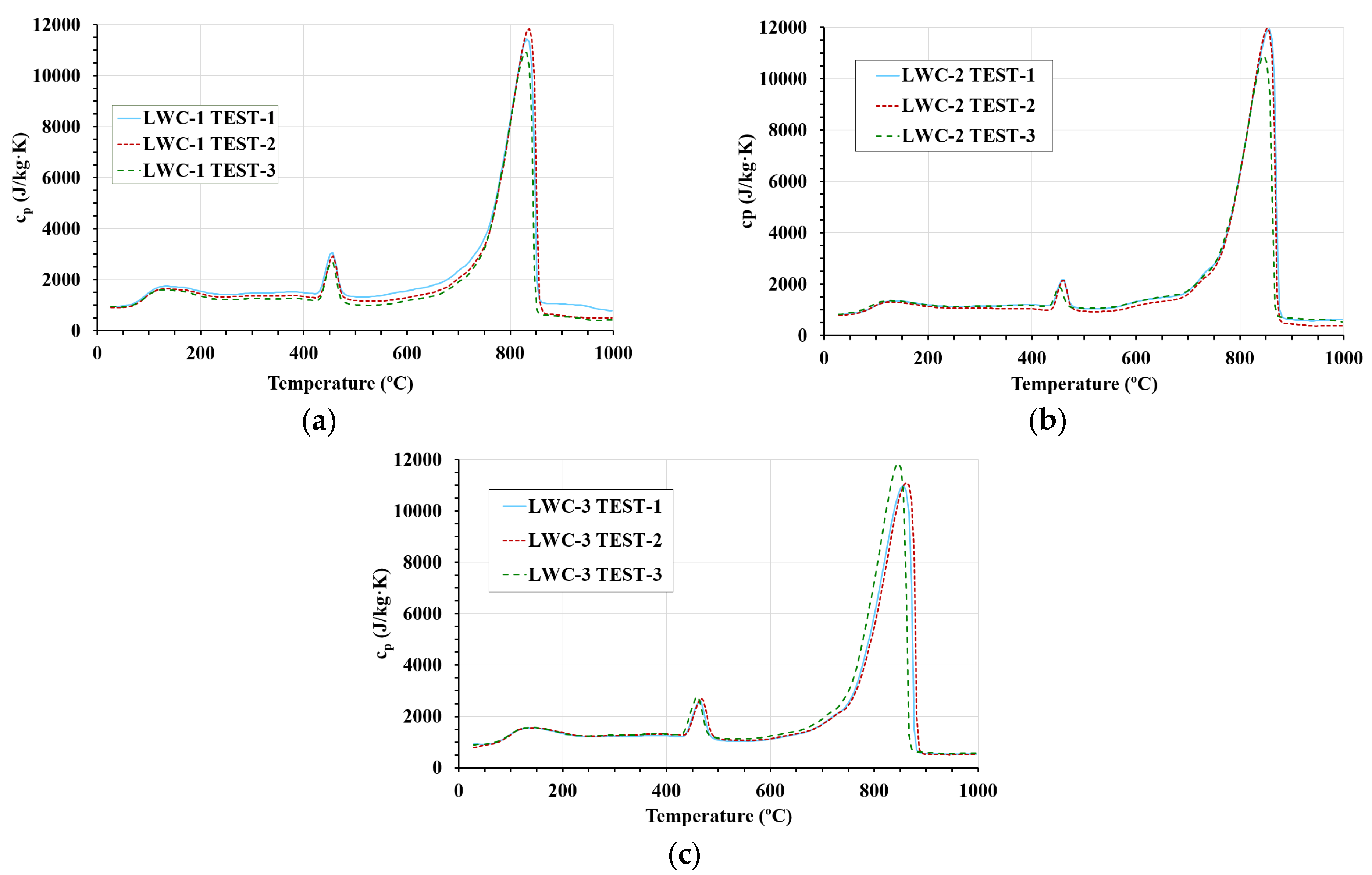
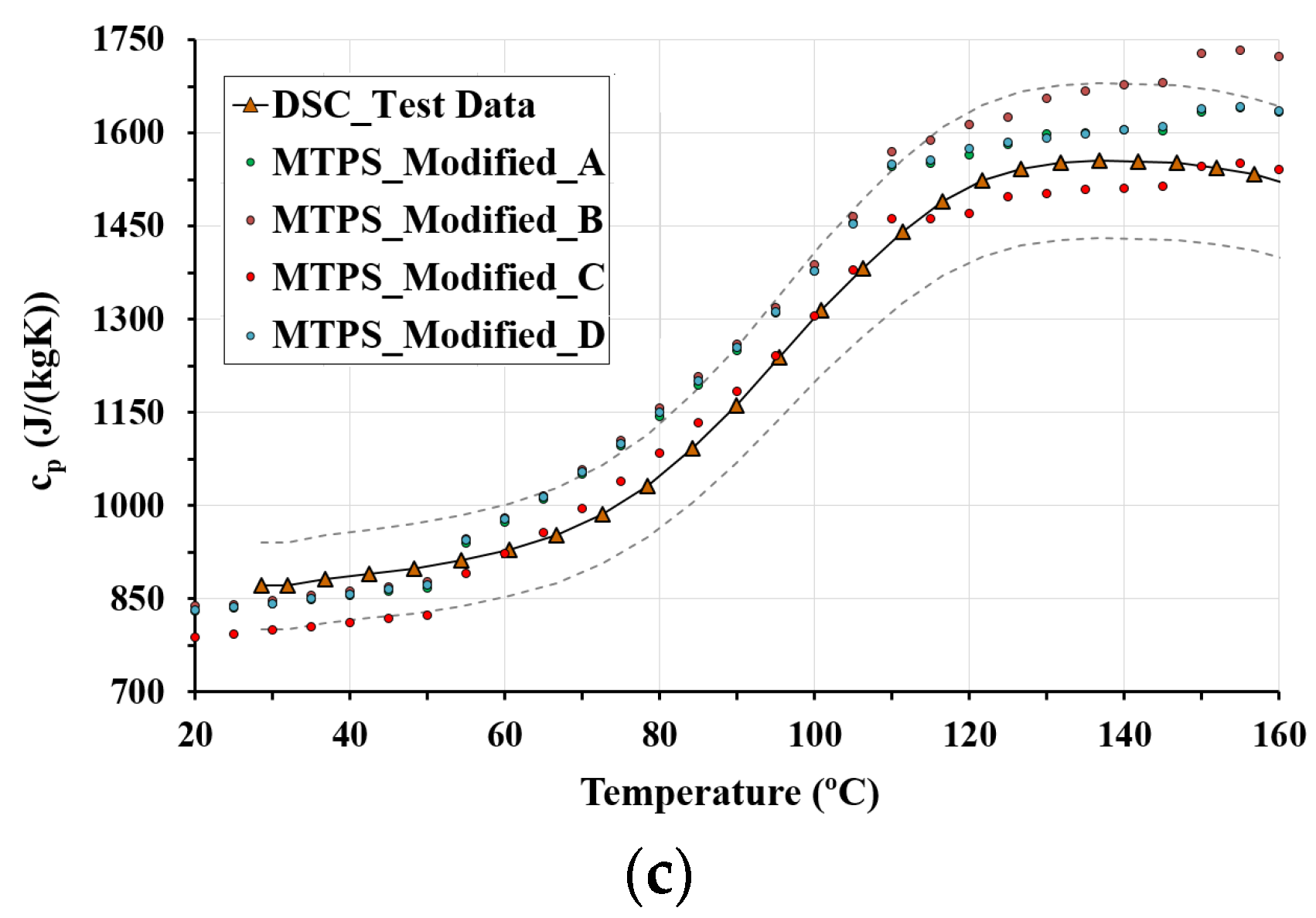
3.3. DSC Results
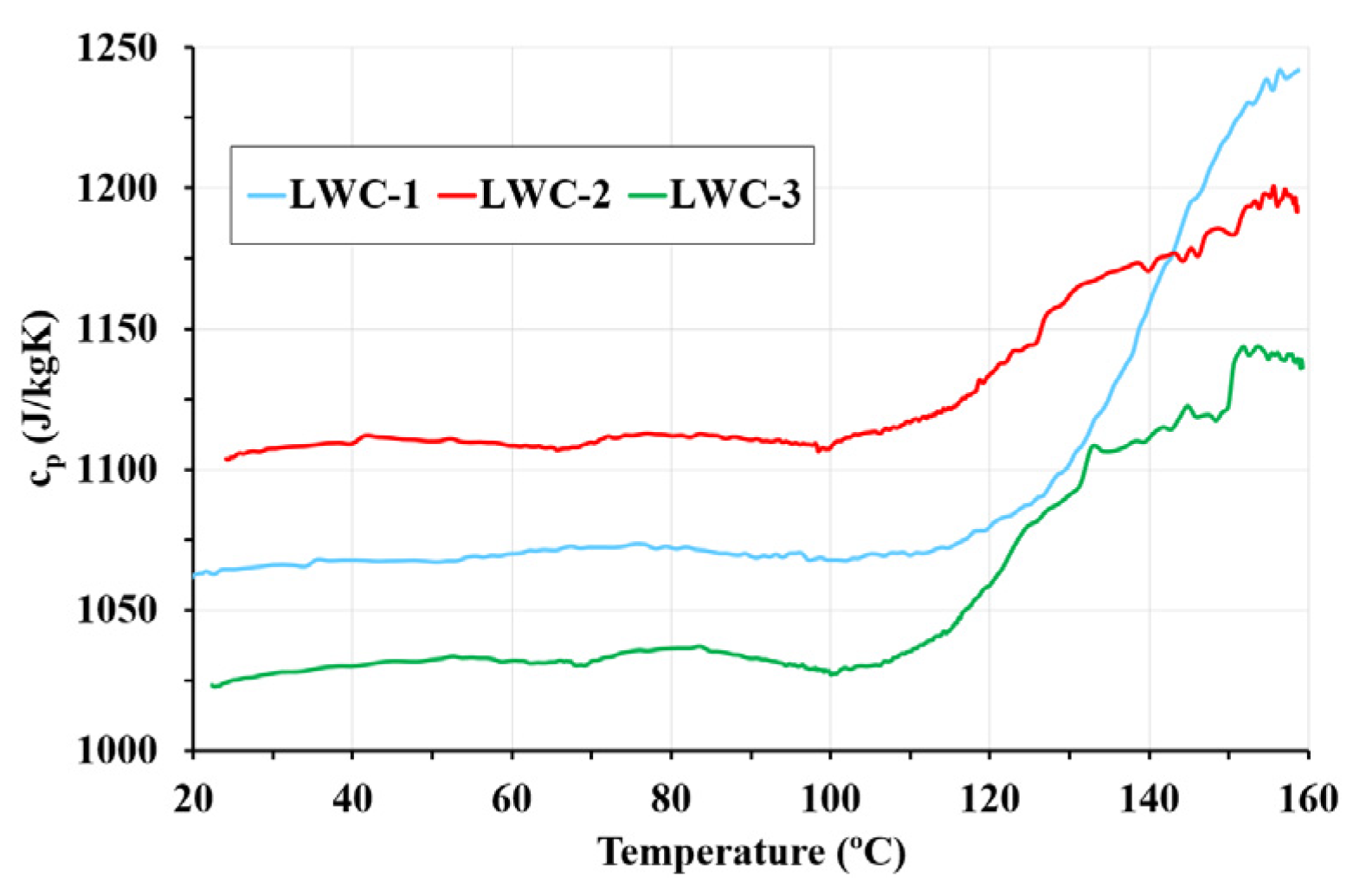
3.4. Specific Heat
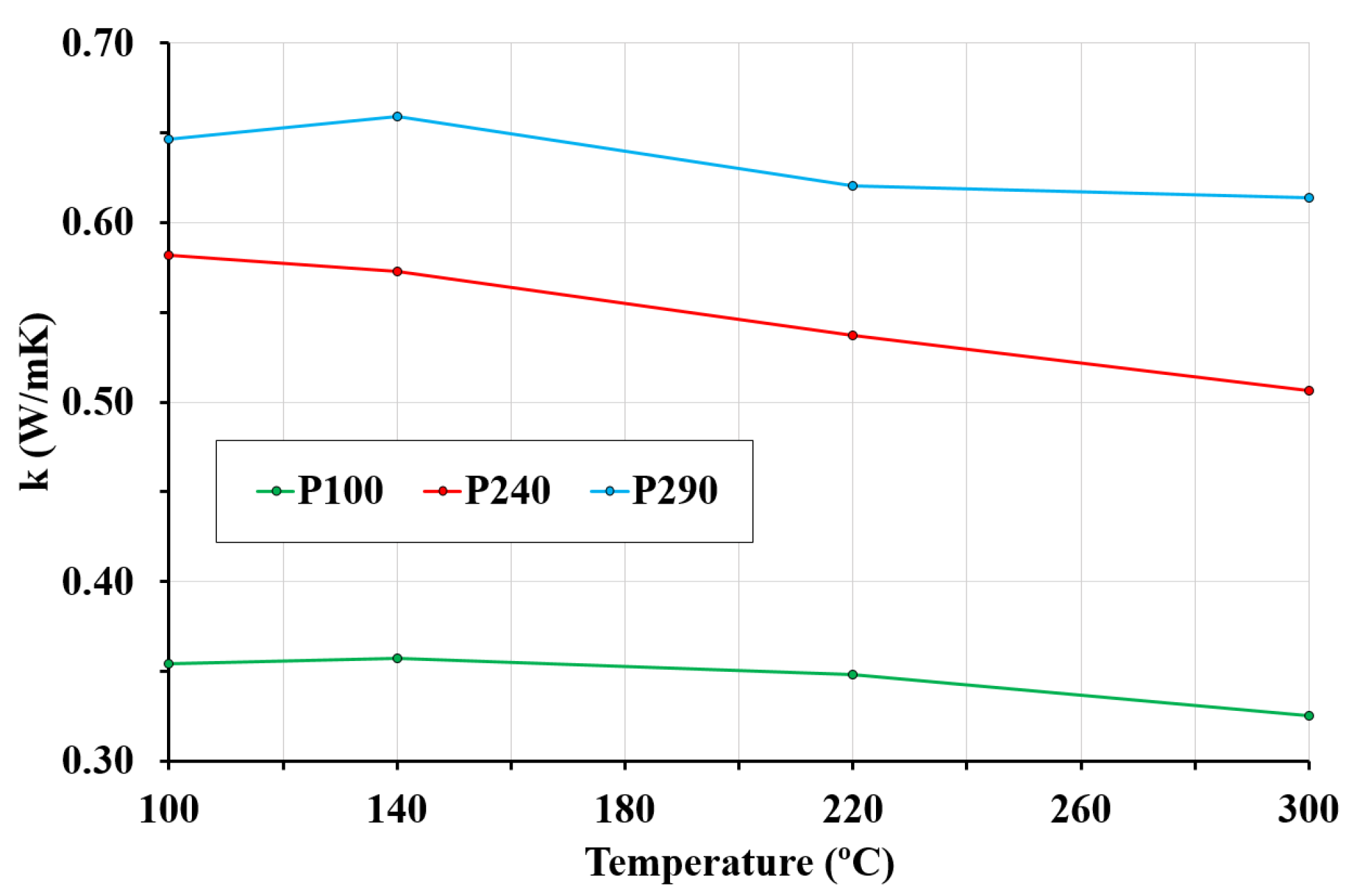
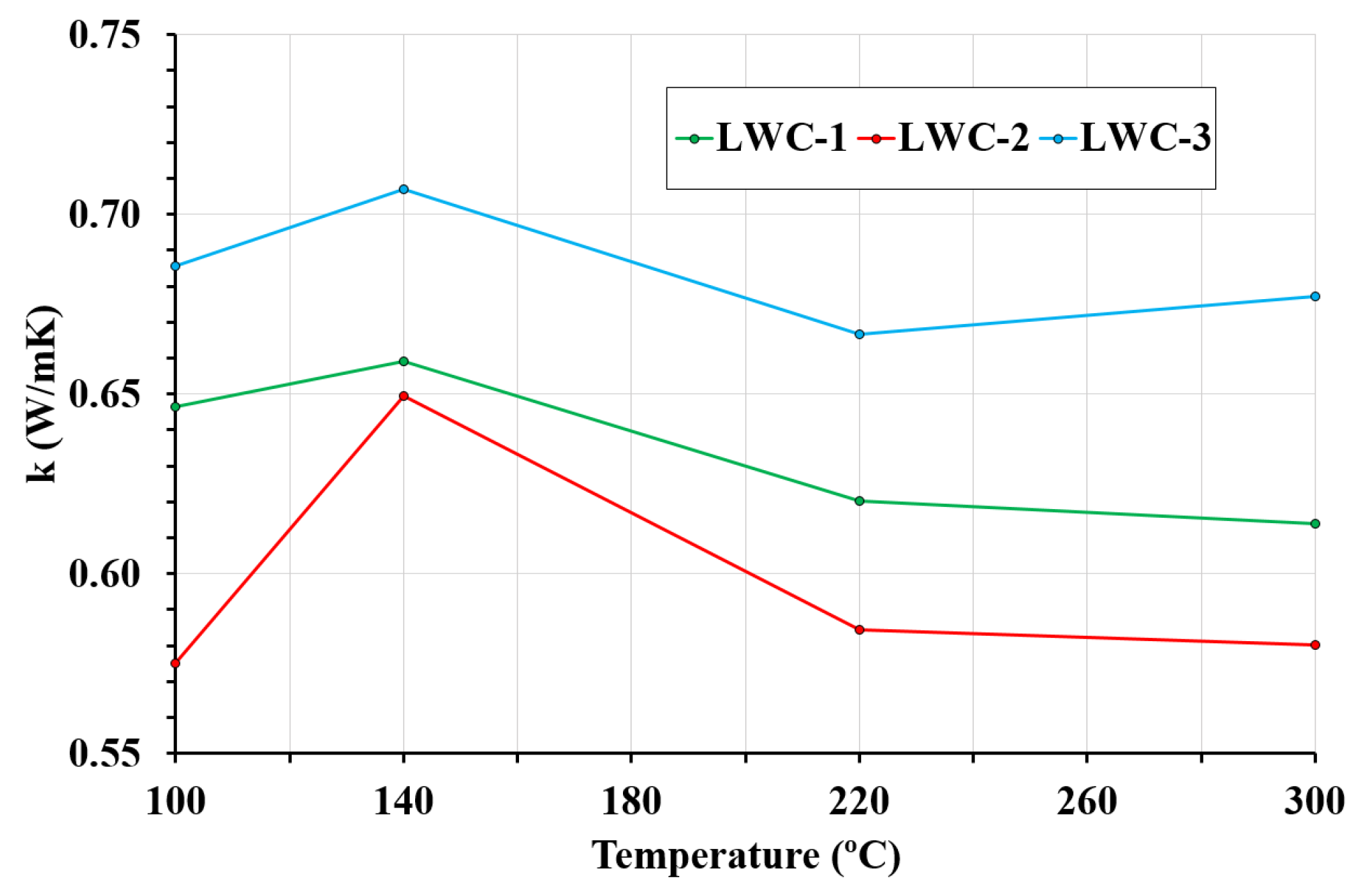
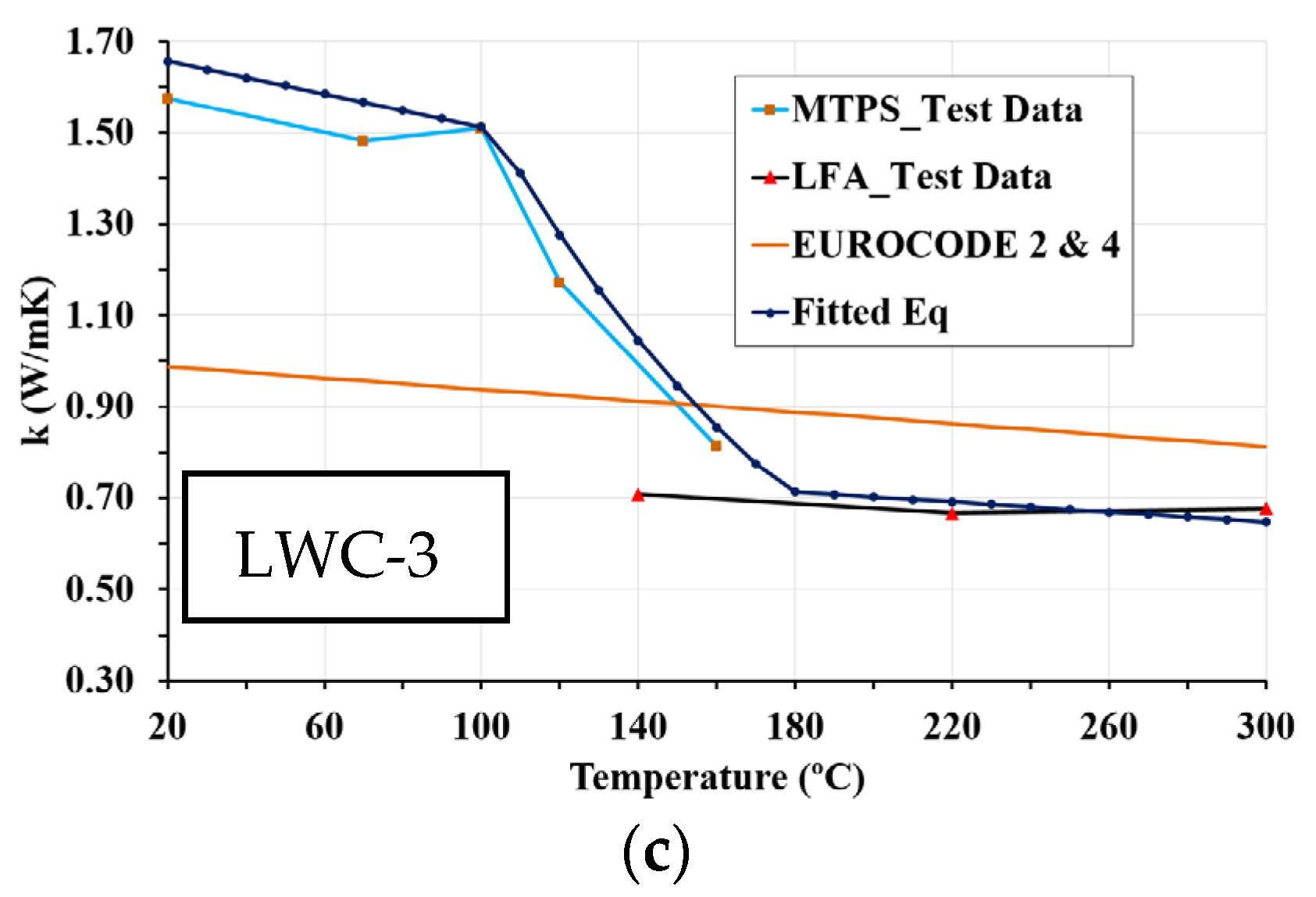
3.5. Thermal Conductivity
4. Proposed Thermal Properties Relationships
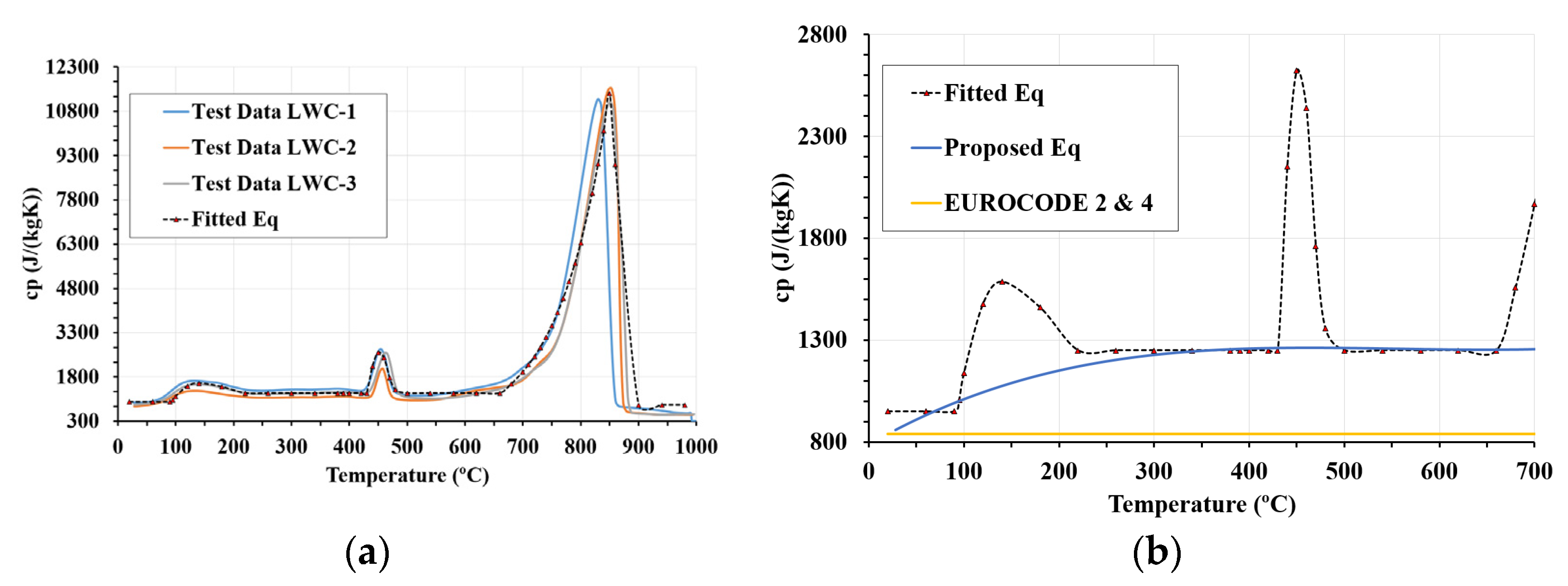
4.1. Specific Heat Equations
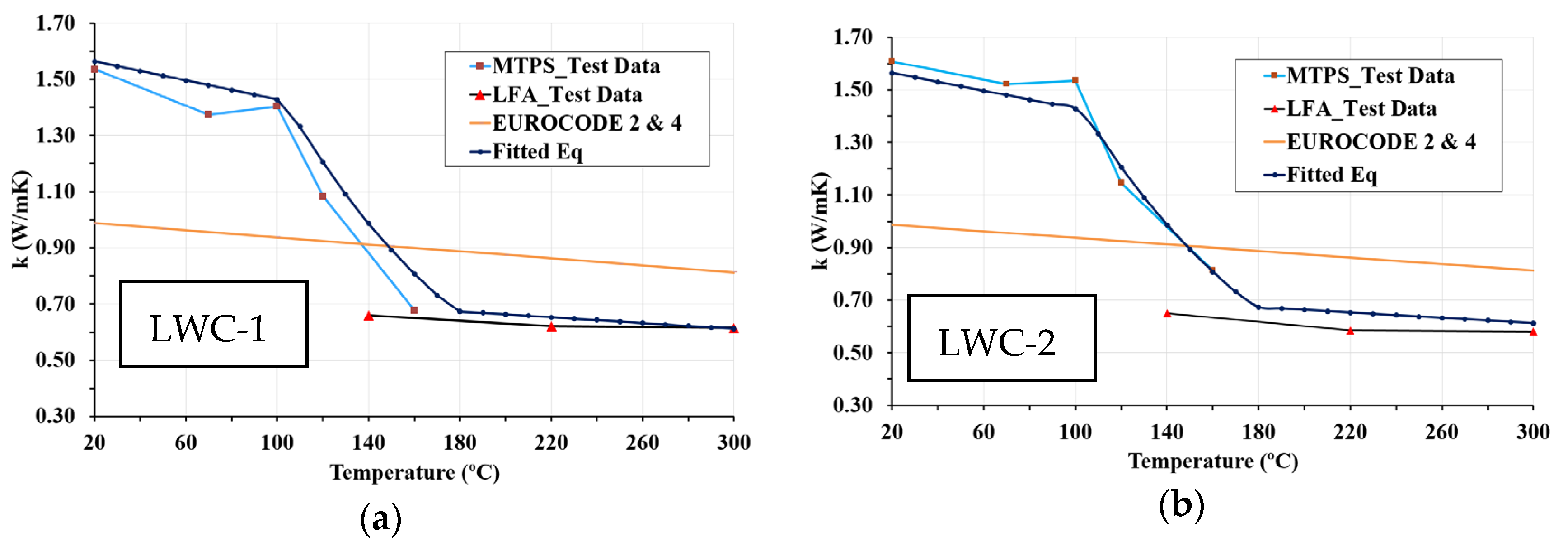
4.2. Thermal Conductivity Equations
5. Conclusions
- General conclusions:
- Porosity and bulk density of LWCs show an inverse relationship at low temperatures: the higher the porosity, the lower the bulk density. LWC-1 has the highest porosity, 28%, and the lowest bulk density, 1740 kg/m3. True density is defined as the relationship between the mass and volume of the concrete, including the pores in the material. Taking into account this relationship, the true density of the three LWCs is similar: between 1.3 and 1.4 times higher than the bulk density.
- The structural LWCs studied have significantly lower thermal conductivity than normal concrete, reducing heat losses. Thermal conductivity of LWC is highly affected by moisture content, which depends on porosity and temperature. In this sense, at low temperatures, the higher the porosity, the higher the thermal conductivity; however, at high temperatures, the higher the porosity is, the lower the thermal conductivity is. The results of the tests reveal this variability in the thermal conductivity of LWCs.
- This research shows interesting differences in the performance of samples manufactured with different dosages of aggregates. This demonstrates the importance of a preliminary phase of material characterization. The standard ISO10456 must be updated to adapt the conversion coefficients when expanded clay is used as the main aggregate. This research work proposes a conversion factor between 6 and 14 for all the LWC mixes with densities between 1700 and 1900 kg/m3.
- The current Eurocodes 2 and 4 used for evaluating the fire resistance of elements assume that specific heat for LWC can be simplified with a constant value of 840 J/kg°C. However, the results of this research work suggest a change to the Eurocodes as temperature has a significant influence on specific heat.
- Thermal techniques:
- The results of this work show the efficiency of combining MTPS and LFA techniques to measure thermal conductivity in a wide temperature range. The MTPS technique measures thermal conductivity from ambient temperature up to 160 °C. Although LFA tests with ground particles have inherent limitations due to parti-cle contact, above 160 °C, at which there is practically no water in the concrete, the values obtained by LFA could be considered valid. Both techniques are complementary, as demonstrated by the equality of the thermal conductivity values at 160 °C. The MTPS technique requires a stabilization time longer than 1 h to reduce the moisture content of the samples.
- The MTPS and DSC techniques show that temperature is an influential parameter and must be taken into account to calculate the specific heat. Both techniques show that the specific heat for LWC is higher than the values specified in Eurocodes 2 and 4. Specific heat is affected by decomposition reactions, as shown in the DSC results. For this reason, the MTPS technique should take into account the loss of mass caused by water vaporization to provide an adjusted value of specific heat. Therefore, in order to use the MTPS technique to obtain an adjusted value of the specific heat at elevated temperatures, the density of the material must be measured as a function of the test temperature, and Equation (4) should be applied to make the corresponding adjustments.
- Proposed equations:
- The proposed equations for specific heat are based on experimental data and dependent on temperature and fitting the experimental values. Although Eurocodes 2 and 4 assume a constant value for specific heat, this research work shows that this assumption has numerous drawbacks. From the assumption of Eurocodes 2 and 4 for normal concrete, an equation is proposed for the temperature range of 20–700 °C. This proposed equation fits the experimental values more accurately.
- The proposed equations for thermal conductivity, based on experimental data, depend on the temperature and density of LWCs. These simplified relations for high-temperature thermal properties of new types of concrete are adequate for incorporation in codes and standards. In addition, these formulae can be used as input for numerical models, which can be used to determine the behavior of LWC structural elements at elevated temperatures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Venkatesh, K. Properties of Concrete at Elevated Temperatures. ISRN Civ. Eng. 2014, 2014, 15. [Google Scholar] [CrossRef]
- Zhou, H.; Brooks, A.L. Thermal and mechanical properties of structural lightweight concrete containing lightweight aggregates and fly-ash cenospheres. Constr. Build. Mater. 2019, 198, 512–526. [Google Scholar] [CrossRef]
- Chalangaran, N.; Farzampour, A.; Paslar, N. Nano Silica and Metakaolin Effects on the Behavior of Concrete Containing Rubber Crumbs. CivilEng 2020, 1, 264–274. [Google Scholar] [CrossRef]
- Yun, T.S.; Jeong, Y.J.; Youm, K.-S. Effect of Surrogate Aggregates on the Thermal Conductivity of Concrete at Ambient and Elevated Temperatures. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Transition to Sustainable Buildings: Strategies and Opportunities to 2050; OECD: Paris, France, 2013. [CrossRef]
- del Coz Díaz, J.J.; Álvarez Rabanal, F.P.; García Nieto, P.J.; Domínguez Hernández, J.; Rodríguez Soria, B.; Pérez-Bella, J.M. Hygrothermal properties of lightweight concrete: Experiments and numerical fitting study. Constr. Build. Mater. 2013, 40, 543–555. [Google Scholar] [CrossRef]
- Gencel, O.; del Coz Díaz, J.J.; Sutcu, M.; Kocyigit, F.; Rabanal, F.P.Á.; Alonso-Martínez, M.; Barrera, G.M. Thermal Performance Optimization of Lightweight Concrete/EPS Layered Composite Building Blocks. Int. J. Thermophys. 2021, 42, 52. [Google Scholar] [CrossRef]
- del Coz Díaz, J.J.; Álvarez-Rabanal, F.P.; Alonso-Martínez, M.; Martínez-Martínez, J.E. Thermal Inertia Characterization of Multilayer Lightweight Walls: Numerical Analysis and Experimental Validation. Appl. Sci. 2021, 11, 5008. [Google Scholar] [CrossRef]
- Lie, T.T.; Kodur, V.K.R. Thermal and mechanical properties of lightweight foamed concrete at elevated temperatures. Mag. Concr. Res. 1996, 23, 511–517. [Google Scholar] [CrossRef]
- Burbano-Garcia, C.; Hurtado, A.; Silva, Y.F.; Delvasto, S.; Araya-Letelier, G. Utilization of waste engine oil for expanded clay aggregate production and assessment of its influence on lightweight concrete properties. Constr. Build. Mater. 2021, 273, 121677. [Google Scholar] [CrossRef]
- Shoukry, S.N.; William, G.W.; Downie, B.; Riad, M.Y. Effect of moisture and temperature on the mechanical properties of concrete. Constr. Build. Mater. 2011, 25, 688–696. [Google Scholar] [CrossRef]
- Al-Sibahy, A.; Edwards, R. Thermal behaviour of novel lightweight concrete at ambient and elevated temperatures: Experimental, modelling and parametric studies. Constr. Build. Mater. 2012, 31, 174–187. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Beaucour, A.L.; Ortola, S.; Noumowé, A. Experimental study on the thermal properties of lightweight aggregate concretes at different moisture contents and ambient temperatures. Constr. Build. Mater. 2017, 151, 720–731. [Google Scholar] [CrossRef]
- Asadi, I.; Shafigh, P.; Hassan, Z.F.B.A.; Mahyuddin, N.B. Thermal conductivity of concrete—A review. J. Build. Eng. 2018, 20, 81–93. [Google Scholar] [CrossRef]
- Khaliq, W.; Kodur, V. High temperature mechanical properties of high-strength fly ash concrete with and without fibers. ACI Mater. J. 2012, 109, 665–674. [Google Scholar] [CrossRef]
- Davie, C.T.; Pearce, C.J.; Bićanić, N. Coupled heat and moisture transport in concrete at elevated temperatures—Effects of capillary pressure and adsorbed water. Numer. Heat Transf. Part A Appl. 2006, 49, 733–763. [Google Scholar] [CrossRef]
- UNE-EN 1992-1-2 Eurocode 2: Design of Concrete Structures—Part 1-2: General Rules—Structural Fire Design; AENOR: Madrid, Spain, 2011.
- UNE-EN 1994-1-2 Eurocode 4—Design of Composite Steel and Concrete Structures—Part 1-2: General Rules—Structural Fire Design; AENOR: Madrid, Spain, 2016.
- Kodur, V.K.R.; Sultan, M.A. Effect of Temperature on Thermal Properties of High-Strength Concrete. J. Mater. Civ. Eng. 2003, 15, 101–107. [Google Scholar] [CrossRef]
- Adl-Zarrabi, B.; Boström, L.; Wickström, U. Using the TPS method for determining the thermal properties of concrete and wood at elevated temperature. Fire Mater. 2006, 30, 359–369. [Google Scholar] [CrossRef]
- Othuman, M.A.; Wang, Y.C. Elevated-temperature thermal properties of lightweight foamed concrete. Constr. Build. Mater. 2011, 25, 705–716. [Google Scholar] [CrossRef]
- Alarcon-Ruiz, L.; Platret, G.; Massieu, E.; Ehrlacher, A. The use of thermal analysis in assessing the effect of temperature on a cement paste. Cem. Concr. Res. 2005, 35, 609–613. [Google Scholar] [CrossRef]
- Yu, Q.L.; Spiesz, P.; Brouwers, H.J.H. Ultra-lightweight concrete: Conceptual design and performance evaluation. Cem. Concr. Compos. 2015, 61, 18–28. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Banerji, S.; Solhmirzaei, R. Test methods for characterizing concrete properties at elevated temperature. Fire Mater. 2020, 44, 381–395. [Google Scholar] [CrossRef]
- UNE-EN 197-1 Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements; AENOR: Madrid, Spain, 2011.
- UNE 83502:2004. Concrete with Fibers. Method of Making in the Laboratory; AENOR: Madrid, Spain, 2004. [Google Scholar]
- UNE 83504:2004. Concrete with Fibers. Making and Maintenance of Specimens for Laboratory Tests; AENOR: Madrid, Spain, 2004. [Google Scholar]
- Wu, A.; Wang, Y.; Wang, H. Estimation model for yield stress of fresh uncemented thickened tailings: Coupled effects of true solid density, bulk density, and solid concentration. Int. J. Miner. Process. 2015, 143, 117–124. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- NETZSCH, Laser Flash Analysis—LFA, Produktfolder LFA 427; ASTM International: West Conshohocken, PA, USA, 2013.
- ASTM International. ASTM Standard E1461−13. Standard Test Method for Thermal Diffusivity by the Flash Method; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ISO 22007-4:2017. Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 4: Laser Flash Method; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- ASTM D7984—16 Standard Test Method for Measurement of Thermal Effusivity of Fabrics Using a Modified Transient Plane Source (MTPS) Instrument; ASTM International: West Conshohocken, PA, USA, 2016.
- Seng, B.; Magniont, C.; Lorente, S. Characterization of a precast hemp concrete. Part I: Physical and thermal properties. J. Build. Eng. 2019, 24, 100540. [Google Scholar] [CrossRef]
- Li, B.; Mao, J.; Nawa, T.; Han, T. Mesoscopic damage model of concrete subjected to freeze-thaw cycles using mercury intrusion porosimetry and differential scanning calorimetry (MIP-DSC). Constr. Build. Mater. 2017, 147, 79–90. [Google Scholar] [CrossRef]
- Romano, A.; Grammatikos, S.; Riley, M.; Bras, A. Determination of specific heat capacity of bio-fibre earth mortars stabilised at different relative humidities using Differential Scanning Calorimetry. J. Build. Eng. 2021, 41, 102738. [Google Scholar] [CrossRef]
- ISO 11358-1:2014. Plastics—Thermogravimetry (TG) of Polymers—Part 1: General Principles; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- DIN 51006:2005-07. Thermal Analysis (TA)-Thermogravimetry (TG)—Principles; Deutsches Institut für Normung e.V: Berlin, Germany, 2015. [Google Scholar]
- DIN 51007:2019-04. Thermal Analysis—Differential Thermal Analysis (DTA) and Differential Scanning Calorimetry (DSC)—General Principles; Deutsches Institut für Normung e.V: Berlin, Germany, 2019. [Google Scholar]
- ISO 10456:2007. Building Materials and Products—Hygrothermal Properties—Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Kodur, V.; Khaliq, W. Effect of Temperature on Thermal Properties of Different Types of High-Strength Concrete. J. Mater. Civ. Eng. 2011, 23, 793–801. [Google Scholar] [CrossRef]
- Gad, E.A.M.; Habib, A.O.; Mousa, M.M. Understanding the mechanism of decomposition reactions of neat and superplasticized ordinary Portland cement pastes using thermal analysis. Epa.-J. Silic. Based Compos. Mater. 2018, 70, 98–103. [Google Scholar] [CrossRef]
| Mixing Compositions | Constituents | ||||
|---|---|---|---|---|---|
| ECF (%) | ECC (%) | Siliceous Aggregate 0/2 (%) | Cement 42.5R (%) | Water (%) | |
| LWC-1 | 5.85 | 6.05 | 40.42 | 32.14 | 15.54 |
| LWC-2 | 5.89 | 4.11 | 44.68 | 30.55 | 14.77 |
| LWC-3 | 3.91 | 4.50 | 44.44 | 31.79 | 15.36 |
| Material | Bulk Density (kg/m3) | True Density (kg/m3) | Porosity (%) |
|---|---|---|---|
| LWC-1 | 1740 | 2430 | 28.2 |
| LWC-2 | 1819 | 2485 | 26.6 |
| LWC-3 | 1906 | 2502 | 24 |
| Type of Concrete | Sample | Moisture Content (%) | k (T = 20 °C) W/mK |
|---|---|---|---|
| LWC-1 | A | 3.1 ± 0.1 | 1.228 |
| LWC-1 | B | 5.8 ± 0.1 | 1.596 |
| LWC-1 | C | 6.2 ± 0.1 | 1.619 |
| LWC-1 | D | 6.4 ± 0.1 | 1.699 |
| LWC-2 | A | 5.8 ± 0.25 | 1.499 |
| LWC-2 | B | 7.4 ± 0.12 | 1.736 |
| LWC-2 | C | 7.5 ± 0.1 | 1.737 |
| LWC-2 | D | 5.6 ± 0.1 | 1.470 |
| LWC-3 | A | 7.3 ± 0.1 | 1.590 |
| LWC-3 | B | 6.4 ± 0.1 | 1.425 |
| LWC-3 | C | 7.1 ± 0.1 | 1.562 |
| LWC-3 | D | 7.6 ± 0.1 | 1.480 |
| Sample | k (LWC-1) W/mK | k (LWC-2) W/mK | k (LWC-3) W/mK |
|---|---|---|---|
| A | 2.120 | 1.611 | 1.562 |
| B | 1.888 | 1.695 | 1.477 |
| C | 1.811 | 1.686 | 1.553 |
| D | 1.848 | 1.599 | 1.428 |
| Mean value | 1.917 | 1.648 | 1.505 |
| σ | 0.139 | 0.050 | 0.064 |
| Error (%) | 7.259 | 3.016 | 4.243 |
| Type of Concrete | Sample | k (70 °C) W/mK | k (100 °C) W/mK | k (120 °C) W/mK | k (160 °C) W/mK |
|---|---|---|---|---|---|
| LWC-1 | A | 1.063 | 1.106 | 0.902 | 0.632 |
| LWC-1 | B | 1.367 | 1.404 | 1.100 | 0.661 |
| LWC-1 | C | 1.492 | 1.531 | 1.127 | 0.670 |
| LWC-1 | D | 1.575 | 1.616 | 1.253 | 0.752 |
| Mean value | 1.478 | 1.517 | 1.160 | 0.679 | |
| Standard deviation | 0.225 | 0.223 | 0.145 | 0.051 | |
| LWC-2 | A | 1.348 | 1.345 | 1.094 | 0.791 |
| LWC-2 | B | 1.704 | 1.719 | 1.196 | 0.819 |
| LWC-2 | C | 1.630 | 1.663 | 1.209 | 0.828 |
| LWC-2 | D | 1.408 | 1.429 | 1.086 | 0.827 |
| Mean value | 1.522 | 1.539 | 1.146 | 0.816 | |
| Standard deviation | 0.171 | 0.181 | 0.065 | 0.017 | |
| LWC-3 | A | 1.486 | 1.503 | 1.223 | 0.867 |
| LWC-3 | B | 1.373 | 1.380 | 1.100 | 0.801 |
| LWC-3 | C | 1.437 | 1.537 | 1.182 | 0.853 |
| LWC-3 | D | 1.423 | 1.495 | 1.181 | 0.842 |
| Mean value | 1.430 | 1.479 | 1.171 | 0.841 | |
| Standard deviation | 0.046 | 0.068 | 0.052 | 0.028 | |
| Type of LWC | Coefficients | R2 | |
|---|---|---|---|
| LWC-1 | a | 0.99 | 0.99 |
| b | 0.9 | 0.9 | |
| LWC-2 | a | 0.98 | 0.98 |
| b | 0.91 | 0.91 | |
| LWC-3 | a | 0.97 | 0.97 |
| b | 0.94 | 0.94 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Martínez, J.E.; Álvarez Rabanal, F.P.; Lázaro, M.; Alonso-Martínez, M.; Alvear, D.; del Coz-Díaz, J.J. Assessment of Lightweight Concrete Thermal Properties at Elevated Temperatures. Appl. Sci. 2021, 11, 10023. https://doi.org/10.3390/app112110023
Martínez-Martínez JE, Álvarez Rabanal FP, Lázaro M, Alonso-Martínez M, Alvear D, del Coz-Díaz JJ. Assessment of Lightweight Concrete Thermal Properties at Elevated Temperatures. Applied Sciences. 2021; 11(21):10023. https://doi.org/10.3390/app112110023
Chicago/Turabian StyleMartínez-Martínez, Juan Enrique, Felipe Pedro Álvarez Rabanal, Mariano Lázaro, Mar Alonso-Martínez, Daniel Alvear, and Juan José del Coz-Díaz. 2021. "Assessment of Lightweight Concrete Thermal Properties at Elevated Temperatures" Applied Sciences 11, no. 21: 10023. https://doi.org/10.3390/app112110023
APA StyleMartínez-Martínez, J. E., Álvarez Rabanal, F. P., Lázaro, M., Alonso-Martínez, M., Alvear, D., & del Coz-Díaz, J. J. (2021). Assessment of Lightweight Concrete Thermal Properties at Elevated Temperatures. Applied Sciences, 11(21), 10023. https://doi.org/10.3390/app112110023








